PROJEKTOWANIE BELEK 

PODSUWNICOWYCH

Wykład KM II.2

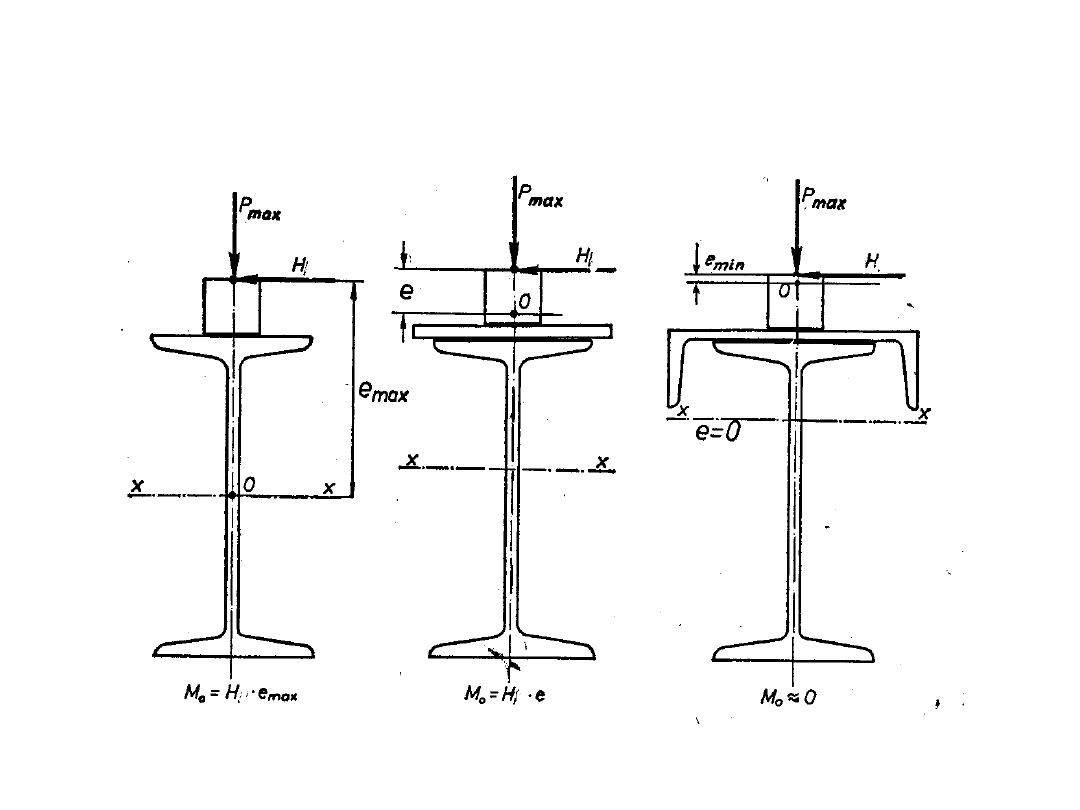
Obliczenia statyczne belek 

podsuwnicowych

P

max

 = Q

r,max

;  H = H

T1

+ H

T3

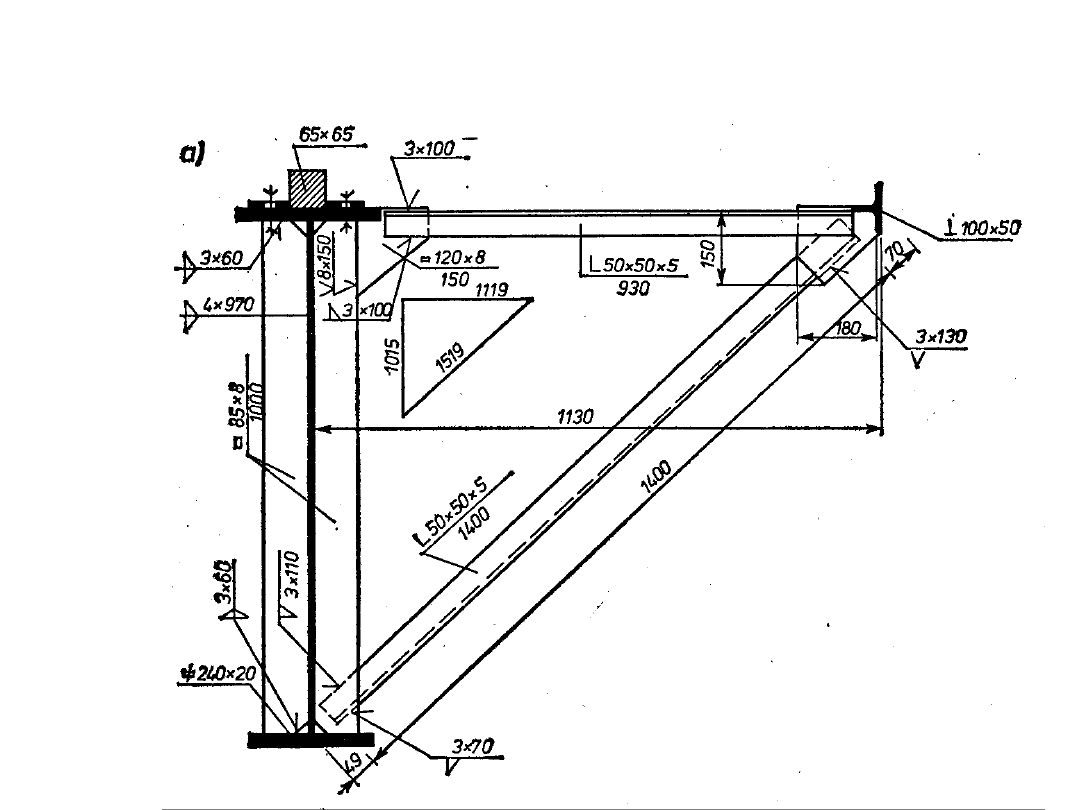
Obliczenia statyczne belek 

podsuwnicowych

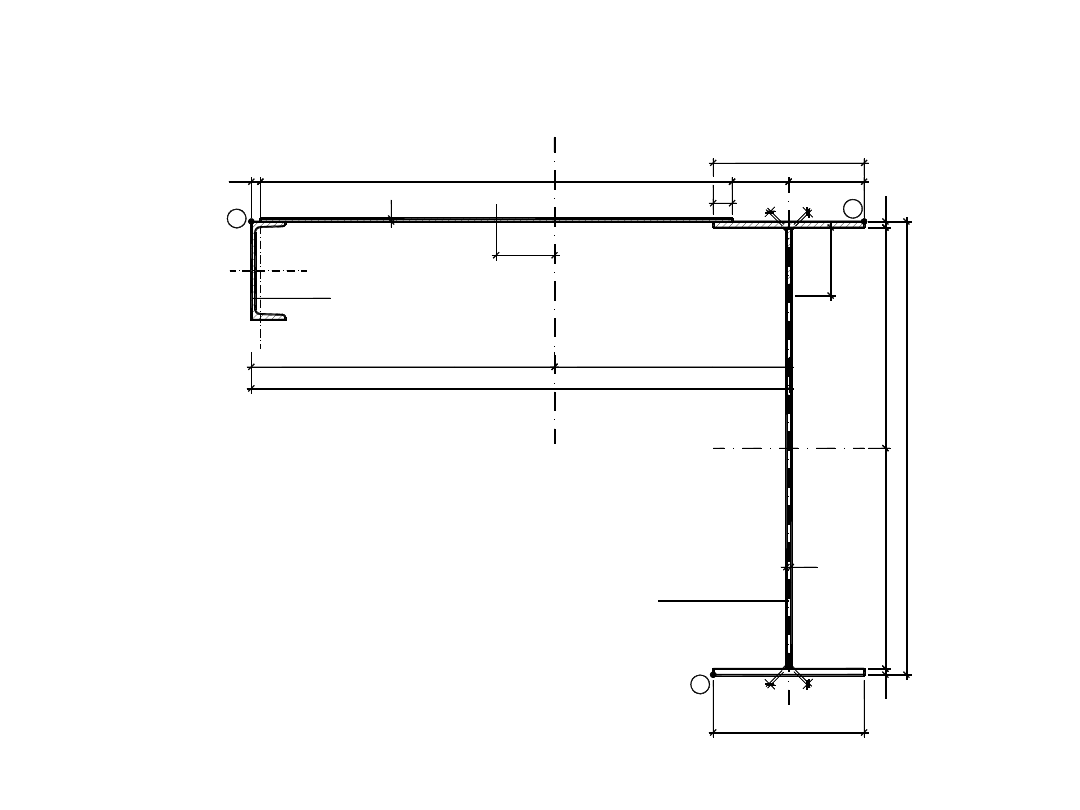
Obliczenia statyczne belek 

podsuwnicowych

8

155

24

1250

150

200

50

400

803,6

620,4

1424

y

y

x

x

1

1

C260

58

4

58

4

16

16

12

00

400

18

0

12

a=

6

a=6

a=6

a=

6

3

1

2

IHKS - 1200 - 12

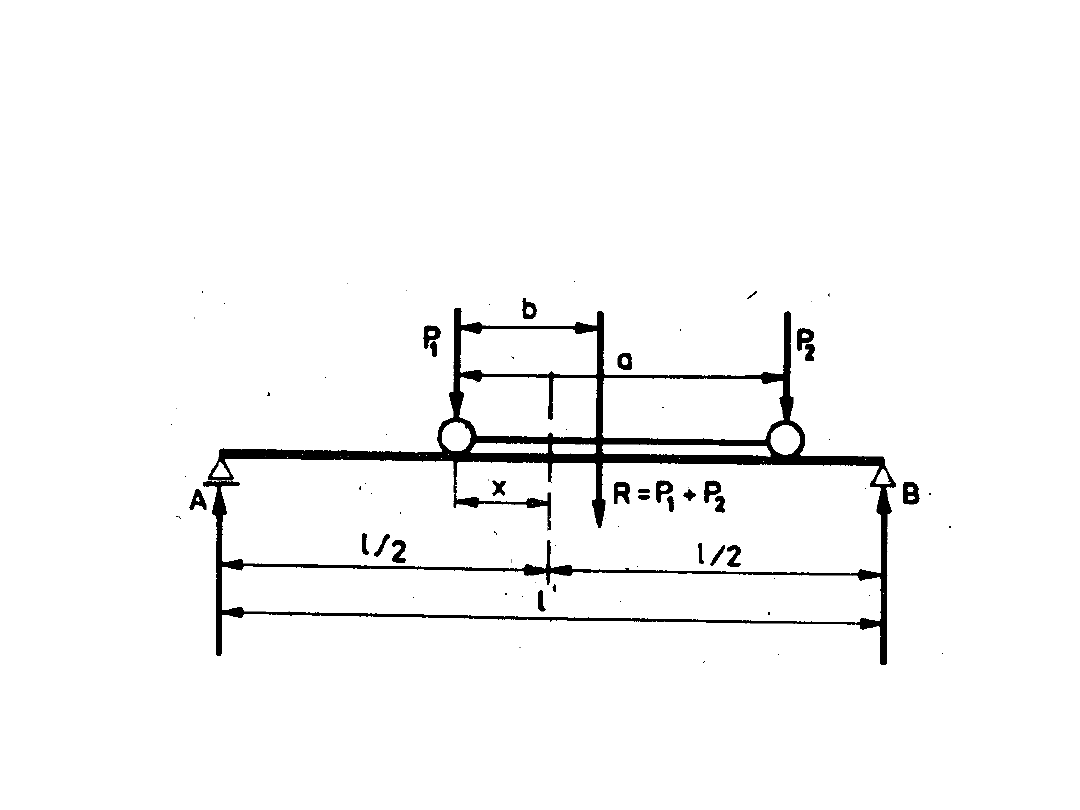
Obliczenia statyczne belek 

podsuwnicowych

  M

max 

= 0,25R(1-b/l)

2

; 

b = P

2

a/R,  x = 0,5b,  R = P

1

+P

2

,  P

1

 > P

2

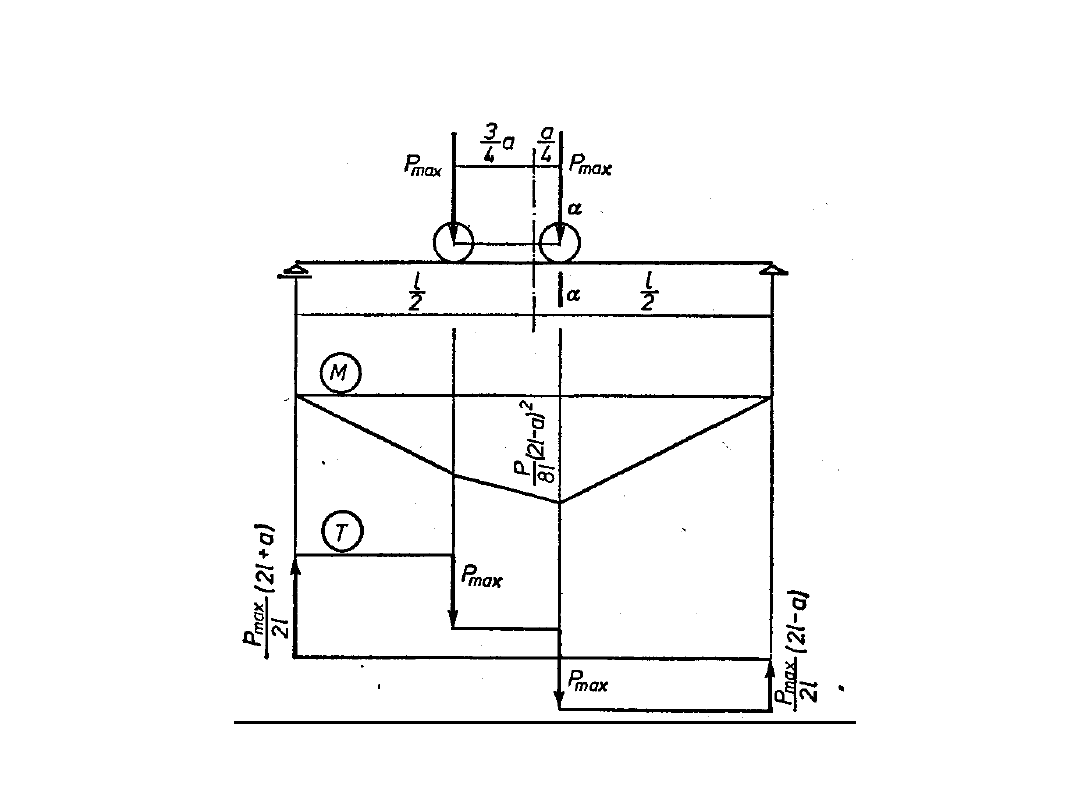
Obliczenia statyczne belek 

podsuwnicowych

 P

max

 = Q

r,max

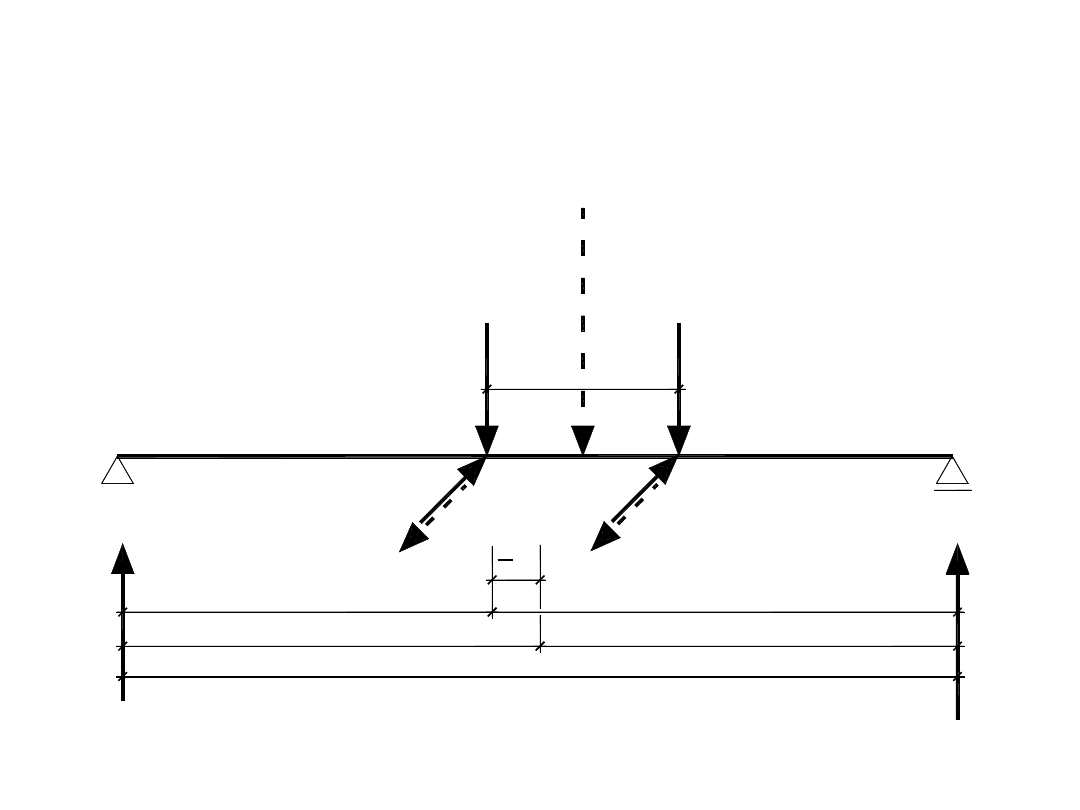
Obliczenia statyczne belek 

podsuwnicowych

2,300

V     =629,2kN

max

V     =629,2kN

max

V     

max



x =4,425

5,000

10,000

5,000

5,575

A

R  =556,7kN

R  =701,6kN

B

A

B

C

H=90,5kN

H=90,5kN

c

2=0,575

c

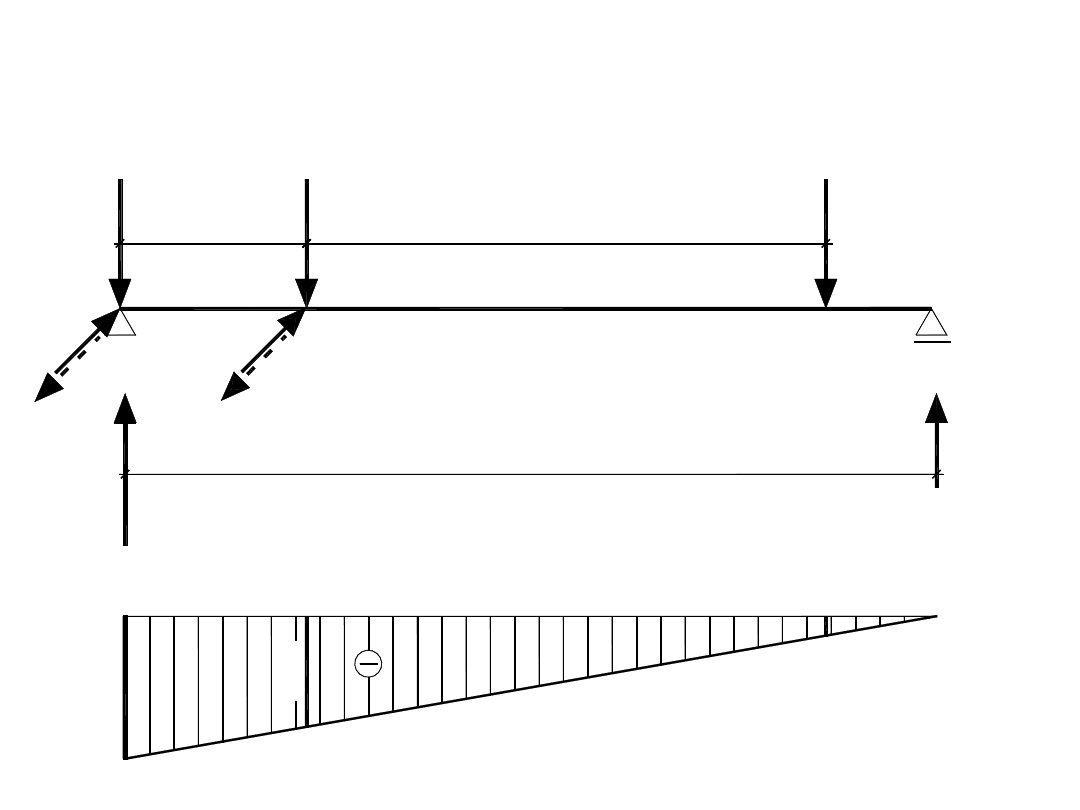
Obliczenia statyczne belek 

podsuwnicowych

R  =1195,5kN

A

R  =692,1kN

B

H=90,5kN

V     =629,2kN

A

H=90,5kN

max

B

2,300

max

V     =629,2kN

V     =629,2kN

max

6,400

10,000

1,

00

0

0,

77

0

0,

13

0

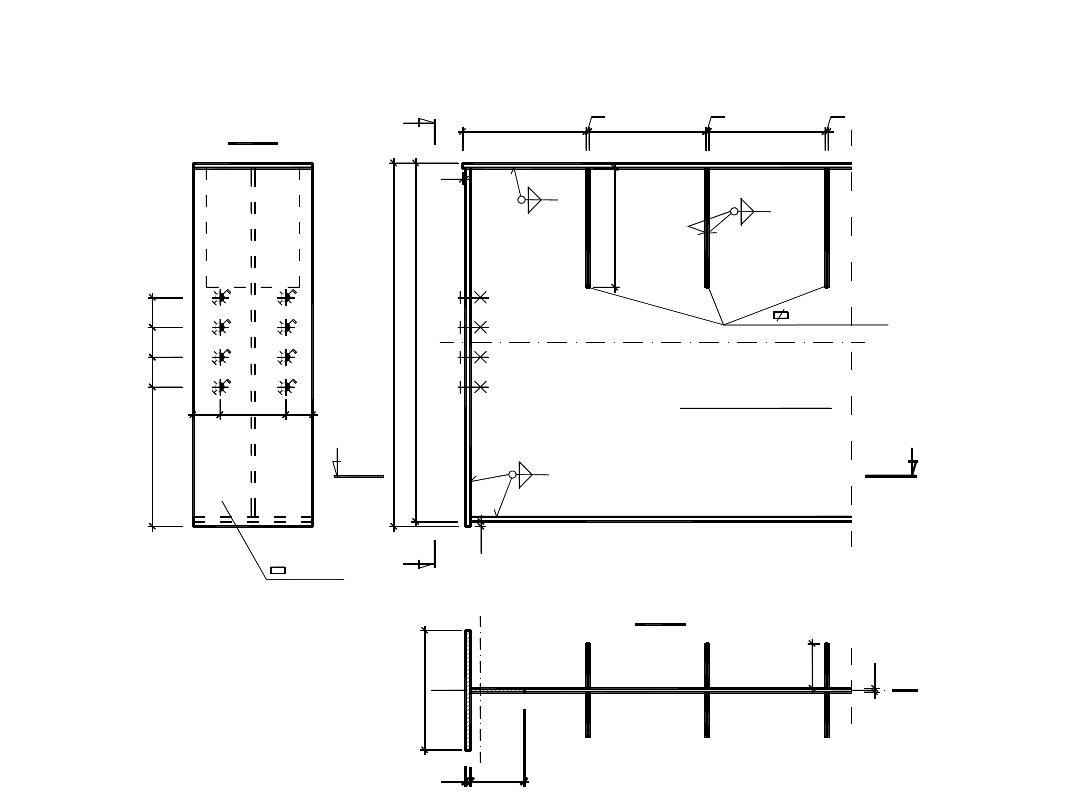
Konstrukcja belek podsuwnicowych

12

x

x

16 15t=180

40

0

1

1

1 - 1

IHKS - 1200 - 12

413

10

390

10

390

10

40

0

16

10

10

0

10

0

10

0

46

6

12

00

12

16

15

0

150x10 - 400

y

y

90

220

90

2

2

2 - 2

400x16

1200

6

4

6

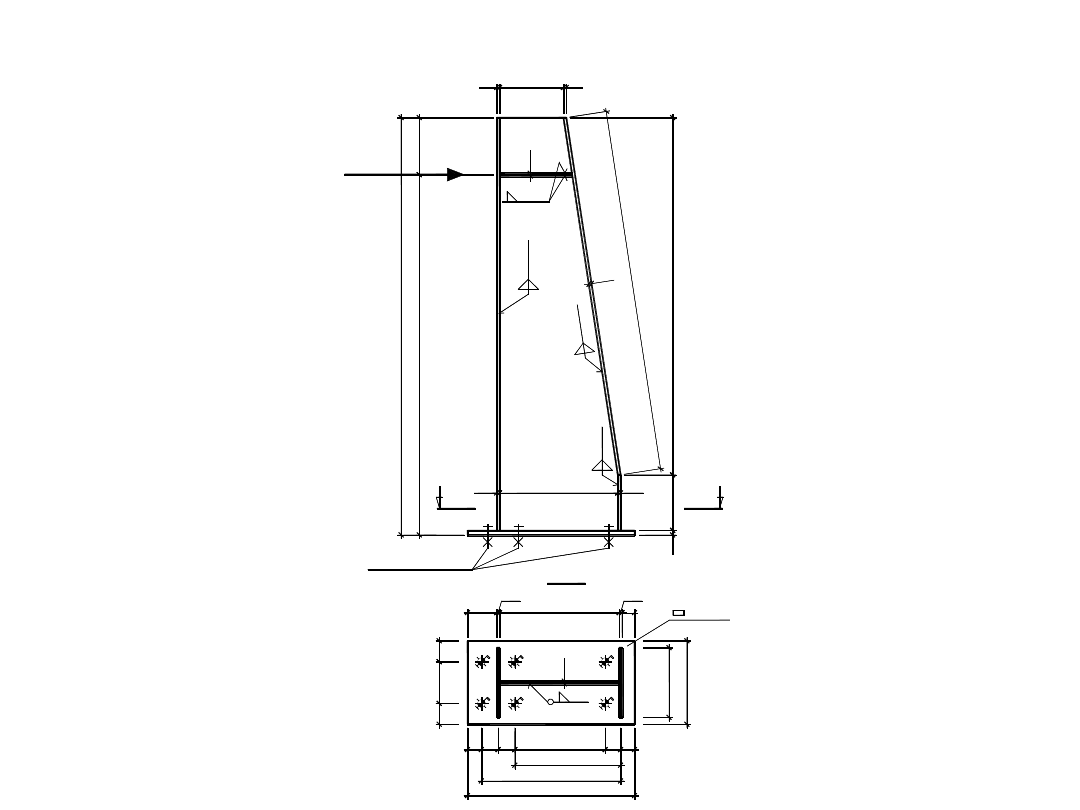
Odbojnice

230

10

10

15

00

12

95

20

5

10

10

10

16

20

0

12

84

13

00

430

10

M24 kl. 5.6

1

1

1 - 1

50

60

60

50

55

325

380

500

600

25



10

430

10

105

10

45

25

0

30

0

75

15

0

75

300x16

600

4

4x260

4x

14

84

4x

13

00

4x

20

0

S=91,5kN

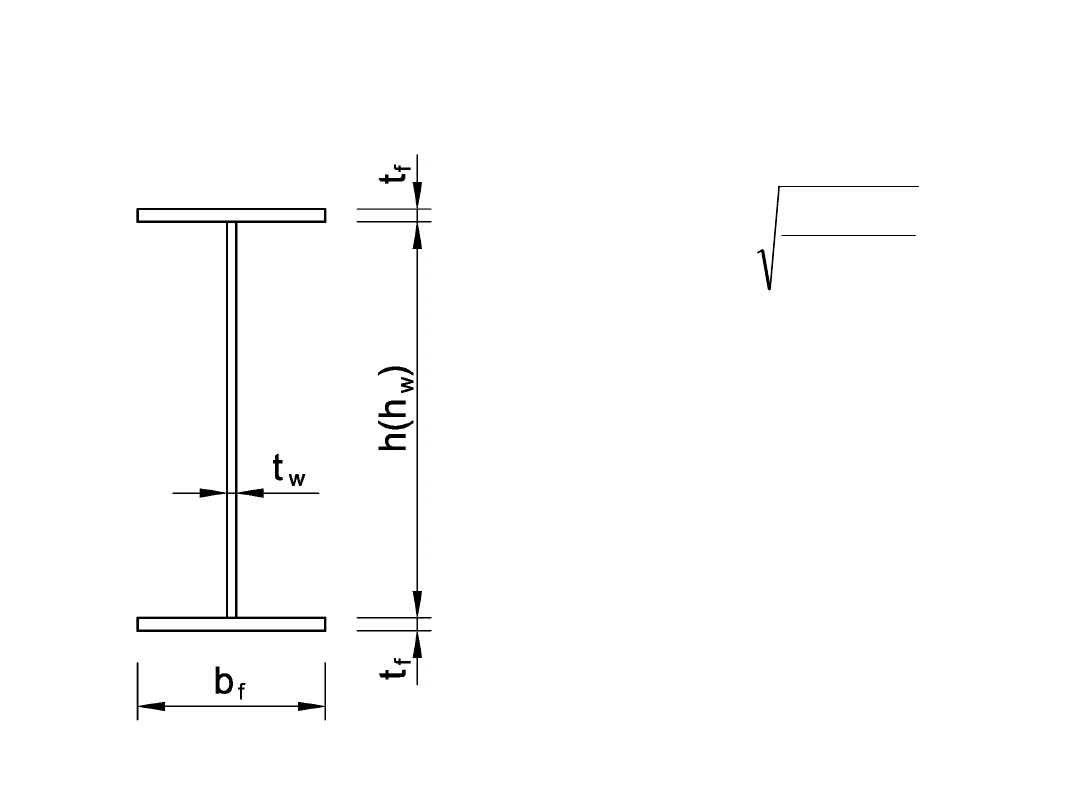
PROJEKTOWANIE BLACHOWNIC

• Dobór wstępny 

wymiarów:

       α = 1,4 - stały przekrój

Klasa 4  h

w

/t

w

 > 124

Klasa 3  h

w

/t

w

 < 124

0,2h

w

 < b

f

 < 0,4h

w

t

f 

< 40 mm dla S235

t

f 

< 30 mm dla S355

MO

y

w

max

w

/

f

t

M

α

h





Wymiarowanie belek podsuwnicowych 

kl 3

• Warunki nośności belki – metoda ogólna wg EN 

1993-1-1:

 

1

M

M

k

M

M

k

N

N

zRd

zEd

yz

yRd

LT

yEd

yy

Rd

y

Ed











1

M

M

k

M

M

k

N

N

zRd

zEd

zz

yRd

LT

yEd

zy

Rd

z

Ed











Wymiarowanie blachownic kl. 3

• Warunek nośności przekroju (środnika)





.

w

ef

zEd

zEd

1

z

zEd

w

y

yEd

Ed

xEd

2

Mo

y

2
Ed

zEd

xEd

2
zEd

2
xEd

t

l

F

σ

y

J

M

2

h

J

M

A

N

σ

/γ

f

3τ

σ

σ

σ

σ

















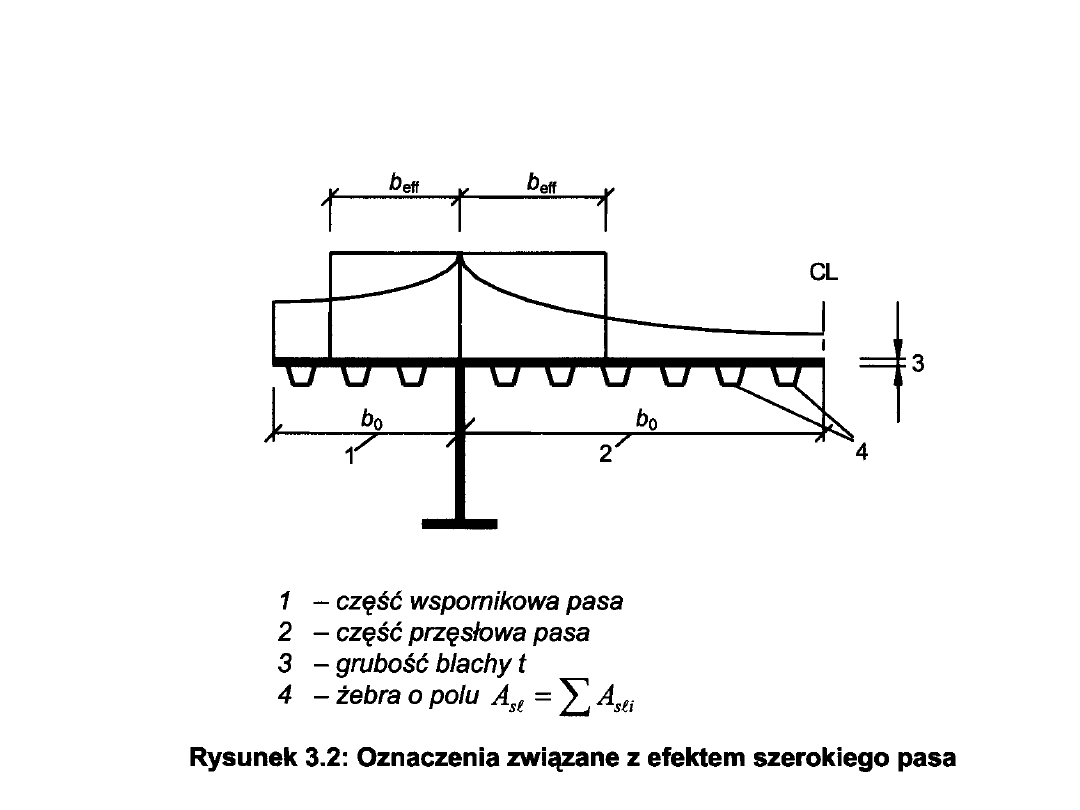
Efekt szerokiego pasa w stanie 

sprężystym

b

ef

 =  b

o

Efekt szerokiego pasa w stanie 

sprężystym

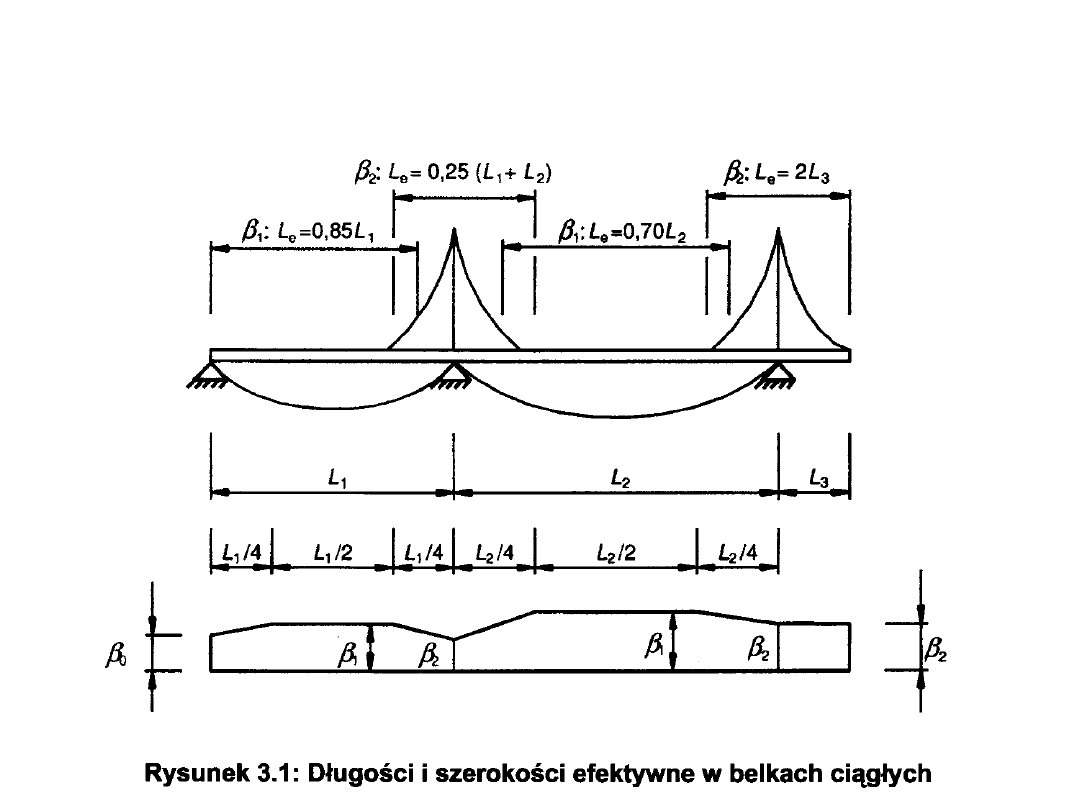
Efekt szerokiego pasa

b

o

 > L

e

/50 →b

ef

 

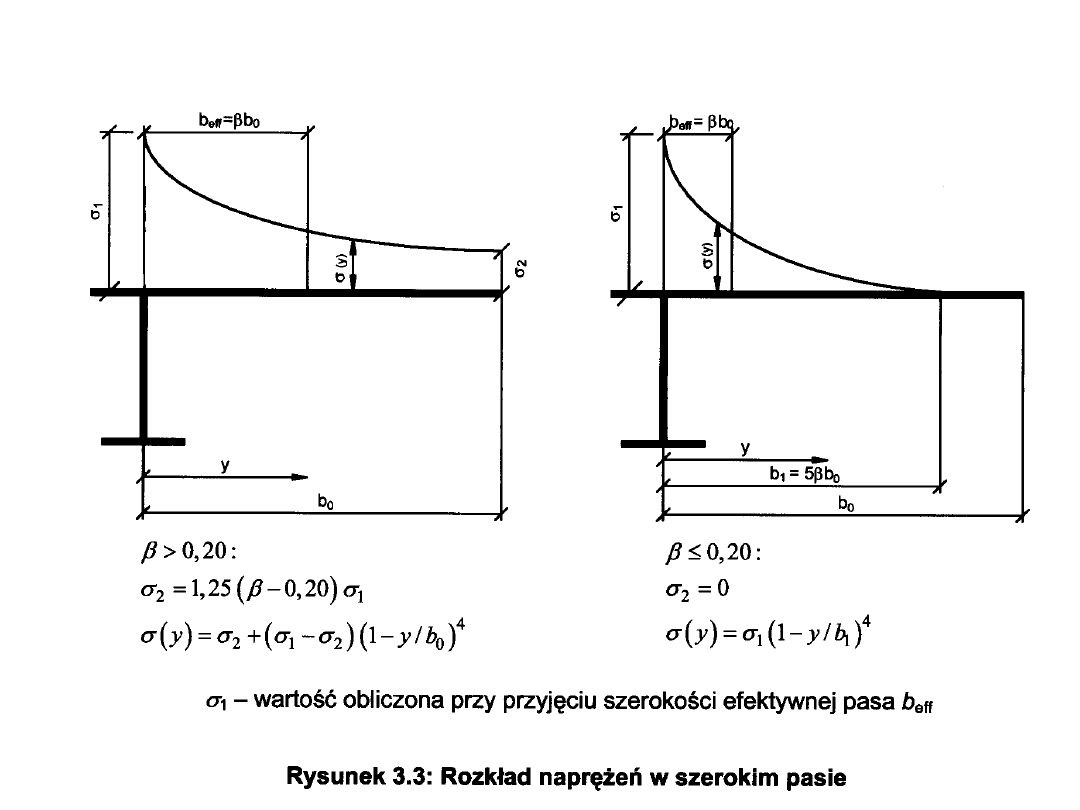
Efekt szerokiego pasa

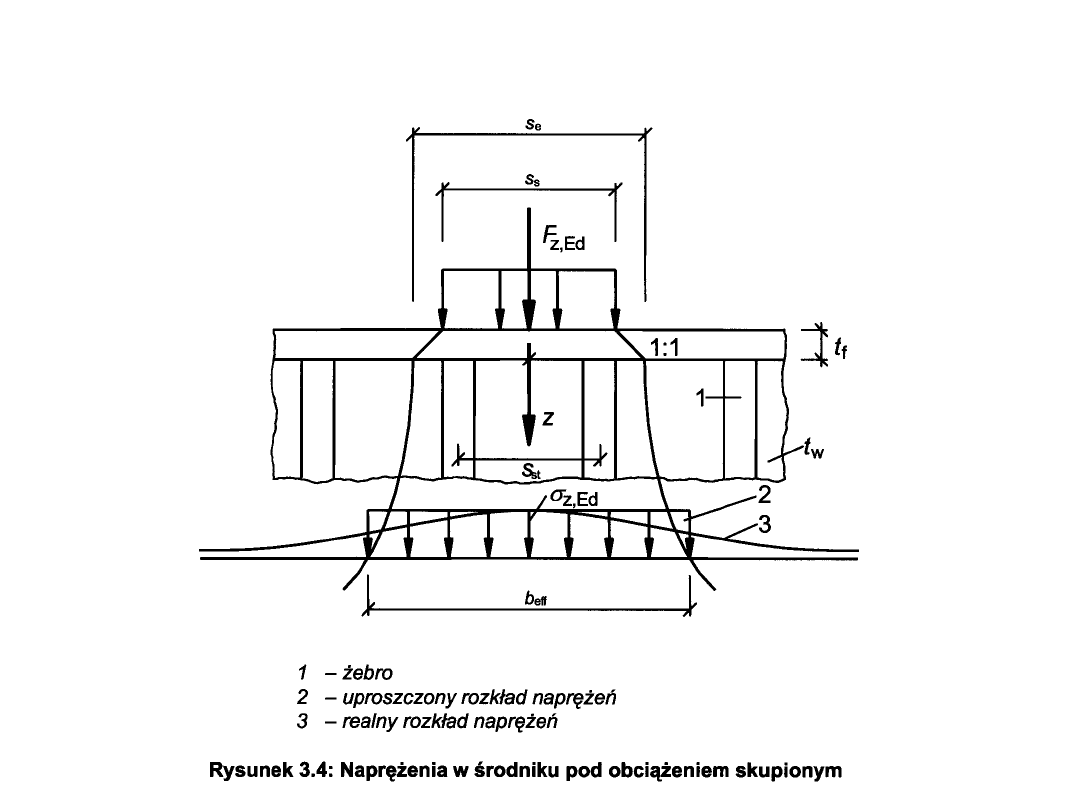
Obciążenia tarczowe środnika

Obciążenia tarczowe środnika

• Naprężenie w środniku od obciążenia tarczowego





st

sl

st

w

st

e

e

ef

s

A

a

t

a

n

n

s

z

s

b

/

'

878

,

0

1

636

,

0

,

1

,

1

,

1

,

1

,

2



























       

          

       

          

     

st,1

w

ef

Ed

z,

Ed

z,

a

t

b

F

σ

Niestateczność ścianek w stanie 

granicznym 

• Nośność blachownic klasy 4  A

ef, 

I

ef

 W

ef

• Efektywne cechy przekroju = efekt szerokiego pasa 

+ stan nadkrytyczny ścianek ściskanych

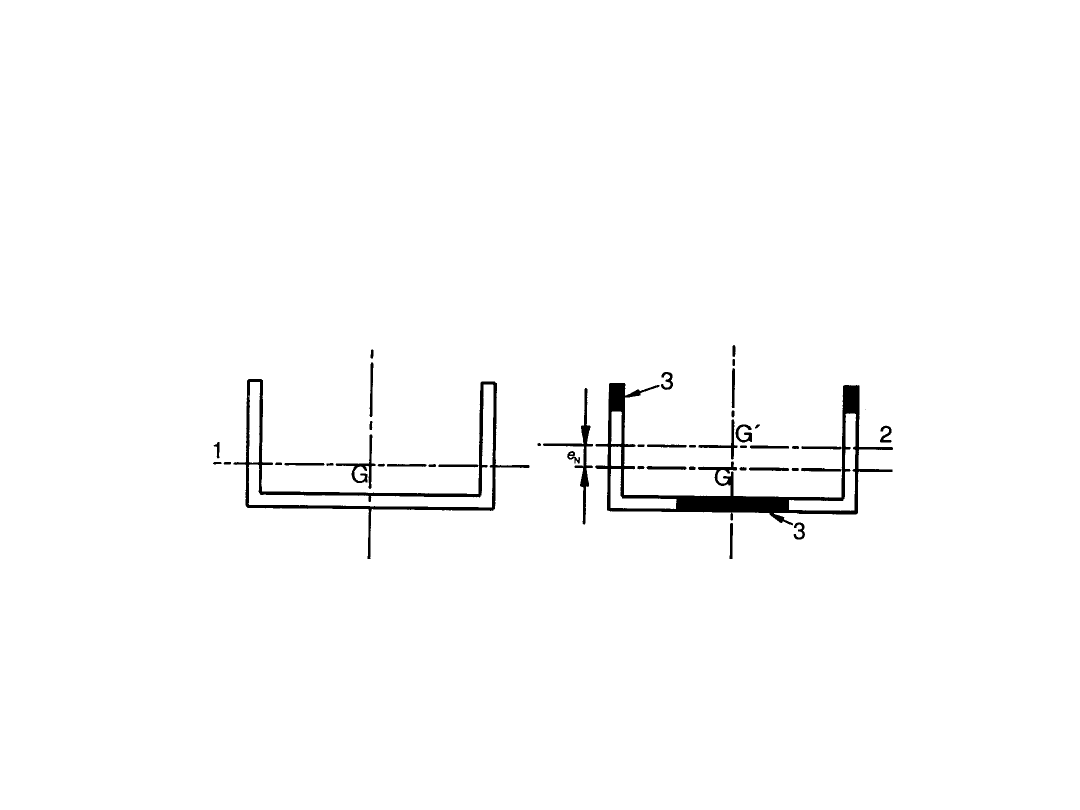
Ścianki bez usztywnień – PN EN 1993-1-

5

Szerokość współpracująca b

ei

 – osiowe ściskanie, klasa 

4:

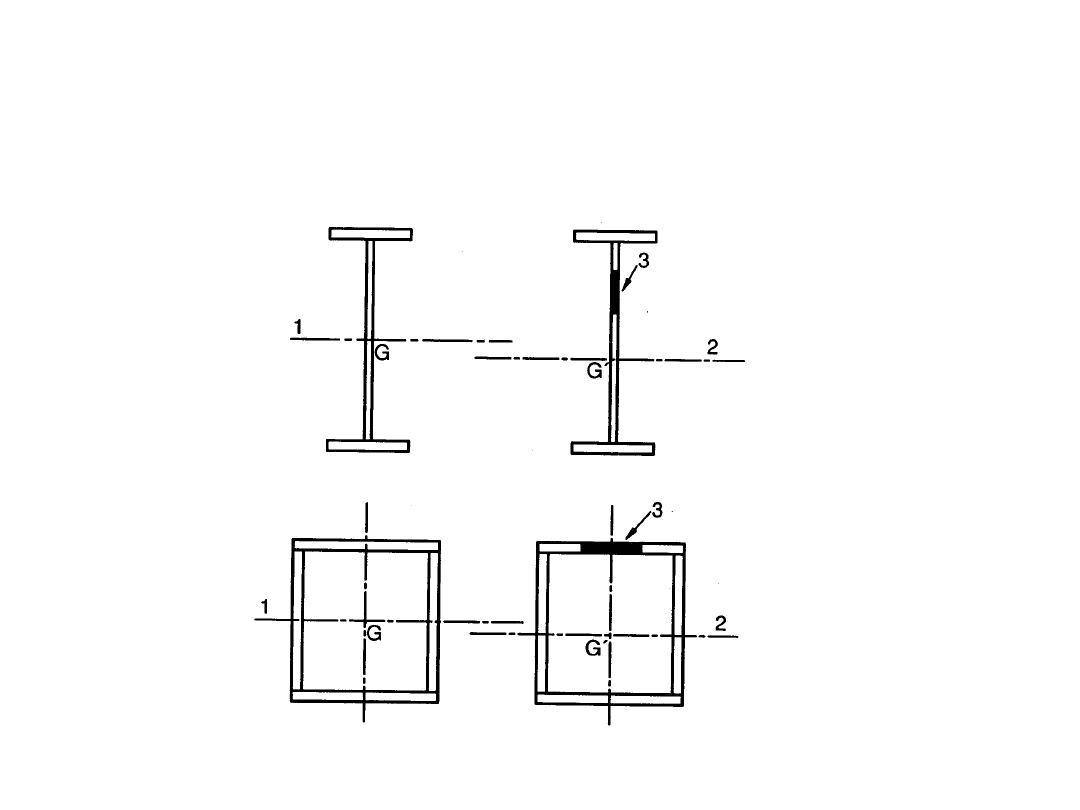
Ścianki bez usztywnień – PN EN 1993-

1-5

Szerokość współpracująca b

ei

 – zginanie, klasa 4:

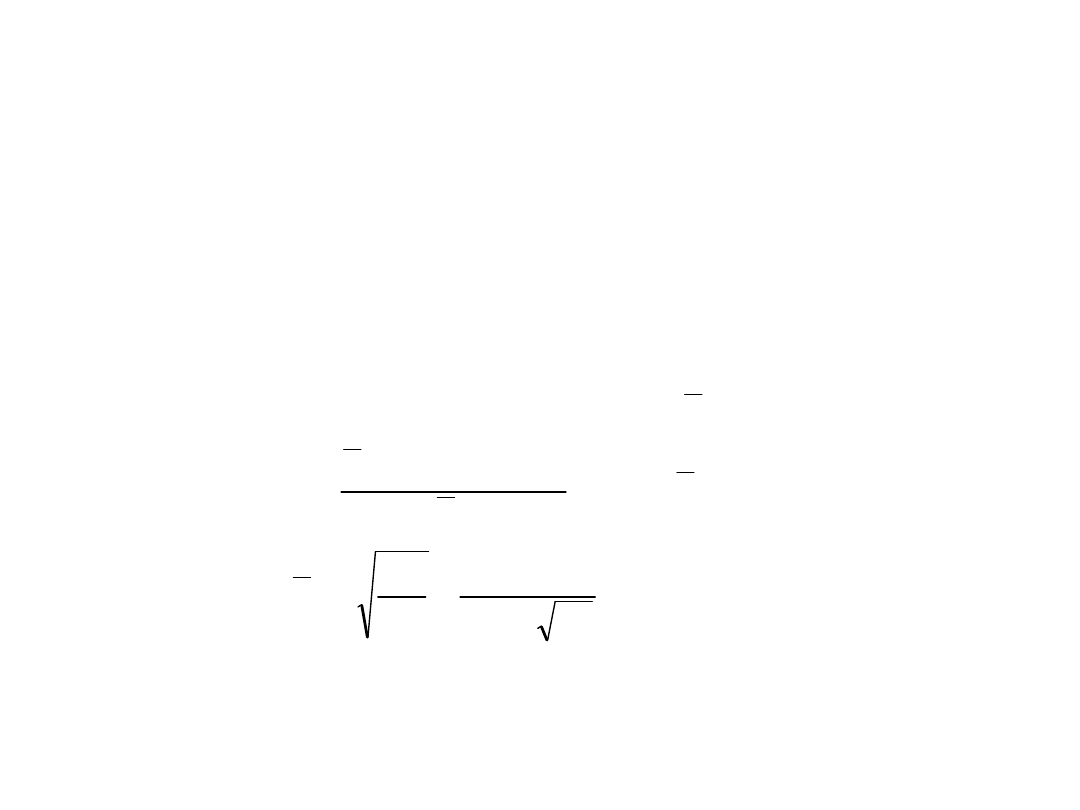
Ścianki bez usztywnień – PN EN 1993-1-

5

współczynnik stateczności miejscowej 

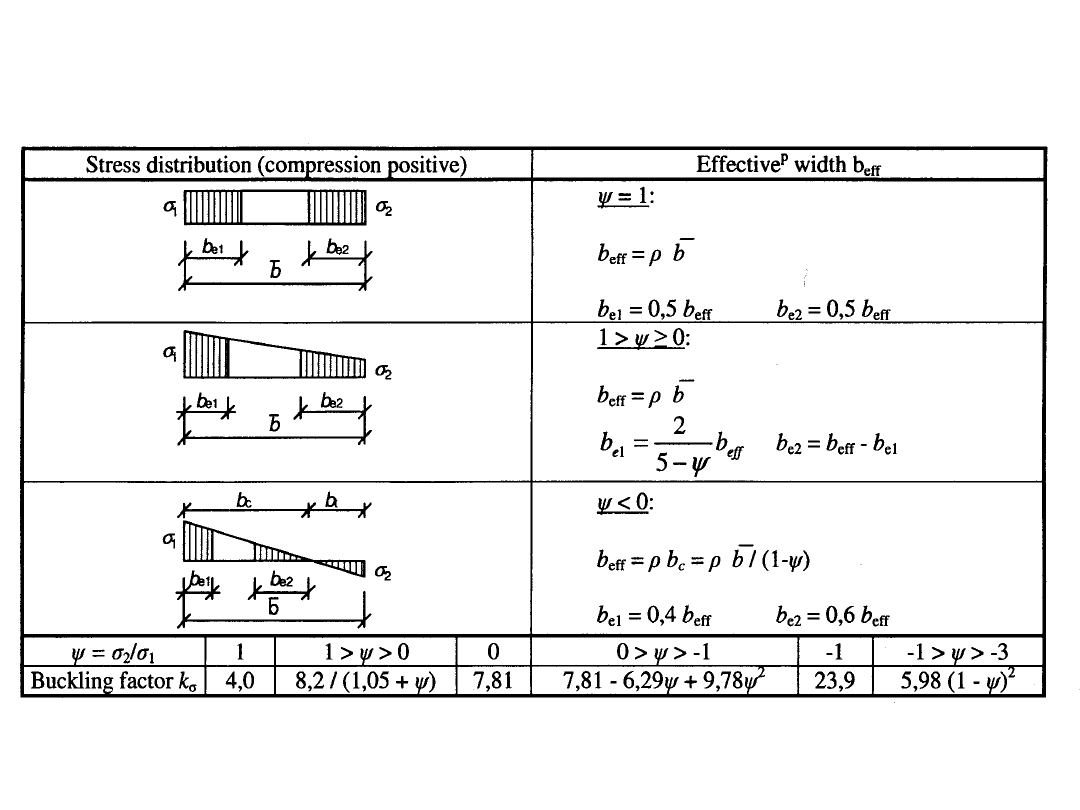
• Szerokość współpracująca ścianki płaskiej b

ei

 

b

e

 = b

p

     dla ścianek wewnętrznych (środnik):





σ

p

cr

y

p

p

2

p

p

p

k

28,4ε

/t

b

σ

f

λ

0,673

λ

  

dla

     

,

λ

ψ

3

0,055

λ

ρ

0,673

λ

  

dla

       

          

          

1,00

ρ

















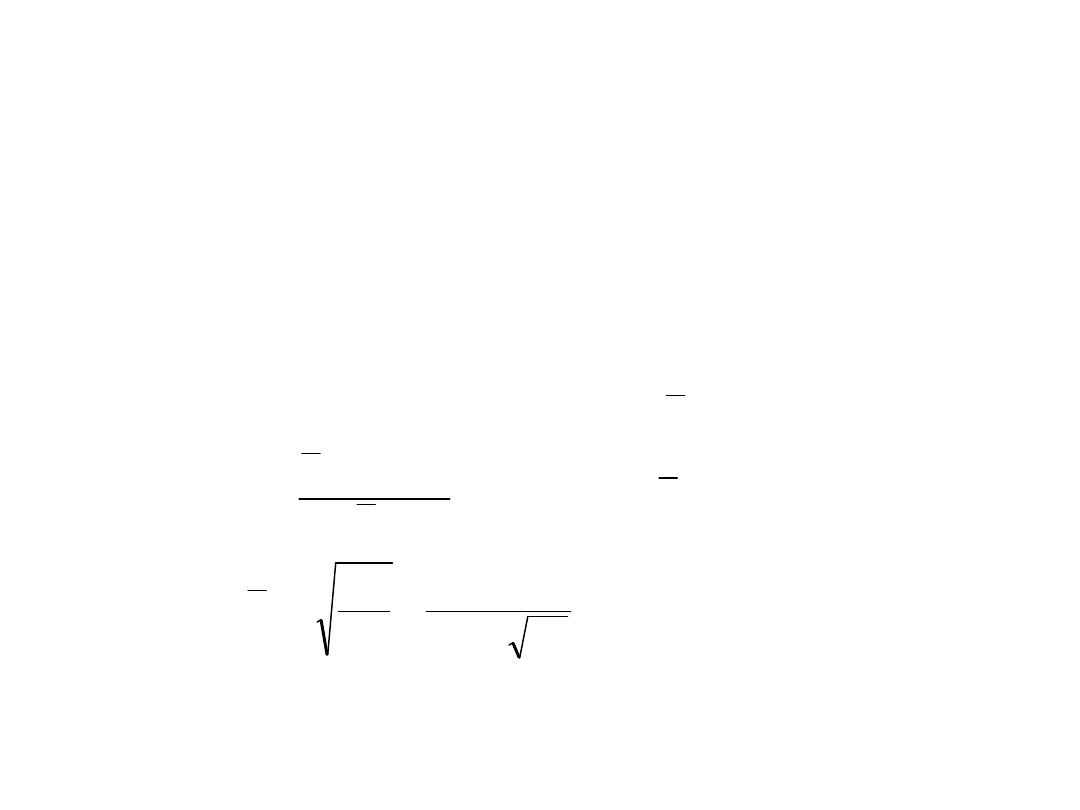
Ścianki bez usztywnień – PN EN 1993-1-

5

 

współczynnik stateczności miejscowej 

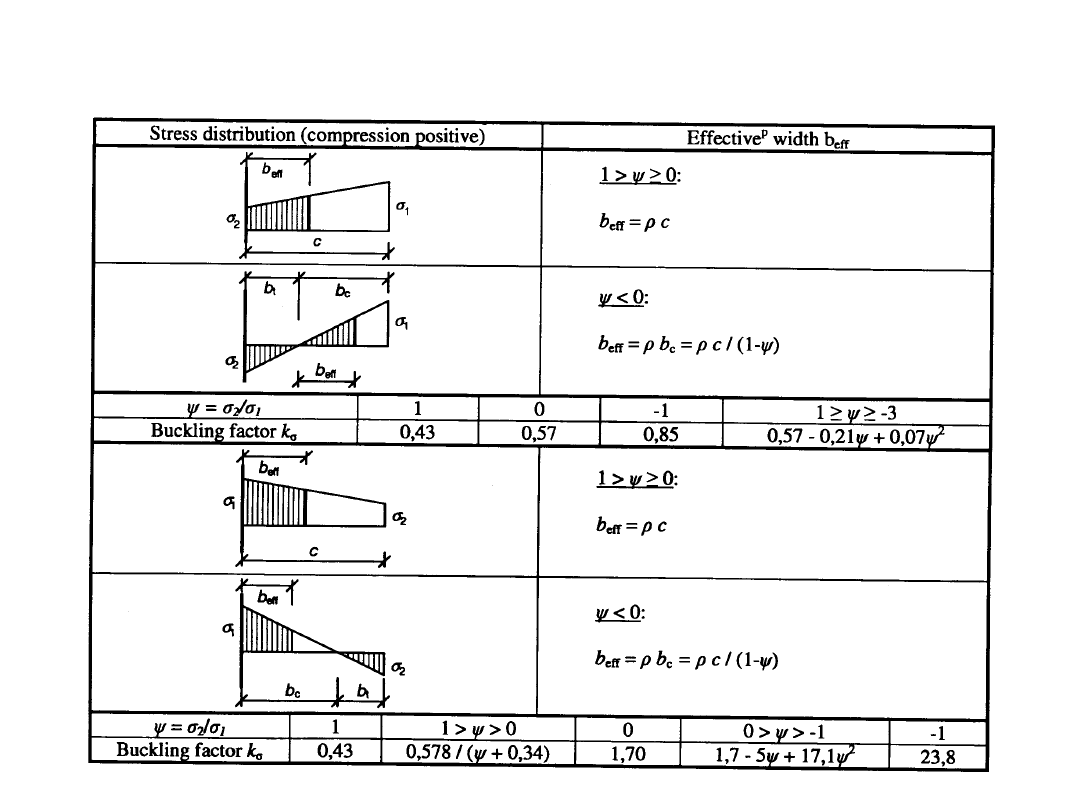
• Szerokość współpracująca ścianki płaskiej b

ei

 

b

e

 = b

p

  A

c,ef

 = A

c

     dla ścianek zewnętrznych (pas):

σ

p

cr

y

p

p

2

p

p

p

k

28,4ε

/t

b

σ

f

λ

0,748

λ

  

dla

     

          

,

λ

0,188

λ

ρ

0,748

λ

  

dla

       

          

          

1,00

ρ















Ścianki bez usztywnień – PN EN 1993-

1-5

Ścianki bez usztywnień – PN EN 1993-

1-5

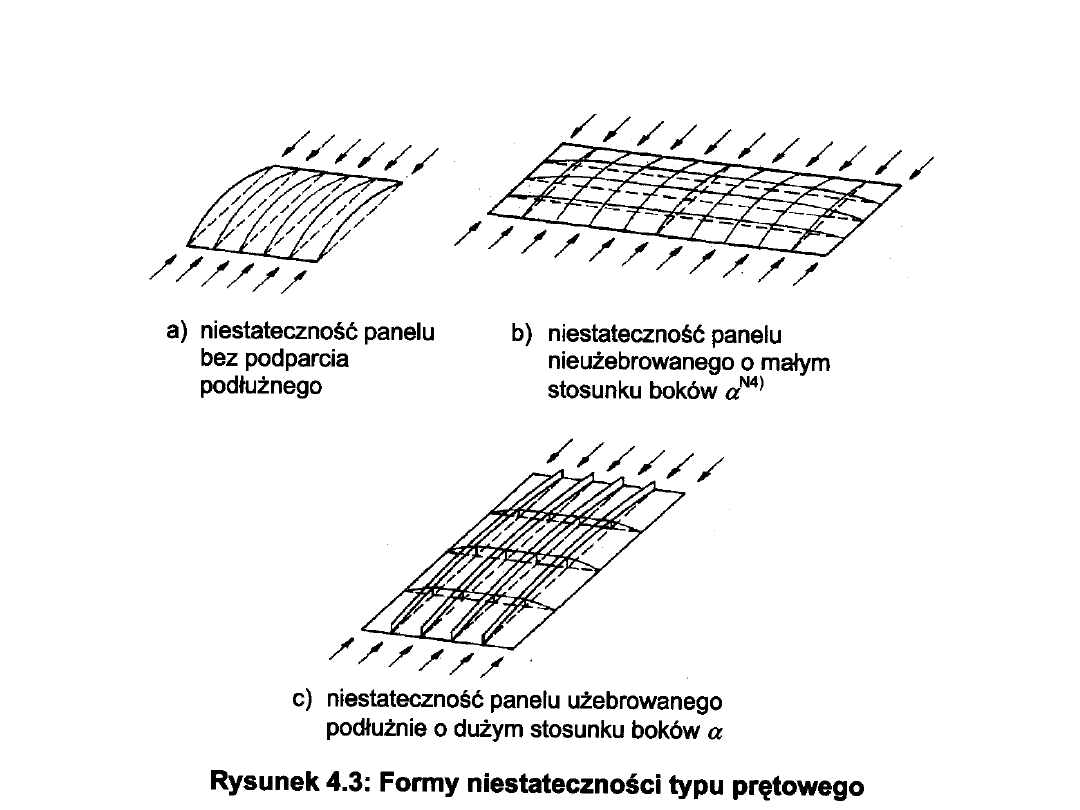
Formy niestateczności typu prętowego

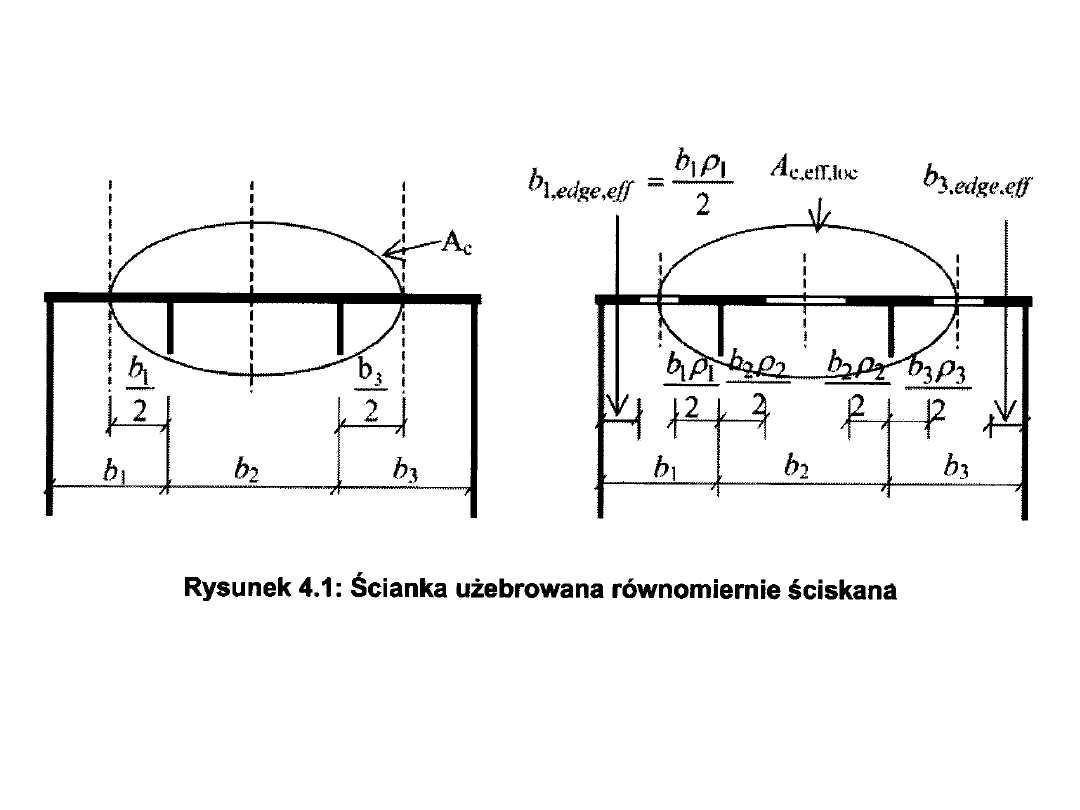
Ścianki podłużnie użebrowane

 A

c,ef

 = 

c

A

c,ef,loc

 +tb

edge,ef 

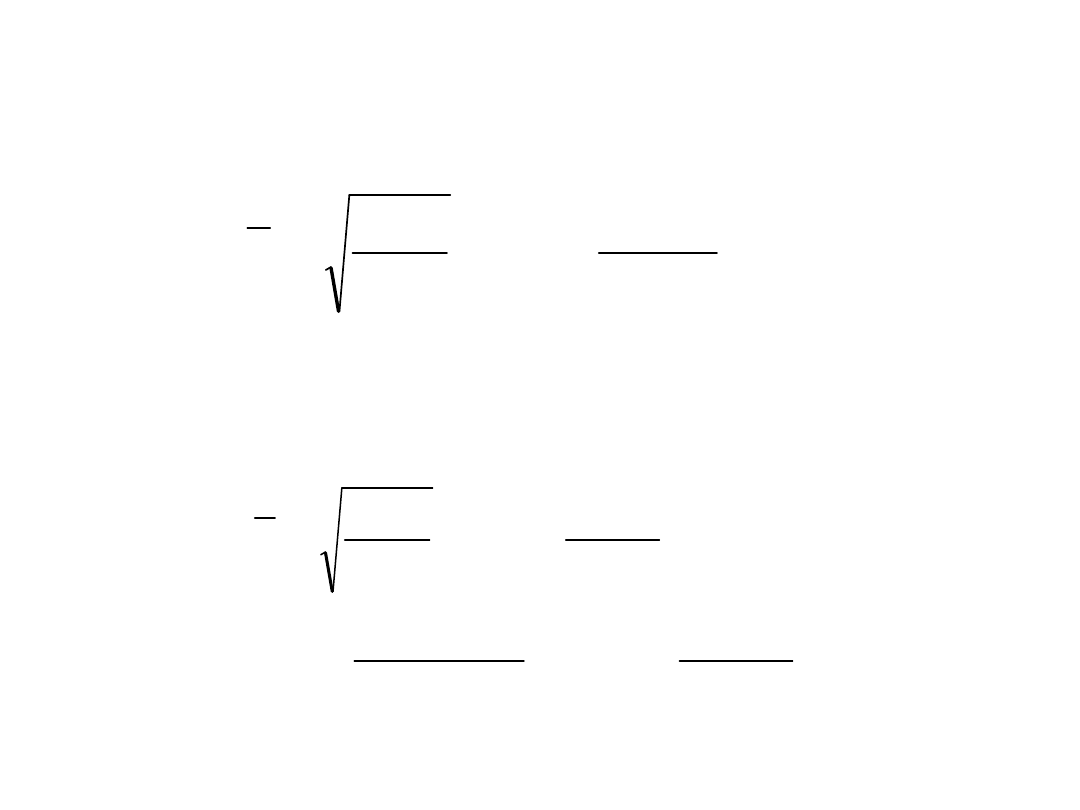
Ścianki podłużnie użebrowane

A

zał

A

A

f

p

cr

c

loc

ef

c

c

A

p

cr

c

A

p

 

   

.

,

,

,

,

,

,

,

























2

1

,

1

,

2

,

2

2

2

2

,

,

1

,

,

,

,

,....

1

12

,

a

A

EI

a

Et

A

A

f

sl

sl

sl

cr

p

cr

c

sl

ef

sl

c

A

c

cr

c

A

c

































   

Ścianki podłużnie użebrowane

• Interakcja niestateczności płytowej i prętowej



 



1

0

,........

,

2

,

,



































c

cr

p

cr

c

c

c

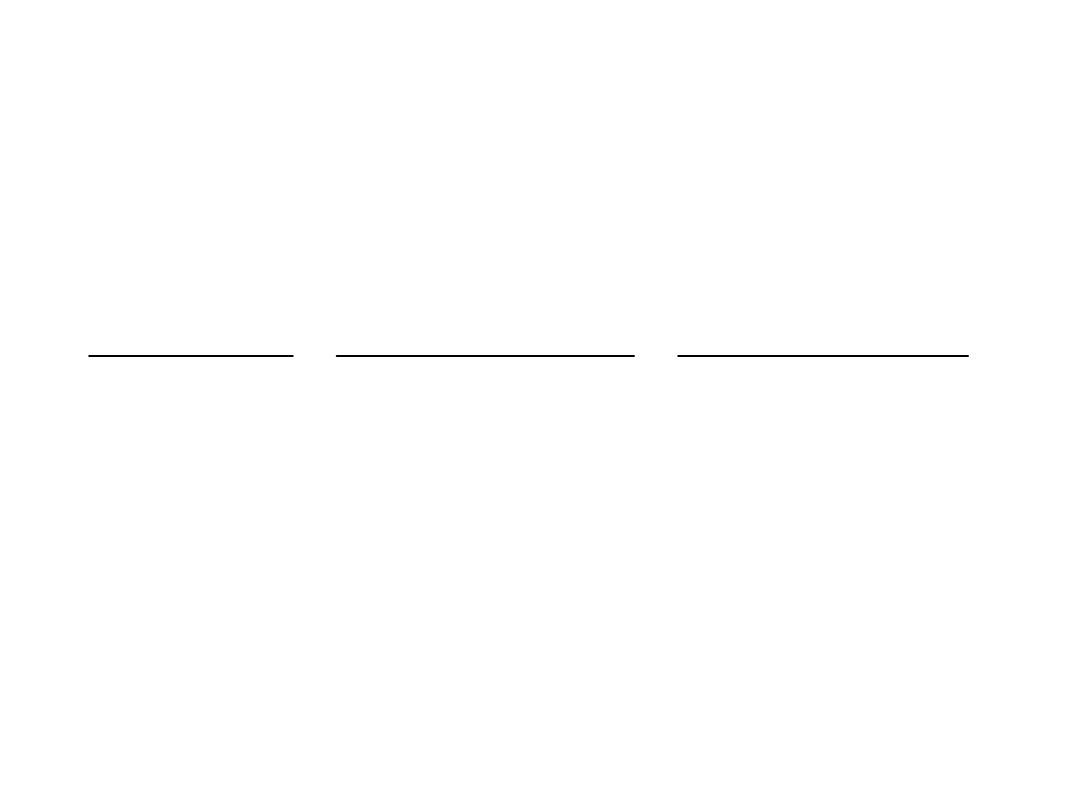
Warunki nośności elementów 

ściskanych i dwukierunkowo zginanych

1,0

/γ

W

f

e

N

M

/γ

W

f

e

N

M

/γ

A

f

N

η

Mo

ef

z,

y

N

z,

Ed

zEd

Mo

ef

y,

y

N

y,

Ed

yEd

Mo

ef

y

Ed

1













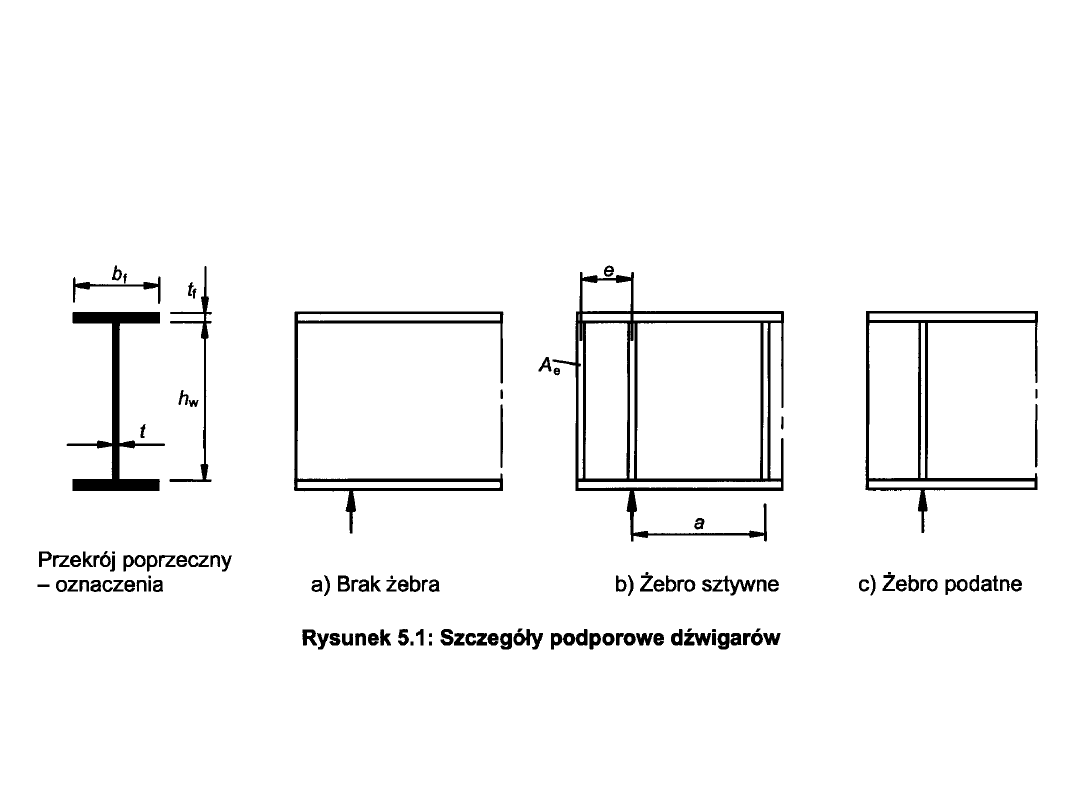
Żebra podporowe 

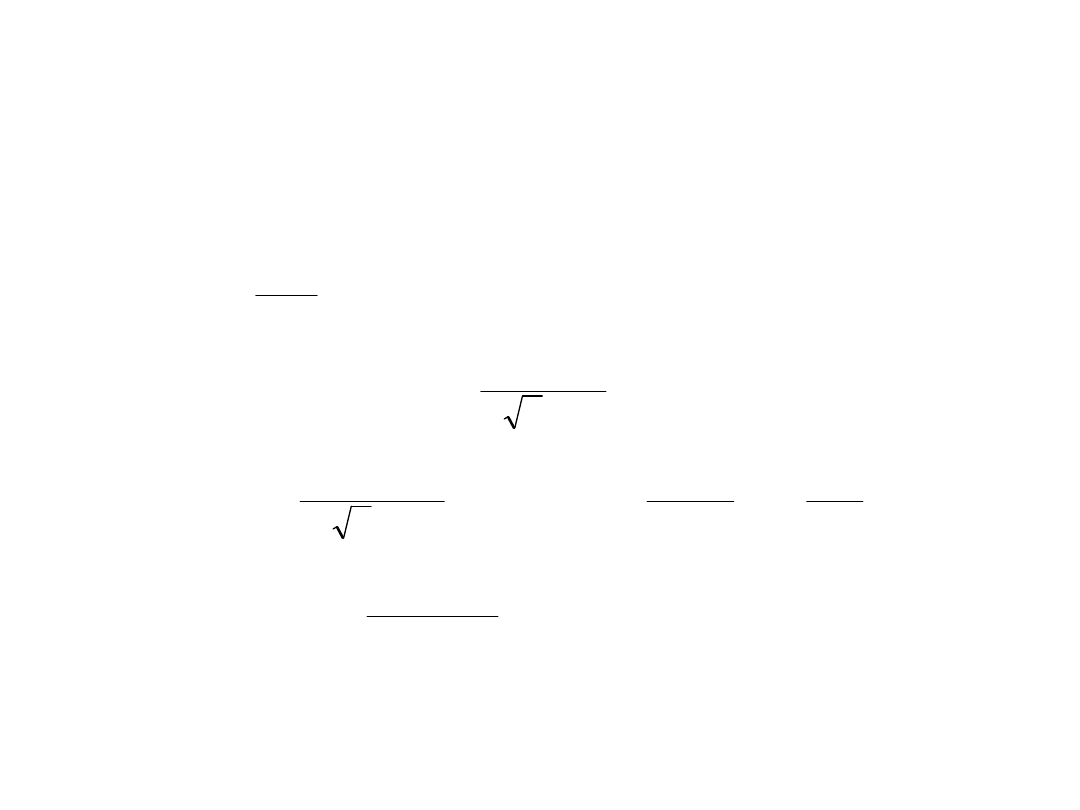
PROJEKTOWANIE BLACHOWNIC KL 4

 

Warunki nośności przekrojów ścinanych

• Warunek ścinania siłą poprzeczną  (przekrój 

podporowy):

•  





























































yw

2

w

w

yf

2

f

f

2

frd

Ed

M1

yf

2

f

f

bfRd

M1

w

w

yw

w

bwRd

M1

w

w

yw

bfRd

bwRd

bRd

bRd

Ed

f

h

t

f

t

1,6b

0,25

a

c

,

M

M

1

c

f

t

b

 V

          

,

3

t

h

f

V

3

t

h

ηf

V

V

V

1,0

V

V









3



PROJEKTOWANIE BLACHOWNIC KL 4

 

Warunki nośności przekrojów ścinanych

• Współczynnik stateczności miejscowej przy ścinaniu 



w

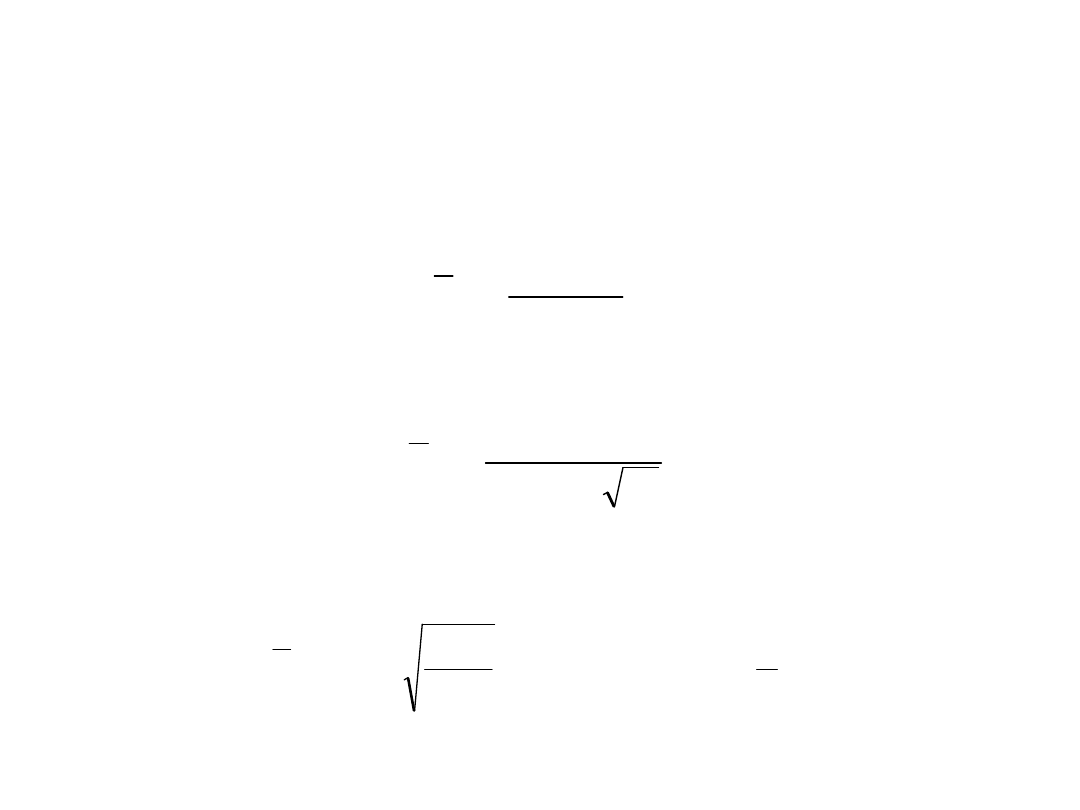
PROJEKTOWANIE BLACHOWNIC KL 4

 

Warunki nośności przekrojów ścinanych

• Smukłość względna gdy żebra występują tylko nad 

podporami

• Smukłość względna gdy żebra występują także poza 

podporami

• Smukłość względna wzór ogólny

 

ε

86,4t

h

λ

w

w

w





k

ε

37,4t

h

λ

w

w

w



2

E

E

yw

w

b

t

190000

σ

        

,

σ

k

f

0,76

λ



















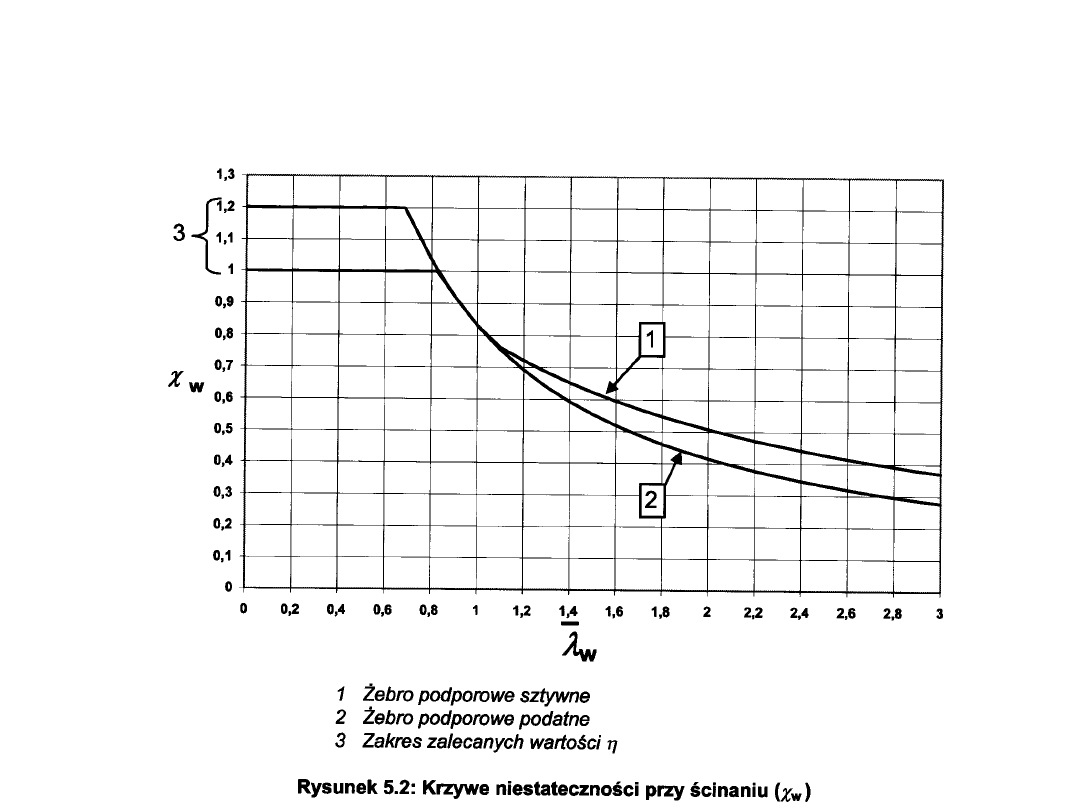
PROJEKTOWANIE BLACHOWNIC KL 4

 

Warunki nośności przekrojów ścinanych

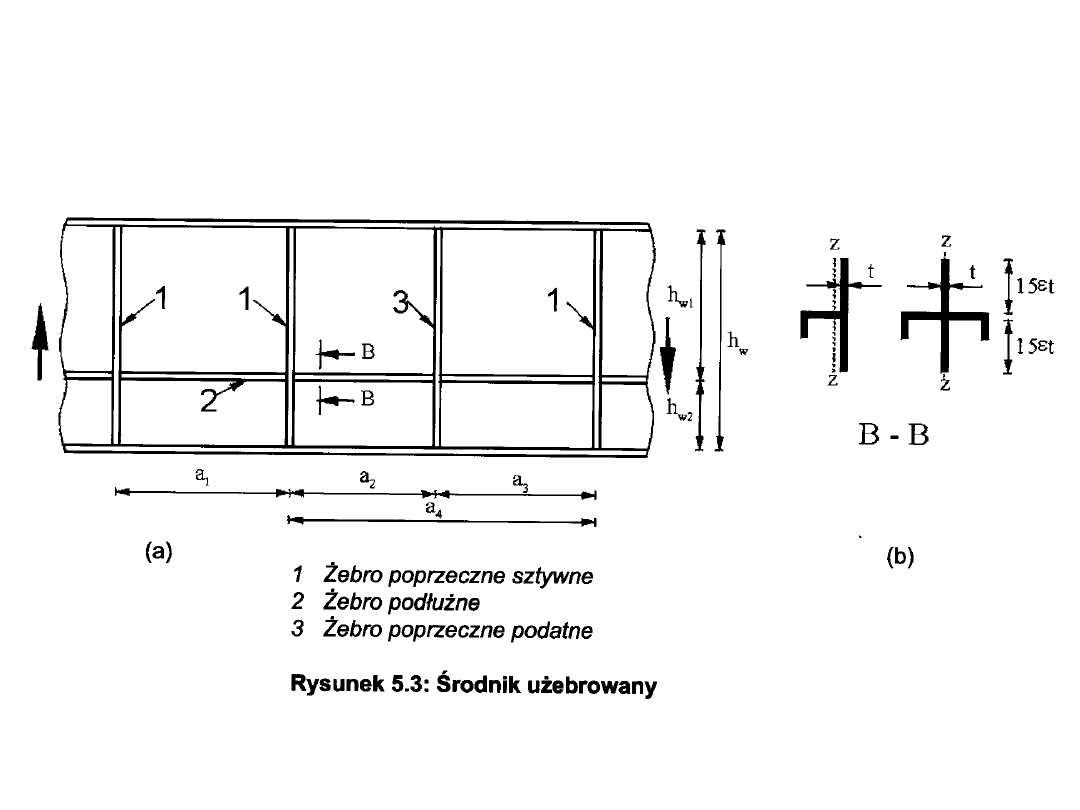
PROJEKTOWANIE BLACHOWNIC KL 4

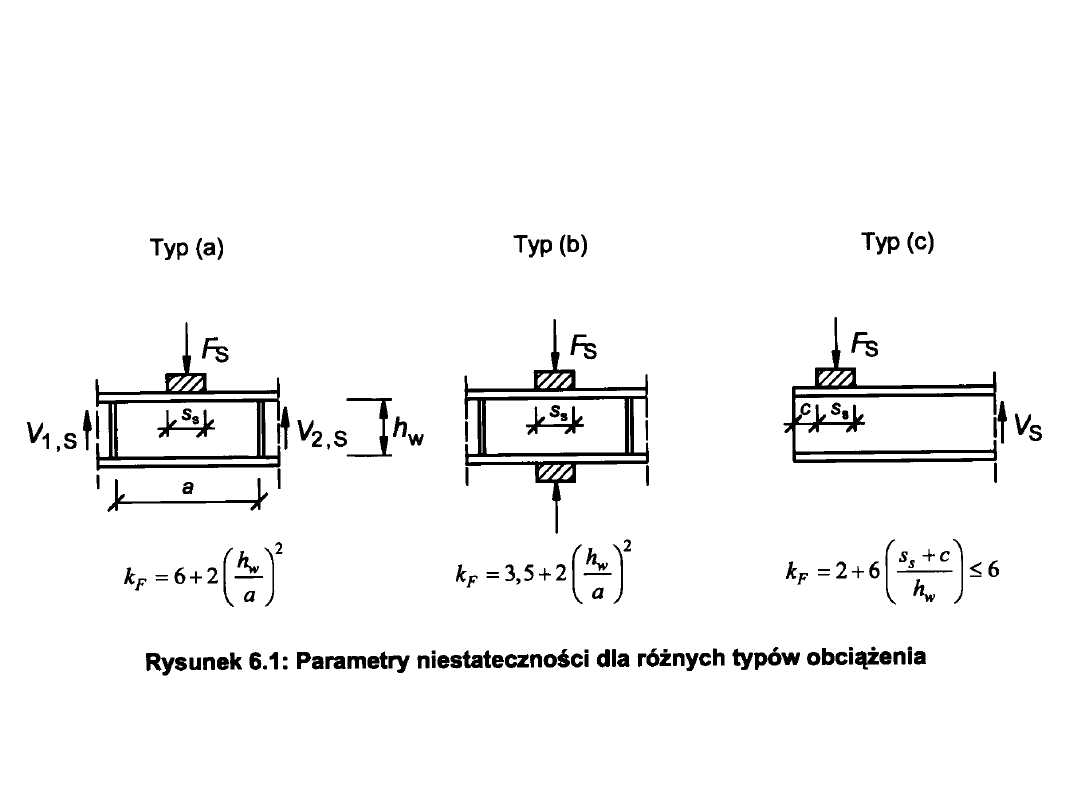
PROJEKTOWANIE BLACHOWNIC KL 4

Nośność przy obciążeniu skupionym

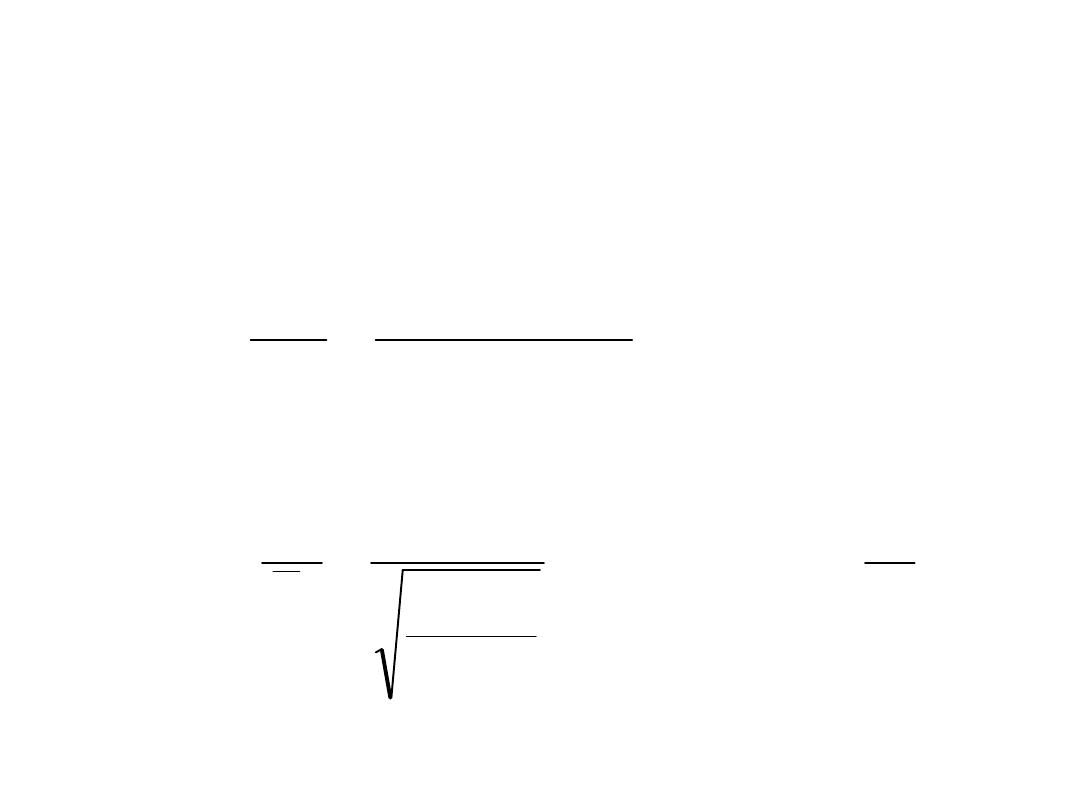
PROJEKTOWANIE BLACHOWNIC KL 4

Nośność przy obciążeniu skupionym

• Warunek nośności

w

w

F

cr

cr

yw

w

y

F

F

y

F

ef

h

t

E

k

F

F

f

t

l

l

L

3

9

,

0

;

5

,

0

5

,

0

,























1,0

/γ

t

L

f

F

F

F

η

M1

w

ef

yw

Ed

Rd

Ed

2

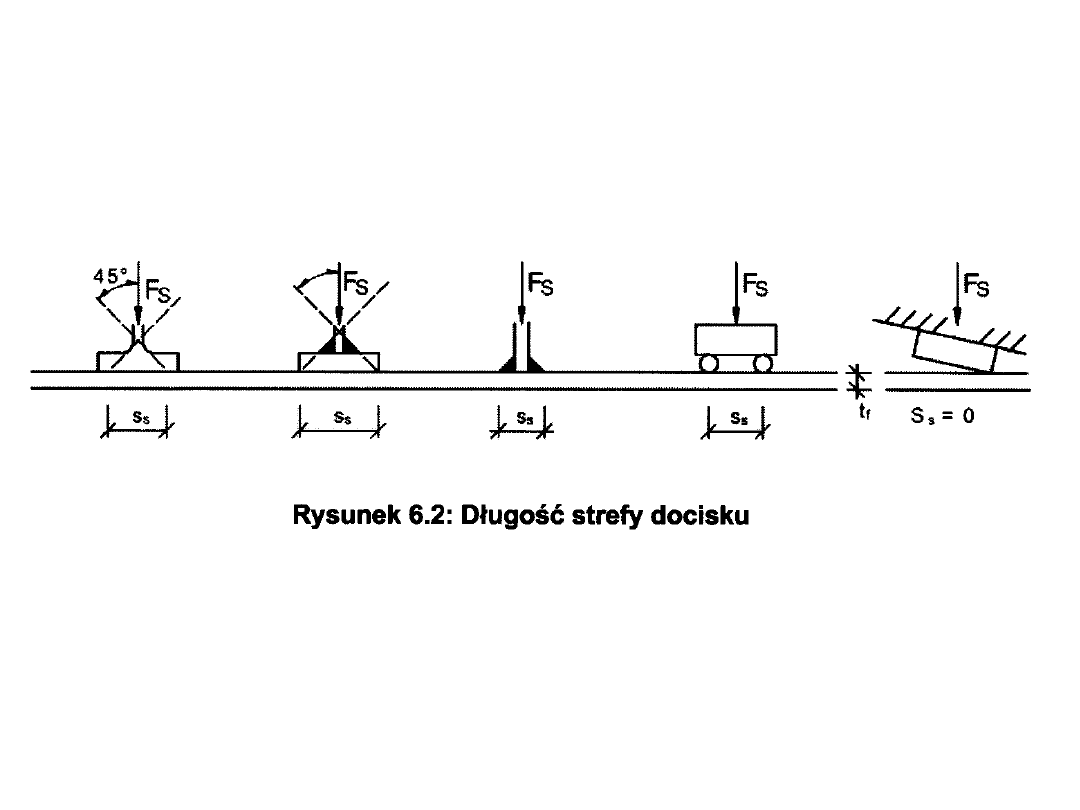
PROJEKTOWANIE BLACHOWNIC KL 4

 Nośność przy obciążeniu skupionym

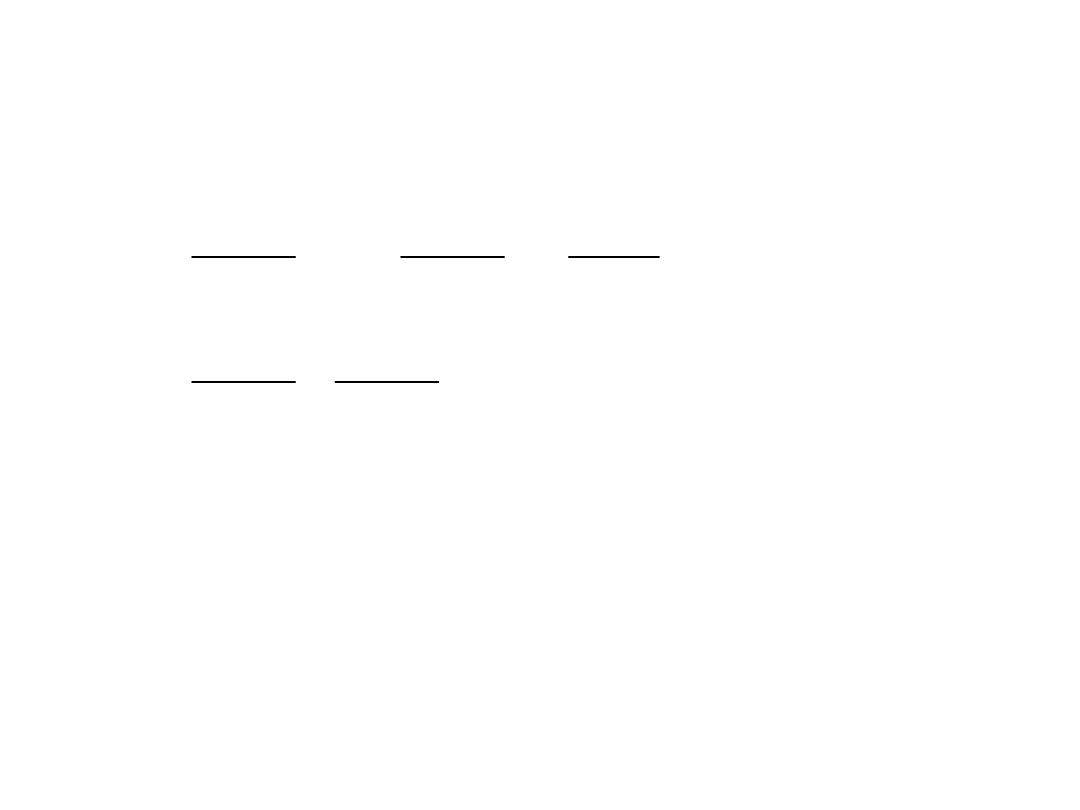
PROJEKTOWANIE BLACHOWNIC KL 4

Interakcyjne warunki nośności M-N-V i M-F-N

1,4

0,8η

η

M

M

M

M

1,00

1

V

V

2

M

M

1

M

M

1

2

Rd

pl,

Rd

f,

Rd

pl,

Ed

2

Rd

bw,

Ed

Rd

pl,

Rd

f,

Rd

pl,

Ed











































,

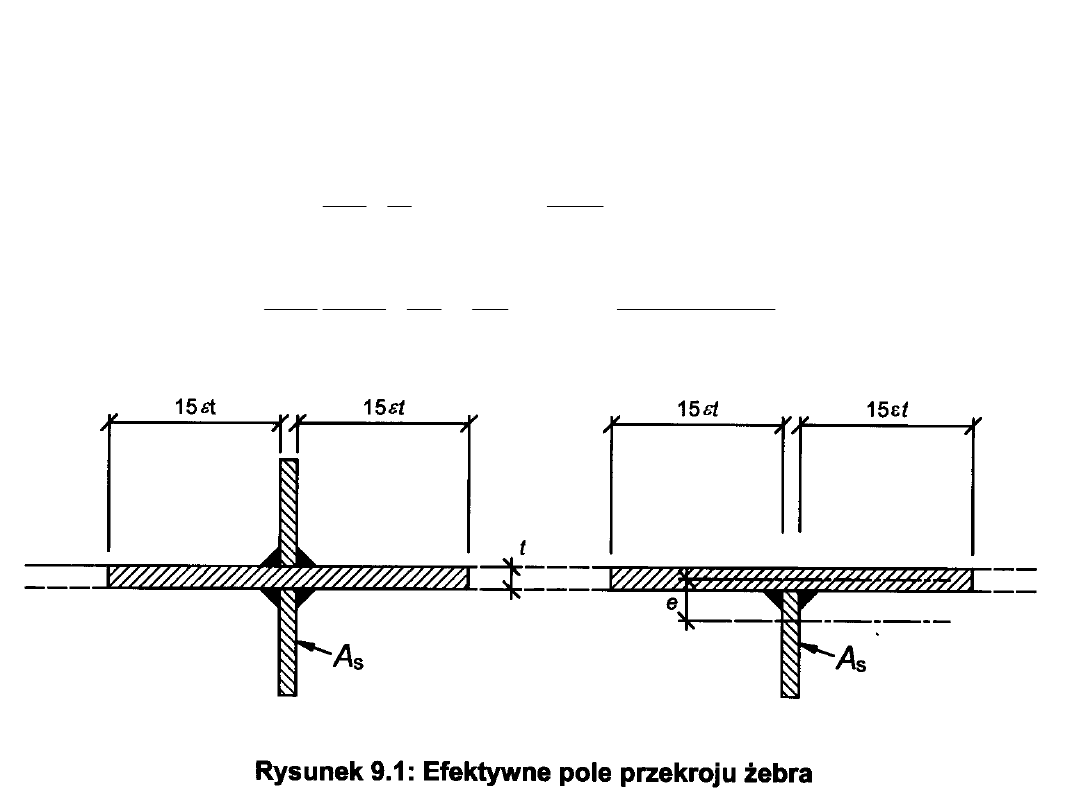
PROJEKTOWANIE BLACHOWNIC KL 4

Żebra usztywniające

1,0

/γ

300bf

Ee

π

u

    

,

a

1

a

1

b

N

σ

σ

σ

u

b

300

w

1

π

b

E

σ

I

I

M1

y

max

2

2

1

Ed

crp

crc

m

o

4

m

st

s































 

















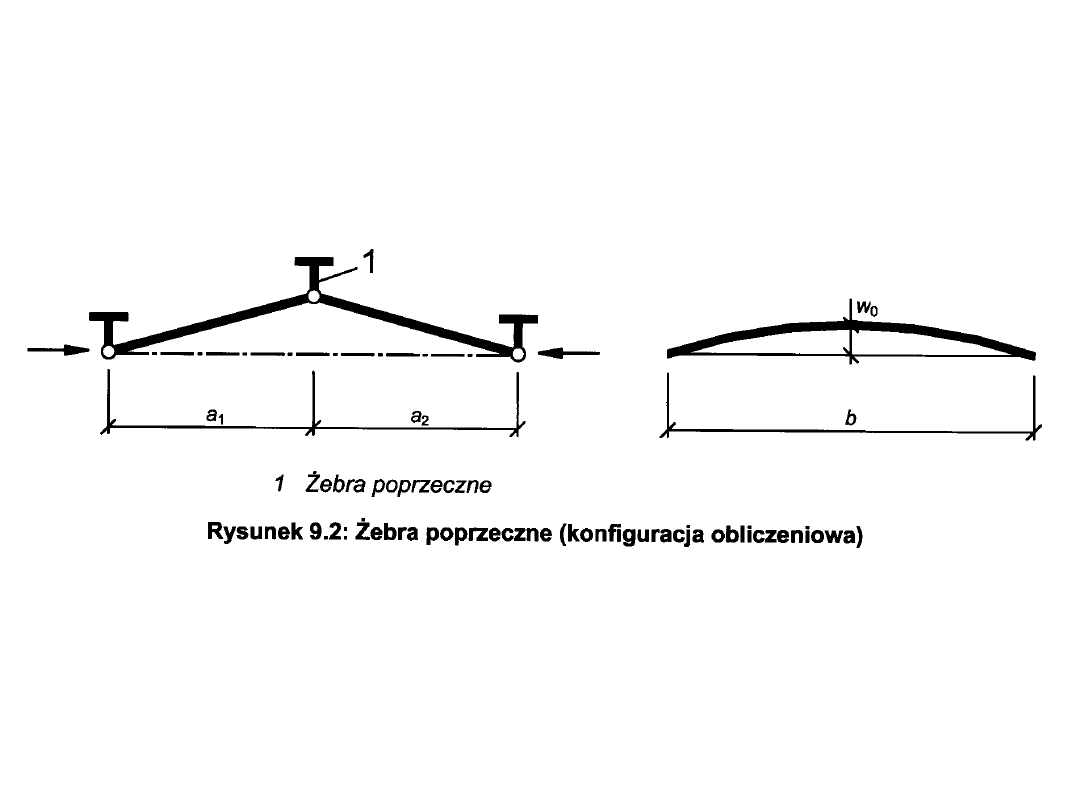
PROJEKTOWANIE BLACHOWNIC KL 4

 

Żebra usztywniające  w

o

  b/300

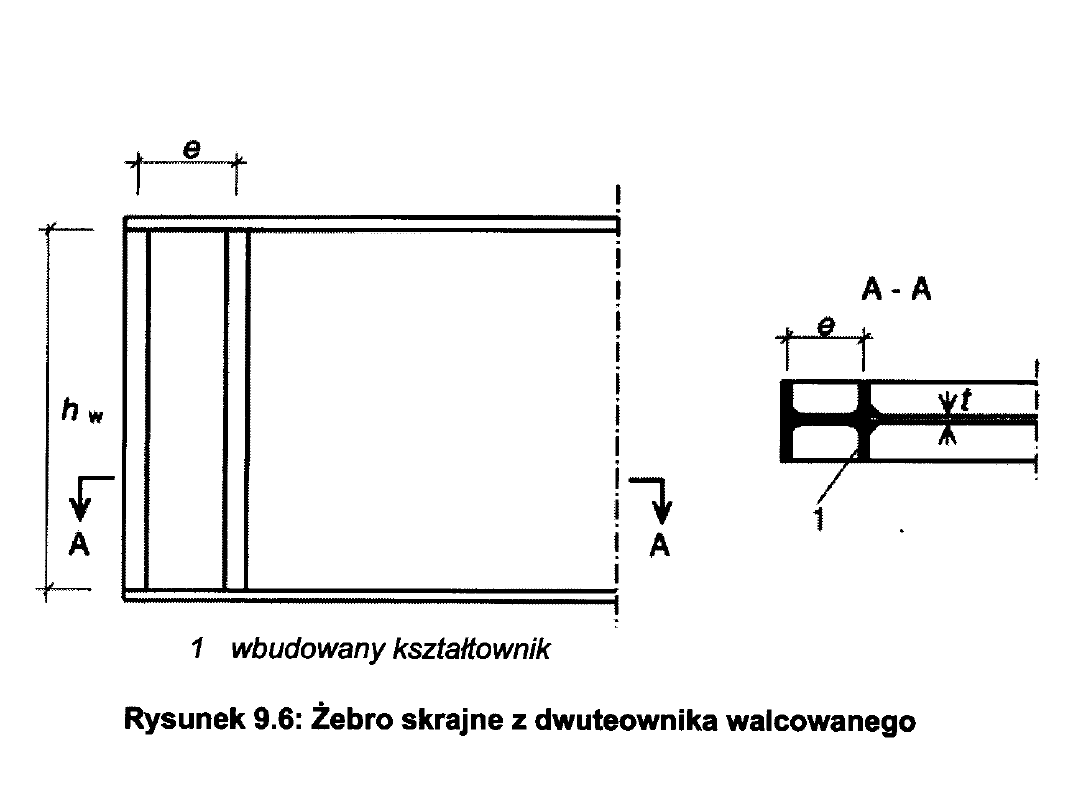
PROJEKTOWANIE BLACHOWNIC

Ścinanie – żebra skrajne sztywne

 

PROJEKTOWANIE BLACHOWNIC KL 4

Metoda Naprężeń Zredukowanych (MNZ)

• Metoda NZ jest alternatywną wobec metody szerokości 

współpracującej (nośności nadkrytycznej)

• Stany graniczne naprężeń mogą stanowić kryterium 

przekrojów współpracujących

• Panele poddane 

xEd

, 

zEd

, 

Ed

 traktujemy jak przekroje 

klasy 3 gdy

1

γ

ρα

M1

ult,k



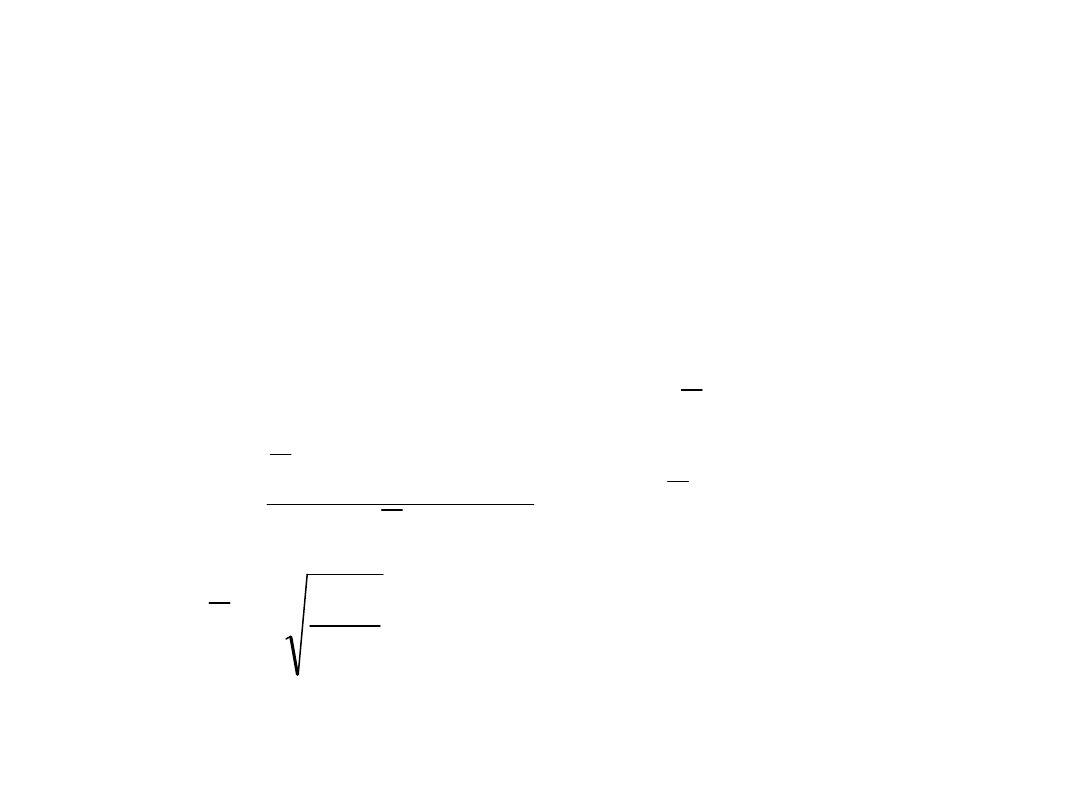
Ścianki bez usztywnień – PN EN 1993-1-

5

współczynnik stateczności miejscowej 

• Szerokość współpracująca ścianki płaskiej b

ei

 

b

e

 = b

p

     dla ścianek wewnętrznych (środnik):





cr

ult,k

α

α















p

p

2

p

p

p

λ

0,673

λ

  

dla

     

,

λ

ψ

3

0,055

λ

ρ

0,673

λ

  

dla

       

          

          

1,00

ρ

PROJEKTOWANIE BLACHOWNIC KL 4

Metoda naprężeń zredukowanych

• Wytężenie środnika belki podsuwnicowej

.

t

I

S

V

   

          

,

t

l

F

σ

y

J

M

2

h

J

M

A

N

σ

w

y

1

Ed

w

ef

zEd

zEd

1

z

zEd

w

y

yEd

Ed

xEd



































2

2

Ed

zEd

xEd

2
zEd

2
xEd

3τ

σ

σ

σ

σ

ult,k

y

α

f

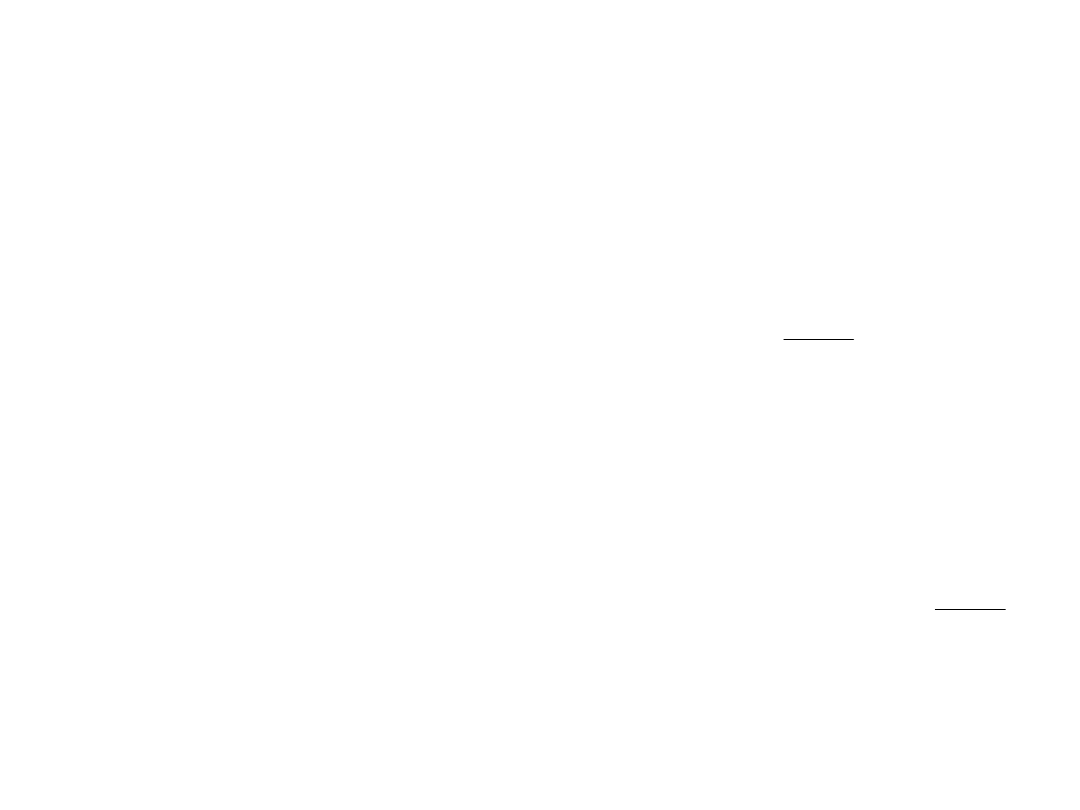
PROJEKTOWANIE BLACHOWNIC KL 4

Metoda naprężeń zredukowanych

• Współczynnik 

 = min (

x

 , 

z

 , 

w

 ) 

-  sposób (a):

• Współczynnik  - sposób (b):

2

2

Ed

zEd

xEd

2
zEd

2
xEd

3τ

σ

σ

σ

σ





















M1

y

f





2

2

Ed

zEd

xEd

2
zEd

2
xEd

3τ

σ

σ

σ

σ





















M1

y

f













2

2

2

/

/

/

/

w

z

x

z

x

PROJEKTOWANIE BLACHOWNIC KL 4

Metoda naprężeń zredukowanych

• Globalny mnożnik 

cr

.

,

,

,

1

2

1

2

1

4

1

4

1

4

1

4

1

1

2

2

2

2

Ed

cr

cr

zEd

crz

crz

xEd

crx

crx

cr

crz

z

crx

x

crz

z

crx

x

crz

z

crx

x

cr



































































































  

          

          

          

  

          

          

          

  

          

          

          

KONSTRUKCJE WSPORCZE SUWNIC

wg PN-EN 1993-6

• Strona tytułowa

KONSTRUKCJE WSPORCZE SUWNIC

wg PN-EN 1993-6

KONSTRUKCJE WSPORCZE

 SUWNIC

wg PN-EN 1993-6

KONSTRUKCJE WSPORCZE SUWNIC

wg PN-EN 1993-6

KONSTRUKCJE WSPORCZE SUWNIC

wg PN-EN 1993-6

PROJEKTOWANIE BLACHOWNIC KL 4

Metoda naprężeń zredukowanych

• Przekroje obliczeniowe belki podsuwnicowej z 

tężnikiem hamownym kratowym