6. SZEREGOWANIE PROCESÓW

Szeregowaniem wykonania procesów zajmuje się zarówno system operacyjny, jak i
programista.

System zarządza wszystkimi wykonywanymi procesami „na niskim poziomie”,
kierując się

jedynie priorytetami procesów i dostępnością zasobów, na które zgłaszają
zapotrzebowanie.

Programista zarządza uruchamianymi przez siebie procesami, korzystając z
mechanizmów

koordynacji dostępnych w używanym przez niego języku programowania.
Koordynacja jest

potrzebna w przypadku korzystania ze wspólnych zasobów. Jakie mogą być
oczekiwania wobec

kolejności udostępniania zasobów procesom ?

Uczciwość słaba

(weak fairness, justice)

Program nazywamy słabo uczciwym, jeżeli dla każdego jego wykonania i dla
każdego jego procesu

zachodzi: jeżeli proces od pewnego momentu nieprzerwanie zgłasza
zapotrzebowanie na pewien

zasób, to kiedyś będzie ono obsłużone.

W praktyce oznacza to, że w momencie zgłoszenia zapotrzebowania proces
zostaje zawieszony

i czeka na przydział zasobu. Czas oczekiwania może być dowolnie długi.

Uczciwość mocna

(strong fairness, compassion)

Program nazywamy mocno uczciwym, jeżeli dla każdego jego wykonania i
każdego procesu

zachodzi: jeżeli proces zgłasza zapotrzebowanie dostatecznie wiele razy, to
kiedyś będzie ono

obsłużone.

Oznacza to, że jeżeli proces wykonując się co pewien czas sprawdza, czy
potrzebny zasób jest już

dostępny, to po pewnym (dowolnie długim) czasie otrzyma przydział tego zasobu.

Oczekiwanie liniowe

Program ma własność oczekiwania liniowego, jeżeli dla każdego jego wykonania
i każdego procesu

zachodzi: jeżeli proces zgłosi zapotrzebowanie, to będzie ono obsłużone, zanim
dowolny inny proces

czekający na ten sam zasób będzie obsłużony więcej, niż raz.

Jest to własność o bardziej praktycznym charakterze, niż dwie poprzednie, gdyż
pozwala oszacować

(choćby tylko z grubsza) czas oczekiwania na przydział.

FIFO (kolejka prosta)

Program ma własność FIFO, jeżeli dla każdego jego wykonania i każdego
procesu zachodzi: jeżeli

proces zgłosi zapotrzebowanie, to będzie ono obsłużone przed każdym
zapotrzebowaniem zgłoszo-

nym później.

Ta definicja może odnosić się jedynie do programu wykonywanego w systemie
ściśle powiązanym,

gdyż tylko w tym przypadku ma sens pojęcie czasu bezwzględnego i
jednoczesności. W przypadku

systemu luźno powiązanego można korzystać co najwyżej z pojęcia oczekiwania
liniowego.

Korzystając z wyżej wprowadzonych pojęć, można teraz dokładniej określić
własności semaforów

związane z szeregowaniem uruchamiania oczekujących procesów:

Semafor ze zbiorem oczekujących jest to semafor, dla którego wybór
procesu do uruchomienia

spośród oczekujących procesów jest niedeterministyczny.

Semafor taki nazywamy też semaforem słabo uczciwym, gdyż jeżeli od
pewnego momentu stale ma

wartość dodatnią, to czas oczekiwania pod nim dla każdego procesu jest
skończony.

Semafor silnie uczciwy to semafor o własności: jeżeli operacja sygnalizuj
będzie wykonana na

semaforze nieskończenie wiele razy, to czas oczekiwania pod tym semaforem dla
każdego procesu

będzie skończony.

Semafor z kolejką oczekujących to semafor, który wstrzymywane procesy
wstawia do kolejki

prostej, a kolejne operacje sygnalizuj uruchamiają je w takiej kolejności, w jakiej
zostały wstrzymane.

Uwaga.

Każdy semafor z kolejką oczekujących jest silnie uczciwy, ale niekoniecznie na
odwrót.

Pojęcia semafora ze zbiorem oczekujących i z kolejką oczekujących są pojęciami
o charakterze

implementacyjnym, pojęcia semafora słabo uczciwego i silnie uczciwego są
pojęciami abstrakcyj-

nymi (odnoszą się do bardziej ogólnych własności).

7. KLASYCZNE PROBLEMY WSPÓŁBIEŻNOŚCI

Dwa klasyczne problemy zostały już przedstawione na poprzednim wykładzie:
problem wzajemnego

wykluczania

(mutual exclusion)

i problem producenta i konsumenta

(producer and consumer)

.

1) Problem wzajemnego wykluczania.

Przedstawione rozwiązanie zakładało istnienie implementacji semaforów w
systemie. Co więcej, dla

liczby procesów większej od 2, brak możliwości głodzenia procesów zależał od
uczciwości użytego

semafora. Obecnie przedstawimy rozwiązania nie korzystające z semaforów, a
jedynie zakładające

niepodzielność operacji podstawienia oraz operacji await.

a) Algorytm Dekkera

kto: 1..2 - zmienna wspólna do zapisu i odczytu, wskazuje, który proces ma
prawo nalegać na

wejście do sekcji krytycznej;

ki: 0..1 - zmienne wspólne do odczytu, ale prywatne do zapisu, ki = 0
wskazuje, że i - ty proces

zgłosił potrzebę wejścia do sekcji krytycznej.

{ k1 = 1, k2 = 1, kto = 1 }

while true do while true do

begin begin

niekrytyczna1;
niekrytyczna2;

k1 := 0; k2 := 0;

while k2 = 0 do

protokół

while k1

= 0 do

if kto = 2 then

wejściowy

if

kto = 1 then

begin
begin

k1 := 1;
k2 := 1;

P1: await (kto = 1); || P2 :
await (kto = 2);

k1 := 0
k2 := 0

end;
end;

krytyczna1;
krytyczna2;

k1 := 1;

protokół

k2 := 1;

kto := 2

wyjściowy

kto := 1

end end

P1
:

|| P2 :

niekrytyczna1

niekrytyczna2

krytyczna1

krytyczna
2

k1 := 0

k2 :=
0

k2 =
1 ?

k1 =
1 ?

k2 = 0
?

kto =
2 ?

k1 := 1

kto =
1 ?

k1 :=
1

kto :=
2

k1 := 0

kto = 1
?

k2 := 1

k1 =
0 ?

kto = 2 ?

kto =
1 ?

k2 := 1

kto =
2 ?

k2 := 0

kto := 1

b) Algorytm Petersona

yi : boolean - zmienne wspólne do czytania, prywatne do pisania, yi = true
oznacza, że

Pi zgłasza chęć wejścia do sekcji krytycznej;

t : boolean - zmienna wspólna do czytania i pisania („przełącznik
dwustanowy”).

{  y1   y2   t }

while true do while true do

begin begin

niekrytyczna1;
niekrytyczna2;

y1 := true; y2 := true;

P1: t := false; || P2 : t := true;

await ( y2  t );

protokół wejściowy

await ( y1  

t );

krytyczna1; krytyczna2;

y1 := false

protokół wyjściowy

y2 := false

end end

Uwaga: testowanie podwójnego warunku powinno być operacją niepodzielną (np.
na bitach 1 bajtu) !

P1:

||
P2 :

niekrytyczna1

niekrytyczna2

y1 := true

y2 := true

t := false

t := true

 y2  t ?

 y1   t ?

krytyczna1

krytyczna2

y1 := false

y2 := false

Powyższe rozwiązania nie dają się w prosty sposób uogólnić dla liczby procesów
większej, niż 2.

Rozwiązania ogólne (nie korzystające z silnie uczciwych semaforów) istnieją, ale
są skomplikowane.

Algorytm „piekarniany” potrzebuje do koordynacji zmiennych przyjmujących
dowolnie duże wartości

naturalne i ma czasochłonny protokół wejściowy (nawet przy braku rywalizacji
procesów). Lepsze

rozwiązania - Peterson 1983, Lamport 1987.

2) Problem producenta i konsumenta

Na poprzednim wykładzie były przedstawione dwa rozwiązania: z buforem
cyklicznym i semaforami,

oraz z kanałem komunikacyjnym. Problem ten ma również wersję ogólniejszą:
wielu producentów

i wielu konsumentów korzysta ze wspólnego bufora.

3) Problem czytelników i pisarzy

Problem ten jest abstrakcją problemu dostępu do wielodostępnej bazy danych.
Każdy proces aktuali-

zujący dane (pisarz) musi mieć wyłączność dostępu do danych (czytelni), ale
procesy, które tylko

czytają (czytelnicy), mogą pracować jednocześnie.

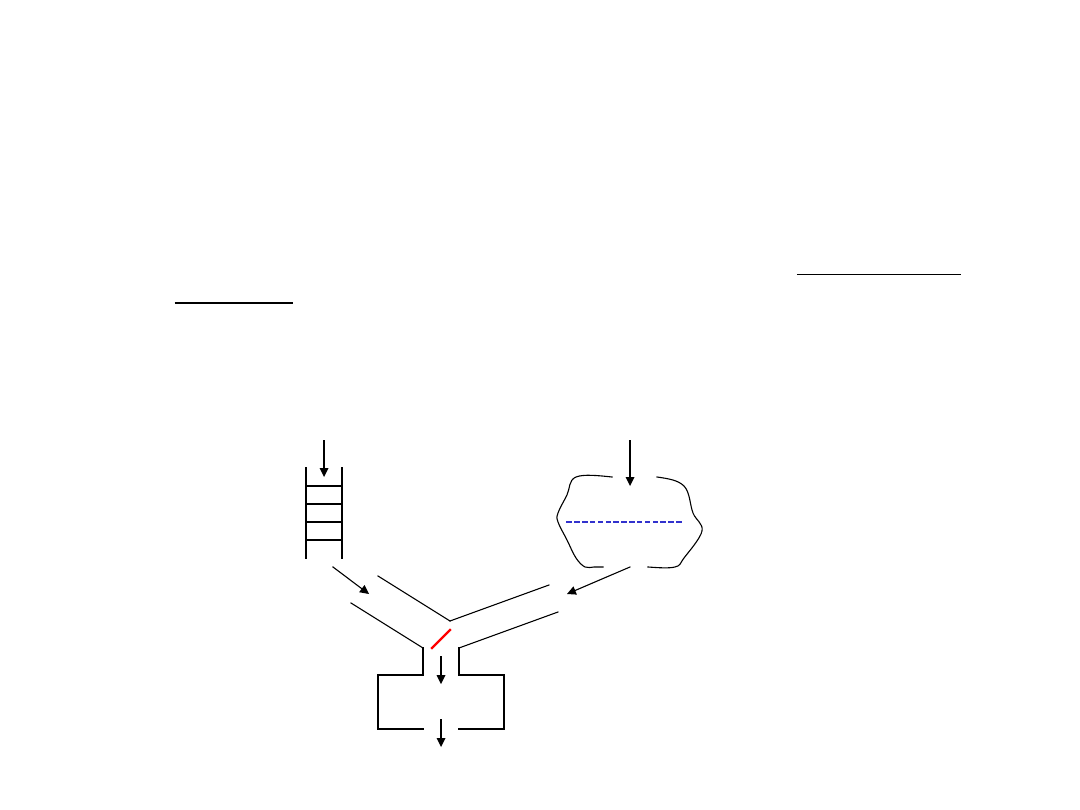
Idea rozwiązania:

(gwarantującego niemożliwość głodzenia zarówno

czytelników, jak i pisarzy)

Przybywający pisarze ustawiani są w kolejkę prostą, przybywający czytelnicy
gromadzeni są

w zbiorze. Mechanizm koordynujący wpuszcza na przemian pojedynczych
pisarzy i cały zbiór

zgromadzonych czytelników. Wpuszczenie może mieć miejsce dopiero po
opuszczeniu czytelni

przez poprzednich użytkowników / użytkownika. Jeżeli kolejka oczekujących
pisarzy jest pusta,

a w czytelni przebywają czytelnicy, każdy nowo przybyły czytelnik jest od razu
wpuszczany.

Jeśli w zbiorze nie oczekują żadni czytelnicy, kolejno przybywający pisarze są
wpuszczani po

zakończeniu pobytu w czytelni przez poprzednika.

Najprostsze rozwiązanie - przy użyciu monitora.

kolejka pisarzy

zbiór
czytelników

czytelnia

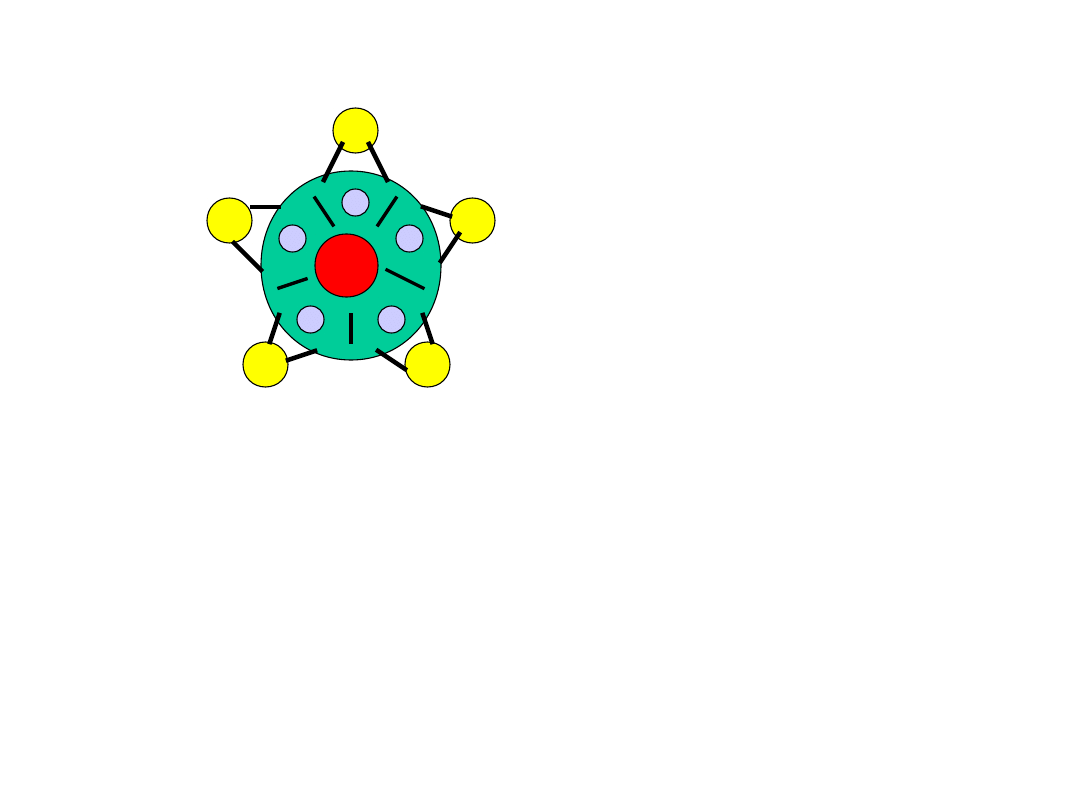
4) Problem ucztujących filozofów

n =

5

Założenia:

a) każdy filozof może przebywać w dwóch stanach:

myślenie

i

jedzenie

;

b) każdy widelec jest zasobem współdzielonym przez dwóch sąsiadów na
zasadzie wyłączności

dostępu;

c) do jedzenia potrzebne są dwa widelce;

d) widelce muszą być brane sekwencyjnie (nie jednocześnie) przez jednego
filozofa;

e) czasy przebywania w stanach

myślenie

i

jedzenie

są zawsze skończone.

F
0

F1

F2

F3

F4

w1

w2

w3

w4

w0

Rozwiązanie symetryczne może doprowadzić do blokady (na przykład wszyscy
filozofowie mogą

jednocześnie podnieść lewe widelce). Rozwiązanie, które nie doprowadzi do
blokady ani do gło-

dzenia jednego z filozofów, musi „psuć” symetrię.

a) Rozwiązanie z ograniczaniem liczby „aktywnych” filozofów do n-1:

jadalnia: semafor = 4;

widelec: array [0..4] of semafor = 1;

while true do

{program i-tego filozofa}

begin

myślenie;

czekaj(jadalnia);

czekaj(widelec[i] );

czekaj(widelec[(i+1) mod 5] );

jedzenie;

sygnalizuj(widelec[i] );

sygnalizuj(widelec[(i+1) mod 5] );

sygnalizuj(jadalnia)

end

b) Rozwiązanie ze zróżnicowaniem programów filozofów:

i = 0, ..., 3 i = 4

widelec : array [0..4] of semafor = 1;

while true do while true do

begin begin

myślenie; myślenie;

czekaj(widelec[i] ); czekaj(widelec[0] );

czekaj(widelec[i+1] ); czekaj(widelec[4] );

jedzenie; jedzenie;

sygnalizuj(widelec[i] ); sygnalizuj(widelec[4] );

sygnalizuj(widelec[i+1] ) sygnalizuj(widelec[0] )

end end

Oba powyższe rozwiązania wykluczają zarówno możliwość blokady, jak i
indywidualnego głodzenia.