ENERGIA

MECHANICZNA

Ważne jest by nigdy nie przestać pytać. Ciekawość nie istnieje bez przyczyny.

Wystarczy więc, jeśli spróbujemy zrozumieć choć trochę tej tajemnicy każdego dnia.

Nigdy nie trać świętej ciekawości. Kto nie potrafi pytać nie potrafi żyć.

Albert Einstein

Czym jest energia

mechaniczna?

• Aby samochód mógł poruszać się, w

jego silniku musi być spalana benzyna.

• Skrzydła wiatraka poruszają się tylko

pod wpływem wiatru.

• Człowiek jest zdolny do życia i pracy

tylko wtedy, gdy jego organizm

otrzymuje odpowiednie ilości

pożywienia.

O człowieku, który może wykonać dużą

pracę mówimy, że ma dużo energii.

Jednak zanim zastanowimy się czy

to stwierdzenie jest słuszne

musimy przypomnieć sobie kilka

pojęć:

Układem ciał nazywamy układ w którym dwa

lub więcej ciał oddziałuje ze sobą.

Siły wzajemnego oddziaływania na siebie

ciał tworzących układ są siłami

wewnętrznymi układu.

Siły pochodzące spoza układu nazywamy

siłami zewnętrznymi.

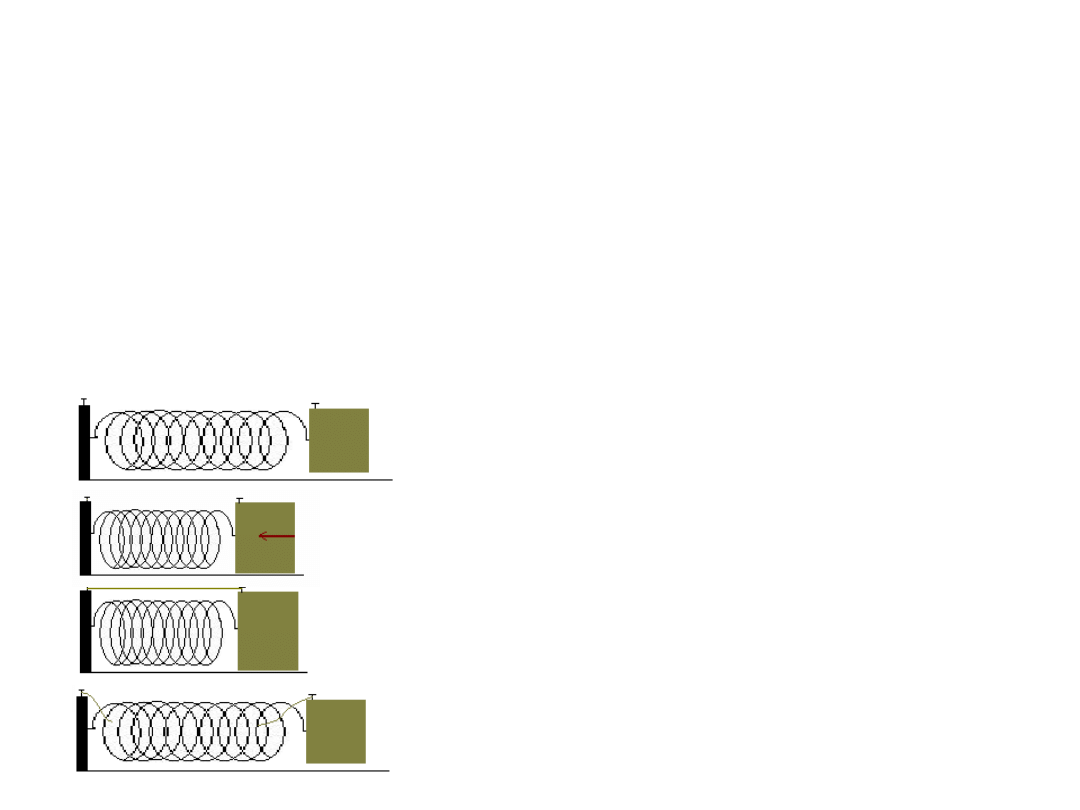
Przykłady układów ciał

wzajemnie oddziałujących.

Układ klocek – luźna sprężyna nie jest w stanie
wykonać pracy.

F



Siła zewnętrzna wykonuje pracę, ściskając
sprężynę i przesuwając klocek.

Sprężyna jest zdolna do wykonania pracy.

Sprężyna wykonała pracę,
przesuwając klocek do początkowego położenia

• Przykład1
Ściśnięta sprężyna i klocek stanowią układ dwóch

ciał, które działają na siebie siłami sprężystości.

Przykłady układów ciał

wzajemnie oddziałujących.

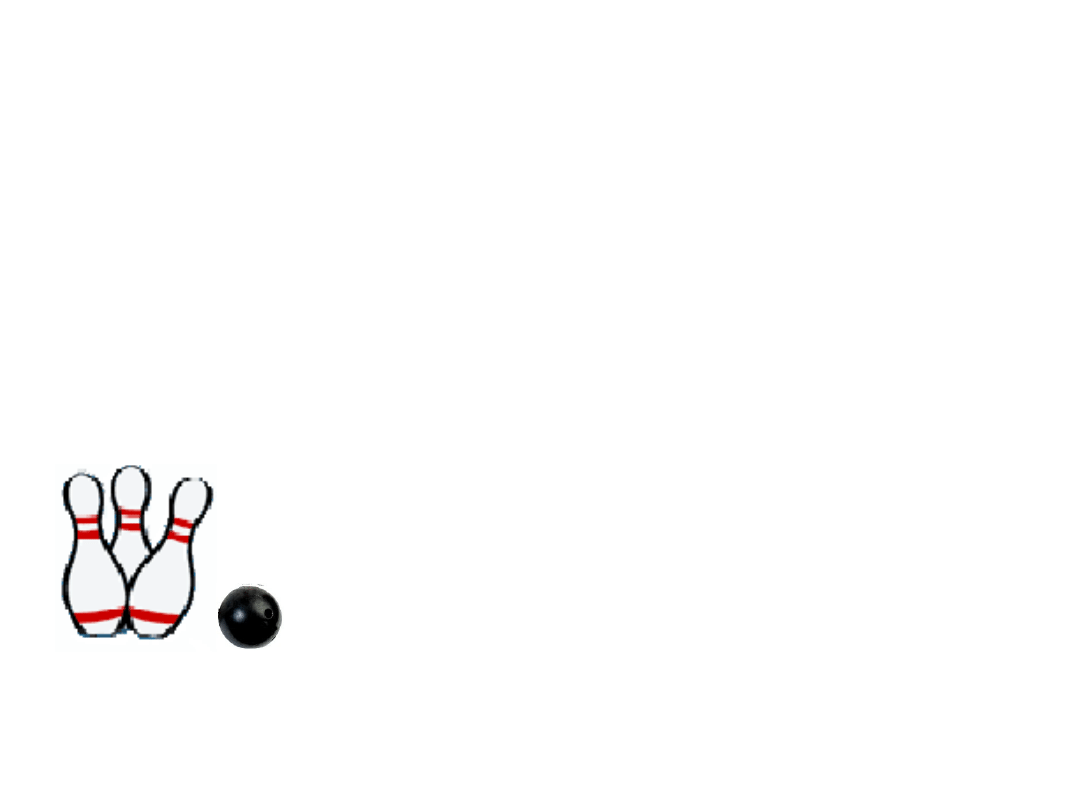
• Przykład 2
Gdy wprawimy w ruch kule ona uderzy w kręgle i je przewróci.
My wykonaliśmy nad kulą pracę, a poruszająca się kula ma energię.

Kula, uderzając w kręgle, przewraca je
wykonując nad nimi pracę.

Kula zatrzymując się, traci energię.

Czym jest energia

mechaniczna?

• O układzie ciał który jest zdolny do

wykonania pracy mówimy, że

posiada energię mechaniczną.

Kiedy zmienia się energia

mechaniczna?

Im większa praca zostanie wykonana

przez siły zewnętrzne, tym większą

energię będzie posiadał układ ciał i

tym większą pracę będzie on mógł

wykonać, wracając do poprzedniego

stanu.

Czemu jest równa energia

mechaniczna?

• Przyrost energii mechanicznej układu ΔE
jest równy pracy sił zewnętrznych

wykonanej nad tym układem:

ΔE=W

Z

• Jednostką energii jest 1J (1dżul)

Podział energii

mechanicznej

Energia mechaniczna

Energia kinetyczna

Energia potencjalna

* Jednostka energii mechanicznej (energii potencjalnej i energii kinetycznej) jest 1 J (dżul)

Energia potencjalna

• Energię taką posiada ciało, które

oddziałuje z innym ciałem siłami

grawitacyjnymi

(energia potencjalna grawitacji)

lub siłami sprężystości

(energia potencjalna

sprężystości).

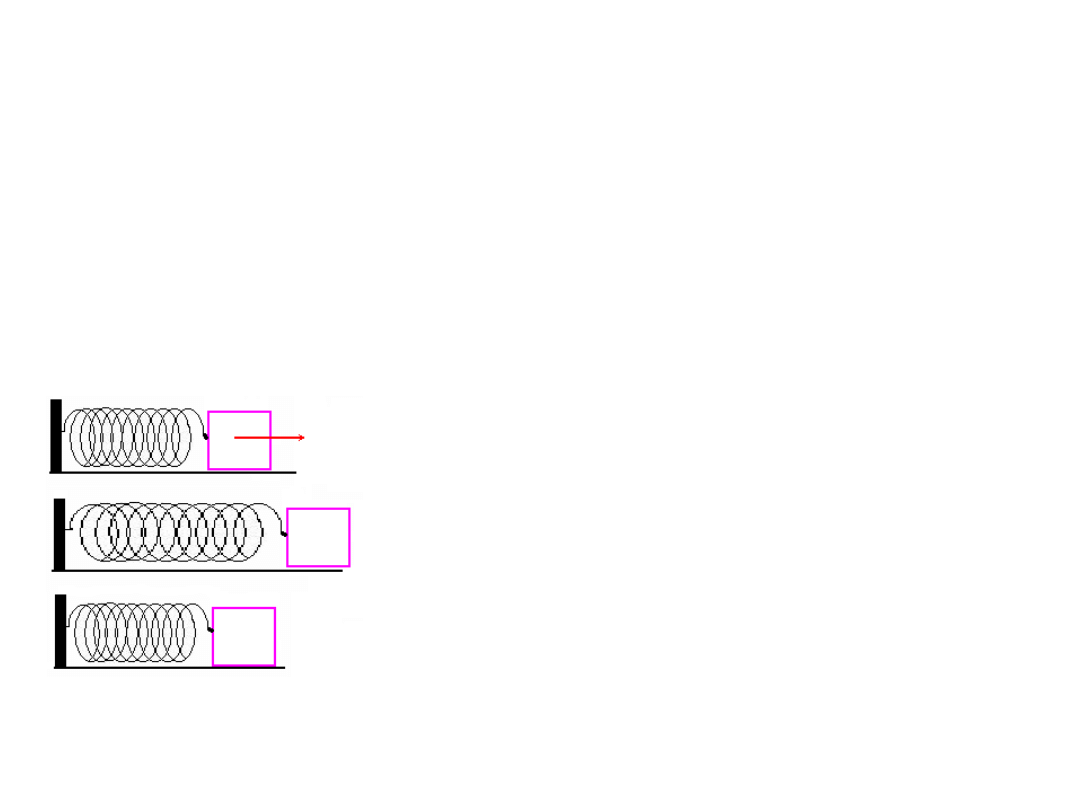
Przykład 1:

• Rozciągając lub ściskając sprężynę, siły zewnętrzne

wykonują nad nią pracę, w wyniku czego uzyskuje
ona energię potencjalną sprężystości.

F



Wykonanie pracy nad sprężyną (rozciągamy ją).

Podczas powrotu sprężyny do stanu początkowego
może ona wykonać pracę kosztem energii
potencjalnej sprężystości.

W tym przypadku sprężyna ma największą
energię potencjalną

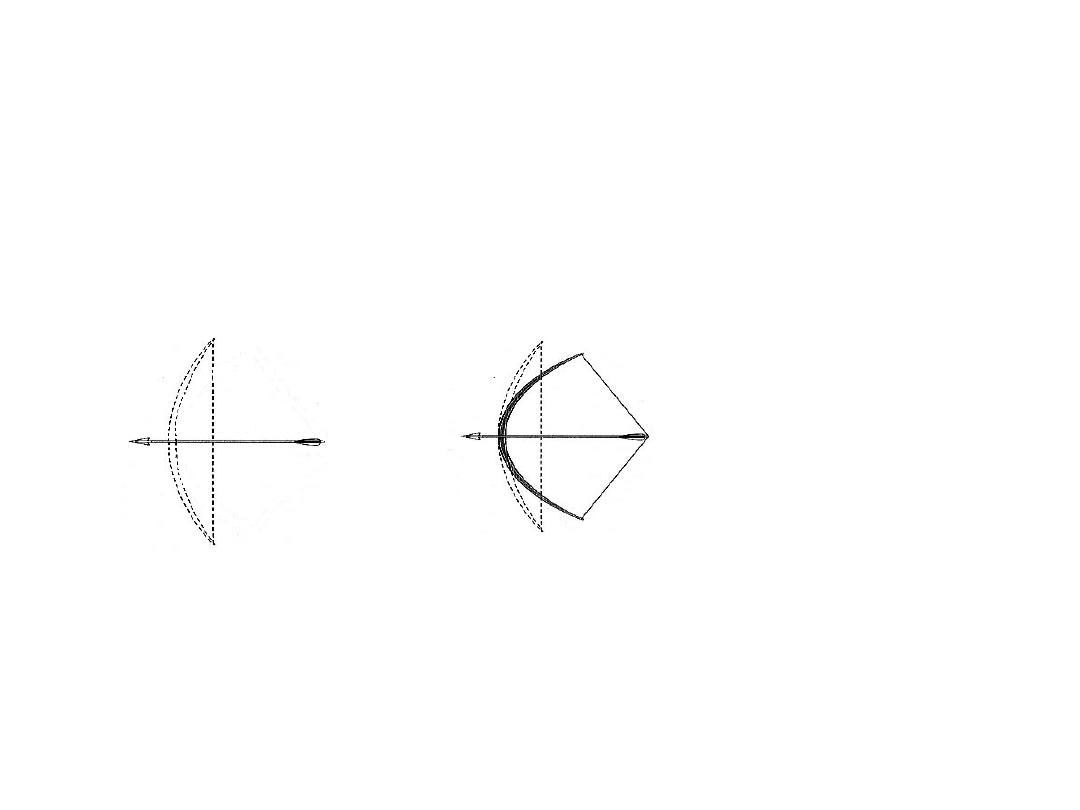
Przykład 2:

• Energię potencjalną sprężystości posiada również

naciągnięty łuk.

W tej sytuacji, gdy nie
naciągniemy cięciwy, łuk
nie posiada energii
potencjalnej sprężystości.

Gdy natomiast wykonamy pracę
i napniemy łuk – cięciwa posiada energię
potencjalną sprężystości. Puśćmy teraz
cięciwę – wraca ona do swojego
poprzedniego stanu.

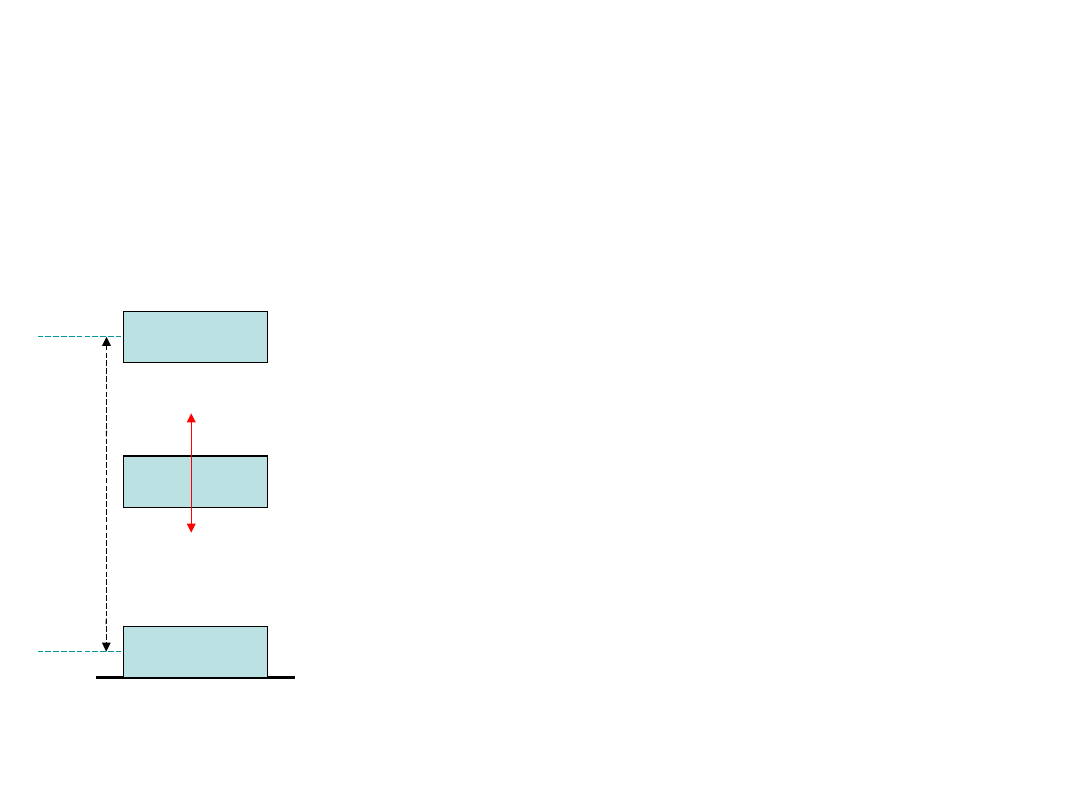
Przykład 3:

• Podnosimy klocek ruchem jednostajnym o masie m na wysokość h.

g

F



h

F



Stan 1

Stan 2

2

p

E

1

p

E

Przez E

p1

oznaczamy energię potencjalną w stanie 1,

natomiast E

p2

energię potencjalną w stanie 2.

Wykonanie pracy W

z

przez siłę zewnętrzną

powoduje wzrost energii potencjalnej
od E

p1

do E

p2

:

W

z

=E

p2

-E

p1

Jak już wiecie pracę tę możemy obliczyć za
pomocą wzoru: W

z

=F h.

Ponieważ ciało podnosimy ruchem jednostajnym,
to wartość siły F jest równa wartości siły jaką Ziemia
przyciąga ciało:
W

z

=F h = m g h

Zatem: E

p2

-E

p1

=m g h

Jeżeli założymy, że na powierzchni Ziemi energia
Potencjalna jest równa zero, to powyższy wzór przyjmie postać:
E

p2

=m g h

F



Wzór na energię

potencjalną grawitacji

• Na wysokości h nad tzw. poziomem

„zerowym” ciało o masie m posiada
energię potencjalną grawitacji równą:

E

p

=mgh

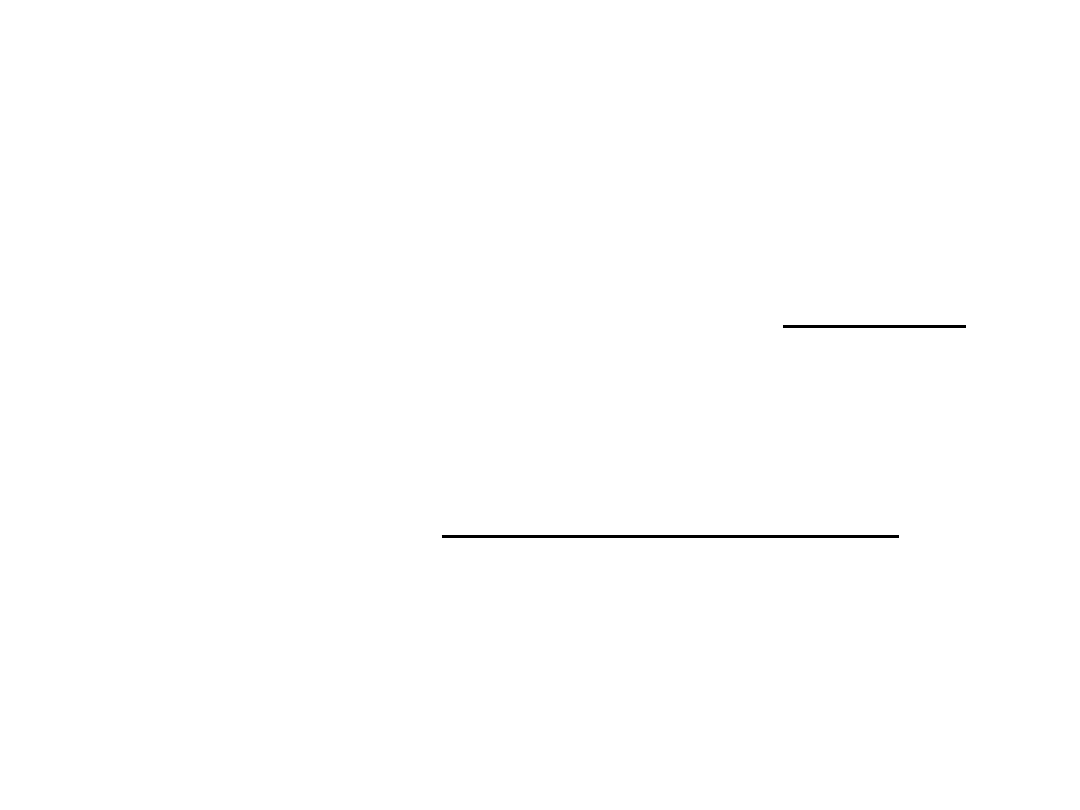
Energia kinetyczna

• Energia ta związana jest z ruchem.

Każde ciało, które w danym układzie

odniesienia jest w ruchu, to mówimy

że posiada energię kinetyczną.

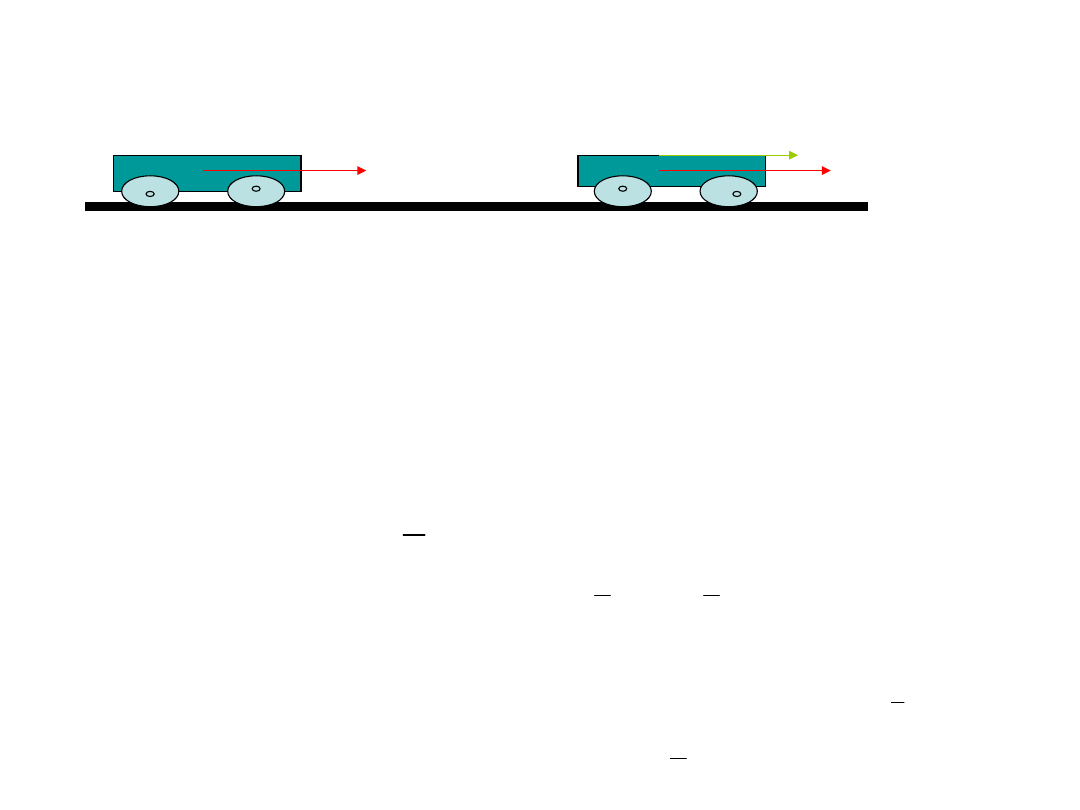
Przykład

• Rozpatrzmy następujący przypadek:

stan1

stan2

0



v



v



F



F



Pod wpływem stałej wypadkowej siły wózek (zgodnie z II zasadą
dynamiki) będzie poruszał się ruchem jednostajnym przyspieszonym o
przyspieszeniu .
Po pewnym czasie t wózek uzyskał energię kinetyczną E

k2

. Przyrost

energii kinetycznej wózka E

k2

-E

k1

równy jest pracy wykonanej przez siłę

wypadkową :

Ponieważ oraz , to przyrost energii kinetycznej
wynosi:

Gdy uwzględnimy fakt, iż szybkość chwilowa po czasie t w ruchu
jednostajnie

przyspieszonym (gdy v

o

=0), równa jest otrzymujemy:

Gdy E

k1

=0 powyższy wzór przyjmie postać:

Na gładkiej powierzchni stołu znajduje się wózek o masie m.
Początkowo jest on w spoczynku (stan1) względem układu odniesienia
jakim jest stół, a zatem jego energia kinetyczna E

k1

równa jest zero.

F



a



F



2

2

1

2

)

(

2

1

2

1

)

(

t

a

m

t

a

a

m

s

F

W

E

E

E

k

k







































a

m

F





2

2

1

t

a

s





t

a

v





2

1

2

2

1

v

m

E

E

k

k







2

2

2

1

v

m

E

k





Wzór na energię kinetyczną

•

Ciało o masie m poruszające się w danym

układzie odniesienia z szybkością v posiada w

tym układzie energie kinetyczna równą:

•

E

k

= mv

2

2

1

ZASADA ZACHOWANIA ENERGII

•

Na co dzień obserwujemy przemianę jednego
rodzaju energii mechanicznej na drugi. Na
przykład energii potencjalnej na kinetyczną w
następującym przypadku:

1. Napięty łuk ma energię potencjalną

sprężystości, ale po wypuszczeniu cięciwy
przekształca się na energię kinetyczną łuku.

2. Jabłko wiszące na gałęzi jabłoni posiada energię

potencjalną grawitacji, kiedy się zerwie i zacznie
spadać energia potencjalna będzie zmieniać się
na energię kinetyczną.

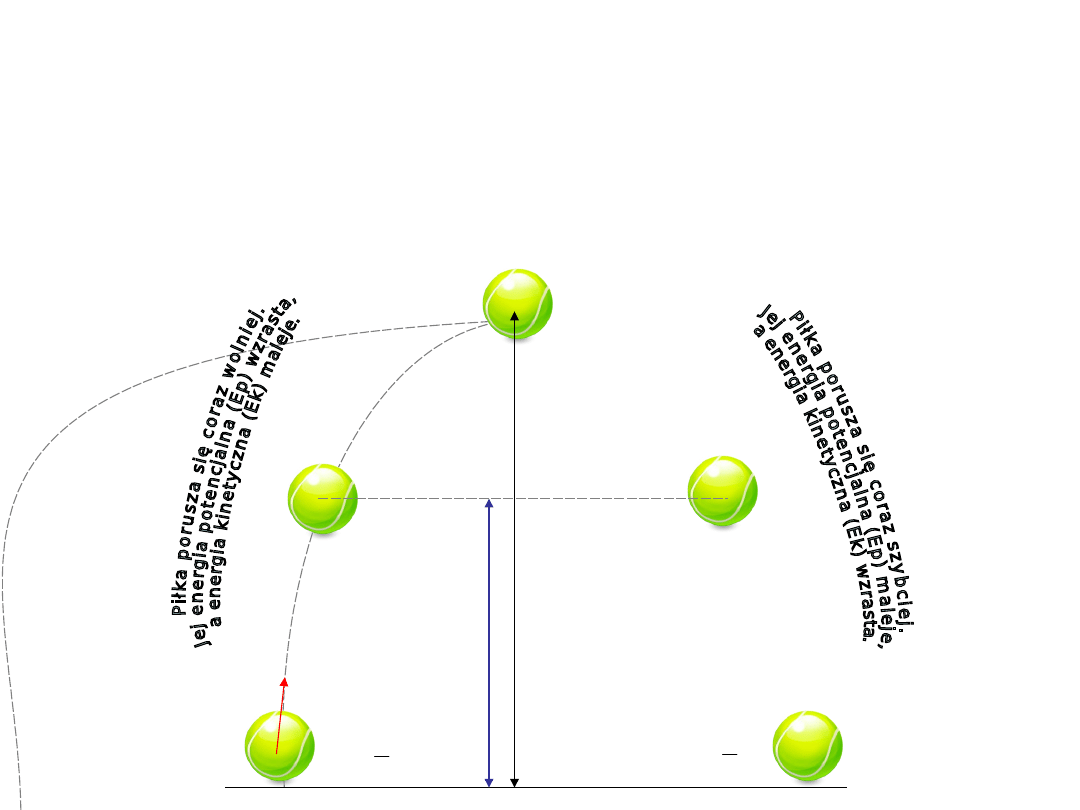
Zasada zachowania energii

• Rozpatrzmy jak w kolejnych etapach wznoszenia i opadania

piłki zmienia się energia kinetyczna i potencjalna ciała (na

wysokości piłeczki podane są wartości danej energii).

h

½ h

2

2

1

0

v

m

E

E

k

p







k

p

E

E 

k

p

E

E 

0









k

p

E

h

g

m

E

0

v

2

2

1

0

v

m

E

E

k

p







Zasada zachowania energii

mechanicznej

Jeśli przemiany energii mechanicznej

zachodzą wewnątrz układu ciał, to
całkowita energia mechaniczna (suma
energii potencjalnej i kinetycznej)
układu jest zachowana – nie zmienia się.

* Zasadę zachowania energii mechanicznej wolno stosować tylko wtedy, gdy możemy pominąć siły tarcia i inne opory ruchu.

ZADANIA

1.Oblicz energię kinetyczną rowerzysty

o masie 50kg jadącego z prędkością 10
.

s

m

s

m

v

kg

m

10

50





k

E

Dane: Szukane:
Rozwiązanie:

J

E

s

m

kg

E

s

m

kg

E

v

m

E

k

k

k

k

2500

100

25

10

50

2

1

2

1

2

2

2

2



























Odpowiedź: Rowerzysta jadąc z prędkością 10 posiadał energię kinetyczną
równą 2500J.

s

m

Wyznaczamy energię kinetyczną:

2.Oblicz energię kinetyczną piłki o masie 0,5kg
poruszającej się z prędkością 4 . Jaka siłą musi
działać bramkarz, by zatrzymać tę piłkę na
odległości 0,5m?

s

m

m

s

s

m

v

kg

m

5

,

0

4

5

,

0







F

E

k

,

Dane: Szukane:
Rozwiązanie:

J

s

m

kg

v

m

E

k

4

4

5

,

0

2

1

2

1

2

2























N

m

J

s

E

F

s

s

F

E

s

F

W

E

8

5

,

0

4

:

//

















Odp: Bramkarz musi działać siłą 8N, aby zatrzymać piłkę o energii kinetycznej 4J.

Aby wyznaczyć siłę z jaka bramkarz
zatrzyma piłkę musimy wykorzystać
fakt iż energia mechaniczna równa jest
wykonanej pracy:

Wyznaczamy energię kinetyczną:

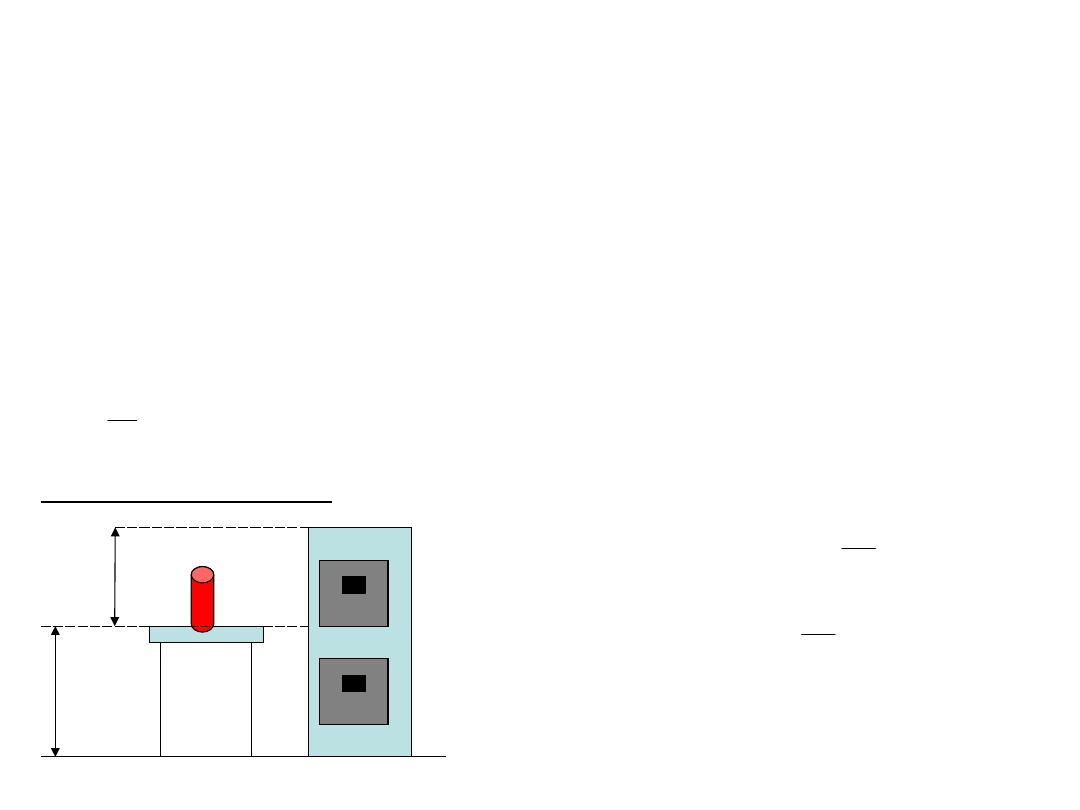
Jaką energię potencjalną ma wazon o masie

0,7kg podniesiony ze stołu o wysokości 1m

na segment.

Szafka segmentu znajduje się na wysokości

0,8m nad poziomem stołu.

2

2

1

10

8

,

1

1

7

,

0

s

m

g

m

h

m

h

kg

m









p

E

J

E

m

s

m

kg

E

m

m

s

m

kg

E

h

h

g

m

E

h

h

h

h

g

m

E

p

p

p

p

p

126

8

,

1

70

)

8

,

0

1

(

10

7

,

0

)

(

2

2

2

1

2

1



































Dane: Szukane:
Rozwiązanie:

Rysunek pomocniczy:

1

h

2

h

Odp: Wazon ma energię potencjalną równą 126J

Wysokość na jakiej będzie wazon to:

Energię potencjalną wyznaczymy ze wzoru:

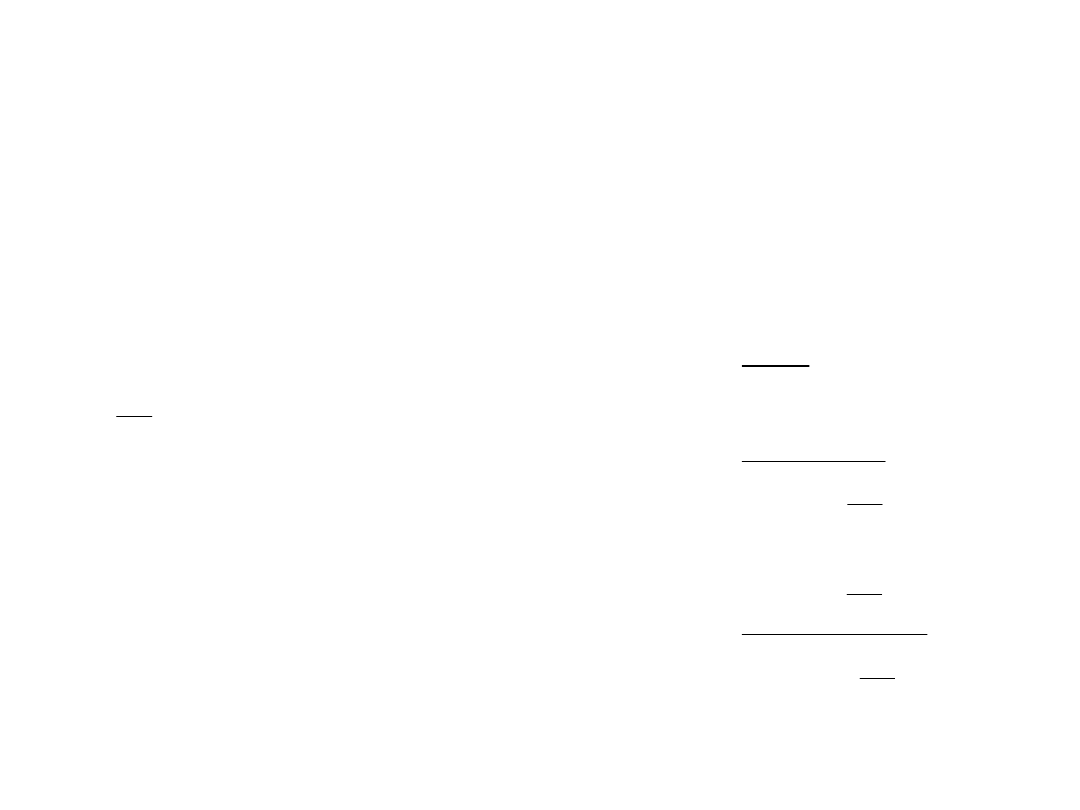
Na jakiej wysokości znajduje się ciało o

masie 2kg, jeżeli jego energia potencjalna

wynosi 0,4kJ.

2

10

400

4

,

0

2

s

m

g

J

kJ

E

kg

m

p









h

Dane: Szukane:
Rozwiązanie:

m

h

s

m

kg

m

s

m

kg

h

s

m

kg

J

h

g

m

E

h

g

m

h

g

m

E

p

p

20

20

400

10

2

400

)

(

:

//

2

2

2



























Odp: Ciało o masie 2kg znajduje się
na wysokości 20m.

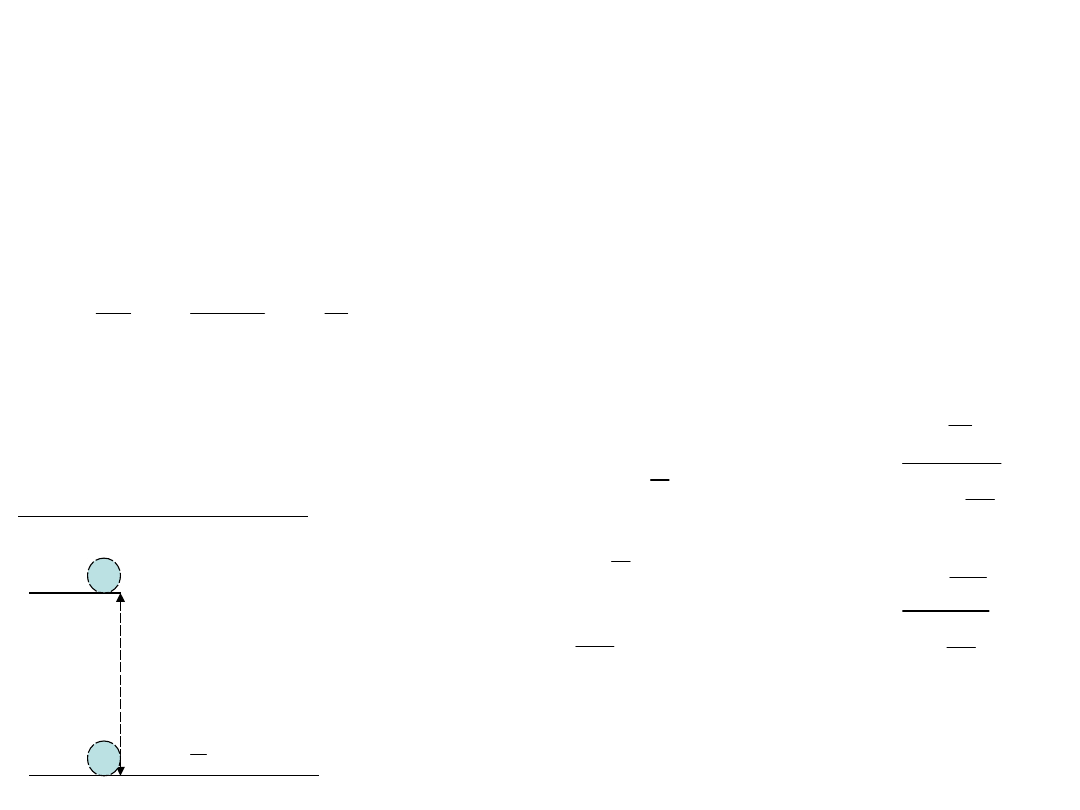
Z jakiej wysokości trzeba zrzucić piłkę, aby

osiągnęła prędkość 72 km/h w chwili

uderzenia o ziemię?

Dane:
Rozwiązanie:

s

m

s

m

h

km

v

20

3600

1000

72

72







h

Rysunek pomocniczy:

2

2

1

v

m

E

h

g

m

E

k

p











h

Zgodnie z zasadą zachowania energii
mechanicznej : energia potencjalna jest
równa energii kinetycznej.

g

v

h

g

v

h

g

m

v

m

h

g

m

E

E

k

p

2

:

//

2

1

:

//

2

1

2

2

2

















m

h

s

m

s

m

h

s

m

s

m

h

20

20

400

10

2

20

2

2

2

2

2





















Szukane:

Odp: Piłkę należy zrzucić z wysokości 20m.

Jaka prędkość końcową osiągnie ciało

spadające z wysokości h=20m? .

2

10

20

s

m

g

m

h





v

Dane: Szukane:
Rozwiązanie:

g

h

v

g

h

v

m

g

h

m

v

m

v

m

g

h

m

E

E

k

p

























2

2

2

2

:

//

2

1

2

2

2

Odp: Ciało spadające z wysokości 20m
osiągnie prędkość 20m/s.

Z zasady zachowania energii wynika, że
energia potencjalna ciała w chwili wyrzucenia
jest równa co do wartości energii kinetycznej,
jaka osiągnie ciało w momencie uderzenia o ziemię

s

m

v

s

m

v

s

m

m

v

20

400

10

20

2

2

2

2









