Teoria Sterowania

Teoria Sterowania

Teoria Sterowania

Teoria Sterowania

Przy badaniu złożonych układów starowania pożyteczne jest
budowanie schematów blokowych (strukturalnych), które
ilustrują zależności funkcjonalne i przepływ sygnałów
pomiędzy blokami składowymi, które mają proste
właściwości przetwarzania sygnałów (są często
podstawowymi członami dynamicznymi).

Teoria Sterowania

Teoria Sterowania

Połączenia członów podstawowych

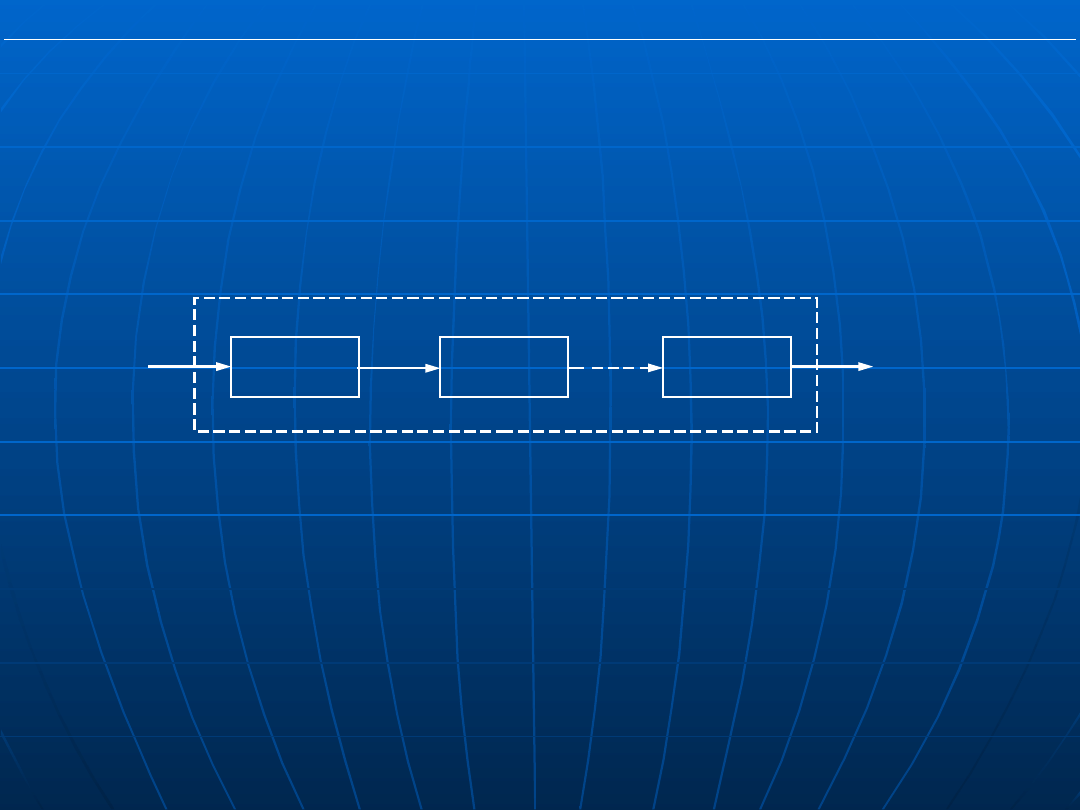
1) połączenie szeregowe

( )

( )

( )

( )

( )

1

2

1

n

n

i

i

G s

G s G s

G s

G s

=

=

�

� �

=

�

K

Rys. Połączenie szeregowe (kaskadowe)

Transmitancja zastępcza połączenia
szeregowego:

G

1

(s)

G

2

(s)

G

n

(s)

G(s)

U(s)

Y(s)

Teoria Sterowania

Teoria Sterowania

2) połączenie równoległe

( )

( )

( )

( )

( )

1

2

1

n

n

i

i

G s

G s G s

G s

G s

=

=

+

+ +

=

�

K

Rys. Połączenie równoległe

(alternatywne oznaczenie węzła sumującego)

G(s)

G

1

(s)

G

2

(s)

G

n

(s)

∑

U(s)

Y(s)

Transmitancja zastępcza połączenia
równoległego:

Teoria Sterowania

Teoria Sterowania

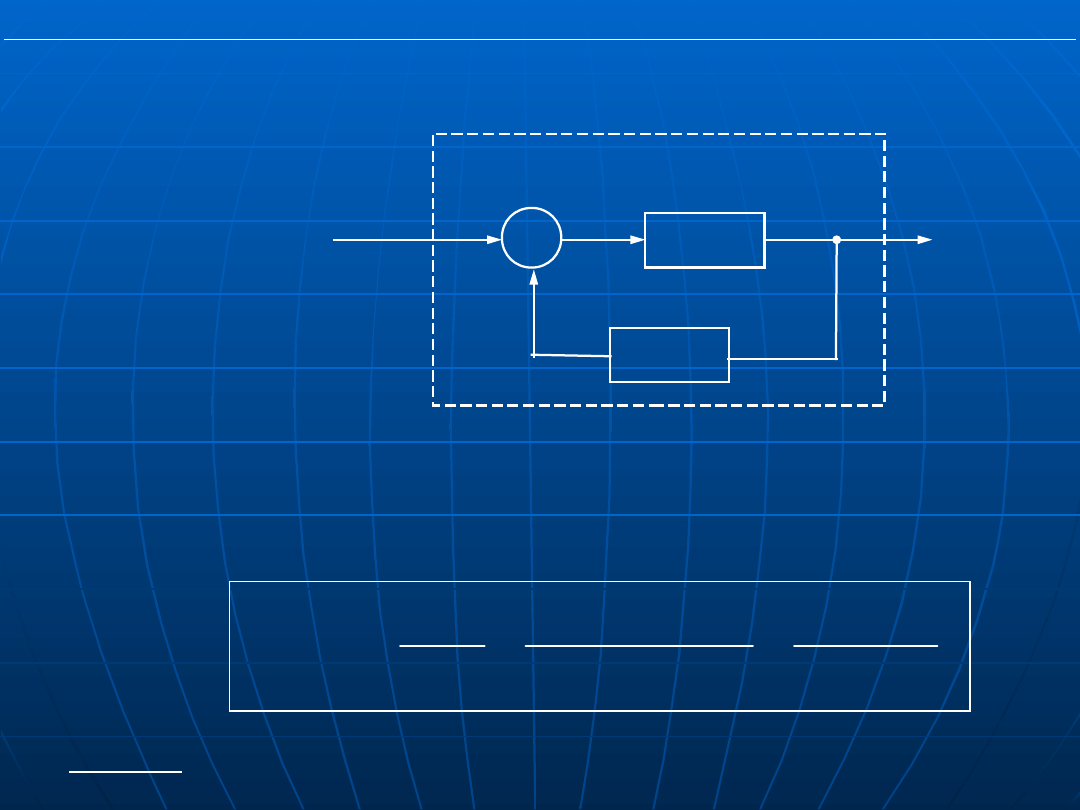
3) połączenie
ze sprzężeniem zwrotnym

Połączenie ze sprzężeniem zwrotnym: (-) ujemnym,

(+)

dodatnim

G(s)

∑

G

z

(s)

U(s)

Y(s)

E(s)

±

H(s)

( )

( )

( )

( )

( )

( )

( )

1

( ) 1

z

o

Y s

G s

G s

G s

U s

G s H s

G s

=

=

=

�

m

m

Transmitancja zastępcza G

z

(s) układu zamkniętego ze sprężeniem

zwrotnym:

Uwaga: (+) we wzorze dla sprzężenia ujemnego, (-) dla
dodatniego

Teoria Sterowania

Teoria Sterowania

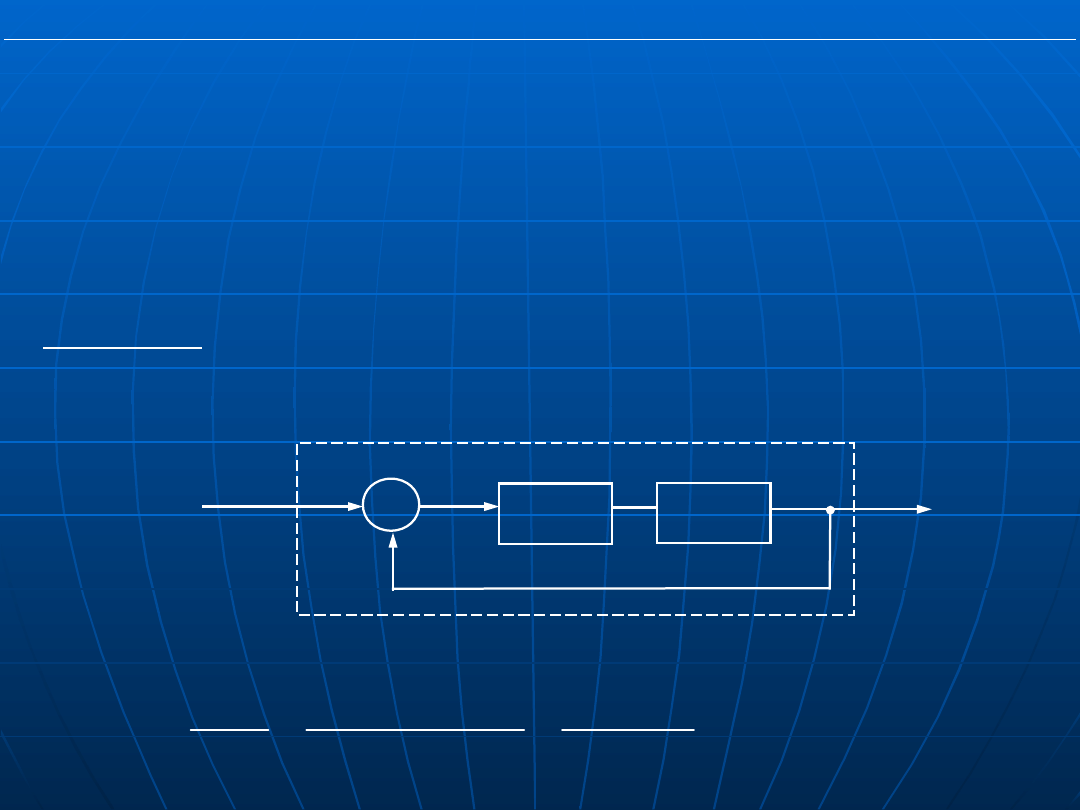
Przykład: Wyznaczyć transmitancję zastępczą układu z pełnym
(sztywnym) sprzężeniem zwrotnym (H(s)=1)

Y(s)

G

1

(s)

∑

G

z

(s)

U(s)

_

G

2

(s)

Odpowied
ź:

( )

( )

( ) ( )

( ) ( )

( )

( )

1

2

1

2

( )

1

1

o

z

o

Y s

G s G s

G s

G s

U s

G s G s

G s

=

=

=

+

+

gdzie G

o

(s)= G

1

(s)G

2

(s)

Określenia:
G(s) – transmitancja toru głównego
H(s) – transmitancja toru sprzężenia zwrotnego
G

o

(s)= G(s)H(s) – transmitancja układu otwartego (przy

przerwanej pętli sprzężenia)

Teoria Sterowania

Teoria Sterowania

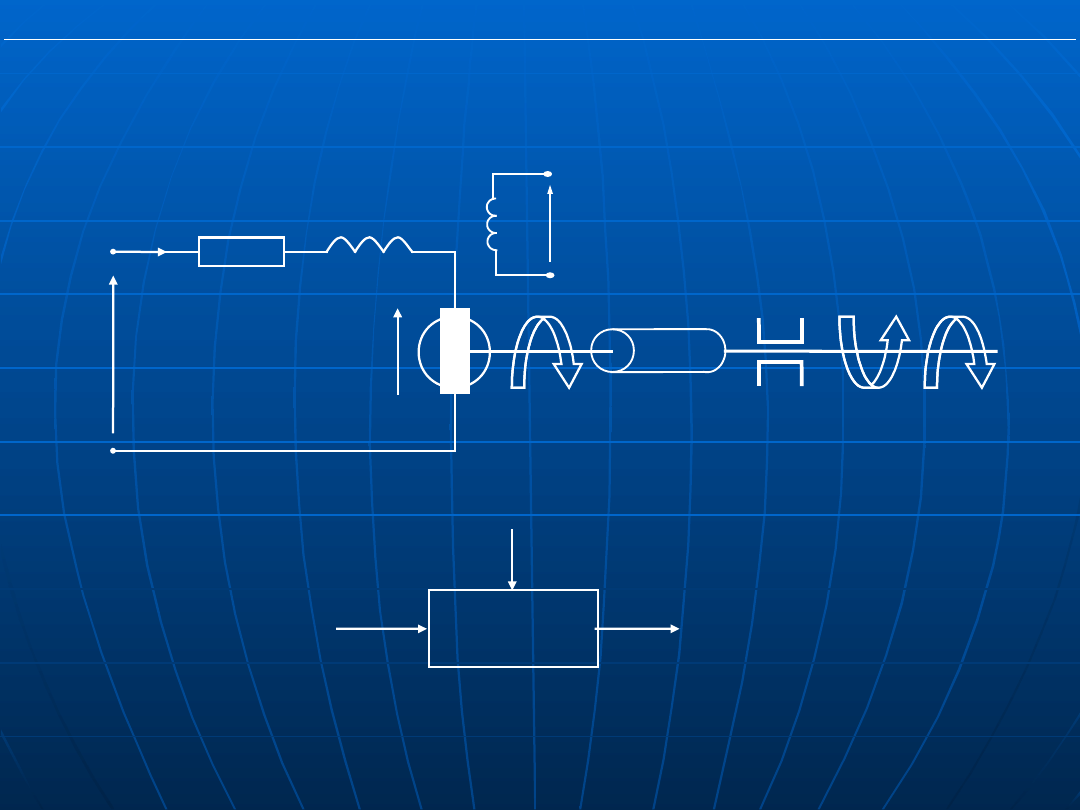
Rys. Schemat zastępczy obwodu twornika silnika prądu

stałego

b) blok wejście-wyjście-zakłócenie

Przykład: budowa schematu blokowego
obcowzbudnego silnika DC

SEM

e

R

t

L

t

i

t

u

M

e

J

B

ω

M

obc

b)

u

t

ω

z(t) = M

obc

a)

u

w

=const



Teoria Sterowania

Teoria Sterowania

Wielkości na schemacie:
u

t

– napięcie zasilające twornika (sygnał wejściowy),

i

t

– prąd twornika,

R

t

– rezystancja zastępcza uzwojeń twornika,

L

t

– indukcyjność zastępcza uzwojeń twornika,

e – siła elektromotoryczna indukcji,
ω – prędkość kątowa wirnika (sygnał wyjściowy),
 - strumień magnetyczny wzbudzenia (const)

M

e

– moment elektryczny (napędowy) silnika,

B – tarcie lepkie wału silnika,
J – moment bezwładności wału silnika,
M

obc

– moment obciążenia silnika (sygnał zakłócenia).

Teoria Sterowania

Teoria Sterowania

Równanie elektryczne wirnika silnika:

t

t t

t

di

u Ri L

e

dt

=

+

+

SEM indukcji jest proporcjonalna do prędkości kątowej wirnika

e

e kw

=

gdzie k

e

– stała elektryczna (zależna m.in. od strumienia

magnetycznego stojana oraz liczby zwojów w uzwojeniu wirnika).
Po podstawieniu otrzymujemy:

.

t

t t

t

e

di

u Ri L

k

dt

w

=

+

+

Teoria Sterowania

Teoria Sterowania

Mechaniczne równanie momentów wywołujących ruch
obrotowy:

e

B

obc

d

J

M

M

M

dt

w

=

-

-

Zakładając, że strumień magnetyczny stojana (wzbudzenia) jest
stały, można przyjąć że moment obrotowy wirnika jest
proporcjonalny do prądu i

t

:

e

m t

M

k i

=

gdzie k

m

– stała mechaniczna (zależna m.in. od strumienia

magnetycznego stojana oraz liczby zwojów w uzwojeniach
wirnika).

Moment związany z oporami ruchu wirnika można zapisać jako

B

M

Bw

=

Po podstawieniu:

m t

obc

d

J

k i B

M

dt

w

w

=

-

-

Teoria Sterowania

Teoria Sterowania

Przekształcając równanie elektryczne:

1

(

)

1

(

)

t

t

t

e

t

t

t

e

t

e

t

L di

i

u k

R dt

R

di

T

i

u k

dt

R

w

w

+ =

-

+ =

-

W formie operatorowej z transmitancją członu inercyjnego:

1

( )(

1)

[ ( )

( )]

1/

( )

[ ( )

( )]

1

t

e

e

t

t

t

e

e

I s T s

U s k

s

R

R

I s

U s k

s

T s

+ =

- W

=

- W

+

T

e

- elektromagnetyczna stała czasowa, 1/R

t

– współczynnik

wzmocnienia

Teoria Sterowania

Teoria Sterowania

Przekształcając równanie mechaniczne (podejście inne niż
poprzednio):

W formie operatorowej z transmitancją członu całkującego:

1

(

)

m t

obc

d

k i B

M

dt

J

w

w

=

-

-

1

( )

[

( )

( )

( )]

1

( )

[

( )

( )

( )]

m t

obc

m t

obc

s s

k I s B s M

s

J

s

k I s B s M

s

Js

W =

- W -

W =

- W -

W formie operatorowej z transmitancją członu inercyjnego:

1

1

(

)

( )

1

[

( )

( )]

1/

( )

[

( )

( )], gdzie

1

m t

obc

m t

obc

m t

obc

m

m

J d

J

k i M

s

s

k I s M

s

B dt

B

B

B

B

J

s

k I s M

s

T

T s

B

w

w

�

�

+ =

-

� W

+ =

-

�

�

�

�

W =

-

=

+

-mechaniczna
stała
czasowa

Teoria Sterowania

Teoria Sterowania

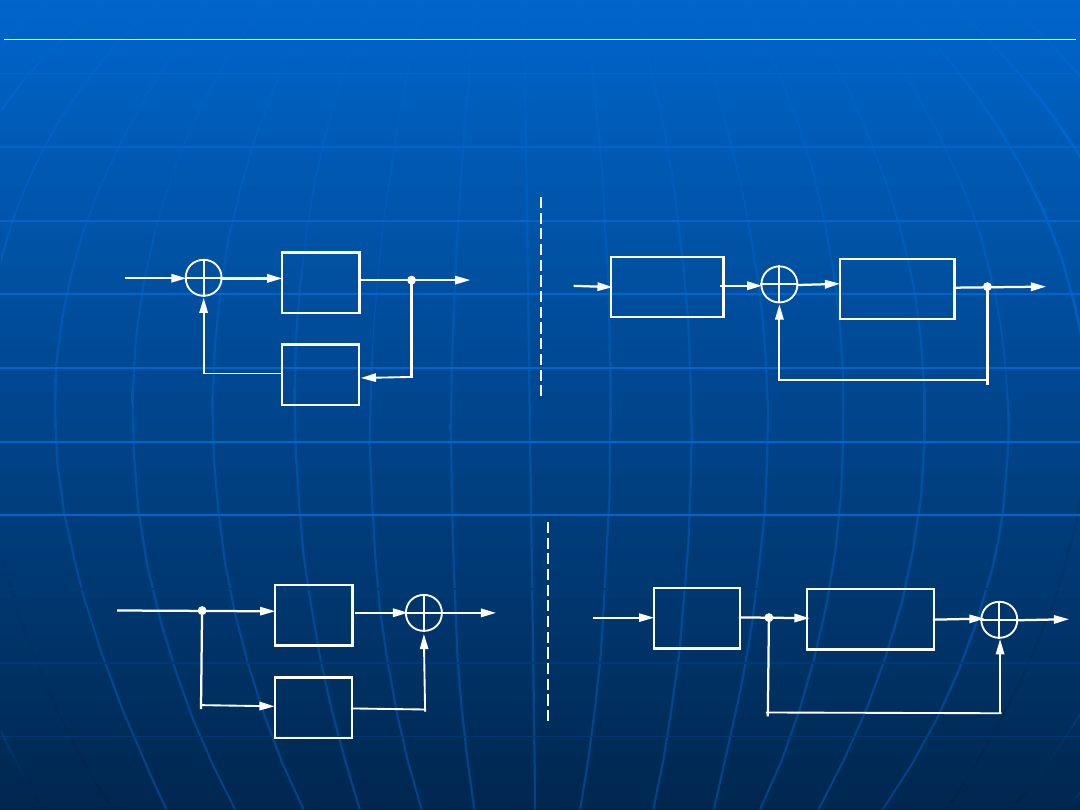
Zmiana sprzężenia zwrotnego niepełnego w
pełne

G

1

U

Y

Reguły przekształcania schematów

blokowych

Wydzielenie członu z gałęzi równoległej

G

2



U

G

1

G

2

Y

1/G

2



G

1

U

Y

G

2



U

G

1

/G

2

Y

G

2



Teoria Sterowania

Teoria Sterowania

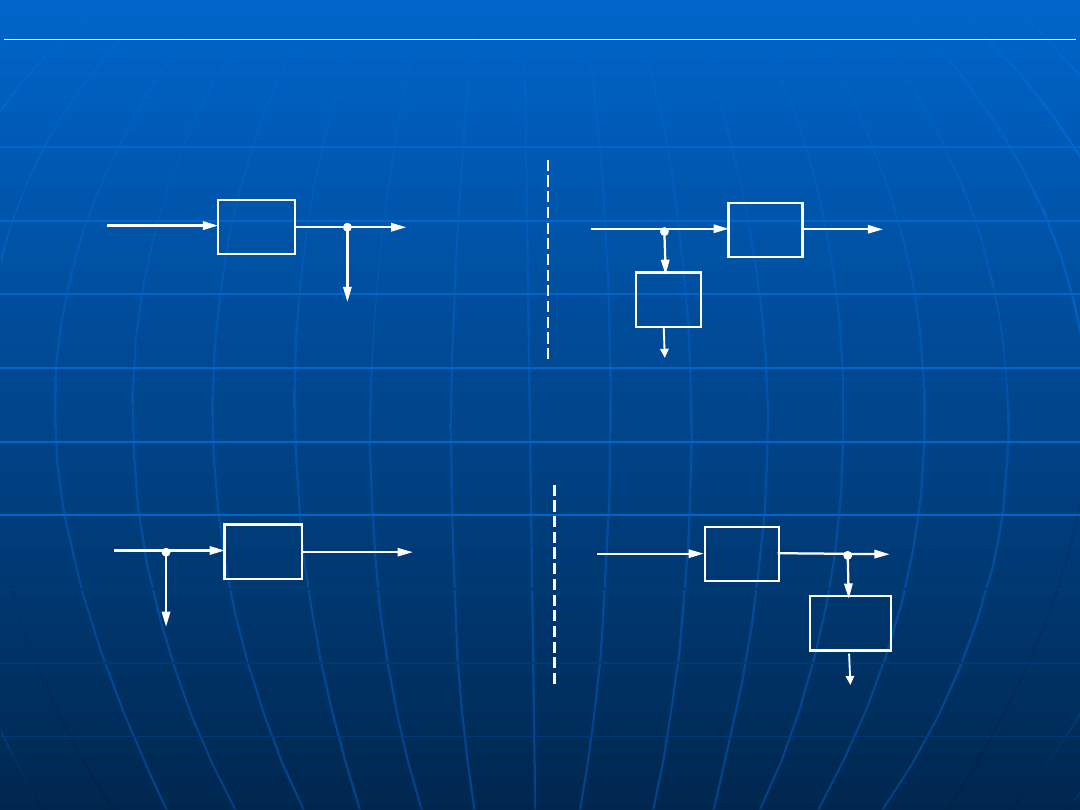
Przeniesienie węzła zaczepowego przed człon

G

U

Y

Y

G

U

Y

Y

G

Przeniesienie węzła zaczepowego za człon

G

U

Y

U

G

U

Y

U

G

-1

Teoria Sterowania

Teoria Sterowania

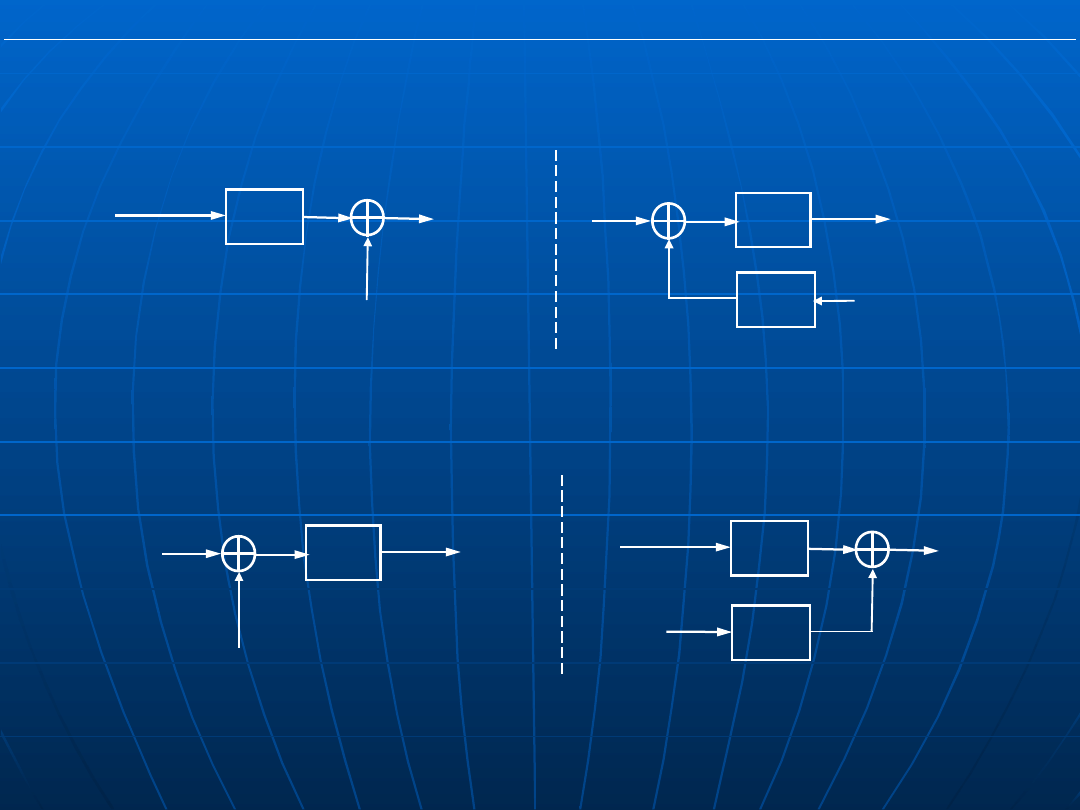
Przeniesienie węzła sumacyjnego przed człon

Przeniesienie węzła sumacyjego za człon

G

U

Y

X

+



G

U

Y

X

G

-1



+

G

U

Y

X



+

G

U

Y

X

+



G

Teoria Sterowania

Teoria Sterowania

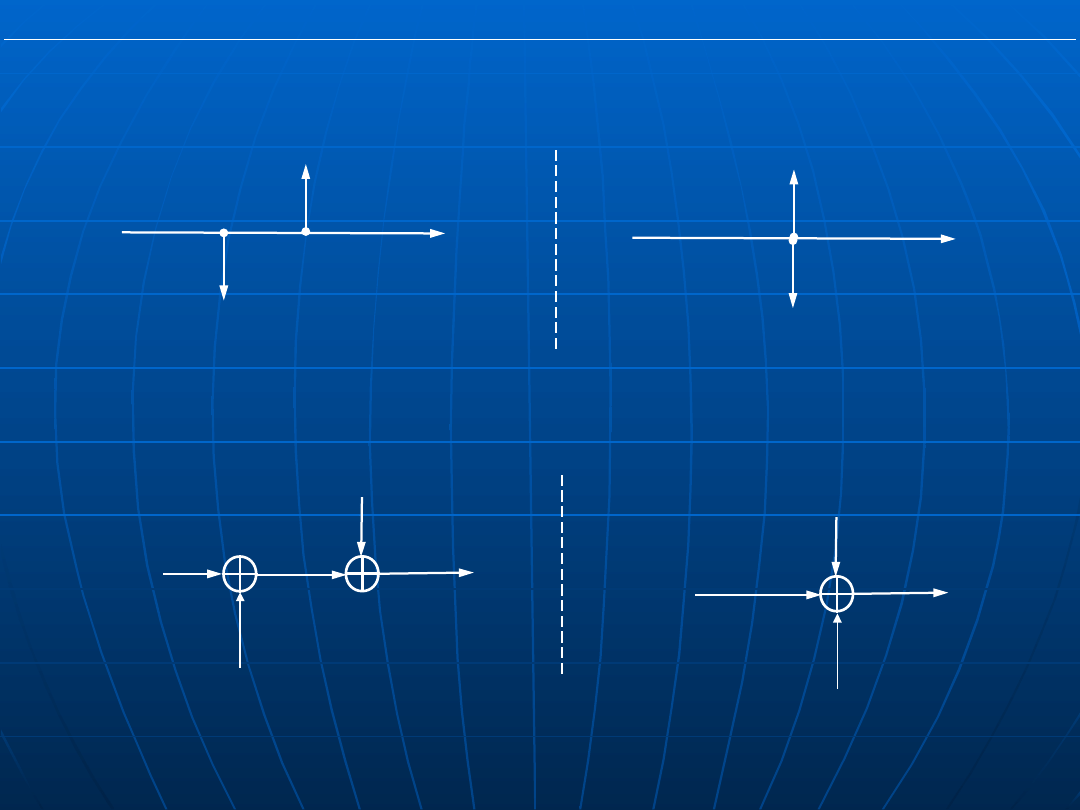
Łączenie/rozdzielanie węzłów zaczepowych

Łączenie/rozdzielanie węzłów sumacyjnych

X

X

X

X

X

X

X

X

U

Z



+

X

Y



+

U

Z



X

Y



+

Teoria Sterowania

Teoria Sterowania

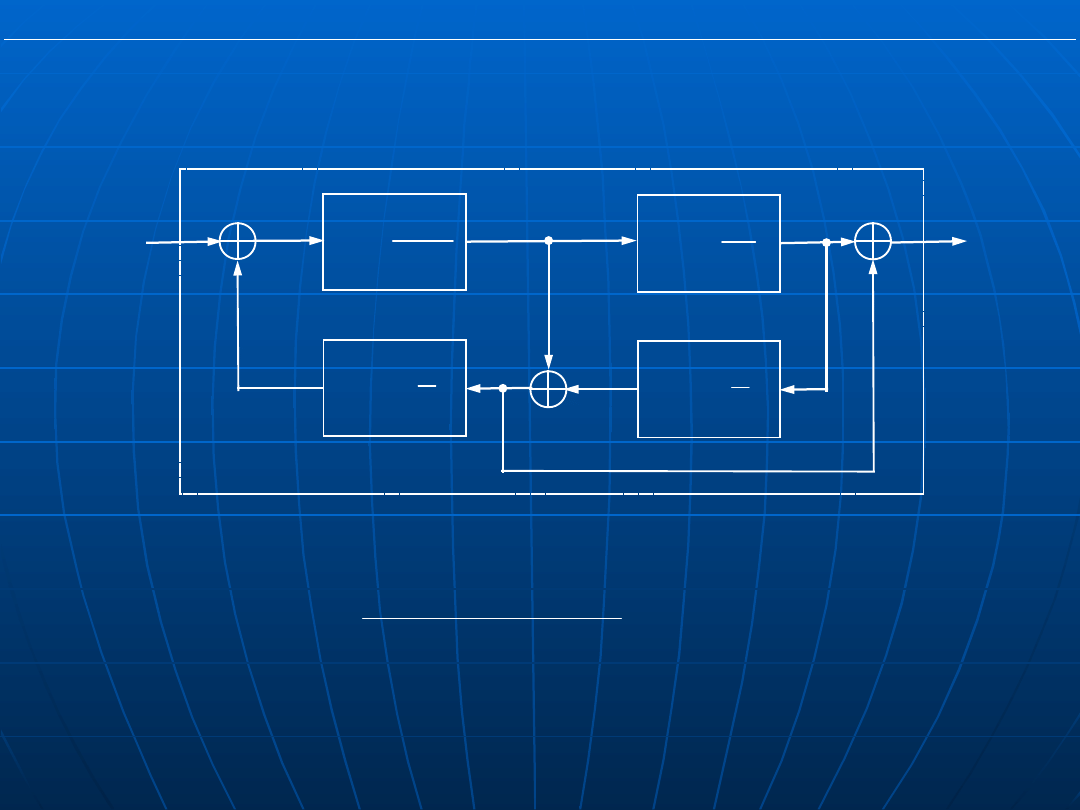
Zadanie: Wyznaczyć transmitancję zastępczą G(s) od u do y
dla podanego schematu blokowego.

y

1

1

4

G

s

=

+

2

1

2

G

s

=

1

1

H

s

=

2

1

H

s

=

x

1

+

+

+

+

_

+

x

4

x

2

x

3

u

Odpowiedź
:

1

2

2

1

1

2

2

1

(1

)

( )

1

(1

)

G

G G H

G s

G H

G H

+ +

=

+

+

Teoria Sterowania

Teoria Sterowania