Informatyka zajmuje się

Informatyka zajmuje się

rozwiązywaniem problemów za

rozwiązywaniem problemów za

pomocą komputerów. Zapis

pomocą komputerów. Zapis

problemu w ścisłej postaci

problemu w ścisłej postaci

pokazującej jak postępować krok

pokazującej jak postępować krok

po kroku, by rozwiązać problem to

po kroku, by rozwiązać problem to

algorytm. Informatyka zatem to

algorytm. Informatyka zatem to

inaczej nauka o algorytmach.

inaczej nauka o algorytmach.

Zapis algorytmu w języku

Zapis algorytmu w języku

zrozumiałym dla komputera to z

zrozumiałym dla komputera to z

kolei program.

kolei program.

Sformalizujmy definicję

Sformalizujmy definicję

algorytmu

algorytmu

Algorytm

to uporządkowany zbiór, jednoznacznych,

wykonywalnych kroków, określający skończony proces,

który dla właściwych danych wejściowych „produkuje”

żądany wynik

Uwagi:
- uporządkowanie kroków ( w sensie
przyczynowo-skutkowym) nie wyklucza
algorytmów równoległych
(wielowątkowych)
- wykonywalność kroków bywa określana jako

obliczalność

- żądanie skończoności eliminuje nieskończone

procesy nie dające rozsądnych wyników

A zatem:

A zatem:



Problem



Algorytm czyli ścisły zapis problemu w

jednej z możliwych notacji (zapis, który

krok po kroku opowiada jak osiągnąć cel)



Program-komputerowa realizacja

algorytmu



Proces – wykonanie programu

Algorytmy mogą wykorzystywać zarówno

znane metody jak i nowo opracowane.

Trudno podać algorytm rozwiązywania problemu
choć były próby (fazy rozwiązywania problemu
wg Polya).

Reprezentacja algorytmów

Reprezentacja algorytmów

Algorytm jest tworem abstrakcyjnym,

tworem fizycznym jest sposób jego
przedstawienia czyli

reprezentacja

algorytmu

Dokładne określenie problemu poprzez

wyszczególnienie danych ( i warunków jakie
mają spełniać) oraz wyników ( i też
warunków jakie mają spełniać) nazywamy

specyfikacją problemu (algorytmu).

Przykłady reprezentacji

Przykłady reprezentacji

algorytmów

algorytmów



słowna



w postaci listy kroków



schematy blokowe



drzewo obliczeń



pseudokod



diagramy Nassi-Schneidermana



w języku programowania (co prowadzi
już do konstrukcji programu)

Przykładowy problem

Przykładowy problem

Dane:

trzy dowolne liczby a,b i c

Wynik:

wartość największej z tych

liczb

Algorytm – opis słowny

Algorytm – opis słowny

Należy przyjąć, że największą

liczbą jest

a

, a następnie porównać

z nią najpierw liczbę

b

zapamiętać

większą liczbę z tej pary, a
następnie porównać ją z liczbą

c

.

Większa liczba z tego drugiego
porównania daje poszukiwaną
wartość.

Algorytm - lista kroków

Algorytm - lista kroków



Krok 1.

Określ wartości a,b i c

.



Krok 2.

Przyjmij, że max = a



Krok 3.

Jeżeli b jest większe niż

max, to przyjmij, że max=b



Krok 4.

Jeżeli c jest większe niż

max, to przyjmij, że max=c



Krok 5.

Wypisz max jako wynik

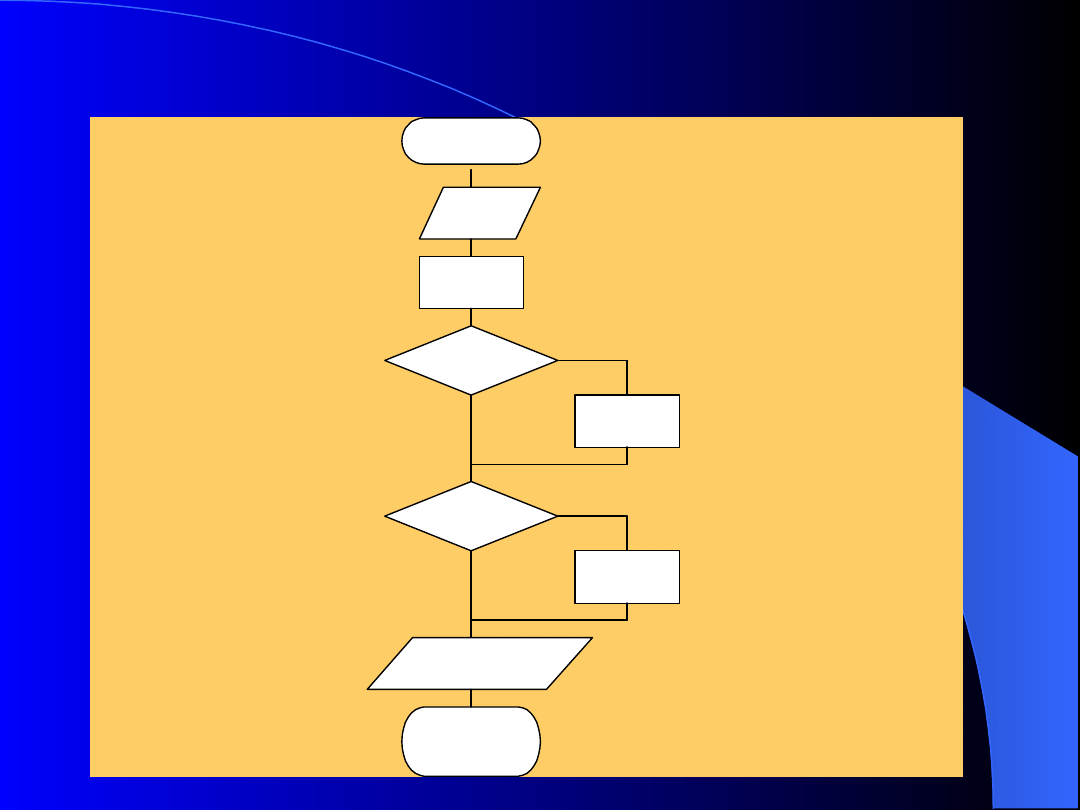
a,b,c

Max:=a

Max<b

b<b

Max:=b

Max<c

Max:=c

Wynik: max

KONIEC

Start

Algorytm- schemat

blokowy

b >=a

c>=b

Wynik :c

Wynik :b

c>=a

Wynik :c

Wynik :a

Algorytm w postaci drzewa obliczeń

Algorytm - pseudokod

Algorytm - pseudokod



Krok 1.

Dane a,b i c

.



Krok 2.

max = a



Krok 3.

Jeżeli b >max, to max=b



Krok 4.

Jeżeli c >max, to max=c



Krok 5.

Wynik: max

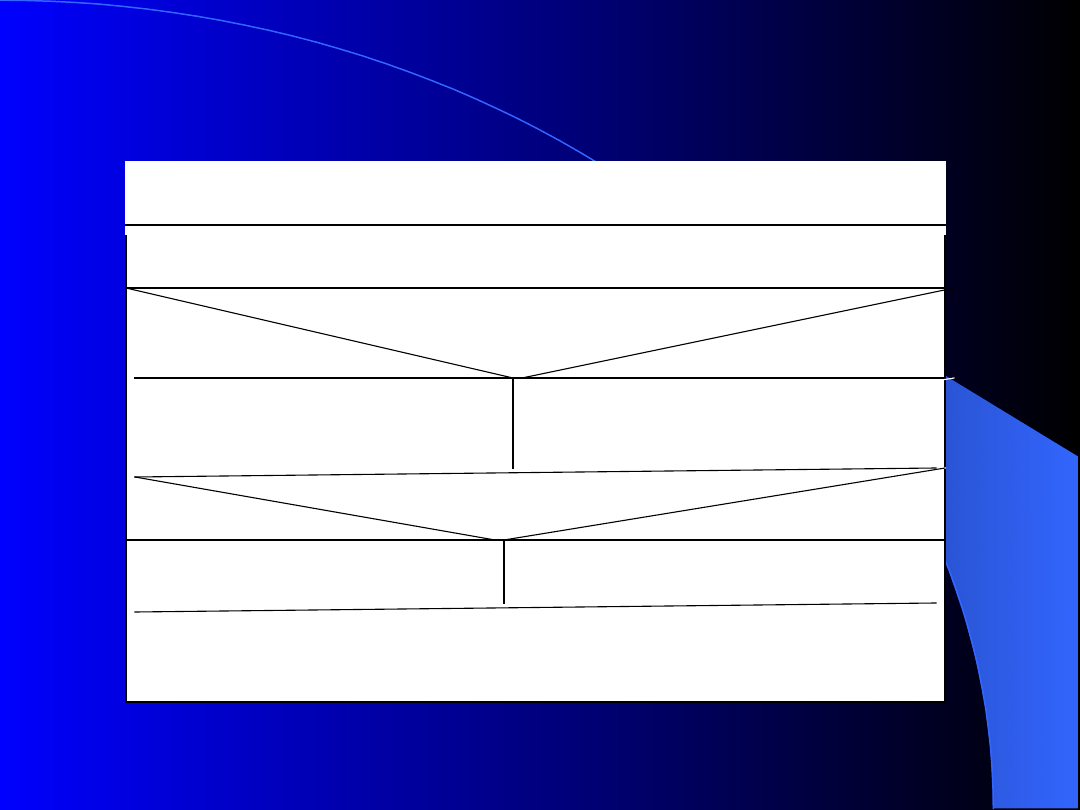
Inne notacje algorytmów-

Inne notacje algorytmów-

diagramy Nassi-

diagramy Nassi-

Schneidermanna

Schneidermanna

a,b

a,b,c <<

max:=a

max<b

TAK

NIE

max:=b

max<c

NIE

TAK

max:=c

Wypisz max

Typy algorytmów

Typy algorytmów



liniowe



rozgałęzione



iteracyjne



rekurencyjne

Języki programowania w

Języki programowania w

ewolucji historycznym

ewolucji historycznym



początki procesu programowania- algorytmy

wyrażane w języku maszynowym



języki asemblerowe (drugiego poziomu)



języki trzeciej generacji



języki wysokiego poziomu -

pełna

niezależność od środowiska komputera i

komunikowanie się z komputerem za

pomocą pojęć i struktur abstrakcyjnych (to

komputer winien dostosowywać się do

charakterystyki człowieka) –duże spektrum

tych języków

Język naturalny, a język

Język naturalny, a język

programowania

programowania



jeden i drugi ma swój zbiór słów, zbiór reguł mówiących jak

tworzyć poprawne zdania (instrukcje języka programowania) czyli

składnię i reguł mówiących jak je rozumieć czyli semantykę,

więcej jest jednak różnic



język naturalny pozostawia wiele interpretacji, wyczuciu, zawiera

zwroty wieloznaczne, idiomy; język programowania nie pozostawia

miejsca na interpretacje i domysły- żądania wobec komputera

muszą być wyartykułowane w sposób ścisły i jednoznaczny



programy w części dotyczącej algorytmiki muszą być uniwersalne,

drobne różnice realizacyjne między komputerami wynikają z

architektury komputera, a nie istoty algorytmu- narzuca to wymóg

odpowiedniej uniwersalności na języki programowania



język naturalny jest zastany, jego bogactwo tworzone jest

wielopokoleniowo, język programowania jest tworem sztucznym,

który konstruuje się praktycznie od zera

Konstrukcja języka metodą

Konstrukcja języka metodą

gramatyk formalnych

gramatyk formalnych



gramatyki te stworzyły N.Chomsky
bezskutecznie próbując opisać nimi
bogactwo języka naturalnego
(angielskiego)- okazały się one
znakomitym narzędziem do opisu
języków programowania, zwłaszcza
część teorii Chomsky’ego dotycząca
tzw. gramatyk bezkontekstowych

Podstawy teorii gramatyk

Podstawy teorii gramatyk

bezkontekstowych

bezkontekstowych



alfabet to dowolny zbiór znaków - A



słowo to dowolny ciąg znaków utworzonych z

dopuszczonych przez alfabet znaków (dopuszczamy

także tzw. słowo puste o zerowej długości –ε)



długość słowa to liczba jego znaków



zbiór wszystkich możliwych słów jaki można

utworzyć przy pomocy alfabetu A oznaczmy przez A*



językiem zdefiniowanym nad alfabetem A nazywamy

dowolny podzbiór A*

Język użyty tu definicyjnie dla rozróżnienia od

rzeczywistych języków programowania

definiowanych później przez te gramatyki nazywamy

językiem formalnym

Podstawy teorii gramatyk

Podstawy teorii gramatyk

bezkontekstowych

bezkontekstowych



Przykład

Jeśli A= {a,b}
to A*=

{ε,a,b,aa,bb,ab,ba,aab,aba…}

Definicja gramatyki

Definicja gramatyki

bezkontekstowej

bezkontekstowej



Jest to uporządkowana czwórka:

{N,T,P,S}
N- zbiór tzw. symboli pomocniczych
T- zbiór symboli końcowych
P- zbiór produkcji czyli konstrukcji postaci

Pojedyncza produkcja to innymi słowy możliwość zastąpienia symbolu

pomocniczego przez słowo, w skład którego mogą wchodzić

zarówno symbole pomocnicze jak i końcowe.

S- wyróżniony symbol pomocniczy gramatyki (tzw. aksjomat)

Idea tworzenia języka generowanego przez taką

gramatykę polega na tym, aby wychodząc z symbolu

pomocniczego tak długo stosować, którąś z produkcji aż

znikną symbole pomocnicze i zostaną wyłącznie końcowe

*

)

(

,

,

:

T

N

w

N

X

w

X









Gramatyki bezkontekstowe-

Gramatyki bezkontekstowe-

przykłady

przykłady

Przykład 1
G1={ {S}, {a}, {S:= ε,S:=aaS},S}
Gramatyka generuje słowa o parzystej

długości (przyjmując, że słowo puste tez ma

parzystą długość) złożone wyłącznie z liter a

Przykład 2
G2={ {S}, {a,b}, {S:= ε,S:=aSa,S=bSb},S}
Gramatyka generuje palindromy o parzystej

długości złożone tylko z liter a oraz b

Gramatyki bezkontekstowe-

Gramatyki bezkontekstowe-

uzupełnienia

uzupełnienia



Gramatyka G jest jednoznaczna jeżeli każde słowo

języka, które można z niej wyprowadzić ma tylko

jeden sposób wyprowadzenia



Gramatyka G jest zgodna z językiem L ze zbioru T*

jeżeli każe słowo wyprowadzalne z G należy do L



Gramatyka G jest pełna względem języka L jeżli każde

słowo tego języka jest wyprowadzalne z gramatyki G

Definiując określony język programowania przy

pomocy gramatyki dążyć się będzie do tego, aby

każdy program (jako zbiór słów tego języka) był

jednoznaczny. Bazą alfabetu są w przypadku

większości języków programowania słowa języka

angielskiego

Przykład gramatyki

Przykład gramatyki

definiujacej liczby całkowite

definiujacej liczby całkowite



Przyjmujmy, że w dowolnym języku
programowania liczba całkowita to
ciąg cyfr poprzedzonych znakiem + lub
–

Mamy wówczas:
G={ {S,Z,C,L}, {-,+,0,1,2,3,4,5,6,7,8,9},

{C::=0|1|2|3|4|5|6|7|8|9,S::=L|
ZL,Z::=+|-, L::=C|LC},S}

Konstrukcja języka

Konstrukcja języka

programowania

programowania



na podobnej zasadzie buduje się definicje

innych typów danych, wyrażeń, a także

konstrukcji programistycznych instrukcji



cały taki zbiór z dbałością o jednoznaczność

gramatyk definiuje nam język programowania



poprawność tej definicji gwarantuje nam

uzupełnienie gramatyki o zbiór odpowiednich

reguł semantycznych jednoznacznie

określających interpretację (przyjmowane

wartości) dla poszczególnych symboli i

wyrażeń

Szczegółowe notacje

Szczegółowe notacje

używane do opisu gramatyk

używane do opisu gramatyk

bezkontekstowych

bezkontekstowych



notacja użyta przykładowo do opisu

produkcji w definicji wyrażenia

całkowitoliczbowego nosi nazwę notacji

BNF (Backusa-Naura) i stanowi właśnie

zestaw reguł produkcji



używana powszechnie do definicji składni

języków programowania, a także protokołów

komunikacyjnych



przy jej pomocy opisano składnię takich

języków programowania jak Fortran

(Backus), czy Algol (Naur)

BNF-przykład

BNF-przykład



<zero>::=0



<cyfra niezerowa>::=1|2|3|4|5|6|7|8|9



<cyfra>::=<zero>|<cyfra niezerowa>



<ciąg cyfr>::=<cyfra>|<cyfra><ciąg cyfr>



<liczba naturalna>::=<cyfra>|<cyfra

niezerowa><ciąg cyfr>

Oprócz notacji BNF do prezentacji składni

języka można stosować postać graficzną tzw.

diagramy syntaktyczne

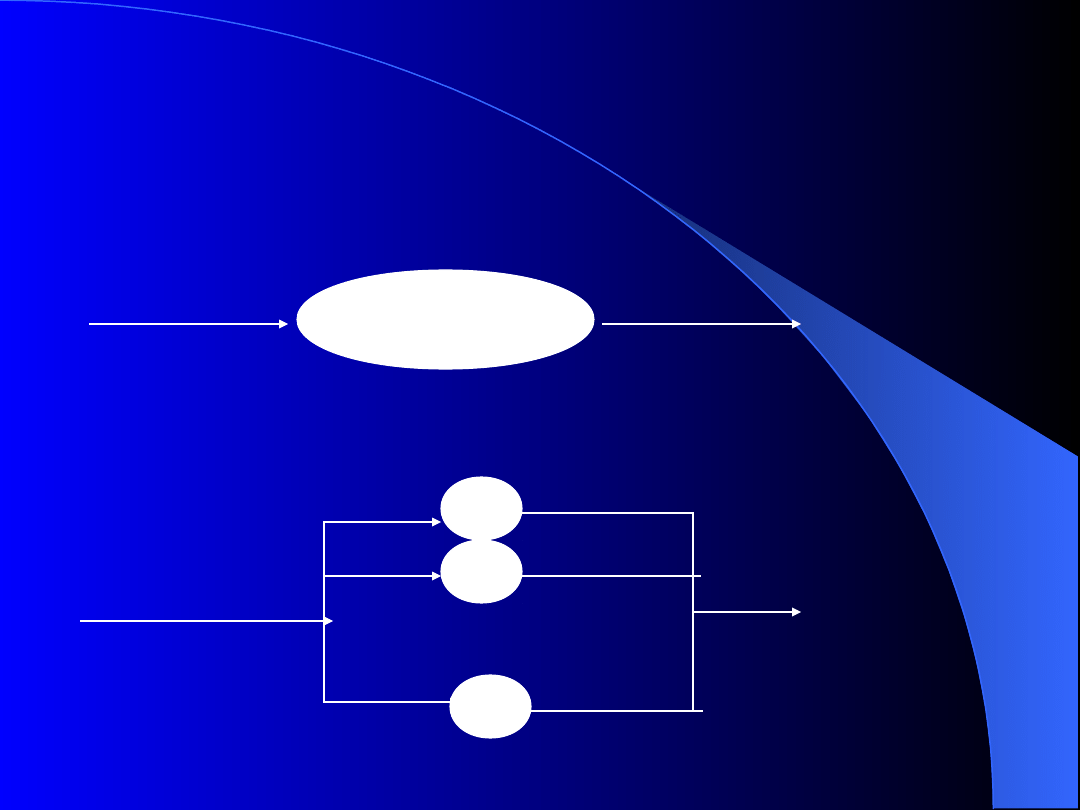
Diagramy syntaktyczne-

Diagramy syntaktyczne-

graficzna postać reguł

graficzna postać reguł

produkcji, liczba

produkcji, liczba

naturalna(pierwsza część)

naturalna(pierwsza część)

zero

cyfra niezerowa

.....

)

0

1

2

9

Typy instrukcji

Typy instrukcji



Instrukcja pusta



Instrukcja złożona –jako zamknięty blok innych instrukcji



Instrukcja przypisania
a:=b (różne konwencje znaku przypisania)



Instrukcja warunkowa np.

if (warunek, test logiczny) then
(instrukcje 1) else (instrukcje 2) –
niekiedy brak słów then lub else
Stosowane operatory porównań oraz logiczne
typu AND, OR lub NOT



Instrukcje iteracyjne (powtórzeń, pętli) – różne składni zależnie od

typu iteracji (znana liczba powtórzeń, liczbę powtórzeń określa

warunek)



Instrukcje wejścia-wyjścia



Instrukcje wywołania procedur lub funkcji

Procedury i funkcje

Procedury i funkcje



wydzielone fragmenty programu o składni zbliżonej

identycznej jak cały program co ma posłużyć tzw.

modularyzacji programu (idea programowania strukturalnego-

wyodrębnienie fragmentów kodu, które następnie mogą być

użyte jako swoiste „czarne skrzynki”)



poza zwiększeniem czytelności kodu programu sprawiają, że

instrukcje raz zapisane mogą być wielokrotnie realizowane

(instrukcja wywołania procedury)



dają praktycznie możliwość wykorzystania rekurencji

(rekursji)

Rekurencja-

polega na odwoływaniu się do obiektu, definicji,

funkcji do samej siebie, w programowaniu najczęściej wiąże

się z tworzeniem tzw. procedur (funkcji) rekurencyjnych, które

w wywołują same siebie

Wybrane pojęcia związane z

Wybrane pojęcia związane z

tradycyjnym programowaniem-

tradycyjnym programowaniem-

proste typy danych

proste typy danych



liczby całkowite



liczby rzeczywiste



dane znakowe



wartości logiczne

Wybrane pojęcia związane z

Wybrane pojęcia związane z

tradycyjnym programowaniem-

tradycyjnym programowaniem-

złożone struktury danych

złożone struktury danych

Związane z implementacją (konkretnym

językiem)



tablice



struktury niejednorodne (np. rekordy)



zbiory

Abstrakcyjne i dynamiczne



stos



listy



kolejki

Zmienne ze względu na

Zmienne ze względu na

używanie pamięci

używanie pamięci



zmienne statyczne- zmiennym
przydziela się z góry pewien
obszar pamięci na podstawie ich
typu (wstępnej deklaracji)



zmienne dynamiczne – pamięć
przydzielona na te zmienne może
być rezerwowana i zwalniana w
trakcie działania programu

Szczególny rodzaj danych

Szczególny rodzaj danych

-pliki

-pliki



pliki binarne – dane w pliku to ciąg bajtów bez
względu na zawartość



pliki ogólne- podzielone na tzw. rekordy
logiczne (niekoniecznie równe fizycznym na
dysku) , obecne w licznych językach
programowania



pliki tekstowe –najbardziej rozpowszechniony
standard, plik o strukturze wierszowej,
jednostka podstawową znak ( w ASCII – 1bajt),
różne standardy kodowania znaków sterujących

Paradygmat

Paradygmat

programowania

programowania

Ogół oczekiwań programisty wobec

języka programowania i komputera,
na którym działa program- innymi
słowy idzie o zbiór mechanizmów
jakich używa programista tworząc
program oraz mechanizmów
związanych z tym jak ten program
jest wykonywany przez komputer

Najważniejsze

Najważniejsze

paradygmaty

paradygmaty

programowania

programowania



programowanie imperatywne czyli – sekwencja poleceń

zmieniająca stan maszyny krok po kroku(mimo pewnych

abstrakcji ALGOL,FORTRAN, C,ADA)



programowanie strukturalne (modularne) – program jako

zbiór zamkniętych „kawałków” (procedur, funkcji,

modułów)-także PASCAL, C (rozwijając się)



programowanie obiektowe – program to zbiór

porozumiewających się ze sobą obiektów zawierających

nie tylko instrukcje jak w programowaniu strukturalnym,

ale także dane; obiekty podlegają mechanizmowi

dziedziczenia- C++,JAVA



inne – np. programowanie w logice

Wiele dzisiejszych języków programowania odzwierciedla

kilka paradygmatów programowania jednocześnie