ALGORYTM to przedstawienie rozwiązania zadania w sposób uporządkowany, tj. z wyszczególnieniem kolejnych czynności.

Algorytm, dokładny przepis podający sposób rozwiązania określonego zadania w skończonej liczbie kroków; zbiór poleceń odnoszących się do pewnych obiektów, ze wskazaniem porządku, w jakim mają być realizowane. Nabrał znaczenia z rozwojem informatyki, gdzie opisuje logiczny ciąg operacji, które ma wykonać program.

Algorytm zapisany przy pomocy języka programowania jest programem.

Wyróżnia się algorytmy numeryczne, operujące na liczbach (np. algorytm Euklidesa), i nienumeryczne, operujące na obiektach nieliczbowych (np. sortowanie dokumentów). Istnieje również podział algorytmów na sekwencyjne (kolejność czynności jest określona jednoznacznie) i niesekwencyjne (równoległe, współbieżne - następstwo między pewnymi operacjami nie jest określone). Algorytmy charakteryzują się możliwością wyrażania ich w różnych językach i przez skończoną liczbę symboli, bez odwoływania się do analogii, a także faktyczną wykonalnością i możliwością wielokrotnej realizacji. Termin algorytm wywodzi się od zlatynizowanej formy (Algorismus, Algorithmus) nazwiska matematyka arabskiego z IX w., Al-Chuwarizmiego.

SPECYFIKACJA ZADANIA - opisanie zadania, czyli szukanie związku, jaki zachodzi między danymi a wynikami

ETAPY ROZWIĄZYWANIA PROBLEMÓW
1) Sformułowanie zadania.
2) Określenie danych wejściowych.
3) Określenie celu, czyli wyniku.
4) Poszukiwanie metody rozwiązania, czyli algorytmu.
5) Przedstawienie algorytmu w postaci:

• opisu słownego

• listy kroków

• schematu blokowego

• jednego z języków programowania

6) Analiza poprawności rozwiązania.
7) Testowanie rozwiązania dla różnych danych - ocena efektywności przyjętej metody.

SPOSOBY ZAPISYWANIA ALGORYTMU.

• ZAPIS ALGORYTMU W POSTACI CIĄGU KROKÓW polega na podaniu kolejnych wykonywanych operacji, składających się na całe rozwiązanie

• ZAPIS ALGORYTMU W POSTACI GRAFICZNEJ - SCHEMATY BLOKOWE.
  Schemat blokowy to graficzne przedstawienie ciągu kroków algorytmu, często stosowane jako ideowy rysunek poprzedzający tworzenie programu.
  W schemacie blokowym poszczególne operacje przedstawiane są za pomocą odpowiednio połączonych skrzynek (klocków, bloków).
  Sposób i kolejność działań programu określane są przez wzajemny układ
  i sposób łączenia bloków ze sobą. Każde działanie (krok) ma w schemacie blokowym swoje standardowe oznaczenie.

ZASADY BUDOWY SCHEMATU BLOKOWEGO
1) Każda operacja jest umieszczona w bloku
2) Schemat ma tylko jeden blok "początek" i przynajmniej jeden blok "koniec"
3) Bloki są ze sobą połączone.
4) Z bloku wychodzi tylko jedno połączenie; wyjątek stanowią bloki:

• "koniec" - z których nie wychodzą już żądne połączenia,

• "warunkowy" - z którego wychodzą dwa połączenia opisane TAK i NIE - w zależności od tego, czy warunek jest spełniony, czy też nie, można wyjść jedną z dwóch dróg.

CECHY ALGORYTMU:

1. skończoność - realizowany ciąg instrukcji powinien mieć swój koniec;

2. określoność - operacje i ich porządek muszą być ściśle określone;

3. ogólność - stosowanie danego algorytmu nie powinno się ograniczać do pojedynczego problemu, ale do całej klasy problemów tego samego typu;

4. efektywność - algorytm prowadzić do rozwiązania najkrótszą drogą;

Przykład algorytmu dodawania dwóch liczb (a + b)

Zadanie do wykonania:

• dane są trzy liczby,

• przedstaw graficznie algorytm obliczania ich sumy.

Sytuacje warunkowe są wtedy, gdy wynik, dalsze działanie zależy od spełnienia warunku.

Przykładem może być obliczanie wartości bezwzględnej liczby x.

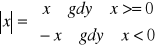
Zadanie:

Dane są dwie liczby. Przedstaw algorytm wyboru większej z nich w postaci ciągu kroków (słownie) i schematu blokowego. Przy liczbach równych wyprowadź „Liczby równe”.

Iteracja, czyli działanie w pętli

Polega na wielokrotnym wykonywaniu tej samej instrukcji. Oszczędza czas programisty, który musiałby powtórzyć (napisać) operację n razy, dla każdej wartości n oddzielny program. Liczba powtórzeń może być z góry określona lub zależeć od podanego warunku.

Poniżej przedstawiono algorytm obliczania sumy N kolejnych liczb naturalnych.

Zadanie:

Napisz algorytm obliczania średniej arytmetycznej sumy N kolejnych liczb naturalnych (zaczynając od jeden).

Sposoby przedstawiania algorytmów 1/3

CZYTAJ A

S <- A + B

STOP

START

CZYTAJ B

WYPISZ S

N

CZY X >= 0 ?

WYPISZ X

WYPISZ -X

CZYTAJ X

STOP

START

START

STOP

Podaj N

S <- 0

L <- N

L > 0 ?

S <- S + L

L <- L - 1

Pisz N

---