WUT

TWG

2005

 

WEDT 

Teoria informacji

Wykład 3

Piotr Gawrysiak

pgawrysiak@supermedia.pl

2005

 

 

WUT

TWG

2005

Projekt

•

Dwie grupy studentów

•

1) 

Piotr Gawrysiak – pgawrysiak@supermedia.pl

•

2) Piotr Andruszkiewicz - P.Andruszkiewicz@elka.pw.edu.pl

•

1) Jabłonka – Marcinkowska

•

2) Mierzejewski - Zyśk

•

Etapy:

•

I    wybór tematu – 1 tydzień / propozycja tematu

•

II   projekt wstępny – 4 tygodnie / wstępna analiza teoretyczna

•

III  implementacja – ost. termin / pełna dokumentacja

•

Ostateczny termin oddania projektu – ostatnie zajęcia (jeśli 

jednak ktoś chce być zwolniony z egzaminu, musi oczywiście 

oddać projekt wcześniej, czas sprawdzania 

•

Zgłoszenie pełnej dokumentacji na konferencję jest dodatkowo 

premiowane ;-)

 

 

WUT

TWG

2005

Teoria informacji

•

Opracowana przez Shannona w latach 40-tych XX 
w.

•

Określenie ilości informacji możliwej do 
przesłania przez nieidealny /„zaszumiony” – 
„noisy channel”/ kanał komunikacyjny

•

Określenie maksymalnych wartości:

•

Szybkości transmisji (pojemność kanału)

•

Stopnia kompresji danych (entropia)

•

Możliwe jest zapewnienie dowolnie małego 
prawdopodobieństwa wystąpienia błędu 
transmisji pod warunkiem zastosowania 
odpowiednio niewielkiej szybkości transmisji i 
stopnia kompresji

 

 

WUT

TWG

2005

Entropia

•

Entropia – miara chaosu, stopnia 
nieuporządkowania

•

Fizyka – entropia układu rośnie, lub pozostaje 
stała, jeśli nie zostanie dostarczona energia

•

Miara niepewności:

•

Niska entropia – wysoka pewność, przewidywalność

•

Wysoka entropia – niska pewność, ale także ilość 
informacji jaką możemy uzyskać przeprowadzając 
eksperyment

•

Miara ilości informacji

 

 

WUT

TWG

2005

Entropia

•

X: dyskretna zmienna losowa

•

pmf p(X) – rozkład zmiennej X

0 log 0 = 0

•

Jednostka – bity (stąd log

2

)

•

Entropia określa ilość informacji w zmiennej 

losowej: średnia długość słowa potrzebnego do 

przekazania wartości tej zmiennej przy użyciu 

optymalnego kodowania

•

Notacja – H(X) = H

p

(X) = H(p) = H

X

(p) = H(p

X

)

p(x)

p(x)log

H(X)

H(p)

X

x

2











 

 

WUT

TWG

2005

Entropia

Przykład: rzucamy 8-ścienną kostką i przekazujemy 

wynik

Entropia:

(bity)

 

3

log(8)

8

1

log

 

8

1

log

8

1

p(i)

p(i)log

H(X)

2

2

2

























8

1

8

1

i

i





























p(x)

1

log

 

E

p(x)

1

p(x)log

p(x)

p(x)log

H(X)

2

X

x

2

X

x

2

Wartość oczekiwana

Średnia ważona 
prawdopodobieństwem 
wystąpień wartości x

1=001, 2=010, ...

 

 

WUT

TWG

2005

Entropia

Przykład: jakiś język polinezyjski

•

Entropia (przesłanie jednej litery):

•

Kodowanie liter (dla częściej występujących liter 
używamy mniejszej liczby bitów)

(bitu)

 

2

1

2

4

1

log

8

1

log

p(i)

p(i)log

H(X)

2

2

2





























4

1

2

8

1

4

}

,

,

,

,

,

{

u

i

a

k

t

p

i

p

t

k

a

i

u

1/8 1/4 1/8 1/4 1/8 1/8

p

t

k

a

i

u

100 00

101 01

110 111

 

 

WUT

TWG

2005

Entropia

Inne interpretacje:

•

Liczba pytań niezbędnych do odgadnięcia 
przekazu – wielkość przestrzeni poszukiwań 
/search space/

1

p(X)

0

H(X)

0

H(X)









Czyli gdy nie ma niepewności

 

 

WUT

TWG

2005

Entropia łączna

•

Podobnie jak dla prawdopodobieństw (łączne, 
warunkowe)

•

Entropia łączna /joint entropy/ - dla dwóch 
dyskretnych zmiennych losowych X, Y, średnia 
długość słowa potrzebnego dla przekazanie ich 
wartości











X

x

Y

y

Y)

y)logp(X,

p(x,

Y)

H(X,

 

 

WUT

TWG

2005

Entropia warunkowa

Zakładając, że odbiorca informacji zna X, entropia 

warunkowa określa długość słowa potrzebną, 
aby przekazać wartość Y

 





X)

|

p(Y

log

E

 

  

x)

|

p(y

y)log

p(x,

x)

|

p(y

x)log

|

p(y

p(x)

x)

X

|

p(x)H(Y

X)

|

H(Y

2

X

x

Y

y

2

X

x

Y

y

2

X

x



































 

 

WUT

TWG

2005

Reguła łańcuchowa dla entropii

•

Logarytmy, więc w odróżnieniu od 
prawdopodobieństw reguła łańcuchowa będzie 
sumą składników

)

,...X

X

|

H(X

....

)

X

|

H(X

)

H(X

)

X

...,

H(X

1

n

1

n

1

2

1

n

1,











X)

|

H(Y

H(X)

x))

|

p(y

(log

E

p(x))

(log

E

x))

|

p(y

log

p(x)

(log

E

x)))

|

(p(x)p(y

(log

E

y))

p(x,

(log

E

 

 

Y)

H(X,

2

y)

p(x,

2

p(x)

2

2

y)

p(x,

2

y)

p(x,

2

y)

p(x,

























 

 

WUT

TWG

2005

Przykład

•

Nasz język polinezyjski modelowaliśmy za 
pomocą zmiennej losowej

•

Załóżmy, że dodatkowe badania pozwoliły 
odkryć strukturę użycia sylab w tym języku: 
wszystkie słowa składają się z ciągów sylab 
złożonych ze spółgłoski (C) i samogłoski (V):

p

t

k

a

1/16 3/8

1/16 1/2

i

1/16 3/16 0

1/4

u

0

3/16 1/16 1/4

1/8

3/4

1/8

 

 

WUT

TWG

2005

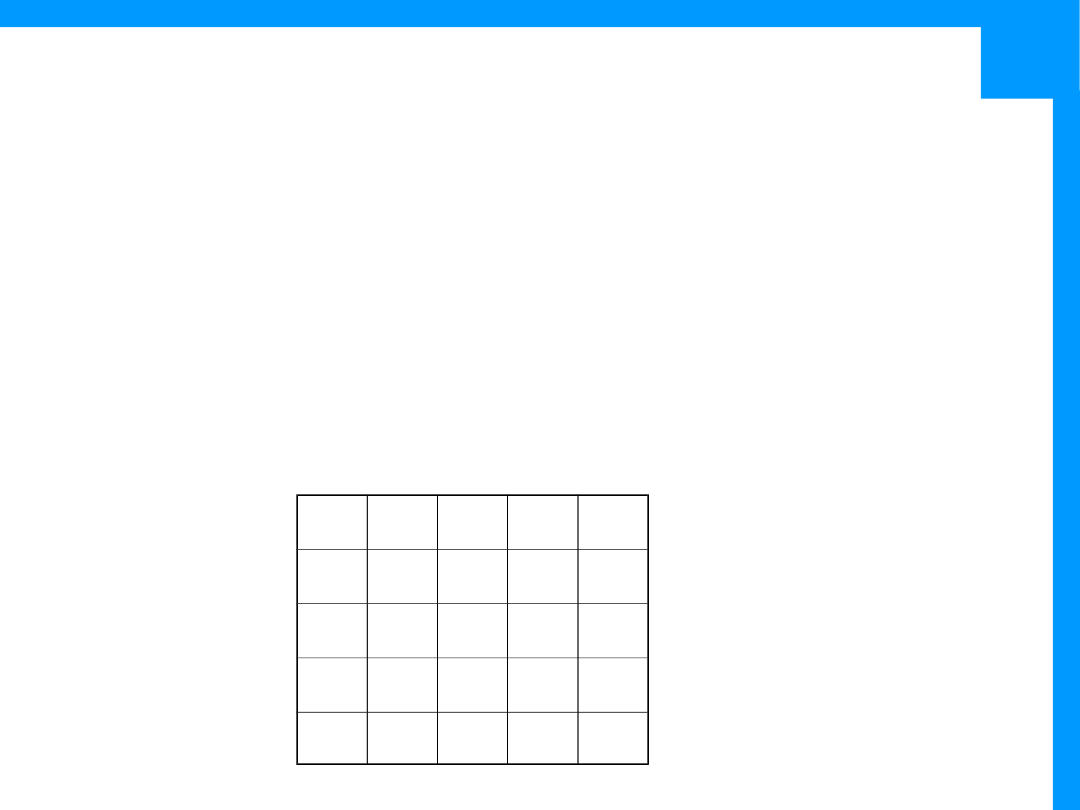
Przykład cd.

•

Używając reguły łańcuchowej dla obliczenia 
H(C,V):

(bitów)

1.061

3

log

4

3

4

9

3)

log

(2

4

3

3

8

1

2

 

 

H(C)

2

2













(bitów)

1.375

8

11

2

3

4

3

4

1

2

4

1

2

2

1

4

3

8

1

2

)

2

1

,0,

2

1

H(

8

1

)

4

1

,

4

1

,

2

1

H(

4

3

,0)

2

1

,

2

1

H(

8

1

)

c

|C

c)H(V

p(C

 

 

|C)

H(V

k}

t,

{p,

c



















































 

 

WUT

TWG

2005

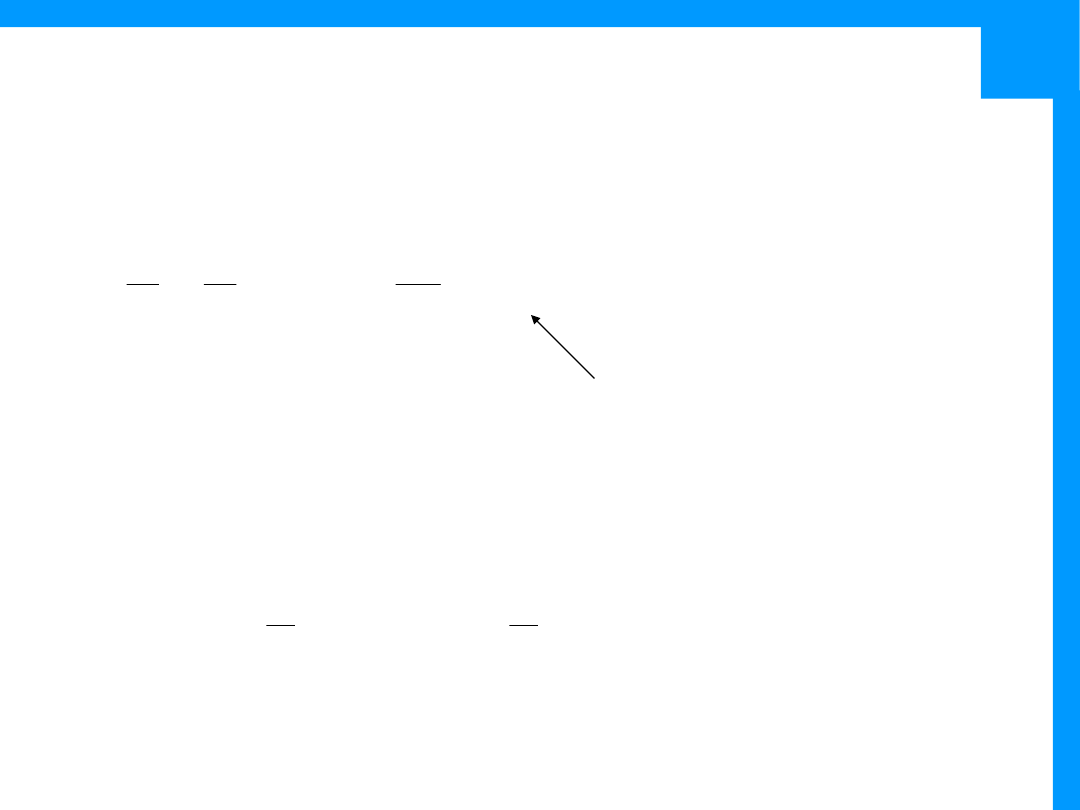
Przykład cd.

•

Entropia ciągu (znaków, wyrazów itd.) zależy od jego 
długości. W praktyce zatem wygodnie definiować 
entropię dla pojedynczych znaków – entropy rate

(bitów)

2.44

8

11

3

log

4

3

4

9

|C)

H(V

H(C)

 

 

V)

H(C,

2













Dla całej sylaby

)

X

,...,

(X

X

gdzie

)

p(x

)log

p(x

n

1

)

H(X

n

1

H

n

1

1n

X

1n

2

1n

1n

rate

1n











 

 

WUT

TWG

2005

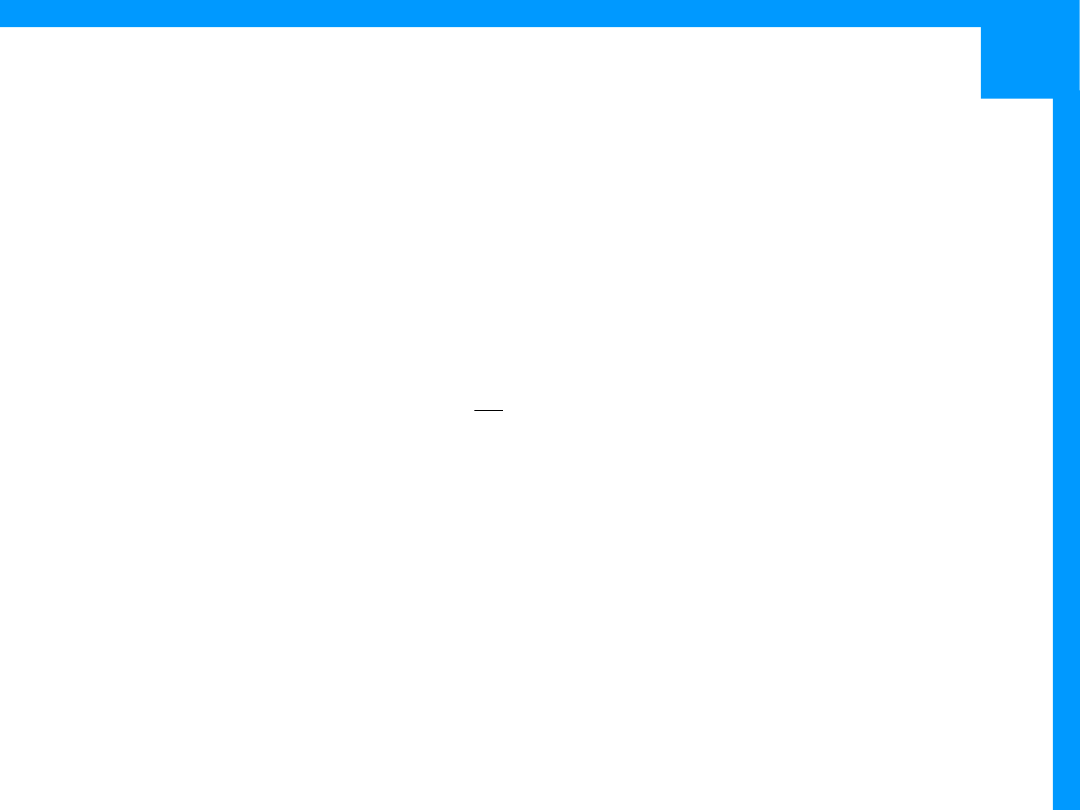
Entropia języka

•

Załóżmy, że język L jest reprezentowany przez 
proces stochastyczny, generujący sekwencję 
tokenów: L=(X

i

)

)

X

,...,

X

,

H(X

n

1

lim

(L)

H

n

2

1

n

rate







 

 

WUT

TWG

2005

Informacja wzajemna /mutual 
information/

•

Informacja o zmiennej losowej Y, którą zawiera 
zmienna losowa X

•

Miara niezależności 

Y)

I(X;

X)

|

H(Y

H(Y)

Y)

|

X(X

H(X)

Y)

|

H(X

H(Y)

X)

|

H(Y

H(X)

Y)

H(X,

















Reguła łańcuchowa

?

p(x)p(y)

y)

p(x,

y)log

p(x,

y)

p(x,

y)log

p(x,

p(y)

1

p(y)log

p(x)

1

p(x)log

Y)

H(X,

H(Y)

H(X)

Y)

|

H(X

H(X)

Y)

I(X;

y

x,

2

y

x,

2

x

x

2

2



























 

 

WUT

TWG

2005

Informacja wzajemna cd.

•

H(X|X)=0 stąd

•

H(X)=H(X)-H(X|X)=I(X;X)

•

Gdy X i Y są niezależne to:

•

H(X|Y) = H(X)

•

I(X;Y) = H(X)-H(X) = 0

•

Interpretacja MI – I(X;Y) mierzy to jak bardzo 

nasza wiedza o Y ułatwia (średnio) 

przewidywanie wartości X

•

Mierzona w bitach

Entropia – miara 
informacji własnej

 

 

WUT

TWG

2005

Model zaszumionego kanału

•

Dualizm pomiędzy kompresją, a jakością transmisji

•

Pojemność kanału – określa maksymalną szybkość 
transmisji informacji

•

Wykorzystamy pojemność kanału, gdy użyjemy 
kodowania X, którego rozkład maksymalizuje wartość 
informacji wzajemnej pomiędzy wejściem i wyjściem dla 
wszystkich możliwych rozkładów wejściowych p(X)

W

X

W*

Y

koder

dekoder

Kanał

 p(y|x)

wiadomość

wejście

wyjście

Y)

I(X;

max

 

 

C

p(X)



 

 

WUT

TWG

2005

Przykład:

•

Symetryczny kanał binarny:

•

Wejście X ~ {0,1}

•

Wyjście Y -> 0->1 oraz 1->0 z prawdopodobieństwem p

•

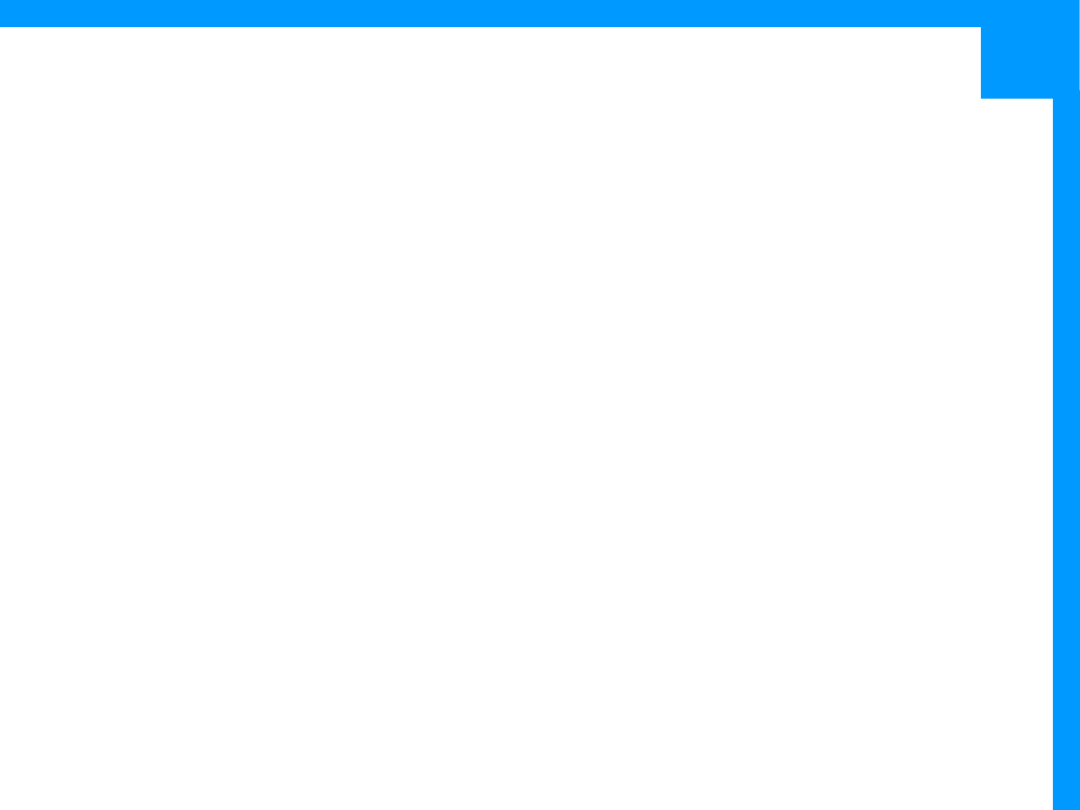
I(X;Y) = H(Y)-H(Y|X)=H(Y)-H(p)

•

Gdy p=0 lub p=1 (kanał zawsze zamienia bity) C=1

•

Gdy p=1/2, C=0; taki kanał nie nadaje się w ogóle do 
transmisji danych

H(p)

-

1

Y)

I(X;

max

p(X)



Gdy kody dla X i Y takie 
same, wymagany 1 bit

 

 

WUT

TWG

2005

Zastosowanie w NLP

•

Pragniemy określić najbardziej prawdopodobną 
wiadomość na wejściu kanału, znając zakodowane 
wyjście 

•

p(i) – model języka, rozkład występowania słów (lub 
innych sekwencji)

•

p(o|i) – „operacja” wykonywana przez kanał

i)

|

p(i)p(o

argmax

 

p(o)

i)

|

p(i)p(o

argmax

 

o)

p(i|

argmax

  

 

I

i

i

i







ˆ

dekoder

Kanał

   p(o|i)

I

O

 

 

WUT

TWG

2005

Zastosowanie w NLP cd.

Zastosowan
ie

Wejście

Wyjście

P(i) 

P(o|i)

Tłumaczenie 
automatyczn
e

Sekwencje 
słów L

Sekwenc
je słów

Prawdopodobieńst
wo wystąpienia L 
wg modelu języka

Model 
tłumaczeni
a

OCR

Skanowany 
tekst

Tekst z 
błędami

Prawdopodobieńst
wo wystąpienia 
tekstu w języku

Model 
błędów 
OCR

POS tagging

Sekwencje 
znaczników 
POS (t)

Sekwenc
je słów 
(w)

Prawdopodobieńst
wo sekwencji 
znaczników

P(w|t)

Rozpoznawa
nie mowy

Sekwencje 
słów

Sygnał 
mowy

Prawdopodobieńst
wo sekwencji słów

Model 
akustyczny

 

 

WUT

TWG

2005

Porównywanie rozkładów

•

Dywergencja Kullbacka-Leiblera

•

Miara różnic pomiędzy pmf p(x), q(x)

•

I(X;Y) = D(p(x,y)||p(x)p(y))

•

D(p||q)>0 oraz D(p||q)=0 wtw. p=q

•

To nie jest miara odległości, nie spełnia warunku 
nierówności trójkąta, ponadto nie jest symetryczna





















q(X)

p(X)

log

E

      

q(x)

p(x)

p(x)log

 

q)

 

||

D(p

p

X

x

Jeszcze jedna definicja MI 
– „odległość” rozkładu 
łącznego dwóch 
zmiennych od rozkładu 
dla zmiennych 
niezależnych

 

 

WUT

TWG

2005

Wyrażenia regularne 

/regular 

expressions/

•

Są wszędzie

•

emacs, vi, perl, python, grep, sed, awk,...

•

Elementy wyrażeń regularnych

•

Ciągi znaków

•

Kleene star

•

Zbiór znaków, dopełnienie zbioru

•

Kotwice

•

Zakres

•

Alternatywa

•

Grupowanie

 

 

WUT

TWG

2005

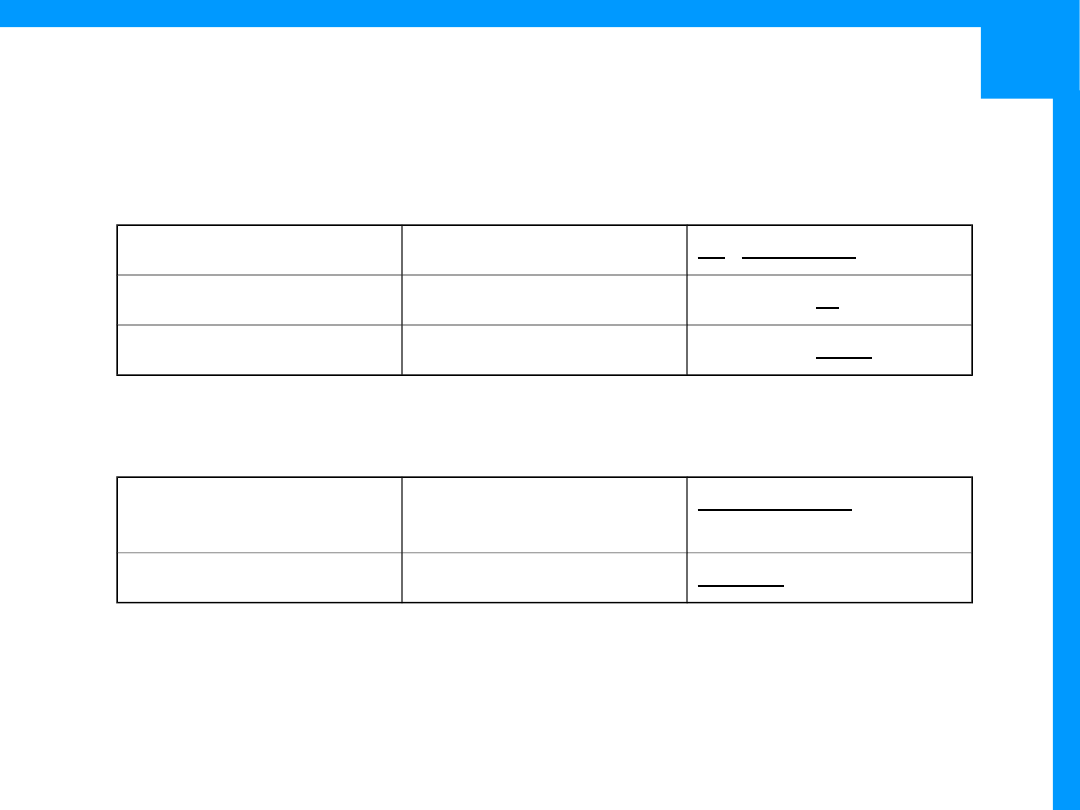
Reguły

•

case sensitive
/woodchuck/

•

Ciągi

•

Zakres

/[wW]oodchuck/

Woodchuck lub 

woodchuck

Woodchuck

/[abc]/

a, b lub c

In uomini, in 

soldati

/[1234567890]/

Dowolna cyfra

Plenty of 7 to 5

/[A-Z]/

Wielka litera

we call it „A great

/[a-z]/

Mała litera

my dear 

/[0-9]/

Dowolna cyfra

Chapter 1: in 

 

 

WUT

TWG

2005

Reguły

•

Dopełnienie

•

Znaki opcjonalne

•

Kleene *

•

Zero lub więcej powtórzeń poprzedzającej sekwencji

•

/[ab]*/ - aaaa, bbbb, abababbba, bbabaaab

/[^A-Z] /

Nie wielka litera

Woodchuck

/[e^]/

e lub ^

Look up ^ now

/a^b/

Ciąg a^b

Look up a^b now

/woodchucks?

woodchuck lub 

woodchucks

woodchuck

/colou?r/

color lub colour

colour

 

 

WUT

TWG

2005

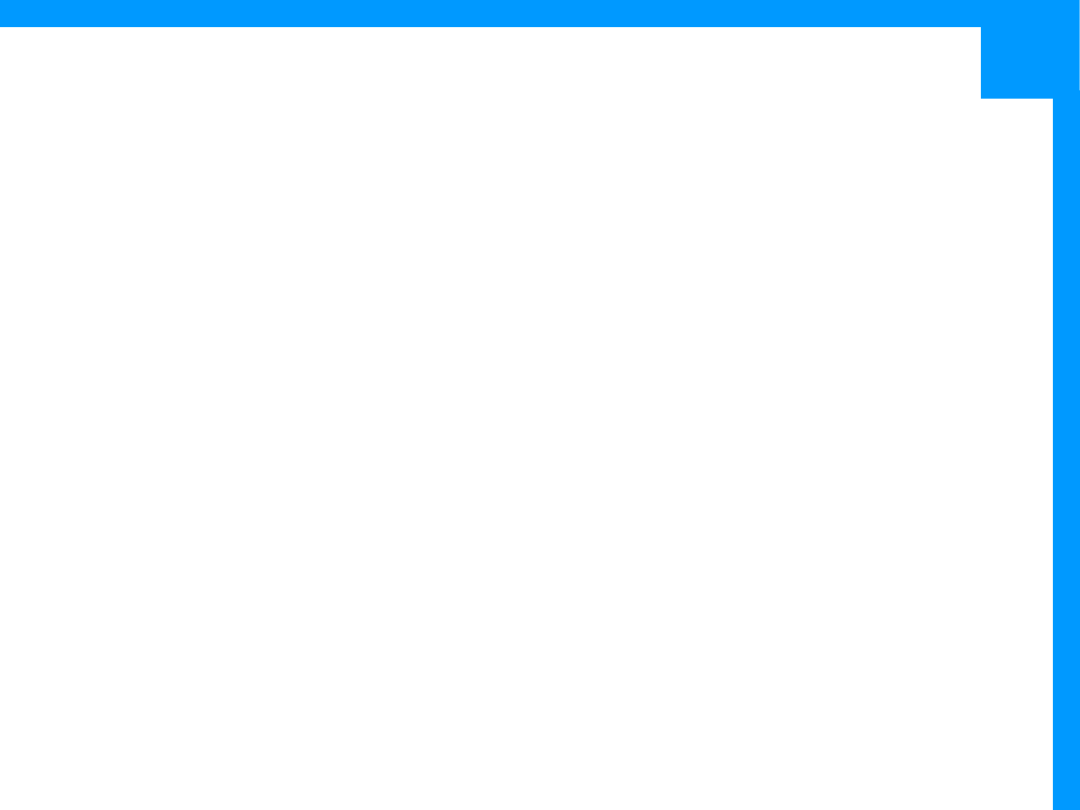
Reguły

•

Alternatywa i grupowanie

•

Kotwice

•

^ - początek ciągu

•

$ - koniec ciągu

•

\b – granica słowa

•

\B – środek słowa

•

Kleene +

•

Przynajmniej jedno wystąpienia sekwencji

•

/[0-9]+/ - liczba całkowita

/cat|dog/

cat lub dog

cat

/gupp(y|ies)/

guppy lub guppies

guppy

/(Column_[0-

9]+_*)*/

Column 1  Column 2  itd.

 

 

WUT

TWG

2005

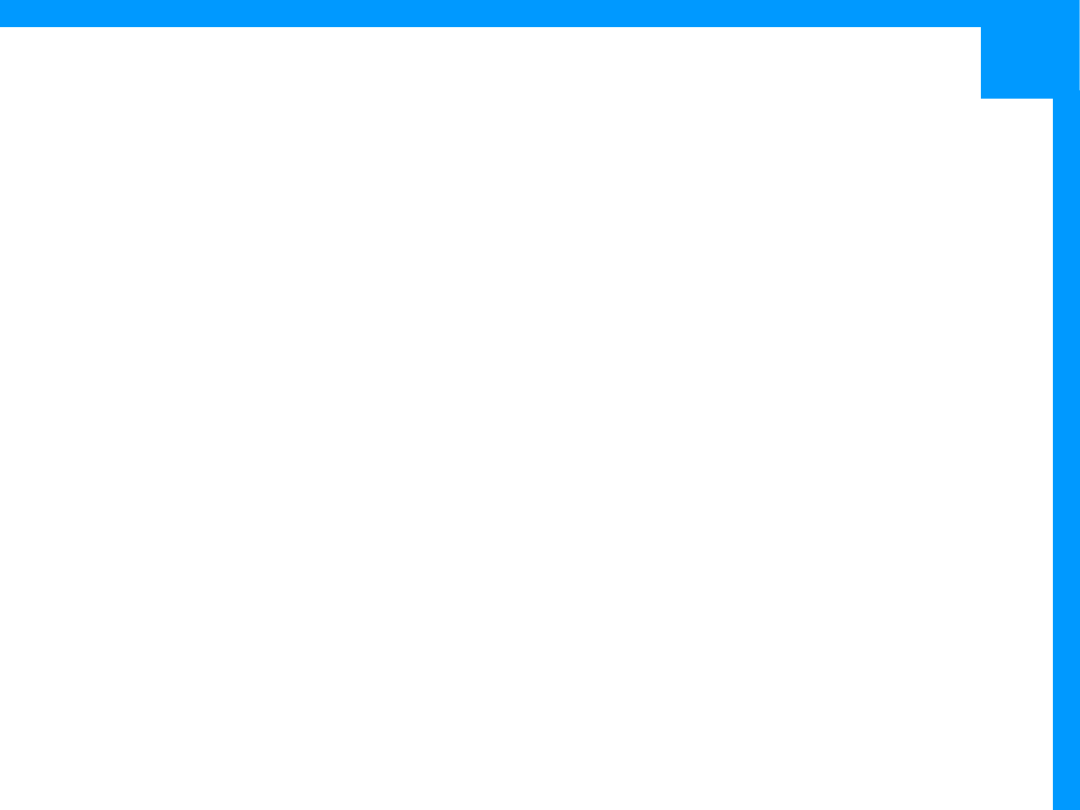
Hierarchia operatorów

1. Grupowanie    ()
2. Liczniki * + ? {}
3. Kotwice the ^my end$
4. Alternatywa

|

{n} – n wystąpień sekwencji
{n,m} – od n do m wystąpień
{n, } - przynajmniej n wystąpień

Character escaping – np. \*, \. itd.

 

 

WUT

TWG

2005

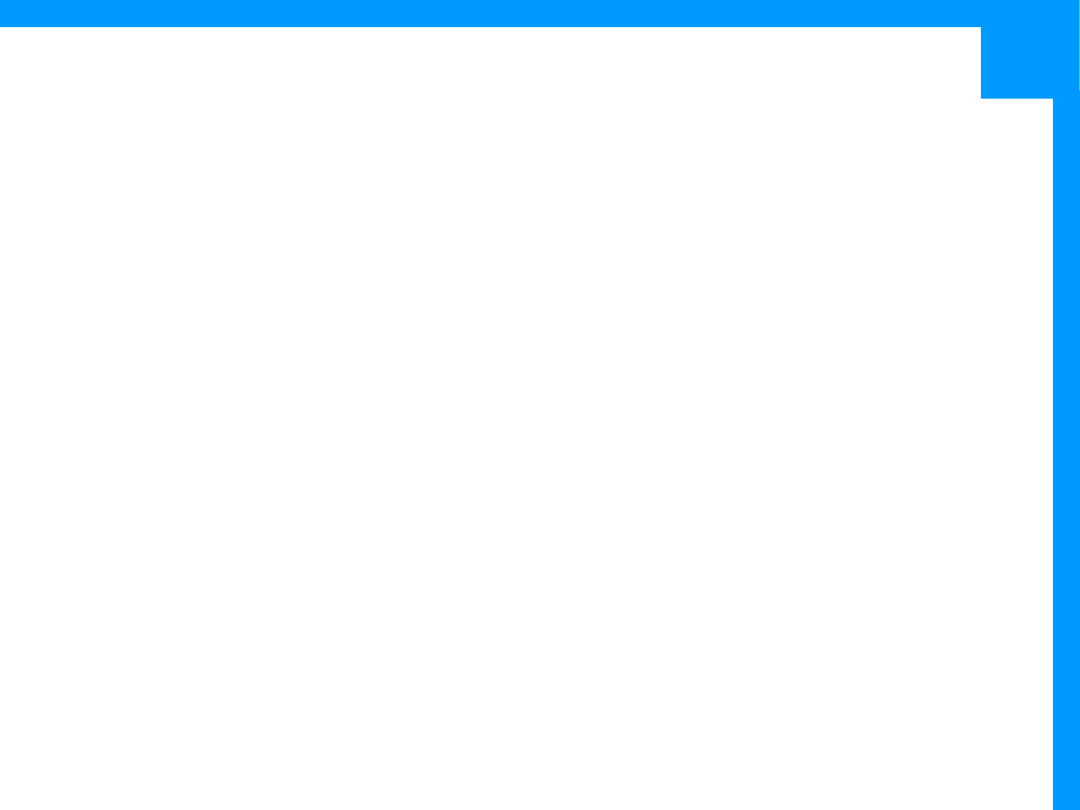
Przykład

•

Znaleźć wystąpienia określnika “the”:

The

 recent attempt by 

the

 police to 

retain their current rates of pay has not 

gathered much favor with 

the

 southern 

factions.

Przykład -  Kathy McCoy

 

 

WUT

TWG

2005

•

Znaleźć wystąpienia określnika “the”:

/the/

The recent attempt by 

the

 police to 

retain 

the

ir current rates of pay has not 

ga

the

red much favor with 

the

 sou

the

rn 

factions.

Przykład

 

 

WUT

TWG

2005

•

Znaleźć wystąpienia określnika “the”:

/[Tt]he/

The

 recent attempt by 

the

 police to 

retain 

the

ir current rates of pay has not 

ga

the

red much favor with 

the

 sou

the

rn 

factions.

Przykład

 

 

WUT

TWG

2005

•

Znaleźć wystąpienia określnika “the”:

/\b[Tt]he\b/

The

 recent attempt by 

the

 police to 

retain their current rates of pay has not 

gathered much favor with 

the

 southern 

factions.

Dwa rodzaje błędów:

• False negatives

• False positives

Przykład

 

 

WUT

TWG

2005

Zastosowania w NLP

•

Wszędzie 

•

ELIZA:

•

U: Men are all alike.

•

E: IN WHAT WAY?

•

They’re always bugging us abouy something or other.

•

CAN YOU THINK OF A SPECIFIC EXAMPLE?

•

Well, my boyfriend made me come here.

•

YOUR BOYFRIEND MADE YOU COME HERE

•

He says I’m depressed much of the time.

•

I AM SORRY TO HEAR YOU ARE DEPRESSED

 

 

WUT

TWG

2005

ELIZA

•

Seria następujących po sobie substytucji ciągów 

znaków

•

1 – zamiana wszystkich wystąpień my na YOUR 

oraz I’m na YOU ARE itd.

•

2 – słownik substytucji:

•

s/.* YOU ARE (depressed|sad) .*/I AM SORRY TO HEAR 

YOU ARE \1/

•

s/.* YOU ARE (depressed|sad) .*/WHY DO YOU THINK 

YOU ARE\1/

•

s/.* all .*/IN WHAT WAY/

•

s/.* always .*/CAN YOU THINK OF A SPECIFIC 

EXAMPLE/

•

Do jednego ciągu może pasować więcej niż jeden 

wzorzec