Pewnego dnia, francuski prawnik, matematyk z

zamiłowania, Pierre Fermat na marginesie czytanej przez

niego książki zapisał jedno twierdzenie i pod nim słowa:

„Znalazłem naprawdę cudowny dowód na to twierdzenie,

ale na marginesie jest za mało miejsca, aby go zapisać”.

Twierdzenie wyglądało mniej więcej tak:

Jeśli x, y, z, należą do zbioru
liczb naturalnych, a n>2 to
równanie:

x

n

+ y

n

= z

n

NIE MA ROZWIĄZANIA!

Matematycy szybko doszli do wniosku, że Fermat ma

rację, jednakże wśród jego zapisków nie znaleziono nigdy

pełnego dowodu na prawdziwość jego założenia. Żeby

było zabawniej, pomimo wieluset prób, żaden z żyjących

matematyków nie umiał udowodnić, że równania nie da

się rozwiązać. Wielu z nich twierdziło nawet, że takiego

dowodu nie ma. Niemniej, poszukiwania trwały. I tak

Twierdzenie Fermata zapisane w XVII wieku bezkarnie

drwiło sobie z kolejnych pokoleń matematyków.

Pierre Fermat

Hehehe.

Z twierdzeniem Fermata wiąże

się również jedna anegdota: Pod

koniec XIX w. Paul Wolfskehl

postanowił zastrzelić się. Uznał,

iż samobójstwo popełni

dokładnie o północy. Do tego

czasu chciał pozałatwiać jeszcze

kilka ostatnich spraw. Kiedy

załatwił, co miał do załatwienia,

do północy sporo jeszcze

brakowało. Dla zabicia czasu

poszedł do biblioteki. Tam trafił

na te słynne twierdzenie. Północ

minęła, a zaaferowany Paul dalej

wertował dzieła francuskiego

prawnika. Matematyka

uratowała mu życie. Zaraz

potem zapisał w testamencie

100 000 marek niemieckich

temu, kto udowodni Wielkie

Twierdzenie Fermata

Któż
pomyślałby,
że matematyka
uratuje mi
życie?

W jednym z odcinków „StarTrek: Nowe Pokolenie”

Kapitan Picard stwierdza:

Akcja StarTreka rozgrywa się w XXIV w. Autorzy w chwili kręcenia odcinka

najwyraźniej sądzili, iż Wielkie Twierdzenie Fermata pozostanie

nieudowodnione przez ponad osiem stuleci.

„Tak jak z Teorią

Fermata; to zagadka,

której możemy nigdy

nie rozwiązać.”

Tymczasem już w niespełna pięć lat po

wyemitowaniu tego odcinka

UDOWODNIONO

TWIERDZENIE FERMATA!

Bez jaj!

Niemożliwe!

A jednak,

Kapitanie.

W 1955 Taniyama przedstawił kilka pytań na temat funkcji

eliptycznych, później zaś prace wraz z André Weilem i

Shimurą postawili hipotezę Shimury-Taniyamy-Weila. W 1986

udowodniono, że istnieje związek między tą hipotezą, a

twierdzeniem Fermata. Późniejsze prace matematyków

pokazały, że gdyby twierdzenie Fermata było fałszywe to i

hipoteza Shimury-Taniyamy-Weila byłaby fałszywa. Teraz

wystarczyło tylko udowodnić, że hipoteza S-T-W jest

prawdziwa. Prościzna, co?

Notabene, pełen dowód

zajmuje ok. 160 stron

maszynopisu. No cóż, Fermat

nie mylił się- „cudowny

dowód” faktycznie nie

zmieściłby się na marginesie

książki

No... niezupełnie. Hipoteza czekała na

udowodnienie do 1994 r. Wtedy Andrew

Wiles napisał pracę, w której udowodnił,

iż

i hipoteza S-T-W i Wielka Teoria Fermata

są prawdziwe.

Triumfujący Andrew

Wiles

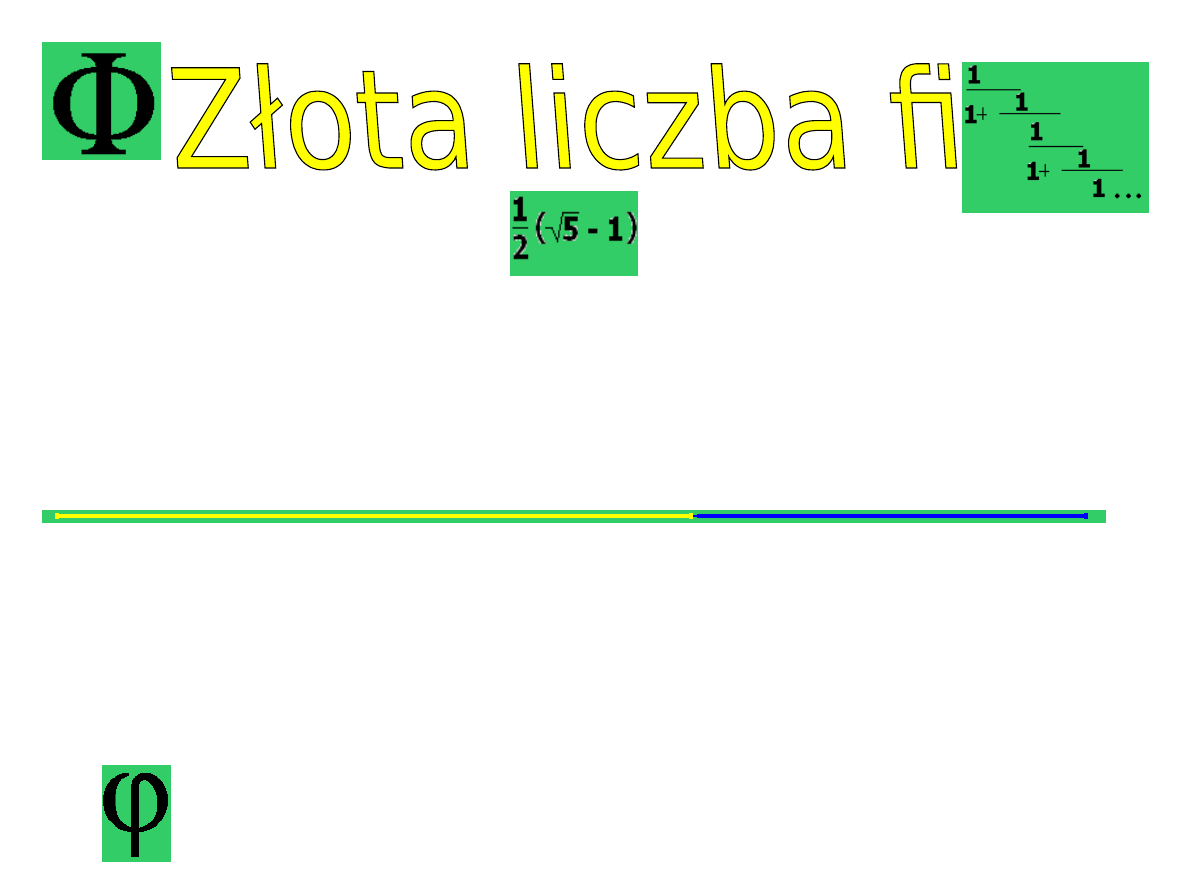
Czy widzicie coś niezwykłego, pięknego w tej liczbie? Nie?

To tylko pozory. 1,61804 (lub 1.1001111000110111011... w

systemie dwójkowym) faktycznie jest złota. Za jej pomocą

można dokonać złotego powdziału, zwanego też niekiedy

boską proporcą.

Czy widzicie w tym odcinku coś szczególnego? Nie? A

jest szczególny. Jeśli zmierzylibyście go i podzielili

długość żółtej części przez długość niebieskiej, a

następnie całego odcinka przez jego żółtą część,

wyjdzie ta sama liczba. Złota Liczba

Fi.

Małe Fi

Duże Fi

Kiedyś liczba Fi była stosowana w wielu dziedzinach:

rzeźbie, architekturze, malarstwie czy astrologii. Ponoć

nawet Antonio Stradivarius wykorzystał ją do budowy

swoich słynnych instrumentów. Przypisywano jej cudowne

właściwości i szukano jej także w naturze. A kto szuka,

znajduje. Na podstawie Złotej Liczby wyznaczono Złoty Kąt,

a ten z kolei występuje między liśćmi niektórych roślin.

Jednakże nie jest AŻ TAK wszechobecna, jak sugerują

niektórzy, np. Down... ups, Dan Brown.

Jeśli podzielimy ilość samic pszczół przez

liczbę samców to w każdym ulu wyjdzie nam

1,618... Ruchy planet i gwiazd i wszelkie inne

zjawiska zachodzące w przestrzeni

kosmicznej dziwnym trafem także hołdują

liczbie Fi... jeśli podzielimy ciężar odchodów

tapira brazylijskiego w kg (zapisany w kodzie

dwójkowym) przez łączne pole jego paznokci

wyrażone w calach...

Tato, o

co temu

panu

chodzi?

Nie przejmuj się

nim. Nikt nie

uwierzy w te

dyrdymały. Miejmy

nadzieję.

Jaką liczbę można uznać za dużą?

10

3

– 1000 -tysiąc?

10

6

– 1000000 – milion ?

10

9

– 1000000000 – miliard?

10

12

- 1 000 000 000 000 - a może bilion?

10

15

- 1 000 000 000 000 000 – no to może

biliard?

10

18

- 1 000 000 000 000 000 000 –

trylion?

10

21

- 1 000 000 000 000 000 000 000 –

tryliard?

A może...

10

60

- decylion? 1 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000 000

A jeśli nawet nie decylion... to może centylion? 10

600

1 000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000 000 000 000 000 000 000 000 000 000

000 000

Jeśli komuś się nudzi, niech policzy. Żeby nie było, że

oszukuję.

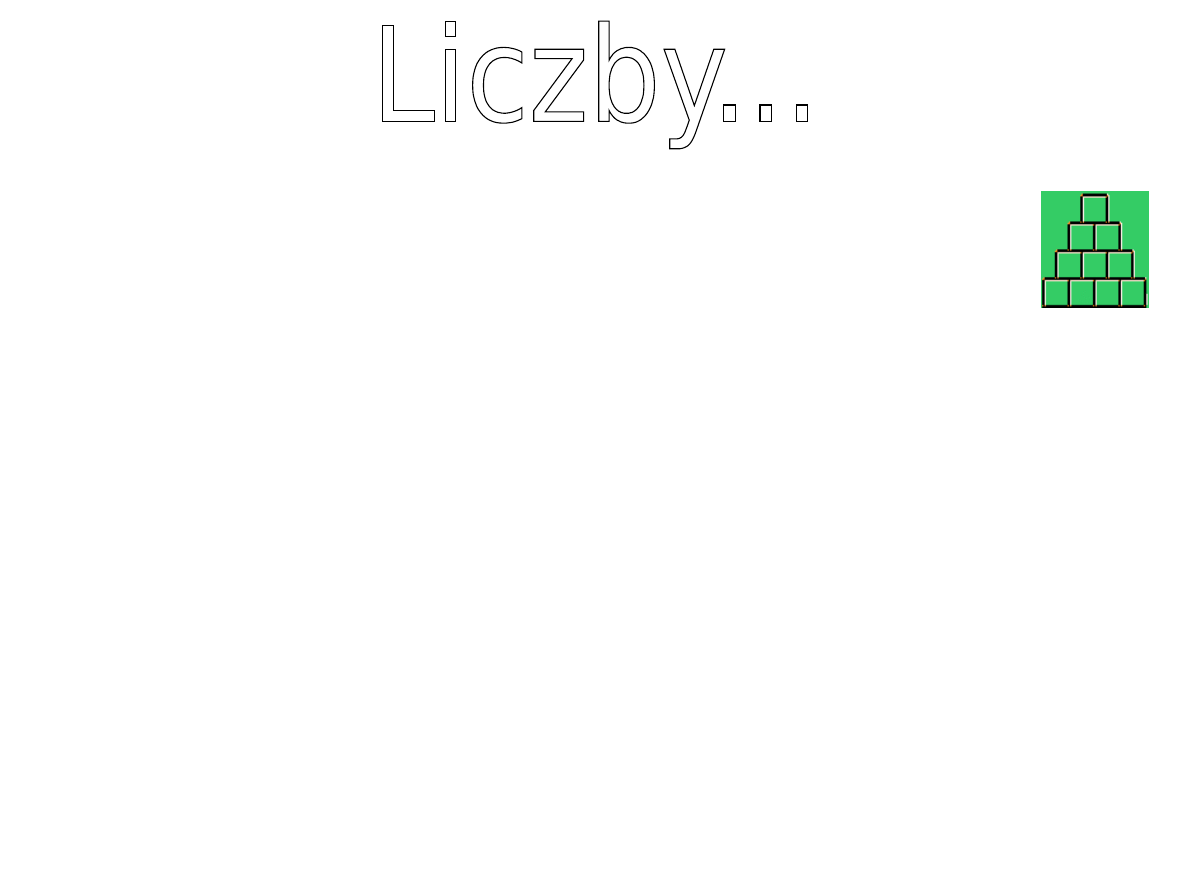
Liczba trójkątna jest sumą n kolejnych liczb naturalnych,

która wyraża się wzorem:

T

n

= n ( n + 1 ) / 2

Mówiąc prosto: to wzór na ilość klocków potrzebnych do

wbudowania piramidy składającej się z n pięter.

Liczby doskonałe to liczby, które są równe sumie

wszystkich ich dzielników prócz nich samych. Np. 6=

1+2+3. Albo 28 = 1 + 2 + 4 + 7 + 14 . W sumie znane są

43 liczby doskonałe. Największa to:

2

30402456

(2

30402457

-1)

Liczby gnomiczne to liczby postaci 2n+1, które dodane do

kwadratu liczby n dają kwadrat następnej liczby.