Sygnały elektryczne

1

2

Sygnał to abstrakcyjny model dowolnej mierzalnej
wielkości zmieniającej się w czasie, generowanej przez
zjawiska fizyczne lub systemy. Tak jak wszystkie
zjawiska może być opisany za pomocą aparatu
matematycznego, np. poprzez podanie pewnej funkcji
zależnej od czasu. Ponieważ sygnał niesie informację o
naturze badanych zjawisk lub systemów, w niektórych
dziedzinach nauk jest on traktowany jak nośnik
informacji. Sygnał oznacza zatem przepływ strumienia
informacji.

DEFINICJA SYGNAŁU

3

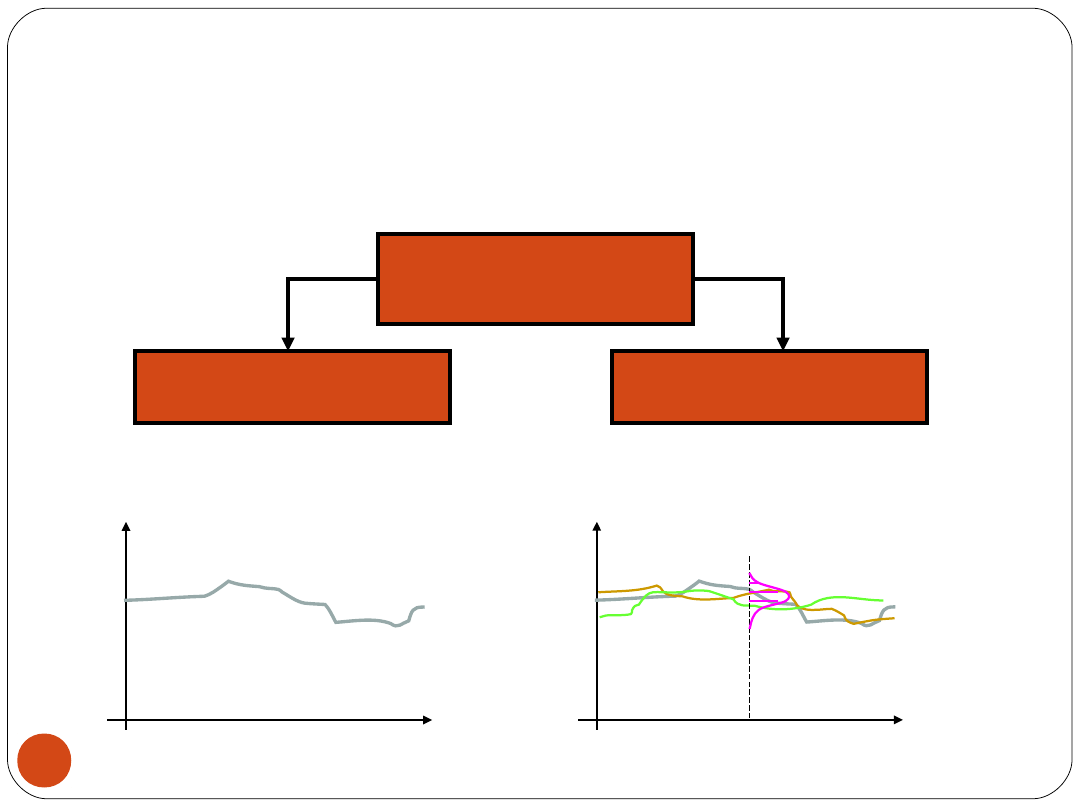
KLASYFIKACJA SYGNAŁÓW

SYGNAŁY

Zdeterminowane

Stochastyczne

f(t)

t

funkcje czasu

f(t)

t

t

0

4

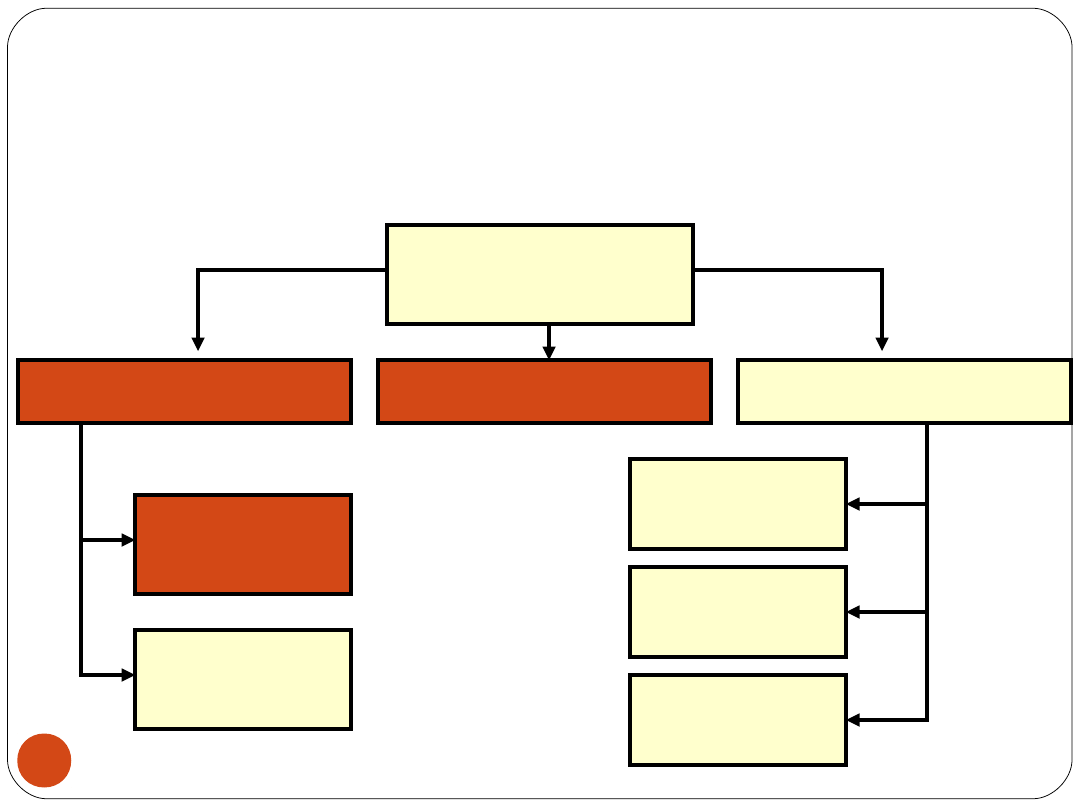
KLASYFIKACJA SYGNAŁÓW ZDETERMINOWANYCH

SYGNAŁY

ZDETERMINOWANE

NIEOKRESOWE

PRAWIE OKRESOWE

OKRESOWE

ZANIKAJĄCE

(stany

nieustalone)

TRWAŁE

(nieograniczone

w czasie)

ODKSZTAŁCONE

HARMONICZNE

IMPULSOWE

KLASYFIKACJA SYGNAŁÓW

ZDETERMINOWANYCH

5

Sygnał prawie okresowy:







)

cos(

)

(

i

i

i

t

Y

t

y





)

2

cos(

cos

)

(

t

t

t

y







PRZYKŁAD:

Sygnał okresowy:

R

T

N

n

T

n

t

y

t

y









,

;

)

(

)

(

6

KLASYFIKACJA SYGNAŁÓW ZDETERMINOWANYCH

SYGNAŁY OKRESOWE

Sygnały harmoniczne:

Sygnały odkształcone:

Sygnały impulsowe:

- prostokątne

- trójkątne

- „szpilkowe”

- inne

)

sin(

)

(









t

U

t

u

m

N

i

t

i

U

U

t

u

i

n

i

m

i













;

)

sin(

)

(

1

0





7

Parametry energetyczne - oznaczenia

u(t

0

) - wartość chwilowa

U

0

- wartość średnia (składowa stała)

U

0w

- wartość średnia wyprostowana

U

- wartość skuteczna

U

M

+

- wartość szczytowa maksymalna

U

M

-

- wartość szczytowa minimalna

U

MM

- wartość międzyszczytowa

8

WSPÓŁCZYNNIKI

k= U/U

0w

- współczynnik kształtu

k

u

= U

M

/U

0w

- współczynnik uśrednienia

k

a

= U

M

/U

- współczynnik amplitudy

k

u

=

kk

a

k  k

a



k

u

9

PARAMETRY ZWIĄZANE Z CZASEM

T

- okres

f=1/T - częstotliwość

=2f - pulsacja


- faza początkowa

10

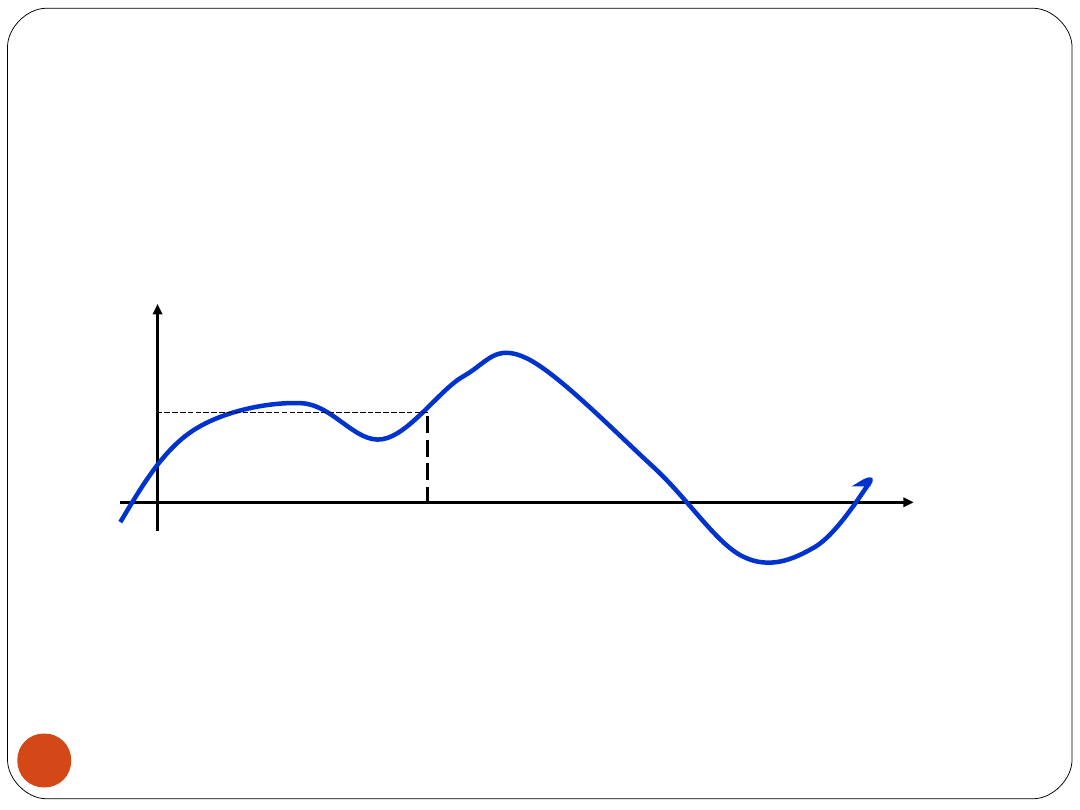
WARTOŚĆ CHWILOWA (u

0

)

u(t)

t

t

0

u(t

0

)

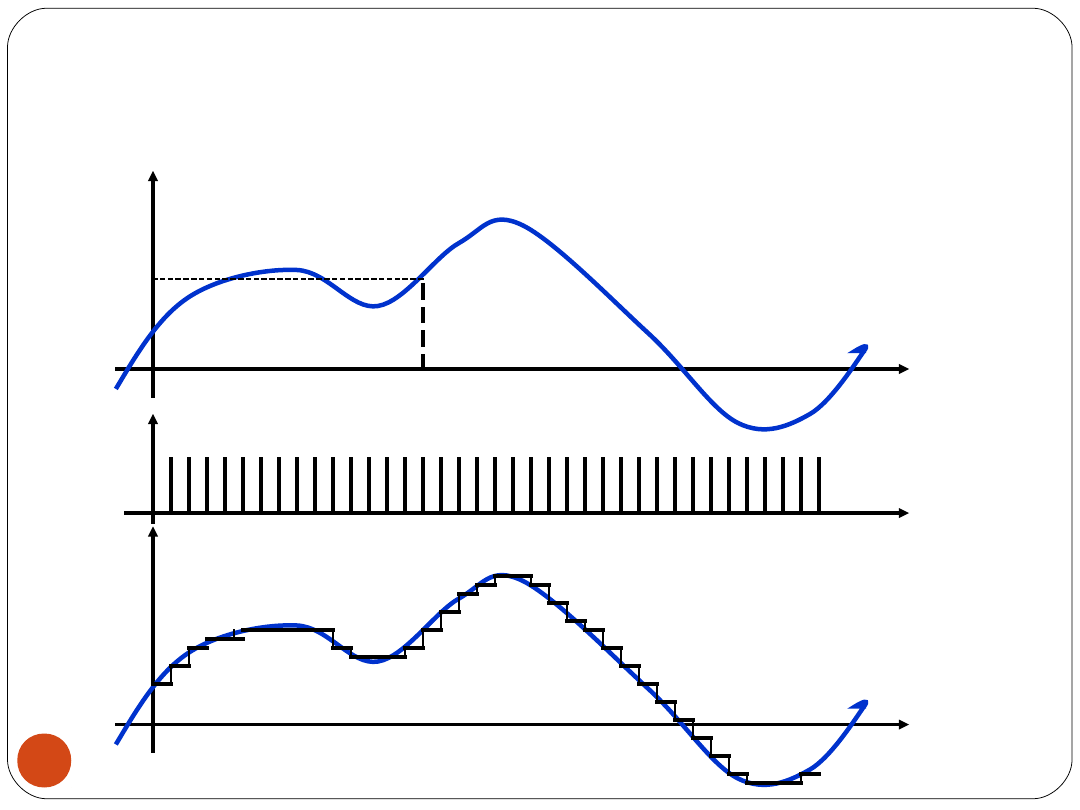
11

PRÓBKOWANIE

u(t)

t

t

0

u(t

0

)

t

u

p

(t)

u(t)

t

u(t

0

)

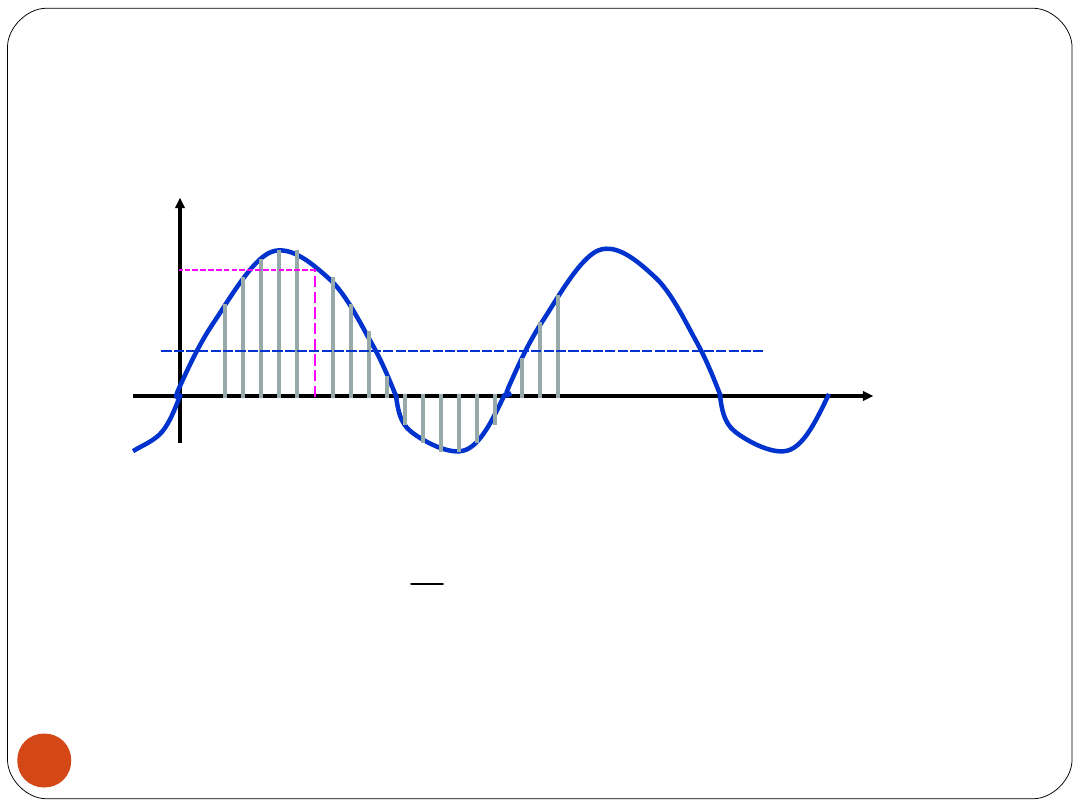
12

WARTOŚĆ ŚREDNIA

u(t)

t

0

t

k

T+t

0

T

0

t

u*(k)

U

0







0

0

)

(

1

0

t

T

t

dt

t

u

T

U

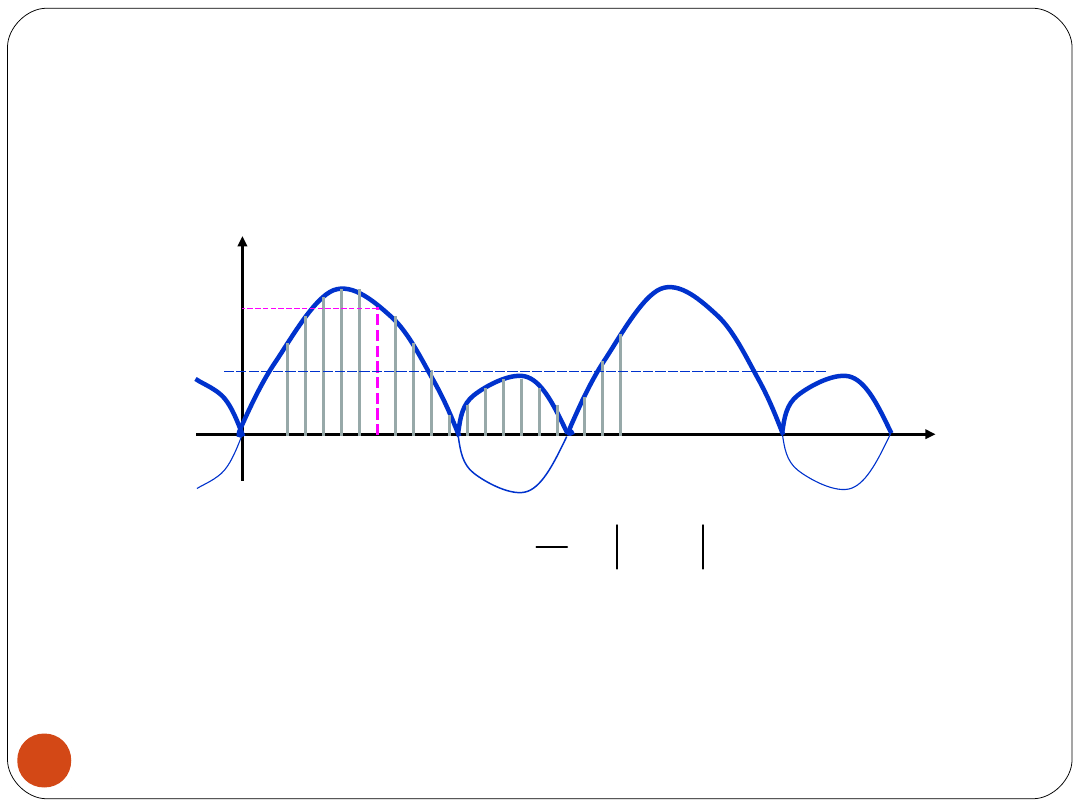
13

WARTOŚĆ ŚREDNIA WYPROSTOWANA

u(t)

t

0

t

k

T+t

0

T

0

t

u*(k)

U

0w







0

0

)

(

1

0

t

T

t

w

dt

t

u

T

U

14

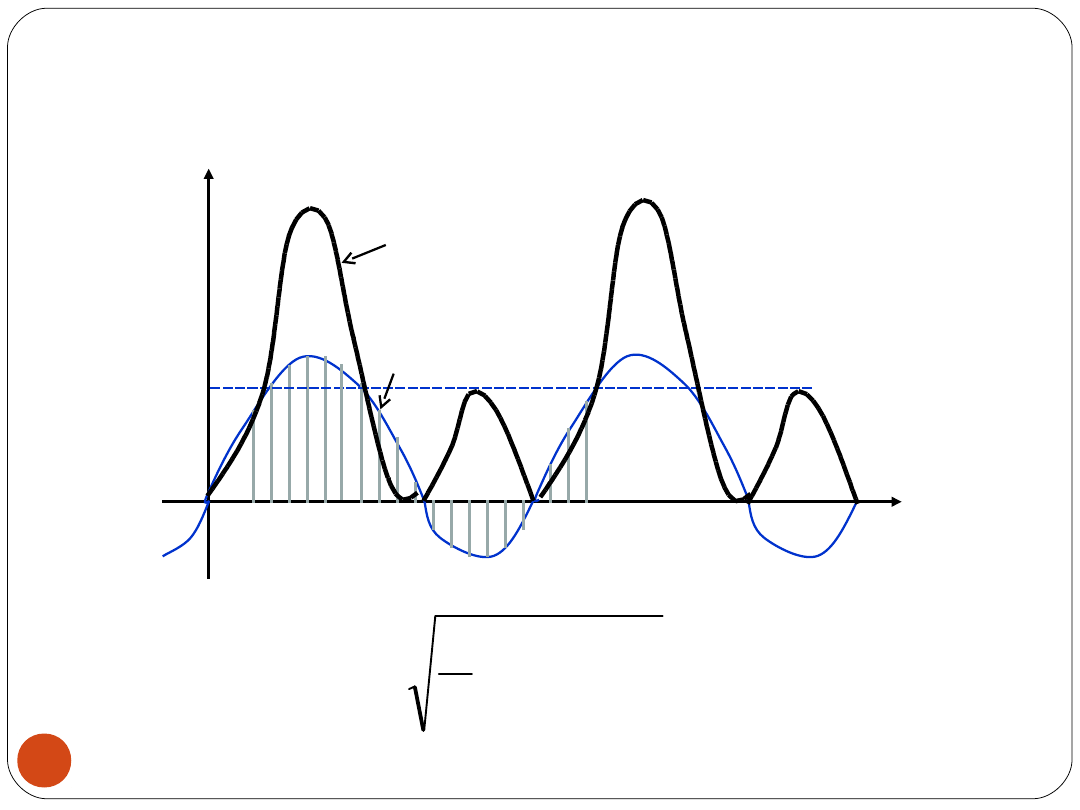
WARTOŚĆ SKUTECZNA

u

2

(t)

t

0

T+t

0

T

0

t

U







0

0

)

(

1

2

t

T

t

dt

t

u

T

U

u(t)

u

15

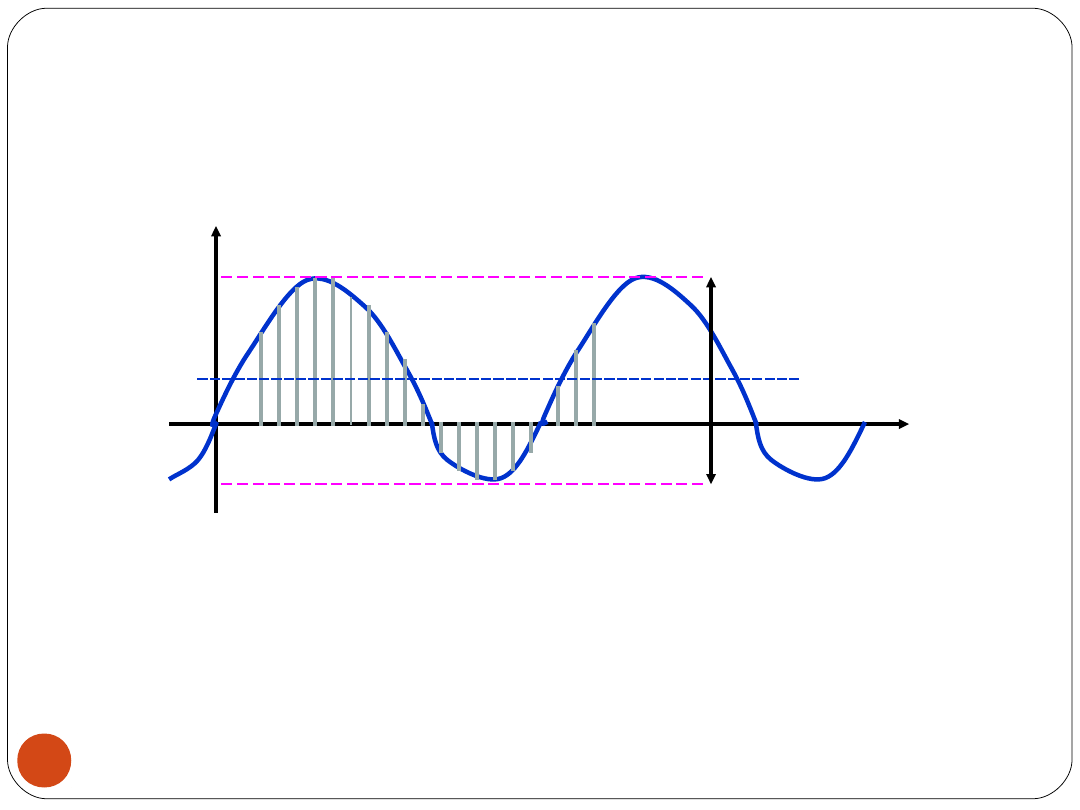
WARTOŚCI SZCZYTOWE

u(t)

t

0

T+t

0

T

0

t

U

0

U

M

+

U

M

-

U

MM

Wartość szczytowa maksymalna: U

M

+

=max[u(t)]

Wartość szczytowa minimalna: U

M

-

=min[u(t)]

Wartość międzyszczytowa: U

MM

= U

M

+

- U

M

-

16

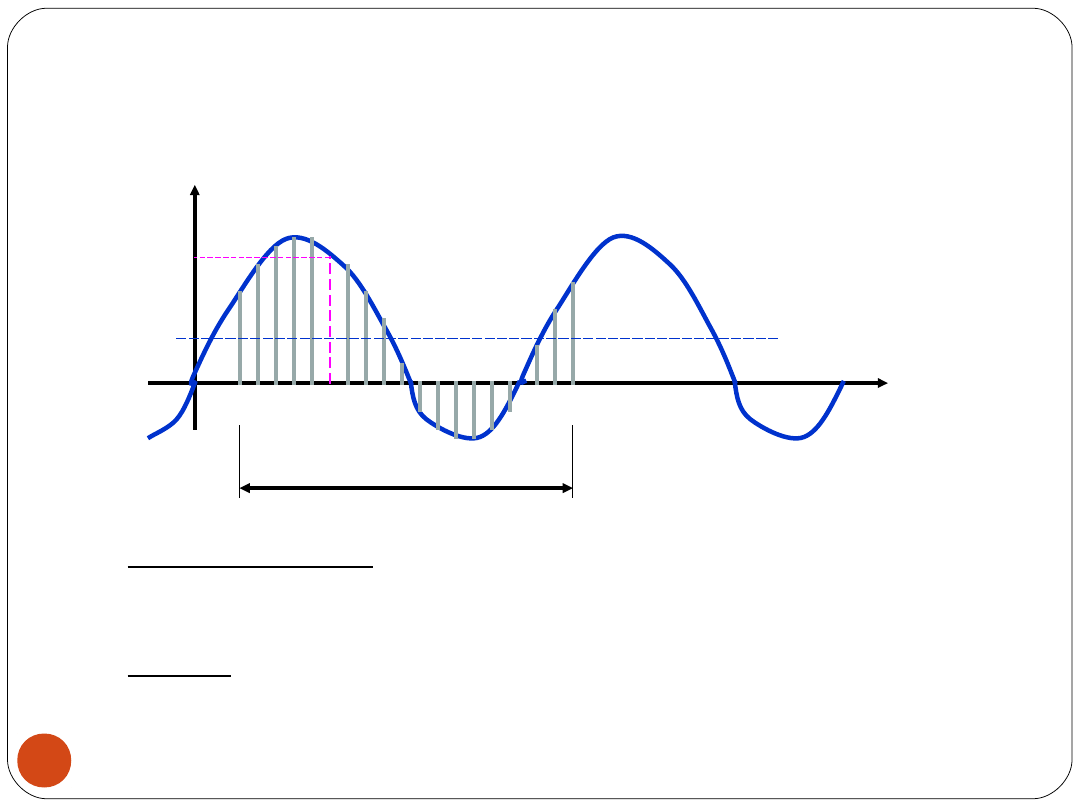
PARAMETRY ZWIĄZANE Z CZASEM

Częstotliwość f – liczba powtórzeń zjawiska
cyklicznego w jednostce czasu

Okres T = 1/f – czas, jaki upływa między
kolejnymi punktami przebiegu okresowego
mającymi tę samą fazę.

u(t)

t

0

t

k

T+t

0

T

0

t

u*(k)

U

0

T

17

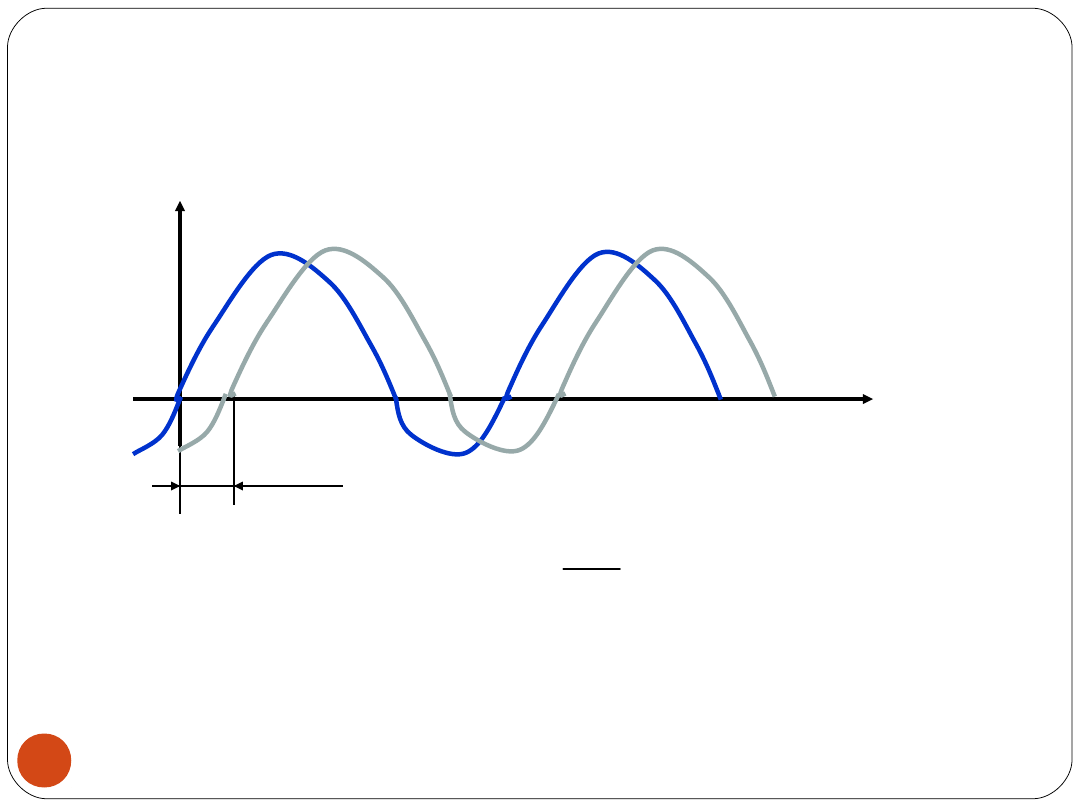
PARAMETRY ZWIĄZANE Z CZASEM

u(t)

T

0

t



Pulsacja:

T

f







2

2





Faza:











t

t)

(

Faza początkowa (przesunięcie fazowe): 

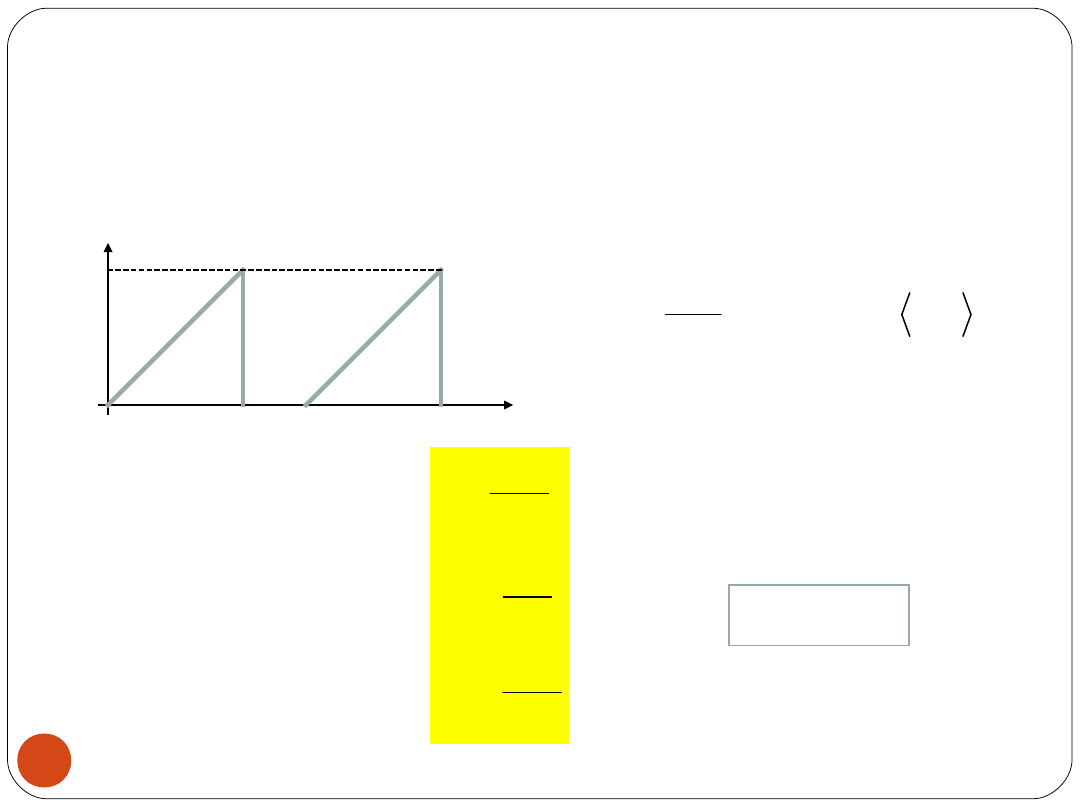
Zadanie 1

18

Obliczyć współczynniki kształtu, amplitudy i uśredniania dla
sygnału przedstawionego na rysunku.

u(t)

U

M

t

0

T

τ

 















T

t

dla

t

dla

t

U

t

u

M

;

0

;

0

)

(







w

m

u

m

a

w

U

U

k

U

U

k

U

U

k

0

0







U

m

= U

M

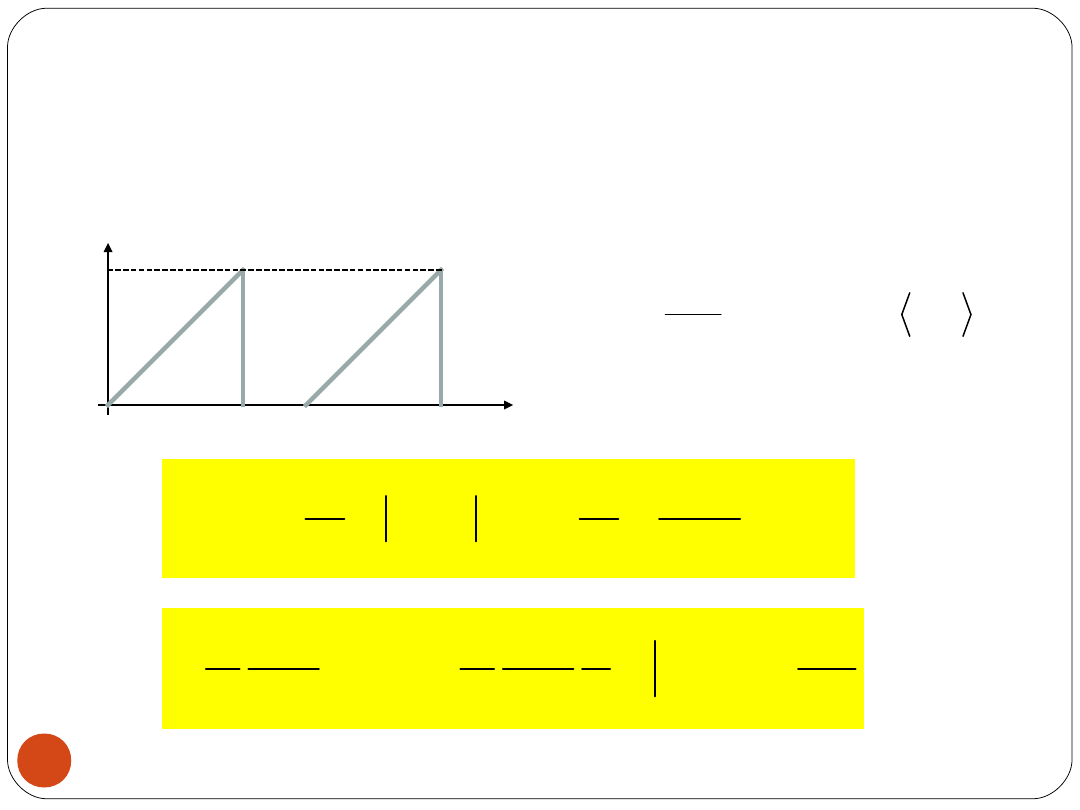
19

Obliczenie wartości średniej wyprostowanej U

0w

u(t)

U

M

t

0

T

τ

 















T

t

dla

t

dla

t

U

t

u

M

;

0

;

0

)

(

















T

M

w

tdt

U

T

dt

t

u

T

U

0

0

0

1

)

(

1





T

U

t

U

T

dt

t

U

T

M

M

M

2

2

1

1

1

0

2

0



















Zadanie 1 c.d.

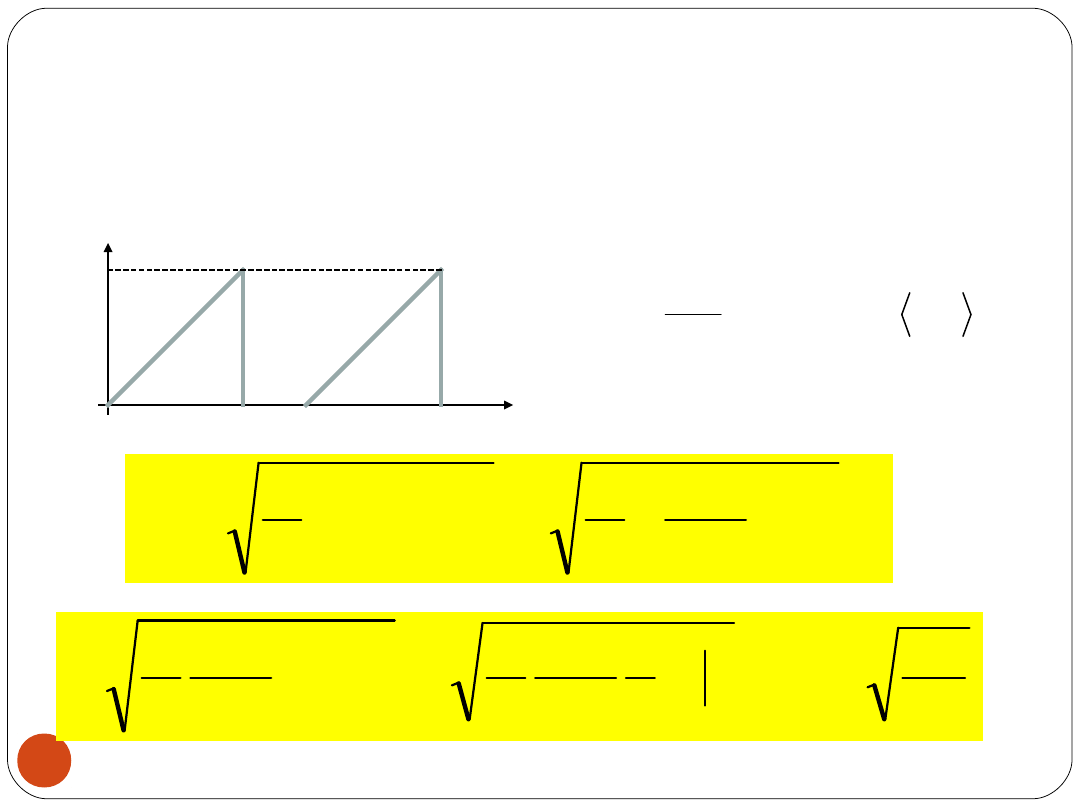
20

Obliczenie wartości skutecznej U

u(t)

U

M

t

0

T

τ

 















T

t

dla

t

dla

t

U

t

u

M

;

0

;

0

)

(





















0

2

2

2

0

2

1

)

(

1

dt

t

U

T

dt

t

u

T

U

M

T

T

U

t

U

T

dt

t

U

T

M

M

M

3

3

1

1

1

0

3

2

2

0

2

2

2



















Zadanie 1 c.d.

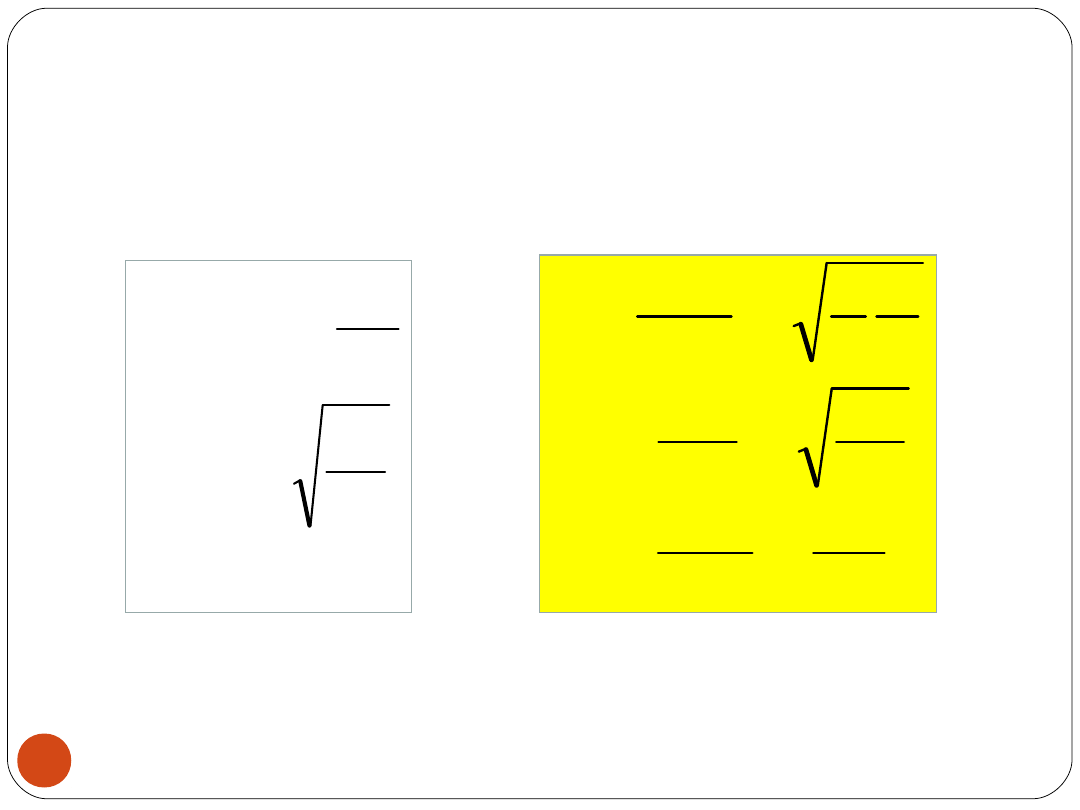
21

Obliczenie współczynników

M

m

M

M

w

U

U

T

U

U

T

U

U







3

2

0











T

U

U

k

T

U

U

k

T

U

U

k

w

m

u

m

a

w

2

3

3

4

0

0













Zadanie 1 c.d.

22

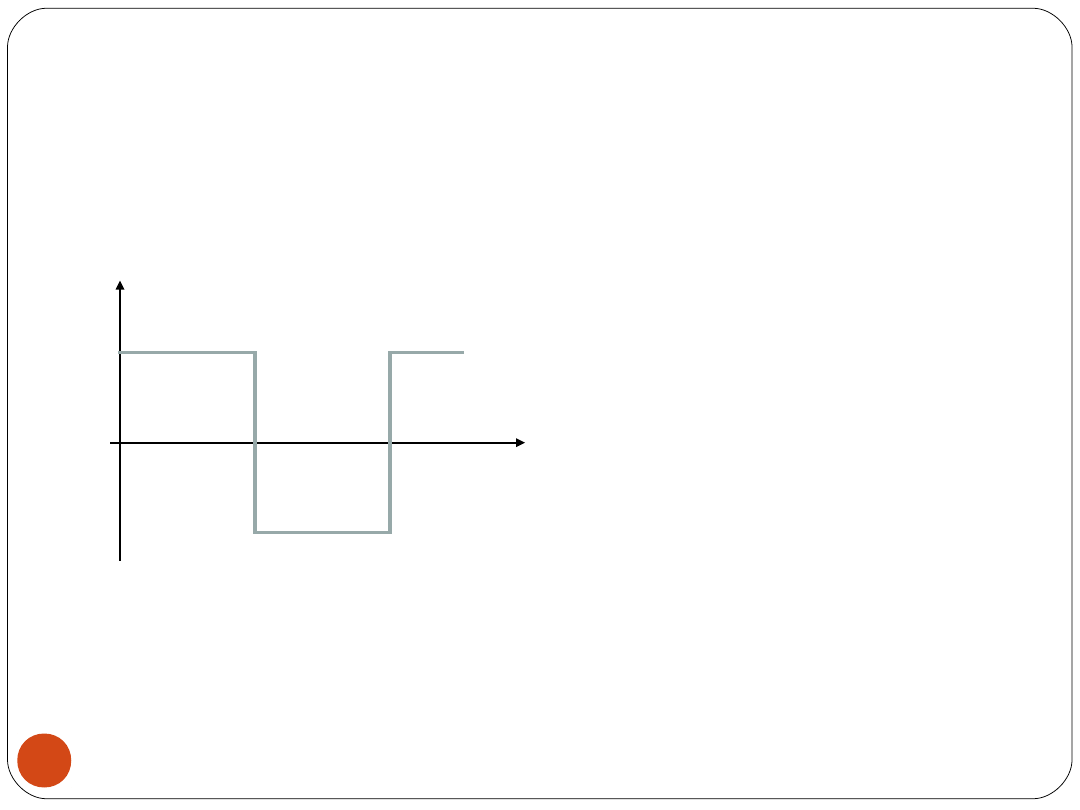
Obliczyć współczynniki kształtu, amplitudy i uśredniania dla
sygnału przedstawionego na rysunku.

u(t)

U

M

t

0

T

½T

-U

M

k= k

a

= k

u

= 1

Zadanie 2

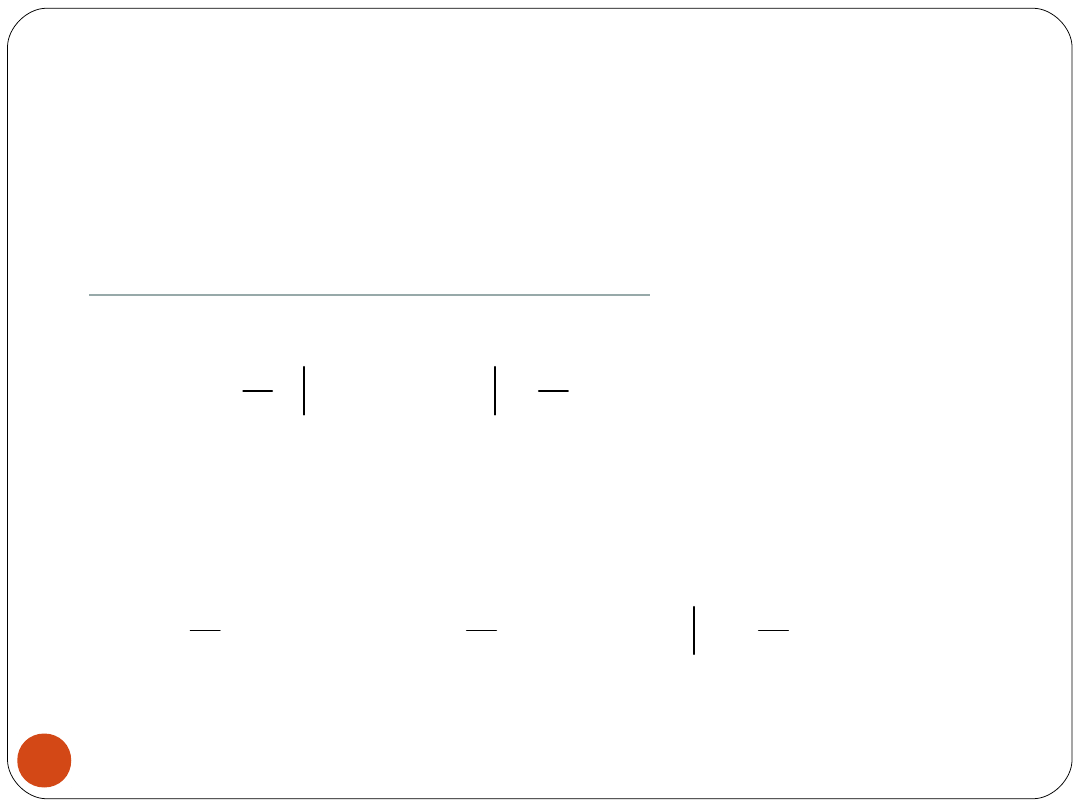
23

Obliczyć współczynniki kształtu, amplitudy i uśredniania dla
sygnału harmonicznego: u(t) = U

M

sint











T

T

M

M

w

tdt

U

T

tdt

U

T

U

0

2

/

0

0

sin

2

sin

1





po zmianie zmiennych:



t = x

M

M

M

U

x

U

dx

x

U











2

)

cos

(

1

sin

1

0

0











Wartość średnia wyprostowana

Zadanie 3

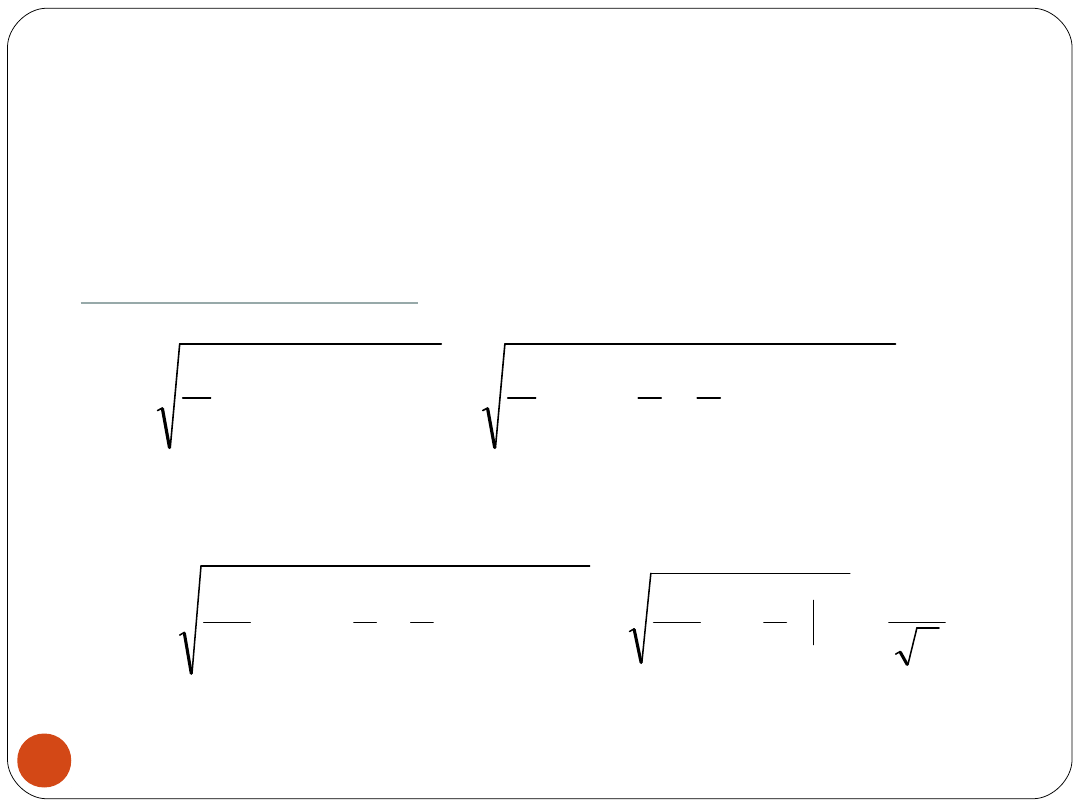
24

Obliczyć współczynniki kształtu, amplitudy i uśredniania dla
sygnału harmonicznego: u(t) = U

M

sint

po zmianie zmiennych:



t = x

Wartość skuteczna













 









T

M

T

M

dt

t

U

T

dt

t

U

T

U

0

2

0

2

2

2

cos

2

1

2

1

1

sin

1





2

2

1

2

1

2

cos

2

1

2

1

2

1

2

0

2

2

0

2

M

M

M

U

x

U

dx

x

U















 













Zadanie 3 c.d.

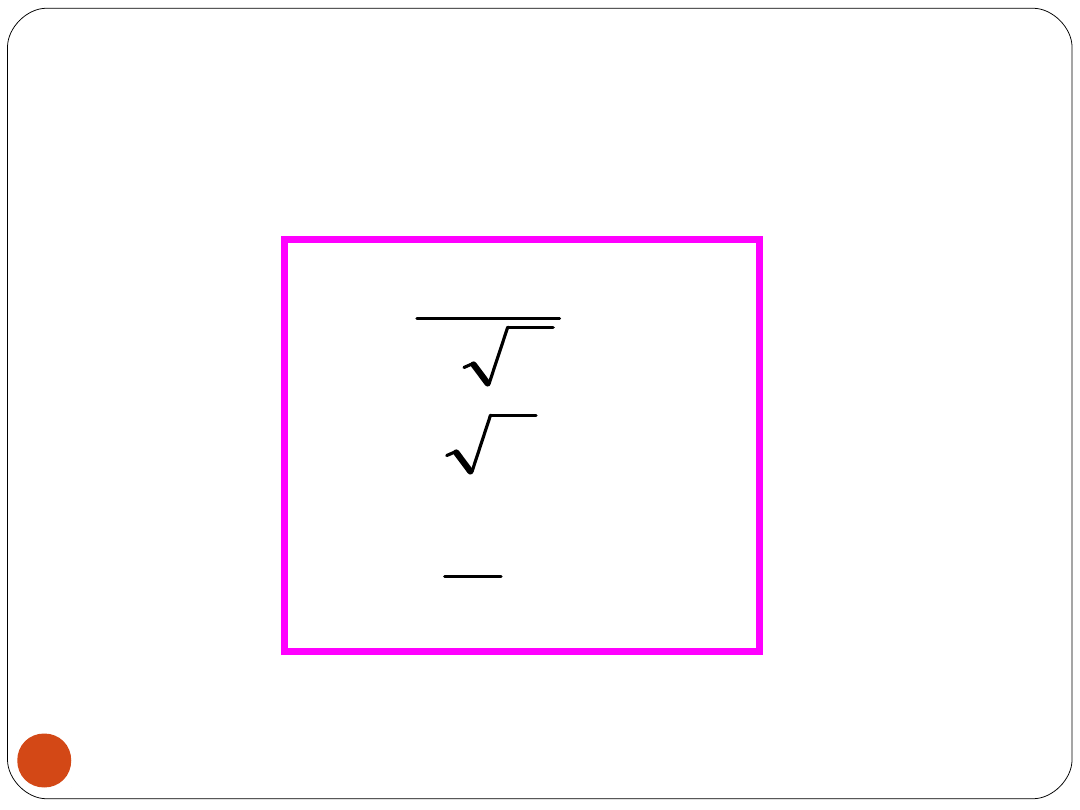
Współczynniki dla sygnału harmonicznego

25

57

,

1

2

41

,

1

2

11

,

1

2

2

















u

a

k

k

k

Zadanie 3 c.d.

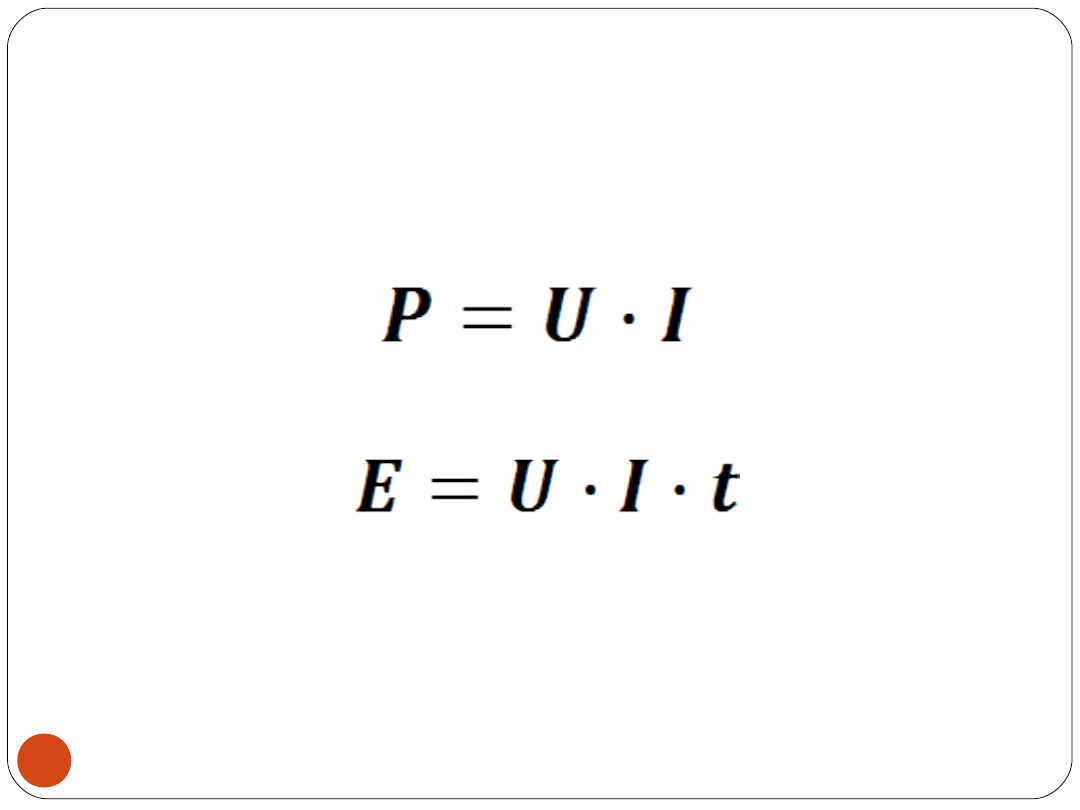
Moc i energia

26

Zadanie

4

27

u(t)

2

t

0

2

1

U

śr

= ?

U = ? P = ?

P

– moc wydzielana w oporniku

R = 2k