1

Wykład XVI i XVII

Tablice, rekordy i zbiory

Podstawy informatyki
Semestr II Transport

2

Tablica

Tablica

(ang.

array)

jest

prawdopodobnie

najbardziej znaną strukturą danych, ponieważ w
wielu językach, jest jedyną bezpośrednio dostępną
strukturą.
Tablica jest strukturą jednorodną; jest złożona ze
składowych tego samego typu zwanego typem
podstawowym.
Tablicę zwie się również strukturą o dostępie
swobodnym (ang. random access); wszystkie
składowe mogą być wybrane w dowolnej kolejności i
są jednakowo dostępne.

3

Definiowanie tablicy

W celu wybrania pojedynczej składowej nazwę
całej struktury uzupełnia się tzw. indeksem
wybierającym składową. Indeks ten powinien
być wartością pewnego typu zwanego typem
indeksującym (ang. index type) tablicy.
Definicja typu tablicowego T zawiera więc
zarówno specyfikację typu podstawowego T

0

,

jak i typu indeksującego I.

type T = array[I] of T

0

4

Przykłady definiowania

tablic

type Wiersz = array [1..5]

of real

type Karta = array [1..80]

of char

type alfa = array [1..10] of

char

5

Tablica typu Wiersz

Konkretną wartość

zmiennej

var x: Wiersz

której

każda

składowa

spełnia

równanie

x

i

=2

-t

,

można zobrazować

tak, jak pokazano

na rysunku

X

1

0.5

X

2

0.25

X

3

0.125

X

4

0.0625

X

5

0.03125

6

Konstruktor tablicowy

Złożoną wartość x typu T o
wartościach składowych c

1,

..., c

n

można

oznaczyć

za

pomocą

konstruktora

tablicowego

i

instrukcji przypisania:

x := T(c

1

,...,c

n

)

7

Selektor tablicowy

Operatorem odwrotnym do konstruktora

jest selektor. Służy on do wybrania

konkretnej składowej tablicy.
Dla danej zmiennej tablicowej x selektor

jest oznaczony nazwą tablicy, po której

występuje

indeks

i

wybierający

odpowiednią składową:

x[i]

8

Zmienna

tablicowa=tablica

zmiennych składowych

Działając na tablicach (zwłaszcza zaś na dużych), stosuje

się technikę selektywnego aktualizowania poszczególnych

składowych zamiast konstruowania całkowicie nowych

wartości złożonych. Wyraża się to traktowaniem zmiennej

tablicowej

jako

tablicy

zmiennych

składowych

i

umożliwieniem

wykonywania

przypisań

wybranym

składowym.

PRZYKŁAD

x[i]:= 0.125

Aczkolwiek aktualizacja selektywna powoduje zmianę

jedynie pojedynczej składowej wartości, jednak z

koncepcyjnego punktu widzenia musimy przyjąć, że

zmienia się również całą wartość złożoną.

9

Indeksy tablicy mogą być

obliczane

Niezwykle ważne konsekwencje pociąga za sobą fakt, że

indeksy tablicy, tzn. „nazwy" składowych muszą być

elementami zdefiniowanego typu skalarnego.
Indeksy mogą być, obliczane, tzn. stała indeksowa może

być zastąpiona wyrażeniem indeksowym. Wyrażenie

to ma być obliczone, a jego wynik decyduje o tym, która

składowa zostanie wybrana.
Wspomniana powyżej możliwość stanowi niezwykle

mocne narzędzie programowania, lecz jednocześnie

umożliwia

popełnianie

jednego

z

najczęściej

spotykanych błędów: wartość wynikowa może znaleźć

się poza przedziałem określonym jako możliwy zakres

indeksu tablicy.

10

Porównywanie tablic

Typ indeksujący powinien być typem skalarnym, tzn. typem

niezłożonym, na którym określona jest pewna relacja porządkująca.

Jeśli typ podstawowy tablicy jest również typem uporządkowanym,

to dostajemy naturalne uporządkowanie typu tablicowego.
Naturalne uporządkowanie dwóch tablic jest zdeterminowane

dwoma odpowiadającymi sobie nierównymi składowymi o

najniższych możliwych indeksach. Formalnie wyraża się to

następująco:

– Dla danych dwóch tablic x i y relacja x < y zachodzi wtedy i tylko

wtedy, gdy istnieje indeks k taki, że x[k]<y[k] oraz x[i]=y[i] dla

wszystkich i<k.

– Na przykład

(2, 3, 5, 7, 9)

< (2, 3, 5, 7, 11)

'LABEL' < 'LIBEL'

11

Moc typu tablicowego

W większości zastosowań nie zakłada się istnienia
relacji porządkującej na typach tablicowych.
Moc typu złożonego otrzymuje się jako iloczyn
mocy jego składowych. Ponieważ wszystkie
składowe typu tablicowego A są tego samego
typu podstawowego B, otrzymujemy

moc(A) = (moc(B))

n

gdzie n=moc(I), I zaś jest typem indeksującym
tablicy.

12

Korzystanie z selektora

tablicowego

Poniższy krótki program ilustruje użycie selektora

tablicowego.

Zadaniem

programu

jest

znalezienie

najmniejszego indeksu i składowej o wartości x.

Poszukiwania dokonuje się, przeglądając sekwencyjnie

tablicę a, zadeklarowaną jako

var a: array[1..N] of T; {N > 0}
i:=0;
repeat
i := i+1
until (a[i] = x) or (i=N);
if a[i] <> x then ShowMessage(

’nie ma takiego elementu

w a’

)

13

Czasem pomoże

wartownik

Inny wariant tego programu ilustruje znaną
metodę

z

wartownikiem

(ang.

sentinel),

ustawionym na końcu tablicy. Zastosowanie
wartownika

znacznie

upraszcza

warunek

zakończenia iteracji.
var a: array[1. .N+1] of T;
i:=0; a[N+1]:=x;
repeat i:=i+1 until a[i]=x;
if i>N then ShowMessage(’nie ma takiego
elementu w a’);

14

Aktualizacja selektywna,

niezmiennik pętli

Przypisanie

a[N+1]:=x

jest

przykładem

aktualizacji

selektywnej

(ang.

selective

updating), tzn. zmiany wybranej składowej

zmiennej złożonej.
Niezależnie od tego, jak często powtórzyło się

wykonanie instrukcji i:=i+1, spełniony jest

warunek
a[j]<>x, dla j = 1... i - 1
Warunek ten jest spełniony w obu wersjach

programu i nazywany jest niezmiennikiem

pętli (ang. loop invariant).

15

Metoda poszukiwania

połówkowego

Jeżeli

elementy

tablicy

zostały

wcześniej

uporządkowane

(posortowane), przeszukiwanie

można znacznie przyspieszyć. W takim przypadku

najczęściej

stosuje

się

metodę

połowienia

przedziału,

w

którym

ma

się

znajdować

poszukiwany element.
Metodę

tę,

nazywa

się

przeszukiwaniem

połówkowym (przeszukiwaniem binarnym; ang.

binary search). Przy każdym powtórzeniu dzieli się

na połowę przedział między indeksami i oraz j.

Górną granicą wymaganej liczby porównań jest

log

2

(N)

16

Przykład - Poszukiwanie

połówkowe

i:=1; j:=N;
repeat k:=(i+j) div 2;
if x>a[k] then i:=k+1 else j:=k-1
until (a[k]=x) or (i>j)

Odpowiednim warunkiem niezmienniczym na wejściu

do instrukcji iteracyjnej repeat jest

a[h]<x, dla h = 1..i –1

a[h]>x, dla h =j+1 .. N

W związku z tym, jeśli wykonanie programu kończy

się przy i>j, oznacza to, że nie istnieje a[h]=x takie,

że 1hN.

17

Składowe typów

tablicowych mogą być

złożone

Składowe typów tablicowych mogą być również

złożone. Tablica, której składowe są również tablicami,

jest zwana macierzą (ang. matrix). Np.

M: array[1..10] of Wiersz

jest tablicą o dziesięciu składowych (wierszach), z

których każda składa się z pięciu składowych typu real,

i

nazywa

się

macierzą

10x5

o

składowych

rzeczywistych.
Selektory mogą być konkatenowane tak, że

M[i][j]

oznacza j-tą składową wiersza M(i), który jest i-tą

składową macierzy M. Oznaczenie to skraca się zwykle
do postaci

M[i,j].

18

Deklarowanie tablic

wielowymiarowych

Podobnie deklaracja

M: array [1. .10] of array [1. .5] of

real

może być napisana w sposób bardziej
zwarty w postaci

M: array [1..10, 1..5] of real

19

Pętla „dla” często przydaje

się przy tablicach

Gdy pewna operacja ma być wykonana dla wszystkich

składowych tablicy (lub kilku kolejnych składowych), wygodnie

jest stosować instrukcję „dla", co ilustruje przykład (następny

slajd).
Załóżmy, że ułamek f jest reprezentowany za pomocą tablicy d w

ten sposób, że

tzn. przez swoje (k-1)-cyfrowe rozwinięcie dziesiętne. Następnie

ma zostać podzielone przez 2. Dokonuje się tego, powtarzając

operację dzielenia dla wszystkich k-1 cyfr, począwszy od i=1.

Operacja ta polega na podzieleniu cyfry przez 2, z

uwzględnieniem ewentualnego przeniesienia z poprzedniej

pozycji i zachowaniem ewentualnej reszty r do następnego kroku.











1

1

10

*

k

i

i

i

d

f

20

Przykład - Reprezentacja

dziesiętna ujemnych

potęg dwójki

program potęga (output);

{reprezentacja dziesiętna ujemnych potęg liczby 2}

{$APPTYPE CONSOLE}
const n=10; type cyfra=0..9; var i, k, r: integer; d: array [1. .n] of

cyfra;

begin for k: = 1 to n do
begin write ('.'); r:= 0;
for i:=1 to k-1 do
begin
r:=10*r+d[i]; d[i]:=r div 2; r:=r-2*d[i]; write(chr(d[i]+ord('0')))
end;
d[k]:=5; writeln('5')
end
end.

21

Przykład - Reprezentacja

dziesiętna ujemnych

potęg dwójki - wyniki

Postępowanie

zastosowano

w

programie (poprzedni slajd) w celu

otrzymania tablicy ujemnych potęg

dwójki.
Powtarzanie

operacji

połowienia

służących do obliczenia wartości 2

-1

,

2

-2

, ..., 2

-n

jest ponownie wyrażone za

pomocą instrukcji „dla", "prowadząc

do zagnieżdżenia dwóch takich

instrukcji.
Wyniki programu dla n = 10

przedstawiono obok.

.5
.25
.125
.0625
.03125
.015625
.0078125
.00390625
.001953125
.0009765625

22

Rekordy

Najbardziej

ogólną

metodą

tworzenia

typów

złożonych jest łączenie w typ złożony elementów o

dowolnych, być może złożonych typach.
Przykładami z matematyki są liczby zespolone

złożone

z

dwóch

liczb

rzeczywistych

bądź

współrzędne punktów złożone z dwóch lub więcej

liczb rzeczywistych w zależności od wymiaru

przestrzeni.
Przykładem z przetwarzania danych jest opis osoby

za pomocą kilku istotnych cech charakterystycznych,

takich jak imię, nazwisko, data urodzenia, płeć i stan

cywilny.

23

Iloczyn kartezjański

W matematyce taki typ złożony zwie się
iloczynem kartezjańskim typów składowych.
Wypływa to z faktu, że zbiór wartości definiujący
ten typ składa się ze wszystkich możliwych
kombinacji wartości wziętych odpowiednio ze
wszystkich typów składowych.
Liczba takich kombinacji jest równa iloczynowi
liczb elementów wszystkich typów składowych,
czyli moc typu złożonego równa jest iloczynowi
mocy typów składowych.

24

Rekord znaczy zapis

W przetwarzaniu danych typy złożone, takie jak
opisy osób czy innych obiektów, służą do
zapisywania

i

rejestracji

ukierunkowanych

problemowo charakterystyk tych osób czy obiektów;
Są one zazwyczaj przechowywane w plikach i
„bankach(bazach) danych”. Fakt ten tłumaczy
stosowanie angielskiego słowa record (zapis, rejestr,
nagranie, przechowywany zestaw informacji) do
oznaczania tego rodzaju danych zamiast terminu
„iloczyn kartezjański".

25

Definiowanie typu

rekordowego

Ogólnie, typ rekordowy T jest zdefiniowany

w następujący sposób:
type T = record
s

1

: T

1

;

s

2

: T

2

;

...
s

n

: T

n

;

end
moc(T)=moc(T

1

) *... * moc (T

n

)

26

Przykłady definicji typów

rekordowych

type Zespolona = record
re: real;
im: real
end

type Data=record
dzien: 1.. 31;
miesiac: 1..12;
rok: 1..3000;
end

type Osoba = record
nazwisko: String[50];
imie: String[50];
dataurodzenia: Data;

plec:

(mezczyzna,

kobieta);

stancywilny: (wolny,

zonaty,

owdowialy,

rozwiedziony)

end

27

Konstruktor rekordowy

Za

pomocą

konstruktora

rekordowego

można

utworzyć

wartość typu T, a następnie przypisać
ją jakiejś zmiennej tego typu:

x:=T(x

1

, x

2

, ..., x

n

)

gdzie x

i

są odpowiednio wartościami z

typów składowych T

i

.

28

Zespolona z

Data d

Osoba p

1.0

1

WIRTH

-1.0

4

CHRIS

1973

18 1 1966

mężczyzna

wolny

Przypisywanie danych

do zmiennych

rekordowych

Dla danych
zmiennych
rekordowych

z: Zespolona
d: Data
p: Osoba

konkretne wartości mogą być przypisane następująco
z:= Zespolona(1.0, -1.0)
d:= Data(1,4,1973)
p:=

Osoba

(‘WIRTH',

‘CHRIS',

Data(18,1,1966),

mezczyzna, wolny)

29

Selektory rekordowe

Identyfikatory s

1

,..., s

n

wprowadzone w

definicji typu rekordowego stanowią nazwy

przydzielone

poszczególnym

składowym

zmiennych tego typu;
Stosuje się je w selektorach rekordowych

odnoszących sięs do zmiennych rekordowych.
Dla danej zmiennej x: T, jej i-ta składowa jest

oznaczona przez

x.s

30

Aktualizacja selektywna

Aktualizację selektywną x prowadzi
się

przy

użyciu

tego

samego

oznacznika selektora stojącego po
lewej stronie instrukcji przypisania:

x.s

i

:=x

i

gdzie x

i

jest wartością (wyrażeniem)

typu T

i

31

Przykłady selektorów

Dla danych zmiennych rekordowych

z: Zespolona
d: Data
p: Osoba

selektory niektórych składowych są następujące:

z.im

(typu real)

d.miesiac

(typu 1..12)

p.nazwisko

(typu String[50])

p.dataurodzenia

(typu Data)

p.dataurodzenia.dzien

(typu 1..31)

32

Typy złożone można

składać

również z typów złożonych

Przykład typu Osoba dowodzi, że typy składowe
rekordu mogą również mieć pewną złożoną
strukturę. Selektory można zatem składać.
Oczywiście operację składania typów o różnych
składowych można wykonywać wielokrotnie
(wielopoziomowo). Na przykład j-ta składowa
tablicy

a,

będącej

składową

zmiennej

rekordowej r, jest oznaczana przez r.a[i] a
składowa o selektorze s i-tej składowej
rekordowej tablicy a jest oznaczana przez a[i].s

33

Poprawna definicja typu

nie gwarantuje

sensownych danych

Charakterystyczną cechą iloczynu kartezjańskiego jest

to, że zawiera on wszystkie kombinacje elementów

typów składowych.
Trzeba jednak pamiętać, że w praktyce nie wszystkie

muszą

być

„prawidłowe”,

tzn.

sensowne.

Np.

zdefiniowany poprzednio typ Data zawiera mógłby

zawierać wartości (31,4,1973) i (29,2,1815), które

odpowiadają datom nie istniejących nigdy dni.
Jak widać, definicja tego typu nie odzwierciedla sytuacji

rzeczywistej.

Niemniej

jednak

praktycznie

jest

dostatecznie bliska rzeczywistości; od programisty

zależy, aby bezsensowne wartości nigdy nie wystąpiły

podczas wykonania programu.

34

Przykład– korzystanie

ze zmiennych

rekordowych

Przytoczony poniżej krótki fragment programu

ilustruje użycie zmiennych rekordowych. Jego

zadaniem jest zliczenie „Osób” reprezentowanych

w tablicy a jako kobiety stanu wolnego.

 

var a: array [1.. N] of Osoba;
licznik: integer;
licznik:=0; for i:=1 to N do
if (a[i].plec=kobieta) and (a[i].stancywilny = wolny)
then licznik:=licznik+1

35

Instrukcja wiążąca

W innym wariancie powyższego fragmentu programu

korzysta się z konstrukcji zwanej instrukcją wiążącą

with:

  for i:=1 to N do

with a[i] do
if (plec=kobieta) and (stancywilny=wolny) then

licznik:=licznik+1

Konstrukcja with r do s oznacza, że można używać nazw

selektorów z typu zmiennej r bez poprzedzenia ich nazwą

zmiennej, ponieważ wiadomo, że będą się do niej odnosiły.
Użycie instrukcji with skraca więc tekst programu, jak

również zapobiega wielokrotnemu obliczaniu od nowa

składowej indeksowanej a[i].

36

Rekordy vs. Tablice

Strukturę rekordu i strukturę tablicy charakteryzuje

wspólnie cecha „dostępu swobodnego”.
Rekord jest strukturą bardziej ogólną w tym sensie,

że nie ma tu wymagania, aby wszystkie typy

składowe były identyczne.
Jednakże stosowanie tablicy zapewnia większą

elastyczność,

ponieważ

selektory

składowych

tablicy mogą być wartościami obliczanymi w

programie (reprezentowanymi przez wyrażenia),

podczas gdy selektory składowych rekordu są

sztywno

ustalonymi

identyfikatorami

wprowadzonymi w definicji odpowiedniego typu.

37

Rekordy z wariantami

W praktyce okazuje się zazwyczaj wygodne i

naturalne traktowanie dwóch typów po prostu jako

wariantów tego samego typu.
Na przykład typ Wspolrzedne można traktować

jako

sumę

dwóch

wariantów,

mianowicie

współrzędnych

kartezjańskich

i

biegunowych,

których składowymi są odpowiednio (a) dwie

wielkości liniowe i (b) wielkość liniowa i kątowa.
W celu rozpoznania wariantu, który aktualnie jest

wartością zmiennej, wprowadza się trzecią składową

zwaną

wyróżnikiem

typu

albo

polem

znacznikowym.

38

Przykład rekordu

wariantowego

type Współrzędne =

record case rodzaj: (kartezjanskie, biegunowe)

of
kartezjanskie: (x, y: real);
biegunowe: (r: real; kat: real)
end
W tym przypadku nazwą pola znacznikowego jest

rodzaj, a nazwy współrzędnych stanowią albo x i

y - wartości współrzędnych kartezjańskich, albo r

i kat - wartości współrzędnych biegunowych.

39

Zbiór wartości typu i jego

moc

Zbiór wartości typu Współrzędne jest
sumą dwóch typów:
T

1

= (x, y: real);

T

2

= (r: real; kat: real)

a jego moc jest sumą mocy T

1

i T

2

40

Rekordy o częściowo

identycznych składowych

Bardzo często jednak nie mamy do czynienia z dwoma

całkowicie różnymi typami, lecz raczej z typami o

częściowo identycznych składowych.
Fakt ten zadecydował o nazwie takiego typu - rekord z

wariantami (ang. variant record).
Przykładem jest typ Osoba zdefiniowany na jednym z

poprzednich slajdów, w którym informacje mogłyby

zależeć od płci osoby.
Na przykład dla mężczyzny charakterystycznymi

informacjami mogą być jego waga oraz to, czy jest

brodaty, podczas gdy dla kobiety informacjami tymi

mogą być trzy charakterystyczne wymiary figury

(natomiast waga może pozostać nieujawniona).

41

Przykład – nowa definicja

typu osoba

Definicja takiego typu wyglądałaby więc następująco:
type Osoba=

record
nazwisko, imie: String[50];
dataurodzenia: data;
stancywilny: (wolny, zonaty, owdowialy, rozwiedziony);
case plec: (mezczyzna, kobieta) b
mężczyzna:

(waga: real;

brodaty: Boolean);
kobieta: (wymiary: array [1..3] of integer)
end

42

Ogólna postać definicji

rekordu z wariantami

type T =

record s

1

: T

1

;...; s

n-1

: T

n-1

;

case s

n

: T

n

of

c

1

: (s

1,1

: T

1,1

; ...; s

1,n1

: T

1,n1

);

……………………………….
c

m

: (s

m,1

: T

m,1

; ...; s

m,nm

: T

1,nm

);

end
Identyfikatory s

i

i s

ij

są nazwami składowych dla typów T

i

i T

ij

, a s

n

jest nazwą wyróżniającego pola znacznikowego o typie T

n

. Stałe

c

1

...c

m

oznaczają wartości typu (skalarnego) T

n

.

Zmienna x typu T zawiera składowe x.s

1

, x.s

2

, …, x.s

n

, x.s

k,1

, ...,

x.s

k,nk

wtedy i tylko wtedy, gdy (bieżąca) wartość x.s

n

jest równa

c

k

. Składowe x.s

1

, ..., x.s

n

tworzą część wspólną m wariantów.

43

Brodata pani

Wynika stąd, że użycie selektora składowej

x.s

k,h

(1≤h≤n

k

),

gdy

x.s

n

≠c

k

,

należy

traktować jako poważny błąd programu,

gdyż

może

to

prowadzić

do

wielu

paradoksalnych konsekwencji.
Dla zdefiniowanego poprzednio typu Osoba

może to spowodować np.

– zapytanie, czy pani jest brodata,
– lub (w przypadku aktualizacji selektywnej)

żądanie, aby taką była.

44

Jeśli chcemy uniknąć

problemów dobrze jest

skorzystać z instrukcji

wyboru

Jak widać, rekordy z wariantami wymagają niezwykle

uważnego programowania. Odpowiednie operacje na

poszczególnych wariantach najlepiej grupować w

instrukcję wybiórczą, tzw. instrukcję wyboru, której

struktura odzwierciedla strukturę definicji rekordu z

wariantami.

case x.s

n

of

c

1

: S

1

;

c

2

: S

2

;

…
c

m

: S

m

;

end

45

Przykład – obliczanie

odległości pomiędzy

dwoma punktami

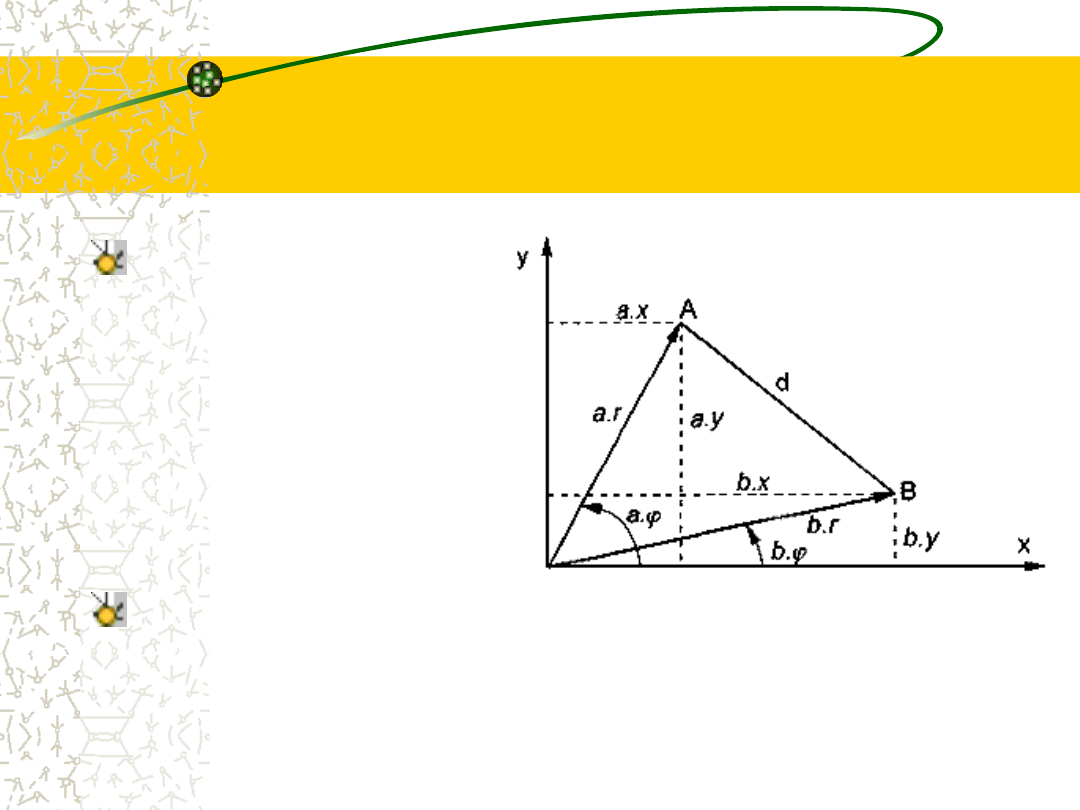
Przytoczony

dalej

fragment programu ma

za zadanie obliczenie

odległości

między

punktami

A

i

B

zadanymi

w

postaci

zmiennych a i b typu

Wspolrzedne, będącego

rekordem z wariantami.

Procedura obliczeń jest odpowiednio odmienna dla każdej

z czterech możliwych kombinacji określania zmiennych za

pomocą współrzędnych kartezjańskich lub biegunowych.

46

Kod realizujący zadanie z

przykładu

case a.rodzaj of

kartezjanskie:case b.rodzaj of
kartezjanskie: d:=sqrt(sqr(a.x-b.x)+sqr(a.y-b.y));
biegunowe:d:=sqrt(sqr(a.x-b.r*cos(b.kat))+sqr(a.y-

b.r*sin(b.kat)))

end;

biegunowe: case b.rodzaj of
kartezjanskie:

d:=sqrt(sqr(a.r*sin(a.kat)-b.x)

+sqr(a.r*cos(a.kat)-b.y))
biegunowe: d:=sqrt(sqr(a.r)+sqr(b.r)-2*a.r*b.r*cos(a.kat-b.kat))

end
end

47

Zbiory

Trzecią podstawową strukturą danych - oprócz

tablicy i rekordu - jest struktura zbioru (ang. set

structure). Definiuje się ją za pomocą deklaracji o

podanej poniżej postaci:

type T = set of T

0

Wartościami zmiennej x typu T są zbiory

elementów typu T

0

.

Zbiór

wszystkich

możliwych

podzbiorów

elementów T

0

nazywa się zbiorem potęgowym

T

0

. W związku z tym typ T stanowi zbiór potęgowy

swego typu podstawowego T

0

.

48

Przykłady typów

zbiorowych

type zbiorcalk

= set of 0..30

type zbiorznakow = set of char
type koloryteczy = set of kolor

Podstawę

dla

drugiego

przykładu

stanowi

standardowy zbiór znaków oznaczony typem char,

podstawą dla trzeciego przykładu jest zbiór kolorów,

który można zdefiniować jako typ skalarny

type kolor=(zolty, pomaranczowy, czerwony,

zielony, niebieski, fioletowy)

opisujący różne kolory, jakie mogą wchodzić w skład

tęczy.

49

Przypisywanie wartości

zmiennym typu

zbiorowego

Dla danych zmiennych
zc

:

zbiorcalk

zz

:

zbiorznakow

t : array [1. .6] of koloryteczy
można wykonać przypisania dla poszczególnych wartości

typu zbiorowego:
zc:= [1, 4, 9, 16, 25] zz := ['+','-','*','/']
t[3]

:

= [zolty] t[5]=[ ]

t[6]=[czerwony..fioletowy]

Wartość

przypisania

zmiennej

t[3]

stanowi

zbiór

jednoelementowy zawierający pojedynczy element zolty;

zmiennej t[5] jest przypisany zbiór pusty, co oznacza, że w

skład piątej tęczy nie wchodził żaden kolor (nie istniała?),

natomiast zmiennej t[6] przypisano zbiór złożony z czterech

spośród możliwych kolorów.

50

Moc typu zbiorowego

Moc typu zbiorowego T jest określona wzorem

Wzór ten wynika bezpośrednio z faktu, że każdy z

elementów T

0

musi być reprezentowany przez jedną

z dwóch wartości: „jest” lub „nie ma” oraz stąd, że

wszystkie elementy są wzajemnie niezależne.
Dla efektywnej i ekonomicznej realizacji jest istotne,

aby typ podstawowy był nie tylko skończony, ale

aby jego moc była stosunkowo niewielka.

 

 

0

2

T

moc

T

moc 

51

Elementarne działania na

zbiorach

Na wszystkich typach zbiorowych są określone

następujące operatory elementarne:

*

przecięcie zbiorów

+

suma zbiorów

-

różnica zbiorów

in

przynależność do zbioru

52

Przykłady działań na

zbiorach

Konstruowanie przecięcia (iloczynu) i sumy zbiorów

nazywa się też często, odpowiednio, mnożeniem i

dodawaniem zbiorów.
Zgodnie z tą analogią określa się też priorytety operatorów

zbiorowych: największy priorytet otrzymuje operator

przecięcia zbiorów, następnie - operator sumy i różnicy,

najmniejszy zaś priorytet - operator przynależności do

zbioru, klasyfikowany na równi z operatorami relacyjnymi.
Poniżej podano przykłady wyrażeń zbiorowych i ich

odpowiedników z nawiasami:
r*s+t=(r*s)+t r-s*t=r-(s*t)
r-s+t=(r-s)+t x in s+t=x in (s+t)

53

Podstawowe statyczne

złożone struktury danych

Strukt

ura

Deklaracja Selektor

Dostęp do

składowych

Typ

składwy

ch

Moc

Tablica

a: array [/]

of T

0

a[i]
(iI)

Selektor

z

obliczanym

indeksem i

Wszystk

ie

jednako

we (T

0

)

moc(T

0

)

m

oc(l)

Rekord

r: record
s

1

: T

1

;

...
s

n

: T

n

;

end

r.s
(s[s

1

,...,

s

n

])

Selektor

z

deklarowaną

nazwą

składowej s

Mogą

być

różne

Zbiór

s : set of

T

0

nie

istnieje

Test

przynależność

za

pomocą

operatora

relacyjnego in

Wszystk

ie

jednako

we

(typu

T

0

)

 





n

i

i

T

moc

1

 

0

2

T

moc