Zajęcia nr 2/3

Analiza wydajności algorytmów

– złożoność i jej miary

Algorytmy i struktury danych

Prowadzący

:

dr hab.inż. ANDRZEJ WALCZAK,

prof.WAT

Złożoność obliczeniowa algorytmów

-

analiza algorytmów

• Analiza algorytmów - złożoność obliczeniowa jest podstawową

własnością określaną dla algorytmów. Zadaniem analizy

algorytmu jest określenie tej złożoności, a co za tym idzie

określenie realizowalności algorytmu oraz jego wydajności..

• Algorytmy

realizowalne

mają

najczęściej

złożoność

aproksymowaną funkcją:

– liniową (wielomianem)
– logarytmiczną.

Mówi się, że takie algorytmy określają zadania ze zbioru

zadań

rozwiązywalnych

(a

co

za

tym

idzie

implementowalnych). Najszybsze są algorytmy o złożoności

logarytmicznej.

• Nie potrafimy skutecznie implementować algorytmów o

złożoności wykładniczej.

Rodzaje złożoności algorytmów

• Złożoność zasobowa (pamięciowa) - wyrażana w skali

zajętości zasobów (PAO, pamięci zewnętrznych itp.)
niezbędnych dla realizacji algorytmu

• Złożoność czasowa - wyrażana w skali czasu wykonania

algorytmu (liczba kroków, aproksymowany czas
rzeczywisty)

• Przykłady szacowania wartości złożoności algorytmów

będziemy realizować przy okazji konkretnych
przykładów na kolejnych wykładach

• De facto wszystko przenosi się w konsekwencji na

koszty eksploatacji oprogramowania, realizującego
analizowany algorytm

Czynniki wpływające na złożoność

algorytmów

• Rozmiar zadania - rozmiar danych niezbędnych dla

realizacji algorytmu. Bierze się pod uwagę:

– rozmiar danych wejściowych
– rozmiar danych roboczych
– rozmiar danych wyjściowych

• Czas działania algorytmu - liczba kroków przekładająca

się na czas faktycznej pracy maszyny realizującej
algorytm. Istotne znaczenie mają w tym przypadku:

– złożoność obliczeniowa rozwiązywanego zadania
– sposób konstrukcji algorytmu
– wydajność maszyny realizującej obliczenia

Funkcja kosztu algorytmu

• Funkcja kosztu zasobowego algorytmu stanowi odwzorowanie

rozmiaru zadania w umowne jednostki kosztu algorytmu (np.
rozmiar zasobów, jednostki monetarne (złotówki, dolary itp.)):

– FKz : RZ -> WKz, gdzie: FKz - funkcja kosztu zasobowego,

RZ - rozmiar zadania,

WKz - wartość kosztu zasobowego,

Dla potrzeb wykładu pozostaniemy jedynie przy

kosztach zasobowych algorytmów.

• Jednak nie tylko koszty zasobowe są brane pod uwagę. Często

analizuje się inne koszty realizacji algorytmów (np. pieniądze).

 Przejrzyj ponownie slajdy z analizą efektywności algrytmu

Fibonacciego. Co możesz powiedzieć na temat jego
złożoności obliczeniowej?

Asymptotyczna złożoność

algorytmów

• Asymptotyczna oznacza, że dla dostatecznie dużych danych

wejściowych n liczymy tylko rząd wielkości czasu działania
algorytmu;

• Zapiszmy formalnie asymptotyczną górną granicę

(pesymistyczny czas działania algorytmu):

•

O( g(n) ) = { f(n): 0 <= f(n) <= c*g(n), c > 0, n > N}

•

Jest to przykład tak zwanej notacji dużego O. Fakt, że
dana wielkość jest rzędu f zapisujemy symbolicznie
jako O(f).

•

W zapisie formalnym złożoności wskazano, że
złożoność zależy od liczby przetwarzanych danych n.

Przykłady asymptotycznej

złożoności algorytmów

• W praktyce, większość algorytmów ma złożoność zaliczaną do

jednej z poniższych klas:

– log n, czyli złożoność logarytmiczna. Podstawa logarytmu

nie ma tu znaczenia, gdyż jej zmiana oznacza jedynie

przemnożenie przez stałą.

– n, n

2

, ..., czyli złożoność liniowa, kwadratowa, sześcienna

lub inaczej złożoność wielomianowa, gdyż funkcje te są

wielomianami zmiennej n. Problemy dla których istnieją

algorytmy o złożonosci co najwyżej wielomianowej,

nazywane są problemami typu P (ang. polynomial, czyli

wielomian).  Jest to bardzo ważna klasa algorytmów, gdyż

algorytmy które mają złożoność czasową co najwyżej

wielomianową, (czyli są O(n

k

), k=1,2,...) dają się w

użytecznym czasie wykonać na komputerach dla większości

rzeczywistych problemów.

– n log n czyli złożoność liniowo logarytmiczna.

– n

log n

 , czyli złożoność podwykładnicza

– 2

n

, czyli złożoność wykładnicza

– n!, czyli złożoność wykładnicza n!

Przykłady asymptotycznej

złożoności algorytmów

• Pojedyncza instrukcja

– s1; s2; …. ; sk

• O(1) dopóki k jest stałą

• Pojedyncza pętla

– for(i=0;i<n;i++) { s; }

• Założenie: s jest O(1)
• Złożoność czasowa jest: n O(1) lub O(n)

• Zagnieżdżona pętla:

– for(i=0;i<n;i++)

for(j=0;j<n;j++) { s; }

– Złożoność jest: n O(n) lub O(n

2

)

Analiza wydajności algorytmów

– złożoność i jej miary

• Do opisu wydajności (złożoności) algorytmów używa się

najczęściej tzw. O notacji. Opisuje ona górne
ograniczenie funkcji z dokładnością do czynnika stałego.

• Wydajność algorytmu rozumiemy ogólnie jako liczbę

operacji wykonywanych w algorytmie w zależności od
liczby przetwarzanych danych. Jeśli dane mają rozmiar n
to złożoność algorytmu zapiszemy jako pewną funkcję
f(n).

• Notacje O rozumiemy jako wskazanie funkcji g(n) takiej,

że istnieje takie n

0

, że dla n>n

0

zawsze f(n)<cg(n) gdzie

c jest stałą. Notacja O wskazuje nam wiec majorantę
albo inaczej ograniczenie górne funkcji złożoności
algorytmu.

Analiza wydajności algorytmów

– złożoność i jej miary

• Symetrycznie do O-notacji stosuje się 

-notację, która oznacza ograniczenie
złożoności od dołu czyli minorantę.

• Notacje  rozumiemy jako wskazanie

funkcji g(n) takiej, że istnieje takie n

0

,

że dla n>n

0

zawsze f(n)>cg(n) gdzie c

jest stałą. Notacja  wskazuje nam wiec

minorantę albo inaczej ograniczenie
dolne funkcji złożoności algorytmu.

Analiza wydajności algorytmów

– złożoność i jej miary

• Łatwo zauważyć, że definicje złożoności

mają charakter asymptotyczny co
oznacza, że rozumiemy je jako zdążanie
złożoności

algorytmu

do

funkcji

wskazanej przez O-notację albo -

notację przy odpowiednio dużej liczbie
zmiennych

w

algorytmizowanym

zdaniu.

Reguły O-notacji

• Oceniając liczbę operacji w algorytmie możemy

pominąć składniki stałe wobec składników
zależnych od n bo wraz ze wzrostem n udział
składników stałych będzie tak mały, że możemy go
zaniedbać. Podobnie w oszacowaniu złożoności
możemy uzasadnić pomijanie czynników stałych.
Jeśli algorytm zawiera kilka składowych
elementów, z których każdy wnosi swoją złożoność
tak, że możemy skonstruować funkcję f(n) =
n

3

+n

2

+n+..., to do oceny majoranty g(n) bierzemy

tylko składnik o najwyższym wykładniku.

Formalizm O-notacji

• Składniki stałe zapisujemy jako O(1) czyli

O(const) = O(1)

• Pomijamy czynniki stałe O(const*f) = c O(f) = O(f)
• Dodawanie elementów składowych jest

uwzględniane przez wybranie składnika o
najwyższej potędze O(f

1

) + O(f

2

) = O(f

1

+f

2

) =

max(O(f

1

), O(f

2

))

• Jeśli mnożone są elementy składowe o różnej

złożoności to mnożenie ulega zachowaniu O(f

1

)

O(f

2

) = O(f

1

*f

2

)

Przykłady O-notacji

złożonoś

ć

przykład

O(1)

Pobieranie pierwszego elementu ze

zbioru danych

O(lg n)

Podział n elementowego zbioru na

pół, następnie podział części na pół
itd.

O(n)

Przeglądanie zbioru n danych

Przykłady O-notacji

złożonoś

ć

przykład

O(n lg n) Kolejne podziały zbioru na pół

połączone z ich przeszukiwaniem

O(n

2

)

Przeglądanie zbioru n

elementowego raz dla każdego

elementu z innego równolicznego

zbioru danych

O(2

n

)

Generowanie wszystkich możliwych

podzbiorów zbioru n danych

Inne typy notacji złożoności

algorytmów

• Definicja: funkcja f(n) ma złożoność



(g(n)) wtedy, kiedy istnieją dwie

dodatnie liczy c oraz N takie, że
f(n)>=cg(n) dla wszystkich n>=N.

• Widać, że g(n) jest ograniczeniem f(n) z

dołu, czyli minorantą badanej funkcji.

Inne typy notacji złożoności

algorytmów

• Definicja: f(n) ma złożoność



(g(n)), jeśli istnieją dodatnie

liczby c

1

, c

2

oraz N takie, że

c

1

g(n)=<f(n)=<c

2

g(n) dla

wszystkich n>=N.

• Czyli szukamy w tej notacji funkcji

g(n) takiego samego rzędu jak f(n)

Inne typy notacji złożoności

algorytmów

• Po co są wprowadzane różne typy

notacji? Otóż dlatego, że notacja
za pomocą majoranty O(f(n)) może
prowadzić do uznania niektórych
algorytmów za zbyt złożone,
podczas, gdy w notacji



(f(n)) albo



(f(n)) mogą zostać przyjęte za

wystarczająco wydajne.

Złożoność pesymistyczna,

optymistyczna i średnia

• Przykład: Złożoność wyszukiwania elementu

w tablicy n-elementowej. Możemy trafić od

razu – przypadek najlepszy- element

szukany to T[0] i złożoność otrzymana to

O(1), albo po przeszukaniu całej tablicy czyli

element szukany to T[n] i złożoność O(n).

• Mówimy, że złożoność pesymistyczna to

taka,

która

poprzez

zadanie

danych

wejściowych do algorytmu powoduje, że

wykona się on maksymalną możliwą liczbę

razy.

Złożoność pesymistyczna,

optymistyczna i średnia

• Złożoność optymistyczna to ten przypadek,

w którym „trafiamy najszybciej jak można
w rozwiązanie”. Każdy z przypadków
zależy od doboru danych wejściowych. Czy
możemy ich dobór przewidzieć „a priori”
czyli przed eksperymentem?

• Definiuje się złożoność średnią ulokowaną

pomiędzy przypadkiem skrajnie złym i
skrajnie dobrym

Złożoność pesymistyczna,

optymistyczna i średnia

• Oznaczmy przez p prawdopodobieństwo, że

element x znajduje się w tablicy i załóżmy, że
wszystkie lokalizacje elementu x są jednakowo
prawdopodobne. Czyli z prawdopodobieństwem
1-p element w tablicy nie występuje. Oznaczmy
przez Z

i, n

zbiór takich i, że 0<i<n oraz x

znajduje się na i-tym miejscu w tablicy. Przez Z

n,n

oznaczymy zbiór, w którym x jest nieobecne.

Wobec założeń zapiszemy:

• P(Z

i,n

) = p/n oraz P(Z

n,n

) = 1-p

Złożoność pesymistyczna,

optymistyczna i średnia

• Złożoność odpowiednią algorytmu oznaczymy

jako:

• f(Z

i,n

) = i oraz f(Z

n,n

) = n

• Średnia złożoność algorytmu w analizowanym

przykładzie to:



 















2

1

1

1

1

,

1

,

p

n

n

p

n

p

i

n

p

Z

f

Z

P

f

n

i

i

n

N

i

i

n

average





































n

i

n

n

i

1

2

1

• Z definicji złożoności w przypadku

średnim widać, że jest ona
równoznaczna z pojęciem wartości
oczekiwanej statystycznie

Złożoność pesymistyczna,

optymistyczna i średnia

   

i

n

n

i

i

n

average

Z

f

Z

P

f

,

0

,







Złożoność pesymistyczna,

optymistyczna i średnia

• Jeśli element znajduje się w tablicy czyli

p=1, to średnia złożoność w
analizowanym przykładzie wynosi:

• f = (n+1)/2.

• Tylu kroków średnio wymaga znalezienie

elementu poszukiwanego wtedy, kiedy
prawdopodobieństwa znalezienia dla
każdego losowania są jednakowe.

• O jakim rodzaju złożoności powinniśmy

mówić kiedy analizujemy O-notację?

Złożoność zamortyzowana

• Widoczne było w przykładzie, że dane

wpływają na złożoność algorytmu. A co

będzie w przypadku algorytmów, w których

poszczególne ich części (podprogramy)

zmieniają

dane

wykorzystywane

w

pozostałych?

Przykładowo

jeśli

przeszukiwana tablica będzie wcześniej

posortowana

czyli

uporządkuje

swoje

elementy

rosnąco

lub

malejąco,

to

znalezienie elementu wybranego będzie z

pewnością trwało krócej. Mówimy, że

złożoność

zostanie

w

takiej

sytuacji

zamortyzowana.

Złożoność zamortyzowana

• Analiza w przypadku zamortyzowanym nie

jest więc analizą złożoności pojedynczego
algorytmu ale analizą sekwencji (albo
ogólniej zbioru) kilku algorytmów. W
najprostszym

przybliżeniu

możemy

przyjmować,

że

oszacowana

złożoność

zamortyzowana jest sumą złożoności każdego
z algorytmów występującego w analizowanej
sekwencji. Można tak przyjąć wówczas, kiedy
poszczególne

algorytmy

są

od

siebie

niezależne i współpracują sekwencyjnie.

Złożoność zamortyzowana

• Wiemy, że złożoność zależy od postaci

danych wejściowych. Definiuje się funkcję

nazywaną funkcją potencjału danych,

która przypisuje danym i-tego rodzaju liczbę

określającą koszty operacji na tych danych.

Wówczas zamortyzowany koszt operacji i-tej

zapiszemy:

• kosztAmort(op

i

)=koszt(op

i

)+f.potencjału

(ds

i

)-f.potencjału(ds

i-1

)

• Jeśli mamy m takich operacji to koszt

zamortyzowany jest sumą kosztów dla

wszystkich m operacji

Techniki wyznaczania złożoności nie

zamortyzowanych

• Budowanie

funkcji

f(n)

zależności

pomiędzy liczbą danych n, a liczbą operacji

w

algorytmie

w

formie

tabeli

przyporządkowania

(pokazano

przy

analizie rekurencji Fibonacciego jako

liczbę podstawień i liczbę dodawań).

• Tworzenie

postaci

kombinatorycznej

funkcji dyskretnej f(n) na podstawie ww.

tabeli lub innych danych z matematyki

dyskretnej i ocena majoranty O(g(n)) dla

tej funkcji (albo innego wariantu notacji).

• Metoda równań rekurencyjnych.

Równania rekurencyjne

• DEFINICJA

• RÓWNANIE POSTACI

JAK PO PRAWEJ

NAZYWAMY

RÓWNANIEM

REKURENCYJNYM,

HOMOGENICZNYM ZE

STAŁYMI

WSPÓŁCZYNNIKAMI ze

względu na t.

• Liniowe bo t występuje

tylko w pierwszej potędze

• Homogeniczne bo prawa

strona jest równa zeru

0

...

1

1

0













k

n

k

n

n

t

a

t

a

t

a

Równania rekurencyjne - przykład

• Szereg

Fibonacciego
opisuje rekurencja
podana obok

• Pierwsze równanie

możemy zapisać
jako homogeniczne,
liniowe równanie
rekurencyjne

1

0

1

0

2

1













t

t

t

t

t

n

n

n

0

2

1











n

n

n

t

t

t

Równania rekurencyjne

• DEFINICJA

• JEŻELI DANE JEST

RÓWNIANIE
REKURENCYJNE TO
JEGO RÓWNANIEM
CHARAKTERYSTYCZNY
M NAZYWAMY
WIELOMIAN ZMIENNEJ
r ZAPISANY OBOK
(czyli metoda
podstawiania)

0

...

0

1

1

0











r

a

r

a

r

a

k

k

k

0

...

1

1

0













k

n

k

n

n

t

a

t

a

t

a

Równania rekurencyjne

• DEFINICJA

• ROZWIAZANIEM

LINIOWEGO,
HOMOGENICZNEGO
RÓWNANIA
REKURENCYJNEGO
WYRAZONEGO W
FORMIE
WIELOMIANOWEJ JEST
KOMBINACJA LINIOWA
POTĘG ZMIENNEJ r.

n

k

k

n

n

n

r

c

r

c

r

c

t









...

2

2

1

1

0

...

0

1

1

0











r

a

r

a

r

a

k

k

k

0

...

1

1

0













k

n

k

n

n

t

a

t

a

t

a

Równania rekurencyjne

• Szereg

Fibonacciego ma
równanie
charakterystyczn
e jak obok

1

0

1

1

0

2

1















t

t

n

gdy

t

t

t

n

n

n

0

1

2





 r

r

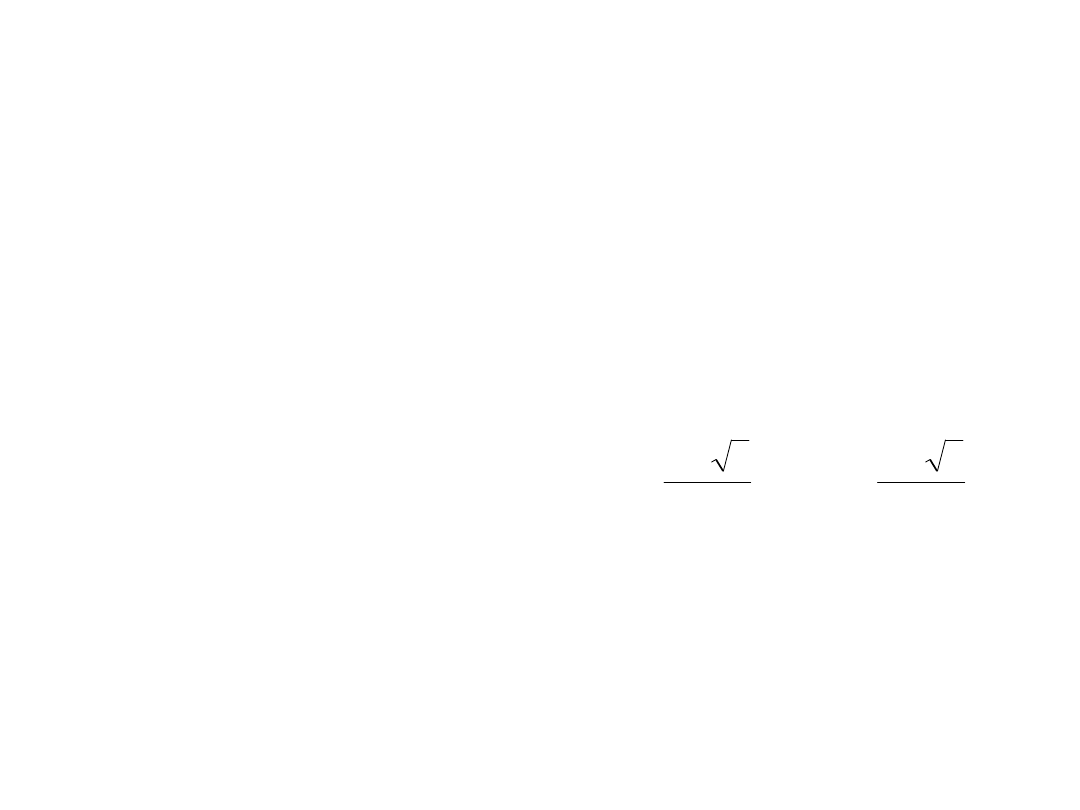
Równania rekurencyjne

• Rozwiązanie dla t

n

ma

postać jak obok.
Współczynniki c

1

i c

2

określamy z
pozostających równań
rekurencji Fibonacciego
dla elementu przy n=0
oraz n=1.

• Takie dodatkowe

równania nazywamy
warunkami
początkowymi

n

n

n

c

c

t











 













 



2

5

1

2

5

1

2

1

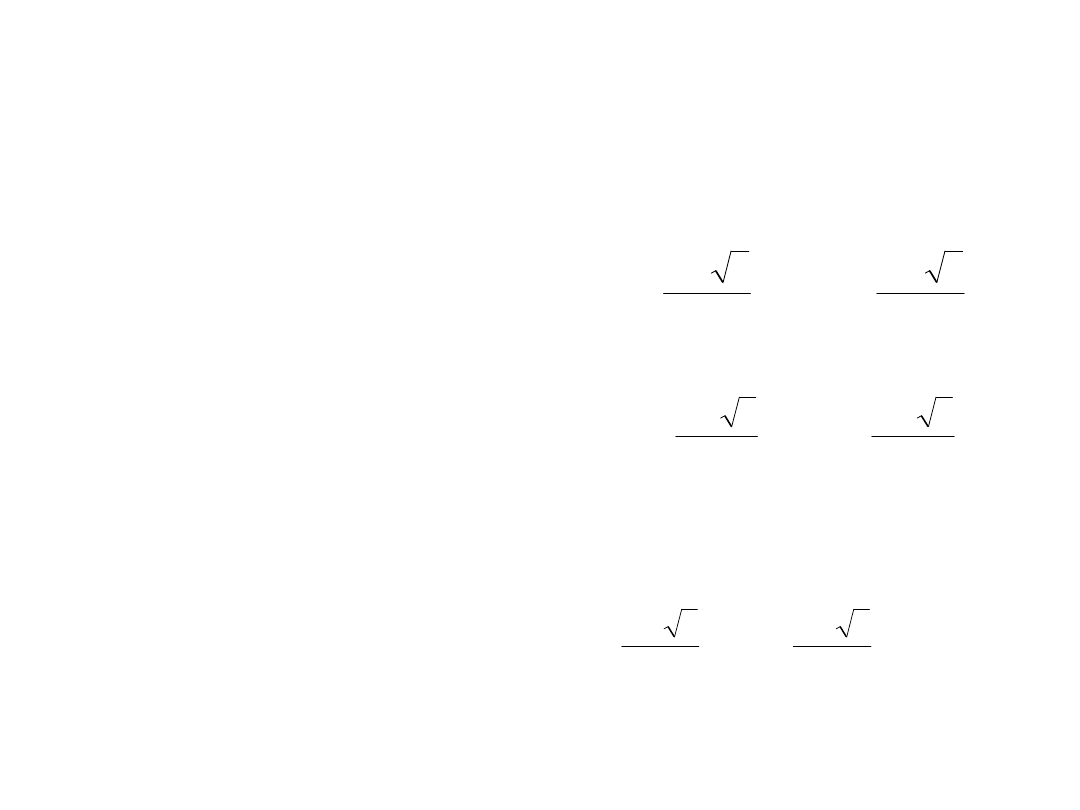
Równania rekurencyjne

• Warunki

początkowe dla
rekurencji
Fibonacciego
mają postać jak
obok

0

2

0

1

0

2

5

1

2

5

1











 













 



c

c

t

1

2

1

1

2

5

1

2

5

1











 













 



c

c

t

n

0

2

1



 c

c

1

2

5

1

2

5

1

2

1













 













 

c

c

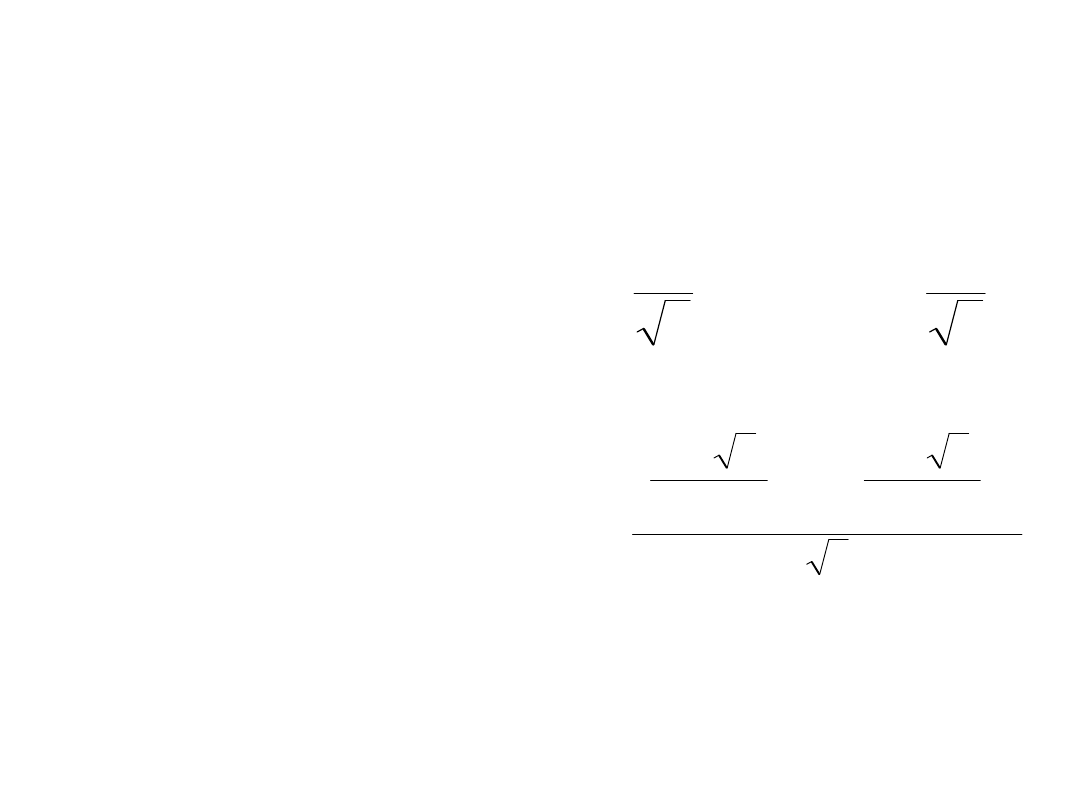
Równania rekurencyjne

• Ostateczna forma

rozwiązania

powoduje, że wraz ze

wzrostem n rośnie

dokładność

potrzebna do

wyrażenia

pierwiastka z 5.

Widać także

jednoznacznie, że

jest to funkcja

wykładnicza.

5

1

,

5

1

2

1







c

c









5

2

5

1

2

5

1

n

n

n

t











 













 



Równania rekurencyjne

• DEFINICJA

• RÓWNANIE POSTACI JAK PO

PRAWEJ NAZYWAMY

RÓWNANIEM

REKURENCYJNYM,

NIEHOMOGENICZNYM ZE

STAŁYMI

WSPÓŁCZYNNIKAMI ze

względu na t. Funkcja f(n) jest

dowolna.

• Liniowe bo t występuje tylko

w pierwszej potędze

• niehomogeniczne bo prawa

strona nie jest równa zeru

• NIE ISTNIEJE OGÓLNA

METODA ANALITYCZNA

ROZWIAZYWANIA TAKICH

RÓWNAŃ

• Pokazać można rozwiązania

m.in.. Dla przypadku gdy

równanie da się sprowadzić do

postaci pokazanej obok gdzie

b to stałą a p(n) to wielomian.

 

n

f

t

a

t

a

t

a

k

n

k

n

n













...

1

1

0

 

n

p

b

t

a

t

a

t

a

k

n

k

n

n













...

1

1

0

Równania rekurencyjne

• Jest to przykład

równania
rekurencyjnego
liniowego
niehomogenicznego z
warunkami
początkowymi. Po
stronie prawej mamy
stałą a więc jest to
przypadek
rozwiązywalny.

4

0

1

4

3

1

0

1













t

t

n

dla

t

t

n

n

n

Równania rekurencyjne

• Jeśli zastąpić w nim n przez

n-1 to jest to równoważne
podzieleniu każdej ze stron
przez 4. Albo inaczej,
ponieważ pierwsze równanie
jest prawdziwe także dla
n=n+1, to dzieląc je przez 4
otrzymamy postać drugą,
która jest równoważna
pierwszej. Ponieważ wyniki
są sobie równoważne to
odejmowanie otrzymanych
równań stronami musi dać
równanie homogeniczne,
którego sposób
rozwiązywania już znamy.

0

3

4

7

4

4

4

3

4

4

3

2

1

1

1

1

2

1





























n

n

n

n

n

n

n

n

n

t

t

t

t

t

t

t

Równania rekurencyjne

• Po pomnożeniu przez 4:

0

12

7

2

1











n

n

n

t

t

t







0

4

3

12

7

2













r

r

r

r

n

n

n

c

c

t

4

3

2

1





 

n

n

n

t

t

t

3

4

4

;

4

;

0

1

1

0











Podsumowanie i spis

zagadnień

• Co to jest złożoność i rozróżnienie złożoności

obliczeniowej oraz czasowej

• Miary złożoności i jej notacje
• Złożoność pesymistyczna, optymistyczna i średnia

algorytmów prostych

• Złożoność zamortyzowana algorytmów

sekwencyjnych i zbioru algorytmów
współpracujących

• Metody wyliczania złożoności
• Sposoby rozwiązywania wybranych typów równań

rekurencyjnych