ARCHITEKTURA

KOMPUTERÓW

dr inż. Janusz Kosiński

Materiały do wykładów

@Janusz Kosiński, 2005

Borowik B., Programowanie równoległe w zastosowaniach.

MIKOM, 2001.

Brookshear G. J., Informatyka w ogólnym zarysie. - WNT,

Warszawa 2003.

Chalk B.S., Organizacja i architektura komputera – WNT,

Warszawa 1998

Metzger P., Anatomia PC – HELION, 2001.
Metzger P., Diagnostyka i optymalizacja komputerów PC.

HELION, 2001.

Mueller S., Soper M.E. – Rozbudowa i naprawa komputerów

PC – HELION 2001.

Stallings W., Architektura komputerów. - WNT, Warszawa

2001.

Zalecana literatura

@Janusz Kosiński, 2005

1. Wprowadzenie do architektury komputerów

• historia i architektura pierwszych komputerów
• podstawowa terminologia
• podstawowe składniki systemu komputerowego
• poziomy logiczne systemu komputerowego
• model von Neumanna

2. Reprezentacja danych w systemach

komputerowych

• typowe reprezentacje numeryczne
• kody BCD, EBCDIC, ASCII i Unicode
• reprezentacja stało i zmiennoprzecinkowa
• zapisywanie danych
• wykrywanie błędów

TREŚĆ ZAJĘĆ

@Janusz Kosiński, 2005

Algebra Boolowska i logika cyfrowa

• algebra Boolowska
• bramki logiczne
• „tablice prawdy”
• mapy Karnaugh
4.

Wprowadzenie do prostego komputera

• cykl pracy

CPU

•

I/O

oraz przerwania

• prosty program
• assembler

TREŚĆ ZAJĘĆ

@Janusz Kosiński, 2005

Instrukcje maszynowe

• instrukcje krótkie
• instrukcje o stałej długości
• typy instrukcji
• adresowanie
• instrukcje potokowe
6.

Pamięć

• typy pamięci
• hierarchia pamięci
• pamięć podręczna
• pamięć wirtualna
• hierarchia pamięci

INTEL

TREŚĆ ZAJĘĆ

@Janusz Kosiński, 2005

Wejście / Wyjście i systemy magazynowania

• prawo Amdahla
• architektura

I/O

– przerwania,

DMA

, system

BUS

• technologia dysków magnetycznych
• dyski optyczne, taśmy magnetyczne; RAID
• kompresja danych
8.

Oprogramowanie systemowe

• system operacyjny
• środowisko chronione
• narzędzia programistyczne asemblery, edytory,

kompilatory, interpretatory

• bazy danych; transakcje
• zarządzanie transakcjami -

CICS

TREŚĆ ZAJĘĆ

@Janusz Kosiński, 2005

Architektury alternatywne - pomiary

wydajności oraz analizy

• maszyna RISC i taksonomia Flynna
• architektury równoległe i wieloprocesorowe;

architektura przepływowa, sieci neuronowe

• podstawowe równanie wydajności komputera
• Clock Rate, MIPS i FLOPS
• benchmarking -

Whetstone

Linpack

, i

Dhrystone

• wydajność dysku

TREŚĆ ZAJĘĆ

Wprowadzenie do architektury

komputerów

Generacja Zero

- Mechaniczne maszyny kalkulujące (1642 – 1945)

Do lat 1550 typowy europejski biznesmen używał

liczydeł

i stosował do swoich obliczeń najpierw

numerację rzymską

a później

arabską

–

pozwalającą na dokonywanie obliczeń z większą
dokładnością.

Wilhelm Schickard

(1592–1635)

– przypisuje

mu się

wynalezienie pierwszego kalkulatora
mechanicznego – tzw,

„zegara kalkulującego”,

umożliwiającego

dodawanie i odejmowanie sześciocyfrowych liczb.

@Janusz Kosiński, 2005

Generacja Zero

- Mechaniczne maszyny kalkulujące (1642 – 1945)

W 1642,

Blaise Pascal

(1623–1662)

zaprojektował kalkulator mechaniczny

„paskalinę”.

Paskalina umożliwiała

dodawanie i

odejmowanie z przeniesieniem

–

prawdopodobnie pierwsze, praktycznie
zastosowane, mechaniczne urządzenie dodające.

@Janusz Kosiński, 2005

Generacja Zero

- Mechaniczne maszyny kalkulujące (1642 – 1945)

Paskalina

@Janusz Kosiński, 2005

Generacja Zero

- Mechaniczne maszyny kalkulujące (1642 – 1945)

Gottfried Wilhelm von Leibniz

(1646–1716),

znany matematyk, wynalazł kalkulator znany
jako

Stepped Reckoner

(schodkowy

rachmistrz),

który mógł dodawać, odejmować,

mnożyć i

dzielić.

Żadne z tych urządzeń nie posiadało pamięci i nie mogło

być programowane – każdy krok w obliczeniach
wymagał „ręcznej interwencji”.

@Janusz Kosiński, 2005

Generacja Zero

- Mechaniczne maszyny kalkulujące (1642 – 1945)

Charles Babbage

(1791–1871) zaprojektował w

1822

Silnik Różnicowy

(Babbage nazywany jest

ojcem techniki komputerowej).

Nazwa była stosowana ze względu
na technikę obliczeniową

(metoda różnic)

– maszyna została

zaprojektowana do rozwiązywania
funkcji wielomianowych –
może być nazywany kalkulatorem
(nie komputerem).

@Janusz Kosiński, 2005

Generacja Zero

- Mechaniczne maszyny kalkulujące (1642 – 1945)

Zastosowanie kart do sterowania zachowaniem się

maszyny zawdzięczamy

Josephowi Marii

Jacquardowi

(1752–1834). W 1801, Jacquard

wynalazł

programowane krosno tkackie

(oferował

Babage’owi gobelin

utkany przy pomocy ponad

10 000 kart
dziurkowanych).

@Janusz Kosiński, 2005

Generacja Zero

- Mechaniczne maszyny kalkulujące (1642 – 1945)

Wśród najważniejszych wynalazków końca XIX w,

znalazła się

„maszyna tablicująca”

Hermana

Holleritha

(1860–1929), zastosowana w 1890 do

spisu ludności US, Hollerith założył firmę, która
później przyjęła
nazwę

IBM

–

80 kolumnowe karty
dziurkowane były
stosowane ponad 50 lat.

@Janusz Kosiński, 2005

Generacja Pierwsza

- Komputery na lampach próżniowych (1945 – 1953)

W latach 1930

Konrad Zuse

(1910–1995) podjął

problem w miejscu, w którym Babbage

zostawił, dodając technologię przekaźników
elektrycznych. Komputer Zuse’go –

, posiadał w

miejscu ręcznych przekładni, przekaźniki
elektromagnetyczne

(Z1 jeszcze nie miał lamp elektronowych).

@Janusz Kosiński, 2005

Generacja Pierwsza

- Komputery na lampach próżniowych (1945 – 1953)

Komputery cyfrowe

, jakie dziś znamy, pochodzą od

wielu prac dokonywanych w latach 1930 i 1940.

Mimo wszystko argumenty, kto był pierwszy,

przemawiają za trzema ludźmi – uważanymi dziś za
„ojców – wynalazców” współczesnych komputerów:

John Atanasof,

John Mauchly,

J. Presper Eckert

@Janusz Kosiński, 2005

Generacja Pierwsza

- Komputery na lampach próżniowych (1945 – 1953)

John Atanasof

(1904–1995) zyskał uznanie za

konstrukcję pierwszego kompletnie elektronicznego
komputera -

Atanasof Berry Computer

(John

Atanasof i Cliford Berry)

ABC

był maszyną binarną , zbudowaną na lampach

elektronowych

- do rozwiązywania systemu

równań liniowych; stąd nie może

być nazywany komputerem

ogólnego zastosowania

@Janusz Kosiński, 2005

Electronic

Numerical

Integrator

And

Computer

lectronic

umerical

ntegrator

omputer

Generacja Pierwsza

- Komputery na lampach próżniowych (1945 – 1953)

John Mauchly

(1907–1980) i

J. Presper Eckert

(1929–1995)

zaprojektowali pierwszy, w pełni elektroniczny komputer
cyfrowy ogólnego stosowania

- ENIAC

(1946). Maszyna ta

wykorzystywała

17 468 lamp elektronowych

, zajmowała

1 800 stóp kwadratowych

powierzchni,

ważyła

30 ton

i zużywała

174 KW energii elektrycznej

ENIAC miał pamięć o pojemności
około

1 000 bitów

(dla

10-cyfrowych

liczb dziesiętnych) i do przechowywania
danych używał kart dziurkowanych.

Generacja Pierwsza

- Komputery na lampach próżniowych (1945 – 1953)

W czasie II Wojny Światowej

, armia USA miała

duże zapotrzebowanie na obliczenia związane z
trajektoriami nowych pocisków armatnich.
Realizacja tego zadania przy pomocy urządzenia
elektronicznego, mogła skrócić obliczanie tablic
balistycznych z dni do minut. Stąd armia byłą
zainteresowana w budowie takiej maszyny.

ENIAC rzeczywiście skrócił czas obliczeń

z 20 godzin

do 30 sekund

, Niestety urządzenie było gotowe

dopiero w 1946 roku – czyli już po wojnie.

@Janusz Kosiński, 2005

biuletyn armii
Stanów
Zjednoczonych:

U.S. Army
1946

@Janusz Kosiński, 2005

Uniwersytet Harvard - model MARK I (1947)

@Janusz Kosiński, 2005

Czym jest lampa elektronowa?

Świat WWW, jaki dziś znamy powstał jako

konsekwencja wynalezienia prostego
urządzenia, nazywanego przez Amerykanów

rurą próżniową

(vacuum tube), a przez

Brytyjczyków

- zaworem

(valve).

Lampa elektronowa steruje przepływem

elektronów, (niektóre lampy elektronowe
połowy dwudziestego wieku nie były próżniowe,
lecz zawierały gazy przewodzące prąd – np,
pary rtęci, stanowiące pożądane środowisko dla
przepływu prądu).

@Janusz Kosiński, 2005

Czym jest lampa elektronowa?

Badanie zjawisk elektrycznych
umożliwiających pracę lamp
elektronowych było konsekwencją
wynalazku

T. A. Edisona

– żarówki.

W 1911, Owen Willams
Richardson analizując te zjawisko,
nazwał je

termoemisją

elektronów.

Lee de Forest – pierwsza trioda

Generacja Druga

- Komputery na tranzystorach (1954 – 1965)

Technologia lamp elektronowych

nie była w pełni

godna zaufania, Krytycy ENIAC-a uważali, że system
nigdy nie będzie działać – lampy wcześniej ulegną
spaleniu nim zostaną wymienione.

Chociaż rzeczywistość systemu była inna, niż

wieszczyli to „prorocy”, to jednak częstotliwość
awarii była większa niż częstotliwość „powodzeń”.

@Janusz Kosiński, 2005

Generacja Druga

- Komputery na tranzystorach (1954 – 1965)

W 1948,

trzej badacze z Bell Laboratories

–

John Bardeen,

Walter Brattain,

William Shockley

wynaleźli

tranzystor,

Ta nowa technologia nie tylko zrewolucjonizowała mnóstwo urządzeń

(radioodbiorniki, telewizory) ale popchnęła przemysł komputerowy
na ścieżkę drugiej generacji

@Janusz Kosiński, 2005

Czym jest Tranzystor ?

Tranzystor

– skrót (ang,) od

transfer resistor

- jest

wersją

triody w stanie stałym. Ponieważ elektrony

lepiej

przemieszczają się w ośrodkach

stałych (solidnych)

niż w próżni czy gazach, nie

potrzebują dodatkowych

elementów, takich jak

siatka sterująca w triodach.

@Janusz Kosiński, 2005

Czym jest Tranzystor ?

Stosowany jest german albo krzem – oba te
pierwiastki stanowią bazę „solidnego” zachowania się
elektronów. W czystej formie, żaden z tych
pierwiastków nie jest dobrym
przewodnikiem elektryczności. Ale kiedy

są one

„domieszkowane”

niewielkimi

(śladowymi) ilościami pierwiastków
sąsiadujących z nimi w układzie

okresowym, stają się przewodnikami

elektryczności w sposób

sterowany

Generacja Trzecia

Komputery na obwodach scalonych (1965 – 1980)

Rzeczywista eksplozja w wykorzystaniu
komputerów przyszła razem z pojawieniem się
obwodów scalonych.

Jack Kilby

- wynalazca pierwszego obwodu

scalonego - IC (microchip),

wykonanego

z germanu,

Robert Noyce

- podobne urządzenie wykonane z

krzemu. Komputery stały się szybsze i tańsze –
korzyści w procesie przetwarzania.

Komputery rodziny IBM System/360 -
pierwsze systemy komercyjne z półprzewodnikami.

@Janusz Kosiński, 2005

Generacja Trzecia

Komputery na obwodach scalonych (1965 – 1980)

Porównanie elementów - zgodnie z

ruchem wskazówek zegara

1) Lampa elektronowa



2) Tranzystor
3) Chip zawierający 3 200 2-

wejściowych

bramek NAND

4) Obwód scalony – w środku

moneta 10

pensowa

@Janusz Kosiński, 2005

Generacja Czwarta -

Komputery VLSI (1980 – ????)

Obecnie są wykorzystywane cztery poziomy w skali
integracji (liczby elementów w chipie):

SSI -

mała skala integracji:

10 do 100 elementów

na chip

MSI -

średnia skala integracji:

100 do 1 000 elementów

chip

LSI -

duża skala integracji:

1 000 do 10 000 elementów

chip

VLSI -

bardzo duża skala integracji:

ponad 10 000

elementów

na chip – powstanie komputerów czwartej

generacji.

(w roku 1997 studenci Uniwersytetu Pensylwania zrobili
odpowiednik ENIAC-a w postaci mikrochipu – był on wielkości
paznokcia kciuka i miał około 174 000 tranzystorów – o rząd
wielkości wyżej niż liczba lamp w Eniacu).

@Janusz Kosiński, 2005

Generacja Czwarta -

Komputery VLSI (1980 – ????)

@Janusz Kosiński, 2005

Generacja Czwarta -

Komputery VLSI (1980 – ????)

INTEL

stworzył w 1971 pierwszy procesor

(4004)

Pierwszym mikrokomputerem był

Altair 8800,

wyprodukowany w 1975 przez firmę Micro
Instrumentation and Telemetry Corporation

Później nastąpiły

Apple I, Apple II, Commodore PET

i Vic 20

W 1981 IBM wprowadził na rynek

pierwszy

(Personal Computer)

@Janusz Kosiński, 2005

Generacja Czwarta -

Komputery VLSI (1980 – ????)

@Janusz Kosiński, 2005

Jeżeli maszyna ma być zdolna do rozwiązywania

szerokiej gamy problemów to powinna
wykonywać programy napisane w różnych
językach, od

FORTRAN-u i C do LISP-u i

PROLOG-u.

Między fizycznymi składnikami a językami

wysokiego poziomu takimi jak C++, istnieje

luka

semantyczna

Żeby system komputerowy był praktyczny, ta

luka

semantyczna musi być niewidoczna dla
użytkownika

tego systemu.

Hierarchia poziomów komputera

@Janusz Kosiński, 2005

Doświadczenie programistyczne uczy, że

kiedy problem jest duży należy podzielić go na

mniejsze części

–

zastosować

metodę „dziel i rządź”

–

części te tworzą wyodrębnione moduły,

wymagające odpowiednich „interfejsów”

pozwalających na współpracę miedzy nimi.

Hierarchia poziomów komputera

@Janusz Kosiński, 2005

Organizacja systemu komputerowego powinna być

realizowana w podobny sposób – maszynę
(komputer) można przedstawić jako pewną

hierarchię zbudowaną z kilku poziomów

, z

których każdy posiada specyficzne funkcje i istnieje
jako wyodrębniona hipotetyczna maszyna.

Taki

hipotetyczny komputer

na każdym poziomie

nosi nazwę

„maszyny wirtualnej”

– wykonującej

(każda) własne zbiory instrukcji.

Hierarchia poziomów komputera

@Janusz Kosiński, 2005

Hierarchia poziomów komputera

Poziom 6

Poziom 5

Poziom 4

Poziom 3

Poziom 2

Poziom 1

Poziom 0

@Janusz Kosiński, 2005

Hierarchia poziomów komputera

Poziom 6 - poziom użytkownika:

jest skomponowany z aplikacji, powszechnie
stosowanych, takich jak edytory tekstów,
pakiety graficzne czy gry.

Z tego poziomu poziomy niższe nie są
widoczne.

@Janusz Kosiński, 2005

Hierarchia poziomów komputera

Poziom 5 - języki wysokiego poziomu:

zawiera takie języki jak

C, C++, FORTRAN, LISP,

Pascal i Prolog

. Języki te muszą być tłumaczone

przy zastosowaniu raczej kompilatorów niż
interpretatorów (interpreterów) do języka, który
będzie zrozumiały dla maszyny.

Języki skompilowane są tłumaczone na język asemblerowy i dalej
„montowane” do kodu maszynowego, (są tłumaczone do języka
niższego poziomu). Użytkownik tego poziomu widzi niewiele z
poziomów niższych. Nawet, jeżeli programista musi znać typy
danych i instrukcje z nimi związane, to nie musi nic wiedzieć o o
tym jakie typy aktualnie są aktualnie realizowane
(implementowane).

@Janusz Kosiński, 2005

Hierarchia poziomów komputera

Poziom 4 - poziom języka asemblera:

zawiera kilka typów języka montażowego
(gromadzenia), Języki wysokiego poziomu są
najpierw tłumaczone do asemblera a potem do
kodu maszynowego. Tu występuje tłumaczenie
„jeden do jednego”, co oznacza że jedna
instrukcja asemblera jest tłumaczona na jedną
instrukcję kodu maszynowego.

Dzięki zastosowaniu oddzielnych poziomów, możliwe jest

zmniejszenie wspomnianej wcześniej „luki semantycznej” między
językami wysokiego poziomu a a aktualnym językiem
maszynowym, który zawiera tylko „0” i „1”.

@Janusz Kosiński, 2005

Hierarchia poziomów komputera

Poziom 3 - poziom oprogramowania systemowego:

„radzący sobie”

z instrukcjami systemu

operacyjnego.

Ten poziom jest odpowiedzialny za
synchronizację procesów, multiprogramowanie,
ochronę pamięci i za wiele innych funkcji.

Często instrukcje tłumaczone z asemblera na język maszynowy
„przechodzą” przez ten poziom niezmienione.

@Janusz Kosiński, 2005

Hierarchia poziomów komputera

Poziom 2 - poziom języka maszynowego:

poziom instrukcji ustalających architekturę

(ISA)

nazywany też poziomem maszynowym, zawiera
język maszynowy, rozpoznawany przez
poszczególne składniki architektury systemu
komputerowego.

Programy napisane w języku maszynowym, dla komputerów z
wbudowanym układem sterowania, mogą być wykonywane
bezpośrednio bez potrzeby interpretatorów, kompilatorów i
edytorów.

@Janusz Kosiński, 2005

Hierarchia poziomów komputera

Poziom 1 - poziom sterowania:

jest tym poziomem na którym jednostka
sterująca nabiera pewności że instrukcje są
rozszyfrowane i wykonane poprawnie oraz że
dane są tam gdzie powinny być, i są wtedy
kiedy powinny być,

Jednostka sterująca interpretuje trafiające do niej jednorazowo
instrukcje maszynowe z wyższego poziomu i powoduje
wymaganą akcję.

@Janusz Kosiński, 2005

Hierarchia poziomów komputera

Innym rodzajem opcji kontrolnych są

mikroprogramy.

Mikroprogramem nazywamy program napisany
w języku najniższego poziomu, stosowany
bezpośrednio przez składniki sprzętowe.

Instrukcje maszynowe wytworzone na Poziomie
2, są wprowadzane do tych programów – co
powoduje interpretację języka maszynowego
przez sprzęt.

Jedna instrukcja z poziomu maszynowego jest często
tłumaczona na kilka instrukcji mikrokodu – kody te można łatwo
modyfikować z tym że stosowanie mikroprogramów
(wprowadzanie dodatkowej warstwy) powoduje spowolnienie
wykonywania instrukcji.

@Janusz Kosiński, 2005

Hierarchia poziomów komputera

Poziom 0 - poziom logiki cyfrowej:

jest tym poziomem gdzie można znaleźć
fizyczne składniki systemu komputerowego:
bramki i przewody.

W tym miejscu znajduje się

implementacja

logiki matematycznej,

wspólnej dla wszystkich

systemów komputerowych.

@Janusz Kosiński, 2005

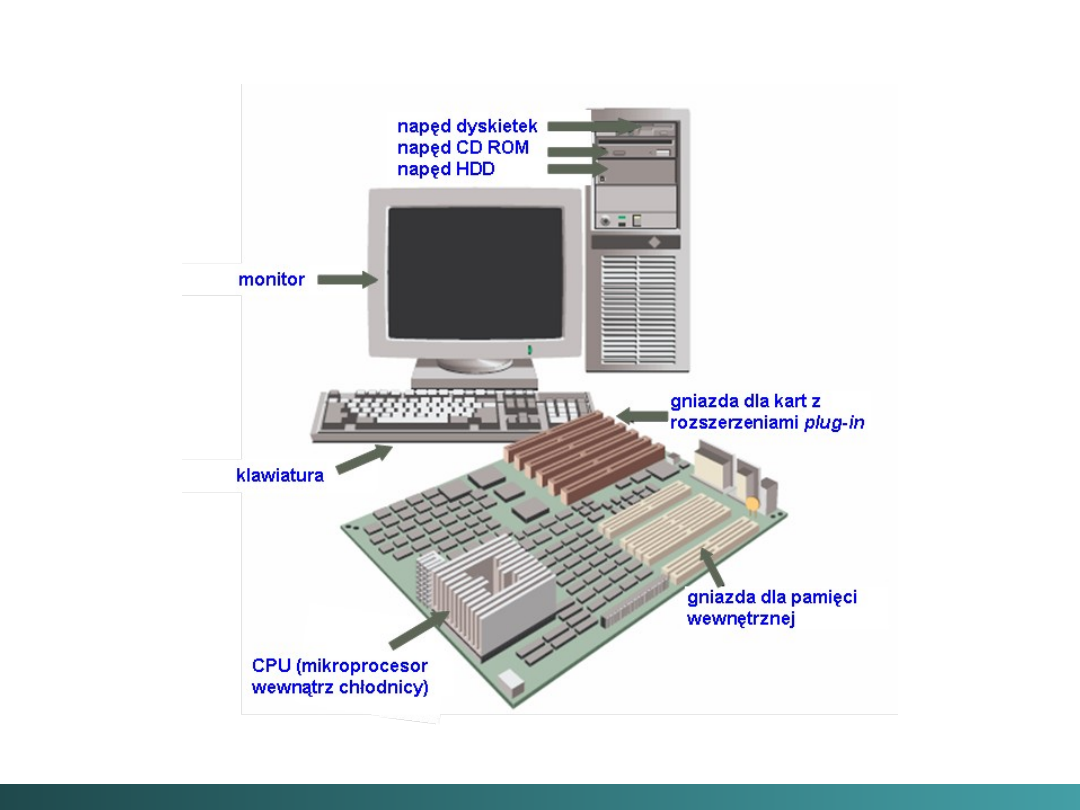
System komputerowy

Cyfrowy system komputerowy

jest systemem

charakteryzującym się sterowaniem programowym i
przeznaczony jest do automatyzacji procesów
algorytmicznego przetwarzania informacji cyfrowej.

Architekturą systemu komputerowego

nazywamy konfigurację podstawowych programowych
i sprzętowych komponentów systemu, w której zostały
uwzględnione wykonywane funkcje i cechy
charakterystyczne każdej części składowej, jak także
współdziałanie tychże części.

@Janusz Kosiński, 2005

System komputerowy

Programem

nazywamy zbiór instrukcji, których

wykonanie w określonej kolejności zapewnia
odpowiednie przetworzenie informacji.

Instrukcja

(rozkaz) jest słowem maszynowym

zawierającym informację o wykonywanej operacji,
miejscu w pamięci gdzie znajdują się operandy,
rezultat i następny rozkaz.

@Janusz Kosiński, 2005

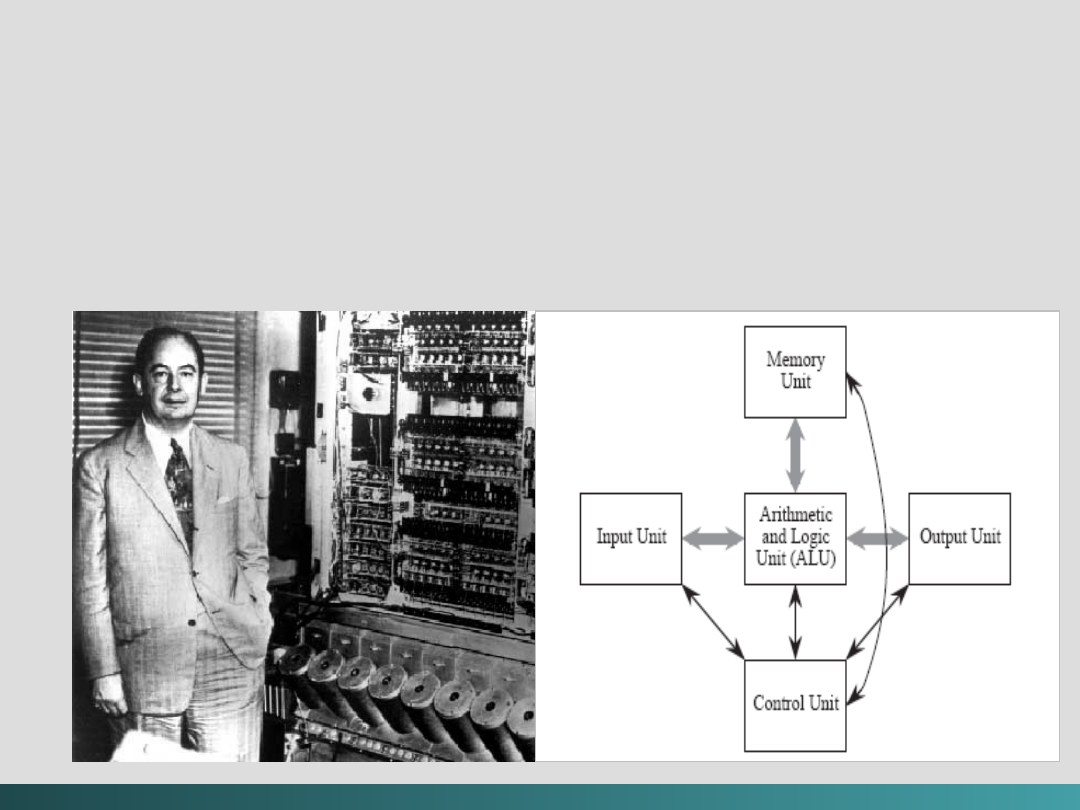
System komputerowy

Większość współczesnych systemów

komputerowych została zbudowana w oparciu o

architekturę von Neumann’a.

@Janusz Kosiński, 2005

Struktura systemu komputerowego von Neumann’a

Von Neumann w 1946 roku po raz pierwszy określił

zasady w jaki sposób jest sterowany uniwersalny
system komputerowy.

System taki powinien:



Mieć skończoną i funkcjonalnie pełną listę rozkazów;



Mieć możliwość wprowadzenia programu do systemu
komputerowego poprzez urządzenia zewnętrzne i jego
przechowywanie w pamięci w sposób identyczny jak
danych;



Dane i instrukcje w takim systemie powinny być jednakowo
dostępne dla procesora;



Informacja jest tam przetwarzana dzięki sekwencyjnemu
odczytywaniu instrukcji z pamięci komputera i wykonywaniu
tych instrukcji w procesorze.

@Janusz Kosiński, 2005

Struktura systemu komputerowego von Neumann’a

Podane warunki pozwalają przełączać system

komputerowy z wykonania jednego zadania
(programu) na inne bez fizycznej ingerencji w
strukturę systemu, a tym samym gwarantują jego
uniwersalność.

System komputerowy von Neumann’a nie posiada

oddzielnych pamięci do przechowywania danych i
instrukcji. Instrukcje jak i dane są zakodowane w
postaci liczb.

Bez analizy programu trudno jest określić czy dany

obszar pamięci zawiera dane czy instrukcje.
Wykonywany program może się sam modyfikować
traktując obszar instrukcji jako dane, a po
przetworzeniu tych instrukcji - danych - zacząć je
wykonywać.

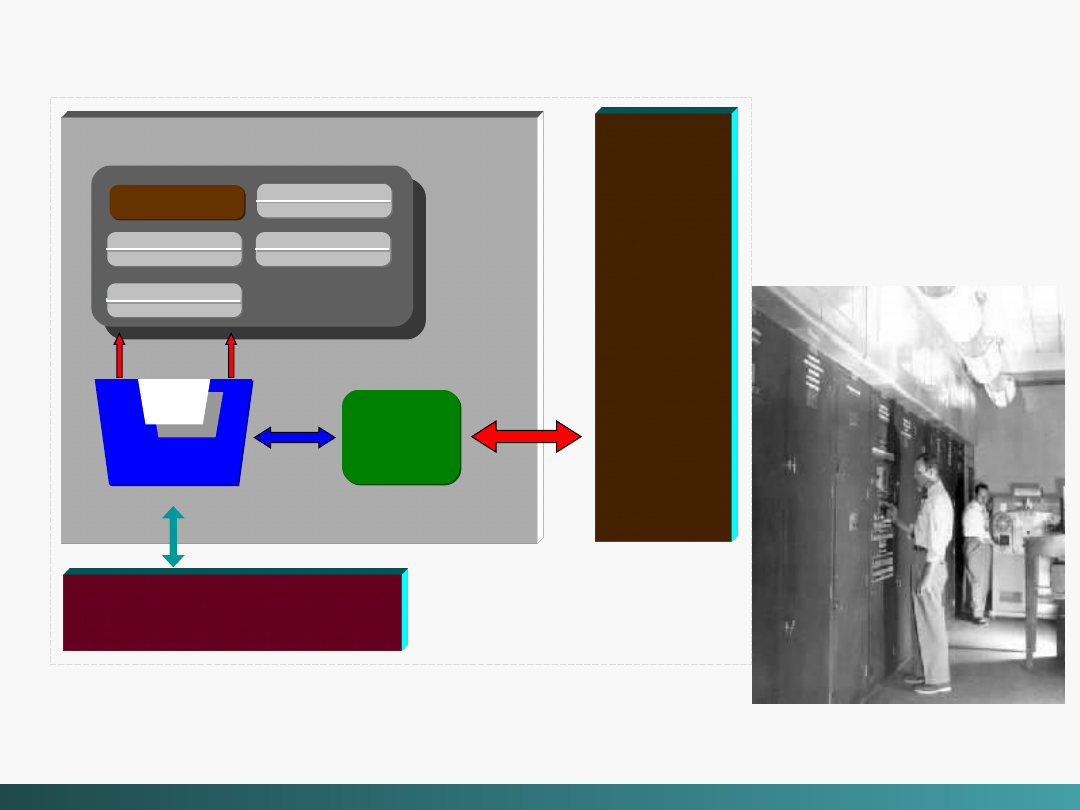
@Janusz Kosiński, 2005

Struktura systemu komputerowego von Neumann’a

EDVAC (Electronic Discrete Variable Automatic

Computer)

1949

CPU

Rejestry

Licznik

Jednostka

arytmetyczn

o - logiczna

Jednostk

kontroln

Jednostk

kontroln

Pamięć

główna

System

Wejścia / Wyjścia

@Janusz Kosiński, 2005

Struktura systemu komputerowego von Neumann’a

System komputerowy składa się z trzech podstawowych części

połączonych magistralą systemową:

1. Pamięci podstawowej
2. Procesora
3. Urządzeń zewnętrznych

Pamięć podstawowa jest przeznaczona do przechowywania

programów i danych. Fizycznie pamięć ta podzielona jest na
dwie części: pamięć operacyjną (RAM), do której informacja
może być zapisywana i odczytywana; oraz pamięć (ROM) -
przeznaczoną tylko do odczytu.

Do urządzeń zewnętrznych zaliczamy urządzenia wejścia,

urządzenia wyjścia i pamięć masową - dyski, streamer’y,

CD-ROM’y itd..

@Janusz Kosiński, 2005

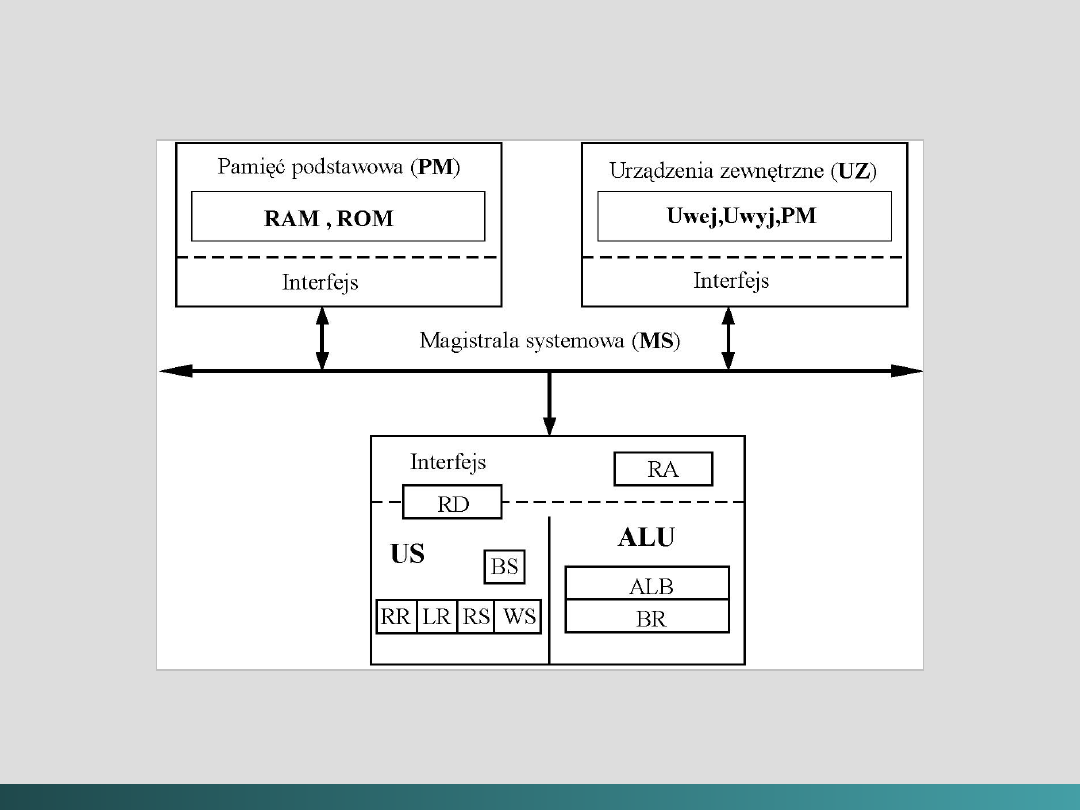
Struktura systemu komputerowego von Neumann’a,

@Janusz Kosiński, 2005

Idea zaprezentowana w architekturze von
Neumann’a

może być rozszerzona

w taki

sposób, że programy i dane magazynowane w
powolnych (co do dostępu) środkach
magazynowania – takich jak dysk twardy (

hard

disk

) mogą być kopiowane do nietrwałych, ale o

szybkim dostępie, środków takich jak

RAM

przed

samym procesem wykonania.

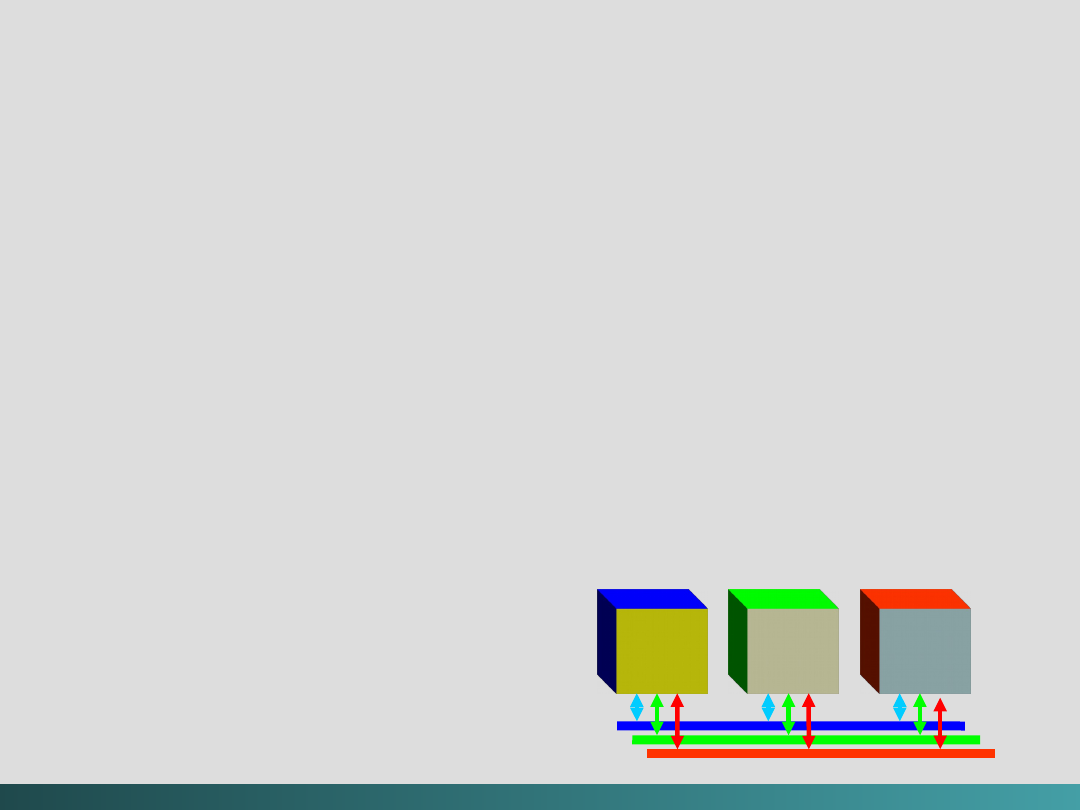
Ta architektura może być również usprawniana wewnątrz
dzięki zastosowaniu modelu

szyn zbiorczych (magistral)

CPU

(ALU,

Rejestry i

Sterowanie

)

Pamięć

Wejście i

Wyjście

(I/O)

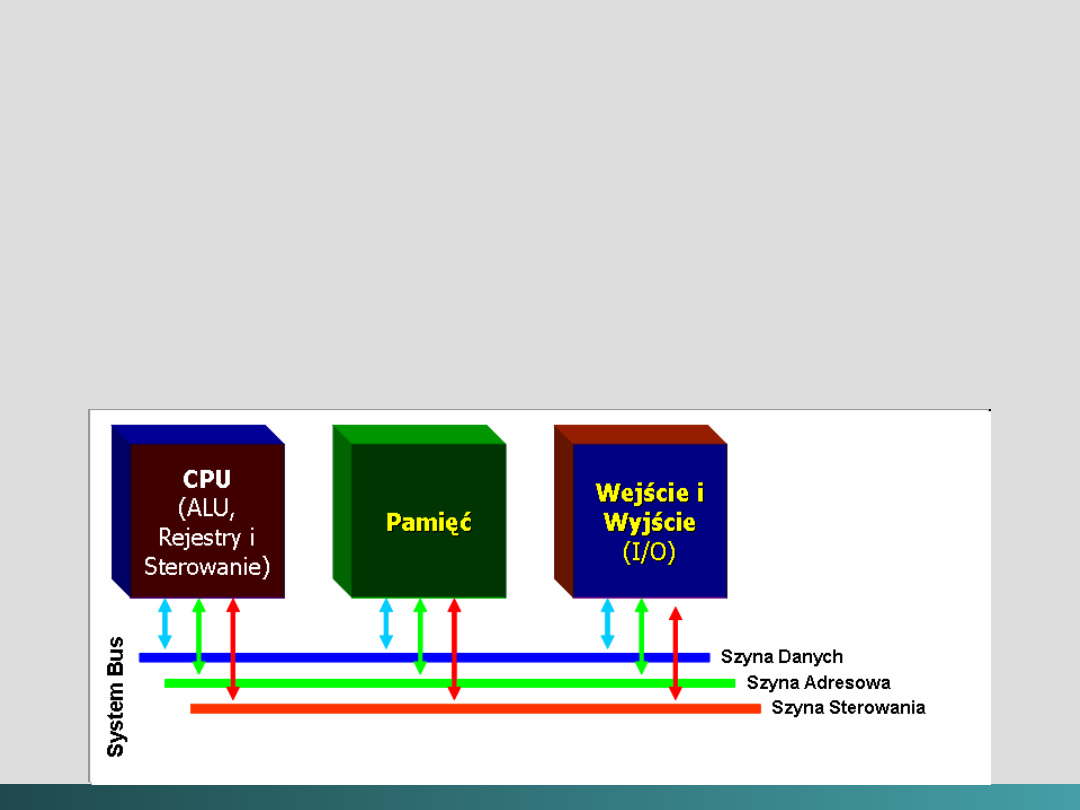
@Janusz Kosiński, 2005

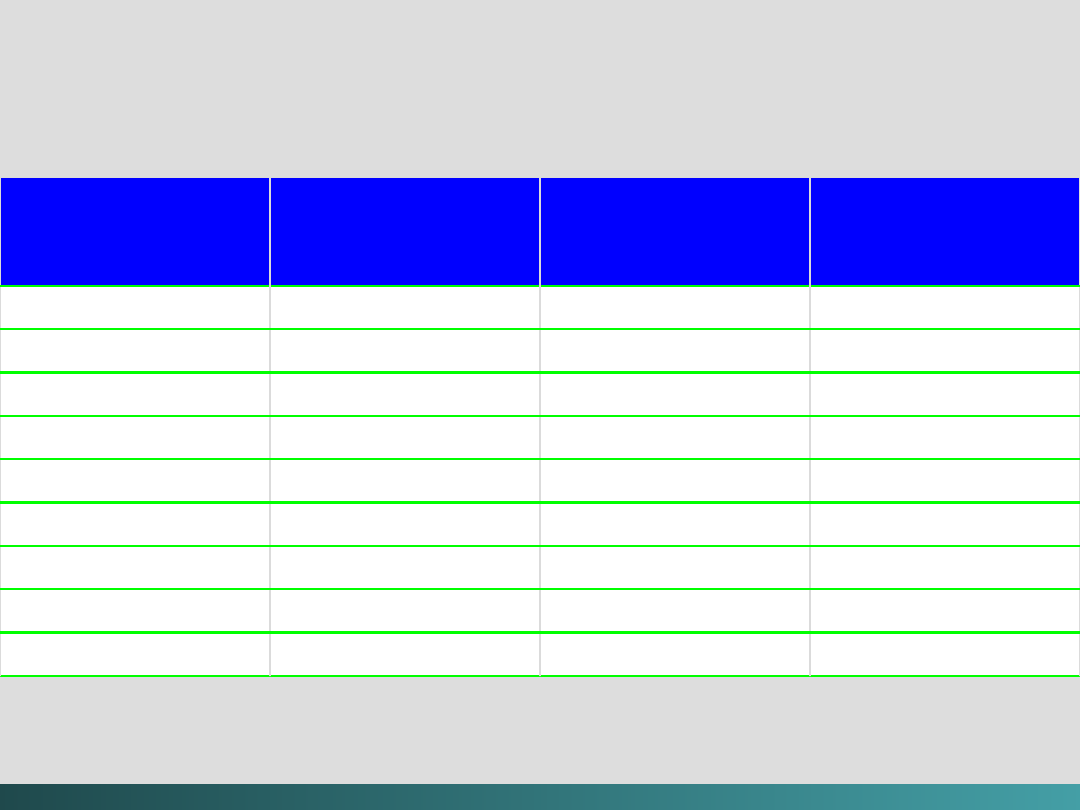
Model szyn zbiorczych (System Bus Model)

Szyna danych

przemieszcza dane między pamięcią

główną a rejestrami CPU – Data Bus

Szyna adresowa

„podtrzymuje” adresy danych do

których szyna danych ma aktualnie dostęp – Address Bus

Szyna sterująca

dostarcza niezbędne sygnały

sterujące transferem danych – Control Bus

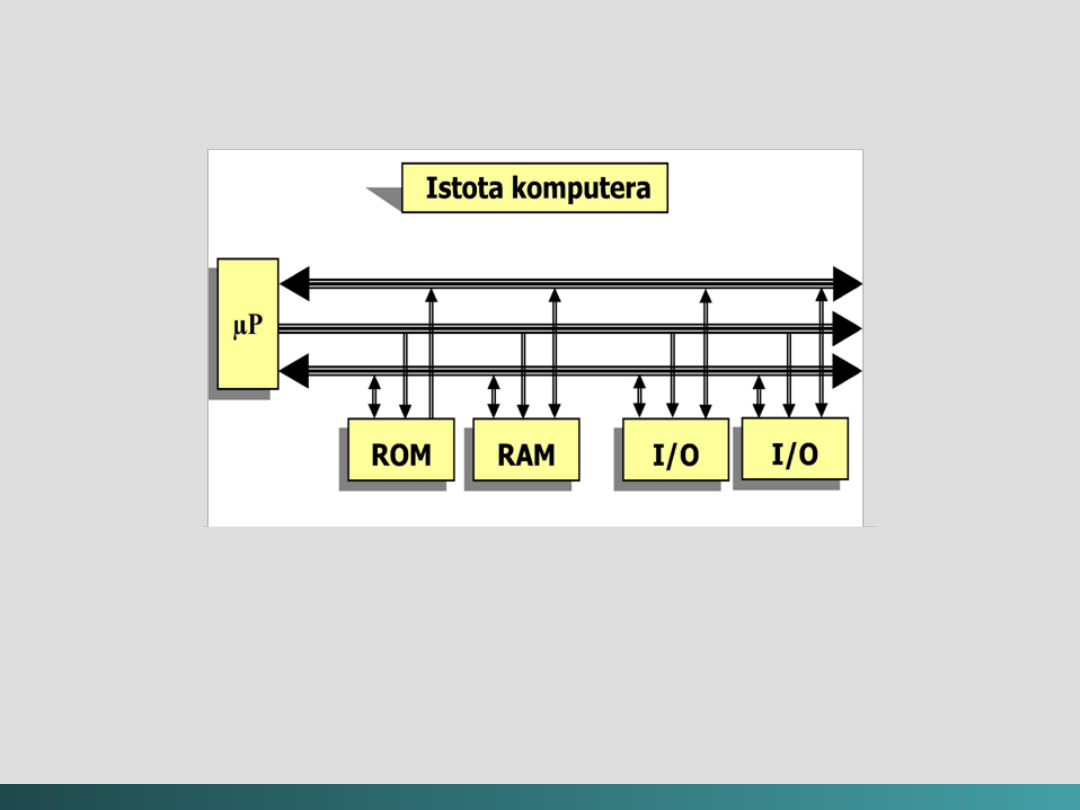
@Janusz Kosiński, 2005

Model szyn zbiorczych (

System Bus Model

)

@Janusz Kosiński, 2005

Model szyn zbiorczych (System Bus Model)

SPECYFIKACJA

1 017,3

66x4

AGP (x4

mode)

508,6

66x2

AGP (x2

mode)

254,3

AGP

508,6

64-bit PCI 2,1

127,2

PCI

127,2

VLB

31,8

8,3

EISA

15,9

8,3

16-bit ISA

7,9

8,3

8-bit ISA

Pasmo

przenoszenia

(MB/sec)

Prędkość

(MHz)

Szerokość

(bity)

BUS

@Janusz Kosiński, 2005

Modele nie - von Neumannowskie

Projektanci, którzy nie są ograniczeni koniecznością
stosowania się do modelu von Neumanna stosują
różne modele obliczeń:

- sieci neuronowe

- algorytmy genetyczne

- przetwarzanie równoległe,

Pierwsze systemy

do obliczeń równoległych

były

zaprojektowane w końcu lat 1960 – posiadały dwa
procesory

@Janusz Kosiński, 2005

Modele nie - von Neumannowskie

W latach 1970 pojawił się wstęp do

superkomputerów

w postaci maszyny 32

procesorowej, zaś w latach 1980 – systemu 1 000
procesorowego.

W roku 1999 IBM ogłosił skonstruowanie

supersystemu

z ponad 1 000 000 procesorów -

każdy z tych procesorów z

pamięcią dedykowaną

(wydzieloną do odrębnych zadań).

Ale i przetwarzanie równoległe ma swoje ograniczenia – ze
wzrostem liczby procesorów powstaje konieczność „wstawiania”

procesorów zarządzających

pozostałymi procesorami i

zasobami.

Reprezentacja danych w systemach

komputerowych

Reprezentacja danych w systemach

komputerowych

243,51

= 2 x 10

+ 4 x 10

+ 3 x 10

+ 5 x 10

-1

+ 1 x

-2

212

= 2 x 3

+ 1 x 3

+ 2 x 3

= 23

10110

= 1 x 2

+ 0 x 2

+ 1 x 2

+ 0 x 2

@Janusz Kosiński, 2005

Potęgi 2

dziesiętne

binarne

4-bity

szesnastkow

-2

= ¼ = 0,25

0000

-1

/2 = 0,5

0001

= 1

0010

= 2

0011

= 4

0100

= 8

0101

= 16

0110

= 32

0111

= 64

1000

= 128

1001

= 256

1010

= 512

1011

= 1 024

1100

= 32 768

1101

= 65 536

1110

1111

Liczbowe systemy
pozycyjne

Podstawowa idea opiera
się na tym,
że wartość liczby jest
reprezentowana
przez wzrastające
potęgi pewnych baz:

Reprezentacja
danych w
systemach
komputerowych

@Janusz Kosiński, 2005

Reprezentacja danych w systemach komputerowych

Liczby całkowite

Przedstawione na poprzednim slajdzie liczby należą do liczb
całkowitych

nieujemnych

(unsigned integer):

Liczby całkowite -

również i ujemne

(signed integer)

wymagają dodatkowych informacji, aby mogły być poprawnie
zaadresowane

W wielu językach programowania następuje automatyczna
alokacja miejsca przechowującego

bit znaku

Stosowana konwencja – skrajny lewy bit wskazuje znak
liczby.

Jeżeli jest to „1” to mamy do czynienia z liczbą ujemną – jeżeli
„0” to z liczbą dodatnią.

@Janusz Kosiński, 2005

Reprezentacja danych w systemach komputerowych

Np, w 8 bitowym słowie

-1

jest reprezentowane jako

10000001

zaś

jest reprezentowane jako

00000001

W systemach komputerowych stosujących taką reprezentację
dla 8 bitów przechowujących liczby całkowite, 7 bitów może być
wykorzystanych do aktualnej reprezentacji liczby.

01111111 → 2

+ 2

= 127

„0” na pierwszej pozycji oznacza liczbę dodatnią

11111111 → - (2

+ 2

)

= -

127

„1” na pierwszej pozycji oznacza liczbę ujemną

Stąd:
N bitów może reprezentować liczby od - 2

(N – 1)

- 1 do 2

(N – 1)

@Janusz Kosiński, 2005

Reprezentacja danych w systemach komputerowych

dodajemy

01001111

(79) do

00100011

(35)  01001111

+ 00100011

= 01110010

(114)

1 1 1 1

 przesunięcie

1 0 0 1 1 1 1

( 7 9 )

0 + 0 1 0 0 0 1 1

+ ( 3 5 )

1 1 1 0 0 1 0

( 1 1 4 )

Odejmujemy

01001111

(79)

od 01100011

(99)  01100011

- 01001111

= 00010100

(20)

0 1 1 2



pożyczanie

1 0 0 0

1 1

( 9 9 )

0 - 1 0 0 1 1 1 1

- ( 7 9 )

0 0 1 0 1 0 0

( 2 0 )

odejmujemy

01100011

(99) od

01001111

(79)  01001111

- 01100011

= 10010100

(-20)

1. Sprawdzamy, która liczba jest większa
2. Odejmujemy mniejszą od większej
3. Zmieniamy wartość pierwszego bitu (z „0” na „1”)

@Janusz Kosiński, 2005

Reprezentacja danych w systemach komputerowych

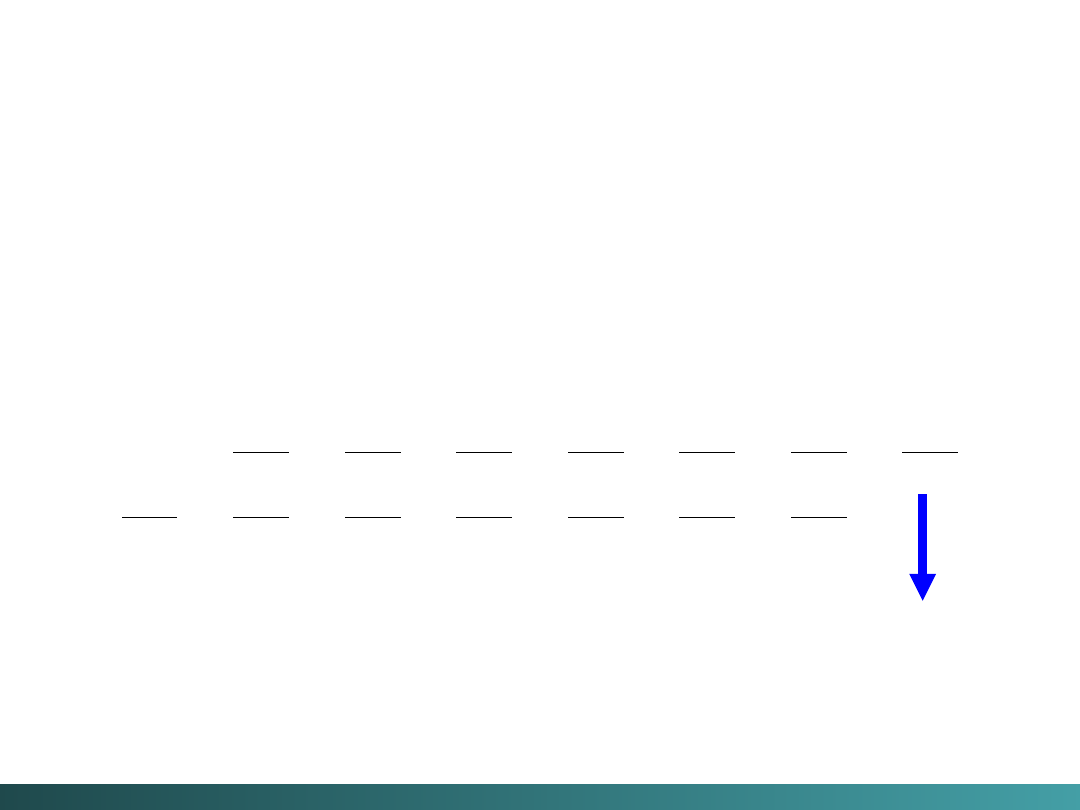
Dodajemy

01001111

(79) do

01100011

(99)



01001111

01100011

= 00110010

(50)



1 1 1 1

 przesunięcie

1 0 0 1 1 1 1

( 7 9 )

0 + 1 1 0 0 0 1 1

+ ( 9 9 )

0 1 1 0 0 1 0

( 5 0 )

Jak widać, przy 8 bitowej reprezentacji otrzymujemy błędny

wynik – rezultat zostanie „obcięty”

@Janusz Kosiński, 2005

Reprezentacja danych w systemach komputerowych

Dla szybkiego przeliczania z systemu dwójkowego na dziesiętny
wymyślona została pewna metoda polegająca na „dublowaniu”
pierwszego od lewej bitu i dodawaniu do następnego (ang, double–
dabble method).

Obliczenia rozpoczynają się od lewego skrajnego bitu

146

147

2

146

10010011

= 147

@Janusz Kosiński, 2005

Reprezentacja danych w systemach komputerowych

odejmujemy:

10011000

(-24) od

10101011

(-43)  10101011

- 10011000

= 00010011

(19)

0 2



pożyczanie

1 0

1 0 1 1

( 4 3 )

0 - 0 0 1 1 0 0 0

- ( 2 4 )

0 0 0 1 0 1 1

( 1 9 )

Odejmujemy

10101011

(-43) od

10011000

(-24)  10011000

- 10101011

= 10010011

(-19)

1. Zamieniamy odjemną na liczbę dodatnią
2. Sprawdzamy która liczba jest większa
3. Jeżeli odjemnik jest mniejszy od odjemnej, odejmujemy

mniejszą liczbę od większej i nie zmieniamy pierwszego bitu

4. Jeżeli odjemnik jest większy, odejmujemy mniejszą liczbę od

większej i zmieniamy wartość pierwszego bitu (z „0” na „1”)

Liczby zmiennoprzecinkowe

W rzeczywistym komputerze, przy zastosowaniu słowa

16 bitowego (a więc małego) i pamiętając o bicie
znaku, największą liczbą, jaką możemy uzyskać, jest
32 767,

Chcąc zwiększyć zakres liczby można zastosować

słowo 32 bitowe,

Ale co robić jeżeli będziemy mieli do czynienia z ułamkami?

@Janusz Kosiński, 2005

Reprezentacja danych w systemach komputerowych

Liczby zmiennoprzecinkowe

Prosty model

W komputerach cyfrowych, liczba zmiennoprzecinkowa zawiera

trzy części

: bit znaku, część wykładniczą (reprezentującą

wykładniki potęgi 2) i część ułamkową – nazywaną znaczącą
(liczba znaków po przecinku),

Liczba bitów

stosowanych dla wykładnika i liczby znaków po

przecinku jest zależna od tego, czy chcemy mieć większą
liczbę (liczba bitów dla wykładników) czy większą dokładność
(liczba bitów dla liczby znaków o przecinku),

Dla celów ilustracyjnych dalej będzie pokazywany znormalizowany 14

bitowy model, z tzw, szczeliną 2 bitową

@Janusz Kosiński, 2005

1 bit

bit znaku

5 bitów

wykładniki

Liczba znaków po przecinku

8 bitów

Reprezentacja danych w systemach komputerowych

Arytmetyka zmiennoprzecinkowa

Przy dodawaniu dwóch liczb dziesiętnych wyrażanych

w notacji naukowej, takich jak

1,5 x 10

+ 3,5 x 10

dokonujemy zmiany liczb w taki sposób aby były

wyrażane jako potęgi przy tych samych podstawach:

1,5 x 10

+ 3,5 x 10

= 0,15 x 10

+ 3,5 x 10

= 3,65 x 10

Dodawanie i odejmowanie zmiennoprzecinkowe działa

według takich samych zasad,

@Janusz Kosiński, 2005

Reprezentacja danych w systemach komputerowych

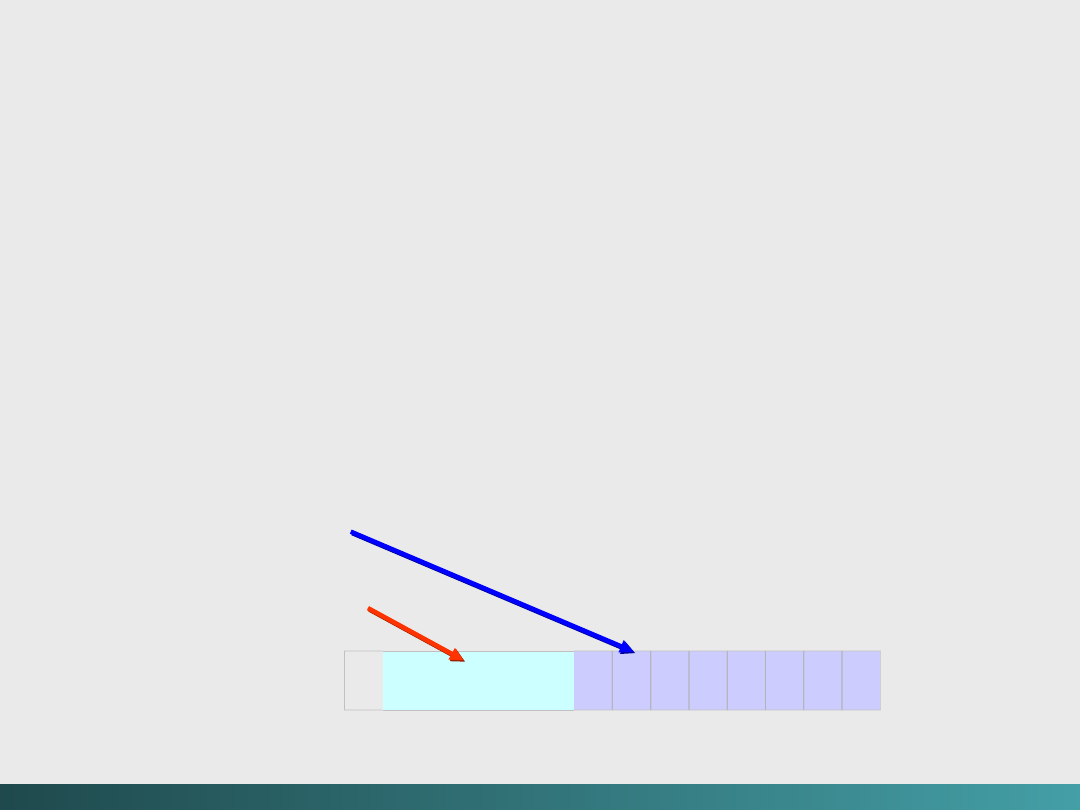
Arytmetyka zmiennoprzecinkowa

Załóżmy, że chcemy przechować liczbę 17 , Wiemy,

że;

17 = 17,0 x 10

= 1,7 x 10

= 0,17 x 10

Analogicznie w formie binarnej:

= 10001

x 2

= 1000,1

x 2

= 100,01

x 2

= 10,001

x 2

= 1,0001

x 2

= 0,10001

x 2

Jeżeli zastosujemy ostatnią formułę, część ułamkowa

będzie równa:

10001000

zaś wykładnik

00101

@Janusz Kosiński, 2005

0 0 0 1 0 1 1 0 0 0 1 0 0 0

Reprezentacja danych w systemach komputerowych

Kod BCD

(Binary-Coded Decimal)

jest

numerycznym systemem kodowania
używanym początkowo przez IBM w
komputerach „mainframe” i
systemach średniej wielkości.

Jak wskazuje nazwa, BCD koduje każdą cyfrę

systemu dziesiętnego, do 4 bitowej formy
binarnej, Jednocześnie stosowane jest
kodowanie dodatkowe (strefowe) dla
odróżniania liczb dodatnich, ujemnych i
nieujemnych.

Liczby nieujemne są znakowane kodem 1111

Liczby dodatnie są znakowane kodem 1100

Liczby ujemne są znakowane kodem 1101

@Janusz Kosiński, 2005

Kody znakowe

cyfra

BCD

0000

0001

0010

0011

0100

0101

0110

0111

1000

1001

Strefy

1111

Nieujemne

1100

Dodatnie

1101

Ujemne

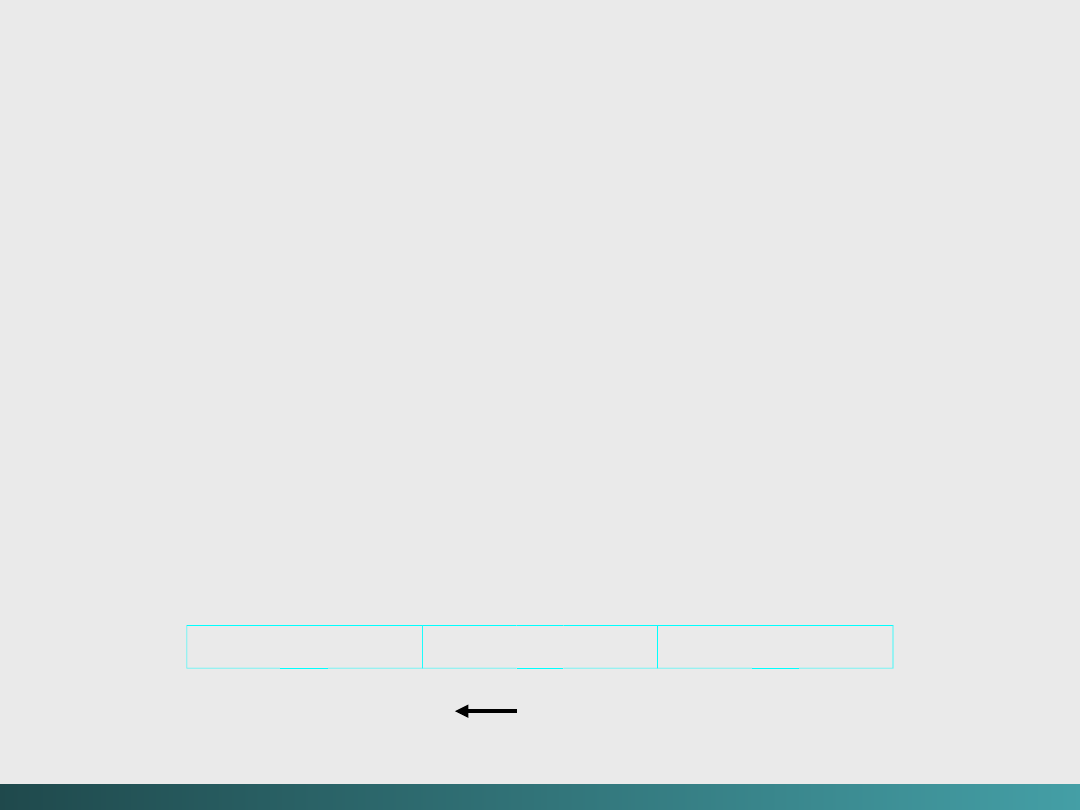
@Janusz Kosiński, 2005

Reprezentacja liczby -1 265 w 3 bajtach (1 bajt = 8
bitów) przy użyciu tzw. spakowanego BCD.

Kodowanie strefowe dla 1 265 ma postać:

1111

0001

1111

0010

1111

0110 1111 0101

Po spakowaniu, string wygląda następująco:

0001 0010 0110 0101

Po dodaniu kodu znaku po cyfrze najniższego poziomu i swoistym
„wyłączeniu przed nawias” kodu znaku liczby nieujemnej, zapis w
trzech bajtach ma postać:

Kody znakowe

1111

0001 0010

0110 0101

1101

0 0 0 0 0 0 0 1 1 1 1 0 0

0 1

Zapis tej samej liczby w słowie 16
bitowym

@Janusz Kosiński, 2005

Kody znakowe

Kod EBCDIC

Przed powstaniem IBM System/360, IBM używał 6
bitowej wersji kodu BCD dla reprezentowania znaków
i liczb.

Kod ten był mocno ograniczony w zakresie możliwości
manipulowania danymi – stąd inżynierowie z IBM
zdecydowali, że najprościej będzie rozszerzyć kod BCD z 6
bitów do 8 bitów.

Ten nowy kod uzyskał nazwę

Extended Binary Coded

Decimal Interchange Code

(EBCDIC).

IBM kontynuuje stosowanie EBCDIC w komputerach
mainframe i systemach komputerowych średniej wielkości.

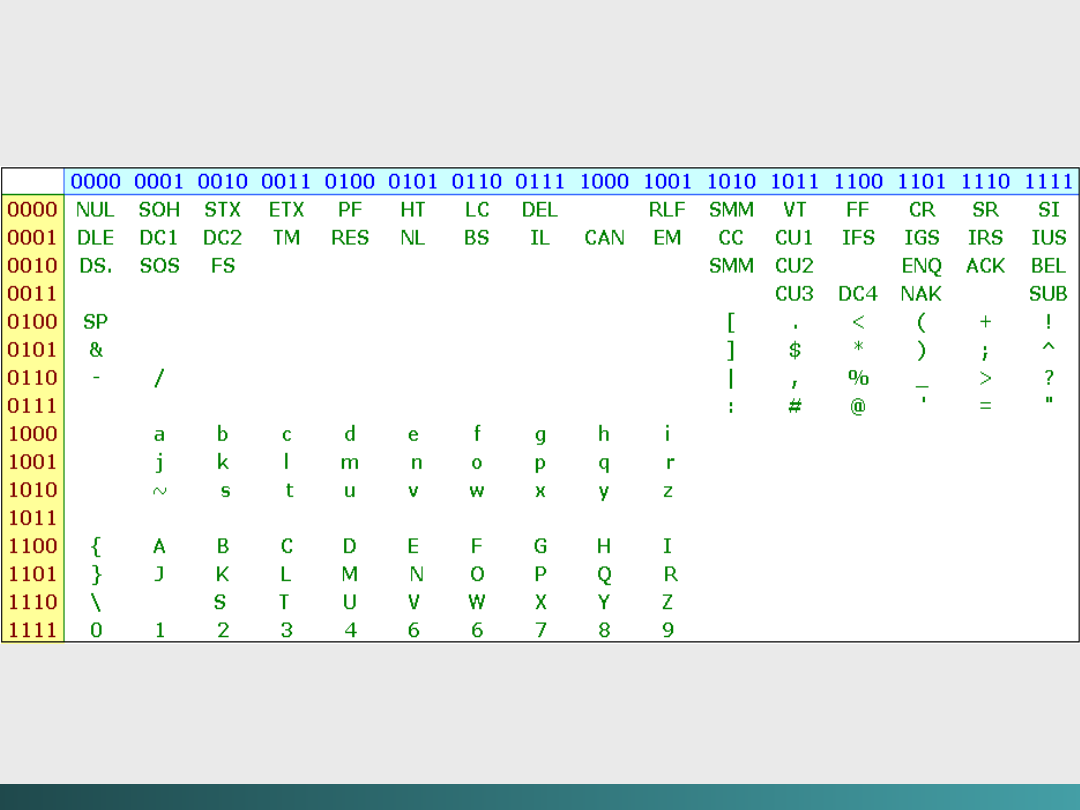
@Janusz Kosiński, 2005

Kody znakowe

Kod
EBCDIC

Stosowane skróty znakowe – opisują czynności wykonywane z treścią
programu

@Janusz Kosiński, 2005

Kody znakowe

Kod ASCII

Podczas gdy IBM był zajęty budową Systemu/360, inni
producenci wyposażenia starali się na znalezieniem
lepszych sposobów transmisji danych między systemami.

American Standard Code for Information
Interchange

(ASCII) jest jednym z produktów tych

wysiłków.

@Janusz Kosiński, 2005

Kody znakowe

Kod ASCII

ASCII jest bezpośrednim potomkiem schematów
kodowania stosowanych w telegrafach (teleksach).
Urządzenia te

wykorzystywały 5 bitowy kod (Murray)

pochodzący od prób

z lat 1880 (Baudet).

International Organization for Standardization (ISO)
zaproponowała 7 bitowy schemat kodowania, nazywany

Międzynarodowym Alfabetem Nr 5.

W 1967 pochodna tego alfabetu stałą się oficjalnym
standardem

nazywanym obecnie ASCII.

@Janusz Kosiński, 2005

Kody znakowe

Kod ASCII

Stosowane skróty znakowe – opisują czynności wykonywane z treścią
programu

@Janusz Kosiński, 2005

Kody znakowe

Unicode

Oba kody EBCDIC i ASCII były zbudowane na podstawie
alfabetu łacińskiego, Lecz większość ludzi na świecie
stosuje alfabety nie łacińskie, W 1991, utworzone zostało
z liderów przemysłu i polityków konsorcjum, do
określenia międzynarodowego standardu kodowania –
nazywanego

UNICODE

(Unicode Consortium).

Unicode jest 16 bitowym alfabetem, podobnym do ASCII z
zestawem znaków Latin 1.

Jest zbieżny z alfabetem ISO/IEC nr 10646-1, Ponieważ
bazą kodowania Unicode jest 16 bitów, to posiada on
możliwość zakodowania praktycznie wszystkich
stosowanych na świecie alfabetów.

@Janusz Kosiński, 2005

Kody znakowe

Typy znaków

Opis zbioru

znaków

Liczba znaków

Wartości

szesnastkowe

Alfabety

Łaciński, grecki,

cyrylica, itp,

8 192

0000 do 1FFF

Symbole

Matematyczne,

geograficzne,

itp,,

4 096

2000 do 2FFF

CJK

Chińskie,

japońskie i

koreańskie

symbole

fonetyczne i

znaki

przystankowe

4 096

3000 do 3FFF

Han

Ujednolicony

chiński, japoński

i koreański

40 960

4000 do DFF

Rozszerzenie Han

4 096

E000 do EFFF

Definiowane

przez

użytkownika

4 095

F000 do FFFE

Unicode

@Janusz Kosiński, 2005

Kody zapisywania i przesyłania danych

ASCII, EBCDIC, czy Unicode są w jednakowy
sposób reprezentowane w pamięci komputera,
Elementy cyfrowe są raczej w pozycji
„włączony” lub „wyłączony” z niczym
„pomiędzy”.

Jednakże, kiedy dane są zapisywane na pewne
rodzaje nośników (taśma, dysk), czy też przesyłane
na duże odległości, sygnały binarne stają się
zamazane, szczególnie w przypadkach długich
stringów „0” lub „1”.

@Janusz Kosiński, 2005

Kody zapisywania i przesyłania danych

Media magnetyczne,

takie jak taśmy czy dyski

mogą gubić synchronizację w wyniku
niestabilności środowiska

(pole magnetyczne w

urządzeniach nadawczych czy odbiorczych jest
wytwarzane przy pomocy prądu elektrycznego),

czy wad materiałowych samych nośników.

@Janusz Kosiński, 2005

Kody zapisywania i przesyłania danych

litera

ASCII

binarnie

1001111

1001011

Bit parzystości

Razem

11001111 01001011

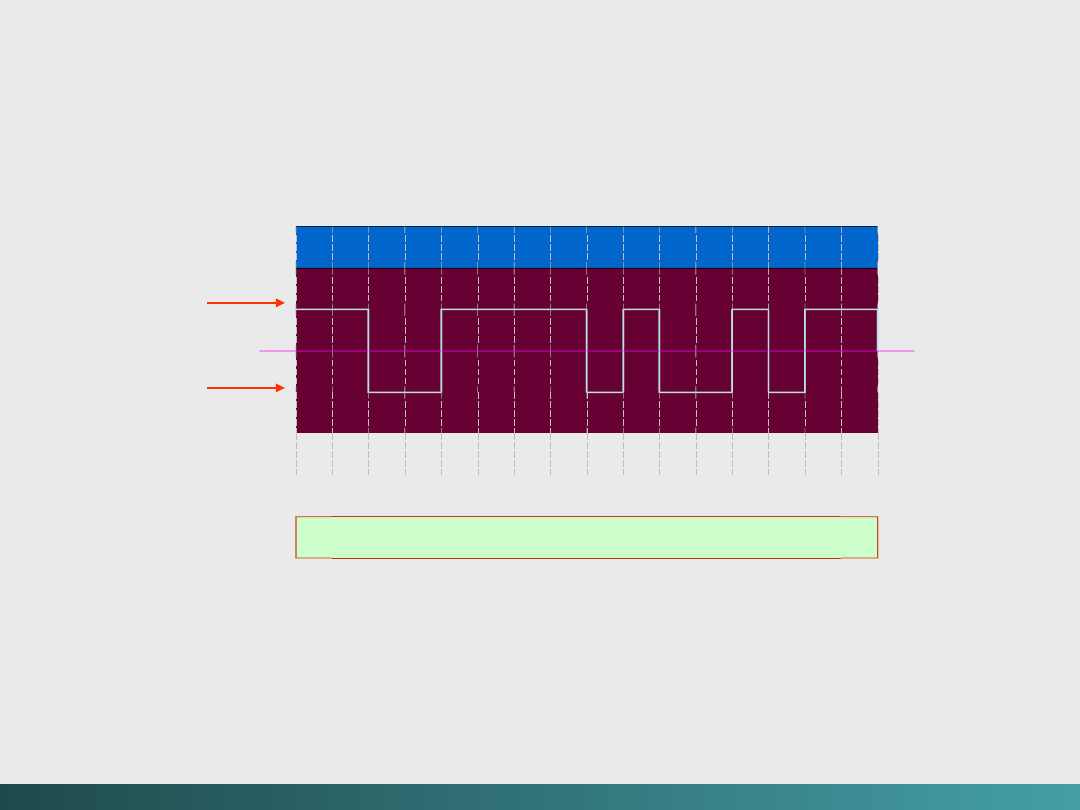
Kod NRZ

(Non-Return-to-Zero)

Najprostszą metodą kodowania danych jest kod
NRZ. Jest on stosowany bezpośrednio – kiedy
mówimy „wysoki” to oznacza to wysoki poziom
napięcia - przeważnie

3 lub 5 V.

zaś kiedy mówimy niski oznacza to niski poziom
napięcia -przeważnie

- 3 lub - 5V.

Na przykład kod ASCII dla angielskiego słowa OK,
z bitem parzystości wynosi:

11001111 01001011

@Janusz Kosiński, 2005

1 1 0 0 1 1 1 1 0 1 0 0 1 0 1 1

               

Wysok

Niski

Zero

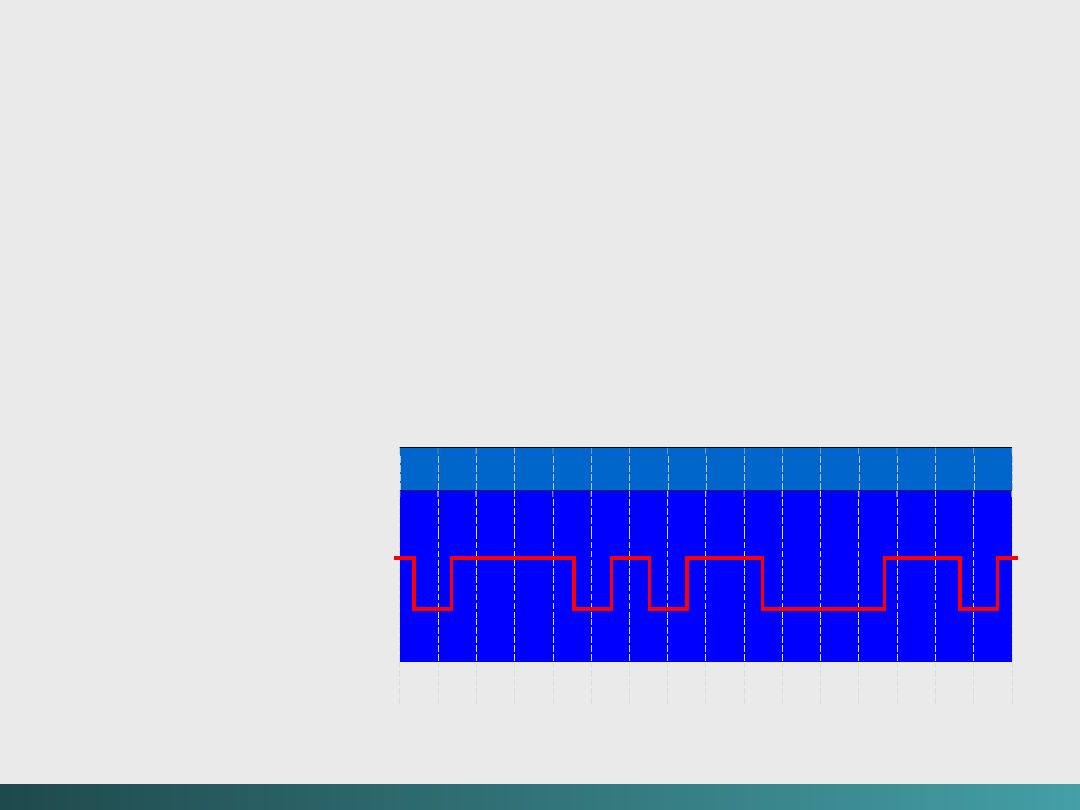
Kodowanie NRZ dla OK

Falowy schemat transmisji

Schemat domen magnetycznych

(

kierunek strzałek

wskazuje polaryzację magnetyczną)

Kody zapisywania i przesyłania danych

Kod NRZ

(Non-Return-to-

Zero)

@Janusz Kosiński, 2005

1 1 0 0 1 1 1 1 0 1 0 0 1 0 1 1

Kody zapisywania i przesyłania danych

Kod NRZI

(Non-Return-to-Zero Invert)

Kodowanie NRZI dla OK

NRZI zapewnia przejścia dla każdej „1” z wysokiego

stanu do niskiego albo z niskiego do

wysokiego, oraz żadnego przejścia dla „0”

To kodowanie rozwiązuje częściowo problem strat
synchronizacji

@Janusz Kosiński, 2005

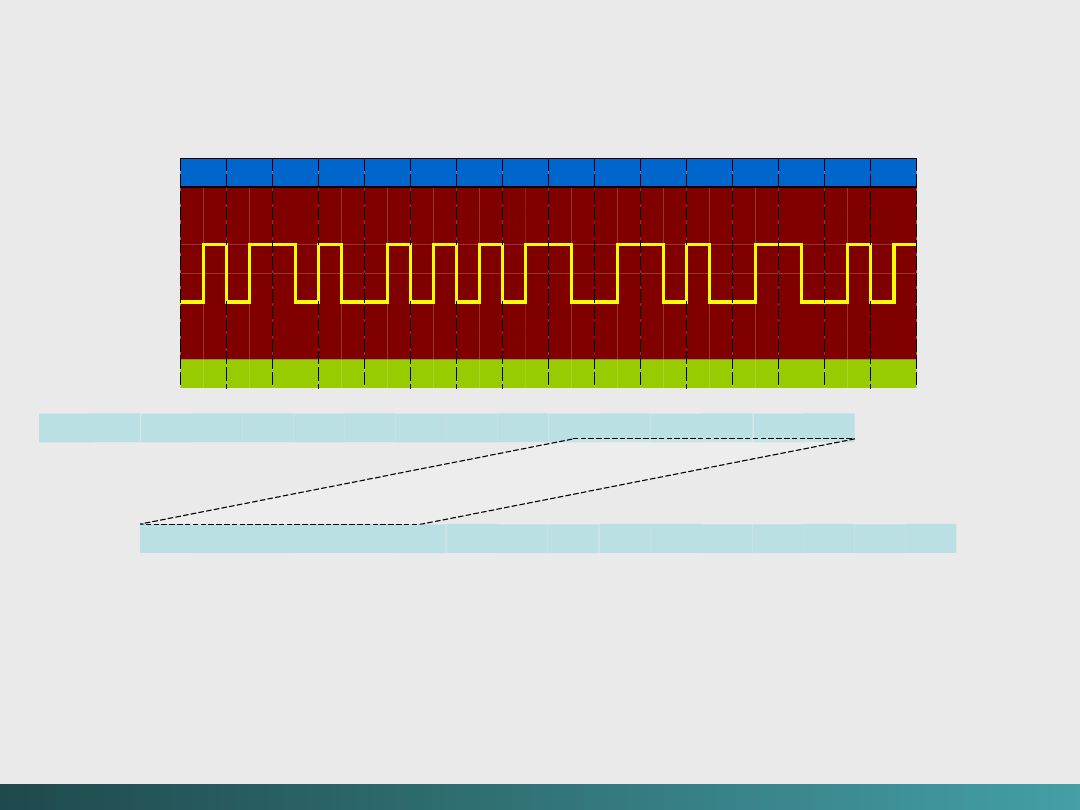
Kody zapisywania i przesyłania danych

Modulacja fazy

(kod Manchester)

Metoda ta zapewnia przejście dla każdego
sygnału, czy to „0” czy też „1”.

W tym kodowaniu,

każde przejście „do góry”

sygnalizuje „1” zaś każde przejście „na dół”
sygnalizuje „0”

– modulacja fazowa jest stosowana m.in. w
sieciach LAN, ale nie jest efektywna dla
przechowywania danych – wymaga dwukrotnej
gęstości w porównaniu z NRZ

@Janusz Kosiński, 2005

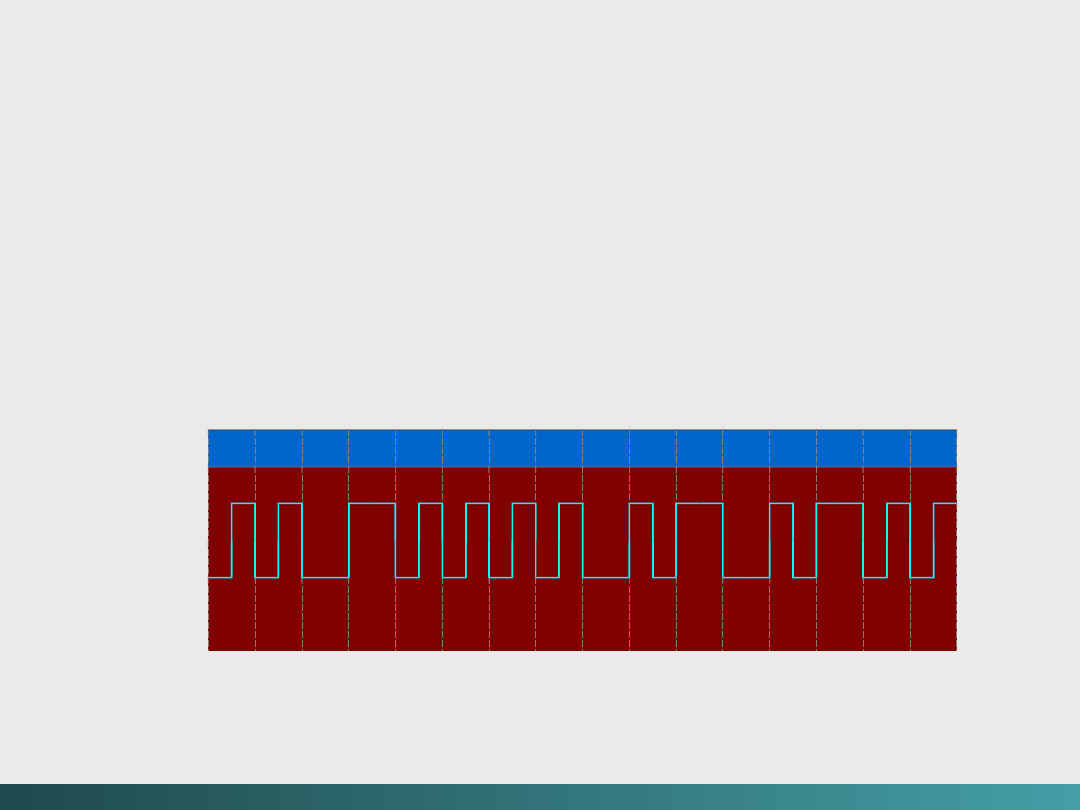
Kody zapisywania i przesyłania danych

Modulacja fazy

(kod Manchester)

Kodowanie Manchester dla OK

Falowy schemat transmisji

Schemat domen magnetycznych

(

kierunek strzałek

wskazuje polaryzację magnetyczną)



@Janusz Kosiński, 2005

1 1 0 0 1 1 1 1 0 1 0 0 1 0 1 1

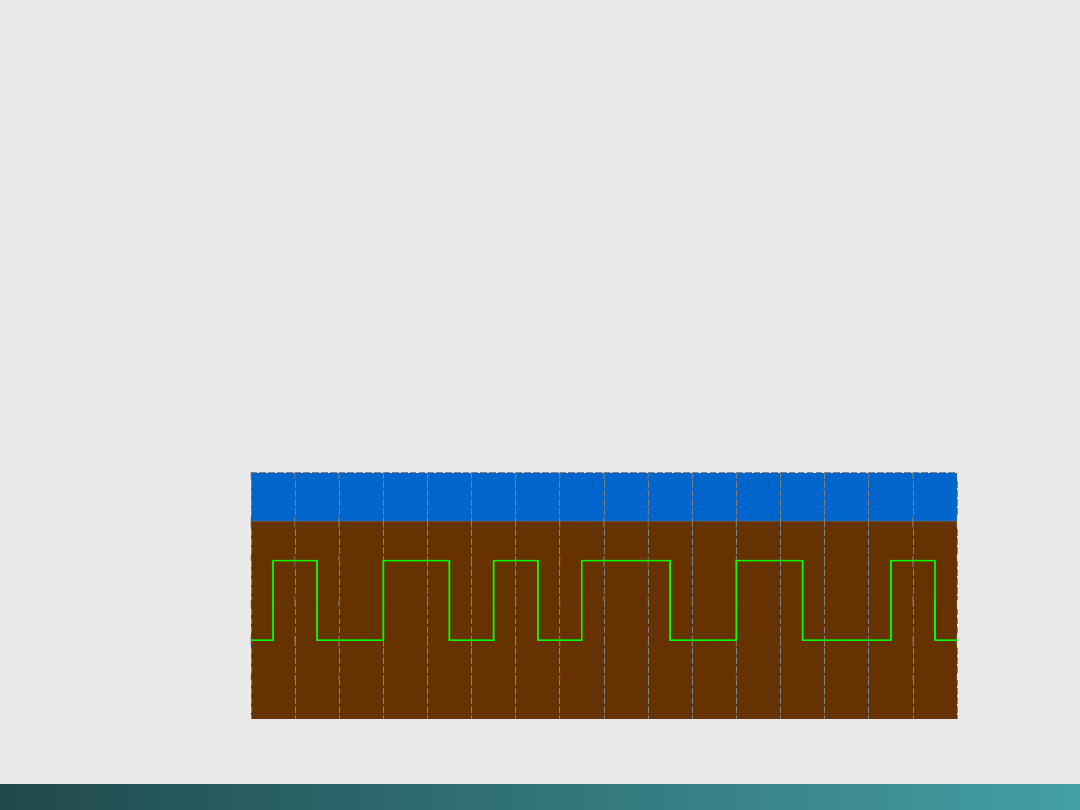
Modulacja częstotliwościowa

Modulacja częstotliwościowa (FM) jest podobna do modulacji

fazowej w tym, że stosowane jest tylko jedno przejście
„wewnętrzne” na każdą „1”, Ta synchronizacja występuje
na początku każdej „komórki bitowej”.

Kody zapisywania i przesyłania danych

Kodowanie FM dla OK

@Janusz Kosiński, 2005

1 1 0 0 1 1 1 1 0 1 0 0 1 0 1 1

Kodowanie MFM

FM jest tylko trochę lepsze niż PM przy uwzględnieniu wymagań
przechowywania. Stąd powstała metoda zmodyfikowana (MFM),
gdzie przejścia miedzy komórkami bitowymi występują tylko przy
następujących po sobie zerach.

MFM jest efektywniejszą metodą kodowania niż FM czy NRZ,
szczególnie przy kontroli błędów –przez wiele lat była stosowana
dla przechowywania danych na dysku.

Kodowanie MFM dla OK

Kody zapisywania i przesyłania danych

@Janusz Kosiński, 2005

Kody zapisywania i przesyłania danych

Kod RLL

Kod RLL (Run-length-limited)

jest metodą kodowania w

której blok znaków kodu ASCII lub EBCDIC jest tłumaczony
w sposób powodujący ograniczanie liczby następujących
po sobie zer.

Kod RLL(d, k) pozwala na występowanie

minimum d

maksimum k

występujących po sobie zer, pomiędzy

dowolną parą następujących po sobie jedynek.

Kodowanie słów z wykorzystaniem RLL zapobiega utracie
synchronizacji danych na dysku, co wydarzało się przy
stosowaniu kodu „płaskiego” (NRZI).

@Janusz Kosiński, 2005

Kody zapisywania i przesyłania danych

Najbardziej rozpowszechnionym wariantem

jest kod RLL(2,

7) stosowany w dyskach magnetycznych. Od strony
technicznej jest 16 bitowym odwzorowaniem kodu ASCII lub
EBCDIC – jest około 50% efektywniejszy niż kod MFM.

Teoretycznie rzecz ujmując,

RLL jest formą kompresji

danych

zwaną kodem Hufmana.

Teoria jest oparta na założeniu, że wystąpienie „1” w
dowolnej komórce bitowej jest tak samo prawdopodobne.

Na podstawie tego założenia możemy wnioskować, że
prawdopodobieństwo wystąpienia układu „10” lub „11”, w dowolnej
parze rozpatrywanych komórek bitowych, jest równe 0,25.

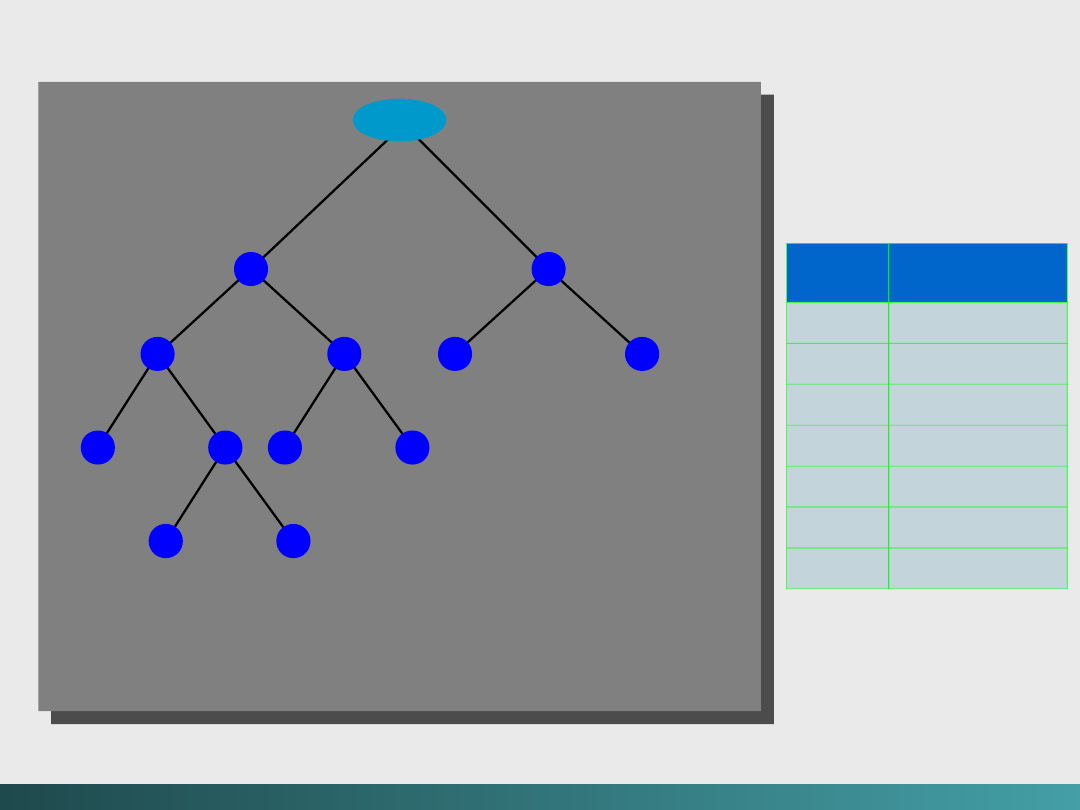
@Janusz Kosiński, 2005

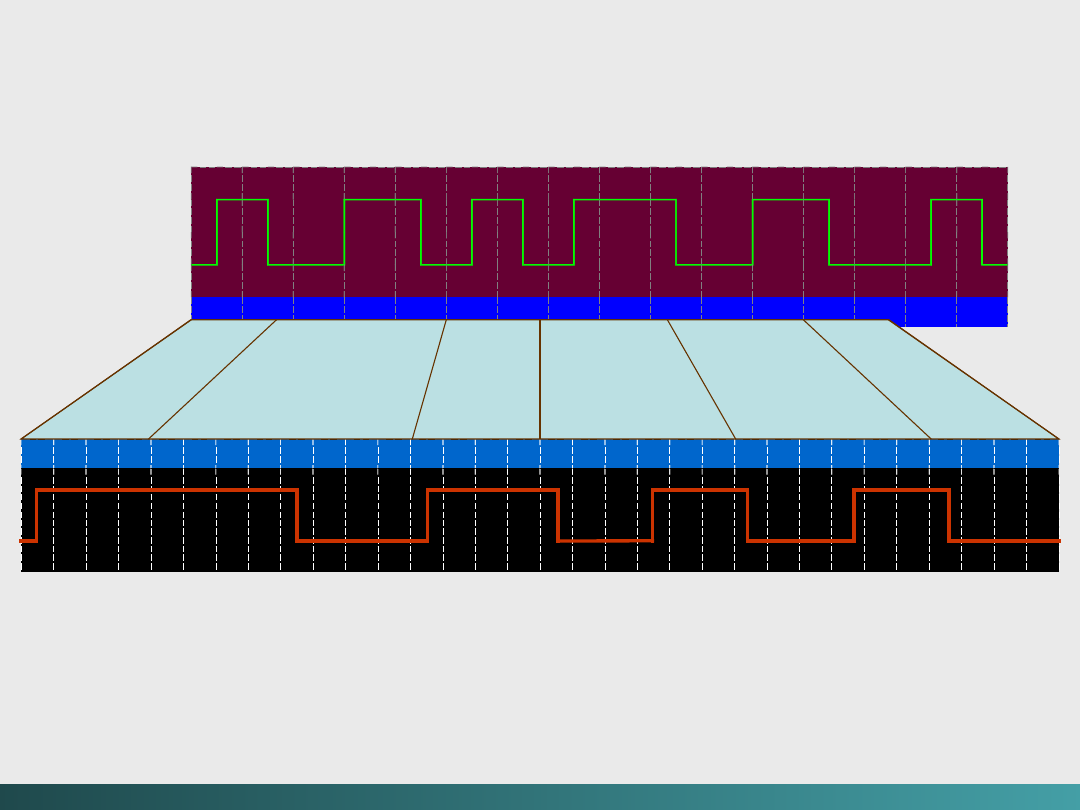
Drzewo prawdopodobieństwa dla RLL(2, 7)
Kodowanie

Kodowanie RLL(2,

Kody zapisywania i przesyłania danych

korzeń

P(000) =

1/8

P(010) =

1/8

P(011) =

1/8

P(0010) =

1/16

P(0011) =

1/16

P(11) =

1/4

P(10) =

1/4

Wzór

bitów

Kod RLL(2, 7)

0100

1000

000

000100

010

100100

011

001000

0010

00100100

0011

00001000

@Janusz Kosiński, 2005

1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0

MFM → 12
przejść

RLL(2, 7)

→

przejść

Porównanie kodowania MFM oraz RLL(2, 7) dla słowa OK

@Janusz Kosiński, 2005

Wykrywanie błędów i korekcja

Niezależnie od stosowanych metod kodowania,
żaden kanał komunikacyjny i środek
magazynowania nie będzie całkowicie wolny od
błędów. Przy zwiększaniu współczynnika
transmisji (bity na sekundę) odstępy między
bitami są coraz ciaśniejsze.

Podobnie przy magazynowaniu – wzrost liczby bitów na milimetr
kwadratowy powoduje zwiększenie gęstości strumienia,
Wskaźnik błędów wzrasta w bezpośredniej proporcji do liczby
transmitowanych bitów na sekundę czy też liczby bitów na
milimetr kwadratowy.

@Janusz Kosiński, 2005

Wykrywanie błędów i korekcja

Cykliczna kontrola redundancji (Cyclic
Redundancy Check)

Sumy kontrolne są szeroko stosowane w różnych
systemach kodowania

(od kodów paskowych do ISBN -

International Standard Book Numbers) –

pozwalają na szybkie

stwierdzenie, że poprzedzająca cyfra jest błędna,
Cykliczna kontrola redundancji jest typem sumy
kontrolnej stosowanej przede wszystkim w przesyłaniu
danych, celem stwierdzenia czy wewnątrz strumienia
bajtów lub bloku danych nie ma błędów.

Sumy kontrolne i CRC są typem systematycznej detekcji
błędów

Słowo cykliczna w CRC odnosi się do teorii
matematycznej, znajdującej się za tym schematem
obliczeniowym.

@Janusz Kosiński, 2005

Reguły dodawania są
następujące:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 0

przykład :

Znaleźć sumę 1011

i 110

modulo 2

1011

+110

1101

(mod 2)

Ta suma ma sens jedynie w
modulo 2

Wykrywanie błędów i korekcja

Arytmetyka Modulo 2

Arytmetyka 12 godzinnego zegara jest systemem modulo 12 – po
dodaniu dwóch godzin do 11:00 otrzymujemy 1:00.

Arytmetyka modulo 2 używa dwóch binarnych operandów bez
przesuwania i pożyczania. Wynik jest binarny i również wchodzi
w skład systemu modulo 2.

Z powodu zastosowania takiego domknięcia w dodawaniu, matematycy
mówią, że system modulo 2 tworzy pole algebraiczne

@Janusz Kosiński, 2005

101

nie dzieli się przez

1011

czyli jest to

reszta,

Iloraz wynosi:

1010

Arytmetyka modulo 2

Dzielenie modulo 2 operuje na serii dodawań modulo
2

Przykład:

Znaleźć iloraz i resztę z dzielenia 1001011

przez

1011

1 0 1 0

1 0 1 1

| 1 0 0 1 0 1 1

1 0 1 1

0 0 1 0
0 0 1 0 0 1

1 0 1 1

0 0 1 0
0 0

1 0 1

Wykrywanie błędów i korekcja

@Janusz Kosiński, 2005

Wykrywanie błędów i korekcja

Obliczanie i stosowanie CRC

Przykład:

Niech bajt informacji wynosi

I = 1001011

, (dowolna liczba

bajtów może być wykorzystana do utworzenia bloku
informacji).

Nadawca i odbiorca zgadzają się na zastosowanie
arbitralnego wzorca binarnego:

P = 1011

, (wzorce

zaczynające i kończące się z „1” „pracują” lepiej).

Przesuwamy I w lewo o jedno miejsce mniej niż liczba bitów
w P tak, że nowa informacja ma postać:

I = 1001011000

Używając I jako dzielnej i P jako dzielnika, przeprowadzamy

dzielenie modulo 2

, ignorujemy wartość ilorazu i

zapisujemy resztę

100

, reszta ta jest aktualną sumą

kontrolną CRC.

@Janusz Kosiński, 2005

Wykrywanie błędów i korekcja

1 0 1 0 1 0 0

1 0 1 1

1 0 0 1 0 1 1

1 0 0

1 0 1 1
0 0 1 0 0 1

1 0 1 1
0 0 1 0
0 0 1 0 1 1

1 0 1 1

0 0 0 0

Obliczanie i stosowanie
CRC

Przykład (c.d.)

Dodając resztę do I,
uzyskujemy wiadomość M:

1001011000

+ 100

1001011100

M jest odkodowane i
sprawdzane

przez odbiorcę wiadomości
przy

zastosowaniu procesu
odwrotnego.

Tym razem P dzieli M
dokładnie:

@Janusz Kosiński, 2005

Reszta różna od zera wskazuje, że w czasie transmisji M powstał
błąd. Metoda ta jest wydajniejsza przy zastosowaniu wielomianów
wysokiego stopnia, Są cztery podstawowe standardy wielomianów
o szerokim zastosowaniu:

CRC-CCITT (ITU-T):

+ X

+ 1

CRC-12:

+ X

+ X + 1

CRC-16 (ANSI):

+ X

+ 1

CRC-32:

+ X

+ X +1

CRC-CCITT

CRC-12

, i

CRC-16

operują na parach bajtów;

CRC-32

używa czterech bajtów, co jest właściwe dla systemów
operujących 32 bitowymi słowami. Zostało dowiedzione, że CRC
wykorzystujące te wielomiany mogą wykryć ponad 99,8%
pojedynczych błędnych bitów,

Wykrywanie błędów i korekcja

@Janusz Kosiński, 2005

Wykrywanie błędów i korekcja

Kod Hamminga

Kanały wymiany danych są bardziej podatne na błędy i bardziej
tolerancyjne niż systemy dyskowe. Wystarczy posiadanie
zdolności do wykrywania błędów. Jeżeli urządzenie
komunikacyjne stwierdzi wystąpienie błędnego bitu, to jedyne
co robi to zamawia ponowna transmisję.

Systemy pamięciowe

systemy magazynowania

nie

posiadają tych możliwości.

Dysk może być wyłącznym repozytorium (przechowalnią) lub
raczej kolekcją nierepredukowalnych danych czasu
rzeczywistego. Stąd dyski i magazyny danych muszą mieć
zdolność do wykrywania i korygowania błędów.

@Janusz Kosiński, 2005

Wykrywanie błędów i korekcja

Kod Hamminga

Kodowanie z wykrywaniem błędów jest problemem
od ponad stu lat, i mimo to jednym z najbardziej
efektywnych i najstarszych kodów jest

kod

Hamminga - adaptacja koncepcji parzystości –

zdolność do korekcji wzrasta wraz z liczbą
dodawanych do słowa bitów parzystości.

Kody Hamminga są stosowane w sytuacjach, gdy mogą
pojawiać się błędy przypadkowe.

W tej sytuacji zakładamy, że każdy błędny bit posiada swoje
prawdopodobieństwo pojawienia się, niezależnie od innych
błędów.

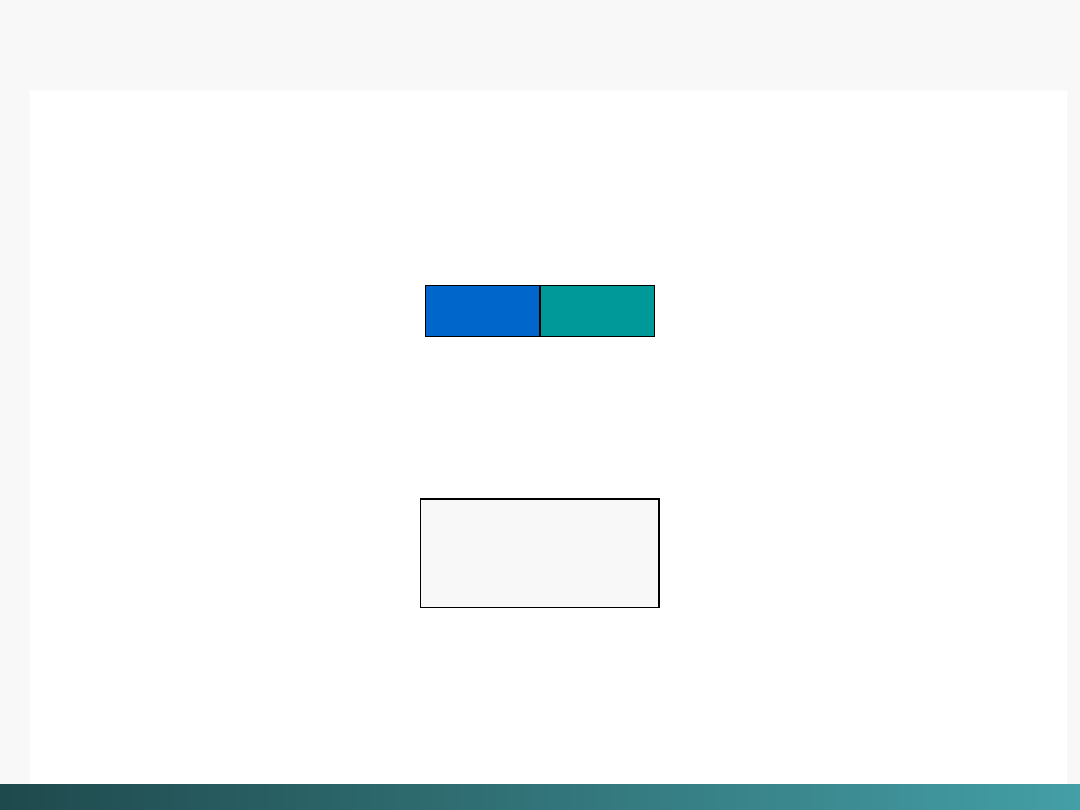
Słowo w pamięci zawiera

m bitów,

ale

r nadmiarowych

bitów

jest dodawanych w celu umożliwienia detekcji i

korekcji błędów.

Stąd słowo końcowe (słowo zakodowane) jest N bitową
jednostką, zawierająca

m bitów danych

r bitów

kontrolnych:

Liczba pozycji bitów, którymi różnią się dwa słowa
kodowane nazywa się

odległością Hamminga.

Np,, jeżeli

mamy dwa słowa zakodowane:

Możemy zobaczyć, że różnią się 3 pozycjami bitów, stąd

odległość Hamminga dla tych słów wynosi 3.

@Janusz Kosiński, 2005

Wykrywanie błędów i korekcja

bitów

10001001

10110001

* * *

@Janusz Kosiński, 2005

Wykrywanie błędów i korekcja

Odległość Hamminga jest ważna w kontekście wykrywania
błędów.

Jeżeli dwa zakodowane słowa są oddalone od

siebie o odległość Hamminga równą d, to wymagane jest
wystąpienie d pojedynczych bitów (błędów) aby
przekonwertować jedno słowo na drugie – taki typ błędu nie
powinien być wykryty.

Stąd wynika, jeżeli chcemy mieć gwarancję detekcji
wszystkich pojedynczych błędnych bitów, wszystkie pary
słów (porównywanych) muszą mieć odległość Hamminga
najwyżej równą 2.

Jeżeli n bitowe słowo kodowe nie jest rozpoznawane jako legalne
słowo danego kodu, to jest sygnalizowany błąd.

@Janusz Kosiński, 2005

Wykrywanie błędów i korekcja

Stosując algorytm do obliczania bitów
kontrolnych, można zestawić kompletną listę
legalnych słów kodowanych.

Najmniejsza odległość Hamminga znaleziona między
wszystkimi parami słów tego kodu jest nazywana

minimalną odległością Hamminga tego kodu
D(min).

Określa ona możliwości wykrywania błędów i
wprowadzania korekt w tym kodzie.

@Janusz Kosiński, 2005

Wykrywanie błędów i korekcja

Załóżmy pamięć z dwoma bitami danych i jednym bitem
parzystości (na końcu słowa).

Z dwoma bitami danych mamy

ogółem 4 możliwe słowa:

Dane

Parzystość Kod

Słowo

Bit

Słowo

000

011

101

110

@Janusz Kosiński, 2005

Wykrywanie błędów i korekcja

Wynikowe słowo kodowe ma 3 bity, Stosując 3 bity dla 8
możliwości mamy: (poprawne słowa kodowe są oznakowane *):

000 *

100

001

101 *

010

110 *

011 *

111

Jeżeli zostanie wykryte słowo kodowe 001 to zostanie
zasygnalizowany błąd. Przypuśćmy, że prawidłowe słowo jest 011,
błąd spowoduje powstanie słowa 001, taki błąd zostanie wykryty
ale nie będzie skorygowany. Jest niemożliwe stwierdzenie jak wiele
bitów może być magazynowanych i ile może zawierać błędy.

Kody

korygujące błędy wymagają więcej niż jednego bitu parzystości.

Algebra Boole’a i logika cyfrowa

George Boole żył w Anglii (1815 – 1864), Boole był
matematykiem i logikiem pracującym nad wyrażaniem
rozważań logicznych przy pomocy symboli
matematycznych – stworzył gałąź matematyki nazywaną
logiką symboliczną lub algebrą Boole’a.

Algebra ta została wykorzystana przez Johna Vincenta

Atanasoffa, który postanowił zbudować maszynę podobną
zasadą działania do maszyn Pascala i Babbage’a – chcąc ją
zastosować do rozwiązywania liniowych równań
algebraicznych.

@Janusz Kosiński, 2005

W odniesieniu do obiektów binarnych, algebra Boole’a posiada

operacje, które mogą być wykonywane na tych obiektach.
Kombinacja tych operacji i zmiennych, daje w wyniku
wyrażenia Boolowskie. Funkcja Boolowska posiada jedną lub
więcej wartości wejściowych i w wyniku daje wyrażenie
bazujące na tych wielkościach, z zakresu {0, 1}.

Trzema wspólnymi operatorami

Boolowskimi są:

AND, OR, i

NOT.

Dla lepszego zrozumienia tych operatorów potrzebny

jest mechanizm, pozwalający na sprawdzenie ich zachowania.
Każdy operator może być opisany przy pomocy tablicy,
wyszczególniającej wejścia z wszystkimi możliwymi
wartościami oraz wartości wyjściowe, reprezentujące
wszystkie możliwe kombinacje tych wejść. Tablica taka jest
nazywana

tablicą prawdy.

@Janusz Kosiński, 2005

Algebra Boole’a i logika cyfrowa

@Janusz Kosiński, 2005

Tablica prawdy dla

AND

Wejścia

Wyjście

Wejścia

Wyjście

x + y

Tablica prawdy dla OR

Tablica prawdy dla

NOT

Wejście

Wyjście

Algebra Boole’a i logika cyfrowa

@Janusz Kosiński, 2005

Tożsamości Boole’owskie

Najczęściej wyrażenia Boole’owskie nie występują w
prostej formie.

Wystarczy przypomnienie z algebry, wyrażenie 2x +
6x nie jest przedstawione w prostej formie; może być
uproszczone do postaci: 8x.

Wyrażenia Boole’owskie również mogą być
upraszczane, ale potrzebne są nowe prawa
wykorzystywane w tej algebrze.

Algebra Boole’a i logika cyfrowa

@Janusz Kosiński, 2005

Podstawowe związki algebry
Boolowskiej

Nazwa

Forma AND

Forma OR

Prawo Tożsamości

1 x = x

0 + x = x

Prawo Dominacji

0 x = x

1 + x = x

Prawo Idempotencji

x x = x

x + x = 1

Prawo Komutatywności

x x = 0

x + y = y + x

Prawo Łączności

(xy)z = x(yz)

(x + y) + z = x + (y +

Prawo Rozdzielności

x + yz = (x + y)(x +

x + (y + z) = xy + yz

Prawo Absorpcji

x(x + y) = x

x + xy = x

Prawo DeMorgana

(xy) = x + y

(x + y) = (xy)

Prawo podwójnego zaprzeczenia

x = x

Algebra Boole’a i logika cyfrowa

@Janusz Kosiński, 2005

Tablica prawdy dla formy

AND

w prawach DeMorgana

(xy)

( )

Algebra Boole’a i logika cyfrowa

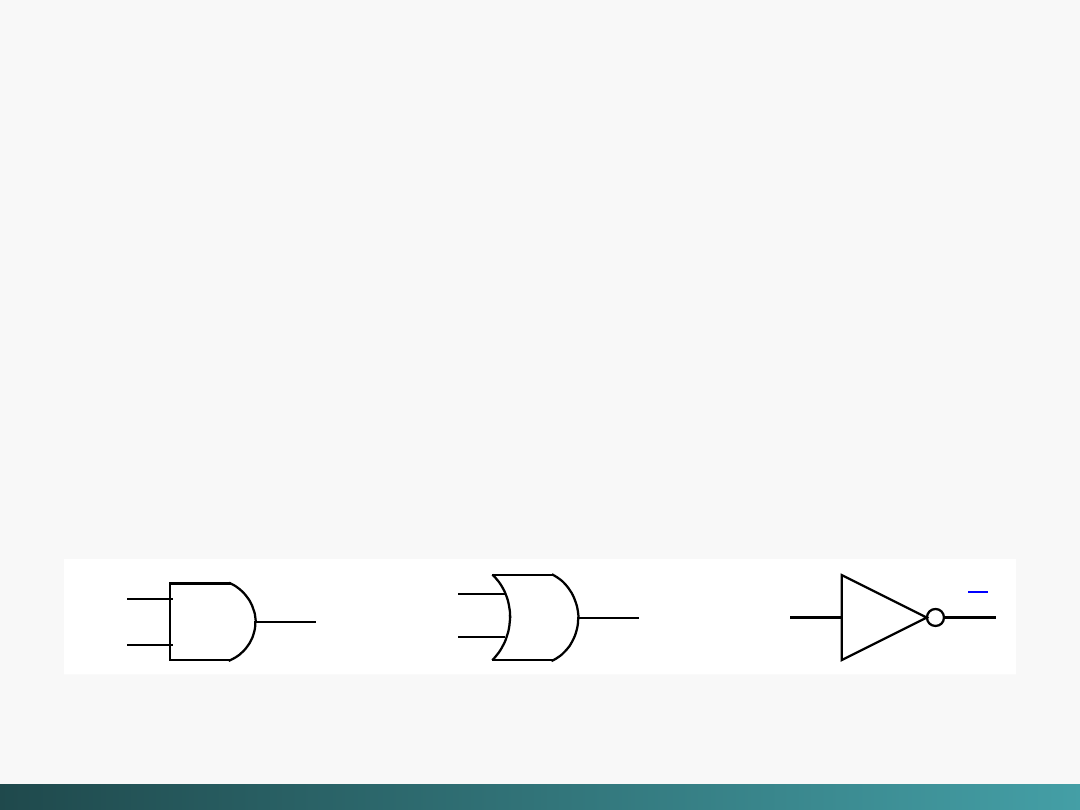
@Janusz Kosiński, 2005

bramka

NOT

x + y

bramka

AND

Algebra Boole’a i logika cyfrowa

Bramki logiczne

Operatory logiczne

AND

OR,

NOT

są reprezentowane w

sensie abstrakcyjnym przy pomocy

tablic prawdy.

Fizyczne

składniki (zwane obwodami scalonymi), pozwalające na
realizację zadań komputera są wykonane z wielkiej liczby
podstawowych elementów zwanych bramkami.

Bramki implementują podstawowe funkcje logiczne jakie realizuje
komputer – urządzenia realizujące dwuwartościowe funkcje (dzięki
dwuwartościowym sygnałom) – implementują podstawowe funkcje
Boolowskie.

Trzy podstawowe bramki

Bramki logiczne

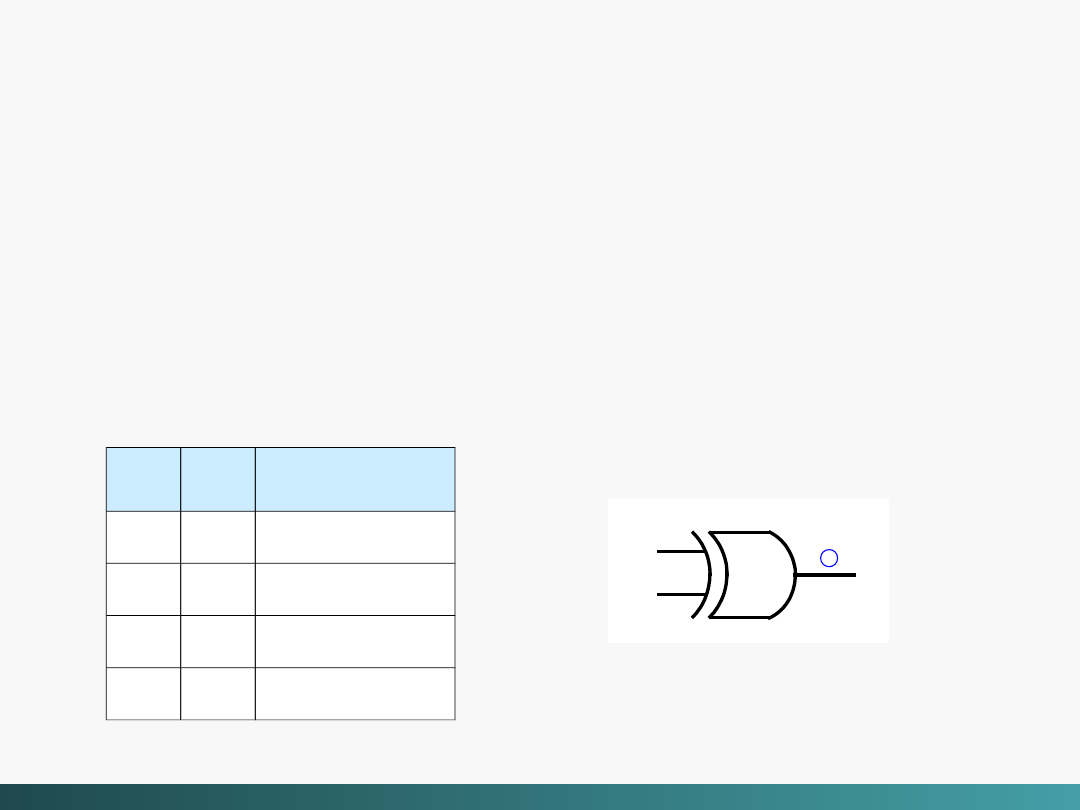
Innym typem wspólnej bramki jest

exclusive-OR

(XOR),

reprezentowana wyrażeniem Boolowskim: x

 y,

XOR

daje FAŁSZ jeżeli oba wejścia są równe i

PRAWDĘ w przeciwnym przypadku

@Janusz Kosiński, 2005

Tablica prawdy dla XOR,

oraz symbol logiczny

XOR

bramka XOR

x XOR y

Algebra Boole’a i logika cyfrowa

@Janusz Kosiński, 2005

Algebra Boole’a i logika cyfrowa

x NAND y

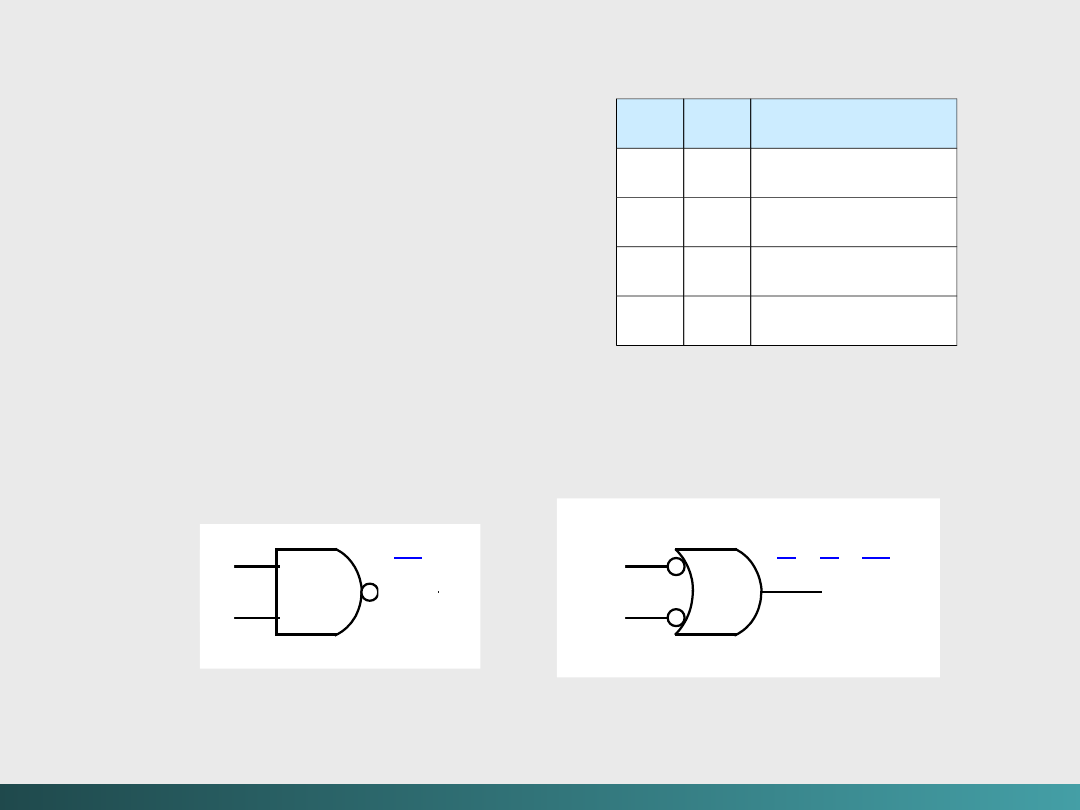
Bramki logiczne

Inną wspólną bramką jest

NAND,

dająca

komplementarne wyjście dla

AND

Bramka logiczna ma dwa
różne symbole,
reprezentujące jej działanie –
por. prawa DeMorgana.

Tablica prawdy dla

NAND,

oraz jej symbole

logiczne

(x + y = xy

)

(xy

)

@Janusz Kosiński, 2005

Algebra Boole’a i logika cyfrowa

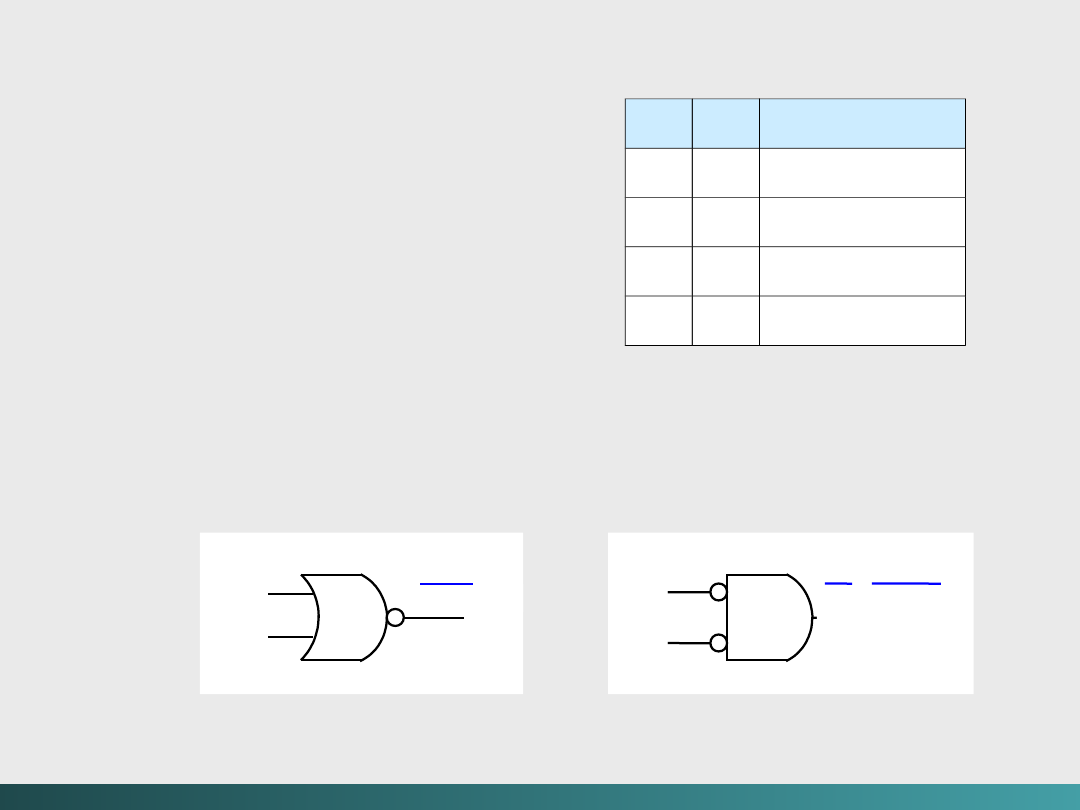
Bramki logiczne

Inną bramką jest bramka

NOR

, dająca

komplementarne wyjścia dla
OR.

Bramka logiczna ma dwa
różne symbole,
reprezentujące jej działanie –
por. prawa DeMorgana.

Tablica prawdy dla NOR,

oraz jej symbole

logiczne

x NOR y

(x + y)

xy =(x +

@Janusz Kosiński, 2005

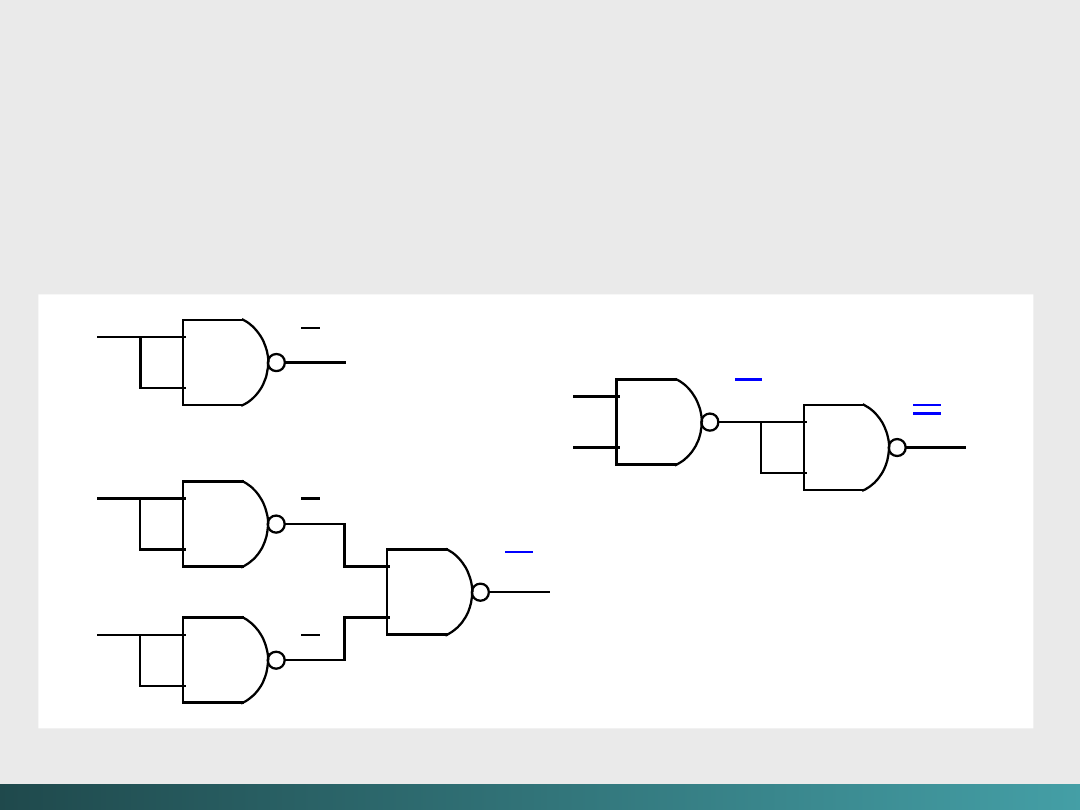
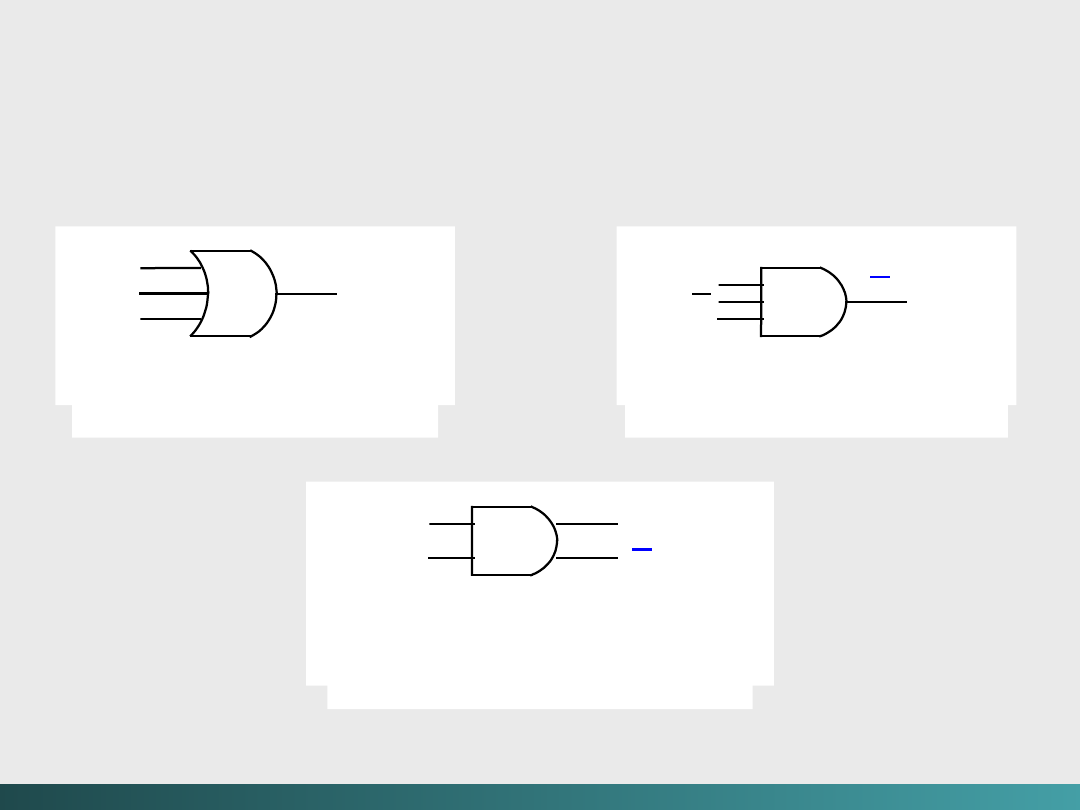
Dlaczego nie stosuje się bramek AND, OR i NOT oddzielnie? –
wytworzenie obwodów z bramkami

NAND

jest łatwiejsze i tańsze!

Konstrukcja trzech
obwodów używających tylko
bramki NAND

Algebra Boole’a i logika cyfrowa

(xy

)

(xy ) =
xy

(xy ) = x +
y

@Janusz Kosiński, 2005

Bramki wielowejściowe

Bramki nie są ograniczone do dwuwejściowych. Istnieją różne warianty
co do liczby i typów wejść oraz wyjść.

Algebra Boole’a i logika cyfrowa

Trzywejściowa

bramka

(x + y + z )

Trzywejściowa

bramka

AND

xyz

Q
Q

x
y

Bramka

AND

z dwoma

wejściami i dwoma
wyjściami

Prosta Boolowska operacja może być reprezentowana przez
prostą bramkę logiczną.

Bardziej złożone wyrażenia Boolowskie są reprezentowane przez

kombinacje bramek AND, OR, i NOT

, wynikające z logicznych

diagramów opisujących wyrażenie wejściowe. Taki logiczny diagram
reprezentuje fizyczną implementację wyrażenia w danym obwodzie
logicznym.

@Janusz Kosiński, 2005

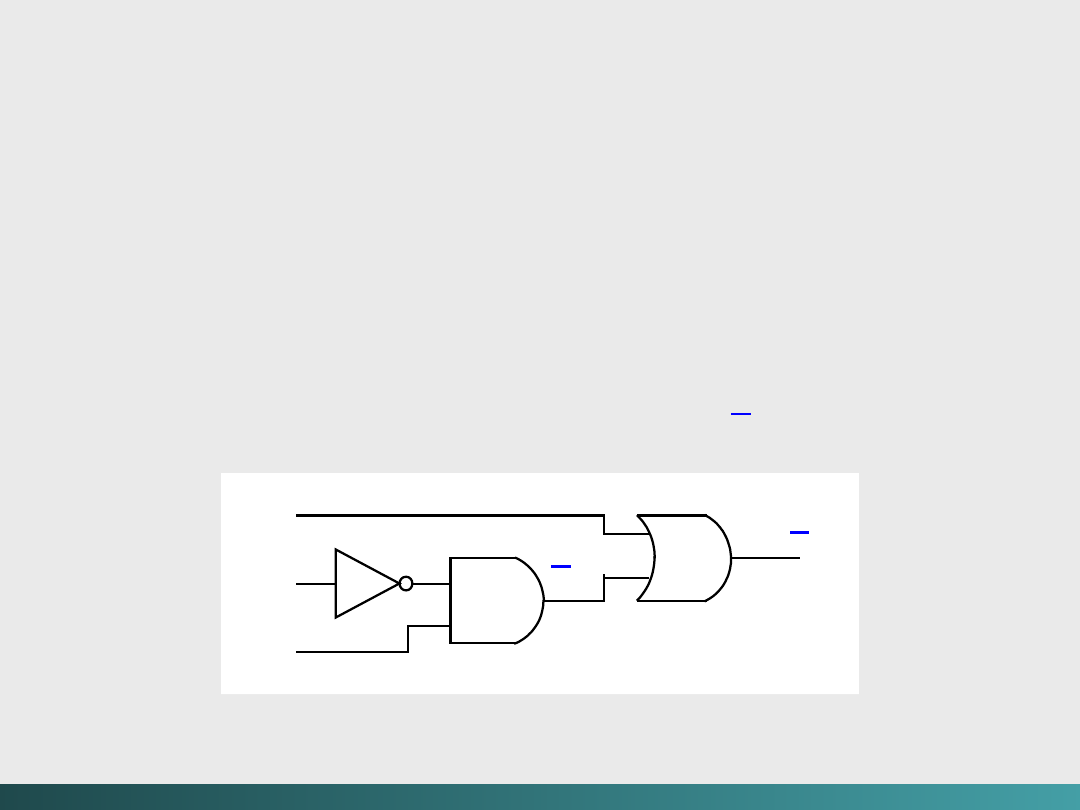
Algebra Boole’a i logika cyfrowa

Diagram logiczny dla F (x, y, z) = x +
yz

x +
yz

@Janusz Kosiński, 2005

Algebra Boole’a i logika cyfrowa

Ziemia

+5 V
DC

Chip (mały kryształ
półprzewodnikowy
z krzemu) jest urządzeniem
zawierającym niezbędne
składniki
elektroniczne (tranzystory,
rezystory
i kondensatory) do
zastosowania w
różnych bramkach – składniki
są
bezpośrednio wykonywane w
chipie, ze względu na
oszczędność
miejsca i bezpośredniość
połączeń.

Chip jest montowany w

plastykowym
lub ceramicznym pojemniku
posiadającym zewnętrzne styki.

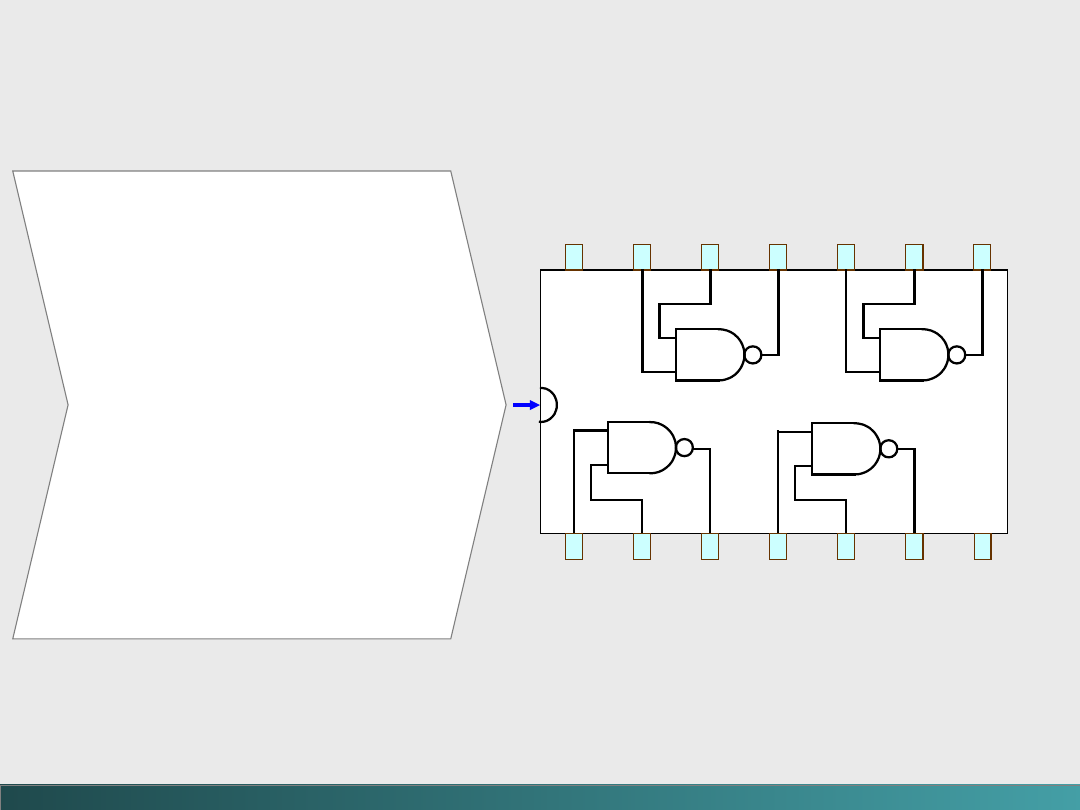
Bramki nie są sprzedawane indywidualnie – są
sprzedawane w jednostkach nazywanych obwodami
scalonymi (integrated circuits - IC).

Rysunek przedstawia budowę
prostego chipu SSI

@Janusz Kosiński, 2005

Do budowy układów scalonych, zawierających podstawowe
operatory Boolowskie wejścia i wyjścia jest stosowana logika
kombinacyjna.

Kluczowym zagadnieniem tej logiki jest założenie, że każde wyjście
zawsze bazuje na sygnałach wejść (jest funkcją wyjść) i w każdej
chwili odpowiada wartościom sygnałów na wejściach.

Dany obwód kombinacyjny może zawierać kilka wyjść, z których
każde może reprezentować odmienną funkcję Boolowską.

Algebra Boole’a i logika cyfrowa

@Janusz Kosiński, 2005

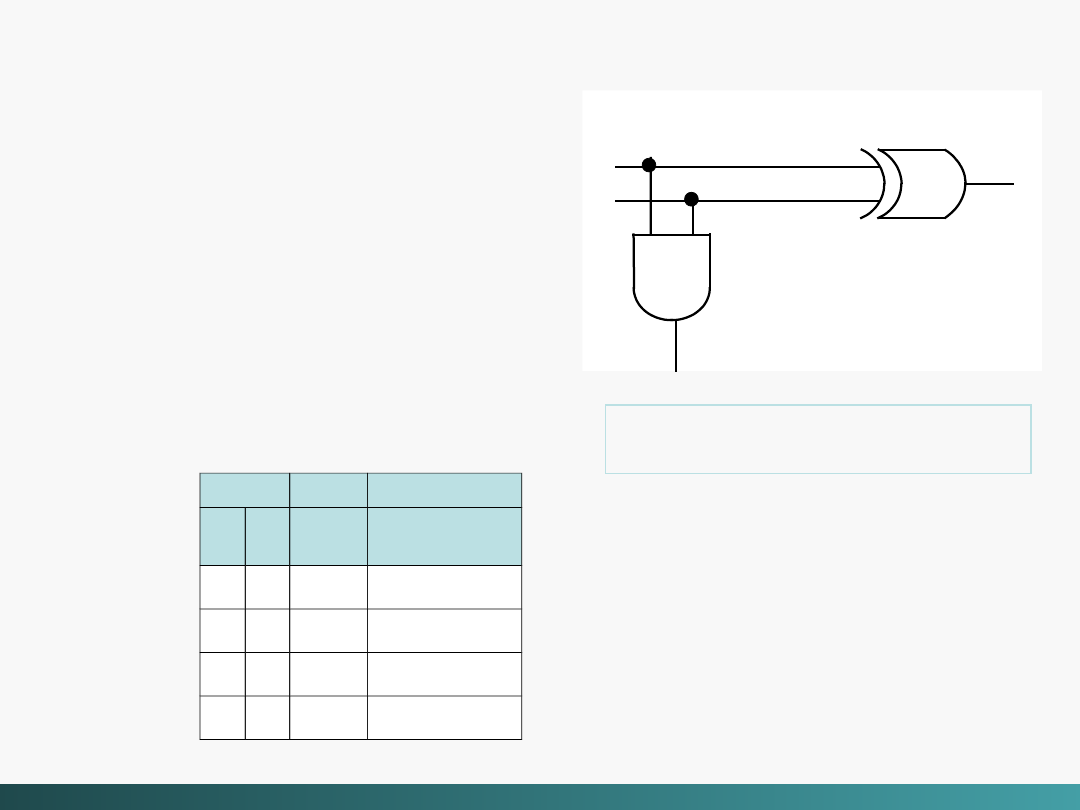
Półsumator

jest bardzo

prostym obwodem, w
rzeczywistości mało
użytecznym ponieważ może
dodać tylko dwa bity.

Można rozszerzyć ten obwód
do postaci umożliwiającej
dodawanie większych liczb
binarnych.

Sum

Przeniesien

0 0

0 1

1 0

1 1

Tablica prawdy

półsumatora

Algebra Boole’a i logika cyfrowa

Diagram logiczny

półsumatora

suma

przeniesienie

0 + 0 = 0, 0 + 1 = 1 + 0 = 1, oraz 1 + 1 =

@Janusz Kosiński, 2005

Algebra Boole’a i logika cyfrowa

Przeniesieni

e WY

suma

Przeniesieni

e WE

Przeniesieni

Suma

Przeniesieni

0 0

0 1

1 0

1 1

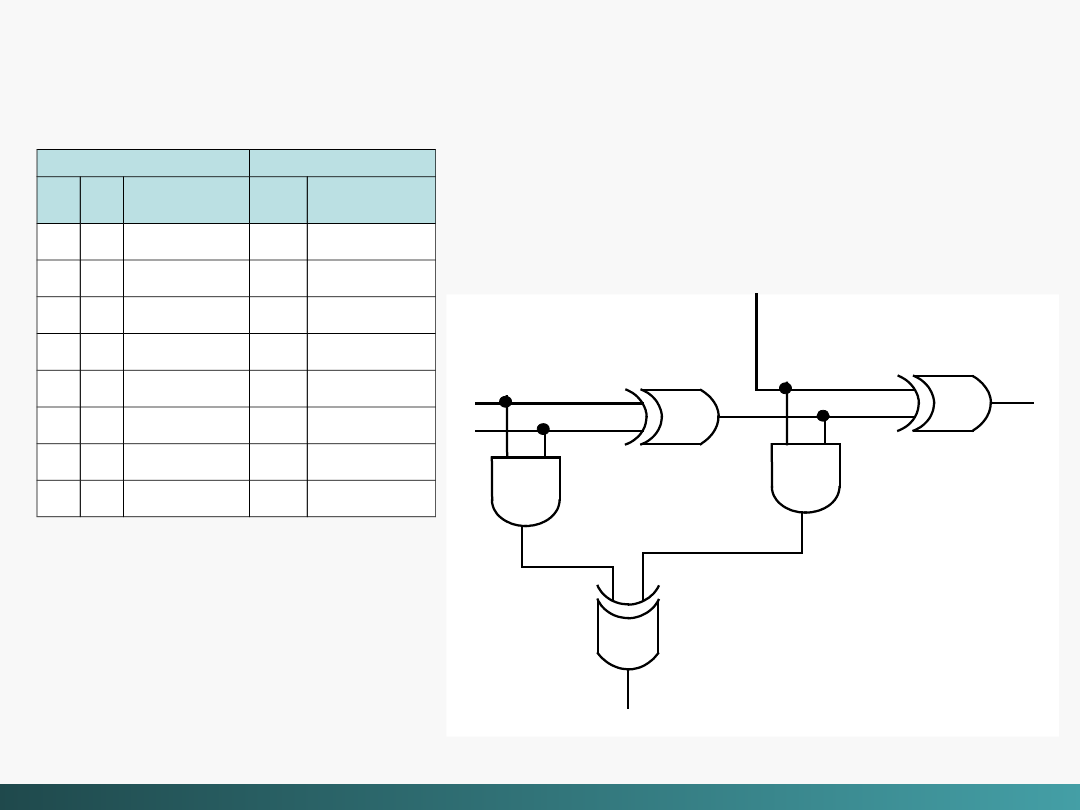
Sumator pełny

składa się z dwóch półsumatorów i jednej bramki

@Janusz Kosiński, 2005

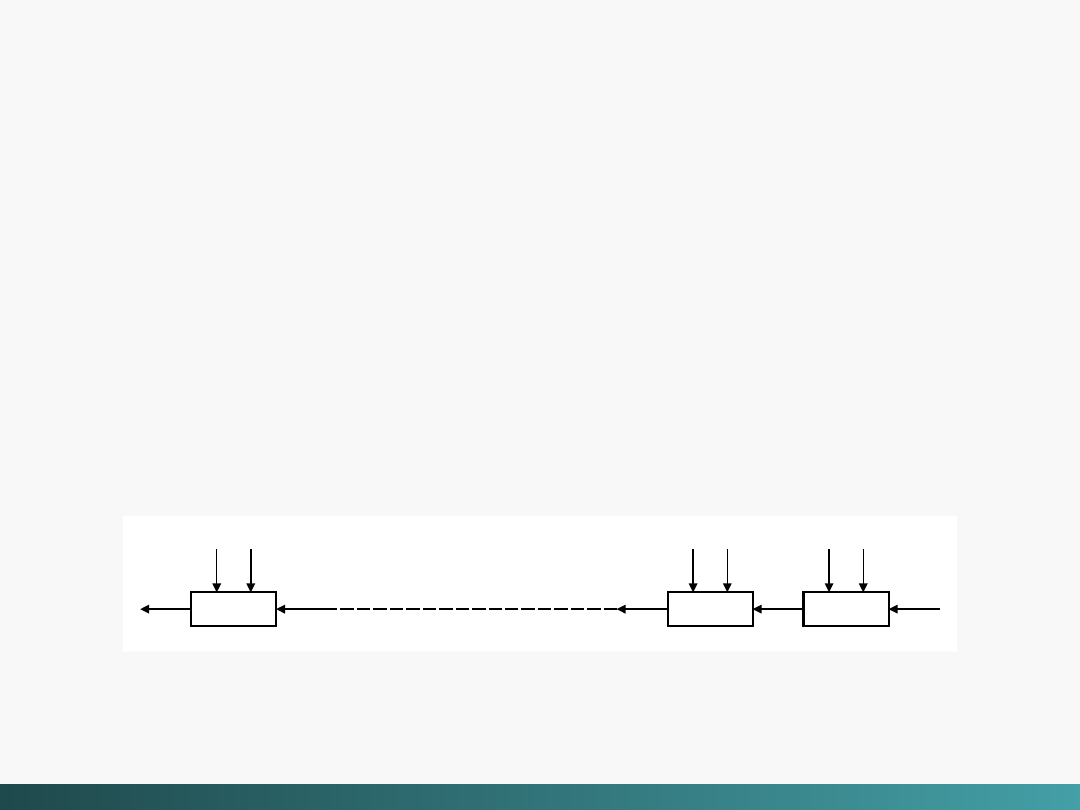
Sumator pełny nie może dodać trzech bitów

. Można

zbudować sumator dodający dwa 16 bitowe słowa poprzez
zastosowanie 16 replikacji pojedynczego sumatora. Z
wyjścia sumatora wprowadzane są dane do następnego
sumatora.

Taki sumator jest bardzo wolny i nie ma praktycznego
zastosowania – pokazany jest celem ilustracji zasady
dodawania. Współczesne sumatory opierają się na modyfikacjach
funkcji przenoszenia – chodzi o skrócenie ścieżki przeniesienia.

Algebra Boole’a i logika cyfrowa

sumator

@Janusz Kosiński, 2005

Sumatory są bardzo ważnymi obwodami –

komputer nie może

istnieć bez możliwości dodawania.

Równie ważną operacją wykonywaną przez komputery jest

dekodowanie binarnych operacji ze zbioru n wejść do 2

wyjść.

Dekoder wykorzystuje wejścia oraz ich wartości do

wyspecyfikowania jednej linii wyjściowej.

To oznacza że tylko jedno wyjście jest ustawiane na „1” przy

pozostałych ustawianych na „0”.

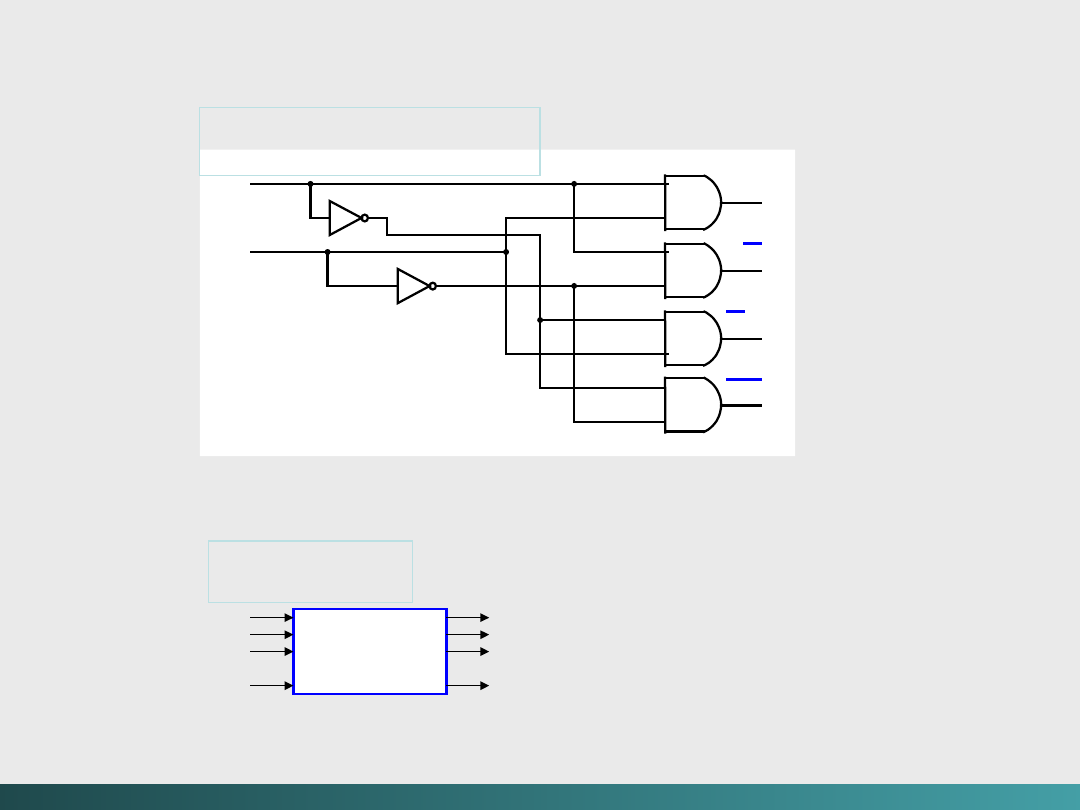
Dekodery są normalnie definiowane poprzez liczbę wejść i
wyjść – np. dekoder o 3 wejściach i 8 wyjściach jest nazywany
dekoderem 3 na 8.

Każdy adres w pamięci komputera jest przedstawiany w postaci
liczby binarnej. Kiedy w operacjach komputerowych występuje
odwołanie do adresu pamięci to wymagane jest zastosowanie
dekodera.

Algebra Boole’a i logika cyfrowa

@Janusz Kosiński, 2005

Algebra Boole’a i logika cyfrowa

Dekoder

n Wejść

Wyjść

x
y

Schemat logiczny

dekodera

Symbol

dekodera

@Janusz Kosiński, 2005

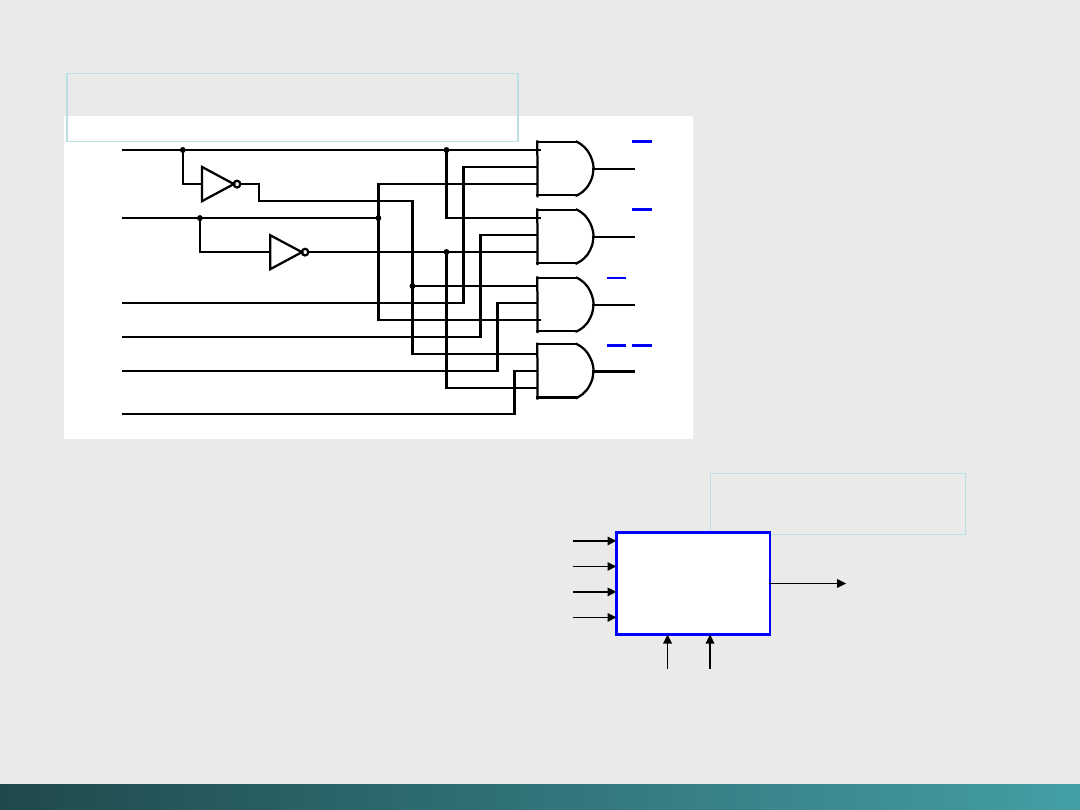
Innym obwodem z obszaru logiki kombinacyjnej jest

multiplekser

. Obwód wybiera informację z jednego wejścia i

przekazuje ją na wyjście. Wybór poszczególnych linii wejściowych
jest dokonywany przy pomocy linii sterujących (zbiór zmiennych
wyboru informacji).

Sytuacje wymagające multiplekserów?

- multipleksowania wejść z terminali użytkowników przez
komputery centralne

- korzystanie ze wspólnych modemów dla wielu
komputerów

- wykorzystanie multipleksowania w generatorach
parzystości i

kontrolerach parzystości

(typowe

generatory i kontrolery

parzystości wykorzystują funkcje

XOR)

Algebra Boole’a i logika cyfrowa

@Janusz Kosiński, 2005

Algebra Boole’a i logika cyfrowa

Schemat logiczny

multipleksera

Symbol

multipleksera

Multiplekser

Jedno WE jest
przekazywane na
WY

Linie

sterujące

@Janusz Kosiński, 2005

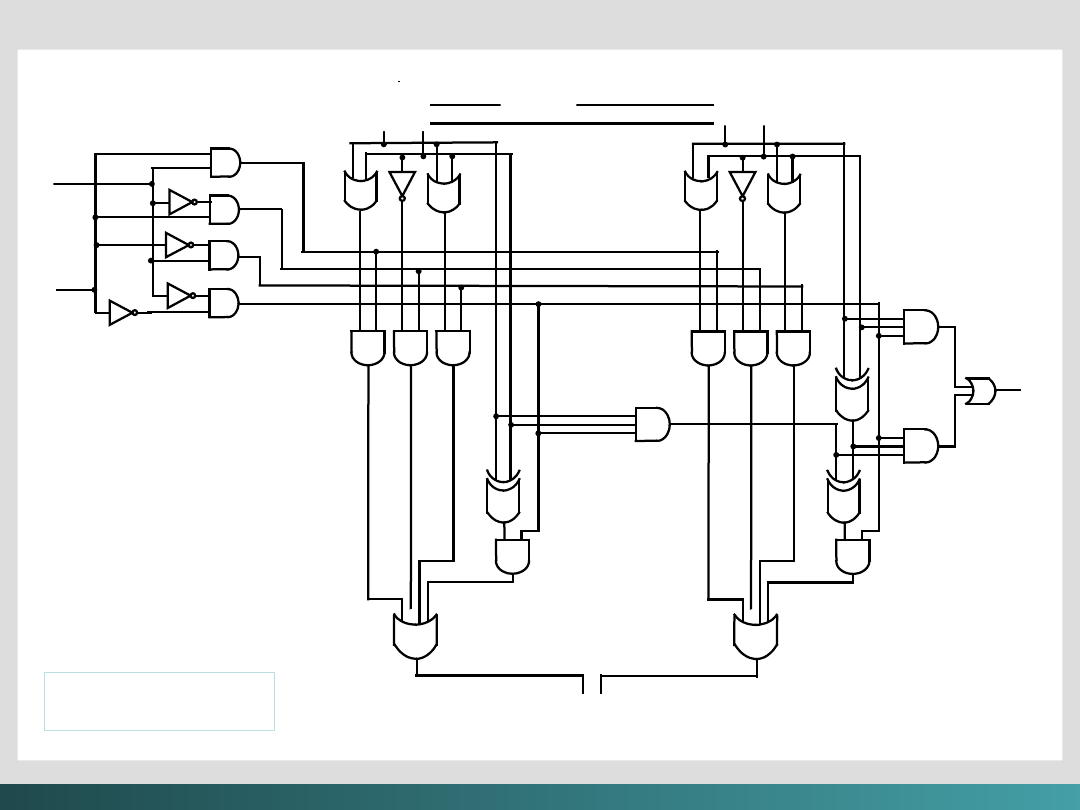
Rysunek na następnym slajdzie ilustruje bardzo prostą ALU z czterema
podstawowymi operacjami –

AND, OR, NOT

oraz

PRZESUNIĘCIE

na dwa słowa

maszynowe, każde po 2 bity.

Linie sterujące f

i f

determinują, która operacja będzie

wykonywana przez CPU.

Sygnał 00

jest używany dla dodawania (A

Sygnał 01

jest używany dla

NOT

Sygnał 10

jest używany dla A

Sygnał 11

jest używany dla A

AND

Linie wejściowe A

i A

wskazują na 2 bity w jednym słowie,

podczas gdy B

and B

wskazują na drugie słowo. C

i C

reprezentują linie wyjściowe.

Algebra Boole’a i logika cyfrowa

@Janusz Kosiński, 2005

Algebra Boole’a i logika cyfrowa

Przep

ełnien

Prosta 2 bitowa

ALU

Wyjście

Dekoder

Wejści

Półsumato

Sumator

Przesunięcie

@Janusz Kosiński, 2005

Główną słabością kombinacyjnych obwodów scalonych
jest

brak pamięci.

Do tego celu stosowane są obwody sekwencyjne.

Do zapamiętywania stanu poprzednich wejść obwód
sekwencyjny musi posiadać pewien rodzaj elementów
magazynujących, w których

Wyjście

jest zależne od stanu

Wejścia.

Powszechnie stosowane jest nazywanie takiego sposobu
przechowywania

przerzutnikiem.

Stan takiego

przerzutnika jest funkcją poprzedniego wejścia do
obwodu. Czyli zmienne wyjście zależy od bieżącego stanu
obwodu i od poprzedniego stanu wejścia.

Algebra Boole’a i logika cyfrowa

@Janusz Kosiński, 2005

Należy więc wprowadzić sposób porządkowania zdarzeń.
Fakt, że obwód sekwencyjny używa wiedzy o poprzednim
wejściu do zdeterminowania wyjścia wymaga ustalania
porządku zdarzeń.

Niektóre obwody sekwencyjne są

asynchroniczne

, co

oznacza że stają się one aktywne w chwili zmiany dowolnej
wartości wejściowej.

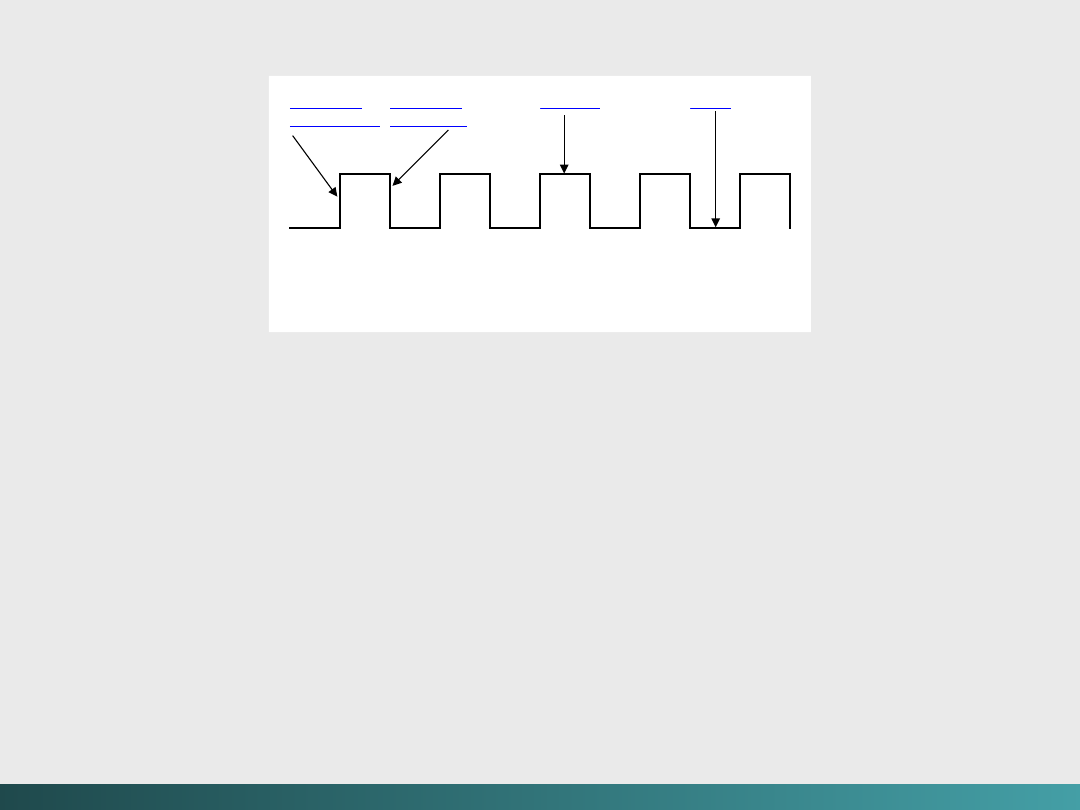
Synchroniczne

obwody sekwencyjne

używają

zegara

do porządkowania zdarzeń.

Zegar jest obwodem, który emituje serie impulsów o dużej
dokładności w zakresie trwania impulsu

(szerokości impulsu)

oraz przerwy miedzy impulsami

(interwałów).

Tak interwał

jest nazywany okresem zegara. Prędkość zegara jest
ogólnie rzecz ujmując mierzona w megahertzach

(MHz)

lub

milionach impulsów na sekundę.

Algebra Boole’a i logika cyfrowa

@Janusz Kosiński, 2005

Zegar jest stosowany przez obwód sekwencyjny do
podejmowania decyzji, kiedy należy uaktualnić stan obwodu
(kiedy

„bieżące”

wartości wejść stają się

„minionymi”

wartościami wejść?). Czyli wejście obwodu może przyjąć

„na

przechowanie”

tylko w określonych chwilach czasu.

Większość obwodów sekwencyjnych jest typu „wyzwalanie
krawędziowe”, to oznacza, że dopuszczają zmianę stanu tylko w
czasie narastania lub opadania impulsu sygnału zegara.

Algebra Boole’a i logika cyfrowa

Sygnał zegara wskazujący

dyskretny upływ czasu

Krawędź
opadania

Wysoki

Niski

Krawędź
narastania

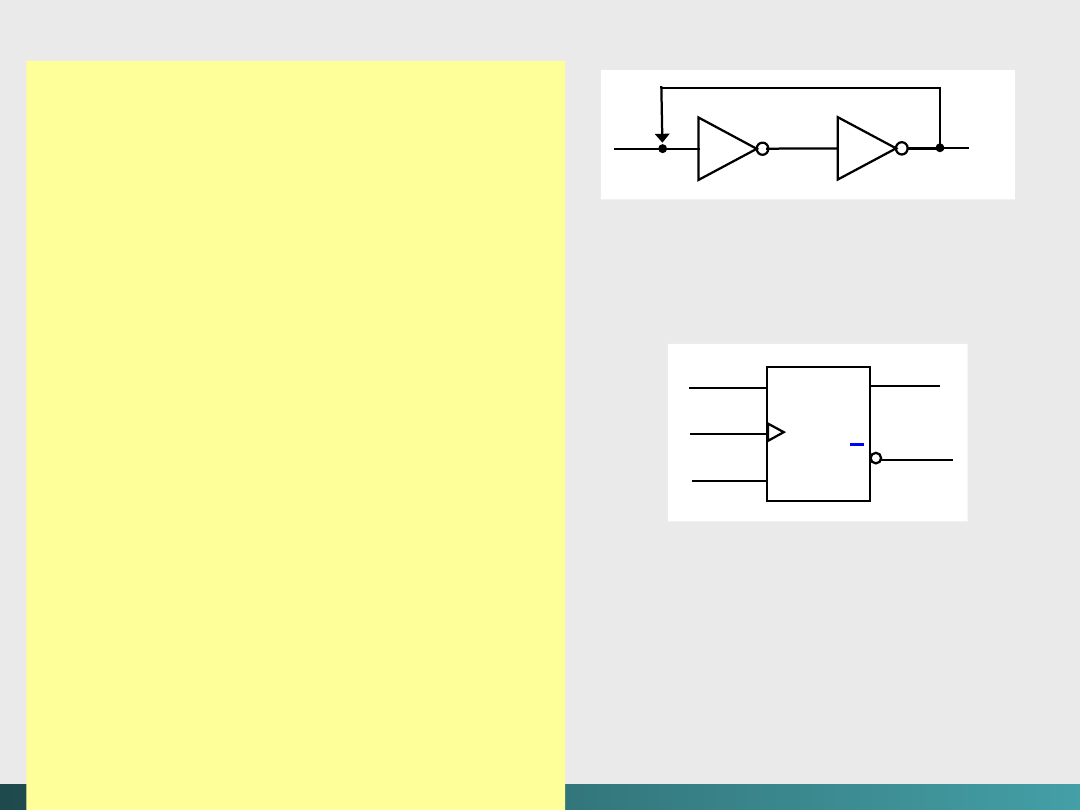
@Janusz Kosiński, 2005

Obwód stosujący wyzwalanie
poziomów pozwala na zmianę
stanu w czasie gdy sygnał zegara
jest wysoki lub niski.

Wielu autorów używa terminu

przerzutnik

lub

flip-flop

wymiennie.

Od strony technicznej przerzutnik
jest wyzwalany poziomem zaś flip-
flop krawędzią (narastaniem lub
opadaniem)

Zapamiętywanie stanu
poprzedniego w obwodach
sekwencyjnych polega na
zastosowaniu sprzężenia
zwrotnego.

Bardzo proste sprzężenie zwrotne
używa dwóch bramek NOT.

Bardziej użyteczny obwód sprzężenia
zwrotnego jest wykonany z dwóch
bramek NOR.

Jest to jedna z podstawowych jednostek
pamięci nazywanych SR Flip-Flop
(przerzutnik)

SR oznacza – SET / RESET

Algebra Boole’a i logika cyfrowa

Przykład prostego sprzężenia
zwrotnego:
Jeżeli Q = 0 to zawsze będzie 0,
Jeżeli Q = 1 to zawsze będzie 1.

@Janusz Kosiński, 2005

Możemy opisać dowolny przerzutnik używając tablicy prawdy -
wskazującej jaki będzie stan następny, bazujący na stanie
aktualnym i stanach poprzednich.

Notacja Q(t) reprezentuje stan bieżący zaś Q(t+1) wskazuje stan
następny (który przerzutnik powinien przyjąć przy następnym
impulsie zegara).

Algebra Boole’a i logika cyfrowa

Q(t+1)

0 Q(t)

– bez zmian

1 0

– resetowanie do 0

0 1

– ustawianie na 1

niezdefiniowane

@Janusz Kosiński, 2005

Q(t)

Q(t+1)

Nie

zdefiniowane

Nie

zdefiniowane

Flip-Flop

wykazuje interesujące zachowania. Posiada on trzy

wejścia: S, R, oraz bieżące wyjście Q(t). Tablica prawdy ilustruje
pracę obwodu.

Jeżeli S = 0 i R= 0, i bieżący stan
Q(t) = 0, to stan następny Q(t+1) =
0.

Jeżeli S = 0 i R = 0, i Q(t) = 1, to
Q(t+1) = 1.

Aktualne wejścia o wartościach
(0,0) dla (S,R) nie powodują zmian
wyjść w czasie zmiany wartości
sygnałów zegara.

Podobnie wejścia (S,R) = (0,1)
wymuszają stan następny Q(t + 1)
= 0 niezależnie od stanu
poprzedniego (wymuszają ponowne
uruchomienie – resetowanie).

Kiedy (S,R) = (1,0), wtedy wyjście
obwodu jest ustawiane na 1.

Algebra Boole’a i logika cyfrowa

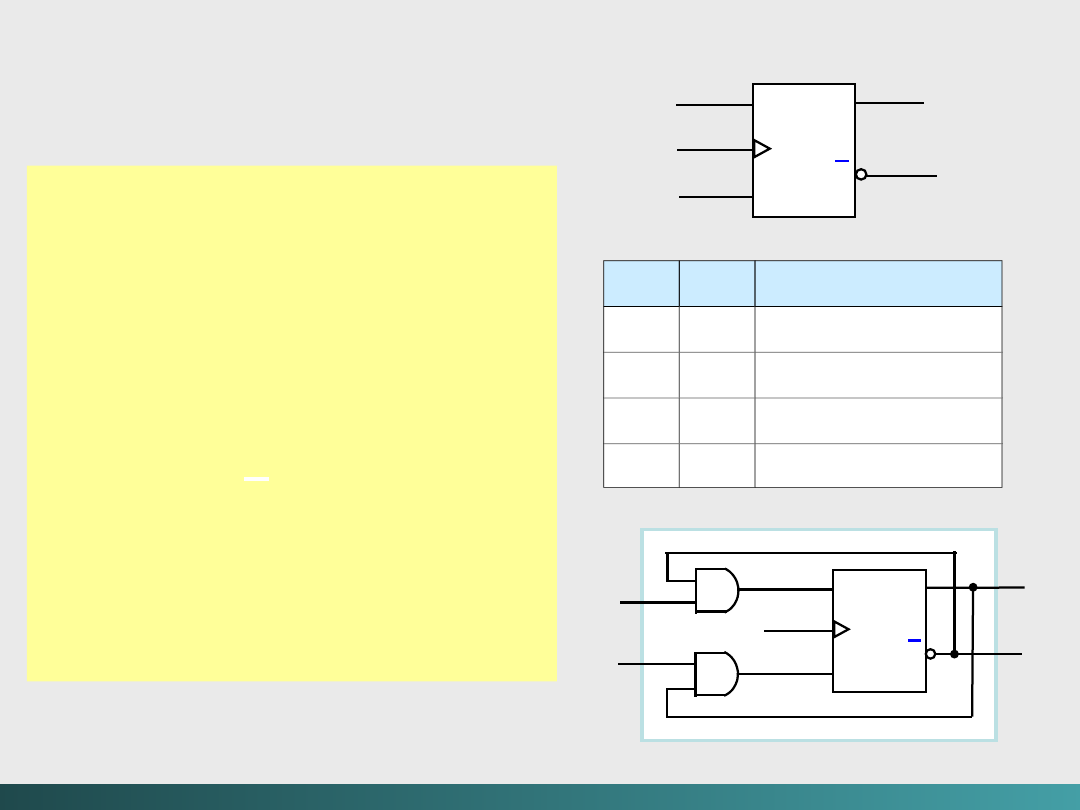
@Janusz Kosiński, 2005

Dodając kilka warunków do
przerzutnika SR, tak że stany
nieustalone się nie pojawią,
uzyskamy

zmodyfikowany SR

Flip-Flop.

Nosi on nazwę

JK Flip-Flop

Nazwa pochodzi od nazwiska
inżyniera z Texas
Instruments,

Jacka Kilby’ego

wynalazcy obwodu scalonego
(1958).

Algebra Boole’a i logika cyfrowa

Q(t+1)

Q(t)

0 -

(resetowanie do 0)

0 –

ustawianie na 1

Q(t)

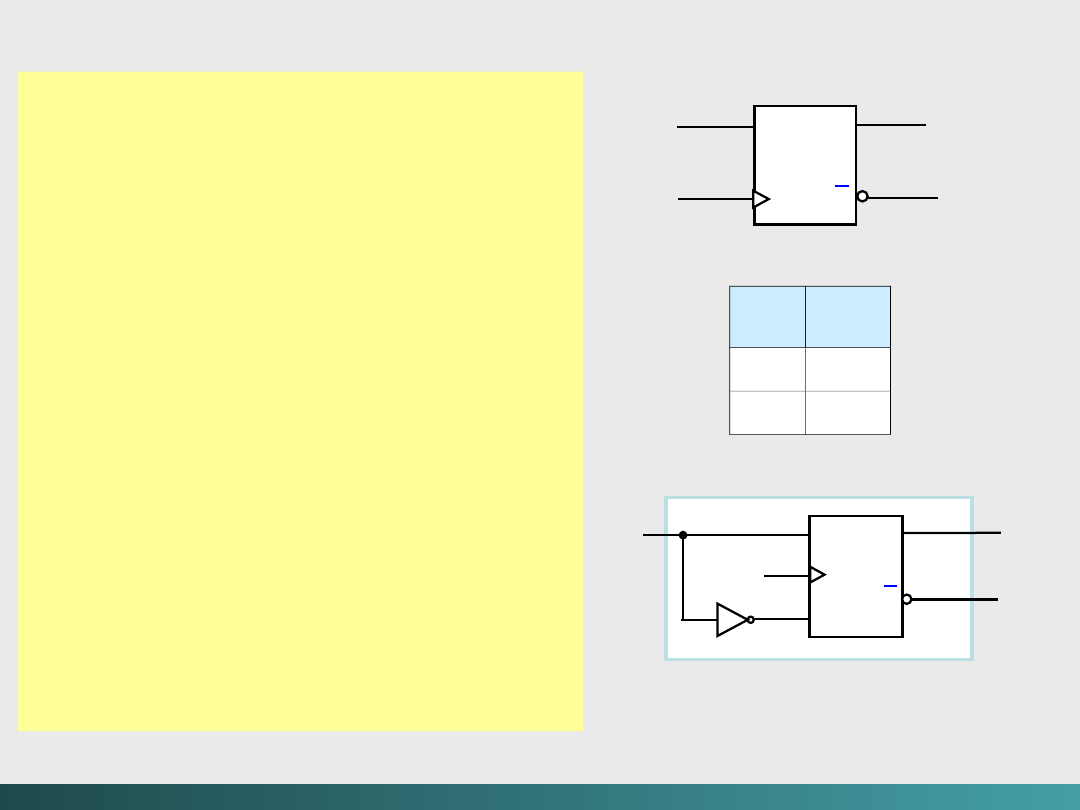
@Janusz Kosiński, 2005

Innym wariantem

SR Flip-Flop

jest

(data)

Flip-Flop.

D Flip-Flop

jest prawdziwą

reprezentacją fizycznej pamięci
komputera.

Ten obwód sekwencyjny przechowuje
jeden bit informacji. Jeżeli na wejściu linii
D jest 1, to na wyjściu Q, w czasie
impulsu zegara pojawi się 1. jeżeli
będzie 0, to przy impulsie zegar na
wyjściu pojawi się 0

(pamiętamy, że Q

reprezentuje bieżący stan obwodu).

Z tego

wynika, że wyjściowa wartość 1 oznacza
bieżące przechowywanie

(magazynowanie)

przez obwód wartości 1.

Algebra Boole’a i logika cyfrowa

Q(t+

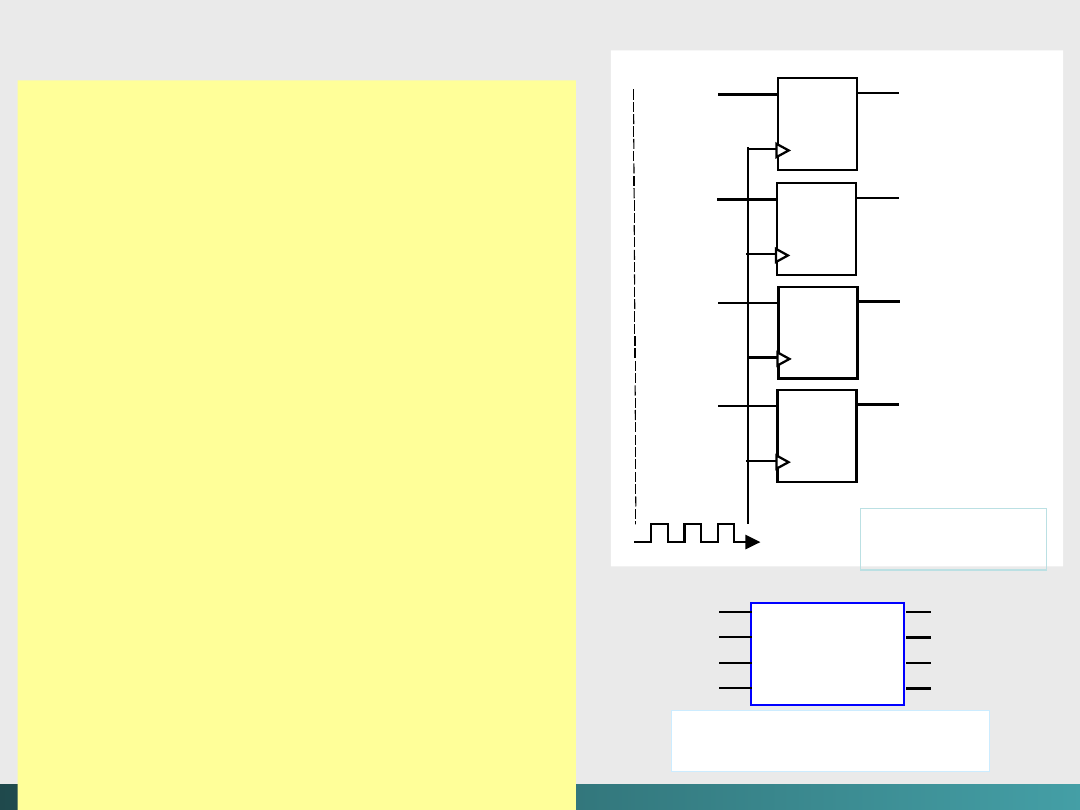
@Janusz Kosiński, 2005

Diagram blokowy dla

rejestru 4 bitowego

Przerzutniki i flip-flopy są stosowane
do budowy bardziej złożonych
obwodów sekwencyjnych. Rejestry,
liczniki, pamięci i przesuwniki
rejestrów - wymagają
przechowywania danych.

Prosty

4 bitowy rejestr

wykorzystuje

cztery

D flip-flopy

. (dla większych słów

należy zastosować większą liczbę
przerzutników).

Należy pamiętać, że

synchroniczny

obwód sekwencyjny nie może zmienić
sam stanu bez wyzwalających impulsów
zegara

Rzeczywiste obwody posiadają jeszcze
linie dla zasilania i uziemienia (dającą
zdolność „zerowania” wszystkich
rejestrów).

Algebra Boole’a i logika cyfrowa

We 0 D Q
Wy 0

We 1 D Q
Wy 1

We 2 D Q
Wy 2

We 3 D Q
Wy 3

Zeg
ar

Rejestr 4

bitowy

Rejestr

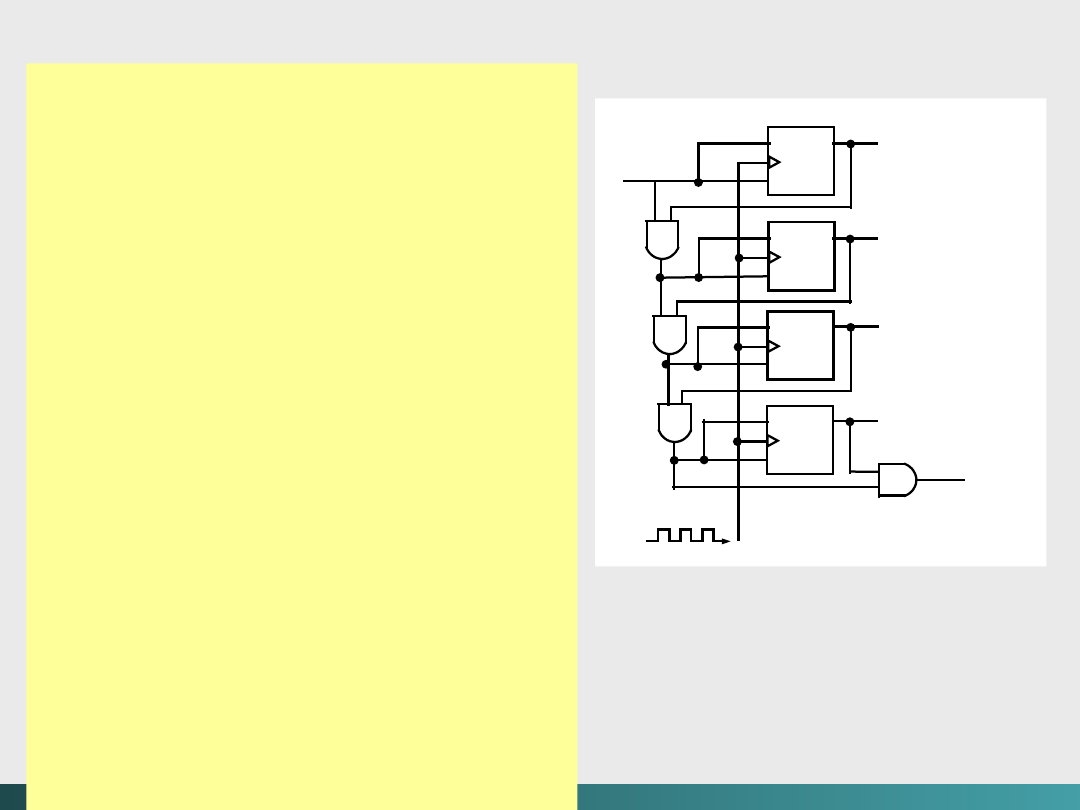
@Janusz Kosiński, 2005

Innym obwodem sekwencyjnym jest

licznik binarny

, (stany

predeterminowane). Jeżeli zaczniemy
odliczanie: 0000, 0001, 0010, 0011, .
. . , to możemy zobaczyć, że bit
najniższy (porządek zapisywania) jest
każdorazowo automatycznie
uzupełniany.

Kiedy nastąpi zmiana stanu z 1 na 0,
to następuje uzupełnienie bitu po lewej
stronie. Każdy następujący bit zmienia
stan z 0 na 1, w chwili gdy wszystkie
bity po prawej stronie są równe 1.

Do tego typu liczników są stosowane

flip-flopy

. Obwód liczy tylko wtedy,

gdy zegar wysyła impulsy i wejście jest
równe 1. Jeżeli wejście jest równe 0, to
obwód nie zmienia stanu.

Algebra Boole’a i logika cyfrowa

4 bitowy licznik synchroniczny

używający JK Flip-Flopów

C
K

B 0

B 1

B 2

B 3

Zeg
ar

Liczenie
dostępn
e

Wyjście
przesunięc
ia

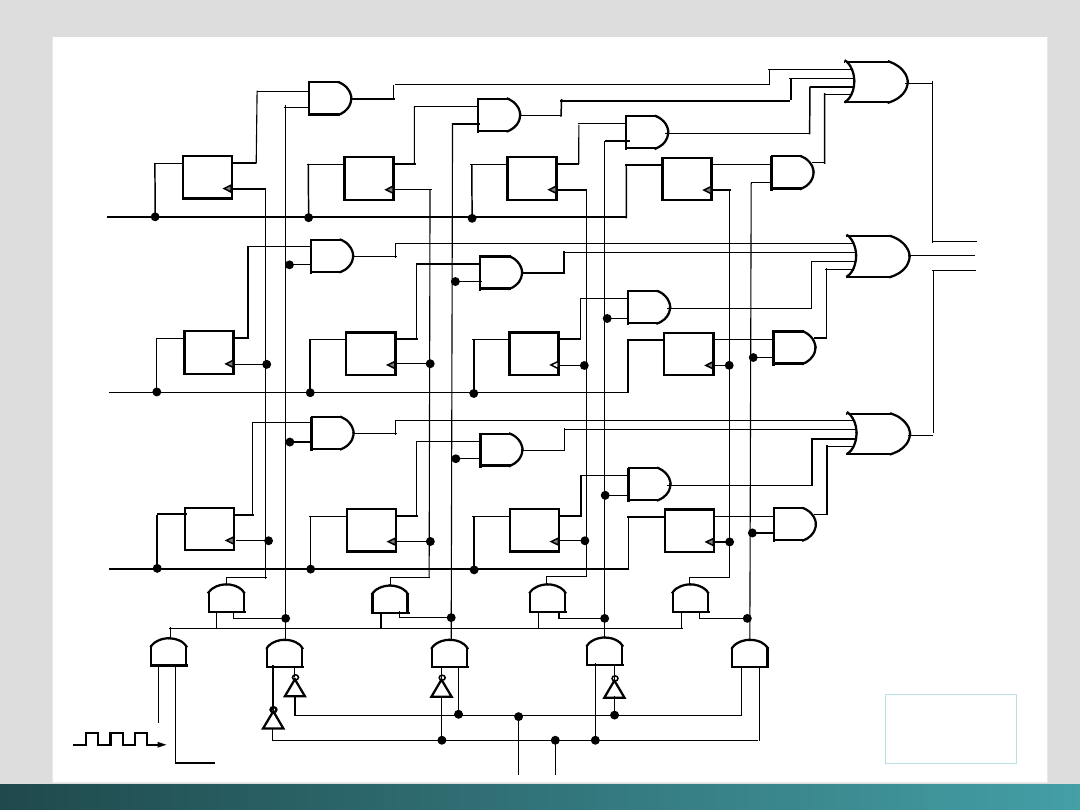
@Janusz Kosiński, 2005

Algebra Boole’a i logika cyfrowa

D Q

Słowo 1

Selekcja

Słowo 2

Selekcja

Słowo 3

Selekcja

Słowo 0

Selekcja

Słowo 1

Słowo 0

Słowo 2

Słowo 3

Zapis
dostępny

Zega
r

Pamięć

4 x 3

@Janusz Kosiński, 2005

Zapamiętywanie czterech 3 bitowych słów (

pamięć 4 x 3

Każda kolumna = jedno 3 bitowe słowo.

Flip-Flopy są synchronizowane zegarem - operacje
zapisywania czy odczytu zawsze dotyczą całego słowa.

Wejścia We

, We

, i We

są liniami używanymi do

przechowywania lub wczytania 3 bitowego słowa do
pamięci.

Linie S

i S

są liniami adresów, stosowanymi do identyfikacji

słowa w pamięci. (S

i S

są liniami wejściowymi dla dekodera

2 na 4, odpowiedzialnego za selekcję właściwego słowa w
pamięci).

Trzy linie wyjściowe (Wy

,Wy

, i Wy

) są używane przy

odczycie słów z pamięci.

Algebra Boole’a i logika cyfrowa

@Janusz Kosiński, 2005

Minimalizacja obwodów logicznych

redukuje liczbę

składników w fizycznej implementacji – mniejsza liczba

składników powoduje szybszą pracę obwodów.

Redukcja wyrażeń Boolowskich może być wykonywana przy
pomocy tzw.

map Karnaugh (siatek Karnaugh)

Mapy Karnaugh

lub K-mapy są graficzną metodą reprezentacji

funkcji Boole’a.

Mapa taka jest po prostu tablicą używaną do wyszczególniania
wartości danych wyrażeń Boolowskich, dla różnych wartości
wejściowych.

Wiersze i kolumny tych tabel odpowiadają możliwym wartościom

„wejść”

funkcji. Każda komórka reprezentuje

„wyjście”

funkcji dla tych

możliwych wejść.

Algebra Boole’a i logika cyfrowa

@Janusz Kosiński, 2005

Jeżeli produkt

term

zawiera wszystkie zmienne dokładnie tylko raz, dopełniające lub

nie, to taki produkt nazywamy

mintermem

. Np. jeżeli są dwie wartości wejściowe

, to mamy cztery mintermy: x y, x y, x y, i x y, reprezentujące wszystkie możliwe

kombinacje wejść dla tej funkcji. I podobnie dla trzech zmiennych: x, y i z, mamy: x y
z, x y z, x y z, x y z, x y z, x y z, x y z, i x y z.

Mintermy dla 2

zmiennych

Mintermy dla 3

zmiennych

Algebra Boole’a i logika cyfrowa

Minterm

XYZ

_ _ _ _

_ _ _ _ _ _ _ _ _ _ _
_

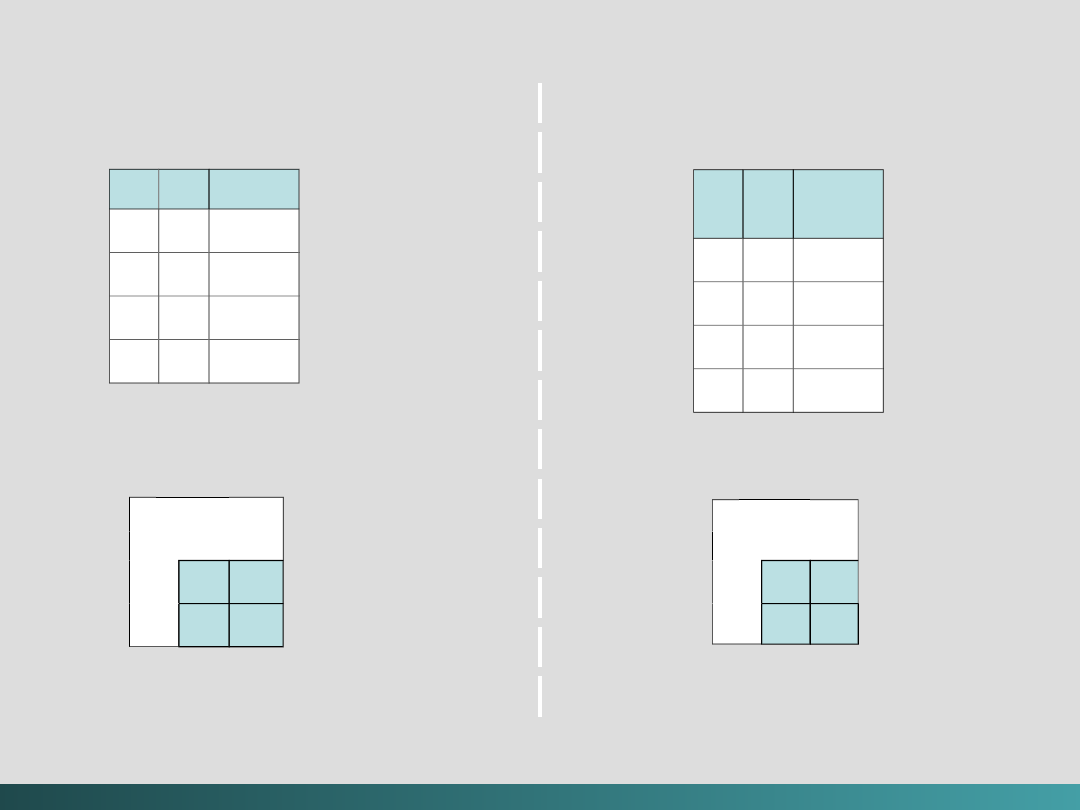
@Janusz Kosiński, 2005

Tablica prawdy dla
funkcji F (x,y) =
xy

Odpowiadająca K-
mapa

Algebra Boole’a i logika cyfrowa

x y

y 0 1

x +

Tablica prawdy dla
funkcji F (x,y) = x +
y

y 0 1

0 1

1 1

Odpowiadająca K-
mapa

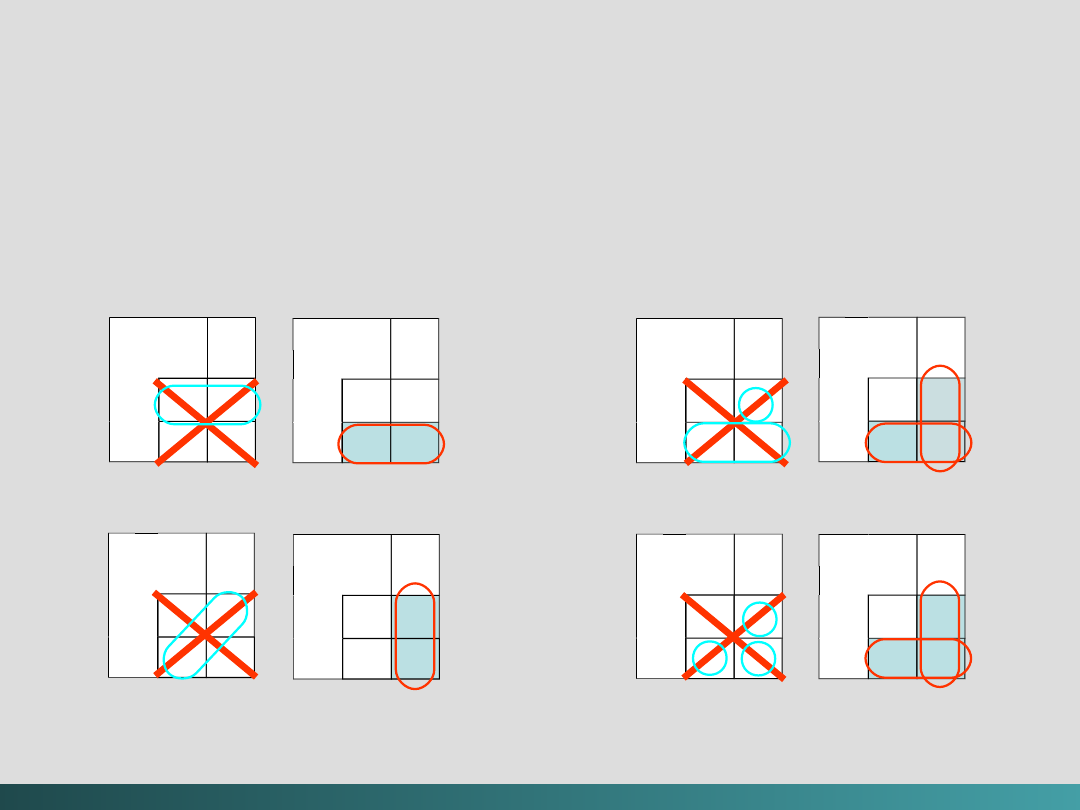
@Janusz Kosiński, 2005

W celu wykorzystania tych map potrzebujemy odpowiedniego pogrupowania komórek.
1. Grupujemy tylko 1.
2. Możemy grupować jedynki w K-mapie jeżeli znajdują się w tych samych wierszach

lub tych samych kolumnach – nie mogą stykać się na przekątnych.

3. Możemy dokonać grupowań jeżeli całkowita liczba wystąpień jedynek w grupie jest

potegą 2.

4. Musimy tworzyć tak duze grupy jak to jest tylko możliwe.

Grupa nie może być na
przekątnej

Groups Must Be as Large as Possible

Algebra Boole’a i logika cyfrowa

y 0 1

0 1

1 1

y 0 1

0 1

1 1

y 0 1

0 1

1 1

y 0 1

0 1

1 1

y 0 1

0 1

1 1

y 0 1

0 1

1 1

y 0 1

0 1

1 1

y 0 1

0 1

1 1

Grupa zawiera tylko 1

Grupa musi być potęgą 2

Grupa musi być tak duża jak to
możliwe

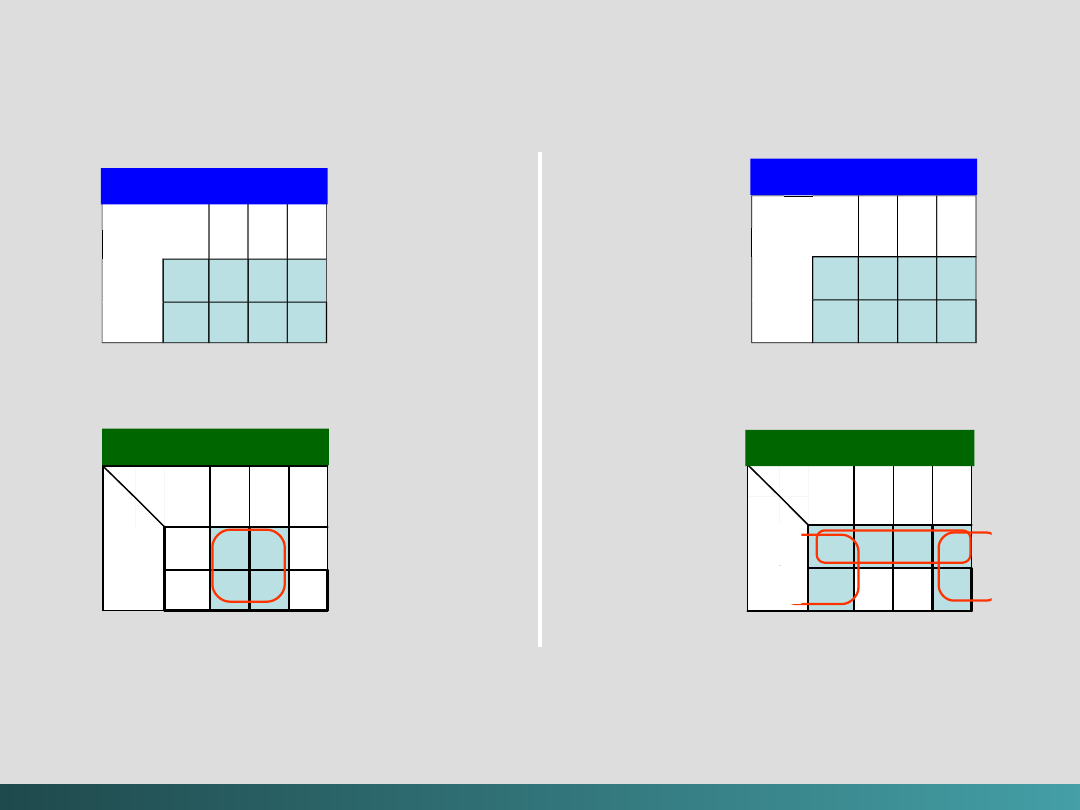
@Janusz Kosiński, 2005

Algebra Boole’a i logika cyfrowa

_ _ _ _

F(x, y, z) =

x y z + x y z + x y z +

x y z

yz 00 01 11 10

0 1 1 0

Tablica prawdy

Mapa Karnaugh

_ _ _ _ _ _ _ _ _ _
_

F(x, y, z) =

x y z + x y z + x y z + x y z

+ xyz + xyz

yz 00 01 11 10

1 1 1 1

1 0 0 1

Tablica prawdy

Mapa Karnaugh

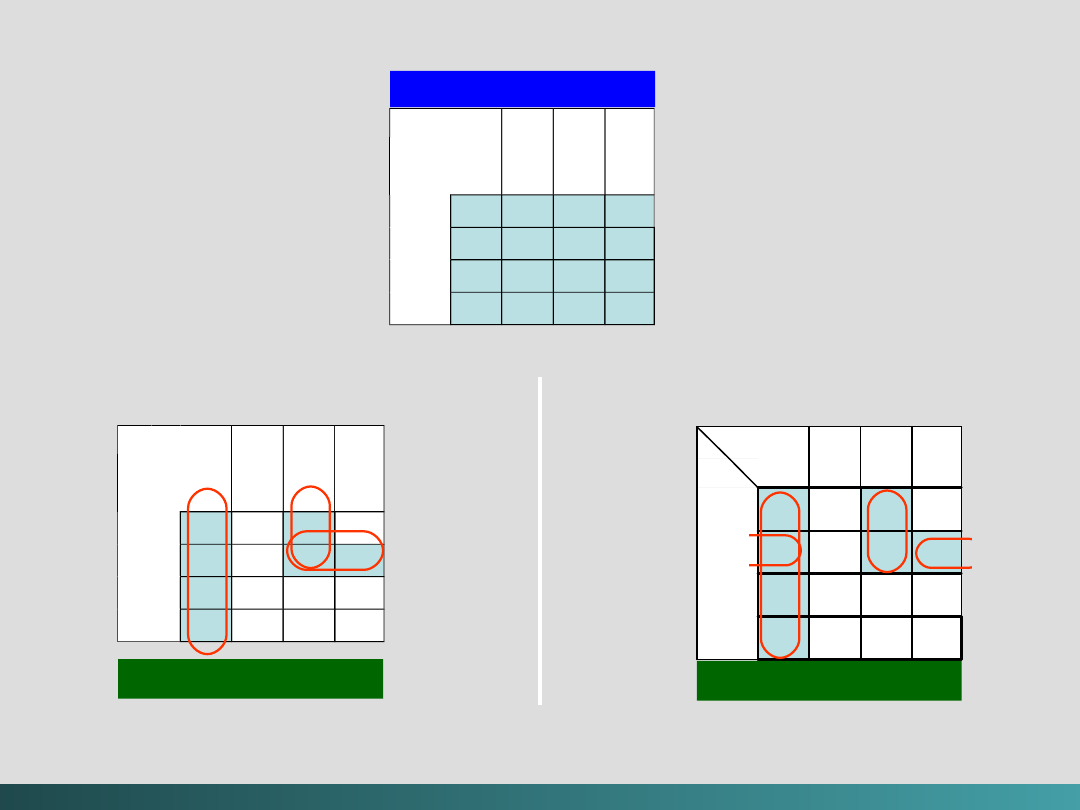
@Janusz Kosiński, 2005

Algebra Boole’a i logika cyfrowa

_ _ _ _

F(w, x, y, z) =

y z + w y z

+ w x y

_ _ _ _
_

F(w, x, y, z) =

y z + w y z

+ w x z

00 01 11 10

Tablica prawdy

00 01 11 10

Mapa Karnaugh (F

)

Mapa Karnaugh (F

)

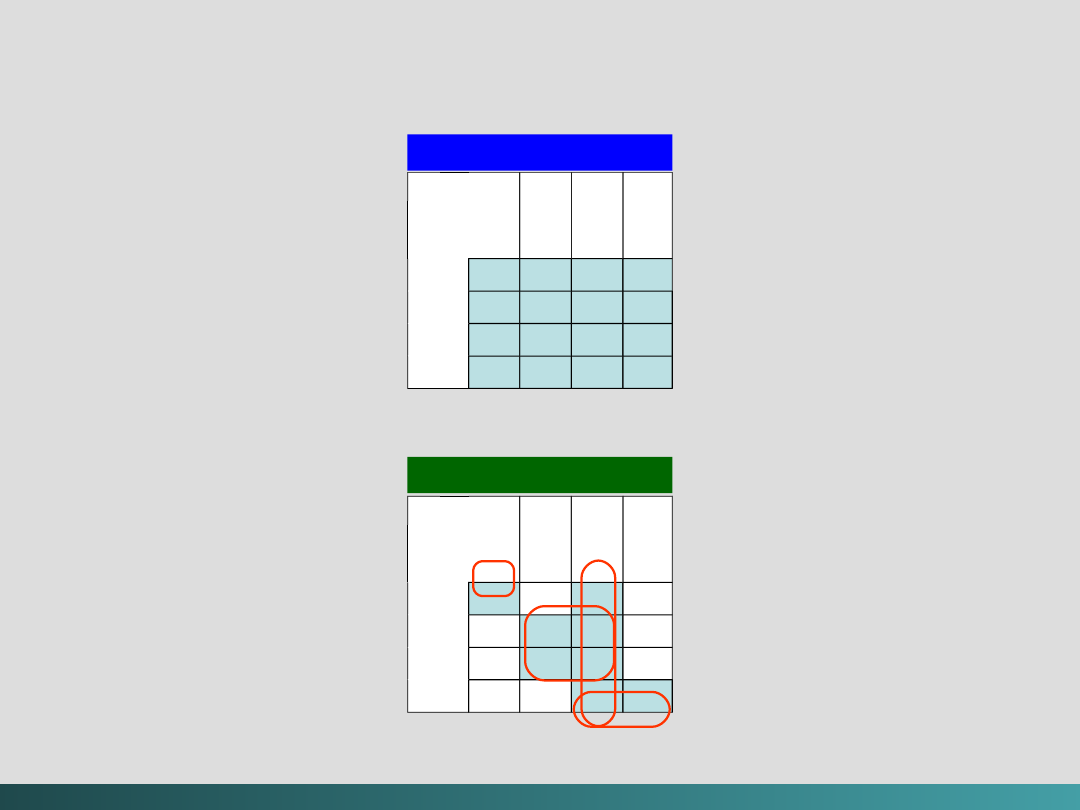
@Janusz Kosiński, 2005

Algebra Boole’a i logika cyfrowa

_ _ _ _ _ _ _ _ _ _ _
_ _

F(w, x, y, z)

w x y z + w x y z + w x y z + w x y z + w x y z + w x y

z + w x y z + w x y z

00 01 11 10

Tablica prawdy

00 01 11 10

Mapa Karnaugh

Wprowadzenie do prostego

komputera

@Janusz Kosiński, 2005

Komputer musi manipulować danymi zakodowanymi
binarnie.
Pamięć jest używana do przechowywania danych i instrukcji

programowych (również w postaci binarnej).

Programy muszą dać się wykonywać, zaś dane muszą być
przetwarzane prawidłowo.

Centralna jednostka przetwarzająca

central processing

unit (CPU

) jest odpowiedzialna za dosięgnięcie każdej

instrukcji,

zdekodowanie jej i zrealizowanie wskazanej

sekwencji

operacji na właściwych danych.

Wszystkie komputery mają CPU.

Każdą taką jednostkę możemy podzielić na dwie części.

CPU - podstawy

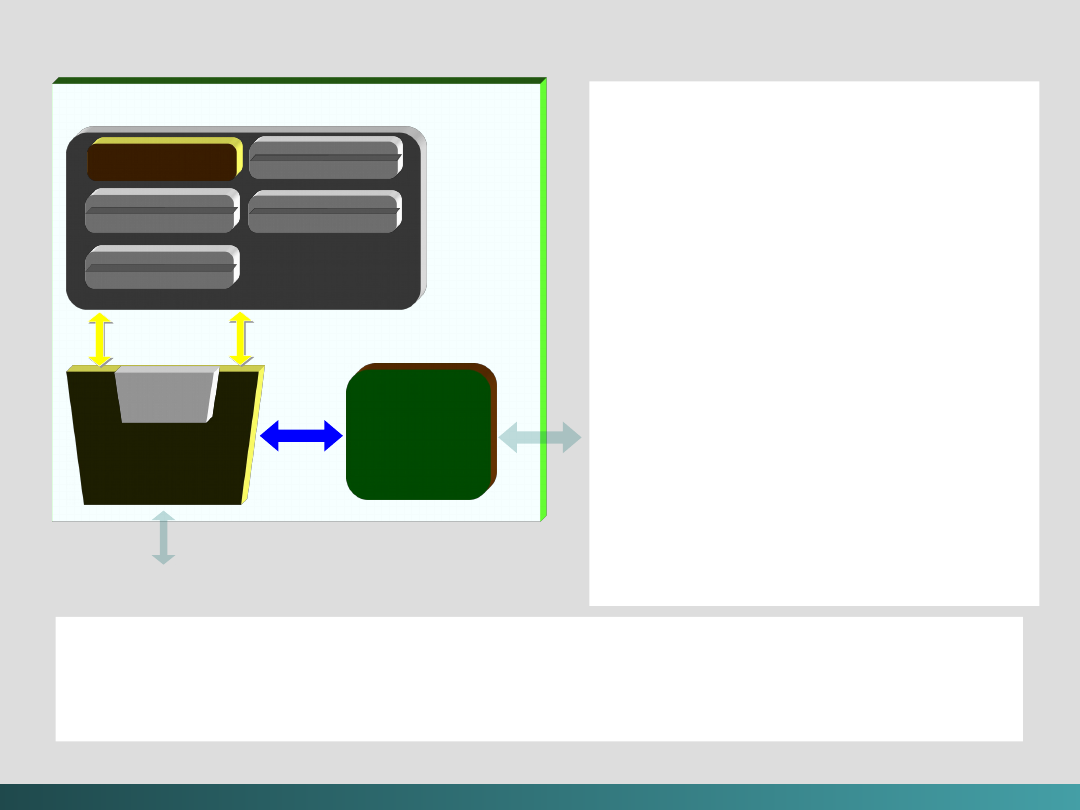
@Janusz Kosiński, 2005

CPU - podstawy

CPU

Rejestry

Licznik

Jednostka

arytmetyczno

- logiczna

Jednostka

kontrolna

Drugim składnikiem CPU jest

jednostka kontrolna

– moduł

odpowiedzialny za kolejkowanie operacji i prawidłowe adresowanie
danych we właściwym czasie.

Pierwszym składnikiem CPU
jest ścieżka danych - sieć

jednostek magazynujących

(rejestrów),

jednostek

arytmetycznych i

logicznych

(dla realizacji różnych operacji
na danych) połączonych w
sposób, umożliwiający
przemieszczanie danych z
miejsca na miejsce (busy), w
której operacje są
synchronizowane przez zegary

@Janusz Kosiński, 2005

Rejestry

są używane w systemach komputerowych jako miejsca

przechowywania różnego rodzaju danych binarnych, takich jak adresy,
liczniki programów czy dane niezbędne do wykonywania programów.
Rejestry są zlokalizowane w procesorze – szybki dostęp do informacji.

Jako rejestry mogą być zastosowane

D flip-flopy

. Jeden D flip-flop jest

ekwiwalentny

1 bitowemu rejestrowi

, tak że do przechowywania

wielobitowych wartości jest potrzebna kolekcja takich D flip-flopów –
np. w celu zbudowania 16 bitowego rejestru jest potrzebne 16 takich
flip-flopów.

Praca takiej kolekcji musi być synchronizowana zegarem

. Każdy impuls zegara

ustawia stany

wejściowe rejestrów i nie może to być zmienione do chwili

następnego sygnału.

Przetwarzanie danych w komputerach jest z reguły

dokonywane w postaci słów o stałych rozmiarach (przechowywanych w
rejestrach) – stąd większość komputerów posiada rejestry o określonym
rozmiarze.

Rozmiary te to przeważnie - 16, 32, i 64 bity. Liczba rejestrów w maszynie różni
się w zależności od architektury ale jest z reguły potęgą 2 – z najczęściej
spotykanymi 16 i 32.

CPU - podstawy

@Janusz Kosiński, 2005

Informacja jest zapisywana do rejestrów, czytana z rejestrów i
przesyłana od rejestru do rejestru.

Rejestry nie są adresowane w taki sam sposób jak adresowana jest
pamięć.

(każde słowo w pamięci posiada unikatowy binarny adres).

Rejestry są adresowane i manipulowane przy pomocy
jednostki sterującej

We współczesnych komputerach występuje wiele wyspecjalizowanych
typów rejestrów: do przechowywania informacji, do przesuwania
wartości, do

porównywania wartości i do liczenia.

Są też rejestry przechowujące wartości tymczasowe, sterujące pętlami

programowymi, wskazujące stan stosu lub rodzaj operacji (np.
przepełnienie, przesunięcie, wyzerowanie,…), czy też rejestry

ogólnego

przeznaczenia – osiągalne dla programistów.

Wiele komputerów posiada zbiory rejestrów (zbiór rejestrów danych,
zbiór rejestrów adresów, ..)

CPU - podstawy

@Janusz Kosiński, 2005

Jednostka arytmetyczno – logiczna

(ALU) odpowiada za operacje

logiczne

(porównywanie) i

arytmetyczne

(dodawanie lub

mnożenie) wymagane podczas wykonywania programów.

Ogólnie rzecz ujmując ALU posiada dwa wejścia i jedno wyjście.

ALU wie które operacje są realizowane dzięki sygnałom z jednostki
sterującej.

CPU - podstawy

Jednostka sterująca

jest ”policjantem” lub „zarządcą ruchu” w CPU.

Monitoruje wykonywanie wszelkich instrukcji i przesyłanie wszelkich
informacji.
Jednostka sterująca „wyciąga” instrukcje z pamięci, dekoduje te
instrukcje,

upewnia się że dane są właściwie rozmieszczone w

odpowiednim czasie, przekazuje informacje do AlU które rejestry
mają być używane,

obsługuje przerwania, …

Jednostka sterująca używa rejestru liczników do poszukiwania
kolejnych

instrukcji wykonawczych i śledzi stan rejestrów czy nie

są przepełnione,

etc ..

@Janusz Kosiński, 2005

System BUS

Układ

BUS

(magistrala)

CPU komunikuje się z innymi składnikami przy pomocy magistrali.
Magistrala jest zbiorem „przewodów” umożliwiających współdzielenie
„ścieżek danych” przez różne podsystemy systemu komputerowego.
Zawierają liczne linie pozwalające na równoległe przemieszczanie bitów.

W jednym czasie, tylko jedno urządzenie

(rejestr, ALU, pamięć lub inny

składnik) może wykorzystywać magistralę- chociaż ten system
współdzielenia doprowadza do swoistych „korków”.

Prędkość magistrali

jest zależna od jej długości i liczby urządzeń

współdzielących. Bardzo często urządzenia są podzielone na główne
(master) i podporządkowane (slave) – gdzie „master” inicjuje działania,
zaś „slave” działa zgodnie z zaleceniami urządzenia nadrzędnego.

Magistrala może mieć postać punkt do punktu (point to point) łącząc
dwa specyficzne składniki lub może być wspólną ścieżką łącząca pewną
liczbę urządzeń wymagających współdzielenia.

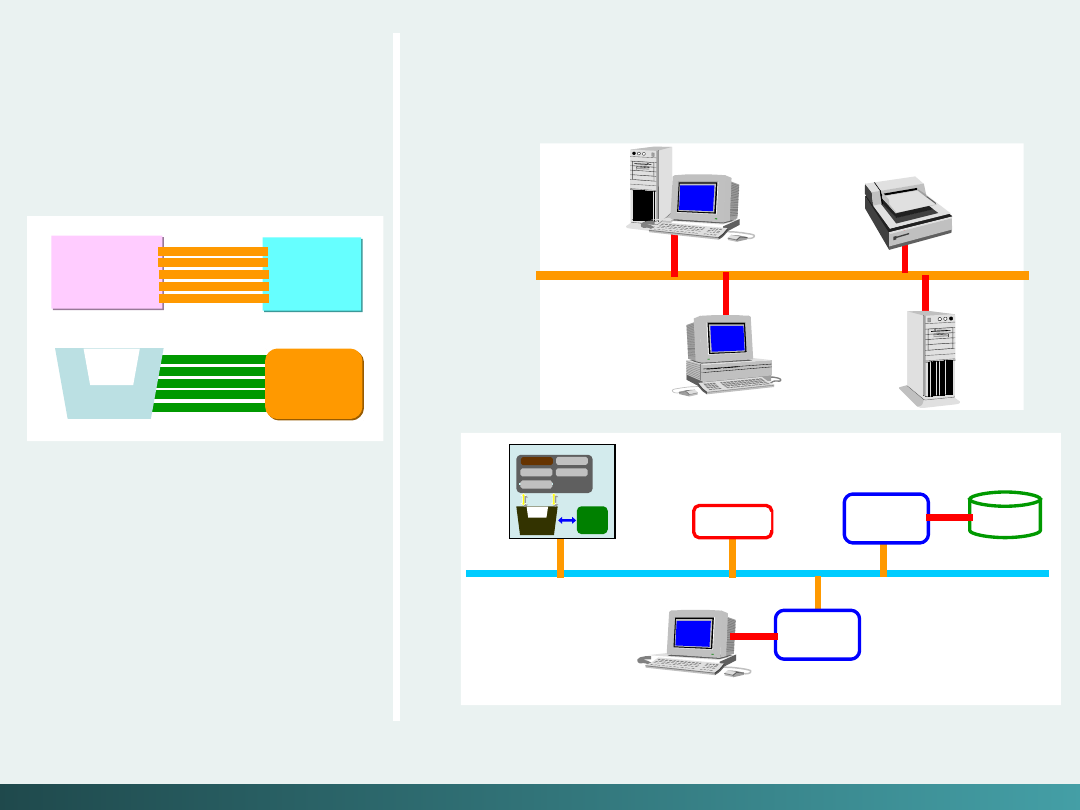
@Janusz Kosiński, 2005

Magistrale

wielopunktowe

Komputer
1

Komputer
2

Serwe
r
plików

Drukark
a

Magistrale „Point-to-

Point”

CPU

Pamięć

Kontrol

dysku

Kontrol

dysku

Monito
r

Dysk

Port

szeregow

Modem

Jednostk

kontrolna

ALU

System BUS

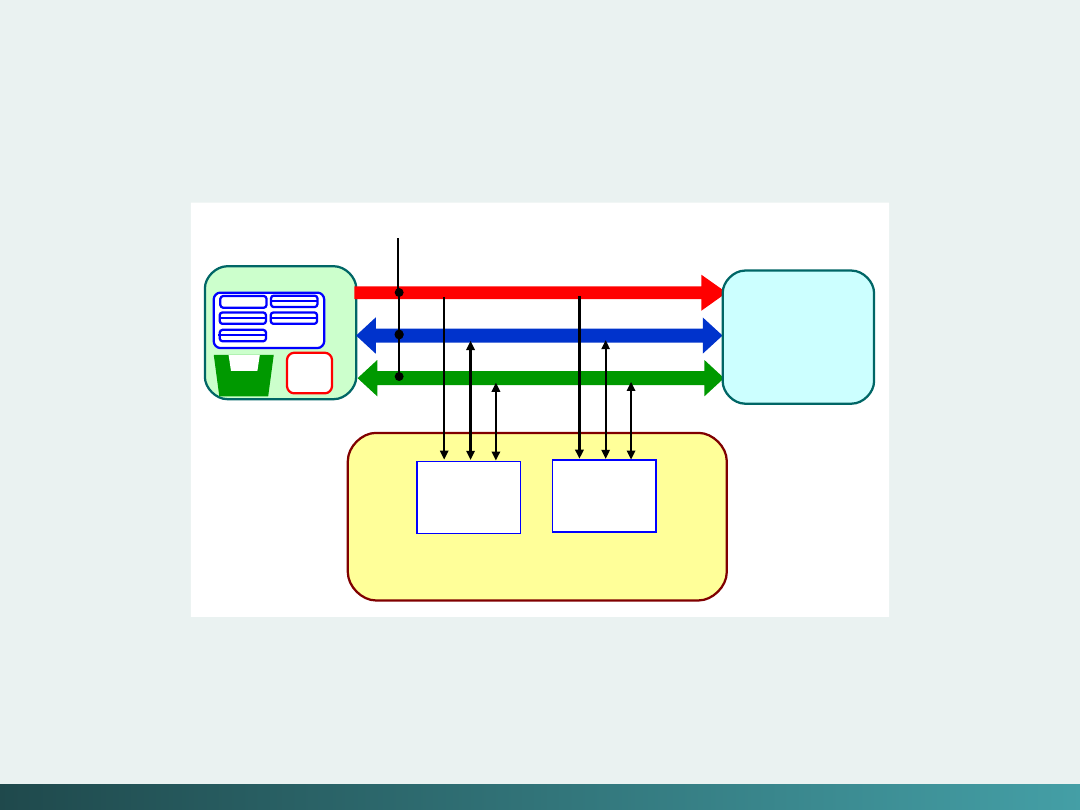
@Janusz Kosiński, 2005

Z powodu tego współdzielenia,

bus protocol

(

zbiór reguł użytkowania

)

jest bardzo ważną sprawą.

CPU

Pamięć

główna

Podsystem WE /WY

Urządzeni

e We / WY

Urządzeni

e We / WY

Szyna
adresowa

Szyna danych

Szyna

sterowania

Zasilan
ie

Składniki typowego układu BUS

Linie danych

(szyny danych)

Linie adresowe

(szyny adresowe)

Linie sterowania

(szyny sterowania) i

linie zasilające

(szyny

zasilające)

System BUS

@Janusz Kosiński, 2005

Linie w magistrali

przeznaczone do transferu danych nazywane są

liniami danych.

Linie danych

zawierają aktualną informację, która musi

być przemieszczona z jednej lokalizacji do drugiej.

Linie sterujące

wskazują które urządzenia ma pozwolenie na

wykorzystywanie

magistrali i w jaki sposób (czytanie lub

zapisywanie do / z pamięci czy urządzeń WE / WY). Linie sterujące
również przekazują wiedzę o

wymaganiach, przerwaniach czy

synchronizacji zegarem.

Linie adresowe

wskazują lokalizację (np. w pamięci) gdzie dane

powinny być

zapisane (odczytane)

Linie zasilania

doprowadzają niezbędne zasilanie do obwodów

logicznych.

Każdy typ transferu jest regulowany cyklem pracy zegara – czasem
między dwoma kolejnymi impulsami.

System BUS

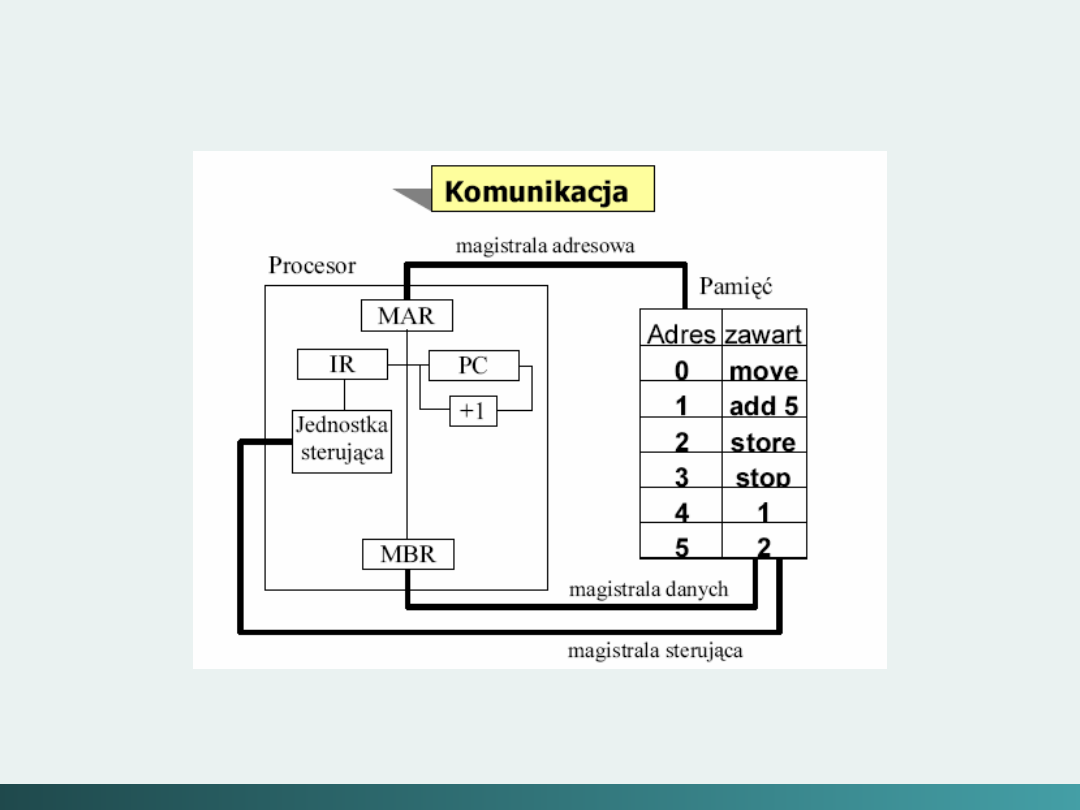
@Janusz Kosiński, 2005

System BUS

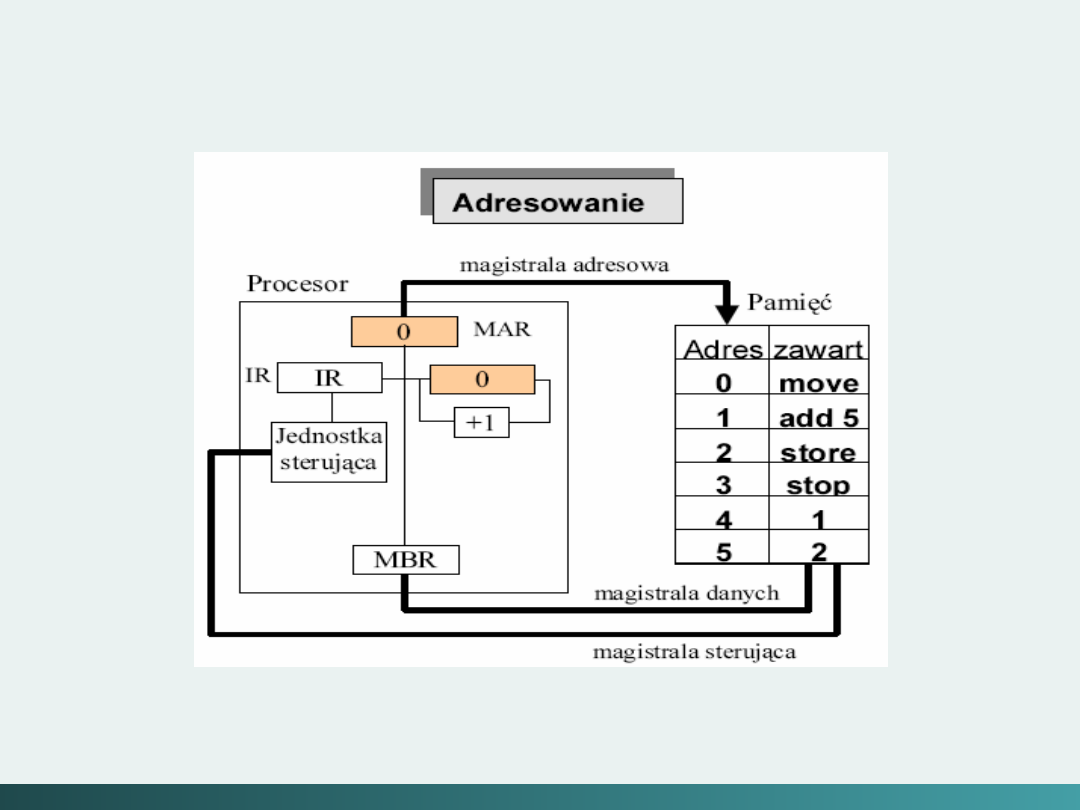
@Janusz Kosiński, 2005

System BUS

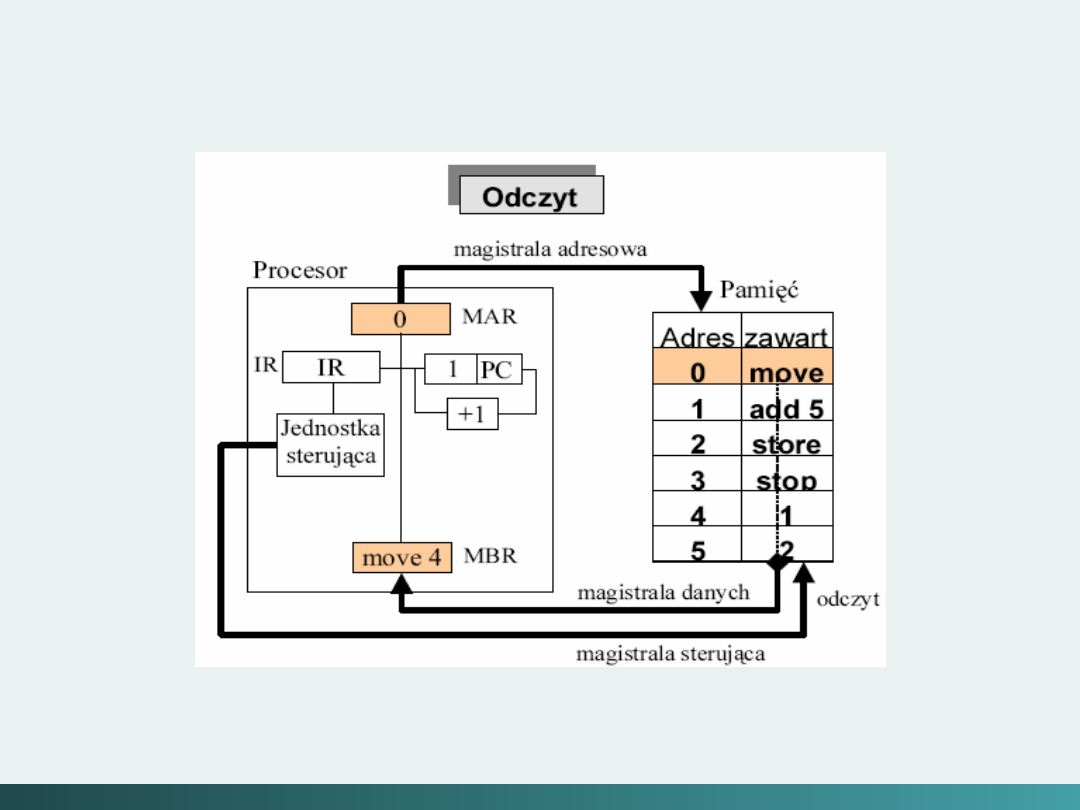
@Janusz Kosiński, 2005

System BUS

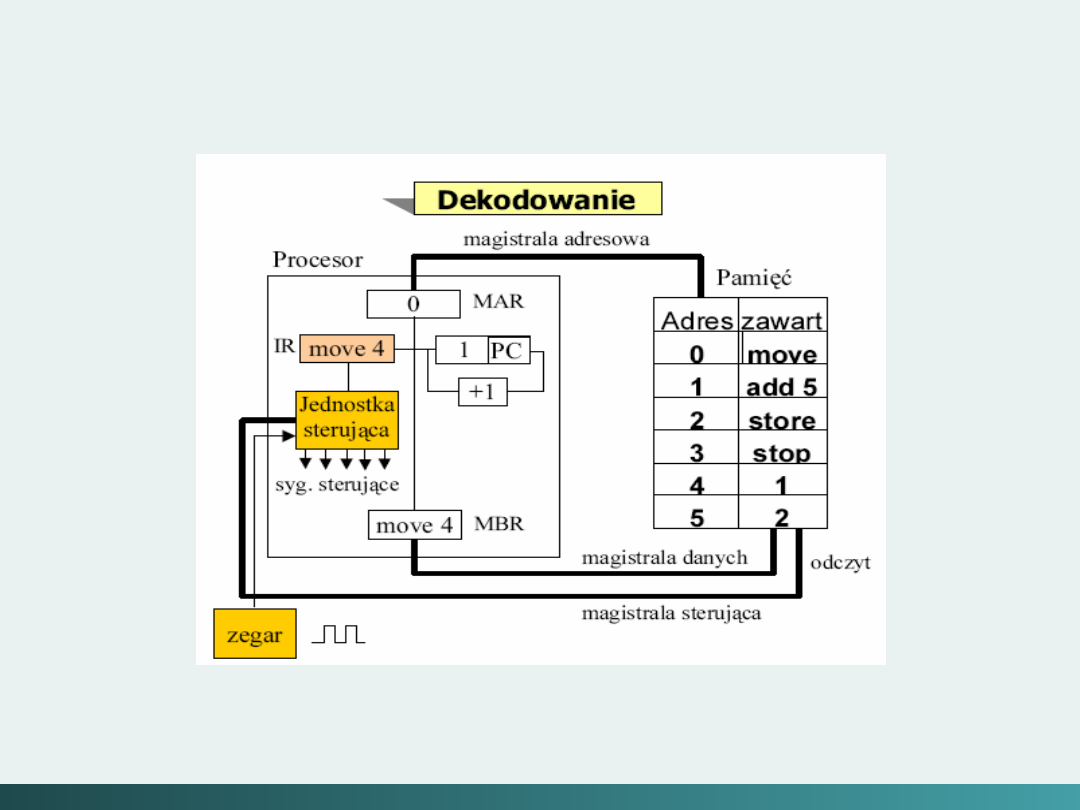
@Janusz Kosiński, 2005

System BUS

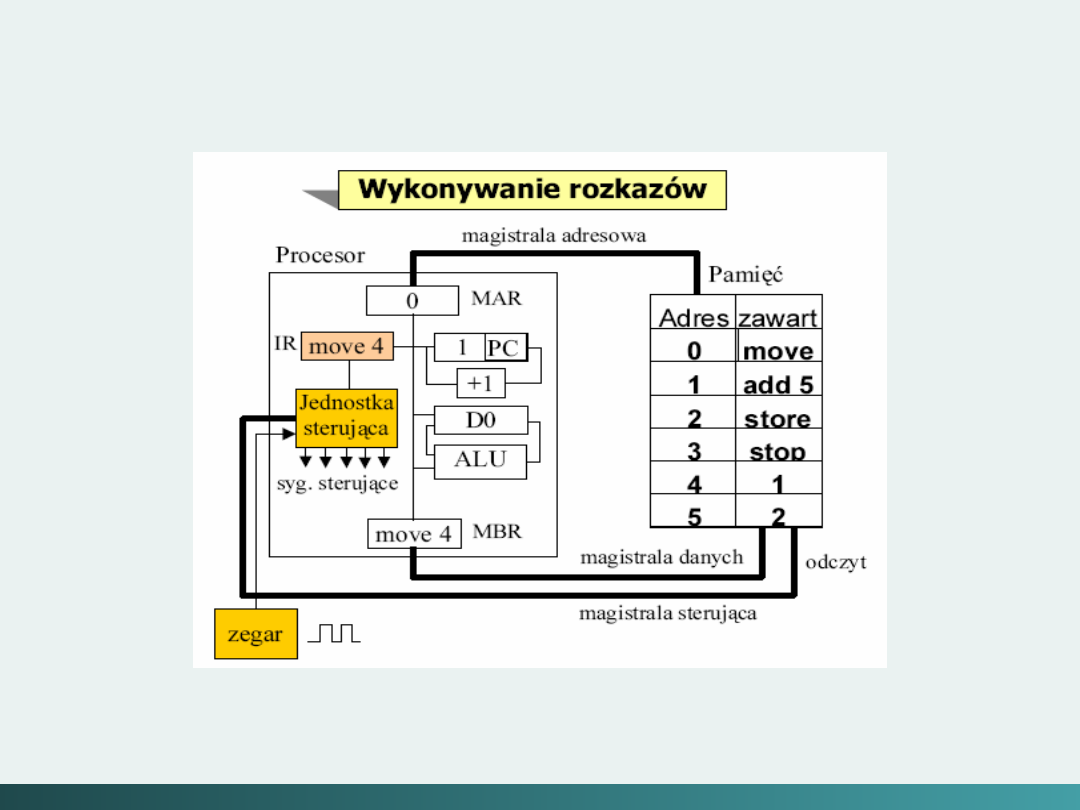
@Janusz Kosiński, 2005

System BUS

@Janusz Kosiński, 2005

Zegary

Każdy komputer zawiera zegar wewnętrzny, regulujący szybkość
wykonywania instrukcji. Zegar również synchronizuje pracę
wszystkich składników systemu.

CPU wykorzystuje zegar do regulowania postępu poszczególnych
procesów,

kontrolując prędkość, nieprzewidywalną w przeciwnym

przypadku,

bramek logicznych.

CPU wymaga określonej liczby „tyknięć” zegara do wykonania każdej
instrukcji.

Stąd wykonywanie instrukcji jest mierzone cyklami

zegara – czasem

pomiędzy dwoma kolejnymi impulsami zegara.

Częstotliwość zegara, jest mierzona w MHz.

Cykl zegara

(okres) jest po prostu odwrotnością częstotliwości – np.

maszyna

800 MHz ma kres równy 1/800 000000 lub 1,25 ns.

Jeżeli maszyna ma okresów 2 ns, to jej częstotliwość wynosi 500 MHz.

Zegary

@Janusz Kosiński, 2005

Większość maszyn jest synchroniczna: główny sygnał zegara
(master clock signal – zegar systemowy), pulsuje (zmieniając się
od 0 do 1 do 0 i tak dalej) w regularnych przedziałach czasu
(interwalach) – rejestry muszą czekać na kolejne „tyknięcia
zegara” zanim będą wprowadzone nowe dane.

Cykl zegara musi być dostatecznie długi aby umożliwić
wprowadzenie tych zmian do następnego zbioru rejestrów. Jeżeli
cykl będzie za krótki, to proces może się zakończyć przed
wprowadzeniem wszystkich instrukcji – to będzie skutkowac w
niestabilnej pracy maszyny.

Stąd minimalny cykl zegara musi być tak duży aby umożliwić
propagację maksymalnej przerwy miedzy rejestrami wejścia i
wyjścia. Np. instrukcja, która powinna wymagać 2 cykli może
potrzebować trzech lub czterech cykli (zależnie od lokalizacji
dodatkowych rejestrów). Większość instrukcji maszynowych
wymaga 1 lub 2 cykli zegara. Poniższa formuła prezentuje relacje
między sekundami a cyklem.

Większość maszyn jest synchroniczna

: główny sygnał zegara

(master clock signal – zegar systemowy), pulsuje (zmieniając się
od 0 do 1 do 0 i tak dalej) w regularnych przedziałach czasu
(interwalach) – rejestry muszą czekać na kolejne „tyknięcia
zegara” zanim będą wprowadzone nowe dane.

Cykl zegara musi być dostatecznie długi

aby umożliwić

wprowadzenie tych zmian do następnego zbioru rejestrów. Jeżeli
cykl będzie za krótki, to proces może się zakończyć przed
wprowadzeniem wszystkich instrukcji – to będzie skutkowac w
niestabilnej pracy maszyny.

Stąd

minimalny cykl zegara

musi być tak duży aby umożliwić

propagację maksymalnej przerwy miedzy rejestrami wejścia i
wyjścia. Np. instrukcja, która powinna wymagać 2 cykli może
potrzebować trzech lub czterech cykli (zależnie od lokalizacji
dodatkowych rejestrów). Większość instrukcji maszynowych
wymaga 1 lub 2 cykli zegara. Poniższa formuła prezentuje relacje
między sekundami a cyklem.

CPU czas =

sekundy

instrukcje

średni
cykl

sekundy

program

instrukcja

cykl

Zegary

@Janusz Kosiński, 2005

System I/O

Podsystem Wejścia / Wyjścia

Urządzenia wejścia/wyjścia (I/O) pozwalają na komunikowanie się z
systemem

komputerowym – różne urządzenia peryferyjne.

Te urządzenia nie są bezpośrednio podłączone do CPU. Występuje tu
interfejs

podtrzymujący transfer danych – ten interfejs

przekształca sygnały

magistrali systemowej do formatu

akceptowalnego przez dna urządzenie.

CPU komunikuje się z tymi urządzeniami przez rejestry
wejścia/wyjścia. Tu

wymiana danych jest realizowana na dwa

sposoby.

W odwzorowujących pamięć I/O, rejestry w interfejsie sa
odwzorowywane w

pamięci i nie ma różnicy pomiędzy dostępem do

pamięci czy dostępem do

urządzenia I/O.

W opartych na poleceniach I/O, CPU posiada wyspecjalizowane
instrukcje

przedstawiające wejścia i wyjścia. Aczkolwiek tu nie ma

używania pamięci,

to jest wymagany specyficzny zbiór instrukcji,

które mogą być użytkowane

tylko przez CPU.

Przerwania odgrywają bardzo ważną rolę w układzie I/O, ponieważ
stanowią

efektywny sposób informowania CPU o osiągalnych w

danej chwili

wejściach lub wyjściach.

Podsystem Wejścia / Wyjścia

Urządzenia wejścia/wyjścia

(I/O) pozwalają na komunikowanie się z

systemem

komputerowym – różne urządzenia peryferyjne.

Te urządzenia nie są bezpośrednio podłączone do CPU. Występuje tu
interfejs

podtrzymujący transfer danych – ten interfejs

przekształca sygnały

magistrali systemowej do formatu

akceptowalnego przez dna urządzenie.

CPU komunikuje się z tymi urządzeniami przez

rejestry

wejścia/wyjścia

. Tu

wymiana danych jest realizowana na dwa

sposoby.

odwzorowujących pamięć

I/O, rejestry w interfejsie sa

odwzorowywane w

pamięci i nie ma różnicy pomiędzy dostępem do

pamięci czy dostępem do

urządzenia I/O.

opartych na poleceniach

I/O, CPU posiada wyspecjalizowane

instrukcje

przedstawiające wejścia i wyjścia. Aczkolwiek tu nie ma

używania pamięci,

to jest wymagany specyficzny zbiór instrukcji,

które mogą być użytkowane

tylko przez CPU.

Przerwania

odgrywają bardzo ważną rolę w układzie I/O, ponieważ

stanowią

efektywny sposób informowania CPU o osiągalnych w

danej chwili

wejściach lub wyjściach.

@Janusz Kosiński, 2005

Pamięć

Organizacja pamięci i adresowanie

Można przedstawić pamięć jako macierz bitów. Każdy wiersz,
wykorzystywany

przez rejestr, posiada długość równoważną do

słowa maszynowego. Każdy

rejestr ma unikatowy adres zazwyczaj

zaczynający się od zera i narastający – adres taki jest zazwyczaj
nieoznaczoną liczbą całkowitą (unsigned integer).

Organizacja pamięci i adresowanie

Można przedstawić pamięć jako macierz bitów. Każdy wiersz,
wykorzystywany

przez rejestr, posiada długość równoważną do

słowa maszynowego. Każdy

rejestr ma unikatowy adres zazwyczaj

zaczynający się od zera i narastający – adres taki jest zazwyczaj
nieoznaczoną liczbą całkowitą (

unsigned integer

Adres

 

8 bitów

 

Adres

 

16 bitów

 

…

N 8 bitowy
rejestr

M 16 bitowy
rejestr

@Janusz Kosiński, 2005

Przeważnie, pamięć jest adresowana bajtami – każdy bajt ma
swój

unikatowy adres. Niektóre maszyny mogą mieć słowo jako

jednostkę

adresową. Np. komputer może operować 32 bitowymi

słowami

(manipuluje cały czas 32 bitami w dowolnych

instrukcjach), ale stale wykorzystuje architekturę adresowaną
bajtami.

W sytuacji, kiedy słowo używa wielu bajtów, bajt z najniższym
adresem

determinuje adres kompletnego słowa.

Jest również możliwe adresowanie słowami – każde słowo (nie jest

niezbędny każdy bajt) posiada swój własny adres, ale

większość

współczesnych maszyn posiada adresowanie oparte

na bajtach (nawet

jeżeli słowa są dłuższe niż 32 bity).

Adres w pamięci, jest przechowywany (typowo) w pojedynczym
słowie maszynowym.

Przeważnie,

pamięć jest adresowana bajtami

– każdy bajt ma

swój

unikatowy adres. Niektóre maszyny mogą mieć słowo jako

jednostkę

adresową. Np. komputer może operować 32 bitowymi

słowami

(manipuluje cały czas 32 bitami w dowolnych

instrukcjach), ale stale wykorzystuje architekturę adresowaną
bajtami.

W sytuacji, kiedy słowo używa wielu bajtów,

bajt z najniższym

adresem

determinuje adres kompletnego słowa.

Jest również możliwe

adresowanie słowami

– każde słowo (nie jest

niezbędny każdy bajt) posiada swój własny adres, ale

większość

współczesnych maszyn posiada adresowanie oparte

na bajtach (nawet

jeżeli słowa są dłuższe niż 32 bity).

Adres w pamięci, jest przechowywany (typowo) w pojedynczym
słowie maszynowym.

Pamięć

@Janusz Kosiński, 2005

Pamięć jest podobna do ulicy pełnej budynków mieszkalnych. Każdy

budynek (słowo) posiada wiele mieszkań (bajtów), zaś każde
mieszkanie ma swój adres. Wszystkie mieszkania są adresowane
kolejno, od 0 do całkowitej liczby mieszkań w tym kompleksie
mieszkalnym.

Budynki obsługują grupę mieszkań – w komputerze słowa robią

dokładnie to samo. Słowa są podstawową jednostką stosowaną w
różnych instrukcjach.

Jeżeli architektura jest adresowana bajtami, oraz słowo

ustalające architekturę instrukcji jest dłuższe niż 1 bajt, musi być
zaadresowane „wyrównanie”. Np. jeżeli chcemy przeczytać słowo
32 bitowe w maszynie adresowanej bajtami, to musimy być pewni,
że:

1. Słowo zostało zmagazynowane w naturalnych granicach
2. Dostęp do słowa rozpoczyna się w tych granicach.
Jest to spełnione w przypadku 32 bitowego słowa, przy zastosowaniu

adresu będącego wielokrotnością 4.

Pamięć jest podobna do ulicy pełnej budynków mieszkalnych. Każdy

Budynki obsługują grupę mieszkań – w komputerze słowa robią

dokładnie to samo. Słowa są podstawową jednostką stosowaną w
różnych instrukcjach.

Jeżeli architektura jest adresowana bajtami, oraz słowo

1. Słowo zostało zmagazynowane w naturalnych granicach
2. Dostęp do słowa rozpoczyna się w tych granicach.

Jest to spełnione w przypadku 32 bitowego słowa, przy zastosowaniu

adresu będącego wielokrotnością 4.

Pamięć

@Janusz Kosiński, 2005

Pamięć jest zbudowana z chipów RAM (random access memory ).

Pamięć jest opisywana, bardzo często, przy pomocy notacji L x W
(length x width = długość x szerokość).

Np., 4M x 16 oznacza, że pamięć ma 4M długości (4M = 2

x 2

= 2

słowa) i

16 bitów szerokości (każde słowo ma 16 bitów).

Szerokość (druga liczba w notacji) reprezentuje rozmiar słowa.

W celu zaadresowania tej pamięci (zakładając adresowanie słowami),
potrzebujemy unikatowej identyfikacji 2

różnych jednostek, co oznacza

konieczność

posiadania 2

różnych adresów.

Ponieważ adresowanie jest dokonywane przy pomocy
nieoznaczonych

liczb binarnych, potrzebujemy odliczania od 0

do (2

– 1) w systemie

Aby liczyć od 0 do 3 w systemie binarnym (dla całkowitej liczby 4
pozycji)

potrzebujemy 2 bity.

Dla liczenia od 0 do 7 w systemie binarnym (dla 8 pozycji),
potrzebujemy 3 bity.

Dla liczenia od 0 to 15 w systemie binarnym (dla 16 pozycji) - 4 bity.

Pamięć jest zbudowana z chipów RAM (random access memory ).

Pamięć jest opisywana, bardzo często, przy pomocy

notacji L x W

(length x width = długość x szerokość).

Np., 4M x 16 oznacza, że pamięć ma 4M długości (4M = 2

x 2

= 2

słowa) i

16 bitów szerokości (każde słowo ma 16 bitów).

Szerokość (druga liczba w notacji) reprezentuje rozmiar słowa.

W celu zaadresowania tej pamięci (zakładając adresowanie słowami),
potrzebujemy unikatowej identyfikacji 2

różnych jednostek, co oznacza

konieczność

posiadania 2

różnych adresów.

Ponieważ adresowanie jest dokonywane przy pomocy
nieoznaczonych

liczb binarnych, potrzebujemy odliczania od 0

do (2

– 1) w systemie

Aby liczyć od 0 do 3 w systemie binarnym (dla całkowitej liczby 4
pozycji)

potrzebujemy 2 bity.

Dla liczenia od 0 do 7 w systemie binarnym (dla 8 pozycji),
potrzebujemy 3 bity.

Dla liczenia od 0 to 15 w systemie binarnym (dla 16 pozycji) - 4 bity.

Pamięć

@Janusz Kosiński, 2005

Pamięć główna jest zazwyczaj większa niż jeden chip RAM. Jako konsekwencja
tego,

chipy są kombinowane w pojedyncze moduły pamięci, spełniające

wymagania

rozmiaru. Np. budowa pamięci 32K x 16 przy pomocy chipów

RAM 2K x 8 –

należy połączyć 16 wierszy i 2 kolumny chipów razem.

Wiersz 0

2K x 8

Wiersz 1

2K x 8

. . .

. . .

Wiersz

2K x 8

Każdy wiersz adresuje 2K słów (zakładamy że maszyna jest adresowana
słowami), ale wymaga, dwóch chipów dla operowania pełną szerokością. Adresy
dla tej pamięci muszą mieć 15 bitów (32K = 2

x 2

dostępnych słów). Każda

para chipów (każdy wiersz) wymaga tylko 11 linii adresowych (każda para
chipów podtrzymuje tylko 2

słów ).

W tej sytuacji potrzebny będzie dekoder, do dekodowania 4 bitów z lewej
strony, aby zdeterminować, która para chipów podtrzymuje pożądany adres.

Jak właściwa para chipów jest zlokalizowana, to pozostałe 11 bitów jest
wprowadzane do następnego dekodera, celem znalezienia dokładnego adresu
wewnątrz tej pary.

x 2

dostępnych słów). Każda

para chipów (każdy wiersz) wymaga tylko 11 linii adresowych (każda para
chipów podtrzymuje tylko 2

słów ).

W tej sytuacji potrzebny będzie dekoder, do dekodowania 4 bitów z lewej
strony, aby zdeterminować, która para chipów podtrzymuje pożądany adres.

Jak właściwa para chipów jest zlokalizowana, to pozostałe 11 bitów jest
wprowadzane do następnego dekodera, celem znalezienia dokładnego adresu
wewnątrz tej pary.

Pamięć

@Janusz Kosiński, 2005

Pojedynczy moduł pamięci współdzielonej jest przyczyną
kolejkowania dostępu. Do ulżenia tej sytuacji jest stosowane
przeplatanie pamięci, powodujące podział pamięci między liczne
moduły pamięci (banki pamięci).

Mniej znaczące przeplatanie (low order interleaving) wykorzystuje
mniej znaczące bity adresów są wykorzystywane do selekcji banków –
dla bardziej znaczących przeplotów (high order interleaving)
wykorzystywane są bity bardziej znaczące.

W przeplocie wysokiego porządku (high order interleaving), każdy
moduł zawiera następujące po sobie adresy.

Pojedynczy moduł pamięci współdzielonej jest przyczyną
kolejkowania dostępu. Do ulżenia tej sytuacji jest stosowane

przeplatanie pamięci

, powodujące podział pamięci między liczne

moduły pamięci (banki pamięci).

Mniej znaczące przeplatanie

(low order interleaving)

wykorzystuje

mniej znaczące bity adresów są wykorzystywane do selekcji banków –
dla bardziej znaczących przeplotów

(high order interleaving)

wykorzystywane są bity bardziej znaczące.

W przeplocie wysokiego porządku (high order interleaving),

każdy

moduł zawiera następujące po sobie adresy.

Moduł

Pamięć

@Janusz Kosiński, 2005

Moduł

W przeplocie niskiego porządku (low order interleaving) kolejne słowa
są umieszczane w pamięci w różnych modułach.

Jeżeli odpowiednie magistrale będą używać przeplotu niskiego
porządku, czytanie lub zapisywanie w jednym module może rozpocząć
się przed skompletowaniem aktualnego odczytu lub zapisu
(nakładanie się operacji – overlapping).

W przeplocie niskiego porządku (

low order interleaving

) kolejne słowa

są umieszczane w pamięci w różnych modułach.

Jeżeli odpowiednie magistrale będą używać przeplotu niskiego
porządku,

czytanie lub zapisywanie w jednym module może rozpocząć

się przed skompletowaniem aktualnego odczytu lub zapisu

(nakładanie się operacji –

overlapping

Pamięć

@Janusz Kosiński, 2005

Przerwania

Przerwania są zdarzeniami modyfikującymi (lub przerywającymi)
normalny tok wykonywania instrukcji w systemie. Przerwania mogą być
wyzwalane z różnych przyczyn, włączywszy:

Wymagania I/O

Błędy arytmetyczne (np. dzielenie przez zero)

Arytmetyczne przepełnienie lub niedomiar

Złe funkcjonowanie sprzętu (np. bład parzystości pamięci)

Punkty przerwań zdefiniowane przez użytkownika (eliminowanie
błędów programu)

Błędy stron

Niepoprawne instrukcje (wyniki złego zastosowania odwołań i
wskaźników)

Różne

Przerwania

Przerwania są zdarzeniami modyfikującymi

(lub przerywającymi)

normalny tok wykonywania instrukcji w systemie. Przerwania mogą być
wyzwalane z różnych przyczyn, włączywszy:

Wymagania I/O

Błędy arytmetyczne (np. dzielenie przez zero)

Arytmetyczne przepełnienie lub niedomiar

Złe funkcjonowanie sprzętu (np. bład parzystości pamięci)

Punkty przerwań zdefiniowane przez użytkownika (eliminowanie
błędów programu)

Błędy stron

Niepoprawne instrukcje (wyniki złego zastosowania odwołań i
wskaźników)

Różne

@Janusz Kosiński, 2005

Czynności podejmowane dla każdego typu przerwań - obsługa
przerwań - są bardzo różne.

Czym innym jest informowanie CPU, że właśnie zostało zakończone
żądanie I/O, a czym innym kończenie programu z powodu dzielenia przez
zero.

Wszystkie muszą być obsługiwane, ponieważ powodują zmiany w
normalnym toku działania programu.

Przerwanie może być:
 inicjowane przez użytkownika lub przez system,
 maskowane (wyłączone lub ignorowane) lub nie maskowane
(przerwanie

wysokiego priorytetu nie może być maskowane),

 może wydarzyć się wewnątrz lub między instrukcjami,
 może być synchroniczne (realizowane w tym samym miejscu
wykonywania programu) lub asynchroniczne (wydarzające się
nieoczekiwanie),
 przyczynić się do zakończenia działania programu lub dalszej realizacji
- jeżeli istnieje obsługa przerwań.

Czynności podejmowane dla każdego typu przerwań - obsługa
przerwań - są bardzo różne.

Czym innym jest informowanie CPU, że właśnie zostało zakończone
żądanie I/O, a czym innym kończenie programu z powodu dzielenia przez
zero.

Wszystkie muszą być obsługiwane, ponieważ powodują zmiany w
normalnym toku działania programu.

Przerwanie może być:

 inicjowane przez użytkownika lub przez system,
 maskowane (wyłączone lub ignorowane) lub nie maskowane
(przerwanie

wysokiego priorytetu nie może być maskowane),

Przerwania

@Janusz Kosiński, 2005

Przykład prostej architektury zawierającej pamięć (do przechowywania
programów i danych) i CPU (zawierającej ALU i kilka rejestrów) oraz wszystkich
niezbędnych składników aby być prostym komputerem:

Binarny, dopełniający do dwóch
Program magazynowany, słowo stałej długości
Adresowanie słowami (ale nie bajtami)
4K słowa pamięci głównej (to powoduje 12 bitów na adres)
16 bitowe dane (słowa mają 16 bitów)
16 bitowe instrukcje, 4 dla kodu operacji i 12 dla adresu
16 bitowy akumulator (AC)
16 bitowy rejestr instrukcji (IR)
16 bitowy rejestr buforów pamięci (MBR)
12 bitowy licznik programu (PC)
12 bitowy rejestr adresów pamięci (MAR)
8 bitowy rejestr wejścia
8 bitowy rejestr wyjścia

Binarny

, dopełniający do dwóch

Program magazynowany, słowo

stałej długości

Adresowanie słowami

(ale nie bajtami)

słowa pamięci głównej (to powoduje 12 bitów na adres)

16 bitowe

dane (słowa mają 16 bitów)

16 bitowe

instrukcje, 4 dla kodu operacji i 12 dla adresu

16 bitowy

akumulator (AC)

16 bitowy

rejestr instrukcji (IR)

16 bitowy

rejestr buforów pamięci (MBR)

12 bitowy

licznik programu (PC)

12 bitowy

rejestr adresów pamięci (MAR)

8 bitowy

rejestr wejścia

8 bitowy

rejestr wyjścia

Prosty
komputer

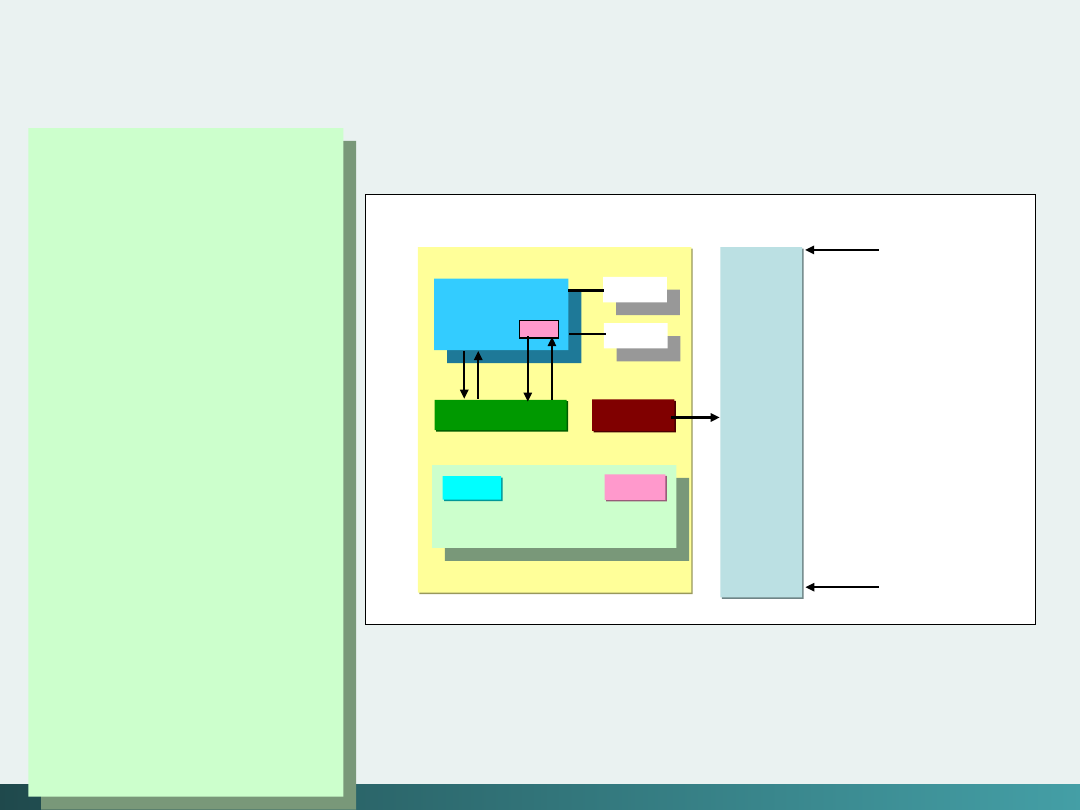
@Janusz Kosiński, 2005

Prosty
komputer

CPU

MBR

MAR

InREG

OutREG

Jednostka kontrolna

ALU

Pamięć

główna

Pamięć

główna

Adres pamięci 4K
- 1

Adres pamięci 0

AC: akumulator - rejestr
ogólnego stosowania,
utrzymuje dane wymagane
przez CPU.

MAR: rejestr adresów
pamięci.

MBR: rejestr buforów
pamięci – utrzymuje dane
właśnie czytane lub gotowe
do zapisu.

PC: licznik programu –
utrzymuje adresy kolejnych
(następujących po sobie)
instrukcji.

IR: rejestr instrukcji –
utrzymuje kolejne
instrukcje.

InREG: rejestr wejścia –
dane z urządzenia
wejściowego.

OutREG: rejestr wyjścia –
dane dla urządzenia
wyjściowego.

AC: akumulator - rejestr
ogólnego stosowania,
utrzymuje dane wymagane
przez CPU.

MAR: rejestr adresów
pamięci.

MBR: rejestr buforów
pamięci – utrzymuje dane
właśnie czytane lub gotowe
do zapisu.

PC: licznik programu –
utrzymuje adresy kolejnych
(następujących po sobie)
instrukcji.

IR: rejestr instrukcji –
utrzymuje kolejne
instrukcje.

InREG: rejestr wejścia –
dane z urządzenia
wejściowego.

OutREG: rejestr wyjścia –
dane dla urządzenia
wyjściowego.

@Janusz Kosiński, 2005

Każde
urządzenie
podłączone do
magistrali
posiada swój
numer,
umożliwiający
prawidłową
realizację
procesów.

Prosty
komputer

MAR

MBR

InREG

OutREG

ALU

Pamięć

Główna

BUS 16 bitowy

Ścieżka danych w prostym
komputerze

@Janusz Kosiński, 2005

Architektura zbioru instrukcji

Architektura zbioru instrukcji (

instruction set architecture - ISA

) dla

maszyny specyfikuje instrukcje, które komputer powinien wykonać oraz
ich format.

ISA jest zasadniczo interfejsem miedzy oprogramowaniem i sprzętem.

W przykładowym komputerze, każda instrukcja zawiera 16 bitów. Bity
najwyższe, od 12 do 15, tworzą kod operacji, specyfikujący instrukcje
wykonawcze – co pozwala na wykonanie wszystkich 16 instrukcji.

Najniższe bity, od 0 do 11 tworzą adres, pozwalający na maksymalny
rozmiar pamięci: 2

- 1.

Prosty
komputer

Adres

Kod

operacji

Bit 15 12 11
0

@Janusz Kosiński, 2005

Pobierz zawartość adresu X do AC

Przechowaj zawartość AC pod adresem X

Dodaj zawartość adresu X do AC i przechowaj wynik w AC

Odejmij zawartość adresu X od AC i przechowaj wynik w AC

Wprowadź wartość z klawiatury do AC

Wyprowadź wartość z AC na wyświetlacz

Zakończ program.

Opuść następną instrukcję w przypadku warunku.

Wprowadź wartość X do PC

Pobierz zawartość adresu X do AC

Przechowaj zawartość AC pod adresem X

Dodaj zawartość adresu X do AC i przechowaj wynik w AC

Odejmij zawartość adresu X od AC i przechowaj wynik w AC

Wprowadź wartość z klawiatury do AC

Wyprowadź wartość z AC na wyświetlacz

Zakończ program.

Opuść następną instrukcję w przypadku warunku.

Wprowadź wartość X do PC

Load X

Store X

Add X

Subt X

Input

Output

Halt

Skipcond

Jump X

Load X

Store X

Add X

Subt X

Input

Output

Halt

Skipcond

Jump X

0001

0010

0011

0100

0101

0110

0111

1000

1001

0001

0010

0011

0100

0101

0110

0111

1000

1001

Hex

Bin

Znaczenie

Instrukcja

Numer instrukcji

Prosty
komputer

@Janusz Kosiński, 2005

Prosty
komputer

Kod operacji

adres

0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1

bit 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

Kod operacji

adres

0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 1

bit 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

Kod operacji

adres

1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1

bit 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

Kod operacji 0001 oznacza w układzie
binarnym pozycję 1, reprezentującą instrukcję
Load. Pozostałe 12 bitów wskazuje adres w
pamięci głównej dla wartości pobieranej (numer
3). Instrukcja ta powoduje skopiowanie do AC
wartości znalezionej w pamięci głównej pod
adresem 3.

Kod operacji 0001

oznacza w układzie

binarnym pozycję 1, reprezentującą instrukcję
Load. Pozostałe 12 bitów wskazuje adres w
pamięci głównej dla wartości pobieranej (numer
3). Instrukcja ta powoduje

skopiowanie do AC

wartości znalezionej w pamięci głównej pod
adresem 3.

Kod operacji 0011 oznacza w układzie
binarnym pozycję 3, reprezentującą instrukcję
Add. Pozostałe 12 bitów wskazuje adres w
pamięci głównej dla wartości pobieranej (numer
13 lub 00D w Hex). Instrukcja ta powoduje
dodanie do AC wartości znalezionej w
pamięci głównej pod adresem 13.

Kod operacji 0011

oznacza w układzie

binarnym pozycję 3, reprezentującą instrukcję
Add. Pozostałe 12 bitów wskazuje adres w
pamięci głównej dla wartości pobieranej (numer
13 lub 00D w Hex). Instrukcja ta powoduje

dodanie do AC wartości znalezionej w
pamięci głównej pod adresem 13.

Kod operacji 1000 oznacza w układzie
binarnym pozycję 8, reprezentującą instrukcję
Skipcond. Bity jedenasty i dziesiąty w adresie
wskazują binarnie 10 (dziesiętnie 2). Jeżeli AC
jest mniejsze od 0, to następuje pominięcie i
przejście do następnej instrukcji. Jeżeli AC jest
większe lub równe 0, to instrukcja ta powoduje
zwiększenie wartości PC o 1.

Kod operacji 1000

oznacza w układzie

binarnym pozycję 8, reprezentującą instrukcję
Skipcond. Bity jedenasty i dziesiąty w adresie
wskazują binarnie 10 (dziesiętnie 2). Jeżeli

jest mniejsze od 0, to następuje pominięcie

przejście do następnej instrukcji.

Jeżeli AC jest

większe lub równe 0,

to instrukcja ta powoduje

zwiększenie wartości PC o 1.

@Janusz Kosiński, 2005

Register Transfer Notation

Notacja symboliczna stosowana do opisywania zachowań w
mikrooperacjach jest nazywana register transfer notation (RTN) lub
register transfer language (RTL).

W notacji tej używamy zapisu M[X] do wskazania aktualnej danej,
magazynowanej na pozycji (pod adresem) X, oraz  do wskazania
transferu informacji.

W rzeczywistości, transfer z jednego rejestru do drugiego jest
dokonywany zawsze za pomocą magistrali (za jej pośrednictwem).

Register Transfer Notation

Notacja symboliczna stosowana do opisywania zachowań w
mikrooperacjach jest nazywana register transfer notation (RTN) lub
register transfer language (RTL).

W notacji tej używamy zapisu

M[X]

do wskazania aktualnej danej,

magazynowanej na pozycji (pod adresem) X, oraz



do wskazania

transferu informacji.

W rzeczywistości, transfer z jednego rejestru do drugiego jest
dokonywany zawsze za pomocą magistrali (za jej pośrednictwem).

Prosty
komputer

@Janusz Kosiński, 2005

Load X

Instrukcja ta pobiera zawartość pamięci z lokalizacji X d oAC – oczywiście
adres musi być najpierw umieszczony w MAR. Wtedy dana z położenia
M[MAR] jest przemieszczana do MBR a dopiero potem do AC.

MAR  X

MBR  M[MAR], AC  MBR

Ponieważ IR musi używać magistrali do kopiowania wartości X do MAR,
zanim dana z lokalizacji X będzie umieszczona w MBR – ta operacja
wymaga dwóch cykli magistrali. Stąd te dwie operacje są na oddzielonych
liniach – nie mogą się pojawić podczas tego samego cyklu.

Store X

Ta instrukcja przechowuje zawartość AC w pamięci na pozycji X:

MAR  X, MBR  AC

M[MAR]  MBR

Load X

MAR  X

MBR  M[MAR], AC  MBR

Store X

Ta instrukcja przechowuje zawartość AC w pamięci na pozycji X:

MAR  X, MBR  AC

M[MAR]  MBR

Prosty
komputer

@Janusz Kosiński, 2005

Add X

Wartość danej przechowywana pod adresem X jest dodawana do AC :

MAR X

MBR  M[MAR]

AC  AC + MBR

Subt X

Podobnie do Add, ta instrukcja odejmuje wartość przechowaną pod
adresem X z akumulatora i umieszcza wynik z powrotem w AC:

MAR  X

MBR  M[MAR]

AC  AC – MBR

Add X

Wartość danej przechowywana pod adresem X jest dodawana do AC :

MAR X

MBR  M[MAR]

AC  AC + MBR

Subt X

Podobnie do Add, ta instrukcja odejmuje wartość przechowaną pod
adresem X z akumulatora i umieszcza wynik z powrotem w AC:

MAR  X

MBR  M[MAR]

AC  AC – MBR

Prosty
komputer

@Janusz Kosiński, 2005

Input

Każde wejście z urządzenia wejściowego jest najpierw kierowane do
InREG. Potem dana jest transferowana do AC.



InREG

Output

Zawartość AC jest umieszczana w OutREG, skąd może być przesłana do
urządzenia wyjściowego:

OutREG  AC

Halt

Maszyna przerywa wykonywanie działania.

Input

Każde wejście z urządzenia wejściowego jest najpierw kierowane do
InREG. Potem dana jest transferowana do AC.



InREG

Output

Zawartość AC jest umieszczana w OutREG, skąd może być przesłana do
urządzenia wyjściowego:

OutREG  AC

Halt

Maszyna przerywa wykonywanie działania.

Prosty
komputer

@Janusz Kosiński, 2005

Skipcond

if IR[11-10] = 00 then {jeżeli bity 10 i 11 w IR są oba równe 0}

If AC < 0 then PC  PC+1

else If IR[11-10] = 01 then {jeżeli bit 11 = 0 i bit 10 = 1}

If AC = 0 then PC  PC + 1

else If IR[11-10] = 10 then {jeżeli bit 11 = 1 i bit 10 = 0}

If AC > 0 then PC  PC + 1

Jeżeli oba bity w pozycji dziesięć i jedenaście są równe jedności, to
powstają warunki sygnalizowania błędu.

Skipcond

IR[11-10] = 00 then

{jeżeli bity 10 i 11 w IR są oba równe 0}

AC < 0

then

PC  PC+1

else If

IR[11-10] = 01

then

{jeżeli bit 11 = 0 i bit 10 = 1}

AC = 0

then

PC  PC + 1

else If

IR[11-10] = 10

then

{jeżeli bit 11 = 1 i bit 10 = 0}

AC > 0

then

PC  PC + 1

Jeżeli oba bity w pozycji dziesięć i jedenaście są równe jedności, to
powstają warunki sygnalizowania błędu.

Prosty
komputer

@Janusz Kosiński, 2005

Jump X

Ta instrukcja jest powodem bezwarunkowego przejścia pod dany adres, X.
do wykonania tej instrukcji, X musi być pobrane do PC.

PC  X

W rzeczywistości, niski lub mało znaczący 12 bit w rejestrze instrukcji (or
IR[11-0]) odpowiada wartości X, tak że transfer jest najczęściej
realizowany:

PC  IR[11-0]

Wprawdzie notacja PC  X jest łatwiejsza do zrozumienia.

Jump X

Ta instrukcja jest powodem bezwarunkowego przejścia pod dany adres, X.
do wykonania tej instrukcji, X musi być pobrane do PC.

PC  X

W rzeczywistości, niski lub mało znaczący 12 bit w rejestrze instrukcji (or
IR[11-0]) odpowiada wartości X, tak że transfer jest najczęściej
realizowany:

PC  IR[11-0]

Wprawdzie notacja

PC  X

jest łatwiejsza do zrozumienia.

Prosty
komputer

@Janusz Kosiński, 2005

Wykonywanie instrukcji

Wszystkie komputery działają według schematu:

pobierz, dekoduj i wykonaj

– czyli w cyklu

Fetch-Decode-Execute

CPU pobiera instrukcje, dekoduje je i wykonuje. Znacząca część czasu jest
zużywana do wielokrotnego (wprawdzie w różnych miejscach) kopiowania
danych.

Kiedy program jest początkowo pobierany, adres pierwszej instrukcji musi
być umieszczony w PC.

Kroki tego cyklu, są pokazane na schemacie –

kroki 1 i 2 tworzą fazę pobierania,

krok 3 – odpowiada za dekodowanie,

zaś krok 4 za wykonanie.

Prosty
komputer

@Janusz Kosiński, 2005

Prosty
komputer

Kopiuj PC do MAR

Kopiuj zawartość

pamięci pod adresem

MAR do IR, zwiększ PC

o 1

Zdekoduj instrukcję

i umieść bity IR[11-

0] w MAR

Instrukcja wymaga

operandu?

Kopiuj zawartość

pamięci o adresie

MAR do MBR

Wykonaj
instrukcję

START

Yes

MAR  PC
IR  M[MAR]
PC  PC+1
MAR  IR[11–

IR[15–12]

MBR  M[MAR]

MAR  PC
IR  M[MAR]
PC  PC+1
MAR  IR[11–

IR[15–12]

MBR  M[MAR]

@Janusz Kosiński, 2005

Program dodający dwie liczby

Adres Hex

Instrukcja

Binarna

zawartość

Adresu Pamięci

Hex

zawartość

Adresu

Pamięci

100
101
102
103
104
105
106

Load

104

Add

105

Store

106

Halt

0023
FFE9
0000

0001000100000100
0011000100000101
0010000100000110
0111000000000000
0000000000100011
1111111111101001
0000000000000000

1104
3105
2106
7000
0023

FFE9

0000

Prosty
komputer

Ten program wprowadza wartość 0023

(dziesiętnie: 35) do AC.

Dodaje potem wartość FFE9

(dziesiętnie: -23), znalezioną pod adresem 105.

Wynikiem jest wartość 12 w AC.

Instrukcja Store magazynuje tę wartość po adresem 106. Kiedy program jest
zakończony, binarna zawartość adresu 106 zmienia się na 0000000000001100, w
układzie hex: 000C, lub w dziesiętnym: 12

Ten program wprowadza wartość 0023

(

dziesiętnie

: 35) do AC.

Dodaje potem wartość FFE9

(

dziesiętnie

: -23), znalezioną pod adresem 105.

Wynikiem jest wartość 12 w AC.

@Janusz Kosiński, 2005

Prosty
komputer

Krok

RTN

MAR

MBR

LOAD 104

(wartości
początkowe)

100

……

FETCH

MAR  PC

100

……

100

……

IR  M[MAR]

100

1104

100

……

PC  PC + 1

101

1104

100

……

DECODE

MAR  IR[11-0]

101

1104

104

……

(DECODE IR[15-
12]

101

1104

104

……

GET OPERAND

MBR  M[MAR]

101

1104

104

0023

……

EXECUTE

AC  MBR

101

1104

104

0023

ADD 105

(wartości początkowe)

101

1104

104

0023

FETCH

MAR  PC

101

1104

101

0023

IR  M[MAR]

101

3105

101

0023

PC  PC + 1

102

3105

101

0023

DECODE

MAR  IR[11-0]

102

3105

105

0023

(DECODE IR[15-
12]

102

3105

105

0023

GET OPERAND

MBR  M[MAR]

102

3105

105

FFE9

0023

EXECUTE

AC  AC + MBR

102

3105

105

FFE9

000C

STORE 106

(wartości początkowe)

102

3105

105

FFE9

000C

FETCH

MAR  PC

102

3105

102

FFE9

000C

IR  M[MAR]

102

2106

102

FFE9

000C

PC  PC + 1

103

2106

102

FFE9

000C

DECODE

MAR  IR[11-0]

103

2106

106

FFE9

000C

(DECODE IR[15-
12]

103

2106

106

FFE9

000C

GET OPERAND

niekonieczne

103

2106

106

FFE9

000C

EXECUTE

MBR  AC

103

2106

106

000C

EXECUTE

M[MAR]  MBR

103

2106

106

000C

@Janusz Kosiński, 2005

Rozwiązania

Każdy członek rodziny x86 w architekturze Intela, jest znany jako
CISC (

Complex Instruction Set Computer

), podczas gdy rodzina

Pentium i architektury MIPS są przykładami RISC (

Reduced

Instruction Set Computer

CISC

posiada dużą liczbę instrukcji zmiennej długości o złożonych

formatach. Duża liczba tych instrukcji jest bardzo skomplikowana -
wykonują liczne operacje podczas wykonywania pojedynczej instrukcji
(np., jest możliwe wykonywanie pętli stosując pojedynczą instrukcję
asemblera). Podstawowym problemem maszyn CISC jest to, że mały
podzbiór złożonych instrukcji spowalnia system.

architekturze RISC

, liczba instrukcji jest zredukowana, aczkolwiek

główną przyczyną jej powstania było uproszczenie instrukcji, w celu
uzyskania szybszego ich wykonywania. Każda instrukcja wykonuje
tylko jedną operację, wszystkie są tej samej długości i tylko w
kilku różnych formatach a wszystkie operacje arytmetyczne muszą
być wykonane między rejestrami (dane w pamięci nie mogą być
operandami).

@Janusz Kosiński, 2005

Pierwszy popularny chip Intel’a – 8086, został wprowadzony w 1979 .
Obsługiwał 16 bitowe dane i pracował z 20 bitowymi adresami – to
pozwalało na zaadresowanie miliona bajtów pamięci. CPU byłą podzielona
na dwie części: wykonawczą (rejestry ogólne i ALU) oraz BUS
(kolejkowanie instrukcji, rejestry segmentów i wskaźnik instrukcji).

8086 miał cztery 16 bitowe rejestry ogólnego zastosowania, nazwane
AX (podstawowy akumulator), BX (rejestr bazowy używany do
rozszerzania adresów), CX (rejestr licznika) i DX (rejestr danych). Każdy z
tych rejestrów był podzielony na dwie części: bardziej znaczące
(oznakowane AH, BH, CH i DH), oraz mniej znaczące (oznakowane AL,
BL, CL, i DL).

Rozwiązania

@Janusz Kosiński, 2005

Asembler w 8086 był podzielony na różne segmenty – bloki obsługujące
specyficzne rodzaje informacji. Był tam segment kodu (CS) –
podtrzymujący program, segment danych (DS) – podtrzymujący dane
programu i segment stosu (SS) – podtrzymujący stos programu. Stąd
pojawiały się odpowiednie rejestry. Był również czwarty segment (ES)
używany prze niektóre operacje stringowe do adresowania pamięci.

Adresowanie było specyficzne: segment/ofset w postaci: xxx:yyy
(wartość segmentu i wartość offsetu).

Rozwiązania

@Janusz Kosiński, 2005

Konwencja nazewnicza zastosowana w 80386, przy przejściu z
16 do 32 bitów, polegała na zastosowaniu przedrostka E
(extended).

Zamiast AX, BX, CX, i DX, rejestry stały się EAX, EBX, ECX, i
EDX.

EA
X

8
bitów

16
bitów

32 bity

Rozwiązania

@Janusz Kosiński, 2005

Rodzina MIPS dla CPU - MIPS R3000, R4000, R5000, R8000, i R10000
są to znaki handlowe należące do MIPS Technologies, Inc.

Chipy MIPS są stosowane w systemach rozszerzonych (dodawanych
do komputerów ) takich jak Silicon Graphics machines i różnych
komputeryzowanych zabawkach (

Nintendo

Sony

używają MIPS CPU).

Cisco, znany producent routerów internetowych stosuje również MIPS
CPU.

MIPS

jest architekturą

pobierz/zmagazynuj

, co oznacza że

wszystkie instrukcje (inne niż LOAD czy STORE) muszą używać
rejestrów jako operandów.

Rozwiązania

Document Outline

ARCHITEKTURA KOMPUTERÓW
Slide 2
Slide 3
Slide 4
Slide 5
Slide 6
Slide 7
Wprowadzenie do architektury komputerów
Slide 9
Slide 10
Slide 11
Slide 12
Slide 13
Slide 14
Slide 15
Slide 16
Slide 17
Slide 18
Slide 19
Slide 20
Slide 21
Slide 22
Slide 23
Slide 24
Slide 25
Slide 26
Slide 27
Slide 28
Slide 29
Slide 30
Slide 31
Slide 32
Slide 33
Slide 34
Slide 35
Slide 36
Slide 37
Slide 38
Slide 39
Slide 40
Slide 41
Slide 42
Slide 43
Slide 44
Slide 45
Slide 46
Slide 47
Slide 48
Slide 49
Slide 50
Slide 51
Slide 52
Slide 53
Slide 54
Slide 55
Slide 56
Slide 57
Slide 58
Slide 59
Slide 60
Slide 61
Slide 62
Reprezentacja danych w systemach komputerowych
Slide 64
Slide 65
Slide 66
Slide 67
Slide 68
Slide 69
Slide 70
Slide 71
Slide 72
Slide 73
Slide 74
Slide 75
Slide 76
Slide 77
Slide 78
Slide 79
Slide 80
Slide 81
Slide 82
Slide 83
Slide 84
Slide 85
Slide 86
Slide 87
Slide 88
Slide 89
Slide 90
Slide 91
Slide 92
Slide 93
Slide 94
Slide 95
Slide 96
Slide 97
Slide 98
Slide 99
Slide 100
Slide 101
Slide 102
Slide 103
Slide 104
Slide 105
Slide 106
Slide 107
Slide 108
Slide 109
Slide 110
Algebra Boole’a i logika cyfrowa
Slide 112
Slide 113
Slide 114
Slide 115
Slide 116
Slide 117
Slide 118
Slide 119
Slide 120
Slide 121
Slide 122
Slide 123
Slide 124
Slide 125
Slide 126
Slide 127
Slide 128
Slide 129
Slide 130
Slide 131
Slide 132
Slide 133
Slide 134
Slide 135
Slide 136
Slide 137
Slide 138
Slide 139
Slide 140
Slide 141
Slide 142
Slide 143
Slide 144
Slide 145
Slide 146
Slide 147
Slide 148
Slide 149
Slide 150
Slide 151
Slide 152
Slide 153
Slide 154
Wprowadzenie do prostego komputera
Slide 156
Slide 157
Slide 158
Slide 159
Slide 160
Slide 161
Slide 162
Slide 163
Slide 164
Slide 165
Slide 166
Slide 167
Slide 168
Slide 169
Slide 170
Slide 171
Slide 172
Slide 173
Slide 174
Slide 175
Slide 176
Slide 177
Slide 178
Slide 179
Slide 180
Slide 181
Slide 182
Slide 183
Slide 184
Slide 185
Slide 186
Slide 187
Slide 188
Slide 189
Slide 190
Slide 191
Slide 192
Slide 193
Slide 194
Slide 195
Slide 196
Slide 197
Slide 198
Slide 199
Slide 200
Slide 201
Slide 202

Wyszukiwarka

Podobne podstrony:
archi wykl 09
archi wykl 13
archi wykl 14
archi wykl 12
archi wykl 07
archi wykl 11
archi wykl 06
wfm5 archi
KRAŚNIK GALERIA RAJ ARCHI BUD OPIS A
debussy La fille aux cheveux de lin archi
archi wykl 08
archi wykl 05
archi wykl1
archi wykl 10
archi wykl 15
Do mówienia Archi
archi wykl 09

więcej podobnych podstron