Rozdział 6

Metoda wskaźników

pojemności

informacyjnej

Sld. 6.2. Metoda wskaźników

pojemności

Idea metody wskaźników pojemności

informacyjnej sprowadza się do wyboru takich
zmiennych objaśniających, które są silnie
skorelowane ze zmienną objaśnianą, a jednocześnie
słabo skorelowane między sobą. Punktem wyjścia tej
metody jest wektor R

0

i macierz R.

Rozpatruje się wszystkie kombinacje

potencjalnych zmiennych objaśniających, których
ogólna liczba wynosi:

L = 2

m

-1.

Dla każdej kombinacji potencjalnych

zmiennych objaśniających oblicza się wskaźniki
pojemności informacyjnej:

indywidualne;

•integralne

.

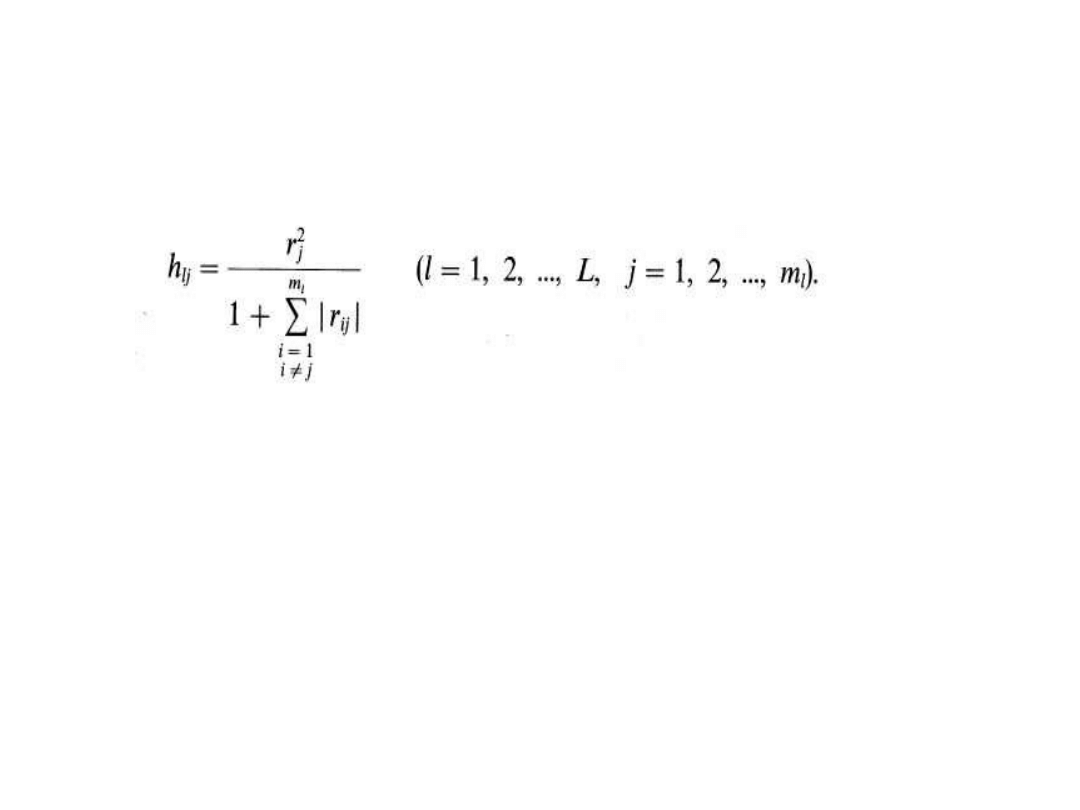
Sld. 6.3. Indywidualne wskaźniki pojemności

l - numer kombinacji (l = 1, 2, ..., L ),

j - numer zmiennej w kombinacji,

m

l

- liczba zmiennych w rozpatrywanej kombinacji.

Indywidualne wskaźniki pojemności informacyjnej :

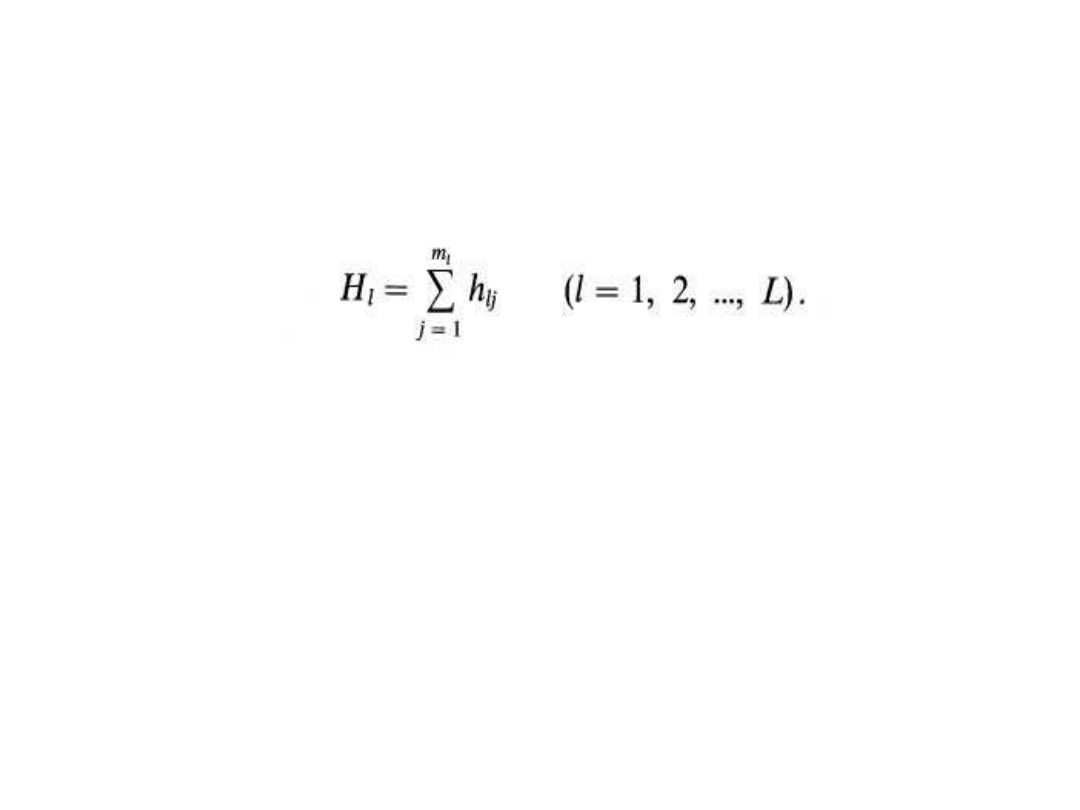
Sld. 6.4. Integralne wskaźniki pojemności

Indywidualne oraz integralne wskaźniki pojemności
informacyjnej są unormowane w przedziale [0; 1]. Przyjmują
one tym większe wartości, im zmienne objaśniające są silniej
skorelowane ze zmienną objaśnianą oraz im słabiej są
skorelowane między sobą.

Jako zmienne objaśniające wybiera się taką kombinację
zmiennych, której

odpowiada maksymalna wartość wskaźnika integralnej
pojemności informacyjnej.

Integralne wskaźniki pojemności :

Sld. 6.5. Przykład

 

Należy wybrać zmienne objaśniające do modelu liniowego wyjaśniającego
kształtowanie się produkcji żywca przypadającej na 1 ha użytków rolnych
Y w pewnym gospodarstwie rolnym. Zestaw potencjalnych zmiennych
objaśniających jest następujący:

X

1

- plony kukurydzy przeznaczonej na paszę,

X

2

-

_

udział wartości produkcji roślinnej w wartości produkcji globalnej,

X

3

- średnie ceny skupu żywca,

X

4

- zużycie pasz treściwych.

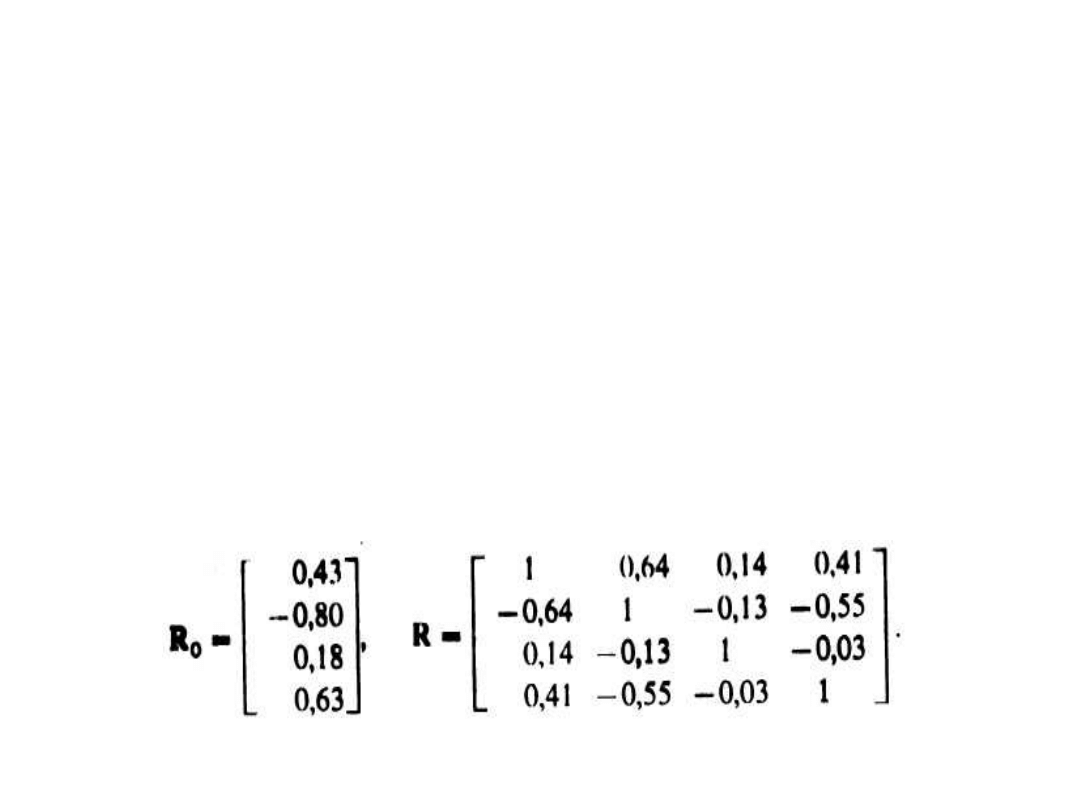
Na podstawie danych statystycznych pochodzących z lat 1986-2000
zbudowano wektor współczynników korelacji między zmienną Y
zmiennymi X

1

, X

2

, X

3

i X

4

, i macierz współczynników korelacji między

zmiennymi X

1

X

2

, X

3

i X

4

Sld. 6.6. Przykład

Należy rozpatrzyć L = 2

4

- 1 = 15 kombinacji zmiennych:

C

1

= (X

l

), C

5

= (X

1

, X

2

) C

11

= (X

1

, X

2

, X

3

),

C

2

= (X

2

), C

6

= (X

1,

X

3

), C

l2

= (X

1

, X

2

, X

4

),

C

3

= (X

3

), C

7

= (X

1

, X

4

), C

13

= (X

1

, X

3

, X

4

),

C

4

= (X

4

), C

8

= (X

2

, X

3

), C

14

= (X

2

, X

3

, X

4

)

C

9

= (X

2

, X

4

)

C

15

= (X

1

,

X

2

, X

3

, X

4

).

C

l0

= (X

3

, X

4

),

Integralne wskaźniki pojemności informacyjnej kombinacji
jednoelementowych są identyczne ze wskaźnikami indywidualnej
pojemności, a te z kolei są równe kwadratom współczynników korelacji
między zmienną objaśnianą i potencjalnymi zmiennymi objaśniającymi:

H

1

= h

11

=r

2

1

= (0,43)

2

= 0,185, H

2

= h

22

= r

2

2

= (-0,80)

2

= 0,640,

H

3

= h

33

= r

2

3

= (0,18)

2

= 0,032, H

4

= h

44

= r

2

4

= (0,63)

2

= 0,370.

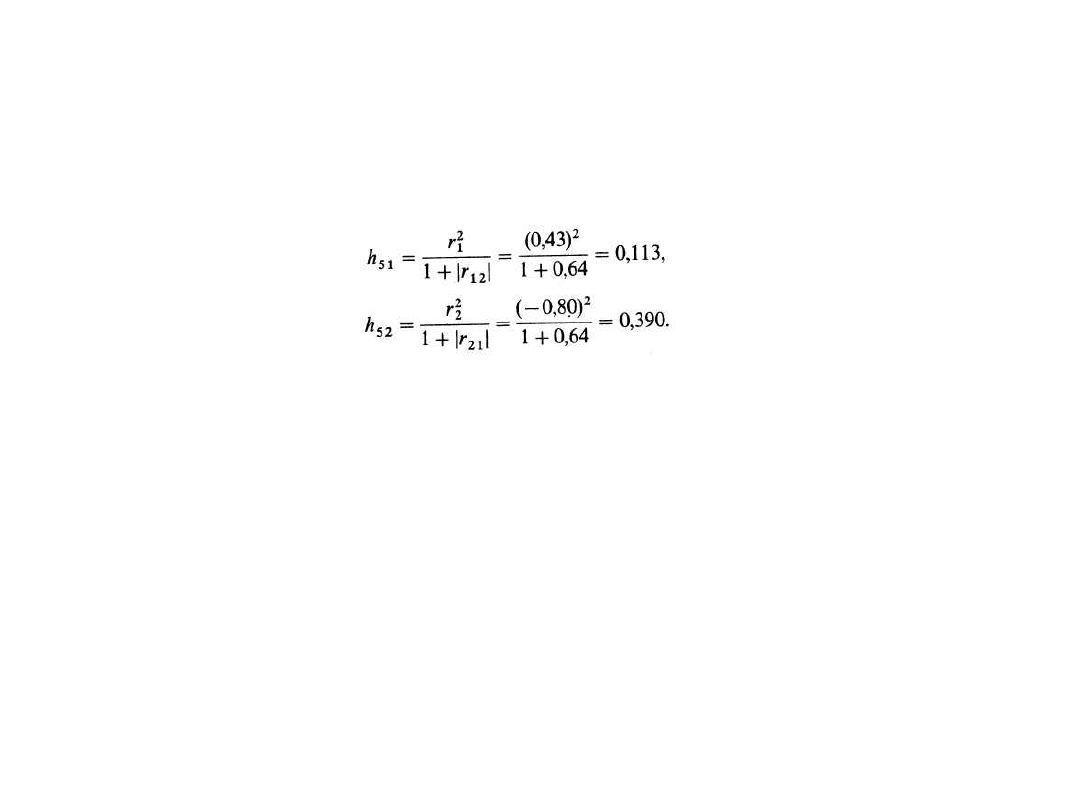
Dla kombinacji dwuelementowej C

5

= (X

1

, X

2

) mamy dwa wskaźniki

indywidualnej pojemności informacyjnej: h

51

dotyczący zmiennej X

1

oraz h

52

dotyczący zmiennej X

2

:

Sld. 6.7. Przykład

Integralny wskaźnik pojemności informacyjnej tej kombinacji
wyniesie:

H

5

= h

51

+ h

52

= 0,113 + 0,390 = 0,503.

Wykonując podobne obliczenia dla pozostałych kombinacji
dwuelementowych
otrzymujemy:

h

61

=0,162, h

63

=0,028, H

6

=0,190,

h

71

=0,131, h

74

. =0,281,H

7

=0,412,

h

82

=0,566, h

83

=0,029, H

8

=0,595,

h

92

=0,413, h

94

=0,255,

H

9

=0,668,

h

10,3

= 0,031, h

10,4

=0,385,H

10

= 0,416.

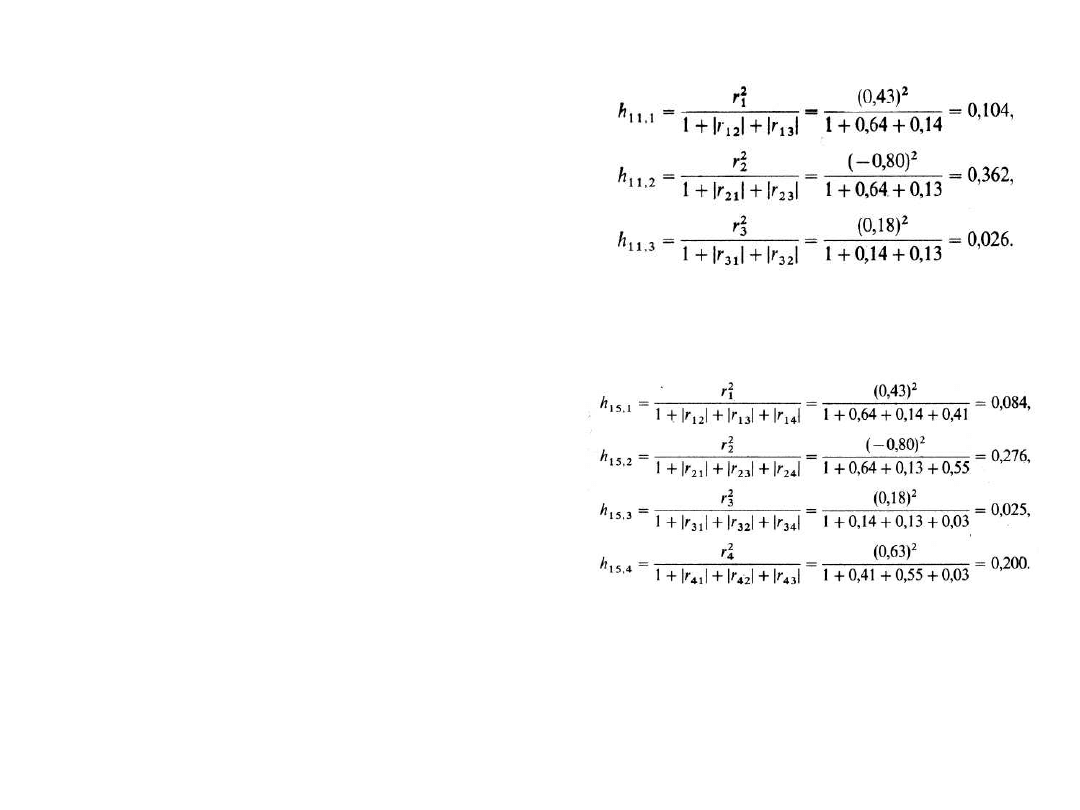
Sld. 6.8. Przykład

Kombinację trójelementową C

11

= (X

1

,, X

2

, X

3

)

Integralny wskaźnik pojemności
informacyjnej tej kombinacji :

H

11

= h

11.1

+ h

11.2

+ h

11.3

= 0,492.

Pozostały kombinacji trójelementowy:

h

12.1

= 0,090, h

12.2

= 0,292, h

12.4

= 0,202, H

12

=

0,584,
h

13.1

=0,119, h

13.3

= 0,028, h

13.4

= 0,276, H

13

=

0,423,
h

14.2

=0,381, h

14.3

= 0,028, h

14.4

= 0,251, H

14

=

0,660.

Wskaźniki indywidualnej pojemności
informacyjnej zmiennych X

1

, X

2

, X

3

i

X

4

(kombinacja C

15

):

Integralny wskaźnik pojemności

informacyjnej

H

15

=h

15.1

+h

15.2

+ h

15.3

+ h

15.4

=

0,585.

Maksymalna wartość wskaźnika integralnej pojemności informacyjnej, wynosi
0,668 i dotyczy kombinacji C

9

, która zawiera zmienne X

2

i X

4

. Oznacza to, że w

modelu liniowym opisującym poziom produkcji żywca przypadającej na 1 ha
użytków rolnych zmiennymi objaśniającymi powinny być X

2

i X

4

.

Model ma postać:

Y = a

0

+ a

1

X

2

+ a

2

X

4

+ ε.

LITERATURA

1.E.Nowak. Zarys metod ekonometrii.

Warszawa 2002