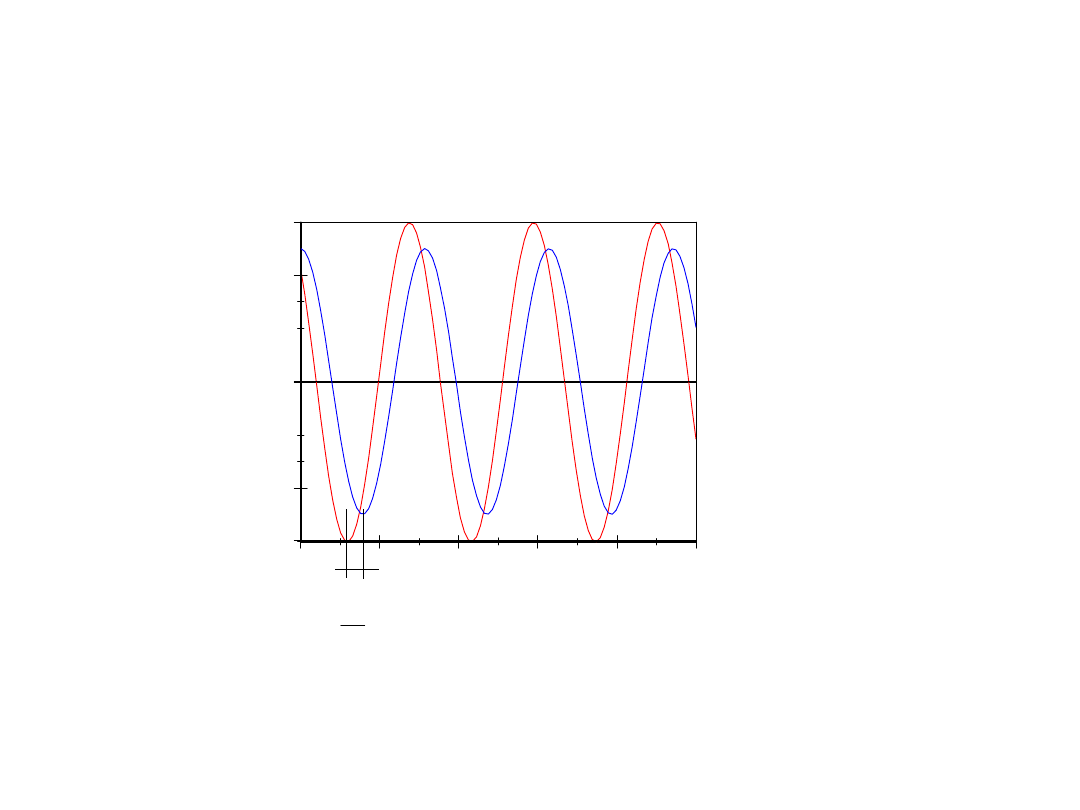
Drgania harmoniczne
– wielkość drgająca zmienia się
sinusoidalnie lub cosinusoidalnie w czasie
Drgania – zjawiska powtarzające się okresowo
Ruch drgający
Przykłady drgań:
• wahadło zegara
• drgania mostu, wywołane przejeżdżającymi pojazdami
• drgania skrzydeł samolotu
• drgania atomów (molekuł) w węzłach sieci krystalicznej
• obwód drgający LC
• .........
Okres
ruchu harmonicznego (T) – czas trwania jednego
pełnego drgania, czas powtarzania się każdego pełnego
przemieszczenia lub cyklu
Częstotliwość
drgań () – liczba drgań (cykli) w jednostce czasu
]
Hz
[
1
T
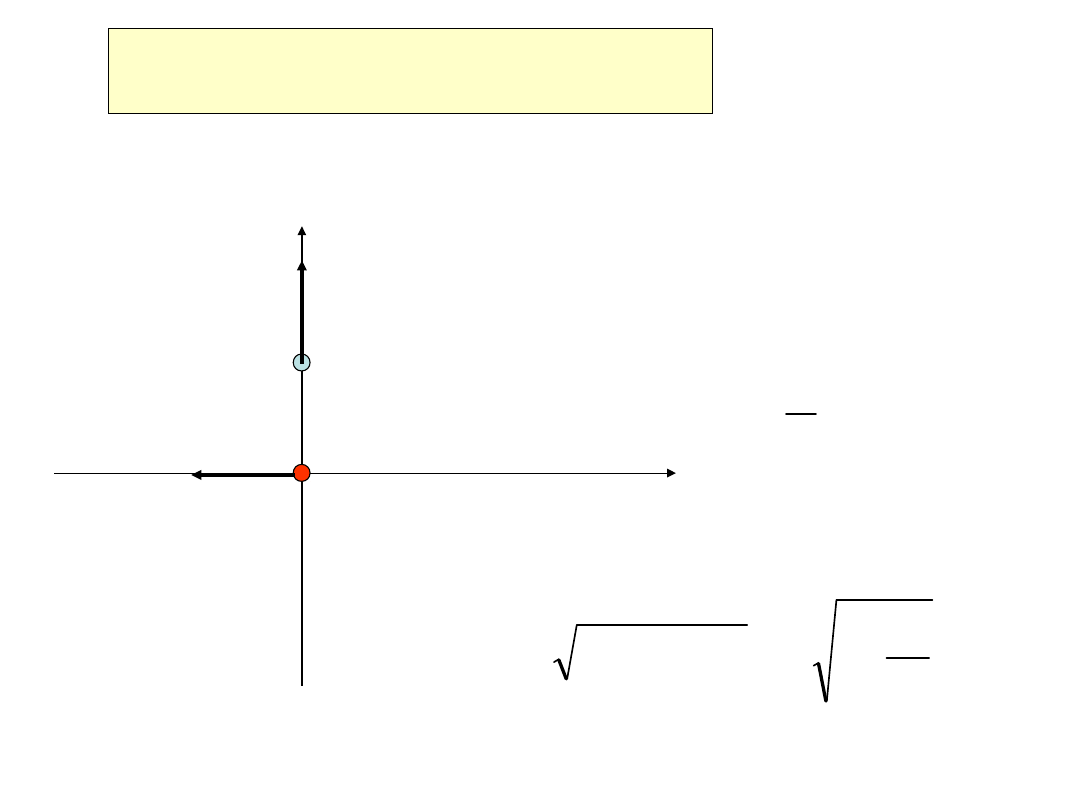
Położenie równowagi
– położenie, w którym na punkt
materialny nie
działa żadna siła
Przemieszczenie
– odległość drgającego punktu od
położenia równowagi w dowolnej chwili
2
2
T
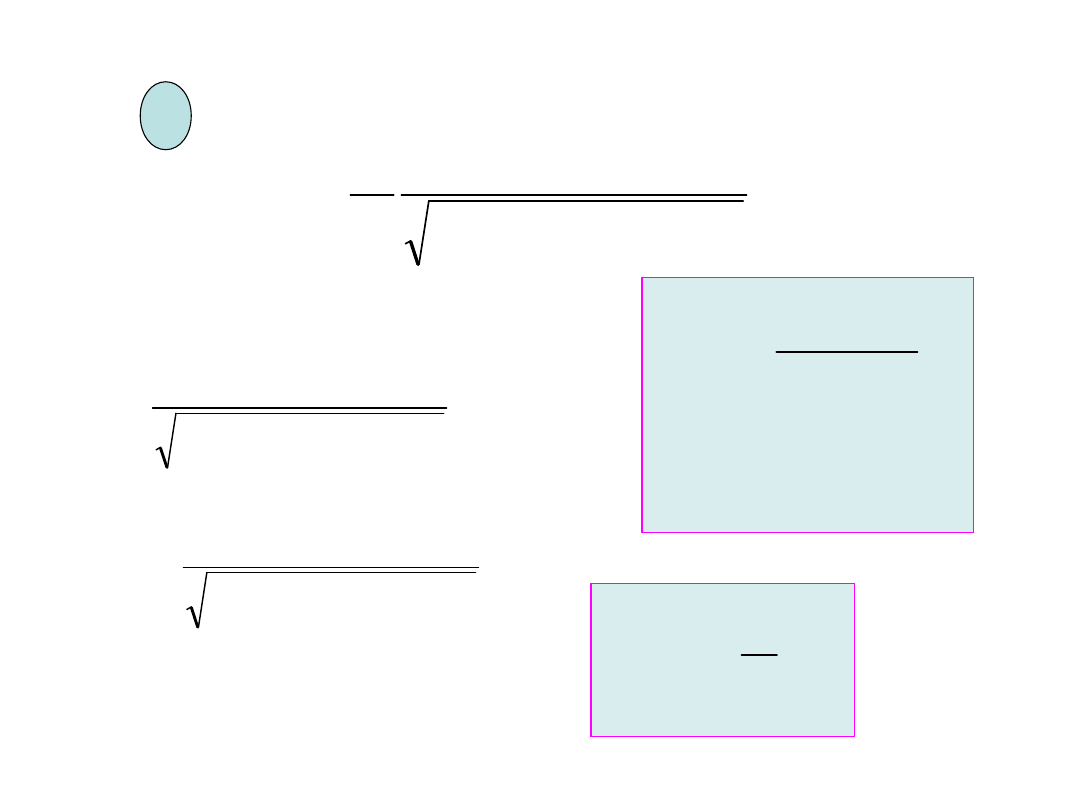
Wielkości opisujące ruch harmoniczny

0
+A
-A
kx
F
2
2
dt
x
d
m
dt
dv
m
F
kx
dt
x
d
m
2
2
0
2
2
x
m
k
dt
x
d
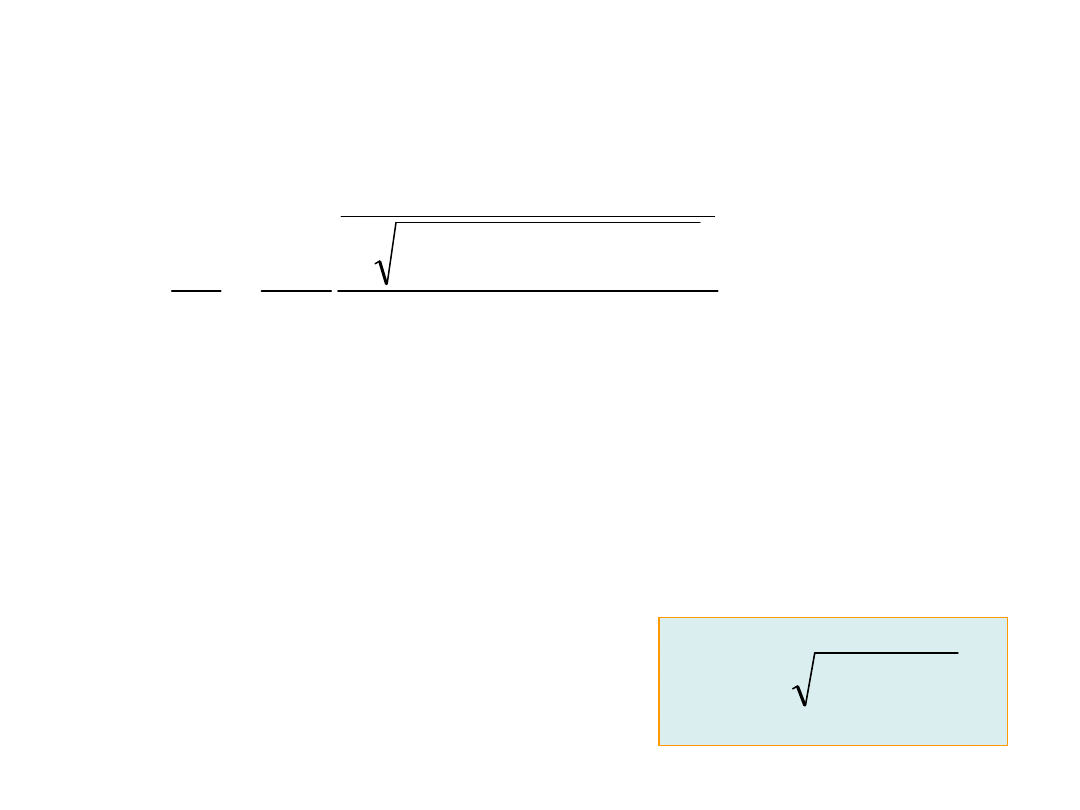
Na oscylator działa siła harmoniczna
Z II zasady dynamiki Newtona
Jest to równanie różniczkowe drgań harmonicznych
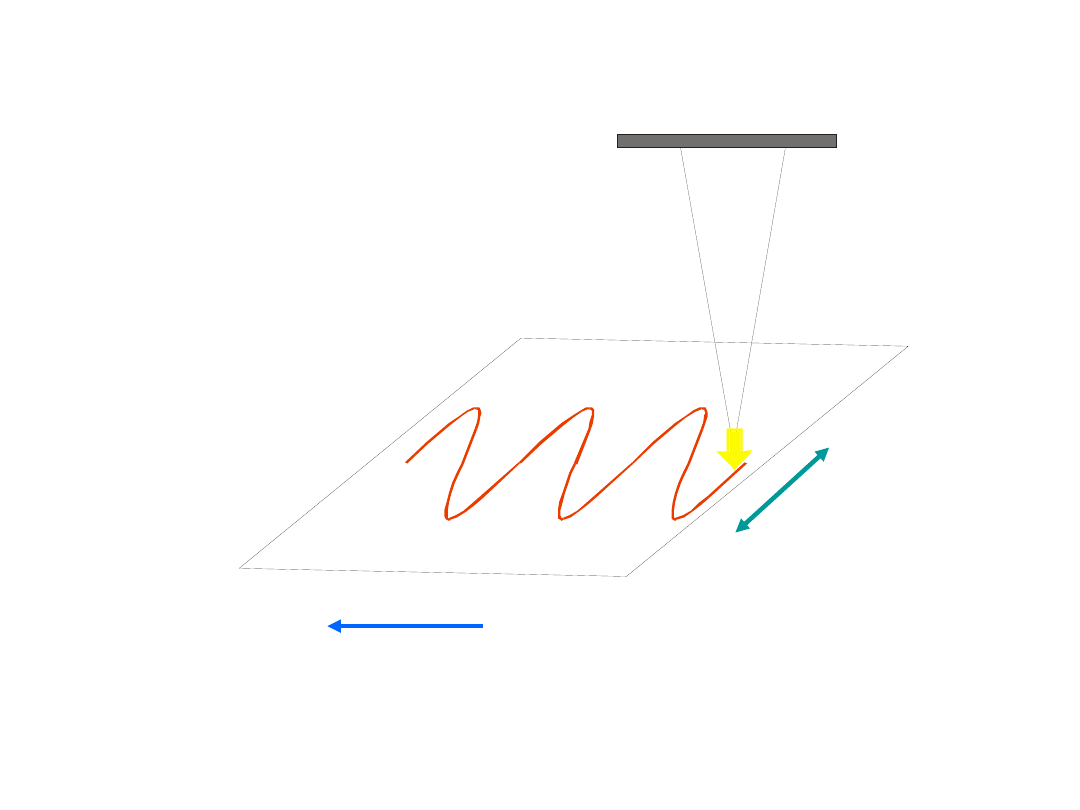
Wahadło wykonuje ruch
harmoniczny. Papier rejestratora
przesuwa się ze stałą prędkością v
– pozostawiony ślad –
wychylenie
wahadła z położenia równowagi
-
można opisać funkcją okresową
v
x(t)
3
2
1
cos
2
cos
2
2
0
cos
0
cos
0
0
0
A
A
A
x
A
x
cos
0
0
A
x
x
t
Jeśli, np.
t
A
x
o
cos
0
+A
-A
x
0
t
A
a
dt
x
d
t
A
v
dt
dx
o
a
o
v
cos
sin
max
max
2
0
2
2
0
t
A
x
o
cos
0
2
2
x
m
k
dt
x
d
0
cos
cos
2
0
t
A
m
k
t
A
o
o
m
k
m
k
0
2
0
0
Przemieszczenie, prędkość i
przyspieszenie zmieniają się w ruchu
harmonicznym okresowo.
częstość
drgań
własnych
częstość drgań
własnych zależy od
współczynnika
sprężystości i masy
ciała
Energia kinetyczna drgań
t
A
m
mv
E
k
0
2
2
0
2
2
sin
2
2
Energia potencjalna drgań
t
A
m
x
m
kx
E
p
0
2
2
2
0
2
2
0
2
cos
2
1
2
1
2
1
Energia całkowita
2
2
0
0
2
2
2
0
0
2
2
2
0
2
1
cos
2
1
sin
2
1
A
m
t
A
m
t
A
m
E
E
E
E
p
k
max
2
2
2
2
2
0
;
0
2
1
2
1
2
1
v
v
x
v
A
x
x
A
m
k
v
kA
kx
mv
E
E
p
k
zależność prędkości
punktu drgającego od
wychylenia
Punkt drgający przechodzi przez położenie równowagi z
maksymalna prędkością. W punktach zwrotnych prędkość = 0.
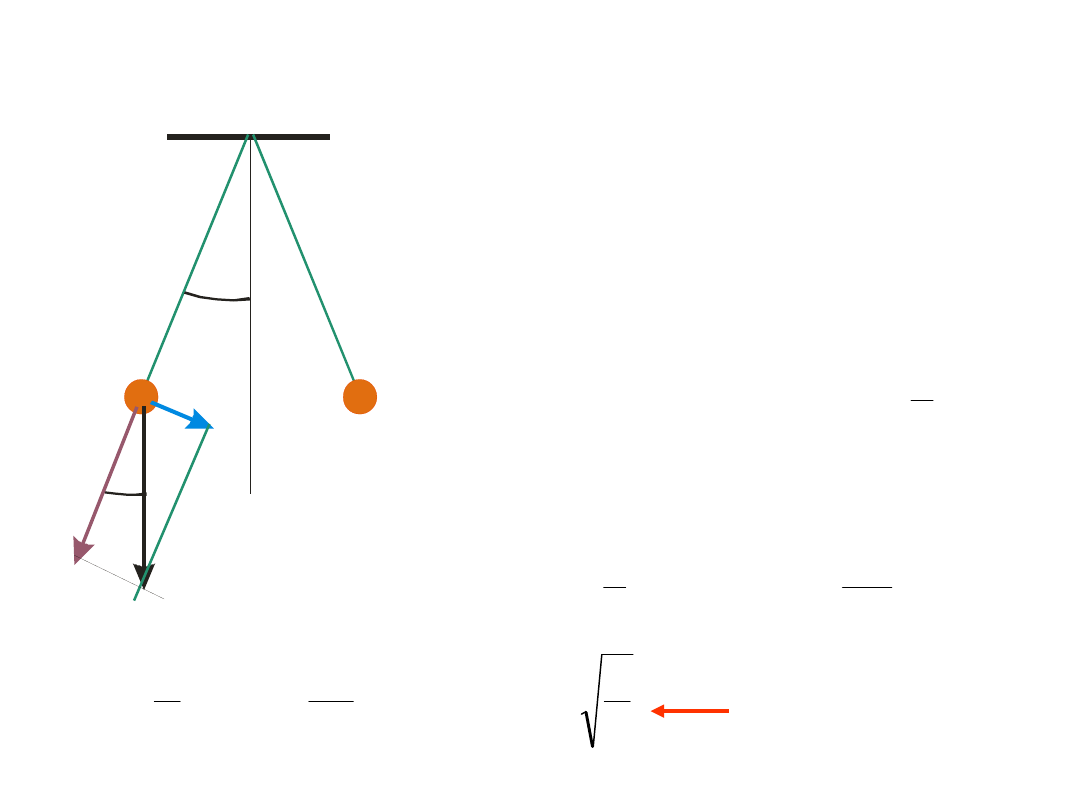
Wahadło wychylone z położenia
równowagi porusza się dzięki
składowej siły ciężkości
dla małych kątów
Z równości tych sił
Wahadło matematyczne
sin
mg
F
kx
F
l
x
mg
mg
F
2
0
m
l
mg
k
kx
l
x
mg
g
l
T
T
l
g
2
2
2
2
0
mg
N
F
okres drgań
wahadła
matematycznego

kąt
[stopnie]
kąt
[radian
y]
sinus
0
0
0
2
0.0349
0.0349
5
0.0873
0.0872
10
0.1745
0.1736
15
0.2618
0.2588
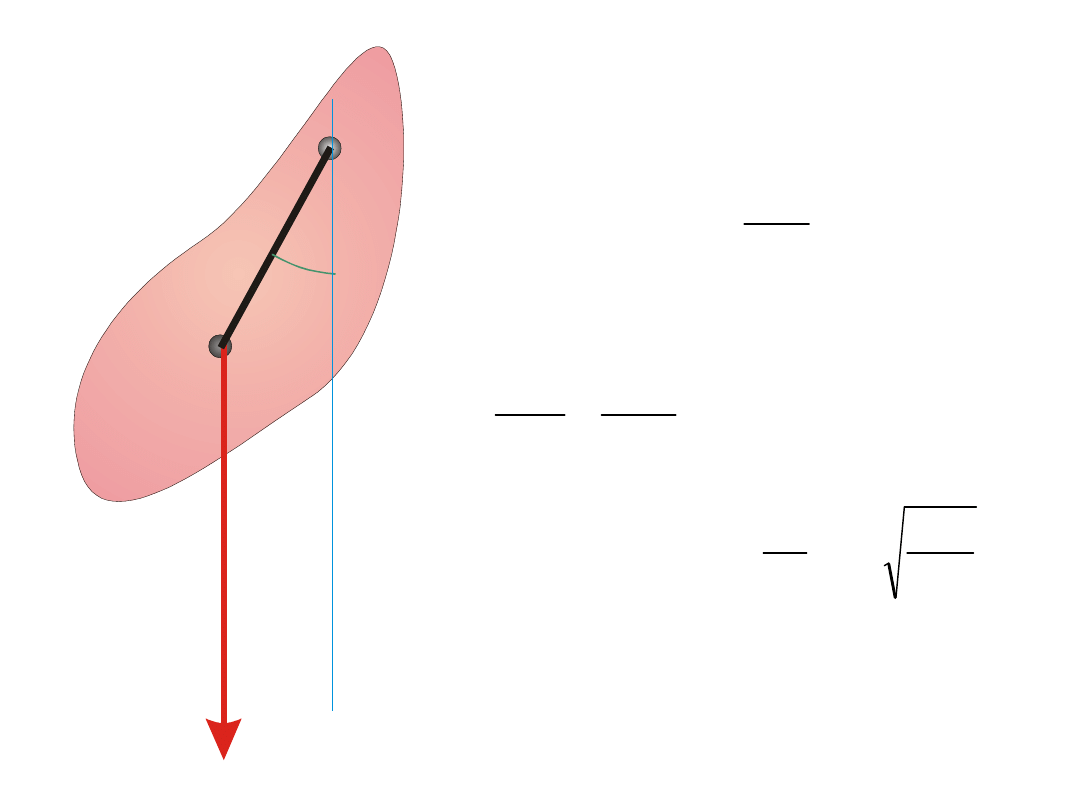
Wahadło fizyczne
mg
d
O
Moment siły
sin
mgd
M
2
2
dt
d
I
I
M
0
2
2
2
o
I
mgd
dt
d
Dla małych kątów
sin
mgd
I
T
o
2
2
D
mgd
D – moment kierujący wahadła

Składanie drgań równoległych
metodą diagramów wektorowych
Wektor obraca się z prędkością kątową - jego rzut na oś x
zmienia się w czasie zgodnie z zależnością
Rzut końca wektora
na oś x wykonuje drgania harmoniczne z
częstością i amplitudą a . Drganie harmoniczne możemy
przedstawić w postaci wektora o długości równej amplitudzie
drgań a kierunek wektora tworzy z osią x kąt równy fazie
początkowej drgań.
t
a
x
o
cos
o
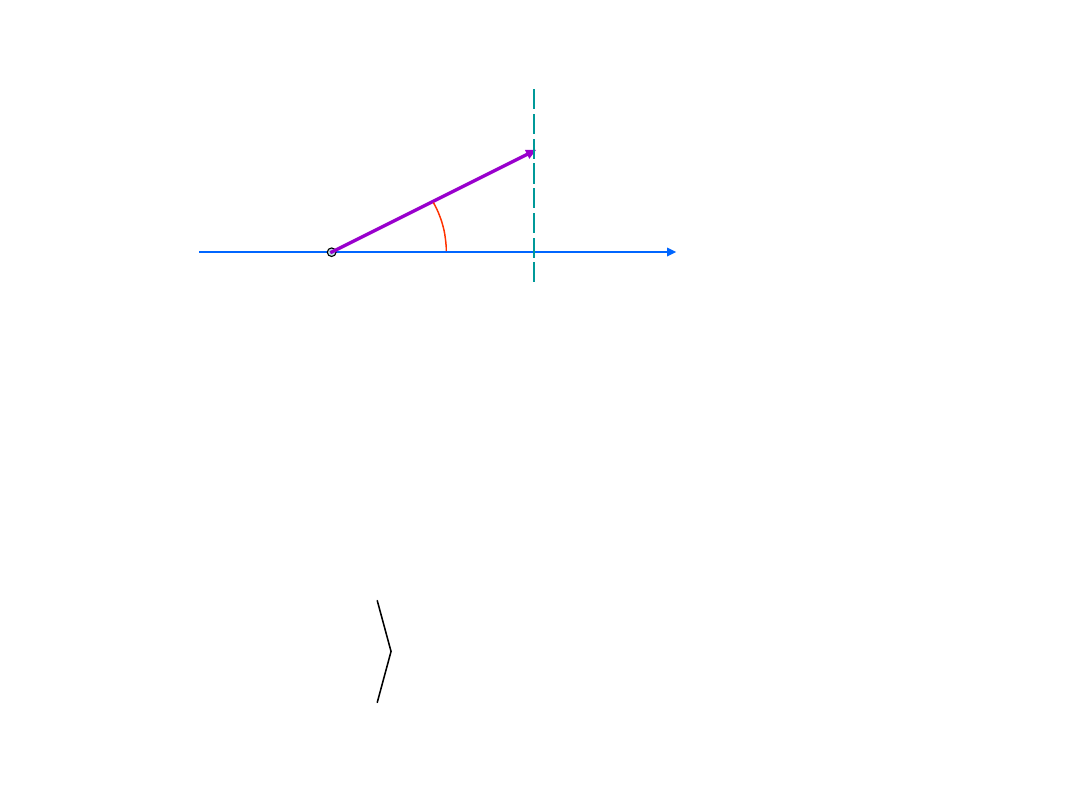
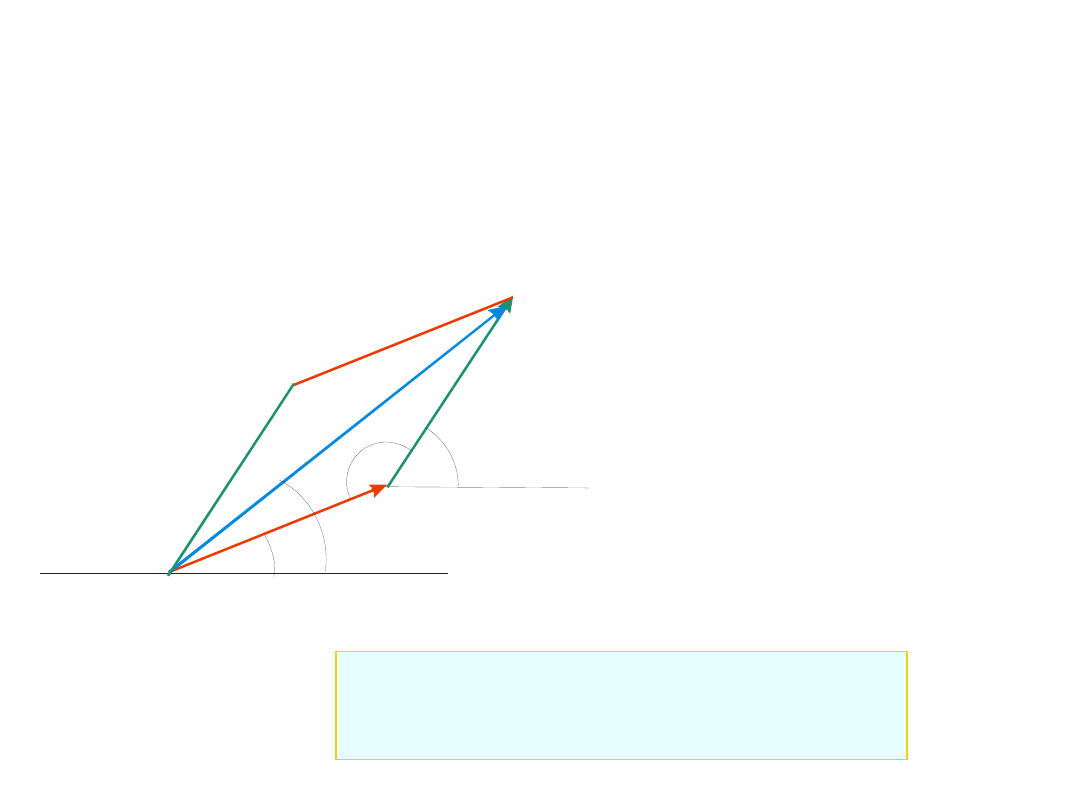
Zgodnie z
zasadą superpozycji
, drganie wypadkowe jest
sumą wektorową drgań składowych. Ponieważ częstość
drgań składowych jest jednakowa, obydwa wektory
amplitud będą obracać się z tą samą prędkością kątową.
Kąt pomiędzy wektorami pozostaje stały w czasie.
2
0
2
1
0
1
2
0
2
2
1
0
1
1
cos
cos
cos
cos
t
a
t
a
x
t
a
x
t
a
x
0
x
a
cos
2
2
1
2
2
2
1
2
a
a
a
a
a
1
2
2
1
180
180
1
2
2
1
2
2
2
1
2
cos
2
a
a
a
a
a
cos
)
180
cos(
1
1
a
2
a
2
a
Twierdzenie cosinusów
2
2
1
1
sin
sin
a
a
sin
cos
cos
sin
sin
1
1
2
2
2
1
sin
cos
cos
sin
sin
cos
cos
sin
a
a
1
1
2
2
2
1
sin
cos
tan
cos
tan
sin
a
a
2
1
1
2
1
2
2
1
cos
cos
sin
sin
tan
a
a
a
a
t
a
x
cos
Twierdzenie sinusów
Składanie drgań prostopadłych
x
y
x
v
y
v
t
a
x
cos
t
b
y
cos
t
a
x
cos
2
2
2
1
cos
1
sin
a
x
t
t
sin
sin
cos
cos
cos
t
t
b
t
b
y
2
2
1
sin
a
x
t
sin
1
cos
2
2
a
x
a
x
b
y
t
a
x
cos
2
2
2
2
sin
1
cos
a
x
a
x
b
y
2
2
2
2
2
2
2
2
2
2
2
2
sin
1
cos
cos
2
sin
1
cos
a
x
a
x
a
x
b
y
b
y
a
x
a
x
b
y
2
2
2
2
2
sin
cos
2
a
x
b
y
a
x
b
y
Ogólne równanie elipsy
x
a
b
y
a
x
b
y
0
2
2
2
2
2
2
2
sin
cos
2
a
x
b
y
a
x
b
y
x
a
b
y
a
x
b
y
0
2
1
0

3
2
1
2
2
2
2
a
x
b
y
b
a
2
2
2
a
x
y
elipsa
okrąg
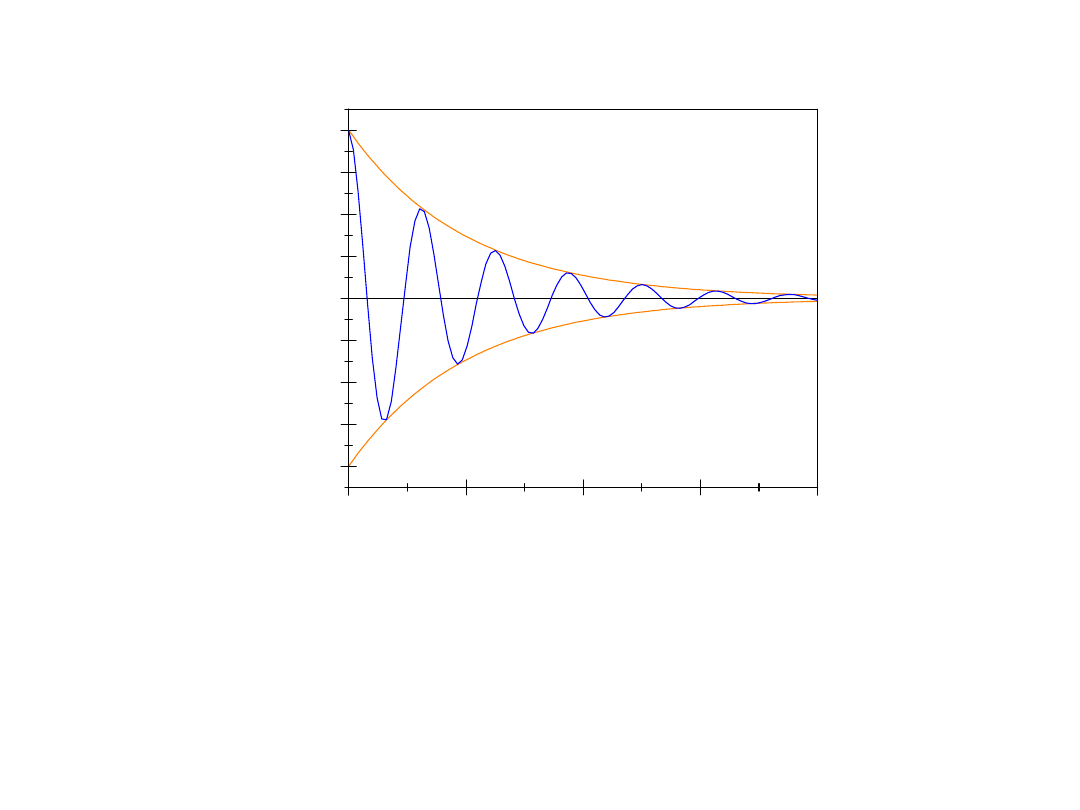
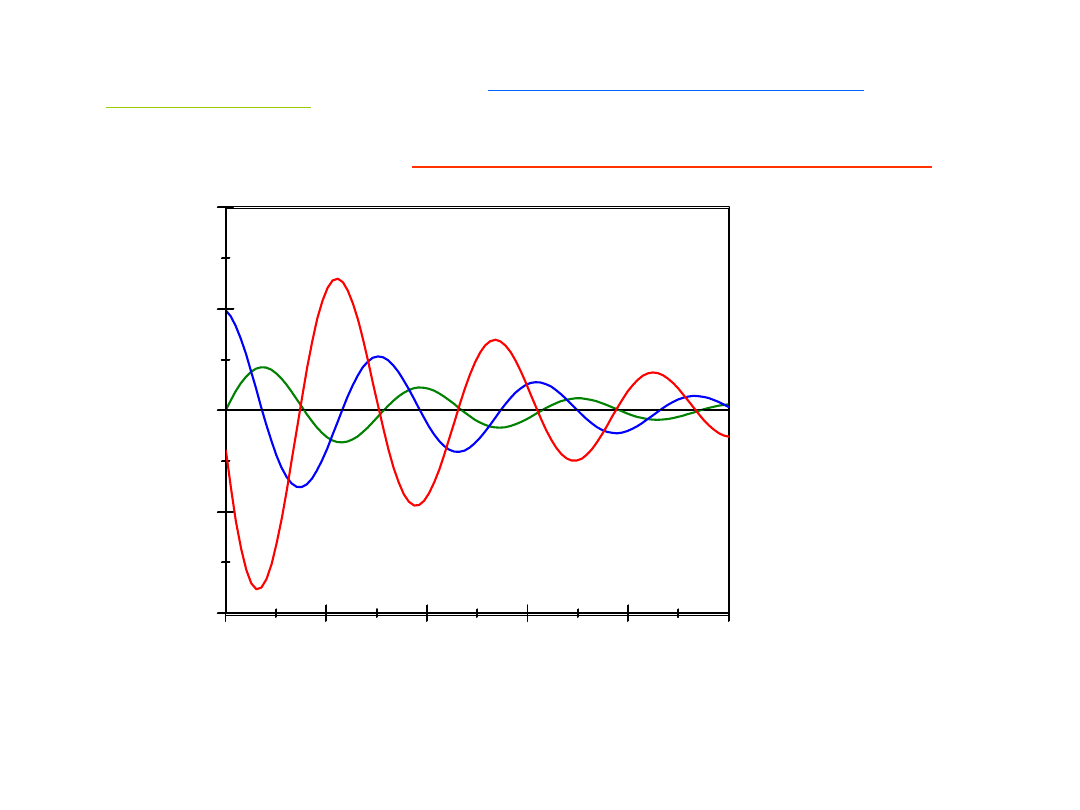
Drgania tłumione
v
F
t
kx
F
0
2
2
2
2
x
m
k
dt
dx
m
dt
x
d
v
kx
dt
x
d
m
Na ciało o masie m działają siły:
Równanie Newtona
0
5
10
15
20
-4
-3
-2
-1
0
1
2
3
4
t
0
20
t
e
A
x
t
sin
0
x
t
e
A
x
t
sin
0
t
t
e
A
t
e
t
e
A
v
dt
dx
t
t
t
cos
sin
cos
sin
0
0
t
t
t
e
A
t
t
e
A
t
t
e
A
a
dt
x
d
t
t
t
sin
cos
2
sin
sin
cos
cos
sin
2
2
0
2
0
0
2
2
Znajdziemy rozwiązanie równania ruchu w postaci
0
2
4
-6
-4
-2
0
2
4
6
x(
t)
t
0
2
4
-6
-4
-2
0
2
4
6
v(
t)
t
0
2
4
-6
-4
-2
0
2
4
6
a(
t)
t
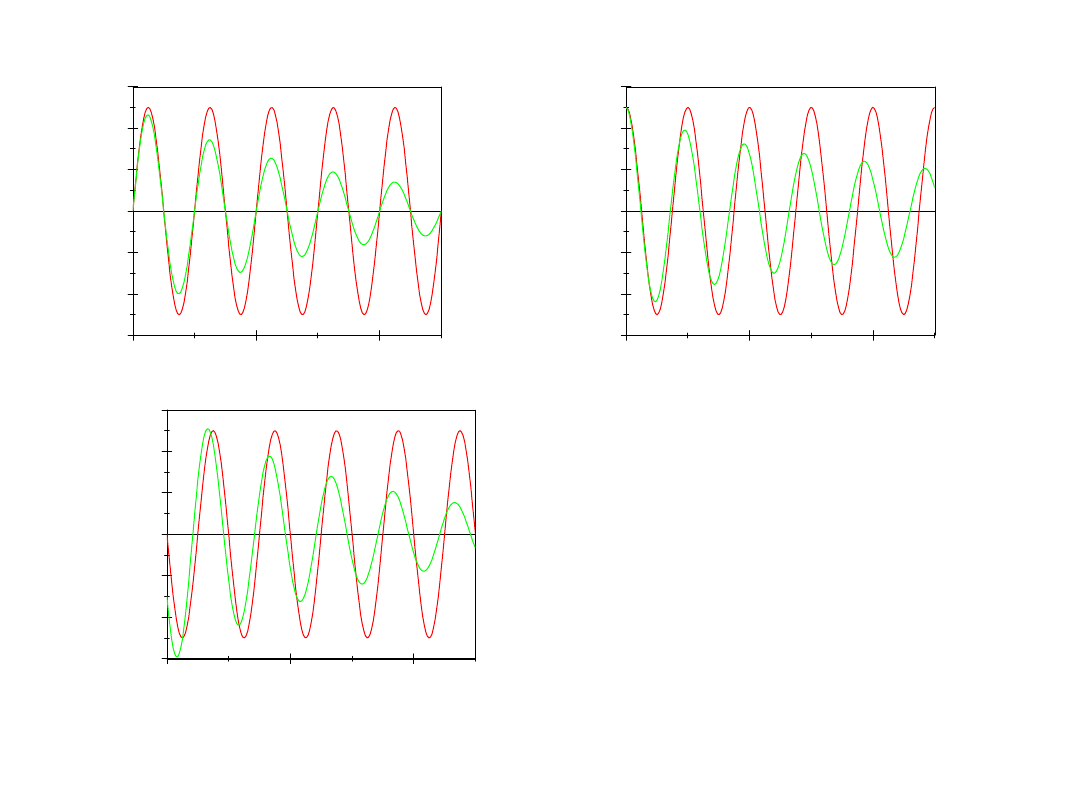
Porównanie zależności od
czasu: wychylenia z położenia
równowagi, prędkości i
przyspieszenia w drganiach
harmonicznych i tłumionych
0
2
4
6
8
10
-8
-4
0
4
8
t
0
2
4
6
8
10
-8
-4
0
4
8
t
e
x
t
2
sin
2
2
.
0
t
t
e
v
t
2
cos
2
2
sin
2
.
0
2
2
.
0
t
t
t
e
a
t
2
sin
4
2
cos
8
.
0
2
sin
04
.
0
2
2
.
0
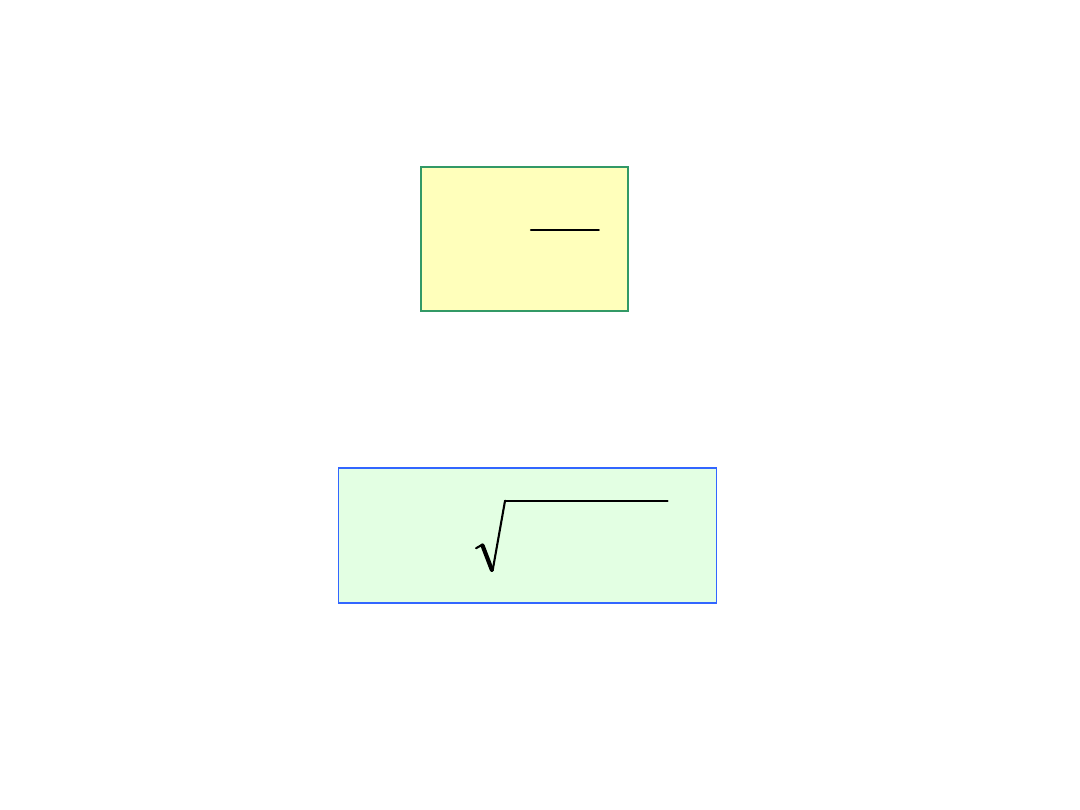
m
2
2
2
0
współczynnik tłumienia
częstość drgań tłumionych
Drgania wymuszone
v
F
t
kx
F
t
m
F
x
m
k
dt
dx
m
dt
x
d
t
F
v
kx
dt
x
d
m
sin
sin
0
2
2
0
2
2
t
A
x
sin
t
F
t
F
sin
)
(
0
t
A
x
sin
Na ciało o masie m działają siły
oraz siła wymuszająca
Równanie ruchu
Rozwiązanie równania ruchu
0
2
4
6
8
10
-2
0
2
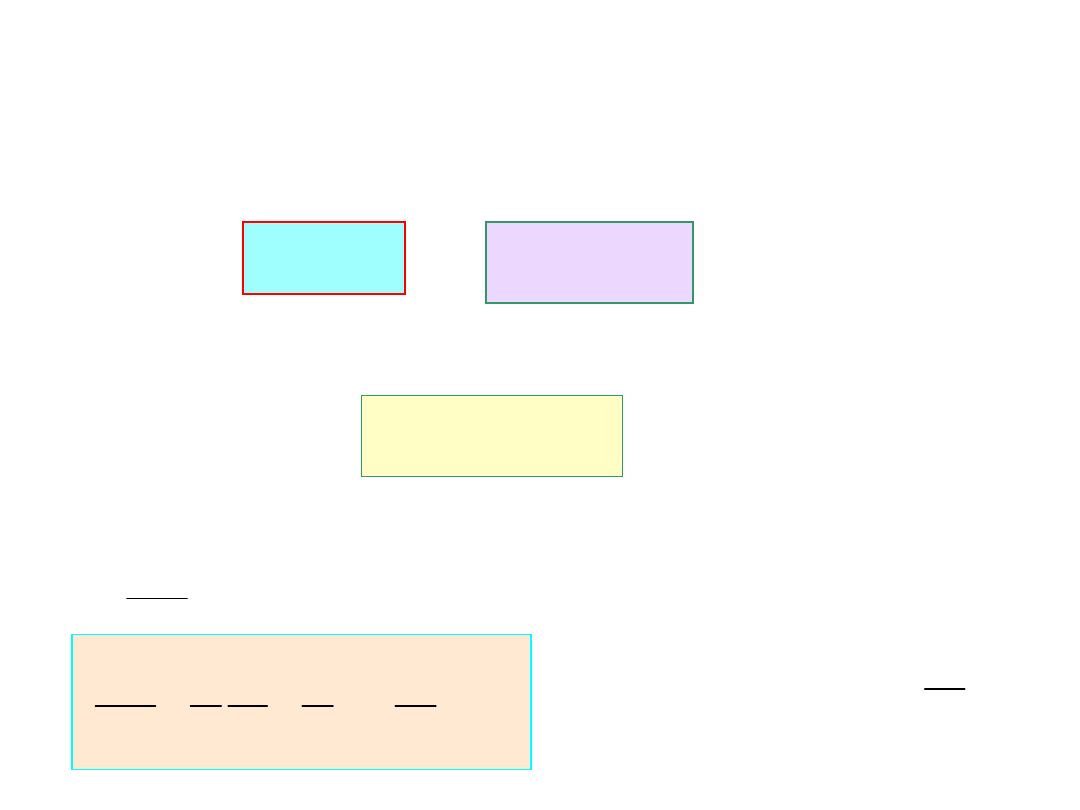
x=
3c
os
(2
t+
4
t
0
10
-6
0
6
F
=
5c
os
2t
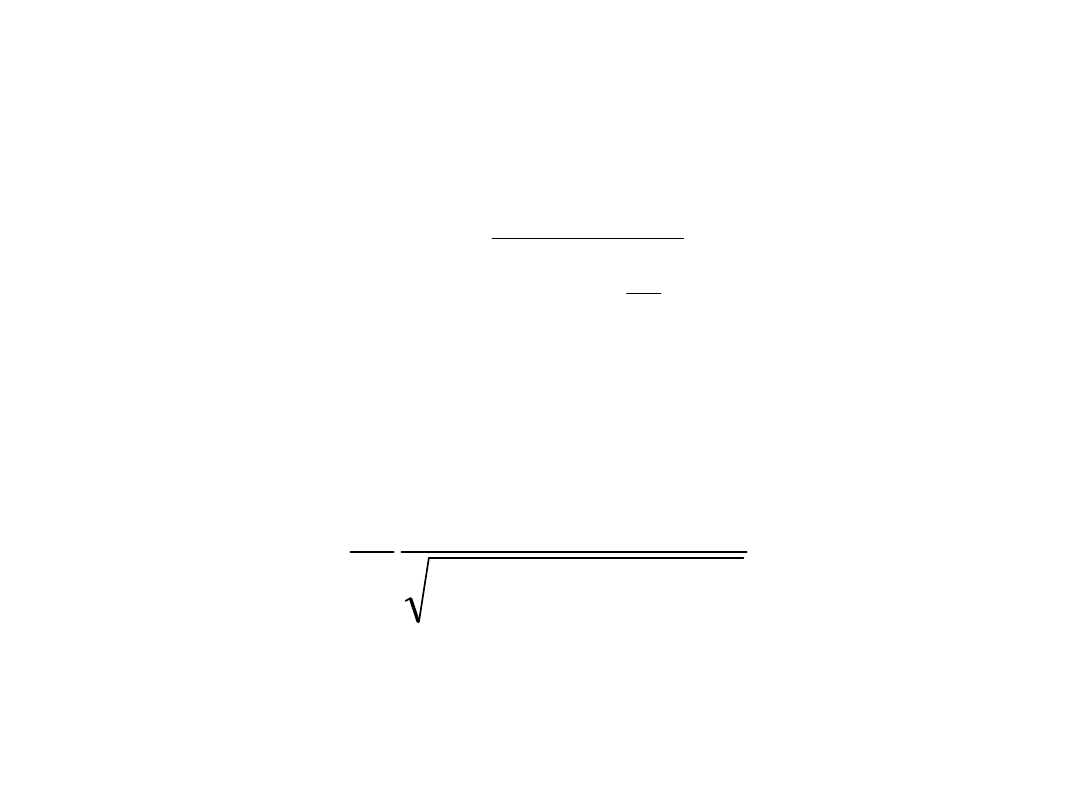
Należy wyznaczyć
amplitudę
drgań wymuszonych A i
przesunięcie fazowe
między siłą a przemieszczeniem
- kąt o jaki maksimum przemieszczenia wyprzedza maksimum siły
m
k
2
2
tan
2
2
2
2
2
0
0
4
1
m
F
A
Przesunięcie fazowe
Amplituda
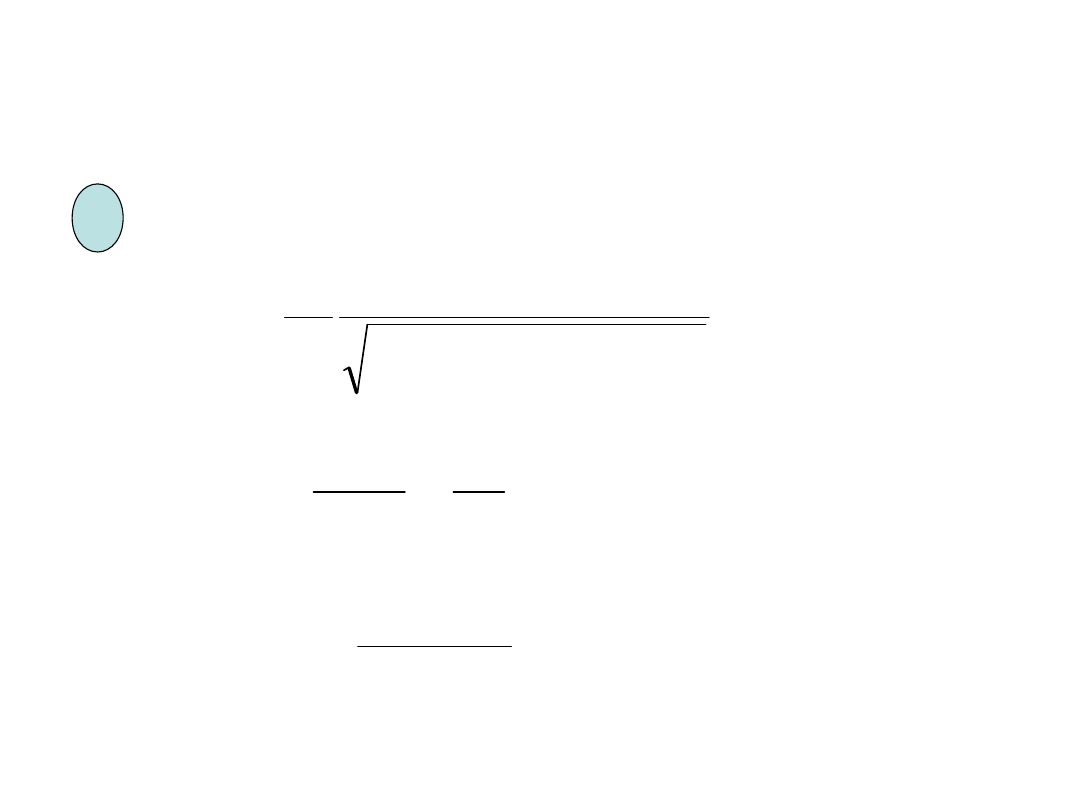
0
0
k
F
m
F
A
0
2
0
0
1.
2
2
2
2
2
0
0
4
1
m
F
A
0
,
0
2
tan
2
0
2
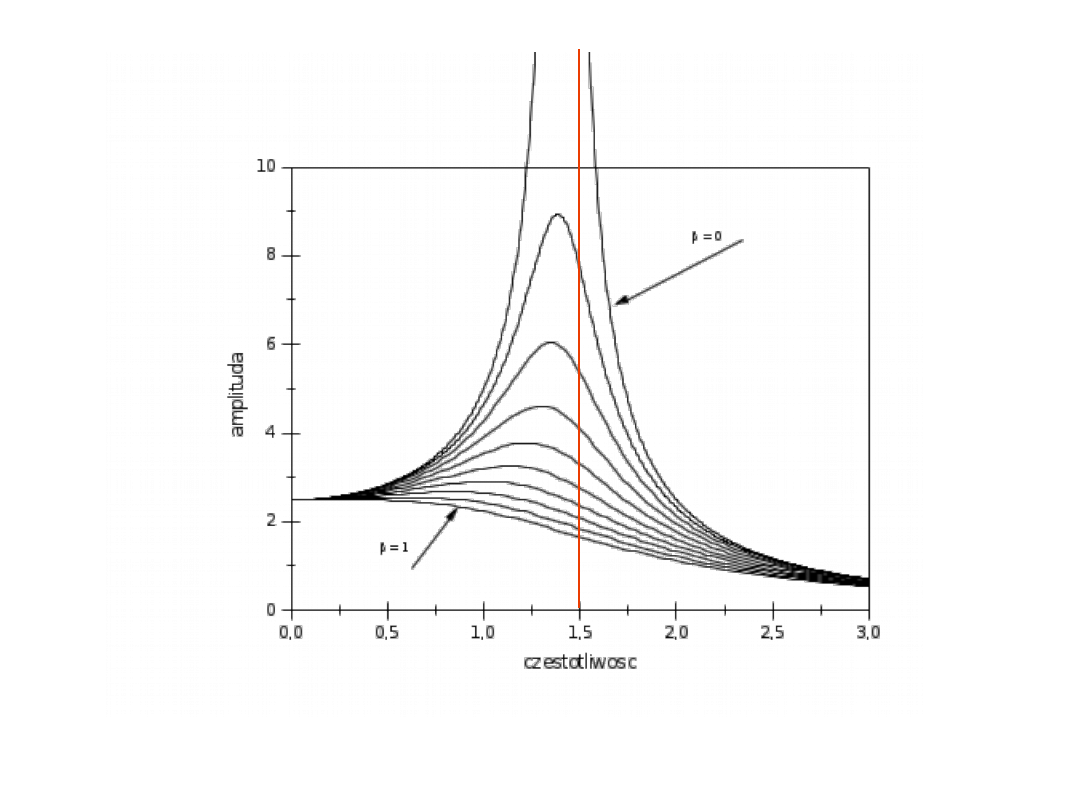
Jak amplituda drgań wymuszonych i przesunięcie fazowe zależą
od częstości siły wymuszającej?
amplituda nie zależy od częstości
0
2
0
m
F
A
2.
2
2
2
0
2
2
4
0
2
2
2
2
2
0
0
4
1
1
4
1
4
1
m
F
m
F
m
F
A
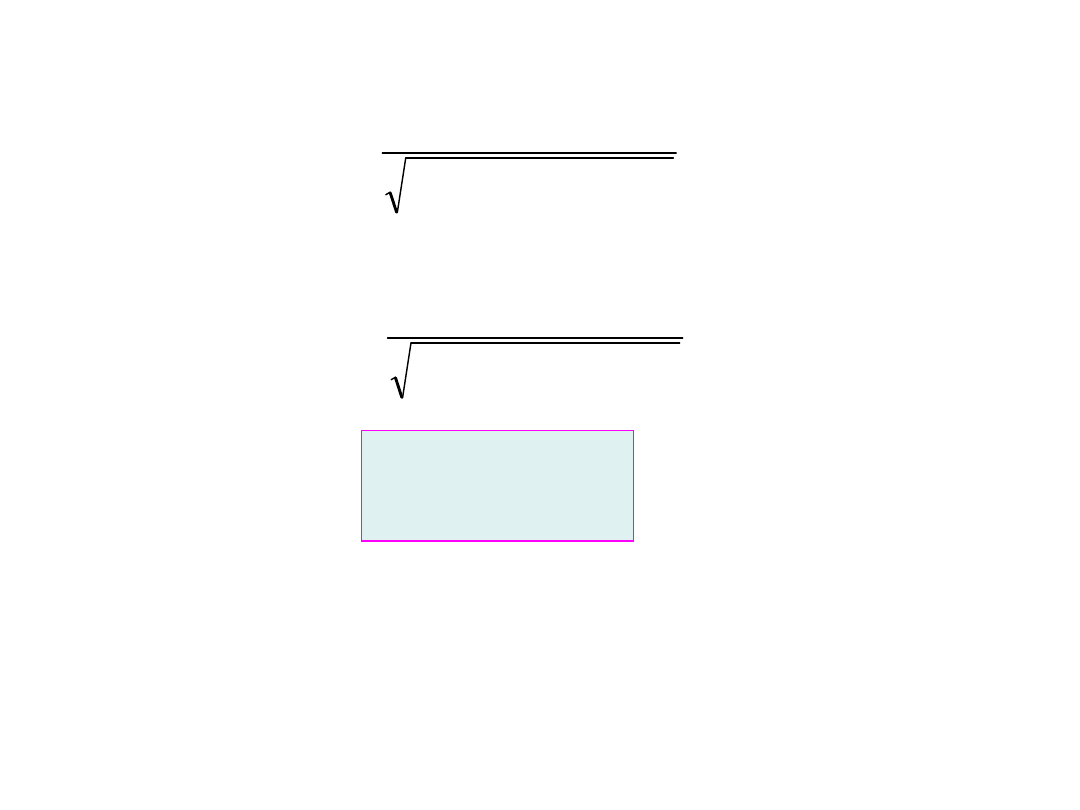
0
4
2
sin
2
2
2
2
2
0
1
4
cos
2
2
2
2
2
0
2
2
0
0
3.
2
2
2
2
2
0
0
4
1
m
F
A
m
F
A
2
0
1
4
2
sin
2
2
2
2
2
0
0
4
cos
2
2
2
2
2
0
2
2
0
2
A
0
0
4
4
2
8
2
2
2
2
2
2
2
0
2
2
2
2
2
0
2
2
2
0
0
m
F
d
dA
2
2
0
2
2
0
2
2
2
2
0
2
2
2
0
2
2
0
2
0
8
2
2
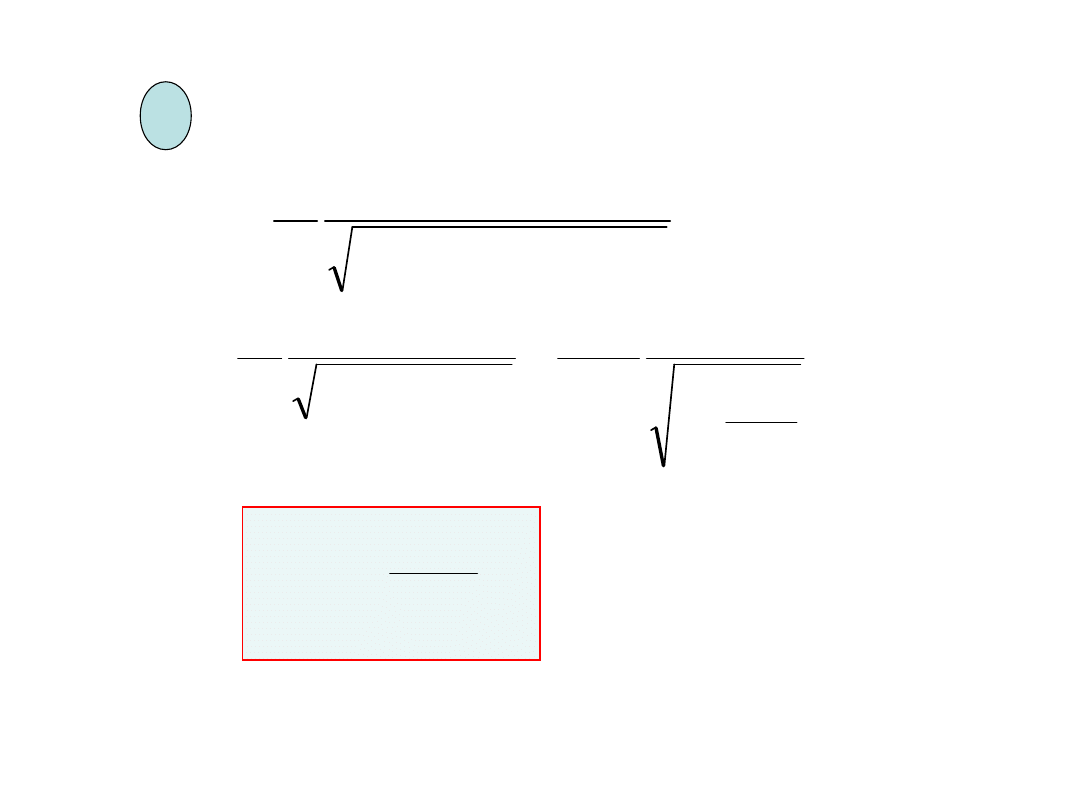
rez
Rezonans – amplituda osiąga wartość
maksymalną
częstość rezonansowa
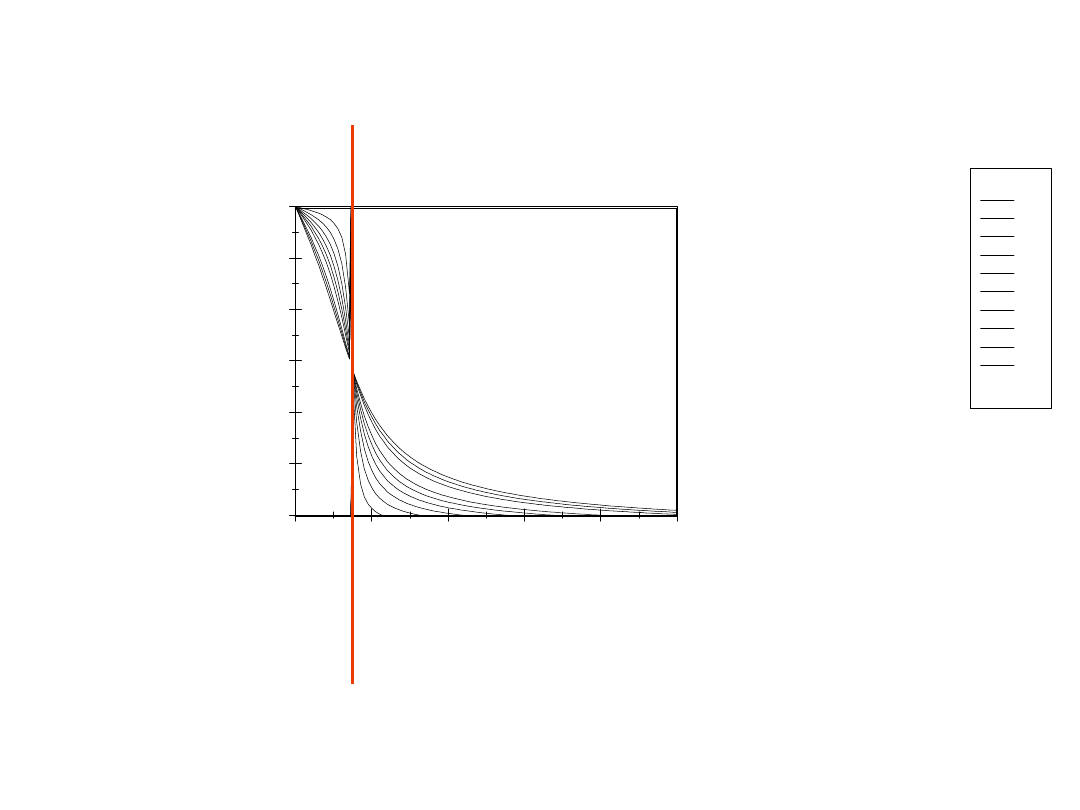
0
2
4
6
8
10
-3,0
-2,5
-2,0
-1,5
-1,0
-0,5
0,0
F1
F2
F3
F4
F5
F6
F7
F8
F9
F10
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
Wyszukiwarka
Podobne podstrony:
WI2
WI2
więcej podobnych podstron