MECHANIKA
TEORETYCZNA I

STATYKA

WYBRANE RYSUNKI

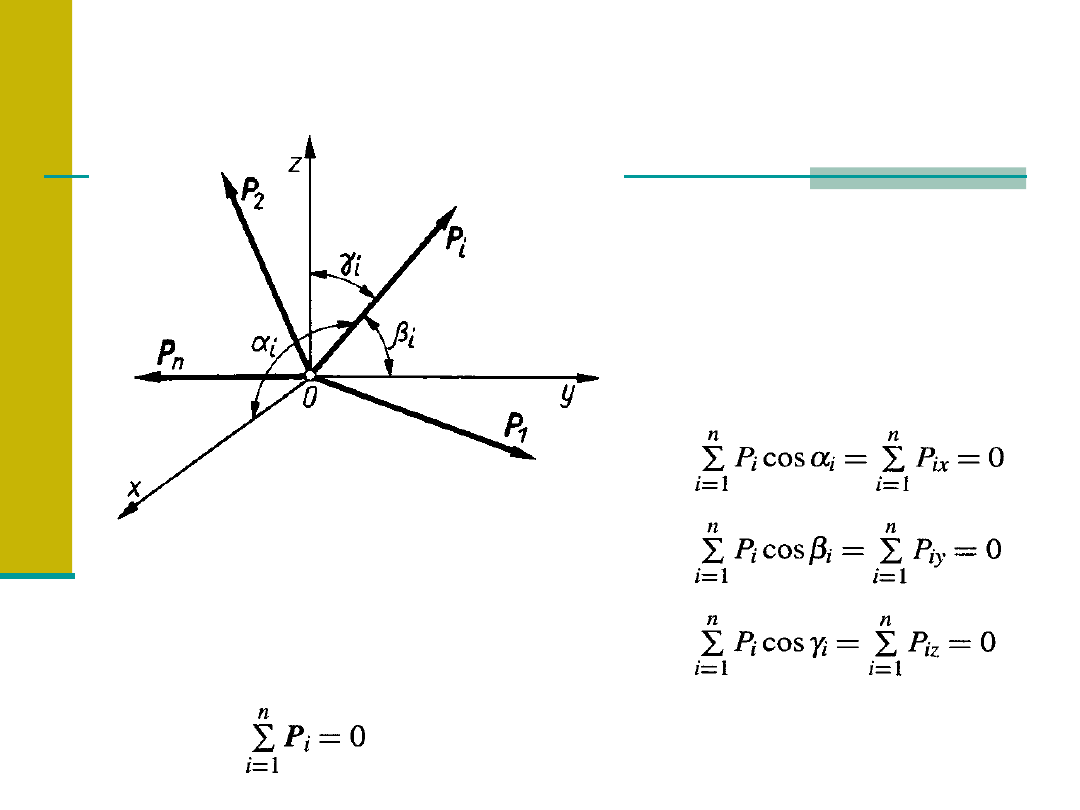
Zbieżne układy sił

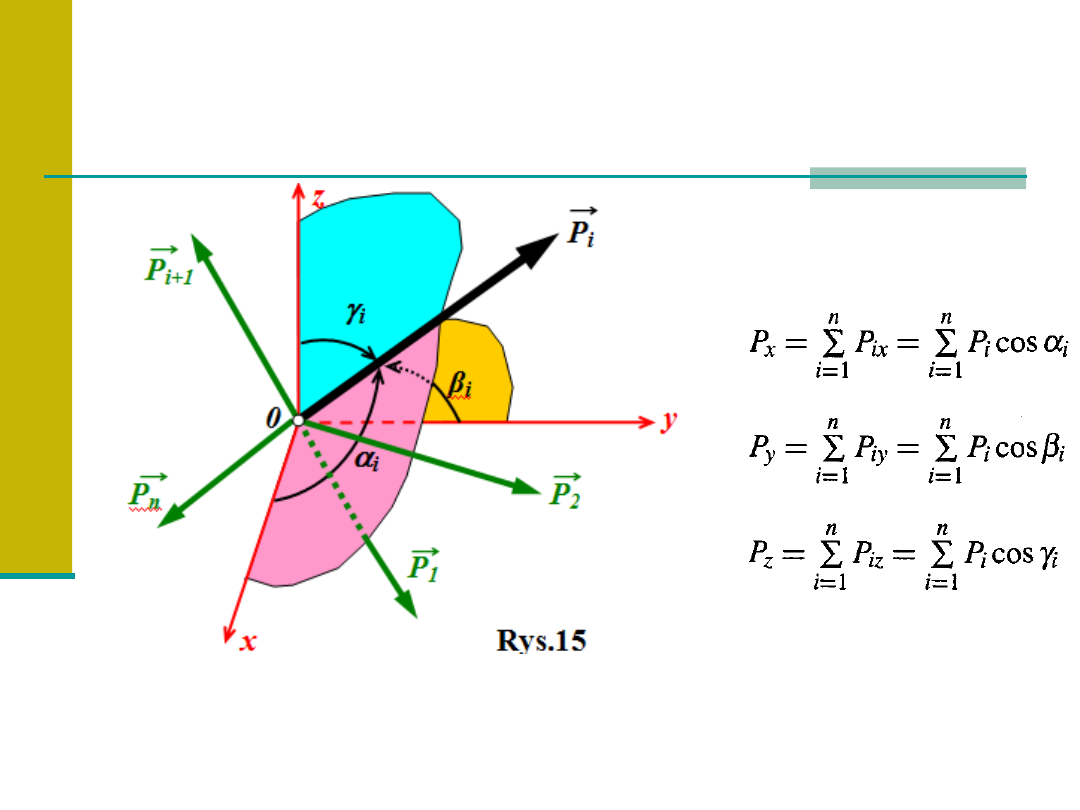
Analityczny sposób wyznaczania
wypadkowej przestrzennego układu sił

zbieżnych (rys.15).

TWIERDZENIE O SUMIE RZUTÓW WEKTORÓW

Rzut sumy geometrycznej wektorów na dowolną oś równy jest

sumie rzutów tych wektorów na tę samą oś.

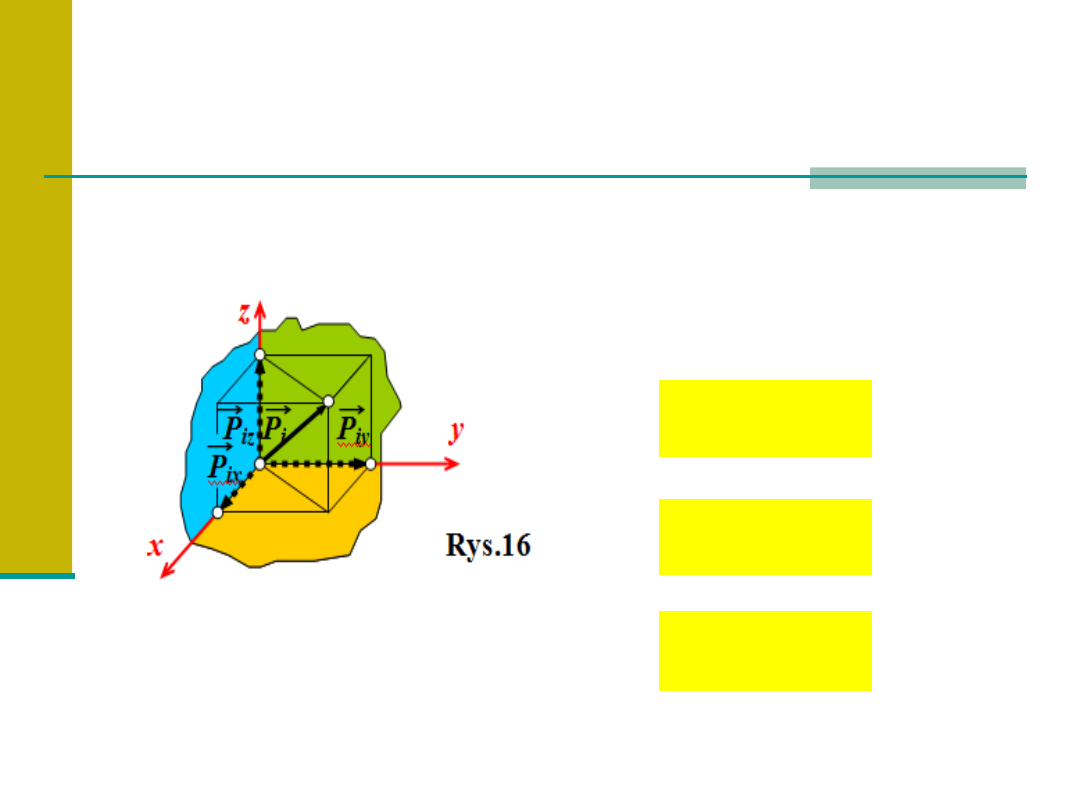
Składowe siły Pi na osie
prostokątnego układu 0xyz (rys.16)



P

ix

= P

i

cos



i

P

iy

= P

i

cosβ

i

(13)

P

iz

= P

i

cos



i









n

i

1

i

i

i

x

cos

P

P











n

i

1

i

i

i

y

cos

P

P











n

i

1

i

i

i

z

cos

P

P



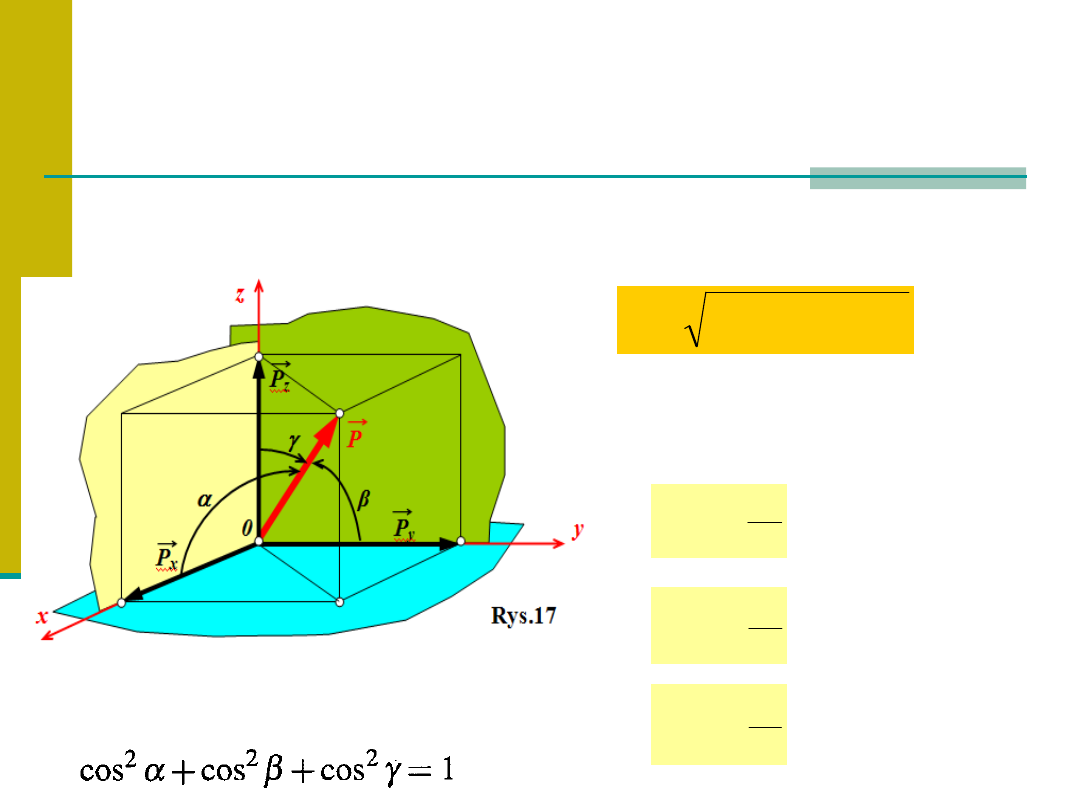
Wartość liczbowa wypadkowej P
określamy z (15) (rys.17)

(15)



cosinusy kierunkowe
określamy z (16)

(16)

2

z

2

y

2

x

P

P

P

P







P

P

cos

x





P

P

cos

y





P

P

cos

z





Cosinusy kierunkowe spełniają zależność.

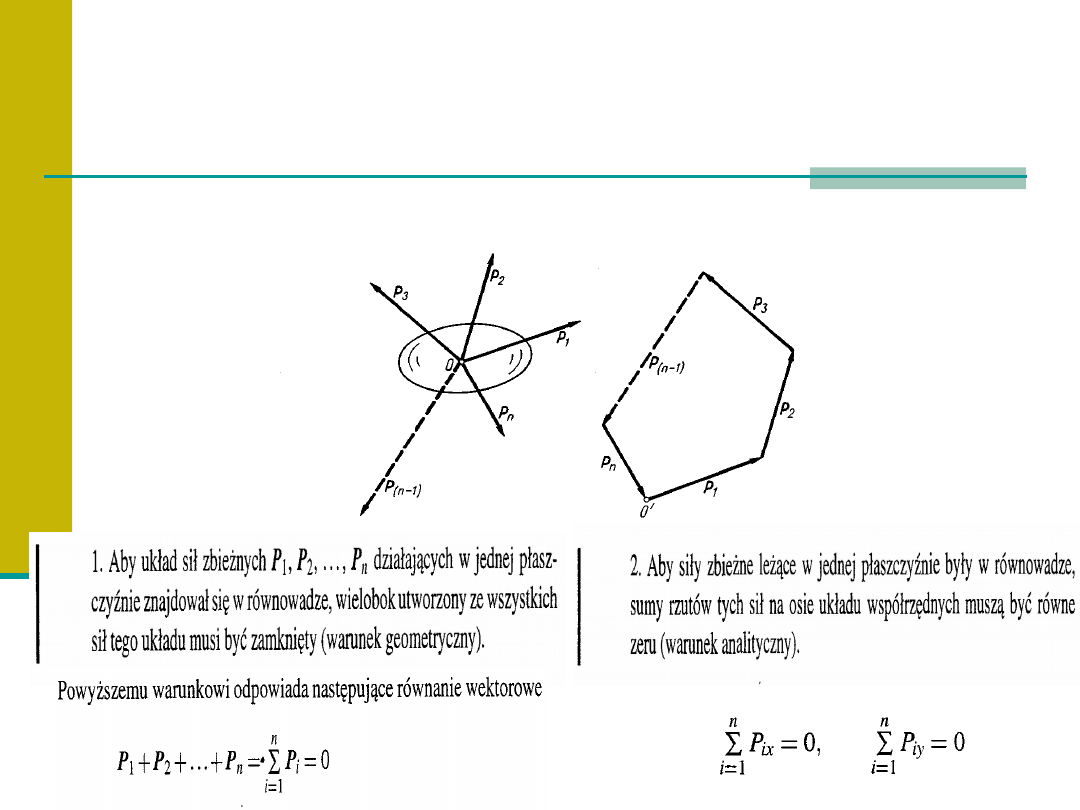
Równowaga płaskiego i
przestrzennego układu sił
zbieżnych

Równowaga płaskiego układu n sił

Równowaga przestrzennego układu n sił

Warunek równowagi
przestrzennego układu sił
zbieżnych w postaci
wektorowej wyraża się
równaniem

Warunek równowagi
przestrzennego układu sił
zbieżnych w postaci
analitycznej wyraża się
równaniem

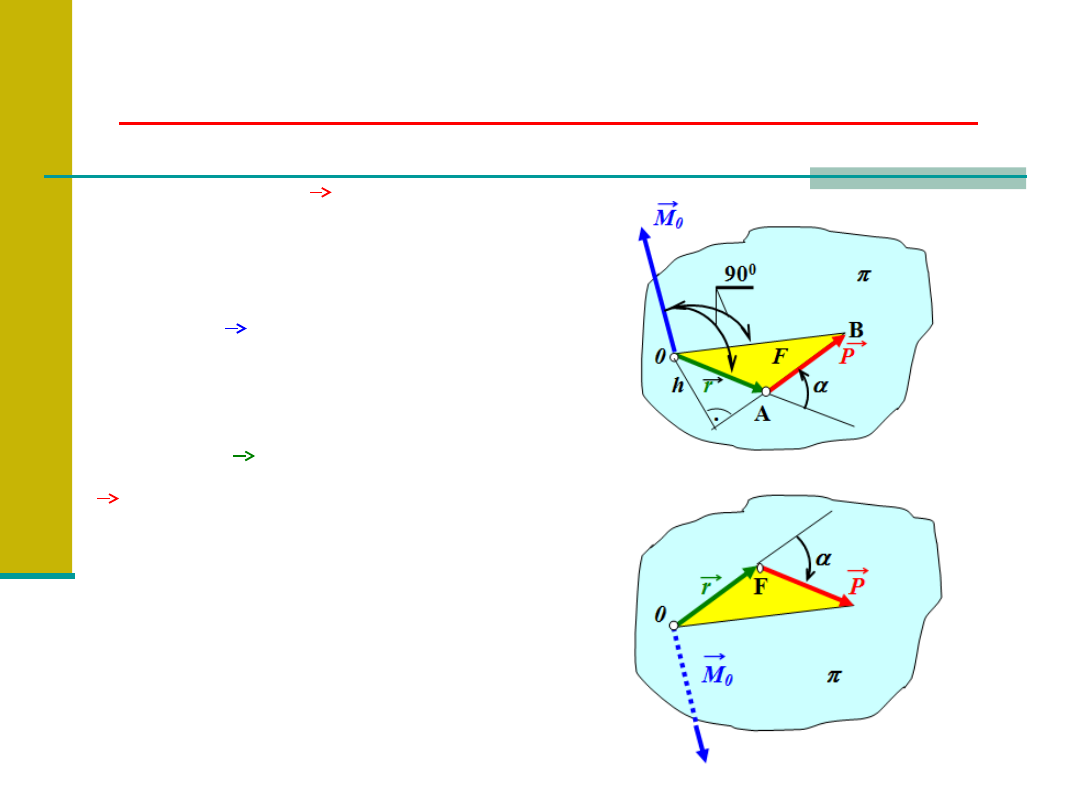
Moment siły względem punktu.

Moment siły

P

względem punktu 0
nazywamy odłożony
z punktu 0 wektor

M

0

, równy iloczynowi

wektorowemu
promienia wektora r
i wektora siły

P

.

P

r

M

0











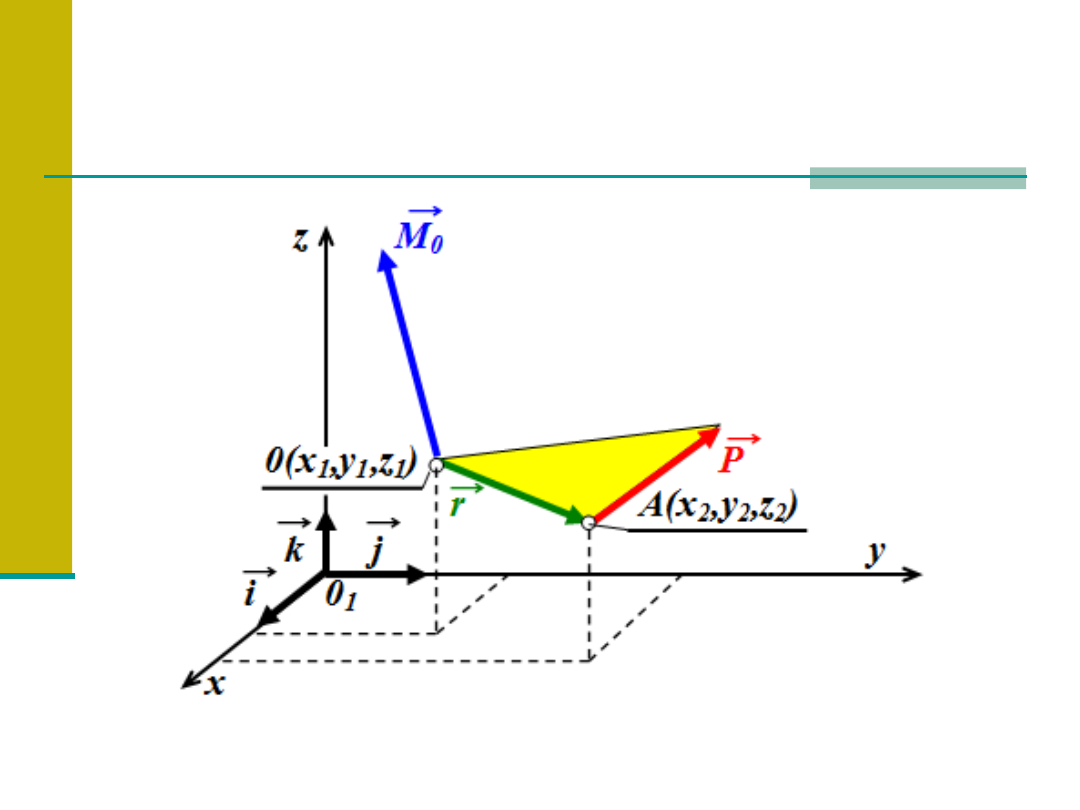
Moment siły względem dowolnego punktu 0

w przestrzeni

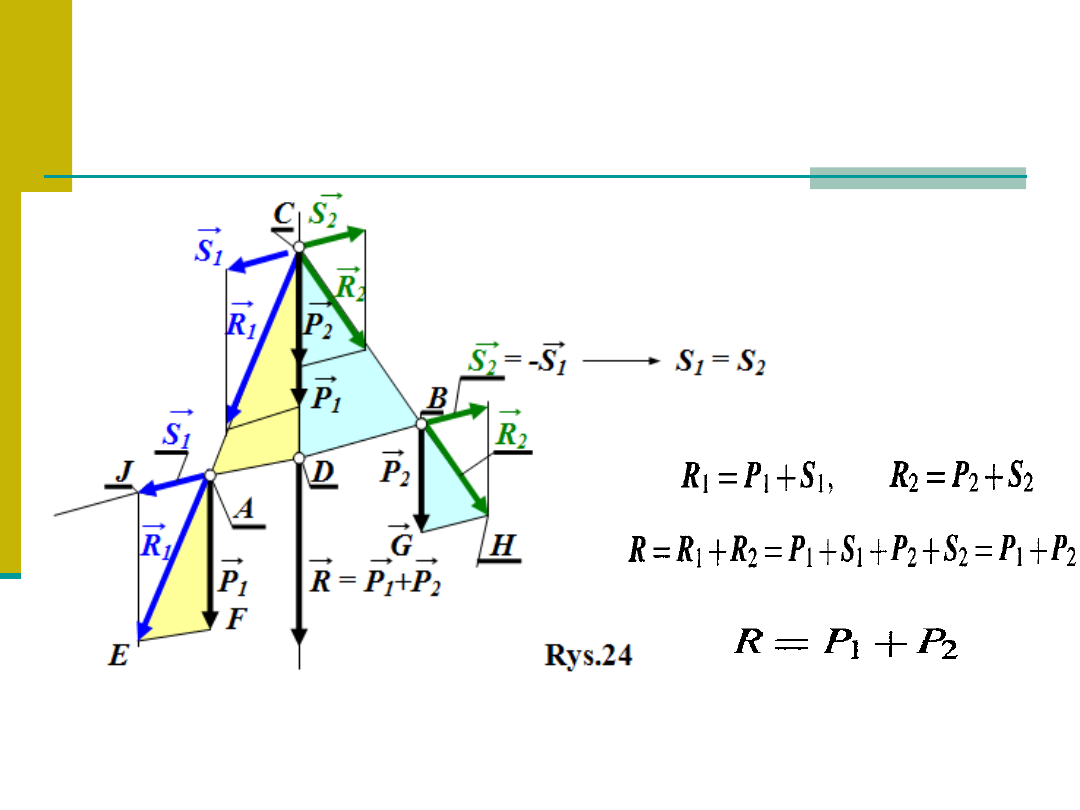
Wypadkowa dwóch sił równoległych zgodnie skierowanych

SIŁY RÓWNOLEGŁE



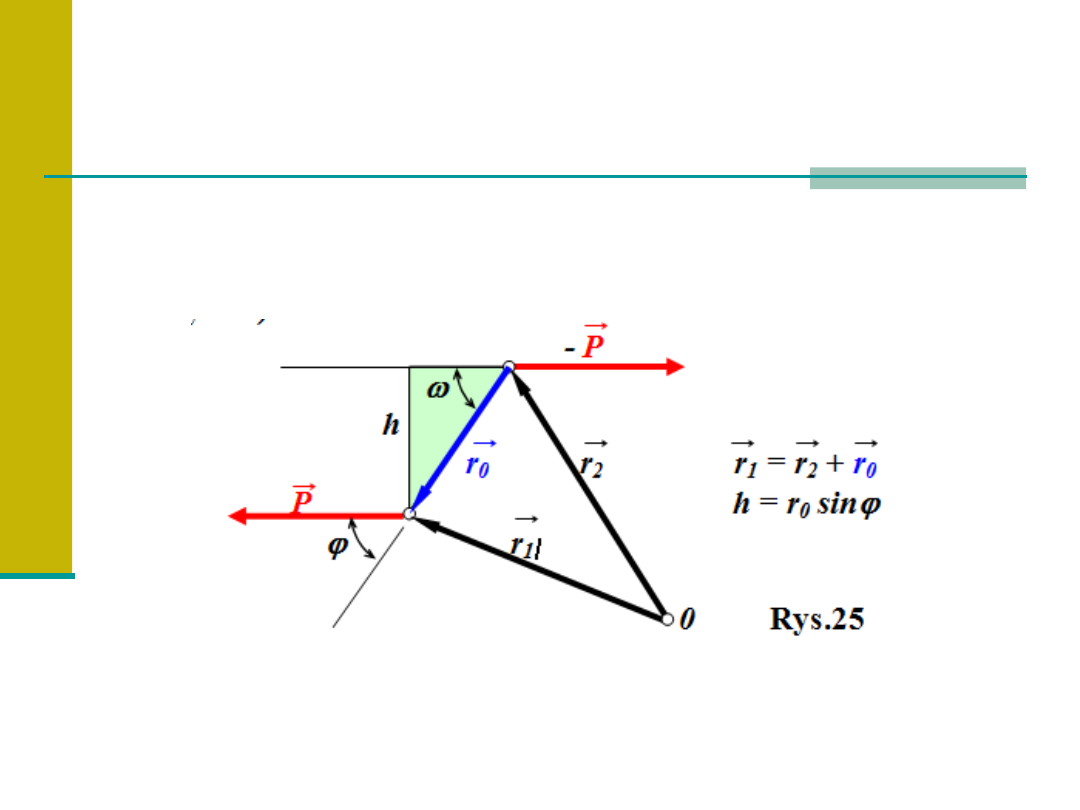
Układ dwóch sił o równych wartościach, lecz

przeciwnych zwrotach nazywamy

parą sił

. (rys.25)

PARA SIŁ

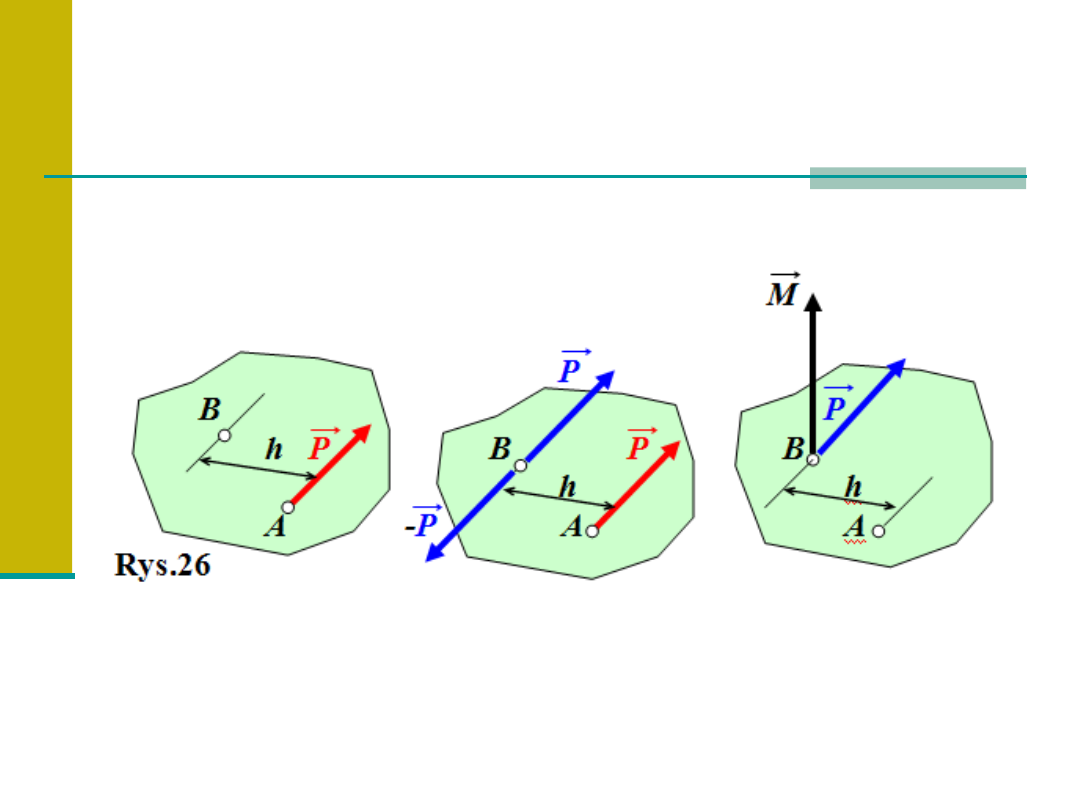
Równoległe

przesunięcie sił (rys.26)

a)

b)

c)

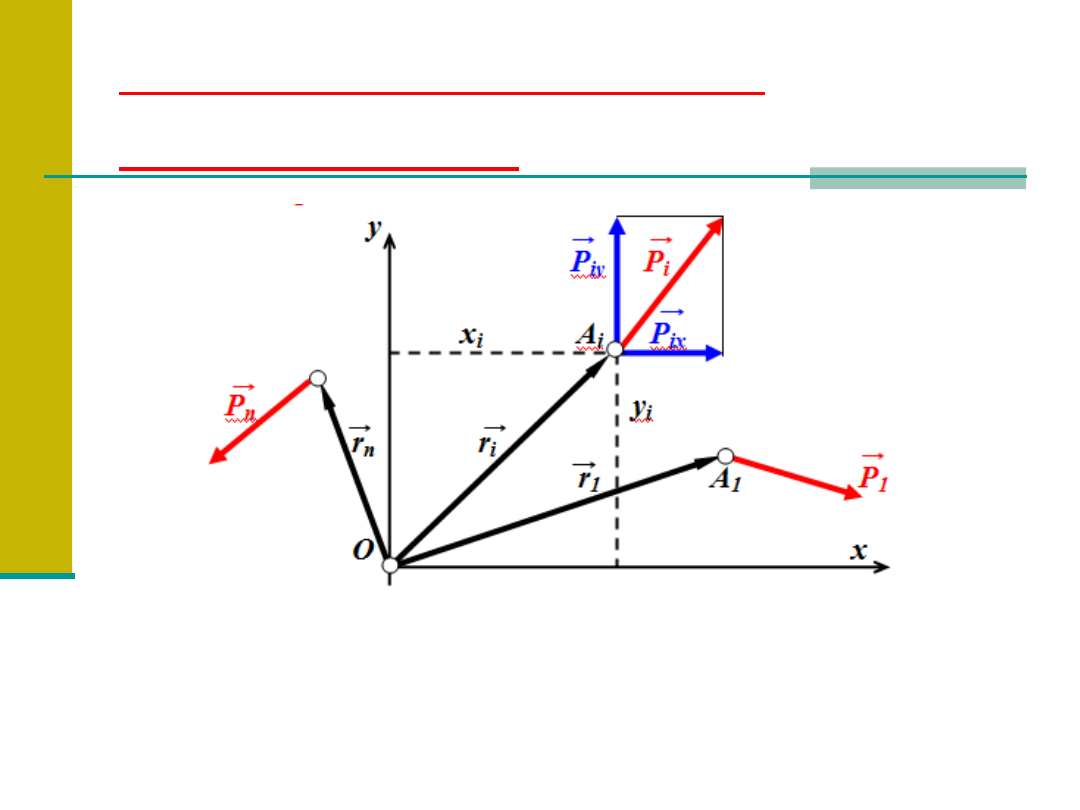
Redukcja płaskich
układów sił



Układ sił, którego siły leżą w jednej

płaszczyźnie, jest nazywany układem płaskim.



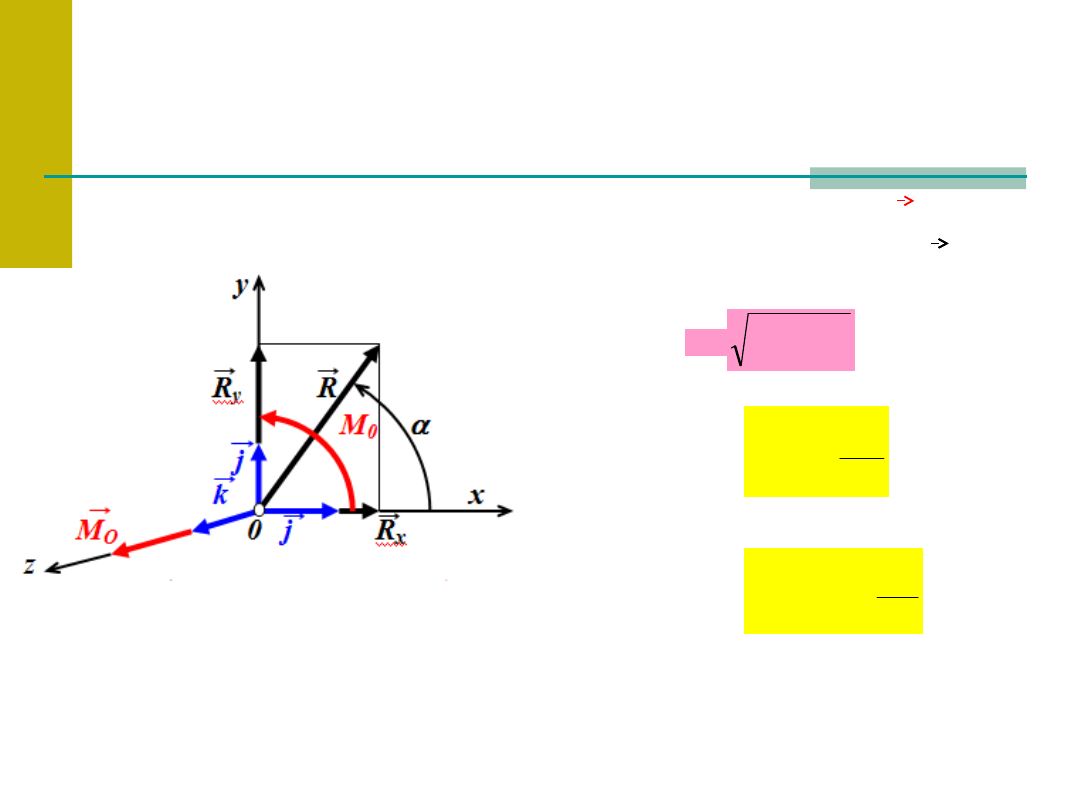
Wektor główny

R

i

moment główny
M

0



R

2

2

x

y

R

R 

R

y

R





sin

R

y

R

arcsin





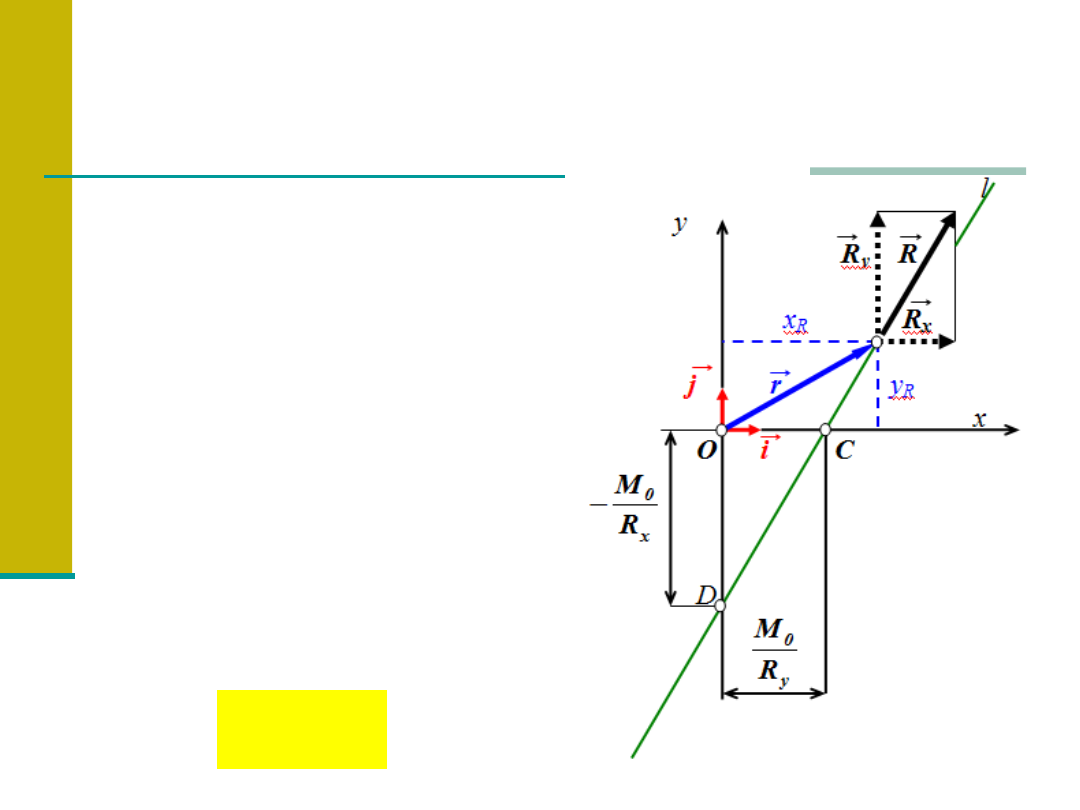
Redukcja płaskiego układu sił do jednej
siły wypadkowej



Równanie linii
działania wypadkowej
wyznacza się z
warunku, że moment
siły wypadkowej
względem początku
układu równa się
momentowi
głównemu M

0

,

równemu sumie
momentów danych sił
względem początku
układu
współrzędnych.











0

M

R

r

Wypadkowa płaskiego układu
sił

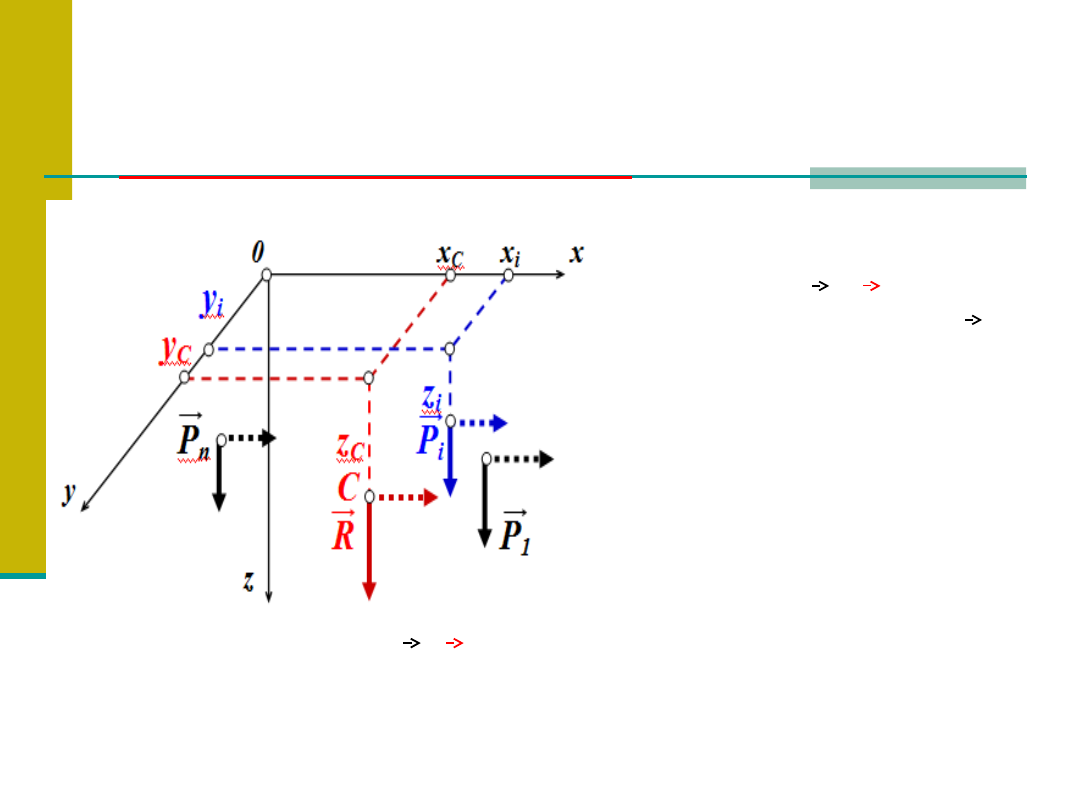
PRZESTRZENNY UKŁAD SIŁ
RÓWNOLEGŁYCH
Środek sił równoległych

Punkt C mający tę

własność, że przechodzi
przez niego stale
wypadkowa W=

R

danego

układu sił równoległych P
niezależnie od kierunku
tych sił (przy niezmiennych
punktach przyłożenia i
wartości sił) nazywa się
środkiem sił równoległych.

Moment siły wypadkowej W=

R

względem dowolnego punktu

równa się sumie momentów układu sił względem tego samego
punktu (

twierdzenie Varingnona

).

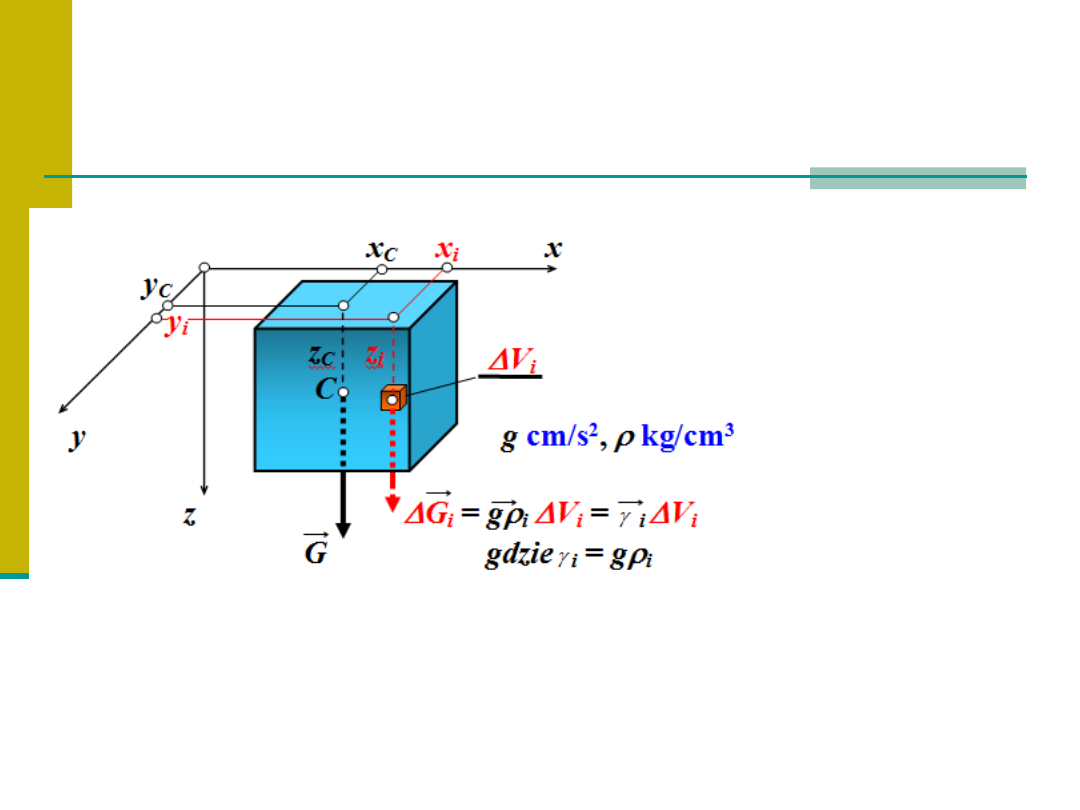
Środek ciężkości

Najczęściej
spotykanym
przykładem sił
równoległych są siły
ciężkości.

Określony poprzednio środek sił równoległych w odniesieniu do sił
ciężkości nazywamy

środkiem ciężkości.

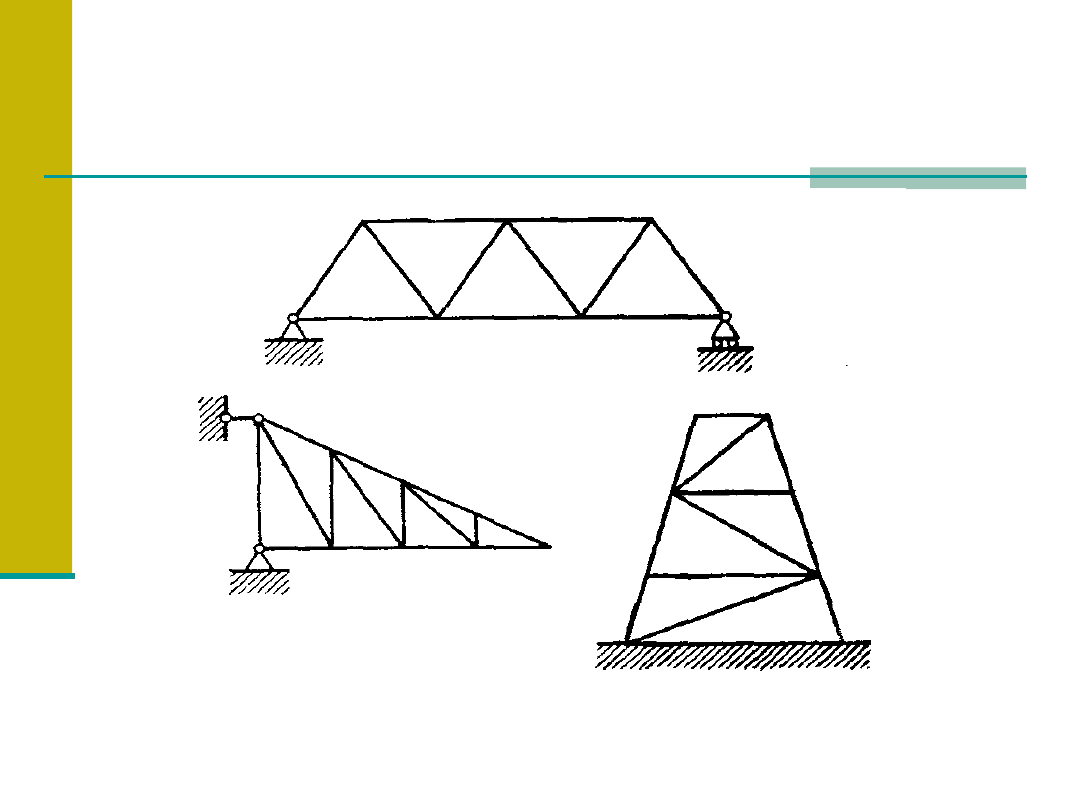
Przykłady kratownic

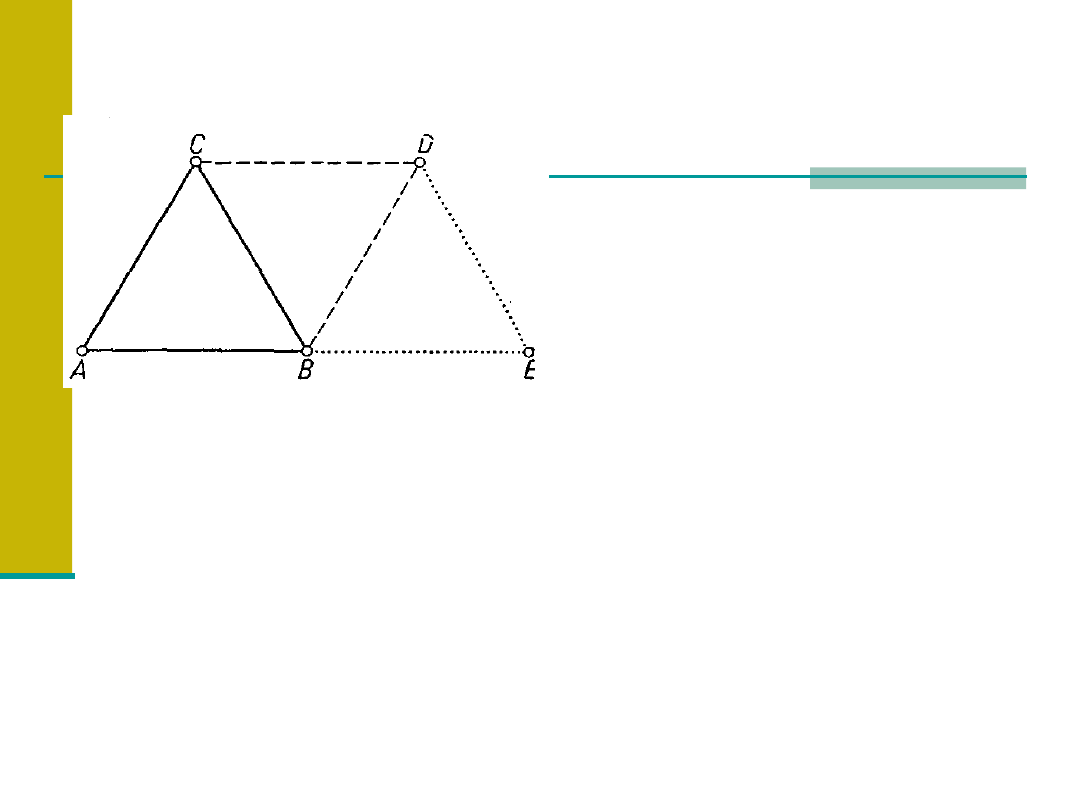
Warunek statycznej wyznaczalności kratownic.

Kratownica ABC składa się z
trzech prętów zakończonych
przegubami. Dla utworzenia
nowego węzła potrzebne są 2
pręty.

Z zasady tworzenia nowych
węzłów wynika związek:

p=2w-3

Jest to związek, który musi być spełniony, aby kratownica

była niezmienna geometrycznie, czyli inaczej, sztywna w

swej płaszczyźnie.

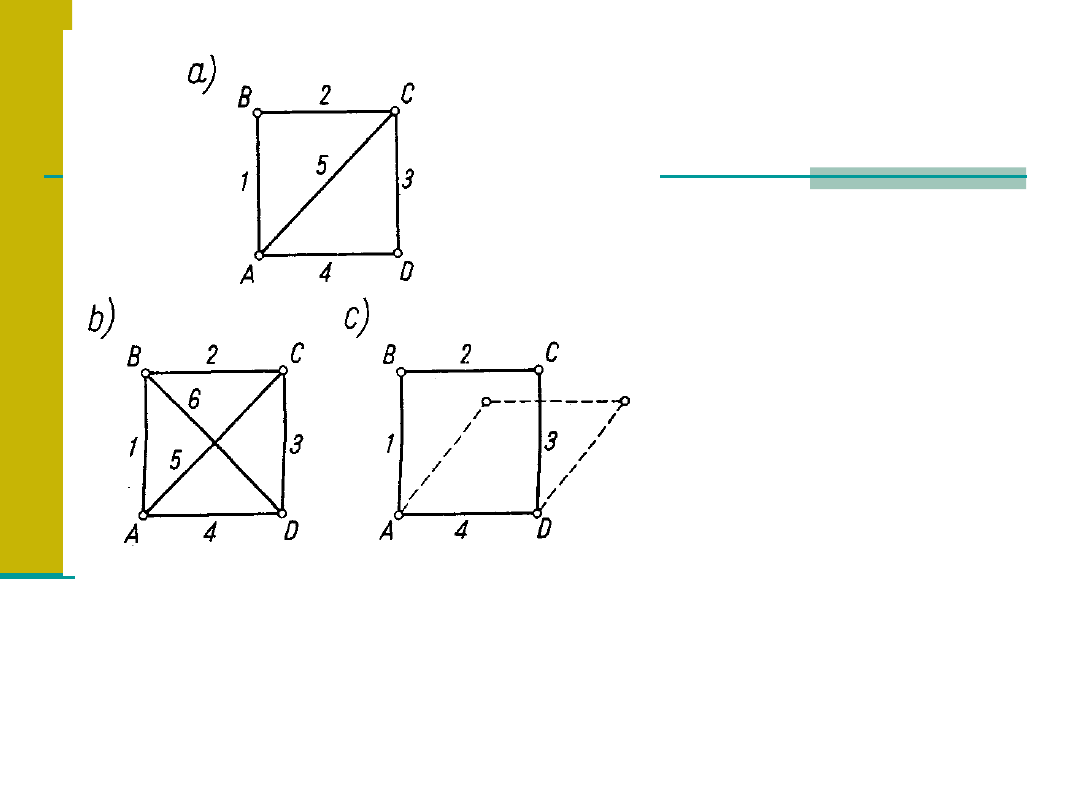
a) p=5; w=4 warunek
sztywności spełniony,.

b) Układ pszesztywniony
ponieważ jeśli usuniemy
jeden pręt, kratownica
nadal będzie układem
niezmiennym,

c) Warunek sztywności
niespełniony, ponieważ

p=4<2w-3=5

Układ może zmieniać
kształt

Warunek sztywności jest konieczny ale niewystarczający w
pewnych przypadkach, jedna część kratownicy może być
przesztywniona, druga zaś niedostatecznie sztywna ( np. b+c).

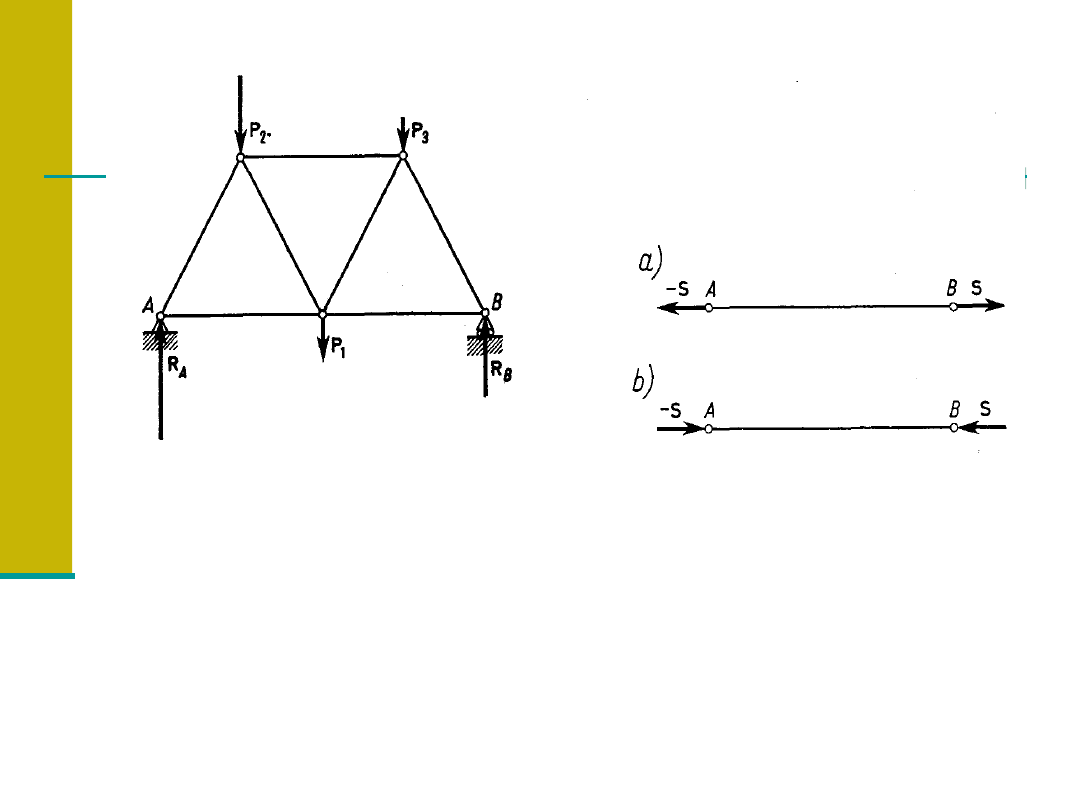
Siły działające na kratownicę w jej płaszczyźnie w węzłach

powodują powstawanie sił w prętach. Ponieważ każdy z prętów
znajduje się w równowadze, przyłożone do niego siły muszą
być równe co do wartości, przeciwne co do kierunku i muszą
działać wzdłuż osi pręta.

a) pręt rozciągany (siła skierowana zawsze „ od węzła”),

b) pręt ściskany (siła skierowana zawsze „ do węzła”),

Znajomość powyższych sił jest niezbędna do projektowania

kratownic.

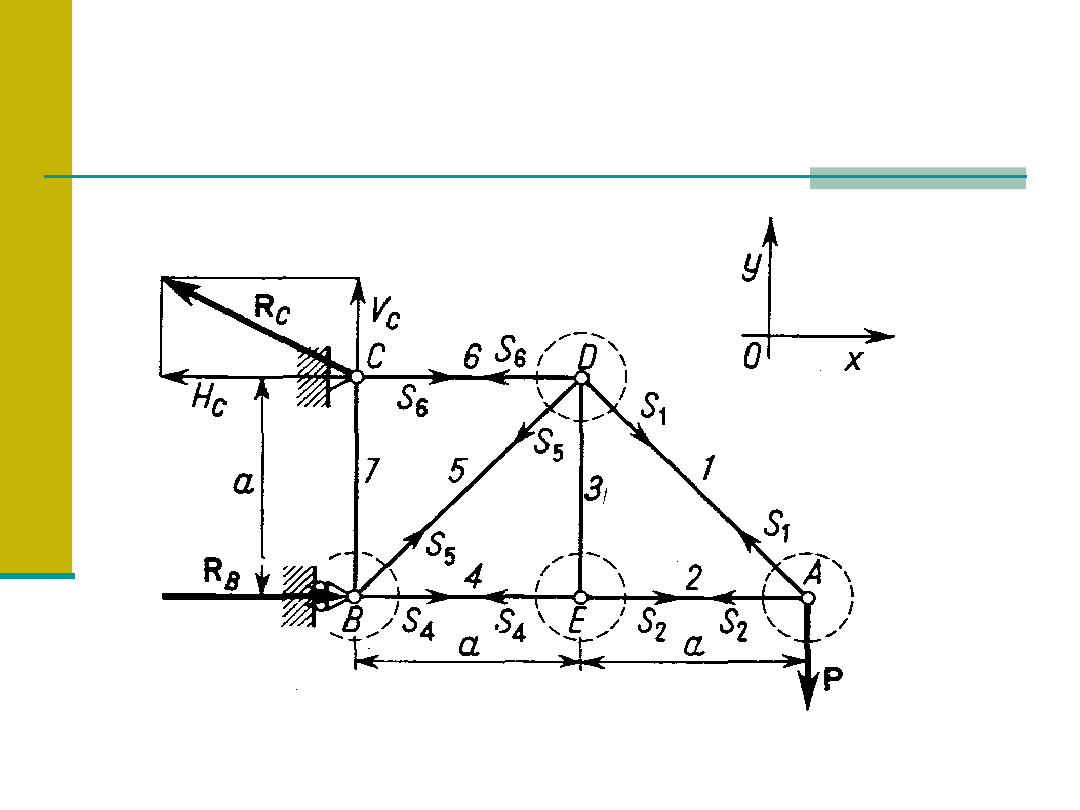
ANALITYCZNE WYZNACZANIE SIŁ

DZIAŁAJĄCYCH NA PRĘTY W KRATOWNICY.

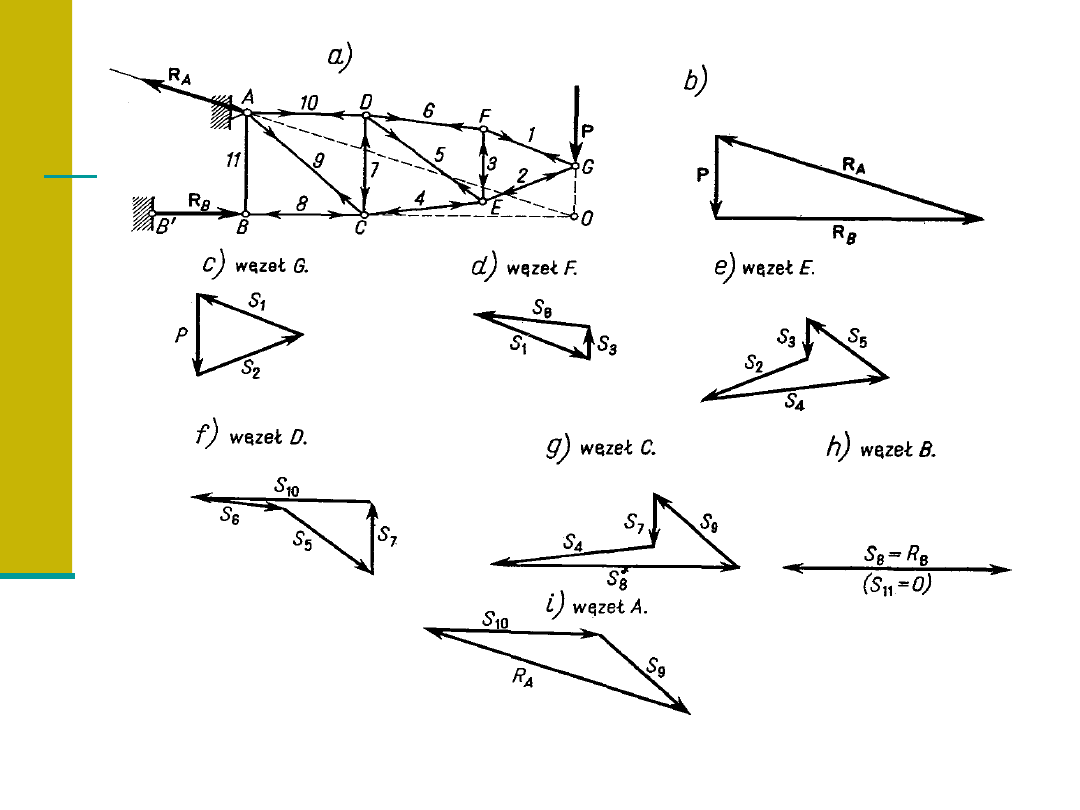
Zaleta-przejrzystość
Wada-kumulacja błędów długości i równoległości

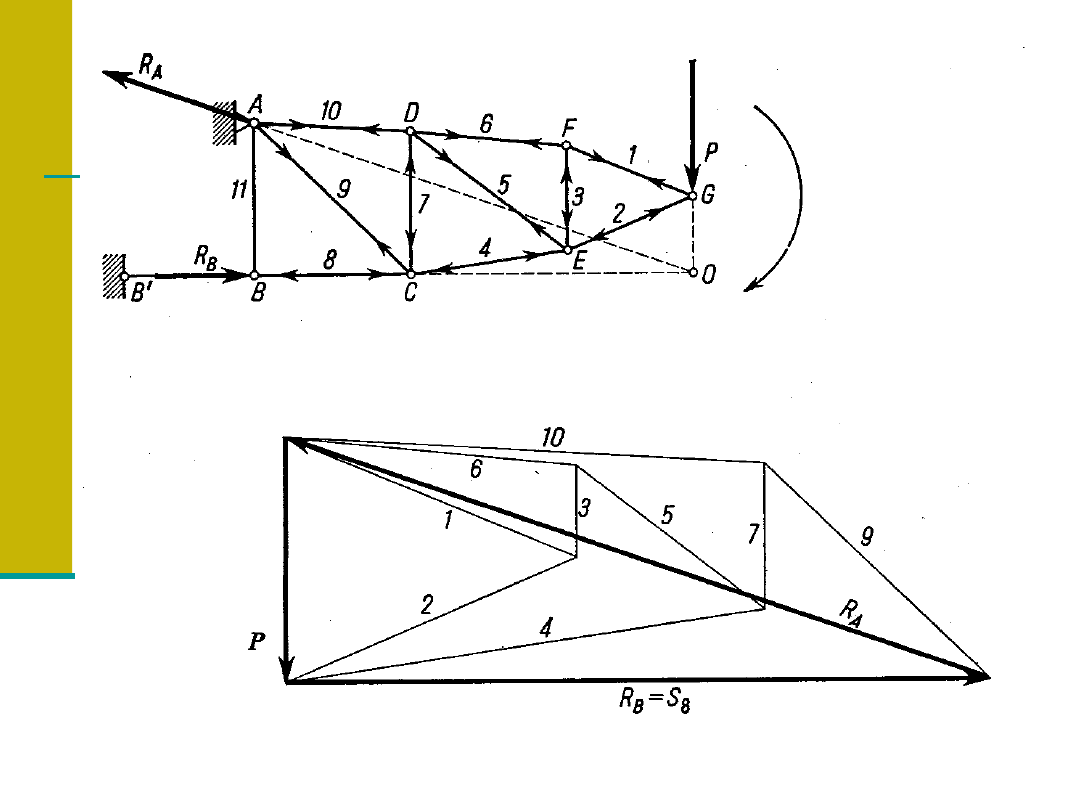
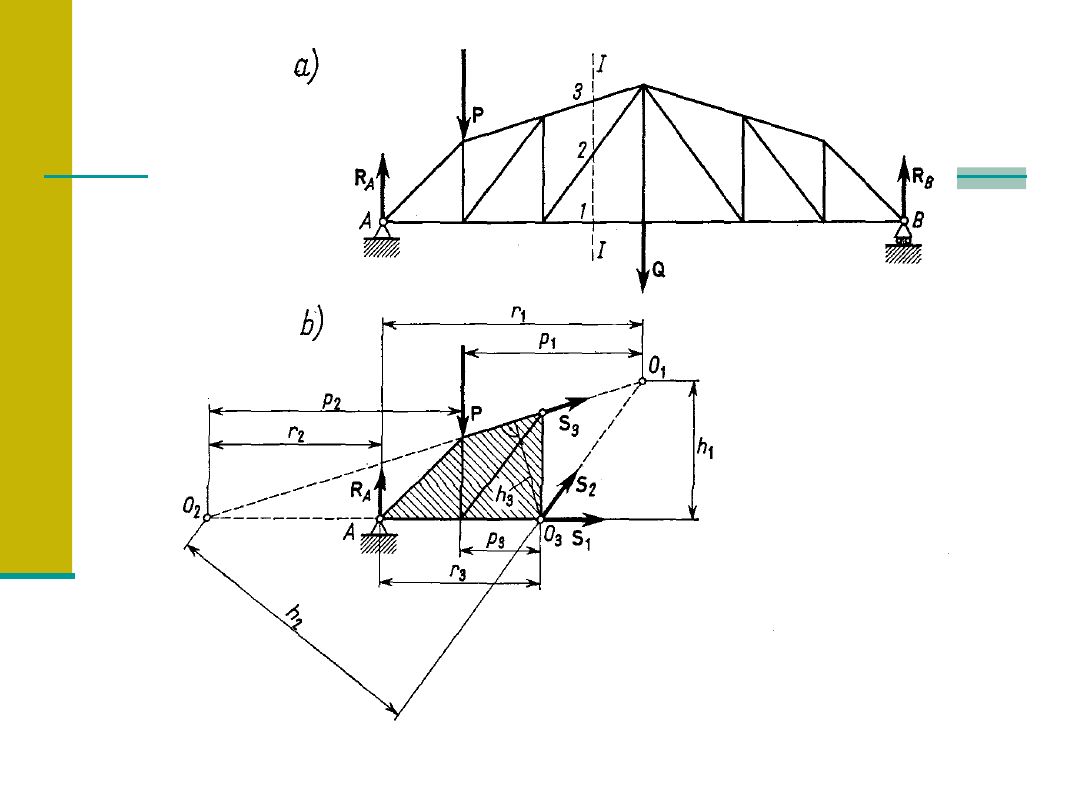
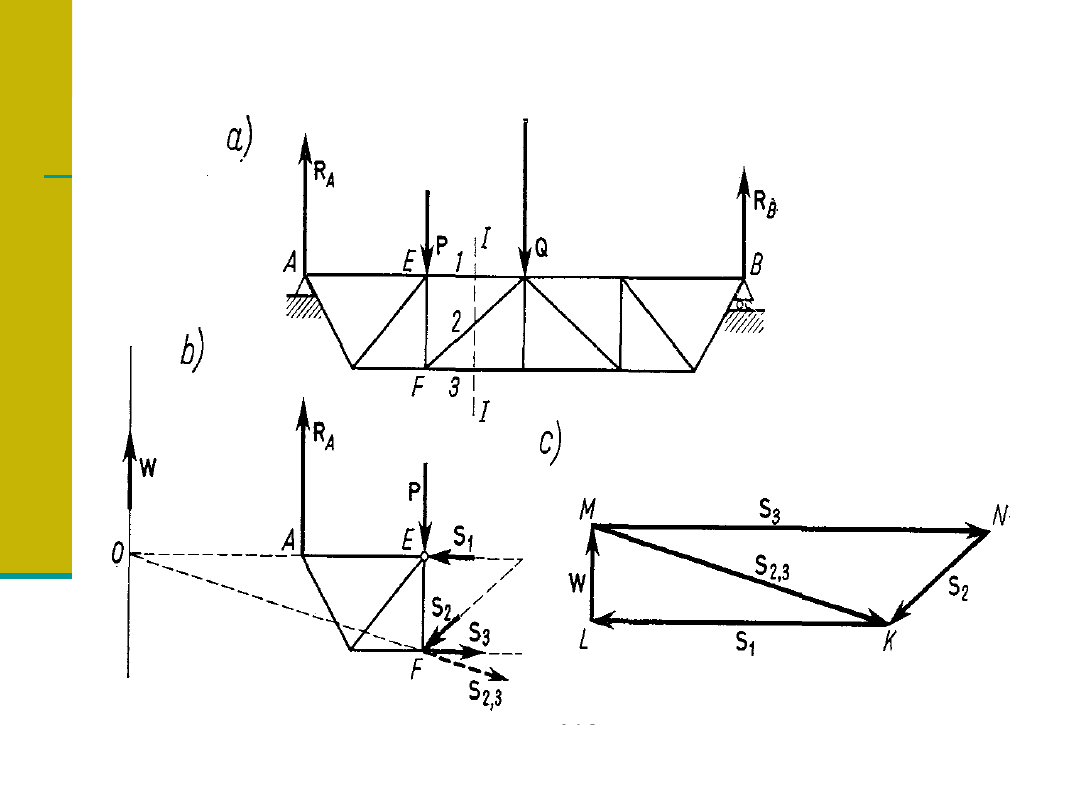
Plan sił Cremony dla kratownicy.

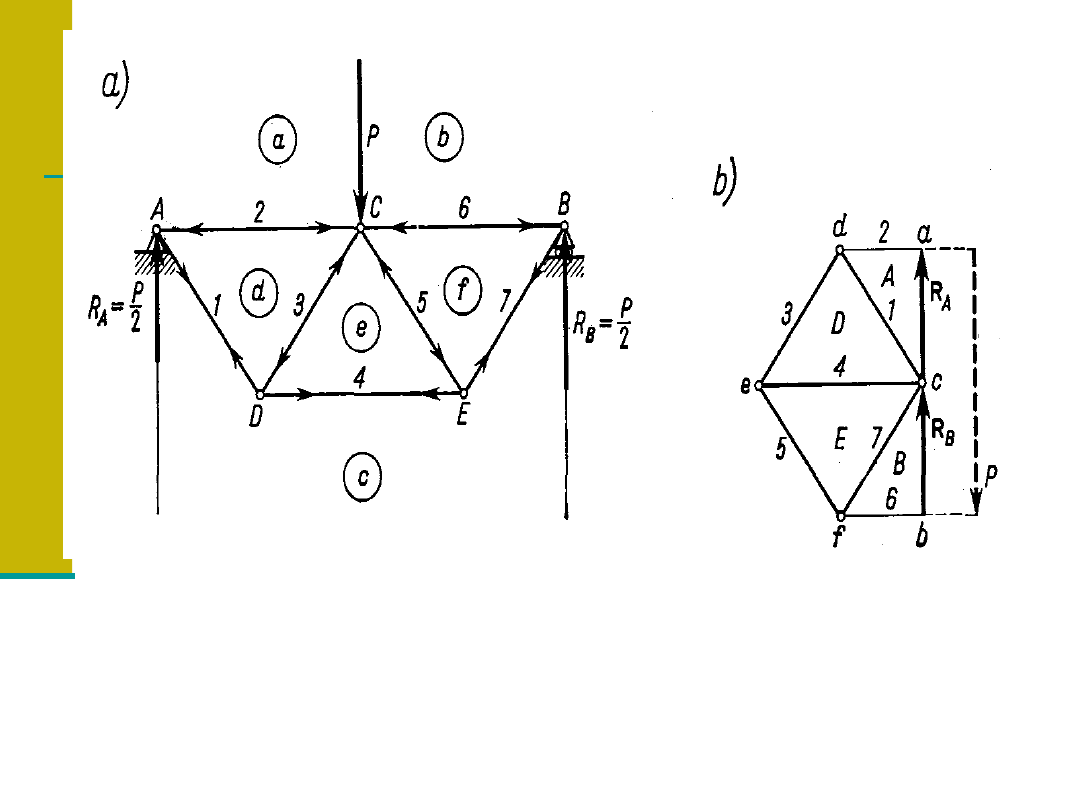
Plan sił Cremony dla kratownicy.

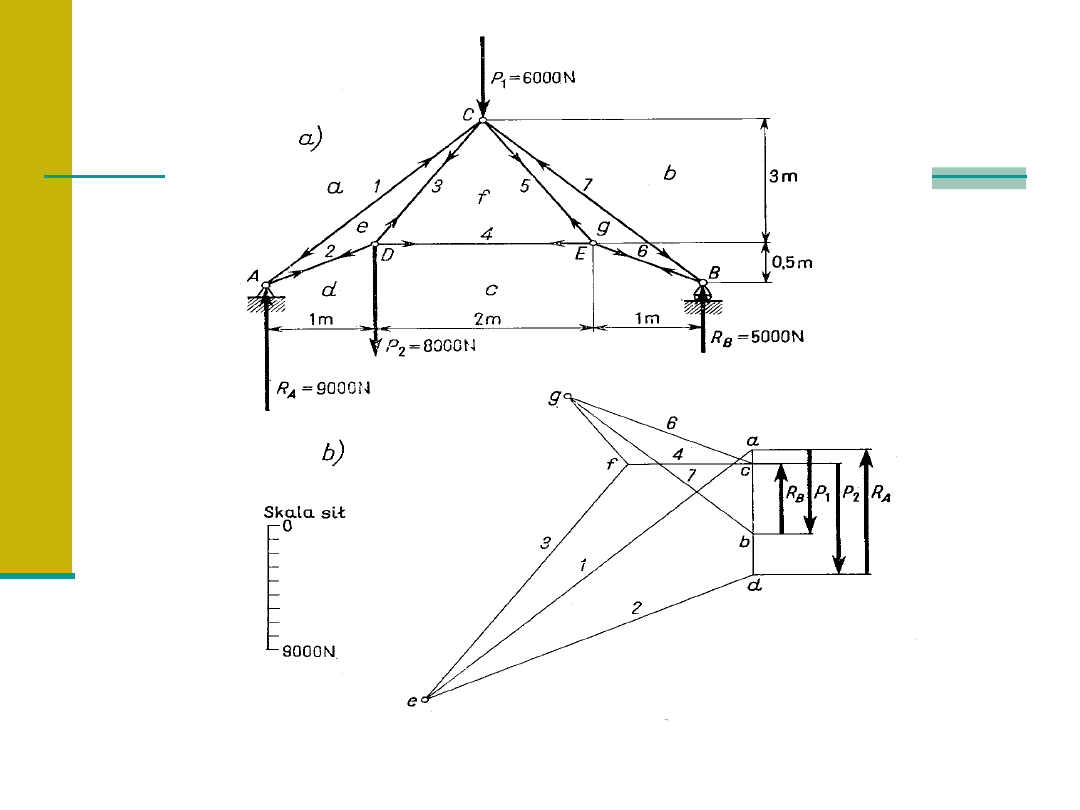
Plan sił Cremony dla kratownicy.

PYTANIA Z MECHANIKI TECHNICZNEJ

STATYKA

(część teoretyczna)



1.Podaj i omów trzy prawa Newtona.



2.Podaj i omów zasady statyki.



3.Omów stopnie swobody, więzy i reakcje (przykłady).



4.Pojęcie skalara i wektora (rodzaje wektorów).



5.Wektor w prawoskrętnym układzie kartezjańskim.



6.Dodawanie i mnożenie wektorów (zapis oraz ilustracja

graficzna).



7.Analityczne wyznaczanie wypadkowej przestrzennego

układu sił zbieżnych.



8.Równowaga płaskiego i przestrzennego układu sił

zbieżnych.



9.Moment siły względem punktu.



10.Moment siły względem dowolnego punktu w przestrzeni

( twierdzenie Varignona).



11.Wypadkowa dwóch sił równoległych zgodnie

skierowanych.



12.Para sił i moment pary sił.



13.Równoległe przesunięcie sił.



14.Redukcja płaskich układów sił.



15.Wyjaśnić pojęcie wektora i momentu głównego.



16.Redukcja płaskiego układu sił do jednej siły

wypadkowej-linia działania wypadkowej.



17.Omówić cztery przypadki redukcji płaskiego układu sił.



18.Równowaga dowolnego płaskiego układu sił.- trzy

sposoby zapisu.



19.Równowaga dowolnego przestrzennego układu sił.



20.Przestrzenny układ sił równoległych. Środek sił

równoległych.



21.Środek ciężkości brył - współrzędne.



22.Warunek statecznej wyznaczalności kratownic – przykłady



23.Rodzaje sił działających na kratownice.



24.Analityczne wyznaczanie sił działających na pręty w

kratownicy – omówienie przykładu.



25.Pojęcie prętów zerowych – przykłady.



26.Metoda graficzna wyznaczania sił w kratownicach –

omówienie przykładu.



27.Metoda Cremony, zasady i kolejność postępowania

(przykład).



28.Metoda Rittera wyznaczania sił w kratownicach (przykład).



29.Metoda Culmana wyznaczania sił w kratownicach

(przykład).



30.Omów pojęcie tarcia ślizgowego.