
Chapter 12
Chapter 12
Software Optimisation
Software Optimisation

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 2
Software Optimisation Chapter
Software Optimisation Chapter
This chapter consists of three parts:
This chapter consists of three parts:
Part 1:
Part 1:
Optimisation Methods.
Optimisation Methods.
Part 2:
Part 2:
Software Pipelining.
Software Pipelining.
Part 3:
Part 3:
Multi-cycle Loop Pipelining.
Multi-cycle Loop Pipelining.

Chapter 12
Chapter 12
Software Optimisation
Software Optimisation
Part 1 - Optimisation
Part 1 - Optimisation
Methods
Methods

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 4
Objectives
Objectives
Introduction to optimisation and optimisation procedure.
Introduction to optimisation and optimisation procedure.
Optimisation of C code using the code generation tools.
Optimisation of C code using the code generation tools.
Optimisation of assembly code.
Optimisation of assembly code.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 5
Introduction
Introduction
Software optimisation is the process of manipulating software code to achieve two main goals:
Software optimisation is the process of manipulating software code to achieve two main goals:
Faster execution time.
Faster execution time.
Small code size.
Small code size.
Note: It will be shown that in general there
Note: It will be shown that in general there
is a trade off between faster
is a trade off between faster
execution type and smaller code size.
execution type and smaller code size.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 6
Introduction
Introduction
To implement efficient software, the programmer must be familiar with:
To implement efficient software, the programmer must be familiar with:
Processor architecture.
Processor architecture.
Programming language (C, assembly or linear assembly).
Programming language (C, assembly or linear assembly).
The code generation tools (compiler, assembler and linker).
The code generation tools (compiler, assembler and linker).
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 7
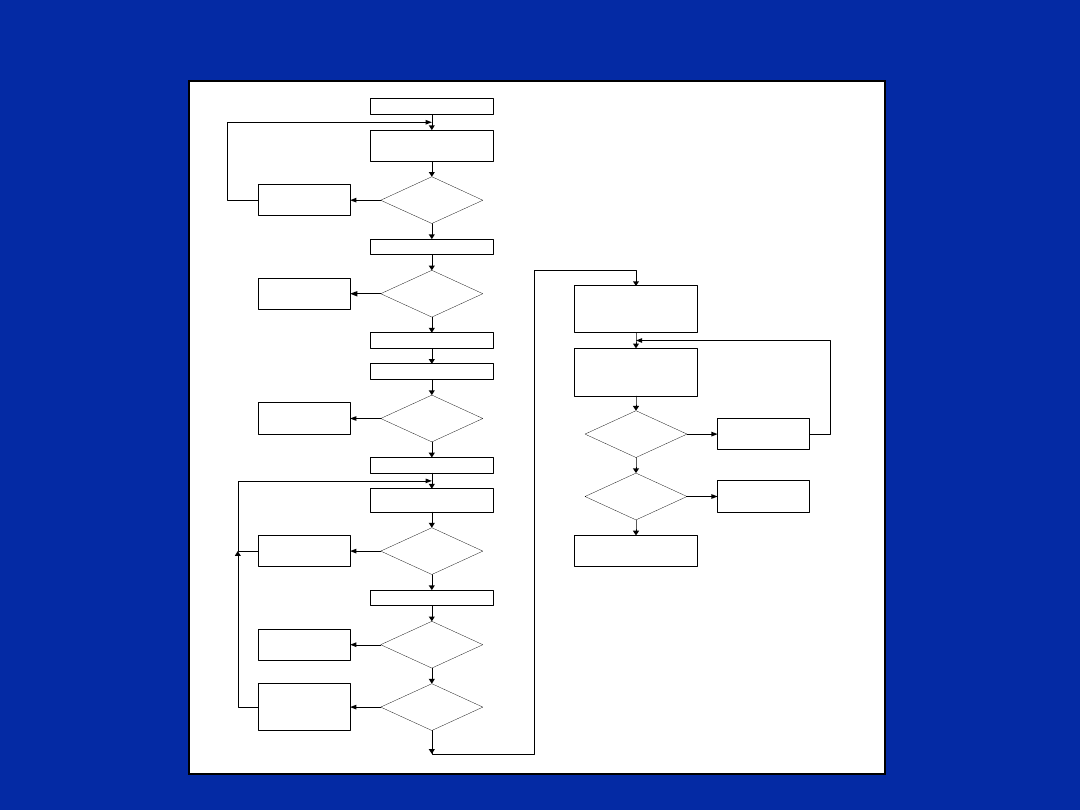
Code Optimisation Procedure
Code Optimisation Procedure
O p t im i s e A l g o r i t h m
P r o g r a m i n 'C '
a n d c o m p il e w i t h o u t
a n y o p ti m i s a t i o n
C o d e
F u n c t io n in g ?
M a k e t h e
n e c e s s a r y
c o r r e c t i o n ( s )
P r o fi l e C o d e
R e s u l t
S a t i s f a c t o r y ?
U s e in t r in s i c s
P r o fi l e C o d e
R e s u l t
S a t i s f a c t o r y ?
S e t n = 0 ( - O n )
C o m p i l e c o d e w i t h
- O n o p t io n
C o d e
F u n c t io n in g ?
M a k e t h e
n e c e s s a r y
c o r r e c t i o n ( s )
P r o fi l e C o d e
R e s u l t
S a t i s f a c t o r y ?
N < 3 ?
N
N
N
Y
N
N
N
N o f u r t h e r
o p t i m i s a t i o n i s
r e q u ir e d
Y
N o f u r t h e r
o p t i m i s a t i o n i s
r e q u ir e d
Y
P a s s t o n e x t
s t e p o f
o p t i m i s a i o n
( N = N + 1 )
y
N o f u r t h e r
o p t i m i s a t i o n i s
r e q u ir e d
I d e n t i f y C o d e
F u n c t i o n s t o b e f u r t h e r
o p ti m is e d f r o m
P r o fi l i n g R e s u l t
C o n v e r t c o d e n e e d i n g
o p t i m is a ti o n t o l in e a r
a s s e m b l y
C o d e
F u n c t i o n i n g ?
M a k e t h e
n e c e s s a r y
c o r r e c t i o n ( s )
R e s u lt
S a t i s f a c t o r y ?
N o f u r t h e r
o p t im is a ti o n i s
r e q u i r e d
W r i t e c o d e i n h a n d
a s s e m b l y
Y
N
Y
N
Y
Y
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 8
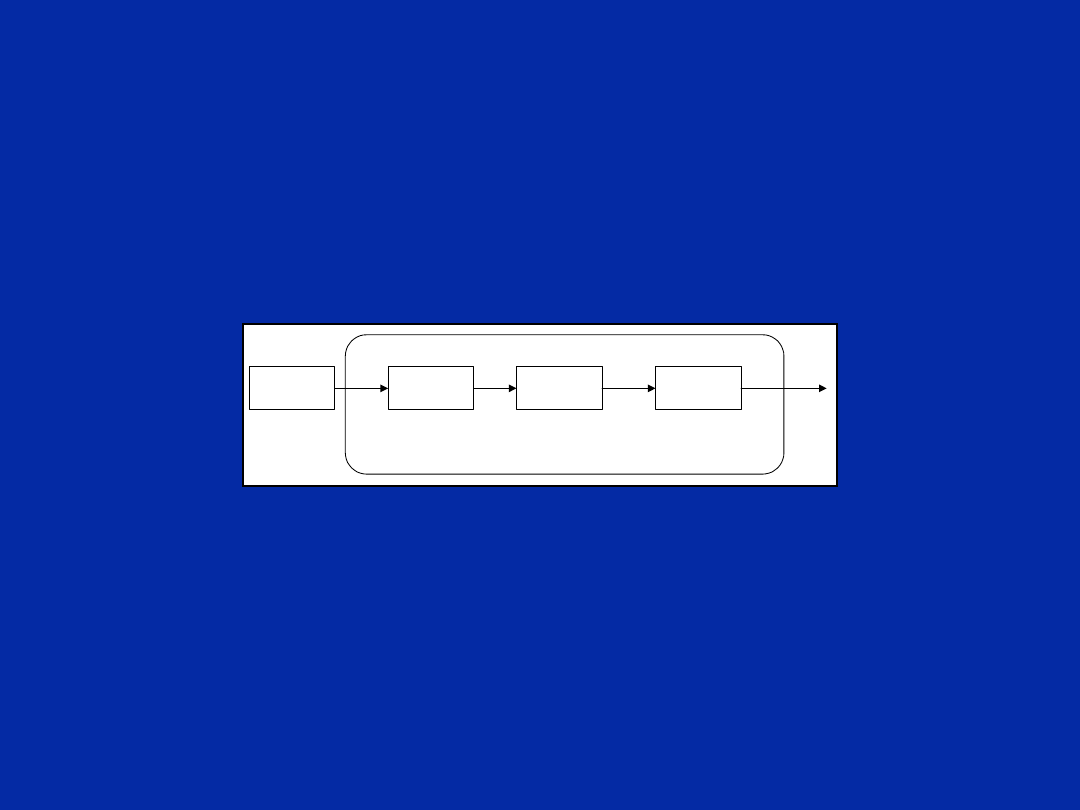
Code Optimisation Procedure
Code Optimisation Procedure
C s o u r c e
fi le
C o d e
g e n e r a to r
O p tim is e r
P a r s e r
. c
. o p t
. a s m
. if
O p tim is in g C o m p ile r

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 9
Optimising C Compiler Options
Optimising C Compiler Options
The ‘C6x optimising C compiler uses
The ‘C6x optimising C compiler uses
the ANSI C source code and can perform optimisation currently up-to about 80% compared with a hand-scheduled assembly.
the ANSI C source code and can perform optimisation currently up-to about 80% compared with a hand-scheduled assembly.
However, to achieve this level of optimisation, knowledge of different levels of optimisation is essential. Optimisation is performed at different stages and levels
However, to achieve this level of optimisation, knowledge of different levels of optimisation is essential. Optimisation is performed at different stages and levels .

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 10
Assembly Optimisation
Assembly Optimisation
To develop an appreciation of how to optimise code, let us optimise an
To develop an appreciation of how to optimise code, let us optimise an
FIR filter:
FIR filter:
For simplicity we write:
For simplicity we write:
1
0
N
k
k
n
x
k
h
n
y
1
0
N
i
i
x
i
h
n
y
[1]
[1]

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 11
Assembly Optimisation
Assembly Optimisation
To implement Equation 1, we need to perform the following steps:
To implement Equation 1, we need to perform the following steps:
(1)
(1)
Load the sample x[i].
Load the sample x[i].
(2)
(2)
Load the coefficients h[i].
Load the coefficients h[i].
(3)
(3)
Multiply x[i] and h[i].
Multiply x[i] and h[i].
(4)
(4)
Add (x[i] * h[i]) to the content of an accumulator.
Add (x[i] * h[i]) to the content of an accumulator.
(5)
(5)
Repeat steps 1 to 4 N-1 times.
Repeat steps 1 to 4 N-1 times.
(6)
(6)
Store the value in the accumulator to y.
Store the value in the accumulator to y.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 12
Assembly Optimisation
Assembly Optimisation
Steps 1 to 6 can be translated into the following ‘C6x assembly code:
Steps 1 to 6 can be translated into the following ‘C6x assembly code:
MVK
.S1
0,B0
; Initialise the loop counter
MVK
.S1
0,A5
; Initialise the accumulator
loop
LDH
.D1
*A8++,A2
; Load the samples x[i]
LDH
.D1
*A9++,A3
; Load the coefficients h[i]
NOP
4
; Add “nop 4” because the LDH has a latency of 5.
MPY
.M1
A2,A3,A4
; Multiply x[i] and h[i]
NOP
; Multiply has a latency of 2 cycles
ADD
.L1
A4,A5,A5
; Add “x [i]. h[i]” to the accumulator
[B0]
SUB
.L2
B0,1,B0
;
[B0]
B
.S1
loop
; loop overhead
NOP
5
; The branch has a latency of 6 cycles

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 13
Assembly Optimisation
Assembly Optimisation
In order to optimise the code, we need to:
In order to optimise the code, we need to:
(1)
(1)
Use instructions in parallel.
Use instructions in parallel.
(2)
(2)
Remove the NOPs.
Remove the NOPs.
(3)
(3)
Remove the loop overhead (remove SUB and B: loop unrolling).
Remove the loop overhead (remove SUB and B: loop unrolling).
(4)
(4)
Use word access or double-word access instead of byte or half-word access.
Use word access or double-word access instead of byte or half-word access.
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 14
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.D1
.D1
.D2
.D2
Cycle
Cycle
.D1
.D1
.D2
.D2
1
1
2
2
3
3
4
4
5
5
6
6
7
7
8
8
9
9
10
10
11
11
12
12
13
13
14
14
15
15
16
16
NOP
NOP
Step 1 - Using Parallel
Step 1 - Using Parallel
Instructions
Instructions
ldh
ldh
mpy
mpy
ldh
ldh
b
b
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
add
add
sub
sub
nop
nop

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 15
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.D1
.D1
.D2
.D2
Cycle
Cycle
.D1
.D1
.D2
.D2
1
1
2
2
3
3
4
4
5
5
6
6
7
7
8
8
9
9
10
10
11
11
12
12
13
13
14
14
15
15
16
16
NOP
NOP
Step 1 - Using Parallel
Step 1 - Using Parallel
Instructions
Instructions
ldh
ldh
mpy
mpy
ldh
ldh
b
b
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
nop
add
add
sub
sub
nop
nop
Note: Not all instructions can be put in
Note: Not all instructions can be put in
parallel since the result of one unit is
parallel since the result of one unit is
used as an input to the following unit.
used as an input to the following unit.
Note: Not all instructions can be put in
Note: Not all instructions can be put in
parallel since the result of one unit is
parallel since the result of one unit is
used as an input to the following unit.
used as an input to the following unit.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 16
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.D1
.D1
.D2
.D2
Cycle
Cycle
.D1
.D1
.D2
.D2
1
1
2
2
3
3
4
4
5
5
6
6
7
7
8
8
9
9
10
10
11
11
12
12
13
13
14
14
15
15
16
16
NOP
NOP
Step 2 - Removing the NOPs
Step 2 - Removing the NOPs
ldh
ldh
mpy
mpy
ldh
ldh
b
b
nop
nop
nop
nop
add
add
sub
sub
nop
nop
loop LDH
.D1 *A8++,A2
LDH
.D1 *A9++,A3
[B0] SUB
.L2 B0,1,B0
[B0] B
.S1 loop
NOP
2
MPY
.M1 A2,B3,A4
NOP
ADD
.L1 A4,A5,A5
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 17
Step 3 - Loop Unrolling
Step 3 - Loop Unrolling
The SUB and B instructions consume at least two extra cycles per
The SUB and B instructions consume at least two extra cycles per
iteration (this is known as branch overhead).
iteration (this is known as branch overhead).
loop
LDH
.D1
*A8++,A2
LDH
.D1
*A9++,A3
[B0]
SUB
.L2
B0,1,B0
[B0]
B
.S1
loop
NOP
2
MPY
.M1
A2,A3,A4
NOP
ADD
.L1
A4,A5,A5
LDH
.D1
*A8++,A2
;Start of iteration 1
||
LDH
.D2
*B9++,B3
NOP
4
MPY
.M1X
A2,B3,A4
;Use of cross path
NOP
ADD
.L1
A4,A5,A5
LDH
.D1
*A8++,A2
;Start of iteration 2
||
LDH
.D2
*B9++,B3
NOP
4
MPY
.M1
A2,B3,A4
NOP
ADD
.L1
A4,A5,A5
;
:
;
:
;
:
LDH
.D1
*A8++,A2
; Start of iteration n
||
LDH
.D2
*B9++,B3
NOP
4
MPY
.M1
A2,B3,A4
NOP
ADD
.L1
A4,A5,A5

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 18
Step 4 - Word or Double Word
Step 4 - Word or Double Word
Access
Access
The ‘C6711 has two 64-bit data buses for data memory access and therefore up to two 64-bit can be loaded into the registers at any time (see Chapter 2).
The ‘C6711 has two 64-bit data buses for data memory access and therefore up to two 64-bit can be loaded into the registers at any time (see Chapter 2).
In addition the ‘C6711 devices have variants of the multiplication instruction to support different operation (see Chapter 2).
In addition the ‘C6711 devices have variants of the multiplication instruction to support different operation (see Chapter 2).
Note: Store can only be up to 32-bit.
Note: Store can only be up to 32-bit.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 19
loop
LDW
.D1
*A9++,A3 ; 32-bit word is loaded in a single cycle
||
LDW
.D2
*B6++,B1
NOP
4
[B0]
SUB
.L2
[B0]
B
.S1
loop
NOP
2
MPY
.M1
A3,B1,A4
||
MPYH
.M2
A3,B1,B3
NOP
ADD
.L1
A4,B3,A5
Step 4 - Word or Double Word
Step 4 - Word or Double Word
Access
Access
Using word access, MPY and MPYH the previous code can be written as:
Using word access, MPY and MPYH the previous code can be written as:
Note: By loading words and using MPY and MPYH instructions the execution time has
Note: By loading words and using MPY and MPYH instructions the execution time has
been halved since in each iteration two 16x16-bit multiplications are performed.
been halved since in each iteration two 16x16-bit multiplications are performed.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 20
Optimisation Summary
Optimisation Summary
It has been shown that there are four complementary methods for code optimisation:
It has been shown that there are four complementary methods for code optimisation:
Using instructions in parallel.
Using instructions in parallel.
Filling the delay slots with useful code.
Filling the delay slots with useful code.
Using word or double word load.
Using word or double word load.
Loop unrolling.
Loop unrolling.
These
These
increase performance
increase performance
and
and
reduce code size.
reduce code size.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 21
Optimisation Summary
Optimisation Summary
This
This
increases performance
increases performance
but
but
increases code size.
increases code size.
It has been shown that there are four complementary methods for code optimisation:
It has been shown that there are four complementary methods for code optimisation:
Using instructions in parallel.
Using instructions in parallel.
Filling the delay slots with useful code.
Filling the delay slots with useful code.
Using word or double word load.
Using word or double word load.
Loop unrolling.
Loop unrolling.

Chapter 12
Chapter 12
Software Optimisation
Software Optimisation
Part 2 - Software
Part 2 - Software
Pipelining
Pipelining

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 23
Objectives
Objectives
Why using Software
Why using Software
Pipelining, SP?
Pipelining, SP?
Understand software
Understand software
pipelining concepts.
pipelining concepts.
Use software pipelining
Use software pipelining
procedure.
procedure.
Code the word-wide software
Code the word-wide software
pipelined dot-product routine.
pipelined dot-product routine.
Determine if your pipelined
Determine if your pipelined
code is more efficient with or
code is more efficient with or
without prolog and epilog.
without prolog and epilog.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 24
Why using Software Pipelining,
Why using Software Pipelining,
SP?
SP?
SP creates highly optimized loop-
SP creates highly optimized loop-
code by:
code by:
Putting several instructions in
Putting several instructions in
parallel.
parallel.
Filling delay slots with useful code.
Filling delay slots with useful code.
Maximizes functional units.
Maximizes functional units.
SP is implemented by simply using
SP is implemented by simply using
the tools:
the tools:
Compiler options -o2 or -o3.
Compiler options -o2 or -o3.
Assembly Optimizer if .sa file.
Assembly Optimizer if .sa file.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 25
Software Pipeline concept
Software Pipeline concept
LDH
LDH
|| LDH
|| LDH
MPY
MPY
ADD
ADD
How many cycles would
How many cycles would
it take to perform this
it take to perform this
loop 5 times?
loop 5 times?
(Disregard delay-slots).
(Disregard delay-slots).
______________ cycles
______________ cycles
To explain the concept of software
To explain the concept of software
pipelining, we
pipelining, we
will assume
will assume
that all
that all
instructions execute in one cycle.
instructions execute in one cycle.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 26
Software Pipeline Example
Software Pipeline Example
LDH
LDH
|| LDH
|| LDH
MPY
MPY
ADD
ADD
How many cycles would
How many cycles would
it take to perform this
it take to perform this
loop 5 times?
loop 5 times?
(Disregard delay-slots).
(Disregard delay-slots).
______________ cycles
______________ cycles
5 x 3 = 15
5 x 3 = 15
Let’s examine hardware
Let’s examine hardware
(functional units) usage ...
(functional units) usage ...

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 27
Non-Pipelined Code
Non-Pipelined Code
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.D1
.D1
.D2
.D2
1
1
Cycle
Cycle
ldh
ldh
ldh
ldh
2
2
mpy
mpy
3
3
add
add
4
4
ldh
ldh
ldh
ldh
5
5
mpy
mpy
6
6
add
add
7
7
ldh
ldh
ldh
ldh
8
8
mpy
mpy
9
9
add
add
.
.
D1
D1
.
.
D2
D2

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 28
Pipelining Code
Pipelining Code
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.D1
.D1
.D2
.D2
1
1
Cycle
Cycle
ldh
ldh
ldh
ldh
2
2
mpy
mpy
ldh
ldh
ldh
ldh
3
3
add
add
mpy
mpy
ldh
ldh
ldh
ldh
4
4
add
add
mpy
mpy
ldh
ldh
ldh
ldh
5
5
add
add
mpy
mpy
ldh
ldh
ldh
ldh
6
6
add
add
mpy
mpy
7
7
add
add
Pipelining these instructions took 1/2 the cycles!
Pipelining these instructions took 1/2 the cycles!

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 29
Pipelining Code
Pipelining Code
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.D1
.D1
.D2
.D2
1
1
Cycle
Cycle
ldh
ldh
ldh
ldh
2
2
mpy
mpy
ldh
ldh
ldh
ldh
3
3
add
add
mpy
mpy
ldh
ldh
ldh
ldh
4
4
add
add
mpy
mpy
ldh
ldh
ldh
ldh
5
5
add
add
mpy
mpy
ldh
ldh
ldh
ldh
6
6
add
add
mpy
mpy
7
7
add
add
Pipelining these instructions takes only 7 cycles!
Pipelining these instructions takes only 7 cycles!

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 30
Loop Kernel
Loop Kernel
Single-cycle “loop”
Single-cycle “loop”
iterated three times.
iterated three times.
Pipelining Code
Pipelining Code
.M1
.M1
.L1
.L1
.D1
.D1
.D2
.D2
ldh
ldh
ldh
ldh
1
1
mpy
mpy
2
2
ldh
ldh
ldh
ldh
add
add
3
3
mpy
mpy
ldh
ldh
ldh
ldh
mpy
mpy
add
add
ldh
ldh
ldh
ldh
4
4
add
add
mpy
mpy
5
5
ldh
ldh
ldh
ldh
add
add
6
6
mpy
mpy
7
7
add
add
Prolog
Prolog
Staging for loop.
Staging for loop.
Epilog
Epilog
Completing final
Completing final
operations.
operations.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 31
Pipelined Code
Pipelined Code
prolog:
prolog:
LDH
LDH
; load 1
; load 1
||
||
LDH
LDH
MPY
MPY
; mpy 1
; mpy 1
||
||
LDH
LDH
; load 2
; load 2
||
||
LDH
LDH
loop:
loop:
ADD
ADD
; add 1
; add 1
||
||
MPY
MPY
; mpy
; mpy
2
2
||
||
LDH
LDH
; load 3
; load 3
||
||
LDH
LDH
ADD
ADD
; add 2
; add 2
||
||
MPY
MPY
; mpy
; mpy
3
3
||
||
LDH
LDH
; load 4
; load 4
||
||
LDH
LDH
.
.
.
.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 32
Software Pipelining Procedure
Software Pipelining Procedure
1.
1.
Write algorithm in C code & verify.
Write algorithm in C code & verify.
2.
2.
Write ‘C6x Linear Assembly code.
Write ‘C6x Linear Assembly code.
3.
3.
Create dependency graph.
Create dependency graph.
4.
4.
Allocate registers.
Allocate registers.
5.
5.
Create scheduling table.
Create scheduling table.
6.
6.
Translate scheduling table to ‘C6x code.
Translate scheduling table to ‘C6x code.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 33
short DotP(short *m, short *n, short count)
short DotP(short *m, short *n, short count)
{ int i;
{ int i;
short product;
short product;
short sum = 0;
short sum = 0;
for (i=0; i < count; i++)
for (i=0; i < count; i++)
{
{
product = m[i] * n[i];
product = m[i] * n[i];
sum += product;
sum += product;
}
}
return(sum);
return(sum);
}
}
Software Pipelining Example (Step
Software Pipelining Example (Step
1)
1)

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 34
Software Pipelining Procedure
Software Pipelining Procedure
1.
1.
Write algorithm in C code & verify.
Write algorithm in C code & verify.
2.
2.
Write ‘C6x Linear Assembly code.
Write ‘C6x Linear Assembly code.
3.
3.
Create dependency graph.
Create dependency graph.
4.
4.
Allocate registers.
Allocate registers.
5.
5.
Create scheduling table.
Create scheduling table.
6.
6.
Translate scheduling table to ‘C6x code.
Translate scheduling table to ‘C6x code.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 35
; for (i=0; i < count; i++)
; for (i=0; i < count; i++)
; prod = m[i] * n[i];
; prod = m[i] * n[i];
; sum += prod;
; sum += prod;
loop:
loop:
ldh
ldh
*p_m++, m
*p_m++, m
ldh
ldh
*p_n++, n
*p_n++, n
mpy
mpy
m, n, prod
m, n, prod
add
add
prod, sum, sum
prod, sum, sum
[count]
[count]
sub
sub
count, 1, count
count, 1, count
[count]
[count]
b
b
loop
loop
1.
1.
No NOP’s required.
No NOP’s required.
2.
2.
No parallel instructions required.
No parallel instructions required.
3.
3.
You don’t have to specify:
You don’t have to specify:
Functional units, or
Functional units, or
Registers.
Registers.
Write code in Linear Assembly
Write code in Linear Assembly
(Step 2)
(Step 2)

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 36
Software Pipelining Procedure
Software Pipelining Procedure
1.
1.
Write algorithm in C code & verify.
Write algorithm in C code & verify.
2.
2.
Write ‘C6x Linear Assembly code.
Write ‘C6x Linear Assembly code.
3.
3.
Create a dependency graph (4 steps).
Create a dependency graph (4 steps).
4.
4.
Allocate registers.
Allocate registers.
5.
5.
Create scheduling table.
Create scheduling table.
6.
6.
Translate scheduling table to ‘C6x code.
Translate scheduling table to ‘C6x code.
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 37
Dependency Graph Terminology
Dependency Graph Terminology
a
a
b
b
na
na
Child Node
Child Node
Parent Node
Parent Node
Path
Path
5
5
.L
.L
.D
.D
.D
.D
LDH
LDH
LDH
LDH
5
5
NOT
NOT
Conditional Path
Conditional Path

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 38
Dependency Graph Steps
Dependency Graph Steps
(a)
(a)
Draw the algorithm nodes
Draw the algorithm nodes
and paths.
and paths.
(b)
(b)
Write the number of cycles it
Write the number of cycles it
takes for each instruction to
takes for each instruction to
complete execution.
complete execution.
(c)
(c)
Assign “required” function
Assign “required” function
units to each node.
units to each node.
(d)
(d)
Partition the nodes to A and
Partition the nodes to A and
B sides and assign sides to all
B sides and assign sides to all
functional units.
functional units.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 39
Dependency Graph (Step a)
Dependency Graph (Step a)
In this step each instruction is
In this step each instruction is
represented by a node.
represented by a node.
The node is represented by a
The node is represented by a
circle, where:
circle, where:
Outside: write instruction.
Outside: write instruction.
Inside: register where result is
Inside: register where result is
written.
written.
Nodes are then connected by
Nodes are then connected by
paths showing the data flow.
paths showing the data flow.
Note: Conditional paths are
Note: Conditional paths are
represented by
represented by
dashed
dashed
lines.
lines.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 40
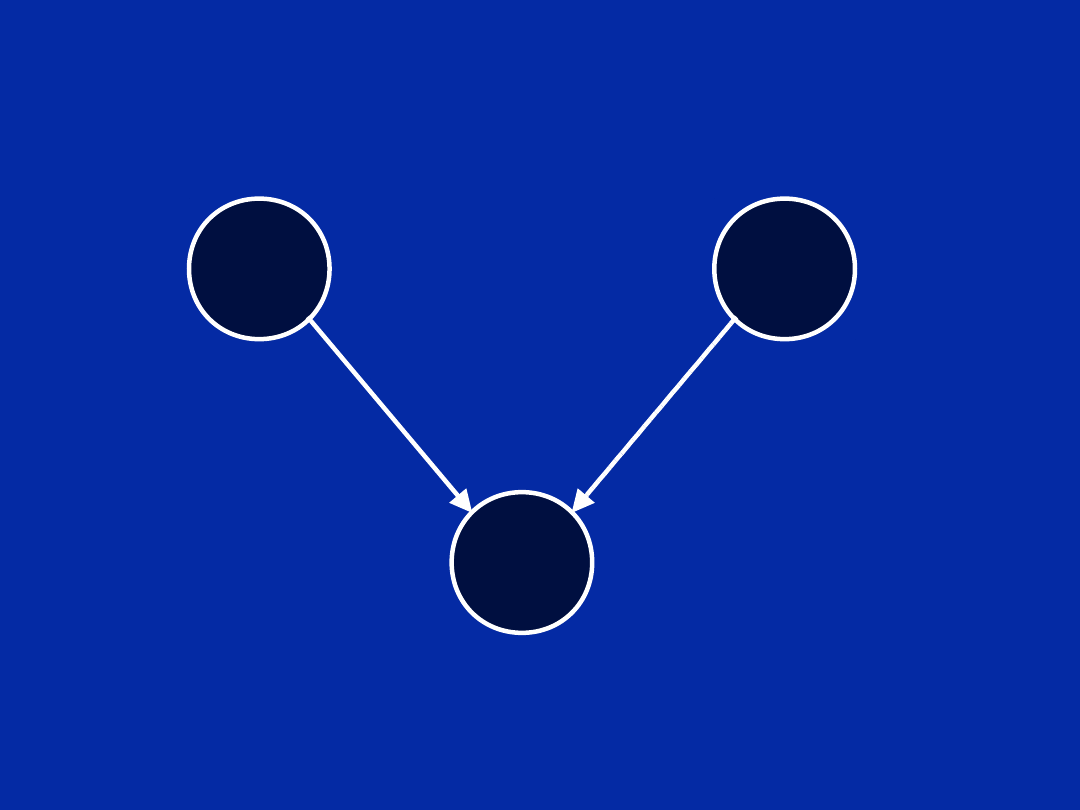
Dependency Graph (Step a)
Dependency Graph (Step a)
m
m
LDH
LDH

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 41
Dependency Graph (Step a)
Dependency Graph (Step a)
m
m
LDH
LDH
n
n
LDH
LDH
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
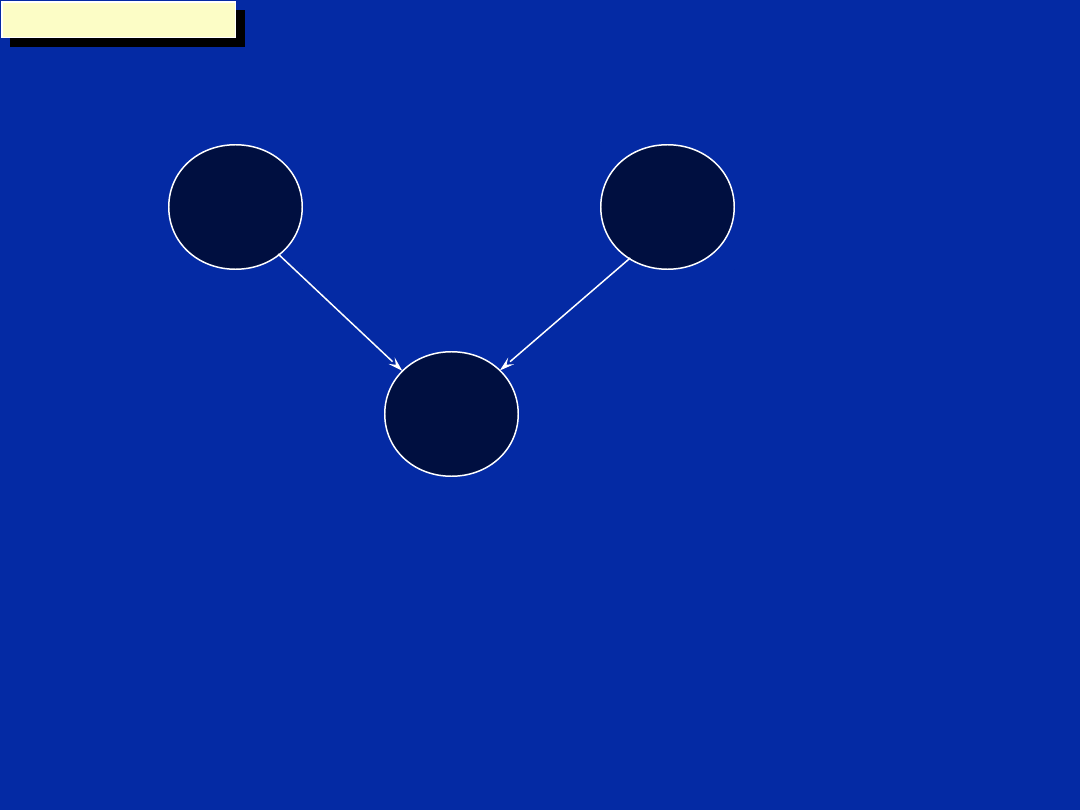
Chapter 12, Slide 42
Dependency Graph (Step a)
Dependency Graph (Step a)
m
m
LDH
LDH
n
n
LDH
LDH
prod
prod
MPY
MPY
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
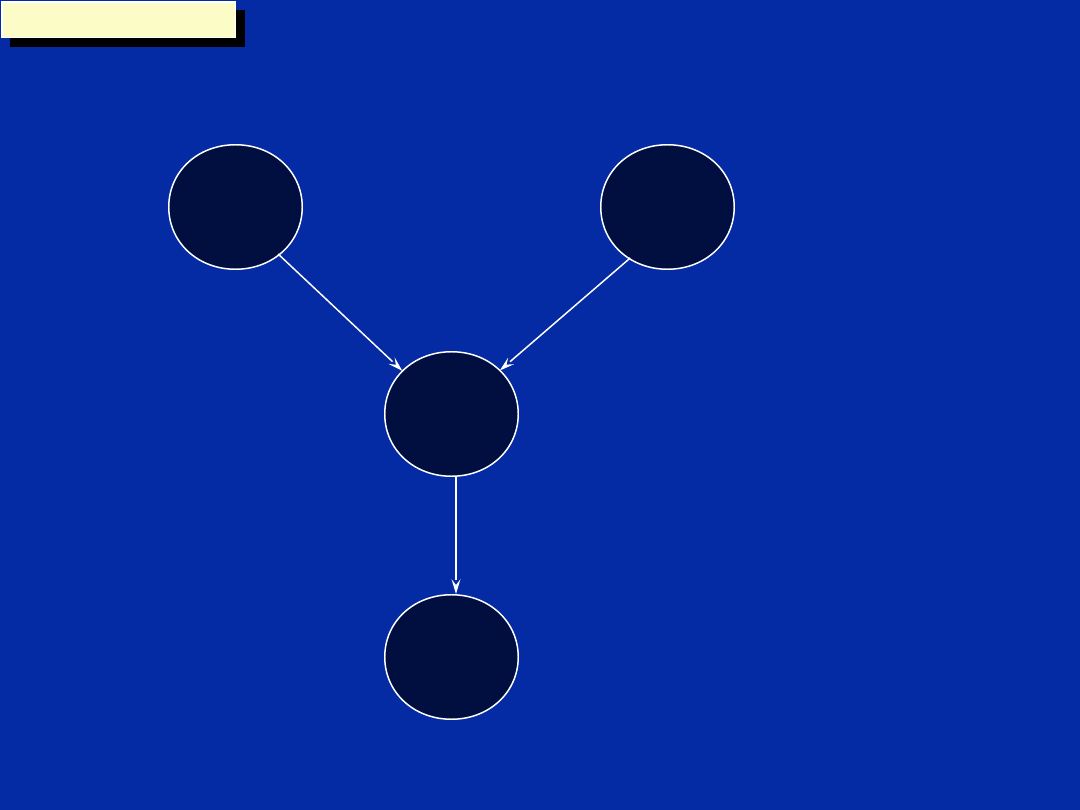
Chapter 12, Slide 43
Dependency Graph (Step a)
Dependency Graph (Step a)
m
m
LDH
LDH
n
n
LDH
LDH
prod
prod
MPY
MPY
sum
sum
ADD
ADD
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
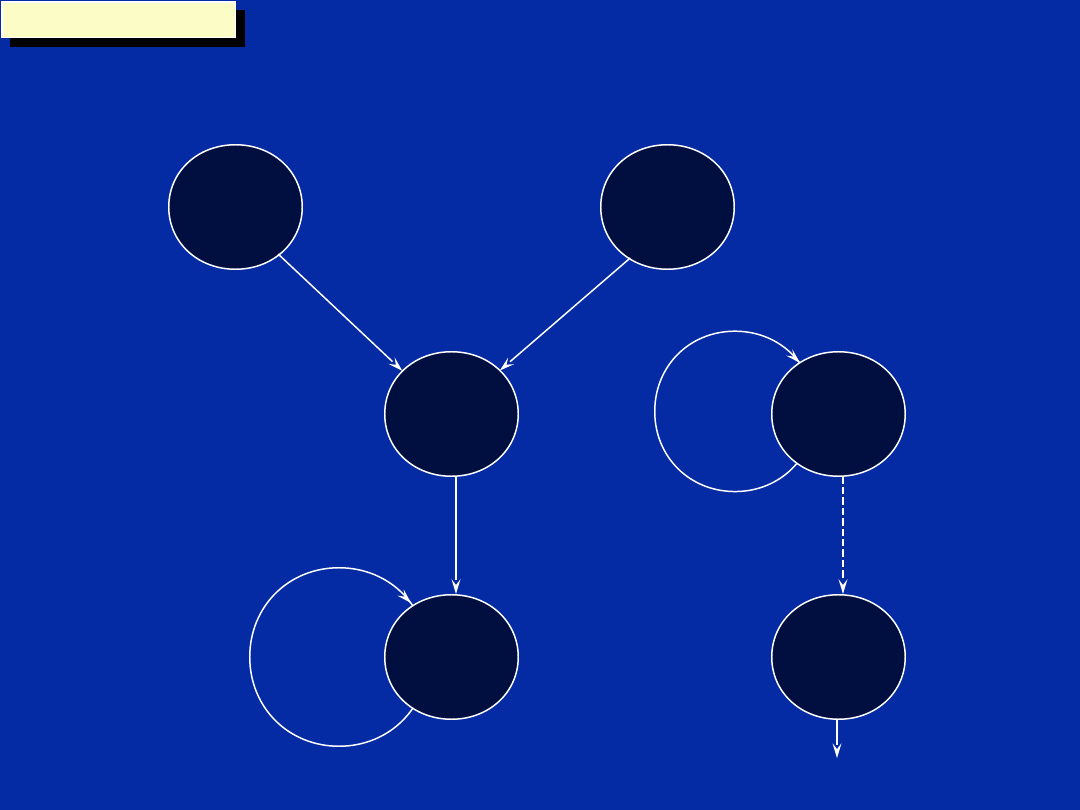
Chapter 12, Slide 44
Dependency Graph (Step a)
Dependency Graph (Step a)
m
m
LDH
LDH
n
n
LDH
LDH
prod
prod
MPY
MPY
sum
sum
ADD
ADD
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
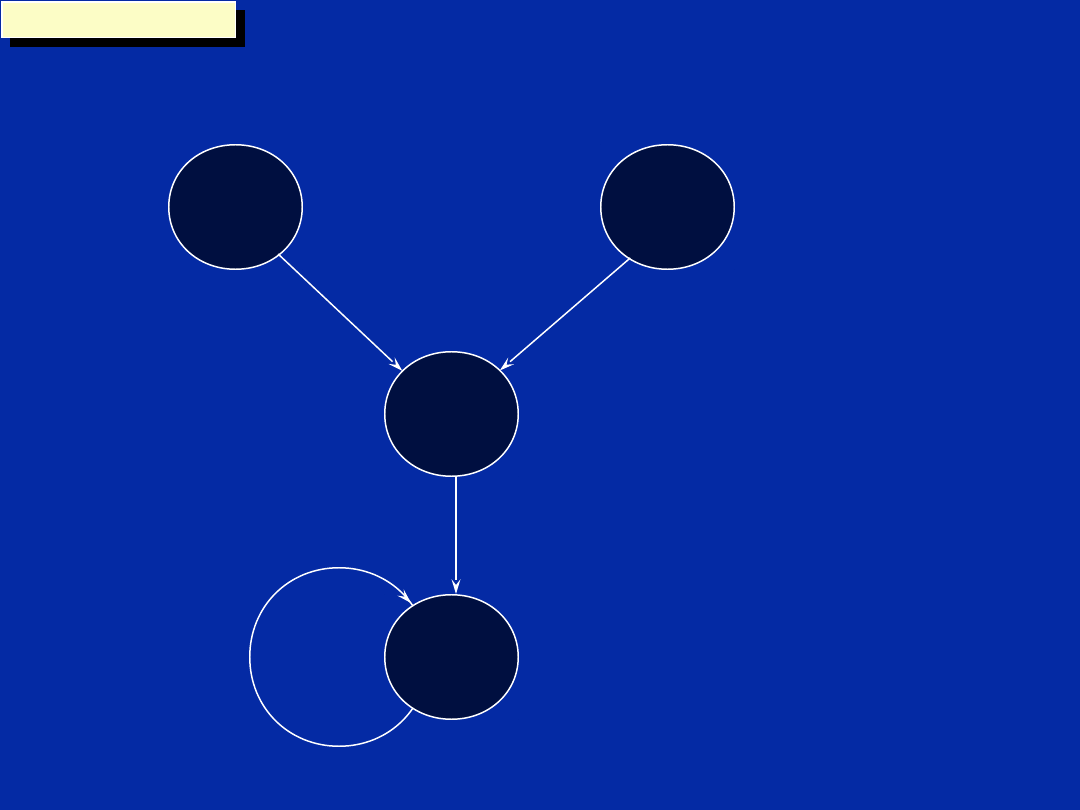
Chapter 12, Slide 45
Dependency Graph (Step a)
Dependency Graph (Step a)
m
m
LDH
LDH
n
n
LDH
LDH
prod
prod
MPY
MPY
sum
sum
ADD
ADD
count
count
SUB
SUB
loop
loop
B
B

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 46
Dependency Graph (Step b)
Dependency Graph (Step b)
In this step the number of
In this step the number of
cycles it takes for each
cycles it takes for each
instruction to complete
instruction to complete
execution is added to the
execution is added to the
dependency graph.
dependency graph.
It is written along the
It is written along the
associated data path.
associated data path.
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 47
Dependency Graph (Step b)
Dependency Graph (Step b)
m
m
LDH
LDH
n
n
LDH
LDH
prod
prod
MPY
MPY
sum
sum
ADD
ADD
5
5
5
5
2
2
1
1
count
count
SUB
SUB
loop
loop
B
B
1
1
1
1
6
6

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 48
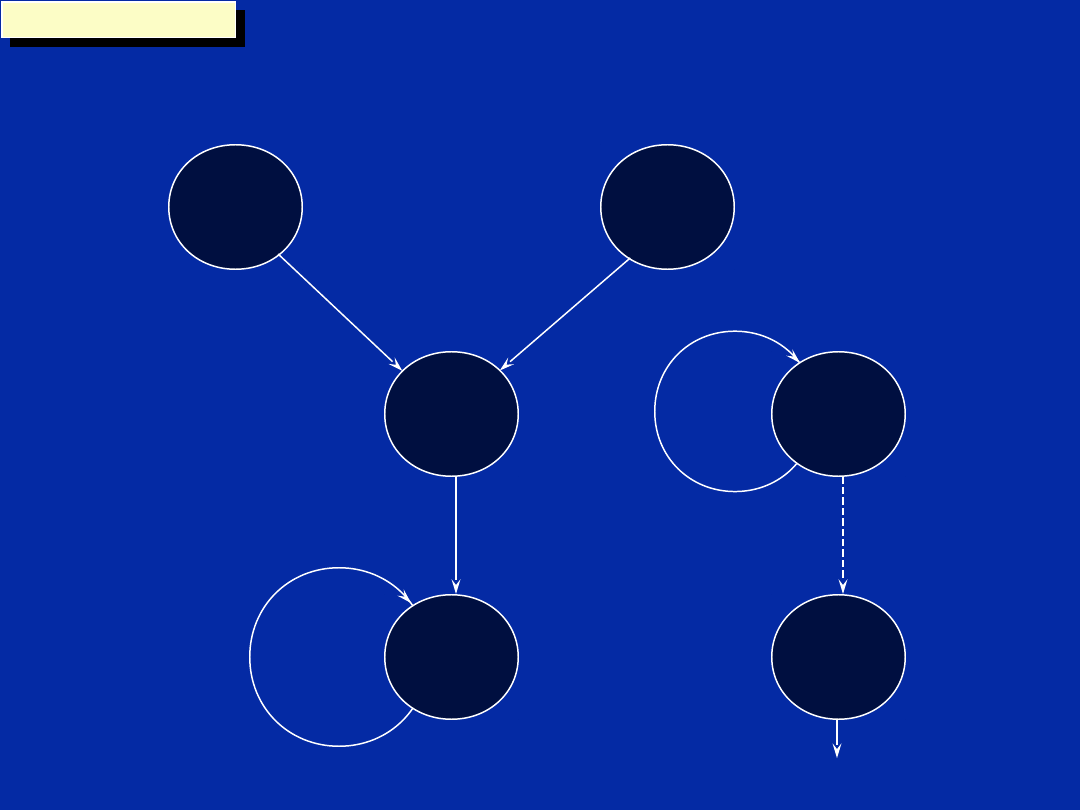
Dependency Graph (Step c)
Dependency Graph (Step c)
In this step functional units are
In this step functional units are
assigned to each node.
assigned to each node.
It is advantageous to start
It is advantageous to start
allocating units to instructions
allocating units to instructions
which require a specific unit:
which require a specific unit:
Load/Store.
Load/Store.
Branch.
Branch.
We do not need to be concerned
We do not need to be concerned
with multiply as this is the only
with multiply as this is the only
operation that the .M unit
operation that the .M unit
performs.
performs.
Note: The side is not allocated at
Note: The side is not allocated at
this stage.
this stage.
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 49
Dependency Graph (Step c)
Dependency Graph (Step c)
m
m
LDH
LDH
n
n
LDH
LDH
prod
prod
MPY
MPY
sum
sum
ADD
ADD
.D
.D
.D
.D
5
5
5
5
2
2
1
1
count
count
SUB
SUB
loop
loop
B
B
1
1
1
1
.M
.M
.S
.S
6
6

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 50
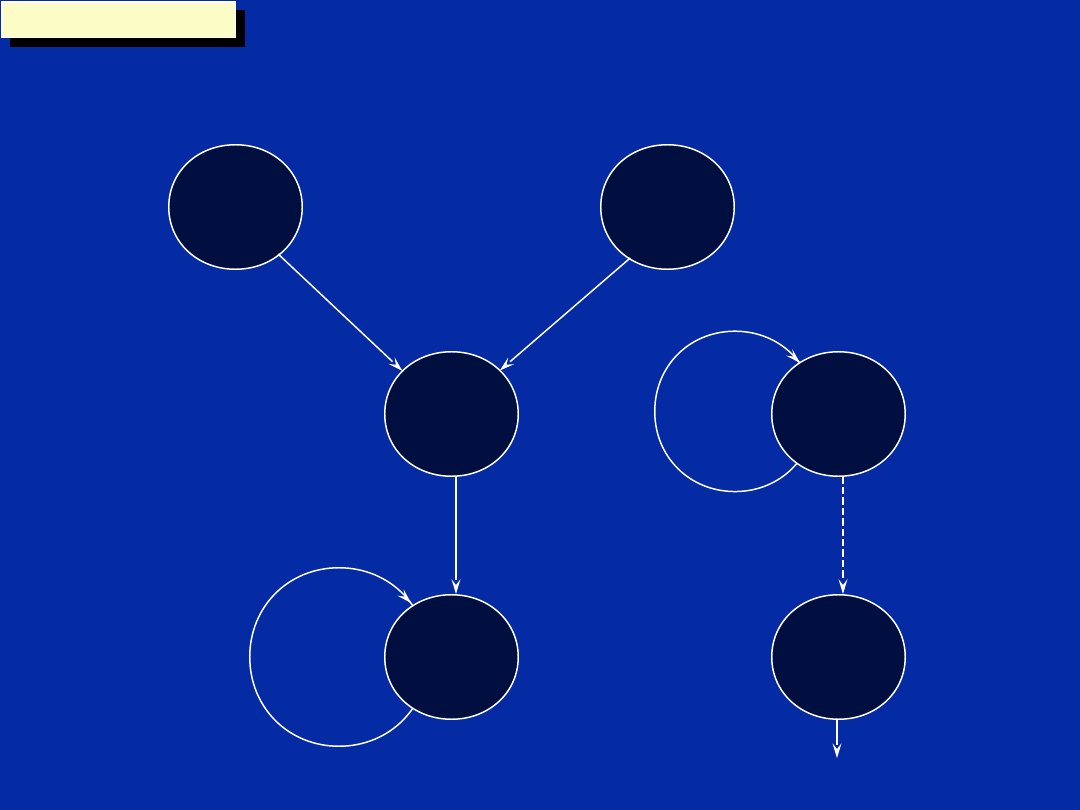
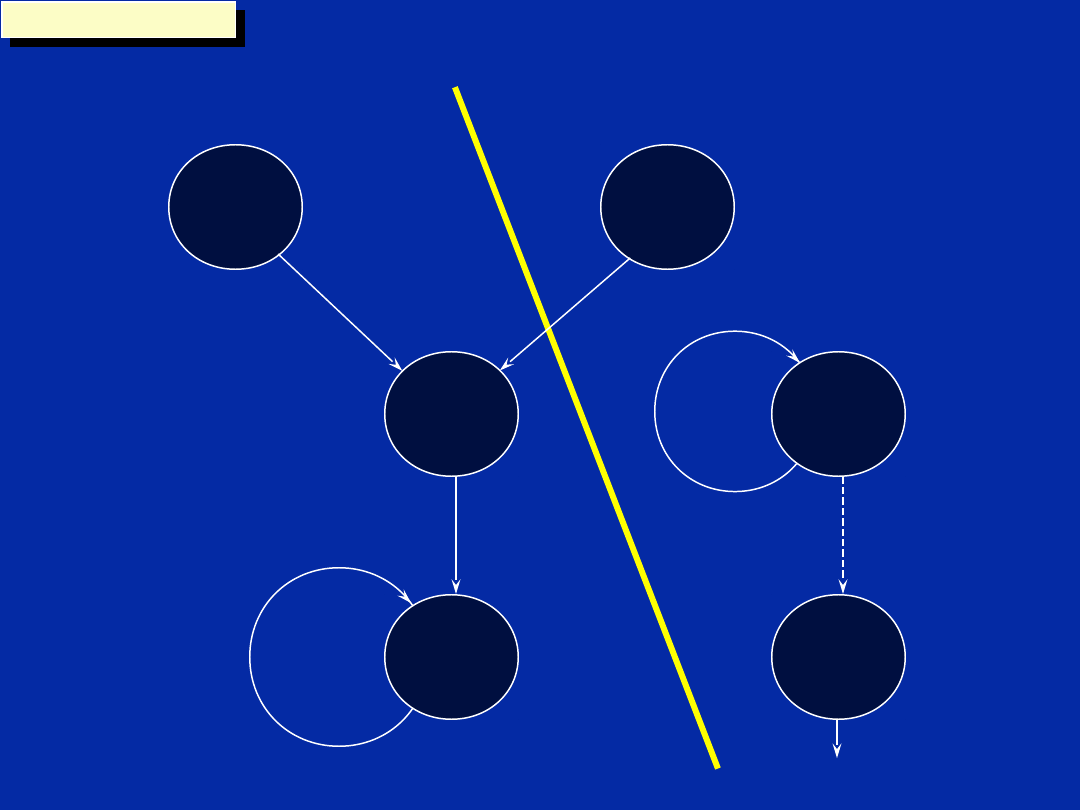
Dependency Graph (Step d)
Dependency Graph (Step d)
The data path is partitioned into
The data path is partitioned into
side A and B at this stage.
side A and B at this stage.
To optimise code we need to
To optimise code we need to
ensure that a maximum number
ensure that a maximum number
of units are used with a
of units are used with a
minimum number of cross
minimum number of cross
paths.
paths.
To make the partition visible on
To make the partition visible on
the dependency graph a line is
the dependency graph a line is
used.
used.
The side can then be added to
The side can then be added to
the functional units associated
the functional units associated
with each instruction or node.
with each instruction or node.
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 51
Dependency Graph (Step d)
Dependency Graph (Step d)
A
A
Side
Side
B
B
Side
Side
m
m
LDH
LDH
n
n
LDH
LDH
prod
prod
MPY
MPY
sum
sum
ADD
ADD
.D
.D
.D
.D
5
5
5
5
2
2
1
1
count
count
SUB
SUB
loop
loop
B
B
1
1
1
1
.M
.M
.S
.S
6
6
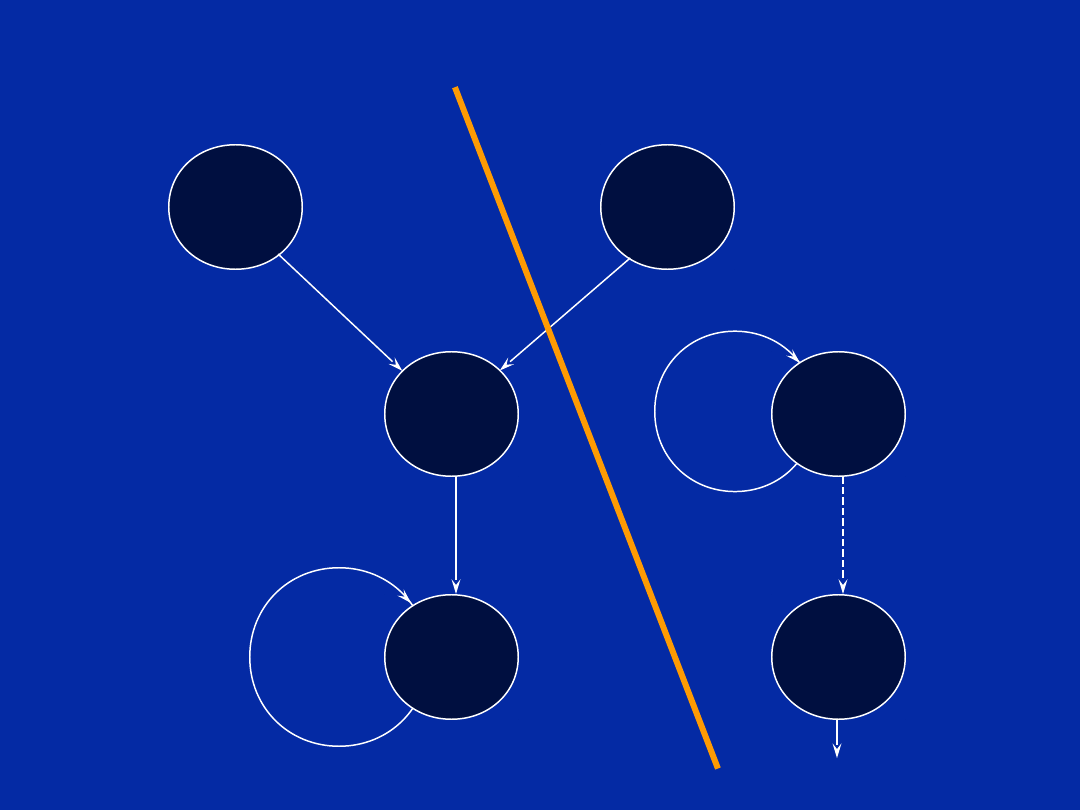
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 52
Dependency Graph (Step d)
Dependency Graph (Step d)
m
m
LDH
LDH
n
n
LDH
LDH
prod
prod
MPY
MPY
sum
sum
ADD
ADD
A
A
Side
Side
.D
.D
1
1
.D
.D
2
2
5
5
5
5
2
2
1
1
count
count
SUB
SUB
loop
loop
B
B
1
1
1
1
.M
.M
1x
1x
.L
.L
1
1
.L
.L
2
2
.S
.S
2
2
B
B
Side
Side
6
6

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 53
Software Pipelining Procedure
Software Pipelining Procedure
1.
1.
Write algorithm in C code & verify.
Write algorithm in C code & verify.
2.
2.
Write ‘C6x Linear Assembly code.
Write ‘C6x Linear Assembly code.
3.
3.
Create a dependency graph (4 steps).
Create a dependency graph (4 steps).
4.
4.
Allocate registers.
Allocate registers.
5.
5.
Create scheduling table.
Create scheduling table.
6.
6.
Translate scheduling table to ‘C6x code.
Translate scheduling table to ‘C6x code.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 54
Step 4 - Allocate Functional Units
Step 4 - Allocate Functional Units
Do we have enough
Do we have enough
functional units to
functional units to
code this algorithm in
code this algorithm in
a
a
single-cycle
single-cycle
loop?
loop?
.L1
.L1
.M1
.M1
.D1
.D1
.S1
.S1
x1
x1
.L2
.L2
.M2
.M2
.D2
.D2
.S2
.S2
x2
x2
sum
sum
prod
prod
m
m
.M1x
.M1x
count
count
n
n
loop
loop
m
m
LDH
LDH
n
n
LDH
LDH
prod
prod
MPY
MPY
sum
sum
ADD
ADD
A
A
Side
Side
.D1
.D1
.
.
D2
D2
5
5
5
5
2
2
1
1
count
count
SUB
SUB
loop
loop
B
B
1
1
1
1
.M1x
.M1x
.L1
.L1
.
.
L2
L2
.S2
.S2
B
B
Side
Side
6
6
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 55
Step 4 - Allocate Registers
Step 4 - Allocate Registers
Content of Register File A
Content of Register File A
&a
&a
a
a
prod
prod
sum
sum
Reg. A
Reg. A
Reg. B
Reg. B
A0
A0
B0
B0
A1
A1
B1
B1
A2
A2
B2
B2
A3
A3
B3
B3
A4
A4
B4
B4
...
...
...
...
A15
A15
B15
B15
Content of Register File B
Content of Register File B
count
count
&b
&b
b
b

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 56
Software Pipelining Procedure
Software Pipelining Procedure
1.
1.
Write algorithm in C code & verify.
Write algorithm in C code & verify.
2.
2.
Write ‘C6x Linear Assembly code.
Write ‘C6x Linear Assembly code.
3.
3.
Create a dependency graph (4 steps).
Create a dependency graph (4 steps).
4.
4.
Allocate registers.
Allocate registers.
5.
5.
Create scheduling table.
Create scheduling table.
6.
6.
Translate scheduling table to ‘C6x code.
Translate scheduling table to ‘C6x code.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 57
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
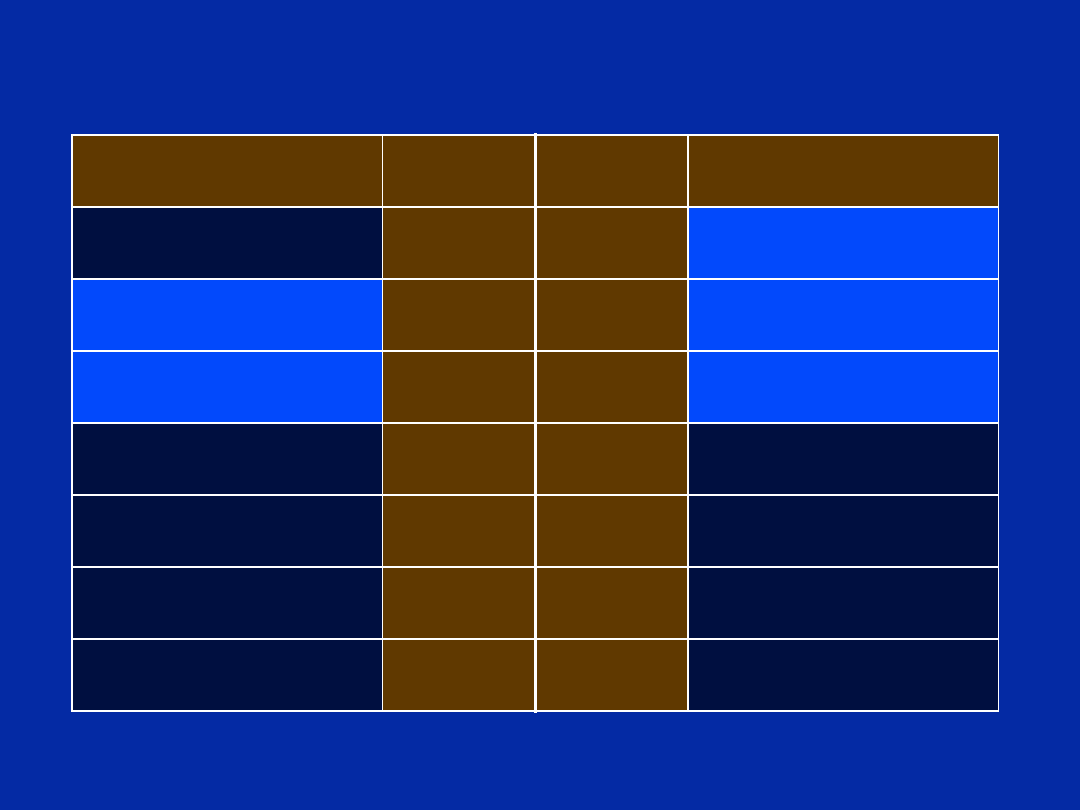
Step 5 - Create Scheduling Table
Step 5 - Create Scheduling Table
How do we know the loop ends up in cycle 8?
How do we know the loop ends up in cycle 8?
LOOP
LOOP
PROLOG
PROLOG
8
8
7
7
6
6
5
5
4
4
3
3
2
2
1
1
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 58
Length of Prolog
Length of Prolog
Answer:
Count up the
length of
longest path, in
this case we
have:
5 + 2 + 1 = 8
cycles
m
m
LDH
LDH
prod
prod
MPY
MPY
sum
sum
ADD
ADD
5
5
2
2
1
1

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 59
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Scheduling Table
Scheduling Table
LOOP
LOOP
PROLOG
PROLOG
8
8
7
7
6
6
5
5
4
4
3
3
2
2
1
1

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 60
Scheduling Table
Scheduling Table
8
8
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
7
7
6
6
5
5
4
4
3
3
2
2
1
1
LOOP
LOOP
PROLOG
PROLOG
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh m
ldh m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh n
ldh n
*
*
*
*
mpy
mpy
add
add
*
*
*
*
*
*
*
*
*
*
B
B
Where do we want to branch?
Where do we want to branch?
Branch here
Branch here

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 61
Scheduling Table
Scheduling Table
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
*
*
*
*
mpy
mpy
*
*
*
*
*
*
*
*
*
*
B
B
8
8
7
7
6
6
5
5
4
4
3
3
2
2
1
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh m
ldh m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh n
ldh n
*
*
*
*
*
*
*
*
*
*
*
*
sub
sub
LOOP
LOOP
PROLOG
PROLOG

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 62
Software Pipelining Procedure
Software Pipelining Procedure
1.
1.
Write algorithm in C code & verify.
Write algorithm in C code & verify.
2.
2.
Write ‘C6x Linear Assembly code.
Write ‘C6x Linear Assembly code.
3.
3.
Create a dependency graph (4 steps).
Create a dependency graph (4 steps).
4.
4.
Allocate registers.
Allocate registers.
5.
5.
Create scheduling table.
Create scheduling table.
6.
6.
Translate scheduling table to ‘C6x code.
Translate scheduling table to ‘C6x code.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 63
Translate Scheduling Table to ‘C6x
Translate Scheduling Table to ‘C6x
Code
Code
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
*
*
*
*
mpy
mpy
*
*
*
*
*
*
*
*
*
*
B
B
7
7
6
6
5
5
4
4
3
3
2
2
1
1
1
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh m
ldh m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh n
ldh n
*
*
*
*
*
*
*
*
*
*
*
*
sub
sub
LOOP
LOOP
PROLOG
PROLOG
C1 ldh .D1 *A1++,A2
C1 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 64
Translate Scheduling Table to ‘C6x
Translate Scheduling Table to ‘C6x
Code
Code
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
*
*
*
*
mpy
mpy
*
*
*
*
*
*
*
*
*
*
B
B
7
7
6
6
5
5
4
4
3
3
2
2
2
2
1
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh m
ldh m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh n
ldh n
*
*
*
*
*
*
*
*
*
*
*
*
sub
sub
LOOP
LOOP
PROLOG
PROLOG
C1 ldh .D1 *A1++,A2
C1 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
C2 ldh .D1 *A1++,A2
C2 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
|| [B0] sub .L2 B0,1,B0
|| [B0] sub .L2 B0,1,B0

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 65
Translate Scheduling Table to ‘C6x
Translate Scheduling Table to ‘C6x
Code
Code
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
*
*
*
*
mpy
mpy
*
*
*
*
*
*
*
*
*
*
B
B
7
7
6
6
5
5
4
4
3
3
3
3
2
2
1
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh m
ldh m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh n
ldh n
*
*
*
*
*
*
*
*
*
*
*
*
sub
sub
LOOP
LOOP
PROLOG
PROLOG
C1 ldh .D1 *A1++,A2
C1 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
C2 ldh .D1 *A1++,A2
C2 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
|| [B0] sub .L2 B0,1,B0
|| [B0] sub .L2 B0,1,B0
C3 ldh .D1 *A1++,A2
C3 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
|| [B0] sub .L2 B0,1,B0
|| [B0] sub .L2 B0,1,B0
|| [B0] B .S2 loop
|| [B0] B .S2 loop

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 66
Translate Scheduling Table to ‘C6x
Translate Scheduling Table to ‘C6x
Code
Code
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
*
*
*
*
mpy
mpy
*
*
*
*
*
*
*
*
*
*
B
B
7
7
6
6
5
5
4
4
4
4
3
3
2
2
1
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh m
ldh m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh n
ldh n
*
*
*
*
*
*
*
*
*
*
*
*
sub
sub
LOOP
LOOP
C1 ldh .D1 *A1++,A2
C1 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
C2 ldh .D1 *A1++,A2
C2 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
|| [B0] sub .L2 B0,1,B0
|| [B0] sub .L2 B0,1,B0
C3 ldh .D1 *A1++,A2
C3 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
|| [B0] sub .L2 B0,1,B0
|| [B0] sub .L2 B0,1,B0
|| [B0] B .S2 loop
|| [B0] B .S2 loop
C4 ldh .D1 *A1++,A2
C4 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
|| [B0] sub .L2 B0,1,B0
|| [B0] sub .L2 B0,1,B0
|| [B0] B .S2 loop
|| [B0] B .S2 loop

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 67
Translate Scheduling Table to ‘C6x
Translate Scheduling Table to ‘C6x
Code
Code
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
*
*
*
*
mpy
mpy
*
*
*
*
*
*
B
B
*
*
B
B
8
8
7
7
6
6
5
5
4
4
3
3
2
2
1
1
*
*
*
*
*
*
ldh
ldh
*
*
*
*
*
*
ldh m
ldh m
*
*
*
*
*
*
ldh
ldh
*
*
*
*
*
*
ldh n
ldh n
*
*
*
*
*
*
sub
sub
*
*
*
*
sub
sub
LOOP
LOOP
C1 ldh .D1 *A1++,A2
C1 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
C2 ldh .D1 *A1++,A2
C2 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
|| [B0] sub .L2 B0,1,B0
|| [B0] sub .L2 B0,1,B0
C3 ldh .D1 *A1++,A2
C3 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
|| [B0] sub .L2 B0,1,B0
|| [B0] sub .L2 B0,1,B0
|| [B0] B .S2 loop
|| [B0] B .S2 loop
C4 ldh .D1 *A1++,A2
C4 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
|| [B0] sub .L2 B0,1,B0
|| [B0] sub .L2 B0,1,B0
|| [B0] B .S2 loop
|| [B0] B .S2 loop
C5 ldh .D1 *A1++,A2
C5 ldh .D1 *A1++,A2
|| ldh .D2 *B1++,B2
|| ldh .D2 *B1++,B2
|| [B0] sub .L2 B0,1,B0
|| [B0] sub .L2 B0,1,B0
|| [B0] B .S2 loop
|| [B0] B .S2 loop

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 68
Translate Scheduling Table to ‘C6x
Translate Scheduling Table to ‘C6x
Code
Code
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
*
*
*
*
mpy
mpy
*
*
*
*
B
B
*
*
*
*
B
B
8
8
7
7
6
6
4
4
4
4
3
3
2
2
1
1
*
*
*
*
ldh
ldh
*
*
*
*
*
*
*
*
ldh m
ldh m
*
*
*
*
ldh
ldh
*
*
*
*
*
*
*
*
ldh n
ldh n
*
*
*
*
sub
sub
*
*
*
*
*
*
sub
sub
LOOP
LOOP
PROLOG
PROLOG
C6
C6
ldh .D1 *A1++,A2
ldh .D1 *A1++,A2
||
||
ldh .D2 *B1++,B2
ldh .D2 *B1++,B2
|| [B0] sub .L2 B0,1,B0
|| [B0] sub .L2 B0,1,B0
|| [B0] B
|| [B0] B
.S2 loop
.S2 loop
|| mpy .M1x A2,B2,A3
|| mpy .M1x A2,B2,A3

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 69
Translate Scheduling Table to ‘C6x
Translate Scheduling Table to ‘C6x
Code
Code
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
*
*
*
*
mpy
mpy
*
*
*
*
B
B
*
*
*
*
B
B
8
8
7
7
6
6
4
4
4
4
3
3
2
2
1
1
*
*
*
*
ldh
ldh
*
*
*
*
*
*
*
*
ldh m
ldh m
*
*
*
*
ldh
ldh
*
*
*
*
*
*
*
*
ldh n
ldh n
*
*
*
*
sub
sub
*
*
*
*
*
*
sub
sub
LOOP
LOOP
PROLOG
PROLOG
C7
C7
ldh .D1 *A1++,A2
ldh .D1 *A1++,A2
||
||
ldh .D2 *B1++,B2
ldh .D2 *B1++,B2
|| [B0] sub .L2 B0,1,B0
|| [B0] sub .L2 B0,1,B0
|| [B0] B
|| [B0] B
.S2 loop
.S2 loop
|| mpy .M1x A2,B2,A3
|| mpy .M1x A2,B2,A3

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 70
Translate Scheduling Table to ‘C6x
Translate Scheduling Table to ‘C6x
Code
Code
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
*
*
*
*
mpy
mpy
*
*
*
*
B
B
*
*
*
*
B
B
8
8
7
7
6
6
4
4
4
4
3
3
2
2
1
1
*
*
*
*
ldh
ldh
*
*
*
*
*
*
*
*
ldh m
ldh m
*
*
*
*
ldh
ldh
*
*
*
*
*
*
*
*
ldh n
ldh n
*
*
*
*
sub
sub
*
*
*
*
*
*
sub
sub
LOOP
PROLOG
PROLOG
* Single-Cycle Loop
* Single-Cycle Loop
loop:
loop:
ldh .D1 *A1++,A2
ldh .D1 *A1++,A2
||
||
ldh .D2 *B1++,B2
ldh .D2 *B1++,B2
|| [B0] sub .L2 B0,1,B0
|| [B0] sub .L2 B0,1,B0
|| [B0] B
|| [B0] B
.S2 loop
.S2 loop
|| mpy .M1x A2,B2,A3
|| mpy .M1x A2,B2,A3
|| add .L1 A4,A3,A4
|| add .L1 A4,A3,A4
See Chapter 14 for practical examples

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 71
With this method we have only created
With this method we have only created
the
the
prolog
prolog
and the
and the
loop
loop
.
.
Therefore if the filter has 100 taps, then
Therefore if the filter has 100 taps, then
we need to repeat the loop 100 times as
we need to repeat the loop 100 times as
we need 100 adds.
we need 100 adds.
This means that we are performing 107
This means that we are performing 107
loads. These
loads. These
7 extra loads
7 extra loads
may lead to
may lead to
some illegal memory acesses
some illegal memory acesses
.
.
Translate Scheduling Table to ‘C6x
Translate Scheduling Table to ‘C6x
Code
Code
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
mpy
mpy
mpy
mpy
mpy
mpy
B
B
B
B
B
B
B
B
B
B
B
B
8
8
7
7
6
6
5
5
4
4
3
3
2
2
1
1
ldh m
ldh m
ldh m
ldh m
ldh m
ldh m
ldh m
ldh m
ldh m
ldh m
ldh m
ldh m
ldh m
ldh m
ldh m
ldh m
ldh n
ldh n
ldh n
ldh n
ldh n
ldh n
ldh n
ldh n
ldh n
ldh n
ldh n
ldh n
ldh n
ldh n
ldh n
ldh n
sub
sub
sub
sub
sub
sub
sub
sub
sub
sub
sub
sub
sub
sub
LOOP
LOOP
PROLOG
PROLOG

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 72
Solution: The Epilog
Solution: The Epilog
We only created
We only created
the
the
Prolog
Prolog
and
and
Loop
Loop
…
…
What about the
What about the
Epilog?
Epilog?
The
The
Epilog
Epilog
can be extracted from
can be extracted from
your results as described below.
your results as described below.
See example in the next slide.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 73
Dot-Product with Epilog
Dot-Product with Epilog
Prolog
Prolog
p1:
p1:
ldh||ldh
ldh||ldh
p2: ldh||ldh
p2: ldh||ldh
|| []sub
|| []sub
p3: ldh||ldh
p3: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p4: ldh||ldh
p4: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p5: ldh||ldh
p5: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p6: ldh||ldh
p6: ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
p7: ldh||ldh
p7: ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
Loop
Loop
loop:
loop:
ldh
ldh
|| ldh
|| ldh
|| mpy
|| mpy
|| add
|| add
|| [] sub
|| [] sub
|| [] b
|| [] b
Epilog
Epilog
Epilog = Loop -
Epilog = Loop -
Prolog
Prolog
And there is no
And there is no
sub
sub
or
or
b
b
in the
in the
epilog
epilog
e1: mpy
e1: mpy
|| add
|| add

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 74
Dot-Product with Epilog
Dot-Product with Epilog
Prolog
Prolog
p1: ldh||ldh
p1: ldh||ldh
p2:
p2:
ldh||ldh
ldh||ldh
||
||
[]sub
[]sub
p3: ldh||ldh
p3: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p4: ldh||ldh
p4: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p5: ldh||ldh
p5: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p6: ldh||ldh
p6: ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
p7: ldh||ldh
p7: ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
Loop
Loop
loop:
loop:
ldh
ldh
|| ldh
|| ldh
|| mpy
|| mpy
|| add
|| add
|| [] sub
|| [] sub
|| [] b
|| [] b
Epilog
Epilog
e1: mpy
e1: mpy
|| add
|| add
e2:
e2:
mpy
mpy
|| add
|| add
Epilog = Loop -
Epilog = Loop -
Prolog
Prolog
And there is no
And there is no
sub
sub
or
or
b
b
in the
in the
epilog
epilog

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 75
Dot-Product with Epilog
Dot-Product with Epilog
Prolog
Prolog
p1: ldh||ldh
p1: ldh||ldh
p2: ldh||ldh
p2: ldh||ldh
|| []sub
|| []sub
p3:
p3:
ldh||ldh
ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p4: ldh||ldh
p4: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p5: ldh||ldh
p5: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p6: ldh||ldh
p6: ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
p7: ldh||ldh
p7: ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
Loop
Loop
loop:
loop:
ldh
ldh
|| ldh
|| ldh
|| mpy
|| mpy
|| add
|| add
|| [] sub
|| [] sub
|| [] b
|| [] b
Epilog
Epilog
e1: mpy
e1: mpy
|| add
|| add
e2: mpy
e2: mpy
|| add
|| add
e3: mpy
e3: mpy
|| add
|| add
Epilog = Loop -
Epilog = Loop -
Prolog
Prolog
And there is no
And there is no
sub
sub
or
or
b
b
in the
in the
epilog
epilog

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 76
Dot-Product with Epilog
Dot-Product with Epilog
Prolog
Prolog
p1: ldh||ldh
p1: ldh||ldh
p2: ldh||ldh
p2: ldh||ldh
|| []sub
|| []sub
p3: ldh||ldh
p3: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p4:
p4:
ldh||ldh
ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p5: ldh||ldh
p5: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p6: ldh||ldh
p6: ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
p7: ldh||ldh
p7: ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
Loop
Loop
loop:
loop:
ldh
ldh
|| ldh
|| ldh
|| mpy
|| mpy
|| add
|| add
|| [] sub
|| [] sub
|| [] b
|| [] b
Epilog
Epilog
e1: mpy
e1: mpy
|| add
|| add
e2: mpy
e2: mpy
|| add
|| add
e3: mpy
e3: mpy
|| add
|| add
e4:
e4:
mpy
mpy
|| add
|| add
Epilog = Loop -
Epilog = Loop -
Prolog
Prolog
And there is no
And there is no
sub
sub
or
or
b
b
in the
in the
epilog
epilog

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 77
Dot-Product with Epilog
Dot-Product with Epilog
Prolog
Prolog
p1: ldh||ldh
p1: ldh||ldh
p2: ldh||ldh
p2: ldh||ldh
|| []sub
|| []sub
p3: ldh||ldh
p3: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p4: ldh||ldh
p4: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p5:
p5:
ldh||ldh
ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p6: ldh||ldh
p6: ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
p7: ldh||ldh
p7: ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
Loop
Loop
loop:
loop:
ldh
ldh
|| ldh
|| ldh
|| mpy
|| mpy
|| add
|| add
|| [] sub
|| [] sub
|| [] b
|| [] b
Epilog
Epilog
e1: mpy
e1: mpy
|| add
|| add
e2: mpy
e2: mpy
|| add
|| add
e3: mpy
e3: mpy
|| add
|| add
e4: mpy
e4: mpy
|| add
|| add
e5:
e5:
mpy
mpy
|| add
|| add
Epilog = Loop -
Epilog = Loop -
Prolog
Prolog
And there is no
And there is no
sub
sub
or
or
b
b
in the
in the
epilog
epilog

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 78
Dot-Product with Epilog
Dot-Product with Epilog
Prolog
Prolog
p1: ldh||ldh
p1: ldh||ldh
p2: ldh||ldh
p2: ldh||ldh
|| []sub
|| []sub
p3: ldh||ldh
p3: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p4: ldh||ldh
p4: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p5: ldh||ldh
p5: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p6:
p6:
ldh||ldh
ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
p7: ldh||ldh
p7: ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
Loop
Loop
loop:
loop:
ldh
ldh
|| ldh
|| ldh
|| mpy
|| mpy
|| add
|| add
|| [] sub
|| [] sub
|| [] b
|| [] b
Epilog
Epilog
e1: mpy
e1: mpy
|| add
|| add
e2: mpy
e2: mpy
|| add
|| add
e3: mpy
e3: mpy
|| add
|| add
e4: mpy
e4: mpy
|| add
|| add
e5: mpy
e5: mpy
|| add
|| add
e6:
e6:
add
add
Epilog = Loop -
Epilog = Loop -
Prolog
Prolog
And there is no
And there is no
sub
sub
or
or
b
b
in the
in the
epilog
epilog

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 79
Dot-Product with Epilog
Dot-Product with Epilog
Prolog
Prolog
p1: ldh||ldh
p1: ldh||ldh
p2: ldh||ldh
p2: ldh||ldh
|| []sub
|| []sub
p3: ldh||ldh
p3: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p4: ldh||ldh
p4: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p5: ldh||ldh
p5: ldh||ldh
|| []sub
|| []sub
|| []b
|| []b
p6: ldh||ldh
p6: ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
p7:
p7:
ldh||ldh
ldh||ldh
|| mpy
|| mpy
|| []sub
|| []sub
|| []b
|| []b
Loop
Loop
loop:
loop:
ldh
ldh
|| ldh
|| ldh
|| mpy
|| mpy
|| add
|| add
|| [] sub
|| [] sub
|| [] b
|| [] b
Epilog
Epilog
e1: mpy
e1: mpy
|| add
|| add
e2: mpy
e2: mpy
|| add
|| add
e3: mpy
e3: mpy
|| add
|| add
e4: mpy
e4: mpy
|| add
|| add
e5: mpy
e5: mpy
|| add
|| add
e6: add
e6: add
e7:
e7:
add
add
Epilog = Loop -
Epilog = Loop -
Prolog
Prolog
And there is no
And there is no
sub
sub
or
or
b
b
in the
in the
epilog
epilog
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 80
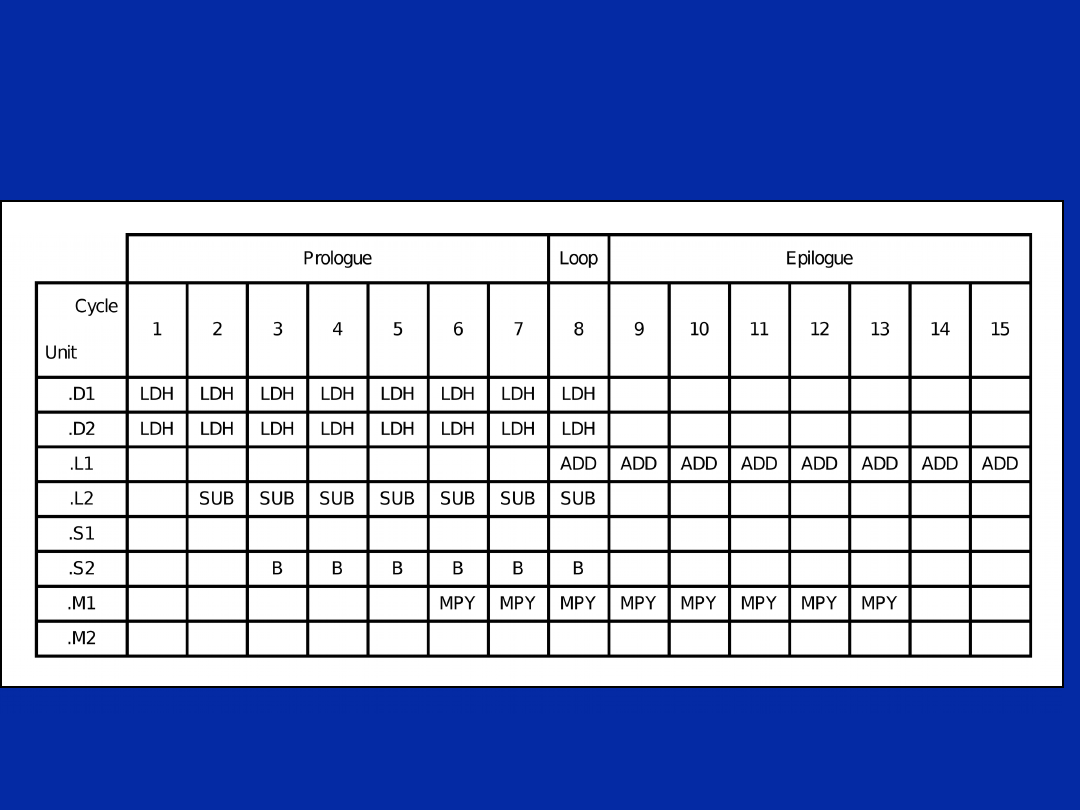
Scheduling Table: Prolog, Loop
Scheduling Table: Prolog, Loop
and Epilog
and Epilog

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 81
Loop only!
Loop only!
Yes!
Yes!
Can the code be written as a
Can the code be written as a
loop only (i.e. no prolog or
loop only (i.e. no prolog or
epilog)?
epilog)?

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 82
Loop only!
Loop only!
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
*
*
*
*
mpy
mpy
*
*
*
*
*
*
*
*
*
*
B
B
8
8
7
7
6
6
5
5
4
4
3
3
2
2
1
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh m
ldh m
*
*
*
*
*
*
*
*
*
*
*
*
*
*
ldh n
ldh n
*
*
*
*
*
*
*
*
*
*
*
*
sub
sub
LOOP
LOOP
PROLOG
PROLOG
(i)
(i)
Remove all
Remove all
instructions except
instructions except
the branch.
the branch.
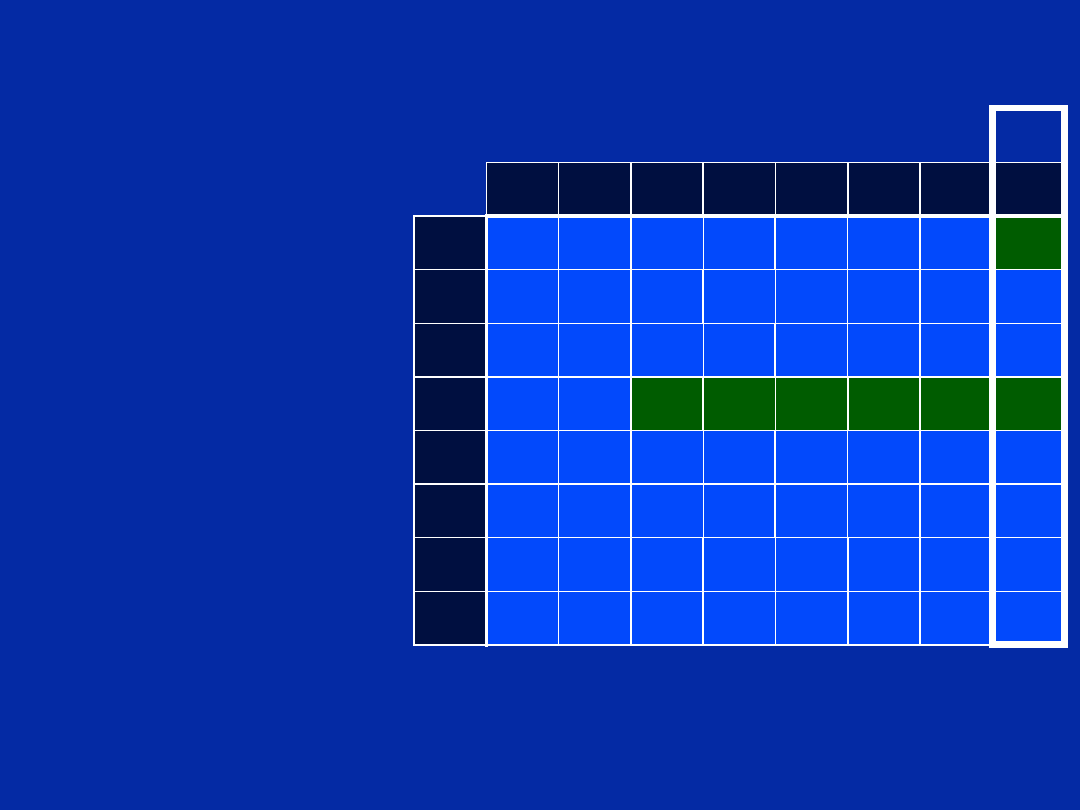
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 83
Loop only!
Loop only!
(i)
(i)
Remove all
Remove all
instructions except
instructions except
the branch.
the branch.
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
B
B
B
B
B
B
B
B
B
B
6
6
5
5
4
4
3
3
2
2
1
1
ldh n
ldh n
sub
sub
LOOP
LOOP
PROLOG
PROLOG
ldh m
ldh m
mpy
mpy
B
B
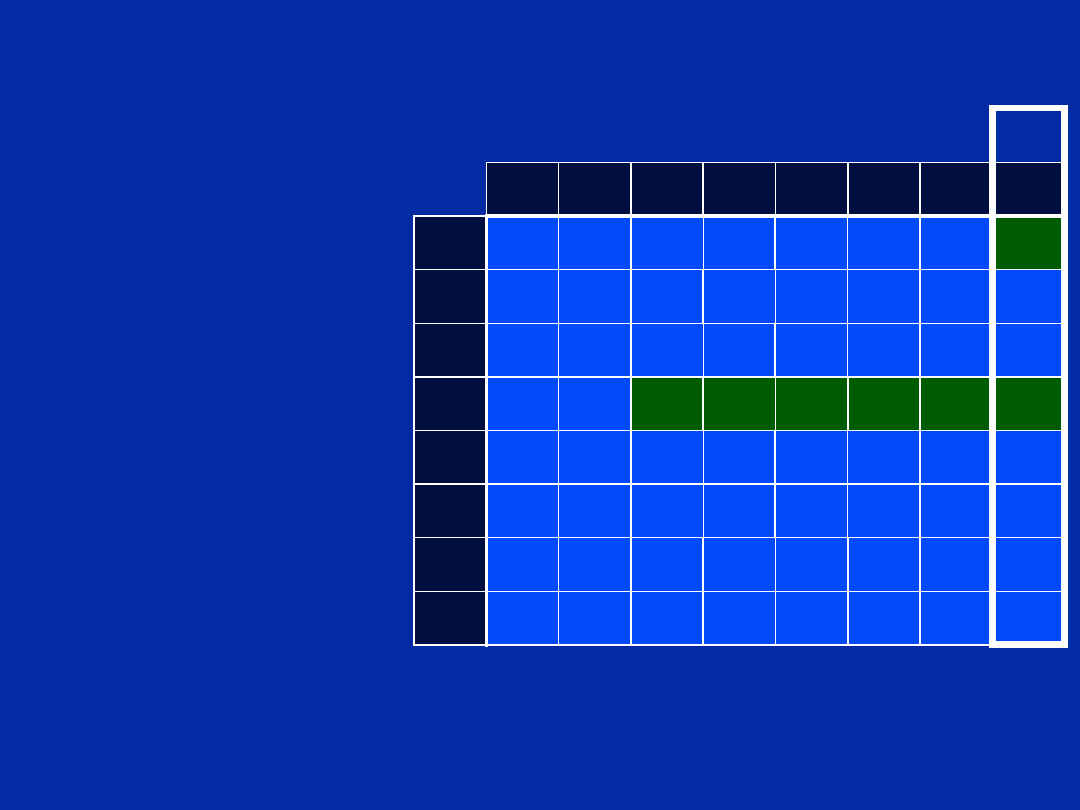
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 84
Loop only!
Loop only!
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
zero
zero
sum
sum
zero a
zero a
B
B
B
B
B
B
B
B
B
B
6
6
5
5
4
4
3
3
2
2
1
1
ldh n
ldh n
sub
sub
LOOP
LOOP
PROLOG
PROLOG
ldh m
ldh m
mpy
mpy
B
B
zero b
zero b
zero
zero
pro
pro
d
d
(i)
(i)
Remove all
Remove all
instructions except
instructions except
the branch.
the branch.
(ii)
(ii)
Zero input
Zero input
registers,
registers,
accumulator and
accumulator and
product registers.
product registers.
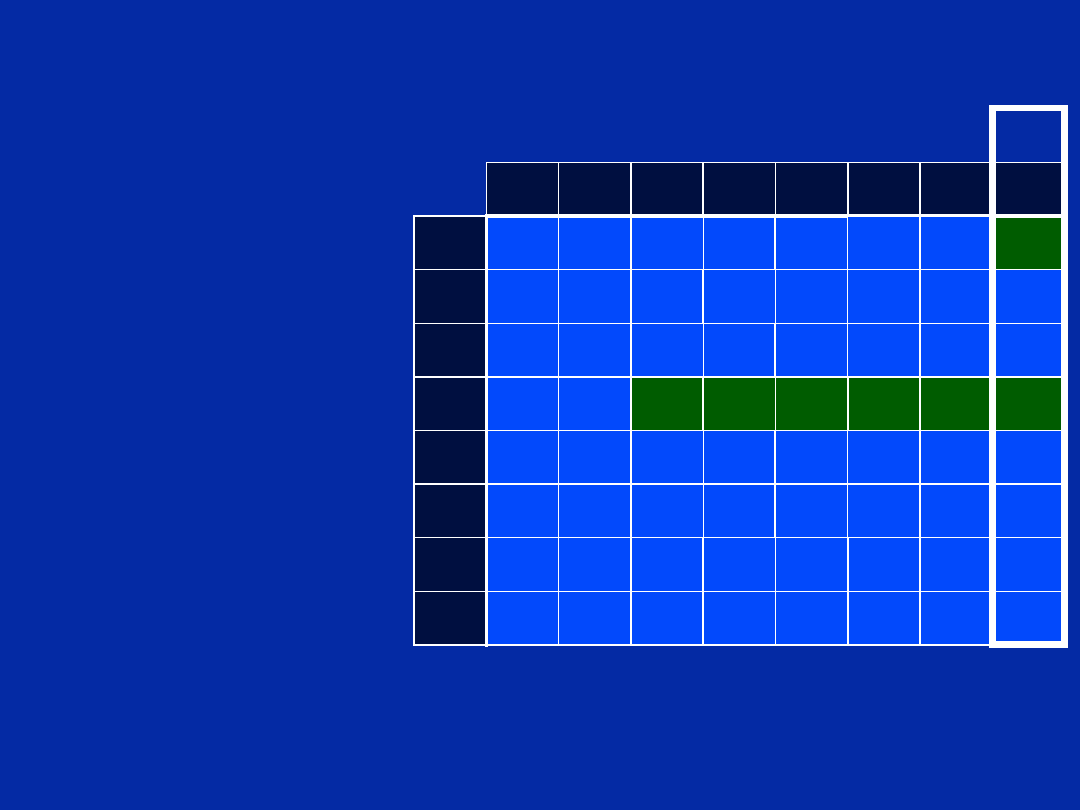
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 85
Loop only!
Loop only!
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
B
B
B
B
B
B
B
B
B
B
6
6
5
5
4
4
3
3
2
2
1
1
ldh n
ldh n
sub
sub
LOOP
LOOP
PROLOG
PROLOG
ldh m
ldh m
mpy
mpy
B
B
sub
sub
zero
zero
sum
sum
zero a
zero a
zero b
zero b
zero
zero
pro
pro
d
d
(i)
(i)
Remove all
Remove all
instructions except
instructions except
the branch.
the branch.
(ii)
(ii)
Zero input
Zero input
registers,
registers,
accumulator and
accumulator and
product registers.
product registers.
(iii)
(iii)
Adjust the
Adjust the
number of
number of
subtractions.
subtractions.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 86
Loop Only - Final Code
Loop Only - Final Code
b
loop
b
loop
b
loop
||
zero m
;input register
||
zero n
;input register
b
loop
||
zero prod
;product register
||
zero sum
;accumulator
b
loop
||
sub
;modify count register
loop
ldh
||
ldh
||
mpy
||
add
|| [] sub
|| [] b
loop
Loop
Loop
Overhead
Overhead

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 87
Laboratory exercise
Laboratory exercise
Software pipeline using the LDW version of
Software pipeline using the LDW version of
the Dot-Product routine:
the Dot-Product routine:
(1)
(1)
Write linear assembly.
Write linear assembly.
(2)
(2)
Create dependency graph.
Create dependency graph.
(3)
(3)
Complete scheduling table.
Complete scheduling table.
(4)
(4)
Transfer table to ‘C6000 code.
Transfer table to ‘C6000 code.
To Epilogue or Not to Epilog?
To Epilogue or Not to Epilog?
Determine if your pipelined code is more efficient
Determine if your pipelined code is more efficient
with or without prolog and epilog.
with or without prolog and epilog.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 88
; for (i=0; i < count; i++)
; for (i=0; i < count; i++)
; prod = m[i] * n[i];
; prod = m[i] * n[i];
; sum += prod; *** count becomes 20 ***
; sum += prod; *** count becomes 20 ***
loop:
loop:
ldw
ldw
*p_m++, m
*p_m++, m
ldw
ldw
*p_n++, n
*p_n++, n
mpy
mpy
m, n, prod
m, n, prod
mpyh
mpyh
m, n, prodh
m, n, prodh
add
add
prod, sum, sum
prod, sum, sum
add
add
prodh, sumh, sumh
prodh, sumh, sumh
[count]
[count]
sub
sub
count, 1, count
count, 1, count
[count]
[count]
b
b
loop
loop
; Outside of Loop
; Outside of Loop
add
add
sum, sumh, sum
sum, sumh, sum
Lab Solution: Step 1 - Linear
Lab Solution: Step 1 - Linear
Assembly
Assembly
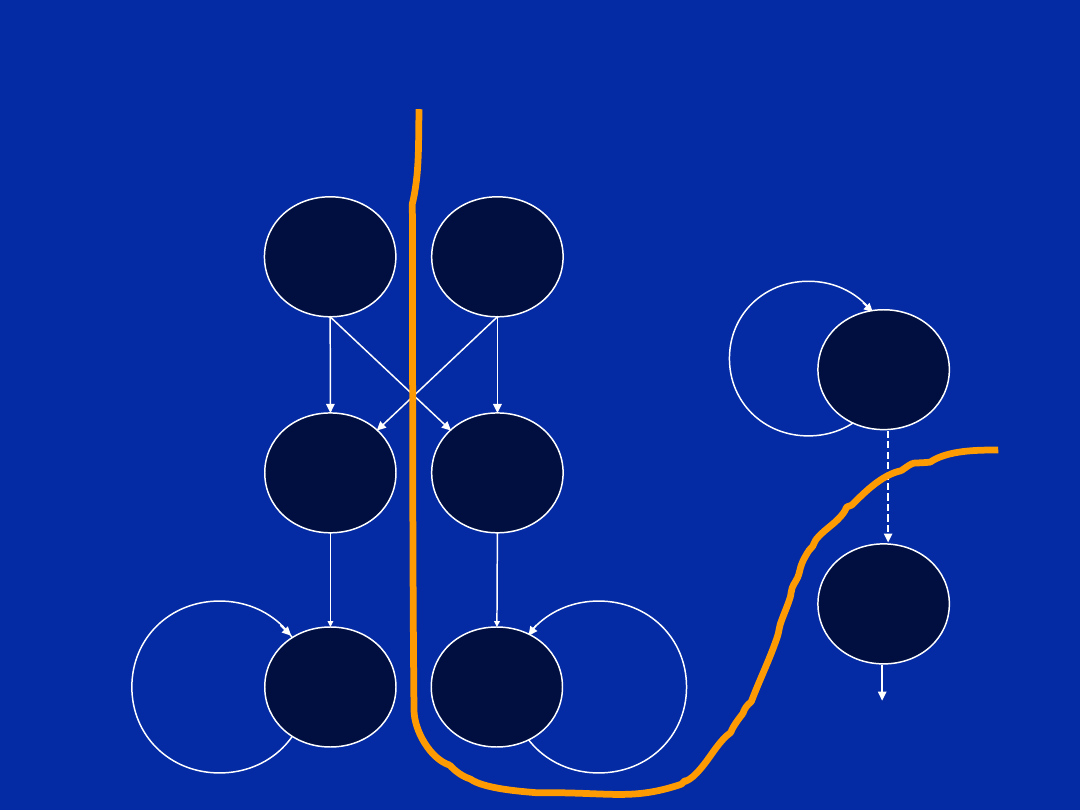
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 89
Step 2 - Dependency Graph
Step 2 - Dependency Graph
prodh
prodh
MPYH
MPYH
m
m
LDW
LDW
.D1
.D1
n
n
LDW
LDW
.D2
.D2
5
5
5
5
2
2
.M1x
.M1x
prod
prod
MPY
MPY
2
2
.M2x
.M2x
1
1
sumh
sumh
ADD
ADD
.L2
.L2
sum
sum
ADD
ADD
.L1
.L1
1
1
count
count
SUB
SUB
loop
loop
B
B
1
1
.S2
.S2
.S1
.S1
6
6
A Side B Side
A Side B Side

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 90
Step 2 - Functional Units
Step 2 - Functional Units
Do we still have enough
Do we still have enough
functional units to
functional units to
code this algorithm
code this algorithm
in a
in a
single-cycle
single-cycle
loop?
loop?
Yes !
Yes !
.L1
.L1
.M1
.M1
.D1
.D1
.S1
.S1
x1
x1
.L2
.L2
.M2
.M2
.D2
.D2
.S2
.S2
x2
x2
sum
sum
prod
prod
m
m
loop
loop
.M1x
.M1x
sumh
sumh
prodh
prodh
n
n
count
count
.M2x
.M2x
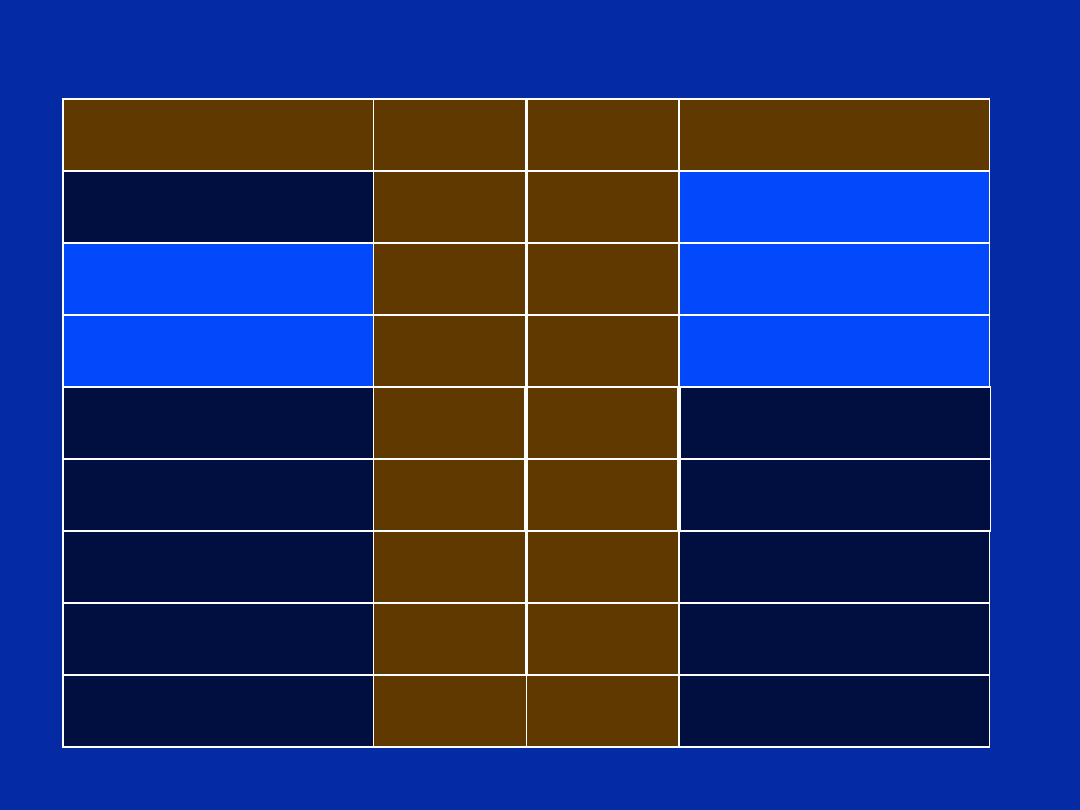
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 91
Step 2 - Registers
Step 2 - Registers
Register File A
Register File A
&a
&a
/ret value
/ret value
a
a
#
#
#
#
A0
A0
B0
B0
A1
A1
B1
B1
A2
A2
B2
B2
A3
A3
B3
B3
A4
A4
B4
B4
A5
A5
B5
B5
Register File B
Register File B
count
count
x
x
count/
count/
prod
prod
A6
A6
B6
B6
prodh
prodh
return address
return address
&x
&x
sum
sum
A7
A7
B7
B7
sumh
sumh
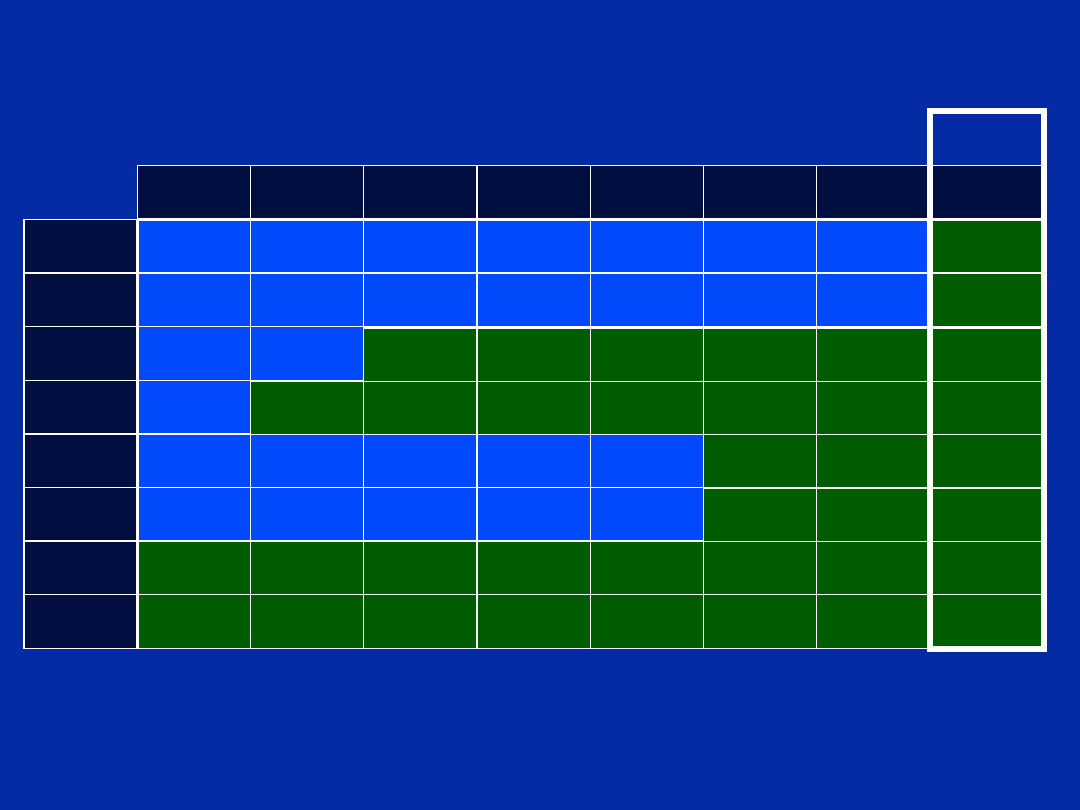
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 92
Step 3 - Schedule Algorithm
Step 3 - Schedule Algorithm
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
add
add
mpy
mpy
3
3
mpy
mpy
2
2
mpy
mpy
8
8
7
7
6
6
5
5
4
4
3
3
2
2
1
1
ldw
ldw
8
8
ldw
ldw
7
7
ldw
ldw
6
6
ldw
ldw
5
5
ldw
ldw
4
4
ldw
ldw
3
3
ldw
ldw
2
2
ldw m
ldw m
ldw
ldw
8
8
ldw
ldw
7
7
ldw
ldw
6
6
ldw
ldw
5
5
ldw
ldw
4
4
ldw
ldw
3
3
ldw
ldw
2
2
ldw n
ldw n
mpyh
mpyh
3
3
mpyh
mpyh
2
2
mpyh
mpyh
sub
sub
7
7
sub
sub
6
6
sub
sub
5
5
sub
sub
4
4
sub
sub
3
3
sub
sub
2
2
sub
sub
1
1
add
add
B
B
6
6
B
B
5
5
B
B
4
4
B
B
3
3
B
B
2
2
B
B
1
1
LOOP
LOOP
PROLOG
PROLOG

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 93
The complete code is available
The complete code is available
in the following location:
in the following location:
Step 4 - ‘C6000 Code
Step 4 - ‘C6000 Code

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 94
loop (count = 0)
loop (count = 0)
(B)
(B)
loop:
loop:
ldh
ldh
*p_m++, m
*p_m++, m
ldh
ldh
*p_n++, n
*p_n++, n
mpy
mpy
m, n, prod
m, n, prod
add
add
prod, sum, sum
prod, sum, sum
[count]
[count]
sub
sub
count, 1, count
count, 1, count
[count]
[count]
b
b
loop
loop
Why Conditional Subtract?
Why Conditional Subtract?
X
X
Without Cond. Subtract:
Without Cond. Subtract:
Loop (count = 1)
Loop (count = 1)
(B)
(B)
loop (count = -1)
loop (count = -1)
(B)
(B)
loop (count = -2)
loop (count = -2)
(B)
(B)
loop (count = -3)
loop (count = -3)
(B)
(B)
loop (count = -4)
loop (count = -4)
(B)
(B)
Loop never ends
Loop never ends
loop (count = 0)
loop (count = 0)
(B)
(B)
X
X
With Cond. Subtract:
With Cond. Subtract:
Loop (count = 1)
Loop (count = 1)
(B)
(B)
loop (count = 0)
loop (count = 0)
(B)
(B)
loop (count = 0)
loop (count = 0)
(B)
(B)
loop (count = 0)
loop (count = 0)
(B)
(B)
loop (count = 0)
loop (count = 0)
(B)
(B)
Loop ends
Loop ends
X
X
X
X
X
X
X
X

Chapter 12
Chapter 12
Software Optimisation
Software Optimisation
Part 3 - Pipelining Multi-
Part 3 - Pipelining Multi-
cycle Loops
cycle Loops

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 96
Objectives
Objectives
Software pipeline the weighted
Software pipeline the weighted
vector sum algorithm.
vector sum algorithm.
Describe four iteration interval
Describe four iteration interval
constraints.
constraints.
Calculate minimum iteration
Calculate minimum iteration
interval.
interval.
Convert and optimize the dot-
Convert and optimize the dot-
product code to floating point code.
product code to floating point code.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 97
What Requires Multi-Cycle Loops?
What Requires Multi-Cycle Loops?
Resource Limitations
Resource Limitations
Running out of resources
Running out of resources
(Functional Units, Registers, Bus Accesses)
(Functional Units, Registers, Bus Accesses)
Weighted Vector Sum example requires
Weighted Vector Sum example requires
three .D units
three .D units
Live Too Long
Live Too Long
Minimum iteration interval defined by length of
Minimum iteration interval defined by length of
time a Variable is required to exist
time a Variable is required to exist
Loop Carry Path
Loop Carry Path
Latency required between loop iterations
Latency required between loop iterations
FIR example and SP floating-point dot product
FIR example and SP floating-point dot product
examples are demonstrated
examples are demonstrated
Functional Unit Latency > 1
Functional Unit Latency > 1
A few ‘C67x instructions require functional
A few ‘C67x instructions require functional
units for 2 or 4 cycles rather than one. This
units for 2 or 4 cycles rather than one. This
defines a minimum iteration interval.
defines a minimum iteration interval.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 98
What Requires Multi-Cycle Loops?
What Requires Multi-Cycle Loops?
Four reasons:
Four reasons:
1.
1.
Resource Limitations.
Resource Limitations.
2.
2.
Live Too Long.
Live Too Long.
3.
3.
Loop Carry Path.
Loop Carry Path.
4.
4.
Double Precision (FUL > 1).
Double Precision (FUL > 1).
Use these four constraints to
Use these four constraints to
determine the smallest Iteration
determine the smallest Iteration
Interval (
Interval (
Minimum Iteration Interval
Minimum Iteration Interval
or MII).
or MII).
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 99
void WVS(short *c, short *b, short *a, short r, short n)
void WVS(short *c, short *b, short *a, short r, short n)
{ int i;
{ int i;
for (i=0; i < n; i++)
for (i=0; i < n; i++)
{
{
c[i] = a[i] + (r * b[i]) >> 15;
c[i] = a[i] + (r * b[i]) >> 15;
}
}
}
}
Step 1 - C Code
Step 1 - C Code
a, b:
a, b:
input arrays
input arrays
c:
c:
output array
output array
n:
n:
length of arrays
length of arrays
r:
r:
weighting factor
weighting factor
Resource Limitation: Weighted
Resource Limitation: Weighted
Vector Sum
Vector Sum
Store
Store
.D
.D
Load
Load
.D
.D
Load
Load
.D
.D
Requires 3 .D
Requires 3 .D
units
units

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 100
Software Pipelining Procedure
Software Pipelining Procedure
1.
1.
Write algorithm in C code & verify.
Write algorithm in C code & verify.
2.
2.
Write ‘C6x Linear Assembly code.
Write ‘C6x Linear Assembly code.
3.
3.
Create dependency graph.
Create dependency graph.
4.
4.
Allocate registers.
Allocate registers.
5.
5.
Create scheduling table.
Create scheduling table.
6.
6.
Translate scheduling table to ‘C6x code.
Translate scheduling table to ‘C6x code.
Write algorithm in C & verify.
Write algorithm in C & verify.
2.
2.
Write ‘C6x Linear Assembly Code.
Write ‘C6x Linear Assembly Code.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 101
Step 2 - ‘C6x Linear Code
Step 2 - ‘C6x Linear Code
loop:
loop:
LDH
LDH
*a++, ai
*a++, ai
LDH
LDH
*b++, bi
*b++, bi
MPY
MPY
r, bi, prod
r, bi, prod
SHR
SHR
prod, 15, sum
prod, 15, sum
ADD
ADD
ai, sum, ci
ai, sum, ci
STH
STH
ci, *c++
ci, *c++
[i]
[i]
SUB
SUB
i, 1, i
i, 1, i
[i]
[i]
B
B
loop
loop
The full code is available here:
The full code is available here:
c[i] = a[i] + (r * b[i]) >> 15;
c[i] = a[i] + (r * b[i]) >> 15;
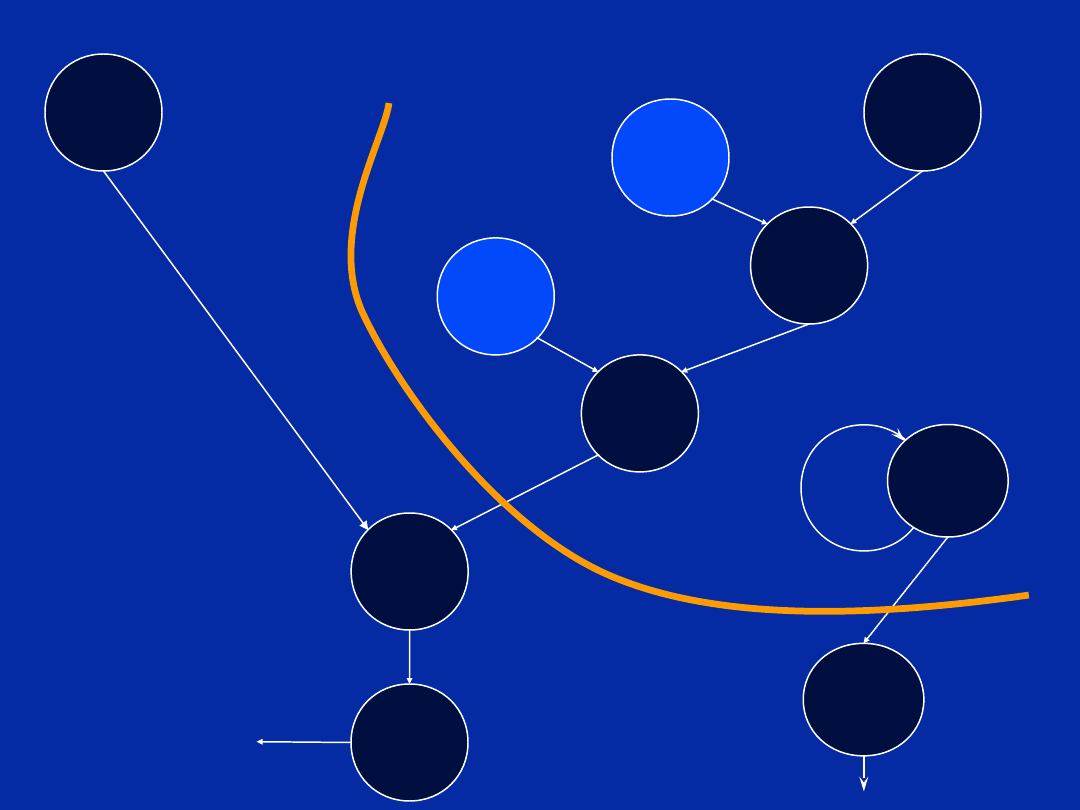
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 102
Step 3 - Dependency Graph
Step 3 - Dependency Graph
5
5
1
1
5
5
2
2
1
1
15
15
ai
ai
LDH
LDH
bi
bi
LDH
LDH
r
r
prod
prod
MPY
MPY
sum
sum
SHR
SHR
ci
ci
ADD
ADD
*c++
*c++
STH
STH
1
1
1
1
1
1
6
6
i
i
SUB
SUB
B
B
loop
loop
A
A
Side
Side
B
B
Side
Side
.D1
.D1
.L1
.L1
.D1
.D1
.S2
.S2
.M2
.M2
.D2
.D2
.L2
.L2
.S1
.S1
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 103
Step 4 -Allocate Functional Units
Step 4 -Allocate Functional Units
ci
ci
ai, *c
ai, *c
i
i
prod
prod
bi
bi
sum
sum
.L1
.L1
.M1
.M1
.D1
.D1
.S1
.S1
.L2
.L2
.M2
.M2
.D2
.D2
.S2
.S2
loop
loop
This requires
This requires
3 .D units
3 .D units
therefore it
therefore it
cannot fit into a
cannot fit into a
single cycle
single cycle
loop.
loop.
This
This
may
may
fit into
fit into
a 2 cycle loop if
a 2 cycle loop if
there are no
there are no
other
other
constraints.
constraints.
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 104
2 Cycle Loop
2 Cycle Loop
Iteration Interval (II):
Iteration Interval (II):
# cycles per loop iteration.
# cycles per loop iteration.
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
loop:
loop:
2 cycles
2 cycles
per
per
loop iteration
loop iteration
Cycle 1
Cycle 1
Cycle 2
Cycle 2

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 105
Multi-Cycle Loop Iterations
Multi-Cycle Loop Iterations
.D1
.D1
.D2
.D2
.S2
.S2
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
.S1
.S1
.D1
.D1
.D2
.D2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
loop 2
loop 2
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
loop 3
loop 3
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
cycle 3
cycle 3
cycle 5
cycle 5
loop 1
loop 1
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
cycle 1
cycle 1
cycle 2
cycle 2
cycle 4
cycle 4
cycle 6
cycle 6

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 106
Multi-Cycle Loop Iterations
Multi-Cycle Loop Iterations
.D1
.D1
.D2
.D2
.S2
.S2
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
.S1
.S1
.D1
.D1
.D2
.D2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
loop 2
loop 2
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
loop 3
loop 3
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
cycle 3
cycle 3
cycle 5
cycle 5
loop 1
loop 1
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
cycle 1
cycle 1
cycle 2
cycle 2
cycle 4
cycle 4
cycle 6
cycle 6

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 107
Multi-Cycle Loop Iterations
Multi-Cycle Loop Iterations
.D1
.D1
.D2
.D2
.S2
.S2
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
.S1
.S1
.D1
.D1
.D2
.D2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
loop 3
loop 3
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
cycle 3
cycle 3
cycle 5
cycle 5
loop 1
loop 1
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
cycle 1
cycle 1
cycle 2
cycle 2
cycle 4
cycle 4
cycle 6
cycle 6
loop 2
loop 2

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 108
Multi-Cycle Loop Iterations
Multi-Cycle Loop Iterations
.D1
.D1
.D2
.D2
.S2
.S2
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
.S1
.S1
.D1
.D1
.D2
.D2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
loop 3
loop 3
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
cycle 3
cycle 3
cycle 5
cycle 5
loop 1
loop 1
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
cycle 1
cycle 1
cycle 2
cycle 2
cycle 4
cycle 4
cycle 6
cycle 6
loop 2
loop 2

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 109
Multi-Cycle Loop Iterations
Multi-Cycle Loop Iterations
.D1
.D1
.D2
.D2
.S2
.S2
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
.S1
.S1
.D1
.D1
.D2
.D2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
cycle 3
cycle 3
cycle 5
cycle 5
loop 1
loop 1
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
cycle 1
cycle 1
cycle 2
cycle 2
cycle 4
cycle 4
cycle 6
cycle 6
loop 2
loop 2
loop 3
loop 3

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 110
Multi-Cycle Loop Iterations
Multi-Cycle Loop Iterations
.D1
.D1
.D2
.D2
.S2
.S2
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
.S1
.S1
.D1
.D1
.D2
.D2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.L1
.L1
.L2
.L2
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
loop 3
loop 3
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
cycle 3
cycle 3
cycle 5
cycle 5
loop 1
loop 1
ldh
ldh
ldh
ldh
shr
shr
mpy
mpy
add
add
sub
sub
b
b
sth
sth
cycle 1
cycle 1
cycle 2
cycle 2
cycle 4
cycle 4
cycle 6
cycle 6
loop 2
loop 2

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 111
How long is the Prolog?
How long is the Prolog?
ai
ai
bi
bi
prod
prod
sum
sum
ci
ci
*c++
*c++
5
5
1
1
5
5
2
2
1
1
1
1
What is the length of the
What is the length of the
longest path?
longest path?
10
10
10
10
How many cycles per loop?
How many cycles per loop?
2
2

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 112
Step 5 - Create Scheduling Chart
Step 5 - Create Scheduling Chart
(0)
0
0
2
2
4
4
6
6
8
8
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
5
5
7
7
9
9

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 113
Step 5 - Create Scheduling Chart
Step 5 - Create Scheduling Chart
0
0
2
2
4
4
6
6
8
8
LDH bi
LDH bi
*
*
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
5
5
7
7
9
9

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 114
Step 5 - Create Scheduling Chart
Step 5 - Create Scheduling Chart
0
0
2
2
4
4
6
6
8
8
LDH bi
LDH bi
*
*
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
5
5
7
7
9
9
MPY mi
MPY mi
*
*
*
*

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 115
Step 5 - Create Scheduling Chart
Step 5 - Create Scheduling Chart
0
0
2
2
4
4
6
6
8
8
LDH bi
LDH bi
*
*
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
5
5
7
7
9
9
MPY mi
MPY mi
*
*
*
*
SHR sum
SHR sum
*
*
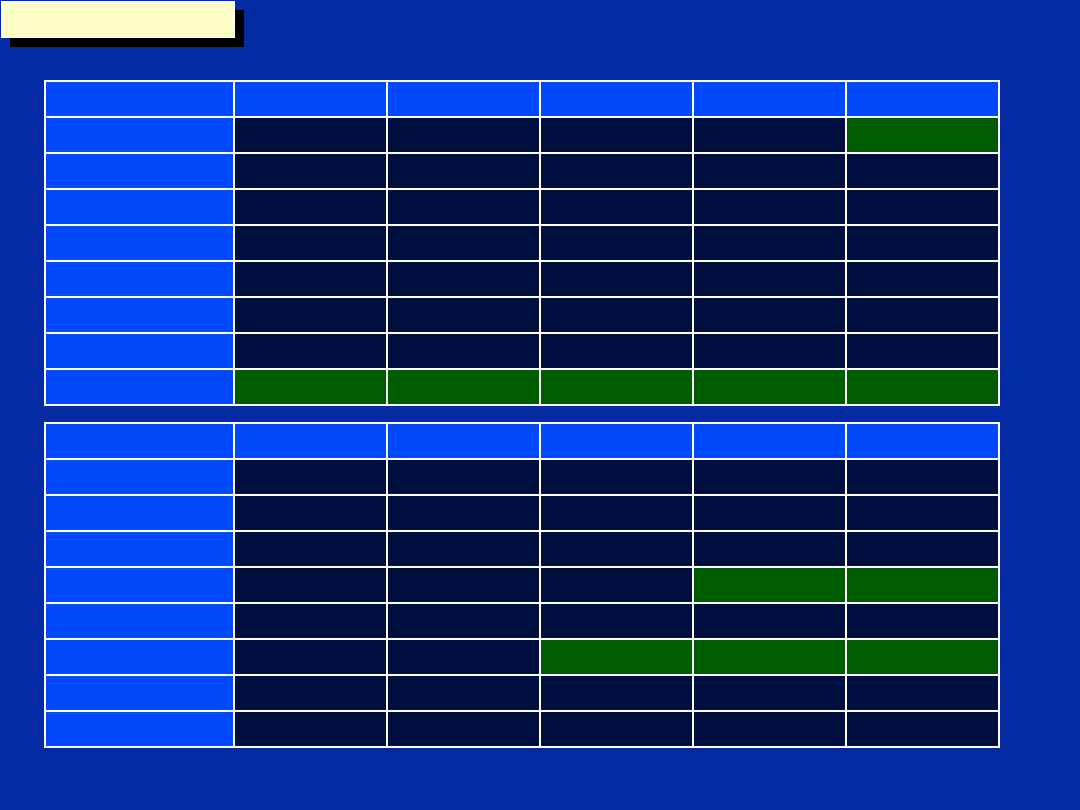
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 116
Step 5 - Create Scheduling Chart
Step 5 - Create Scheduling Chart
0
0
2
2
4
4
6
6
8
8
LDH bi
LDH bi
*
*
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
5
5
7
7
9
9
MPY mi
MPY mi
*
*
*
*
SHR sum
SHR sum
*
*
ADD ci
ADD ci
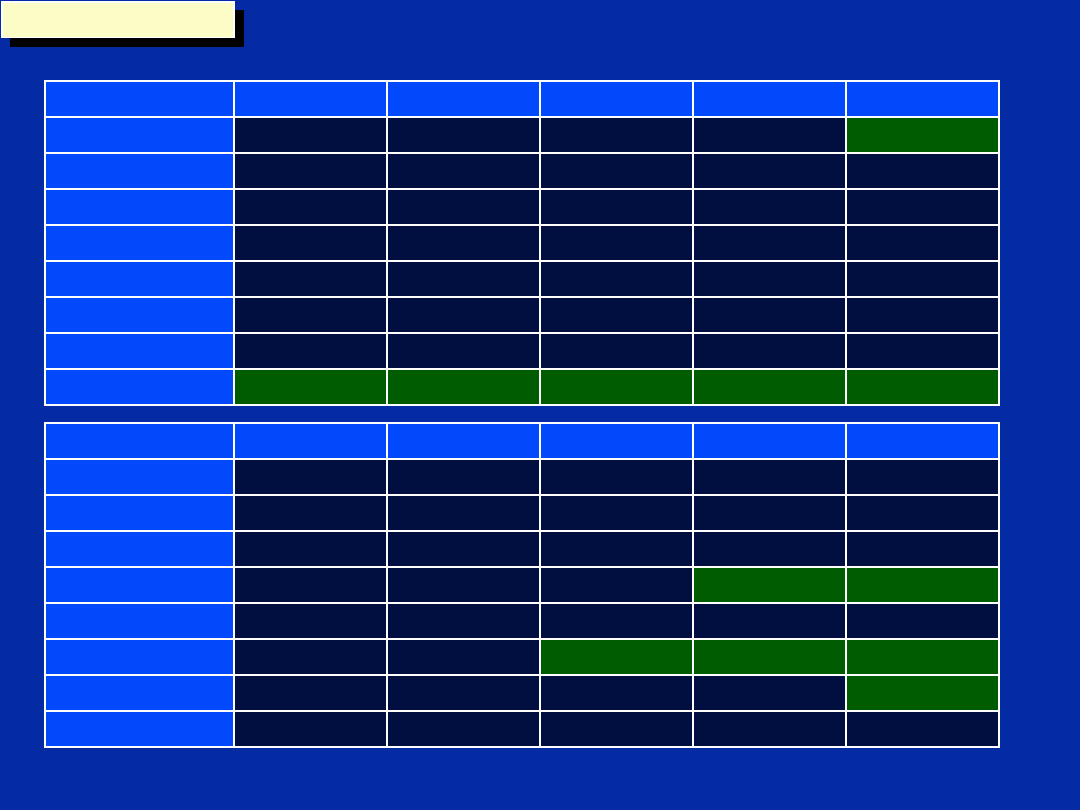
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 117
Step 5 - Create Scheduling Chart
Step 5 - Create Scheduling Chart
0
0
2
2
4
4
6
6
8
8
LDH bi
LDH bi
*
*
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
5
5
7
7
9
9
MPY mi
MPY mi
*
*
*
*
SHR sum
SHR sum
*
*
ADD ci
ADD ci
*
*
STH c[i]
STH c[i]
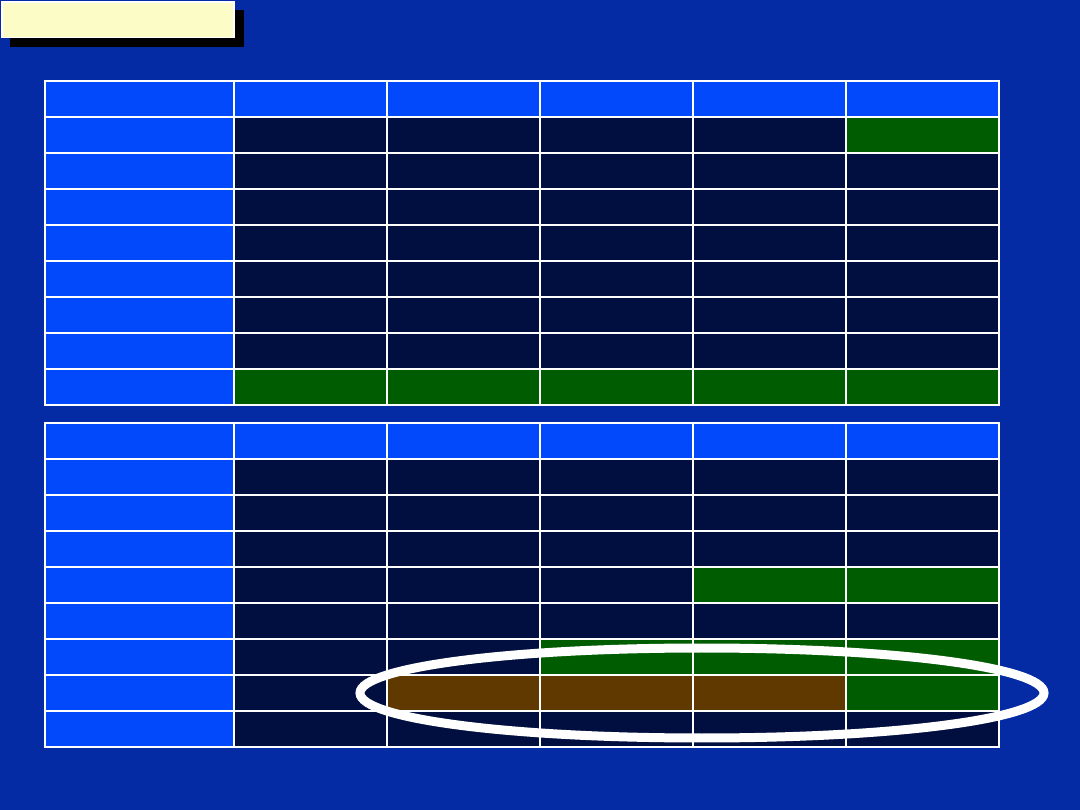
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 118
Step 5 - Create Scheduling Chart
Step 5 - Create Scheduling Chart
0
0
2
2
4
4
6
6
8
8
LDH bi
LDH bi
*
*
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
5
5
7
7
9
9
MPY mi
MPY mi
*
*
*
*
SHR sum
SHR sum
*
*
ADD ci
ADD ci
*
*
STH c[i]
STH c[i]
*
*
*
*
LDH ai
LDH ai

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 119
Step 5 - Create Scheduling Chart
Step 5 - Create Scheduling Chart
0
0
2
2
4
4
6
6
8
8
LDH bi
LDH bi
*
*
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
5
5
7
7
9
9
MPY mi
MPY mi
*
*
*
*
SHR sum
SHR sum
*
*
ADD ci
ADD ci
*
*
STH c[i]
STH c[i]
*
*
*
*
LDH ai
LDH ai
Con
flic
t
Con
flic
t

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 120
Conflict Solution
Conflict Solution
0
0
2
2
4
4
6
6
8
8
LDH bi
LDH bi
*
*
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
5
5
7
7
9
9
MPY mi
MPY mi
*
*
*
*
SHR sum
SHR sum
*
*
*
*
STH c[i]
STH c[i]
*
*
*
*
LDH ai
LDH ai
LDH ai
LDH ai
LDH ai
LDH ai
Here are two possibilities ...
Here are two possibilities ...
Which is better?
Which is better?

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 121
Conflict Solution
Conflict Solution
Here are two possibilities ...
Here are two possibilities ...
Which is better?
Which is better?
Move the LDH to cycle 2.
Move the LDH to cycle 2.
(so you don’t have to go back and recheck crosspaths)
(so you don’t have to go back and recheck crosspaths)
0
0
2
2
4
4
6
6
8
8
LDH bi
LDH bi
*
*
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
5
5
7
7
9
9
MPY mi
MPY mi
*
*
*
*
SHR sum
SHR sum
*
*
*
*
STH c[i]
STH c[i]
*
*
*
*
LDH ai
LDH ai
LDH ai
LDH ai
LDH ai
LDH ai

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 122
Step 5 - Create Scheduling Chart
Step 5 - Create Scheduling Chart
0
0
2
2
4
4
6
6
8
8
LDH bi
LDH bi
*
*
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
5
5
7
7
9
9
MPY mi
MPY mi
*
*
*
*
SHR sum
SHR sum
*
*
ADD ci
ADD ci
LDH ai
LDH ai
*
*
*
*
*
*
LDH ai
LDH ai
STH c[i]
STH c[i]
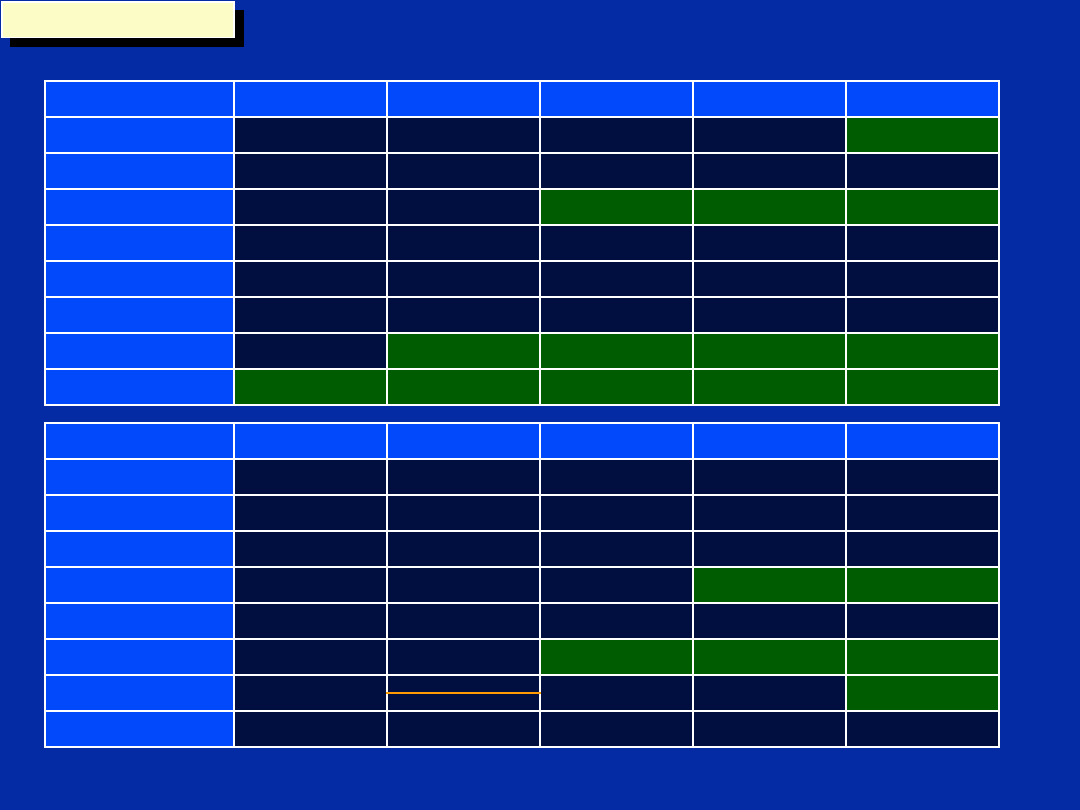
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 123
Step 5 - Create Scheduling Chart
Step 5 - Create Scheduling Chart
0
0
2
2
4
4
6
6
8
8
LDH bi
LDH bi
*
*
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
5
5
7
7
9
9
MPY mi
MPY mi
*
*
*
*
SHR sum
SHR sum
*
*
ADD ci
ADD ci
LDH ai
LDH ai
*
*
*
*
*
*
LDH ai
LDH ai
STH c[i]
STH c[i]
[i] B
[i] B
*
*
*
*
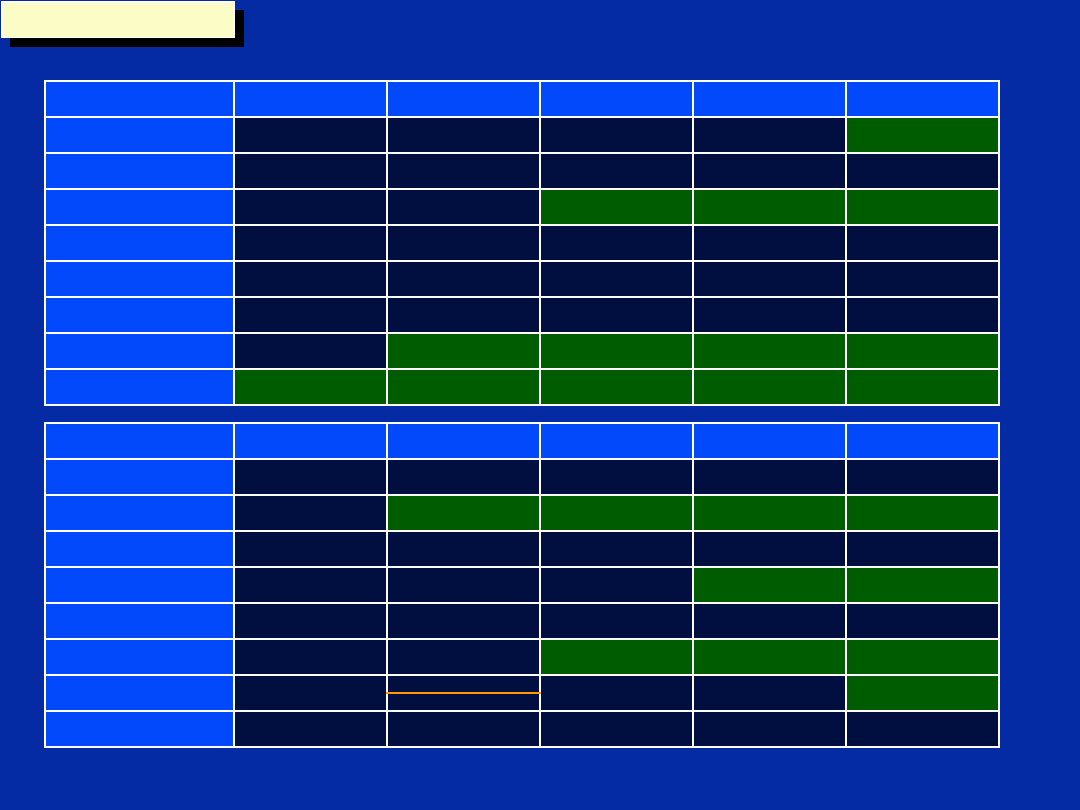
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 124
Step 5 - Create Scheduling Chart
Step 5 - Create Scheduling Chart
0
0
2
2
4
4
6
6
8
8
LDH bi
LDH bi
*
*
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
5
5
7
7
9
9
MPY mi
MPY mi
*
*
*
*
SHR sum
SHR sum
*
*
ADD ci
ADD ci
LDH ai
LDH ai
*
*
*
*
*
*
LDH ai
LDH ai
STH c[i]
STH c[i]
[i] B
[i] B
*
*
*
*
[i] SUB i
[i] SUB i
*
*
*
*
*
*
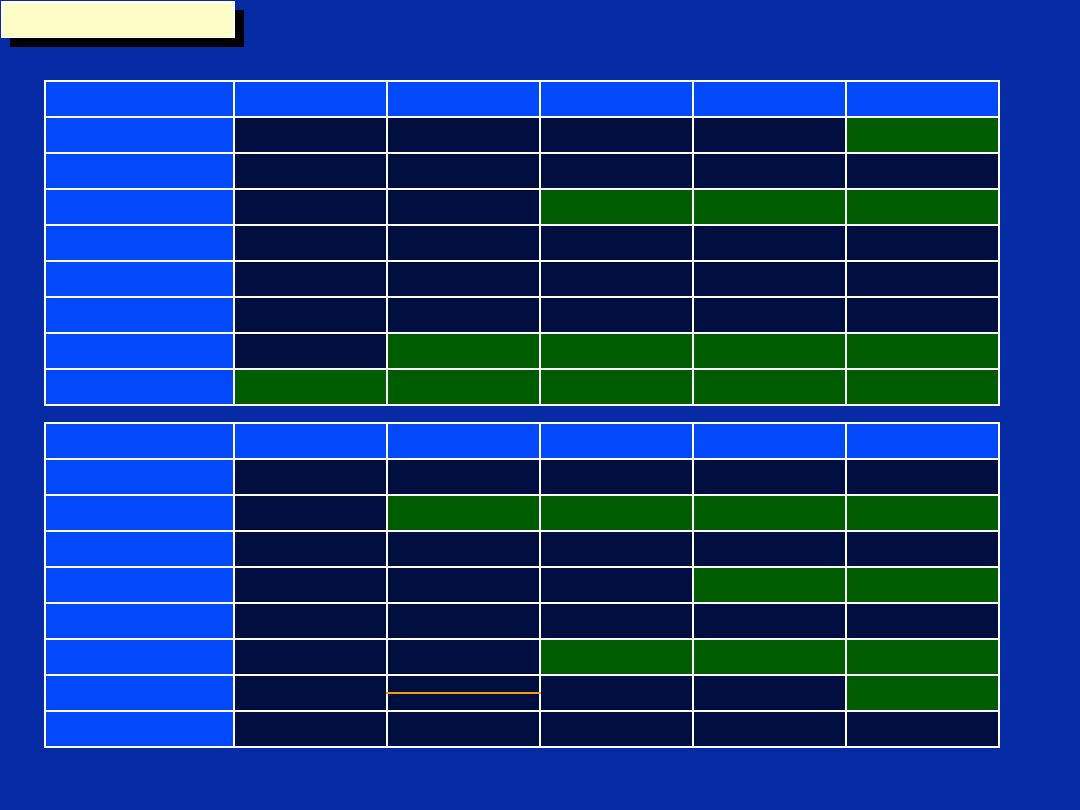
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 125
Step 5 - Create Scheduling Chart
Step 5 - Create Scheduling Chart
0
0
LDH bi
LDH bi
2
2
LDH ai
LDH ai
*
*
4
4
[i] B
[i] B
*
*
*
*
6
6
*
*
*
*
*
*
8
8
ADD ci
ADD ci
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
[i] SUB i
[i] SUB i
LDH ai
LDH ai
5
5
*
*
MPY mi
MPY mi
7
7
*
*
SHR sum
SHR sum
*
*
9
9
*
*
*
*
*
*
STH c[i]
STH c[i]

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 126
2 Cycle Loop Kernel
2 Cycle Loop Kernel
0
0
LDH bi
LDH bi
2
2
LDH ai
LDH ai
*
*
4
4
[i] B
[i] B
*
*
*
*
6
6
*
*
*
*
*
*
8
8
ADD ci
ADD ci
*
*
*
*
*
*
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
Unit\cycle
Unit\cycle
.L1
.L1
.L2
.L2
.S1
.S1
.S2
.S2
.M1
.M1
.M2
.M2
.D1
.D1
.D2
.D2
1
1
3
3
[i] SUB i
[i] SUB i
LDH ai
LDH ai
5
5
*
*
MPY mi
MPY mi
7
7
*
*
SHR sum
SHR sum
*
*
9
9
*
*
*
*
*
*
STH c[i]
STH c[i]

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 127
What Requires Multi-Cycle Loops?
What Requires Multi-Cycle Loops?
Four reasons:
Four reasons:
1.
1.
Resource Limitations.
Resource Limitations.
2.
2.
Live Too Long.
Live Too Long.
3.
3.
Loop Carry Path.
Loop Carry Path.
4.
4.
Double Precision (FUL > 1).
Double Precision (FUL > 1).
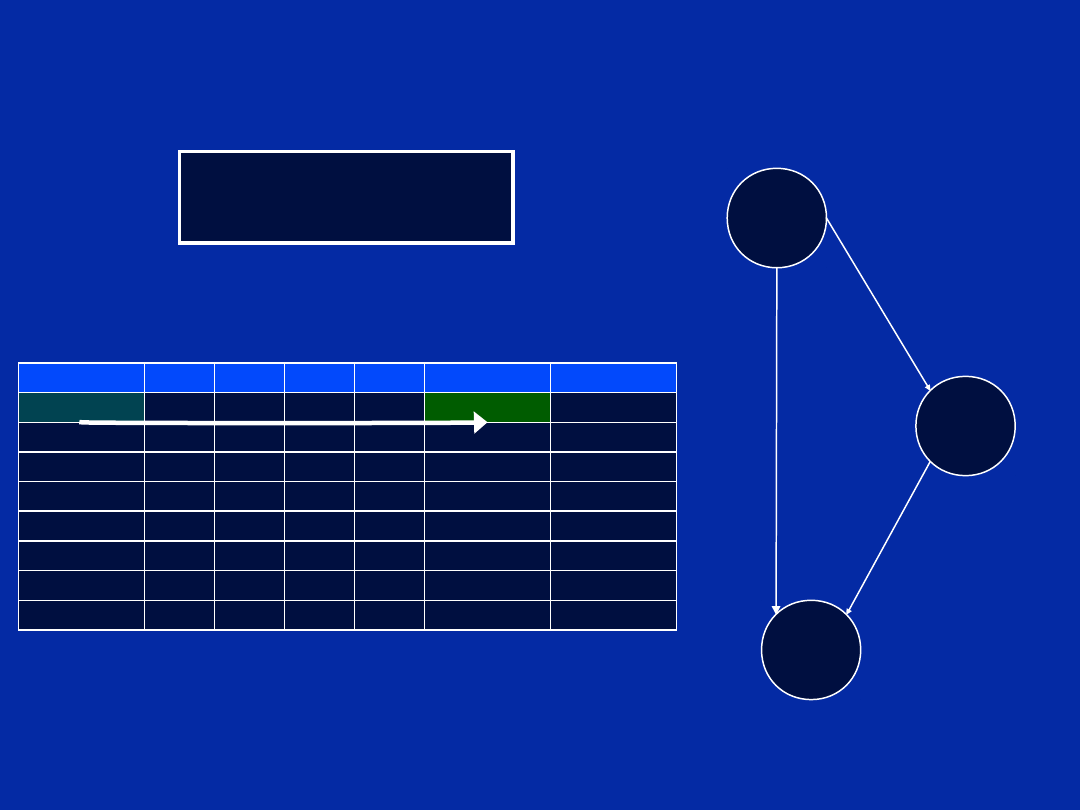
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 128
Live Too Long - Example
Live Too Long - Example
0
0
LDH ai
LDH ai
5
5
a0 valid
a0 valid
6
6
1
1
LDH
LDH
2
2
LDH
LDH
3
3
LDH
LDH
4
4
LDH
LDH
ai
ai
LDH
LDH
ci
ci
ADD
ADD
5
5
1
1
5
5
x
x
SHR
SHR
.S1
.S1
.L1
.L1
.D1
.D1
c = (a >>
c = (a >>
5) + a
5) + a
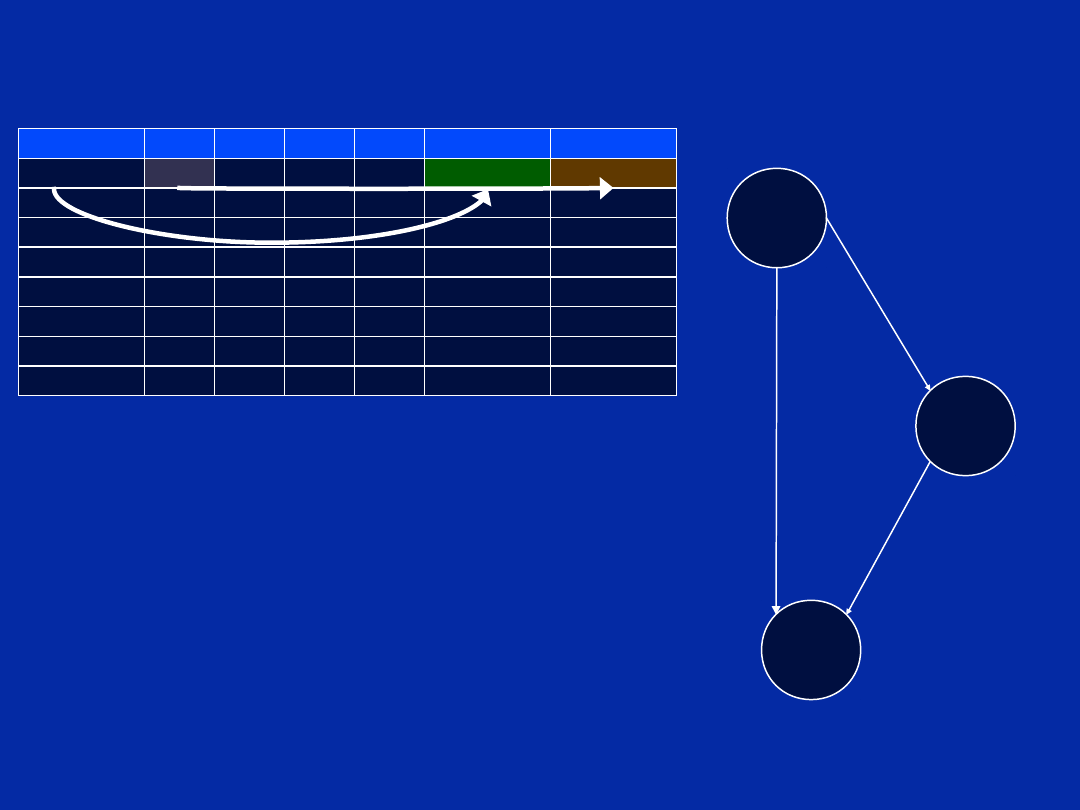
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 129
Live Too Long - Example
Live Too Long - Example
0
0
LDH ai
LDH ai
5
5
a0 valid
a0 valid
6
6
a1
a1
1
1
LDH
LDH
2
2
LDH
LDH
3
3
LDH
LDH
4
4
LDH
LDH
ai
ai
LDH
LDH
ci
ci
ADD
ADD
5
5
1
1
5
5
x
x
SHR
SHR
.S1
.S1
.L1
.L1
.D1
.D1
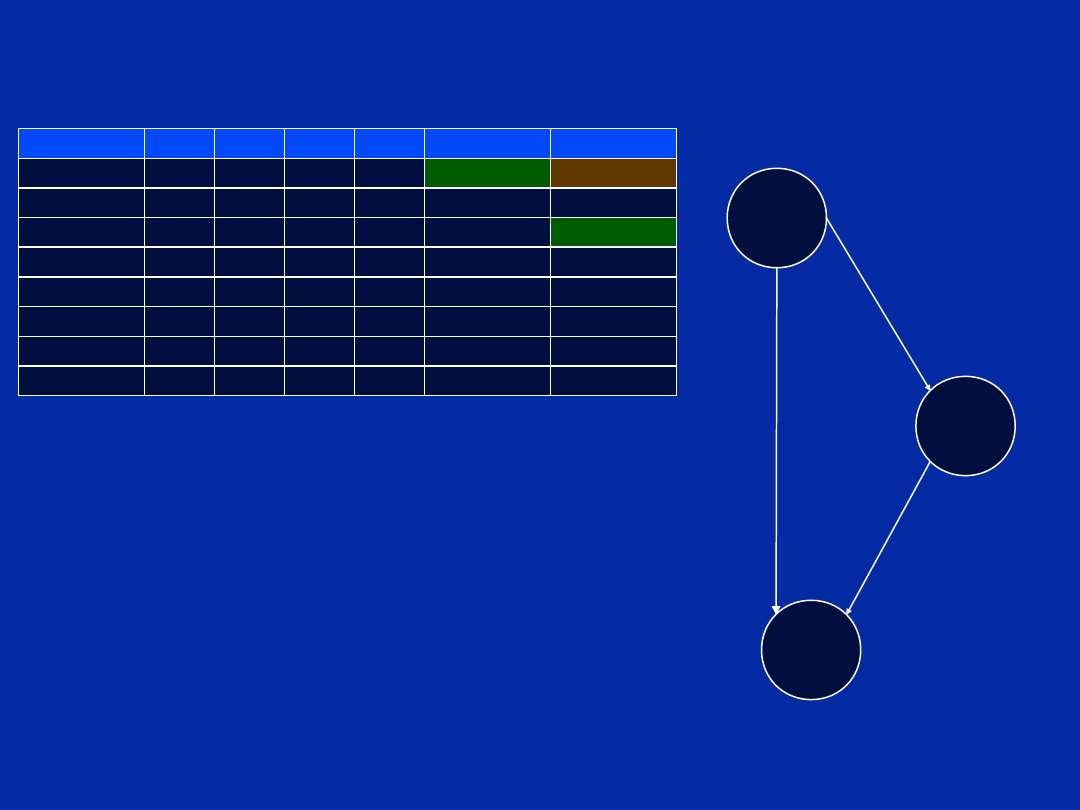
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 130
Live Too Long - Example
Live Too Long - Example
0
0
LDH ai
LDH ai
5
5
a0 valid
a0 valid
SHR
SHR
6
6
a1
a1
x0 valid
x0 valid
1
1
LDH
LDH
2
2
LDH
LDH
3
3
LDH
LDH
4
4
LDH
LDH
ai
ai
LDH
LDH
ci
ci
ADD
ADD
5
5
1
1
5
5
x
x
SHR
SHR
.S1
.S1
.L1
.L1
.D1
.D1
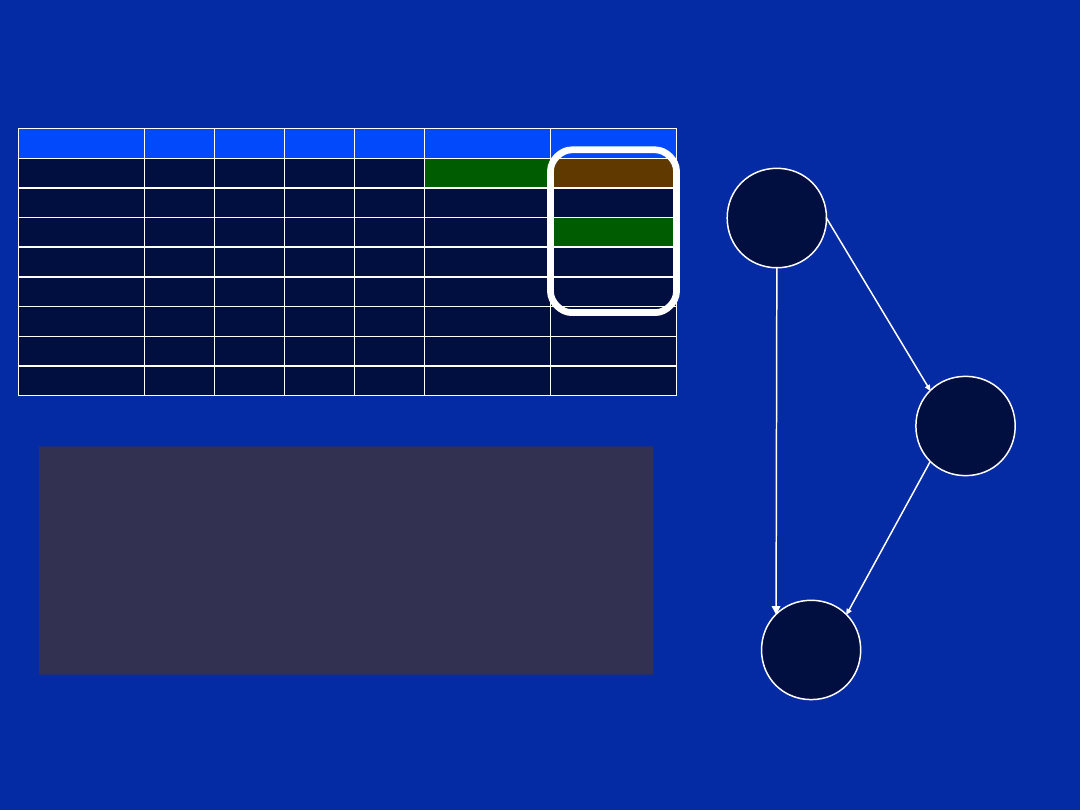
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 131
Live Too Long - Example
Live Too Long - Example
0
0
LDH ai
LDH ai
5
5
a0 valid
a0 valid
SHR
SHR
6
6
a1
a1
x0 valid
x0 valid
ADD
ADD
1
1
LDH
LDH
2
2
LDH
LDH
3
3
LDH
LDH
4
4
LDH
LDH
ai
ai
LDH
LDH
ci
ci
ADD
ADD
5
5
1
1
5
5
x
x
SHR
SHR
.S1
.S1
.L1
.L1
.D1
.D1
Oops, rather than adding
Oops, rather than adding
a0 + x0
a0 + x0
we got
we got
a1 + x0
a1 + x0
Let’s look at one solution ...
Let’s look at one solution ...

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 132
Live Too Long -
Live Too Long -
2 Cycle Solution
2 Cycle Solution
0
0
LDH ai
LDH ai
2
2
LDH
LDH
4
4
LDH
LDH
6
6
a0 valid
a0 valid
1
1
3
3
5
5
a0 valid
a0 valid
7
7
a1
a1
With a 2 cycle loop,
With a 2 cycle loop,
a0 is valid for
a0 is valid for
2 cycles.
2 cycles.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 133
Live Too Long -
Live Too Long -
2 Cycle Solution
2 Cycle Solution
0
0
LDH ai
LDH ai
2
2
LDH
LDH
4
4
LDH
LDH
6
6
a0 valid
a0 valid
x0 valid
x0 valid
1
1
3
3
5
5
a0 valid
a0 valid
SHR
SHR
7
7
a1
a1
x0 valid
x0 valid
Notice, a0 and x0 are
Notice, a0 and x0 are
both valid for 2 cycles
both valid for 2 cycles
which is the length of the
which is the length of the
Iteration Interval
Iteration Interval
Adding them ...
Adding them ...

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 134
Live Too Long -
Live Too Long -
2 Cycle Solution
2 Cycle Solution
0
0
LDH ai
LDH ai
2
2
LDH
LDH
4
4
LDH
LDH
6
6
a0 valid
a0 valid
x0 valid
x0 valid
ADD
ADD
1
1
3
3
5
5
a0 valid
a0 valid
SHR
SHR
7
7
a1
a1
x0 valid
x0 valid
Works!
Works!
But what’s the drawback?
But what’s the drawback?
2 cycle loop is slower.
2 cycle loop is slower.
Here’s a better solution ...
Here’s a better solution ...
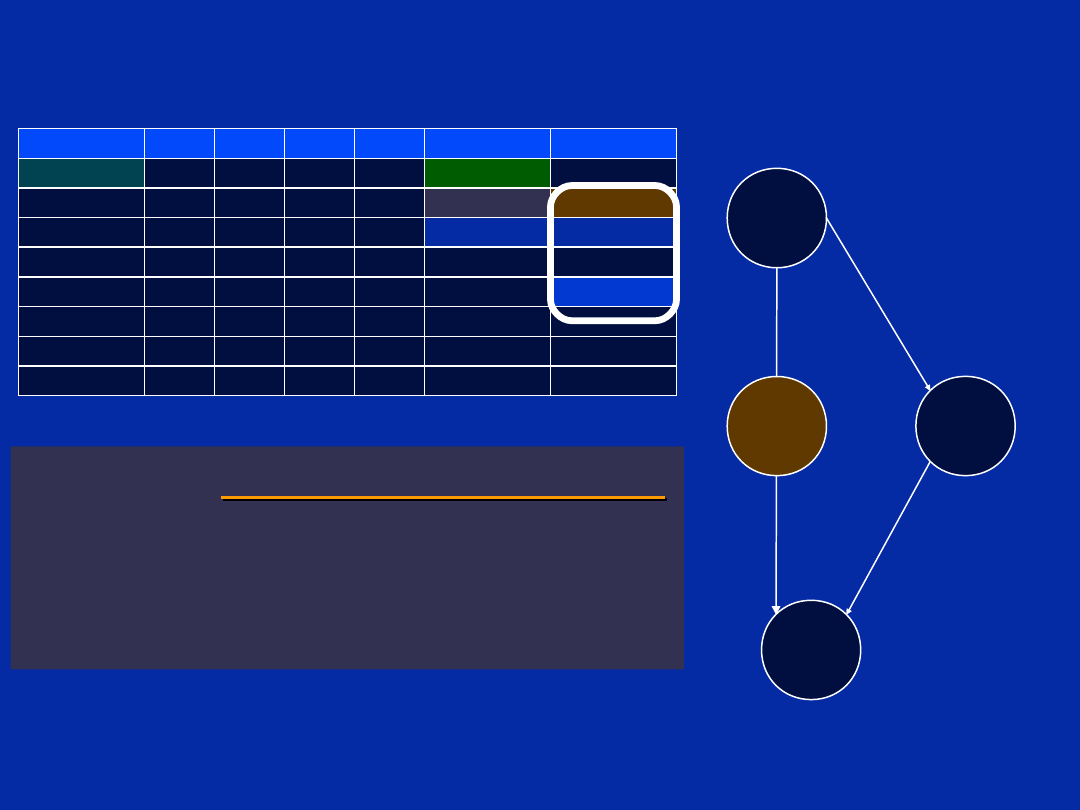
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 135
Live Too Long -
Live Too Long -
1 Cycle Solution
1 Cycle Solution
ai
ai
LDH
LDH
ci
ci
ADD
ADD
5
5
1
1
5
5
x
x
SHR
SHR
.S1
.S1
.L1
.L1
.D1
.D1
1
1
b
b
MV
MV
.S2
.S2
Using a
Using a
temporary register
temporary register
solves this problem without
solves this problem without
increasing the
increasing the
Minimum Iteration Interval
Minimum Iteration Interval
0
0
LDH ai
LDH ai
5
5
a0 valid
a0 valid
MV b
MV b
SHR
SHR
1
1
LDH
LDH
2
2
LDH
LDH
3
3
LDH
LDH
4
4
LDH
LDH
6
6
a1
a1
b valid
b valid
x0 valid
x0 valid
ADD
ADD

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 136
What Requires Multi-Cycle Loops?
What Requires Multi-Cycle Loops?
Four reasons:
Four reasons:
1.
1.
Resource Limitations.
Resource Limitations.
2.
2.
Live Too Long.
Live Too Long.
3.
3.
Loop Carry Path.
Loop Carry Path.
4.
4.
Double Precision (FUL > 1).
Double Precision (FUL > 1).
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 137
Loop Carry Path
Loop Carry Path
The loop carry path is a path which feeds one variable from part of the
The loop carry path is a path which feeds one variable from part of the
algorithm back to another.
algorithm back to another.
p2
p2
st_y0
st_y0
MPY.M2
MPY.M2
STH.D1
STH.D1
2
2
1
1
e.g. Loop carry
e.g. Loop carry
path = 3.
path = 3.
Note: The loop carry path is not the
Note: The loop carry path is not the
code loop.
code loop.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 138
Loop Carry Path, e.g. IIR Filter
Loop Carry Path, e.g. IIR Filter
IIR Filter Example
IIR Filter Example
y0 = a0*x0 + b1*y1
y0 = a0*x0 + b1*y1

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 139
IIR.SA
IIR.SA
IIR:
IIR:
ldh
ldh
*a_1, A1
*a_1, A1
ldh
ldh
*x1, A3
*x1, A3
ldh
ldh
*b_1, B1
*b_1, B1
ldh
ldh
*y0, B0
*y0, B0
; y1 is previous y0
; y1 is previous y0
mpy
mpy
A1, A3, prod1
A1, A3, prod1
mpy
mpy
B1, B0, prod2
B1, B0, prod2
add
add
prod1, prod2, prod2
prod1, prod2, prod2
sth
sth
prod2, *y0
prod2, *y0
IIR Filter Example
IIR Filter Example
y0 = a0*x0 + b1*y1
y0 = a0*x0 + b1*y1
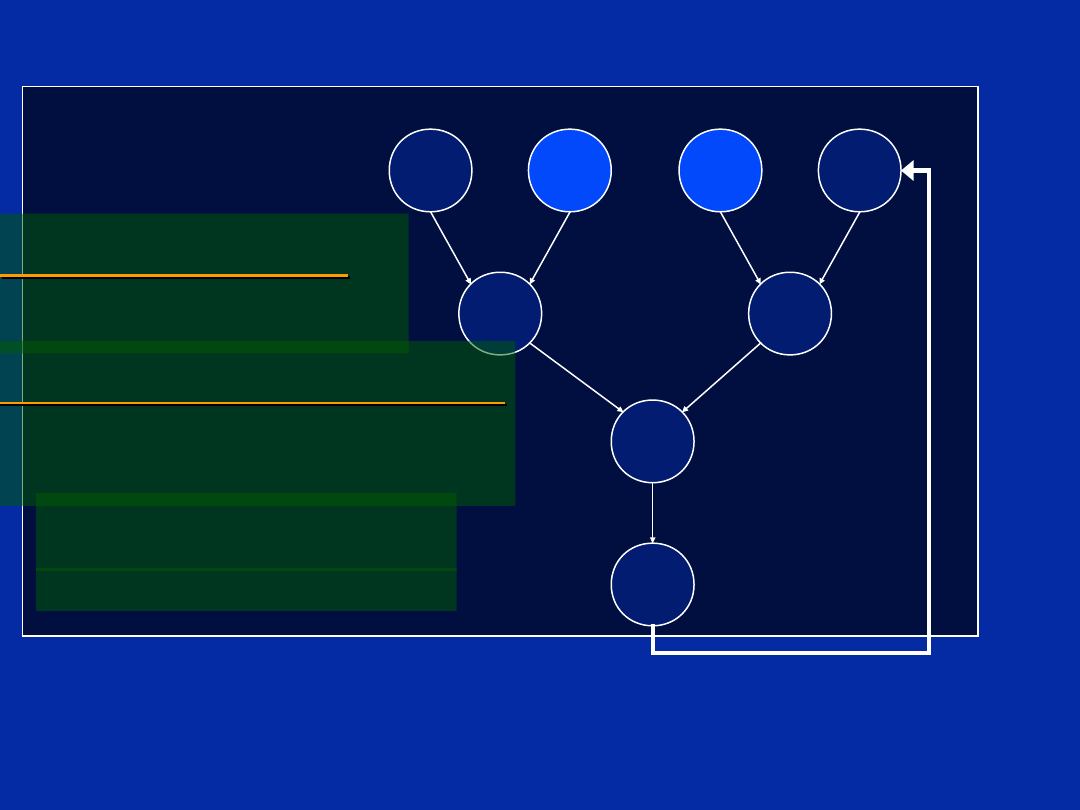
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 140
Loop Carry Path - IIR Example
Loop Carry Path - IIR Example
p1
p1
x1
x1
A1
A1
p2
p2
B1
B1
y1
y1
y0
y0
st_y0
st_y0
LDH.D1
LDH.D1
LDH.D2
LDH.D2
MPY.M1
MPY.M1
MPY.M2
MPY.M2
ADD.L1
ADD.L1
STH.D1
STH.D1
5
5
2
2
1
1
IIR Filter Loop
IIR Filter Loop
y0 = a1*x1 + b1*y1
y0 = a1*x1 + b1*y1
Min Iteration Interval
Min Iteration Interval
Resource = 2
Resource = 2
(need 3 .D units)
(need 3 .D units)
1
1
Result carries over from
Result carries over from
one iteration of the loop
one iteration of the loop
to the next.
to the next.
Loop Carry Path = 9
Loop Carry Path = 9
(9 = 5 + 2 + 1 + 1)
(9 = 5 + 2 + 1 + 1)
therefore, MII = 9
therefore, MII = 9
Can it be minimized?
Can it be minimized?
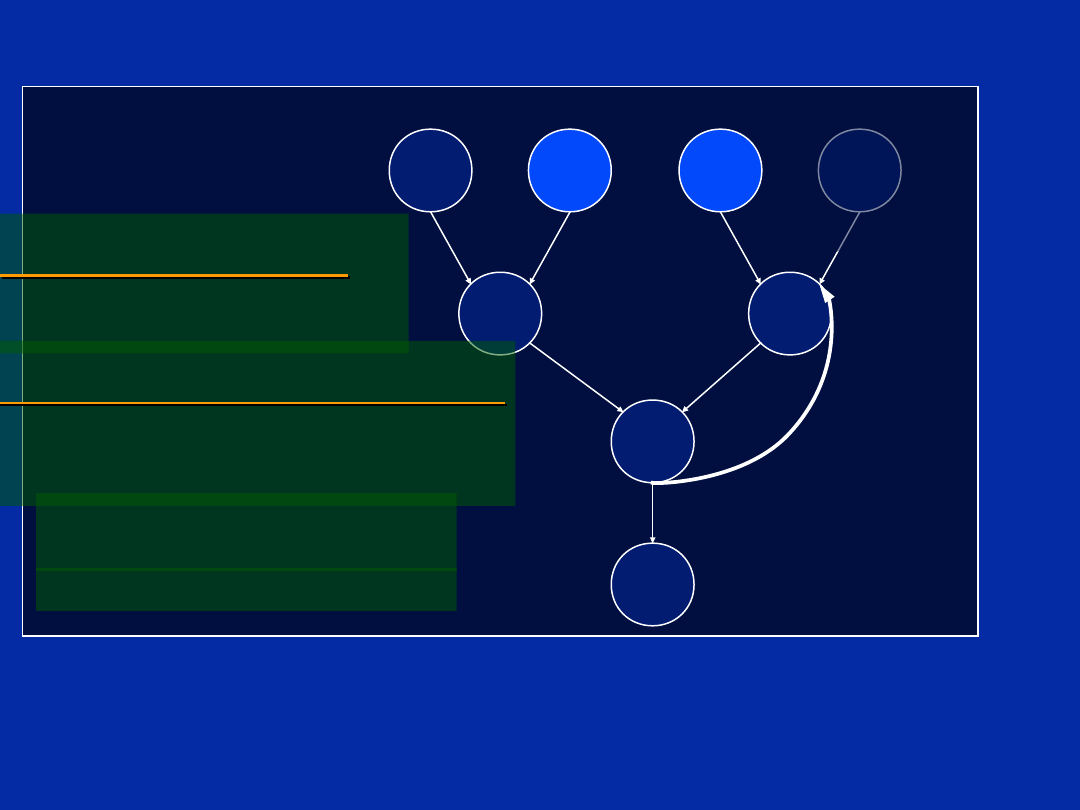
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 141
Loop Carry Path - IIR Example
Loop Carry Path - IIR Example
(Solution)
(Solution)
p1
p1
x1
x1
A1
A1
p2
p2
B1
B1
y1
y1
y0
y0
st_y0
st_y0
LDH.D1
LDH.D1
LDH.D2
LDH.D2
MPY.M1
MPY.M1
MPY.M2
MPY.M2
ADD.L1
ADD.L1
STH.D1
STH.D1
5
5
2
2
1
1
IIR Filter Loop
IIR Filter Loop
y0 = a1*x1 + b1*y1
y0 = a1*x1 + b1*y1
Min Iteration Interval
Min Iteration Interval
Resource = 2
Resource = 2
(need 3 .D units)
(need 3 .D units)
1
1
New
New
Loop Carry Path = 3
Loop Carry Path = 3
(3 = 2 + 1)
(3 = 2 + 1)
therefore, MII = 3
therefore, MII = 3
Since y0 is stored in a CPU register,
Since y0 is stored in a CPU register,
it can be used directly by MPY
it can be used directly by MPY
(after the first loop iteration).
(after the first loop iteration).
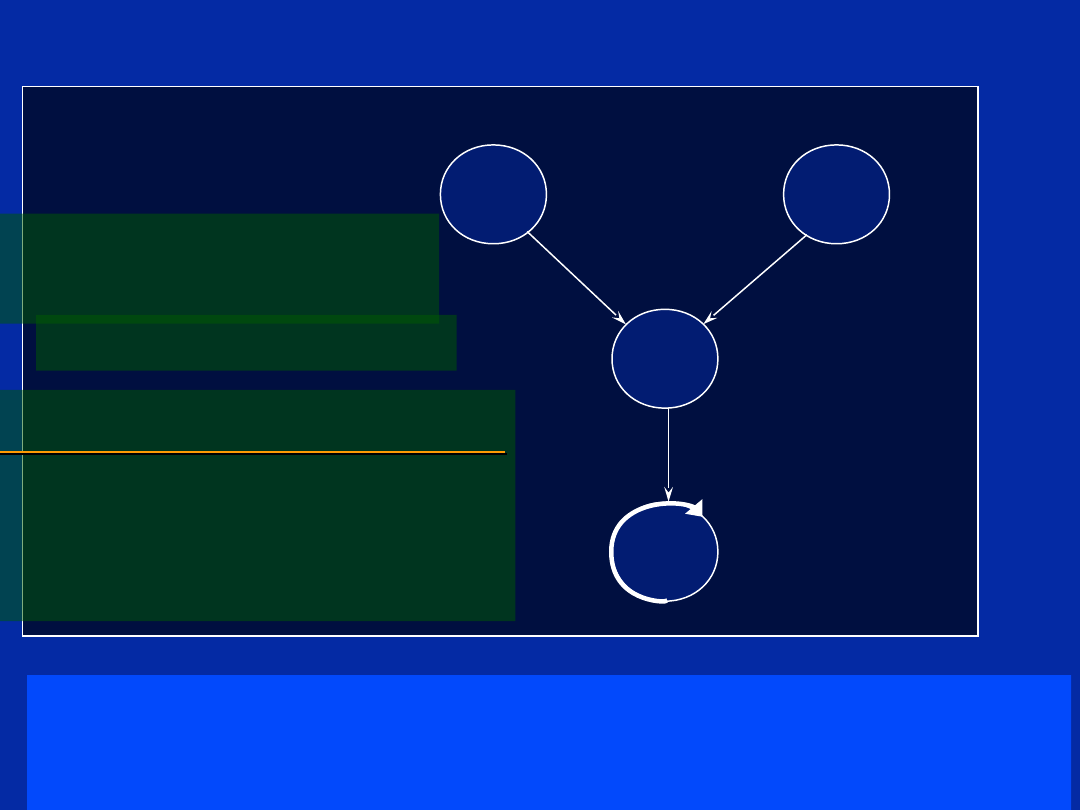
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 142
Reminder: Fixed-Point Dot-
Reminder: Fixed-Point Dot-
Product Example
Product Example
m
m
LDH
LDH
n
n
LDH
LDH
prod
prod
MPY
MPY
sum
sum
ADD
ADD
.D1
.D1
.D2
.D2
5
5
2
2
.M1x
.M1x
.L1
.L1
Is there a loop carry
Is there a loop carry
path in this example?
path in this example?
1
1
Yes, but it’s only “1”
Yes, but it’s only “1”
Min Iteration Interval
Min Iteration Interval
Resource = 1
Resource = 1
Loop Carry Path = 1
Loop Carry Path = 1
MII = 1
MII = 1
For the fixed-point implementation, the
For the fixed-point implementation, the
Loop Carry Path was not taken into
Loop Carry Path was not taken into
account because it is equal to 1.
account because it is equal to 1.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 143
Loop Carry Path
Loop Carry Path
IIR Example.
IIR Example.
Enhancing the IIR.
Enhancing the IIR.
Fixed-Point Dot-Product
Fixed-Point Dot-Product
Example.
Example.
Floating-Point Dot Product
Floating-Point Dot Product
Example.
Example.
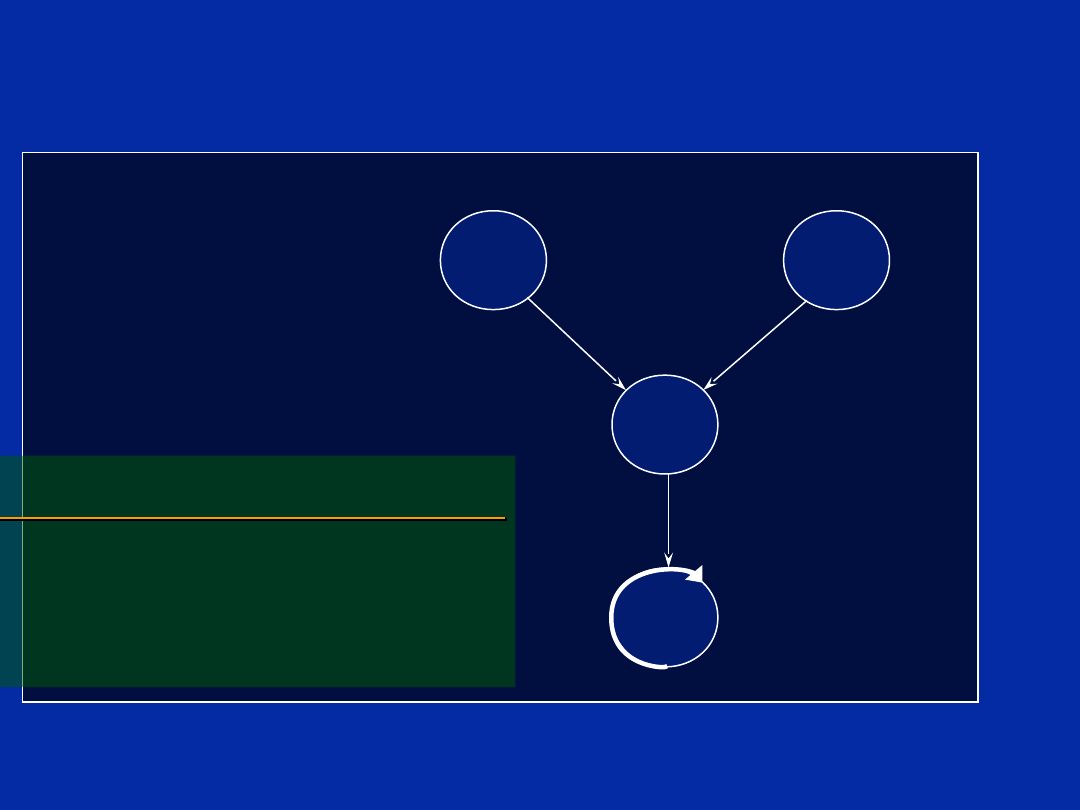
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 144
Loop Carry Path due to FUL > 1
Loop Carry Path due to FUL > 1
Floating-Point Dot-Product
Floating-Point Dot-Product
Example
Example
m
m
LDW
LDW
n
n
LDW
LDW
prod
prod
MPYSP
MPYSP
sum
sum
ADDSP
ADDSP
.D1
.D1
.D2
.D2
5
5
4
4
.M1x
.M1x
.L1
.L1
4
4
Min Iteration Interval
Min Iteration Interval
Resource = 1
Resource = 1
Loop Carry Path = 4
Loop Carry Path = 4
MII = 4
MII = 4
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 145
Unrolling the Loop
Unrolling the Loop
If the MII must be four cycles
If the MII must be four cycles
long, then use all of them to
long, then use all of them to
calculate four results.
calculate four results.
m1
m1
LDW
LDW
n1
n1
LDW
LDW
prod1
prod1
MPYSP
MPYSP
sum1
sum1
ADDSP
ADDSP
.D1
.D1
.D2
.D2
4
4
.M1x
.M1x
.L1
.L1
m2
m2
LDW
LDW
n2
n2
LDW
LDW
prod2
prod2
MPYSP
MPYSP
sum2
sum2
ADDSP
ADDSP
.D1
.D1
.D2
.D2
4
4
.M1x
.M1x
.L1
.L1
m3
m3
LDW
LDW
n3
n3
LDW
LDW
prod3
prod3
MPYSP
MPYSP
sum3
sum3
ADDSP
ADDSP
.D1
.D1
.D2
.D2
4
4
.M1x
.M1x
.L1
.L1
m4
m4
LDW
LDW
n4
n4
LDW
LDW
prod4
prod4
MPYSP
MPYSP
sum4
sum4
ADDSP
ADDSP
.D1
.D1
.D2
.D2
4
4
.M1x
.M1x
.L1
.L1

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 146
ADDSP Pipeline (Staggered
ADDSP Pipeline (Staggered
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
sum = x1 + x5
sum = x1 + x5
10
10
sum = x2 + x6
sum = x2 + x6
11
11
sum = x3 + x7
sum = x3 + x7
12
12
sum = x0 + x4 +
sum = x0 + x4 +
x8
x8
ADDSP takes 4 cycles or three
ADDSP takes 4 cycles or three
delay slots to produce the result.
delay slots to produce the result.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 147
ADDSP Pipeline (Staggered
ADDSP Pipeline (Staggered
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
sum = x1 + x5
sum = x1 + x5
10
10
sum = x2 + x6
sum = x2 + x6
11
11
sum = x3 + x7
sum = x3 + x7
12
12
sum = x0 + x4 +
sum = x0 + x4 +
x8
x8

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 148
ADDSP Pipeline (Staggered
ADDSP Pipeline (Staggered
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
sum = x1 + x5
sum = x1 + x5
10
10
sum = x2 + x6
sum = x2 + x6
11
11
sum = x3 + x7
sum = x3 + x7
12
12
sum = x0 + x4 +
sum = x0 + x4 +
x8
x8

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 149
ADDSP Pipeline (Staggered
ADDSP Pipeline (Staggered
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
sum = x1 + x5
sum = x1 + x5
10
10
sum = x2 + x6
sum = x2 + x6
11
11
sum = x3 + x7
sum = x3 + x7
12
12
sum = x0 + x4 +
sum = x0 + x4 +
x8
x8

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 150
ADDSP Pipeline (Staggered
ADDSP Pipeline (Staggered
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
sum = x1 + x5
sum = x1 + x5
10
10
sum = x2 + x6
sum = x2 + x6
11
11
sum = x3 + x7
sum = x3 + x7
12
12
sum = x0 + x4 +
sum = x0 + x4 +
x8
x8

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 151
ADDSP Pipeline (Staggered
ADDSP Pipeline (Staggered
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
sum = x1 + x5
sum = x1 + x5
10
10
sum = x2 + x6
sum = x2 + x6
11
11
sum = x3 + x7
sum = x3 + x7
12
12
sum = x0 + x4 +
sum = x0 + x4 +
x8
x8

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 152
ADDSP Pipeline (Staggered
ADDSP Pipeline (Staggered
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
sum = x1 + x5
sum = x1 + x5
10
10
sum = x2 + x6
sum = x2 + x6
11
11
sum = x3 + x7
sum = x3 + x7
12
12
sum = x0 + x4 +
sum = x0 + x4 +
x8
x8

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 153
ADDSP Pipeline (Staggered
ADDSP Pipeline (Staggered
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
sum = x1 + x5
sum = x1 + x5
10
10
sum = x2 + x6
sum = x2 + x6
11
11
sum = x3 + x7
sum = x3 + x7
12
12
sum = x0 + x4 +
sum = x0 + x4 +
x8
x8

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 154
ADDSP Pipeline (Staggered
ADDSP Pipeline (Staggered
Results)
Results)
There are effectively four
There are effectively four
running sums:
running sums:
sum (i)
sum (i)
= x(i) + x(i+4) + x(i+8)
= x(i) + x(i+4) + x(i+8)
+ …
+ …
sum (i+1)
sum (i+1)
= x(i+1) + x(i+5) +
= x(i+1) + x(i+5) +
x(i+9) + …
x(i+9) + …
sum (i+2)
sum (i+2)
= x(i+2) + x(i+6) +
= x(i+2) + x(i+6) +
x(i+10) + …
x(i+10) + …
sum (i+3)
sum (i+3)
= x(i+3) + x(i+7) +
= x(i+3) + x(i+7) +
x(i+11) + …
x(i+11) + …
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
NOP
NOP
sum = x1 + x5
sum = x1 + x5
10
10
NOP
NOP
sum = x2 + x6
sum = x2 + x6
11
11
NOP
NOP
sum = x3 + x7
sum = x3 + x7
12
12
NOP
NOP
sum = x0 + x4 +
sum = x0 + x4 +
x8
x8

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 155
ADDSP Pipeline (Staggered
ADDSP Pipeline (Staggered
Results)
Results)
There are effectively four
There are effectively four
running sums:
running sums:
sum (i)
sum (i)
= x(i) + x(i+4) + x(i+8)
= x(i) + x(i+4) + x(i+8)
+ …
+ …
sum (i+1)
sum (i+1)
= x(i+1) + x(i+5) +
= x(i+1) + x(i+5) +
x(i+9) + …
x(i+9) + …
sum (i+2)
sum (i+2)
= x(i+2) + x(i+6) +
= x(i+2) + x(i+6) +
x(i+10) + …
x(i+10) + …
sum (i+3)
sum (i+3)
= x(i+3) + x(i+7) +
= x(i+3) + x(i+7) +
x(i+11) + …
x(i+11) + …
These need to be combined after
These need to be combined after
the last addition is complete...
the last addition is complete...

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 156
ADDSP Pipeline (Combining
ADDSP Pipeline (Combining
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
MV
MV
sum, temp
sum, temp
sum = x1 + x5
sum = x1 + x5
10
10
sum = x2 + x6
sum = x2 + x6
11
11
sum = x3 + x7
sum = x3 + x7
12
12
sum = x0 + x4 + x8
sum = x0 + x4 + x8

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 157
ADDSP Pipeline (Combining
ADDSP Pipeline (Combining
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
MV
MV
sum, temp
sum, temp
sum = x1 + x5
sum = x1 + x5
10
10
ADDSP
ADDSP
sum, temp, sum1
sum, temp, sum1
sum = x2 + x6,
sum = x2 + x6,
temp =
temp =
x1 + x5
x1 + x5
11
11
sum = x3 + x7
sum = x3 + x7
12
12
sum = x0 + x4 + x8
sum = x0 + x4 + x8

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 158
ADDSP Pipeline (Combining
ADDSP Pipeline (Combining
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
MV
MV
sum, temp
sum, temp
sum = x1 + x5
sum = x1 + x5
10
10
ADDSP
ADDSP
sum, temp, sum1
sum, temp, sum1
sum = x2 + x6,
sum = x2 + x6,
temp =
temp =
x1 + x5
x1 + x5
11
11
MV
MV
sum, temp
sum, temp
sum = x3 + x7
sum = x3 + x7
12
12
sum = x0 + x4 + x8
sum = x0 + x4 + x8

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 159
ADDSP Pipeline (Combining
ADDSP Pipeline (Combining
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
MV
MV
sum, temp
sum, temp
sum = x1 + x5
sum = x1 + x5
10
10
ADDSP
ADDSP
sum, temp, sum1
sum, temp, sum1
sum = x2 + x6,
sum = x2 + x6,
temp =
temp =
x1 + x5
x1 + x5
11
11
MV
MV
sum, temp
sum, temp
sum = x3 + x7
sum = x3 + x7
12
12
ADDSP
ADDSP
sum, temp, sum2
sum, temp, sum2
sum = x0 + x4 + x8,
sum = x0 + x4 + x8,
temp = x3
temp = x3
+ x7
+ x7

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 160
ADDSP Pipeline (Combining
ADDSP Pipeline (Combining
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
MV
MV
sum, temp
sum, temp
sum = x1 + x5
sum = x1 + x5
10
10
ADDSP
ADDSP
sum, temp, sum1
sum, temp, sum1
sum = x2 + x6,
sum = x2 + x6,
temp =
temp =
x1 + x5
x1 + x5
11
11
MV
MV
sum, temp
sum, temp
sum = x3 + x7
sum = x3 + x7
12
12
ADDSP
ADDSP
sum, temp, sum2
sum, temp, sum2
sum = x0 + x4 + x8,
sum = x0 + x4 + x8,
temp = x3
temp = x3
+ x7
+ x7
13
13
NOP
NOP
14
14
NOP
NOP
sum1 = x1 + x2 + x5 + x6
sum1 = x1 + x2 + x5 + x6

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 161
ADDSP Pipeline (Combining
ADDSP Pipeline (Combining
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
MV
MV
sum, temp
sum, temp
sum = x1 + x5
sum = x1 + x5
10
10
ADDSP
ADDSP
sum, temp, sum1
sum, temp, sum1
sum = x2 + x6,
sum = x2 + x6,
temp =
temp =
x1 + x5
x1 + x5
11
11
MV
MV
sum, temp
sum, temp
sum = x3 + x7
sum = x3 + x7
12
12
ADDSP
ADDSP
sum, temp sum2
sum, temp sum2
sum = x0 + x4 + x8,
sum = x0 + x4 + x8,
temp = x3
temp = x3
+ x7
+ x7
13
13
NOP
NOP
14
14
NOP
NOP
sum1 = x1 + x2 + x5 + x6
sum1 = x1 + x2 + x5 + x6
15
15
NOP
NOP
16
16
ADDSP
ADDSP
sum1, sum2, sum
sum1, sum2, sum
sum2 = x0 + x3 + x4 + x7 + x8
sum2 = x0 + x3 + x4 + x7 + x8

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 162
ADDSP Pipeline (Combining
ADDSP Pipeline (Combining
Results)
Results)
Cycle
Cycle
Instruction
Instruction
Result
Result
0
0
ADDSP
ADDSP
x0, sum, sum
x0, sum, sum
sum = 0
sum = 0
1
1
ADDSP
ADDSP
x1, sum, sum
x1, sum, sum
sum = 0
sum = 0
2
2
ADDSP
ADDSP
x2, sum, sum
x2, sum, sum
sum = 0
sum = 0
3
3
ADDSP
ADDSP
x3, sum, sum
x3, sum, sum
sum = 0
sum = 0
4
4
ADDSP
ADDSP
x4, sum, sum
x4, sum, sum
sum = x0
sum = x0
5
5
ADDSP
ADDSP
x5, sum, sum
x5, sum, sum
sum = x1
sum = x1
6
6
ADDSP
ADDSP
x6, sum, sum
x6, sum, sum
sum = x2
sum = x2
7
7
ADDSP
ADDSP
x7, sum, sum
x7, sum, sum
sum = x3
sum = x3
8
8
ADDSP
ADDSP
x8, sum, sum
x8, sum, sum
sum = x0 + x4
sum = x0 + x4
9
9
MV
MV
sum, temp
sum, temp
sum = x1 + x5
sum = x1 + x5
10
10
ADDSP
ADDSP
sum, temp, sum1
sum, temp, sum1
sum = x2 + x6,
sum = x2 + x6,
temp =
temp =
x1 + x5
x1 + x5
11
11
MV
MV
sum, temp
sum, temp
sum = x3 + x7
sum = x3 + x7
12
12
ADDSP
ADDSP
sum, temp sum2
sum, temp sum2
sum = x0 + x4 + x8,
sum = x0 + x4 + x8,
temp = x3
temp = x3
+ x7
+ x7
13
13
NOP
NOP
14
14
NOP
NOP
sum1 = x1 + x2 + x5 + x6
sum1 = x1 + x2 + x5 + x6
15
15
NOP
NOP
16
16
ADDSP
ADDSP
sum1, sum2, sum
sum1, sum2, sum
sum2 = x0 + x3 + x4 + x7 + x8
sum2 = x0 + x3 + x4 + x7 + x8
17
17
NOP
NOP
18
18
NOP
NOP
19
19
NOP
NOP
20
20
NOP
NOP
sum = x0 + x1 + x2 + x3 + x4 + x5 + x6
sum = x0 + x1 + x2 + x3 + x4 + x5 + x6
+ x7 + x8
+ x7 + x8

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 163
What Requires Multi-Cycle Loops?
What Requires Multi-Cycle Loops?
Four reasons:
Four reasons:
1.
1.
Resource Limitations.
Resource Limitations.
2.
2.
Live Too Long.
Live Too Long.
3.
3.
Loop Carry Path.
Loop Carry Path.
4.
4.
Double Precision (FUL > 1).
Double Precision (FUL > 1).
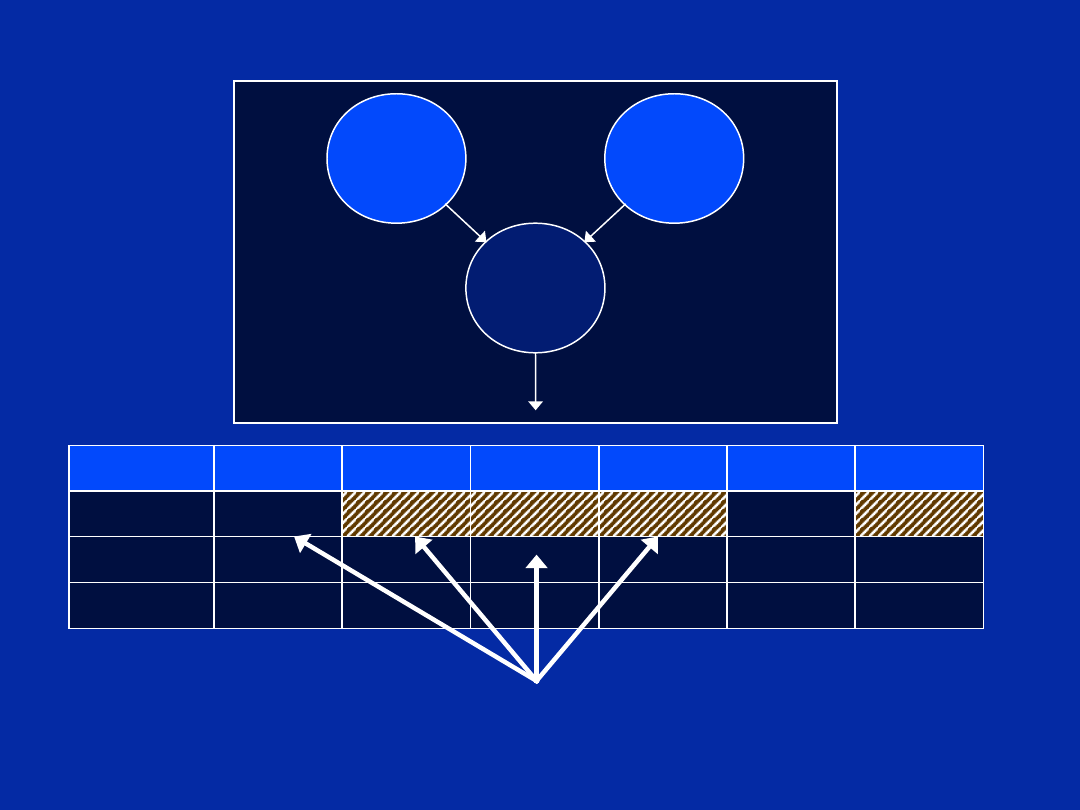
Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 164
Simple FUL Example
Simple FUL Example
prod
prod
3
3
5
5
MPYDP
MPYDP
10 (4.9)
10 (4.9)
.M1
.M1
1
1
MPYDP
MPYDP
2
2
3
3
4
4
5
5
MPYDP
MPYDP
6
6
...
...
MPYDP ties up the functional unit
MPYDP ties up the functional unit
for 4 cycles.
for 4 cycles.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 165
A Better Way to Diagram this ...
A Better Way to Diagram this ...
.M1
.M1
1
1
MPYDP
MPYDP
5
5
MPYDP
MPYDP
9
9
MPYDP
MPYDP
13
13
MPYDP
MPYDP
.M1
.M1
2
2
6
6
10
10
14
14
.M1
.M1
3
3
7
7
11
11
prod1
prod1
15
15
prod2
prod2
.M1
.M1
4
4
8
8
12
12
16
16
Since the MPYDP
Since the MPYDP
instruction has a
instruction has a
functional unit
functional unit
latency (FUL) of
latency (FUL) of
“
“
4”, .M1 cannot be
4”, .M1 cannot be
used again until
used again until
the fifth cycle.
the fifth cycle.
Hence,
Hence,
MII
MII
4.
4.

Dr. Naim
Dahnoun,
Bristol U
niversity
, (c) Te
xas Instr
uments 20
04
Chapter 12, Slide 166
What Requires Multi-Cycle Loops?
What Requires Multi-Cycle Loops?
1.
1.
Resource Limitations.
Resource Limitations.
2.
2.
Live Too Long.
Live Too Long.
3.
3.
Loop Carry Path.
Loop Carry Path.
4.
4.
Double Precision
Double Precision
(FUL > 1).
(FUL > 1).
Lab: Converting your dot-
Lab: Converting your dot-
product code to Single-Precision
product code to Single-Precision
Floating-Point.
Floating-Point.

Chapter 12
Chapter 12
Software Optimisation
Software Optimisation
- End -
- End -
Document Outline
- Slide 1
- Software Optimisation Chapter
- Slide 3
- Objectives
- Introduction
- Slide 6
- Code Optimisation Procedure
- Slide 8
- Optimising C Compiler Options
- Assembly Optimisation
- Slide 11
- Slide 12
- Slide 13
- Step 1 - Using Parallel Instructions
- Slide 15
- Step 2 - Removing the NOPs
- Step 3 - Loop Unrolling
- Step 4 - Word or Double Word Access
- Slide 19
- Optimisation Summary
- Slide 21
- Slide 22
- Slide 23
- Why using Software Pipelining, SP?
- Software Pipeline concept
- Software Pipeline Example
- Non-Pipelined Code
- Pipelining Code
- Slide 29
- Slide 30
- Pipelined Code
- Software Pipelining Procedure
- Software Pipelining Example (Step 1)
- Slide 34
- Write code in Linear Assembly (Step 2)
- Slide 36
- Dependency Graph Terminology
- Dependency Graph Steps
- Dependency Graph (Step a)
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Dependency Graph (Step b)
- Slide 47
- Dependency Graph (Step c)
- Slide 49
- Dependency Graph (Step d)
- Slide 51
- Slide 52
- Slide 53
- Step 4 - Allocate Functional Units
- Step 4 - Allocate Registers
- Slide 56
- Step 5 - Create Scheduling Table
- Length of Prolog
- Scheduling Table
- Slide 60
- Slide 61
- Slide 62
- Translate Scheduling Table to ‘C6x Code
- Slide 64
- Slide 65
- Slide 66
- Slide 67
- Slide 68
- Slide 69
- Slide 70
- Slide 71
- Solution: The Epilog
- Dot-Product with Epilog
- Slide 74
- Slide 75
- Slide 76
- Slide 77
- Slide 78
- Slide 79
- Scheduling Table: Prolog, Loop and Epilog
- Loop only!
- Slide 82
- Slide 83
- Slide 84
- Slide 85
- Loop Only - Final Code
- Laboratory exercise
- Lab Solution: Step 1 - Linear Assembly
- Step 2 - Dependency Graph
- Step 2 - Functional Units
- Step 2 - Registers
- Step 3 - Schedule Algorithm
- Step 4 - ‘C6000 Code
- Why Conditional Subtract?
- Slide 95
- Slide 96
- What Requires Multi-Cycle Loops?
- Slide 98
- Resource Limitation: Weighted Vector Sum
- Slide 100
- Step 2 - ‘C6x Linear Code
- Step 3 - Dependency Graph
- Step 4 -Allocate Functional Units
- 2 Cycle Loop
- Multi-Cycle Loop Iterations
- Slide 106
- Slide 107
- Slide 108
- Slide 109
- Slide 110
- How long is the Prolog?
- Step 5 - Create Scheduling Chart (0)
- Step 5 - Create Scheduling Chart
- Slide 114
- Slide 115
- Slide 116
- Slide 117
- Slide 118
- Slide 119
- Conflict Solution
- Slide 121
- Slide 122
- Slide 123
- Slide 124
- Slide 125
- 2 Cycle Loop Kernel
- Slide 127
- Live Too Long - Example
- Slide 129
- Slide 130
- Slide 131
- Live Too Long - 2 Cycle Solution
- Slide 133
- Slide 134
- Live Too Long - 1 Cycle Solution
- Slide 136
- Loop Carry Path
- Loop Carry Path, e.g. IIR Filter
- IIR.SA
- Loop Carry Path - IIR Example
- Loop Carry Path - IIR Example (Solution)
- Reminder: Fixed-Point Dot-Product Example
- Slide 143
- Loop Carry Path due to FUL > 1 Floating-Point Dot-Product Example
- Unrolling the Loop
- ADDSP Pipeline (Staggered Results)
- Slide 147
- Slide 148
- Slide 149
- Slide 150
- Slide 151
- Slide 152
- Slide 153
- Slide 154
- Slide 155
- ADDSP Pipeline (Combining Results)
- Slide 157
- Slide 158
- Slide 159
- Slide 160
- Slide 161
- Slide 162
- Slide 163
- Simple FUL Example
- A Better Way to Diagram this ...
- Slide 166
- Slide 167
Wyszukiwarka
Podobne podstrony:
Figures for chapter 5
Figures for chapter 12
Figures for chapter 6
Chapter16
Chapter21a
Chapter22
Dictionary Chapter 07
Chapter1
Chapter 8 Magnetostratigraphic polarity units
JNC 2013 Chapter 18 Matthews and Anwar
Matlab Class Chapter 1
więcej podobnych podstron