Lech Gładysiewicz

Lech Gładysiewicz

Instytut Górnictwa

Instytut Górnictwa

Politechniki Wrocławskiej

Politechniki Wrocławskiej

Właściwości dynamiczne

taśmy przenośnikowej

 

Lech Gładysiewicz

Lech Gładysiewicz

Instytut Górnictwa

Instytut Górnictwa

Politechniki Wrocławskiej

Politechniki Wrocławskiej

Do typowych procesów wyróżniających taśmę
pod względem zmiennych obciążeń zaliczyć
można

:

  zmieniające się w zależności od miejsca na trasie oraz

chwilowej strugi urobku siły rozciągające w ruchu ustalonym

  silne oscylacje sił o różnym charakterze w zależności od

miejsca na trasie przenośnika w czasie rozruchu i hamowania;

  cyklicznie powtarzające się na każdej podporze

krążnikowej naciski i zginanie poprzeczne;

  wielokrotne zginanie taśmy na bębnach;

  nierównomierność obciążeń rdzenia taśmy na odcinkach

przejściowych

  odkształcenia trwałe oraz zmiana sprężystości w czasie w

wyniku wielocyklowych obciążeń;

  zależność modułu sprężystości taśmy od szybkości

narastania naprężeń.

Lech Gładysiewicz

Lech Gładysiewicz

Instytut Górnictwa

Instytut Górnictwa

Politechniki Wrocławskiej

Politechniki Wrocławskiej

 
 

Właściwości taśmy w trakcie cyklicznego

rozciągania

(ε

0

-odkształcenie trwałe taśmy; moduł

sprężystości podłużnej E=tgβ)

wydłużenie

(odkształcenie)

si

ła

r

oz

ci

ąg

aj

ąc

a

(n

ap

rę

że

ni

e)

pierwsze cykle obciążeń

po stabilizacji





Lech Gładysiewicz

Lech Gładysiewicz

Instytut Górnictwa

Instytut Górnictwa

Politechniki Wrocławskiej

Politechniki Wrocławskiej





E

a)

c)

b)









E

0

E

U



v



v

E

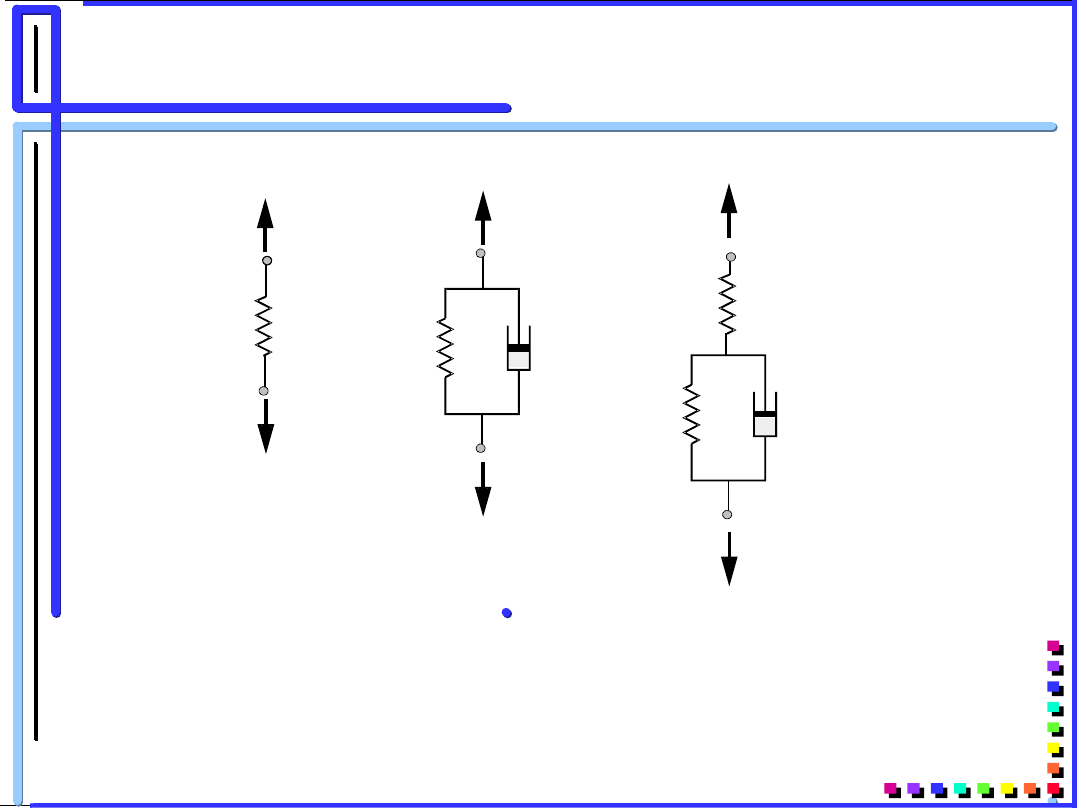
Stosowane w obliczeniach modele

reologiczne taśmy przenośnikowej

:

a) – jednoparametrowy

b) - dwuparametrowy Kelvina-Voigtha,

c) - trójparametrowy (standardowy)

Lech Gładysiewicz

Lech Gładysiewicz

Instytut Górnictwa

Instytut Górnictwa

Politechniki Wrocławskiej

Politechniki Wrocławskiej















(t)



(t)





0



t

t

K

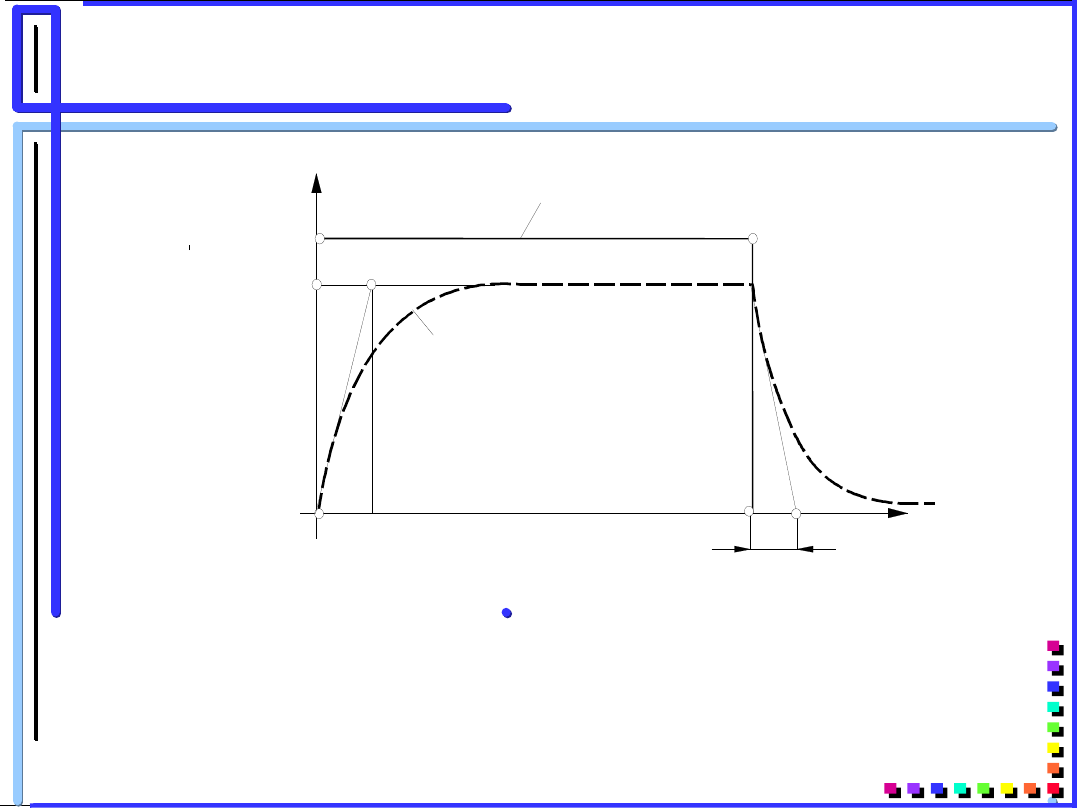
Zachowanie się modelu

dwuparametrowego przy skokowych

zmianach naprężeń

Lech Gładysiewicz

Lech Gładysiewicz

Instytut Górnictwa

Instytut Górnictwa

Politechniki Wrocławskiej

Politechniki Wrocławskiej









t

















 



przesunięcie fazowe

a)









pierwszy

cykl

kolejne cykle

b)









E

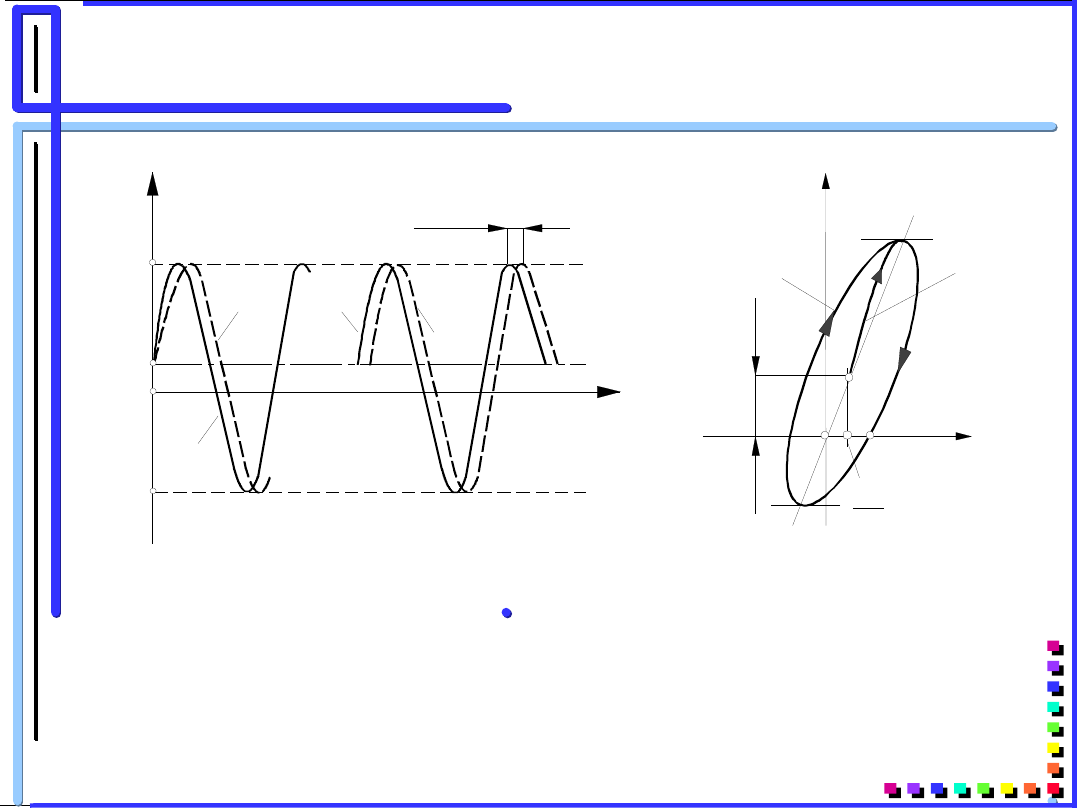
Zachowanie się modelu dwuparametrowego

przy wymuszeniu harmonicznym:

a) - przebieg naprężeń i odkształceń w czasie

b) - pętla histerezy

Lech Gładysiewicz

Lech Gładysiewicz

Instytut Górnictwa

Instytut Górnictwa

Politechniki Wrocławskiej

Politechniki Wrocławskiej

t













t

b)















const



const

a)

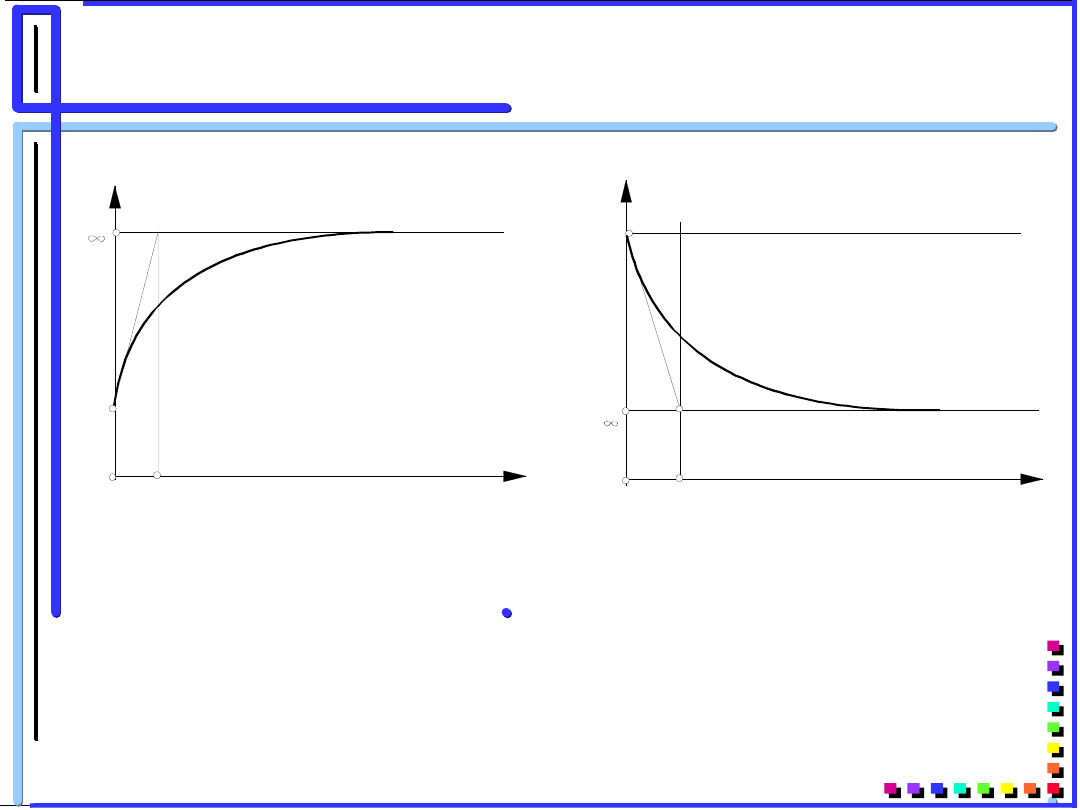
Właściwości taśmy odwzorowane

modelem trójparametrowym:

a)  – krzywa pełzania

b) – krzywa relaksacji naprężeń

Lech Gładysiewicz

Lech Gładysiewicz

Instytut Górnictwa

Instytut Górnictwa

Politechniki Wrocławskiej

Politechniki Wrocławskiej

S



S



S



S









1

2

3

4

L













v

t

 t =

v

t

L

v

t

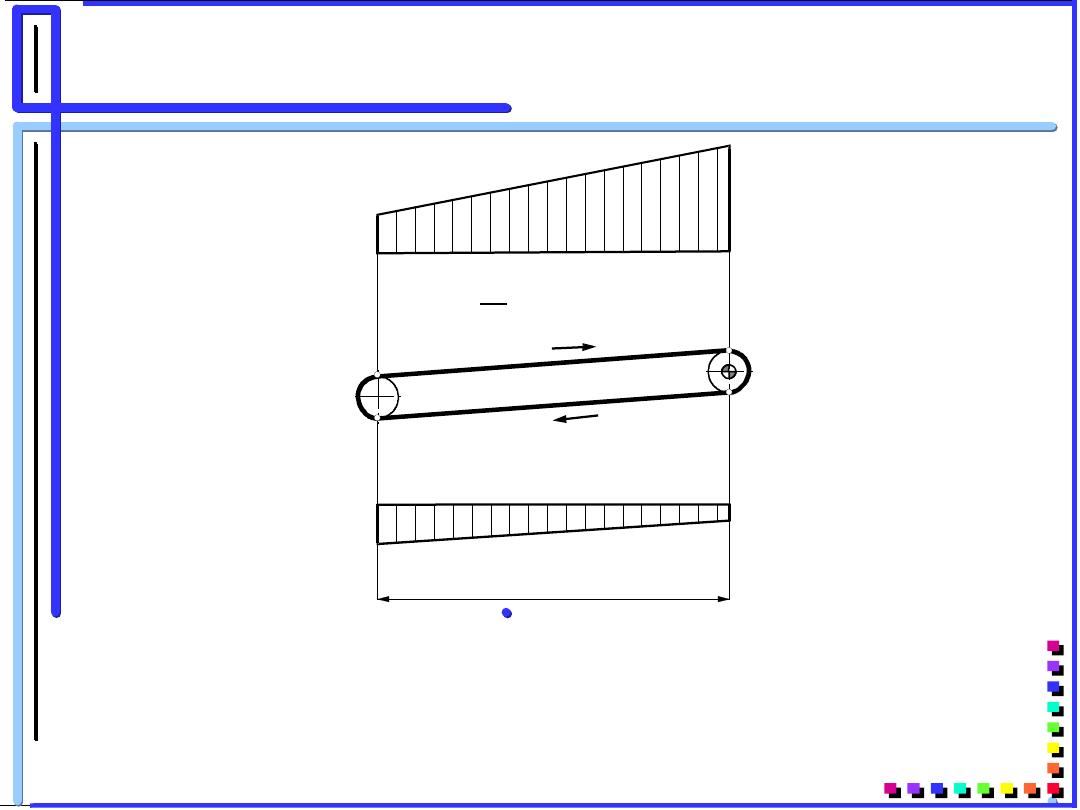
Zmiany sił (naprężeń) w

cięgnie górnym i dolnym

przenośnika w ruchu

ustalonym

Lech Gładysiewicz

Lech Gładysiewicz

Instytut Górnictwa

Instytut Górnictwa

Politechniki Wrocławskiej

Politechniki Wrocławskiej

Moduł dynamiczny taśmy na

trasie przenośnika w ruchu

ustalonym:

- dla modelu dwuparametrowego





























t

1

M

E

R

d

- dla modelu trójparametrowego

t

1

E

E

0

d









Lech Gładysiewicz

Lech Gładysiewicz

Instytut Górnictwa

Instytut Górnictwa

Politechniki Wrocławskiej

Politechniki Wrocławskiej

2

1

P

O

P

O

P

O

= P

O

+ P

O

S



S



S



S



1

2

P

O

S



S



S



S



1

2

3

4

c

H

W

d

-

W

ht

W

G

+

W

ht

+

W

hn

a

b

Siły w taśmie w ruchu ustalonym przenośnika z

napędem czołowym

a) - rozkład sił w cięgnie górnym i dolnym,

b) - rozkład sił na stacji napędowej jednobębnowej

c) - rozkład sił na stacji napędowej dwubębnowej

Lech Gładysiewicz

Lech Gładysiewicz

Instytut Górnictwa

Instytut Górnictwa

Politechniki Wrocławskiej

Politechniki Wrocławskiej

Moduł dynamiczny taśmy

na bębnie napędowym

U

R

db

E

M

E



















1

E

E

b

0

db

















model trójparametrowy

model dwuparametrowy
(ω

b

- prędkość kątowa bębna)

Lech Gładysiewicz

Lech Gładysiewicz

Instytut Górnictwa

Instytut Górnictwa

Politechniki Wrocławskiej

Politechniki Wrocławskiej

Przykład:

Przenośnik długości L=800 m i prędkości taśmy v

t

=3,25 m/s

taśma z rdzeniem tkaninowym opisana modelem reologicznym
trójparametrowym,moduł relaksacji sprężystej M

R

=2,8·10

6

N/m,

czas relaksacji naprężeń τ

ε

=40s oraz czas relaksacji odkształceń

τ

σ

=60 s

czas przyrastania naprężeń w cięgnie górnym i dolnym

moduł dynamiczny dla warunków zmian występujących w
cięgnie dolnym lub górnym w ruchu ustalonym

moduł dynamiczny dla warunków na bębnie
napędowym

s

v

L

t

t

246

25

,

3

800









m

N

t

M

E

R

d

/

10

5

,

2

7

,

152

40

60

1

10

8

,

2

1

6

6





















































m

N

E

M

E

U

R

db

/

10

2

,

4

40

60

10

8

,

2

6

6

























Lech Gładysiewicz

Lech Gładysiewicz

Instytut Górnictwa

Instytut Górnictwa

Politechniki Wrocławskiej

Politechniki Wrocławskiej

Wnioski:

 

Występują istotne różnice wartości
modułów dynamicznych taśmy w zależności
od szybkości zmian naprężeń.
Przy analizowaniu obciążeń jednostek
napędowych w napędzie głównym
wielobębnowym należy rozróżniać moduł
dynamiczny dla warunków panujących na
trasie przenośnika (względnie mały
przyrosty naprężeń) od modułu
adekwatnego dla warunków panujących na
bębnie napędowym (szybkie zmiany
naprężeń)