Wydział Fizyki, Matematyki i Informatyki Stosowanej
Instytut Modelowania Komputerowego
Zakład Grafiki Komputerowej i Obliczeń Wysokiej Wydajności
wykład 6:
Histogram obrazu rastrowego
Poprawa jakości obrazu
(operacje geometryczne i arytmetyczne)
Grafika Komputerowa
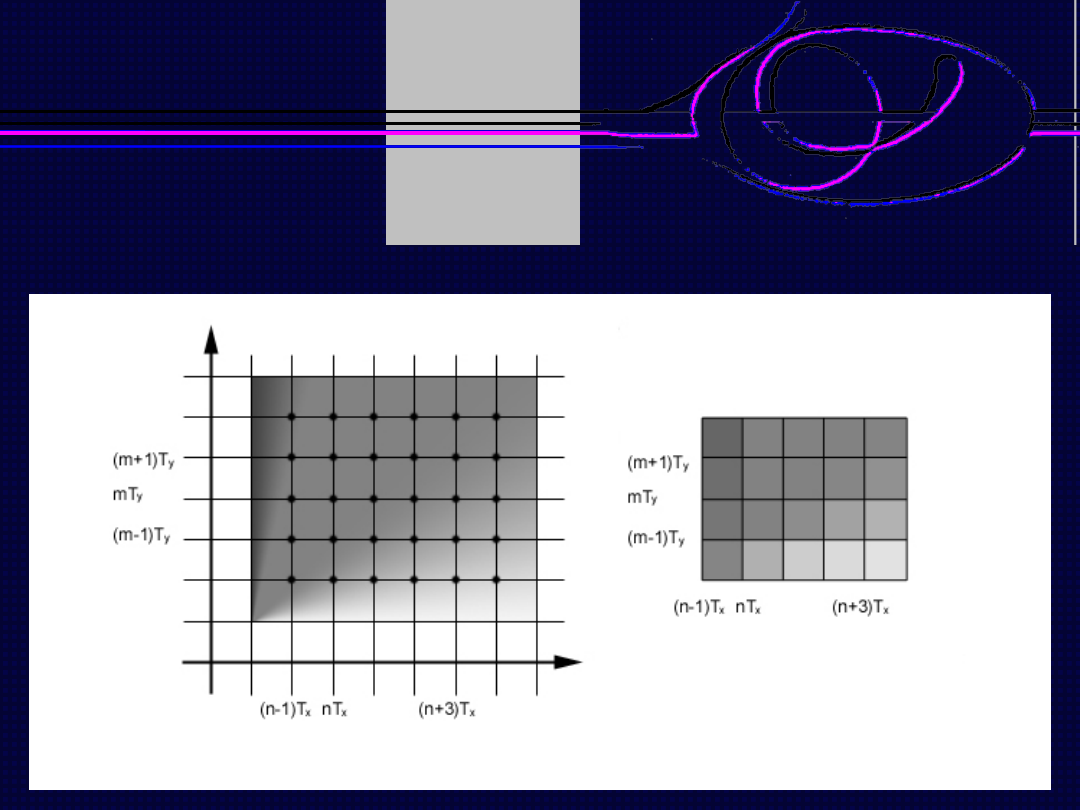
Dyskretyzacja obrazu w oparciu o dwuwymiarowe próbkowanie
Grafika komputerowa
– wykład 6
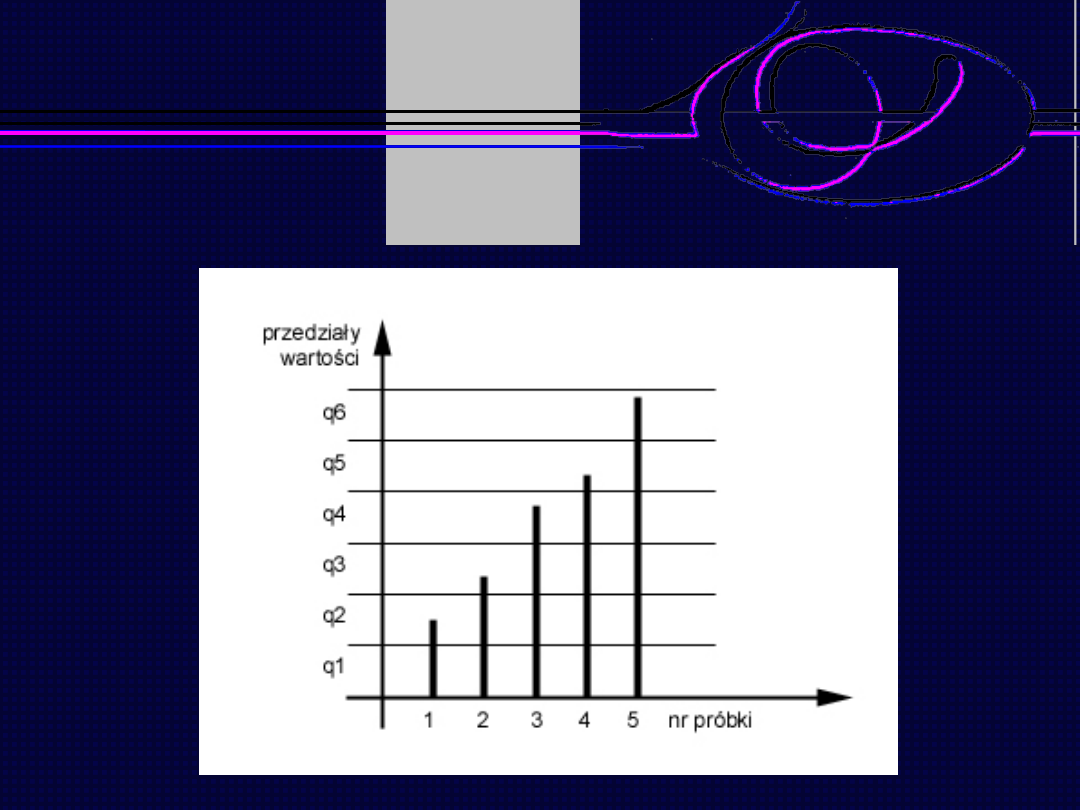
Kwantyzacja obrazu
Grafika komputerowa
– wykład 6
Obraz zapisany jako tablica
punktów (pikseli) o wartościach
parametru jasności od 0 do 255
(grayscale), przy czym:
• wartość J=0 odpowiada
barwie czarnej,
• J=255 odpowiada barwie
białej.
Grafika komputerowa
– wykład 6
Histogram obrazu
Histogram jest to jeden z graficznych sposobów przedstawiania
rozkładu cechy.
Jeżeli będziemy analizować parametr jasności, histogram
podaje informacje na temat ilości pikseli o zadanym poziomie
jasności występujących w danym obrazie.
Obliczanie składowych histogramu odbywa się zgodnie z
wzorem:
gdzie n
i
oznacza liczbę pikseli o
danym
poziomie jasności i (J
i
),
M – rozmiar obrazu względem osi
X,
N – rozmiar obrazu względem osi
Y
g
i
(x,y) = 1 gdy J(x,y) = i,
0 w przeciwnym razie
)
y
,
x
(
g
n
M
x
N
y
i
i
1
0
1
0
Grafika komputerowa
– wykład 6
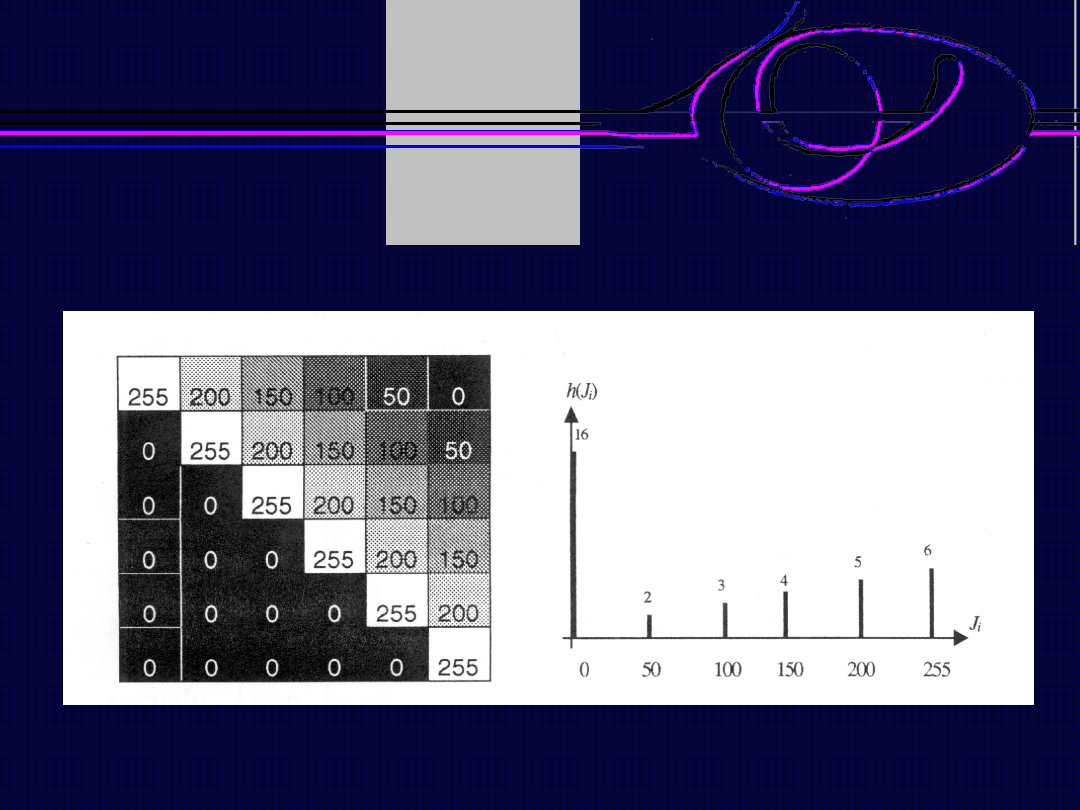
Histogram obrazu
Przykładowy obraz i histogram ilościowy cechy jasności
tego obrazu
Grafika komputerowa
– wykład 6
Histogram obrazu
Schemat tworzenia
histogramu
Grafika komputerowa
– wykład 6
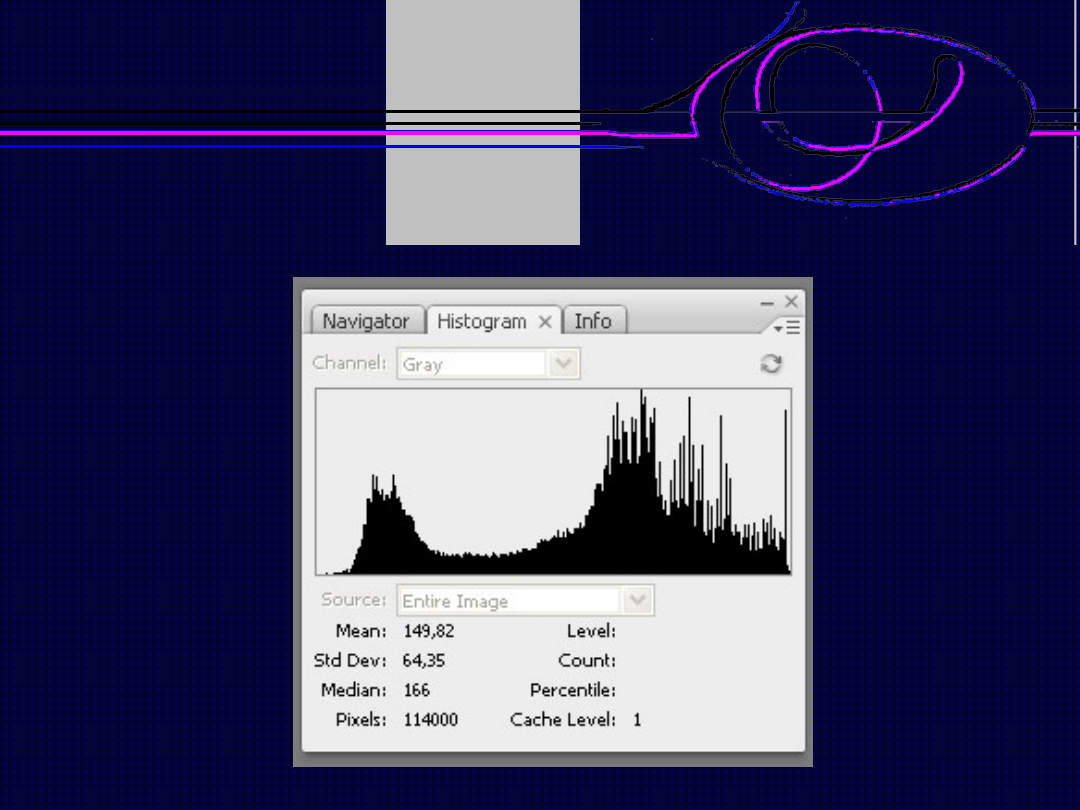
Histogram obrazu
Grafika komputerowa
– wykład 6
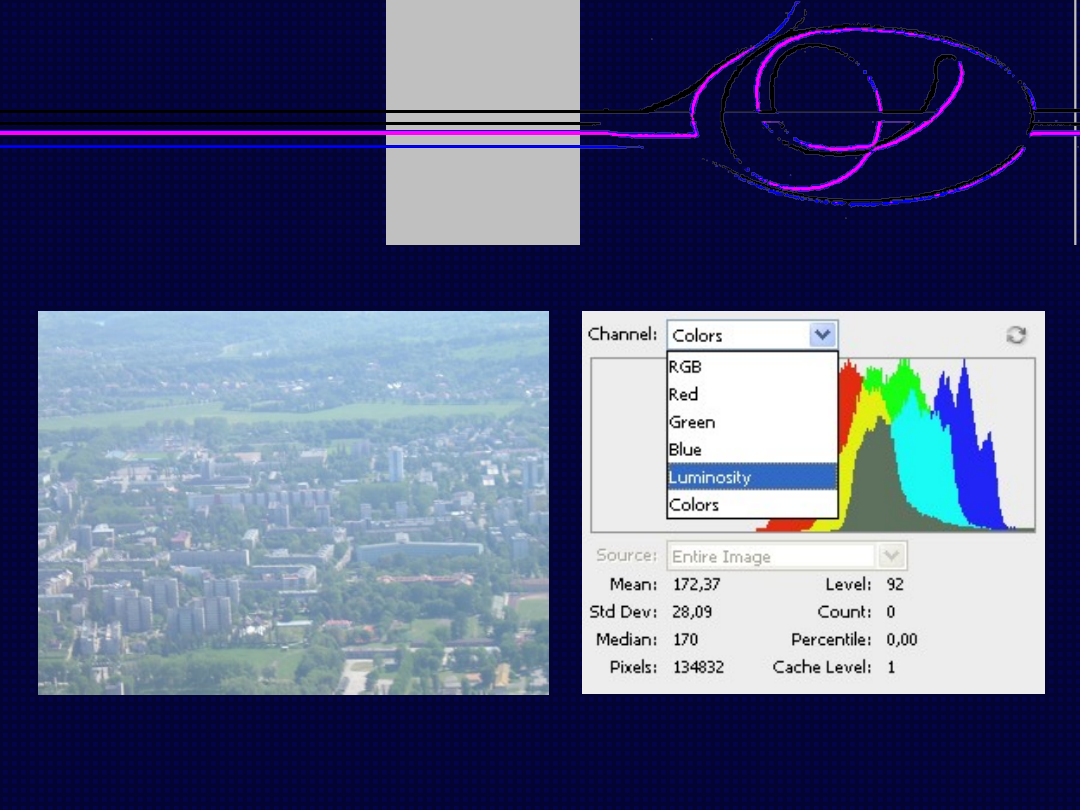
Histogram obrazu
Histogramy jasności oraz poszczególnych składowych
koloru
Grafika komputerowa
– wykład 6
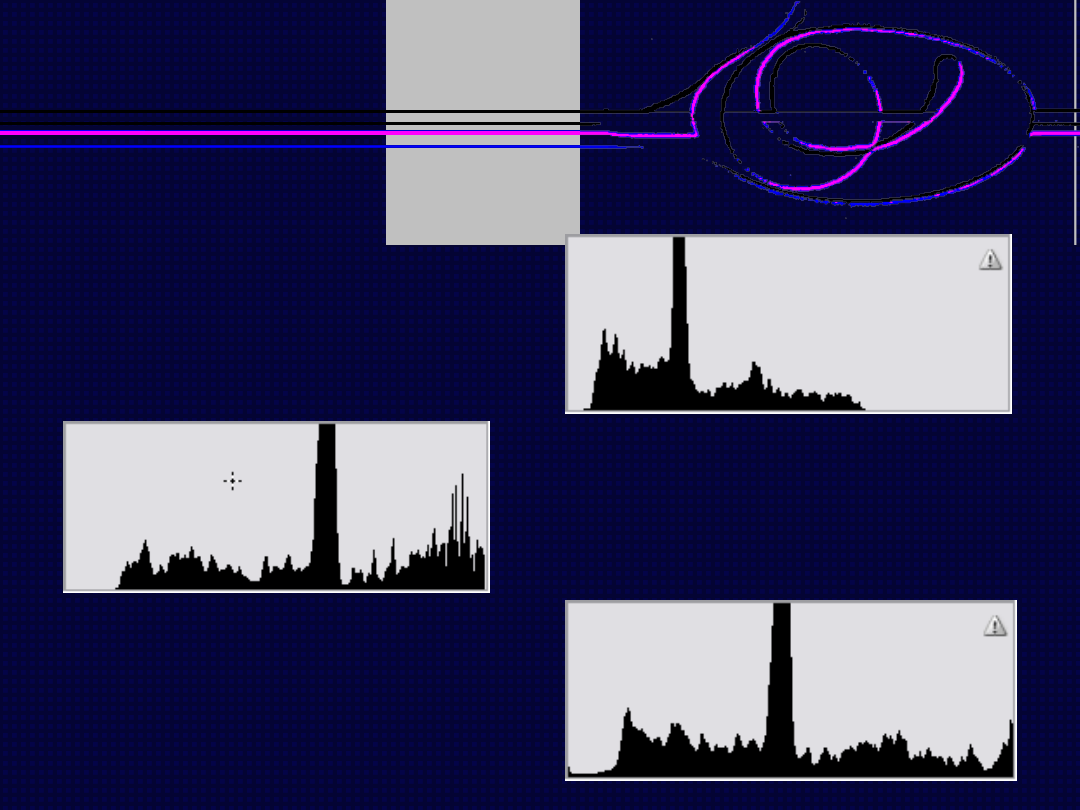
Histogram obrazu
poprawnego – wyzyskanie
pełnego zakresu poziomów
jasności
Histogram obrazu zbyt
ciemnego – w obrazie
występują głównie piksele o
niskiej jasności, brak pikseli
o wysokiej
jasności
Histogram obrazu zbyt jasnego –
w obrazie występują
głównie piksele o wysokiej
jasności, brak pikseli o
niskiej jasności
Grafika komputerowa
– wykład 6
Histogram obrazu
o niskim kontraście
Histogram obrazu o
wysokim kontraście
Grafika komputerowa
– wykład 6
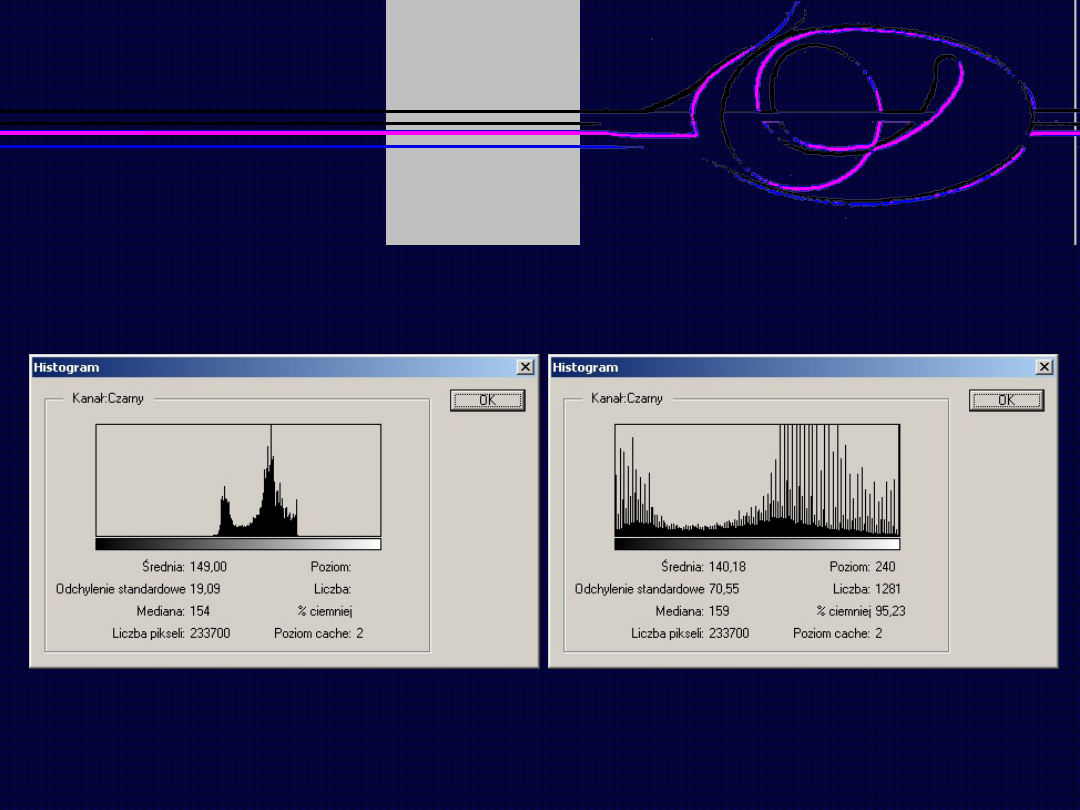
W praktyce często stosuje się histogram oparty o procentowy
rozkład jasności. Wówczas jego rzędne oblicza się ze wzoru:
gdzie n
i
oznacza liczbę pikseli
o poziomie jasności J
i
,
n jest liczbą pikseli całego
obrazu.
Jeżeli zakres dostępnych poziomów danej cechy (w tym
przypadku jasności) nie jest w pełni wykorzystany, stosuje się
modyfikacje histogramu, prowadzące do zmiany kształtu jego
obwiedni.
Histogram obrazu
n
n
)
J
(
h
i
i
Grafika komputerowa
– wykład 6
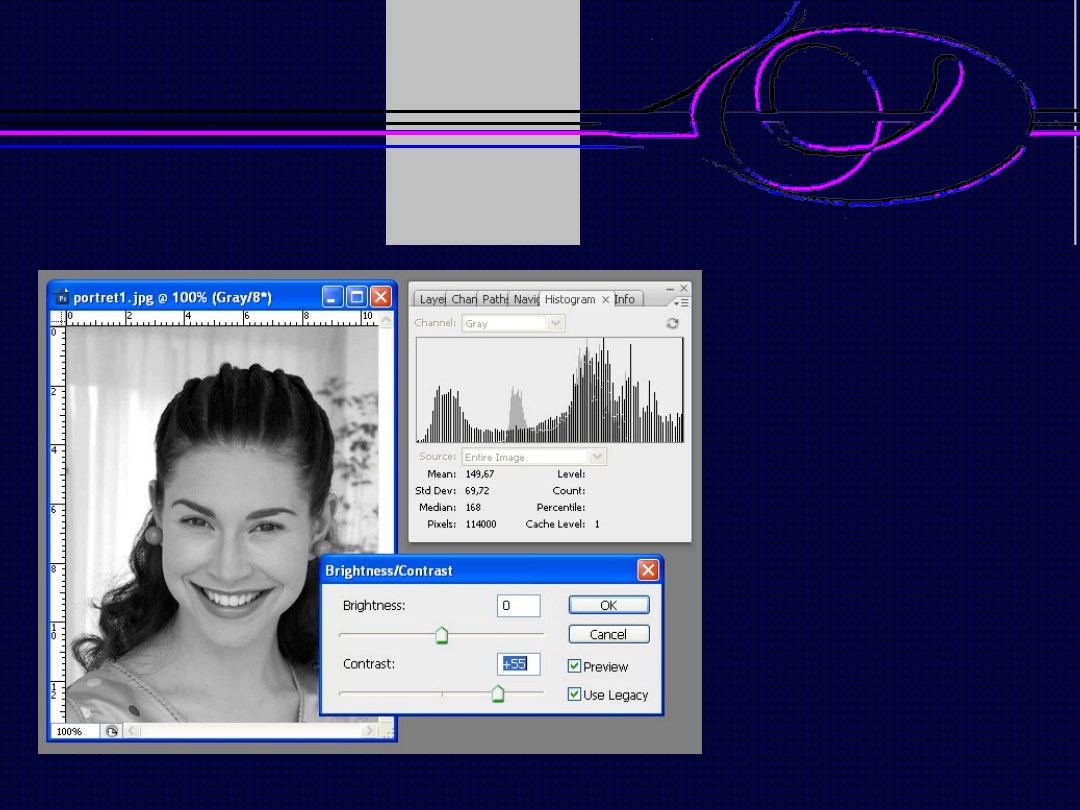
Operacje na histogramie
Rozszerzanie zakresu jasności
Transformacja obrazu wykonywana wówczas, gdy zakres
jasności pikseli obrazu nie obejmuje całego dostępnego
zakresu. Efektem tej operacji jest zwiększenie kontrastowości
obrazu, ponieważ jego piksele o wartościach minimalnych i
maksymalnych przyjmą dostępne ekstremalne jasności,
natomiast pomiędzy pośrednimi odległości zwiększą się.
dla
Operację transformacji można wykonywać na pewnych
zakresach jasności, celem uwypuklenia ich.
max
min
min
min
max
w
J
)
y
,
x
(
J
J
)
J
)
y
,
x
(
J
(
J
J
)
y
,
x
(
J
255
Grafika komputerowa
– wykład 6
Operacje na histogramie
Obraz źródłowy
Obraz po rozszerzeniu zakresu jasności
Grafika komputerowa
– wykład 6
Operacje na histogramie
Obraz źródłowy
Obraz po rozszerzeniu zakresu jasności
Grafika komputerowa
– wykład 6
Operacje na histogramie
Rozciąganie
histogramu
Zwiększanie kontrastu
Wykorzystanie całego
zakresu jasności
Grafika komputerowa
– wykład 6
Operacje na histogramie
Obraz źródłowy
Obraz po rozszerzeniu zakresu koloru
Grafika komputerowa
– wykład 6
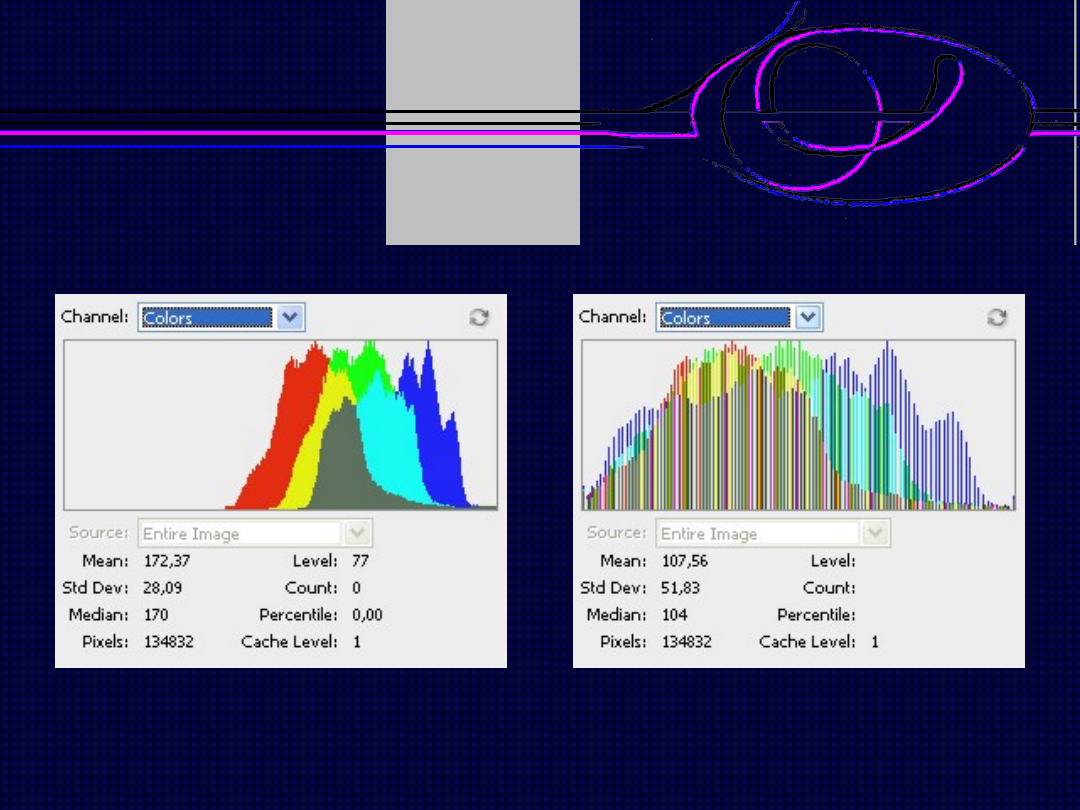
Operacje na histogramie
Obraz źródłowy
Obraz po rozszerzeniu zakresu koloru
Grafika komputerowa
– wykład 6
Operacje na histogramie
Obraz źródłowy
Obraz po rozszerzeniu zakresu koloru
Grafika komputerowa
– wykład 6
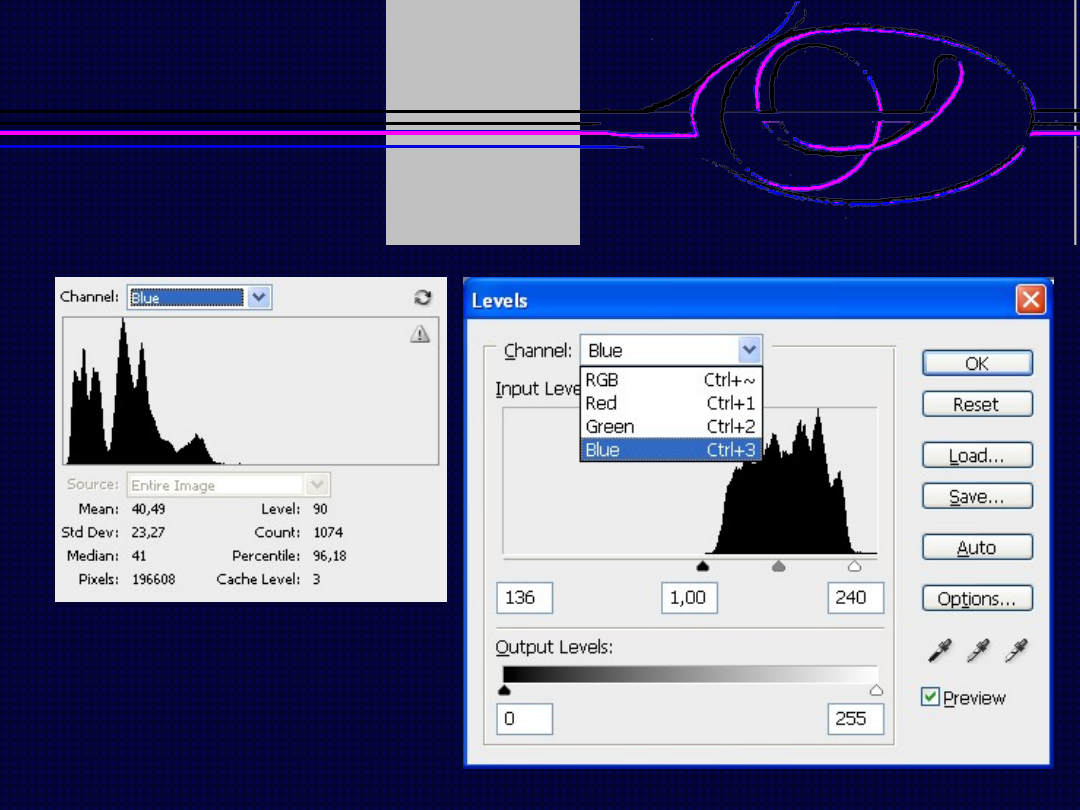
Operacje na histogramie
Rozszerzanie zakresu
jasności lub koloru
(kontrolowane przez
użytkownika)
Grafika komputerowa
– wykład 6
Metody przekształcania obrazów
Przekształcenia geometryczne
obrazu
Przekształcenia dotyczące geometrii obrazu:
• zmiana rozdzielczości przestrzennej
• przesunięcie (translacja),
• odbicie symetryczne,
• obrót,
• zniekształcenia,
• powielanie skrajnych wierszy lub kolumn.
Grafika komputerowa
– wykład 6
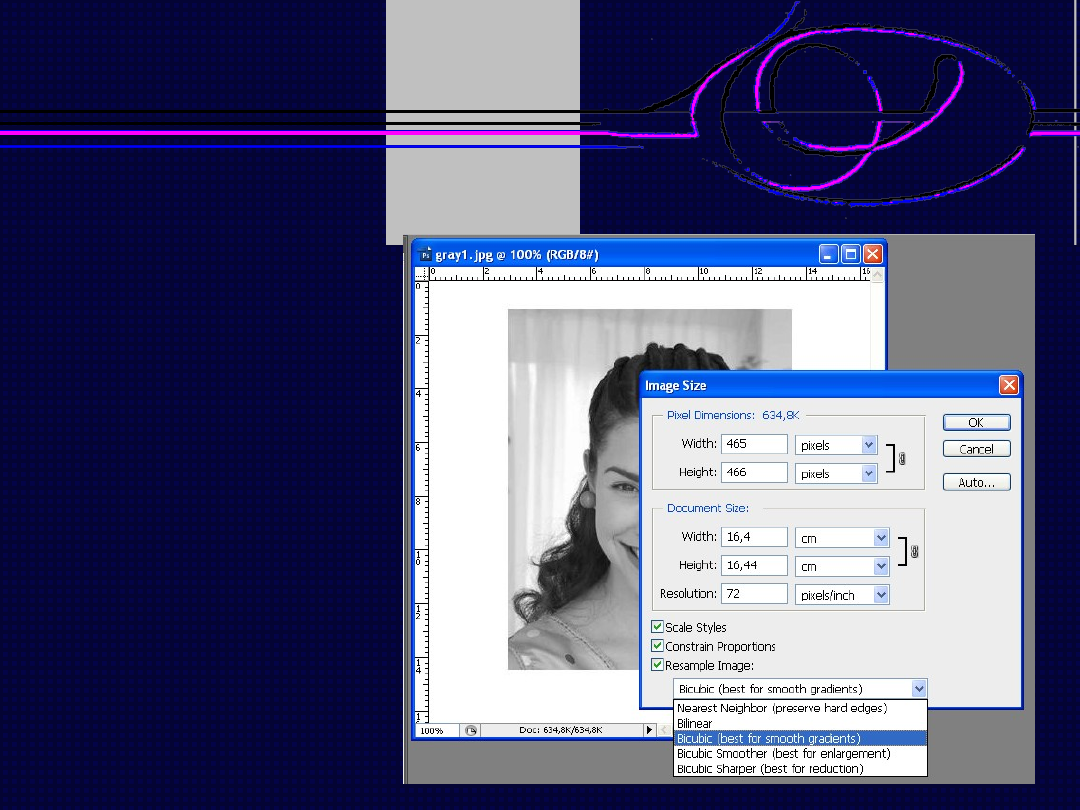
Zmiana rozdzielczości przestrzennej obrazu
Grafika komputerowa
– wykład 6
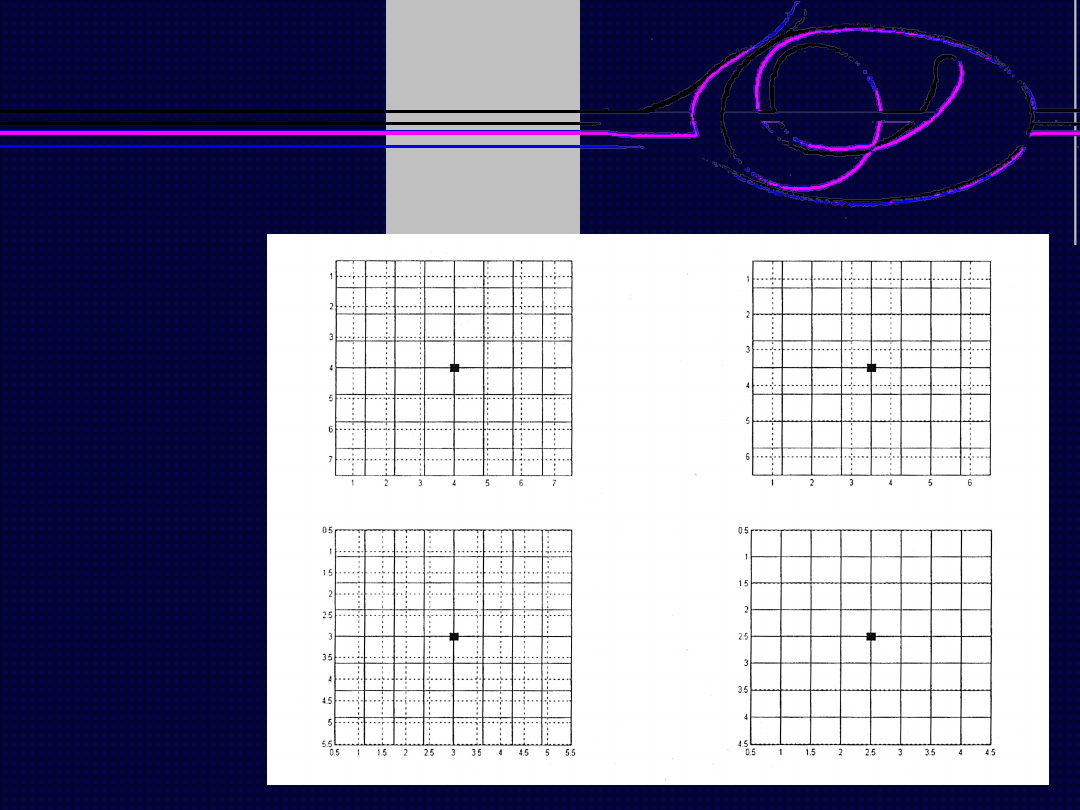
Zmiana rozdzielczości przestrzennej obrazu
Grafika komputerowa
– wykład 6
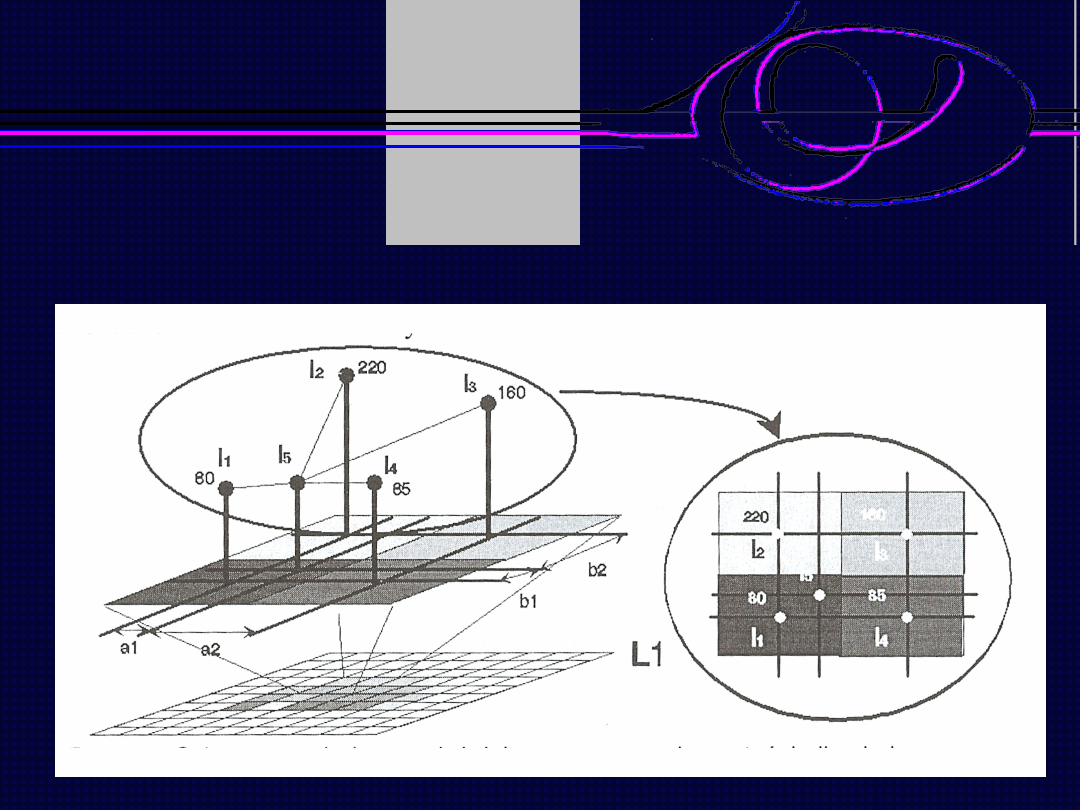
Metoda najbliższego sąsiada
Zmiana rozdzielczości przestrzennej obrazu
Grafika komputerowa
– wykład 6
Metoda najbliższego sąsiada
Wartość pikseli nowopowstałych w obrazie obliczana jest poprzez
wybór wartości jednego z czterech najbliżej położonych pikseli
obrazu źródłowego.
Analizowany piksel przyjmuje wartość piksela znajdującego się
najbliżej niego w sensie odległości euklidesowej.
Oznacza to powielanie (w przypadku zwiększenia rozdzielczości)
lub eliminację niektórych pikseli (w przypadku zmniejszania
rozdzielczości obrazu).
Brak nowych wartości wprowadzanych do obrazu.
Brak interpolacji nie powoduje zmniejszenia ostrości krawędzi.
Jeżeli dwa piksele obrazu źródłowego są równooddalone od
nowego piksela, wybór może przebiegać według dowolnej
metody, lecz powinna być ona stosowana konsekwentnie
względem wszystkich nowopowstałych pikseli.
Zmiana rozdzielczości przestrzennej obrazu
Grafika komputerowa
– wykład 6
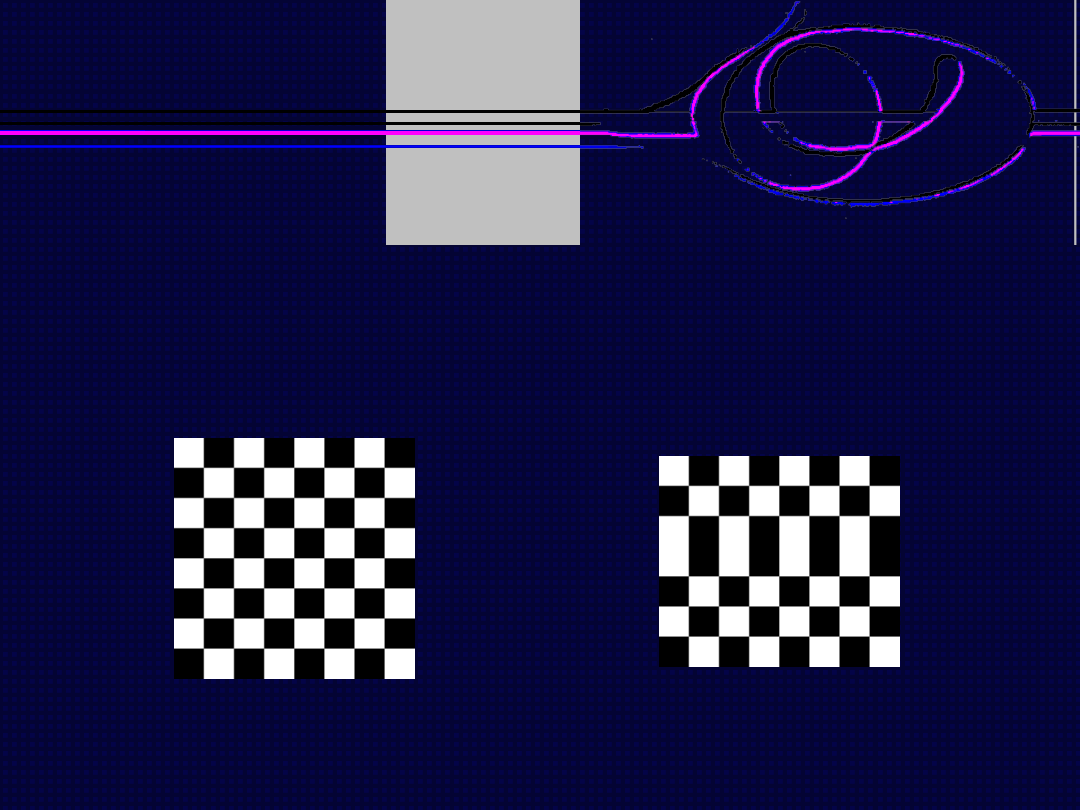
Metoda najbliższego sąsiada
Zmiana rozdzielczości przestrzennej obrazu
Metoda daje zadawalające wyniki w przypadku zwielokrotniania
rozdzielczości. W innych przypadkach rezultat jej zastosowania
nie jest optymalny.
Rozdzielczość przestrzenna
80x80 pikseli
Rozdzielczość przestrzenna
70x80 pikseli
Grafika komputerowa
– wykład 6
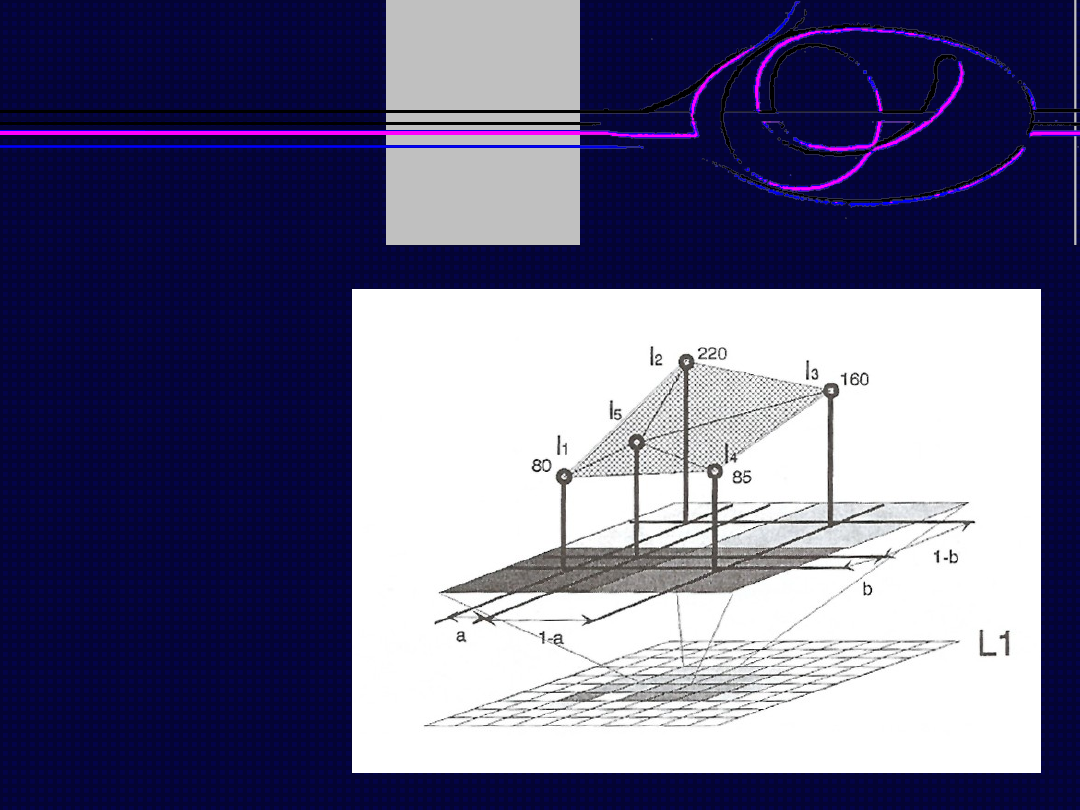
Metoda interpolacji dwuliniowej
Zmiana rozdzielczości przestrzennej obrazu
Grafika komputerowa
– wykład 6
Metoda interpolacji dwuliniowej
Zmiana rozdzielczości przestrzennej obrazu
W tej metodzie interpolacji liniowej poddawane są piksele
występujące najczęściej w układzie 4-sąsiedztwa.
Poszukiwana wartość nowopowstałego piksela obliczana jest ze
wzoru:
b
a
l
b)
a(1
l
b
a)
(1
l
b)
a)(1
(1
l
l
3
4
2
1
5
Im bliżej analizowanego punktu położony jest piksel z jego
sąsiedztwa, z tym większą wagą wpływa na wartość
obliczanego piksela.
W porównaniu z metodą najbliższego sąsiada, wszystkie piksele
z sąsiedztwa (a nie tylko jeden) mają wpływ na wartość
nowopowstałego piksela. W tej metodzie powstają nowe
wartości pikseli (nieobecne w obrazie źródłowym). Kontury
obiektu ulegają rozmyciu.
Grafika komputerowa
– wykład 6
Metoda interpolacji dwuliniowej
Zmiana rozdzielczości przestrzennej obrazu
Rozdzielczość przestrzenna
80x80 pikseli
Rozdzielczość przestrzenna
70x80 pikseli
Grafika komputerowa
– wykład 6
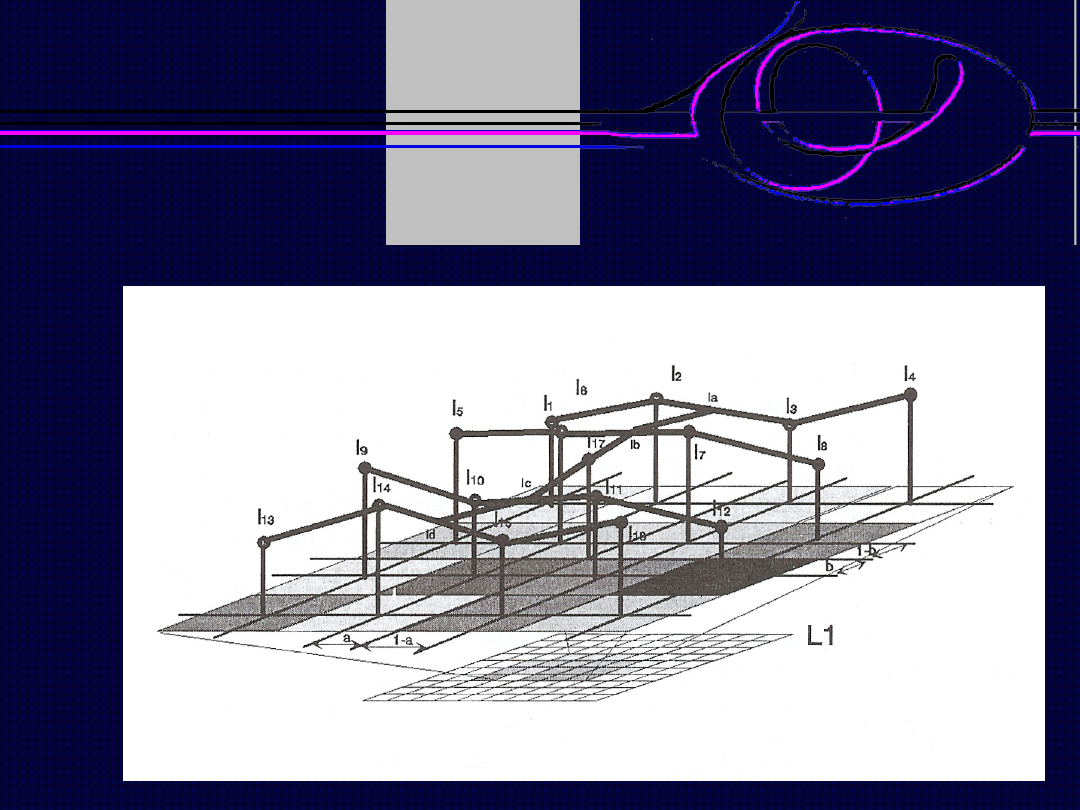
Metoda interpolacji dwukubicznej
Zmiana rozdzielczości przestrzennej obrazu
Grafika komputerowa
– wykład 6
Metoda interpolacji dwukubicznej
Zmiana rozdzielczości przestrzennej obrazu
W tej metodzie brane jest pod uwagę 16 sąsiadujących pikseli.
Wyznaczane są wartości pomocnicze l
a
, l
b
, l
c
, l
d
, obliczane ze
wzoru:
2
1
3
2
1
2
4
3
3
1
2
3
4
a
l
a
)
l
(l
a
)
l
2
l
2
l
(l
a
)
l
l
l
(l
l
Na ich podstawie wartość piksela l
17
obliczana jest z zależności:
b
a
c
2
a
b
d
c
3
a
b
c
d
17
l
b
)
l
(l
b
)
l
2
l
2
l
(l
b
)
l
l
l
(l
l
Grafika komputerowa
– wykład 6
Metoda interpolacji dwukubicznej
Zmiana rozdzielczości przestrzennej obrazu
Funkcja wyznaczająca nową wartość piksela ma charakter
sześcienny:
d
x
c
x
b
x
a
f(x)
2
3
Wadą tej metody jest znaczna złożoność obliczeniowa.
Podobnie, jak w przypadku interpolacji dwuliniowej, do obrazu
zostają wprowadzone nowe wartości, co powoduje rozmycie
krawędzi.
Grafika komputerowa
– wykład 6
Metoda interpolacji dwukubicznej
Zmiana rozdzielczości przestrzennej obrazu
Rozdzielczość przestrzenna
80x80 pikseli
Rozdzielczość przestrzenna
70x80 pikseli
Grafika komputerowa
– wykład 6
Obraz rzeczywisty - zastosowanie metody najbliższego
sąsiada
Zmiana rozdzielczości przestrzennej obrazu
Obraz źródłowy
Obraz wynikowy
Grafika komputerowa
– wykład 6
Obraz
rzeczywisty
-
zastosowanie
interpolacji
dwuliniowej
Zmiana rozdzielczości przestrzennej obrazu
Obraz źródłowy
Obraz wynikowy
Grafika komputerowa
– wykład 6
Obraz
rzeczywisty
-
zastosowanie
interpolacji
dwukubicznej
Zmiana rozdzielczości przestrzennej obrazu
Obraz źródłowy
Obraz wynikowy
Grafika komputerowa
– wykład 6
Obraz rzeczywisty - zastosowanie metody najbliższego
sąsiada
Zmiana rozdzielczości przestrzennej obrazu
Grafika komputerowa
– wykład 6
Przekształcenia geometryczne obrazu
Przesunięcie obrazu w poziomie i pionie opisuje wzór:
x
2
= x
1
+ x
0
y
2
= y
1
+
y
0
gdzie:
x
0
, y
0
– wartość wektora przesunięcia pikseli obrazu,
odpowiednio w poziomie i w pionie,
x
1
, y
1
oraz x
2
, y
2
– odpowiednio kolumna i wiersz
macierzy
obrazu źródłowego i
wynikowego.
Grafika komputerowa
– wykład 6
Przekształcenia geometryczne
obrazu
Obraz źródłowy
Obraz po przesunięciu o
wektor
(z zachowaniem pola powierzchni
obrazu)
Grafika komputerowa
– wykład 6
Przekształcenia geometryczne
obrazu
Wartość piksela w obrazie powstałym po wykonaniu obrotu
obrazu źródłowego o zadany kąt α względem początku układu
współrzędnych można opisać wzorem:
x
2
= x
1
∙cosα – y
1
∙sinα
y
2
= x
1
∙cosα + y
1
∙sinα
Operacje przesuwania i obrotu są używane często w
przypadku łączenia obrazów (np. zeskanowanych fragmentów,
tworzenia kolaży itp.)
Grafika komputerowa
– wykład 6
Obraz źródłowy
Obraz po wykonaniu obrotu o
zadany kąt
(z zachowaniem pola powierzchni
obrazu)
Przekształcenia geometryczne
obrazu
Grafika komputerowa
– wykład 6
Obraz źródłowy
Obraz po
wykonaniu odbicia
względem osi pionowej
Przekształcenia geometryczne
obrazu
Grafika komputerowa
– wykład 6
Obraz źródłowy
Obraz po
wykonaniu odbicia
względem osi poziomej
Przekształcenia geometryczne
obrazu
Grafika komputerowa
– wykład 6
Obraz źródłowy
Obraz po dodaniu
wierszy i kolumn
Przekształcenia geometryczne
obrazu
Grafika komputerowa
– wykład 6
Obraz źródłowy
Obraz po powieleniu skrajnych
wierszy i kolumn
Przekształcenia geometryczne
obrazu
Grafika komputerowa
– wykład 6
Obraz źródłowy Obraz po lustrzanym odbiciu
fragmentów
Przekształcenia geometryczne
obrazu
Grafika komputerowa
– wykład 6
Obraz źródłowy
Obraz po
zniekształceniu
Przekształcenia geometryczne
obrazu
Grafika komputerowa
– wykład 6
Obraz źródłowy Prostowanie perspektywy za pomocą
zniekształcenia
Przekształcenia geometryczne
obrazu
Grafika komputerowa
– wykład 6
Operacje bezkontekstowe – najprostsze metody przekształcania
obrazów, które dokonywane są na pojedynczym pikselu, bez
uwzględniania pikseli sąsiadujących.
Operacje kontekstowe – uwzględniają wartości pikseli
sąsiadujących.
Wyjaśnienia mają charakter poglądowy i przedstawiane będą
jedynie w odniesieniu do parametru jasności, jednak
większość operacji można wykonywać na poszczególnych
składowych parametru barwy (np.: kanałach RGB)
Metody przekształcania obrazów
Grafika komputerowa
– wykład 6
Operacje arytmetyczne wykonywane są na każdym pikselu
obrazu źródłowego, którego barwa (lub stopień jasności) jest
przeliczana w oparciu o daną funkcję. Jako wynik
otrzymywana jest barwa odpowiedniego piksela w obrazie
wynikowym.
Przy konieczności przeprowadzania obliczeń na każdym
kolejnym pikselu, przekształcenie byłoby bardzo czasochłonne.
Powszechnie do tego celu stosuje się tablice przekodowań (LUT
– Look Up Table).
Każdej wartości jasności obrazu źródłowego przypisywana jest
wartość, jaką uzyska w obrazie wynikowym po wykonaniu
danego przekształcenia.
Operacje arytmetyczne
Grafika komputerowa
– wykład 6
Nowa wartość obliczana jest według wzoru:
J
w
(x,y) = Ψ(J
0
(x,y)
gdzie:
Ψ – funkcja, zgodnie z którą nowe wartości obrazu
wynikowego
są przyporządkowane wartościom
obrazu
wyjściowego.
Grafika komputerowa
– wykład 6
Operacje arytmetyczne
Przykład tabeli LUT dla obrazu w skali
szarości
Wartości poziomów jasności wszystkich punktów
Obrazu źródłowego
Obrazu wynikowego
00000000
J
0
00000001
J
1
…………
………
11111111
J
255
Grafika komputerowa
– wykład 6
Operacje arytmetyczne
Operacje arytmetyczne - liniowe
Dodanie lub odjęcie od obrazu stałej wartości powoduje jego
rozjaśnienie lub przyciemnienie (zwiększenie lub
zmniejszenie jasności).
J
w
(x,y) = J
0
(x,y) ± b,
gdzie:
J
w
(x,y) – jasność wynikowa,
J
0
(x,y) – jasność początkowa,
b - stała
Istnieje niebezpieczeństwo przekroczenia maksymalnej lub
minimalnej wartości jasności (w tym przypadku odpowiednio
255 oraz 0).
Grafika komputerowa
– wykład 6
Obraz źródłowy
Obraz po dodaniu stałej wartości
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
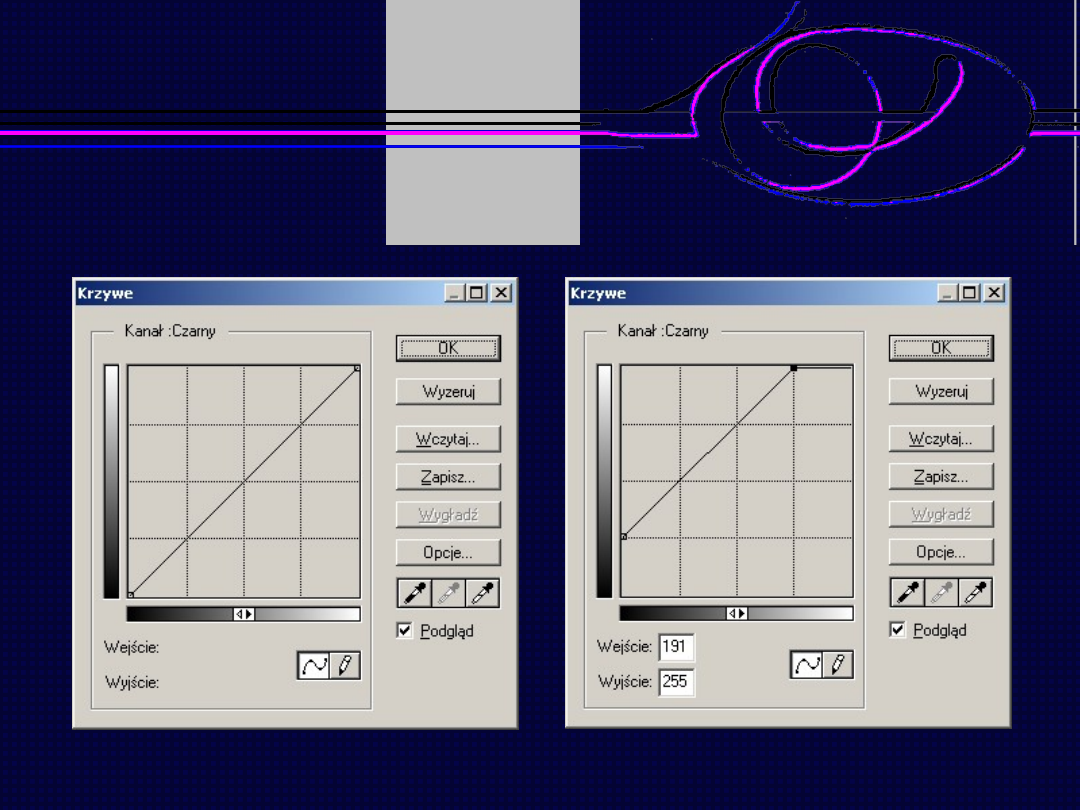
Obraz źródłowy
Obraz po dodaniu stałej wartości
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
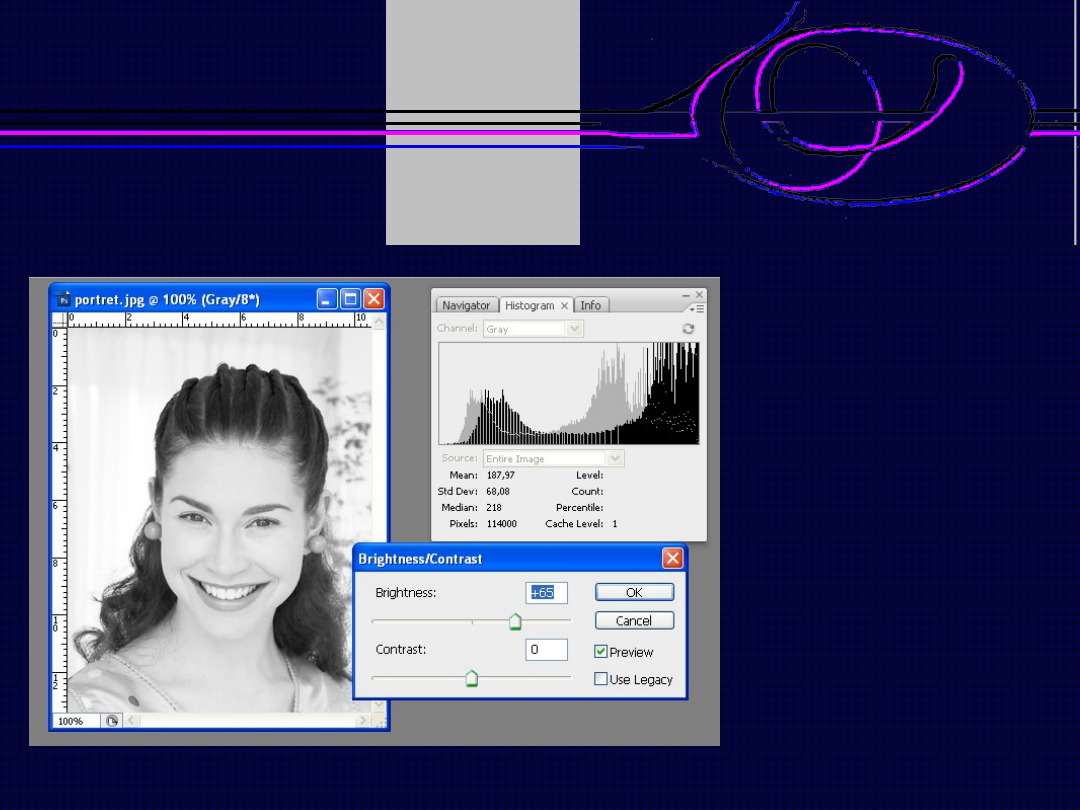
Dodawanie
wartości
Rozjaśnianie
Przesuwanie
wykresu w prawo
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
Obraz źródłowy
Obraz po odjęciu stałej wartości
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
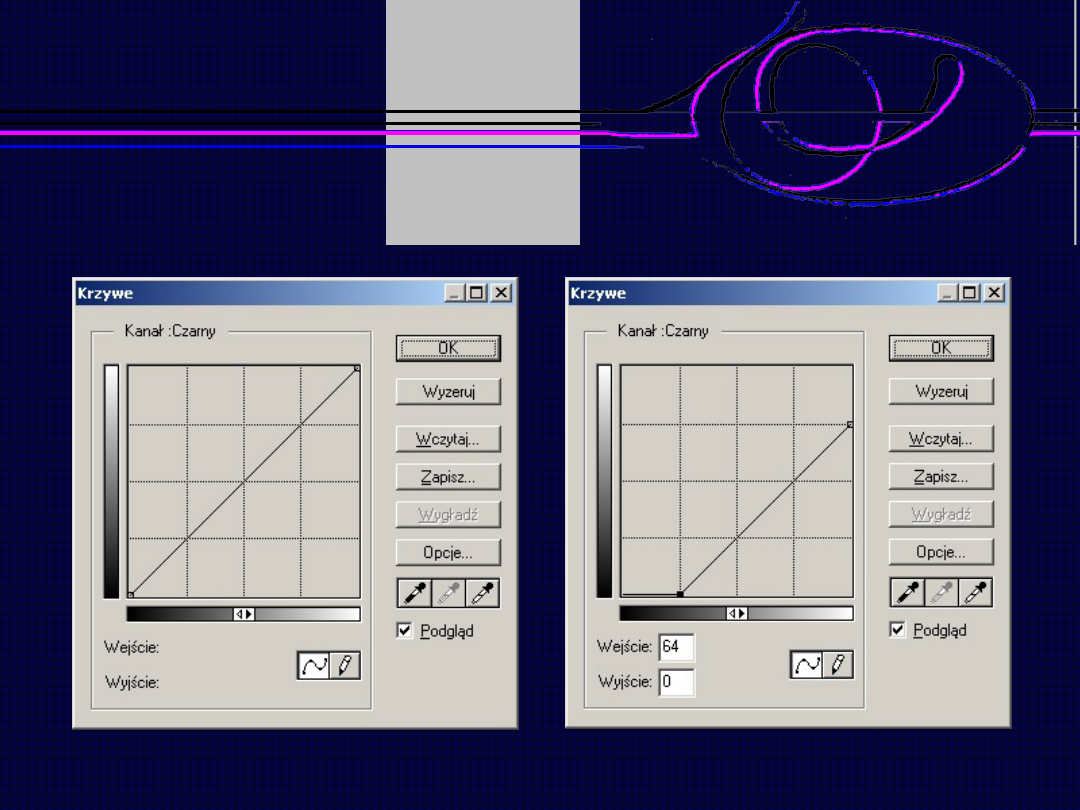
Obraz źródłowy
Obraz po odjęciu stałej wartości
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
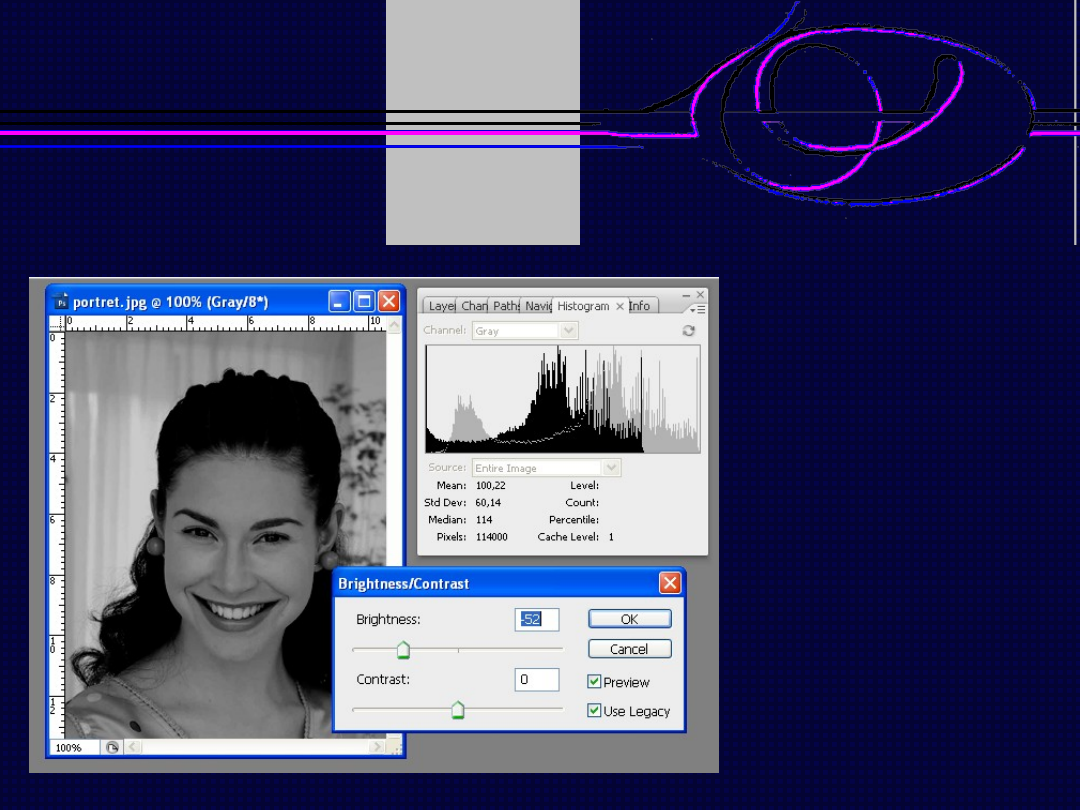
Odejmowanie
wartości
Przyciemnianie
Przesuwanie wykresu
w lewo
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
Odjęcie wartości jasności obrazu od maksymalnej wartości
jasności
(w tym przypadku 255) daje w wyniku obraz negatywowy.
J
w
(x,y) = 255 -
J(x,y)
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
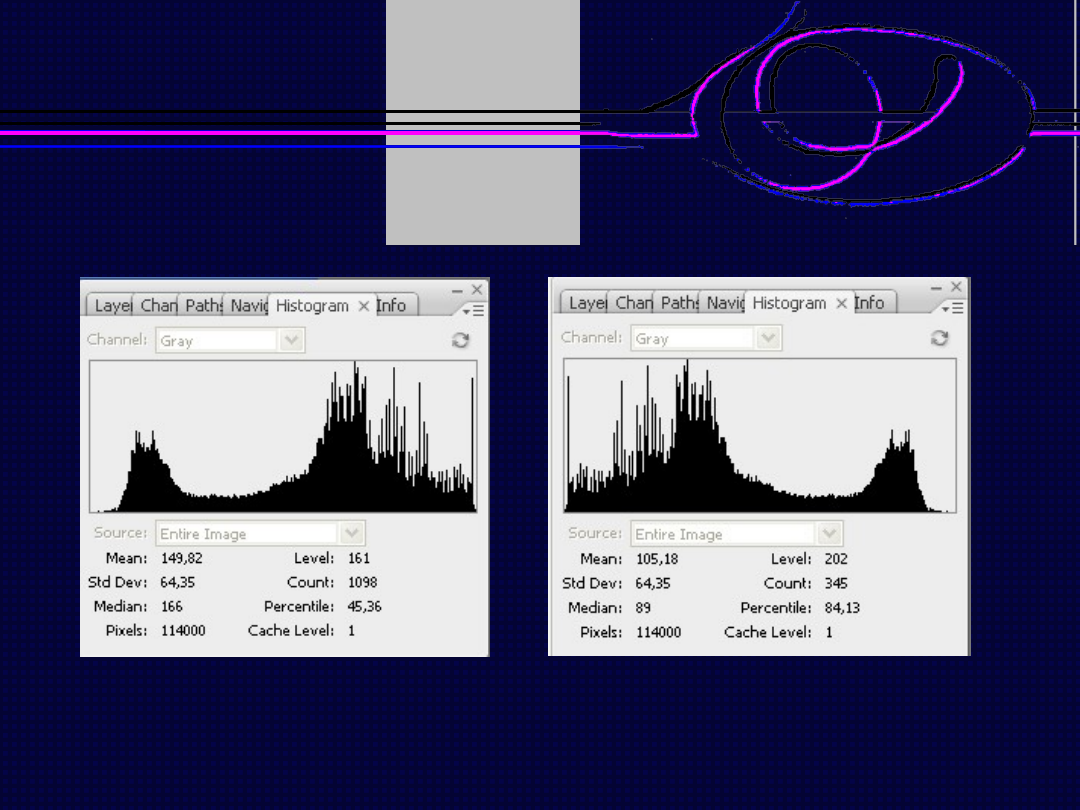
Histogram obrazu
Histogram negatywu
J
w
(x,y) = 255 -
J(x,y)
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
Mnożenie obrazu jest zwykle stosowane w celu poprawy jego
jakości.
J
w
(x,y) = a · J
0
(x,y)
W wyniku wykonania mnożenia uzyskujemy:
• zwiększenie kontrastu (większe zróżnicowanie szarości),
jeżeli a>1,
• zmniejszenie kontrastu, jeżeli 0<a<1.
Przy przekroczeniu maksymalnej lub minimalnej wartości
jasności (w tym przypadku odpowiednio 255 oraz 0) może
nastąpić utrata części danych.
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
Obraz
źródłowy
Obraz po mnożeniu przez stałą wartość
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
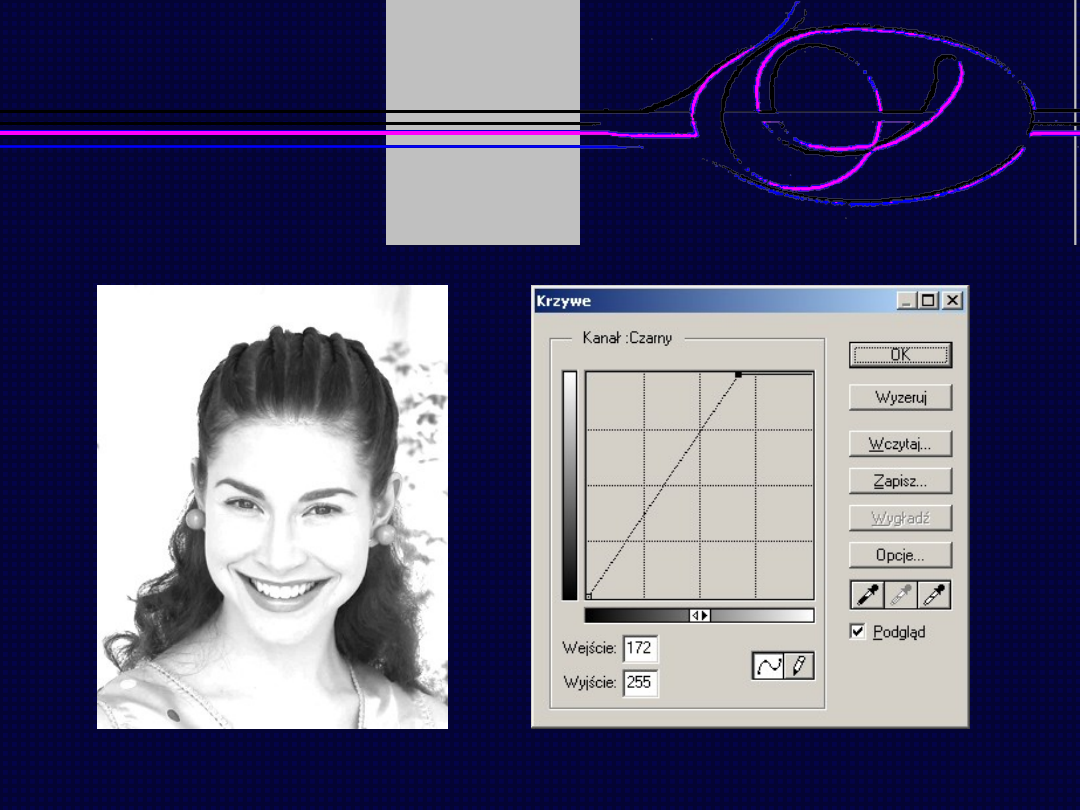
Obraz po mnożeniu przez stałą wartość
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
Obraz po dzieleniu przez stałą wartość
Obraz
źródłowy
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
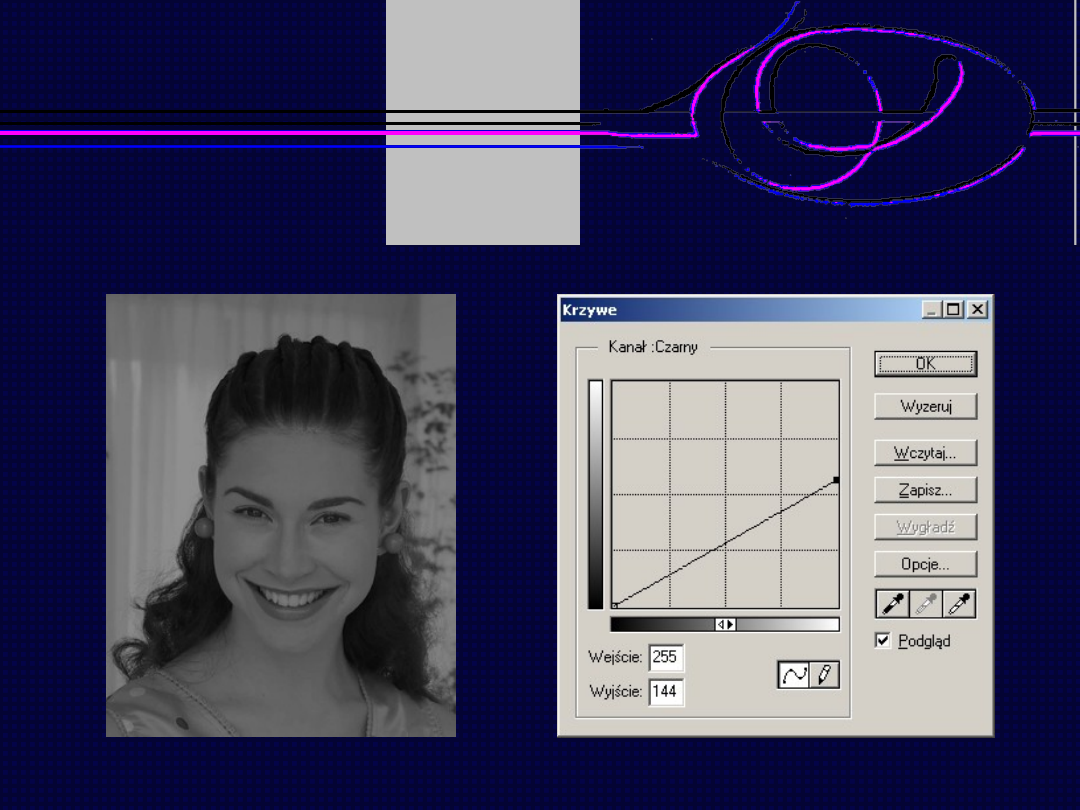
Obraz po dzieleniu przez stałą wartość
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
Omówione powyżej operacje określane są jako operacje
liniowe, gdyż mogą zostać opisane wzorem:
J
w.
(x,y) = a · J
0
(x,y) + b
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
Efekt solaryzacji
Zmiana poziomów jasności pikseli
Grafika komputerowa
– wykład 6
Operacje arytmetyczne - liniowe
Omawianym przekształceniom obrazów towarzyszy problem
możliwego przekroczenia maksymalnej bądź minimalnej wartości
parametru jasności (lub barwy).
W przypadku otrzymania w wyniku przekształcenia piksela o
wartości wykraczającej poza dopuszczalny zakres, możliwe są trzy
podejścia:
• Stosowanie zasad arytmetyki przepełnieniowej – obcinanie
wartości na poziomie dopuszczalnego maksimum czy minimum.
Towarzyszy temu efekt negatywny – utrata części informacji o
obrazie (metoda nasycenia).
• Traktowanie punktów o wartości większej niż 255 jako wynik
modulo p (p=256). W efekcie przekroczenie maksymalnej jasności
podczas sumowania obrazów może dać jako wynik piksel ciemny,
a w wyniku odejmowania piksela jaśniejszego od ciemniejszego
możemy otrzymać piksel jasny (metoda modulo).
Grafika komputerowa
– wykład 6
Operacje arytmetyczne
• Trzecie rozwiązanie polega na normalizacji jasności.
Może się ona odbywać poprzez:
• podzielenie obrazu wynikowego przez największą wartość
piksela w którymś z obrazów składowych,
• podzielenie przez średnią wartość piksela w obrazach
składowych.
W wyniku normalizacji otrzymujemy obraz o średniej jasności
zbliżonej do obrazów składowych, a dodatkowo zmniejsza
się szum w obrazie.
Grafika komputerowa
– wykład 6
Operacje arytmetyczne
Metoda
nasycenia
Obraz źródłowy
Obraz po pomnożeniu
przez stałą
Grafika komputerowa
– wykład 6
Operacje arytmetyczne
Metoda modulo
Obraz źródłowy
Obraz po pomnożeniu
przez stałą
Grafika komputerowa
– wykład 6
Operacje arytmetyczne
Normalizacja
jasności
Obraz źródłowy
Obraz po pomnożeniu
przez stałą
Grafika komputerowa
– wykład 6
Operacje arytmetyczne
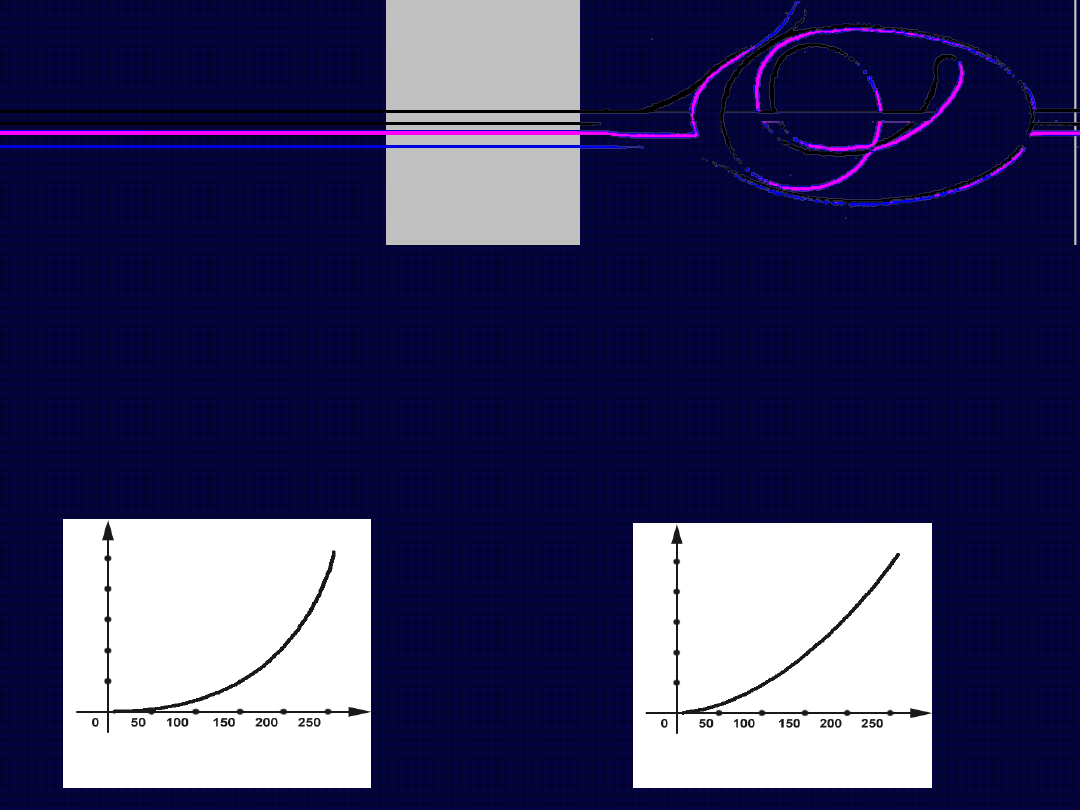
Operacje nieliniowe
Potęgowanie obrazu wykonywane jest dla każdego piksela
zgodnie ze wzorem:
J
w
(x,y) = J
0
(x,y)
α
gdzie α>0
Jeżeli założymy, że minimalna jasność wynosi 0, to wzór będzie
wyglądać następująco:
J
w
(x,y) = 255 ·
gdzie J
max
≤ 255
Operacje arytmetyczne
J
max
0
)
,
(
J
y
x
J
Grafika komputerowa
– wykład 6
Operacje arytmetyczne nieliniowe
Dla α > 1 i całkowitego potęgowanie obrazu sprowadza się do
mnożenia go przez siebie samego. Najczęściej używane jest
podnoszenie obrazu do „kwadratu”, rzadziej do „sześcianu”.
Operacja ta jest wykonywana w celu większego zróżnicowania
wysokich wartości atrybutu jasności. Po zastosowaniu koniecznej
normalizacji, powoduje przyciemnienie obrazu oraz zmniejszenie
zróżnicowania niskich wartości parametru jasności.
α = 2
α = 3
Grafika komputerowa
– wykład 6
Obraz źródłowy
Obraz po transformacji Obraz po
transformacji
kwadratowej
sześciennej
Grafika komputerowa
– wykład 6
Operacje arytmetyczne nieliniowe
Potęgowanie
obrazu
Grafika komputerowa
– wykład 6
Operacje arytmetyczne nieliniowe
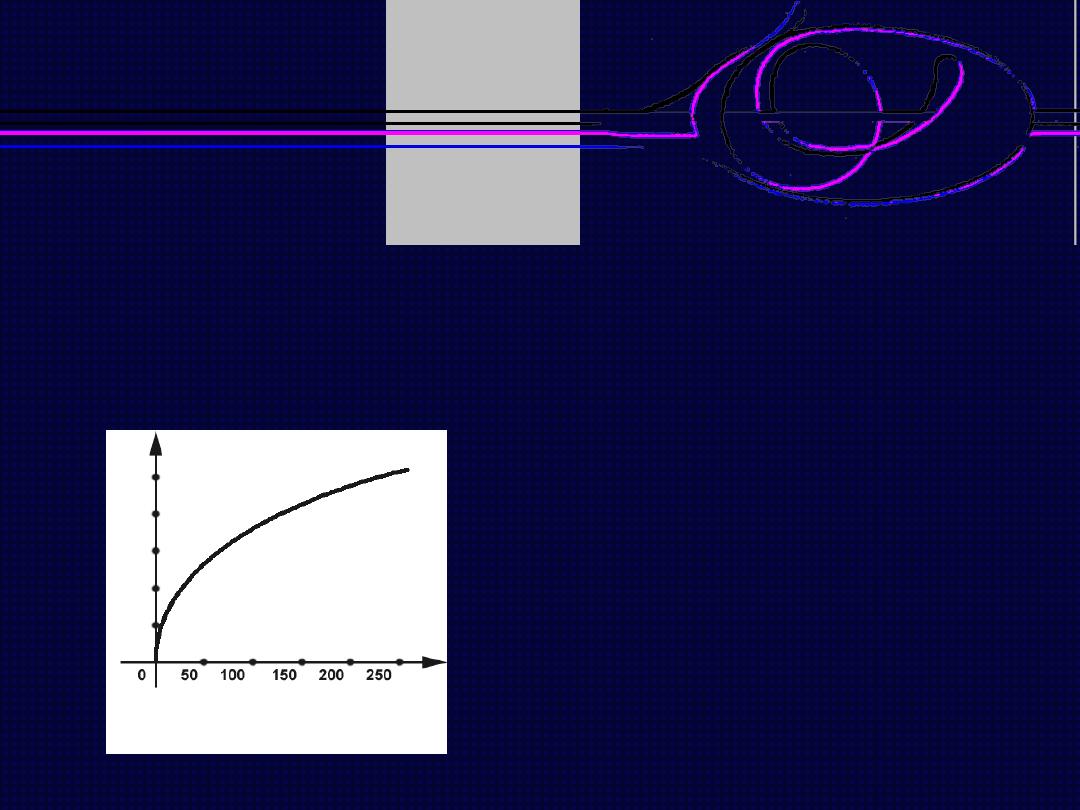
Jeżeli α < 1, mamy do czynienia z pierwiastkowaniem obrazu.
W wyniku tej operacji następuje zwiększenie kontrastu w
ciemnych partiach obrazu (o niskich wartościach jasności).
Wykres funkcji pierwiastka
kwadratowego
Potęgowanie obrazu znajduje
zastosowanie w korekcji lamp
analizujących obraz.
Korekcja gamma ma na celu
poprawę percepcji zmian
jasności wraz ze zmianą
luminancji.
Grafika komputerowa
– wykład 6
Operacje arytmetyczne nieliniowe
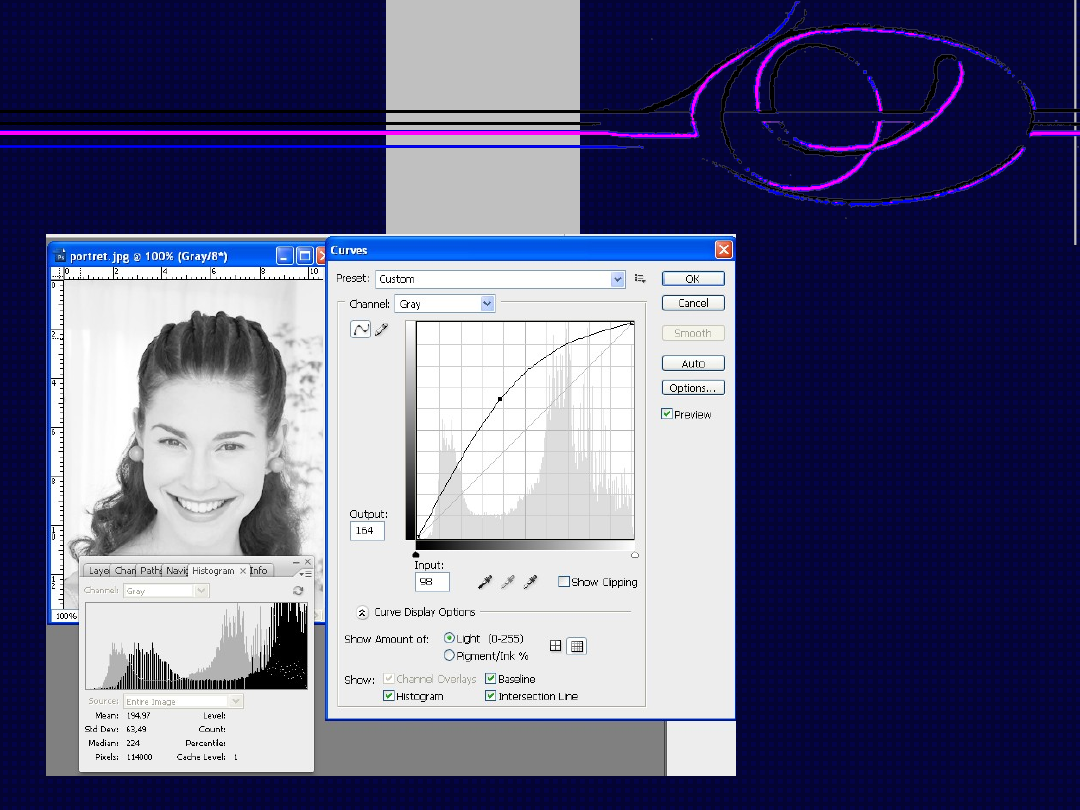
Pierwiastkowani
e obrazu
Grafika komputerowa
– wykład 6
Operacje arytmetyczne nieliniowe
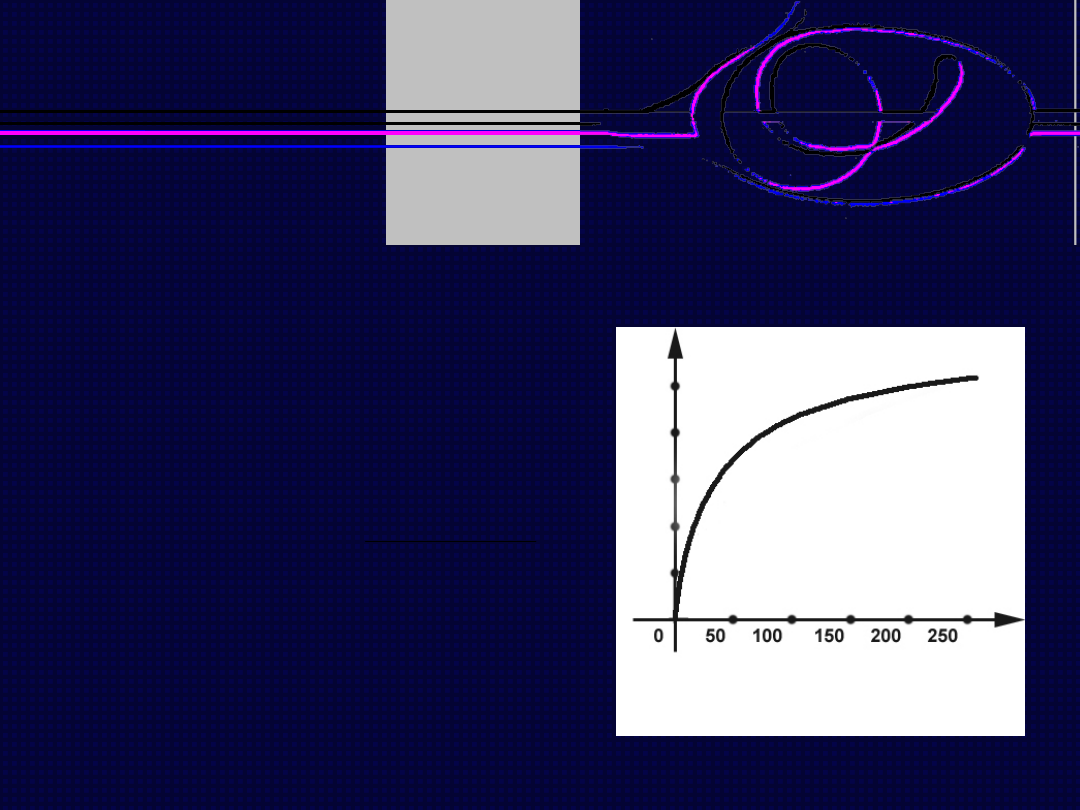
Logarytmowanie obrazu
J
w.
(x,y) = log (1 + J
0
(x,y))
Przy założeniach podobnych, jak
dla potęgowania, otrzymujemy
wzór:
J
w
(x,y) = 255 ·
Ze względu na nieokreśloność
funkcji w zerze, wykres musi być
przesunięty o jeden.
W wyniku operacji następuje silne
rozjaśnienie ciemnych partii
obrazu.
)
J
(1
log
y))
(x,
J
(1
log
max
0
Grafika komputerowa
– wykład 6
Operacje arytmetyczne nieliniowe
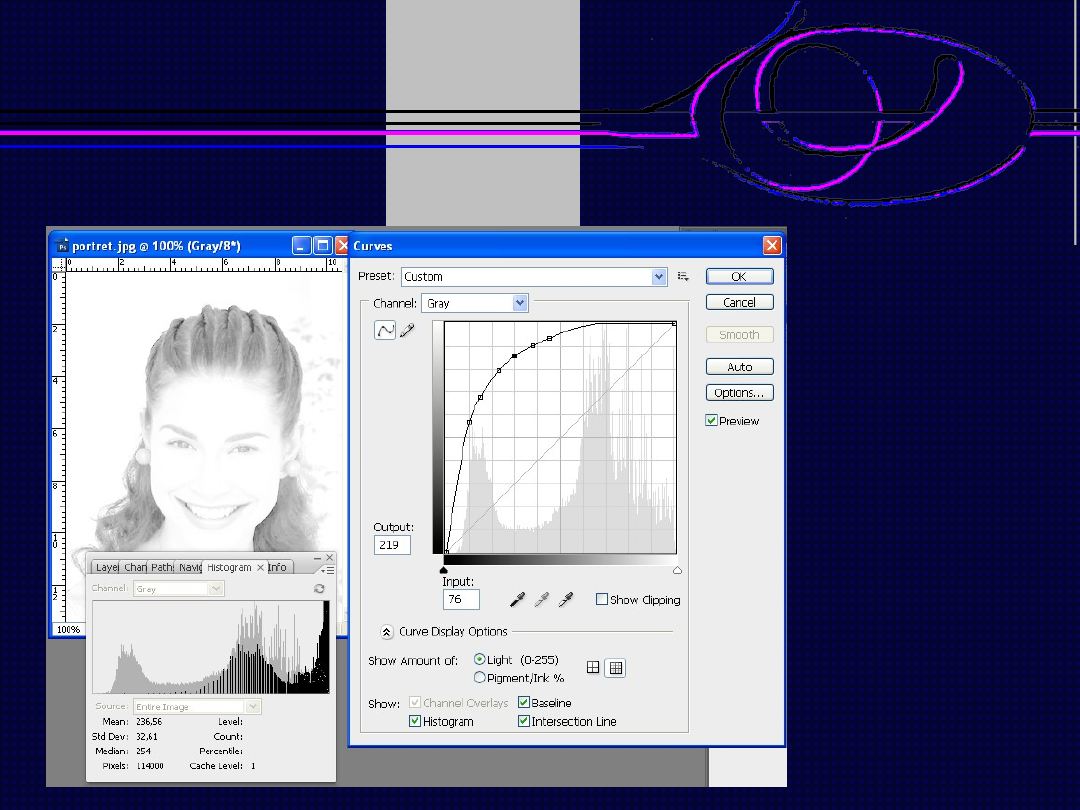
Logarytmowa
nie obrazu
Grafika komputerowa
– wykład 6
Operacje arytmetyczne nieliniowe
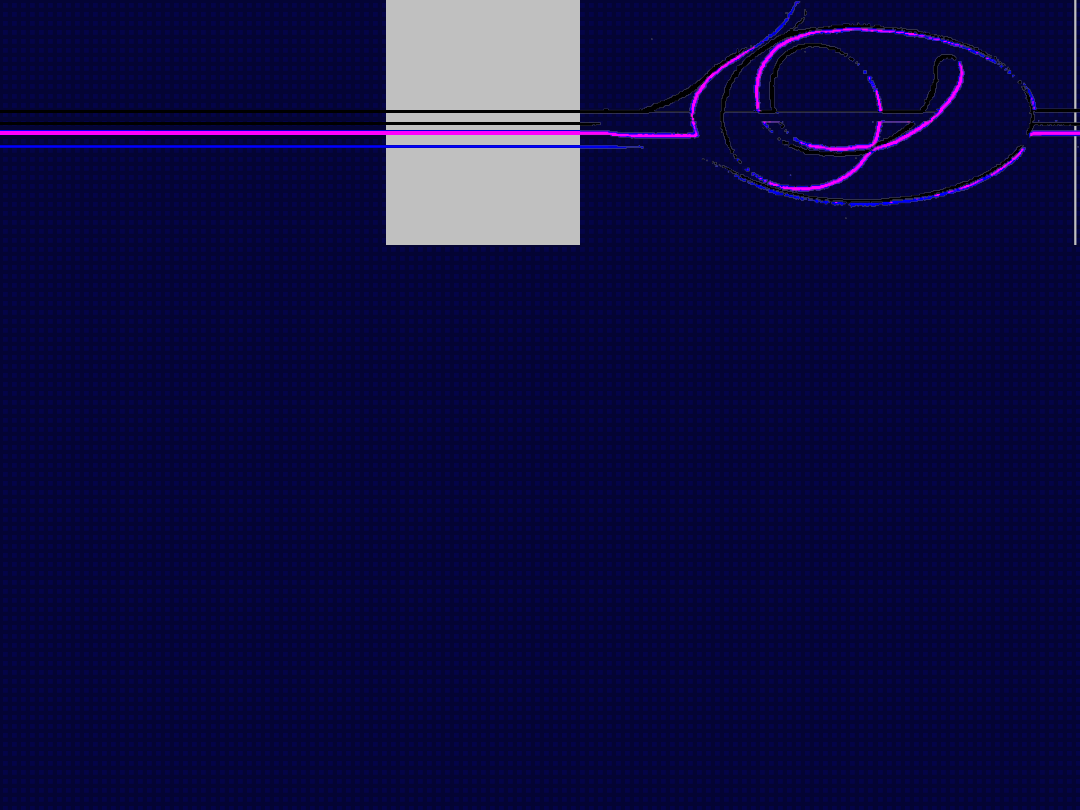
Korekcja gamma jest to bezkontekstowa (punktowa) transformacja
wykonywana na obrazie monochromatycznym lub poszczególnych
kanałach barw w obrazie kolorowego.
Podstawowym celem jej stosowania jest korekcja nieliniowej
charakterystyki kineskopu.
L2 = k ( X ' )γ ,
gdzie:
L2 oznacza luminancję kineskopu zależną od napięcia
sterującego X '.
k – wartość parametru zależna od aktualnych ustawień
monitora
γ = 2.3 - 2.6 stała dla danego kineskopu (zależna od jego
fizycznych właściwości)
Grafika komputerowa
– wykład 6
Operacje arytmetyczne nieliniowe
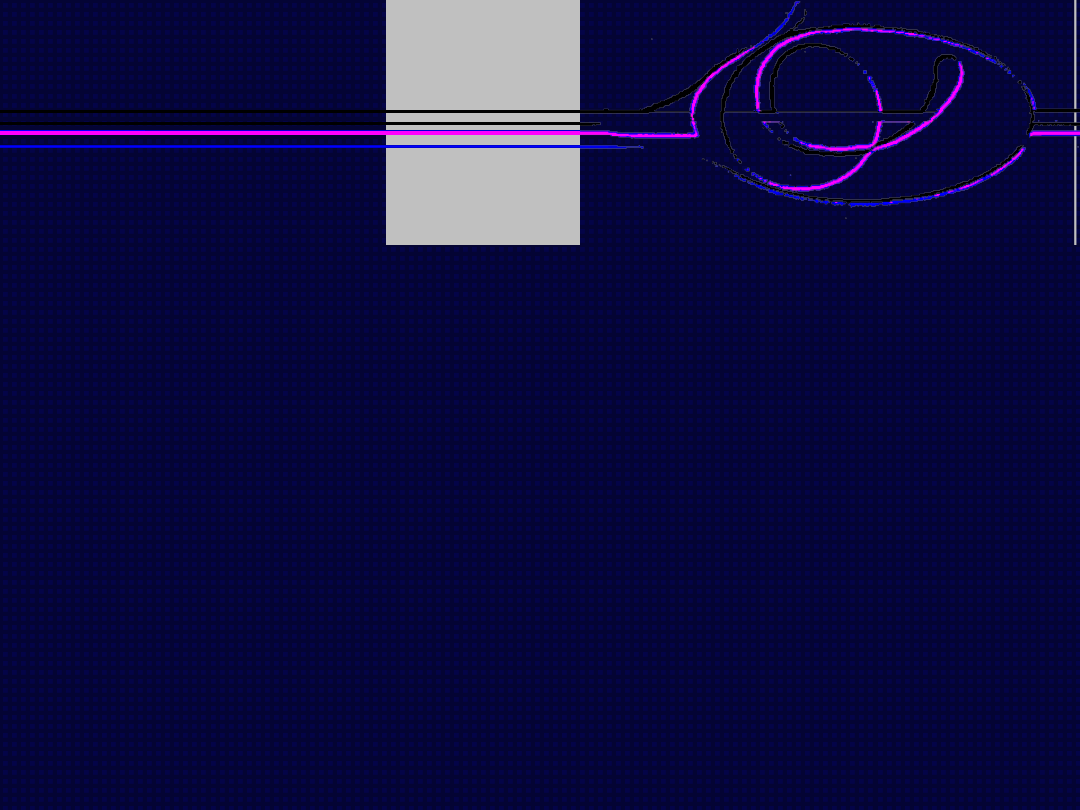
Korekcja gamma dana jest funkcją:
X ' = X 1/γ
Często wartość γ zastosowana do korekcji materiału źródłowego
nie jest znana. Jeżeli wypadkowa charakterystyka całego systemu
pozostaje wykładnicza (γ > 1), obraz wydaje się ostrzejszy.
Niestety zakres poziomów jasności w wyświetlanym obrazie jest
ograniczony.
Jeśli wynikowa charakterystyka jest logarytmiczna (γ < 1) obraz
wydaje się „miękki".
W systemach telewizyjnych stosuje się
γ = 2,8 dla systemu PAL (Europa),
γ = 2,2 dla systemu NTSC (USA).
Dzięki zastosowaniu korekcji gamma poprawiona zostaje
charakterystyka percepcji jasności obrazu, gdyż zmysł wzroku nie
odbiera zmian luminancji w sposób liniowy.
Grafika komputerowa
– wykład 6
Korekcja gamma
Grafika komputerowa
– wykład 6
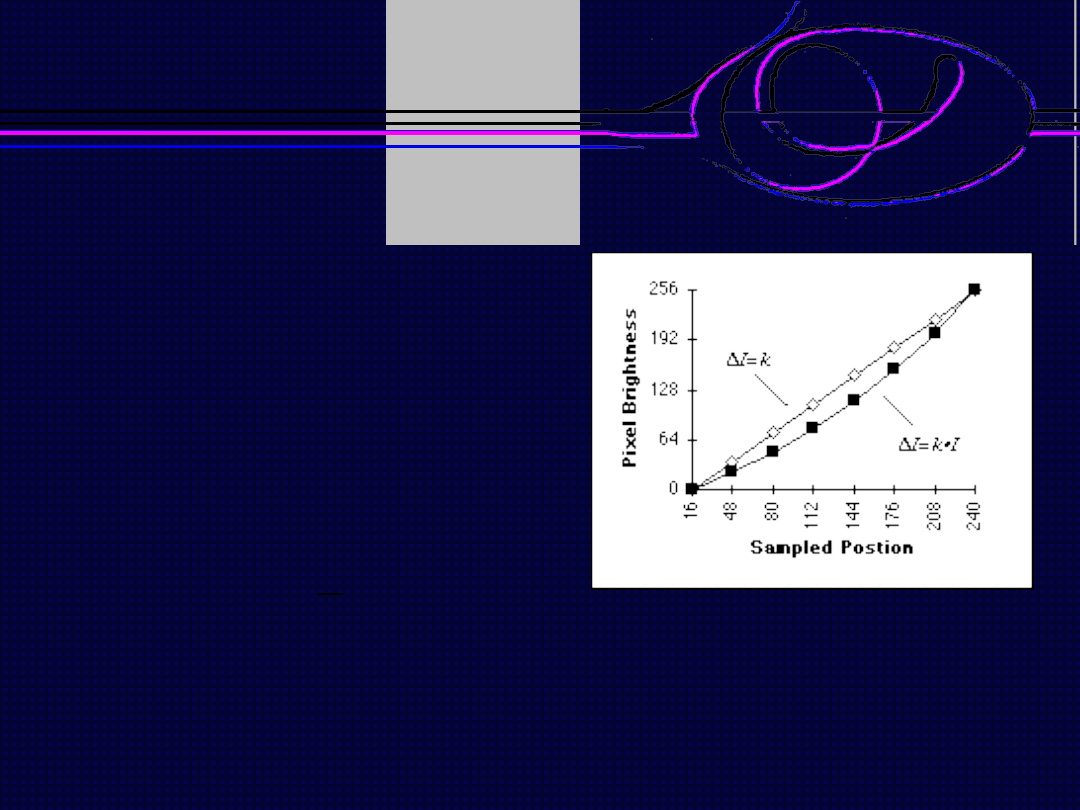
Czułość oka na poziom jasności
Prawo Webera-Fechnera
Wartość reakcji układu
biologicznego jest
proporcjonalna do
logarytmu bodźca.
gdzie:
R - reakcja układu biologicznego (wrażenie zmysłowe),
I - natężenie danego bodźca,
I
0
- wartość progowa natężenia danego bodźca,
log - logarytm o podstawie 10.
0
I
I
log
k
R
Grafika komputerowa
– wykład 6
Czułość oka na poziom jasności
Linearny wzrost obiektywnej
jasności
Logarytmiczny wzrost jasności
odczuwalnej
Wykładniczy wzrost obiektywnej
jasności
Linearny wzrost jasności
odczuwalnej
Grafika komputerowa
– wykład 6