AREA, ARC LENGTH

VOLUME





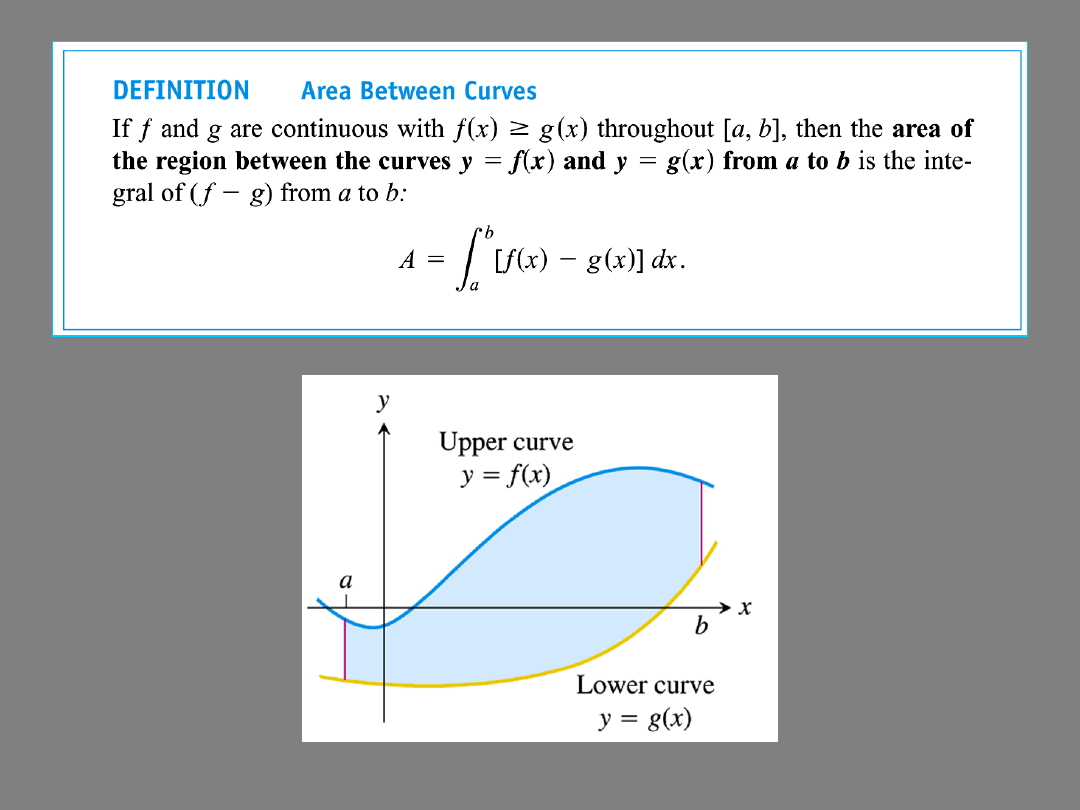
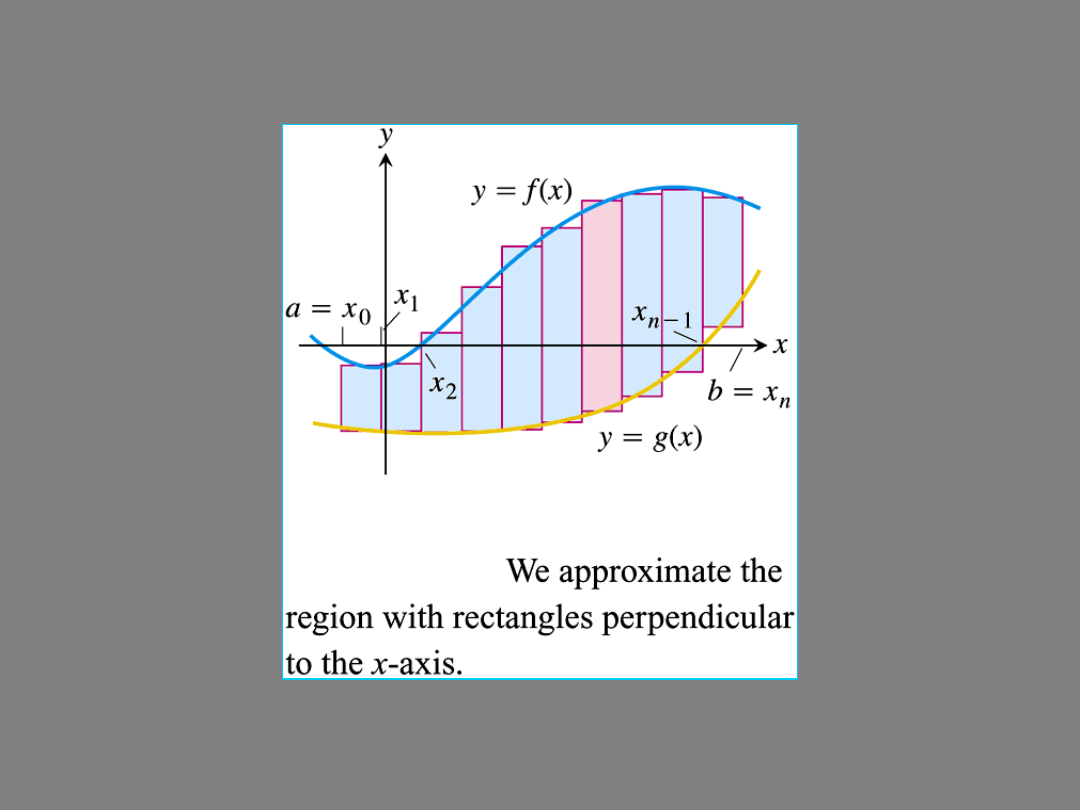
b

a

dx

x

f

A

)

(

AREA between f (x) and the OX-axis

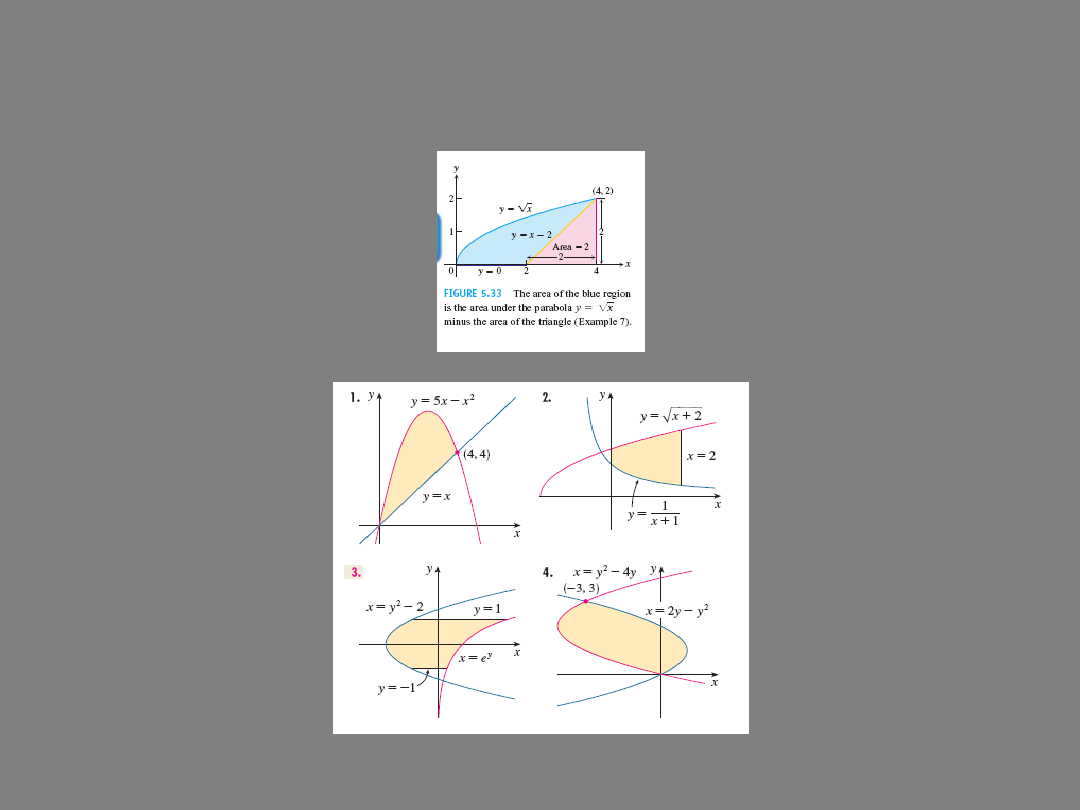
Find the following areas

(*)

Figure (*)

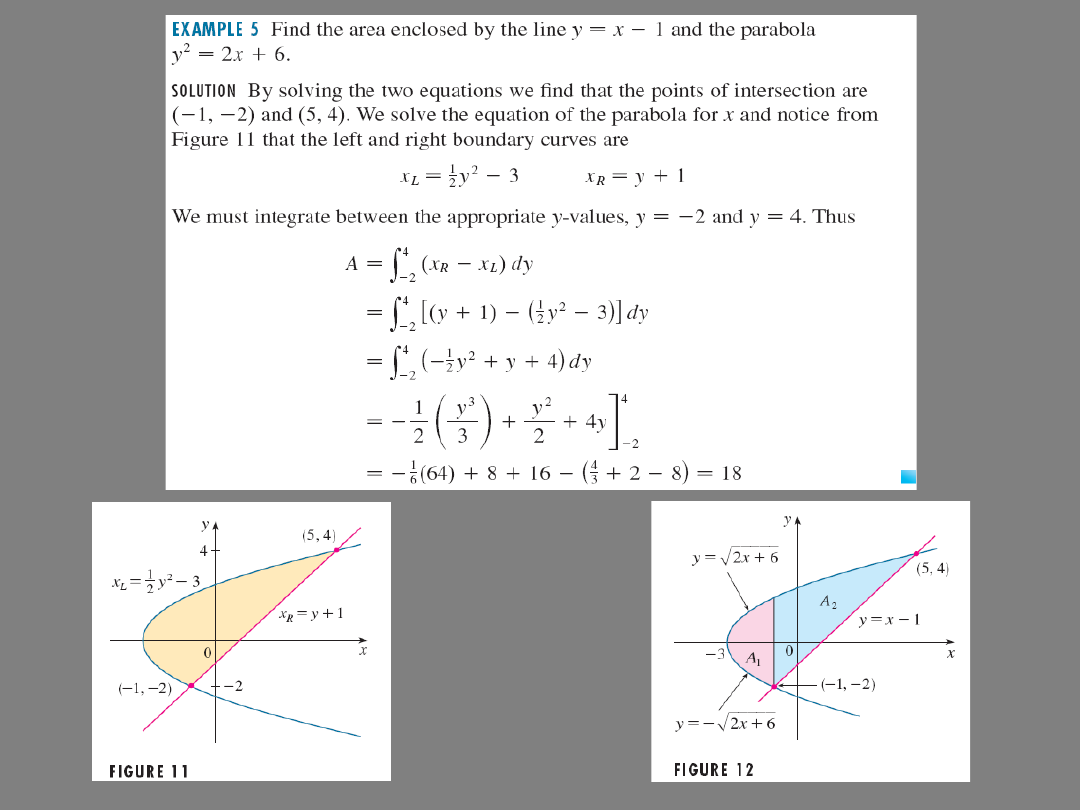
ARC LENGTH

The circumferance of a circle approximated by the perimeters
of inscribed polygons (Archimedes).

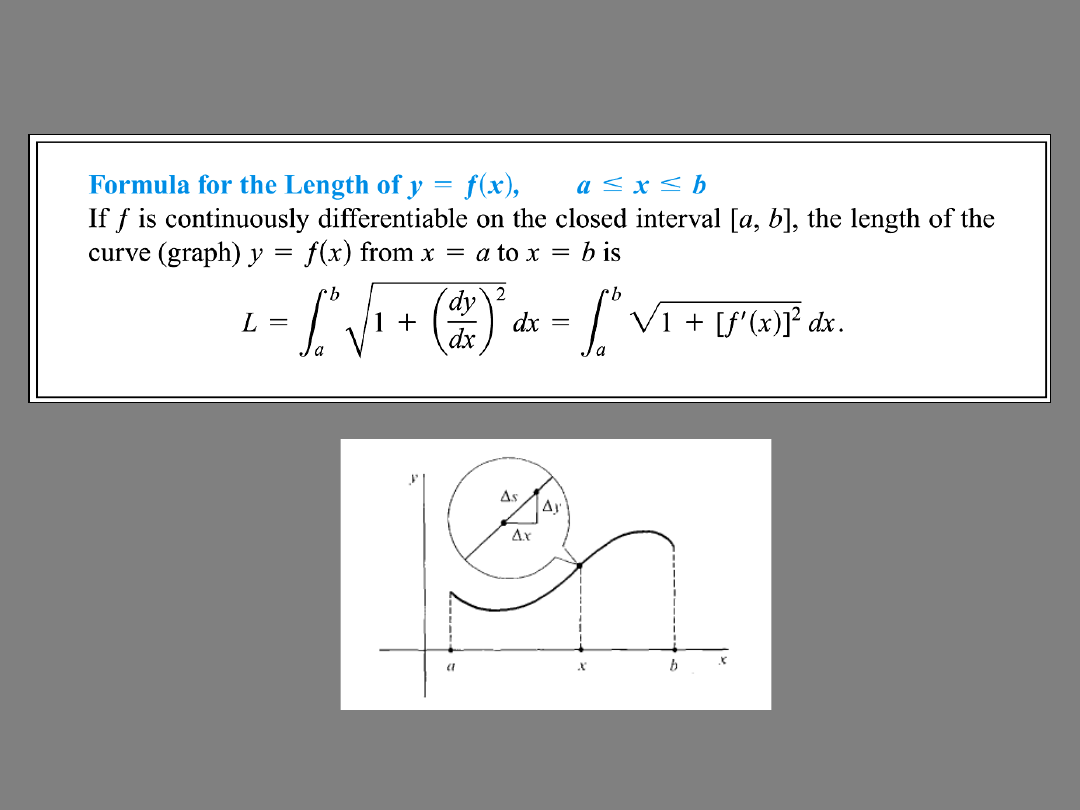
LENGTH OF A CURVE













b

a

2

dx

)

x

(

f

1

s

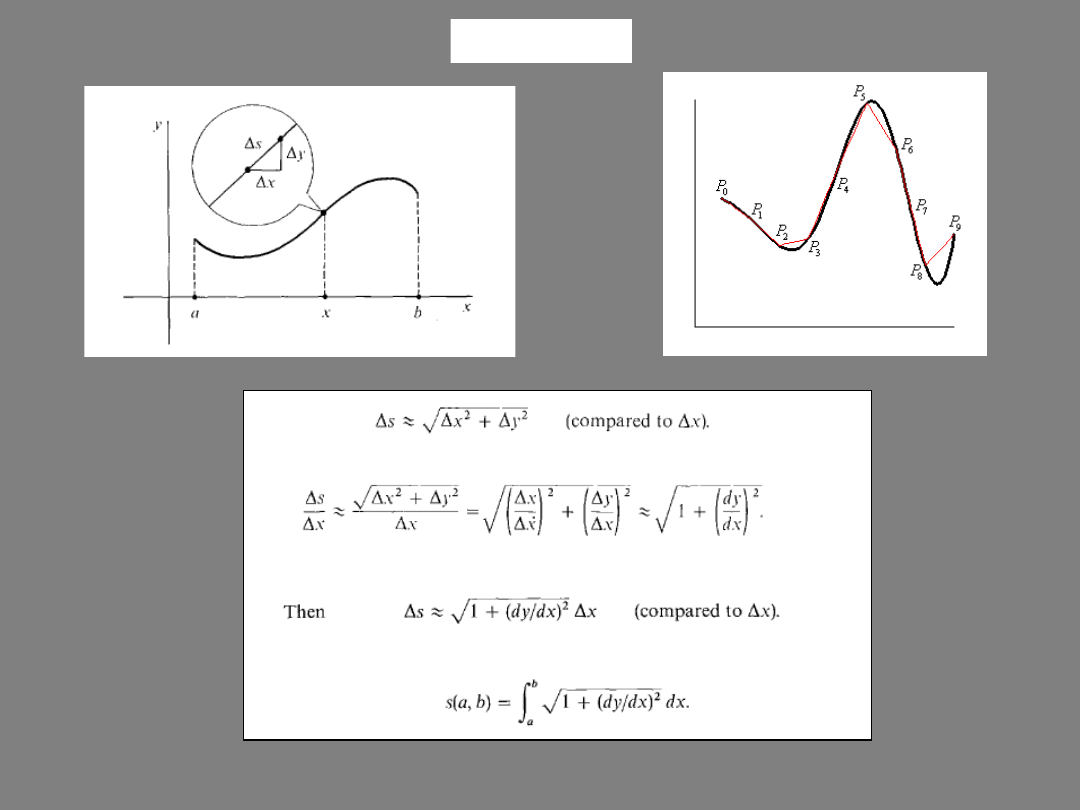
INTUITION

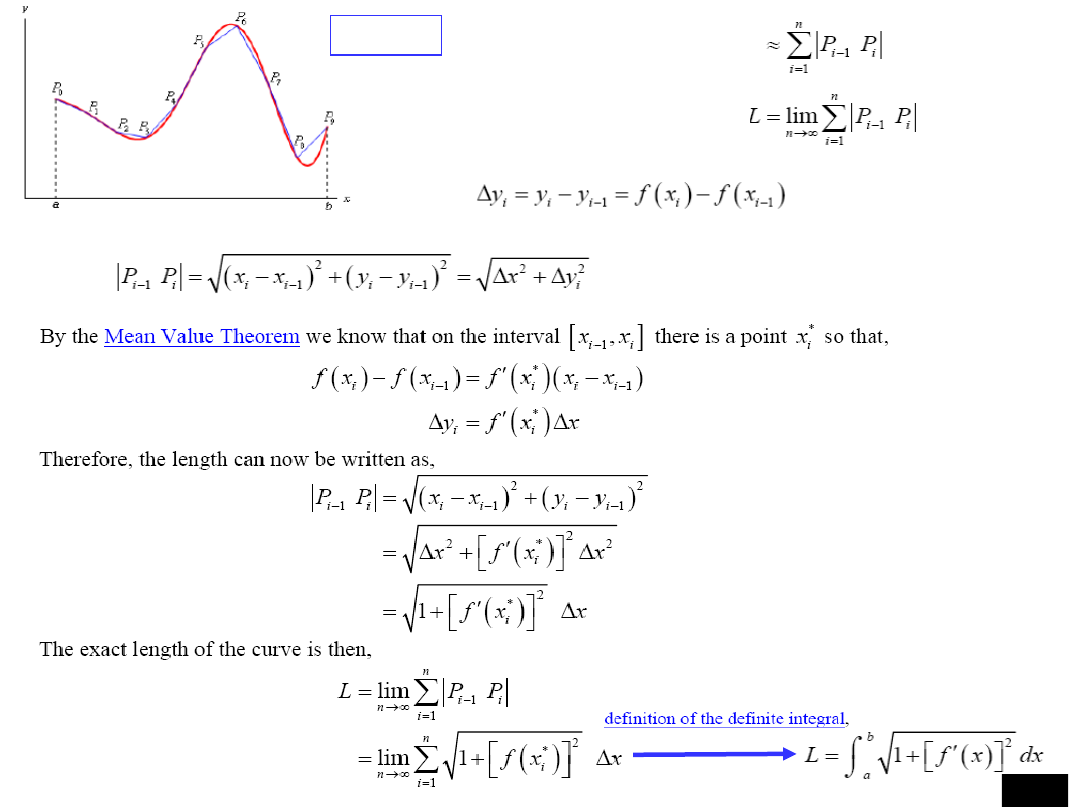
The exact length

The approximate length

Let

Then

QED

PROOF

x

x

cos

1

sec 

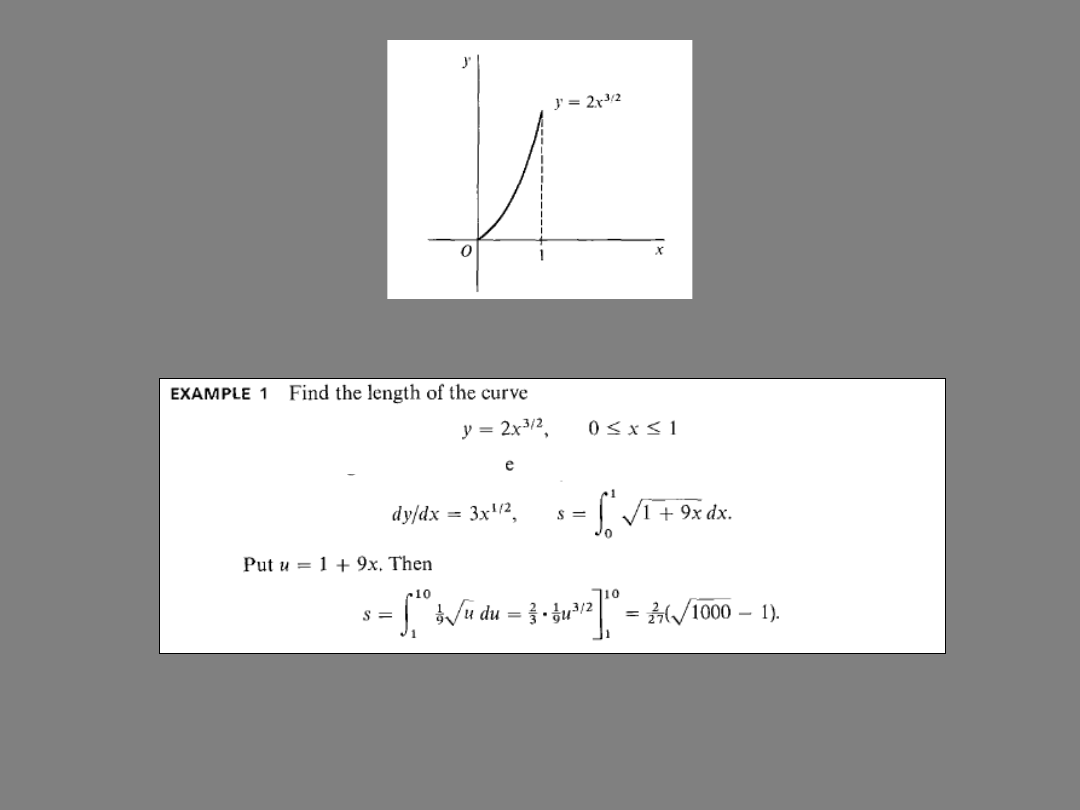
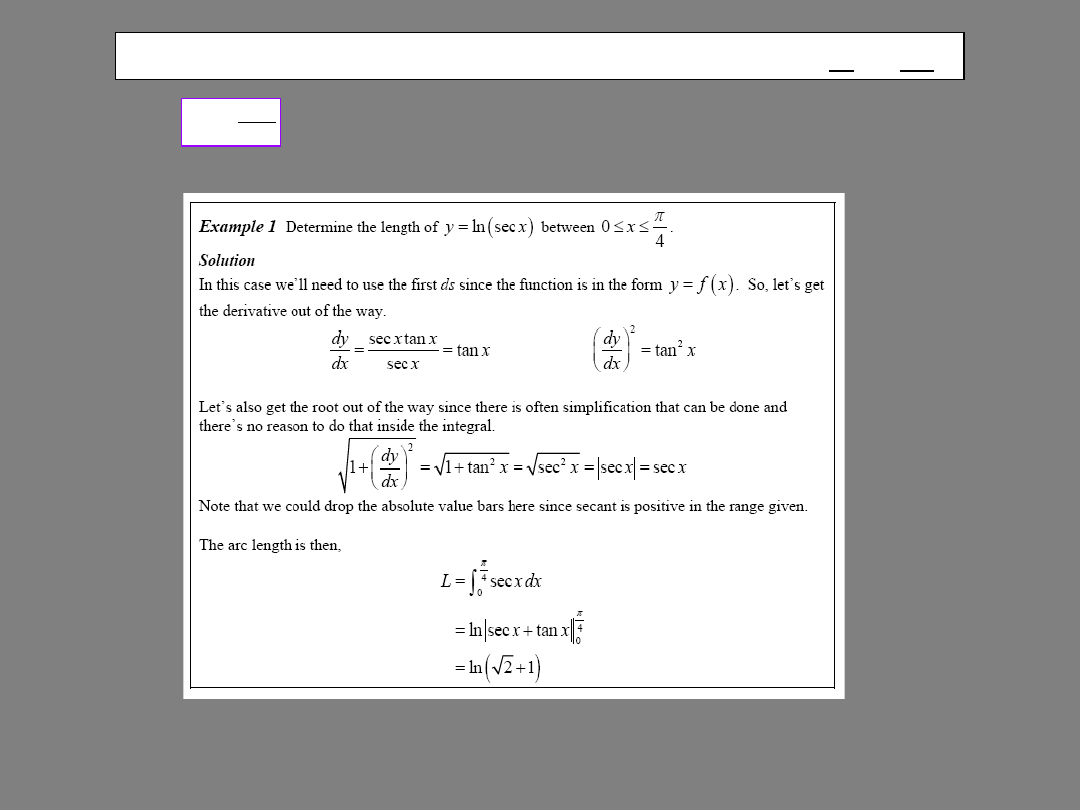
Detrmine the length of

y = ln(1/cos

x)

between

0 < x < 4

the end 26.06

VOLUME OF A SOLID

trapezium
rhombus
prism
pyramid
cylinder
cone
frustrum

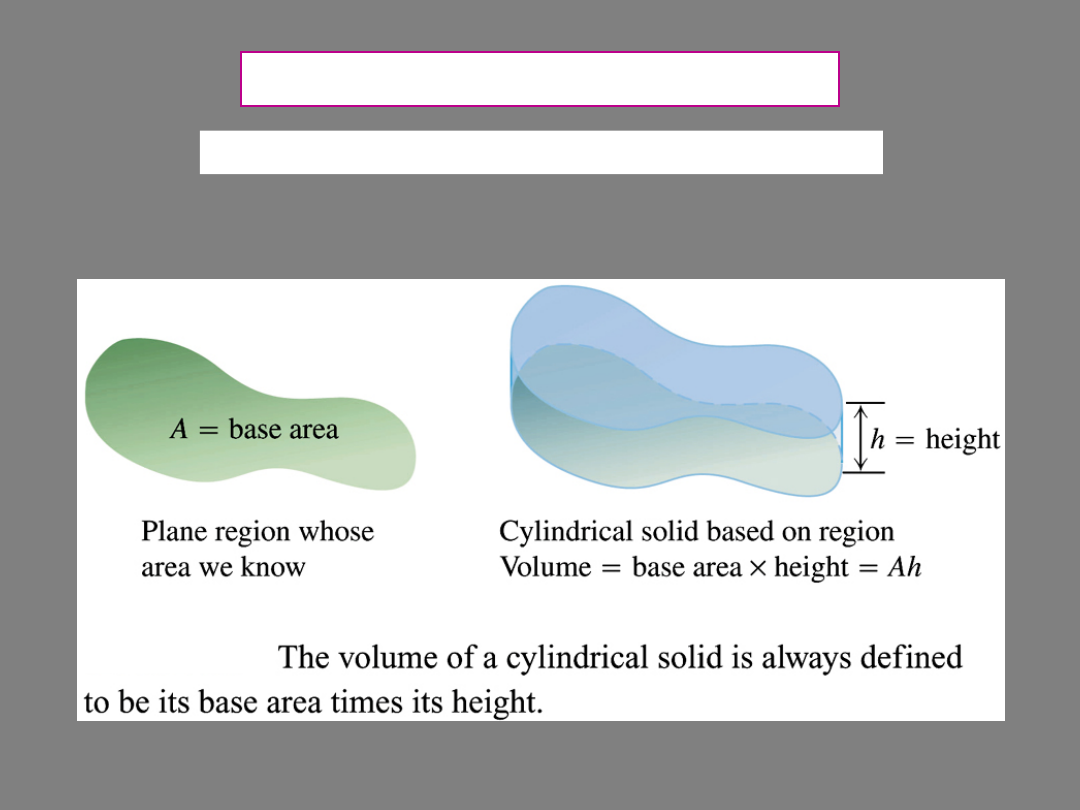
volume = (base area)

x

(height)

when the top base is parallel to the bottom base

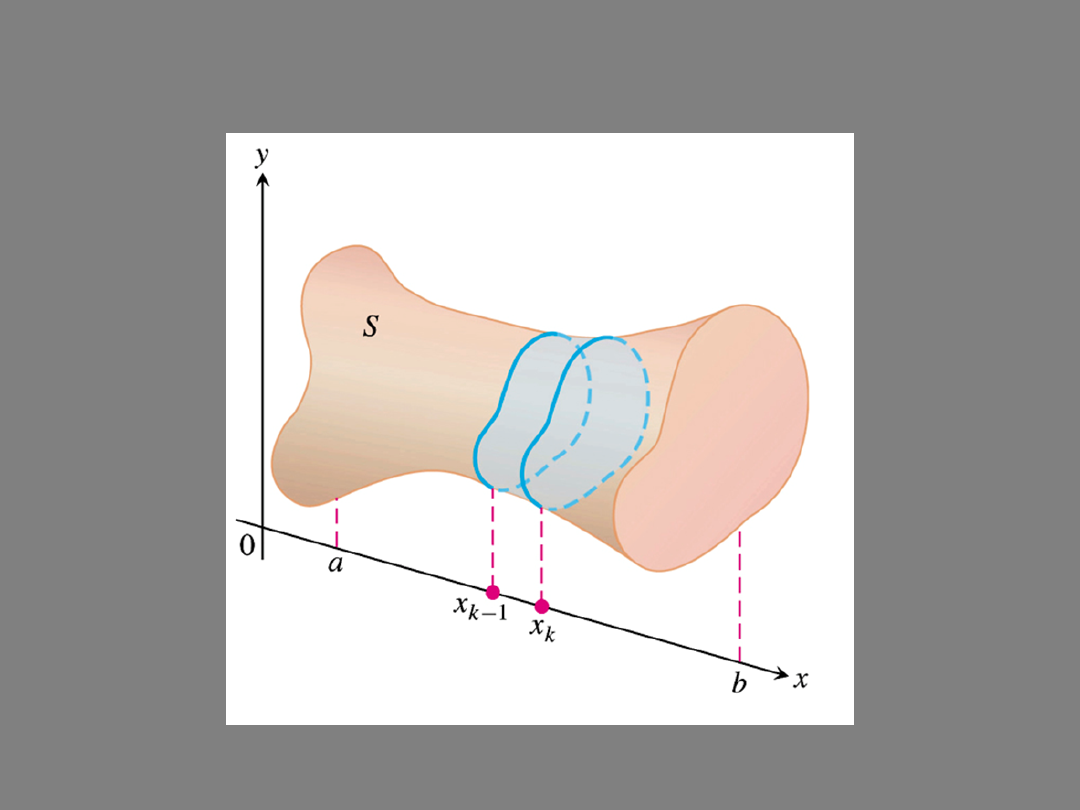
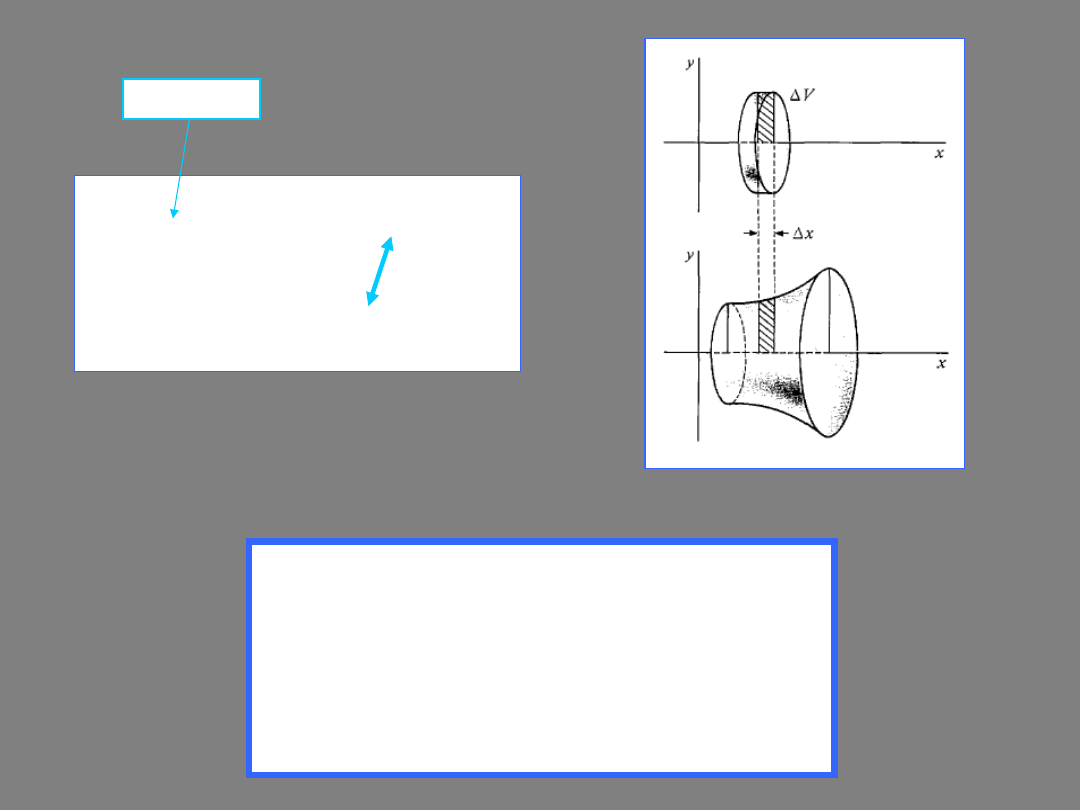
A thin slab of height Δx

k

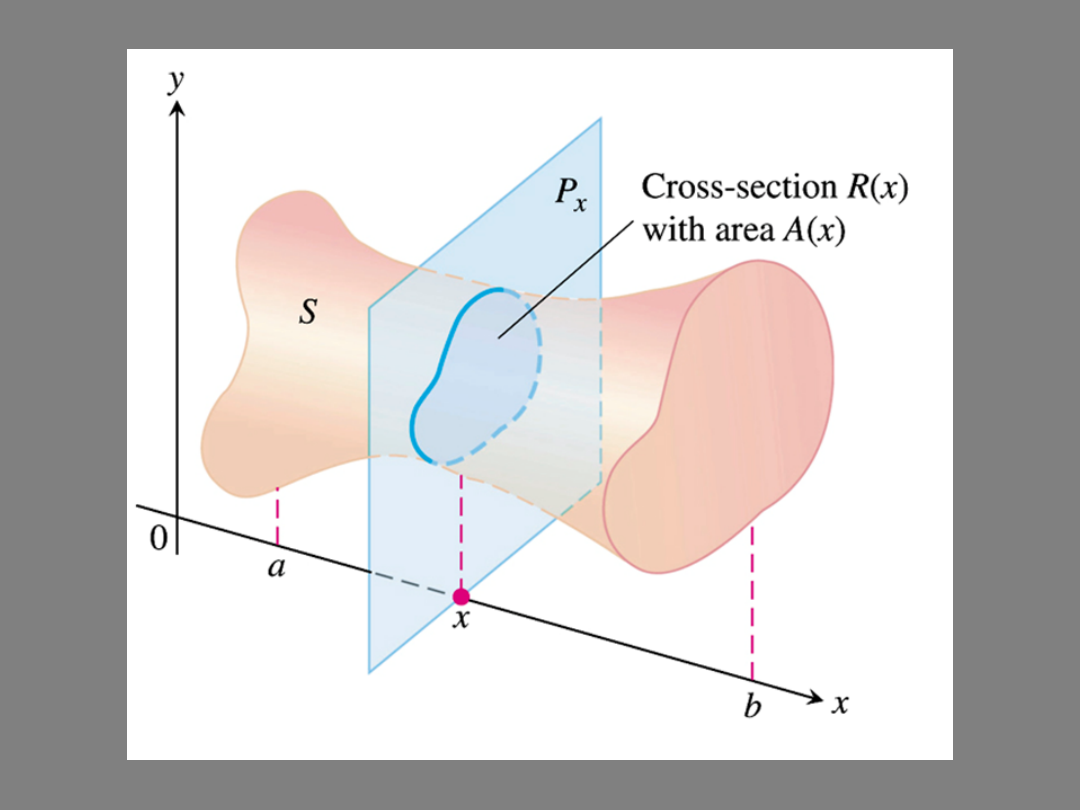
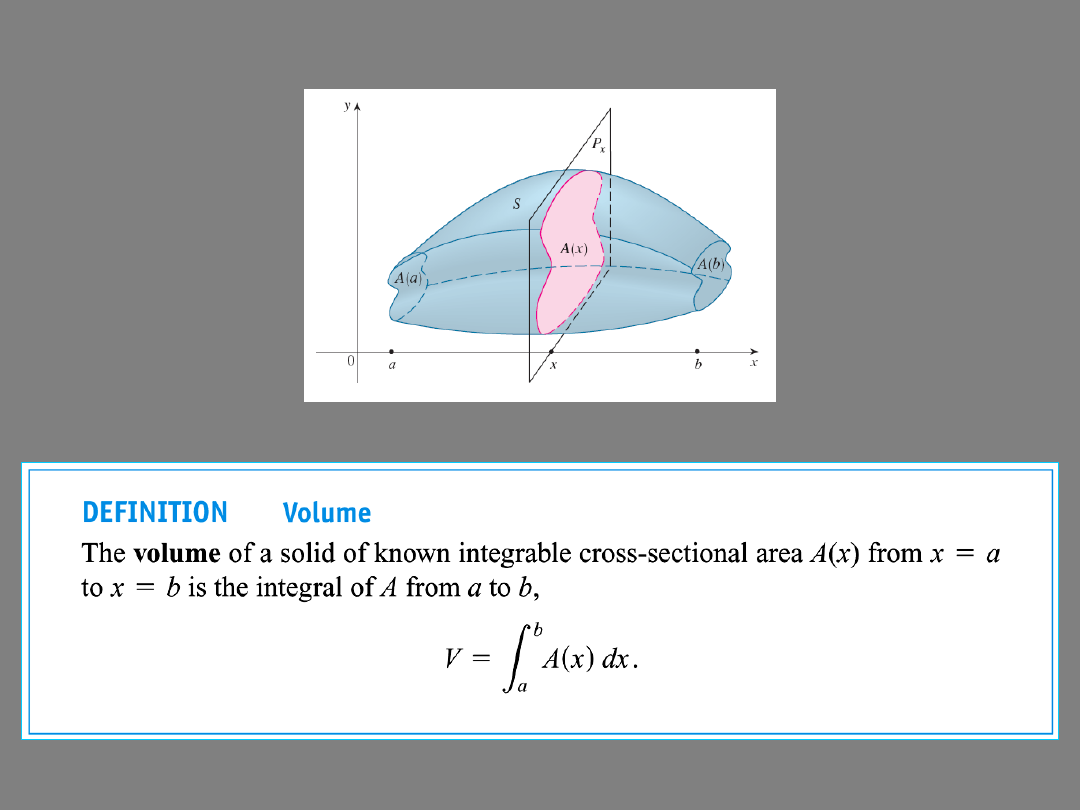
Definition of volume

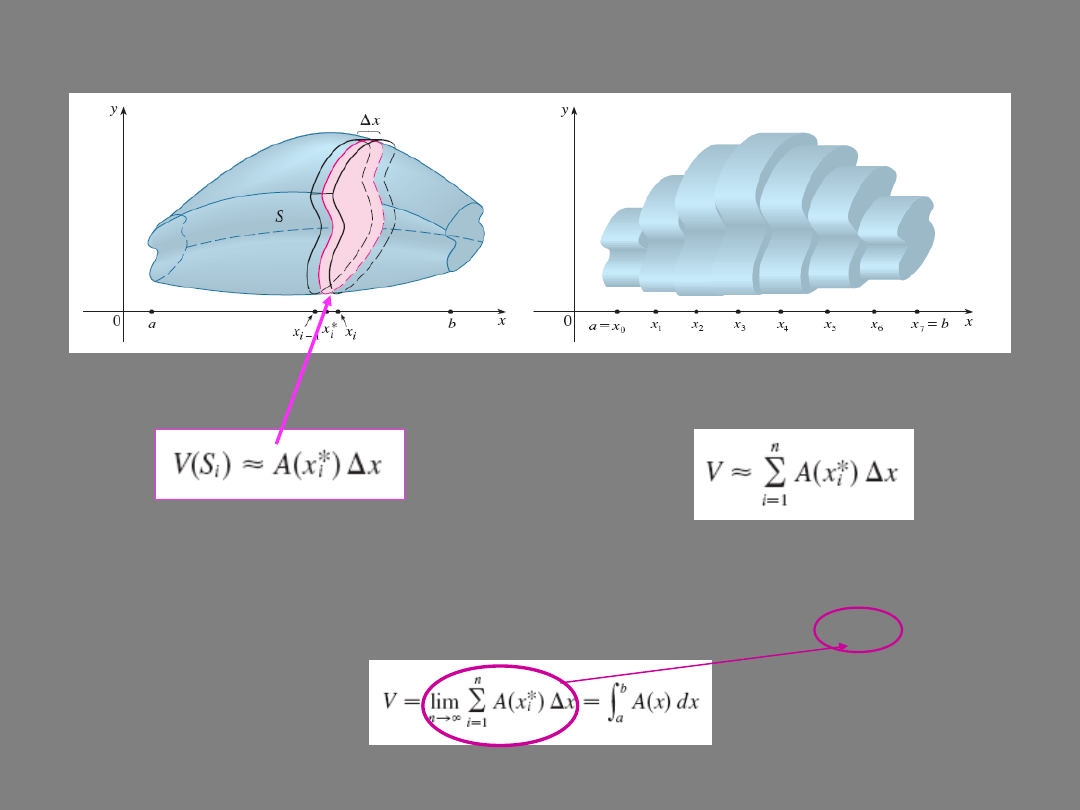
Justification:

the volume of the i-th slab

total volume

This approximation appears to become better and better as





n

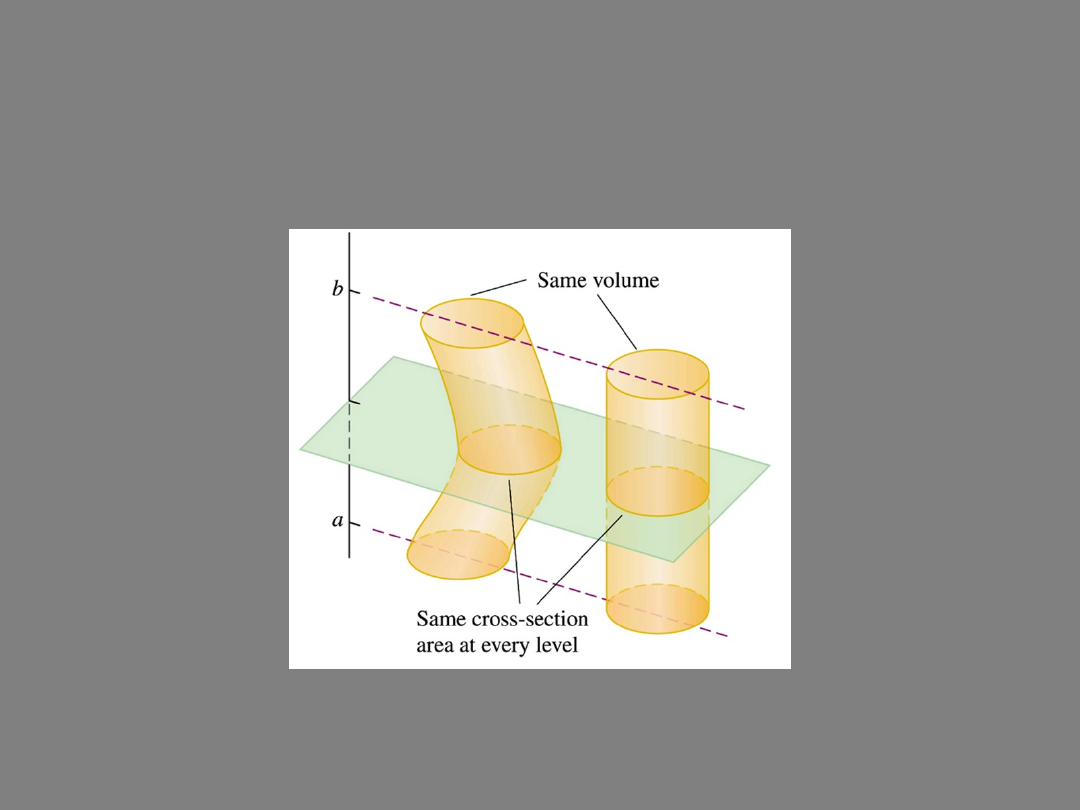
These solids have the same volumes – the same cross-sections,
Cavalieri’s Principle

SOLID OF
REVOLUTION

ROTATING A REGION ABOUT THE x- AXIS

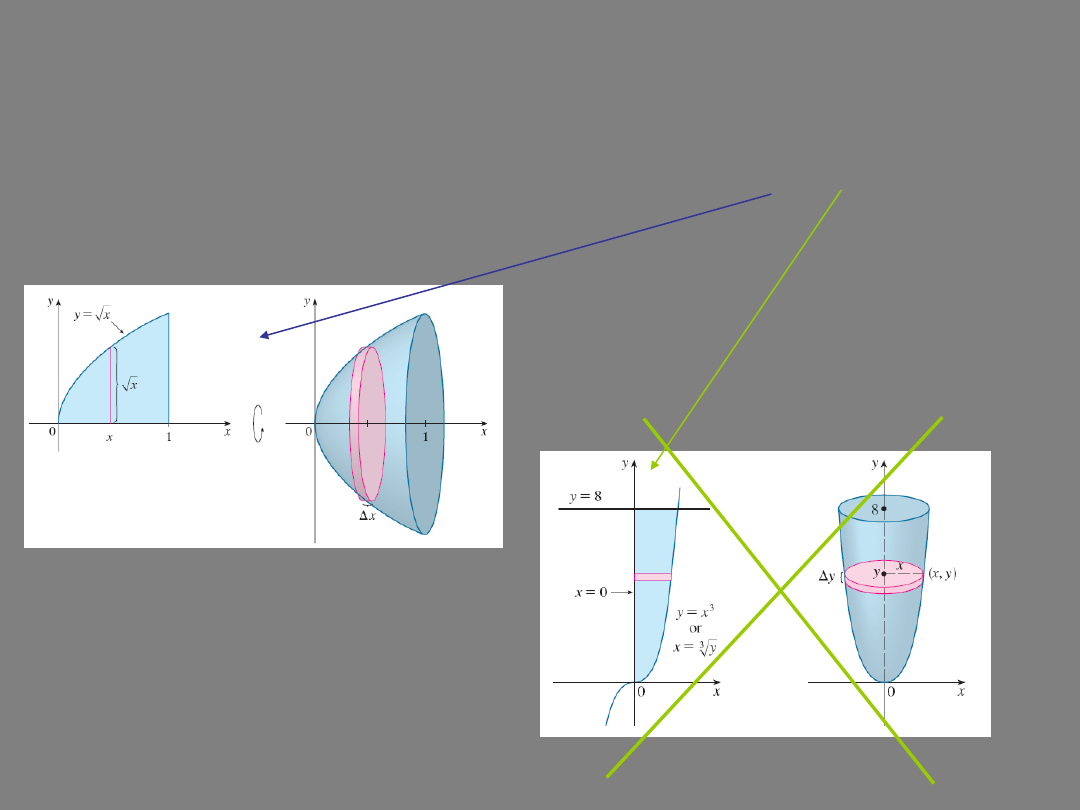
SOLIDS OF REVOLUTION
A solid of revolution is generated by taking a region in
the first quadrant of the plane and rotating it in space
about the

x

- or

y

-axis:

not obligatory

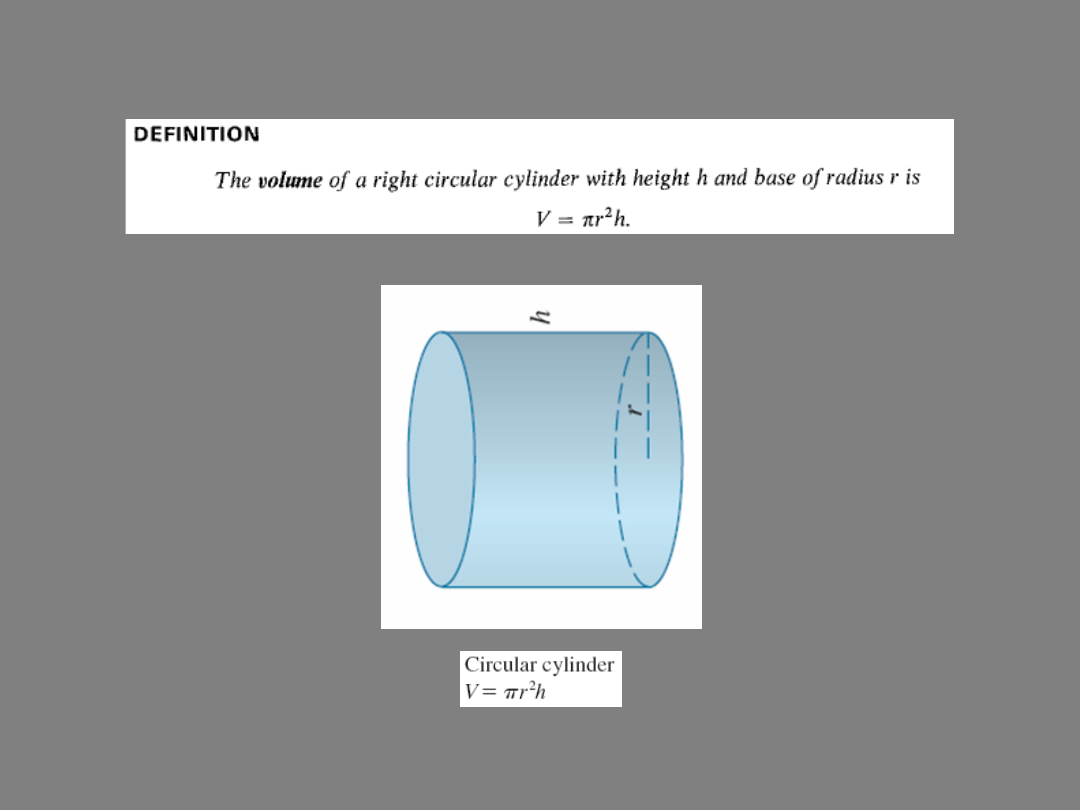
Revision

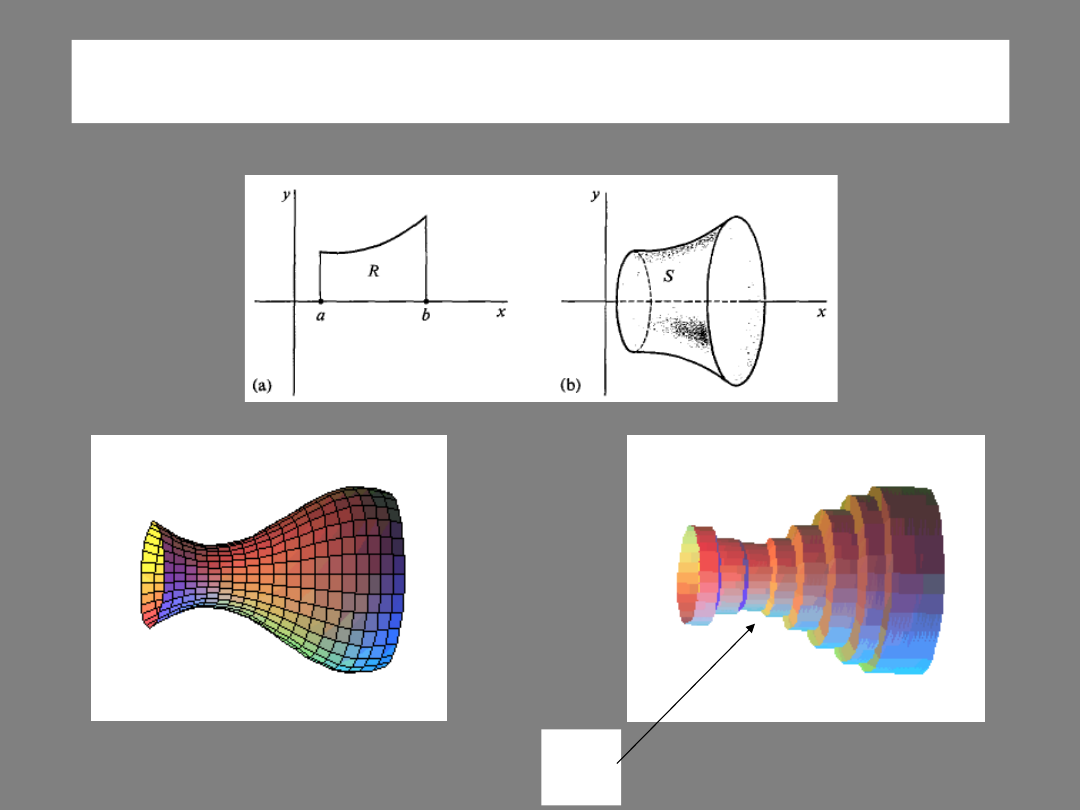
VOLUME

By the

DISC

METHOD

:

disc
s

The diagram demonstrates this formula, and why it is called the disc method







b

a

dx

x

f

V

2

))

(

(

VOLUME OF SOLID OF REVOLUTION

















b

a

b

a

b

a

dx

x

f

dx

radius

dx

x

A

2

2

))

(

(

)

(

)

(

Volume

Definition

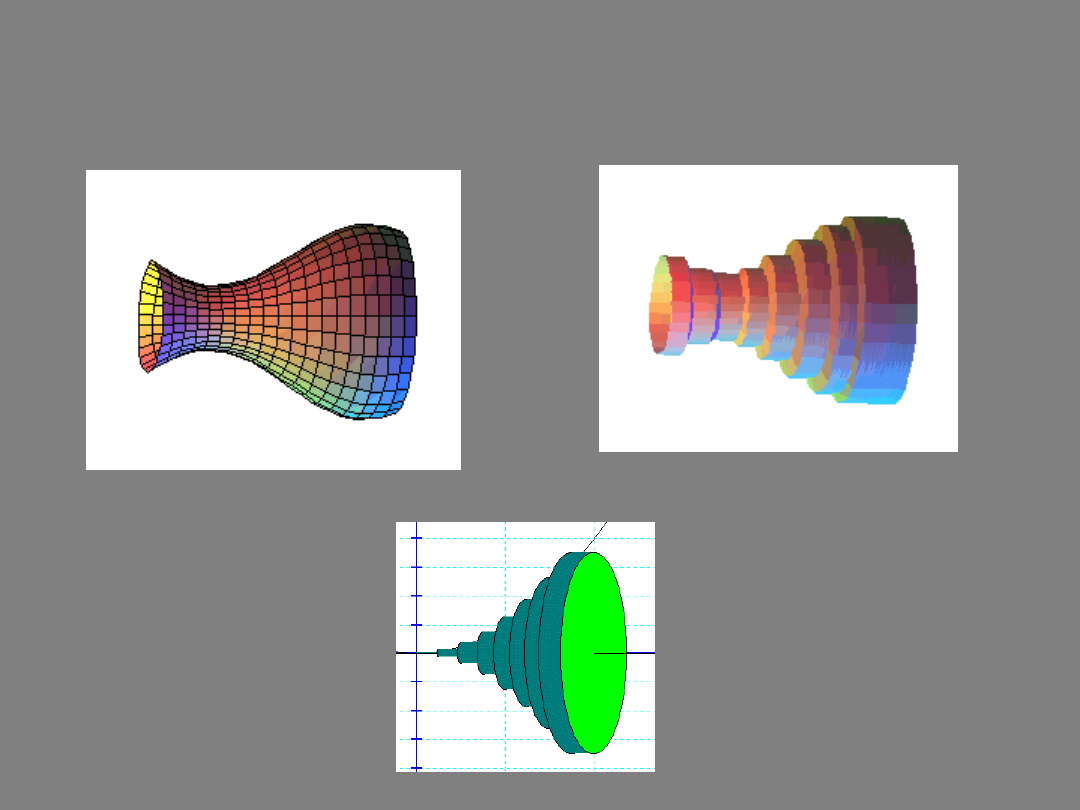
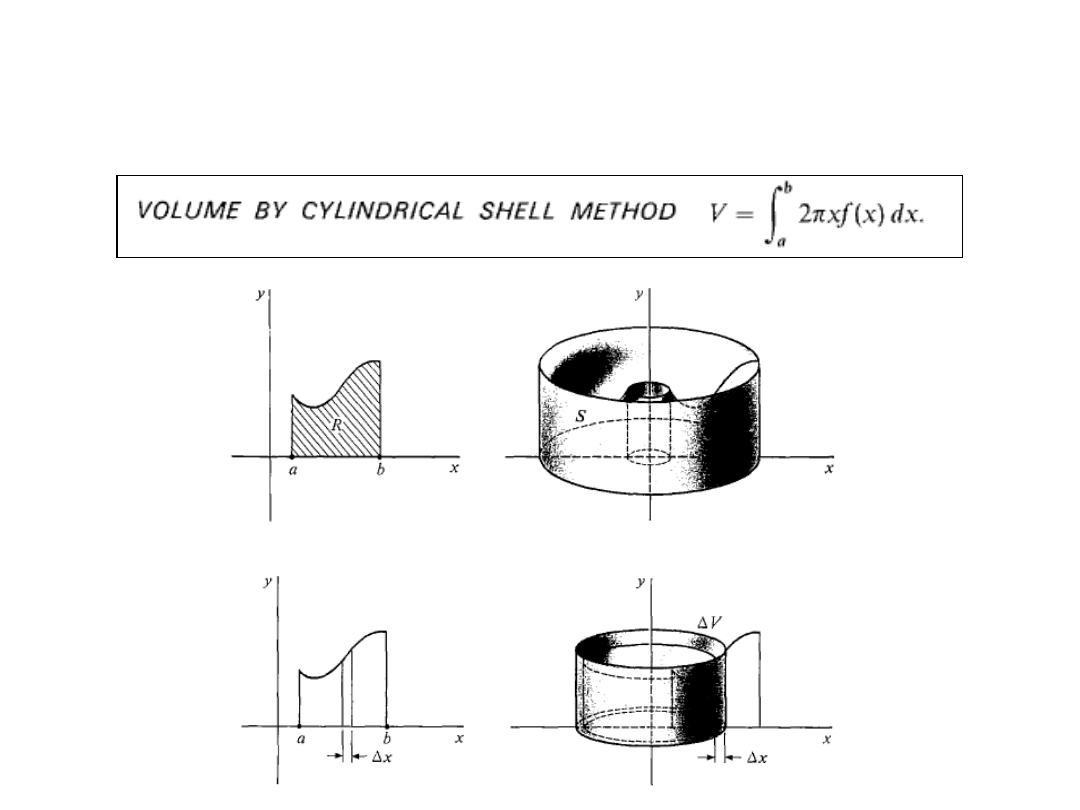
Cutting the solid of revolution into cylinders

EXAMPLE

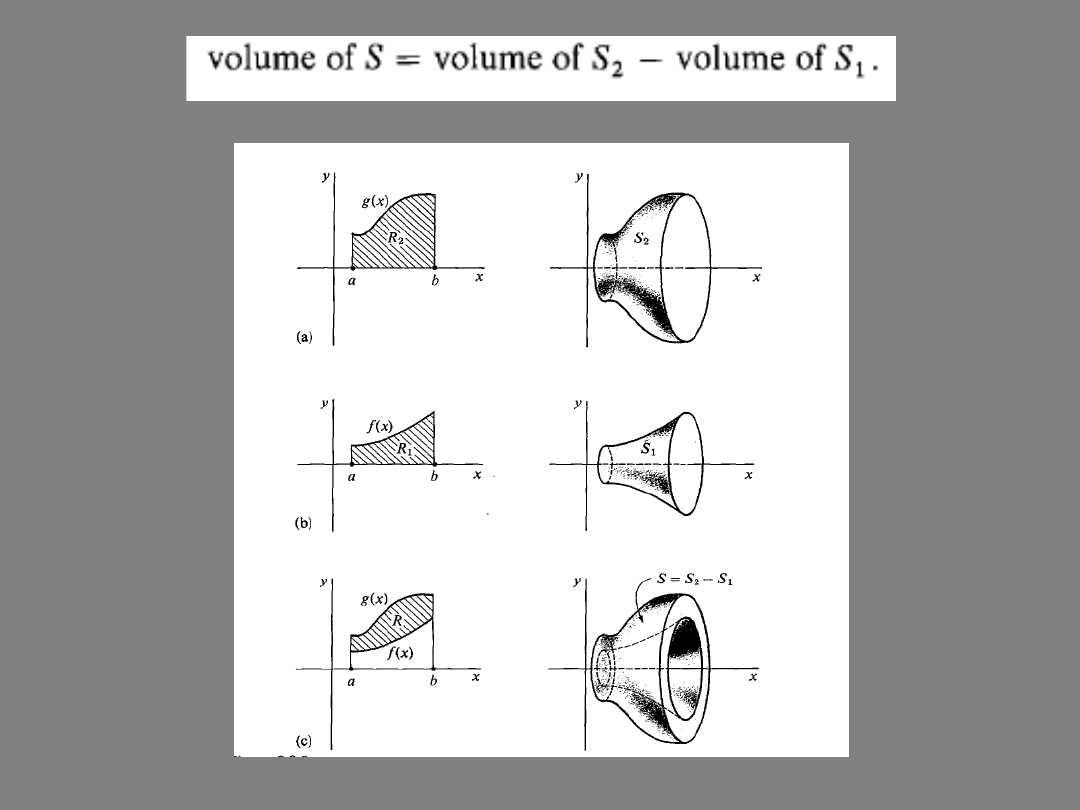
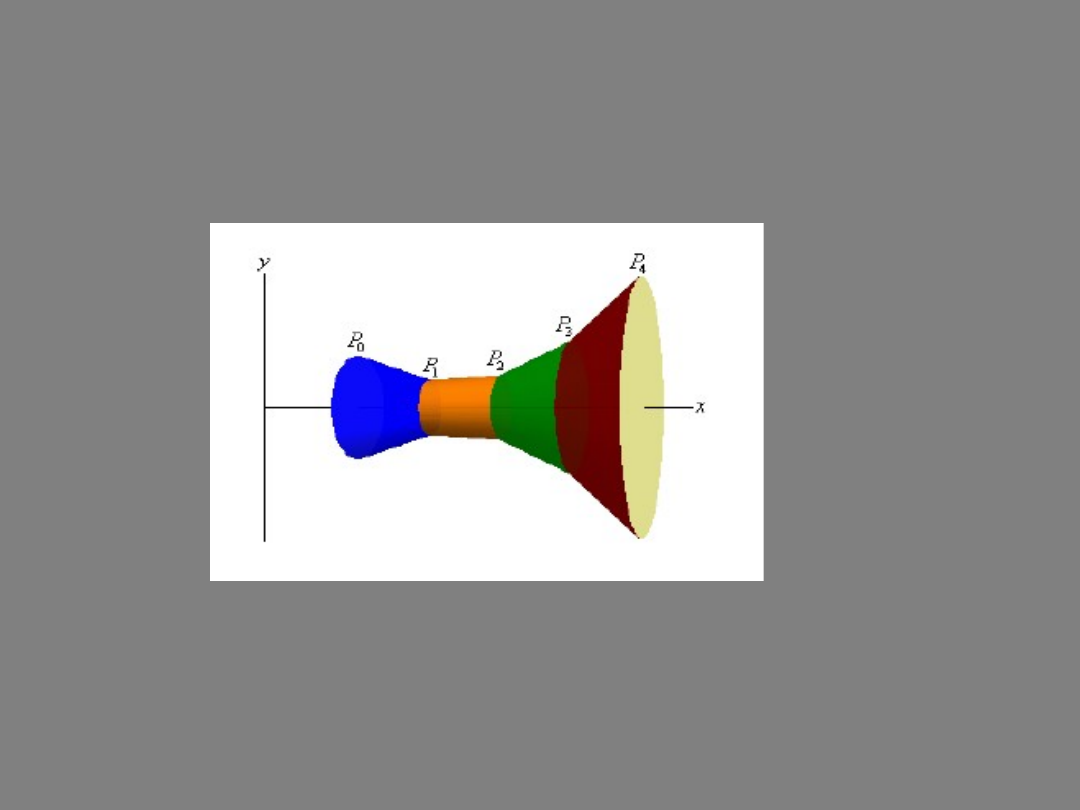
Find the volumes of the solids generated by revoloving the shaded region
about the x-axis.

SURFACE
AREA

)

(

2

1

R

R

s

side

of

Area

S









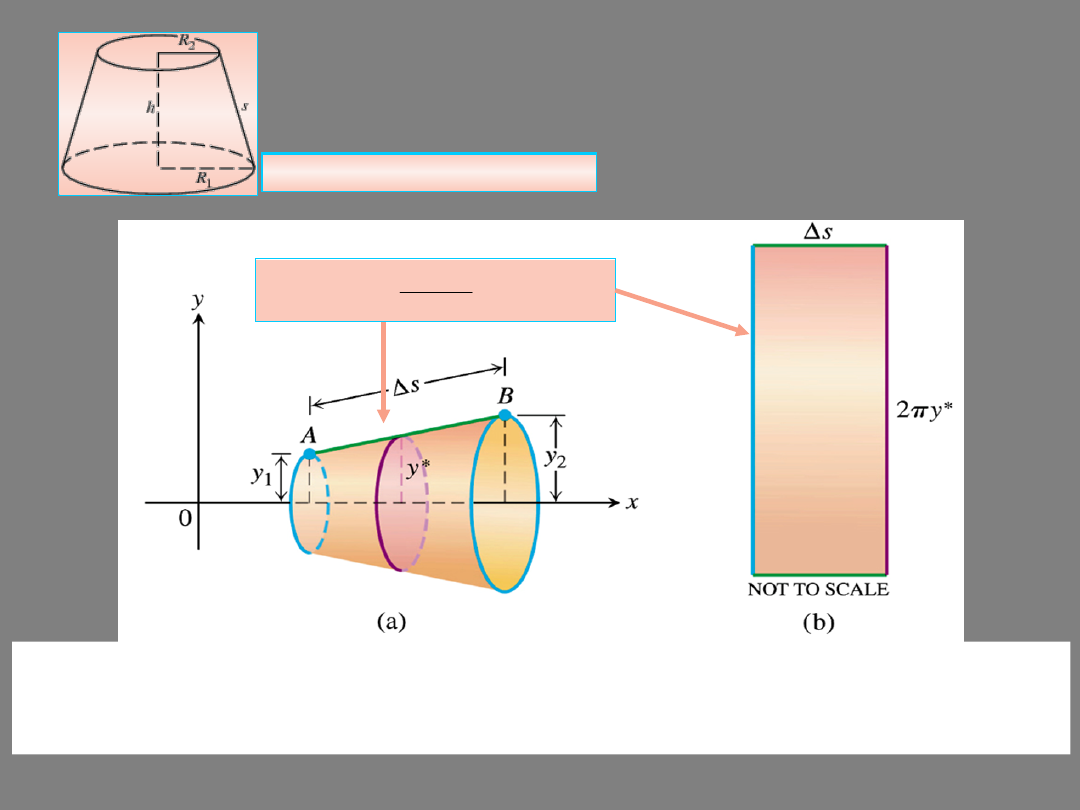
The area of the frustum of a cone generated by rotating the slanted
line segment AB of lenght Δs about the x-axis has area 2πy

*

Δs – the area of

the rectangle on the right for y

*

= (y

1

+ y

2

)/2

s

y

s

y

y

Area

S

















*

2

1

2

2

2

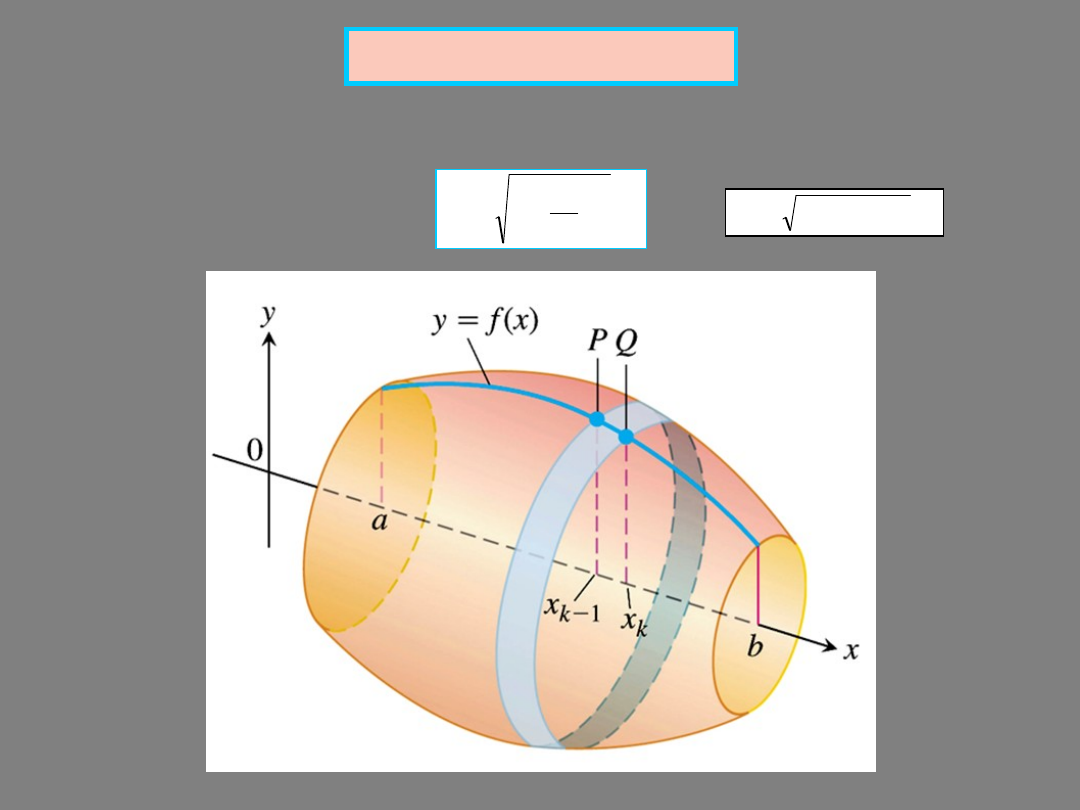
The frustums are ”curved” , so is calculated from the integral formula.

s



x

x

y

s

























2

1





dx

x

f

ds

2

)

(

'

1



We still need

!!!

s



Revolving a curve about an axis generates a
surface area.

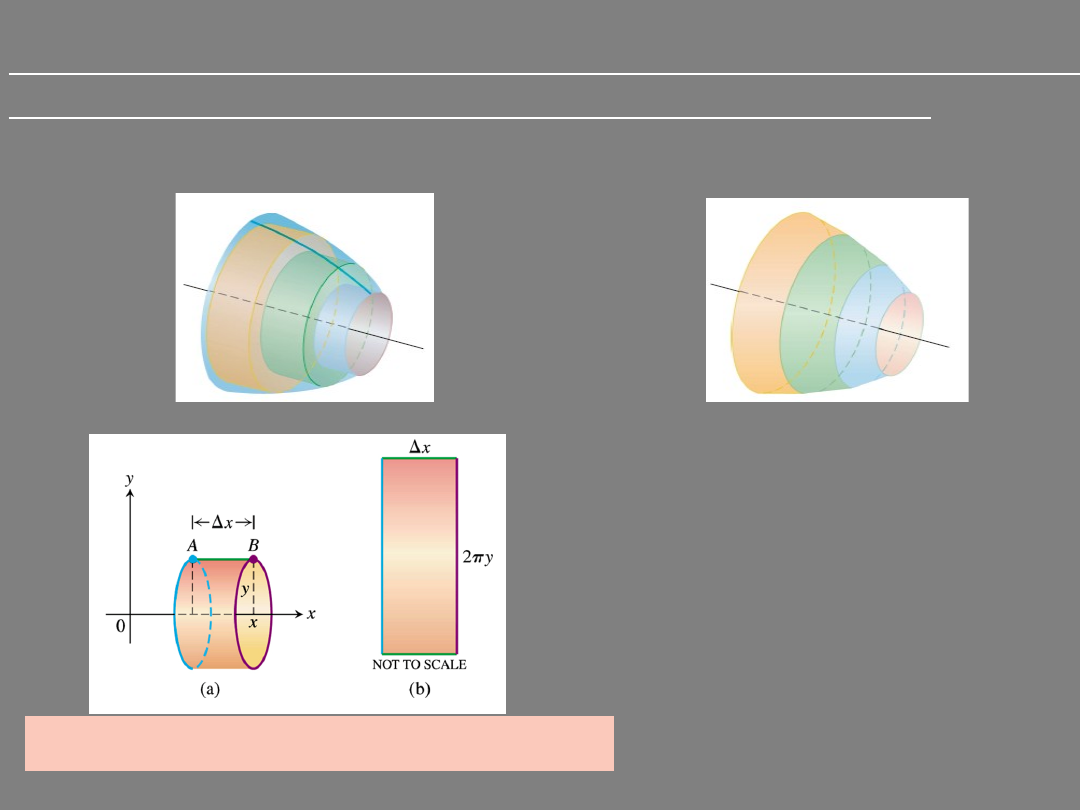
WHY NOT find the approximate area by approximating
with conical bands instead of conical bands??

Why not

instead of

x

y

cylinder

of

area

side

S









2

The Riemann sums we get this way converge just as nicely as the the ”conical” ones,
and the resulting integral is simpler. It leads to the formula:

(*)

)

(

2

*







b

a

dx

x

f

S

But this new formula fails to give results consistent with the surface area formulas
from classical geometry.

CAUTION
Do not use the above formula

(*)

to calculate surface area

(*
)

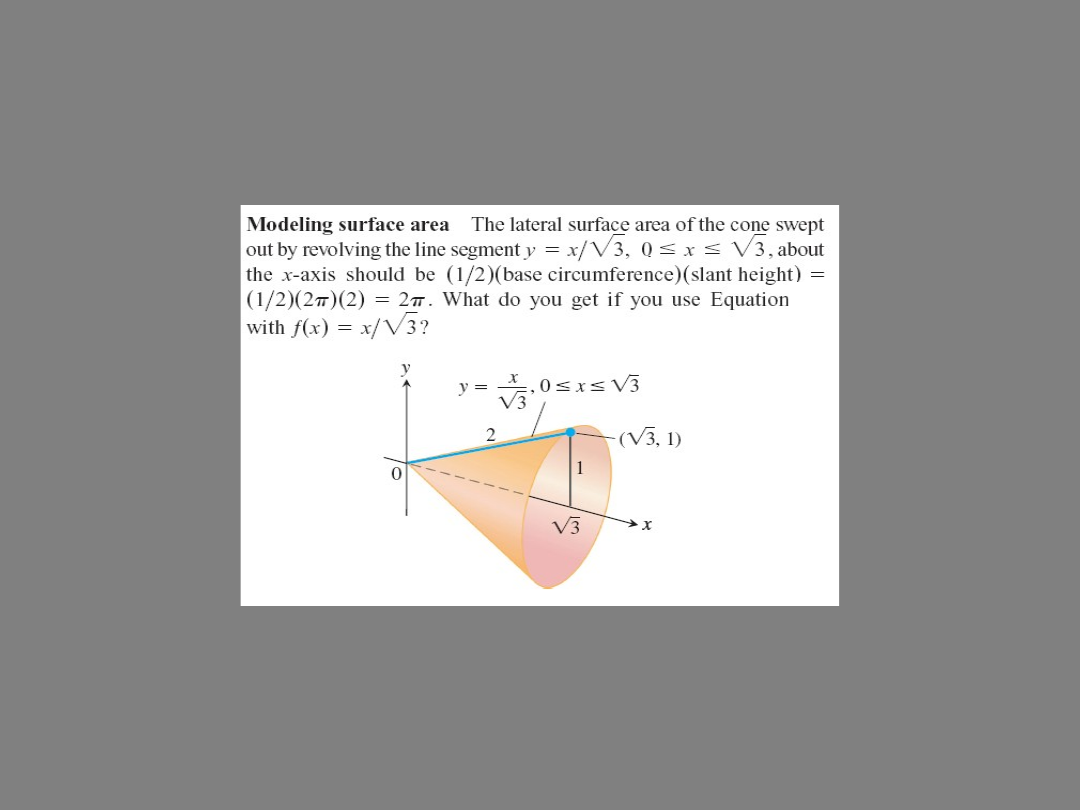
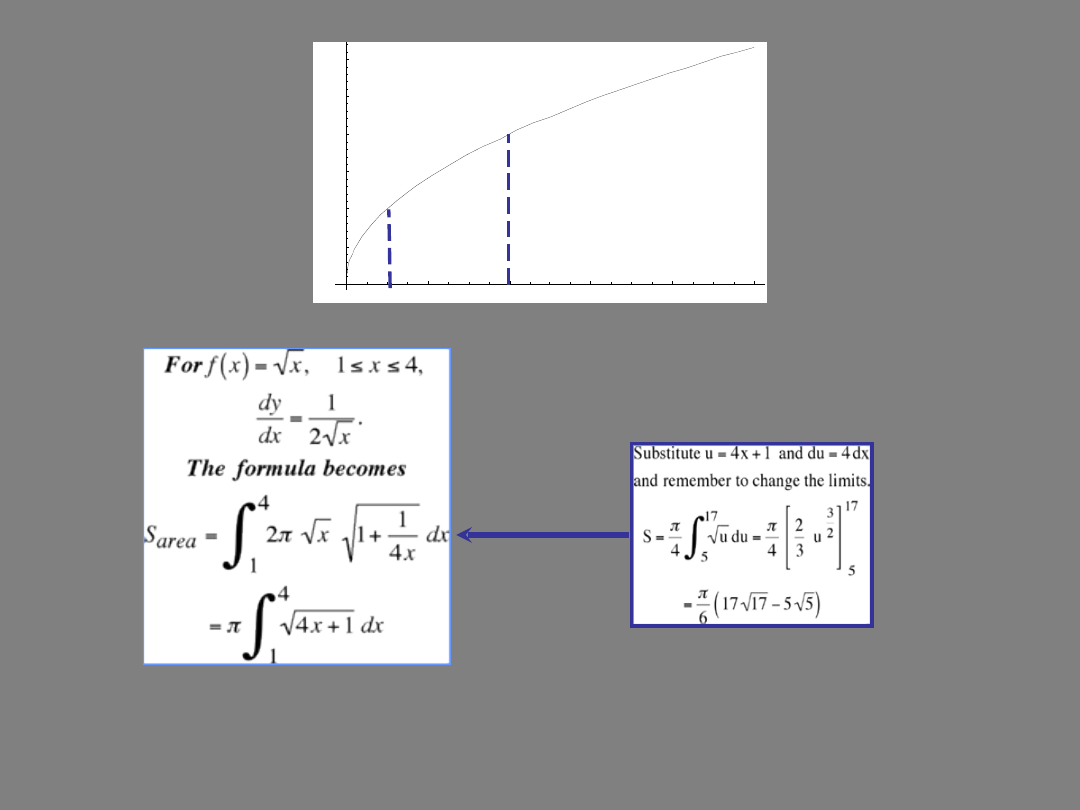
2

4

6

8

10

0.5

1

1.5

2

2.5

3

This curve is rotated

INFINITE SURFACES - IMPROPER INTEGRALS

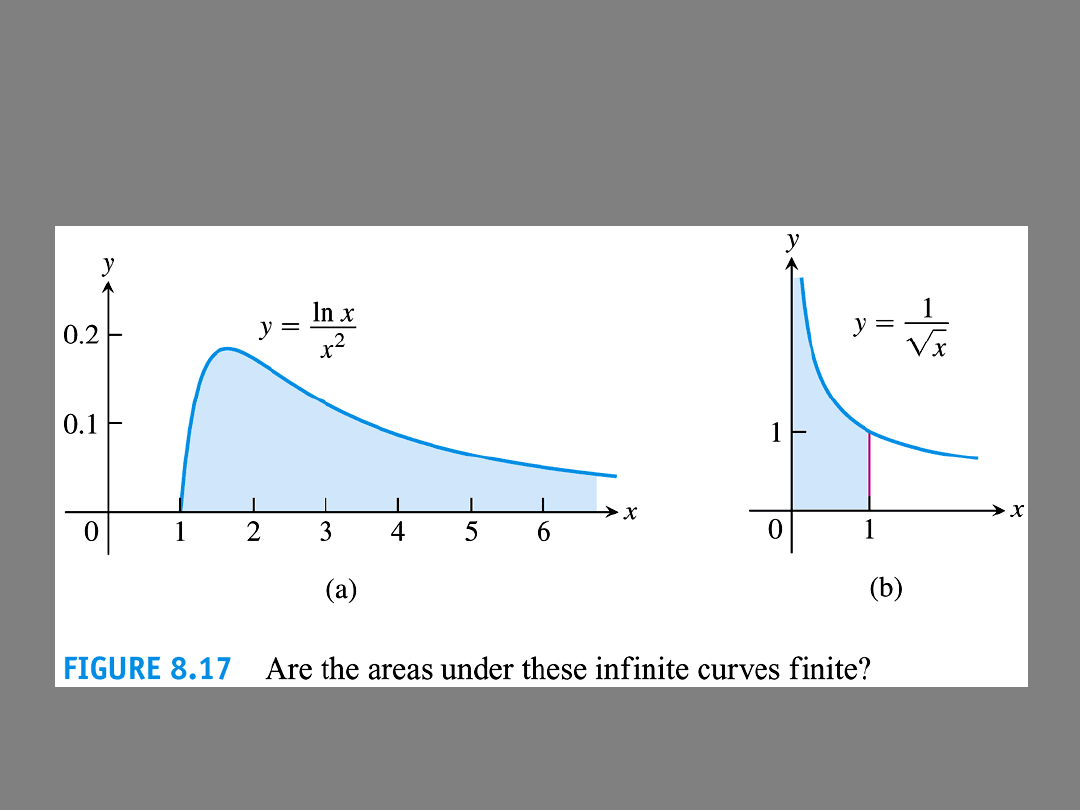
Unfortunately, the integrals involving surface area are often quite tricky.

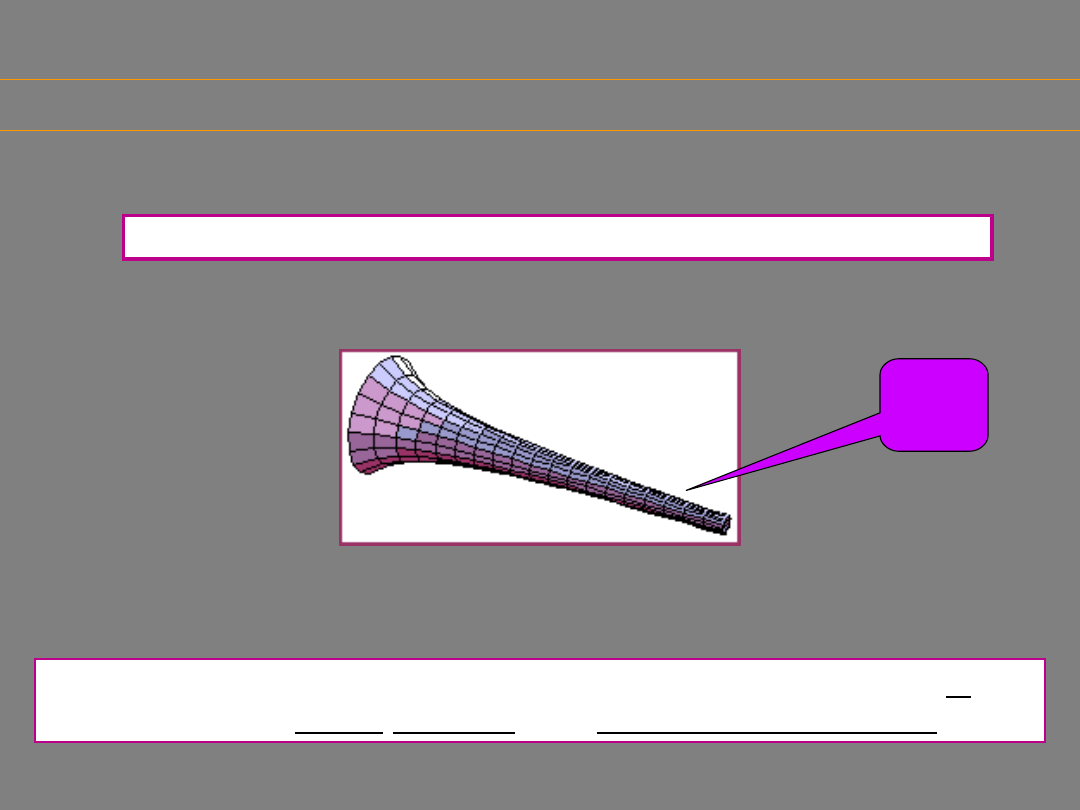
A Famous Paradox:   Gabriel's Horn or Torricelli's Trumpet

If the function  y = 1/x   is revolved around the x-axis for x > 1,
the figure has a finite volume, but infinite surface area.

infinit
e
lengt
h

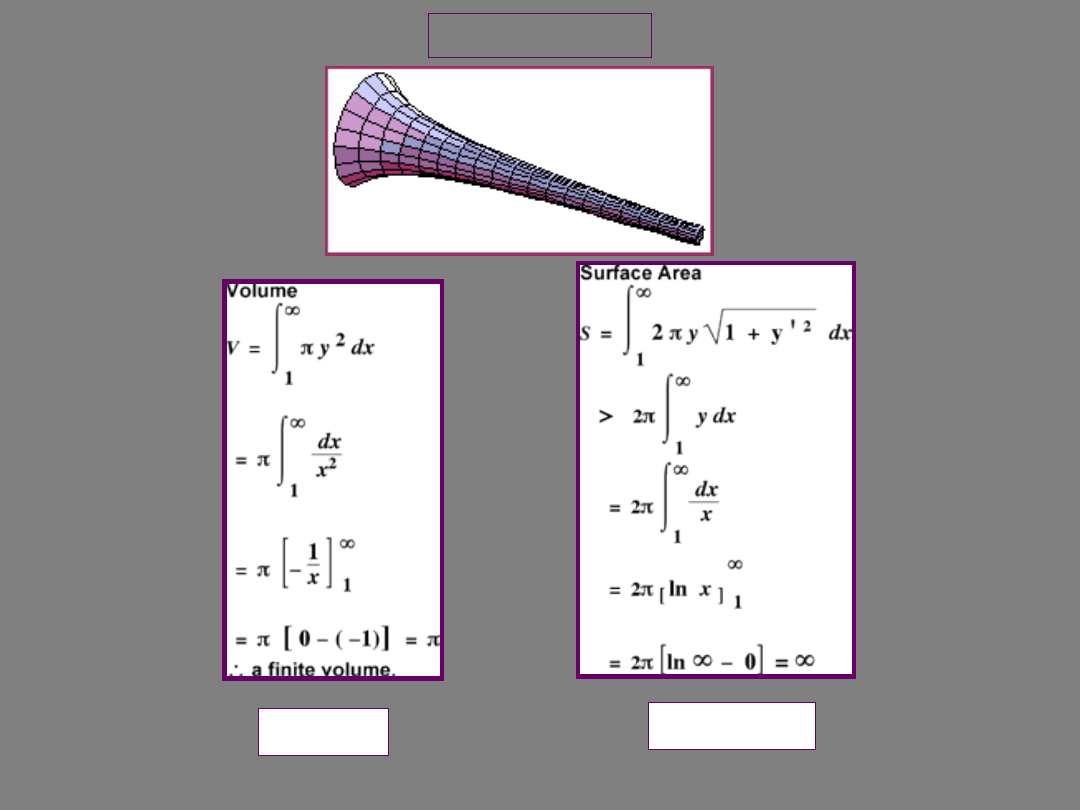
Gabriel's Horn

FINITE

INFINITE

This leads to the paradoxical consequence that
while Gabriel's horn can be filled up with π
cubic units of paint, an infinite number of square
units of paint are needed to cover its surface!

APPENDIX
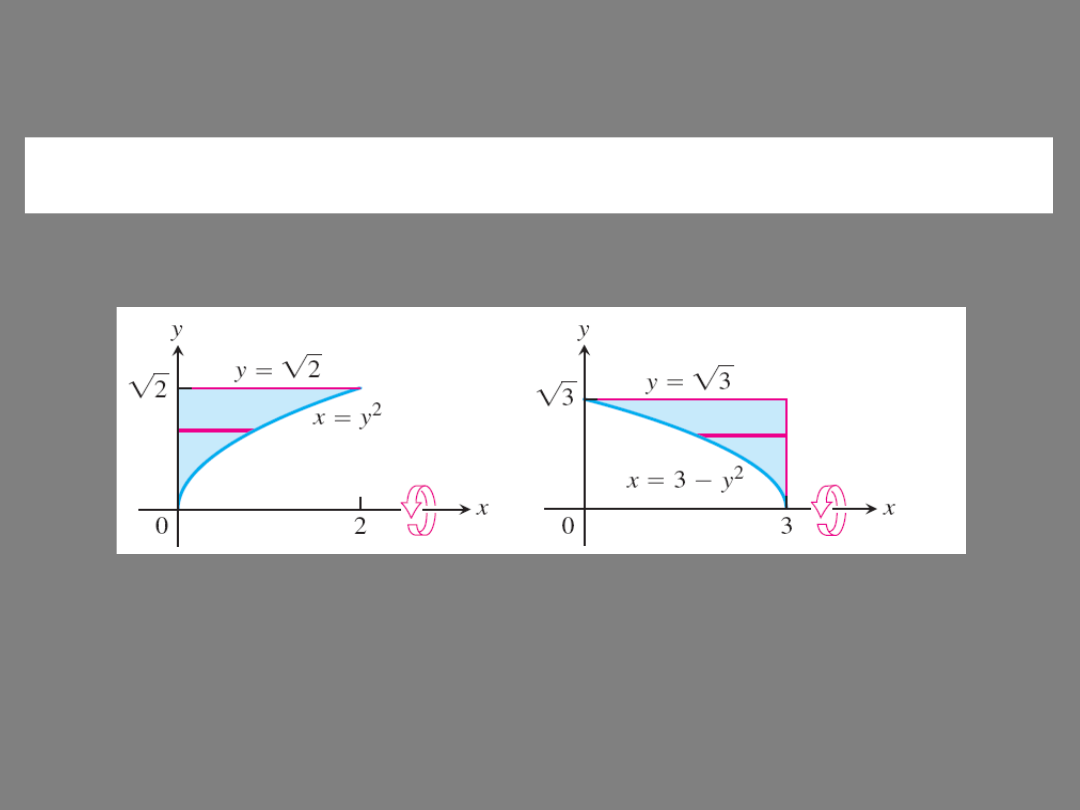
In a similar way we can the volume of a solid of revolution
obtained by rotating a curve about the y-axis:

An engineer, a chemist and a mathematician are staying in three
adjoining cabins at an old motel. First the engineer's coffee maker
catches fire. He smells the smoke, wakes up,

unplugs

the coffee maker

,

throws it out the window, and goes back to sleep.

Later that night the chemist smells smoke too. He wakes up and sees
that a cigarette butt has set the trash can on fire. He says to himself,
"Hmm. How does one put out a fire? One can reduce the temperature of
the fuel below the flash point,

isolate the burning material from oxygen

,

or both. This could be accomplished

by applying water

." So he picks up

the trash can, puts it in the shower stall, turns on the water, and, when
the fire is out, goes back to sleep.
The mathematician, of course, has been watching all this out the window.
So later, when he finds that his pipe ashes have set the bedsheet on fire,
he is not in the least taken aback. He says:

"Aha! A solution exists!"

and

goes back to sleep.