KINEMATYCZNE

WŁASNOŚCI PRZEKŁADNI

Wielkości charakteryzujące koło zębate:

 liczba zębów

z

,

 cechy geometryczne

m

,

d, h

,

h

a

,

h

f

, itp.

 kształt zarysu boku zęba.

Warunki współpracy zazębienia

Pamiętamy, że koła zębate mogą ze sobą
współpracować, kiedy mają ten sam
moduł

m

.

Kształt zarysu boku zęba w zasadzie
może być dowolny, ponieważ znana
jest metoda

REALAUX

, pozwalająca

wyznaczyć

przeciwzarys

danego

zarysu.

linia zarysu boku zęba

Jednakże

dla

prawidłowej

pracy

przekładni linia zarysu boku zęba musi
zapewniać:

1. stałość przełożenia
2. ciągłość zazębienia

Niespełnienie

pierwszego

warunku

powoduje, że w przekładni przy



=

const. części napędzającej, wystąpi
rozpędzanie

lub

hamowanie

części

napędzanej,

zależnie

od

chwilowej

wartości przełożenia

i

.

Z

pierwszym warunkiem związana jest tzw.

główna zasada zazębienia (zasada Willisa).

Z drugim warunkiem związana jest tzw. liczba
przyporu.

Spełnienie obu warunków zależy w głównej
mierze od kształtu linii zarysu boku zęba.

Zasadniczo kształt zarysu zęba może być
dowolny, jednakże nie wszystkie zarysy spełniają
przedstawione warunki, tj. stałości przełożenia i
ciągłości zazębienia.

Najkorzystniejsze okazały się zarysy utworzone
przez krzywe cykliczne, a więc wszelkiego rodzaju
cykloidy oraz ewolwenta koła, jako szczególny
przypadek cykloidy.

Krzywe cykliczne używane w kołach
zębatych to:
a) cykloida zwyczajna (ortocykloida),

b)epicykloida,

c) hipocykloida,

d)ewolwenta zwyczajna.

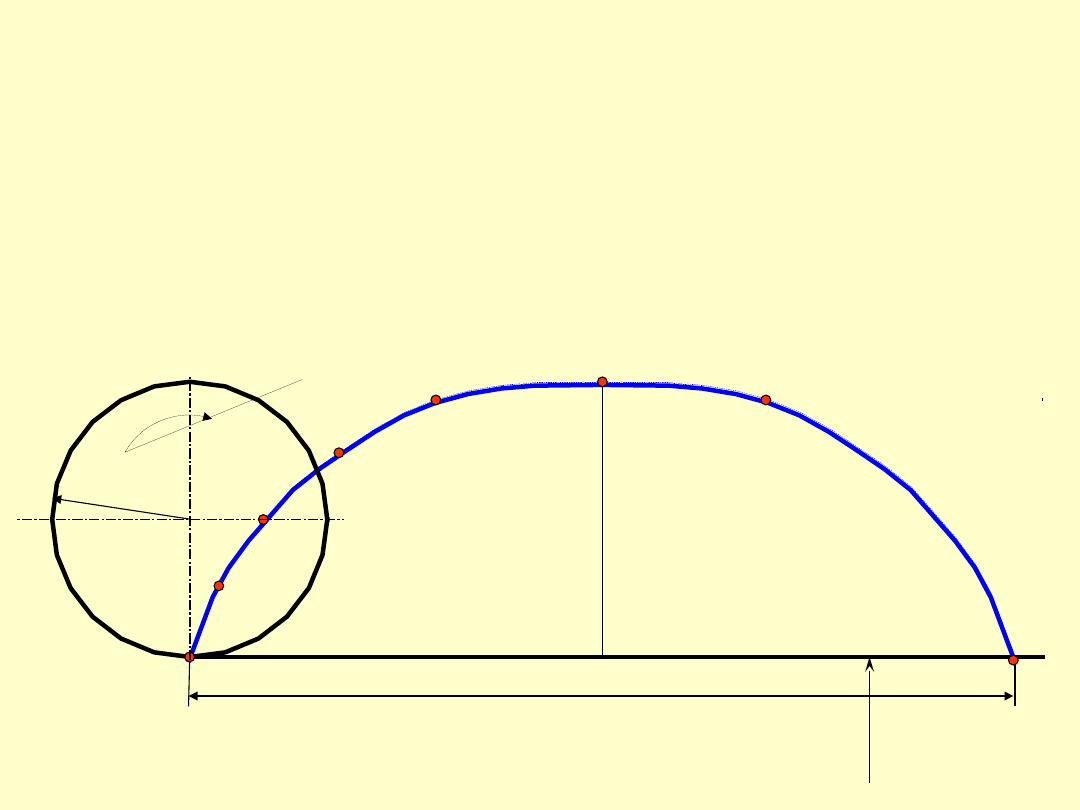
a) Cykloida zwyczajna (ortocykloida) – krzywa, którą

kreśli punkt koła toczącego się po innym kole.

Koło toczące się o promieniu



nazywamy kołem

odtaczającym, a koło nieruchome o promieniu

r

z

=



nazywamy kołem zasadniczym.



2





r

z

=



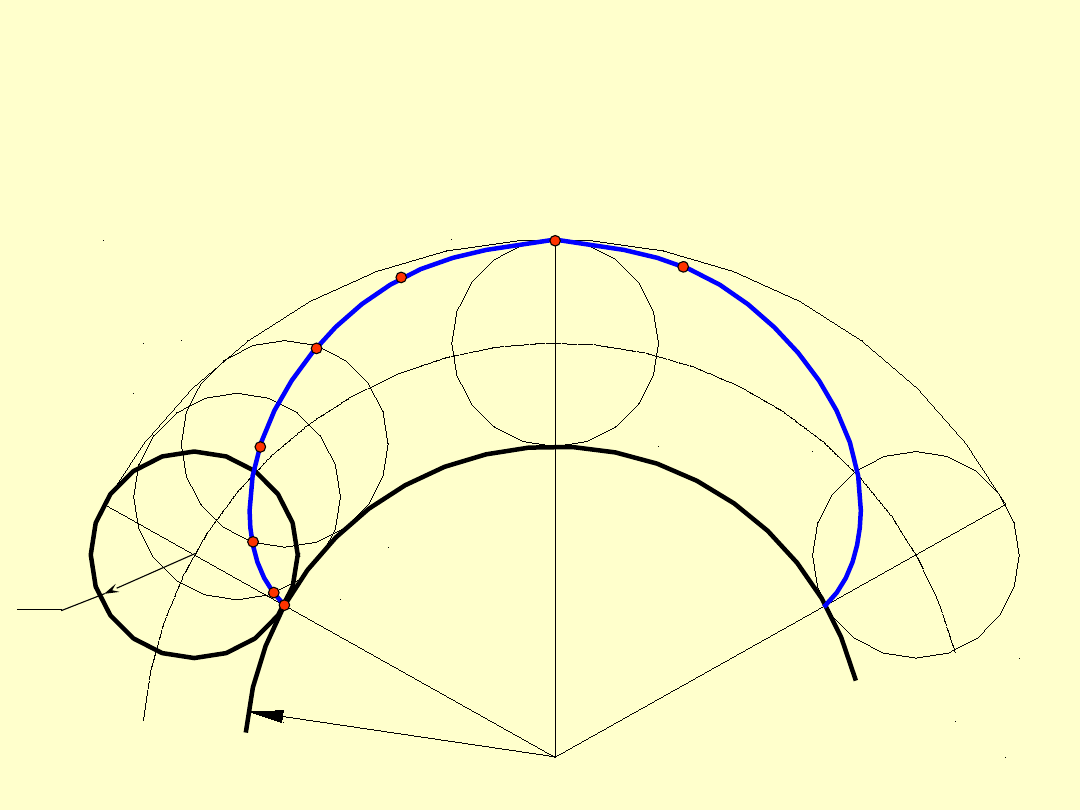
b) Epicykloida - uzyskuje się ją wówczas, gdy koło

odtaczające



toczy się po zewnętrznej części koła

zasadniczego

r

z

.

r

z



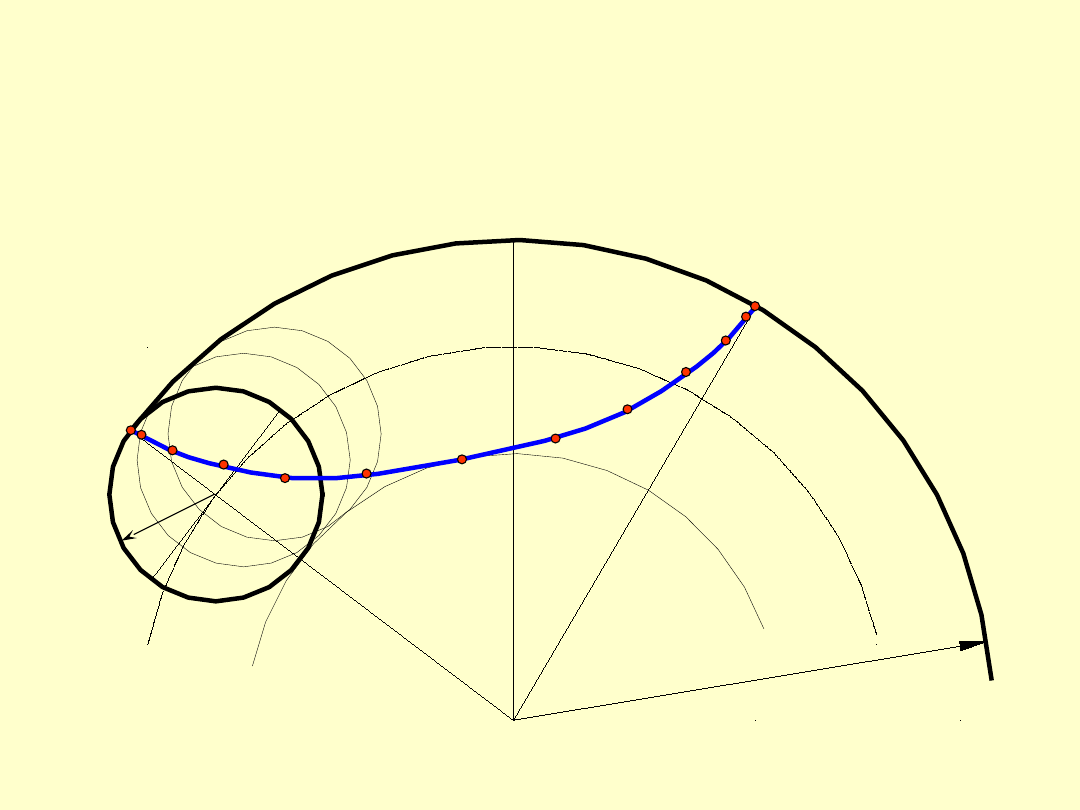
c) Hipocykloida - uzyskuje się ją wówczas, gdy koło

odtaczające



toczy się po wewnętrznym torze koła

zasadniczego

r

z

.

r

z

O



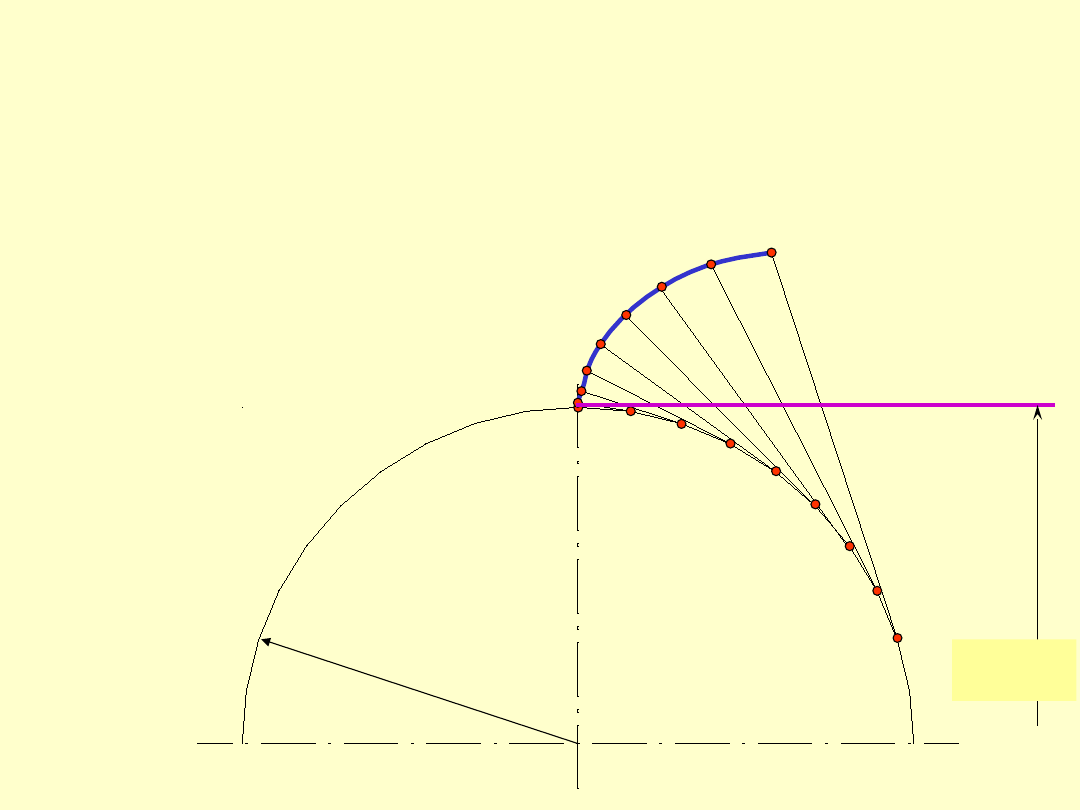
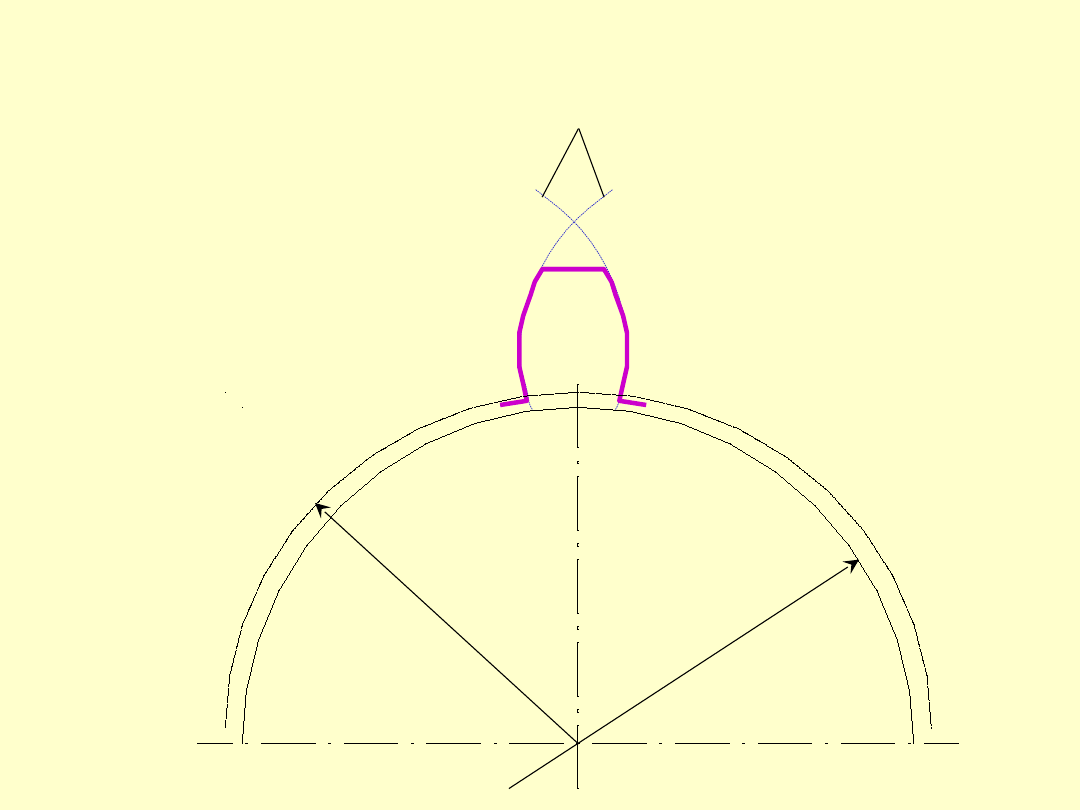
d) Ewolwenta zwyczajna - (odwinięcie koła) jako

szczególny przypadek cykloidy uzyskuje się, gdy
prosta toczy się po torze kołowym (kole
zasadniczym)

r

z

. W danym przypadku promień koła

odtaczającego



=



.

1 2

3

4

5

6

7

8

r

z



=



0

d

f

r

z

ewolwenta

ZASADA ZAZĘBIENIA (zasada

Willisa)

Z kinematycznego punktu widzenia od
zazębienia wymaga się równomierności
przenoszenia ruchu obrotowego.

Z tego zadania wynika główna zasada
zazębienia.

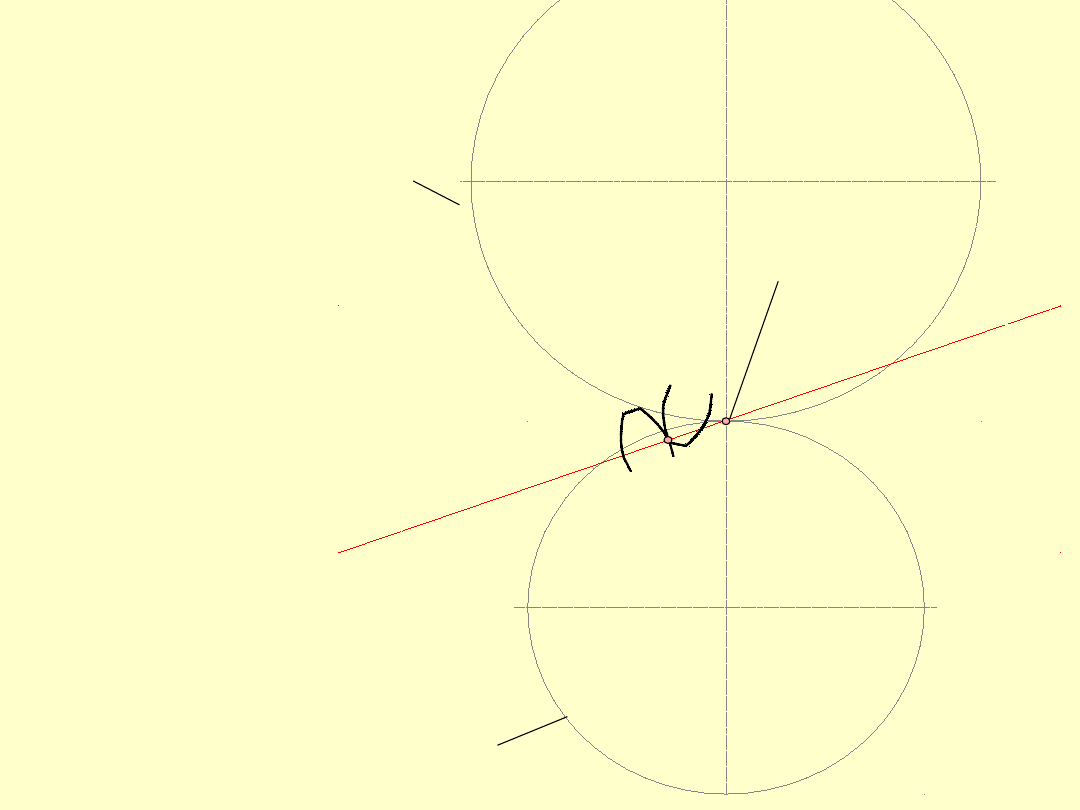
Prosta normalna do boku zęba w
punkcie

styku

B

zębów

kół

współpracujących musi przechodzić
przez punkt styku kół tocznych.

styczna do boku
zęba w punkcie

B

normalna do boku
zęba w punkcie

B

B

Prosta normalna do boku zęba

B

KT

1

KT

2

wspólna normalna
do zarysów zębów
w punkcie ich styku

punkt styczności kół
tocznych

Aby dwa zarysy współpracujących ze
sobą zębów miały wspólną normalną w
punkcie ich styku to muszą być one
utworzone

przez

to

samo

koło

odtaczające.

W przypadku zarysu ewolwentowego
kołem odtaczającym jest linia prosta, a
więc ten warunek zawsze jest spełniony.

Dowód
:

Koła

1

i

2

obracają się dokoła swoich

środków

O

1

i

O

2

w ten sposób, że ich zęby

pozostają w stałym styku. Koło

1

obracając się z chwilową prędkością



1

,

wskutek styku zębów w punkcie

B

, nadaje

kołu

2

chwilową prędkość



2

.

Równocześnie

zgodnie

z

zasadami

kinematyki otrzymujemy w punkcie

B

chwilowe prędkości obwodowe

V

1

i

V

2

.

1

1

1

B

r

ω

V





2

2

2

B

r

ω

V





(1
)

(2
)

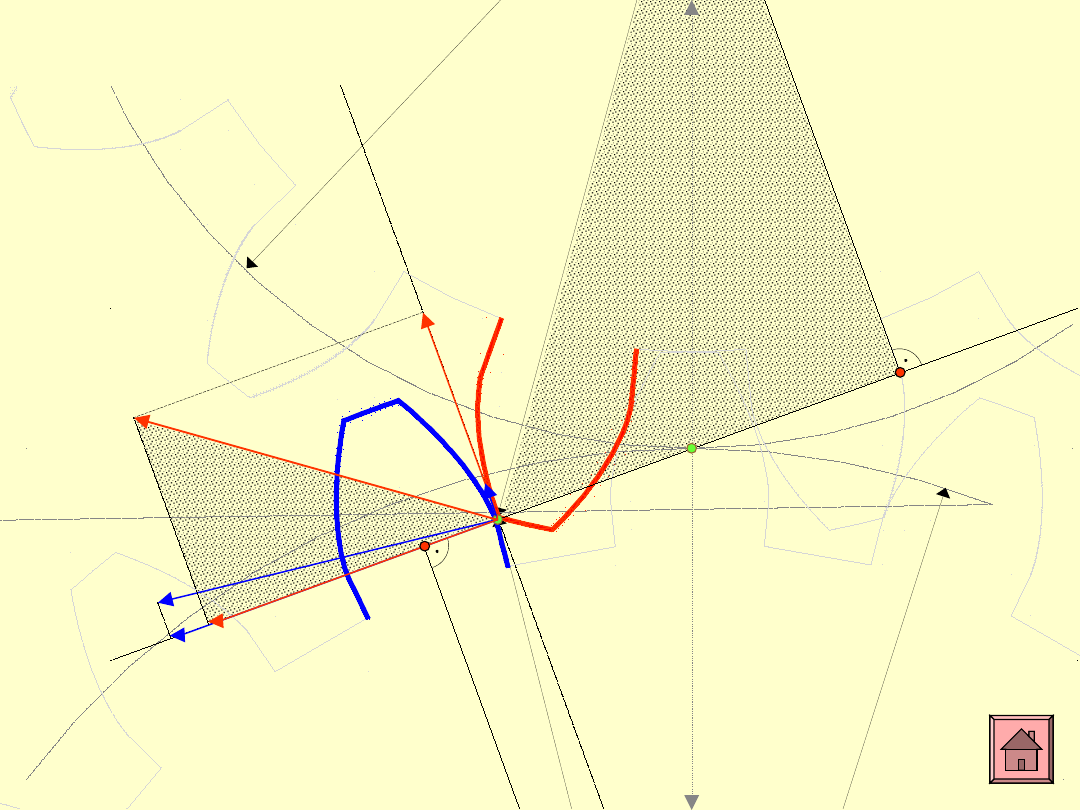
B

O

1

O

2

KT

1

KT

2

r

1

r

2

r

B1

r

B2

C

r

z1

r

z2

N

2

N

1

V

1

V

2

H

D

E

F

C

1

W

1

C

2

W

2

Prędkości obwodowe

V

1

i

V

2

można

rozłożyć na składowe styczne do boków
zębów

W

1

i

W

2

oraz prostopadłe do nich

C

1

i

C

2

.

Rozpatrzmy podobne do siebie
trójkąty:

O

1

N

1

B będzie podobny do

BDH

O

2

N

2

B będzie podobny do

BEF

Z podobieństwa trójkątów wynika, że
stosunki podobnych boków muszą być
takie same.

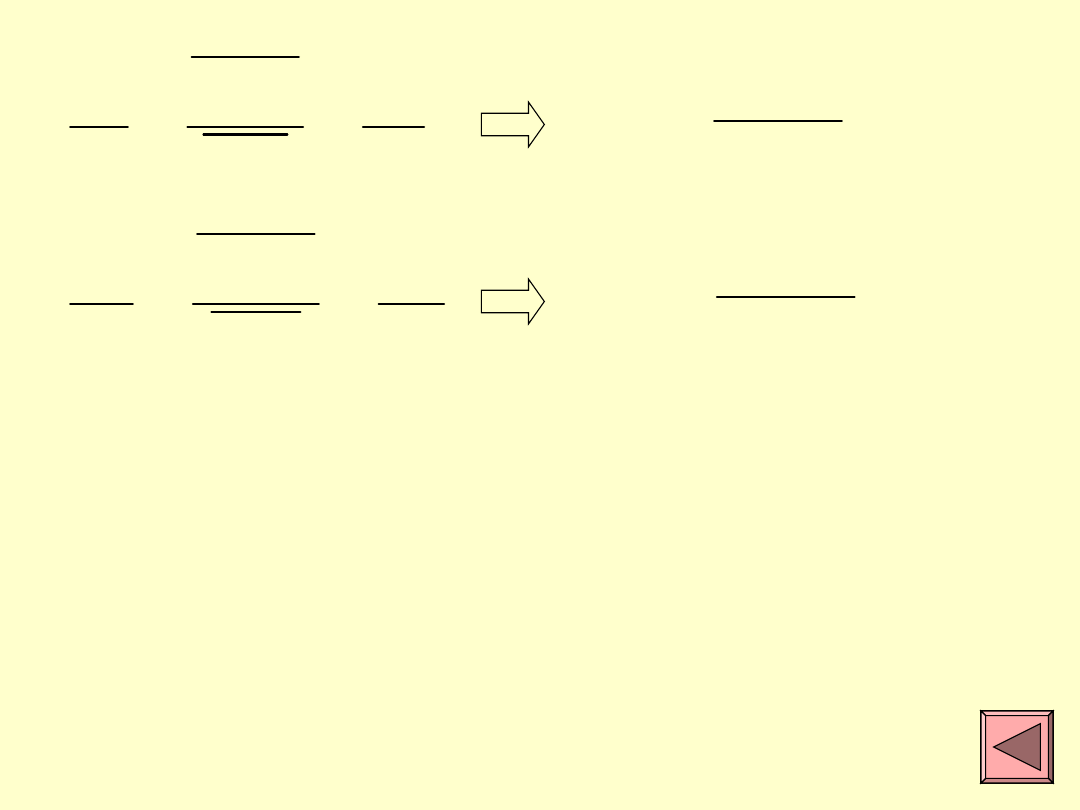
1

1

1

1

1

1

1

B

z

r

r

B

O

N

O

V

C





1

1

1

1

B

z

r

r

V

C





2

2

2

2

2

2

2

B

z

r

r

B

O

N

O

V

C





2

2

2

2

B

z

r

r

V

C





(4
)

(3
)

Ponieważ zgodnie z założeniem zęby
powinny być w ciągłym styku przeto musi
być spełniony warunek:

2

1

C

C 

(5
)

W przypadku gdy C

1

< C

2

wówczas ząb

koła drugiego „wyprzedzałby” ząb koła
pierwszego, a to jest absurdem.

W przypadku przeciwnym, gdy C

1

> C

2

,

ząb koła pierwszego „wciskałby” się w
ząb koła drugiego, co również jest
nonsensem.

Po zestawieniu wzorów (3), (4) i (5)
otrzymamy:

2

2

2

1

1

1

B

z

B

z

r

r

V

r

r

V







(6)

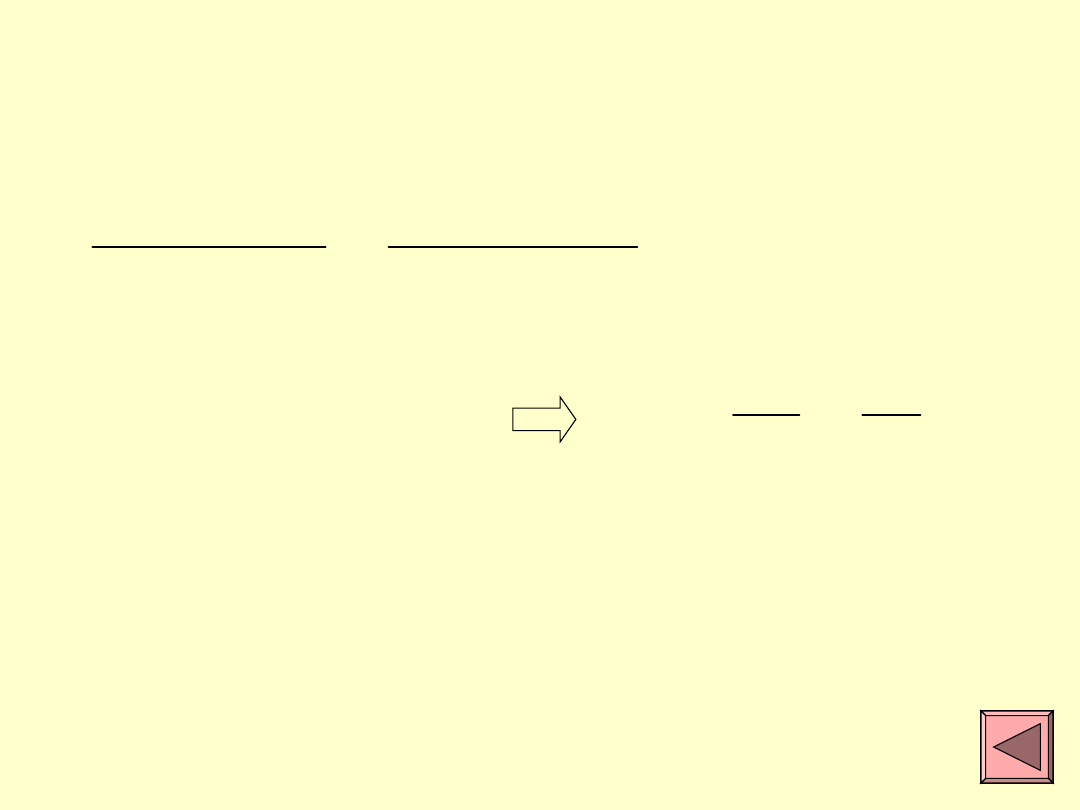
Po podstawieniu do wzoru (6) zależności
(1) i (2) uzyskuje się:

2

2

2

2

1

1

1

1

B

z

B

B

z

B

r

r

ω

r

r

r

ω

r



















2

1

2

1

ω

r

ω

r

z

z







1

2

2

1

z

z

r

r

ω

ω

i





Rozpatrzmy podobne do siebie trójkąty
O

1

N

1

C i O

2

N

2

C.

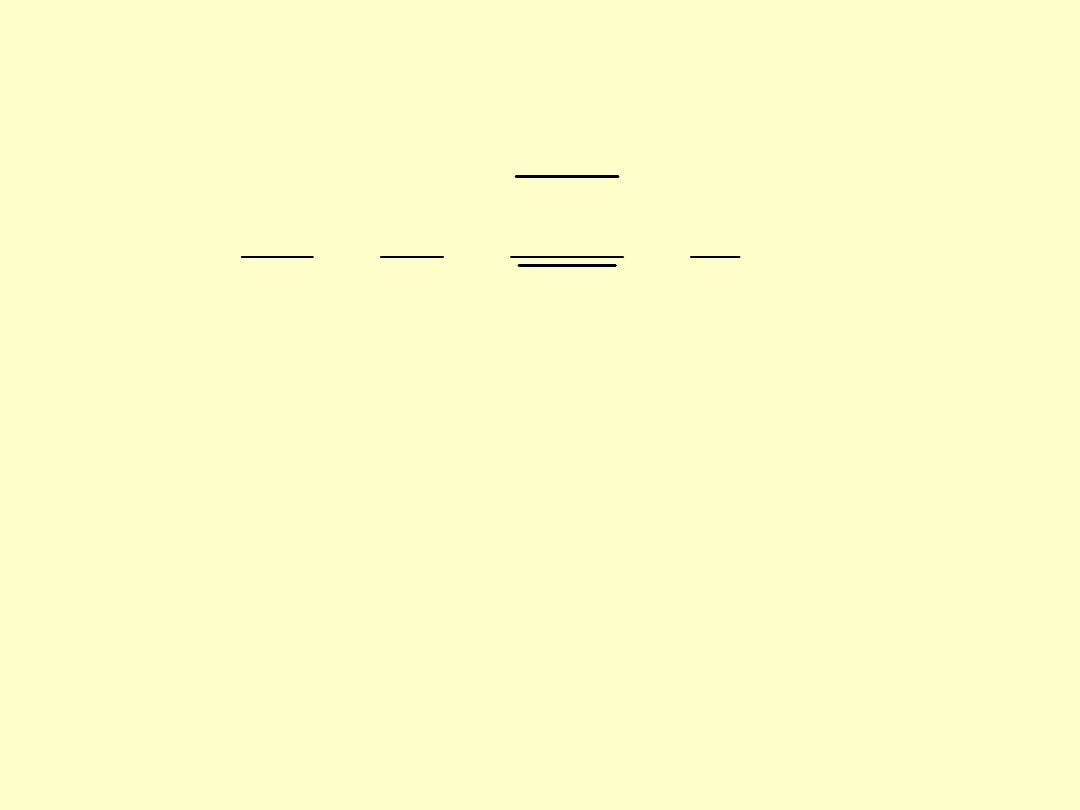
Ponieważ

r

z1

i

r

z2

są bokami podobnymi do

siebie trójkątów przeto możemy napisać:

1

2

1

2

2

1

1

2

r

r

C

O

C

O

r

r

ω

ω

i

z

z









Wynika stąd, że linia łącząca średnice kół
zębatych O

1

i O

2

została podzielona przez

punkt

C

proporcjonalnie do prędkości

kątowych



1

i



2

.

Stosunek



1

/



2

wyraża zaś przełożenie

kinematyczne

i

przekładni, a zatem

można sformułować już podstawową
zasadę zazębienia, tzw. zasadę Willisa.

Jeżeli

przełożenie

kinematyczne

i

przekładni ma pozostać niezmienne, to
stosunek promieni kół tocznych

r

1

do

r

2

również musi pozostawać niezmienny, a
więc przy stałych obrotach osi kół

O

1

i

O

2

,

punkt

C

musi pozostać stale w tym

samym miejscu.

Punkt styczności kół tocznych

C

nosi

nazwę

centralnego punktu zazębienia

lub

bieguna zazębienia

.

Punkt

C

wynika z przecięcia odcinka z

linią łączącą środek kół

O

1

O

2

wobec czego

udowodniliśmy twierdzenie postawione
na początku.

2

N

N

1

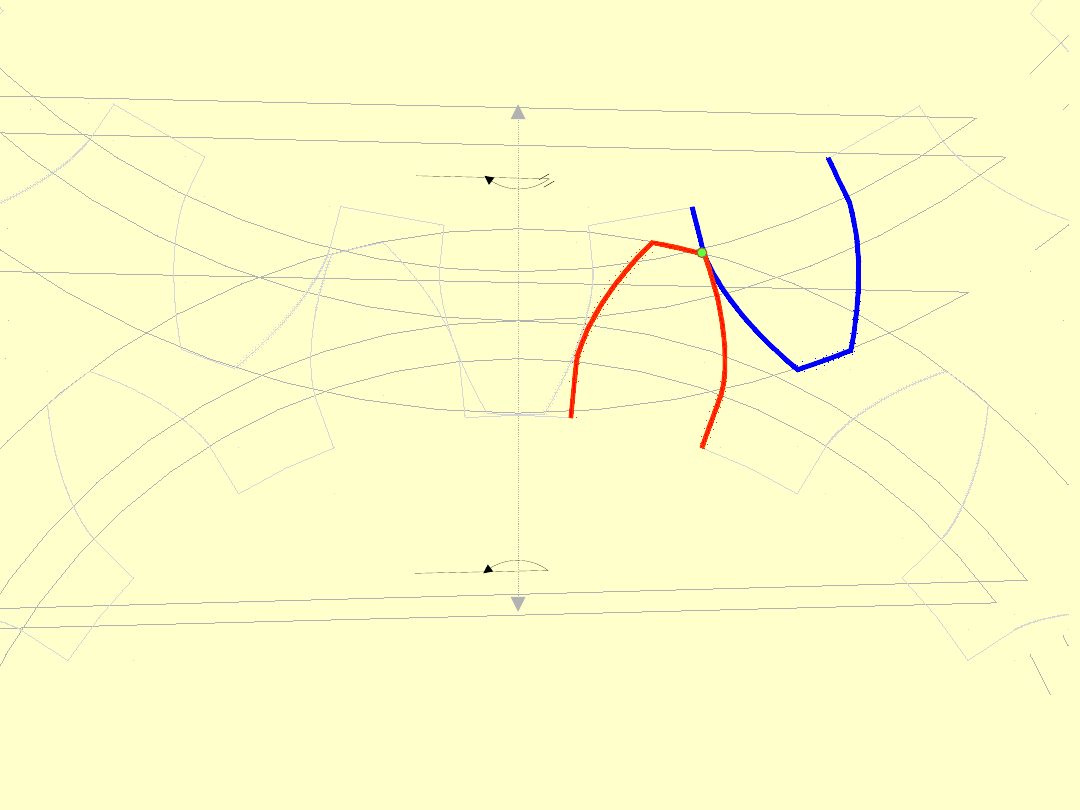
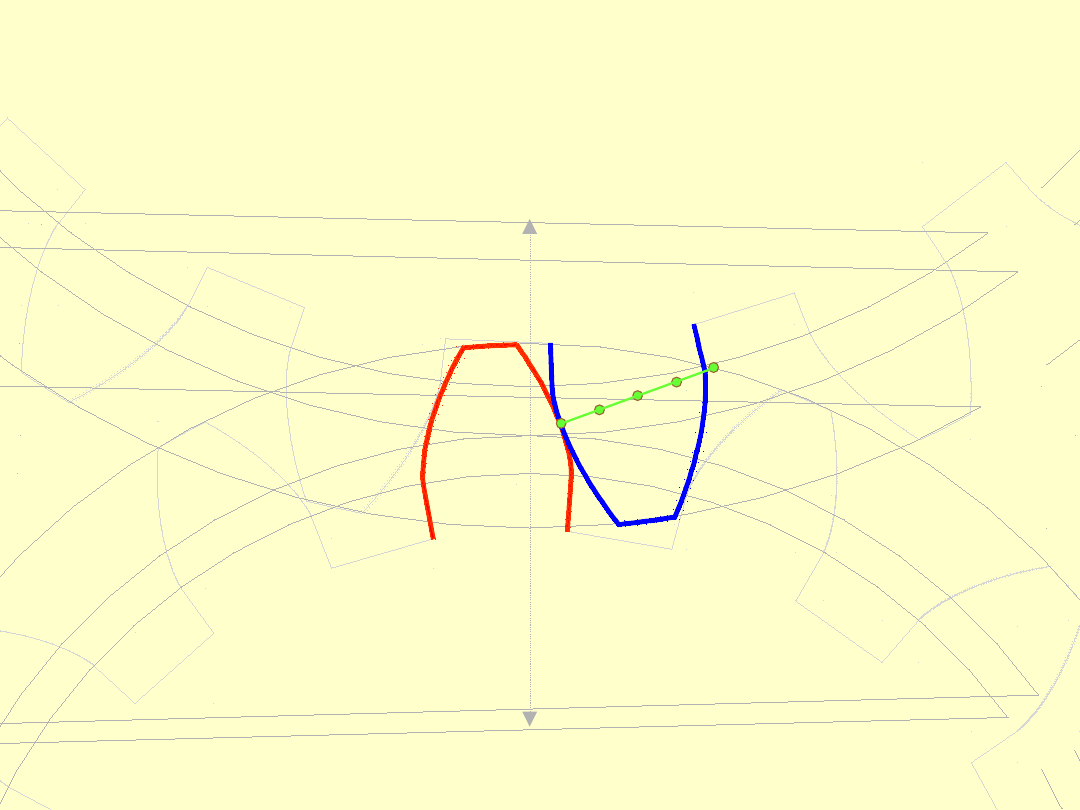
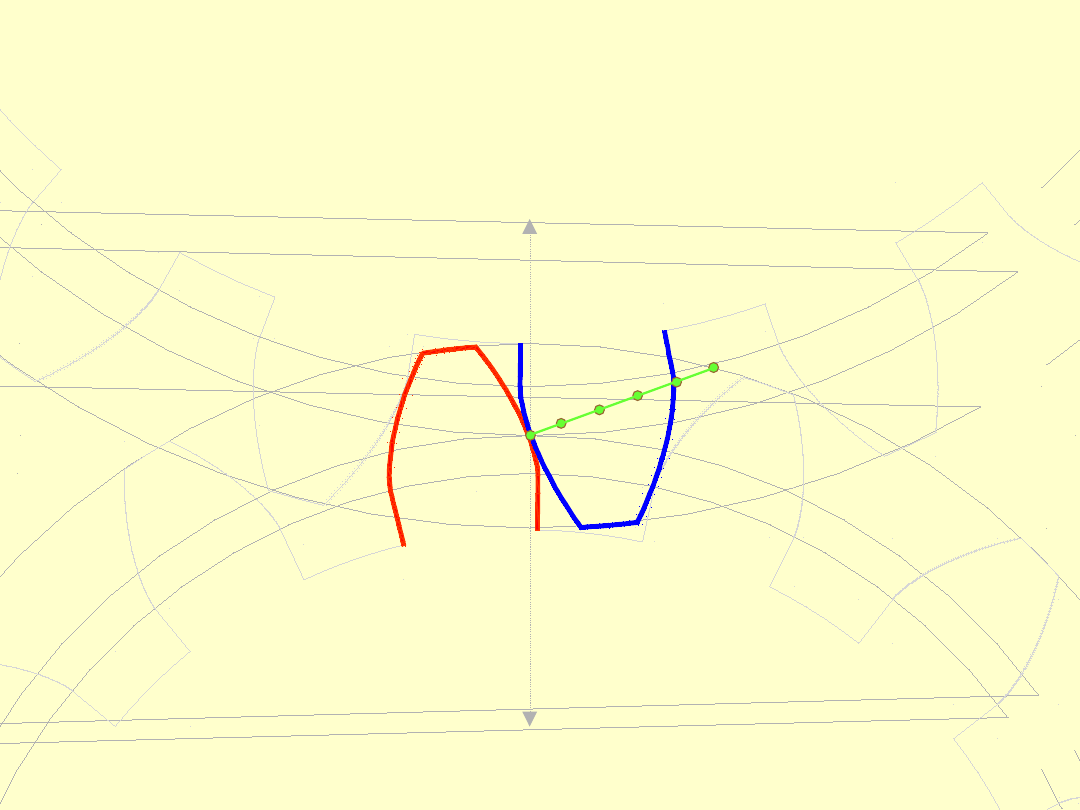
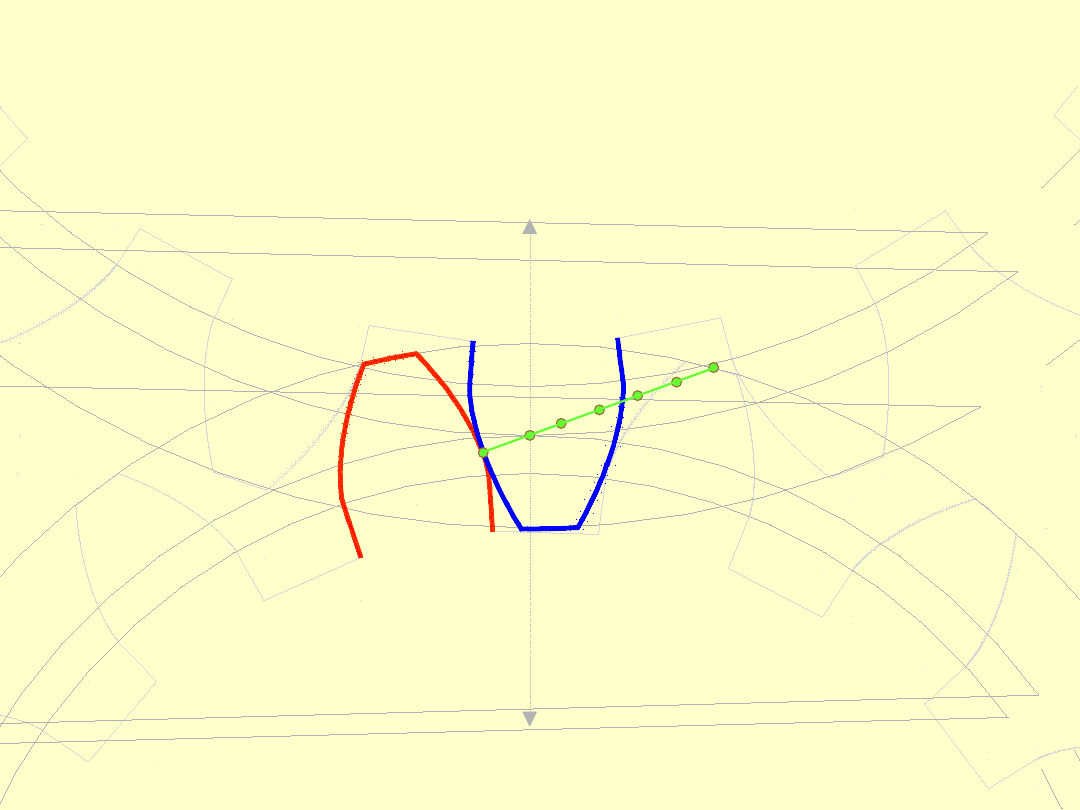
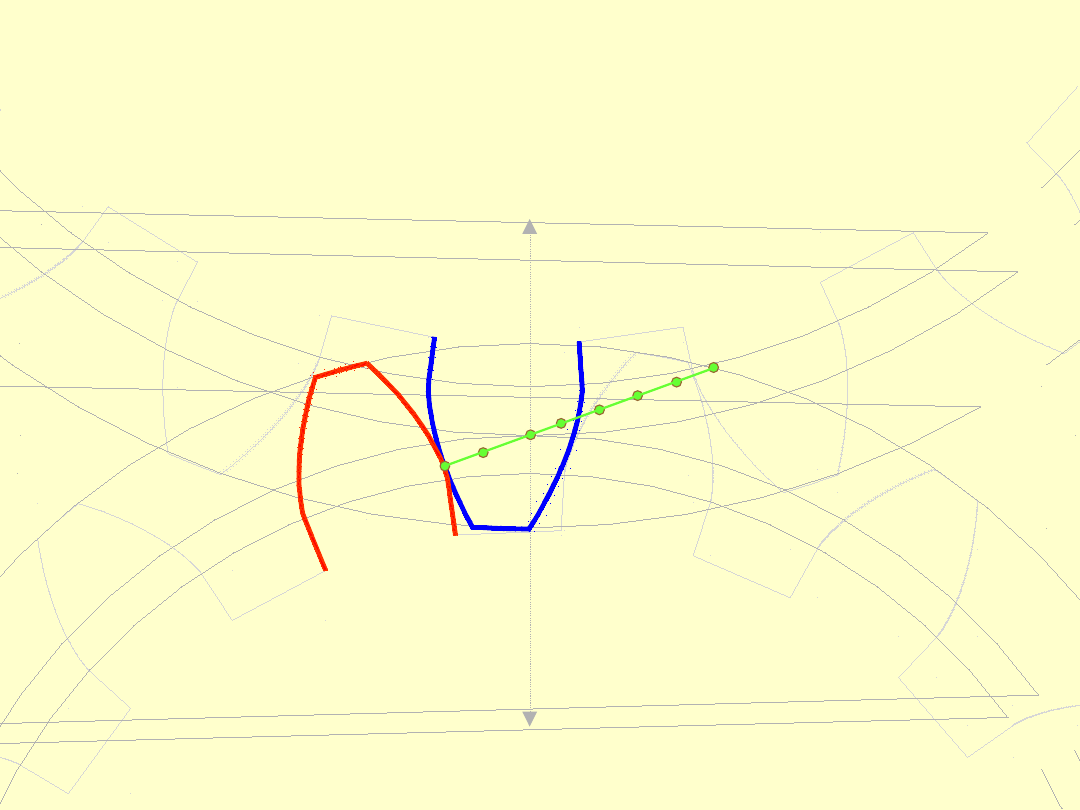
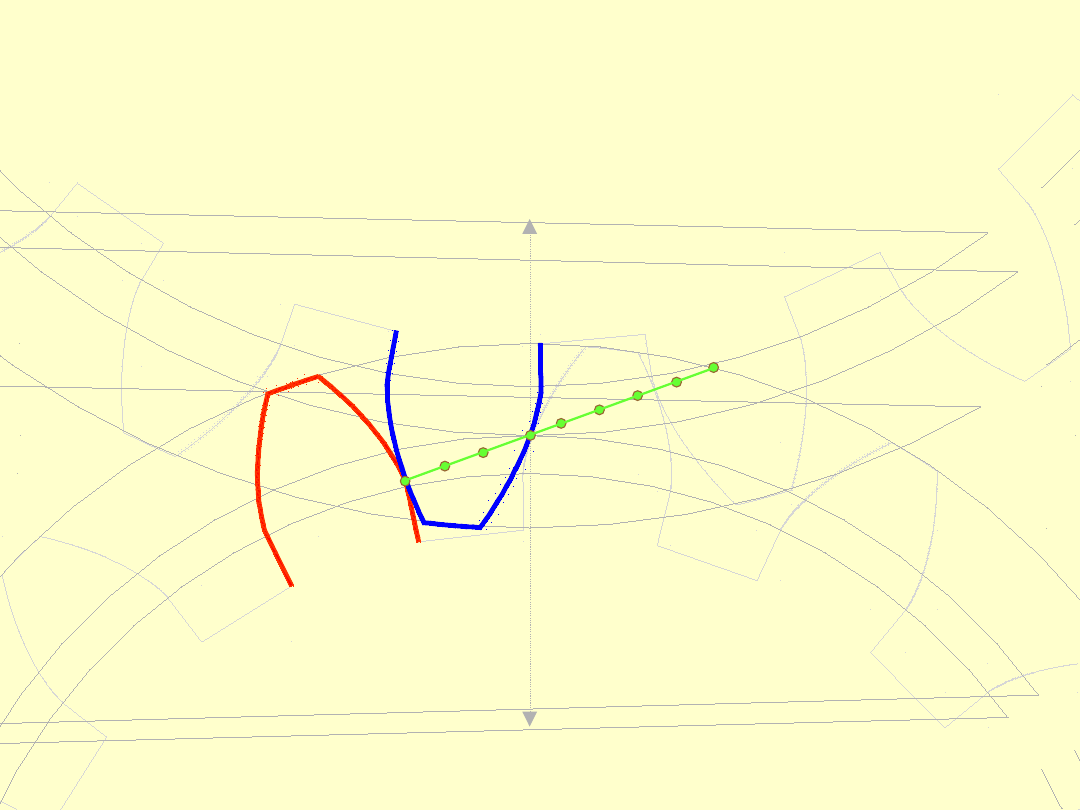
Linią przyporu

(linia zazębienia)

nazywamy

miejsce

geometryczne

wszystkich punktów styku (przyporu)
zębów podczas zazębiania.

LINIA PRZYPORU

O

2

O

1



2



1

E

1

O

2

O

1



2



1

O

2

O

1



2



1

O

2

O

1



2



1

O

2

O

1



2



1

O

2

O

1



2



1

C

O

2

O

1



2



1

O

2

O

1



2



1

O

2

O

1



2



1

O

2

O

1



2



1

O

2

O

1



2



1

E

2

E

1

O

2

O

1



2



1

E

2

C

linia

przyporu

Weźmy pod uwagę współpracę dwóch zębów.

Zęby te stykają się ze sobą po raz pierwszy w punkcie

E

1

, gdzie stopa zęba koła

1

(napędzającego) spotyka

się po raz pierwszy z wierzchołkiem zęba koła

2

(napędzanego). Jest to pierwszy z punktów przyporu
wykorzystywany w danym zazębieniu.
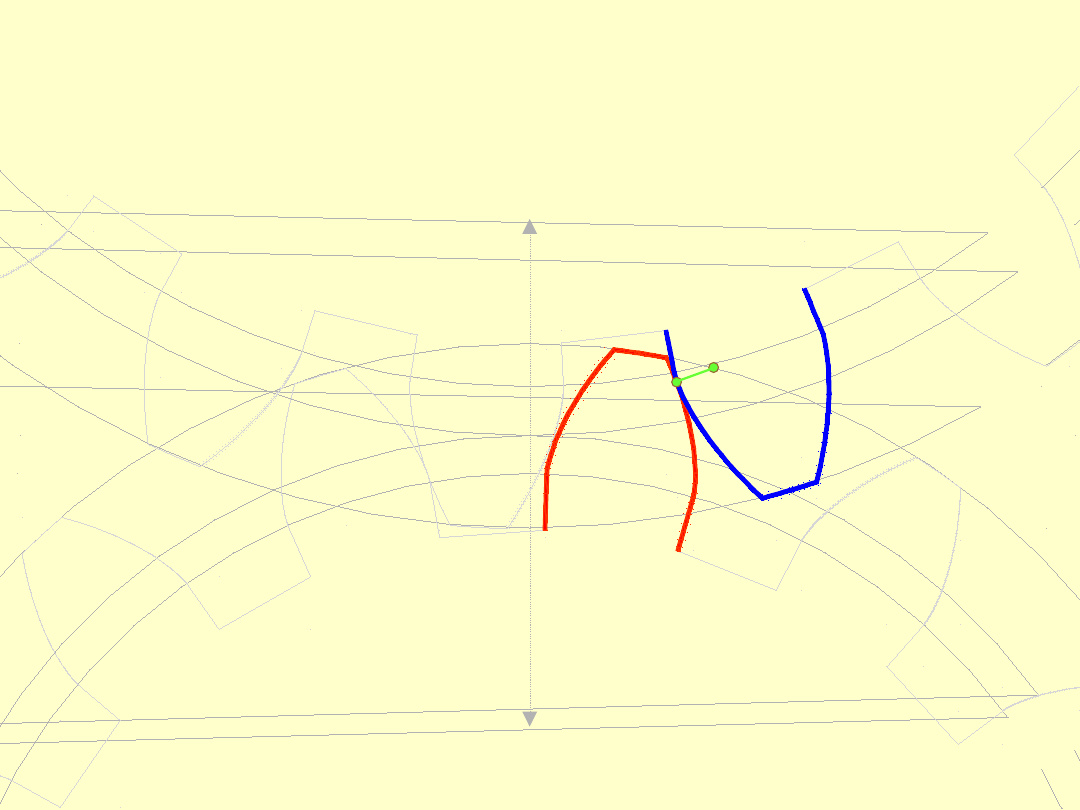
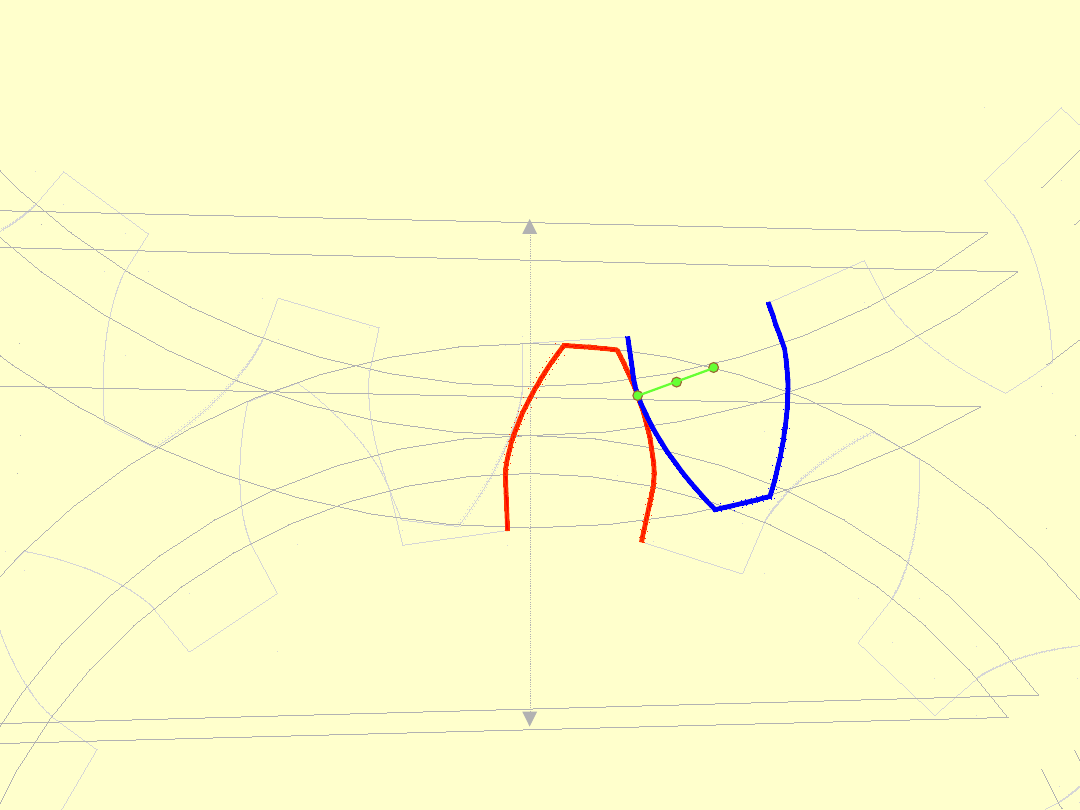
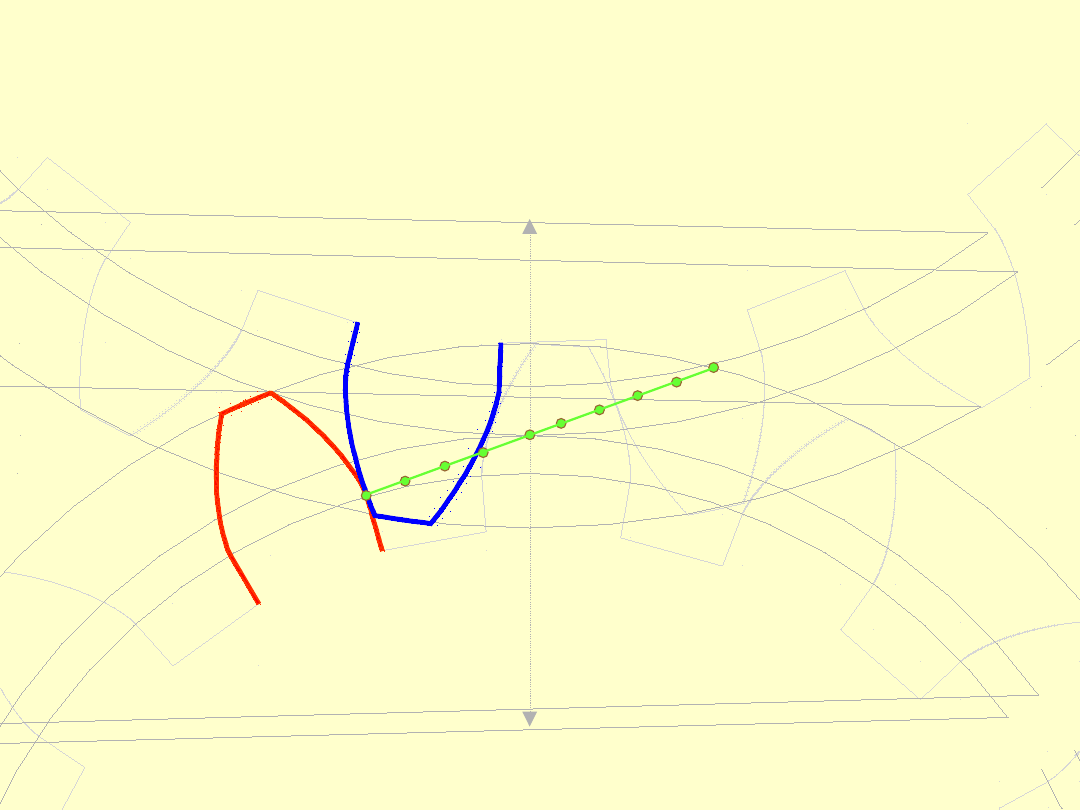
Następnie punkt ten przesuwa się zajmując położenia
pośrednie. Trajektoria tego punktu nazywa się linią
przyporu.

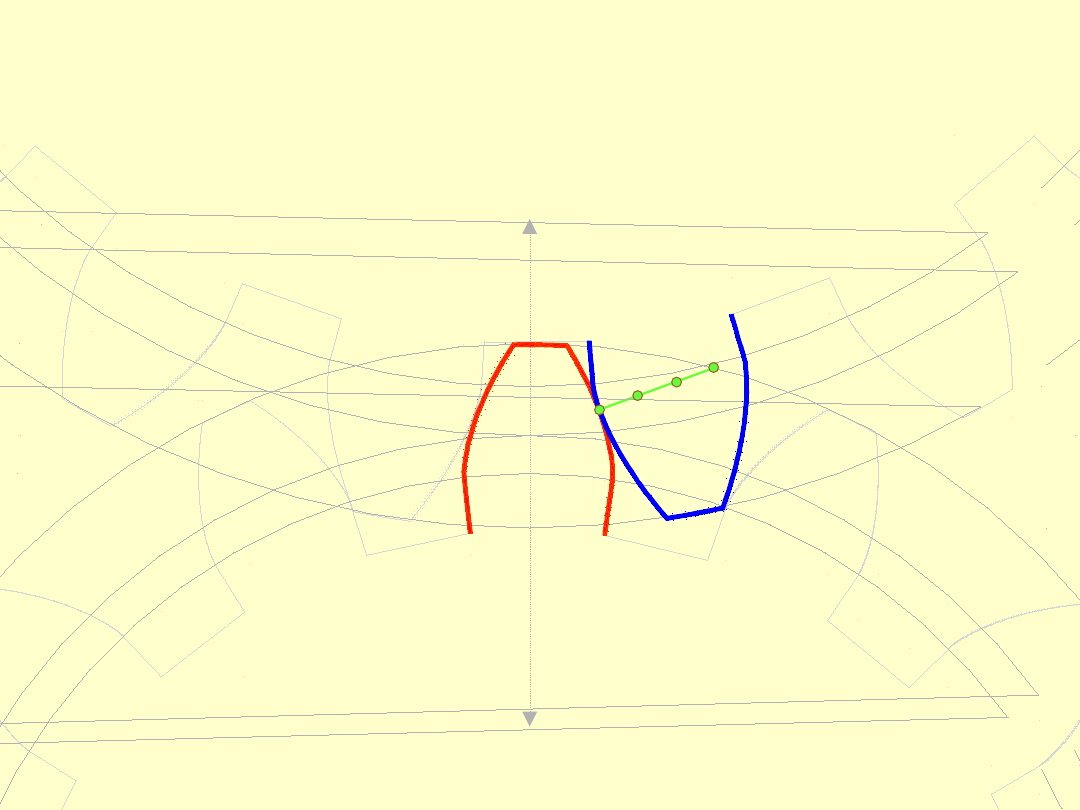
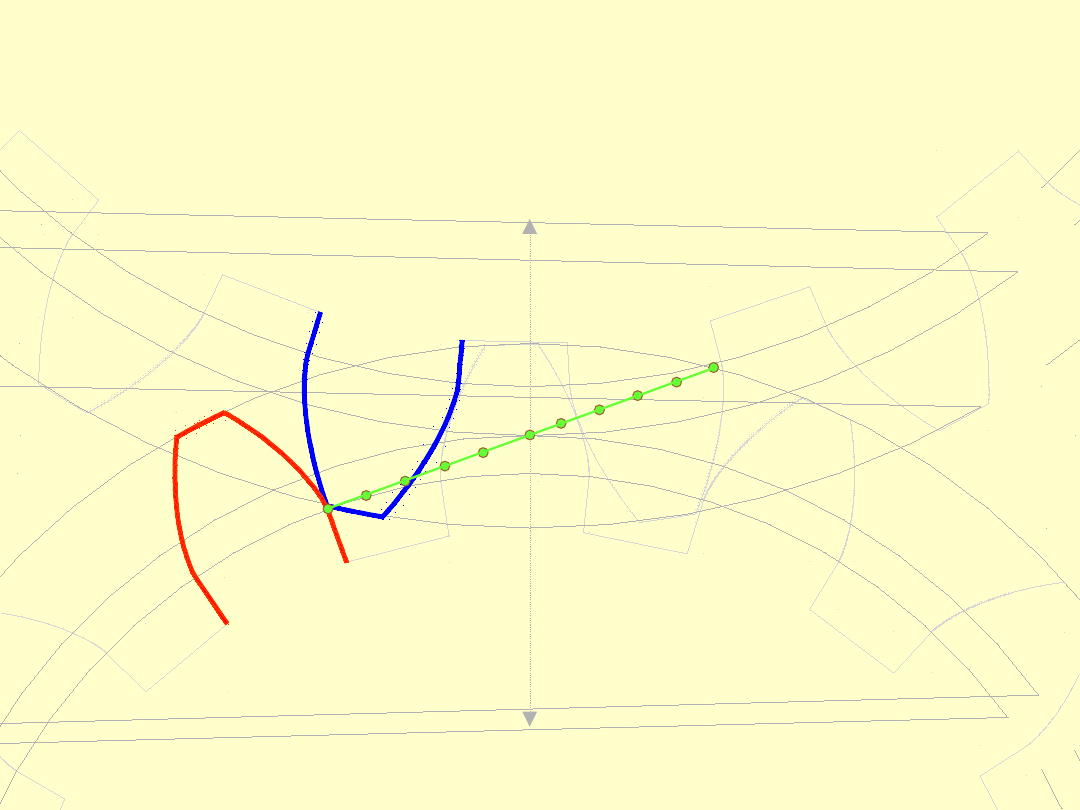
Ostatnim punktem przyporu jest punkt

E

2

, gdzie

wierzchołek zęba koła

1

„rozstaje się” ze stopą zęba

koła

2

.

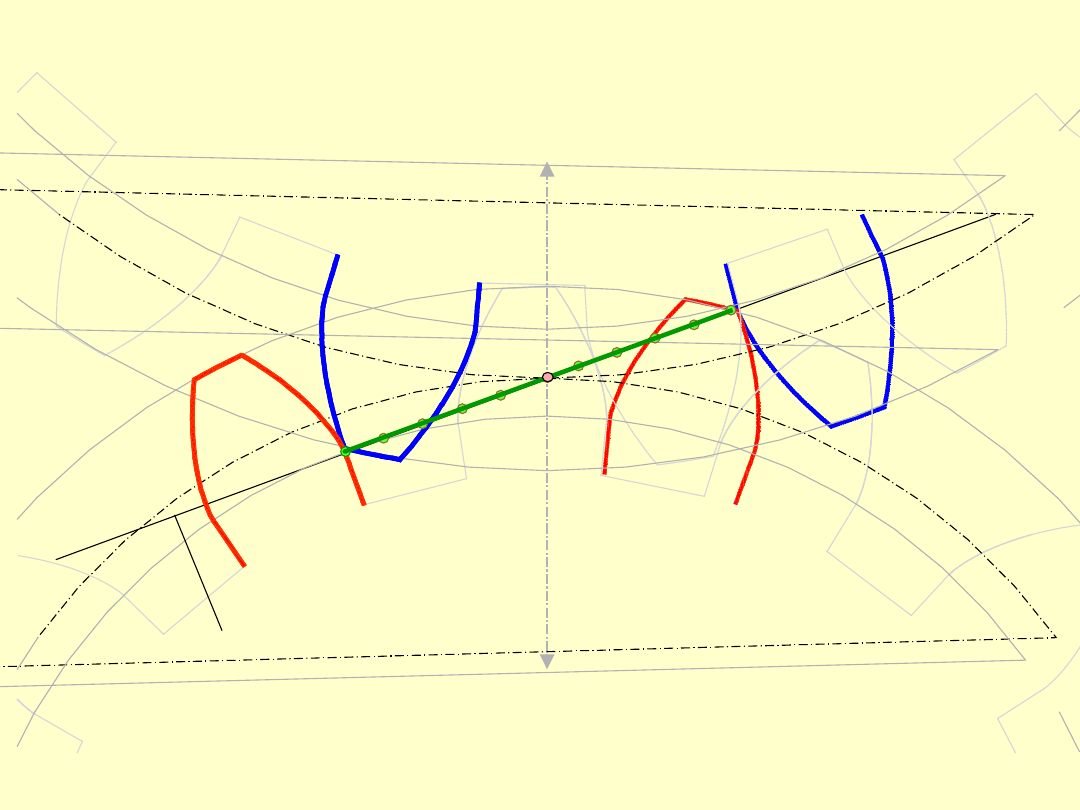
Odcinek linii przyporu nazywa się odcinkiem
przyporu.

2

1

E

E

Kąt zawarty między wspólną normalną do

zarysów zębów w punkcie styku zębów

B

a

styczną do kół tocznych nazywa się kątem
przyporu



.

O

2

O

1

wspólna normalna
do zarysów

styczna do kół
tocznych



KT1

KT2

B

C

linia przyporu

Kąt przyporu

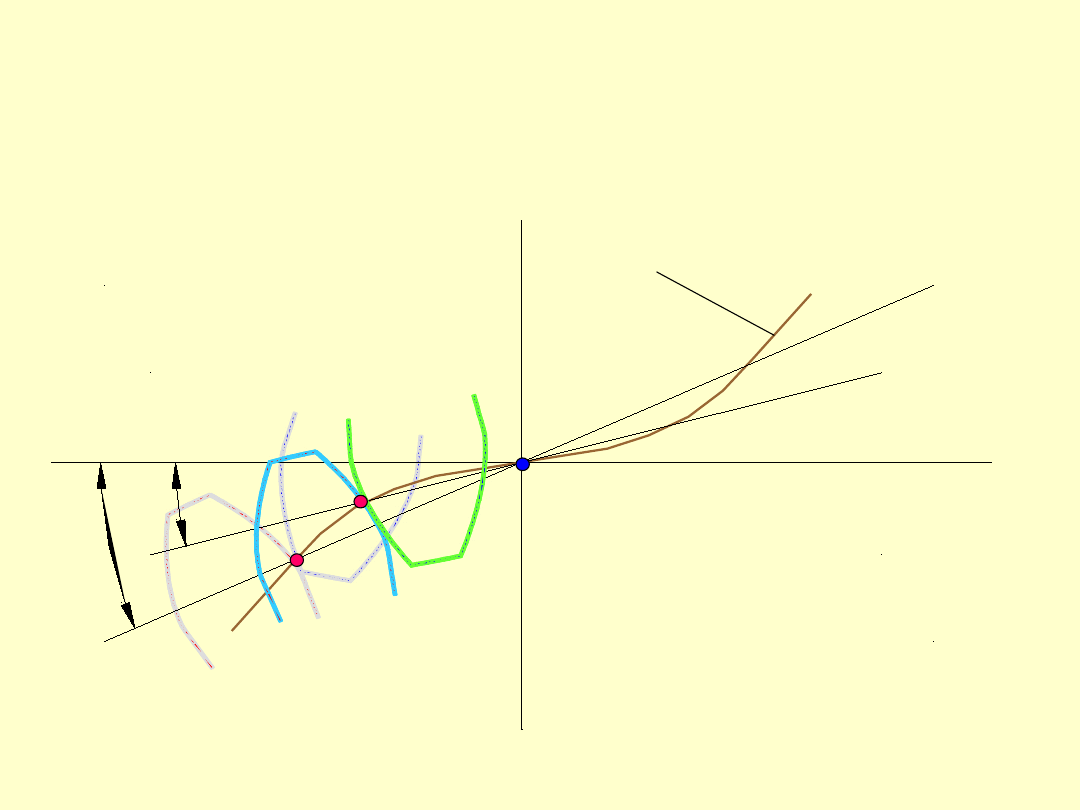
Jeżeli linia przyporu jest krzywoliniowa to
kąt przyporu jest zmienny.

B



B



A

C

O

2

O

1

linia przyporu

A

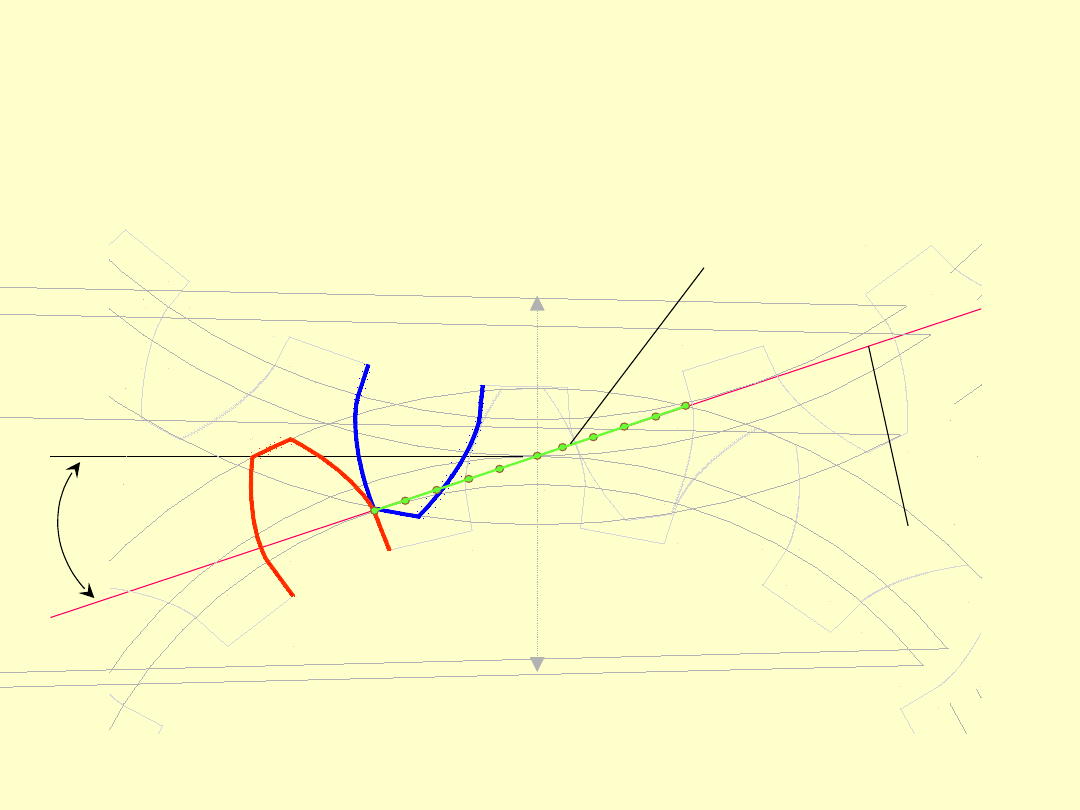
Jeżeli linia przyporu jest prostą to
wyznacza ona również kierunek wspólnej
normalnej do zarysów, a zatem kąt
przyporu jest stały



= const.

O

2

O

1



2



1

E

2



=

const.

wspólna
normalna do
zarysów

linia przyporu

E

1

C

Z

warunku

ciągłości

zazębienia

niezbędne jest aby jedna para zębów
wychodząc

z

zazębienia

została

zastąpiona przez następną parę zębów.

O tym decyduje tzw. liczba przyporu
(wskaźnik przyporu, stopień pokrycia).

Rozpatrzmy współpracę dwóch zębów.

LICZBA PRZYPORU

(wskaźnik przyporu, stopień

pokrycia)

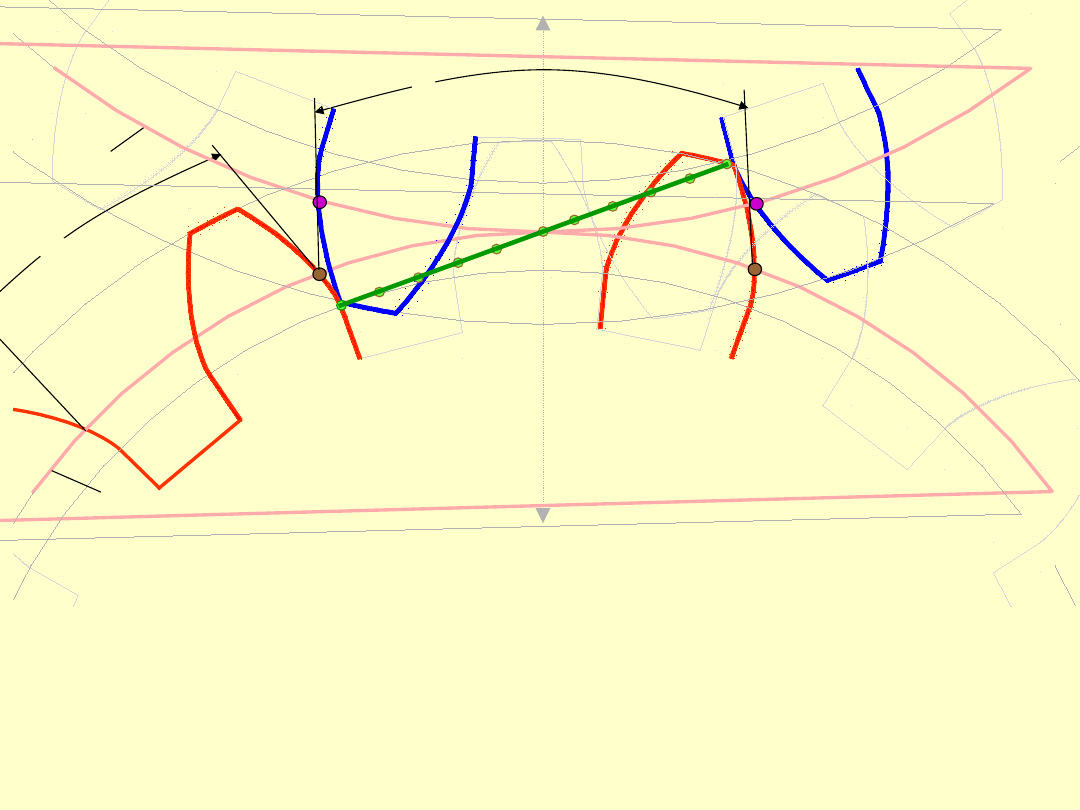
l



W czasie, gdy punkt przyporu przejdzie z
punktu

E

1

do punktu

E

2

, to punkt

A

1

, znajdujący

się na kole tocznym koła

1

, „przewędruje” w

tym czasie w położenie

A

2

.

E

1

O

2

O

1



2



1

E

2

KT1

A

1

A

2

B

1

B2

KT2

p



Natomiast punkt

B

1

, znajdujący się na kole

tocznym koła

2

, „przewędruje” w tym czasie w

położenie

B

2

.

Każdej długości odcinka przyporu

E

1

,

E

2

odpowiada łuk zazębień

A

1

A

2

i

B

1

B

2

mierzony

na okręgach kół tocznych.

Każdej długości odcinka przyporu

E

1

,

E

2

odpowiada łuk zazębień

A

1

A

2

i

B

1

B

2

mierzony

na okręgach kół tocznych.

A

1

A

2

= B

1

B

2

= l

Aby każda para zębów została w czasie pracy
zastąpiona przez następną parę zębów w
sposób ciągły to łuk zazębienia

l

musi być

większy od podziałki tocznej

p

mierzonej na

kole tocznym.

Liczba przyporu



(stopień pokrycia,

wskaźnik przyporu) jest to stosunek łuku
zazębienia

l

do podziałki tocznej

p

:

Liczba przyporu określa średnią liczbę
par

zębów

równocześnie

współpracujących.



p

l

ε





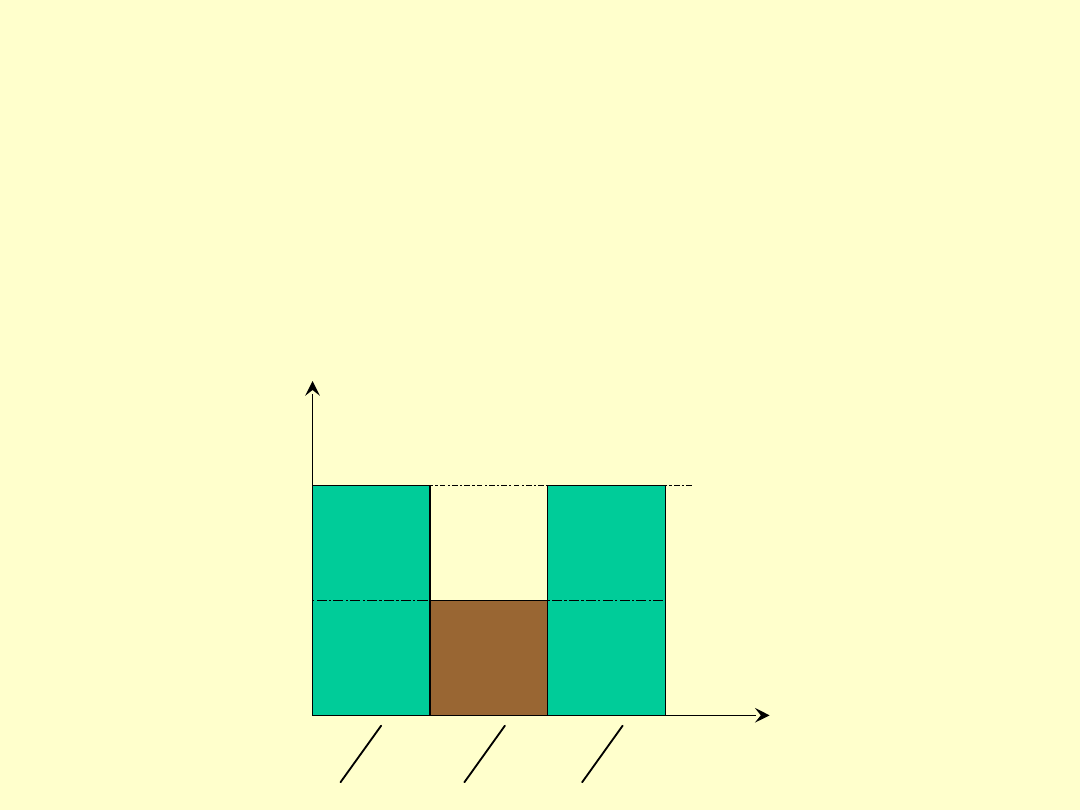
Jeżeli liczba przyporu



=1.5

, wówczas

każda para zębów pracuje przez 1/3 łuku
zazębienia samotnie, a na początku i
końcu łuku zazębienia współpracują dwie
pary zębów, również przez 1/3 łuku
zazębienia.

liczba
par
zębów

1

2

łuk
zazębienia

3

1

3

1

3

1

Uogólniając: jeżeli

1 <



< 2

, wówczas

odcinek czasu, przez który pracuje tylko
jedna para zębów wynosi (

2-



), a odcinek

czasu, w którym pracują dwie pary zębów
(



-1

).

Natomiast: jeżeli

2 <



< 3

, wówczas

odcinek czasu, przez który pracuje tylko
jedna para zębów wynosi (

3-



), a odcinek

czasu, w którym pracują dwie pary zębów
(



-2

).

Im większa jest liczba przyporu



tym

korzystniejsza (równiejsza) jest praca
przekładni.

POŚLIZG ZĘBÓW

Zjawisko

opisane

różnymi

prędkościami

stycznymi nazywa się

poślizgiem

.

Z rysunku wynika, że zęby ślizgają się po sobie
z prędkości

V

p

= |W

1

-W

2

|

.

Prędkości styczne

W

1

i

W

2

są równe zeru tylko w

punkcie

C

.

Poza tym punktem są one różne, a więc zawsze
występuje ślizganie się zębów.

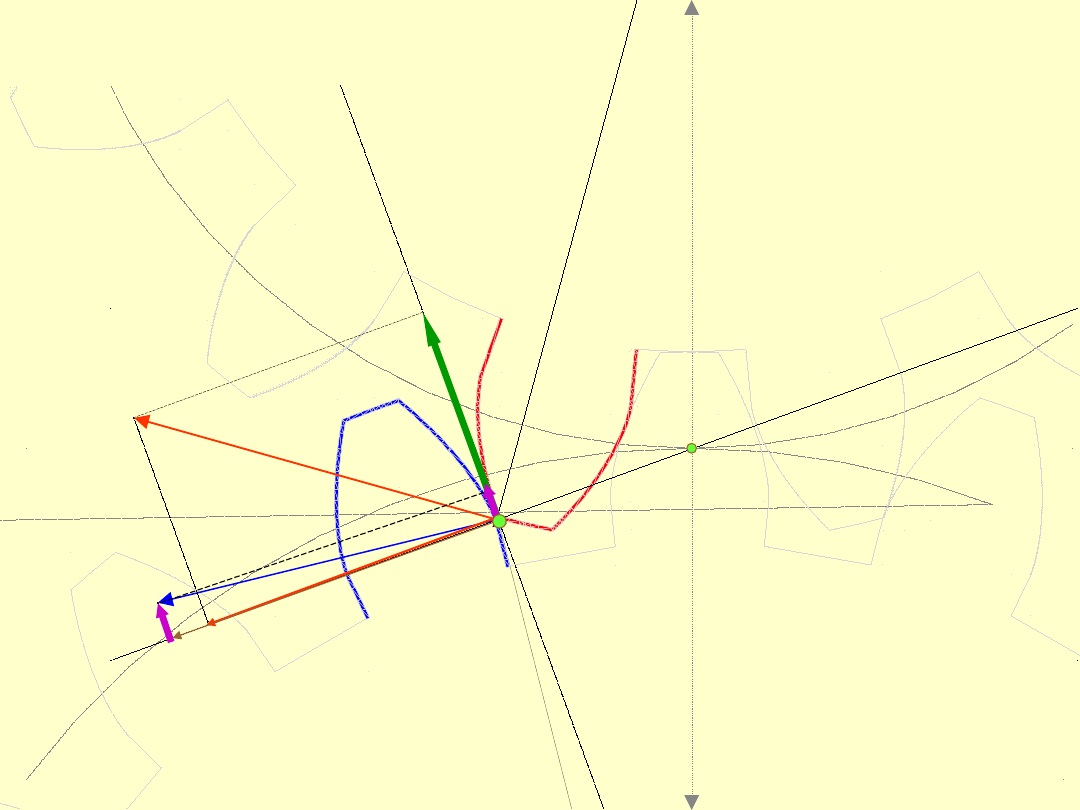
B

O

1

O

2

KT

1

KT

2

r

B1

r

B2

C

V

1

V

2

W

1

W

2

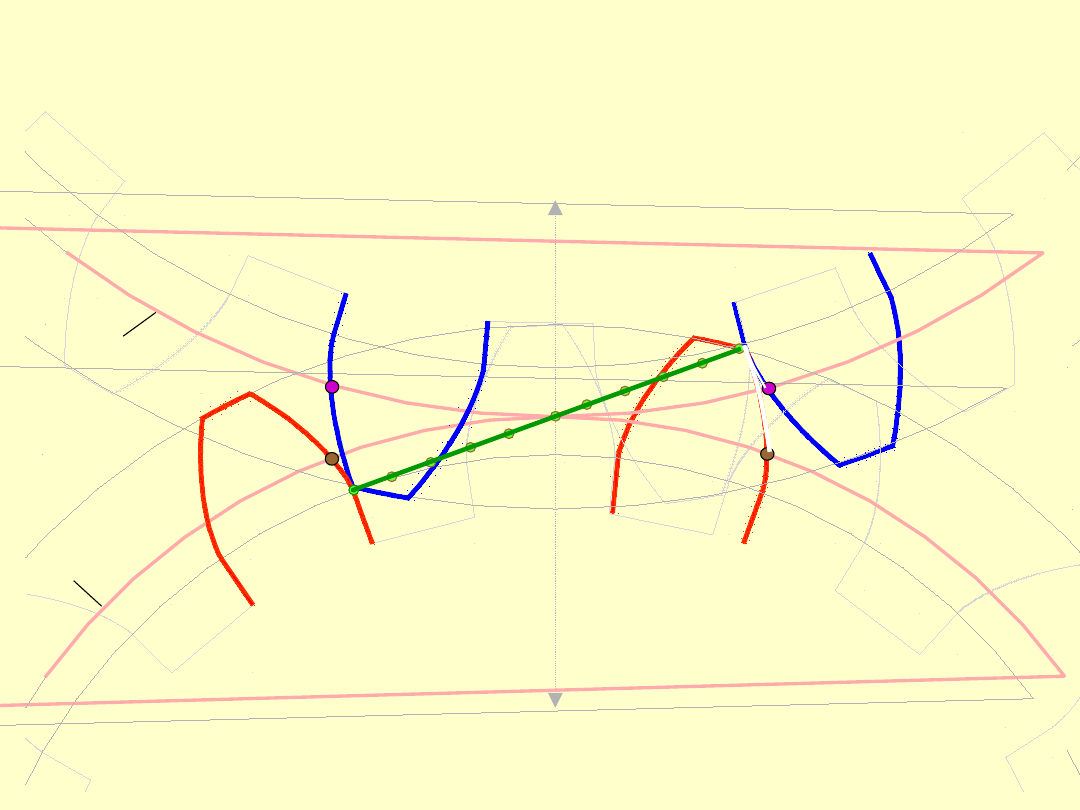
E

1

O

2

O

1



2



1

E

2

KT2

KT1

A

1

A

2

B

1

B

2

Ponieważ

współpracujące

odcinki

zarysów |

E

1

A

1



E

1

B

1

|, to wielkość drogi

poślizgu wyniesie |

E

1

A

1

–

E

1

B

1

|.

Głowa zęba koła

1

ślizga się po stopie

zęba koła współpracującego

2

przy czym

odcinek czynnej wysokości stopy |

E

1

A

1

|

jest mniejszy od czynnej wysokości głowy
|

E

1

B

1

| zęba współpracującego, a zatem

stopa zęba zużywa się silniej niż jego
głowa.

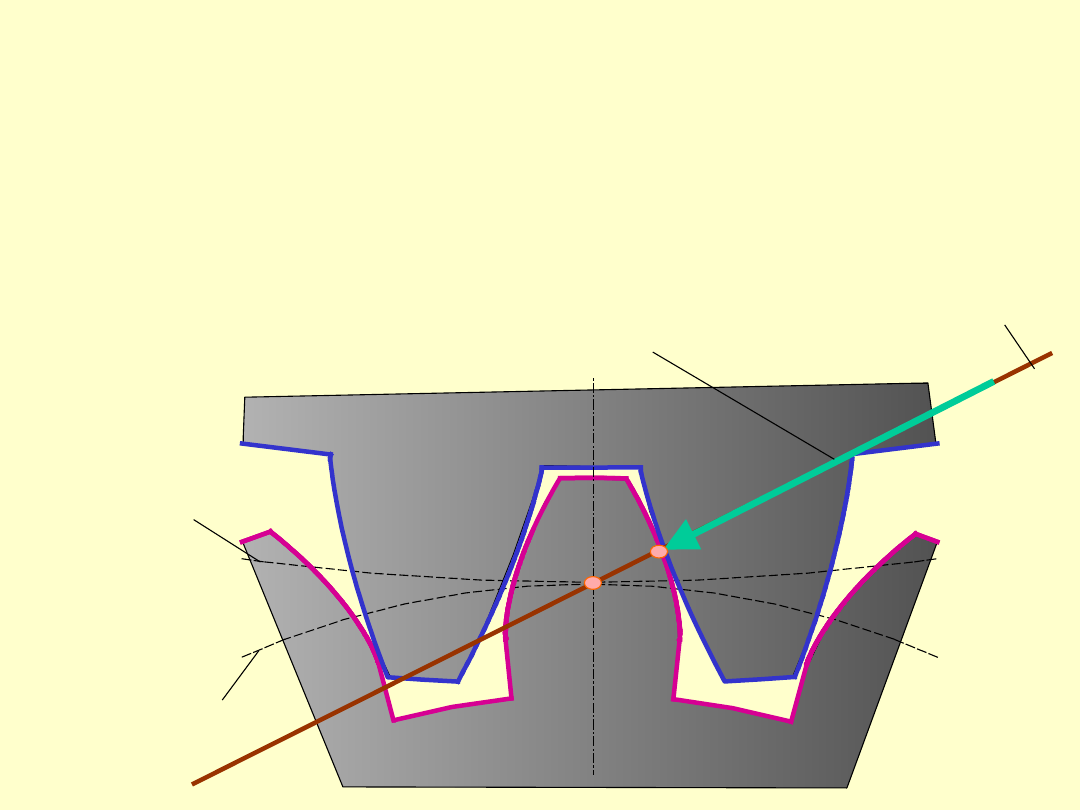
Siły występujące w zazębieniu

Siła wynikająca z oddziaływania jednego zęba
na drugi zawsze działa wzdłuż wspólnej
normalnej do zarysów w punkcie ich styku.

kp

1

kp

2

C

linia przyporu

B

siła miedzyzębna

B

C

O

2

O

1

linia przyporu

A

P

OA

P

OB

P

RA

P

RB

P

NA

P

NB

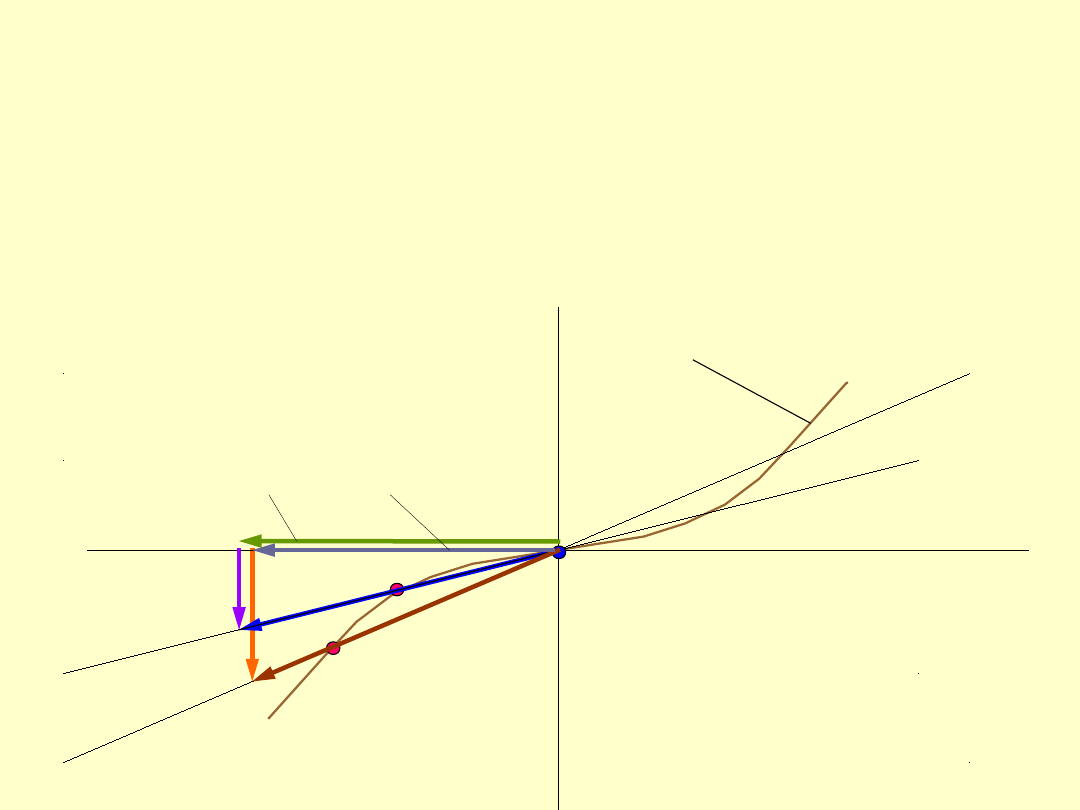
W przypadku krzywoliniowej linii przyporu, siła
międzyzębna

P

N

zmienia kierunek

oddziaływania, zaś jej składowe: obwodowa

P

O

oraz promieniowa

P

R

zmieniają swoje wartości.

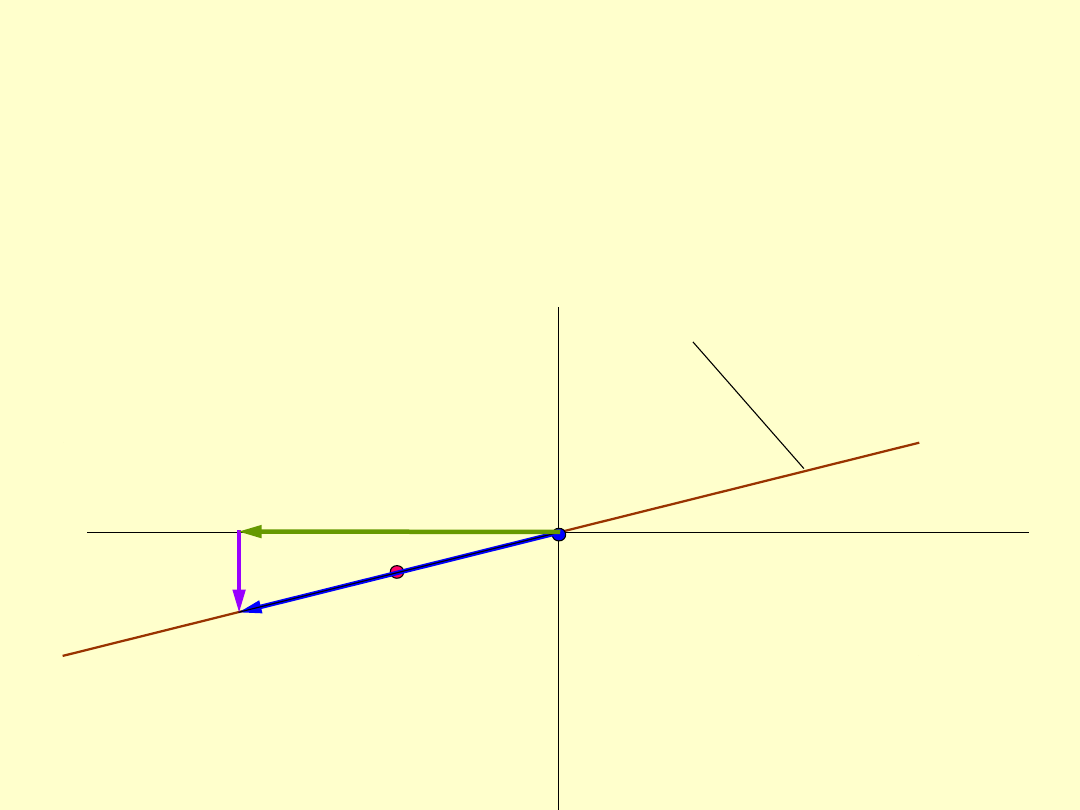
W przypadku prostej linii przyporu, zarówno
siła międzyzębna

P

N

jak i jej składowe:

obwodowa

P

O

oraz promieniowa

P

R

maja te

same wartości i kierunki.

C

O

2

O

1

linia przyporu

B

P

OB

P

RB

P

NB