OGÓLNE PODSTAWY

MATEMATYCZNE

POMIARÓW I OBLICZEŃ

GEODEZYJNYCH

NA MAŁYCH

OBSZARACH

Definicja obszaru małego

Obszarem małym (lub niedużym) z
geodezyjnego punktu widzenia
nazywamy obszar nie przekraczający 750
km

2

.

Na obszarze do 750 km

2

(o promieniu nie

większym niż 15,5 km) można wykonać
pomiary liniowe i kątowe z zaniedbaniem
wpływu zakrzywienia powierzchni
ziemskiej.

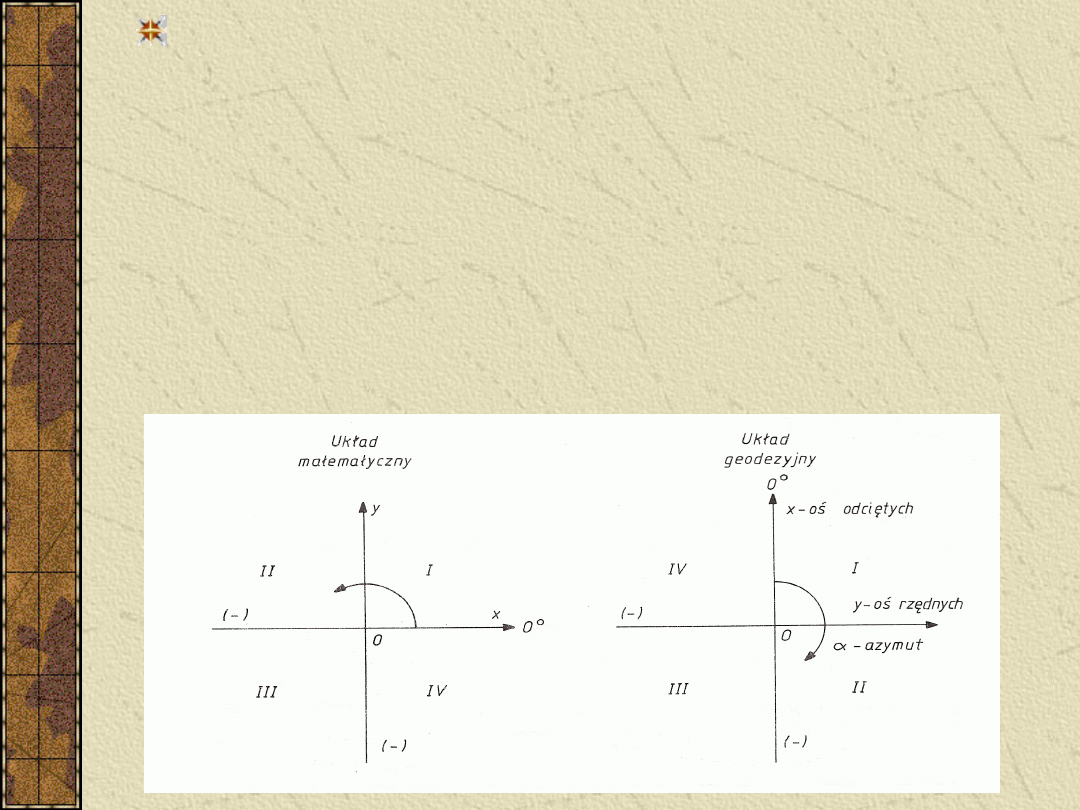
W geodezji na płaszczyźnie do

wyznaczania położenia punktów
stosujemy najczęściej układ
współrzędnych prostokątnych. Ze
względu na stosowanie w geodezji jako
kąta kierunkowego azymutu, liczonego
od kierunku północnego (dodatniego
kierunku osi x) zgodnie z ruchem
wskazówek zegara, układ współrzędnych
w geodezji różni się od układu przyjętego
w matematyce.

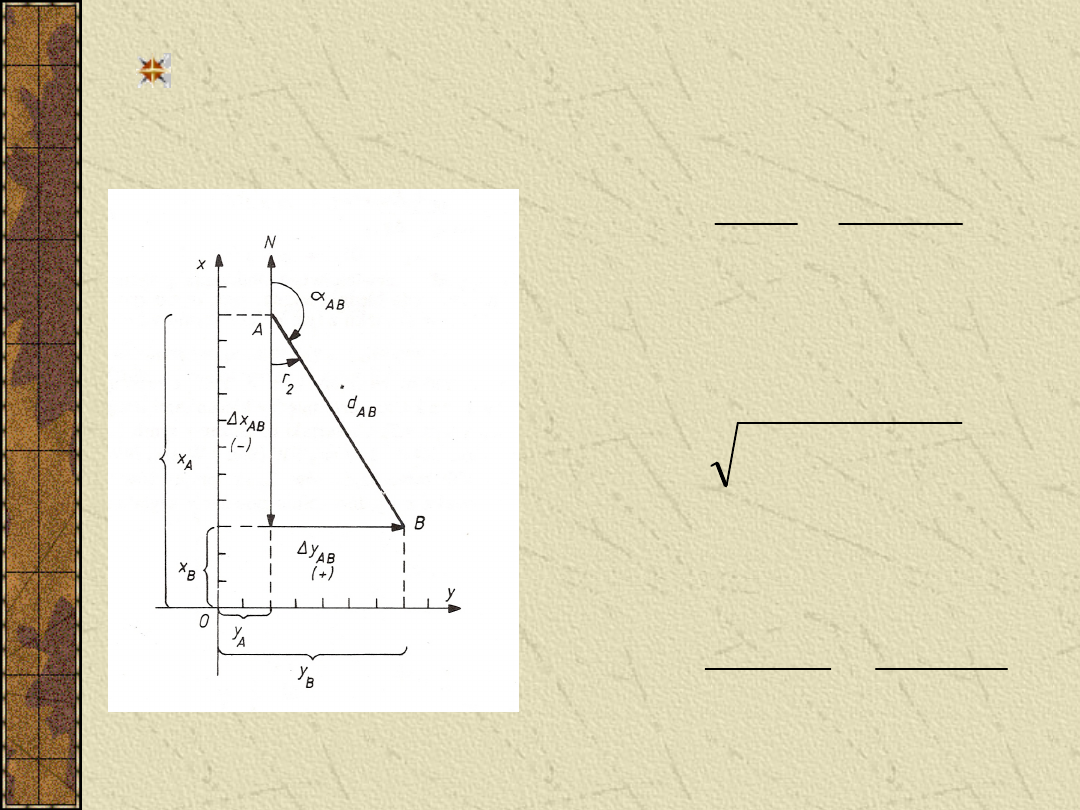
Obliczenie azymutu i długości linii.

Azymut 

AB

obliczamy ze

wzoru:

Długość linii AB:

lub

A

B

A

B

AB

AB

AB

x

x

y

y

x

y

tg















2

2

AB

AB

AB

y

x

d









AB

AB

AB

AB

AB

x

y

d





cos

sin









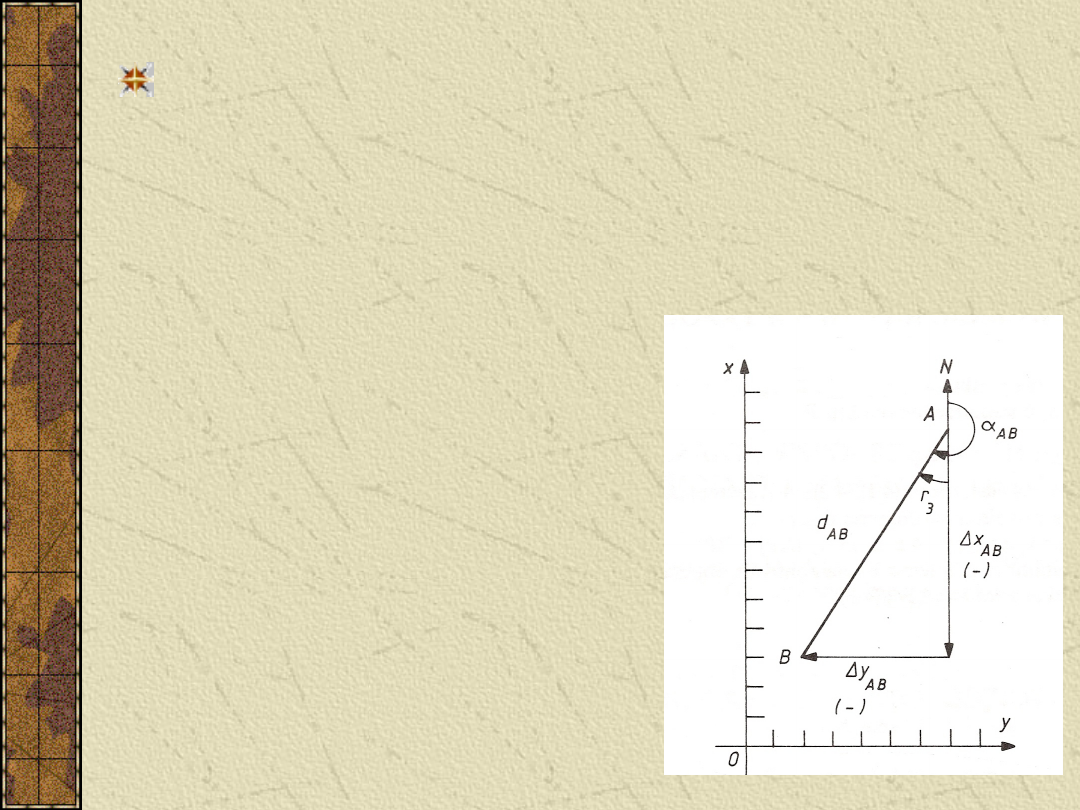
Obliczenie współrzędnych punktu.

Dane: współrzędne punktu A(x

A

,y

A

), azymut linii



AB

oraz jej długość d

AB

.

Szukane: współrzędne punktu B(x

B

, y

B

).

Współrzędne obliczamy ze wzorów:

AB

AB

A

AB

A

B

d

x

x

x

x



cos











AB

AB

A

AB

A

B

d

y

y

y

y



sin











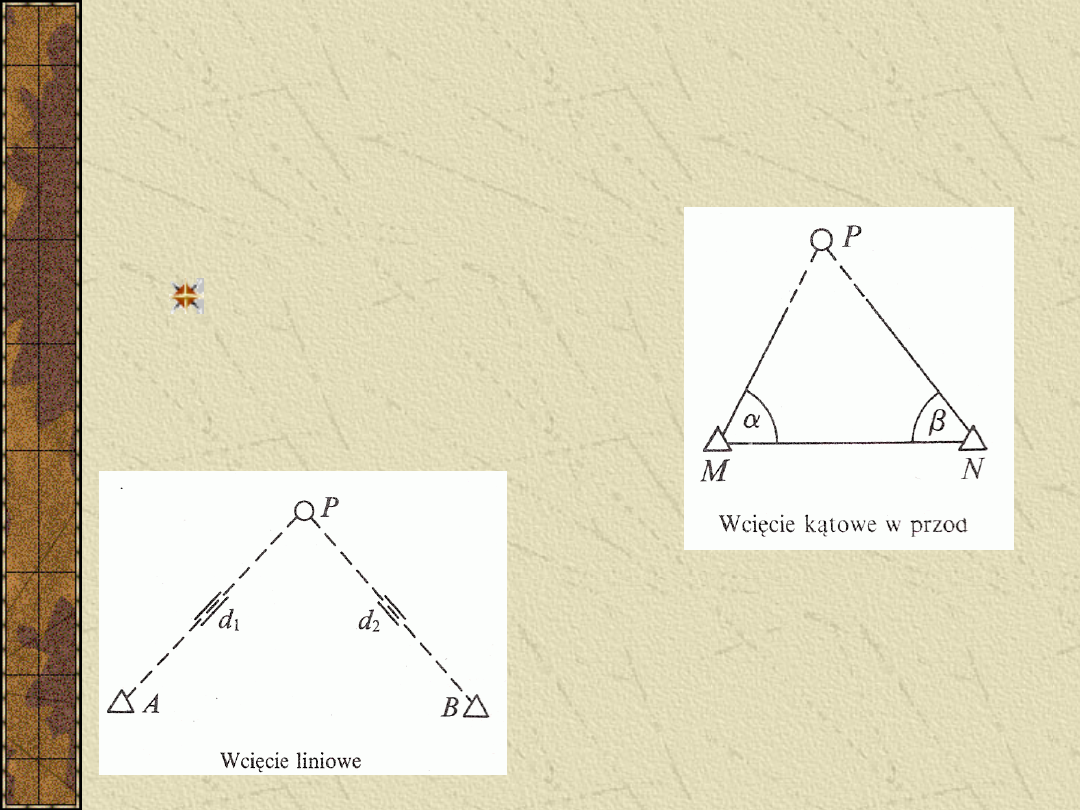
W praktyce geodezyjnej bardzo

często wyznacza się współrzędne
punktów za pomocą specjalnych
konstrukcji takich jak:

Wcięcie kątowe w przód

Wcięcie liniowe w przód

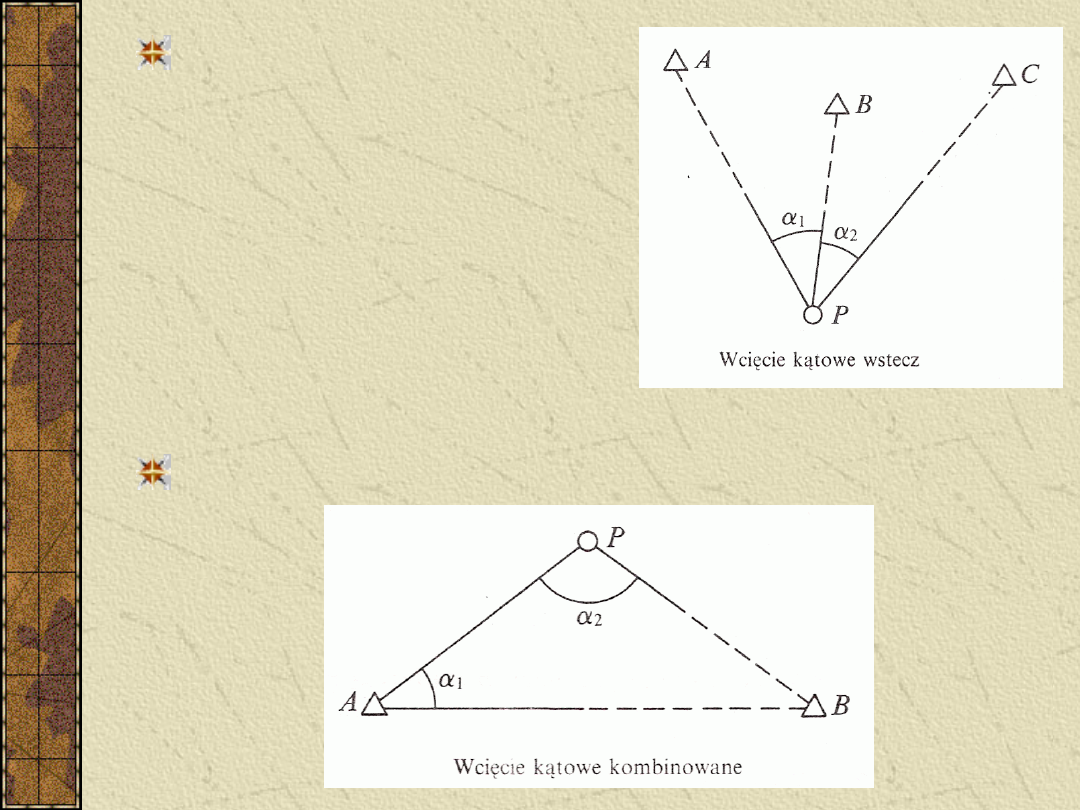
Wcięcie kątowe wstecz

Wcięcie kątowe kombinowane

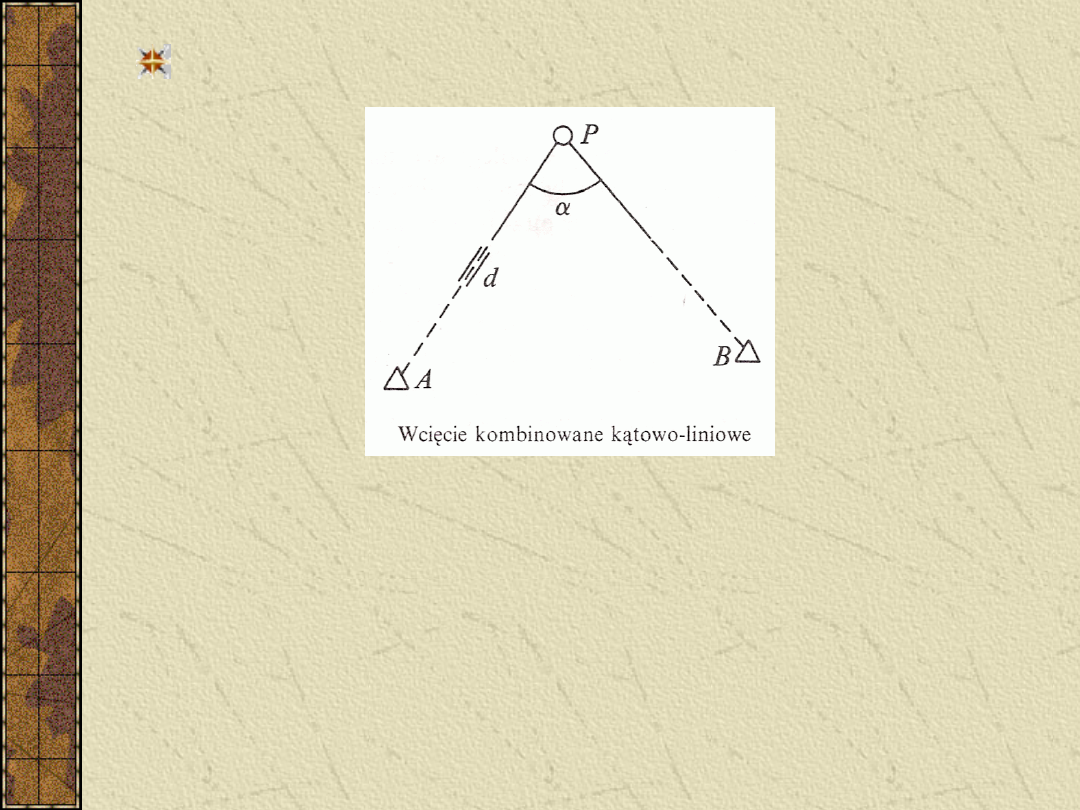
Wcięcie kombinowane kątowo-
liniowe

Ciągi poligonowe zamknięte i

otwarte

Azymut linii następnej w ciągu

poligonowym, gdy znany jest azymut linii

poprzedniej i kąt zawarty między danymi liniami,

wyznaczamy na podstawie następujących wzorów:

dla kąta prawego

dla kąta lewego

Wzór na określenie azymutu końcowego

ostatniej linii w ciągu o n kątach:

dla kątów prawych

dla kątów lewych

pr















180

1

2

l















180

1

2

 

pr

p

k

n

















180

 

l

p

k

n

















180

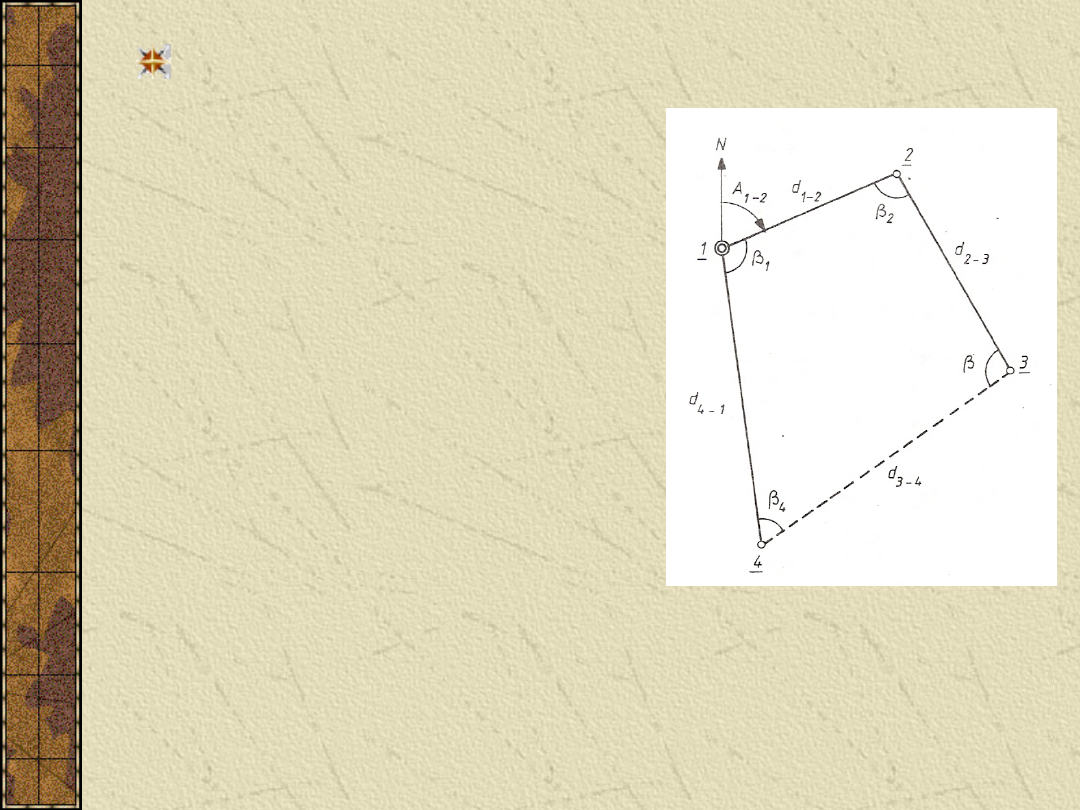
Ciąg poligonowy zamknięty

Suma pomierzonych kątów
wewnętrznych wieloboku:

sumy obliczonych przyrostów
x i y:

 

)

2

(

180 





n

w



 

0



x

 

0



y

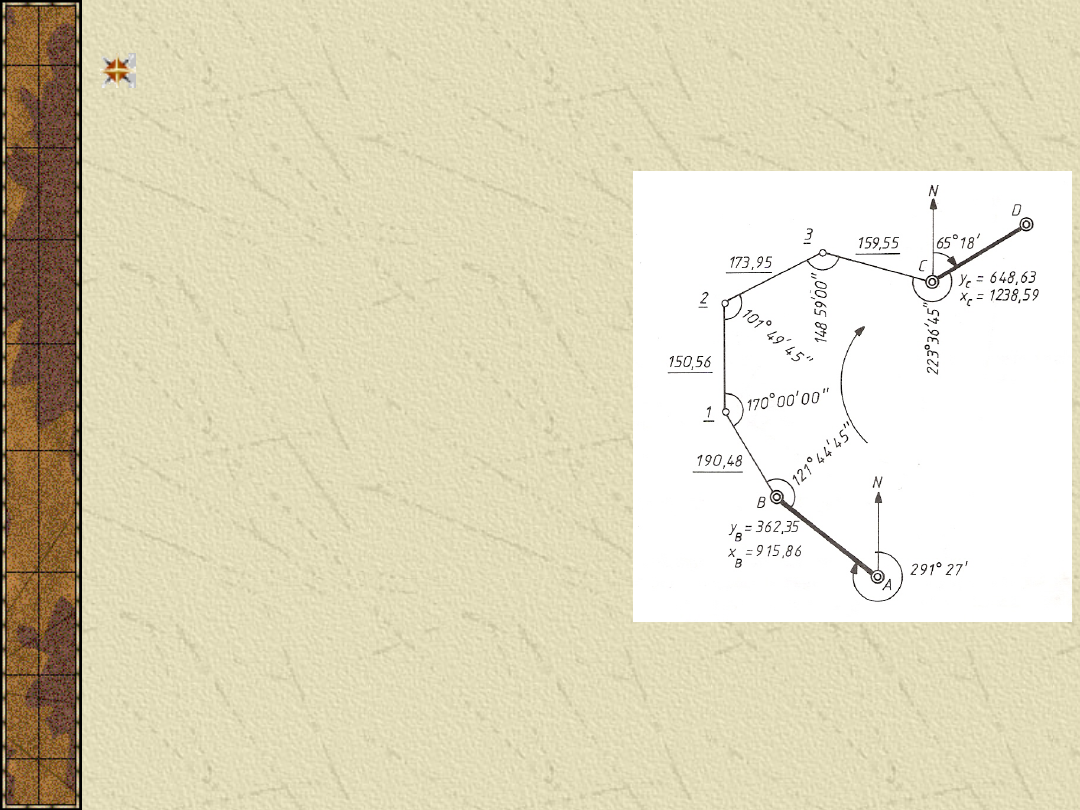
Ciąg poligonowy otwarty

Suma pomierzonych kątów
wewnętrznych ciągu:

sumy obliczonych przyrostów
x i y:

 













180

)

(

n

A

A

k

p

p

l



 

p

k

x

x

x







 

p

k

y

y

y







Reguły rachunkowe

Kryłowa-Bradisa

stosuje się podczas działań na liczbach

o różnej ilości cyfr znaczących lub znaków

dziesiętnych.

cyfry znaczące – wszystkie cyfry danej

liczby oprócz zer położonych na lewo od

pierwszej różnej od zera cyfry
znaki dziesiętne – cyfry danej liczby

położone na prawo od znaku ułamkowego

cyfry znaczące

znaki dziesiętne

24,5

trzy

24,

5

jeden

0,0

245

trzy

0,

0245

cztery

0,00

20500

0

sześć

0,

00205

000

osiem

1

jedna

1

zero

10

dwie

10

zero

1,000

cztery

1,

000

trzy

1) Przy dodawaniu i odejmowaniu liczb
przybliżonych w wyniku należy
zachować tyle znaków dziesiętnych, ile
ich zawiera liczba przybliżona o
najmniejszej ilości znaków dziesiętnych.

np. dodajmy liczby: 2,34 oraz 0,621

2,34

+ 0,621
2,96

1

Po zastosowaniu reguły otrzymujemy:

2,96

2) Przy mnożeniu i dzieleniu należy
w wyniku zachować tyle cyfr
znaczących, ile zawiera ich liczba
przybliżona o najmniejszej ilości cyfr
znaczących.

np. pomnóżmy liczby: 1,2 oraz 3,11

3,11
* 1,2
3,7

32

Po zastosowaniu reguły otrzymujemy:

3,7

3)

Przy podnoszeniu do kwadratu i

sześcianu należy w wyniku zachować

tyle cyfr znaczących, ile ich zawiera

potęgowana liczba przybliżona, przy

czym ostatnia cyfra potęgi jest mniej

pewna od ostatniej cyfry potęgowanej

liczby.

np. podnieśmy do kwadratu liczbę 1,2

(1,2)

2

= 1,4

4

Po zastosowaniu reguły otrzymujemy:

1,4

4)Przy wyciąganiu pierwiastka kwadratowego

i sześciennego należy w wyniku zachować

tyle cyfr znaczących, ile ich zawiera liczba

pierwiastkowana, przy czym ostatnia cyfra

pierwiastka będzie pewniejsza od ostatniej

cyfry pierwiastkowanej liczby.

np. wyciągnijmy pierwiastek z liczby 9,32

= 3,05

2867504...

Po zastosowaniu reguły otrzymujemy:

3,05

32 , 9

5)Przy obliczaniu wyników pośrednich
stadiów rachunku należy brać zawsze
o jedną cyfrę więcej, niż to wskazują
wcześniejsze zasady, przy czym w
rezultacie końcowym tę zapasową
cyfrę odrzucamy. Zaleca się pisać ją
drobniejszym pismem.

np. dodajmy liczby 1,5 oraz 2,2431

1,5

+ 2,2431
3,74

31

Do dalszych obliczeń używamy liczby:

3,74 (zalecany zapis: 3,7

4

)

6) Jeżeli niektóre dane zawierają więcej znaków

dziesiętnych (w działaniach I stopnia) lub więcej cyfr

znaczących (w działaniach II i III stopnia) niż

pozostałe, to należy je przede wszystkim zaokrąglić,

zachowując przy tym jedną, zbędną według reguł

cyfrę.

np. dodajmy liczby: 0,1436 i 2,31 i 6,229188.

Po zaokrągleniu dodajemy 0,144
2,31
+ 6,229
8,68

3

Po zastosowaniu reguły otrzymujemy:

8,68 – jeśli jest to wynik ostateczny

8,683 – jeśli wynik ma być użyty do dalszych obliczeń

7) Jeżeli dane wyjściowe do rachunku

można brać z dowolną dokładnością,

to aby otrzymać wynik o k cyfrach

należy brać dane z taką ilością cyfr,

która zgodnie z regułami 1-4 daje

(k+1) cyfr wyniku.

8) Przy obliczaniu logarytmicznym

jednomianu należy używać tablic

zawierających o jedną cyfrę więcej od

ilości cyfr znaczących, zawartych w

tym czynniku, który zawiera najmniej

cyfr. W wyniku końcowym odrzucamy

wówczas ostatnią cyfrę znaczącą.