Równowaga sił w

układzie mięśniowo

szkieletowym człowieka

w warunkach statyki

Warszawa, 19 października

2007

Mechanika

• 1) Dział fizyki zajmujący się badaniem

równowagi, ruchu i oddziaływania ciał

• Siły są miarą oddziaływania ciał
• 1N jest to siła, która działając na ciało o

masie 1kg nadaje mu przyspieszenie 1
m/s

2

• 2) Nauka o budowie, działaniu i

konstruowaniu maszyn oraz mechanizmów

Mechanika

• Z gr. Mechaniké ‘sztuka budowania maszyn’ od mechané

‘maszyna’

• M. klasyczna – mechanika oparta na teorii Newtona,

badająca ruch makroskopowych ciał materialnych

• M. relatywistyczna – mechanika uwzględniająca w swoich

badaniach elementy wynikające z teorii względności

• M. kwantowa
• M. płynów
• M. nieba – dział astronomii badający ruch ciał niebieskich
• M. techniczna dział nauki zajmujący się konstruowaniem i

budowaniem maszyn, mechanizmów, aparatów

Prekursorzy

• Mechanika jako nauka ścisła powstała w

Egipcie w IV w p.n.e.

• Arystoteles (384-322 p.n.e.), Archytas z

Tarentu – maszyny proste

• Archimedes (287-212 p.n.e.) siły

równoległe teoria dźwigni

• Mikołaj Kopernik (1473-1543) układy

odniesienia

• Isaak Newton (1642-1727) Philosophiae

naturalis principia mathematica. 1687,

Londyn – podstawy mechaniki klasycznej

opartej na faktach doświadczalnych, prawa

powszechnego ciążenia i klasycznej

dynamiki

Mechanika Techniczna

• Mechanika techniczna:

»Mechanika ogólna (teoretyczna)
»Wytrzymałość

• Mechanika ogólna zajmuje się

ustalaniem ogólnych praw ruchu i

równowagi ciał materialnych oraz

zastosowaniem tych praw do pewnych

wyidealizowanych schematów ciał

materialnych: punktu materialnego,

ciała doskonale sztywnego

Mechanika ogólna

• Mechanika

ogólna dzieli się na:

– Kinematykę

(badanie ruchu bez wnikania w

jego przyczyny, bez uwzględniania działających
sił)

– Dynamikę

(badanie działających sił), która

dzieli się na:

•Statykę: zajmuje się badaniem

równowagi sił

•Kinetykę: bada ruch ciał oraz siły

wywołujące go

Kinematyka

•a – stałe przyspieszenie
•V(t) = v

0

+ at

•X(t) = x

0

+ v

0

t + ½at

2

II zasada dynamiki Newtona

m

F

a 

Zmiana pędu

•Π = Δp

•Popęd siły = Przyrost pędu
•Popęd siły to pole pod

krzywą siły zmieniającej się w

czasie (całka)

•Pęd = mv

Zasady statyki (aksjomaty)

• Zasada równoległoboku: Działanie dwóch sił F

1

i F

2

można zastąpić działaniem jednej siły R

• Jeżeli do ciała przyłożone są dwie siły to równoważą się

one tylko wtedy, gdy mają tę samą linię działania, te

same wartości i przeciwne zwroty

• Skutek działania dowolnego układu sił przyłożonego do

ciała nie zmieni się jeżeli dodamy lub odejmiemy

dowolny układ sił równoważących się (układ zerowy)

• Jeżeli ciało odkształcalne znajduje się w równowadze pod

działaniem pewnego układu sił, to również pozostanie w

równowadze ciało doskonale sztywne (nieodkształcalne)

identyczne z poprzednim, pod działaniem tego samego

układu sił.

• Każdemu działaniu towarzyszy równe co do wartości o

przeciwnym zwrocie i leżące na tej samej prostej

przeciwdziałanie.

• Każde ciało nieswobodne można myślowo oswobodzić z

więzów, zastępując ich działanie reakcjami, a następnie

rozpatrywać jako ciało swobodne, znajdujące się pod

działaniem sił czynnych i biernych

Ruch

• Ruch – wzajemne przemieszczanie

się w przestrzeni, w miarę upływu
czasu jednych ciał względem innych

• Ruch jest względny
• Układ współrzędnych związany z

ciałem lub zbiorem ciał, względem
których opisujemy ruch innego ciała
nazywamy układem odniesienia

Modele, pojęcia podstawowe

• Opisując zjawiska fizyczne posługujemy się

modelami:

• Punkt materialny – ciało którego wymiary można

pominąć w opisie ruchu

• Bryła sztywna – zbiór wielkiej liczby punktów

materialnych znajdujących się w stałej niezmiennej

odległości

• Tor ruchu – linia krzywa lub prosta po której odbywa

się ruch

• Droga s – długość toru (skalar)

• Δr – przemieszczenie (wektor)

• W postaci wektorowej kinematyczne równanie ruchu

jest zależnością określającą wektor położenia ciała

jako funkcję czasu r = r(t); r = xi + yi + zj

• Eliminując czas otrzymujemy równanie toru

Siła bezwładności

•B = - am

• Siły B są wywołane przyspieszeniem układu

odniesienia a nie oddziaływaniem między ciałami

• Siły B działają na ciała tylko w nieinercjalnych

układach odniesienia

• Siły B zależą od masy, zawsze przeciwne do

przyspieszenia nieinercjalnego układu odniesienia

• Dla dowolnego układu ciał w nieinercjalnym

układzie odniesienia Siły B są siłami

zewnętrznymi dlatego nie są zachowane w tych

układach zasada zachowania energii i pędu

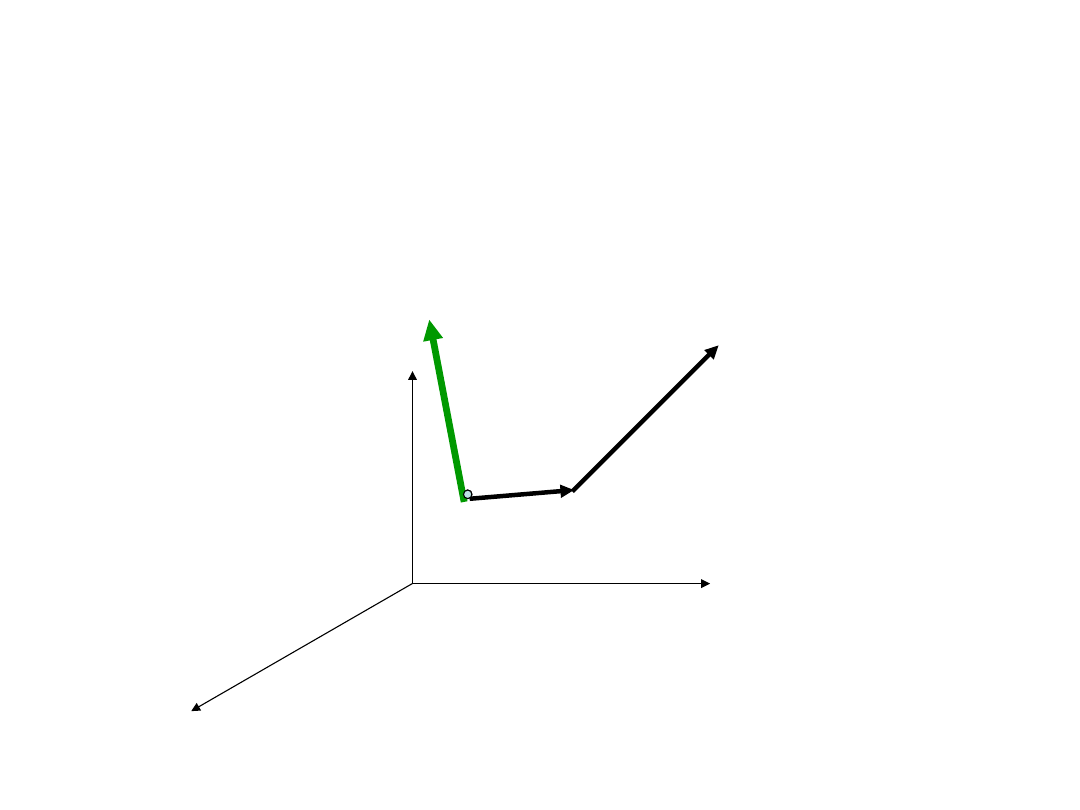
Moment siły

• Momentem siły F względem punktu 0

nazywamy odłożony z punktu 0
wektor M

0

równy iloczynowi

wektorowemu promienia wektora r i
wektora siły F ; M

0

= r×F

y

y

x

z

0

F

r

M

0

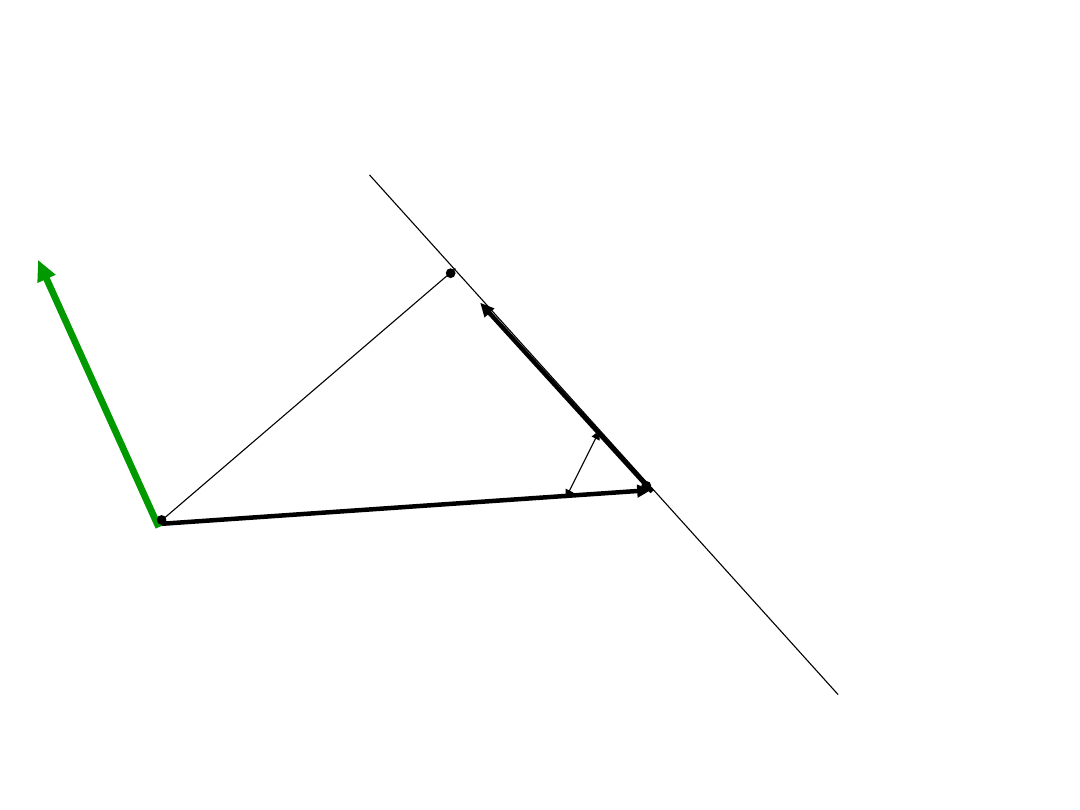
Moment siły

r

F

B

A

l

M

0

0

M

0

= Frsinα =

Fl

α

l – ramię działania siły

Redukcja dowolnego przestrzennego

układu sił

• Załóżmy, że na ciało sztywne działa dowolny

przestrzenny układ n sił F

i

przyłożonych w

różnych punktach przestrzenia. Aby ten układ
zredukować przyjmujemy dowolny punkt 0
zwany środkiem redukcji układu sił

• Korzystając z równoległego przesunięcia

otrzymujemy układ sił zbieżnych przyłożonych
do punktu 0 oraz n par sił o momentach M

i0

• Układ sił zbieżnych zastępujemy:







n

i

i

F

R

1

i

n

i

i

F

r

M







1

0

Równowaga przestrzennego

układu sił

• Przestrzenny układ n sił jest w równowadze,

jeżeli jego suma geometryczna R jest
równa zeru oraz moment M

0

od tych sił

względem dowolnego punktu 0 jest równy
zero

0

1









n

i

i

F

R

0

1

0









i

n

i

i

F

r

M

Równowaga przestrzennego

układu sił

• Dowolny przestrzenny układ sił F

i

jest w

równowadze, jeżeli suma rzutów wszystkich sił
na trzy osie układu równa jest zeru i suma
momentów sił względem trzech osi układu jest
równa zeru







n

i

iz

M

1

0







n

i

ix

M

1

0







n

i

iy

F

1

0







n

i

ix

F

1

0







n

i

iz

F

1

0







n

i

iy

M

1

0

Równowaga płaskiego układu

sił

• Płaski dowolny układ sił znajduje się w

równowadze, jeżeli sumy rzutów
wszystkich sił na osie układu są równe
zeru i moment wszystkich sił względem
dowolnego punktu płaszczyzny działania
sił jest równy zeru







n

i

ix

F

1

0







n

i

iy

F

1

0







n

i

i

M

1

0

0

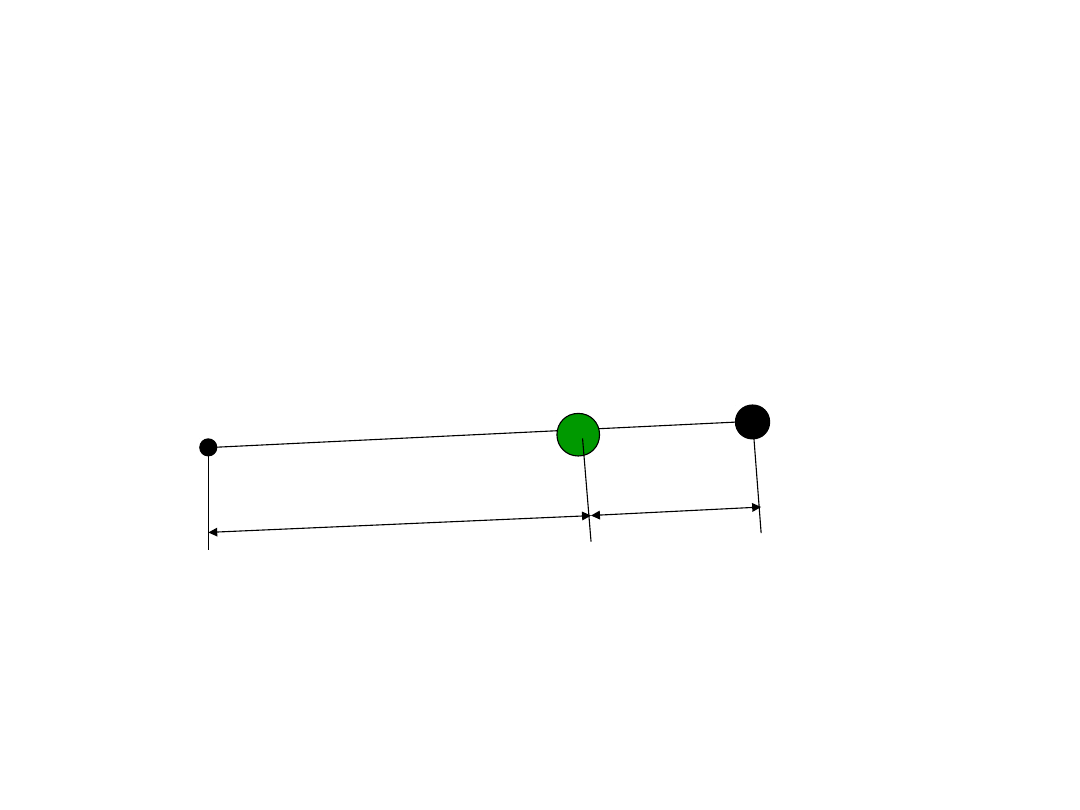
Środek masy (Środek

ciężkości)

• Środek masy dwóch punktów

materialnych

m

A

m

B

a

b

m

A

a =

m

B

b

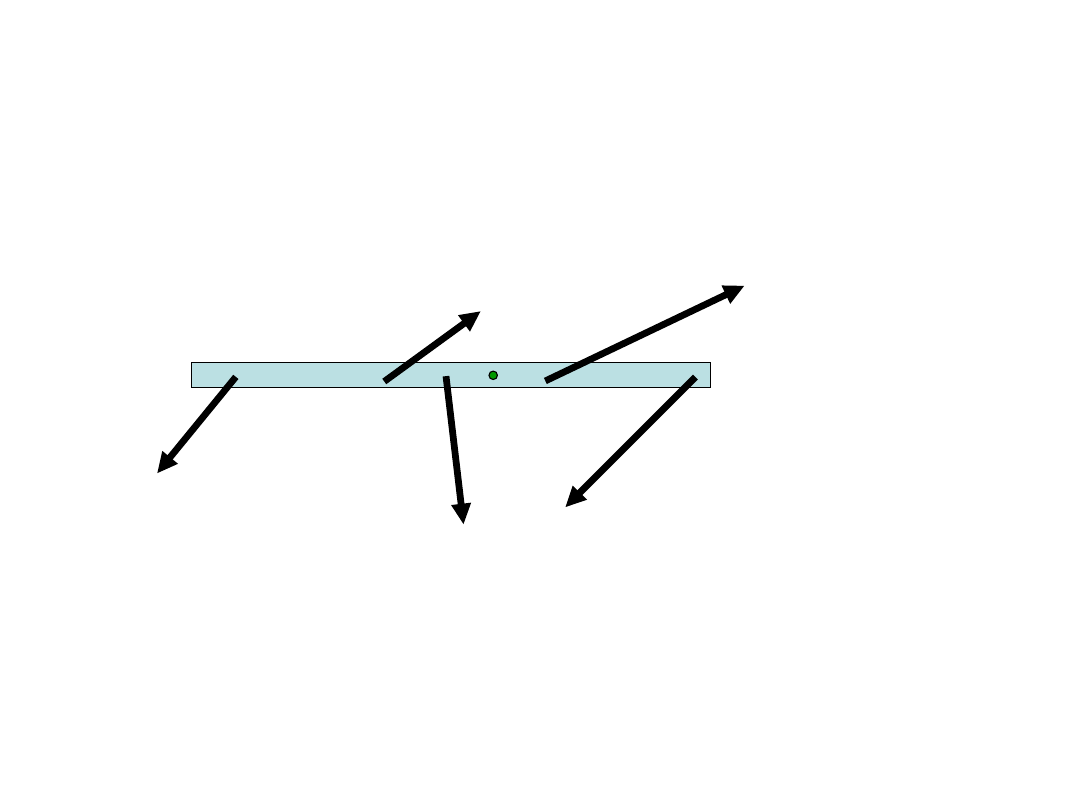
Dźwignie

• Dźwignia jest to sztywna belka,

mogąca obracać się dookoła osi
0

0

0

1







n

k

k

M

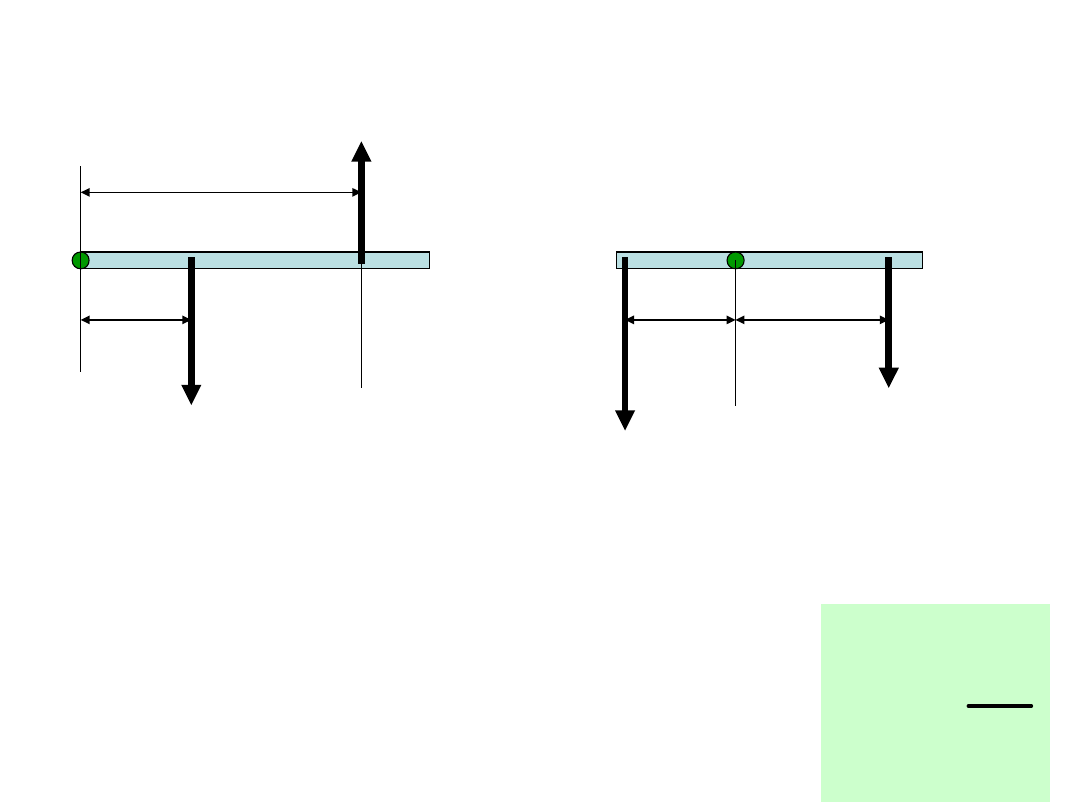
Dźwignie

0

0

P

Q

a

b

P

Q

Dźwignia jednostronna Dźwignia dwustronna

Pa – Qb = 0; czyli Pa = Qb

Jeżeli P jest siłą z jaką działamy,
a Q siła którą pokonujemy to zysk mechaniczny Z:

P

Q

Z 

a

b