Opis struktury zbiorowości

dr Aneta Włodarczyk

Parametry stosowane w analizach struktury
zbiorowości statystycznych:



Miary tendencji centralnej (położenia)



Miary zmienności (dyspersji,

rozproszenia)



Miary asymetrii (skośności)



Miary koncentracji

Podział miar tendencji
centralnej



przeciętne miary klasyczne
(średnia arytmetyczna, harmoniczna,
geometryczna)



przeciętne miary pozycyjne
(dominanta, kwantyle)

Średnia arytmetyczna



Dla szeregu szczegółowego:

x

i

- kolejne wartości badanej cechy,

n - liczba jednostek zbiorowości.

n

x

x

n

i

i







1

Średnia arytmetyczna



Dla szeregu
rozdzielczego
punktowego:

n

i

-liczebności klas, k- liczba klas



Dla szeregu
rozdzielczego
przedziałowego:

- środek przedziału
klasowego

i

k

i

k

i

i

i

n

n

x

x











1

1

i

k

i

k

i

i

i

n

n

x

x











1

1



i

x



Średnia grupowa

wyznaczono wartości średnich arytmetycznych w każdej

z r grup ( )

gdzie: n

i

-liczebność i-tej grupy,











r

i

i

r

i

i

i

n

n

x

x

1

1

i

x

Średnia harmoniczna



Dla szeregu szczegółowego:



Dla szeregu rozdzielczego
punktowego:



Dla szeregu rozdzielczego
przedziałowego:







n

i

i

H

x

n

x

1

1











k

i

i

i

i

k

i

H

x

n

n

x

1

1











k

i

i

i

i

k

i

H

x

n

n

x

1

1



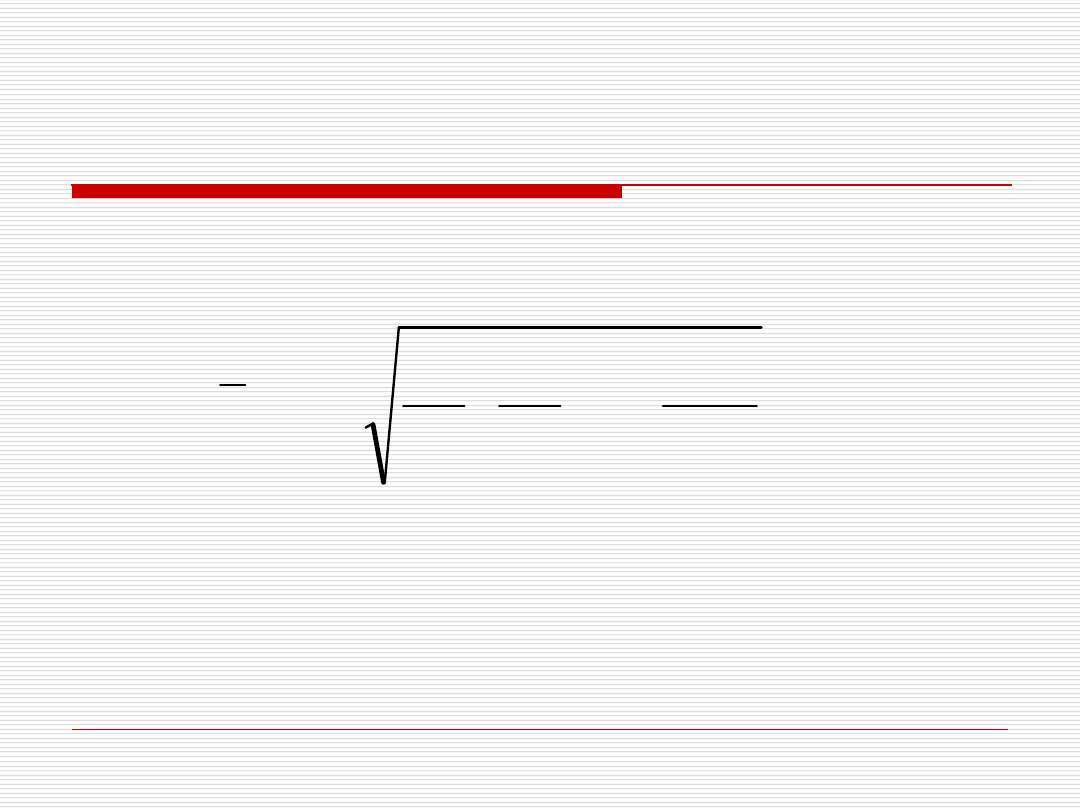
Średnia geometryczna liczona jest
ze wzoru:

1

1

2

3

1

2

...













n

n

n

G

x

x

x

x

x

x

x

W szeregu rozdzielczym przedziałowym
modę liczy się ze wzoru:

m

m

m

m

m

m

m

m

h

n

n

n

n

n

n

x

Mo





















)

(

)

(

1

1

1

X

m

- dolna granica przedziału, w którym występuje dominanta,

n

m

- liczebność przedziału, w którym występuje dominanta,

n

m-1

-liczebność przedziału poprzedzającego przedział z modą,

n

m+1

– liczebność przedziału następującego bezpośrednio

po przedziale z modalną,

h

m

-rozpiętość przedziału klasowego, w którym znajduje się dominanta

W szeregu rozdzielczym klasowym o
różnej rozpiętości przedziałów modę
liczy się ze wzoru:

i

i

i

h

n

g 

gdzie g

i

oznacza gęstość przedziału

klasowego
o numerze i

m

m

m

m

m

m

m

m

h

g

g

g

g

g

g

x

Mo





















)

(

)

(

1

1

1

Wyznaczanie kwartyla pierwszego
w szeregach szczegółowych:



Szereg wartości należy uporządkować w
sposób niemalejący

4

1

1





n

N

Q

1

1

Q

N

x

Q 

Przykład:

Wydatki (w zł) na pewne dobro w 12

gospodarstwach domowych wynosiły:

31 32 33 34 35 36 37 38 39 40 41 42

Pozycja kwartyla: (n+1)/4 = 13/4= 3,25
x

3

=33 zł x

4

= 34zł

Q

1

jest wartością większą od 33 zł o 0,25

odległości między 34 a 33, czyli 33,25 zł

[0,25*(34-33)+33].

Wzór na kwartyl pierwszy (Q

1

) dla szeregu

rozdzielczego przedziałowego:

m

m

m

i

i

m

h

n

n

n

x

Q















1

1

1

4

gdzie:
m - numer przedziału, w którym znajduje się Q

1

x

m

- dolna granica przedziału z Q

1

n- liczebność analizowanej zbiorowości

n

m

- liczebność przedziału z Q

1

h

m

-rozpiętość przedziału z Q

1

.

W szeregu szczegółowym medianę
Me wyznacza się ze wzoru:

szereg wartości liczbowych należy

uporządkować w sposób niemalejący!
























parzystego

n

dla

x

x

ego

nieparzyst

n

dla

x

Me

n

n

n

2

1

2

2

2

1

Przykład:

Wydatki (w zł) na pewne dobro w 12

gospodarstwach domowych wynosiły:

31 32 33 34 35

36 37

38 39 40 41 42

Pozycja mediany: n – parzyste
n/2 = 12/2 = 6 (n/2)+1 = 7
x

6

=36 zł x

7

= 37zł

Me = (36+37)/2 = 36,5 zł.

Wzór na kwartyl drugi (Me) dla szeregu
rozdzielczego przedziałowego:

m

m

m

i

i

m

h

n

n

n

x

Me















1

1

2

m-numer przedziału, w którym znajduje się Me,

x

m

- dolna granica przedziału z Me,

n - łączna liczebność analizowanej zbiorowości,
n

m

- liczebność przedziału z Me,

h

m

-rozpiętość przedziału z Me.

Wyznaczanie kwartyla trzeciego w
szeregach szczegółowych:



Szereg wartości należy uporządkować w
sposób niemalejący

4

)

1

(

3

3







n

N

Q

3

3

Q

N

x

Q 

Przykład:

Wydatki (w zł) na pewne dobro w 12

gospodarstwach domowych wynosiły:

31 32 33 34 35 36 37 38 39 40 41 42

Pozycja kwartyla: 3*(n+1)/4 = 39/4= 9,75
x

9

=39 zł x

10

= 40 zł

Q

3

jest wartością większą od 39 zł o 0,75

odległości między 40 a 39, czyli 39,75 zł
[(0,75*(40-39)+39].

Wzór na kwartyl trzeci (Q

3

) dla szeregu

rozdzielczego przedziałowego:

m

m

m

i

i

m

h

n

n

n

x

Q















1

1

3

4

3

gdzie:
m - numer przedziału, w którym znajduje się
Q

3

x

m

- dolna granica przedziału z Q

3

n- liczebność analizowanej zbiorowości
n

m

- liczebność przedziału z Q

3

h

m

-rozpiętość przedziału z Q

3

.

Miary zmienności (dyspersji,
rozproszenia) dzielą się na:



pozycyjne (rozstęp, odchylenie

ćwiartkowe),



klasyczne (odchylenie przeciętne,

odchylenie standardowe, wariancja)

Rozstęp (empiryczny obszar
zmienności, amplituda wahań)

R= x

max

-x

min

Odchylenie
ćwiartkowe:

2

1

3

Q

Q

Q





Typowy obszar zmienności:

Q

Me

x

Q

Me

typ









Odchylenie przeciętne



dla szeregu szczegółowego:









n

i

i

x

x

n

d

1

1

Odchylenie przeciętne



dla szeregu rozdzielczego
punktowego:



dla szeregu rozdzielczego
przedziałowego:

i

k

i

i

n

x

x

n

d









1

1

i

k

i

i

n

x

x

n

d









1

1



Wariancja



dla szeregu szczegółowego:









n

i

i

x

x

n

S

1

2

2

)

(

1

Wariancja



dla szeregu rozdzielczego
punktowego:



dla szeregu rozdzielczego
przedziałowego:











k

i

i

i

n

x

x

n

S

1

2

2

)

(

1











k

i

i

i

n

x

x

n

S

1

2

2

)

(

1



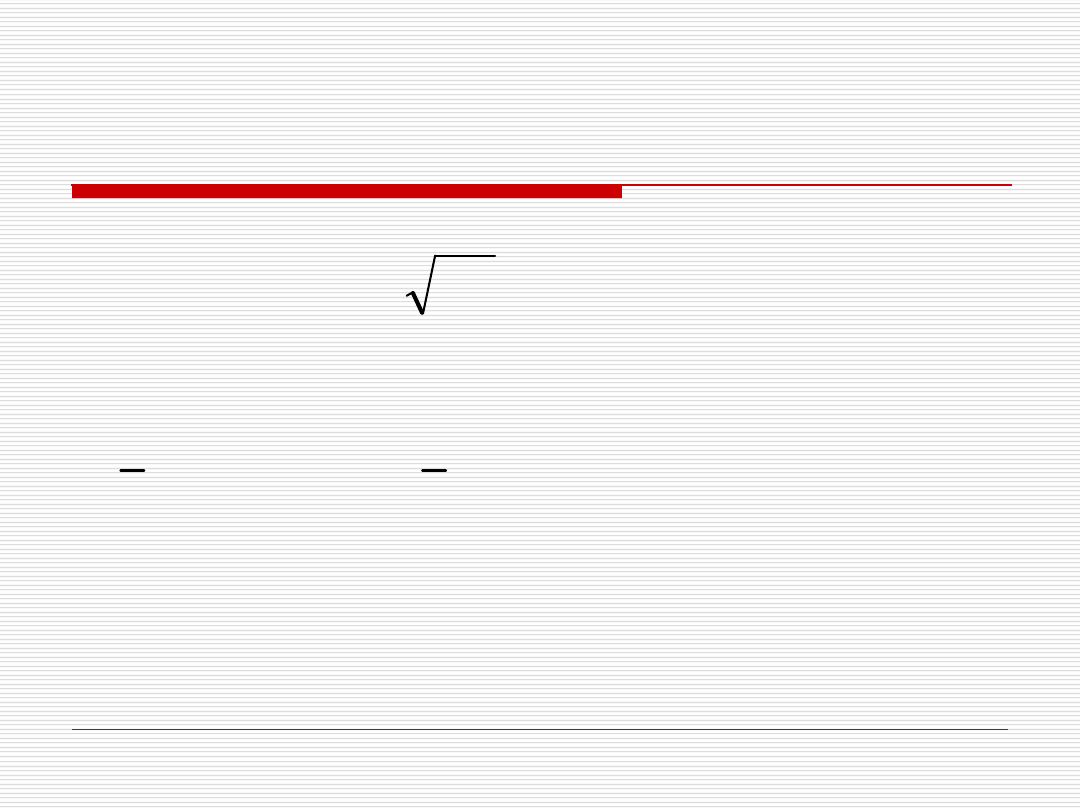
Odchylenie standardowe

2

S

S 

Typowy obszar zmienności:

S

x

x

S

x

typ







