METODY

TWORZENIA

ALGORYTMÓW

METODA PRZYROSTOWA

SORTOWANIE PRZEZ WSTAWIANIE

DANE : 6, 5 2 4 6 1 3

1 2 3 4 5 6

posortowany ciąg

1 2 4 5 6

posortowany podciąg 5-

elementowy

2 4 5 6

posortowany podciąg 4-

elementowy

2 4 5

posortowany podciąg 3-

elementowy

2 5

posortowany podciąg 2-

elementowy

5

posortowany podciąg 1-

elementowy

"DZIEL I ZWYCIĘŻAJ"

Zasada : problem rozmiaru n jest dzielony
na kilka problemów podobnych do problemu
początkowego
ale rozmiarów mniejszych niż n;
problemy "mniejsze" są rozwiązywane
i ich rozwiązania są łączone w rozwiązanie wyjściowego
problemu.

Wykorzystuje rekurencję.

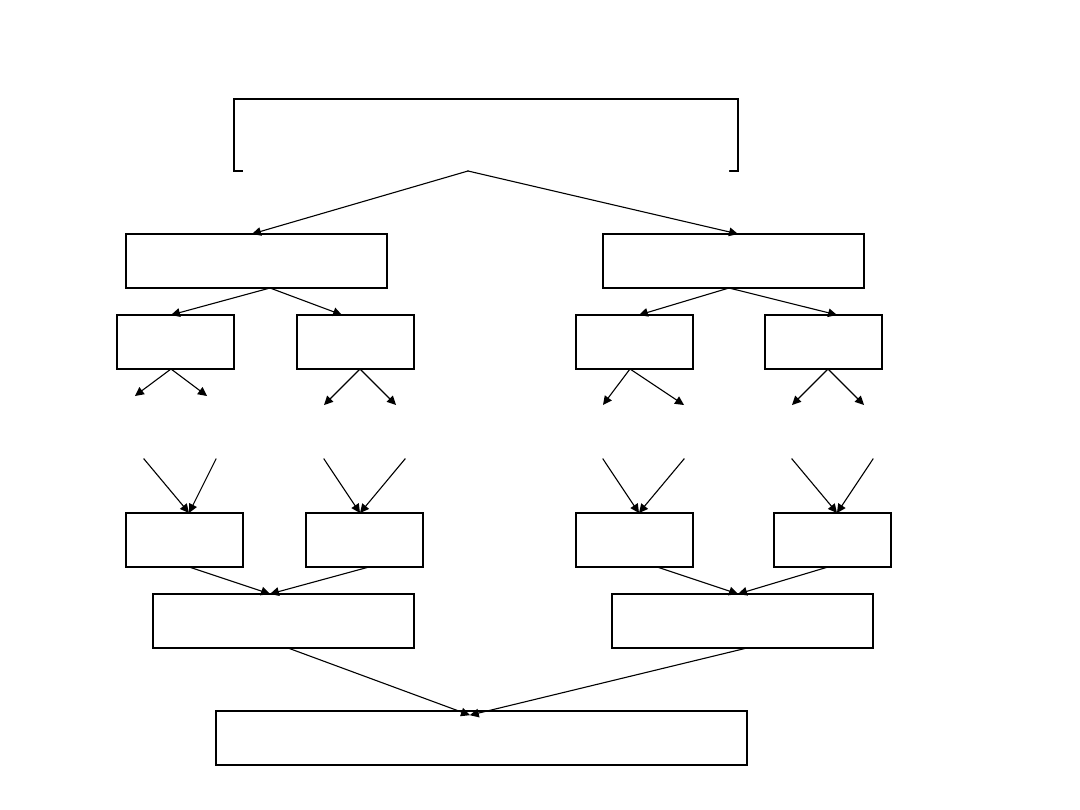
SORTOWANIE

5 2 4 6 1
3 2 6

2 5

4 6

2 6

1 3

5 2 4 6

1 3 2 6

5 2

4 6

1 3

2 6

2 4 5 6

1 2 3 6

1 2 2 3 4 5
6 6

5 2 4 6 1 3
2 6

MERGE-SORT ( A, p, k);

{ Sortuje elementy w podtablicy A[p..k];
jeśli p >= k to podtablica jest już posortowana;
jeśli p < k to dzielimy A[p..k] na dwie podtablice i sortujemy każdą
z nich }

begin
if p < k then
begin
q := (p+k)/2 ;

MERGE-SORT ( A, p, q );

MERGE-SORT ( A, q+1, k );
MERGE (A, p, q, k);

end

end;

MERGE-SORT( A, 1, n ) -

sortuje tablicę A[1..n]

Złożoność : T(n) =



(nlgn)

ALGORYTMY ZACHŁANNE

(GREEDY ALGORITHMS)

Zasada: w każdym kroku wykonuje działanie,
które w danej chwili jest najkorzystniejsze,
czyli wybiera lokalnie optymalną możliwość
w nadziei , że doprowadzi to do globalnie optymalnego
rozwiązania

Uwaga: Nie zawsze prowadzi do optymalnego rozwiązania

DANE :

Z = {1, 2, ... n } - zbiór n zajęć , n>0

[ p

i

, k

i

) p

i

- czas rozpoczęcia zajęcia i

k

i

- czas zakończenia zajęcia i p

i



k

i

WYNIK:

Największy podzbiór PZ zbioru Z, który zawiera zajęcia

zgodne,

tzn.: i, j



PZ , to [ p

i

, k

i

)



[ p

j

, k

j

) =



PLANOWANIE ZAJĘĆ

GREEDY-ACTIVITY-SELECTOR ( p, k);

{ p- tablica początków zajęć, k- tablica końców zajęć;
zakładamy, że k [1]



k [2]



...



k [n] }

begin

n := length [p];
PZ := {1};
j := 1;

for i := 2 to n do

if p [i]  k [j] then

begin
PZ := PZ  {i};

j := i
end;
return PZ;
{ PZ - największy podzbiór
zajęć
parami zgodnych }
end;

PROGRAMOWANIE DYNAMICZNE



Rozwiąż "małe" problemy.



Zapamiętaj rozwiązania.



Użyj tych rozwiązań do rozwiązania "dużych" problemów

Zasada:



Liczby Fibonacciego

DANE :

n



N; n>0

WYNIK :

n - ta liczba Fibonacciego



metoda rekurencyjna

-

złożoność

O(n

n

)

fib( n: integer) : integer;
begin
if ( (n =1) or (n= 2)) then fib := 1;
else

fib := fib(n-1) +

fib(n-2)

end;



Liczby

Fibonacciego



metoda dynamiczna

-

złożoność

O(n)

fib ( n: integer ) : integer;
f1, f2, f, k : integer;
begin
if ( n < 2 ) then fib := n;
else
begin

f1 = f2 = 1;

for k:= 2 to k := n-1 do
begin

f := f1 + f2;

f2 := f1;
f1 := f;

end;
end
end;



Mnożenie ciągu macierzy

DANE

:

n



N

,

p

0

, p

1

, ... , p

n



N

A

1

, ... , A

n

- macierze prostokątne o elementach

rzeczywistych,
A

i

ma rozmiar p

i-1

* p

i

.

WYNIK :

A

1

* ... * A

n

obliczony w sposób optymalny, tzn.:

liczba wykonanych mnożeń elementów
macierzy
jest najmniejsza

Optymalne nawiasowanie

DANE : A

1

- 10x100 A

2

- 100x5 A

3

- 5x50

WYNIK : A

1

A

2

A

3

- optymalnie

(A

1

A

2

)A

3

A

1

(A

2

A

3

)

A

1

A

2

10x100x5

= 5000 => A

1

A

2

(10x5)

(A

1

A

2

)A

3

10x5x50 = 2500





7500

A

2

A

3

100x5x50

= 25000 => A

2

A

3

(100x50)

A

1

(A

2

A

3

) 10x100x50

= 5000





75000

Przykład :

Struktura optymalnego nawiasowania :

m [i,j] = minimalna liczba mnożeń potrzebna do obliczenia
iloczynu A

i

*...*A

j

0 dla i = j

m [i,j] =

min { m [i,k] + m [k+1, j ] + p

i-1

* p

k

* p

j;

} dla

i < j

i  k < j

MATRIX-CHAIN-ORDER ( p );

{

p[0..n] – tablica rozmiarów macierzy A

1

, ... , A

n

,

tzn .: A

i

ma rozmiar p[i-1] * p[i] }

begin

n := length (p) -
1;
for i := 1 to n
do

m [i,i] :=

0;

for r := 2 to n do
for i := 1 to n-r+1 do
begin
j := i + r – 1;
m [i,j] := ;

for k := i to j–1 do
begin

q := m [i,k] + m [k+1, j ] + p

i-1

*

p

k

* p

j;

if q < m [i,j ] then begin

m [i,j ] := q ;

s [i,j] := k

end end end
return m and s
end ;

MATRIX-CHAIN-MULTIPLY ( A, s, i, j);

{Oblicza optymalnie iloczyn A

i

* A

i+1

* ... * A

j

}

begin
if j > i then
begin
X := MARTIX-CHAIN-MULTIPLY(A, s, i,s[i,j]);
Y := MARTIX-CHAIN-MULTIPLY(A, s, s[i,j ] +1, j);
Z := MATRIX-MULTIPLY ( X, Y );
return Z
end
else return A

i

end;

MATRIX-MULTIPLY ( A, B );

{ Oblicza iloczyn : C = A * B }

begin
if kol(A) <> rows(B) then error
else for i := 1 to rows (A) do
for j := 1 to kol (B) do
begin
C [i,j ] := 0;
for k := 1 to kol (A) do
C [i,j ] := C [i,j] + A [i,k] * B [k,j] ;

end;

return C;
end;