Bilans cieplny

suszarni

Bilans cieplny

suszarni

teoretycznej

Bilans cieplny suszarni

teoretycznej

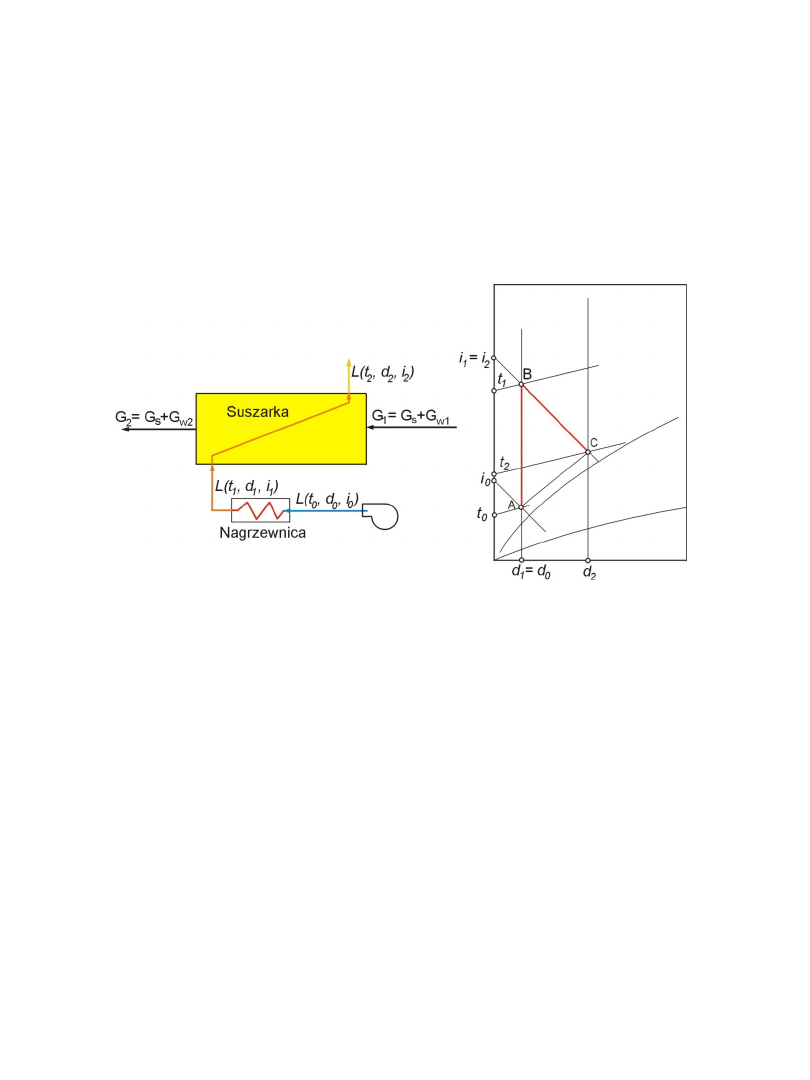
Schemat ideowy suszarni i przebieg suszenia w suszarni
jednostopniowej

z

podgrzewaczem

zewnętrznym

przedstawia poniższy rysunek:

W suszarni teoretycznej całe dostarczone ciepło zużywa się
tylko

na

odparowanie

wody.

Przebieg

procesu

podgrzewania i suszenia przedstawia wykres i – d. Stan
początkowy powietrza reprezentuje na wykresie punkt A.
Ponieważ

podczas

nagrzewania

zawartość

wilgoci

pozostaje stała, to proces ten na wykresie reprezentuje
prosta AB prostopadła do osi odciętych. Powietrze
wchodzące do suszarni ma parametry określone
położeniem punktu B. Proces suszenia materiału, a tym
samym nawilżania się powietrza, reprezentuje na wykresie
linia prosta BC biegnąca równolegle do linii stałych entalpii.
Powietrze opuszczające ma parametry odpowiadające
punktowi C.

Bilans cieplny suszarni

teoretycznej - obliczenia

Zgodnie z prawem zachowania energii, ilość ciepła

wprowadzonego do suszarki musi być równa ilości
ciepła, które jest z suszarki wynoszone. Pozycje bilansu
ciepła takiej suszarni obejmują:

• ciepło dostarczone z powietrzem zewnętrznym

tłoczonym do nagrzewnicy:

Q

1

= i

o

· L, kJ

[4.10]

• ciepło pobrane z nagrzewnicy dla nagrzania powietrza

zewnętrznego do temperatury t

1

:

Q

2

= L(i

1

– i

o

), kJ

[4.11]

• ciepło wnoszone do powietrza z wilgocią odparowaną

podczas suszenia

:

Q

3

= M

w

· C

w

· t

w

, kJ

[4.12]

• ciepło zawarte w powietrzu opuszczającym suszarkę

:

Q

4

= L · i

2

, kJ

[4.13]

Równanie bilansu cieplnego suszarni teoretycznej ma więc

postać:

Q

1

+ Q

2

+Q

3

= Q

4

Podstawiając odpowiednie wyrażenia otrzymamy:

L · i

o

+ L(i

1

– i

o

) + M

w

· C

w

· t

w

= L· i

2

gdzie:

L – ilość powietrza suchego dostarczanego do suszarni,
t

m

– temperatura wchodzącego do suszarni materiału

wilgotnego (i wody w nim zawartej),

M

w

– masa odparowanej wilgoci.

Bilans cieplny suszarni

teoretycznej – obliczenia (2)

Równanie bilansu służy najczęściej dla określenia ilości
ciepła, które musi być dostarczone do powietrza w
nagrzewnicy. Przekształcając równanie [6] otrzymamy:

L(i

1

- i

0

) = Q

2

= L(i

2

– i

o

) - M

w

· C

w

· t

w

[4.14]

Jeżeli obie strony podzielimy przez ilość odparowanej wody
M

w

to otrzymamy:

,

[kJ/kg]

[4.15]

lub

q = L

ps

· (i

2

– i

o

) - C

w

· t

w

= L

ps

· (i

1

– i

o

), [kJ/kg]

[4.16]

gdzie:

q = Q

2

/M

w

- zużycie ciepła na odparowanie 1 kg

wody,

- ilość powietrza suchego potrzebnego

do

odparowania 1 kg wody.

Jeżeli temperatura suszonego materiału t

w

= 0°C, to z

równania [4] wynika, że i

2

= i

1

, czyli podczas suszenia

teoretycznego entalpia powietrza nie zmienia się. Ciepło
oddane przez powietrze na odparowanie wody zostaje mu
w procesie suszenia zwrócone w postaci pary wodnej
zawierającej w sobie ciepło potrzebne do jej wytworzenia.
Dlatego na wykresie i – d przebieg suszenia reprezentuje
linia równoległa do linii stałych entalpii.





w

w

o

w

w

t

C

i

i

M

L

M

Q

q











2

2

1

2

1

d

d

L

M

L

ps

w







Bilans cieplny suszarni

teoretycznej – przykład

Do suszarni jednostopniowej podawane jest powietrze
atmosferyczne o temperaturze 20°C i zawartości wilgoci d
= 11 g/kg suchego powietrza, które w podgrzewaczu
zostaje podgrzane do temperatury 85°C, a następnie
wprowadzone do suszarni.

Powietrze odlotowe z suszarni ma zawartość wilgoci d =
24 g/kg przy temperaturze 50°C. Do suszarni, w ilości
1000 kg/godz., podawany jest materiał, którego wilgotność
bezwzględna wynosi 8%. W suszarni materiał ten
wysuszony jest do wilgotności bewzględnej 0,5%. Ciepło
właściwe wody C

w

= 4,2119 kJ/(kg·K).

Przy założeniu teoretycznego przebiegu przeprowadzić
należy

graficzną

analizę

procesu

oraz

określić

zapotrzebowanie powietrza atmosferycznego oraz ciepła
na odparowanie 1 kg wilgoci.

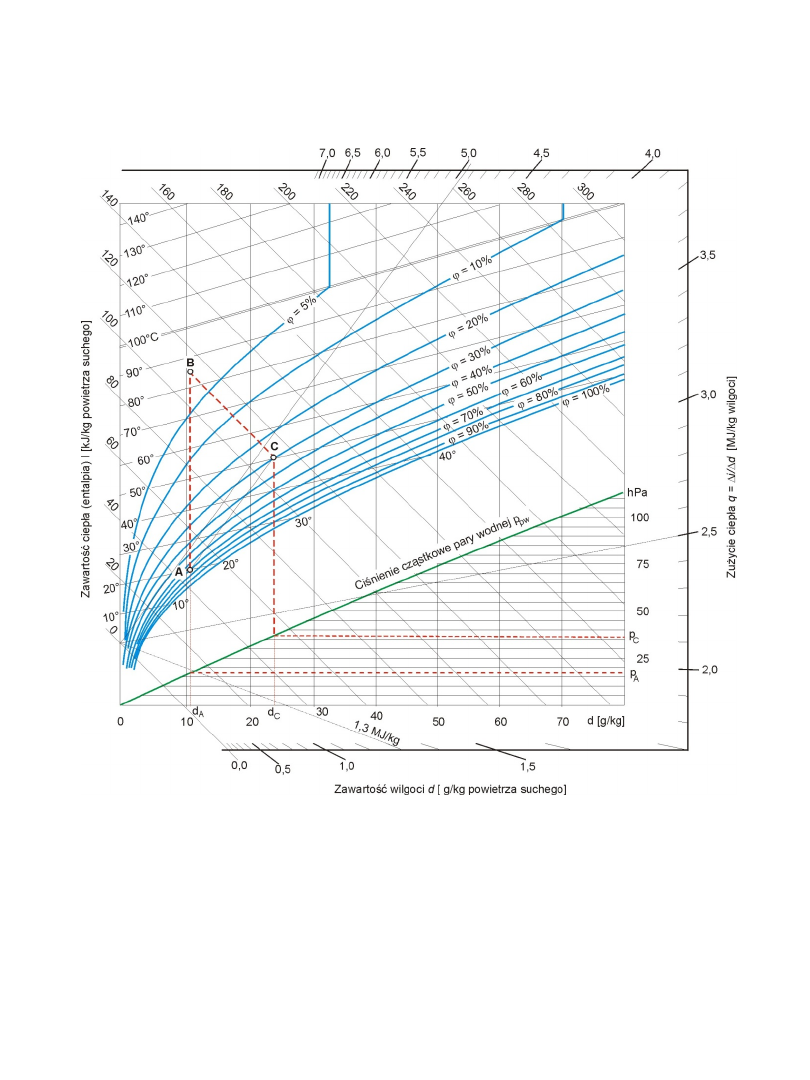
Bilans cieplny suszarni teoretycznej –

przykład – graficzna analiza procesu

Parametry powietrza początkowe, punkt A: i

A

=48 kJ/kg;



A

=70%,

Parametry powietrza podgrzanego, punkt B: d

A

=d

B

=11g/kg; i

B

=115

kJ/kg;



B

3%,

Ilość ciepła zużyta na podgrzanie powietrza w nagrzewnicy (równa
różnicy końcowej i początkowej pojemności ciepła): i

B

-i

A

=67kJ/kg,

Parametry powietrza opuszczającego suszarnię, punkt C (leżący na
tej samej linii pojemności ciepła i

B

- suszenie teoretyczne):



C

=30%.

Bilans cieplny suszarni teoretycznej – przykład –

określenie zapotrzebowania na powietrze

atmosferyczne potrzebne do odparowania 1 kg

wilgoci

Ilość odparowanej w suszarni wilgoci, przypadającej na 1 kg
powietrza suchego, równa jest oczywiście ilości wilgoci, o którą
powietrze się wzbogaciło, a więc: d

C

– d

B

= d

C

– d

A

= 24 – 11 = 13

g/kg suchego powietrza. Strumień suchego wsadu wynosi:

, kg/h

Strumień odparowanej wilgoci wynosi:

, kg/h

Zapotrzebowanie na suche powietrze suszenia:

, kg/h

Stąd ilość suchego powietrza potrzebna na odparowanie 1 kg
wilgoci:

, kg/kg wilgoci

odpowiadającą ilości powietrza atmosferycznego równej:

, kg/kg wilgoci

926

8

100

1000

100

100

100















W

G

G

s

69

100

5

,

0

8

926

100

2

1













W

W

G

M

s

w

5308

11

24

1000

69

1000















B

C

w

ps

d

d

M

L

77

13

1000

69

5308

1000













A

C

w

ps

p

d

d

M

L

L

8

,

77

11

24

11

1000

1000















A

C

A

a

d

d

d

L

Bilans cieplny suszarni teoretycznej –

przykład – określenie zapotrzebowania na

ciepło potrzebne do odparowania 1 kg wilgoci

Ogólne zapotrzebowanie na ciepło wynosi:

, kJ/h

Zużycie ciepła przypadające na odparowanie 1 kg wilgoci
wyznacza na wykresie poprowadzona z punktu zerowego linia
prosta równoległa do odcinka łączącego punkty A i C, tj. punkty
początkowego i końcowego stanu powietrza. Z wykresu
odczytujemy, że na odparowanie 1 kg wilgoci zużywane jest 4980
kJ ciepła.

Z równania na zużycie ciepła na odparowanie 1 kg wody
wyliczymy, że

,MJ/kg odparowanej wody

349823

20

2119

,

4

69

67

5308

)

(

2























w

w

w

A

C

ps

t

C

M

i

i

L

Q

07

,

5

69

349823

2







w

M

Q

q