Fizyka II

Zagadnienia

• Elektromagnetyzm
• Elementy mechaniki kwantowej
• Elementy fizyki ciała stałego

Elektromagnetyzm

• Elektrostatyka
• Prąd stały
• Magnetyzm
• Zjawiska elektro-magnetyczne

Elektrostatyka

• Ładunek elektryczny
• Prawo Coulomba
• Pole elektryczne
• Natężenie pola
• Potencjał pola i napięcie

Ładunek elektryczny

-

Elektryzowanie przedmiotów przez pocieranie

- Przyciąganie , odpychanie dwa rodzaje elektryczności

- Ładunek elektryczny q

- Dodatni (szkło, skóra), ujemny (futro, ebonit)

-[q] – 1 C (kulomb) -= 1 A s

Elektroskop

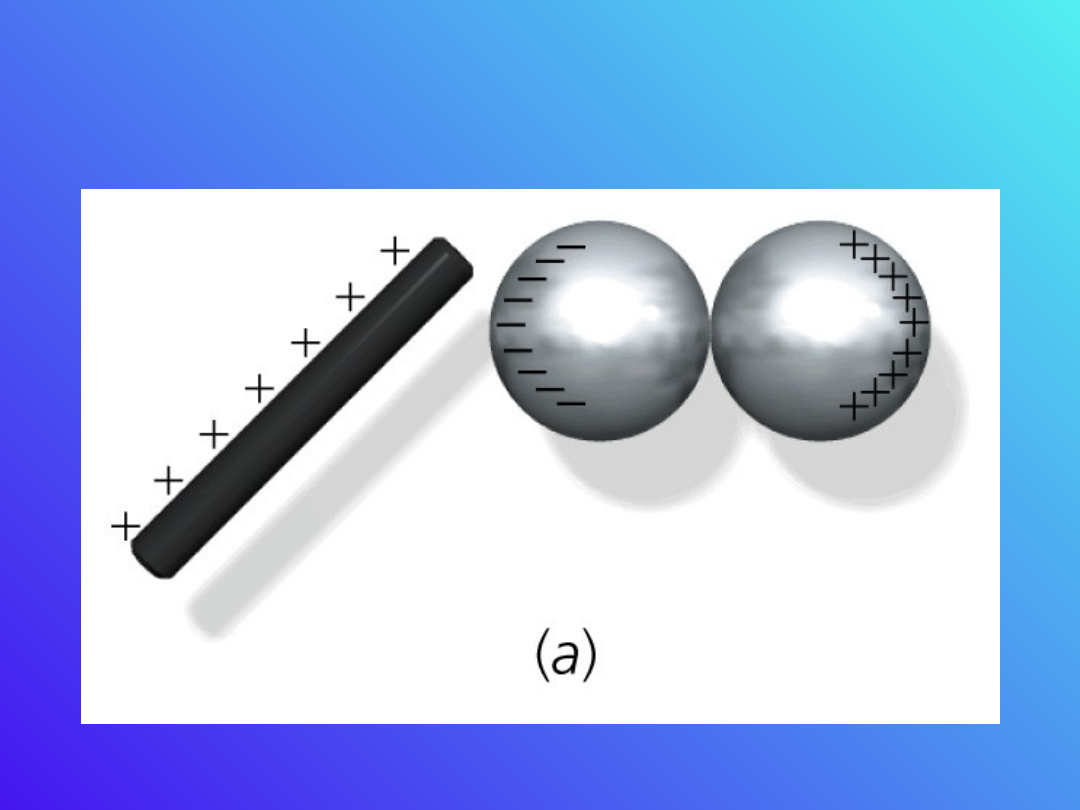
Elektryzowanie przez tarcie i

przez indukcję

Prawo Coulomba

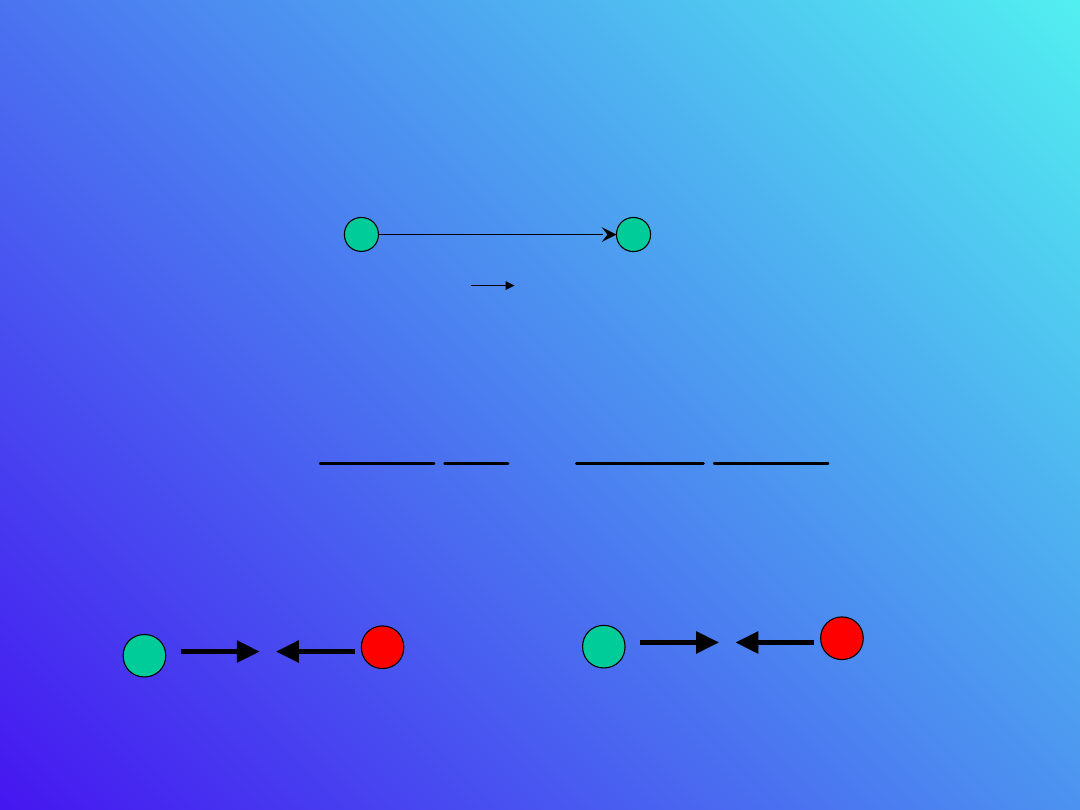
Siła Coulomba

12

3

12

2

1

0

12

12

2

12

2

1

2

1

r

r

q

q

4

1

r

r

r

q

q

k

F















q

1

q

2

r

12

+

-

+

-

Superpozycja sił Coulomba

Pole elektryczne

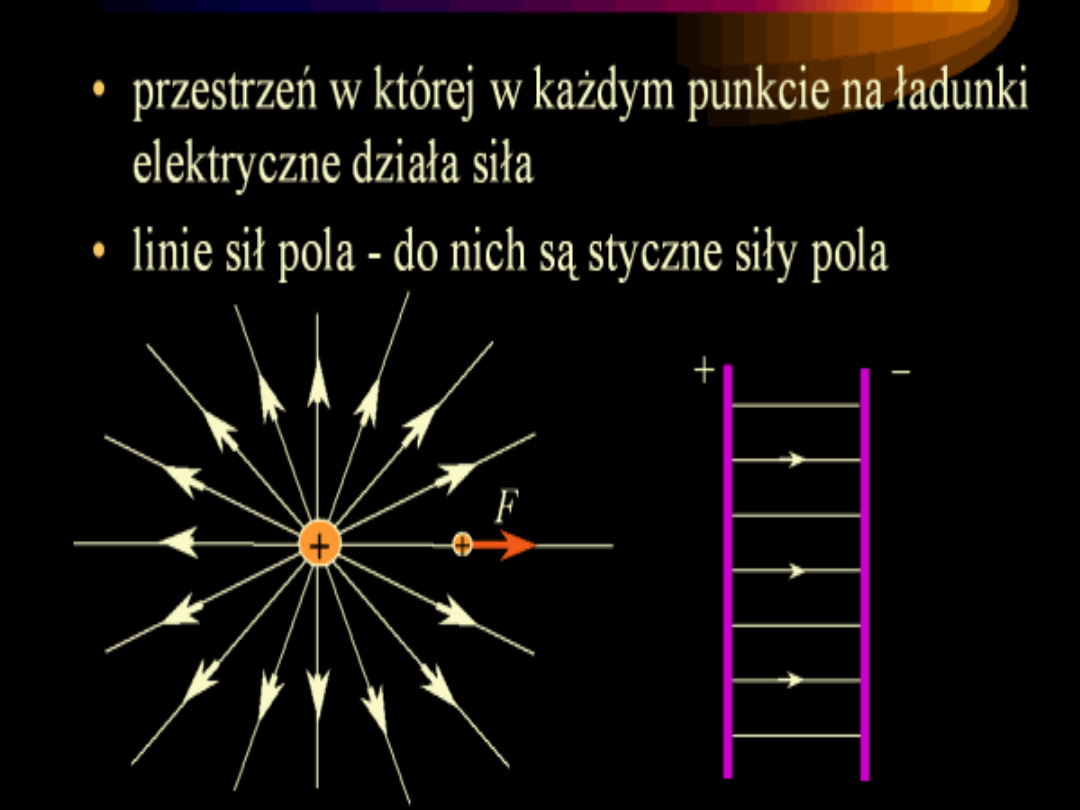
Pole

elektryczne

Pole ładunku punktowego

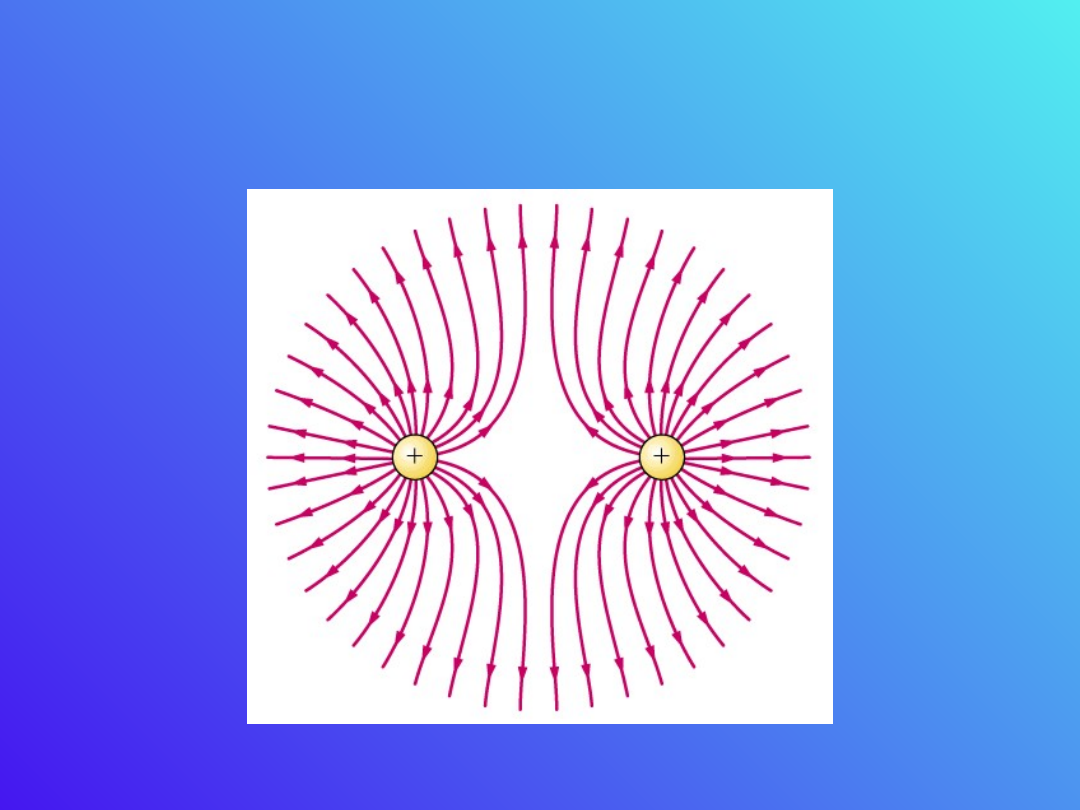
Pole ładunków jednakowego

znaku

Dipol elektryczny

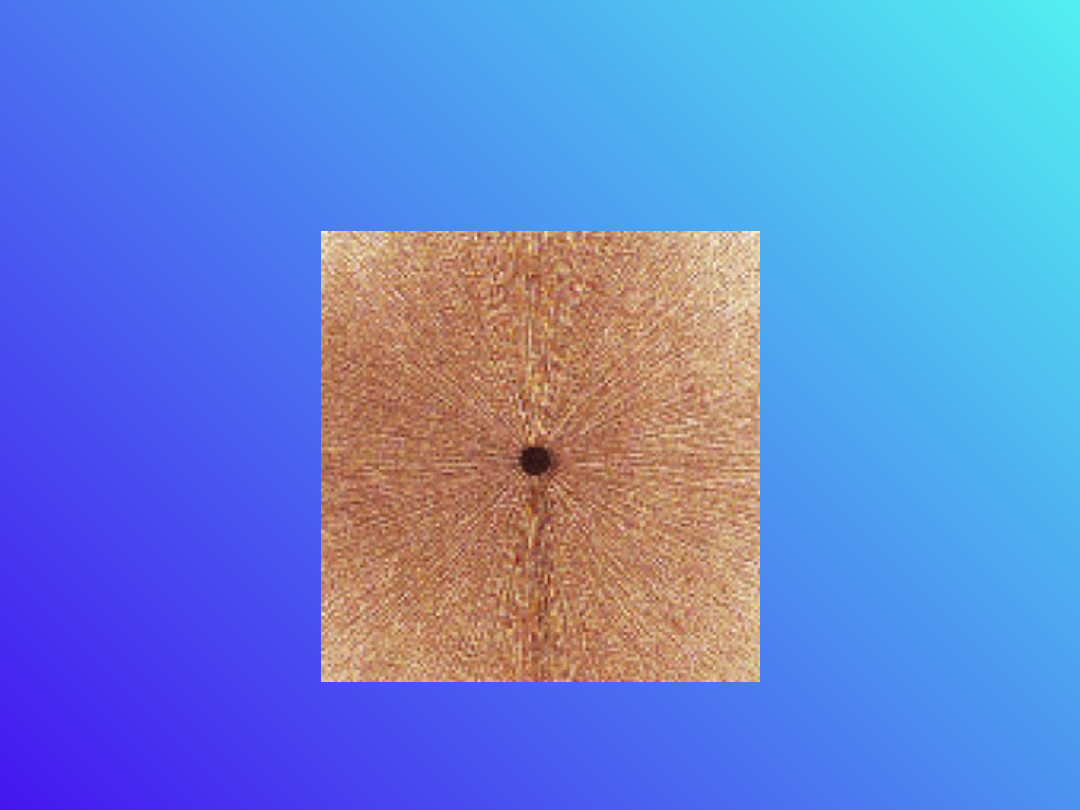
Jak można zobaczyć linie

pola?

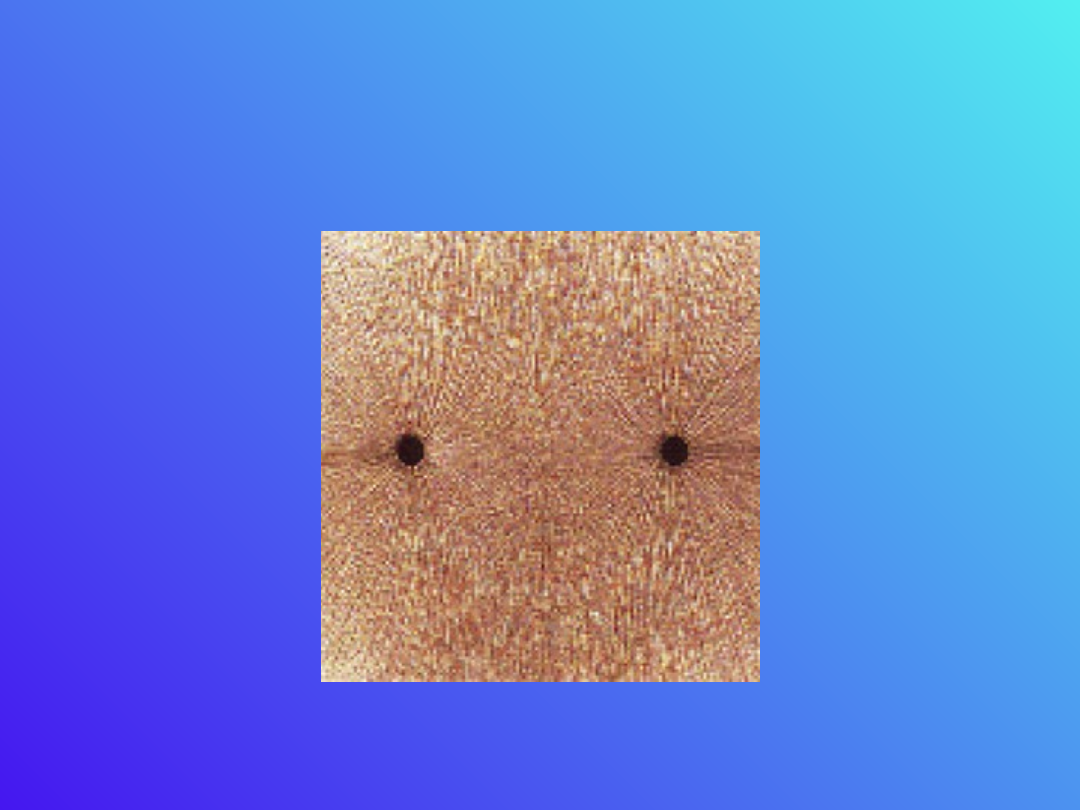
Obraz pola ładunków

jednoimiennych

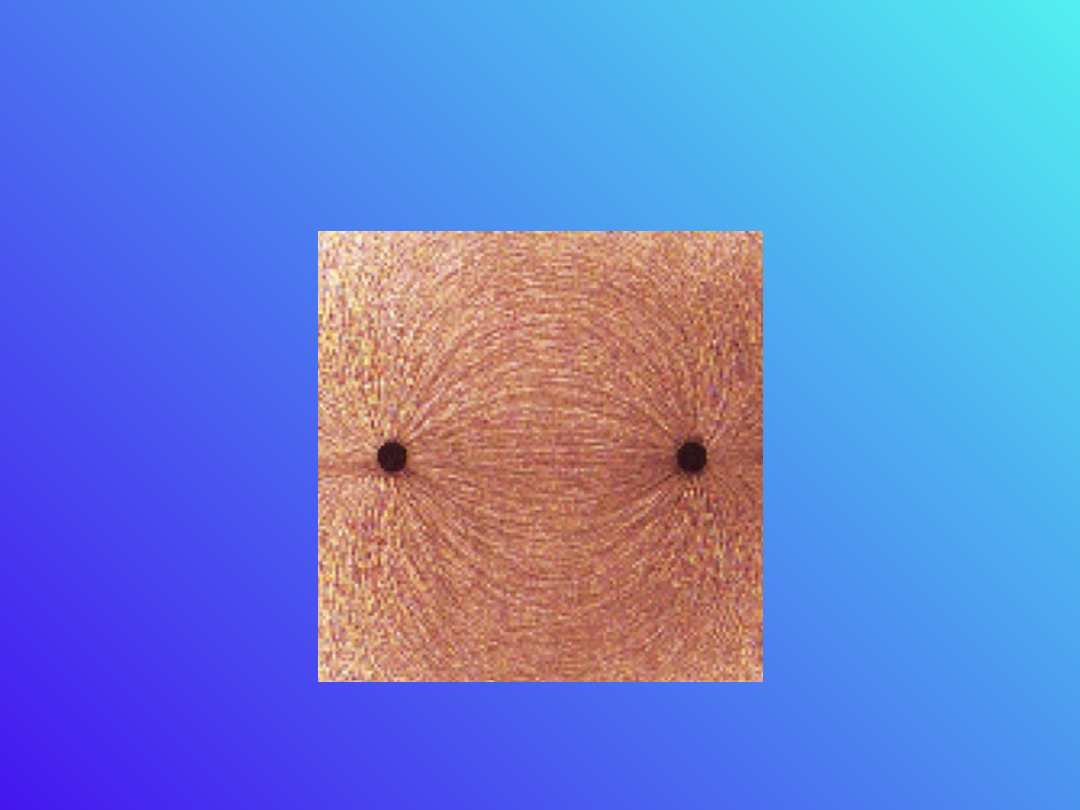
Obraz pola dipola

elektrycznego

Pole dipola magnetycznego

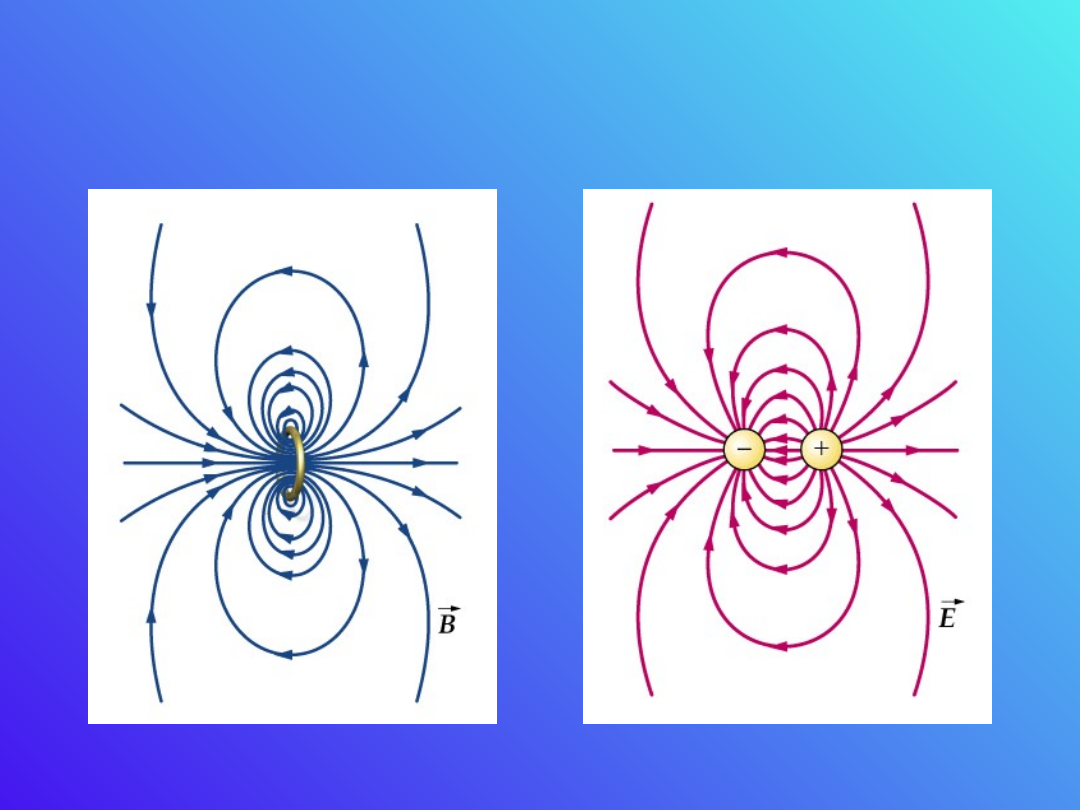
Porównanie dipoli elektr. i

magnet.

Natężenie pola

Jak liczyć natężenie pola
gdy ładunek nie jest punktowy?

Potencjał
pola

Napięcie

Dipol w jednorodnym polu

elektryczny

Elektrostatyka

• Prawo Gaussa
• Przewodnik izolowany
• Pojemność elektryczna
• Kondensatory
• Dielektryki
• Energia pola elektrycznego

Definicja pola

Pole możemy zdefiniować na dwa sposoby

:

• matematycznie

jako

przestrzenny rozkład
liczb

(pole

skalarne),

lub przestrzenny rozkład wektora,

(pole wektorowe)

• fizycznie

jako przestrzenny

rozkład

wielkości fizycznej

Zajmijmy się w dalszym ciągu polami
fizycznymi

.

Wiemy, że wielkości fizyczne mogą być
skalarne, wektorowe, a nawet tensorowe.
Zobaczmy poniższe przykłady.

W danym punkcie przestrzeni pole
opisane jest przez pewną funkcję:

)

,

,

(

z

y

x

f

f 

Pole może być płaskie lub przestrzenne.
Stałe wartości pola są wyznaczone przez

izopowierzchnie

lub

izolinie

.

Pole wektorowe scharakteryzowane jest przez
wektor pola

)

(r

v 



.

Liniami pola wektorowego nazywamy linie
wyznaczające kierunek pola.
Wektor pola jest w każdym punkcie styczny do
linii pola.

v

S

dS









S

S

d

v







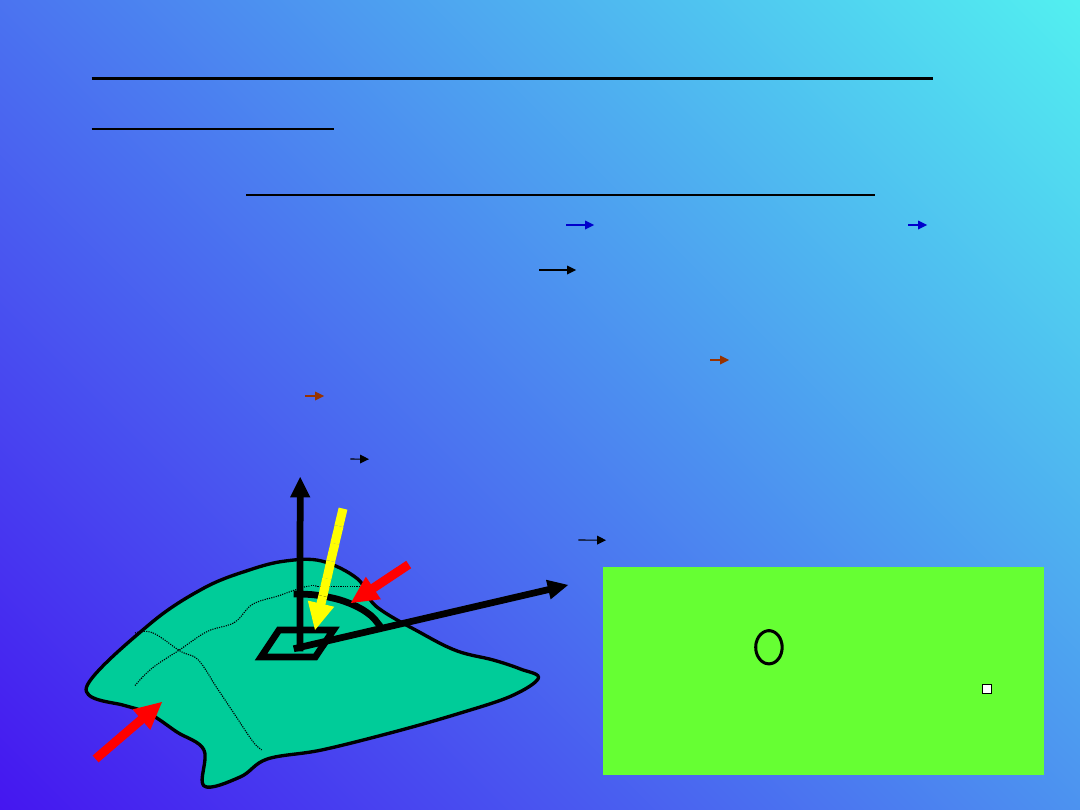
Pojęcia matematyczne przydatne do
opisu pola

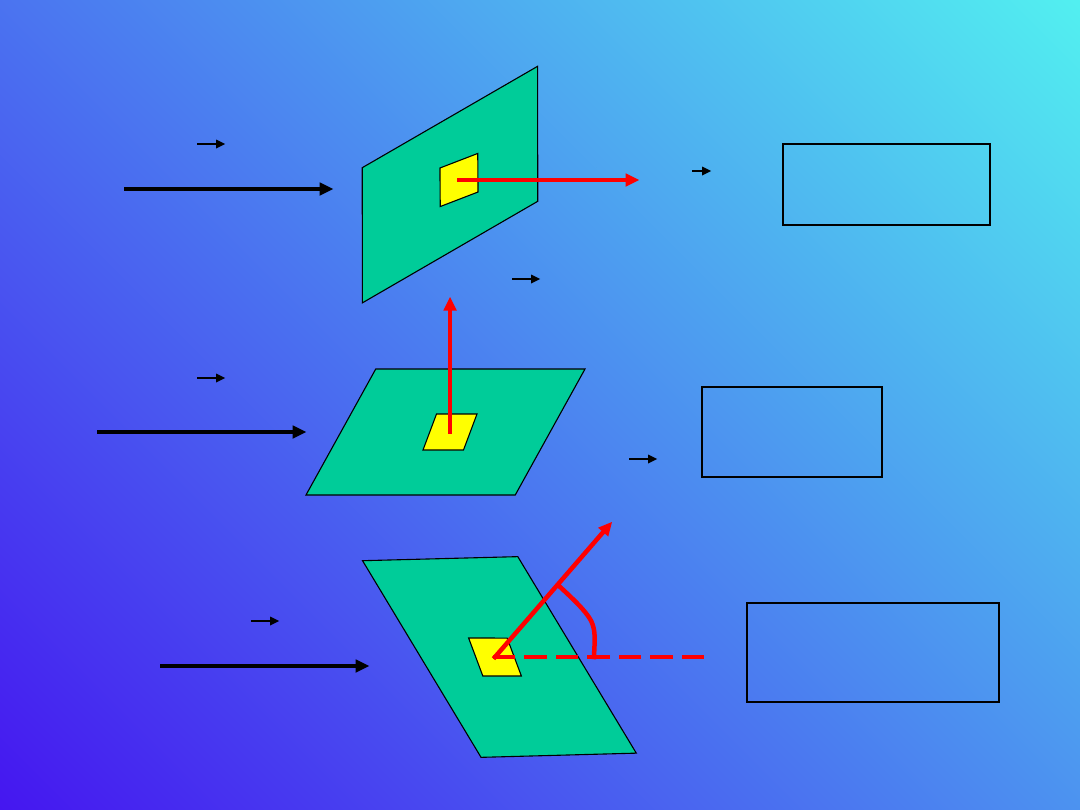
Strumień wielkości wektorowej

Strumień wielkości wektorowej

v przez

powierzchnię ds. reprezentowanej przez wektor
dS. normalny skierowany na zewnątrz
powierzchni zamkniętej powierzchni jest równy

iloczynowi składowej normalnej wektora v przez
pole powierzchni dS

dS

dS

dS

v

v

v

v













0

v
S

60

o

½ v
S

Gradient pola

Jeśli chcemy wyznaczyć

przyrost funkcji

pola skalarnego

)

(r

s 

przy zmianie

położenia

r

d

to w układzie kartezjańskim

gdzie

)

,

,

(

z

y

x

f

s 

,

przyrost ten

jest

sumą iloczynów pochodnych funkcji

f

względem współrzędnych i
różniczek współrzędnych.

dz

z

f

dy

y

f

dx

x

f

ds



















Przyrost ten możemy przedstawić jako iloczyn skalarny dwóch
wektorów,

r

d

gradf

ds







gdzie

0

0

0

z

dz

y

dy

x

dx

r

d















a

0

0

0

z

z

f

y

y

f

x

x

f

f

grad

























Aby uzyskać gradient funkcji musimy na nią podziałać pewnym
operatorem, który nazywamy

 -

nabla.

0

0

0

z

z

y

y

x

x





























f

f

grad







Dla przypomnienia zdefiniujmy sobie jeszcze dwie pozostałe

wielkości przy pomocy których możemy scharakteryzować

pole fizyczne.

Są to:

Diwergencja

i

rotacja

Dywergencja funkcji wektorowej

Dywergencję wektora pola

v(r)

otrzymamy, jeśli dodamy dodamy do siebie
pochodne składowych wektora względem
odpowiednich współrzędnych.

z

v

y

v

x

v

v

div

z

y

x





















Pamiętając, że wektor

0

0

0

z

v

y

v

x

v

v

z

y

x















,

możemy napisać, że

v

v

div













Strumień wektora
powierzchnię zamkniętą
jest powiązany
z dywergencją tego
wektora
następującą zależnością:

dV

v

v

dV

v

div

S

d

v

S













S





W oparciu o ten wzór możemy stwierdzić, że

dywergencja

jest

przestrzenną gęstością strumienia pola wektorowego.



















S

V

S

S

d

v

S

d

v

dV

v

div

V











1

lim

0

1

Cyrkulacja (krążenie) pola wektorowego.

Niech będzie dowolnym polem wektorowym, a

ds

v

s

d

v

C

t



















v

s

d

s

d

s

d

v

v

v



s

d

niech będzie styczną
do

zaznaczonej
krzywej



wtedy całkę
krzywoliniową

nazywamy

cyrkulacją pola wektorowego

po krzywej
zamkniętej.

t

v

Rotacja pola wektorowego.

Rotacją pola wektorowego

nazywamy iloczyn wektorowy

Operatora wektorowego i wektora pola .





v

v

v

rot

v













Rotacja jest wektorem, którego
składowe są równe:

v

0

x

0

z

0

z

z

)

y

v

x

v

(

y

)

x

v

z

v

(

)

z

v

y

v

(

v

rot













































y

x

y

x

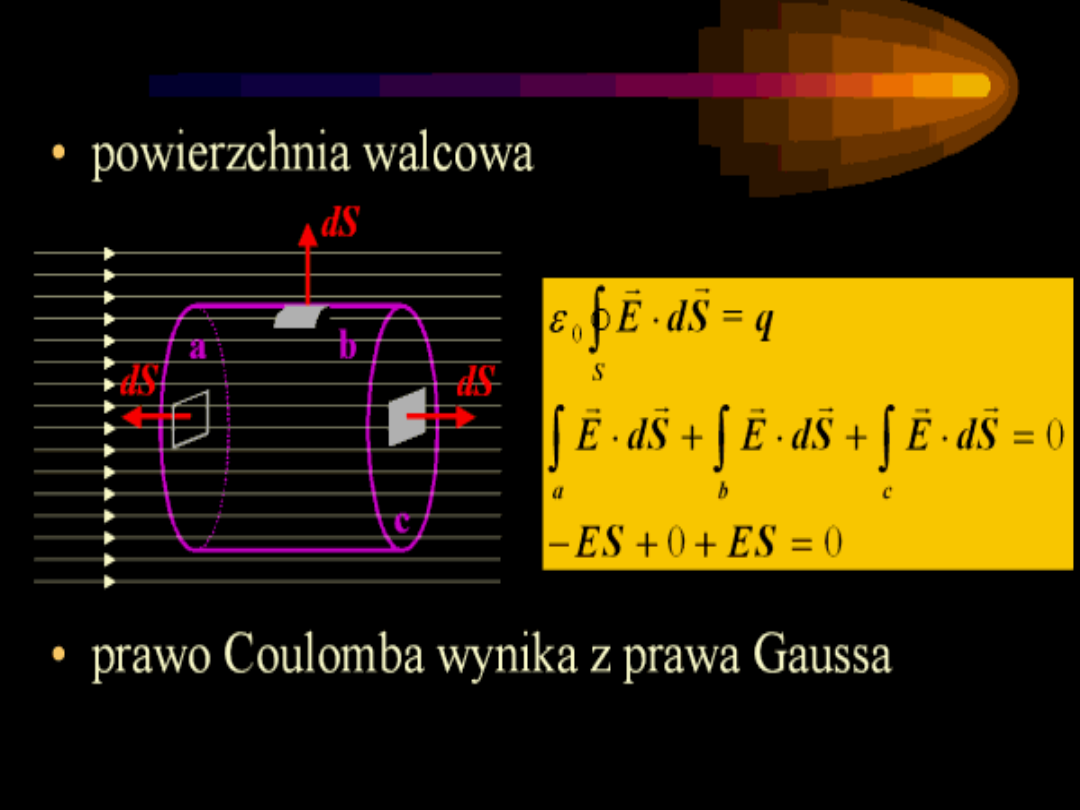
Przewodnik izolowany

Wyznaczanie natężenia pola

elektrycznego od obiektów o wysokiej

symetrii

.

•Jednorodna przewodząca kula

•Jednorodny nieskończony pręt

•Nieskończona naładowana płaszczyzna

Pojemność
elektryczna

Kondensatory

Pojemność
elektryczna

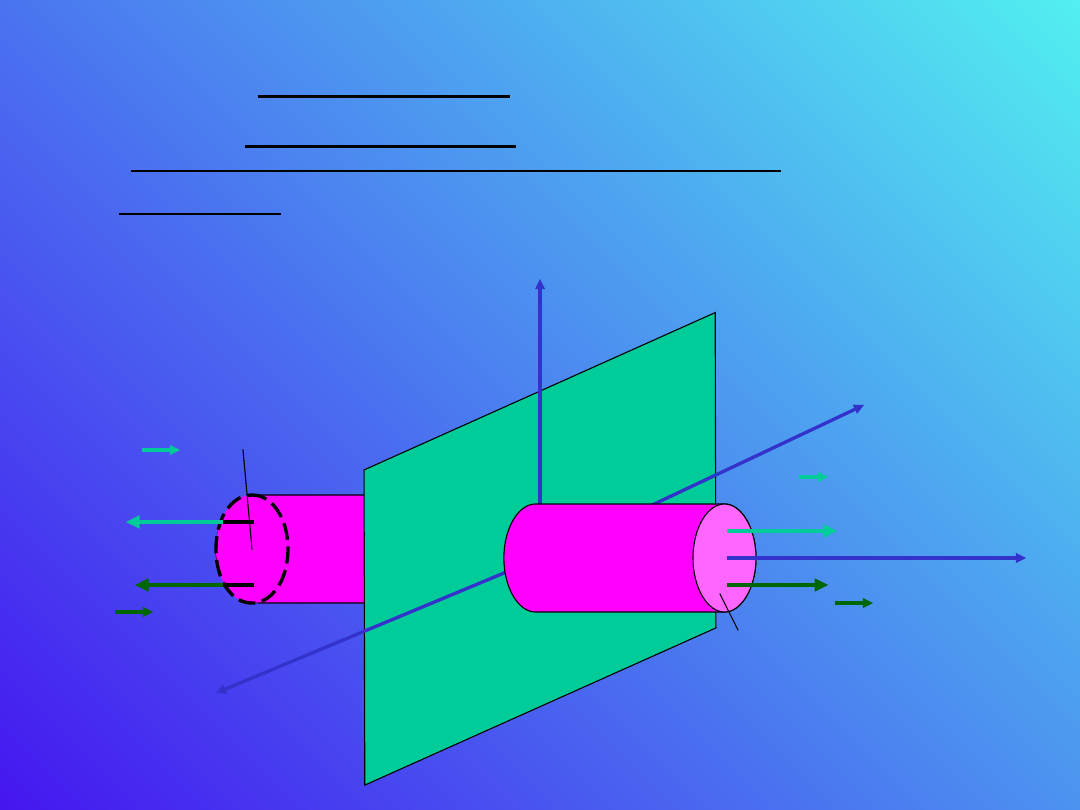
Pole nieskończonej naładowanej
warstwy

x

z

y

+


E

1

dS

1

S

1

E

2

dS

2

S

2

-ładunek

powierzchniow
y

Natężenie pola elektrycznego pochodzące od
nieskończonej naładowanej warstwy możemy
wyznaczyć dwoma sposobami, metodą superpozycji,
oraz w oparciu o prawo Gaussa.

Zgodnie z prawem Gaussa całkowity strumień
jest równy

0



Q





Linie natężenia pola elektrycznego są prostopadłe
do naładowanej płaszczyzny, wobec tego całkowity
strumień wynosi:

)

(

2

2

1

1











S

S

d

E

S

d

E











Widzimy z
rysunku, że

2

1

2

1

,

E

E

S

d

S

d

















Całkowity strumień jest więc
równy:

0

0

2









S

Q

S

E











Czyli:

0

2







E



Pole pochodzące od tej warstwy wygląda
następująco:

y

z

0

0

ˆ

2

y

E









0

0

ˆ

2

y

E











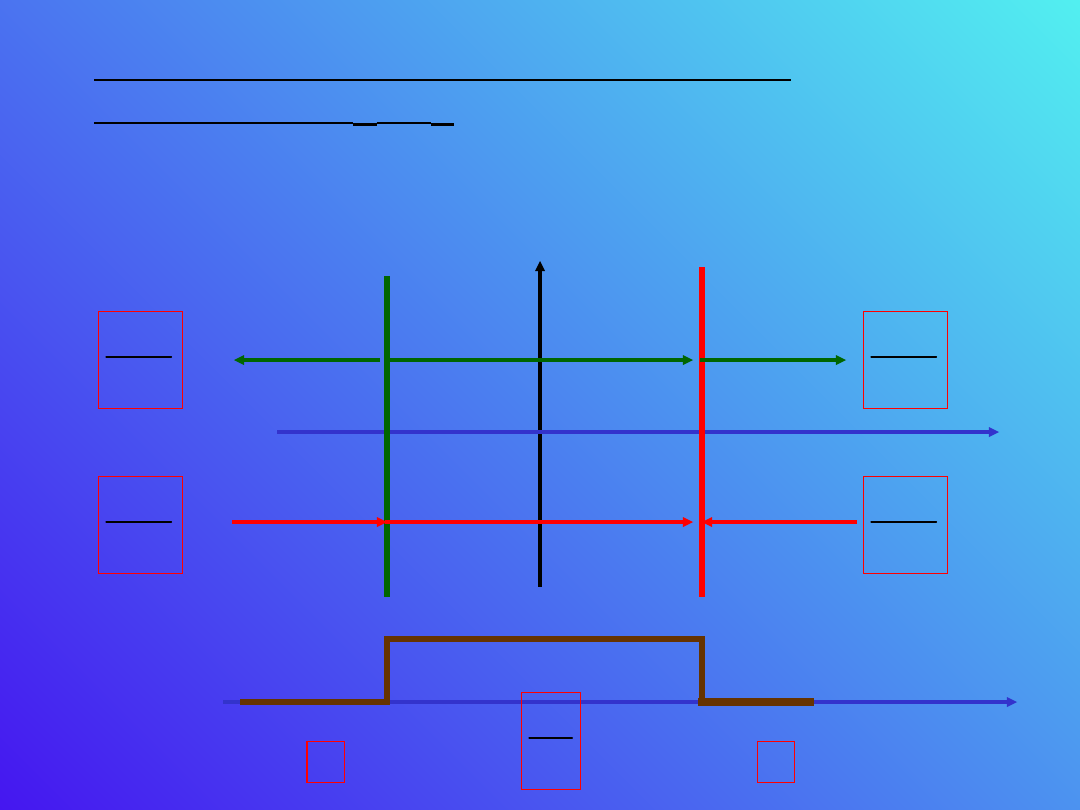
Pole między dwoma naładowanymi
warstwami + i -

Zastanówmy się jaka jest wartość pola pomiędzy
dwoma przeciwnie naładowanymi warstwami.

+

-

0

2





0

2





0

2





0

2





y

0





0

0

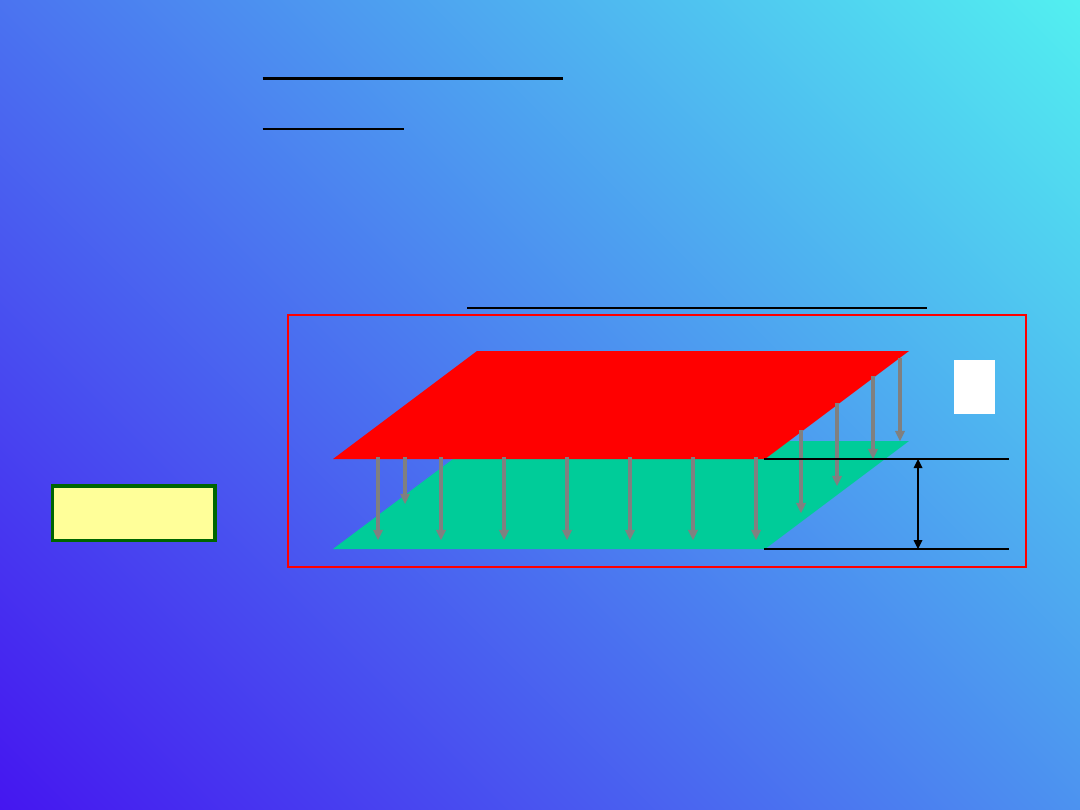
Kondensator

płaski

+Q

-Q

Eˆ

Zajmijmy się układem dwóch płasko-równoległych
przewodników (elektrod) o powierzchni S
położonych w odległości d od siebie. Elektrody są
naładowane odpowiednio ładunkami +Q i –Q.
Układ taki nazywamy kondensatorem płaskim.

d

S

Gęstość
powierzchnio
wa ładunku
wynosi:

 = Q/S

Pole wewnątrz elektrod z pominięciem efektów
brzegowych jest jednorodne.

Niech różnica potencjałów pomiędzy elektrodami
wynosi V.

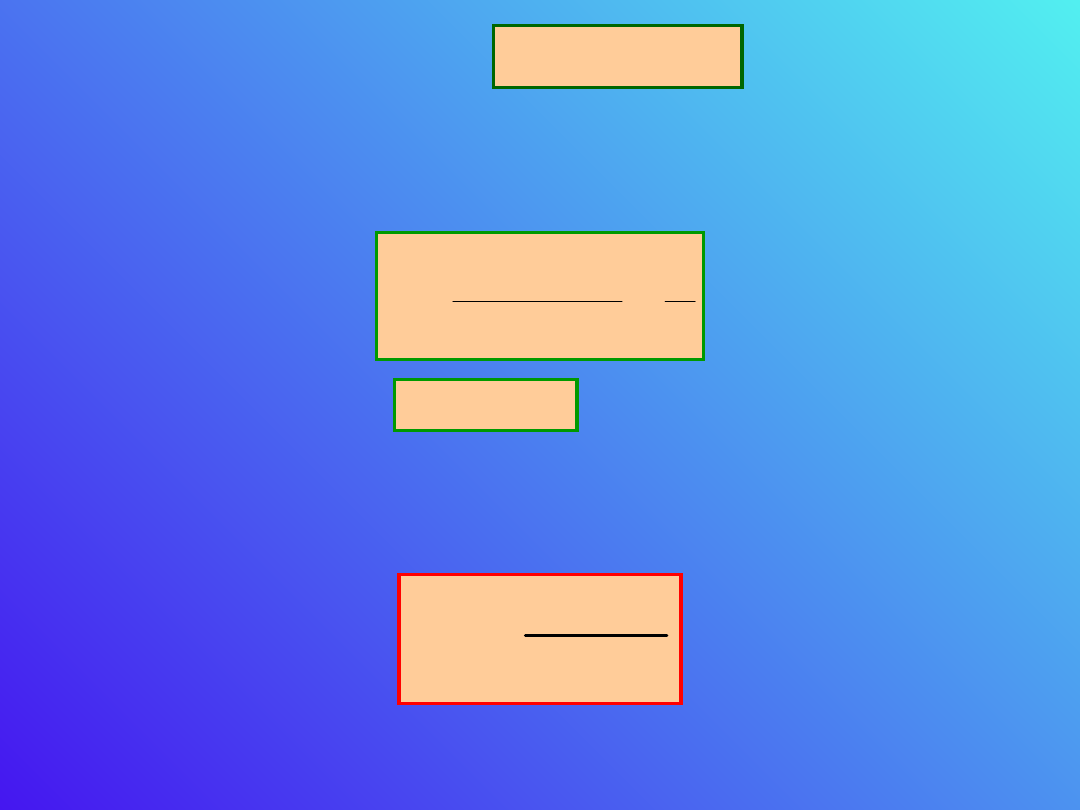
Oznaczmy tą różnicę
przez

)

(

2

)

(

1









V

V

V

.

Z zależności pomiędzy potencjałem a natężeniem
pola elektrycznego otrzymujemy, że:

d

V

d

V

V

E











)

(

2

)

(

1

Widzimy więc,
że:

d

E

V





, a korzystając z
obliczonej

poprzednio wartości natężenia pola
elektrycznego pomiędzy dwoma naładowanymi
płaszczyznami otrzymujemy:

S

d

Q

V







0



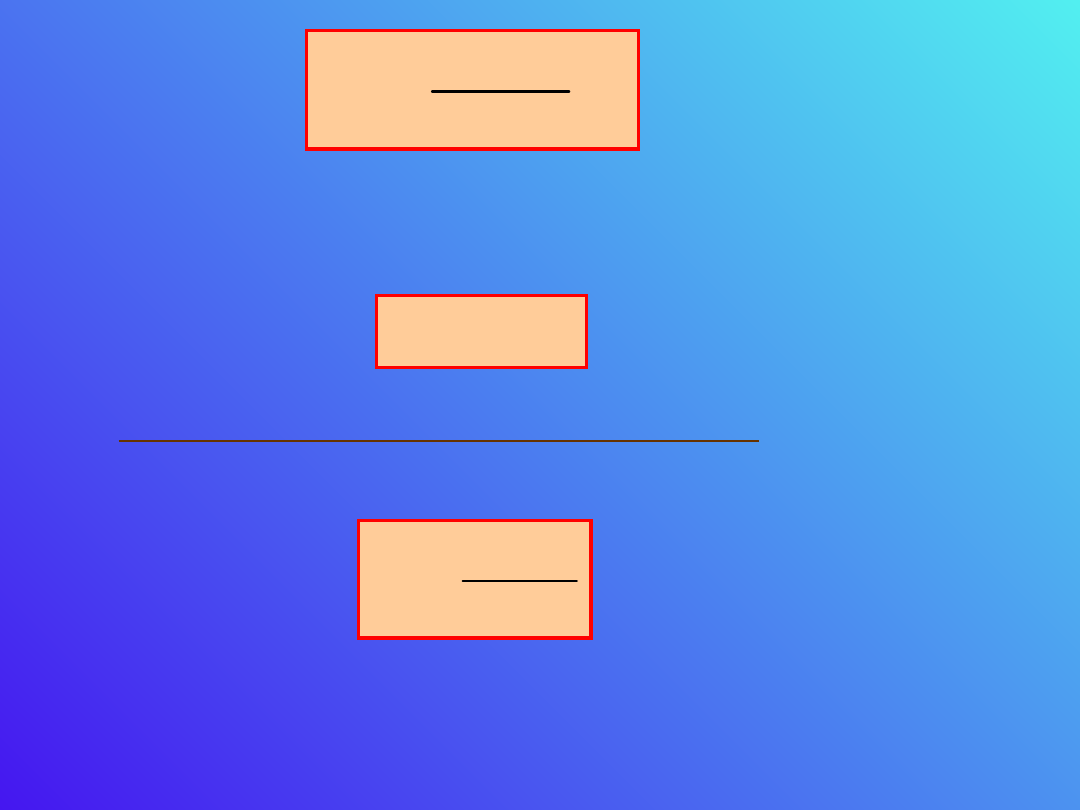
Wprowadźmy pojęcie pojemności

kondensatora

jako

współczynnika we wzorze:

V

C

Q





Pojemność kondensatora płaskiego
wynosi więc:

d

S

C





0



V

d

S

Q





0



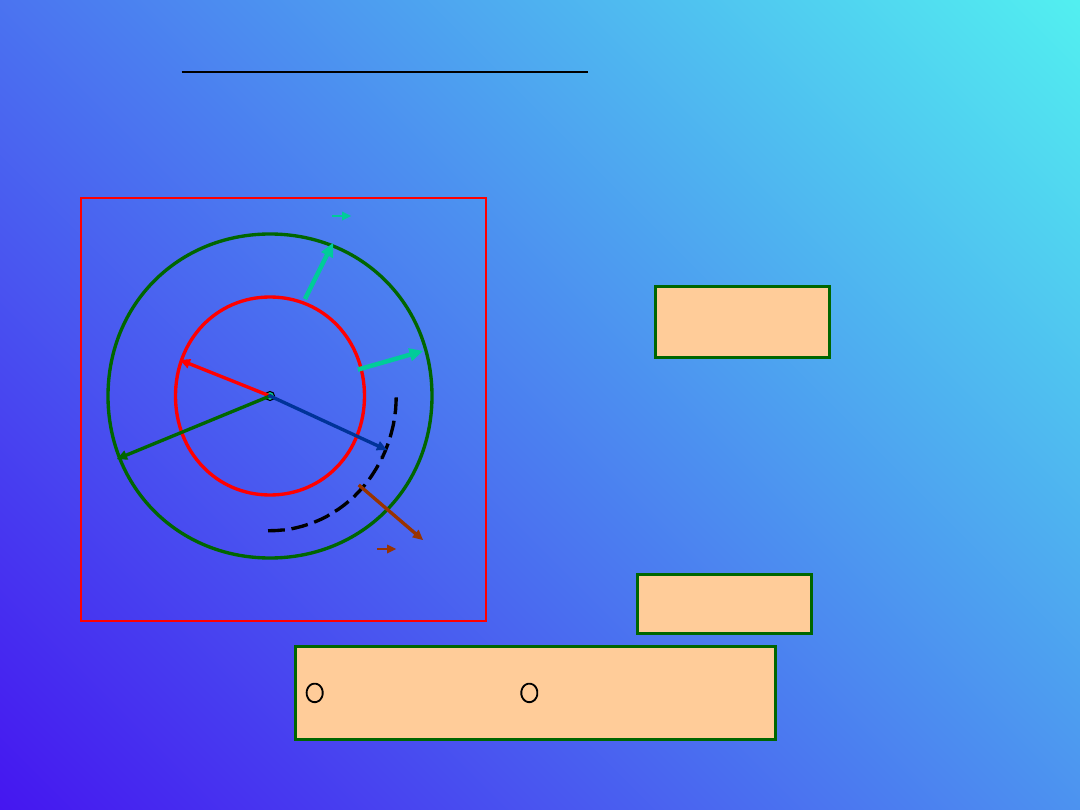
Kondensator kulisty

Rozpatrzmy układ dwóch współśrodkowych czasz
kulistych naładowanych odpowiednio ładunkami
+Q i –Q.

-Q

+
Q r

1

r

2

E

d
S

Pole elektryczne dla
takiego układu jest polem
radialnym, więc

)

(r

E

E







Policzmy strumień pola
elektrycznego
przechodzącego przez
powierzchnię kuli w
środku „0” i promieniu R

2

1

r

R

r





.

E

R

S

d

E

S

d

E











2

4









R

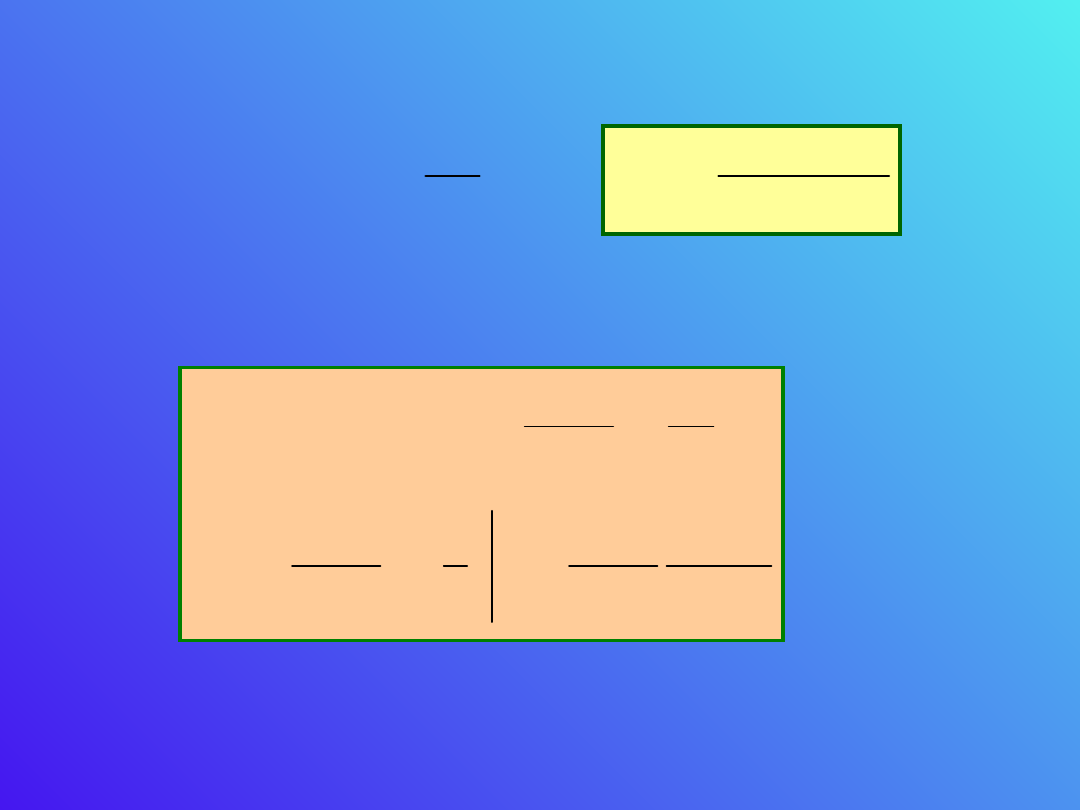
Z prawa Gaussa
otrzymamy:

2

0

0

2

4

4

R

Q

E

Q

E

R













dla dowolnego R z podanego poprzednio
przedziału.

Różnica potencjałów V=V

1

– V

2

wartość:

2

1

1

2

0

0

2

0

4

1

4

4

2

1

2

1

2

1

r

r

r

r

Q

r

Q

r

dr

Q

dr

E

V

r

r

r

r

r

r

r

















 



























Zgodnie z wzorem otrzymujemy na pojemność
kondensatora złożonego z dwóch czasz kulistych
wyrażenie:

1

2

2

1

0

4

r

r

r

r

C









Z wyrażenia tego widać, że gdy
pojemność kondensatora kulistego, inaczej
mówiąc pojemność przewodnika będącego kulą
jest równa:





2

r

1

0

4

r

C







Jednostką pojemności w układzie SI jest
FARAD.





2

4

1

2

1

1

1

1

A

s

kg

m

V

C

F









Pojemność kuli ziemskiej, R~6.4 10

6

m, C = 710

F, a kula o pojemności 1F ma promień 9 10

6

km.

Pow.

+Q

-Q

a

b

l

r

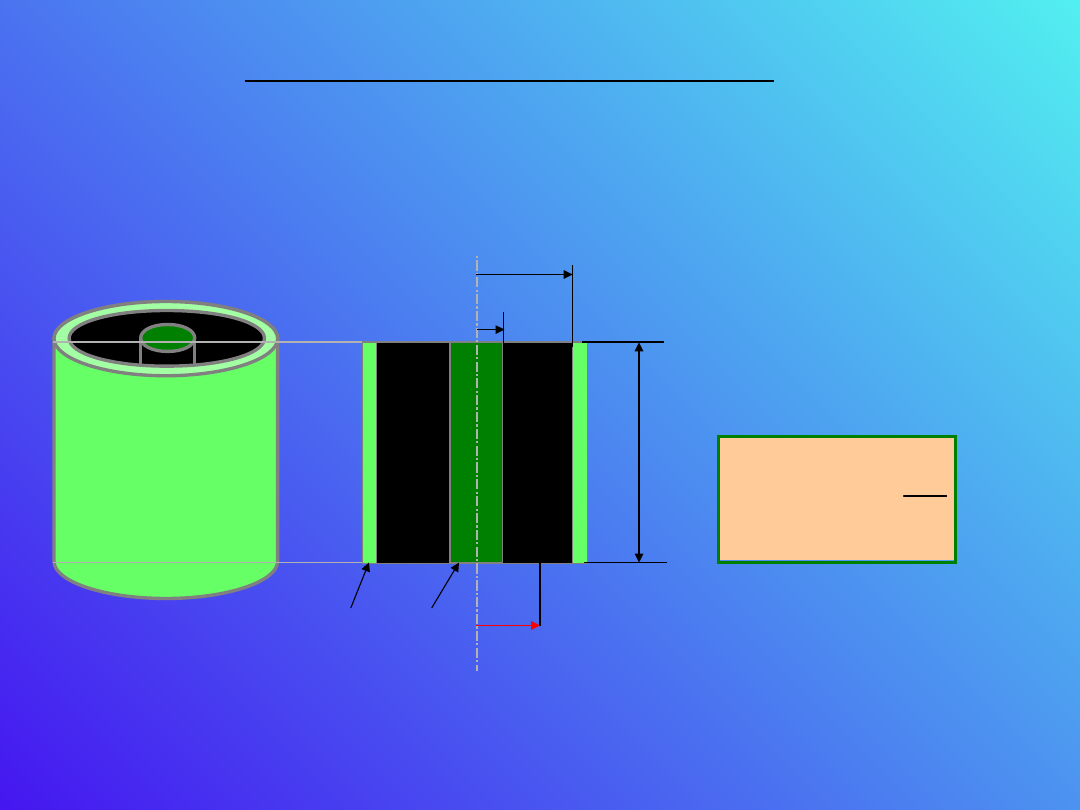
Kondensator cylindryczny.

Kondensator cylindryczny składa się z dwóch
współśrodkowych cylindrów o p promieniach a i b.

Stosując Prawa
Gaussa dla
dowolnej
odległości r od
środka walców
otrzymujemy, że

0

2





Q

rl

E





Na wartość potencjału otrzymamy więc
wyrażenie:





















































a

b

l

Q

a

b

l

Q

b

a

l

Q

dr

r

l

Q

dr

rl

Q

Edr

V

a

b

a

b

a

b

ln

2

ln

ln

2

ln

ln

2

1

2

2

0

0

0

0

0



























a

b

l

V

Q

C

ln

2

0



Pojemność kondensatora cylindrycznego
wynosi więc:

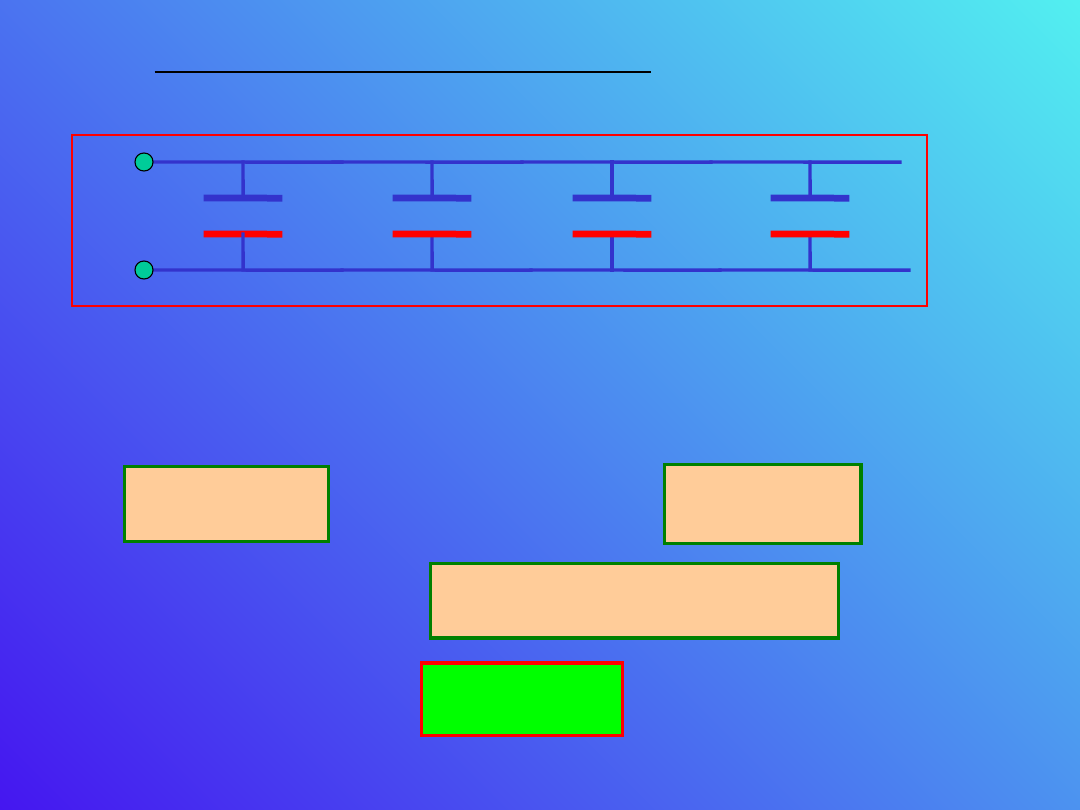
Łączenie kondensatorów
Połączenie równoległe

+Q

1

-Q

4

C

1

V

1

V

2

C

2

C

3

C

4

+Q

2

+Q

3

+Q

4

-Q

2

-Q

3

-Q

1

Potencjał V = V

1

– V

2

jest taki sam na każdym

kondensatorze.

Ładunek, który znajduje się na każdym z
kondensatorów

V

C

Q

i

i





, a całkowity ładunek





i

i

Q

Q

.

Otrzymujemy więc













i i

i i

C

V

V

C

Q

. Czyli





i

i

C

C

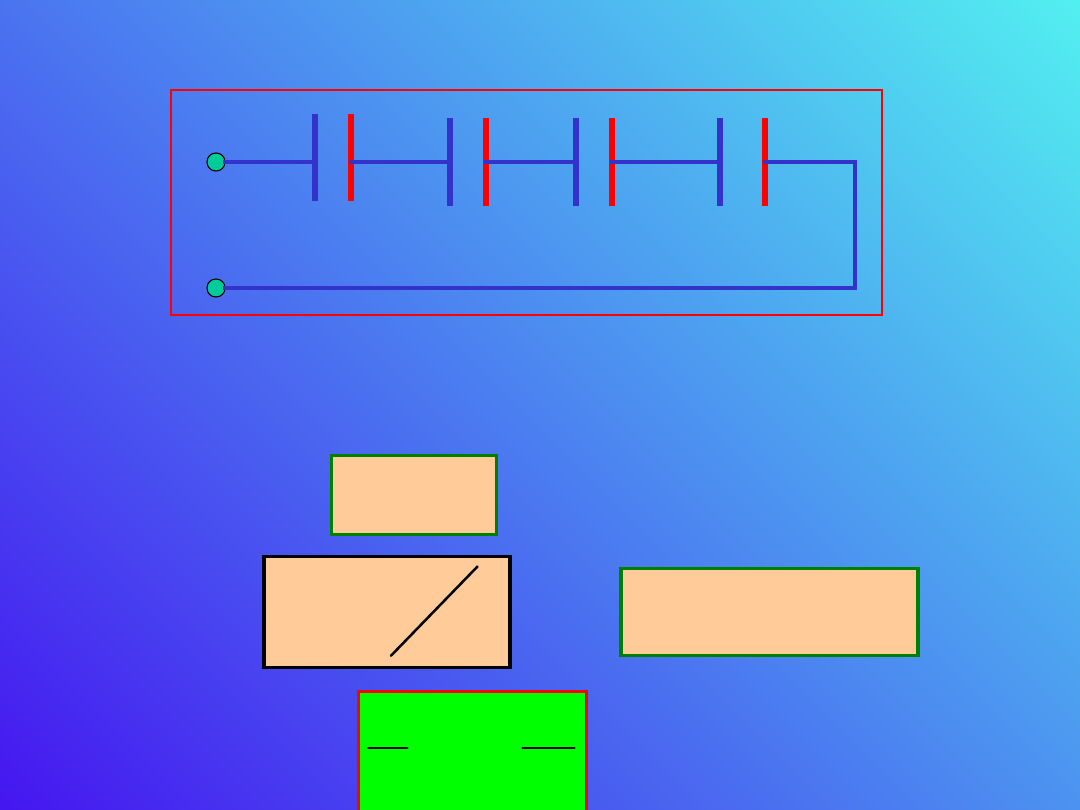
Połączenie szeregowe

V

1

+Q

+Q

+Q

+Q

-Q

-Q

-Q

-Q

V

C

1

C

2

C

3

C

4

V

2

V

3

V

4

Ładunki na okładkach kondensatorów połączonych
szeregowo są jednakowe. Całkowita różnica
potencjałów jest równa sumie różnic potencjałów
między okładkami poszczególnych kondensatorów
.





i i

V

V

i

i

C

Q

V 

Wiemy, że
czyli







1

/

1

i

C

Q

V

.





i

i

C

C

1

1

Ziemia jako kondensator
kulisty

Mimo, że wydaje się nam, że Ziemia jest ładunkowo
obojętna, to doświadczenie uczy, że tak nie jest. Na
Ziemi zachodzi szereg zjawisk charakterystycznych
dla ciał naładowanych. Znane nam są wszystkim
wyładowania atmosferyczne w czasie burz, ale jak
jest w czasie gdy nie ma burz.
Okazuje się, że w atmosferze istnieje pionowe pole
elektryczne o natężeniu E ~ 100V/m. Co 1 m
wysokości potencjał wzrasta o
100 V. Ładunek Ziemi jest ujemny.

Warunkiem istnienia pola jest:

1. Obecność jonów w atmosferze,

2. Rozdzielenie istniejących ładunków przez

jakiś mechanizm.

Ad. 1. Przypuszczano, że obecność jonów w
atmosferze związana jest z naturalna
promieniotwórczością. Wtedy liczba

jonów powinna być największa przy powierzchni
Ziemi. Stwierdzono jednak, że liczba jonów rośnie z
wysokością i osiąga maksimum na wysokości
powyżej 50 km, na wysokości gdzie rozciąga się
tzw. jonosfera.

Jonizacja jest wywoływana przez

promieniowanie kosmiczne.

Ad 2. Ziemia ma ładunek ujemny a potencjał
powietrza jest dodatni.

+ + + + + + + + + +

50 km

400000
V

Prąd
10

-2

jonu/(s m

2)

Stale więc
płynie prąd
ładunków
dodatnich z
atmosfery do
Ziemi.

Całkowity prąd
ma moc ok. 700
MW

Materia w polu
elektrycznym

Na każdy ładunek umieszczonej w polu
elektrycznym materii działa siła wynikająca z
prawa Coulomba. Ze względu na różną ruchliwość
ładunków w różnych materiałach można
zaobserwować następujące zjawiska:

a).

W przewodniku

ruchliwe elektrony

zostają przesunięte w stosunku do dodatnich
atomów, co daje rozdzielenie ładunków
dodatnich od ujemnych, czyli tzw.

zjawisko

indukcji.

b).

W izolatorach

nośniki ładunku zostają

przesunięte tylko nieznacznie, obserwujemy
tzw.

polaryzację.

Rozważmy przewodnik umieszczony w polu
elektrycznym. Znajdujące się w nim swobodne
elektrony będą przesuwały się w określonym
kierunku.

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-
-
-
-
-
-
-

+
+
+
+
+
+
+

Eˆ

.

ˆ

Cond

E

Doprowadzi to do nagromadzenia się na ściankach
przewodnika tzw. ładunku indukcyjnego. Ładunek
ten generuje wewnątrz przewodnika pole
elektryczne skierowane przeciwnie do pola
zewnętrznego.

Przesuwanie się ładunku trwa tak długo, aż
wypadkowe pole wewnątrz przewodnika osiągnie
wartość zero.

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-
-
-
-
-
-
-

+
+
+
+
+
+
+

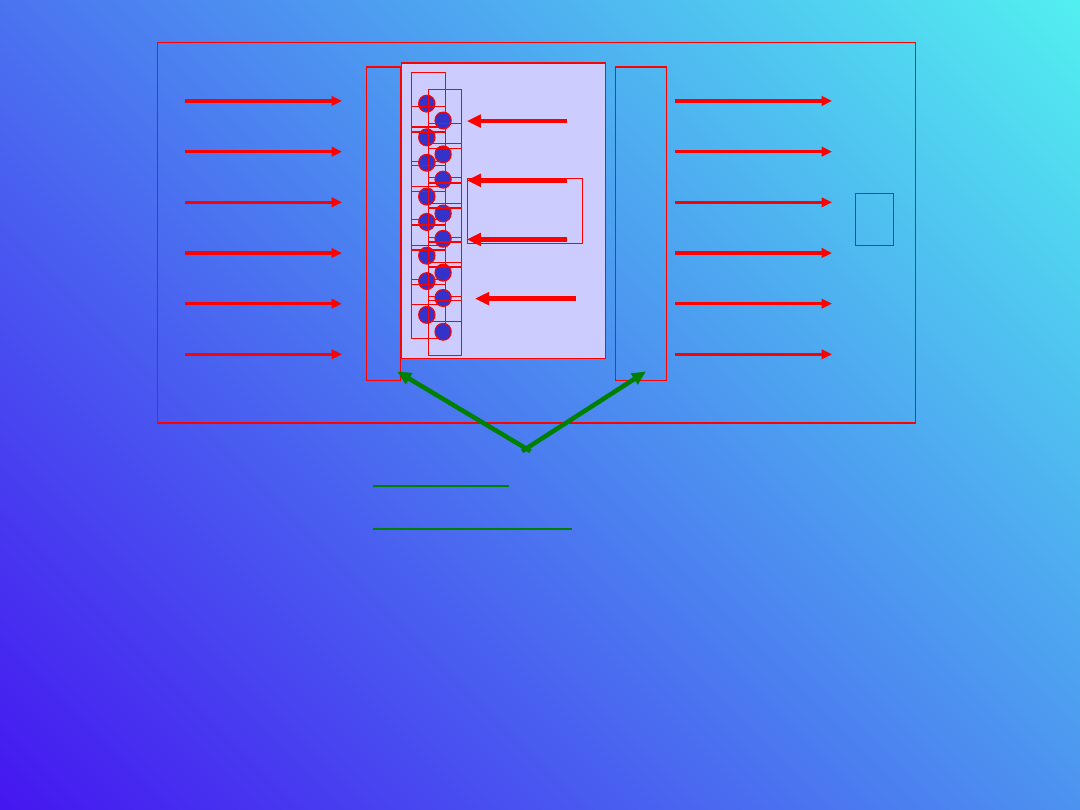
Eˆ

.

ˆ

Cond

E

ładunki
indukcyjne

Zastanówmy się teraz jak wygląda sytuacja, gdy w
polu elektrycznym umieścimy materiał nie
przewodzący ładunku.

Doświadczenie uczy nas, że jeśli pomiędzy dwa
ładunki wprowadzimy izolator, to maleje siła
kolumbowska działająca pomiędzy ładunkami.

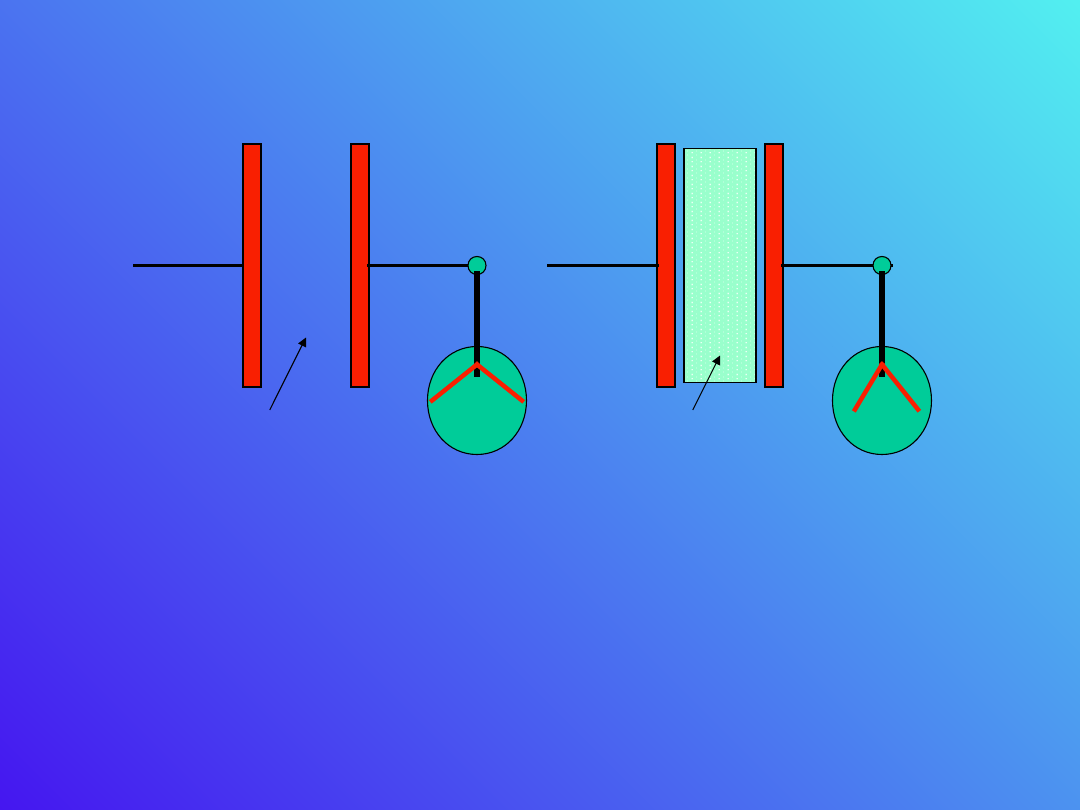
Omówmy ten problem na przykładzie kondensatora
płaskiego.

C

1

C

2

powietrz
e

dielektr
yk

Po włożeniu dielektryka pomiędzy okładki
kondensatora płaskiego, na pewno nie zmienił się
ładunek na okładkach a jednak zmalał potencjał jak
wskazał elektroskop. Zgodnie ze wzorem musiała
wzrosnąć pojemność kondensatora. Równocześnie
spadek potencjału na okładkach oznacza spadek
natężenie pola elektrycznego wewnątrz okładek.

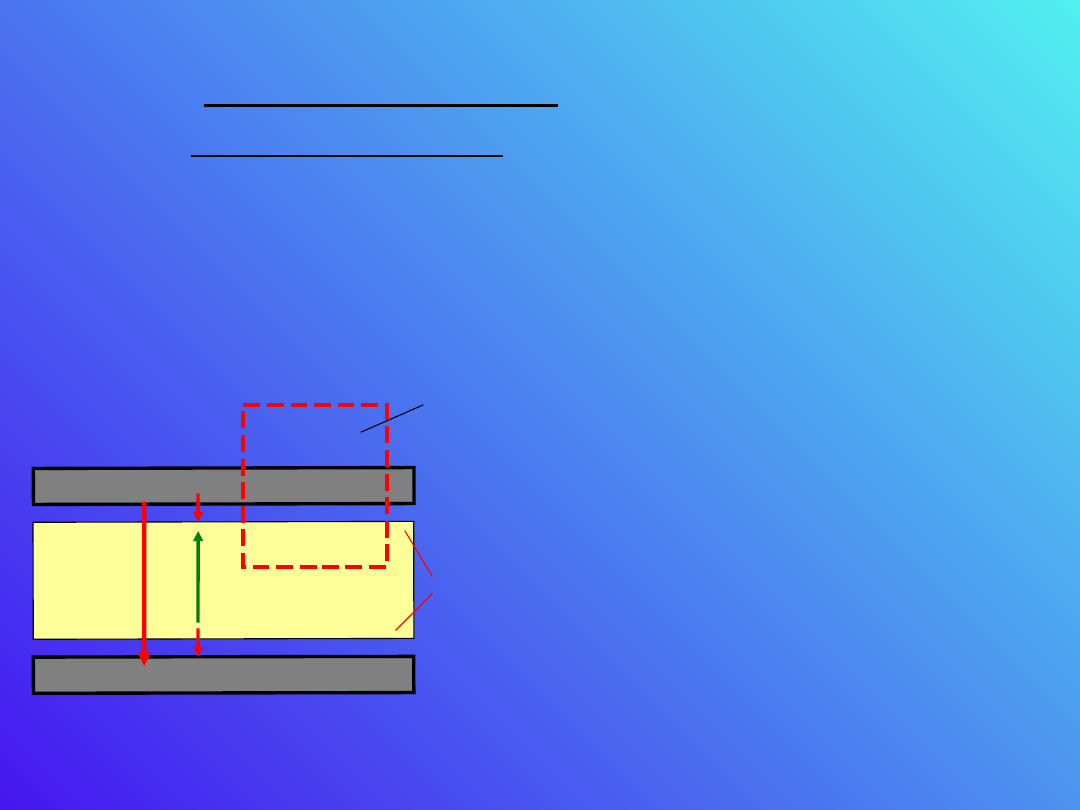
Materia w polu
elektrycznym

Zastanówmy się nad faktem wzrostu pojemności
kondensatora, do wnętrza którego włożyliśmy
dielektryk. Jak wytłumaczyć fakt zmniejszenia się
natężenia pola elektrycznego wewnątrz
kondensatora.

– –

–

– –

–

– –

–

– –

– –

+ +

+

+

+

+

+

+

+

–

–

–

–

–

–

–

–

–

–

+ +

+

+

+

+

+

+

+ +

+

+

E

0

E

A

Według prawa Gaussa strumień
natężenia pola elektrycznego
jest bezpośrednio związany z
ładunkiem wewnątrz
powierzchni A dla której ten
strumień liczymy. Zmniejszenie
się natężenia pola oznacza że
wypadkowy ładunek wewnątrz
powierzchni A jest mniejszy niż
wtedy gdy nie ma tam
dielektryka. Wynika stąd, że na
powierzchni dielektryka
wewnątrz powierzchni A muszą
być ładunki ujemne.



pol

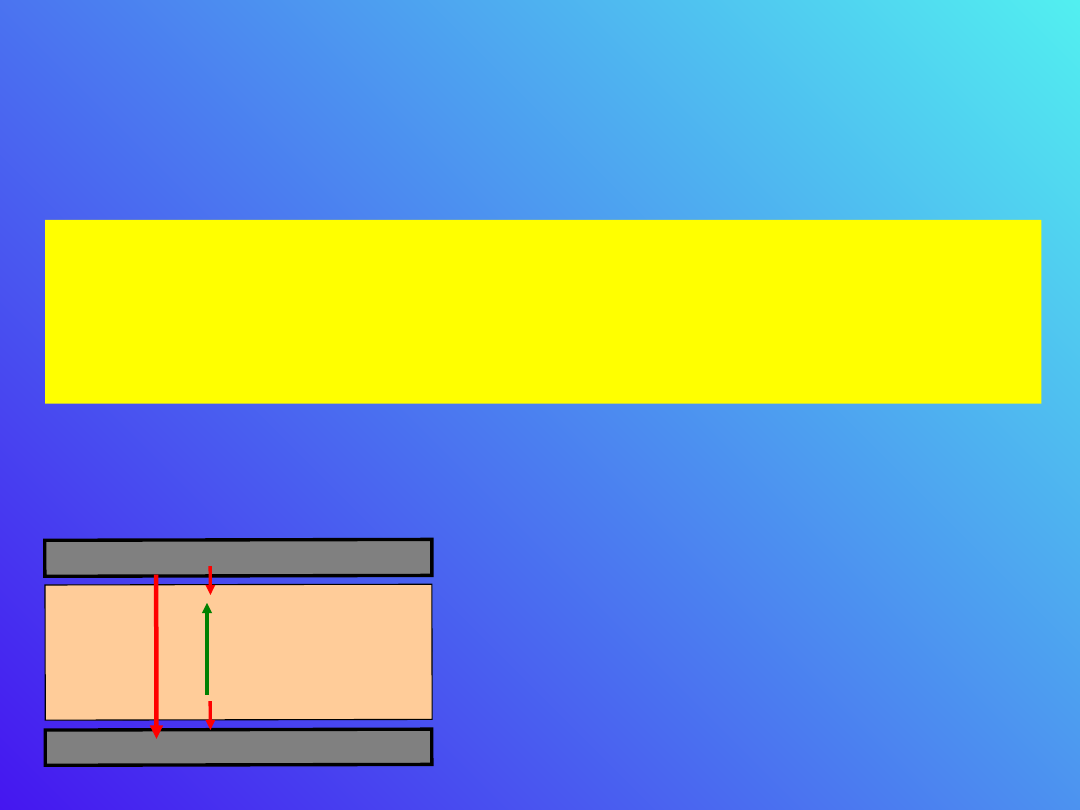
Ładunków jest mniej niż dodatnich, gdyż pole nie
znika zupełnie. Na drugiej powierzchni izolatora
wytwarza się ładunek dodatni.
Ładunek pojawiający się na izolatorze umieszczonym
w polu elektrycznym nazywamy ładunkiem
polaryzacyjnym.

Pojawianie się tego ładunku związane jest z
indukowaniem się i uszeregowaniem dipoli
elektrycznych w dielektryku, lub tylko
uszeregowaniem istniejących dipoli.

Gdybyśmy pomiędzy okładki kondensatora włożyli
przewodnik, to ładunek polaryzacyjny byłby
identyczny jak ten na okładkach. Pole wewnątrz
przewodnika byłoby równe 0. Pole istniałoby tylko w
małych szczelinach między okładkami a
przewodnikiem.

– –

–

– –

–

– –

–

– –

– –

+

+

+

+

+

+

+

+

+

–

–

–

–

–

–

–

–

–

–

+ +

+

+

+

+

+

+

+ +

+

+

E

0

E

Również w tym
przypadku
zaobserwujemy wzrost
pojemności
kondensatora.

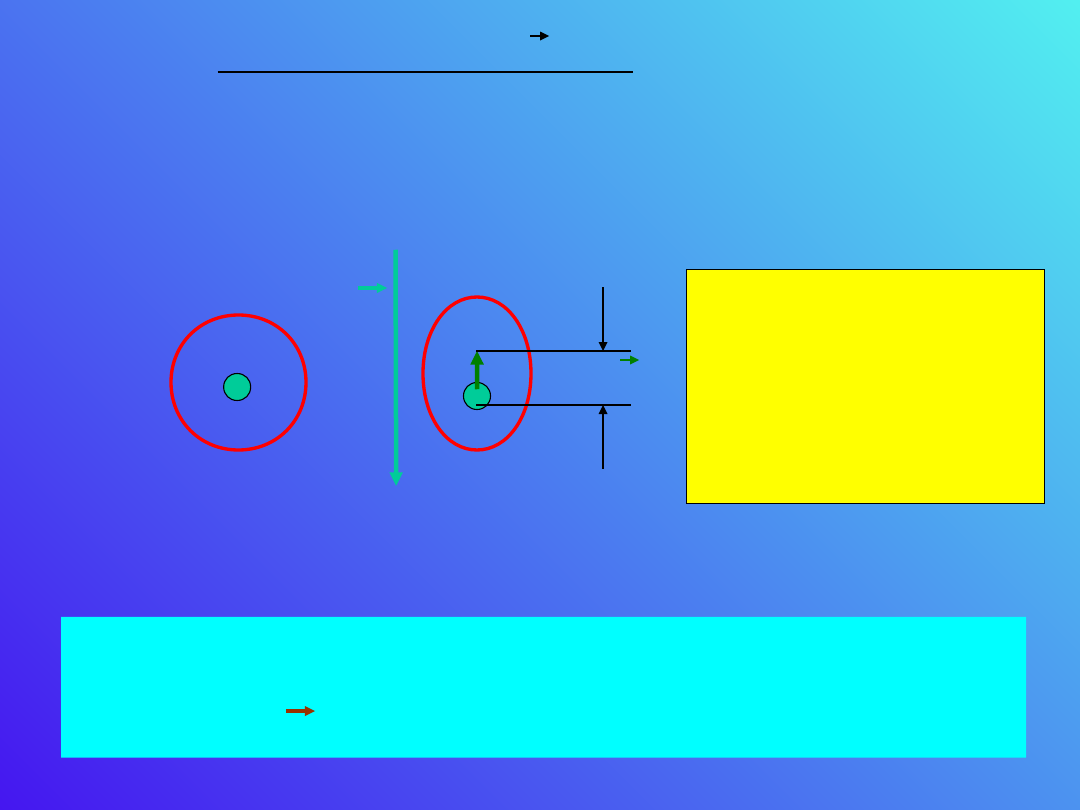
Wektor polaryzacji P

W izolatorach w przeciwieństwie do przewodników
ładunki nie mogą się swobodnie poruszać. Jednak w
atomach i cząsteczkach może nastąpić
przemieszczenie się ładunku pod wpływem pola
elektrycznego.

-

-

- - -

-

-

-

-

-

+

-

- -

-

-

-

-

-

--

-

+



E

Na wskutek
działania pola
nastąpiło
przesunięcie
ładunków o

.

Pod wpływem pola elektrycznego następuje
również przesunięcie jonów w kryształach.

Istnieją również cząsteczki posiadające moment
dipolowy wynikający z ich struktury. Dipole te
polaryzują się pod wpływem pola E.

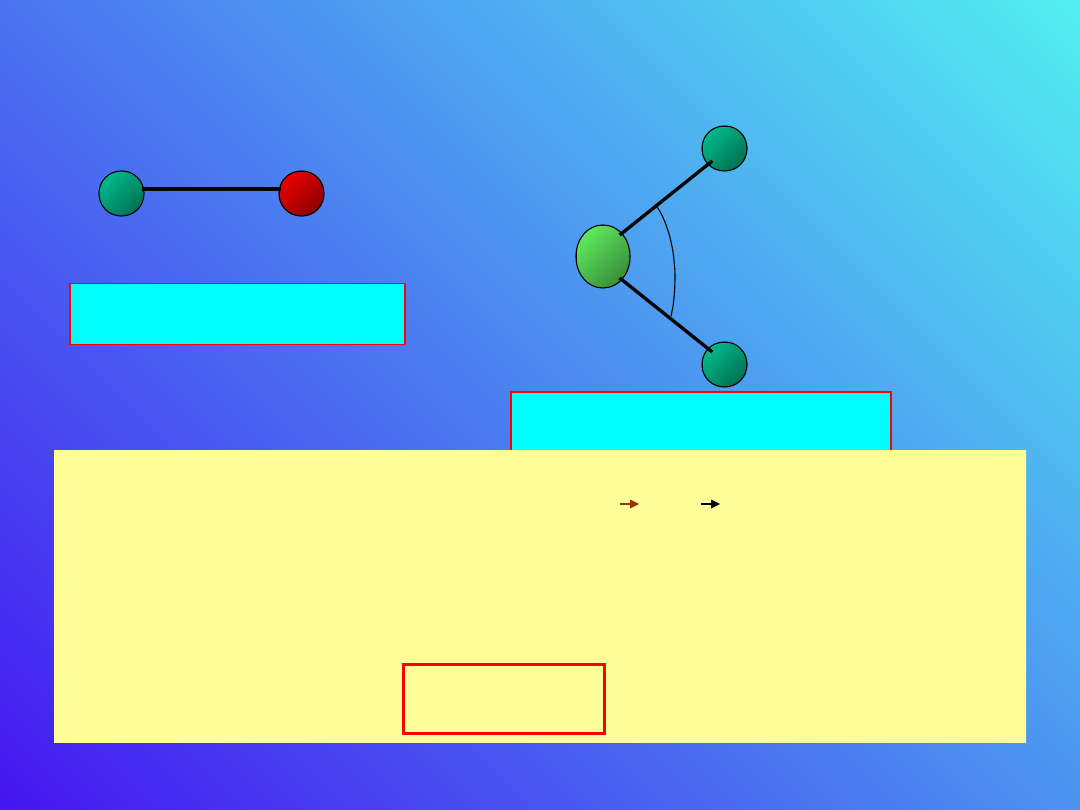
Przykładem struktur posiadających moment
dipolowych są np. CO, SO

2

, H

2

O, HCl, NH

3

, C

2

H

5

OH.

H

+

H

+

H

+

-

O

105

0

Cl

-

p

e

=3.4·10

-30

C·m

p

e

=6.2·10

-30

C·m

Jeśli w przypadku atomu czy cząsteczki ładunek
przesunie się o , to moment dipolowy będzie

równy p = q .
Jeżeli w jednostce objętości znajduje się N atomów
które mogą polaryzować, to moment dipolowy na
jednostkę objętości







q

N

P 

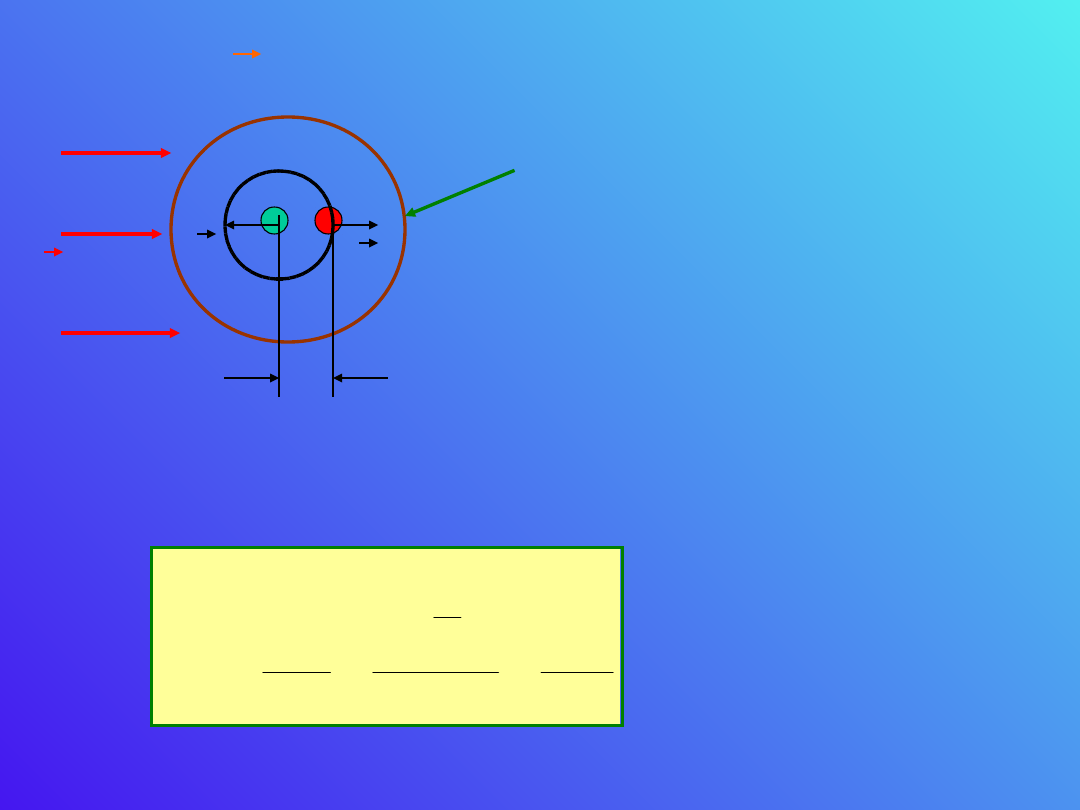
Wektor P nazywamy wektorem
polaryzacji.

+Z
e

-Ze



Zastanówmy się od czego
ten wektor zależy.
Przesunięty o  ładunek Ze

oddziaływuje tylko z częścią
chmury elektronowej o
promieniu .

E

F

1

F

2

Natężenie pola elektrycznego pochodzące od
ładunku polaryzacyjnego ma wartość:

3

2

3

2

a

Ze

a

Ze

Q

E

pol

pol





























Ze jest ładunkiem
całej kuli o
promieniu a.

Promień
a

Równowaga nastąpi wtedy gdy .
Oznacza to, że

E

E

pol







E

a

Ze



3





.

Widać więc, że moment dipolowy jest
proporcjonalny do natężenia zewnętrznego pola
polaryzującego. Jest tak przynajmniej dla
niedużych pól.

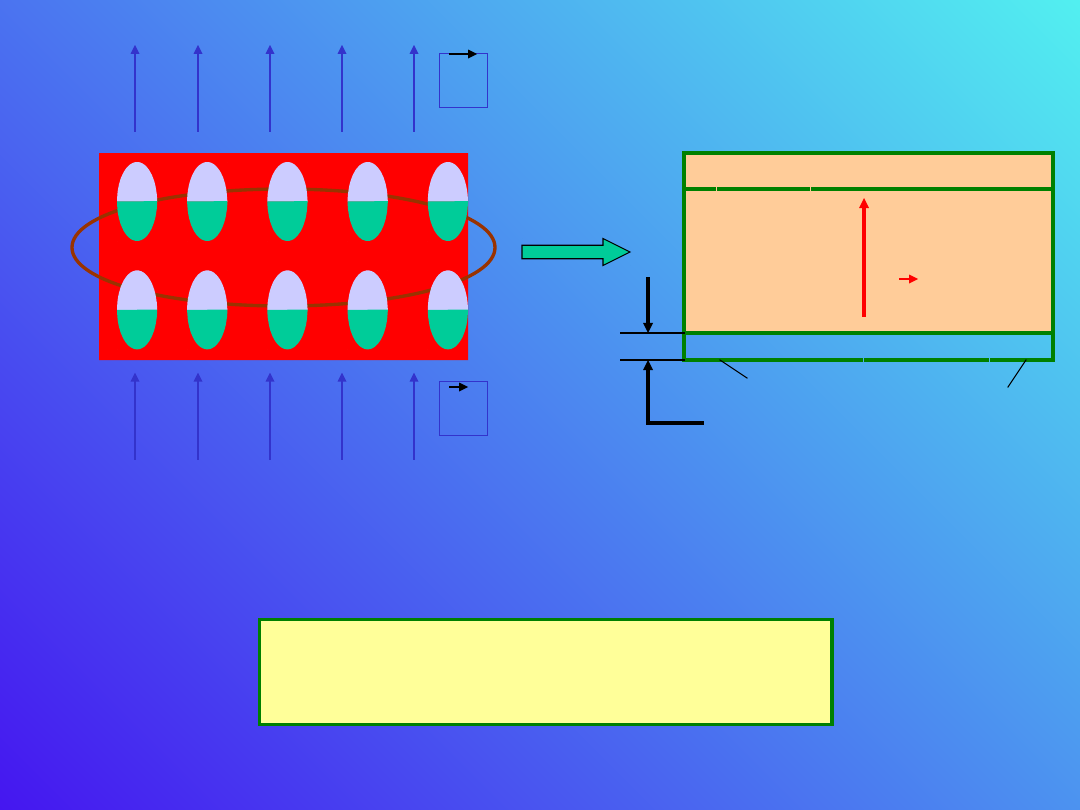
Ładunek polaryzacyjny

Wewnątrz dielektryka wprowadzonego do
kondensatora pojawi się ładunek
polaryzacyjny.
Rozważmy płytkę dielektryka umieszczoną w
jednorodnym polu elektrycznym

E

E

– – – – – – – – – –

+ + + + + + +
+ + +



± ± ± ± ± ± ±
± ± ±

P

Pole
powierzchni
A

Widzimy, że na wskutek polaryzacji dielektryka w
polu elektrycznym następuje przesuniecie się
ładunku. Na powierzchni A pojawia się ładunek

N

q

A

q

A











.

+

-

+

-

+

-

+

-

+

-

+

-

+

-

+

-

+

-

+

-

Gęstość powierzchniowa ładunku
polaryzacyjnego wynosi więc:

N

q

A

N

q

A

pol













.

Jest to dokładnie bezwzględna wartość wektora
polaryzacji| |P| , czyli

P

pol







Widzimy więc, że gęstość powierzchniowa
ładunku na powierzchni dielektryka jest równa
wartości wektora polaryzacji w jego wnętrzu.

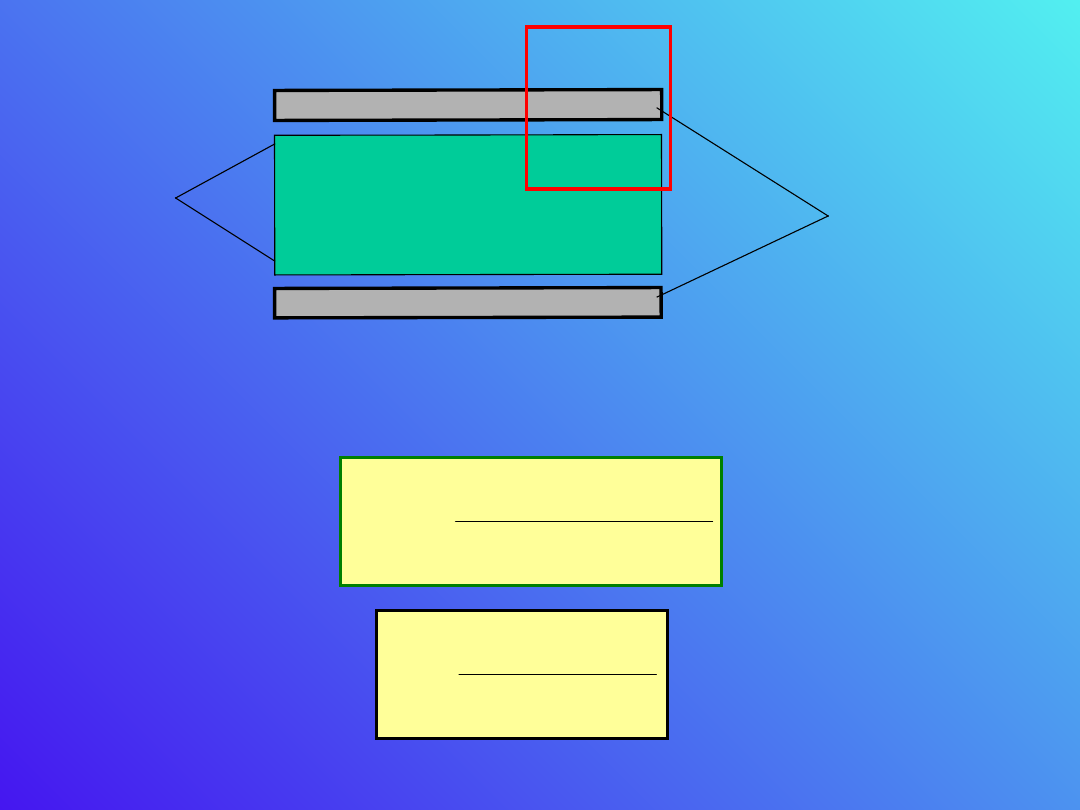
Rozważmy jeszcze raz naładowany kondensator
wypełniony dielektrykiem.

– –

–

– –

–

– –

–

– –

– –

+

+

+

+

+

+

+

+

+

–

–

–

–

–

–

–

–

–

–

+ +

+

+

+

+

+

+

+ +

+

+



pol



swob

A

W celu znalezienia wypadkowego natężenia pola
elektrycznego, zastosujmy do zaznaczonej czerwonej
powierzchni Prawo Gaussa .

0







A

A

A

E

pol

swob











0







pol

swob

E





0





P

E

swob







.

Pamiętamy, że wektor polaryzacji dielektryka P
zależy od natężenia zewnętrznego pola
elektrycznego E. Tą zależność zapisuje się zwykle
w postaci:

E

P





0







Wielkość



nazywamy

podatnością

elektryczną

dielektryka.

Podatność elektryczna nie zawsze musi być
liczbą.W wielu przypadkach jest wielkością
tensorową. Gdy mamy cząsteczkę o wyróżnionej
osi symetrii ( nie sferę), to można się
spodziewać się innego przesunięcia ładunku
wzdłuż osi

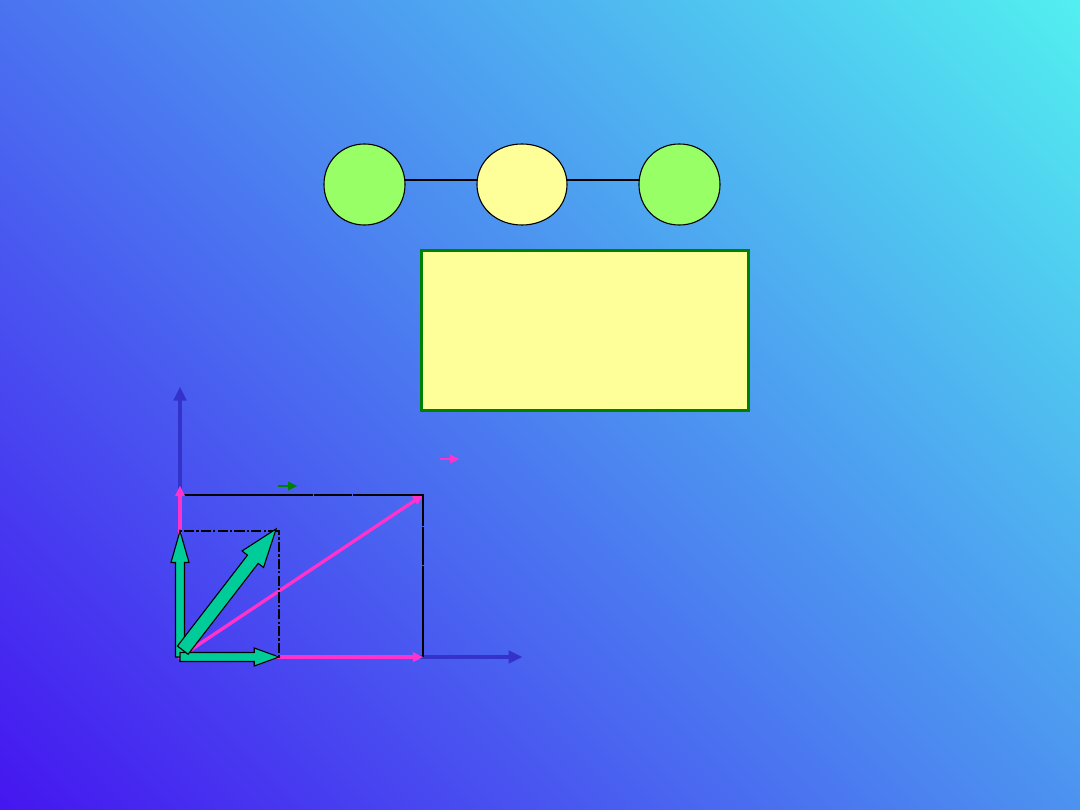
Cząsteczki niż w kierunku prostopadłym do niej.
Zachodzi to np. dla cząsteczki CO

2

.

O

O

C

Może być tak,
że:

E

P

E

P









2

0

||

1

0

||

















E

E

||

E



P

P



P

||

Widzimy więc, że
wektor polaryzacji może
nie być równoległy do
wektora pola
elektrycznego.

z

y

x

z

y

x

E

P

,

,

0

,

,











Gdzie,























zz

zy

zx

yz

yy

yx

xz

xy

xx





















,

,

,

,

,

,

Element 

xz

oznacza, że składowa E

x

natężenia

pola elektrycznego daje przyczynek do składowej
P

z

wektora polaryzacji, itp..

Zwykle tensor podatności elektrycznej jest
symetryczny, tzn.


xy

= 

yx

, 

xz

= 

zx

, 

zy

= 

yz

.

Tensor ten jest więc opisany przez sześć elementów.
Można znaleźć układ współrzędnych w którym  jest tensorem

diagonalnym.

W oparciu o te wzory możemy napisać:

0

0







E

E

swob





Po krótkich przekształceniach
otrzymujemy:

























1

1

0

swob

E

Widzimy więc, że E < E

swob

. Wielkość









1

Wielkość  nazywamy

stałą dielektryczną lub

przenikalnością elektryczną ośrodka.

Możemy napisać wyrażenie na pojemność
kondensatora płaskiego wypełnionego
dielektrykiem.

d

A

A

d

d

E

A

V

Q

C

swob

0

0

)

1

(





















Równania elektrostatyki w
dielektrykach

Prawo Gaussa w formie całkowej ma następującą
postać:

0

0





















A

swob

pol

swob

a

A

d

P

Q

Q

Q

A

d

E









Można to również
zapisać tak:

0

0





swob

A

Q

A

d

P

E



























Forma różniczkowa Prawa Gaussa wygląda
następująco:

0

0











P

div

E

div

swob

pol

swob













.

Po przekształceniu ostatniego wzoru otrzymujemy:

0

0







swob

P

E

div





























 

0

1









swob

E

div

E

div











,

oraz







A

swob

Q

A

d

E

0









.

Wektor przesunięcia D

Ze względów historycznych przyjęło się
wprowadzać wektor D zwany wektorem
przesunięcia zdefiniowany następująco:

P

E

D











0



Wprowadzając do tego wzoru wyrażenie na
polaryzację możemy napisać:

E

E

E

E

D











0

0

0

0

)

1

(

























Należy pamiętać, że  i  są tensorami.

Współczynnik



(

 (1+)

)

nazywamy

względną przenikalnością dielektryczną
ośrodka.

Wszystkie dotychczasowe rozważania nie
wpływają na zachowawczość pola E . Dalej
słuszne jest równanie rot E = 0. Równanie to
razem z prawem Gaussa w formie różniczkowej
pozwala wyznaczyć pole E z dokładnością do
stałej addytywnej.









A

swob

swob

Q

A

d

D

D

div









Dielektryk z trwałymi momentami
dipolowymi

Przyłożone pole elektryczne może uszeregować
dipole. To porządkujące działanie pola jest
niszczone przez ruchy termiczne. Można więc
przypuszczać, że stopień uporządkowania
dielektryka polarnego będzie określony przez
relację pomiędzy energią potencjalną uzyskiwaną
przez działania zewnętrznego pola o natężeniu E, a
energią kinetyczna ruchu termicznego.

Energia potencjalna dipola umieszczonego w polu
o natężeniu E jest dane przez :



cos

PE

E

P

E

pot















kT

E

Np

P

3

2

0





Zgodnie z wzorami (P=

0

E) i (1+=),

otrzymujemy, że:

kT

Np

0

2

0

3

1









.

Polaryzacja dielektryka polarnego jest
proporcjonalna do przyłożonego natężenia pola
elektrycznego i odwrotnie proporcjonalna do
temperatury.

Zależność polaryzacji od 1/T

nazywamy prawem Curie.

Widzimy również, że dla dielektryków polarnych
podatność dielektryczna czy też stała dielektryczna
jest malejącą funkcją temperatury T.

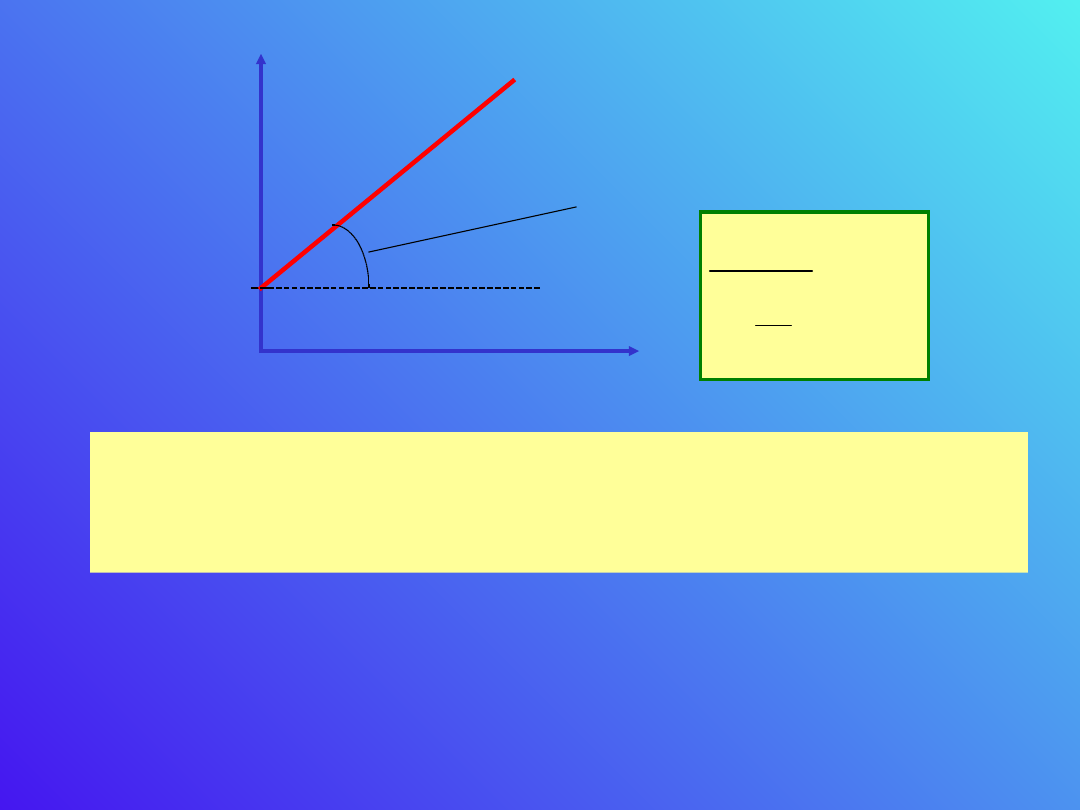
1/T



1

Ten kąt jest miarą
polaryzacji, gdyż

2

0

)

1

(

p

T









Pomiar  dla różnych temperatur pozwala ustalić

czy mamy do czynienia z dielektrykiem polarnym
czy nie.

Gęstość energii pola elektrycznego

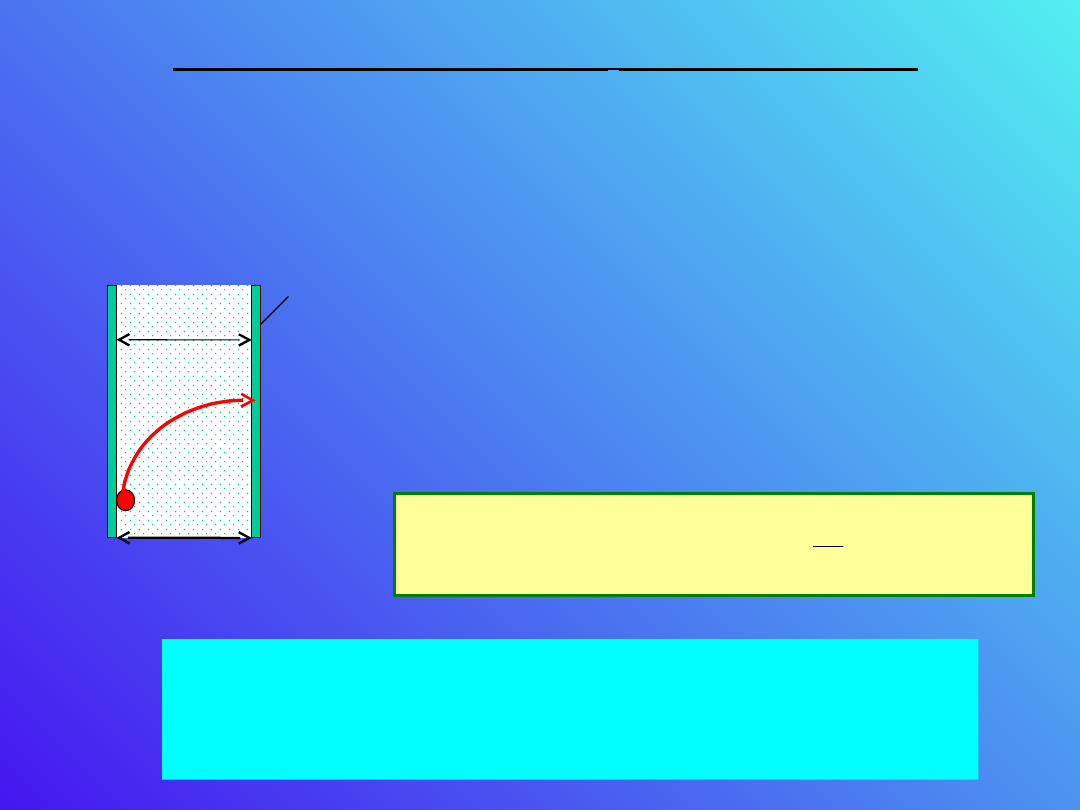
Gęstość energii pola

elektrycznego

Rozważmy jednorodne pole elektryczne zawarte
pomiędzy okładkami kondensatora płaskiego
naładowanego ładunkiem Q. Przeniesienie z
okładki na okładkę ładunku dQ wymaga
wykonania
pracy dW.

-Q

+Q

V

L

dQ

+



Jeżeli przeniesiemy z ujemnej
płyty ładunek +dQ na dodatnią
płytę, to wykonamy pracę
przeciwko polu elektrycznemu
równą

V

dQ

L

L

V

dQ

l

d

E

dQ

dW

l

























Na wskutek przeniesienia ładunku z
okładki ujemnej na dodatnią napięcie na
kondensatorze wzrośnie o dV.

A

powierzchnia

-
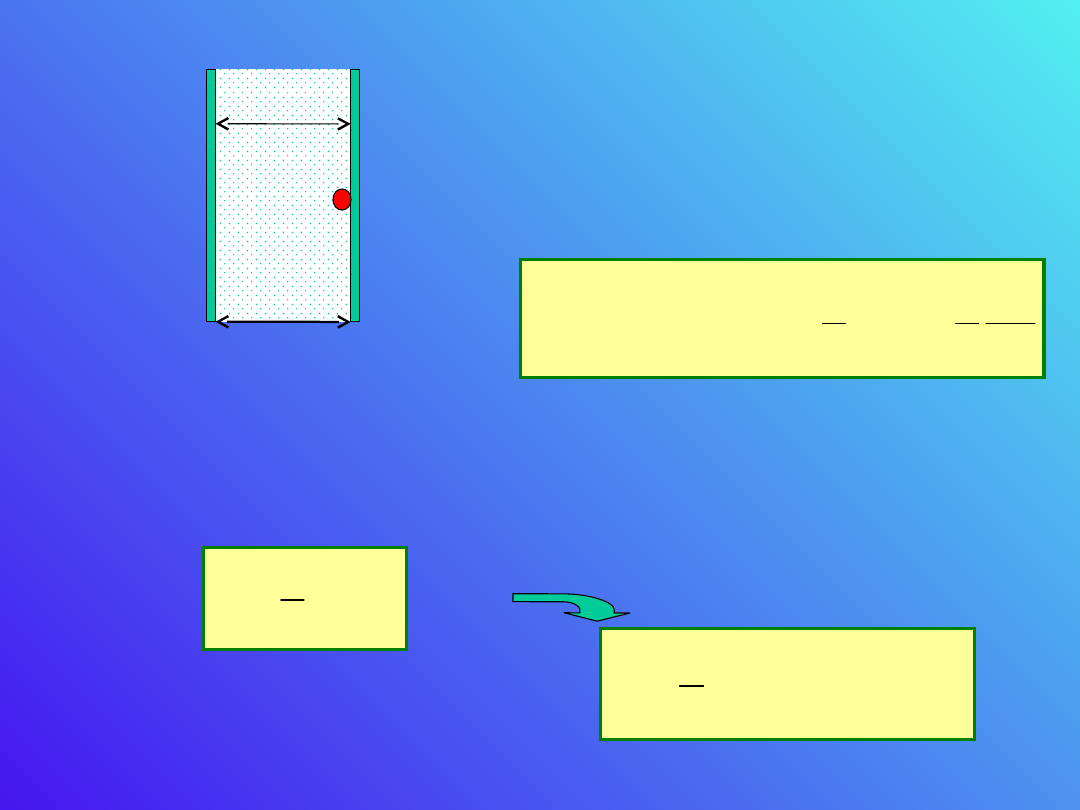
(Q+dQ
)

L

dQ

+



+
(Q+dQ)

V+dV

Wobec tego

dQ = C dV.

Możemy więc napisać:

dW = C V dV .

Po całkowaniu,
otrzymujemy:

C

Q

CV

dV

V

C

W

V

2

2

0

2

1

2

1













Wykonana praca została zmagazynowana w
kondensatorze jako energia potencjalna (W = U

).

Może ona zostać wykorzystana do wykonania
pracy przez kondensator.
Czyli,

2

2

1

V

C

U





Pamiętając, że

C =

0

A/L, a

V=L E,

2

0

}

{

2

1

E

L

A

U















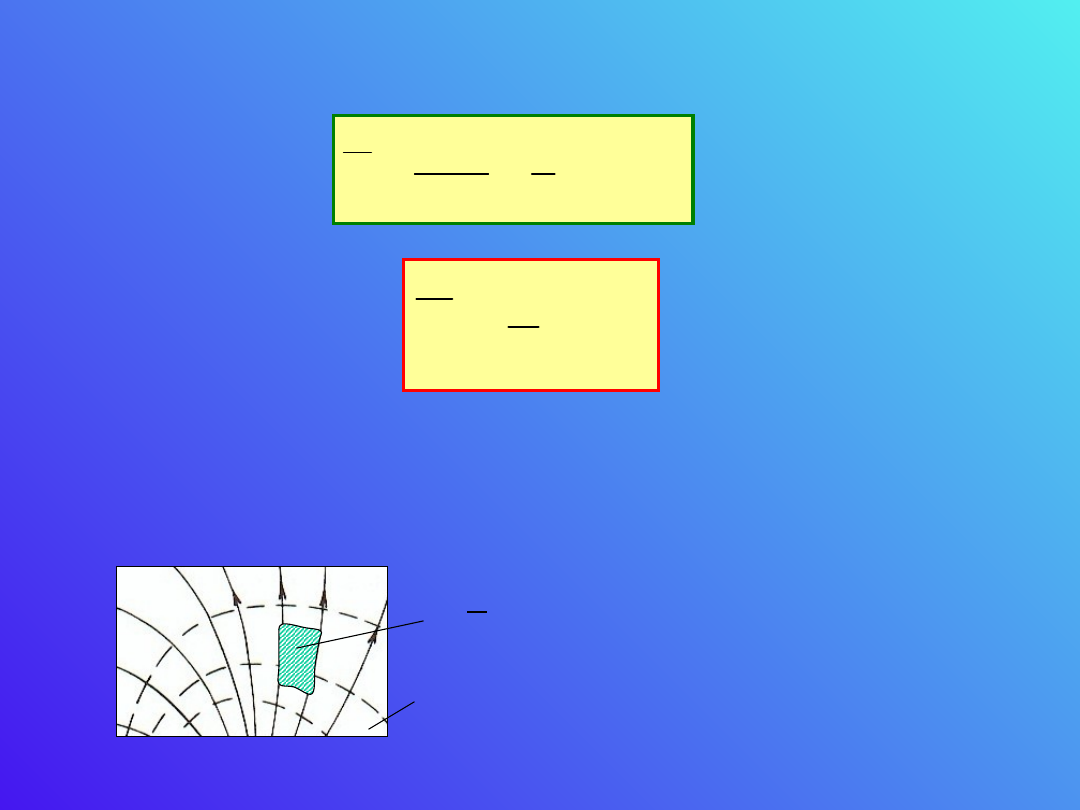
Możemy więc wyliczyć gęstość energii pola
elektrycznego, która wynosi:

E

E

L

A

E

U

p













0

2

1



i dalej:

E

D

U









2

1

Ponieważ dowolne pole można na małym obszarze
traktować jako jednorodne, wzór ten stosuje się
również do pól niejednorodnych.

d

Linie
ekwipotencja
lne

mikro-objętość pola , którą
można uważać za mały
kondensator.

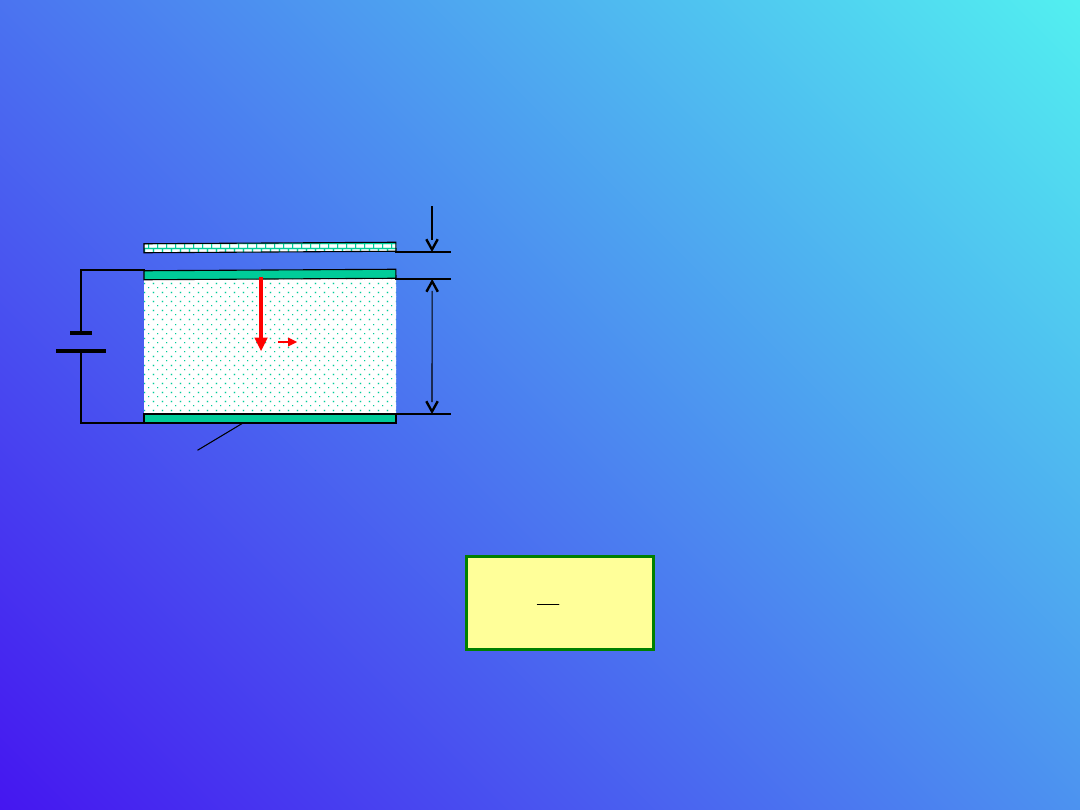
Pomiędzy okładkami kondensatora działają siły,
które można wykorzystać do dokładnego pomiaru
napięcia.

-Q

+
Q

A

F

x

dx Wirtualne rozsunięcie

okładek o dx powoduje
zmniejszenie energii
pola. Ładunek spływa z
powrotem do baterii.
Wiemy, że energia pola
jest równa

V

2

2

1

V

C

U





.

Prąd elektryczny

Natężenie prądu, wektor gęstości prądu

Prawo zachowania
ładunku

Model przewodnictwa elektrycznego

Prąd elektryczny

Natężenie prądu, wektor gęstości

prądu

Opuszczamy rozważanie stabilnych rozkładów
ładunków i od tej chwili pozwalamy im się
poruszać.

W
elektrostatyce:

1. Powierzchnie przewodników są powierzchniami

ekwipotencjalnymi,

2. Ładunki są rozmieszczone na powierzchni i

spoczywają,

3. Wewnątrz przewodników natężenie pola E jest

równe zero,

Połączmy przewodnikiem dwa naładowane
elektroskopy i zobaczmy co się dzieje.

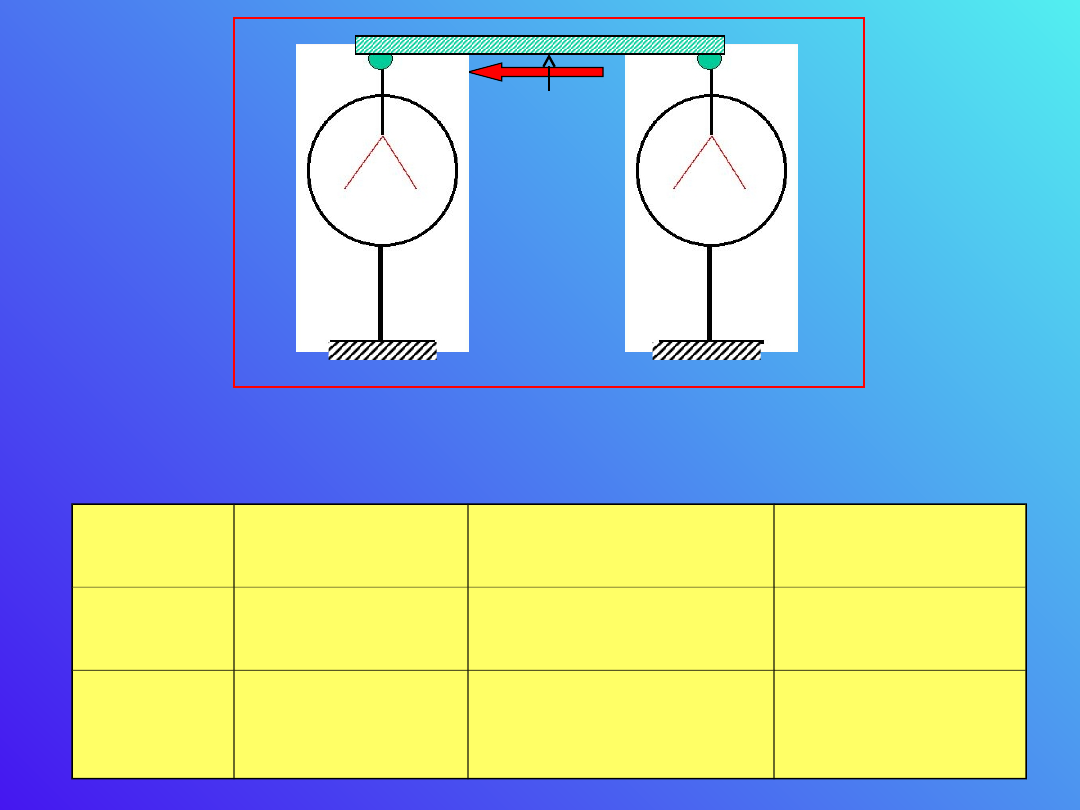
+Q

-Q

V

1

V

2

Po połączeniu elektroskopów następuje w
krótkim czasie wyrównanie ładunków. Co
natomiast dzieje się z potencjałem?

t=0

V

0

= V

1

– V

2

Przypadek

statyczny

2 powierzchnie

ekwipotencjalne

t=duże

V

0

= 0

Przypadek
statyczny

1 powierzchnia

ekwipotencjalna

t=t’

V

0

maleje

Przypadek
niestatyczny

Potencjał zależy

od miejsca

pomiaru

V

3

Oznacza to, że

w czasie przepływu ładunku mamy

do czynienia ze spadkiem potencjału

, czyli, że

w

przewodniku pojawia się pole elektryczne.

Przepływ ładunków przewodniku zarówno

dodatnich jak i ujemnych nazywamy prądem

elektrycznym.

Na rysunku na poprzedniej stronie poruszają się
elektrony i zachodzi to z prawej strony na lewą.

Prąd elektryczny charakteryzowany jest przez
swoje

natężenie,

które definiujemy jako całkowity

ładunek przepływający przez daną powierzchnię
w jednostce czasu

.

dt

dQ

I 

Jednostką natężenie prądu jest amper. [1
A=1C/1sek].

Do pomiaru natężenia prądu wykorzystuje się
wszelkie efekty wywoływane przez płynący prąd.
Nośnikami prądu w metalach są elektrony, a w
gazach i elektrolitach – jony.

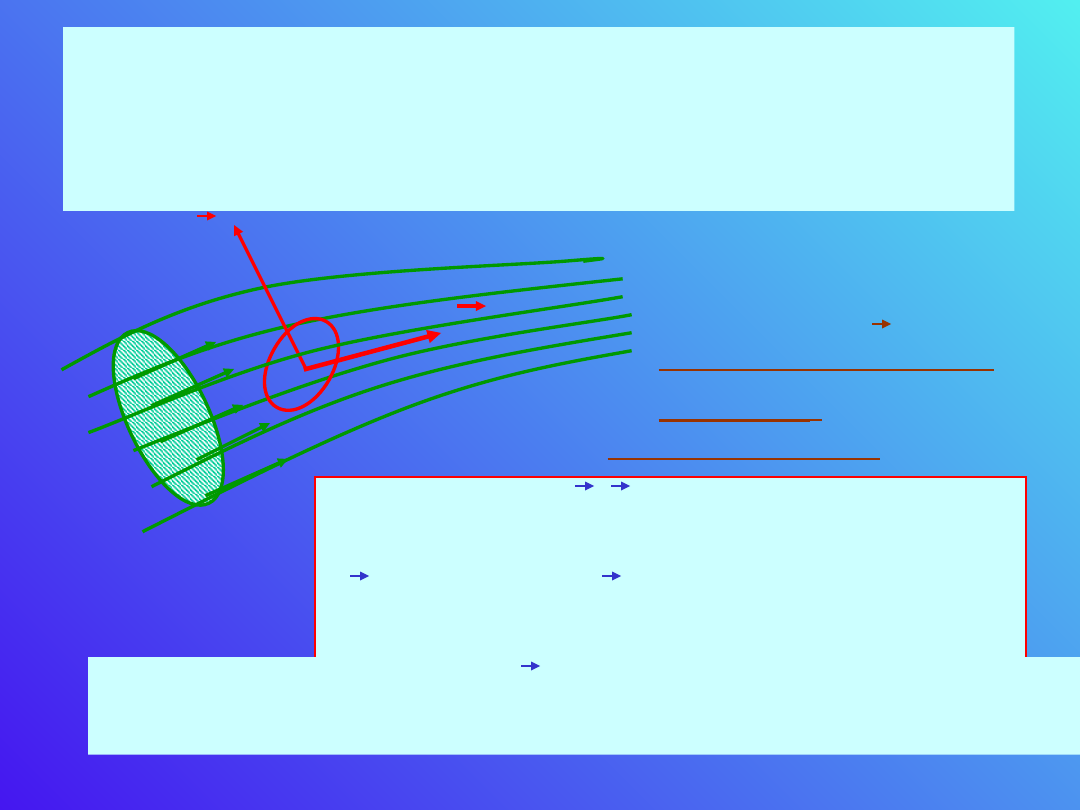
dA

A

j

Ważną wielkością
charakteryzującą
prąd elektryczny jest

wektor gęstości
prądu j

.

Jego

kierunek jest
określony

przez

ruch ładunków

dodatnich.

Wartość wektora j ,| j | jest równa
ładunkowi przepływającemu przez
jednostkę powierzchni dA
prostopadłej do j na jednostkę czasu.

Przez element powierzchni dA przepływa w czasie dt
ładunek

dt

A

d

j

dt

A

d

j

dA

j

dQ























)

,

cos(

n

n

dA

dI

dt

dA

dQ

j





|

|



Przy czym

)

,

cos( A

d

j

dA

dA

n







Jednostką gęstości prądu w układzie SI
jest [A/m

2

].

W oparciu o wzór znajdujemy na natężenie prądu
przepływającego przez całą powierzchnię A
wyrażenie;

A

d

j

dt

dQ

I

A













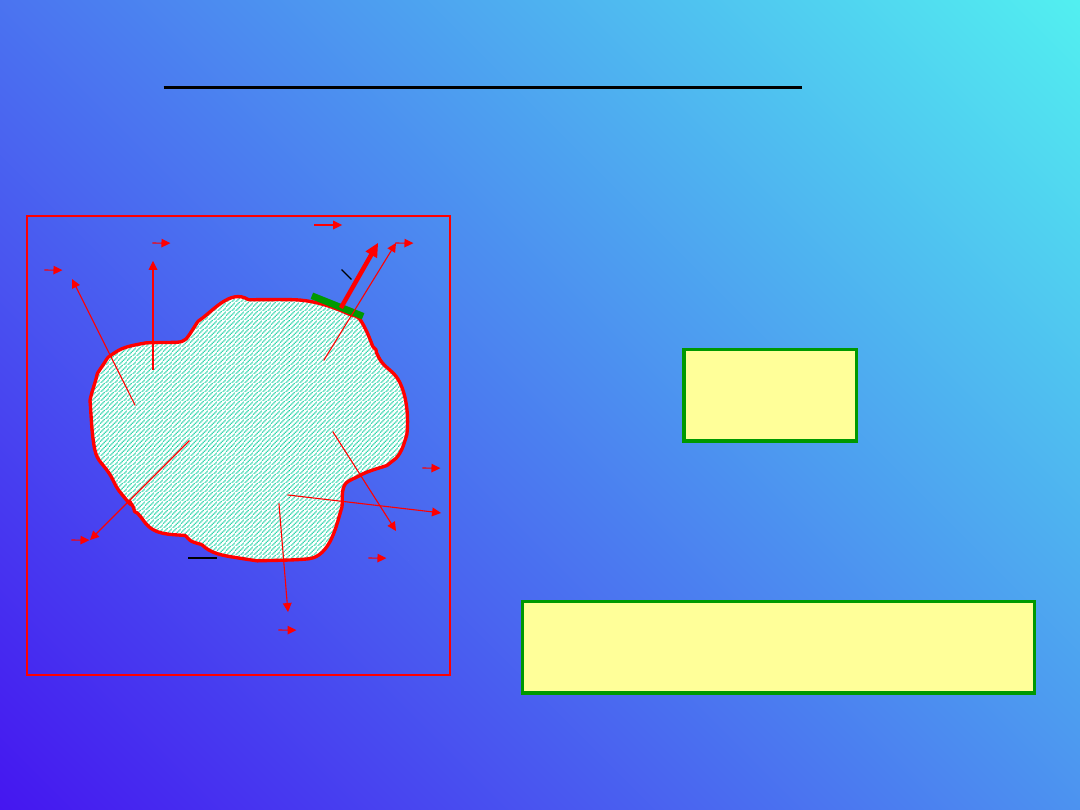
Prawo zachowania ładunku

W jaki sposób sformułować prawo zachowania
ładunku, kiedy mamy przepływ prądu.



A

dA

j

j

j

j

j

j

j

j

Wiemy ile na sekundę
przepływa ładunku przez całą
powierzchnie przewodnika,
mianowicie







 









d

j

div

A

d

j

A

Gauss











A

A

d

j





W oparciu o twierdzenie
Gaussa mamy:

Na jednostkę czasu w przewodniku ubywa
ładunku.
Bilans ładunku wynosi
więc:















d

t























d

t

d

j

div



Wyrażenie to jest ważne dla każdej objętości , a
więc również dla objętości d. Otrzymujemy więc
równanie, które nazywamy

równaniem

ciągłości:

0









t

j

div





Dla prądu o stałym natężeniu I=0 wektor gęstości
też jest niezależny od czasu. Tyle
samo ładunku wpływa co wypływa z danej
objętości.

0



j

div



Model przewodnictwa elektrycznego

Pamiętamy, że nośnikami ładunków mogą być
elektrony, jak również jony dodatnie i ujemne.
Najlepszymi przewodnikami są metale w których
znajduje się wiele swobodnych elektronów.

Zastanówmy się nad mechanizmem przewodzenia
prądu w metalicznym przewodniku.

• Każdy atom siatki oddaje średnio jeden elektron
do całej sieci (elektrony przewodnictwa).
Elektrony te zachowują się jak gaz. Gęstość tego
gazu jest bardzo wysoka. Do elektronów jako
fermionów stosuje się statystyka Fermiego-
Diraca.

• Przyjmuje się, że prędkość elektronu przed
zderzeniem nie wpływa na prędkość po zderzeniu.
Oznacza to, że zderzenia „wymazują pamięć”
elektronów. Oznaczmy średni czas pomiędzy
dwoma kolejnymi zderzeniami przez .

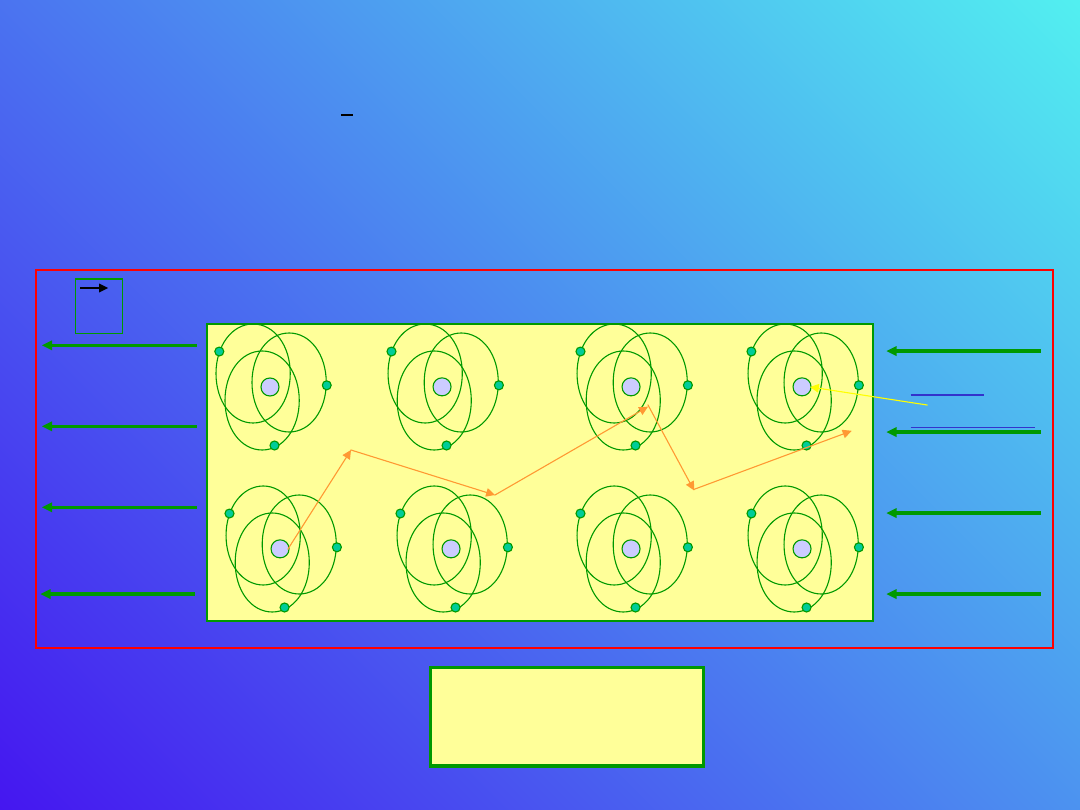
E

Jądro
atomowe

Co zachodzi w czasie przepływu prądy w
przewodniku. W przewodniku istnieje pole
elektryczne . Elektrony w czasie ruchu w polu
elektrycznym zderzają się głównie z elektronami
związanymi w atomach. Tor przypadkowego
elektronu jest przedstawiony na poniższym
rysunku.

E



Na elektrony działa siła
.

E

e

F









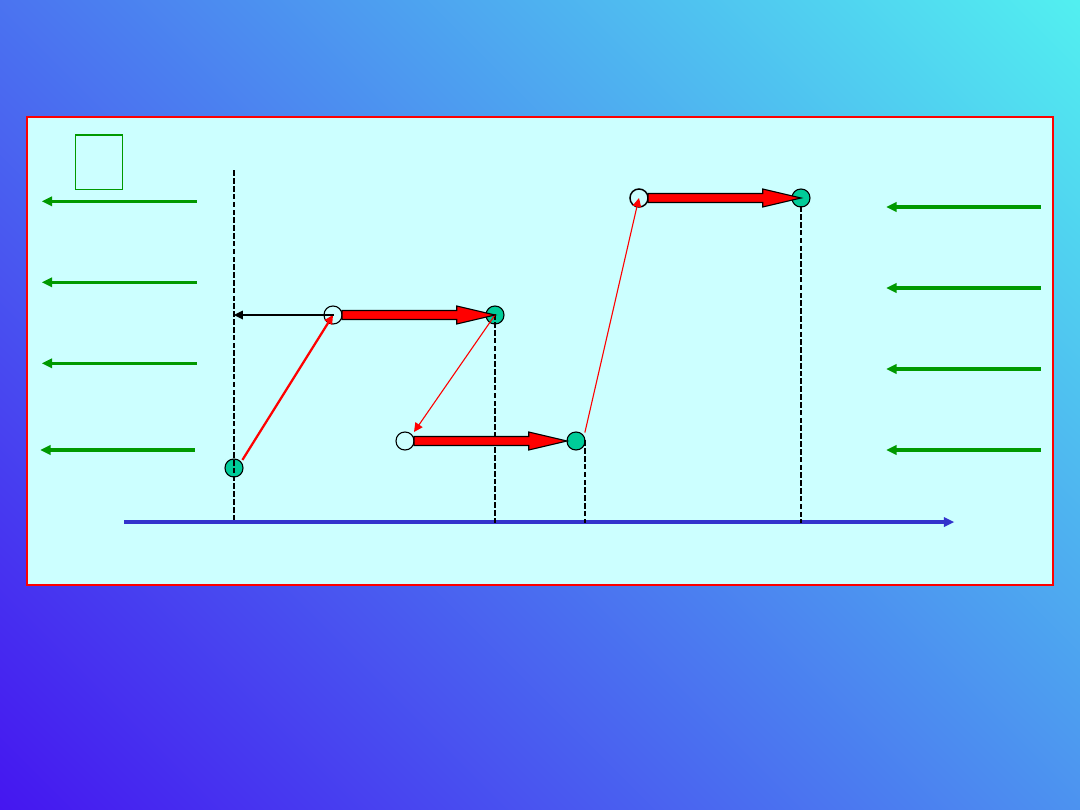
Na ukierunkowany ruch elektronów pod wpływem
pola elektrycznego nakładają się izotropowe ruchy
termiczne

E

x

x

0

x

1

x

2

x

3

v

x0



v

0



v

1



v

2



1

/

2

b

2

1

/

2

b

2

1

/

2

b

2

Pomiędzy kolejnymi zderzeniami następującymi po
średnim czasie  elektron porusza się w kierunku osi

x ruchem jednostajnie przyśpieszonym.

Ruch elektronu odbywa się zgodnie z II zasada
dynamiki Newtona,

m

E

e

b

dt

x

d

E

e

dt

x

d

m











2

2

2

2

.

Licząc kolejne odcinki przebyte między zderzeniami,
otrzymujemy,

2

2

1

)

1

(

1

2

2

1

1

1

2

2

2

1

0

0

1













b

v

x

x

b

v

x

x

b

v

x

x

N

x

N

N

x

x























Sumujemy te równania po N zdarzeniach, przy
czym N>>1.

W wyniku
otrzymujemy:

2

2

1

0

0





b

N

v

x

x

N

i

xi

N











Ze względu na izotropowy rozkład kierunków ruchów
termicznych, pierwszy wyraz po prawej stronie jest
równy zero, gdyż tyle samo cząstek może mieć
prędkości –v

x

jak i +v

x

. Średnia prędkość elektronów

w kierunku x (prędkość dryfu) jest więc równa:

E

m

e

b

N

x

x

v

N

D

















2

2

1

0









.

Zdefiniujmy jeszcze czas relaksacji jako <

R

> = /2.

Wtedy

E

m

e

v

R

D









Ruchliwością nośników prądu nazywamy:

E

v

m

e

D

R













.

Mimo, że ruch pod wpływem siły eE powinien być
przyśpieszony, ze względu na występujące
zderzenia, nie ma przyśpieszenia. Średnia
prędkość dryftu jest stała. Ruch elektronu wygląda
tak, jakby istniała siła tarcia. Wpływ zderzeń na ruch
ilustruje poniższa animacja.

W rzeczywistości poprzez zderzenia sieci
dostarczana jest energia, tzw. „

ciepło Joule’a”

.

Równanie możemy też interpretować następująco.
W sieci w której poruszają się elektrony działa na
nie poza siłą przyspieszającą F = eE, również siła
tarcia

R

D

v

m

R











.

Zachodzi więc równowaga F + R =0.
Z tego faktu wynika jednostajny
ruch elektronów.

Na podstawie definicji wektora gęstości prądu oraz
średniej prędkości dryfu, możemy wyrazić wektor
gęstości prądu jako:

dl = <v

D

>

dt

dA

n

d

V

dI

D

D

V

n

n

v

v

d

dQ

dl

dl

dt

dA

dQ

dA

dI

j























Znajdujemy więc, że ,
przy czym pamiętamy, że
ruchliwość

E

E

m

e

j

R





















R

m

q











.

Równanie na gęstość prądu możemy więc
zapisać jako:

E

j











Tym wzorem sformułowaliśmy

prawo

Ohma

.

Współczynnik  określa

przewodnictwo właściwe

, które jest

odwrotnością oporu właściwego 

el

przewodnika.

Należy pamiętać, że przewodnictwo właściwe może
być

wielkością tensorową.

.

W przypadku gdy nośnikami ładunku nie są
elektrony, możemy w podanych wzorach zastąpić
ładunek e przez q.

Omówmy jeszcze ogólny przypadek, kiedy w
przepływie prądu poza ładunkami ujemnymi q = -e,
są również zaangażowane ładunki dodatnie q = +e.
Pole E nadaje tym ładunkom prędkości dryfu w
przeciwnych kierunkach.

E

m

e

E

v

E

m

e

E

v

R

D

R

D



























































Można w tym miejscu zaznaczyć, że czas dryfu
można wyrazić przez średnią drogę swobodną i
średnią prędkość ruchu cieplnego ładunków.















/

R

Wektor gęstości prądu wyrazi się więc
następująco:

E

e

n

e

n

v

e

n

v

e

n

j

D

D

































)

(





Wielkości n

+

e=

0

+

oraz n

-

e=

0

-

określają gęstości

ładunków. Otrzymujemy na przewodnictwo
właściwe następujące wyrażenie;

)

(

)

(

2





























m

n

m

n

e

n

n

e

R

R











W oparciu o podaną poprzednio definicję czasu
dryfu, możemy napisać, że

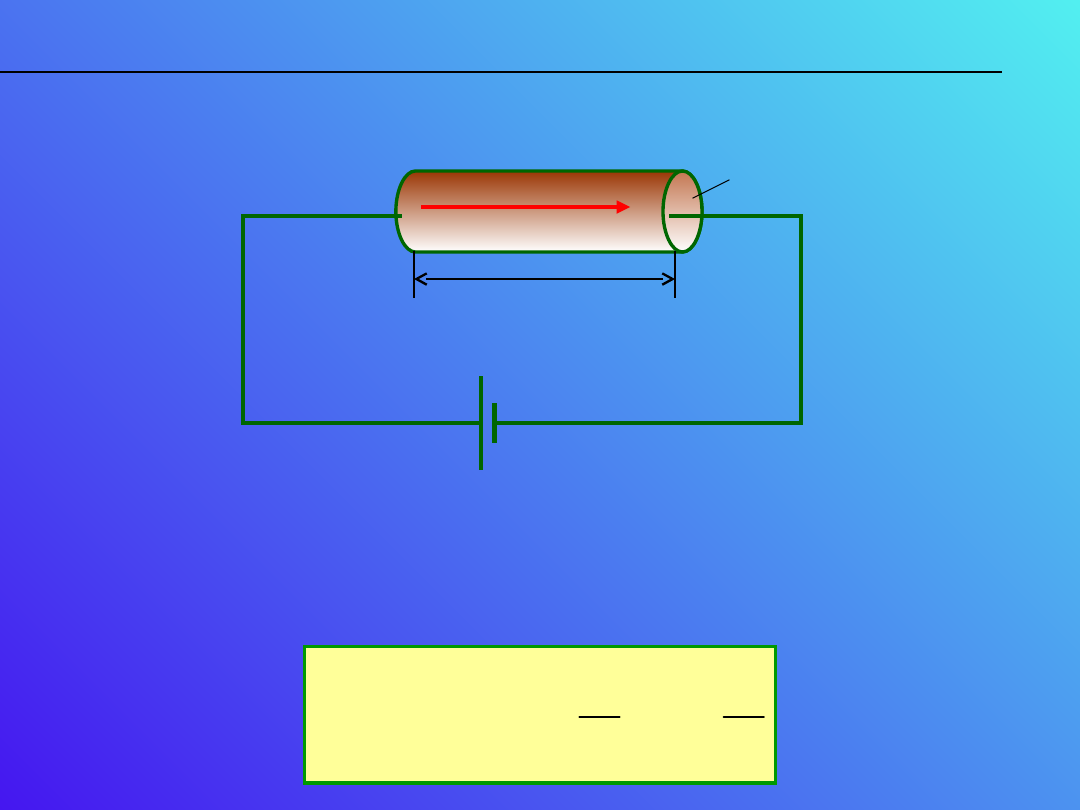
Techniczna postać prawa Ohma. Opór elektryczny

I(A)

Ogniwo
V

R

L

A

Powyższy rysunek przedstawia najprostszy
obwód elektryczny – opór R zasilany przez
baterię o napięciu V. Dla przewodnika ważne
jest prawo Ohma. Mamy więc

L

V

A

I

E

j













Poprzedni wzór możemy przekształcić do postaci
nazywanej zwykle prawem Ohma.

R

V

A

L

V

I







1

Z równania tego wynika wzór na opór
przewodnika.

A

L

R

0





Dla układu o dowolnej geometrii możemy opór
policzyć z wzoru:





















A

A

A

d

E

l

d

E

A

d

j

l

d

E

R























Trywialną konsekwencją prawa Ohma są wyrażenia
na wypadkowy opór połączenie równoległego i
szeregowego oporników.

1

i

N

1

i

N





i

i

R

R

1

1





i i

R

R

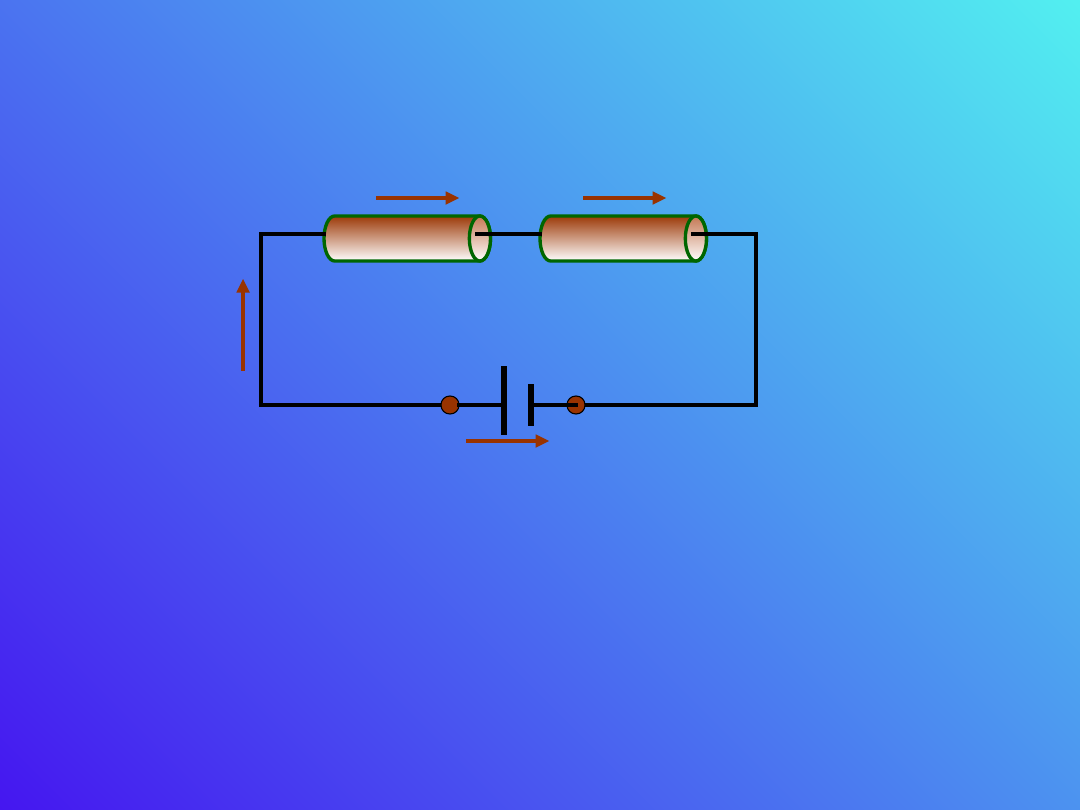
Jak już wspomniano, najprostszy obwód składa się
z baterii na zaciskach której panuje napięcie V

Є

,

oraz z jednego lub wielu oporów./

+ -

V

Є

V

1

V

2

I

W układzie tym płynie prąd o natężeniu I = V

Є

/R,

gdzie R jest całkowitym oporem . Prąd ten jest
spowodowany przez siłę elektromotoryczną V

Є

,

która również dostarcza energii zużytej na
pokonanie oporu przewodników. Ze względu na to,
że pole elektryczne jest zachowawcze,









0

s

d

E





Gdzie  biegnie wzdłuż całego obwodu.

Wynika z tego, że

0

2

1









V

V

V

.

Wynika z tego, że w obwodzie
zamkniętym suma wszystkich spadków
potencjałów jest równa zero.

Siła elektromotoryczna

Przy omawianiu prawa Ohma zakładaliśmy, że
między końcami rozważanego przewodnika istnieje
stała różnica potencjałów. Siły kulombowskie
zawsze będą dążyły do wyrównania się potencjałów
w przewodniku, likwidując tą różnicę. Utrzymanie
różnicy potencjału wymaga istnienia
dodatkowych sił zewnętrznych. Muszą one
wykonywać pracę na przemieszczanie ładunków.

Pracę sił zewnętrznych przypadającą na
jednostkę ładunku dodatniego nazywamy siłą
elektromotoryczną.

Є = W/Q

Rozważmy następujący
układ:

+ -

I

R

Przeniesienie ładunku z jednej zacisku baterii
na drugi wymaga wykonania pracy:

l

d

E

Q

l

d

E

Q

W

zewn

kul



























Pierwsza całka ze względu na zachowawczość pola
elektrycznego (krążenie wektora E znika). Wobec
tego siła elektromotoryczna
jest równa:

l

d

E

zewn















1

2



Sformułujmy prawo Ohma dla przypadku,
obecności w obwodzie siły elektromotorycznej.

)

(

zewn

kul

E

E

j















Pomnóżmy obydwie strony równania przez
element długości dl
styczny do wektora gęstości prądu j. Otrzymamy
wtedy:

l

d

E

l

d

E

l

d

j

zewn

kul



























1

2



12

Scałkujmy to równanie pomiędzy punktami 1 a 2
(patrz poprzedni rysunek) przewodnika, wiedząc,
że

dl

A

I

l

d

j









Otrzymamy wtedy:

l

d

E

l

d

E

A

dl

I

zewn

kul























2

1

2

1

2

1

1



Całka po lewej stronie reprezentuje opór
odcinka przewodu pomiędzy punktami 1 a 2.
Wynik jest następujący:

12

12

2

1

12

U

V

V

IR











Wzór ten wyraża uogólnione

Prawo

Ohma

dla dowolnego odcinka

obwodu. Jeśli obwód jest zamknięty,
potencjały punktów 1 i 2 są takie
same..

Zwykle źródło siły elektromotorycznej, którym może
być ogniwo, bateria itp.. posiada własny opór
wewnętrzny

R

w

.

Oznaczając opór przewodników

włączonych do obwodu przez

R

z

,

mamy:













w

z

w

z

IR

IR

R

R

I

)

(

Wyrażenie IR

z

określa spadek napięcia na oporze

zewnętrznym, możemy więc napisać,

w

IR

U







Równocześnie w zamkniętym obwodzie suma
wszystkich spadków potencjału jest równa zero.

0





n

n

V

Jeżeli w obwód byłoby włączonych więcej
oporów i sił elektromotorycznych, wtedy w
oparciu o prawo Ohma











n

i

i

i

n

i

i

R

I

1

1



(*)

Obwód taki jest przedstawiony na poniższym
rysunku.



1



2



3

R

1

R

2

R

3

I

1

I

3

I

2

Wzór (*) stanowi sformułowanie tzw.

Drugiego Prawa

Kirchoffa

,

które mówi, że

w dowolnym oczku obwodu suma iloczynów natężeń

prądu i oporów odpowiednich odcinków obwodu jest

równa sumie sił elektromotorycznych występujących

w tym obwodzie.

Z kolei

Pierwsze Prawo Kirhoffa

dotyczy

węzłów, w których spotykają się elementy obwodu.

I

1

I

2

I

3

I

n

Prawo to mówi, że

algebraiczna suma
natężeń prądów
schodzących się w
węźle jest równa zero

.

0

1







n

i

i

I

Łączenie ogniw

Zależność oporu metali od temperatury.

Prawo Wiedemana - Franza

Prawo Joule’a - Lenza

Zależność oporu metali od
temperatury.

Zgodnie z rozważaną poprzednio hipotezą
przenoszenia ładunku, jako nałożenia się
uporządkowanego ruchu elektronów w polu E,
oraz ruchu związanego ze zderzaniem się

elektronów z cząstkami poruszającymi się ruchami
termicznymi, oraz faktem, że energia cząstek
wzrasta wraz z temperaturą, opór powinien rosnąć
wraz z temperaturą. Jest tak rzeczywiście.
Możemy powiedzieć, że opór właściwy metali
zmienia się następująco:





)

(

1

0

0

T

T 











Wskaźnik

0

odpowiada temperaturze 0

0

C, czyli

273 K. Współczynnik temperaturowy oporu 

można wyliczyć z wyrażenia:

273

1

273

273







T

K

K









Współczynnik temperaturowy oporu właściwego
niewiele różni się od wartości 1/273 K

-1

, co

oznacza, że jest podobny do temperaturowego
współczynnika rozszerzalności gazów.



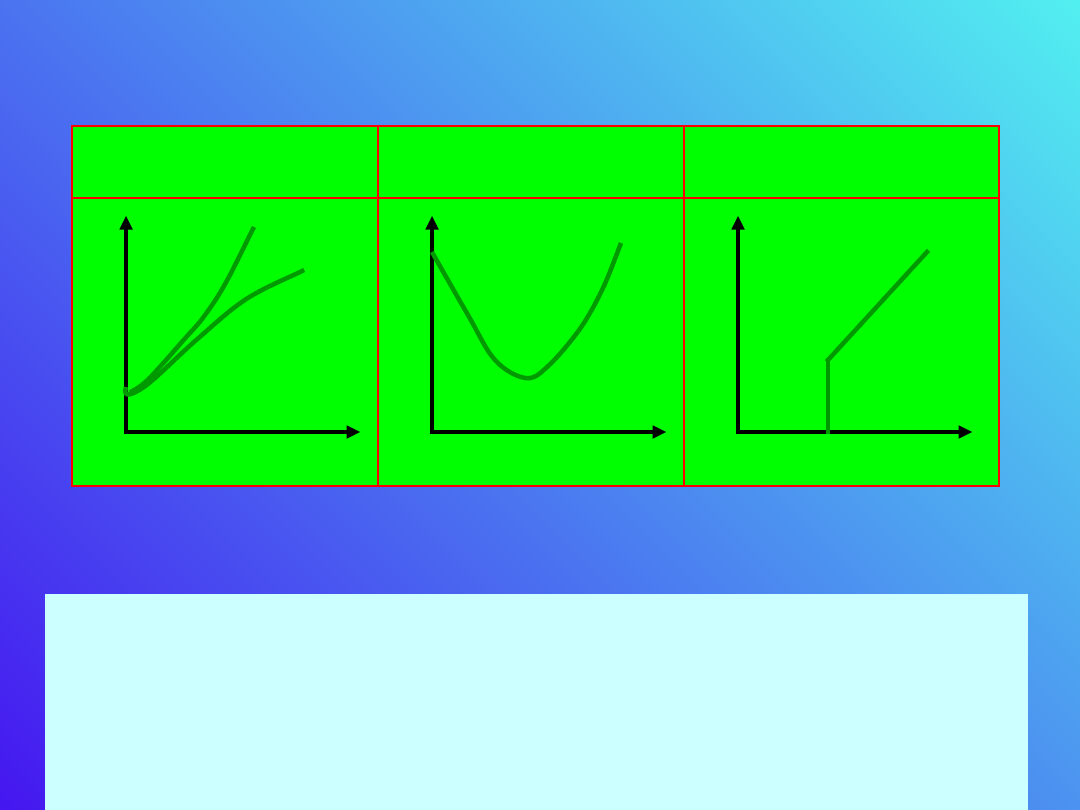
Metal Półprzewodnik
Nadprzewodnik

T

T

T







Powyższa tabela przedstawia przebieg oporów z
temperaturą dla różnych materiałów.

Współczynnik temperaturowy oporu zależy w dużym
stopniu od czystości materiału. Bardzo małe
domieszki zwiększają opór właściwy, a przez
odpowiednie stopy można uzyskać słabą zależność
oporu od temperatury.

Współczynnik  nie jest stały i zależy od

temperatury. Najsilniej z temperaturą rośnie opór
ferromagnetyków.

Prawo Wiedemana - Franza

Omawiając zależność oporu, czy też przewodnictwa
właściwego od temperatury, należy wspomnieć o

związku pomiędzy przewodnictwem cieplnym a
przewodnictwem elektrycznym

. Związek ten

został odkryty w r. 1853 przez Wiedemana i Franza i
jest znany pod ich nazwiskami jako

Prawo

Wiedemana – Franza .

Jeżeli przez



oznaczymy współczynnik

przewodnictwa cieplnego, a przez



współczynnik przewodnictwa elektrycznego, to
dla stałej temperatury T,

const







Oznacza to, że

dobre przewodniki ciepła są też

dobrymi przewodnikami elektryczności.

Później Lorenz stwierdził, że stosunek ten jest
proporcjonalny do temperatury bezwzględnej

T.





LT



L oznacza Liczbę Lorenza

, która można

wyznaczyć w oparciu o teorię przewodnictwa i
zjawisk transportu. Okazuje się, że ;

2

2

8

2

2

/

10

228

.

2

3

K

V

e

k

L









Prawo Joule’a - Lenza

Drugim podstawowym prawem dotyczącym przepływu
prądu elektrycznego poza prawem Ohma jest

Prawo

Joule’a – Lenza.
Prawo to określa wielkość energii wydzielonej w
przewodniku w czasie przepływu w nim prądu.

Jeżeli ładunek dQ jest przenoszony przez różnicę
potencjałów U, to jest wykonywana praca:

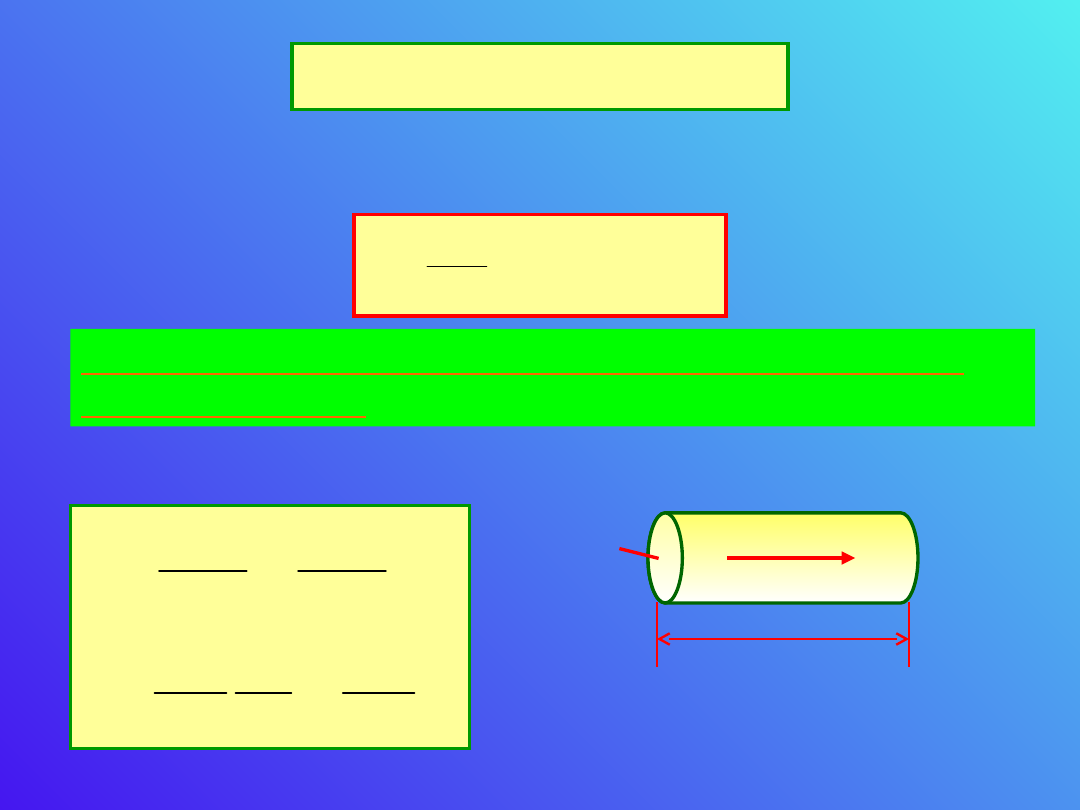
Rdt

I

dt

UI

UdQ

dW

2









Moc wydzielana w przewodniku wynosi więc:

R

I

I

U

dt

dW

P











2

(**)

Równanie(**) stanowi sformułowanie Prawa
Joule’a-Lenza.

Możemy również zdefiniować gęstość objętościową
mocy wydzielonej w przewodniku.

I

A

U

L

2

2

2

2

j

L

A

R

A

I

L

A

R

L

A

I

R

L

A

P

w















W oparciu o prawo Ohma I = U/R mamy:

j

E

L

A

R

R

L

E

A

j













Ostatecznie otrzymujemy na gęstość mocy
wyrażenie:

2

E

j

E

w









Gęstość mocy wydzielanej w przewodniku w
czasie przepływu prądu jest proporcjonalna do E

2

.

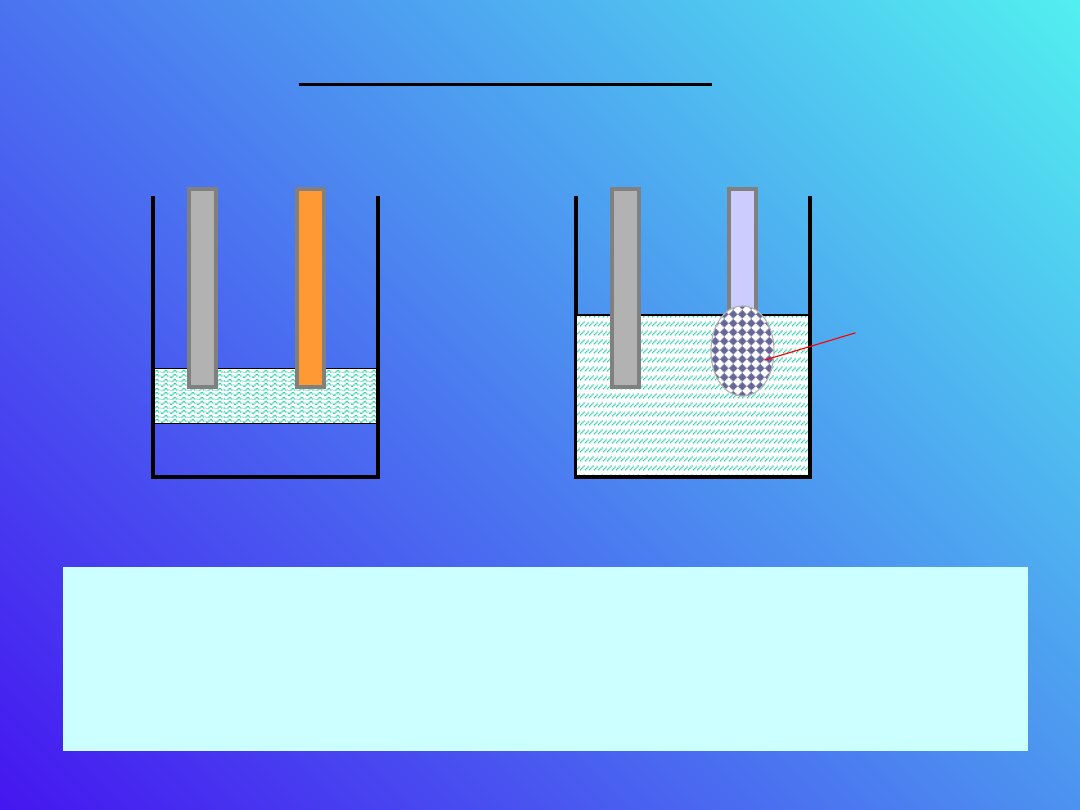
H

2

S

O

4

NH

4

Cl

Zn

Zn

Cu

C

-

-

+

+

MnO

2

+C

Łączenie ogniw

Ogniwa możemy łączyć podobnie jak opory.
Sposób połączenia zależy od tego, czy chcemy
aby w obwodzie płynął duży, albo aby napięcie
było wysokie.

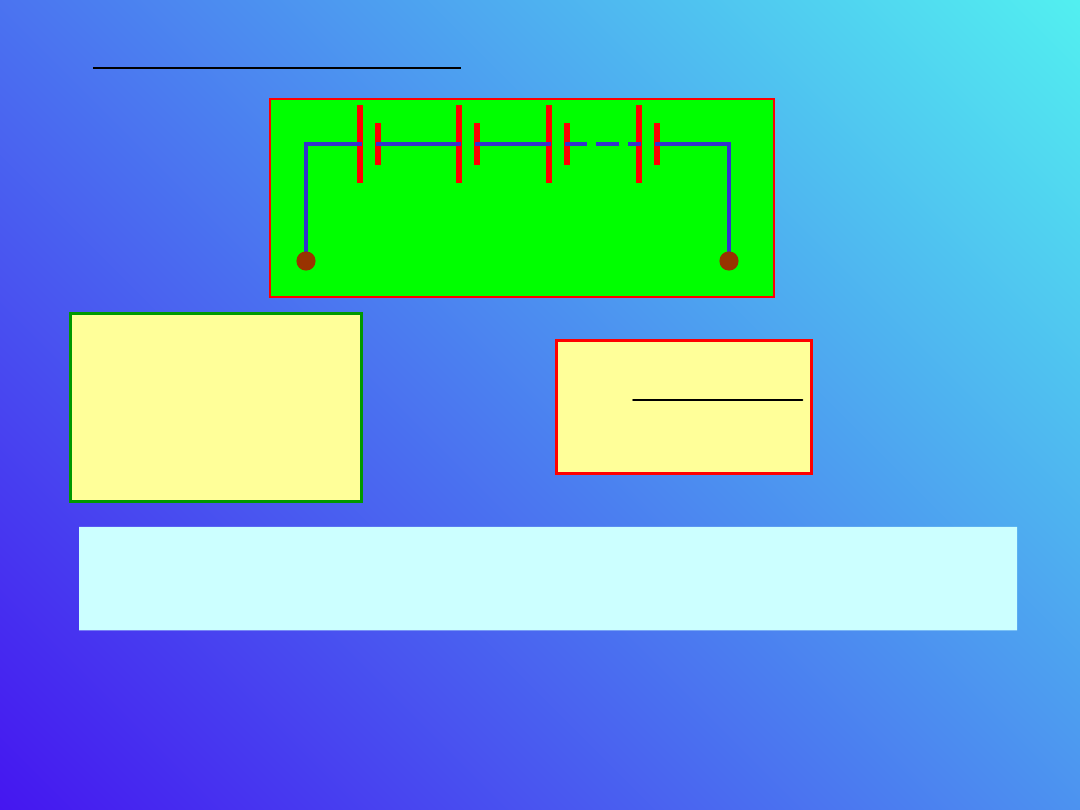
a) Łączenie szeregowe

n

i

i

w

i

w

w

i

i

i

nR

R

R

n



















wted
y

z

w

i

R

nR

n

I

i







Gdy R

z

>> nR

w

, dostajemy większą siłę

elektromotoryczną, oraz większe natężenie.

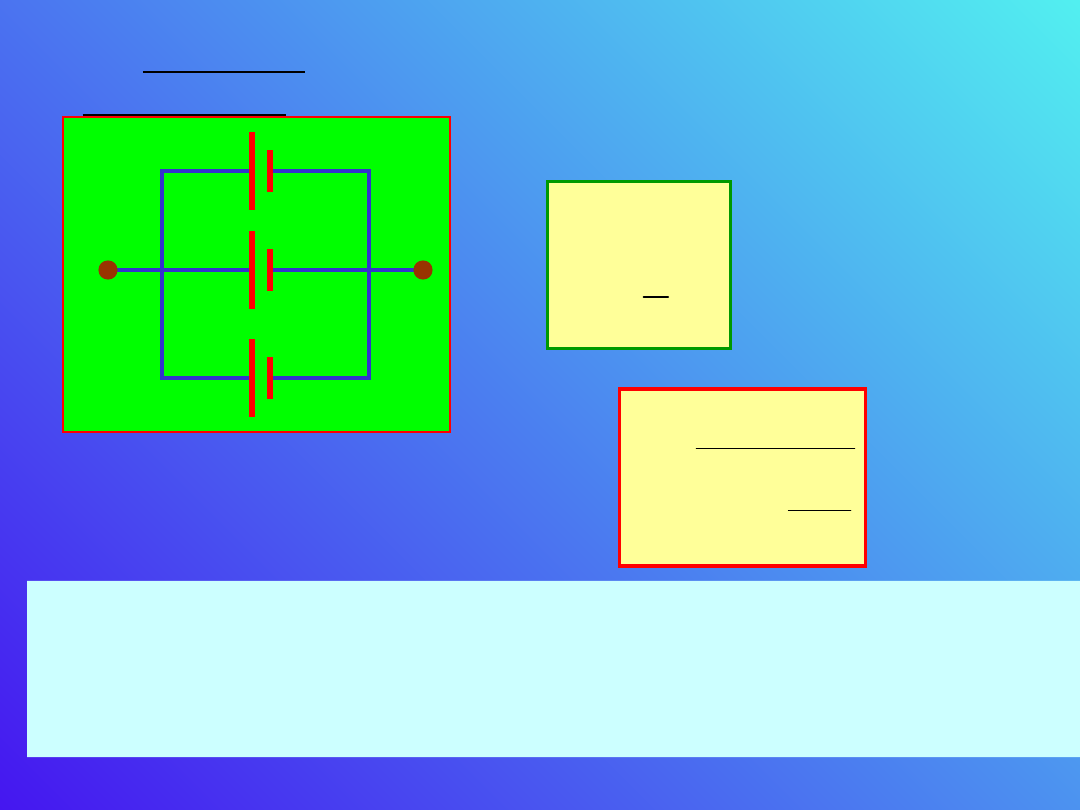
b). Łączenie
równoległe

i

w

w

i

R

n

R

1









Natężenie prądu będzie
równe:

n

R

R

I

i

w

z

i







Gdy R

z

>> nR

w,

prąd jest taki sam jak dla

jednego ogniwa.
Gdy R

z

<< R

w,

prąd jest n razy większy.

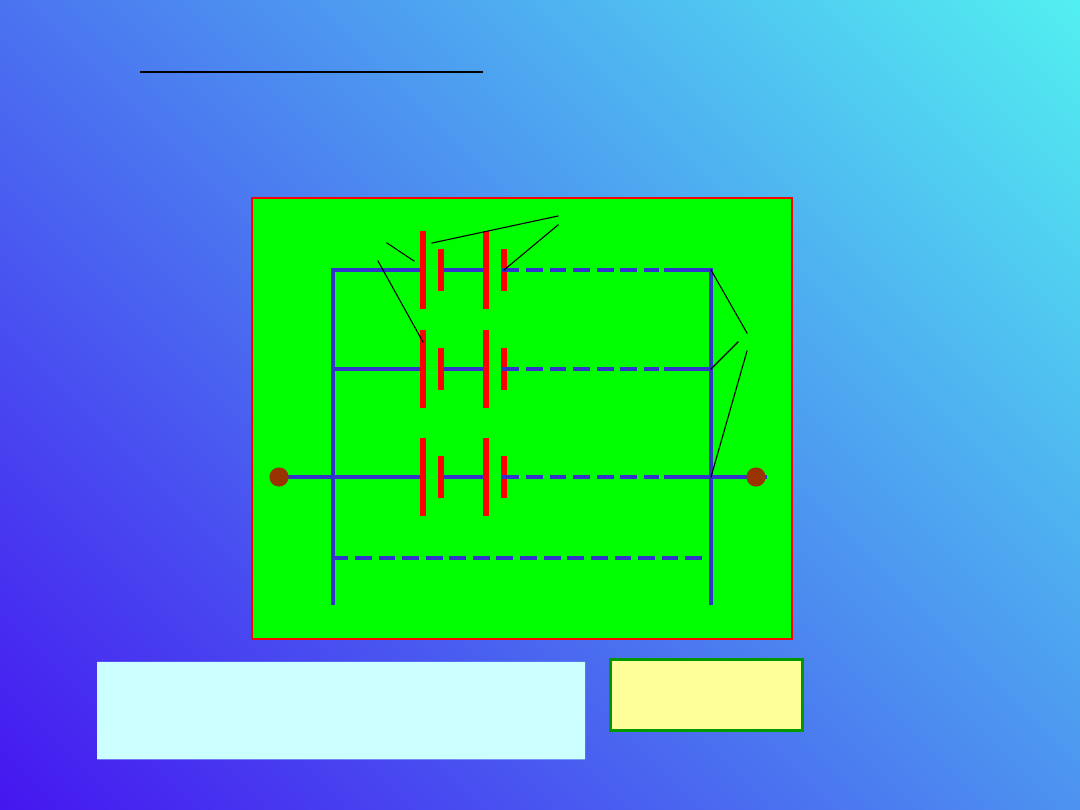
c). Łączenie mieszane

n

m

W każdym szeregu mamy n baterii, i połączonych
równolegle m szeregów. Każda bateria ma opór
wewnętrzny R

wi

.

Siła elektromotoryczne
wynosi;

i

n







Є

i

.

Całkowity opór takiego połączenia wynosi;















m

R

n

R

i

w

Natężenie prądu, które popłynie w obwodzie, gdy
włączymy baterię w obwód o oporze R

z,

będzie

równe;

z

w

i

R

R

m

n

n

I

i







Gdy mamy łącznie (m · n) ogniw, uzyskamy
maksymalny prąd , gdy;

z

w

R

R

n

m



Najprostsze obwody elektryczne

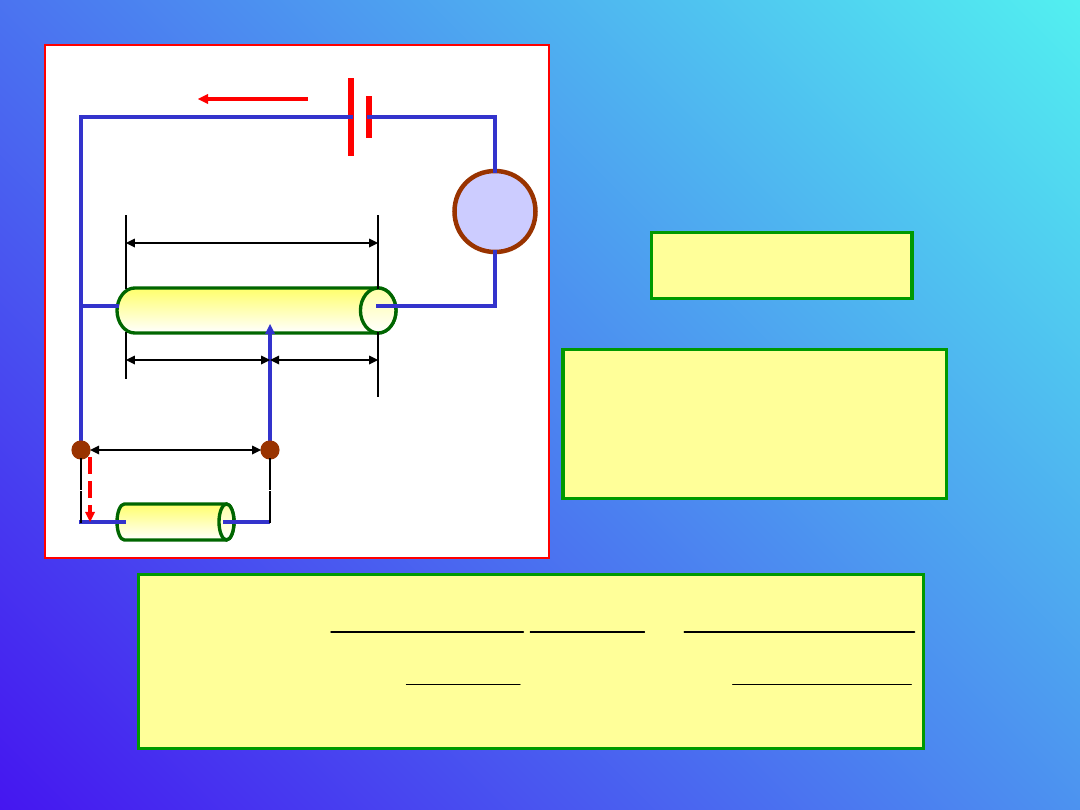
A. Dzielnik
napięcia.

B. Mostek
Wheatstone’a

C. Kompensacyjna metoda pomiaru siły
elektromotorycznej

D. Prosty układ
RC

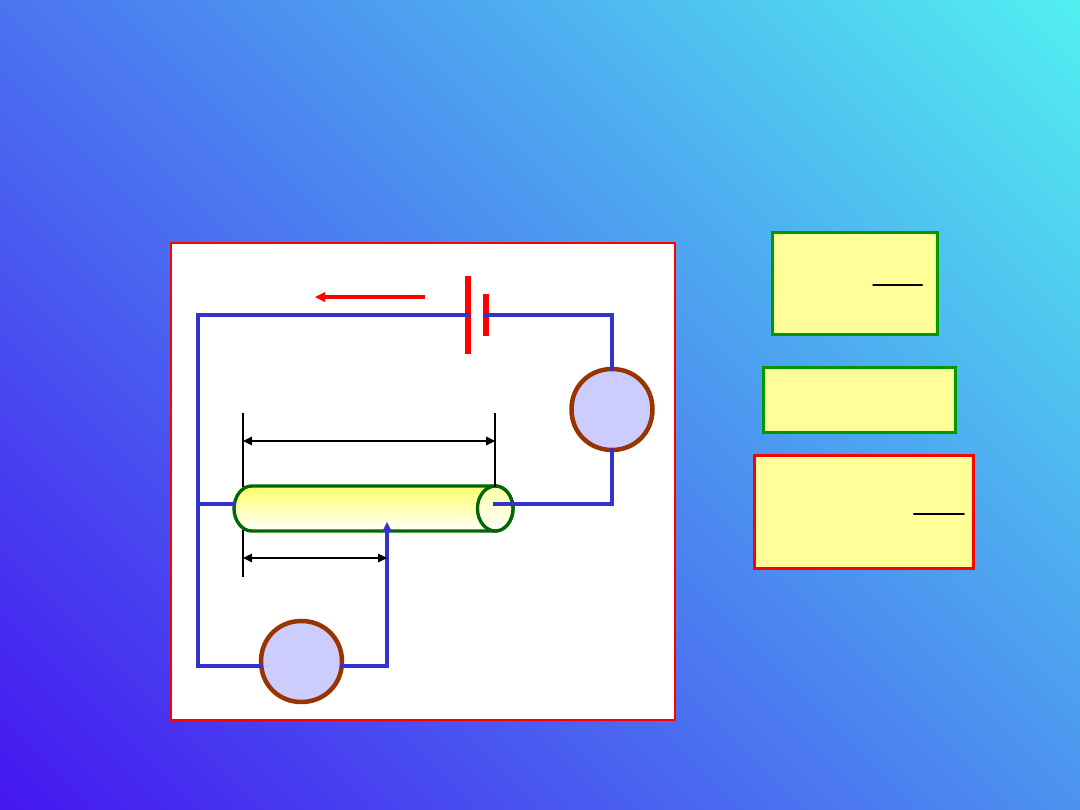
A. Dzielnik napięcia.

A

V

R

R

x

U

R

U

I 

I

x

x

R

I

U





R

R

U

U

x

x





A

R

R

1

U

I

’

R

A

R

2

I

A

U

A’

W przypadku gdy
obciążymy dzielnik
oporem R

A

napięcie

U

a

ulegnie zmianie na

U

A’

, przy czym

'

1

'

'R

I

U

A



gdzi
e

)

/(

)

(

2

'

1

'

1

1

'

1

R

R

U

I

R

R

R

R

R

A

A









Napięcie U

A’

będzie więc

równe:

A

A

A

A

A

A

A

R

R

R

R

R

U

R

R

R

R

R

R

R

R

R

U

R

I

U

1

1

2

1

1

1

1

2

'

1

'

'

)

(

1

















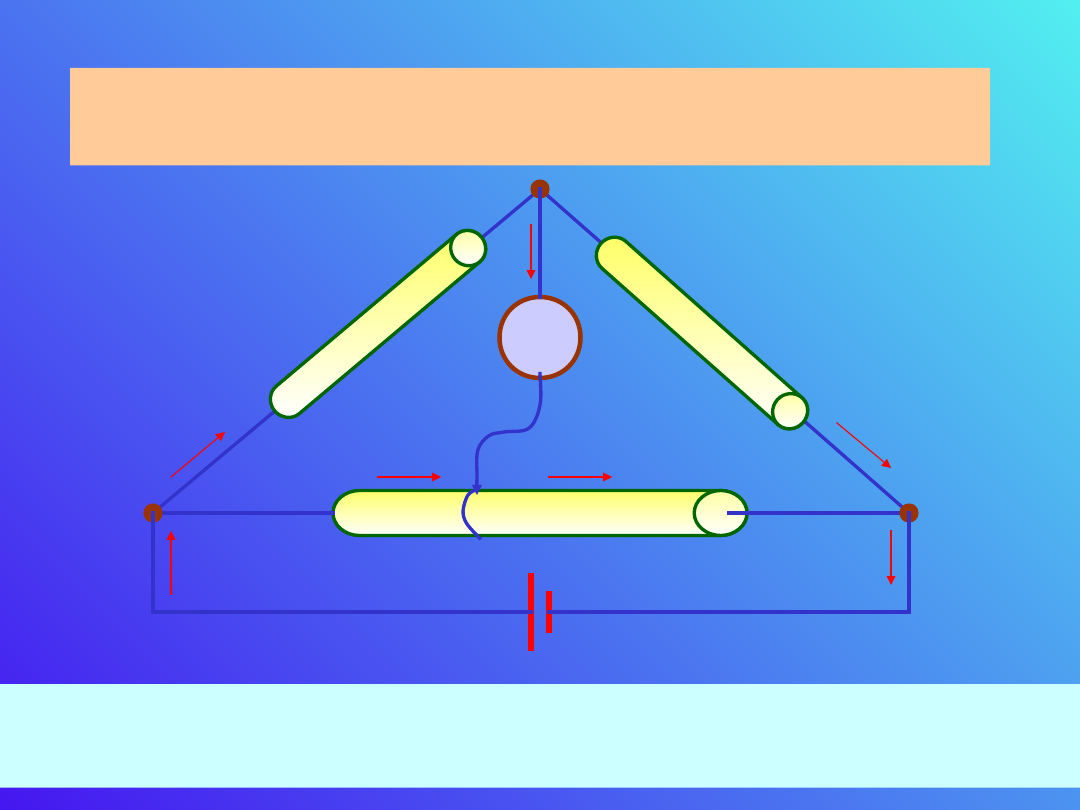
B. Mostek Wheatstone’a

Mostek Wheatstone’a jest najbardziej znanym
układem do pomiaru oporu elektrycznego.

G

A

B

R

0

R

x

C

U

I

1

I

D

I

1

I=
0

I

2

I

2

R

1

R

2

Opór mierzony wpinamy pomiędzy punktami C i B. R

0

jest

znanym oporem.

Suwak na oporze AB przesuwamy tak długo, aż w gałęzi CD nie
popłynie prąd. Oznacza to równość potencjałów w punktach C i D.
Rozważając oczko ACD otrzymujemy;

2

1

1

0

2

1

1

0

0

I

R

I

R

I

R

I

R







.

Z kolei rozważając oczko CBD otrzymujemy;

2

2

1

2

2

1

0

I

R

I

R

I

R

I

R

x

x







.

Dzieląc drugą linijkę tych równań przez siebie,
otrzymujemy;

1

2

0

R

R

R

R

x



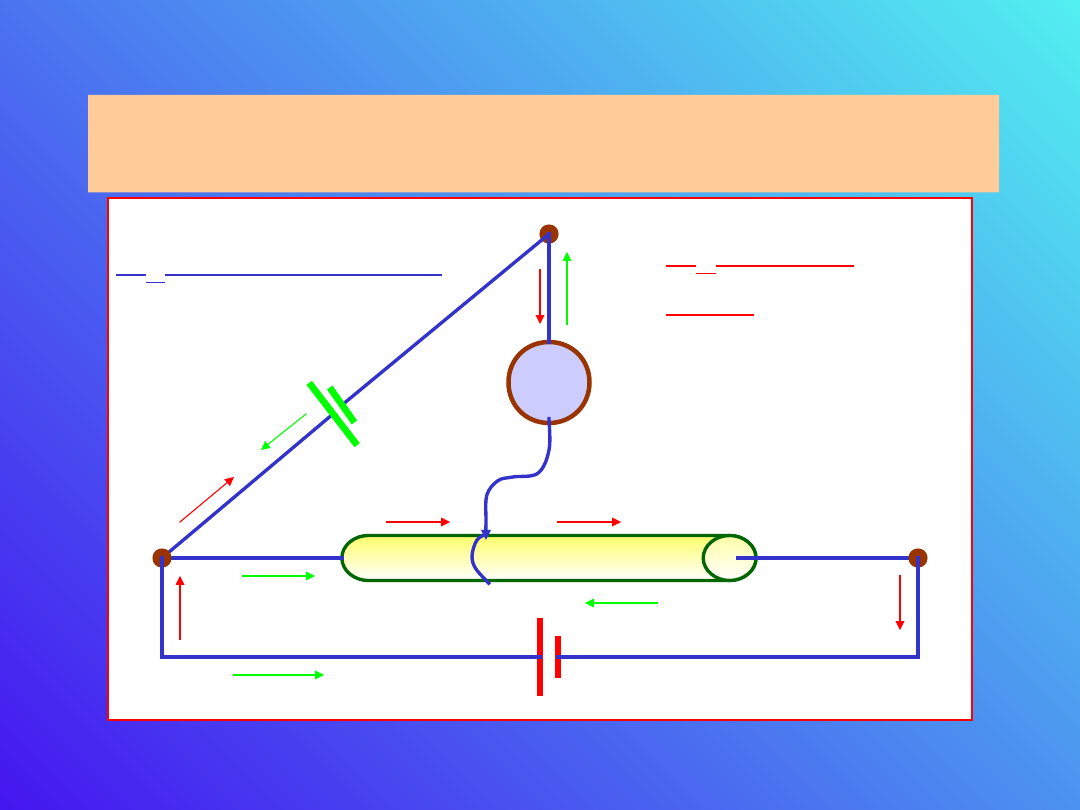
G

A

B

C

I

02

I

0

D

I

02

I

01

I

0

R

1

R

2

C. Kompensacyjna metoda pomiaru siły
elektromotorycznej

U

0

U

x

R

wx

I

x

I

x

I

x2

I

x1

I

x2

Metoda ta jest podobna do wyznaczania oporów
w oparciu o mostek Wheatstone’a.

U

x

– szukana SEM

U

0

– znana

SEM

R

g

R

w0

-

+

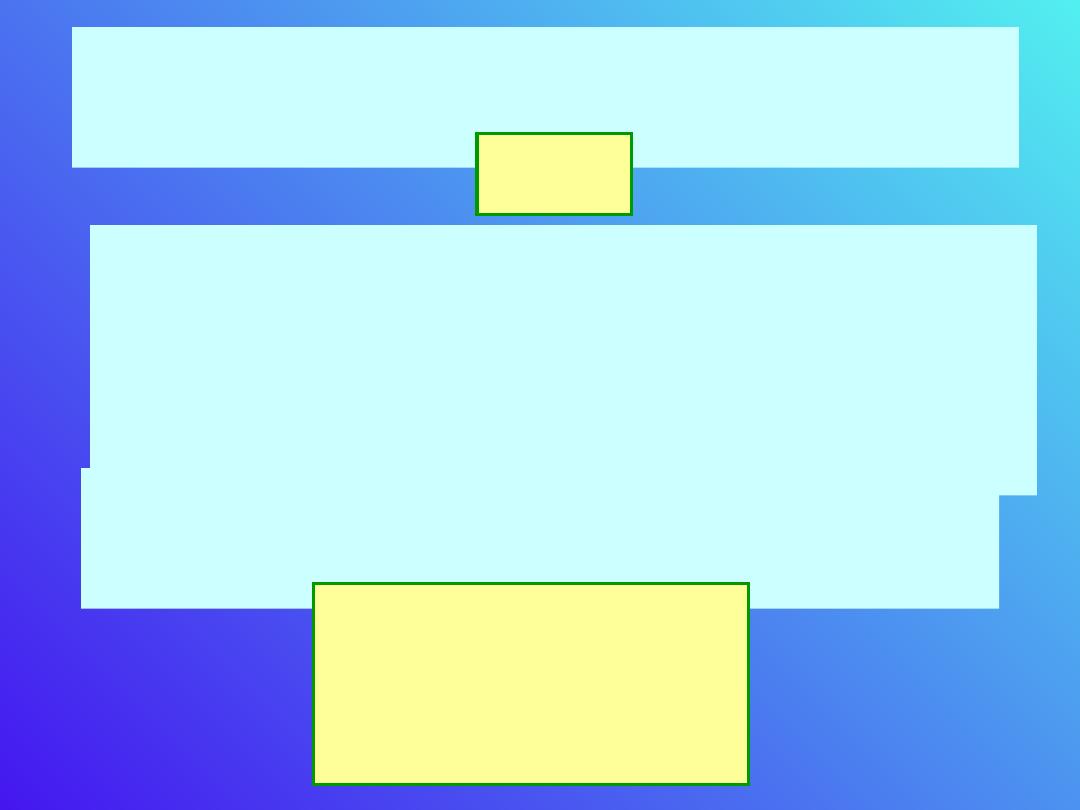
Zmieniamy ustawienie suwaka na oporze AB tak
długo, aż w galwanometrze przestanie płynąć
prąd. Wtedy wiemy, że;

02

I

I

x



Prąd w każdej gałęzi jest algebraiczną sumą
prądów pochodzących od każdej siły
elektromotorycznej oddzielnie, przy czym muszą
zostać uwzględnione opory wewnętrzne
wszystkich ogniw. Musimy również uwzględnić
opór galwanometru.

Dla prądów związanych z szukaną siłą
elektromotoryczną otrzymamy w oparciu o
Prawa Kirchoffa;

0

)

(

)

(

1

1

0

2

2

1

1

2

1

















R

I

R

R

I

U

R

I

R

R

I

I

I

I

x

w

x

x

x

wx

g

x

x

x

x

.

Dla prądów wywołanych przez siłę
elektromotoryczną U

0

otrzymamy;

0

1

01

0

2

0

1

01

02

02

01

0

)

(

0

)

(

U

R

I

R

R

I

R

I

R

R

I

I

I

I

w

wx

g

















Z układu podanych równań można znaleźć I

x1

i I

x2

w

funkcji oporów i U

x

, oraz I

01

i I

02

w funkcji tych

samych oporów i U

0

.

Z warunku znikania prądu w galwanometrze

x

I

I 

02

otrzymujemy,

0

2

1

0

1

U

R

R

R

R

U

w

x







.

.

Gdy R

w0

<< R=R

1

+R

2,

metoda ta jest dokładna.

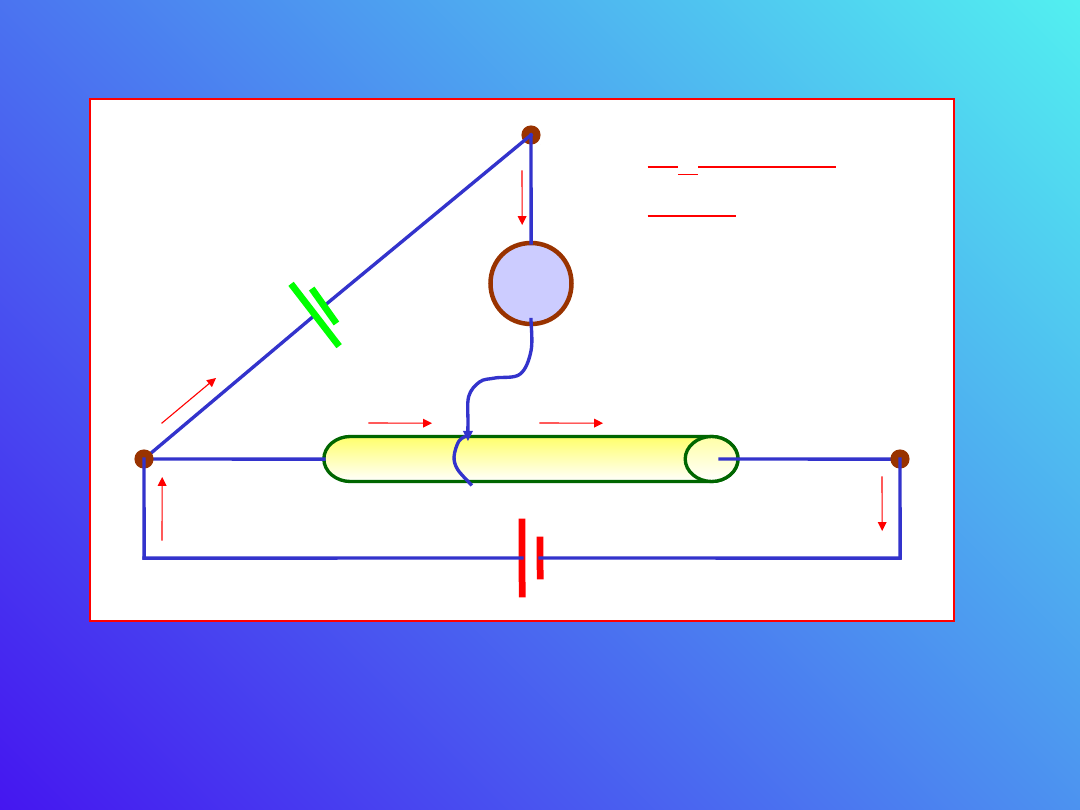
G

A

B

C

I

2

I

0

D

I

2

I

1

I

0

R

1

R

2

U

0

U

x

R

wx

U

0

– znana

SEM

R

g

R

w0

+ -

Zakładając kierunki prądu takie jak na rysunku,
oraz że opór wewnętrzny galwanometru R

g

= 0,

możemy napisać

Zakładając wypadkowe prądy w poszczególnych gałęziach mamy;

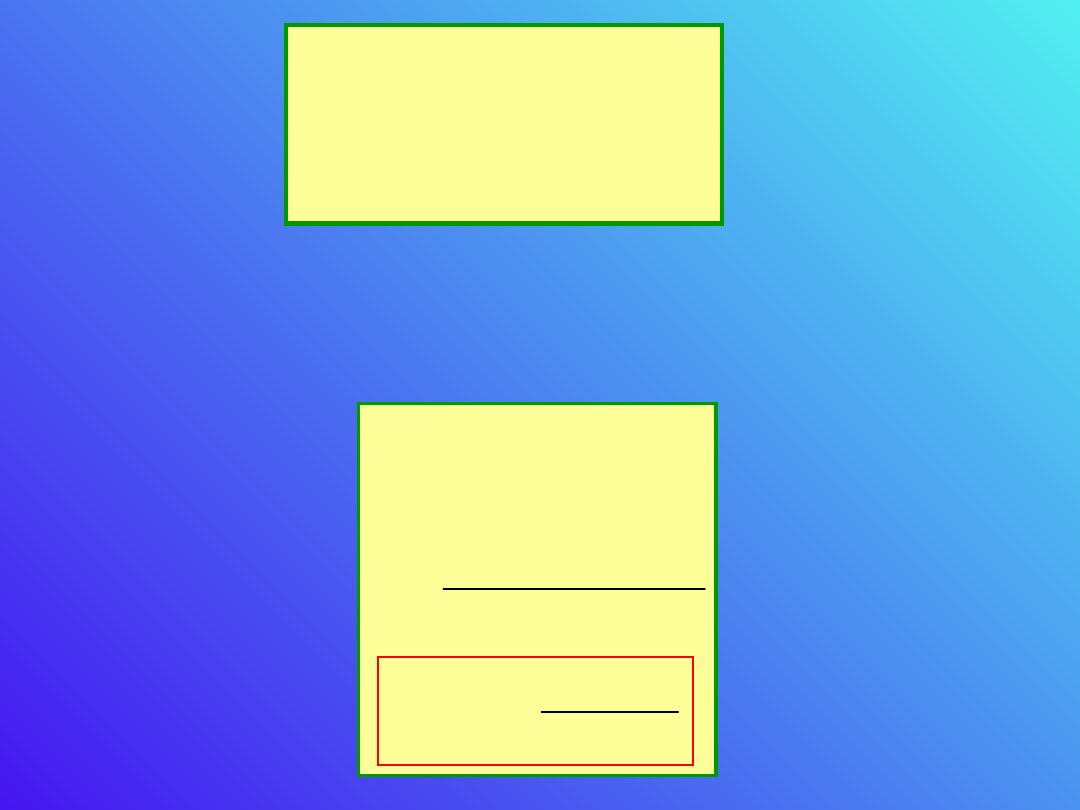
x

wx

w

U

R

I

R

I

U

R

I

R

R

I

I

I

I

















1

1

2

0

1

1

0

2

0

2

1

0

)

(

Ustawiając suwak w punkcie D tak, aby przez
galwanometr nie płynął prąd, czyli I

2

= 0, mamy

0

1

0

0

2

1

0

1

1

1

1

0

)

(

w

x

w

x

R

R

R

U

U

R

R

R

U

I

R

I

U

I

I



















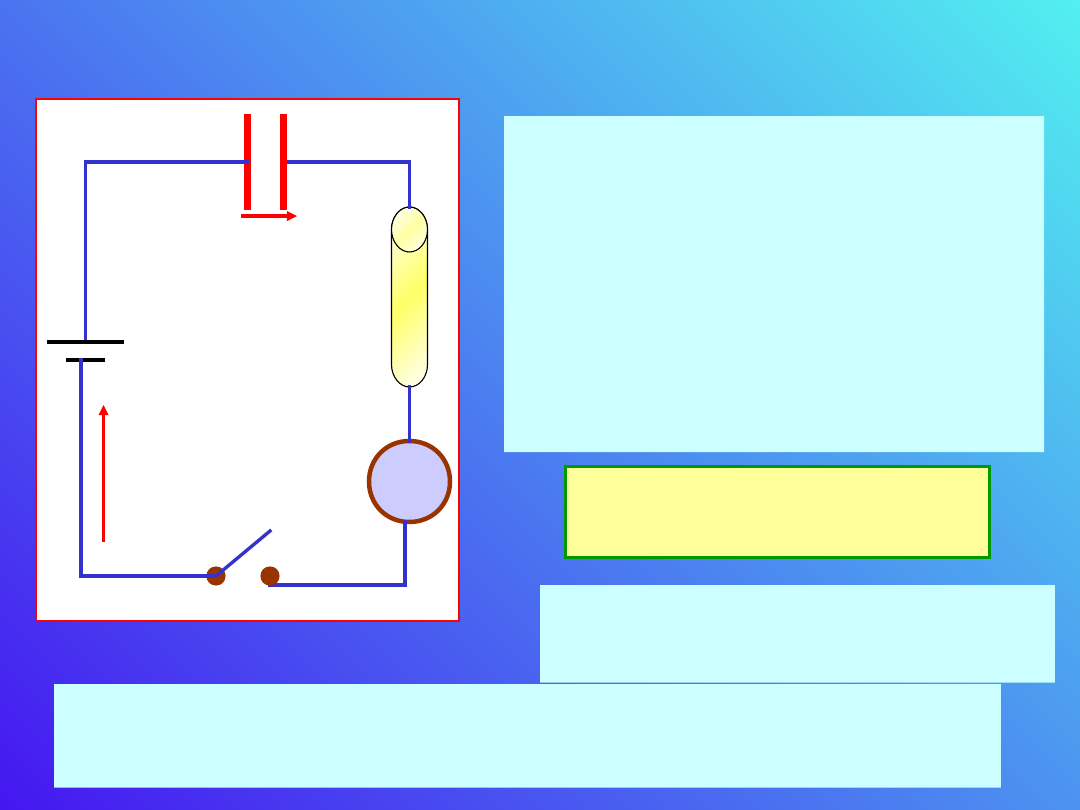
D. Prosty układ RC

G

R

U

C

K

I

Jeśli zamykamy obwód
kluczem K, to w chwili t=0
łączymy nie naładowany
kondensator ze źródłem siły
elektromotorycznej U.

W oparciu o II Prawo
Kirchoffa mamy;

U

0







IR

U

U

C

Oznaczając chwilowe
natężenie

Prądu w obwodzie

I

, oraz chwilowe napięcie na

okładkach kondensatora przez

U

C

, otrzymamy:

-

+

+ -

C

Q

U

dt

dQ

I

C





0







dt

dQ

R

C

Q

U

Po przekształceniu i podzieleniu przez R
otrzymamy:

Rozwiązanie tego równania ma postać:

0

1







R

U

Q

RC

dt

dQ

Po podstawieniu do poprzedniego równania
otrzymamy:

)

1

(

1

t

RC

C

e

CU

Q







Ponieważ :

C

Q

U

C

C

/



napięcie na kondensatorze, będzie się więc
zmieniało zgodnie z równaniem:



















t

RC

C

e

U

U

1

1

Iloczyn RC ma wymiar czasu i jest nazwany
czasem

relaksacji

.

,

.

Wstawiając wyrażenie na czasową zależność
napięcia na kondensatorze do naszego
wyjściowego równania, otrzymamy wzór na
czasową zależność natężenia prądu ładującego
kondensator.

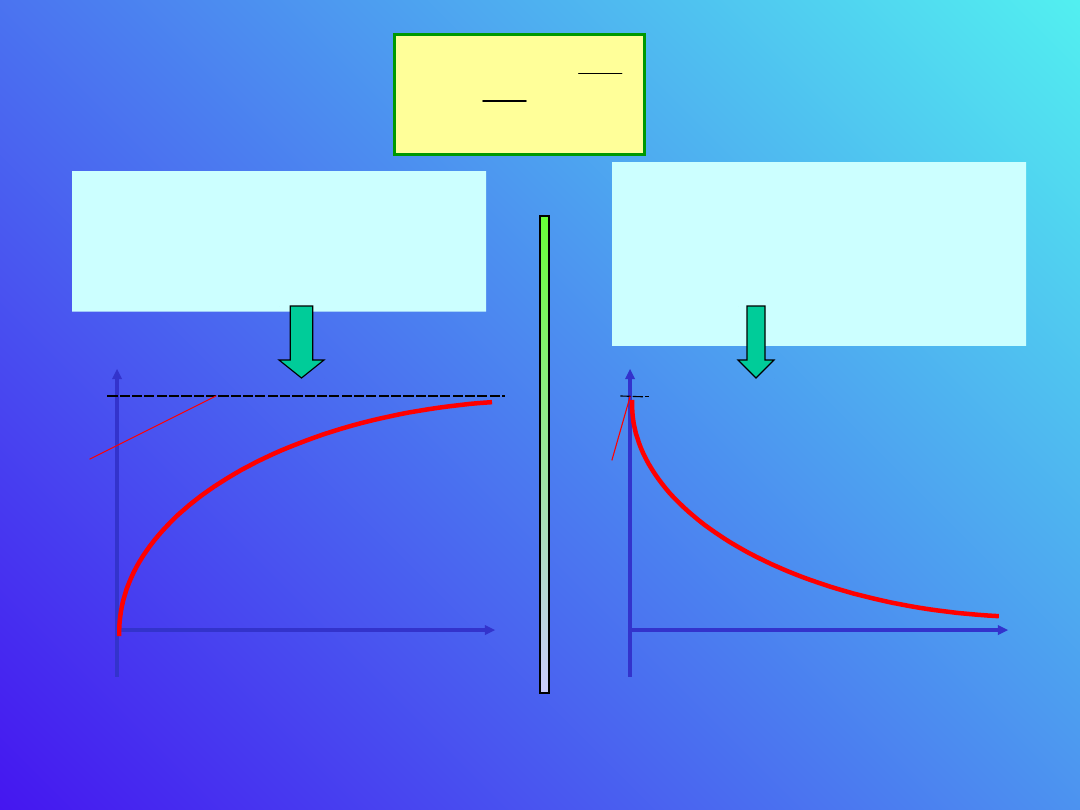
t

RC

e

R

U

I

1





U

t

Przebieg napięcia na
kondensatora w
czasie ładowania.

U

C

I

t

U/R

Przebieg natężenia
prądu w obwodzie w
czasie ładowania
kondensatora.

Półprzewodniki

Półprzewodniki

Przewodnictwo ciał stałych zależy od wzajemnego
położenia pasma walencyjnego i pasma
przewodnictwa, oraz od liczby elektronów, które
mogą dojść do pasma przewodnictwa.
W półprzewodniku typowy rozkład energii pasma
walencyjnego i przewodnictwa wygląda
następująco.

• • • • • • • • •
• • • •

° ° ° ° ° ° ° ° ° °
° °

Pasmo
walencyjne

Pasmo
przewodnictwa

E

P

E

D

E

F

E

A

E

W

E-przerwa

energetyczna

Oznaczenia energii na osi pionowej są następujące:

E

W

- górna energia pasma walencyjnego,

E

A

- energia poziomu energetycznego akceptorów,

E

F

- energia Fermiego,

E

D

- energia poziomu energetycznego donorów,

E

P

- najniższa energia pasma przewodnictwa.

E = E

P

– E

W

– szerokość przerwy energetycznej

Szerokość przerwy energetycznej dla germanu(Ge)
wynosi 0.66eV.

Donory

Sb

P

As

Li

E

P

-

E

D

(eV)

0.009

7

0.0120 0.0127 0.009

Akceptor

y

Al

Ga

In

B

E

A

-

E

W

(eV)

0.010

2

0.0108 0.0112 0.0100

Rodzaje półprzewodników

Półprzewodniki klasyfikuje się w zależności od
koncentracji donorów (N

D

) i akceptorów (N

A

).

Wpływają one na koncentrację nośników
nadmiarowych (elektronów) typu n (ujemnych) i
niedomiarowych(dziur), typu p (dodatnich).

Rozróżniamy więc następujące półprzewodniki:

A).

samoistne

, dla których N

D

=N

A

=0. Posiadają

one własne przewodnictwo, czyli odpowiednią
koncentrację elektronów i dziur. Koncentracja ta
jest proporcjonalna do,

)

2

exp(

~

2

3

kT

E

T

n

p

n

opt









Następstwem takiej zależności koncentracji jest
zależność temperaturowa przewodnictwa
właściwego czystych półprzewodników.

)

2

exp(

~

)

(

kT

E

T







B).

Typu-n

z N

D

>>0 i N

A

=0. Dla tego typu

półprzewodników nośnikami są elektrony,
których istnieje duży nadmiar n>>p. W niskich
temperaturach współczynnik przewodnictwa
właściwego zależy od energii stanów
donorowych E

D

.









kT

E

E

T

P

D

2

/

exp

~

)

(





Nośnikami są dziury. Występuje w nich niedomiar
elektronów n<<p. W niskich temperaturach
współczynnik przewodnictwa właściwego zależy od
temperatury zgodnie z zależnością;









kT

E

E

T

A

W

2

/

exp

~

)

(





Przewodnictwo półprzewodników typu n i p
jest w wysokich temperaturach takie jak typu
samoistnego.

C).

Typu-p

z N

D

=0 i N

A

>>0 Dla tego typu

półprzewodników

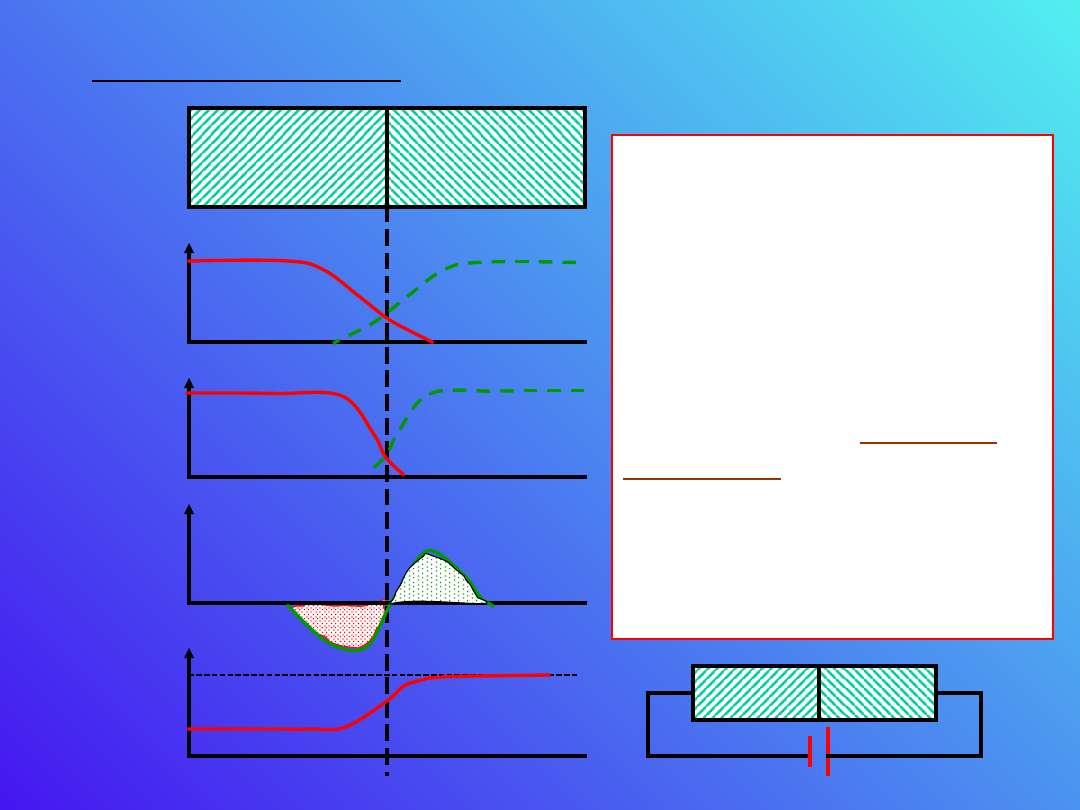
Złącze typu n-p

p

n

Złącze n-p

Koncentracja
donorów i
akceptorów

Koncentracja

dziur

i

elektronów

dziury

elektrony

Gęstość
ładunk
u

potencjał

Dzięki dyfuzji
elektronów z n do p i
dziur z p do n powstaje
w warstwie przejściowej
strefa ujemnego i
dodatniego ładunku
przestrzennego
stanowiącego

warstwę

zaporową

. W warunkach

równowagi
termodynamicznej nie
płynie prąd elektryczny.

Na wysokość bariery U

możemy wpływać przez
przyłożenie napięcia do
złącza n-p.

U

p

n

Pole magnetyczne

Pole magnetyczne

Podstawowe informacje

doświadczalne

Poza polem elektrycznym E istnieje również pewne
inne pole wektorowe B, które możemy określić jako
pewien stan przestrzeni. Pole to jest wytwarzane
przez np. stałe magnesy i wszelkiego rodzaju prądy
elektryczne. Można go uwidocznić przez np. igłę
kompasową, opiłkami żelaza, oraz siłą, którą to pole
działa na poruszające się ładunki.
Nauka o magnesach stałych rozwijała się
niezależnie, lecz prawie równolegle z
elektrostatyką. Bazowała ona na znanych
materiałach magnetycznych.
Jaka jest

ewidencja doświadczalna

dotycząca pól

magnetycznych.

Stwierdzono, że w magnesach naturalnych efekty
magnetyczne są najsilniejsze na końcach magnesu,
nazywanych

biegunami. Obserwacje można przeprowadzić przy
pomocy

igły magnetycznej

lub

opiłków żelaza.

Biegunów magnesu nie da się wyizolować, tak
jak można rozdzielić ładunki elektryczne.

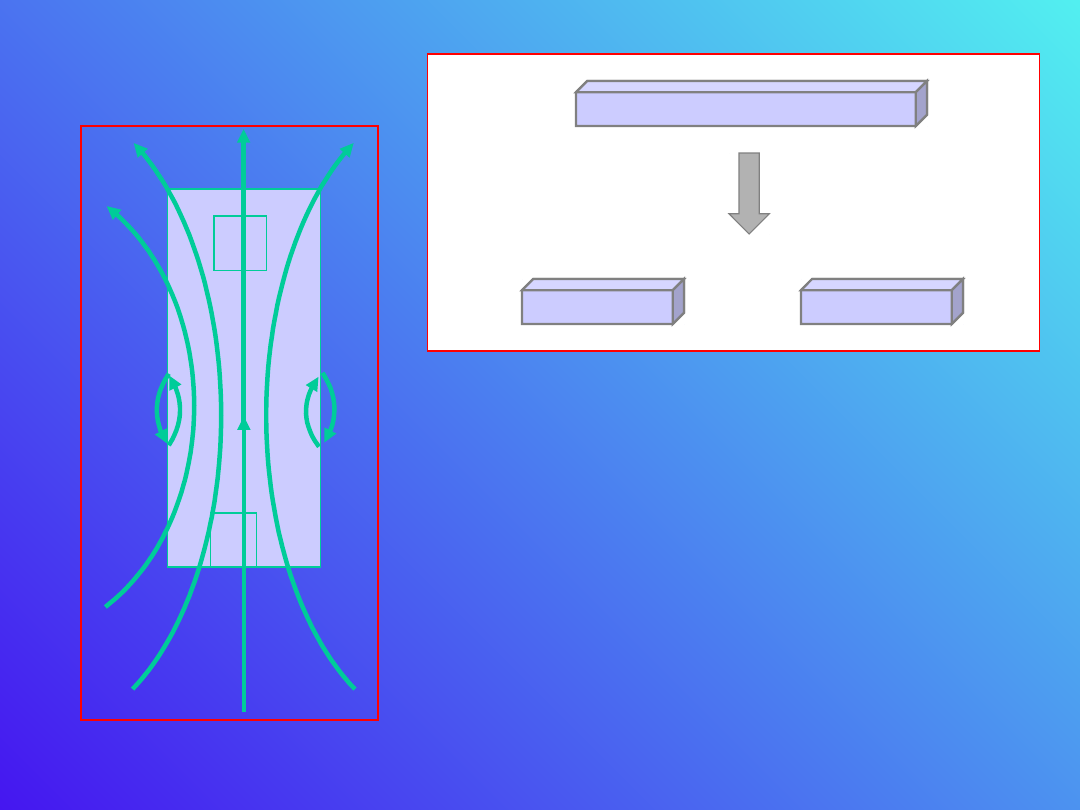
N

S

N

S N

S

N

S

Wokół magnesów stałych
rozchodzą
się linie pola
magnetycznego,

podobnie jak było to dla pola
elektrycznego. Zobaczymy
jednak, że linie pola
magnetycznego są
zamknięte.

Bieguny magnetyczne występują zawsze parami
(dwa przeciwne) o tej samej wielkości.

Dla biegunów magnetycznych możemy analogicznie
do ładunków w elektrostatyce, zdefiniować wielkość
charakteryzującą siłę tych biegunów. Oznaczmy tą
wielkość przez M, którą możemy nazywać masą
magnetyczną.

2

0

2

1

4

r

M

M

F







Oddziaływanie biegunów magnetycznych odbywa
się zgodnie z równaniem;

.

Wielkości M

1,2

, określają siłę biegunów

magnetycznych, r odległość pomiędzy nimi, a 

0

oznacza przenikalność magnetyczną próżni, przy
czym.



o

= 4·10-7 V s A

-1

m

-1

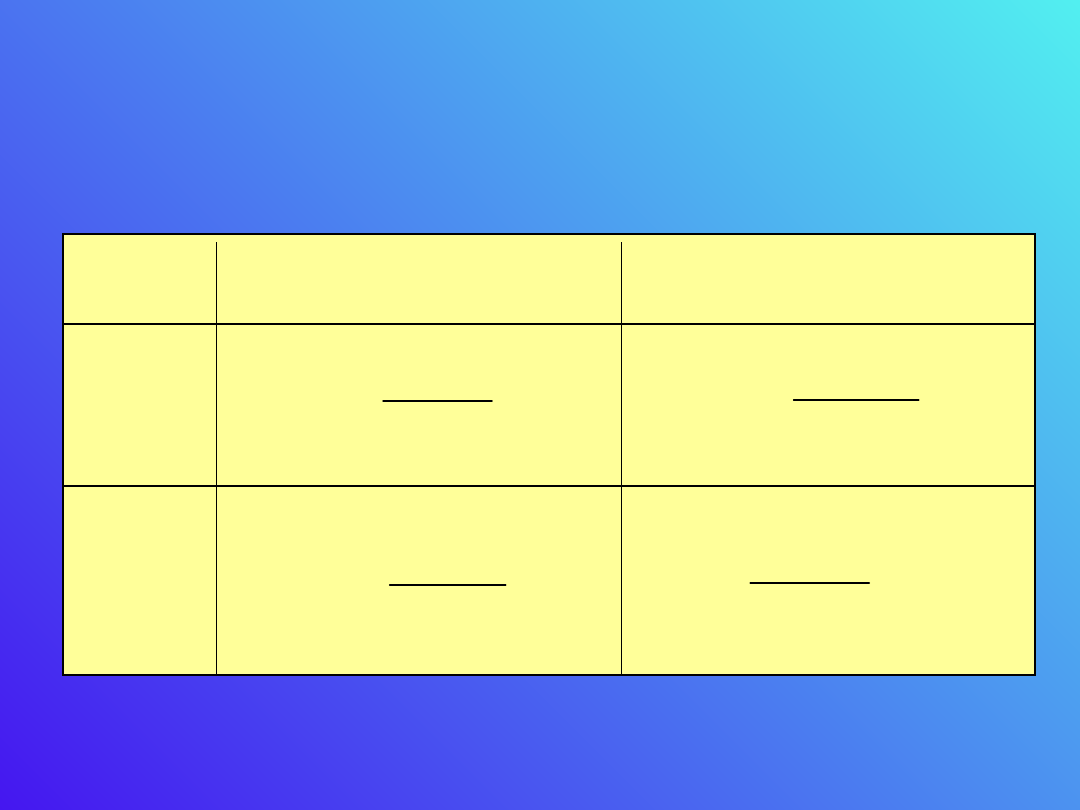
Z zależności siły działającej pomiędzy biegunami
magnetycznymi wynika, że możemy zastosować
tutaj dobrze nam znany formalizm dotyczący
grawitacji i elektrostatyki, wprowadzając m.in.
natężenie i potencjał pola magnetycznego.

r

r

Q

Q

F





3

0

2

1

4





Elektrostatyka

Magnetostatyka

Siła

r

r

M

M

F





3

0

2

1

4





Natężenie
Pola

r

r

Q

E





3

0

1

4





)

/

(

4

3

0

1

m

A

r

r

M

H









Geograficz
na
Północ

Geograficzne
Południe

Magnetycz
ne
Południe

Magnetycz
na
Północ

Ziemskie
pole
magnetyc
zne

Ziemskie
pole
magnetyc
zne

Ziemia posiada również własne pole magnetyczne.
Bieguny magnetyczne nie pokrywają się z
biegunami geograficznymi.

Powiedzieliśmy, że pole magnetyczne wytwarzane
jest również przez wszelkiego rodzaju prądy
elektryczne. Pole magnetyczne wpływa na
poruszające się ładunki elektryczne, działając na
nie siłą.

Wprowadzone w tabelce natężenie pola
magnetycznego jest wielkością, którą uwzględnia
się ze względów historycznych podobnie jak wektor
przesunięcia w elektrostatyce. Drugą wielkością
charakteryzującą pole magnetyczne jest wektor
indukcji magnetycznej B.

H

B





0





Okazało się, że właściwe pole magnetyczne
opisane jest przez wektor indukcji magnetycznej
B, a wektor natężenia pola magnetycznego
opisuje tą część pola, która jest wytwarzana

przez makroskopowe prądy elektryczne o
natężeniu I, dipoli atomowych i prądów okrężnych
ośrodka materialnego.

Jednostkami natężenia pola magnetycznego H,
oraz indukcji magnetycznej B w układzie SI są
odpowiednio:

 

 

2

1

1

1



















m

s

V

T

Tesla

B

m

A

H





W podanym kształcie równanie ogranicza się do
próżni. Będziemy również rozważali zachowanie
się tych pól w obecności materii.

Wróćmy w tej chwili do doświadczalnej ewidencji
siły, którą pole indukcji magnetycznej wywiera
na poruszające się ładunki.

Znane są następujące fakty doświadczalne dotyczące
oddziaływania
pola indukcji magnetycznej na poruszające się
elektrony:

a). Poruszające się elektrony są odchylane ,
b). Działająca na ładunki siła F jest prostopadła do
kierunku wskazywanego przez igłę magnetyczną,
czyli do kierunku wektora B,
c). Siła F prostopadła do prędkości ładunku v,
d). Siła F ~ | v |,
e). Wartość
siły F ~ q.

Wszystkie te wyniki doświadczalne zebrał
Hendrik Lorentz(1853-1928) definiując siłę
nazwaną obecnie

siłą Lorentza

)

(

B

v

q

k

F















W układzie SI stała proporcjonalności

(k

*

=1

).

Równanie to jest równocześnie definicją wektora
indukcji magnetycznej B przez znane wielkości,
siłę F, ładunek q, oraz prędkość v.

W ogólnym przypadku na cząstkę o ładunku q
poruszającą się w jakimś układzie współrzędnych
działa siła:

)

(

B

v

q

E

q

F















Zauważając, że przewodnik z prądem zawiera
poruszające się ładunki, możemy rozszerzyć
prawo Lorentza

I

dl

B

l

d

I

dt

v

dt

dq

v

dq

B

v

dq

F

d





























)

(

Otrzymujemy wyrażenie na siłę działającą na
element przewodu ds, przez który płynie prąd I.

Jest to siła Biota – Savarta

.

)

(

B

l

d

I

F

d













Analogicznie do strumienia pola elektrycznego
możemy zdefiniować strumień wektora indukcji
magnetycznej .

dA

B







A

B

A

d

B







Ze względu na to, że linie pola indukcji
magnetycznej są zamknięte zgodnie z

prawem

Gaussa

zachodzi:

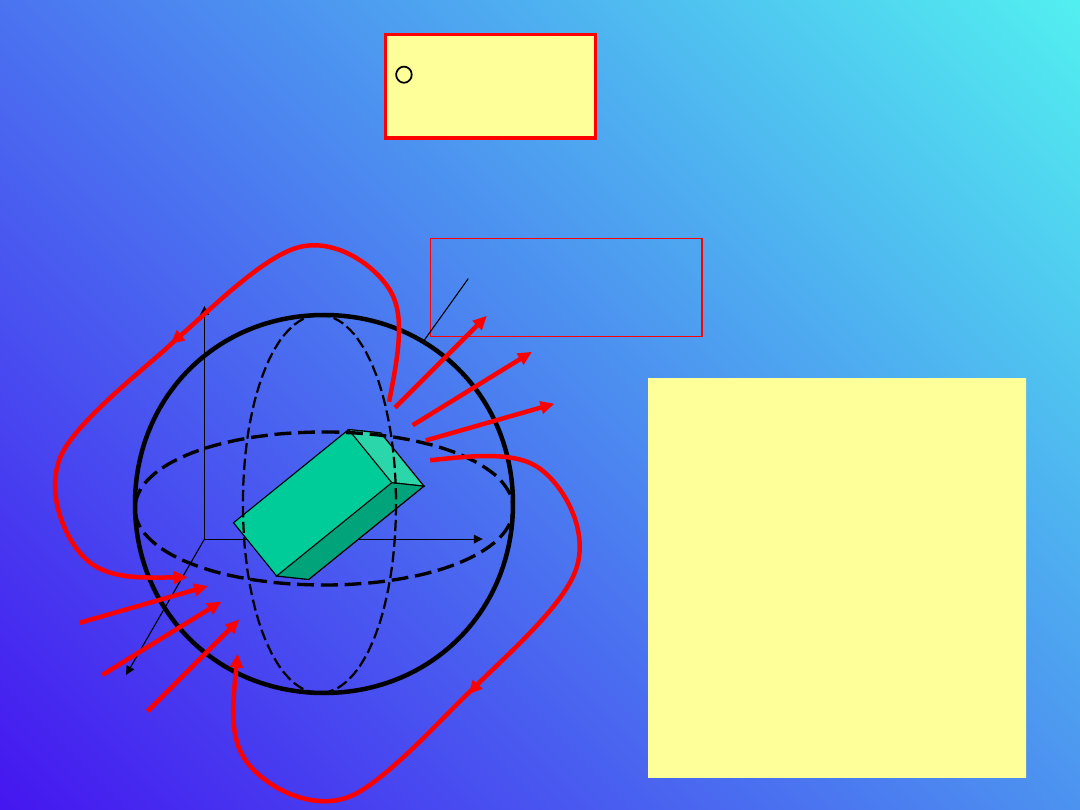
0







A

A

d

B





Rezultat ten jest niezależny od tego, czy
powierzchnia A zawiera przewodniki, izolatory,
ładunki, natężenia prądu, czy magnesy.

x

y

z

N

S

B

Powierzchnia
A

Ponieważ nie
istnieją monopole
magnetyczne,
strumień pola
indukcji
magnetycznej
przez powierzchnie
A musi być równy
zero.

W oparciu o twierdzenie Ostrogradzkiego-Gaussa możemy napisać;

0

















d

B

div

A

d

B

A







Równanie to jest spełnione dla każdej objętości



, a

więc również dla objętości

d.

Otrzymujemy więc;

0



B

div



Równanie to opisuje fundamentalną własność
pola indukcji magnetycznej. Jest to pole
bezźródłowe. Linie pola B nie mają ani początku
ani końca. Tworzą one więc wiry. Dla
natężenia pola elektrycznego zgodnie z
równaniem

0







E

div



Nie ma rozdzielonych ładunków
magnetycznych.

Z

bezźródłowości

pola indukcji magnetycznej którą

inaczej nazywamy

solenoidalnością

wynika, że pole

to charakteryzuje się pewnym potencjałem
wektorowym A. Zakładamy, że potencjał ten też
jest bezźródłowy, oraz że znika w nieskończoności .
Definiujemy go następującym wzorem.

A

rot

B







Zgodnie z twierdzeniem Stokes’a możemy zdefiniować strumień
indukcji pola magnetycznego jako krążenie(cyrkulację) potencjału w
wektorowego A.

dl

A

d

rot

A

d

B

A

A

B



































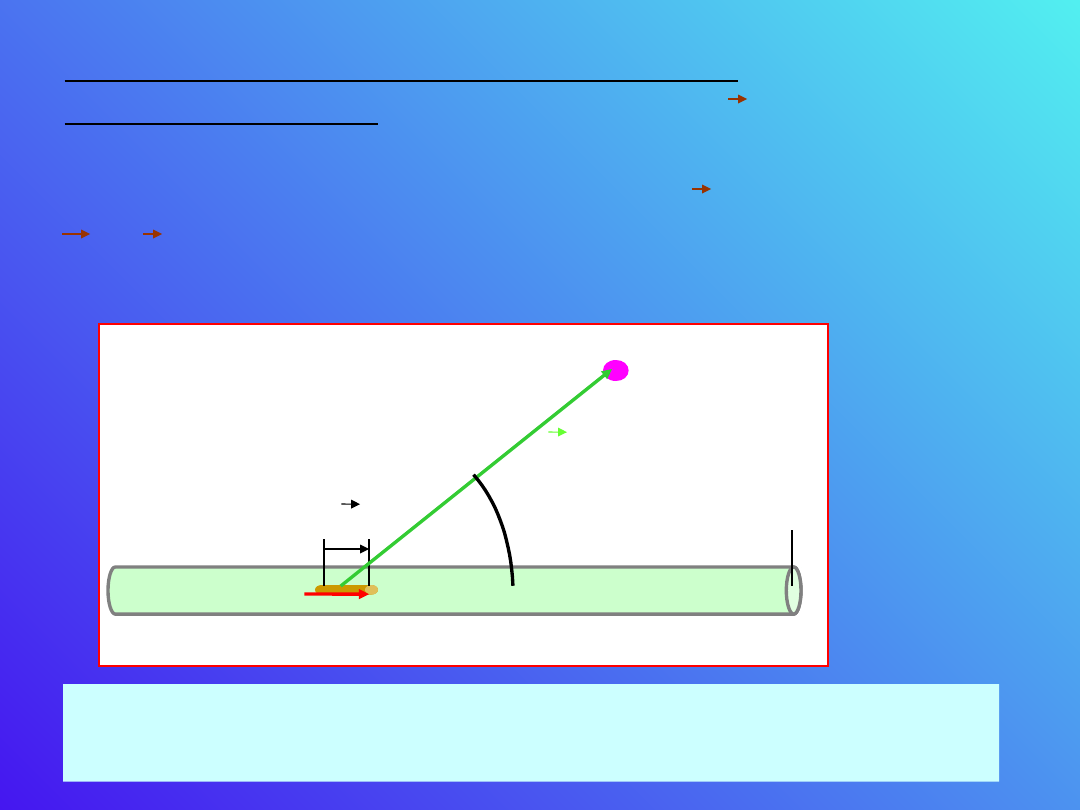
Prąd elektryczny jako źródło pola
magnetycznego

Rozważmy element przewodnika o długości

dl,

przekroju

A

, w którym płynie prąd, którego nośniki

o ładunku

q

i o liczbie

N

w jednostce objętości,

mają średnią prędkość

v

. Gęstość prądu

j=Nqv

, a

natężenie prądu

I=Aj.

Zakładamy, że ładunki

poruszają się równolegle do przewodnika.

Jeśli w przewodniku znajduje się n nośników, to
wytwarzają one pole

I

dl

P

r



A

















r

r

l

d

r

I

B

d







2

0

4



























 



r

r

v

nq

r

r

r

v

r

q

n

B

d











)

(

4

4

2

0

2

0









Wiemy, że

n = N·d =

N·A·dl

,wobec tego

dl

I

dl

A

j

dl

A

Nqv

v

q

dl

A

N

v

q

n

















)

(

Ponieważ zachodzi, że

nqv=Idl,

stąd;

Jest to prawo Biota-Savarta.

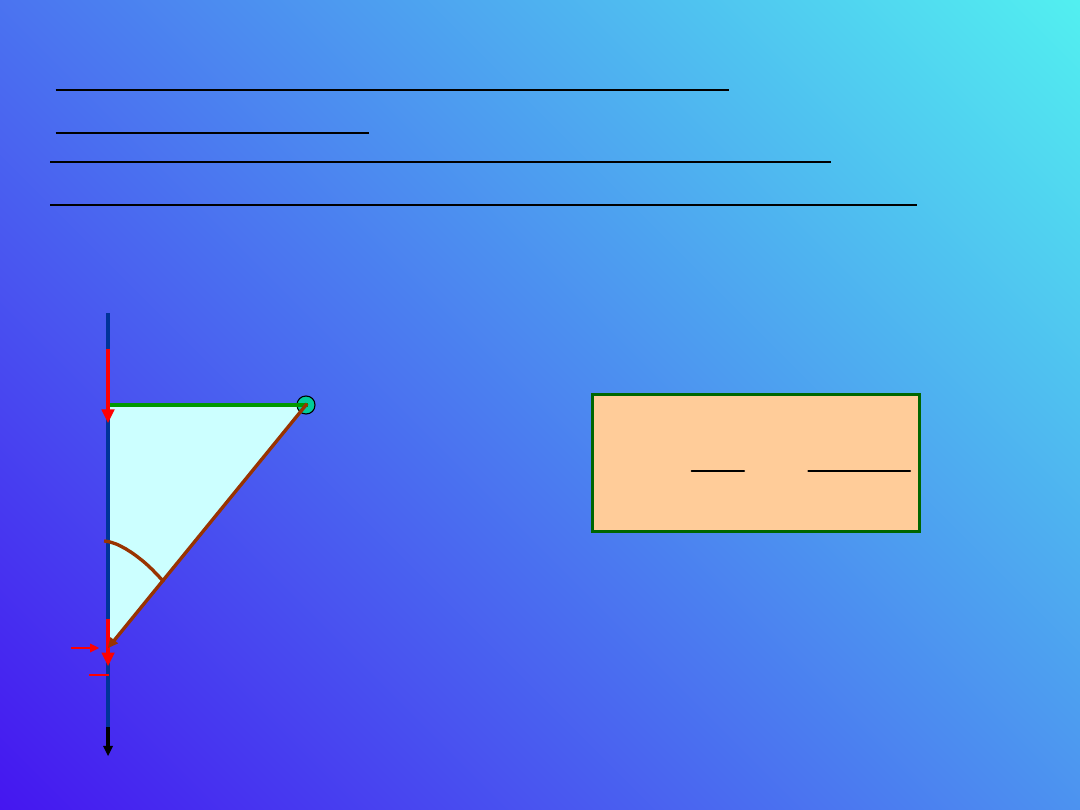
Prąd elektryczny jako źródło pola
magnetycznego

Pole indukcji magnetycznej pochodzące od
nieskończenie długiego przewodnika z prądem.

I

dl

r

0

r = r

0

/sin

P

Chcemy znaleźć pole indukcji w punkcie
P oddalonym o r

0

od przewodnika.

3

0

4

r

r

l

d

I

B

d



















Przyjmując, że przewodnik leży na
osi x, mamy

x/r

0

= ctg  dx=dl=-r

0

/sin

2



·d

r=r

0

/sin



r

x

























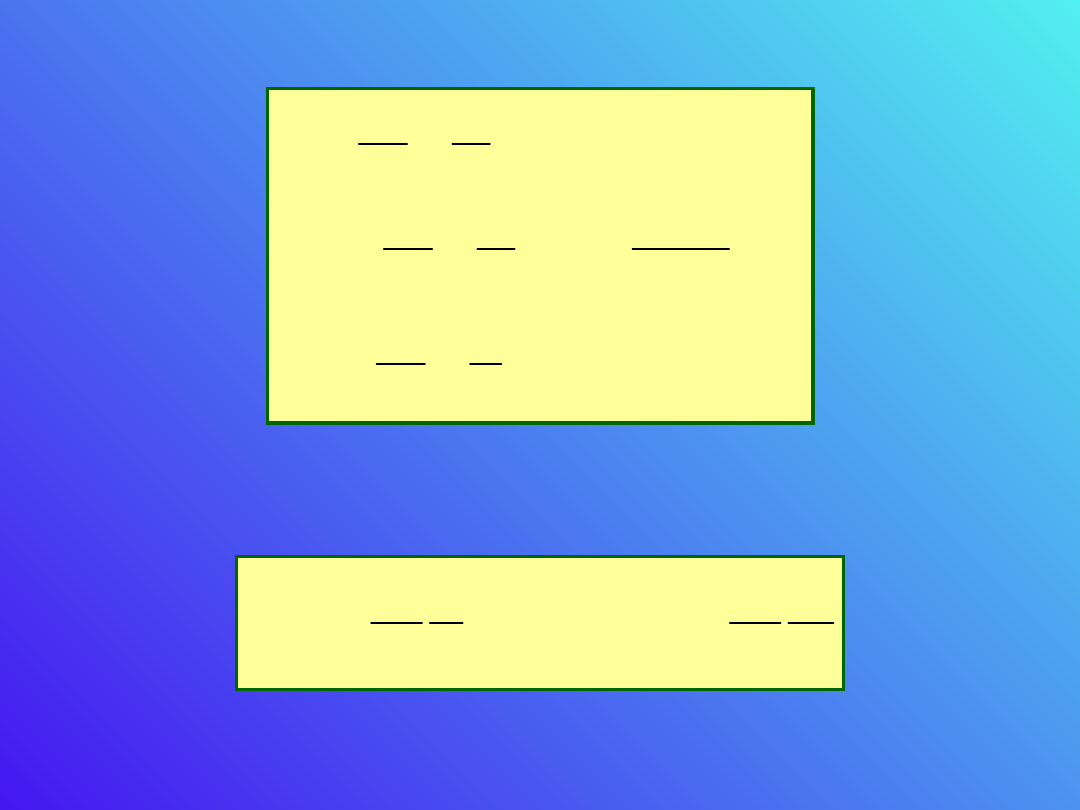
d

r

I

r

d

r

r

I

r

dl

r

I

dB

sin

1

4

sin

sin

1

4

sin

1

4

0

0

0

2

0

3

3

0

0

3

0





























Po podstawieniach otrzymamy:

Wektor indukcji w odległości r

0

od przewodnika

wynosi więc:

0

0

0

0

0

2

4

)

sin

(

4

)

(

r

I

d

r

I

r

B

o























I

Policzyliśmy wartość wektora
indukcji. Jaki zaś będzie jego
kierunek? Musi on
być prostopadły zarówno do

dl

jak

i

I

.

Ze względu na symetrię
cylindryczną
i fakt, że div B = 0,

(muszą

to być zamknięte
linie),

jedyną

możliwością są

koncentryczne
okręgi wokół
przewodnika

.

Stosuje się regułę śruby prawej tak jak na
rysunku powyżej.

r

0

B(r

0

)



1. Policzmy cyrkulację wektora B po
podanym okręgu.

I

r

r

B

l

d

B

0

0

0

2

)

(





















dl

Wynik ten nie zależy od wartości r

0

. Wartość

indukcji B(r

0

) jest więc równa:

0

0

2

)

(

r

I

r

B







2. Policzmy cyrkulację dla dowolnej krzywej
przestrzennej.

.

dl

db

dz

dr



I

Rozkładamy element
krzywej dl. na składowe
db, dz i dr. Do cyrkulacji
przyczynek będzie
pochodził tylko od
elementu db, gdyż dz i dr
są prostopadłe do B.
Położenie pętli nie
odgrywa więc żadnej
roli.

I

l

d

B









0







Pętla  może obejmować wiele przepływających

prądów.

I

1

I

2

I

3

I



I

N



Zawsze wtedy jest
słuszny wzór:













N

wewn

I

l

d

B

1

0











Wzór przedstawia

prawo Ampera.

Z prawa Ampera wynika, że prądy poza pętlą nie
dają żadnego przyczynku do liczonej cyrkulacji.
Należy również przyjąć negatywną wartość dla
prądu I

N

, pamiętając o stosowaniu reguły prawej

śruby.

Poniżej przedstawione są dwa przykłady dla
innych konfiguracji przewodników.



I

1

I

2



I

)

(

(

2

1

0

I

I

l

d

B

















nI

l

d

B









0







n