Wyznaczanie

współczynnika

sprężystości

sprężyny;

ważenie za pomocą

drgań.

1. Cel doświadczenia:

• W trzecim semestrze spotkań z fizyką w ramach

projektu FENIKS zajęliśmy się badaniem sprężyn.

Zainteresowało nas to, że identycznie wyglądające

sprężyny, podczas ich rozciągania zachowują się

różnie – jedne są „miękkie”, a inne „twarde”. Z

informacji jakie odszukaliśmy na temat sprężyn

wynika, że cechy te zależą od współczynnika

sprężystości sprężyny, a ten od masy ciała

wprawiającego sprężynę w drgania i od czasu

trwania jednego drgania. A skoro tak jest, to czy

uda się zważyć ciało przy pomocy sprężyny lub

gumki? I tak określiliśmy cele naszego

eksperymentu:

–

wyznaczyć współczynnik sprężystości sprężyny

–

wyznaczyć masę ciała za pomocą drgań

2. Trochę teorii:

Ruch drgający – ruch lub zmiana stanu, które charakteryzuje powtarzalność w

czasie wartości wielkości fizycznych, określających ten ruch lub stan.

 

Wielkości służące do opisu ruchu drgającego:

Amplituda drgań to największe wychylenie z położenia równowagi.

Oznaczamy ją literą A. Jednostką amplitudy jest 1 metr , [A] = 1 m

Okres drgań to czas jednego pełnego drgania. Oznaczamy go literą T.

Jednostką okresu jest 1 sekunda , [T] = 1 s

Okres drgań wahadła wyznacza się, mierząc czas t określonej liczby n pełnych

drgań, a następnie dzieląc go przez tę liczbę:

T=

Częstotliwość jest to liczba drgań w ciągu jednej sekundy. Oznaczamy ją literą

f. Jej

jednostką jest herc, [f] = = 1 Hz

f= ( związek częstotliwości z okresem)

Drgania gasnące- gdy nie uzupełniamy energii ciała drgającego. Amplituda

maleje w czasie takich drgań.

Drgania niegasnące- gdy uzupełniamy energię ciała drgającego. Amplituda

drgań się nie zmienia.

Siła wywołująca ruch drgający ma zwrot zawsze ku położeniu równowagi

 

1

T

t

n

t

n

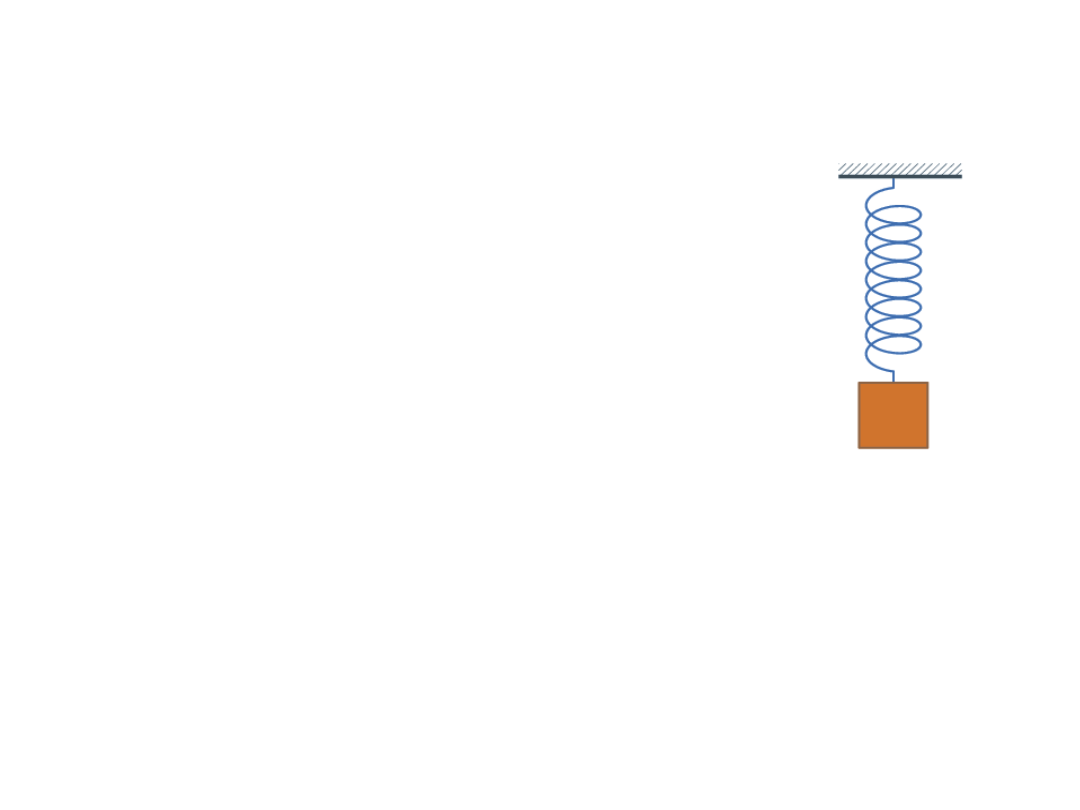
Gdy zawiesimy ciało o masie m na sprężynę o współczynniku

sprężystości k, otrzymamy wahadło sprężynowe. Zakładamy, że

wahadło pod wpływem sił sprężystości i grawitacji wykonuje drgania

harmoniczne. Działanie innych sił pomijamy.

• k- współczynnik sprężystości
• T- okres drgań wahadła
• m- masa ciała zawieszonego na sprężynie
• x- wychylenie z położenia równowagi
• ω-częstość kołowa ( pulsacja- nazwa rzadko używana)

Okres drgań T wahadła sprężynowego zależy od masy m

wykonującej drgania i od właściwości k gumki czy

sprężyny, którą to właściwość nazywamy

współczynnikiem sprężystości (stałą sprężyny).

Warunkiem jest, by ta gumka czy sprężynka spełniała

prawo Hooke'a wymagające by x = F/k to znaczy by

wydłużenie było wprost proporcjonalne do siły

wydłużającej (czyli, żeby stała k była rzeczywiście stała).

Jeśli tak jest to mamy:

2

2

2

2

2

2

2

2

2

2

2

4

4

4

4

F

kx

mw x

T

kx

m

x

T

k

m

T

T k

m

kT

m

m const T

p

w

p

p

p

p

=-

=-

=

=

=

=

=

=

�

Ciężarek zawieszony na sprężynie lub na nitce, po

wychyleniu z położenia równowagi wykonuje

ruch drgający, zwany w fizyce ruchem

harmonicznym.

Ciało drgające wraca do położenia równowagi

ruchem przyspieszonym, a oddala się od niego

ruchem opóźnionym.

W czasie ruchu wahadła cyklicznie następują

przemiany energii potencjalnej w kinetyczną i

odwrotnie. Energia potencjalna wahadła ma

wartość największą w punktach maksymalnego

wychylenia- wtedy energia kinetyczna ma

wartość zero. W położeniu równowagi energia

kinetyczna wahadła jest największa, natomiast

potencjalna ma wartość najmniejszą.

3. Opis układu i czynności:

Pomoce:

•

sprężyny (różne)

•

stoper

•

odważniki o masach 50 g, 20 dag, 25 dag

•

ciało, którego masę chcemy wyznaczyć

•

waga (niekoniecznie – dla porównania z masą wyznaczoną za pomocą drgań).

 
 
 
Czynności:
 
a) Wyznaczanie współczynnika sprężystości sprężyny:

•

 

•

Mocujemy sprężynę na statywie.

•

Zawieszamy na sprężynie odważnik, wprawiamy sprężynę w drgania.

•

Dokonujemy serii pomiarów czasu trwania 20 drgań sprężyny (oscylatora harmonicznego).

•

Wyniki zapisujemy w przygotowanej tabeli pomiarów.

•

Powtarzamy pomiary dla sprężyny obciążonej innymi masami.

•

Wykonujemy obliczenia współczynnika sprężystości (kalkulatorem lub w arkuszu

kalkulacyjnym).

•

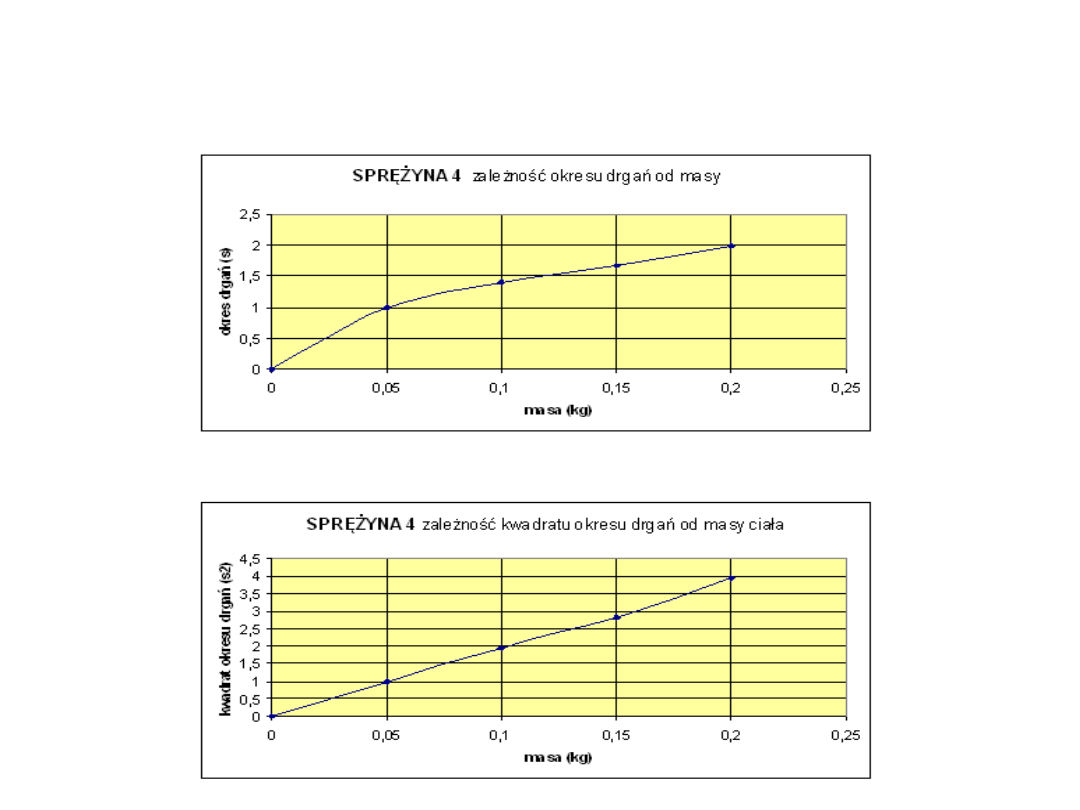
Sporządzamy wykresy zależności T(m) i T

2

(m).

 
b) Wyznaczanie masy ciała:

•

 

•

Na sprężynie zawieszamy badane ciało.

•

Mierzymy czas trwania 20 drgań, obliczamy okres drgań i kwadrat okresu.

•

Z wykresu T

2

(m) odczytujemy masę (i możemy porównać ją z masą wyznaczoną wagą).

 

4. Wyniki pomiarów i obliczeń:

 
• tabele pomiarów (wielkości

mierzone wpisano na czerwono)

• wykres zależności okresu drgań

odważników od ich masy T(m)

• wykres zależności kwadratu

okresu drgań odważników od ich
masy T

2

(m).

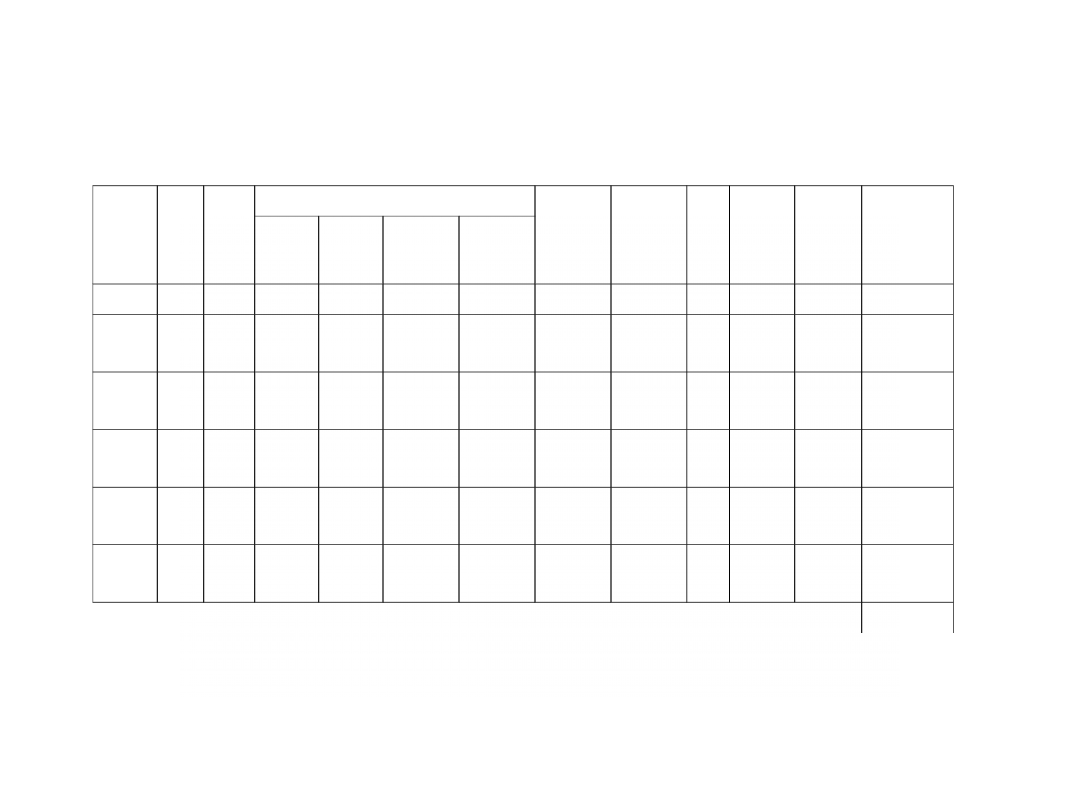
Sprężyna 1

l.p.

m(g) m(kg)

t = 20T

T(s)

T

2

(s

2

)

π

π

2

4π

2

m

k=4π

2

m/T

2

(kg/s

2=

N/

m)

t

1

(s)

t

2

(s)

t

3

(s)

t

śr

0

0

0

0

0

0

0

0

0  

 

 

 

1

50

0,05

9,35

9,31

9,28

9,3133

33 0,465667 0,216845 3,14

9,8596 1,97192

9,093666

2

100

0,1

12,65

12,69

12,73

12,69

0,6345

0,40259 3,14

9,8596 3,94384

9,796164

3

150

0,15

15,51

15,46

15,42

15,46333 0,773167 0,597787 3,14

9,8596 5,91576

9,896105

4

200

0,2

17,41

17,38

17,39

17,39333 0,869667

0,75632 3,14

9,8596 7,88768

10,42902

5

250

0,25

19,71

19,69

19,65

19,68333 0,984167 0,968584 3,14

9,8596

9,8596

10,1794

średnie k

9,878871

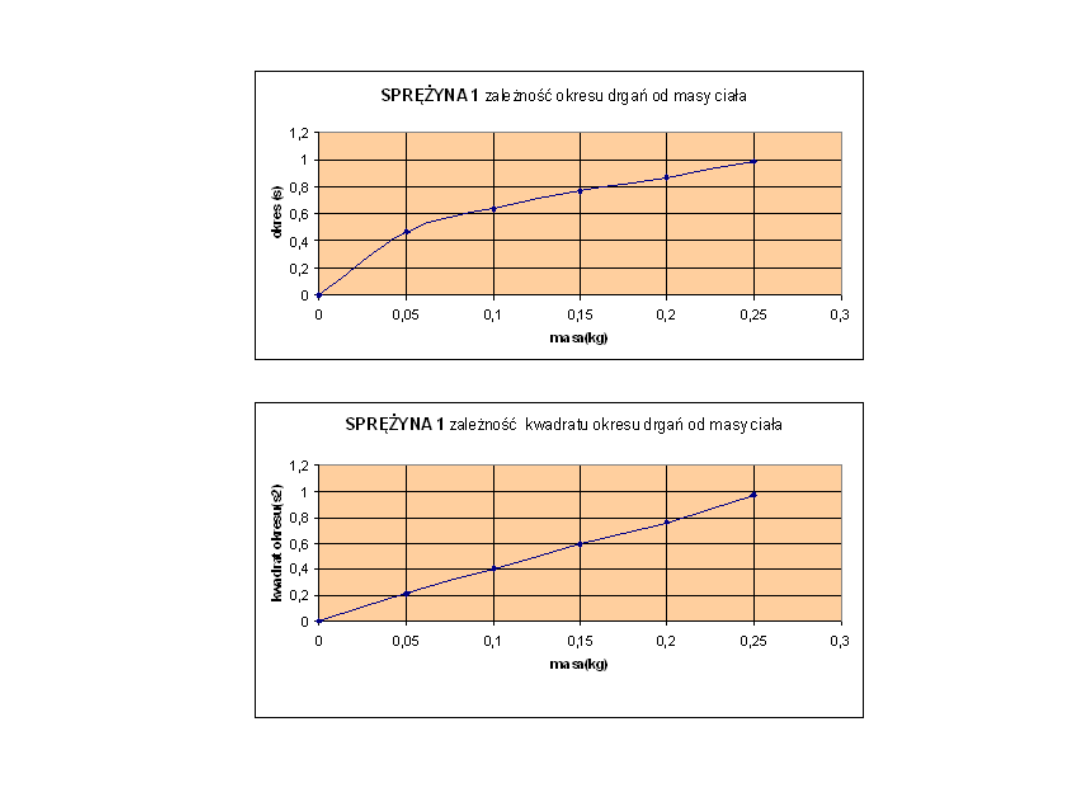
5. Ważenie za pomocą drgań

sprężyny 2:

Wyznaczamy masę kalkulatora.
Przykładowy pomiar 20 pełnych drgań kalkulatora:
t

1

= 5,15 s

t

2

= 5,21 s

t

3

= 5,19 s

t

śr

= 5,18(3) s

6. Dyskusja błędów:

a) czynniki, które mogły mieć wpływ na dokładność

uzyskanych wyników:

– w doświadczeniu przyjęliśmy masy używanych odważników

takie, jakie były podane na nich – w rzeczywistości mogły one

nieco różnić się od rzeczywistych

– używaliśmy stopera w telefonie, czasu reakcji przy włączaniu i

wyłączaniu stopera nie uwzględnialiśmy ; aby zwiększyć

dokładność pomiarów, wykonywaliśmy je trzykrotnie

– okres T wyliczaliśmy ze średniej 20 okresów, byłoby

dokładniejszy dla np. średniej z 50 (lub 100) okresów

– do obliczeń przyjęliśmy przybliżoną do części setnych wartość

liczby π ≈ 3,14 ( wyniki obliczonego współczynnika

sprężystości k dla większego przybliżenia np. π ≈

3,1415926559 będą o 0,1% większe)

– dla sprężyn 1,3 i 4 przyczepialiśmy odważniki bezpośrednio do

sprężyny, ale dla sprężyny 2 umieszczaliśmy je w pojemniku,

którego masy nie uwzględniliśmy w obliczeniach

– przy wyznaczaniu masy kalkulatora nie uwzględniliśmy masy

pojemnika, do którego był on włożony;

b) sprężyna 4 miała metryczkę ze współczynnikiem

sprężystości k = 2 N/m; obliczyliśmy błąd procentowy:

Autorzy: Michał Pająk i Przemysław

Kozłowski

Nr szkoły w projekcie FENIKS:  45
Nazwa szkoły:  Gimnazjum Nr 1, ul. Armii

Krajowej 2, 26-200 Końskie

Imię i nazwisko nauczyciela: Małgorzata

Piecuch 

Tytuł pracy: Wyznaczanie współczynnika

sprężystości sprężyny; ważenie za
pomocą drgań.