Opracowała:

Opracowała:

Jolanta

Jolanta

Brzozowska

Brzozowska

KLASYFIKACJA

TRÓJKĄTÓW

W niniejszej prezentacji

W niniejszej prezentacji

zostały użyte następujące

zostały użyte następujące

przyciski akcji:

przyciski akcji:

Powrót do menu głównego

Powrót do menu głównego

Powrót do slajdu poprzedniego.

Powrót do slajdu poprzedniego.

Przejście do slajdu następnego.

Przejście do slajdu następnego.

Koniec prezentacji.

Koniec prezentacji.

KLASYFIKACJ
A

TRÓJKĄTÓW

SPIS TREŚCI

SPIS TREŚCI



Definicja trójkąta

Definicja trójkąta



Zależności między bokami trójkąta.

Zależności między bokami trójkąta.

Suma miar kątów wewnętrznych trójkąta.

Suma miar kątów wewnętrznych trójkąta.



Podział trójkątów ze względu na kąty.

Podział trójkątów ze względu na kąty.



Podział trójkątów ze względu na boki.

Podział trójkątów ze względu na boki.



Podsumowanie.

Podsumowanie.



Test sprawdzający wiadomości o trójkątach

Test sprawdzający wiadomości o trójkątach

.

.

Definicja trójkąta

Definicja trójkąta

wierzchołek trójkąta

wierzchołek trójkąta

Trójkąt

Trójkąt

to część

to część

płaszczyzny ograniczona

płaszczyzny ograniczona

łamaną zwyczajną

łamaną zwyczajną

zamkniętą złożoną

zamkniętą złożoną

z trzech odcinków, razem

z trzech odcinków, razem

z tą łamaną.

z tą łamaną.

bok

bok

trójkąta

trójkąta

kąt

kąt

trójkąta

trójkąta

A

B

C

Każdy bok trójkąta jest mniejszy od
sumy dwóch pozostałych boków,
a większy od ich różnicy.

IABI<IBCI+ICAI i IABI>IBCI-ICAI

IBCI<IACI+IABI i IBCI>IACI-IABI

ICAI<IABI+IBCI i ICAI>IACI-IABI

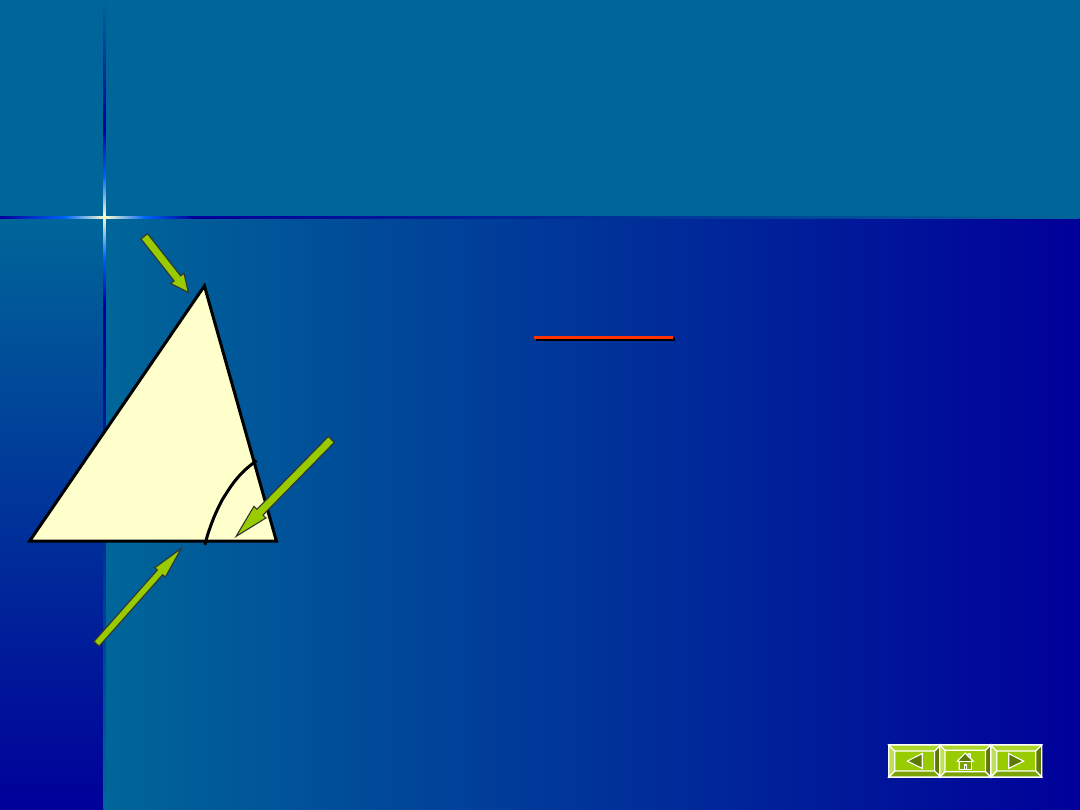
Suma miar kątów
wewnętrznych dowolnego
trójkąta jest równa 180°.







 +  +  =

180°

Podział trójkątów

Podział trójkątów

ze względu na boki:

ze względu na boki:

Trójkąt różnoboczny

Trójkąt różnoboczny

Trójkąt równoramienny

Trójkąt równoramienny

Trójkąt równoboczny

Trójkąt równoboczny

Podział trójkątów

Podział trójkątów

ze względu na kąty:

ze względu na kąty:

Trójkąt ostrokątny

Trójkąt ostrokątny

Trójkąt prostokątny

Trójkąt prostokątny

Trójkąt rozwartokątny

Trójkąt rozwartokątny

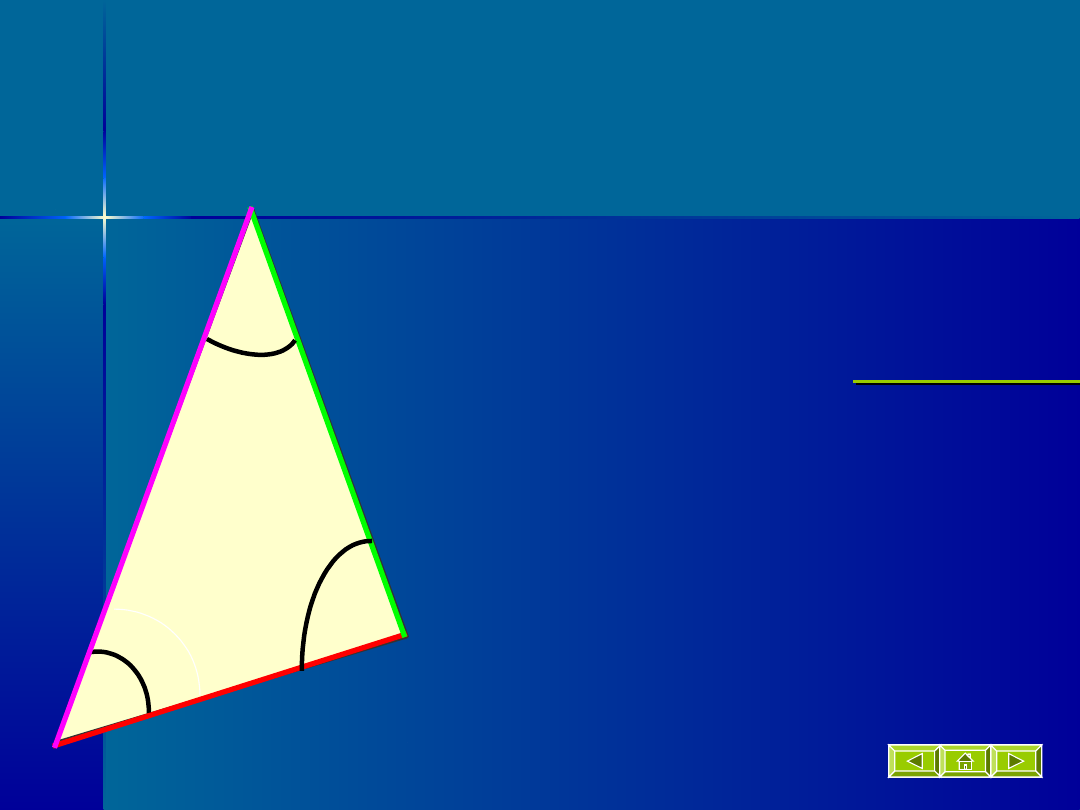
Trójkąt

Trójkąt

różnoboczny

różnoboczny

Trójkąt, który ma

Trójkąt, który ma

wszystkie

wszystkie

boki różnej długości.

boki różnej długości.

b

a

c

A

B

C







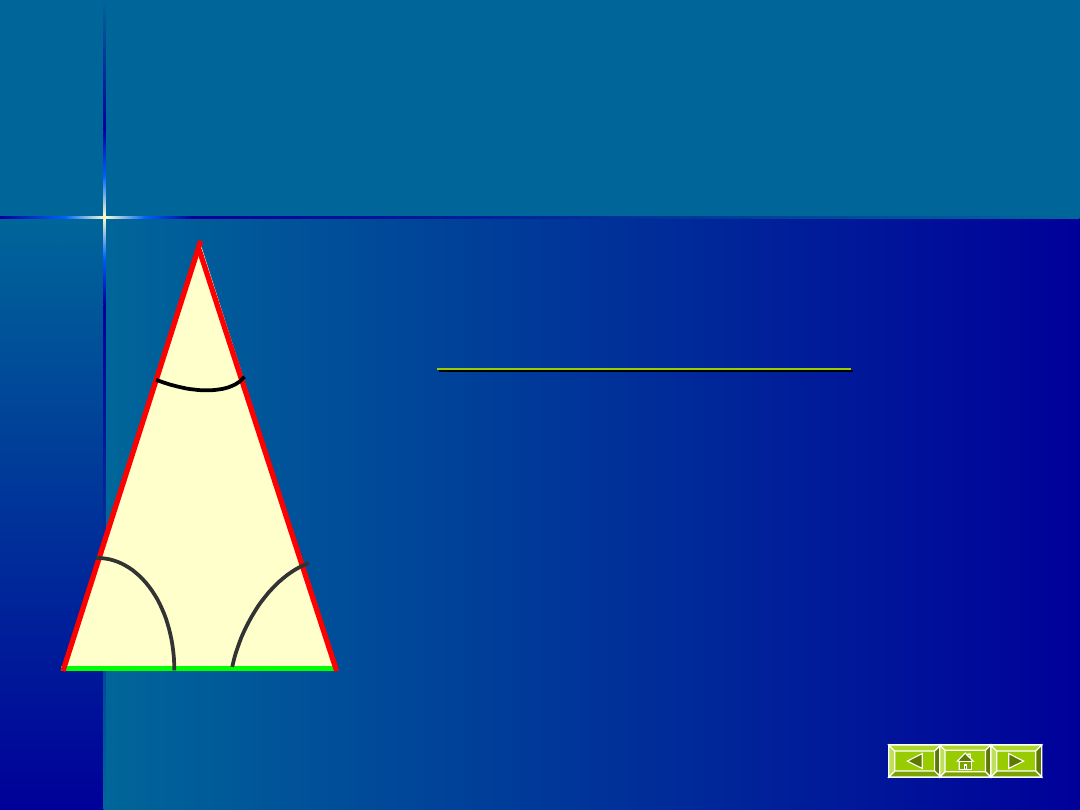
Trójkąt

Trójkąt

równoramienny

równoramienny

Trójkąt, który ma

Trójkąt, który ma

przynajmniej dwa

przynajmniej dwa

boki

boki

równej długości.

równej długości.

Kąty przy podstawie

Kąty przy podstawie

mają równe miary.

mają równe miary.

r a

m

i

ę

podstawa

r

a

m

i

ę







A

B

C

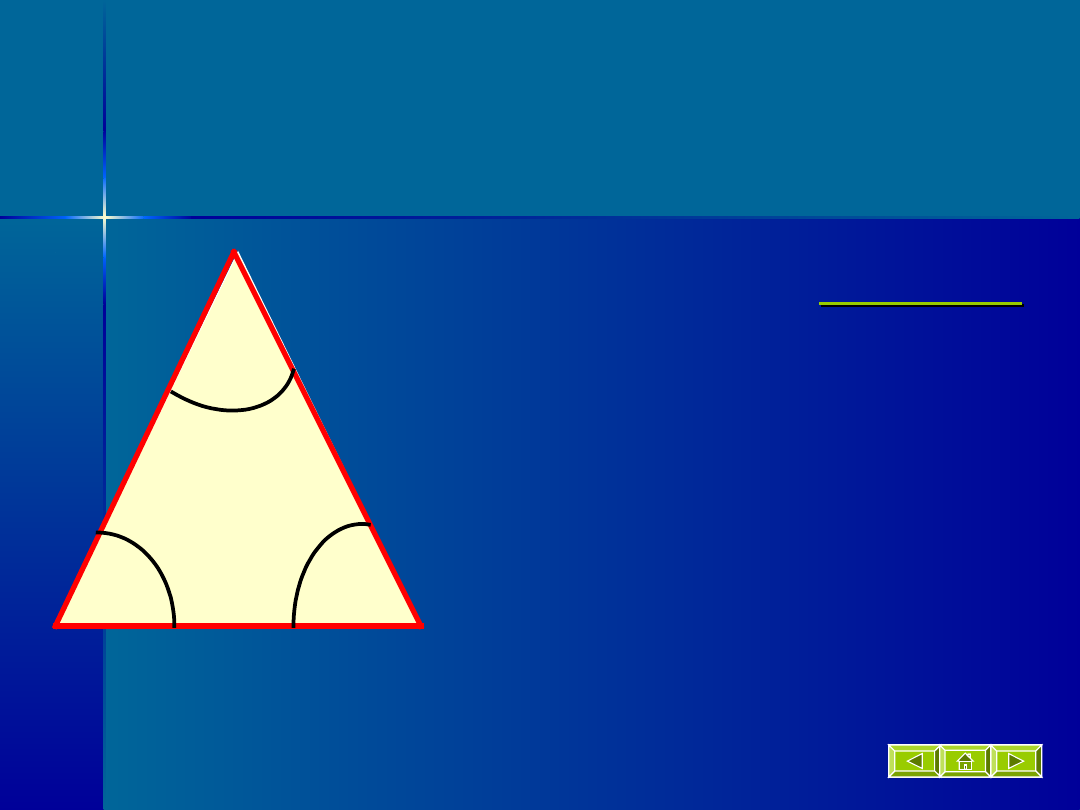
Trójkąt

Trójkąt

równoboczny

równoboczny

Trójkąt, który ma

Trójkąt, który ma

wszystkie

wszystkie

boki równej długości.

boki równej długości.

60

°

°

60

°

°

60

°

°

Trójkąt równoboczny jest także

Trójkąt równoboczny jest także

trójkątem równoramiennym.

trójkątem równoramiennym.

Każdy kąt ma 60

Każdy kąt ma 60

°

°

.

.

A

B

C

a

a

a

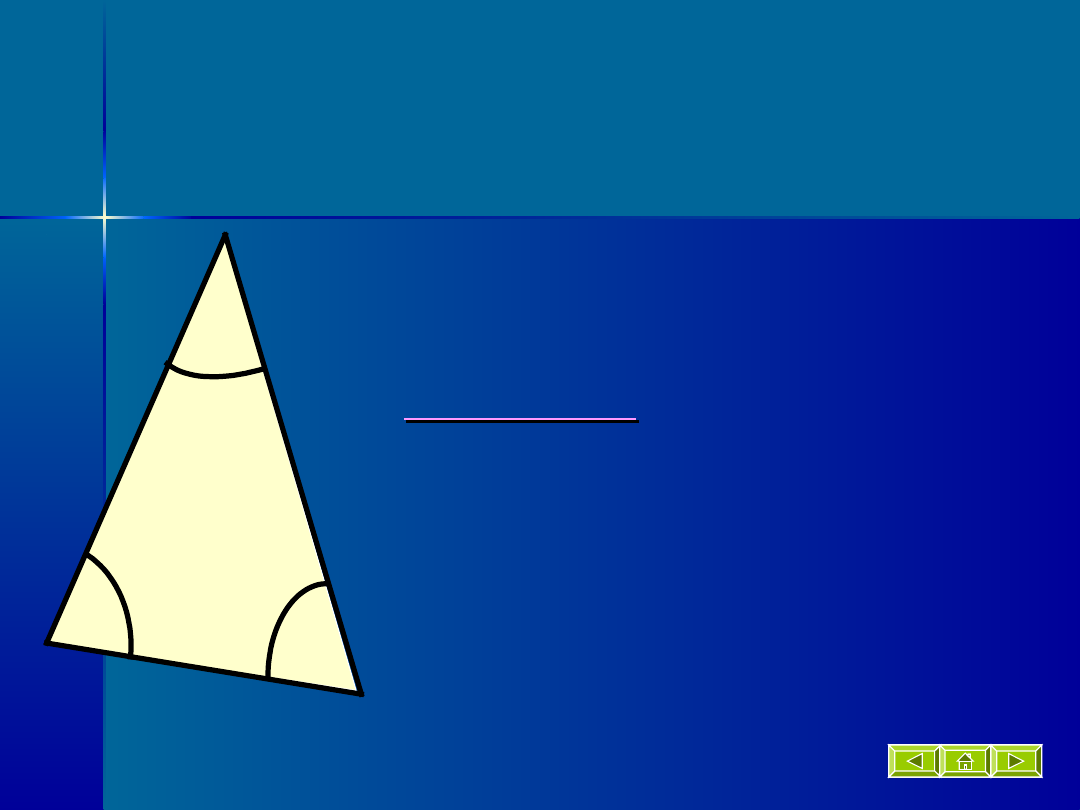
Trójkąt ostrokątny

Trójkąt ostrokątny

Trójkąt, który ma

Trójkąt, który ma

wszystkie

wszystkie

kąty wewnętrzne ostre.

kąty wewnętrzne ostre.

A

B

C







 < 90
 < 90
 < 90

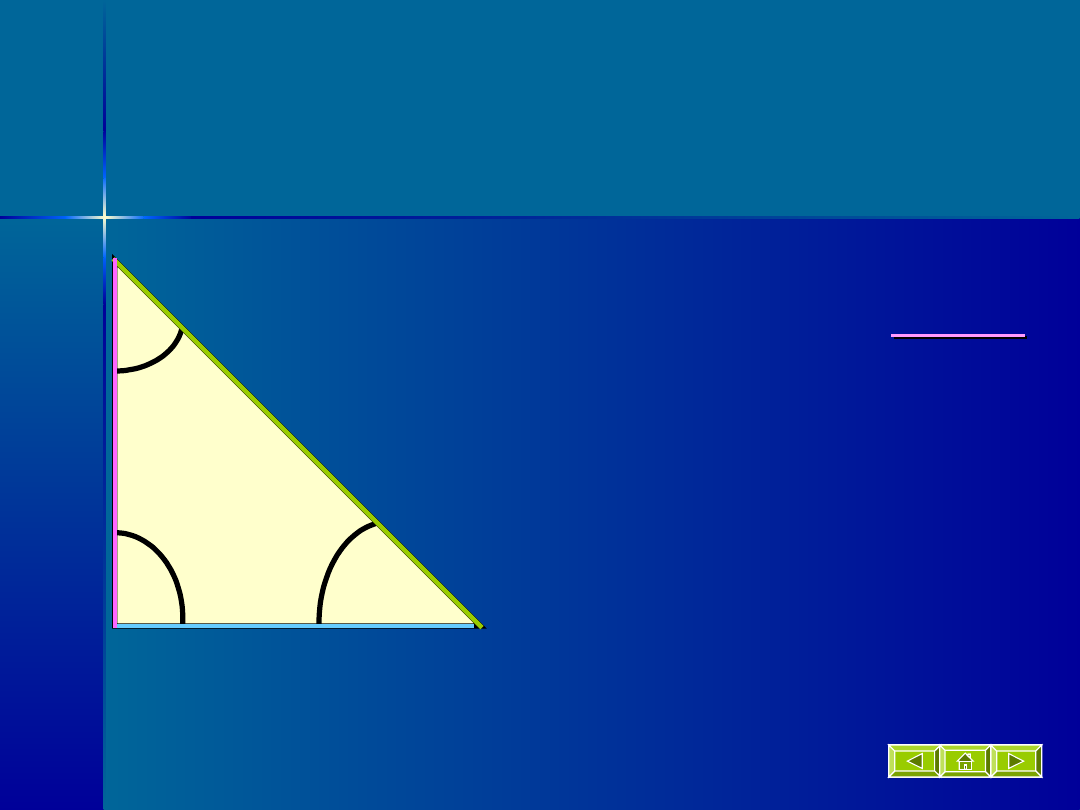
Trójkąt

Trójkąt

prostokątny

prostokątny

Trójkąt, który ma

Trójkąt, który ma

jeden

jeden

kąt wewnętrzny prosty.

kąt wewnętrzny prosty.

A

B

C

przyprostokątna

p

rz

y

p

ro

st

o

k

ą

tn

a

prz

ec

iw

pro

sto

ką

tna

.





ICABI = 90
 < 90
 < 90

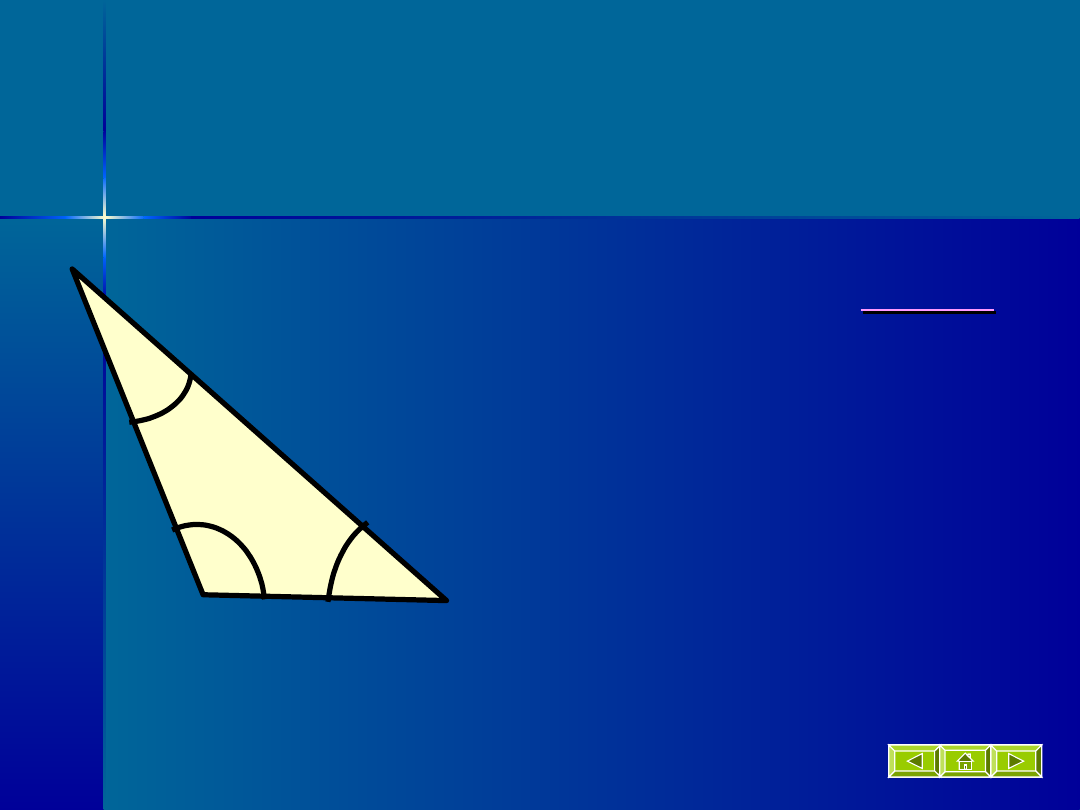
Trójkąt rozwartokątny

Trójkąt rozwartokątny

Trójkąt, który ma

Trójkąt, który ma

jeden

jeden

kąt wewnętrzny

kąt wewnętrzny

rozwarty.

rozwarty.

A

B

C







 > 90
 < 90
 < 90

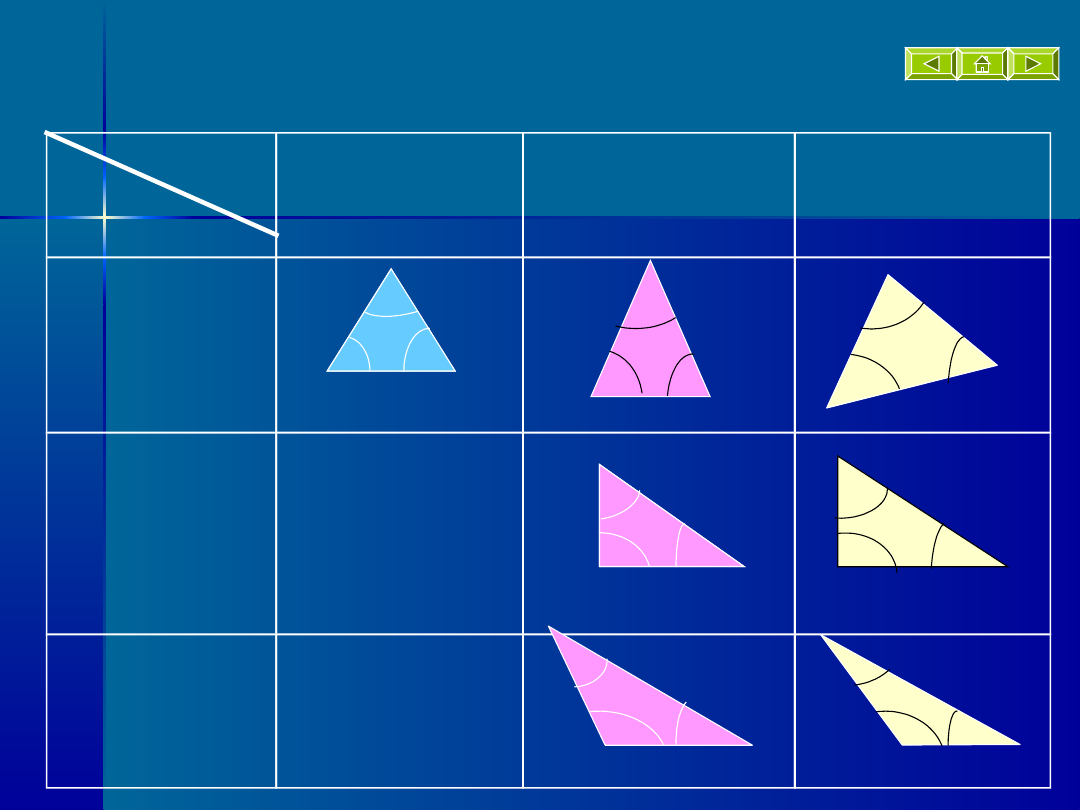
równoboczn

równoboczn

e

e

równoramien

równoramien

ne

ne

różnoboczne

różnoboczne

ostrokątne

ostrokątne

prostokątn

prostokątn

e

e

nie istnieje

nie istnieje

rozwarto-

rozwarto-

kątne

kątne

nie istnieje

a





Podział

wg boków

Podział

wg. kątów

P o d s u m o w a n i e

















a

b

c

.





a







a

b

a

a

b

b

b

a

a

a

a

.









.







a

b

c

c

b

a

Zadanie 1.

Zadanie 1.

Suma miar kątów wewnętrznych trójkąta jest

Suma miar kątów wewnętrznych trójkąta jest

równa:

równa:

Zadanie 2.

Zadanie 2.

W narysowanym trójkącie suma miar kątów ostrych

jest równa:

A. 90

A. 90





B. 360

B. 360





C. 180

C. 180





D. 150

D. 150





110

°

A. 180

A. 180





B. 35

B. 35





C. 360

C. 360





D. 70

D. 70





A. 90

A. 90





Zadanie 3.

Zadanie 3.

Kąt wewnętrzny trójkąta równobocznego ma:

Kąt wewnętrzny trójkąta równobocznego ma:

A. 90

A. 90





C. 45

C. 45

C. 120

C. 120





D. 30

D. 30





Zadanie 4.

Zadanie 4.

Kąt ostry trójkąta prostokątnego równoramiennego ma:

Kąt ostry trójkąta prostokątnego równoramiennego ma:

A. 60

A. 60





C. 30

C. 30





D. 90

D. 90

Zadanie 5.

Zadanie 5.

Nie istnieje trójkąt:

Nie istnieje trójkąt:

A. różnoboczny

A. różnoboczny

rozwartokątny

rozwartokątny

B. równoramienny prostokąt

B. równoramienny prostokąt

ny

ny

C. różnoboczny ostrokątny

C. różnoboczny ostrokątny

D. równoboczny prostokątny

D. równoboczny prostokątny

B. 60

B. 60





Zadanie 6.

Zadanie 6.

Nie istnieje trójkąt o bokach długości:

Nie istnieje trójkąt o bokach długości:

A. 1 cm, 2 cm, 3 cm

A. 1 cm, 2 cm, 3 cm

B. 1 cm, 2 km, 2 km

B. 1 cm, 2 km, 2 km

C. 3 m, 5 m, 7 m

C. 3 m, 5 m, 7 m

D. 300 cm, 50 dm, 7

D. 300 cm, 50 dm, 7

m

m

Zadanie 7.

Zadanie 7.

Wskaż zdanie prawdziwe:

Wskaż zdanie prawdziwe:

A. Najdłuższy bok trójkąta prostokątnego to

A. Najdłuższy bok trójkąta prostokątnego to

przyprostokątna.

przyprostokątna.

B. Każdy trójkąt równoramienny jest

B. Każdy trójkąt równoramienny jest

równoboczny.

równoboczny.

C. Trójkąt może mieć dwa kąty rozwarte.

C. Trójkąt może mieć dwa kąty rozwarte.

D. Każdy trójkąt równoboczny jest

D. Każdy trójkąt równoboczny jest

równoramienny.

równoramienny.

Dobra odpowiedź.

Dobra odpowiedź.

Brawo!

Brawo!

Zastanów się

Zastanów się

jeszcze raz!

jeszcze raz!