Model hydrauliczny

Sieci wodociągowej

Stan hydrauliczny sieci

Parametrami określającymi stan

hydrauliczny sieci wodociągowej są :



natężenia przepływów wody przez

elementy (odcinki) sieci

wodociągowej,



spadki linii ciśnień na tych

elementach,



oraz wynikające z nich rzędne linii

ciśnień

w węzłach sieci.

I-sze prawo Kirschhoffa

Dla każdego punktu sieci suma natężeń

przepływu jest równa 0.

Równania wynikające z 1 prawa opisują stan

hydrauliczny sieci o strukturze rozgałęźnej (bez

obwodów).

Liczba równań = w-1 ,

gdzie :

w - liczba węzłów,

a

w-1 - liczba

odcinków=

liczbie

zmiennych.

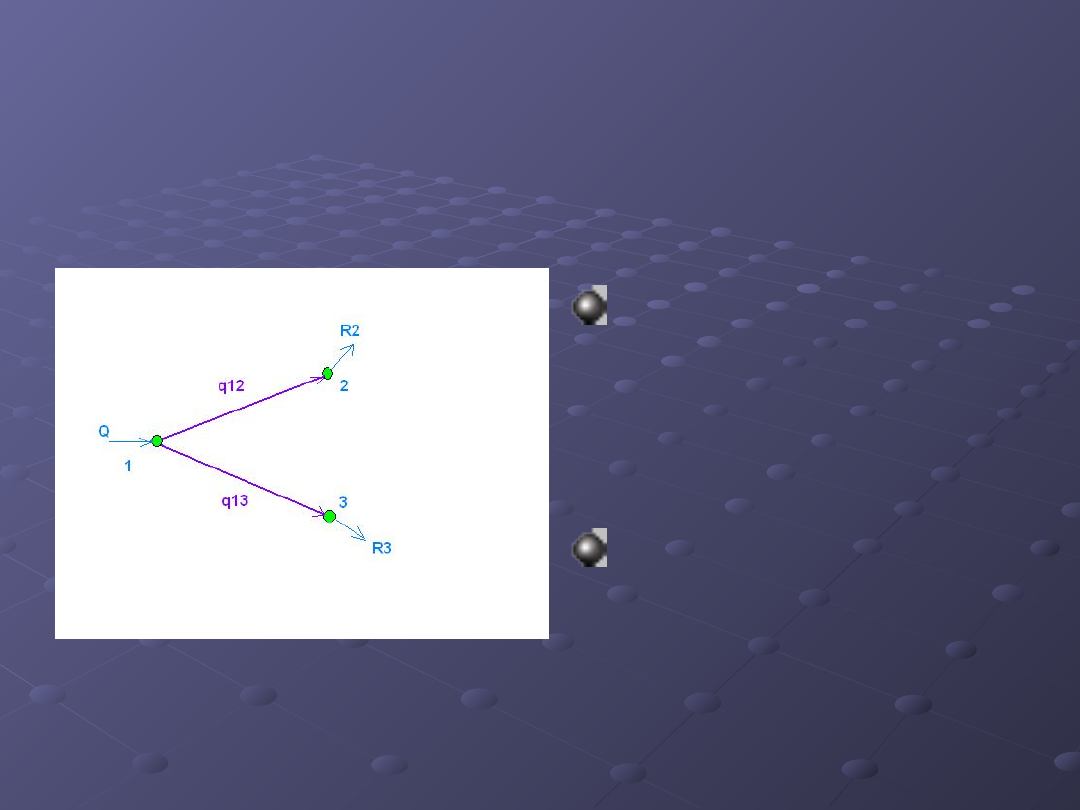
Model hydrauliczny sieci

rozgałęźnej

Dla węzła 2

q

12

- R2 = 0

Dla węzła 3

q

13

- R3 = 0

Postać algebraiczna równań

wynikających z I-szego prawa

Kirchhoffa

a

r

[w-1,l]

* q

[l,1]

= R ,

gdzie : a

r

- macierz incydencji

węzłów i odcinków

sieci.

a

wl

= 1 gdy, odcinek skierowany do

węzła

a

wl

= 0 brak incydencji odcinka i

węzła

a

wl

= -1

gdy, odcinek skierowany od

węzła

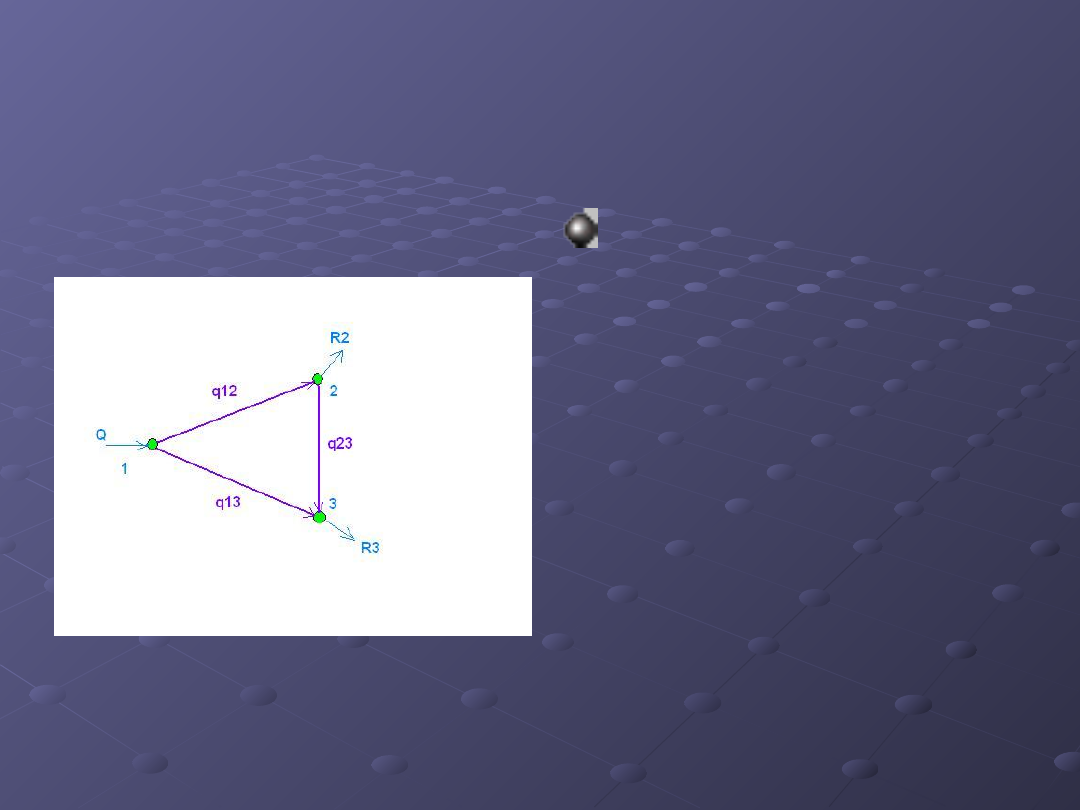
Sieć obwodowa

Zamknięcie nawet
jednego obwodu w
sieci rozgałęźnej
powoduje, że :

- liczba zmiennych q

ij

równa ilości

odcinków

jest większa niż

liczba równań
wynikających z 1-
szego prawa
Kirchhoffa

II-gie prawo Kirschhoffa

Dla każdego obwodu sieci suma spadków ciśnień
na odcinkach stanowiących obwód jest równa 0.
Równania wynikające z drugiego prawa
Kirschhoffa dopełniają układ równań opisujący
stan hydrauliczny sieci obwodowej.

Liczba równań = l-w+1,

gdzie:
l – liczba odcinków,
w – liczba węzłów,
l-w+1 – liczba obwodów.

Postać algebraiczna równań

wynikających z II-giego prawa

Kirchhoffa

B

[l-w+1,l]

* dh

[l,1]

= 0 ,

gdzie : b

- macierz incydencji

obwodów i odcinków

sieci.

b

ol

= 1 gdy, odcinek skierowany w

prawo

b

ol

= 0 brak incydencji odcinka i

obwodu

b

ol

= -1

gdy, odcinek skierowany w

lewo

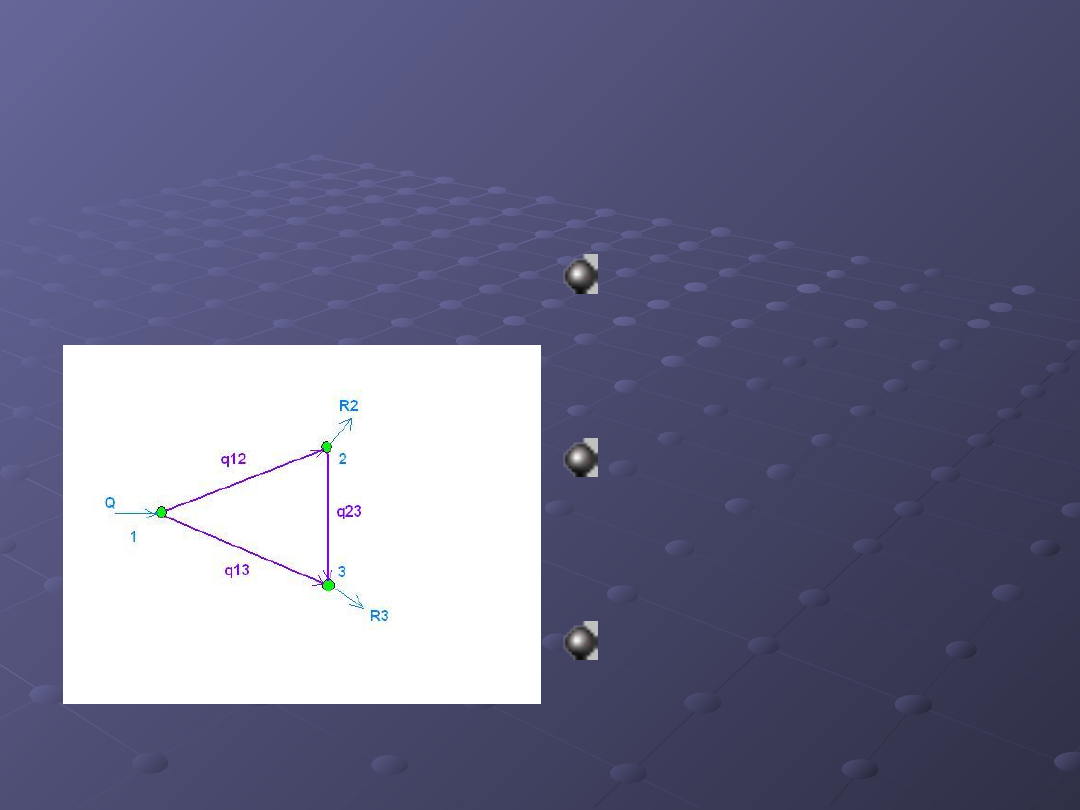
Model hydrauliczny sieci

obwodowej

Dla węzła 2

q

12

- q

23

- R2 = 0

Dla węzła 3

q

13

+ q

23

- R3 = 0

Dla obwodu 1

dh

12

+ dh

23

-

dh

13

=

0

Metoda aproksymacji Newtona

obliczania stanu

hydraulicznego sieci.

1. q

12

- q

23

- R2 = 0

2.

q

13

+ q

23

- R3 = 0

3.

K

12

*q

12

2

+ K

23

*q

23

2

-

K

13

*q

13

2

= 0

Rozwinięcie w szereg

Taylora

Każdą ciągłą i różniczkowalną funkcję
n-tego stopnia możemy rozwinąć w
szereg Taylora w epsilonowm
otoczeniu punktu:

f(q

1

,q

2

,…,q

l

)=f(q

1

,q

2

,

…,q

l

)

o

+Sdf/dq

i

*dq

i

+

Sd

2

f/dq

i

2

*(dq

i

2

/2!)+….+ Sd

n

f/dq

i

n

*(dq

i

n

/n!),

gdzie q

i

= q

i o

+ dq

i

Iteracyjny model liniowy stanu

hydraulicznego sieci po

transformacji

1. q

12

o

- q

23

o

- R2 + dq

12

- dq

23

= 0

2. q

13

o

+ q

23

o

- R3 + dq

13

+ dq

23

= 0

3. (K

12

*q

12

2

+ K

23

*q

23

2

-

K

13

*q

13

2

)

o

+

2*(K

12

*q

12

o

*dq

12

+ K

23

*q

23

o

*dq

23

-

K

13

*q

13

o

*dq

13

)

= 0

gdzie q

ij

= q

ij o

+ dq

ij

Standardowa postać modelu

liniowego stanu hydraulicznego

sieci

1. dq

12

- dq

23

= R2 - q

12

o +

q

23

o

2. dq

13

+ dq

23

= R3 - q

13

o

- q

23

o

3. K

12

*q

12

o

*dq

12

+ K

23

*q

23

o

*dq

23

-

K

13

*q

13

o

*dq

13

=

-(K

12

*q

12

2

+ K

23

*q

23

2

-

K

13

*q

13

2

)

o

/2

Iteracyjny proces wyznaczania

stanu hydraulicznego sieci

(1/2).

1. Założyć początkowe wartości

natężeń

przepływu w odcinkach sieci.
2. Obliczyć parametry modelu, czyli :



K

ij

*q

ij

o

oraz K

ij

*q

ij

o

*q

ij

o

dla każdego odcinka sieci, oraz



(S K

ij

*q

ij

o

*q

ij

o

) dla każdego obwodu

3. Sprawdzić, czy



(S K

ij

*q

ij

o

*q

ij

o

) dla każdego obwodu <

założonej dokładności wyrównywania

ciśnień.

Iteracyjny proces wyznaczania

stanu hydraulicznego sieci

(2/2).

4. Jeżeli warunek z p.3 jest spełniony dla
każdego obwodu to wyznaczone

natężenia

przepływu określają stan hydrauliczny

sieci.

„STOP”
5. Jeżeli nie, należy przejść do p.6.
6. Rozwiązać układ równań liniowych
wyznaczając poprawki natężeń przepływu.
7. Obliczyć skorygowane natężenia

przepływu i

przejść do p.2.

Redukcja wymiarowości

modelu hydraulicznego sieci

Możliwe jest zredukowanie zadania

wyznaczania stanu hydraulicznego

sieci z „l” wymiarowego do „l-w+1”

wymiarowego.

W iteracyjnym procesie

obliczeniowym należy założyć takie

początkowe wartości natężeń

przepływu w odcinkach sieci, aby

spełnione było I-sze prawo

Kirschhoffa.

Wyznaczenie natężeń

przepływów spełniających I-sze

prawo Kirschoffa

1. dq

12

- dq

23

= R2 - q

12

o +

q

23

o

=0

2. dq

13

+ dq

23

= R3 - q

13

o

- q

23

o

=0

Stąd :
dq

12

= dq

23

oraz

dq

23

= -dq

13

czyli

dq

12

= dq

23

= -dq

13

= dQ

I

Zredukowany model

hydrauliczny sieci

Po wprowadzeniu poprawek

korygujących przepływy w

obwodach, równanie :

3. K

12

*q

12

o

*dq

12

+ K

23

*q

23

o

*dq

23

-

K

13

*q

13

o

*dq

13

=

-(K

12

*q

12

2

+ K

23

*q

23

2

-

K

13

*q

13

2

)

o

/2

przyjmuje postać :
(K

12

*q

12

o

+ K

23

*q

23

o

+

K

13

*q

13

o

)*dQ

I

=

-(K

12

*q

12

2

+ K

23

*q

23

2

-

K

13

*q

13

2

)

o

/2

Równanie Crossa wyznaczania

poprawek natężenia przepływu

Rozwiązując równanie :
(K

12

*q

12

o

+ K

23

*q

23

o

+ K

13

*q

13

o

)*dQ

I

=

-(K

12

*q

12

2

+ K

23

*q

23

2

-

K

13

*q

13

2

)

o

/2

Otrzymujemy
dQ

I

= -(K

12

*q

12

2

+ K

23

*q

23

2

-

K

13

*q

13

2

)

o

/

2(K

12

*q

12

o

+ K

23

*q

23

o

+ K

13

*q

13

o

),

Co możemy zapisać jako :
dQ

I

= - (S dh)/(S|dh

’

|)