Podstawy chemii

kwantowej

Układ okresowy pierwiastków

1887 - 1961

1887 - 1961

Ernest

Schrödinger

Ernest

Schrödinger

e

e

B

v

m

h





MECHANIKA FALOWA

(KWANTOWA)

MECHANIKA FALOWA

(KWANTOWA)

rok 1926

rok 1926

2

Spróbujemy opisać ruch elektronu, zakładając, że zachowuje się
on jak UMOWNA fala de Broglie’a, która jest związana z
poruszającym się elektronem

Ponieważ

atom

jest

układem

STACJONARNYM,

to

znaczy

nie

zmieniającym się w czasie, trzeba przyjąć,
że fala związana z elektronem w atomie jest
FALĄ STOJĄCĄ

E. Schrödinger

E. Schrödinger

lata 1925 - 1927

3

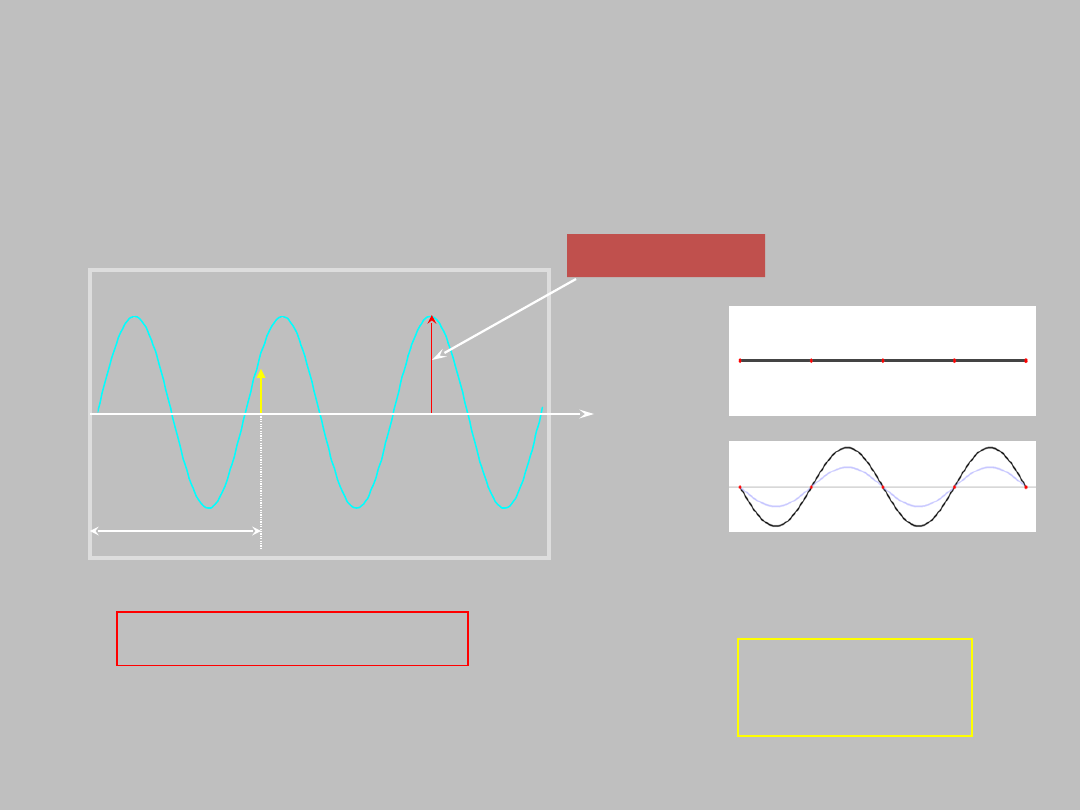
Obecność fali w jakiejkolwiek przestrzeni oznacza drganie
elementu w każdym punkcie tej przestrzeni czyli odchylanie
się elementu o Da od tak zwanego POŁOŻENIA RÓWNOWAGI
(PR)

Da

A

Da = F(x,t)

PR

*)

dla fali stojącej Da także nazywa się amplitudą

Funkcja falowa:

x

x

fala

stojąca:

Da = F(x)

*)

amplituda

4

W ujęciu mechaniki kwantowej elektron w przestrzeni
wokół jądra atomu reprezentowany jest przez falę
stojącą, która zadana jest FUNKCJĄ FALOWĄ Y(x,y,z)

x

y

z

x

0

y

0

z

0

P(x

0

,y

0

,z

0

)

odchylenie

od

położenia

równowagi (amplituda) tego co
drga w fali de Broglie’a w
punkcie P...

odchylenie

od

położenia

równowagi (amplituda) tego co
drga w fali de Broglie’a w
punkcie P...

5

Da(P) = Y(x

0

,y

0

,z

0

)

Energia „ukryta” w fali znajdującej się w jakimś

ośrodku jest wprost proporcjonalna do natężenia

fali, które z kolei jest wprost proporcjonalne do

kwadratu amplitudy fali

E(x,y,z) ~ Y

2

(x,y,z)

E(x,y,z) ~ Y

2

(x,y,z)

6

..czas przypomnieć sobie o dualizmie

korpuskularno-falowym - fala, o której

mówimy musi czasem ujawnić swoje

korpuskularne właściwości....

Przyjmijmy,
że...

.. natężenie fali de Broglie’a
elektronu w jakiejś przestrzeni
jest związane z ...

...PRAWDOPODOBIEŃSTWEM

zaobserwowania elektronu jako

cząstki...

...PRAWDOPODOBIEŃSTWEM

zaobserwowania elektronu jako

cząstki...

7

W tych miejscach przestrzeni, gdzie jest większe
natężenie

fali

-

tam

jest

też

większe

prawdopodobieństwo napotkania elektronu jako
cząstki*

*) tzw. interpretacja kopenhaska

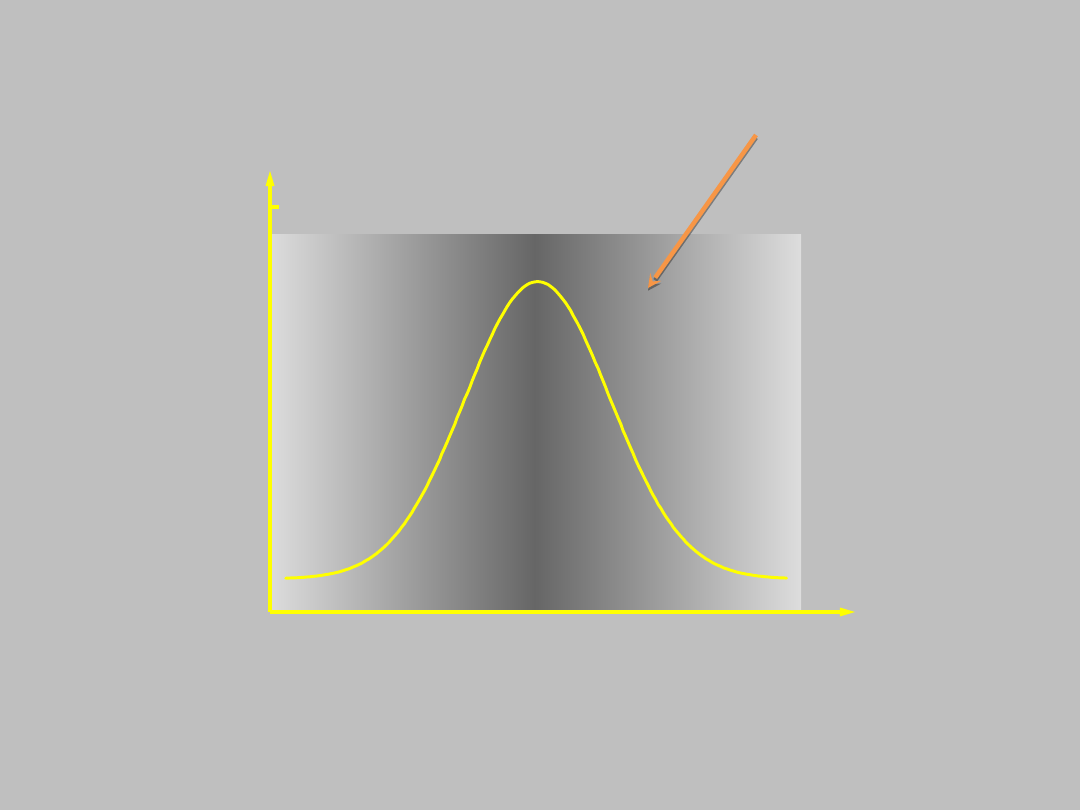
Rozważmy przykład...

..

im ciemniej tym większe

natężenie fali
elektronowej

Pr

a

w

d

o

p

o

d

o

b

ie

ń

st

w

o

x

1

8

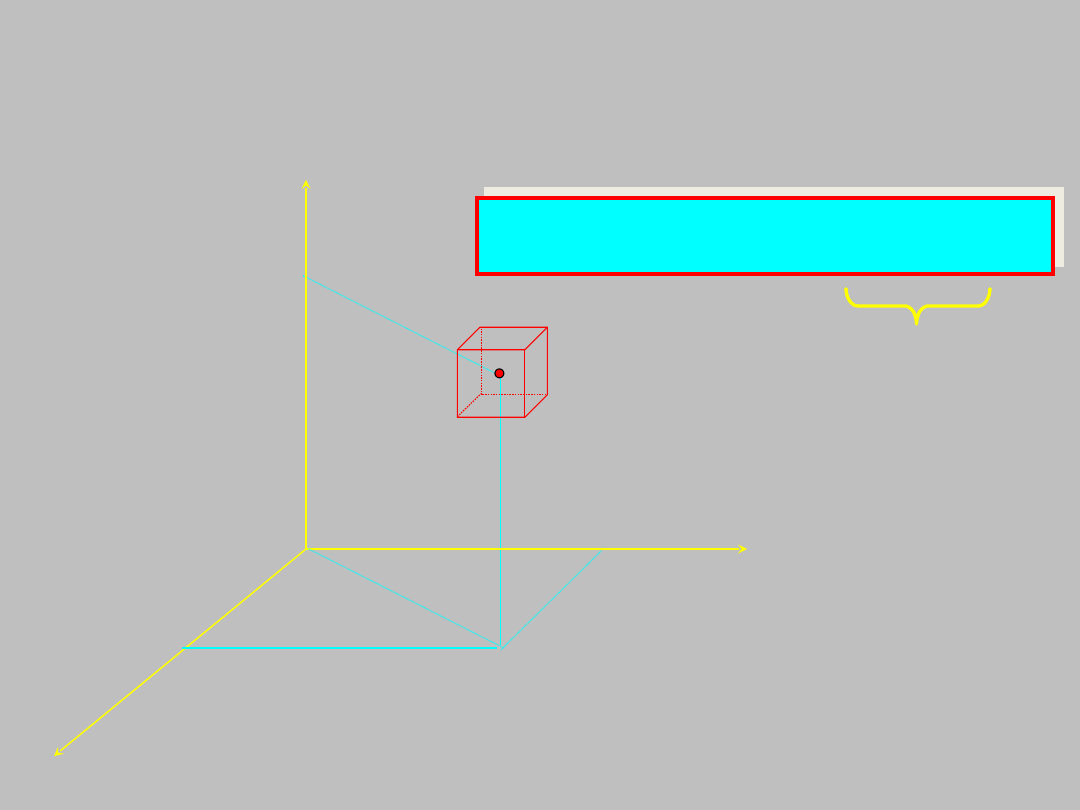
x

y

z

Dx

Dy

Dz

Prawdopodobieństwo P napotkania elektronu w
otoczeniu punktu (x

0

,y

0

,z

0

)

x

0

y

0

z

0

P ~ Y

2

(x

0

,y

0

,z

0

)DxDyDz

P ~ Y

2

(x

0

,y

0

,z

0

)DxDyDz

DV

9

Erwin Schrödinger

1887-1961

Erwin Schrödinger

1887-1961

1926
Austria

10

Jak znaleźć funkcję falową elektronu
Y(x,y,z) w atomie wodoru?

Jeżeli umiemy napisać wyrażenie
na całkowitą energię elektronu E

c

w atomie wodoru, to można
zbudować równanie różniczkowe,
którego

rozwiązaniem

jest

poszukiwana

funkcja

falowa

Y(x,y,z).

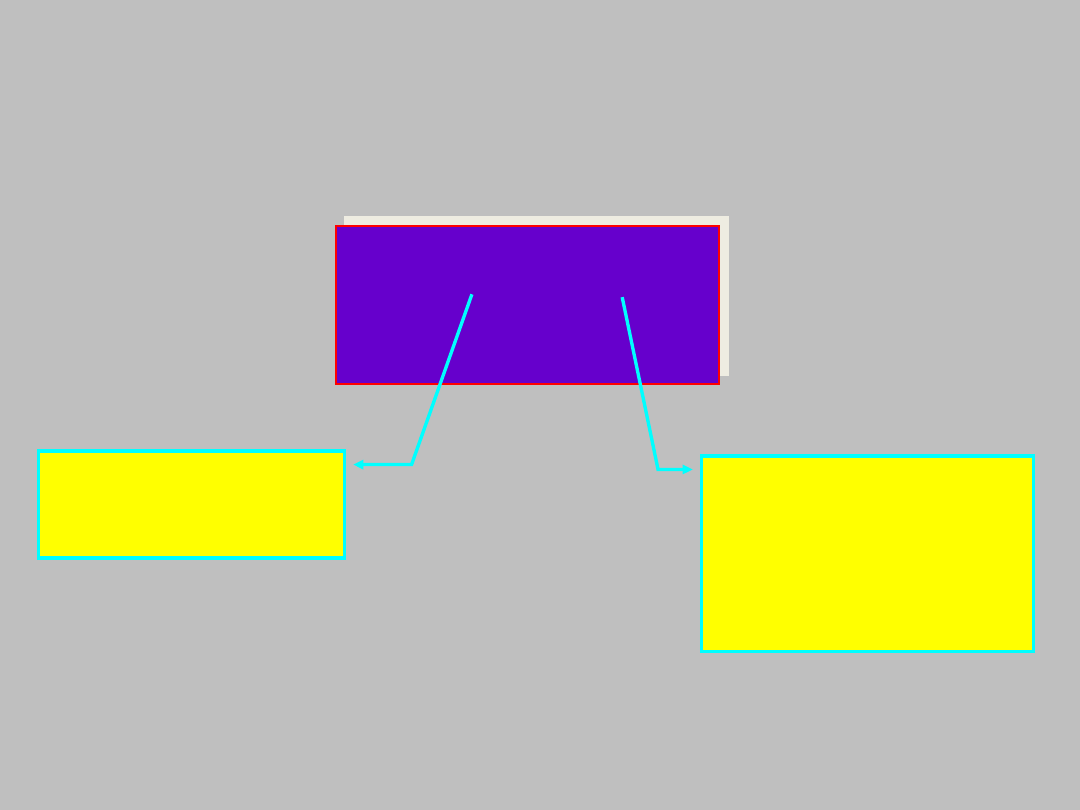
E

c

= E

kin

+

E

pot

E

c

= E

kin

+

E

pot

związana z ruchem

elektronu

związana z

oddziaływaniami

elektrostatycznymi i

magnetycznymi

11

ENERGIA CAŁKOWITA ELEKTRONU W

ATOMIE WODORU

Już w 1925 roku George
Uhlenbeck i Samuel
Goudsmit...

G. Uhlenbeck

G. Uhlenbeck

S. Goudsmit

S. Goudsmit

stwierdzili, że elektron posiada własne pole magnetyczne zachowując
się jak elementarny magnes i cechę tą nazwali

SPINEM

elektronu

...okazało się, że także proton i neutron posiadają spin,

zatem zachowują się jak elementarne magnesy...

12

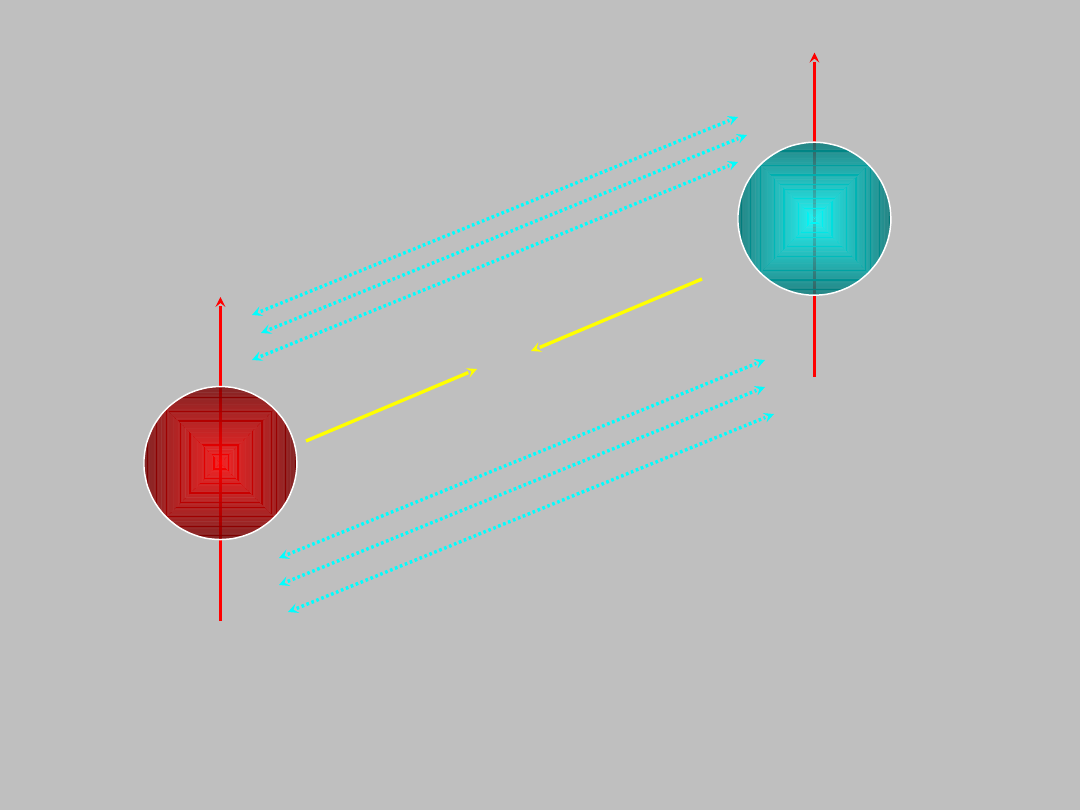
N

S

+

proton

N

S

-

odd

ział

ywa

nie

elek

tros

taty

czn

e

odd

ział

ywa

nie

ma

gne

tycz

ne

odd

ział

ywa

nie

ma

gne

tycz

ne

..z każdym z tych

oddziaływań wiąże się

wkład do energii atomu

....

elektron

13

energia potencjalna E

pot

H

^

HY(x,y,z) = E

c

·

Y(x,y,z)

^

-

operator Hamiltona (hamiltonian), którego postać

jest jednoznacznie określona przez wyrażenie na
energię całkowitą elektronu E

c

^

HY = E

c

·

Y

w
uproszczeniu:

14

RÓWNANIE SCHRÖDINGERA

15

RÓWNANIE SCHRÖDINGERA DLA ATOMU

WODORU

^

HY = E

c

·

Y

Rozwiązać powyższe równanie, to znaczy

znaleźć takie funkcje Y(x,y,z) i takie

wartości E

c

, dla których równanie to jest

spełnione

Przyjmijmy (zgodnie z prawdą), że rozwiązano
równanie Schrödingera, czyli znaleziono funkcję
Y(x,y,z) spełniającą to równanie, a wraz z nią
znaleziono wartości E

c

.

lub skrótowo:

16

Rozwiązania równania Schrödingera dla
atomu wodoru

Jakie cechy ma ta funkcja?

Funkcja ta zależy od czterech parametrów

liczbowych

n, l, m, s

co

zanotujemy jako:

Y

nlms

(x,y,z)

Y

nlms

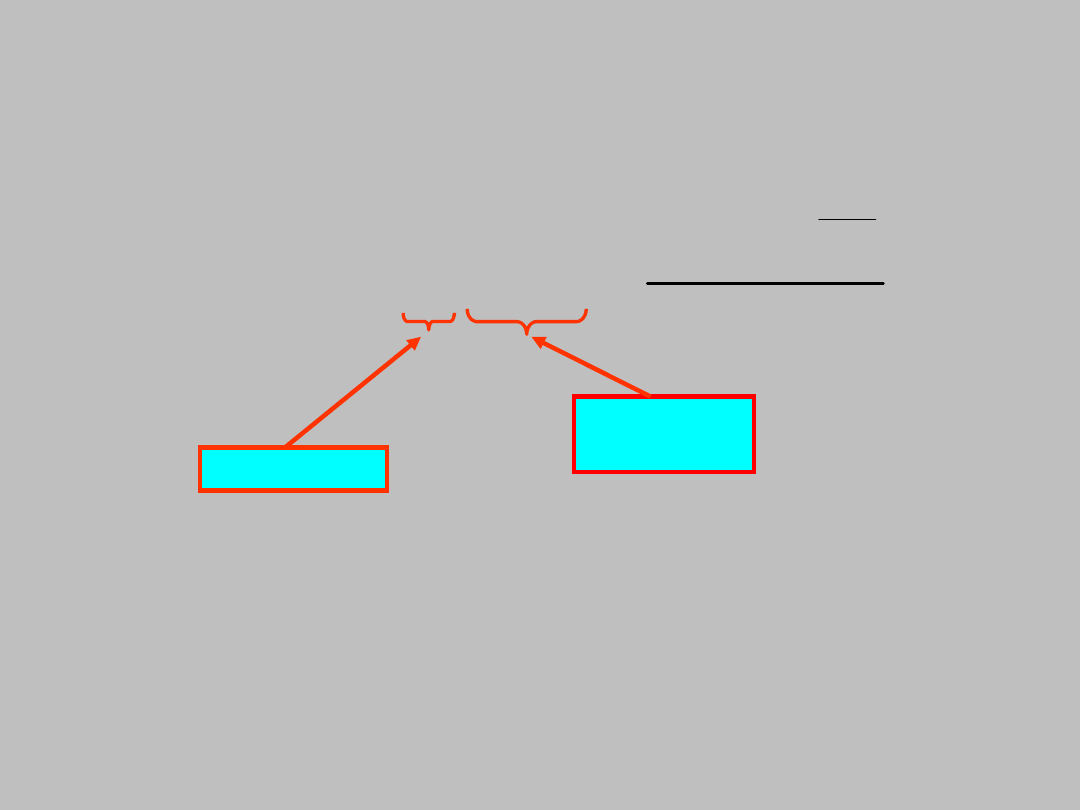
Co to znaczy, że funkcja zależy od
parametrów?

weźmy przykład:

1

log(k)

n k

nk

n

y

z

f (x,y,z)

1 x

-

�

=

-

Przy ZADANYCH wartościach n i k ZMIENIAMY
wartości x, y i z

Aby funkcja f

nk

(x,y,z) miała sens:

n > 0 n > k

k > 0

zmienne

niezależne

parametry

17

Parametry n, l, m, s (LICZBY KWANTOWE) nie
mogą być dowolne jeżeli funkcja Y

nlms

ma mieć

sens

Parametry n, l, m, s (LICZBY KWANTOWE) nie
mogą być dowolne jeżeli funkcja Y

nlms

ma mieć

sens

n = 1, 2, 3......

n = 1, 2, 3......

główna liczba kwantowa

l = 0, 1, 2...... (n-1)

l = 0, 1, 2...... (n-1)

orbitalna liczba kwantowa

-l  m  l

-l  m  l

magnetyczna liczba kwantowa

s = ±
1/2

spinowa liczba kwantowa

18

Parametry n, l, m,s w funkcji falowej dla
atomu wodoru

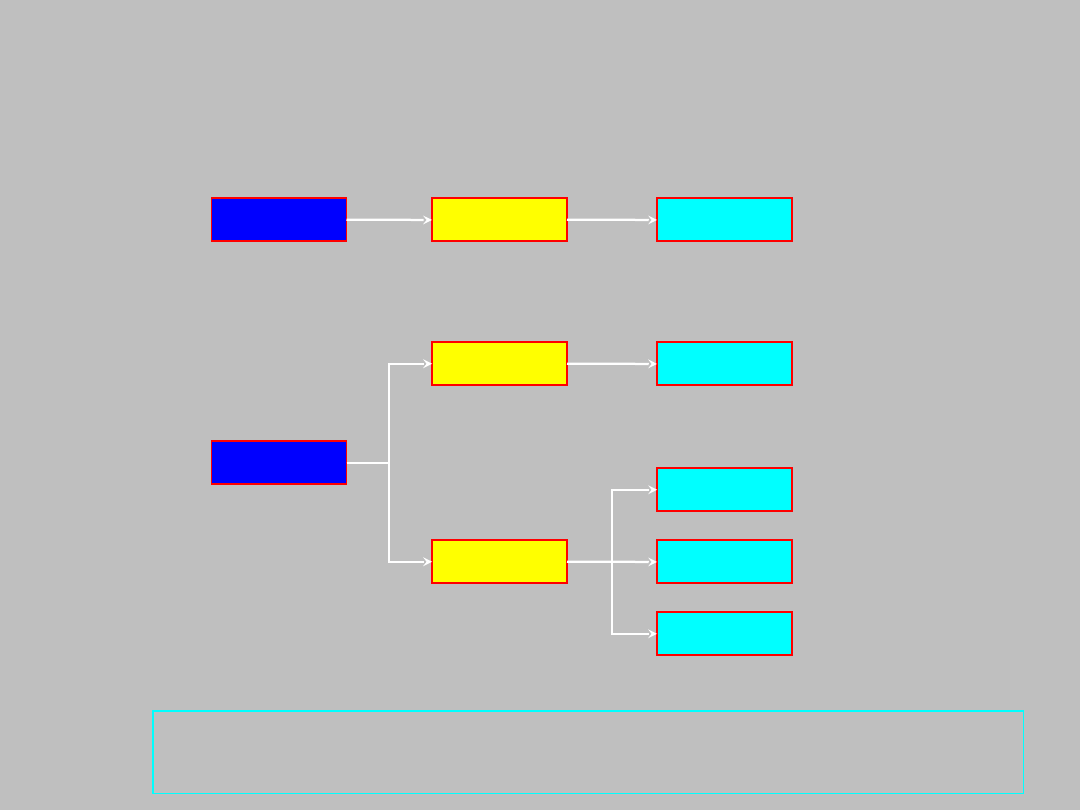
Zatem przykładowe dozwolone zestawy liczb
kwantowych kształtują się następująco:

n = 1

l = 0

m = 0

n = 2

l = 0

l = 1

m = 0

m = -1

m = 0

m = 1

dla każdego zestawu n, l, m liczba s może przyjąć dwie
wartości: ±1/2

19

Nowa notacja i nazewnictwo

Funkcję falową Y

nlm

opisującą rozkład prawdopodobieństwa

napotkania elektronu w jakimkolwiek atomie nazywamy:

ORBITALEM ATOMOWYM

nowa notacja:

Y

nlm

h nl

ind

n - główna liczba kwantowa podana cyfrą arabską

l - orbitalna liczba kwantowa oznaczona literą wg klucza: 0 - s, 1 - p, 2
- d, 3 - f

ind - indeks związany z wartością magnetycznej liczby kwantowej m,
dodawany tylko wtedy, gdy jest to konieczne

20

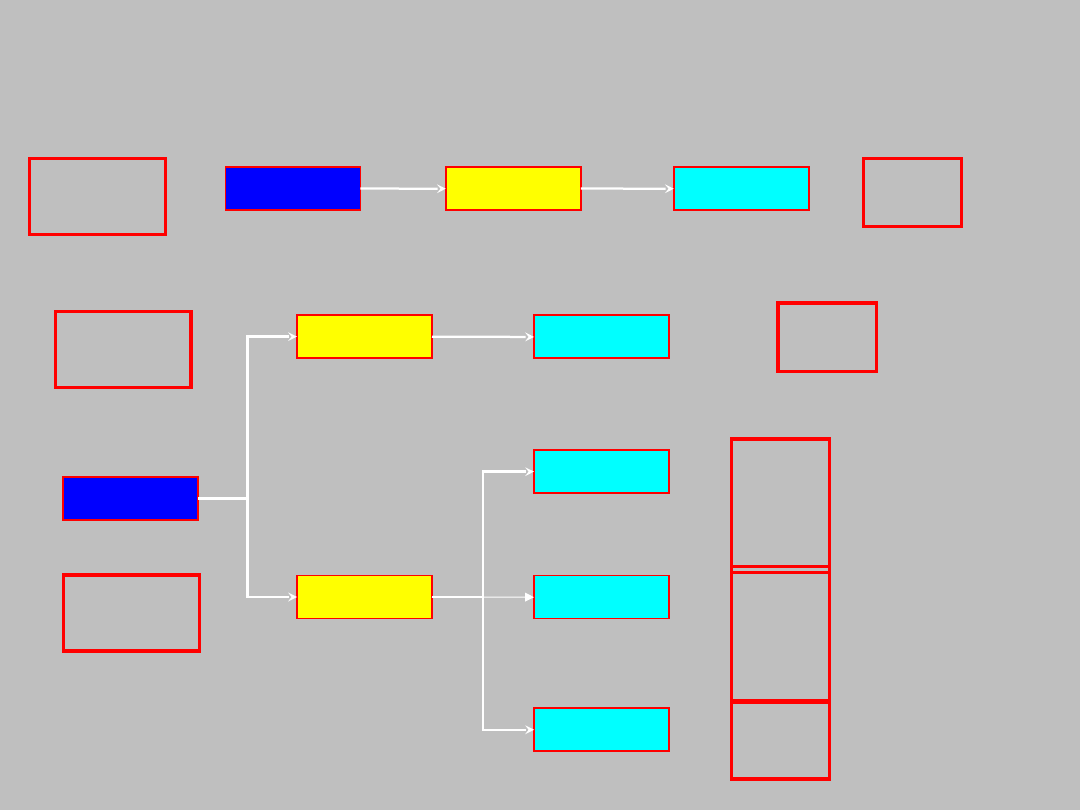
Nowa notacja orbitali:

n = 1

l = 0

m = 0

n = 2

l = 0

l = 1

m = 0

m = -1

m = 0

m = 1

Y

100

1s

Y

200

2s

Y

210

2p

x

2p

y

2p

z

21

n = 3

l = 0

m = 0

l = 1

m = -1

m = 0

m = 1

Y

300

3s

Y

31m

l = 2

m = -2

m = -1

m = 0

m = 1

m = 2

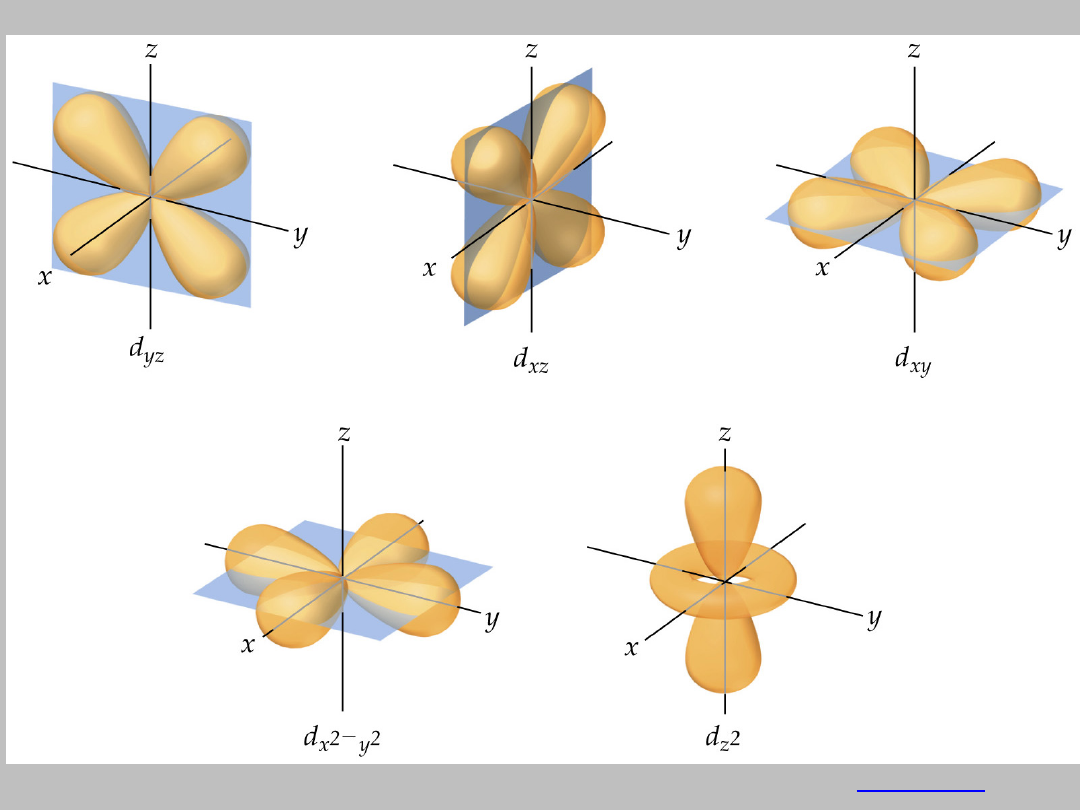
2

2

2

xy

xz

yz

z

x y

3d

3d

3d

3d

3d

-

3p

x

3p

y

3p

z

Y

32m

22

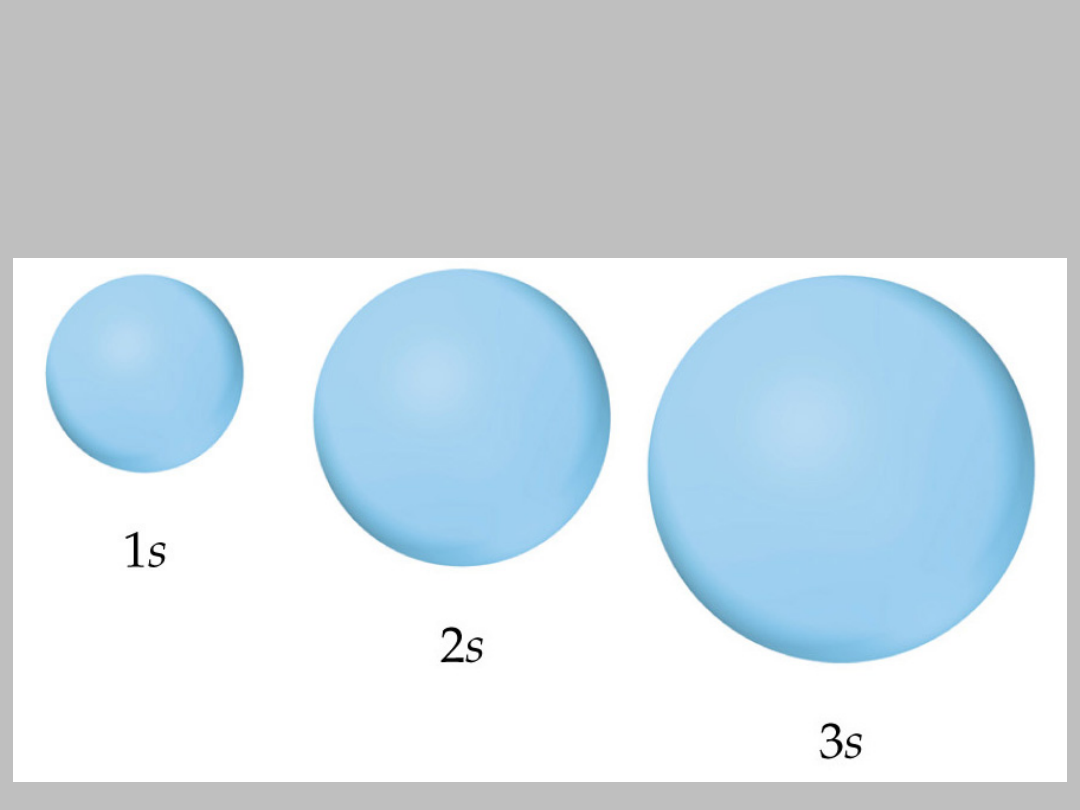
orbitale typu s

Reprezentacja geometryczna orbitali

Orbitale typu p

Reprezentacja orbitali

d-orbitals

Jak zmienia się energia E

c

orbitalu Y

nlms

w zależności od

wartości liczb kwantowych
n,l,m,s?

H

H

Y = E

c

·

Y

^

1 2 3 4 5 6
7

s s s s s s
s

p p p p p
p

d d d
d

f f

główna liczba kwantowa
n

o

rb

it

a

ln

a

l

ic

z

b

a

k

w

a

n

to

w

a

l

..można też przedstawić to inaczej..

Kolejność energetyczna orbitali atomowych

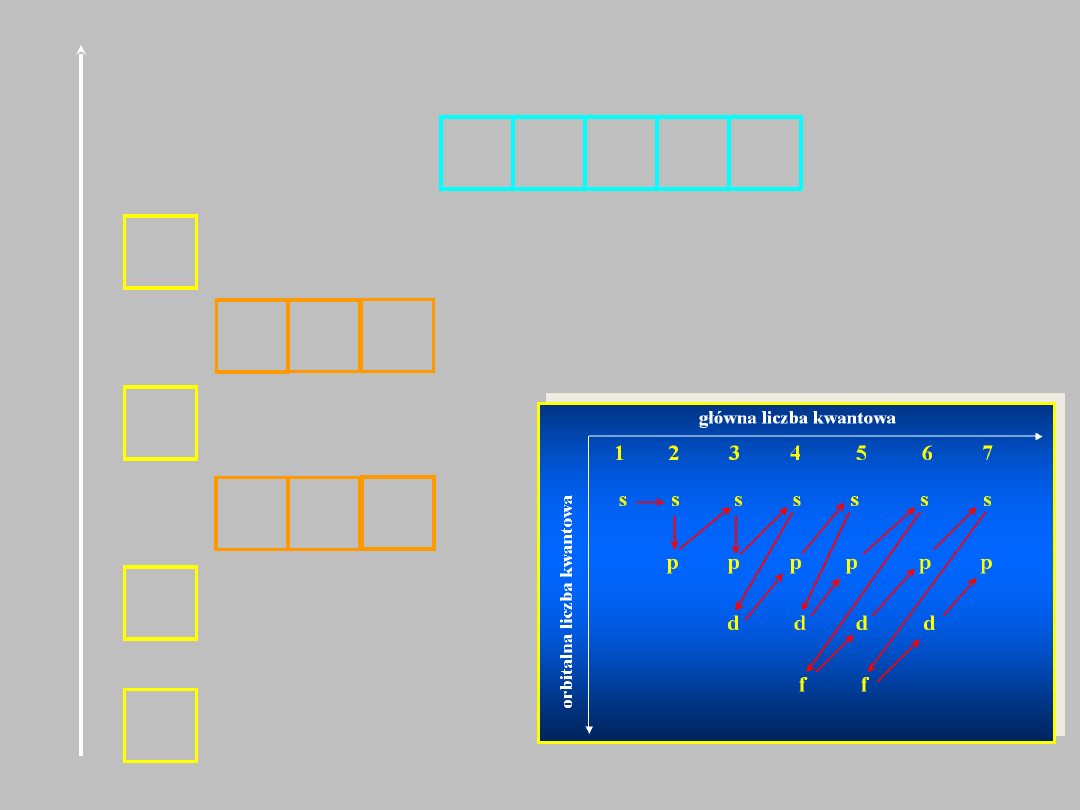
E

1s

2s

2p

3s

3p

4s

3d

zapis

„klatkowy”

Jesteśmy przygotowani do przedstawienia
struktury elektronowej atomów....

..wystarczy wiedzieć, że:

Liczba elektronów w obojętnym atomie jest równa jego liczbie

atomowej

Elektrony w atomie w stanie podstawowym „starają się”

przyjmować jak najniższe energie

Każdy orbital atomowy opisuje zachowanie dwóch elektronów

różniących się spinową liczbą kwantową (zakaz Pauliego)

Jeżeli elektrony opisywane są różnymi orbitalami o tej samej energii

to zajmują je tak aby liczba niesparowanych spinów była jak

największa

(reguła Hunda)

E

n

e

rg

ia

1s

2s

2p

3s

3p

4s

3d

konfiguracja

elektronowa atomu:

wodoru
(Z=1)

H: 1s

1

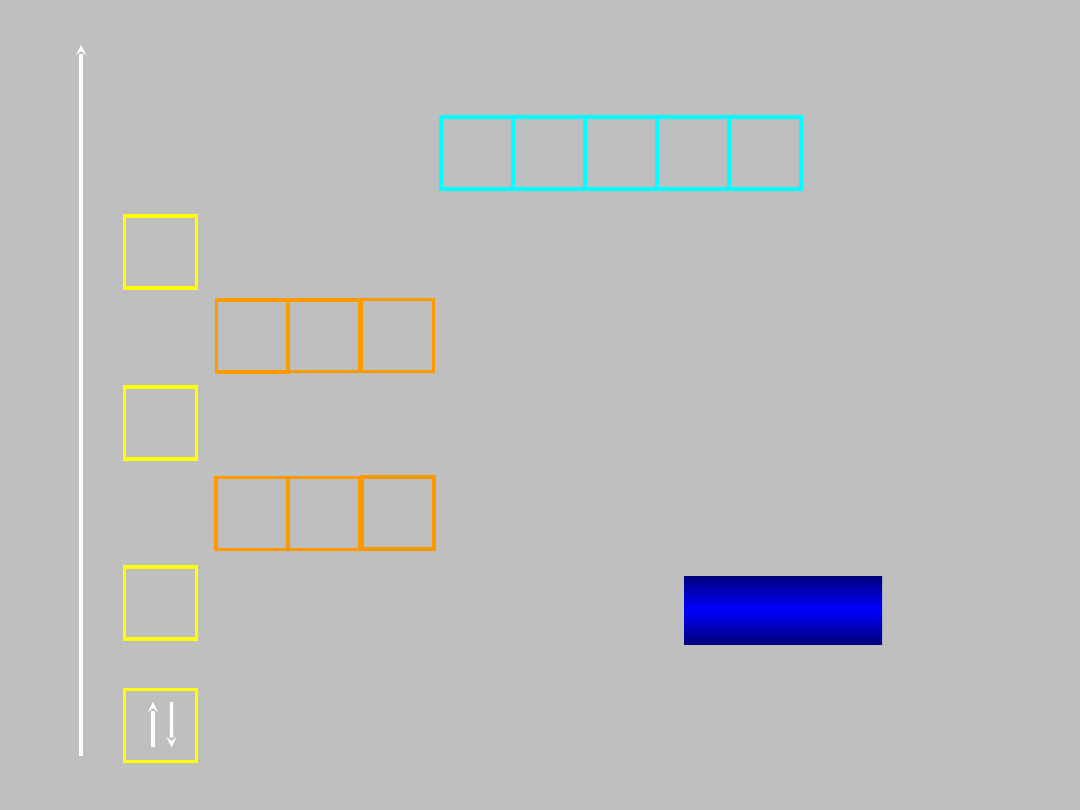
E

1s

2s

2p

3s

3p

4s

3d

konfiguracja

elektronowa atomu:

He: 1s

2

helu (Z=2)

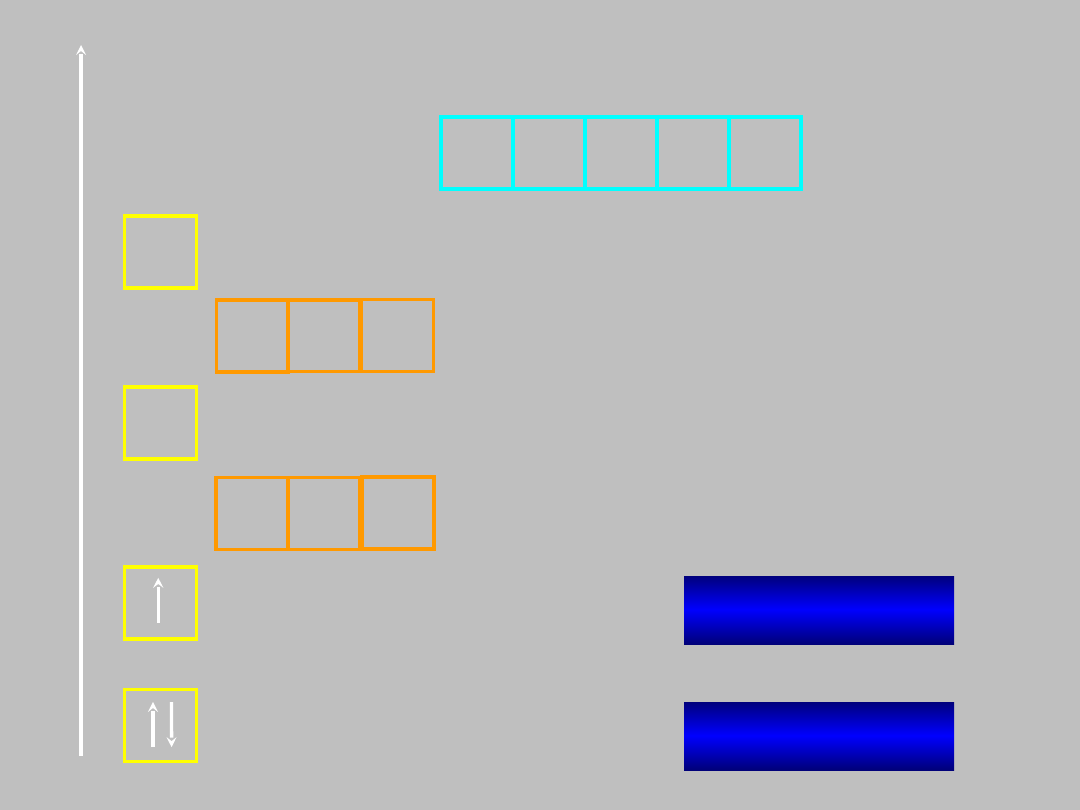
E

1s

2s

2p

3s

3p

4s

3d

konfiguracja

elektronowa atomu:

Li: 1s

2

2s

1

litu (Z=3)

Li: He2s

1

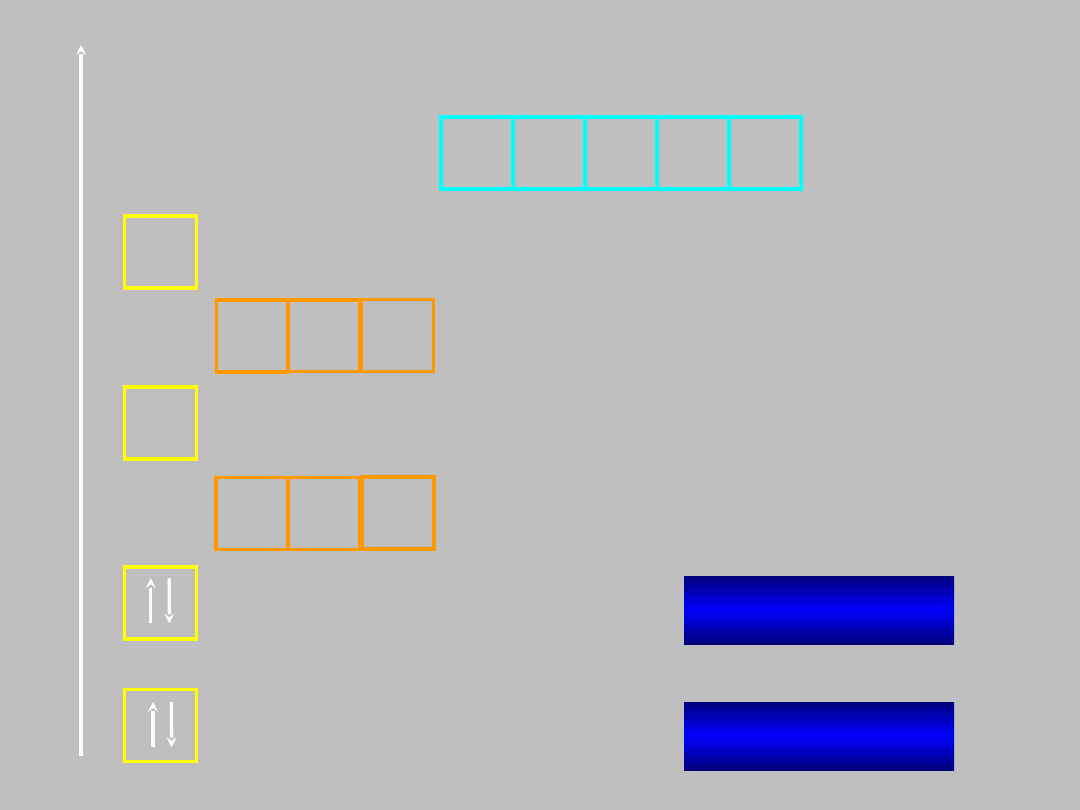
E

1s

2s

2p

3s

3p

4s

3d

konfiguracja

elektronowa atomu:

Be: 1s

2

2s

2

berylu

(Z=4)

Be: He2s

2

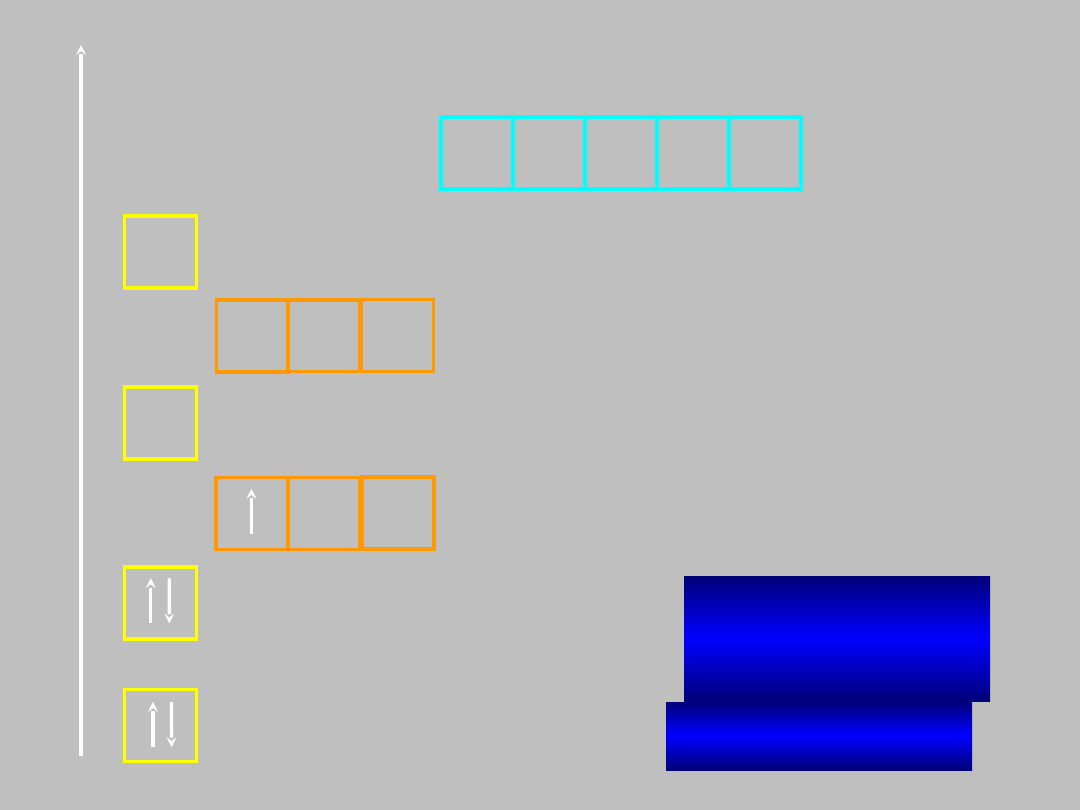
E

1s

2s

2p

3s

3p

4s

3d

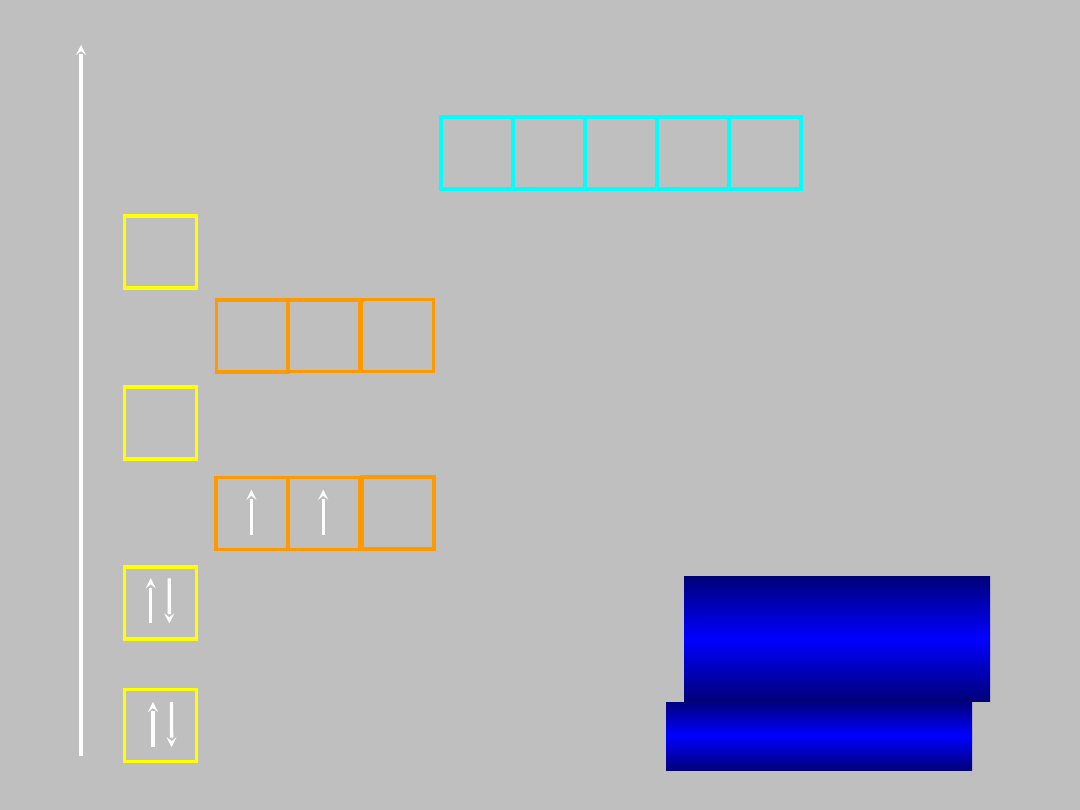
konfiguracja

elektronowa atomu:

B:
1s

2

2s

2

2p

1

boru (Z=5)

B: He2s

2

2p

1

E

1s

2s

2p

3s

3p

4s

3d

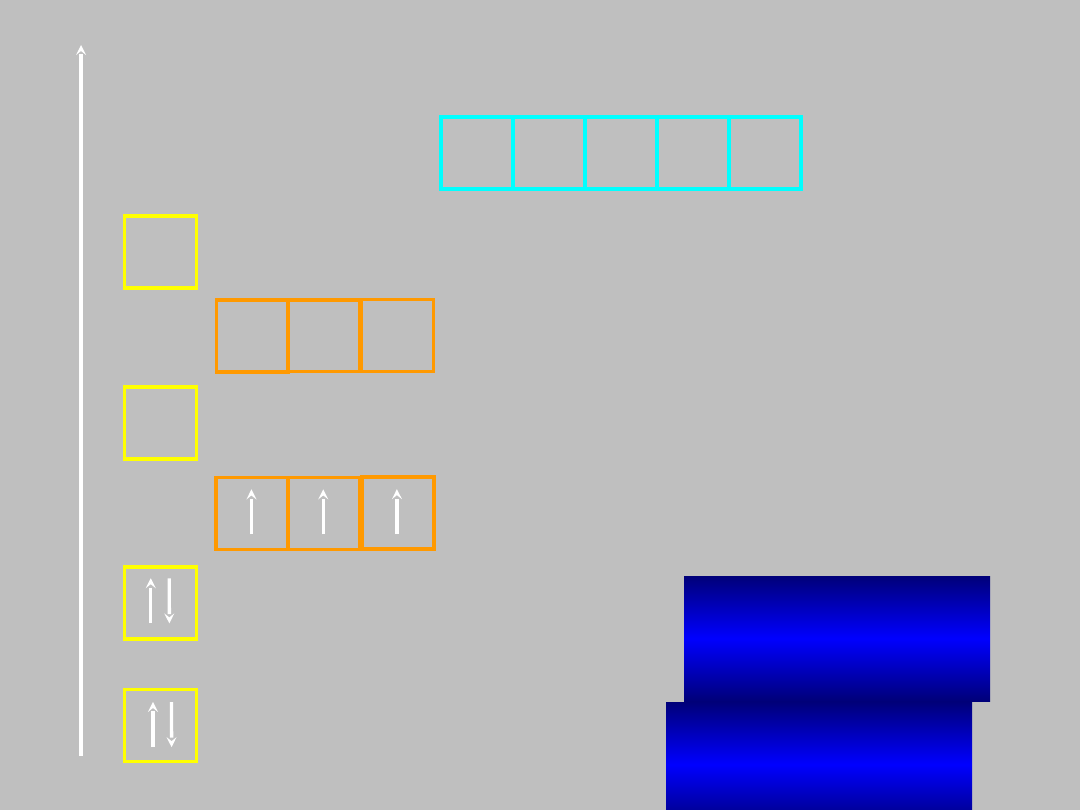
konfiguracja

elektronowa atomu:

C:

1s

2

2s

2

2p

2

węgla (Z=6)

C: He2s

2

2p

2

E

1s

2s

2p

3s

3p

4s

3d

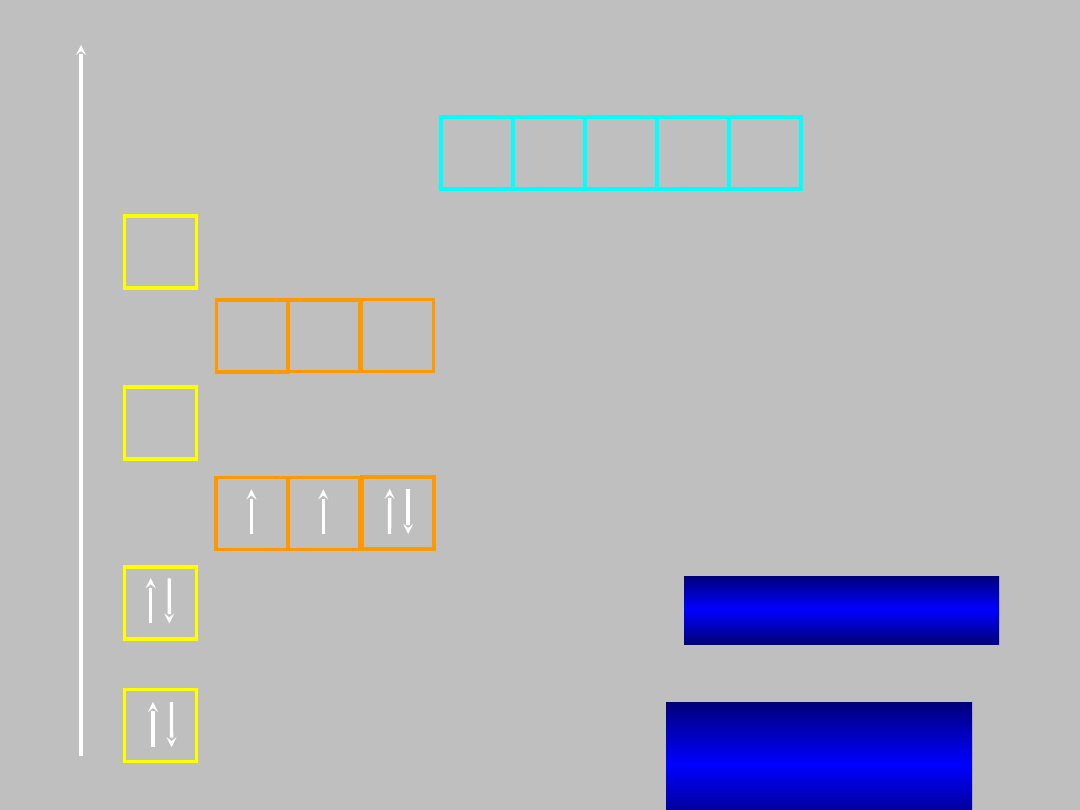
konfiguracja

elektronowa atomu:

N:

1s

2

2s

2

2p

3

azotu (Z=7)

N:

He2s

2

2p

3

E

1s

2s

2p

3s

3p

4s

3d

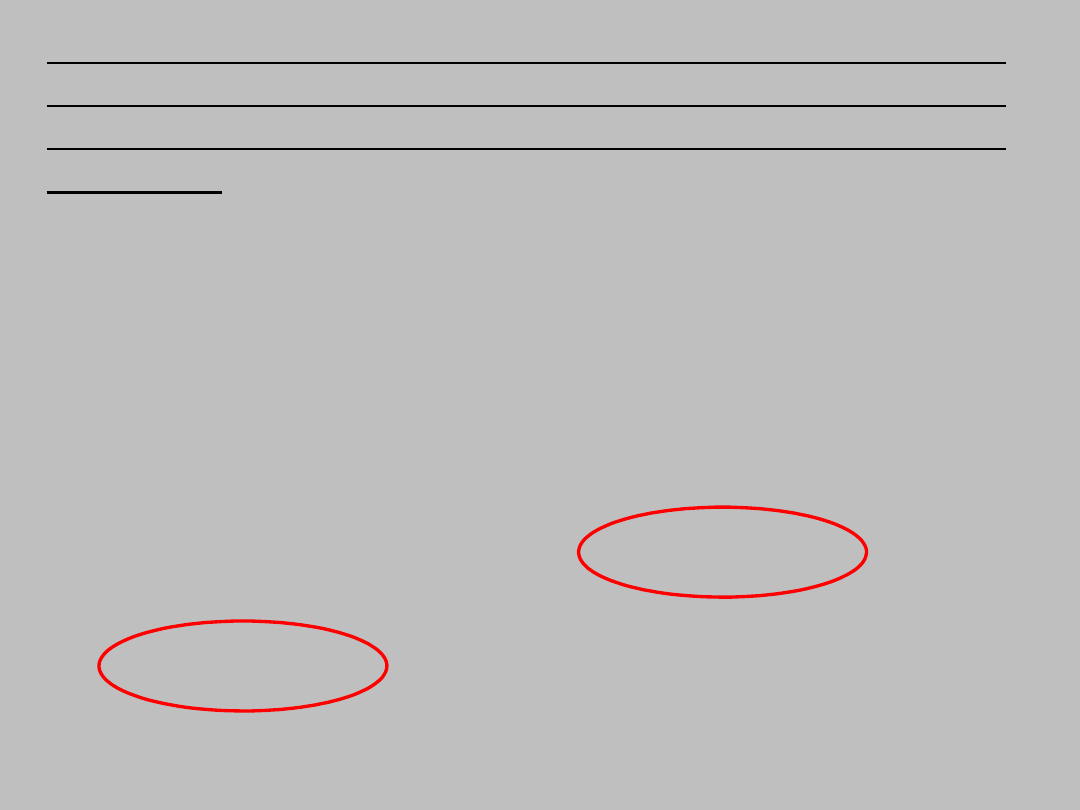
konfiguracja

elektronowa atomu:

O: 1s

2

2s

2

2p

4

tlenu (Z=8)

O:

He2s

2

2p

4

Należy pamiętać, że istnieje szereg wyjątków
od przedstawionego schematu zapełniania
poziomów energetycznych przez elektrony w
atomach

przykładowo dla pierwiastków 4 okresu

:

K: Ar4s

1

Ca: Ar4s

2

Sc: Ar4s

2

3d

1

Ti: Ar4s

2

3d

2

V: Ar4s

2

3d

3

Cr: Ar4s

1

3d

5

Mn: Ar4s

2

3d

5

Fe: Ar4s

2

3d

6

Co: Ar4s

2

3d

7

Ni: Ar4s

2

3d

8

Cu: Ar4s

1

3d

10

Zn: Ar4s

2

3d

10

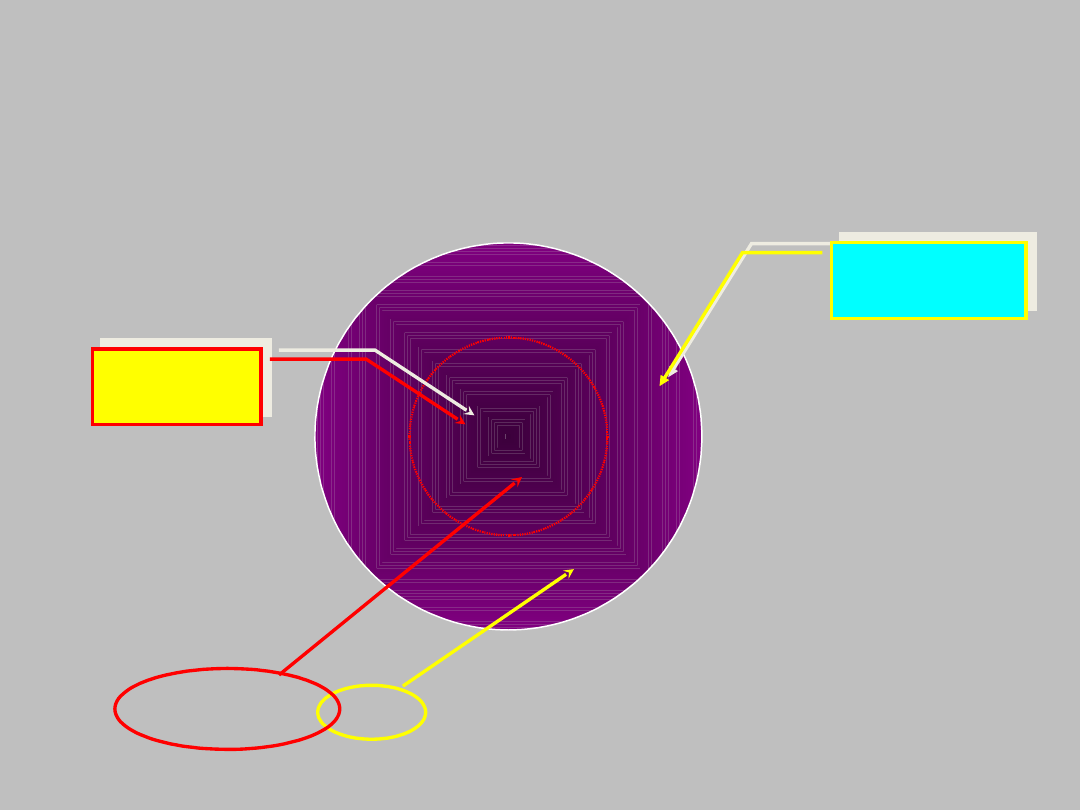
Im wyższa jest energia elektronów, tym bardziej
maksimum prawdopodobieństwa ich napotkania
oddala się od jądra

pozwala to podzielić elektrony w atomie na dwie grupy:

rdzeń

atomowy

rdzeń

atomowy

elektrony

walencyjne

elektrony

walencyjne

Na: 1s

2

2s

2

2p

6

3s

1

przykład:

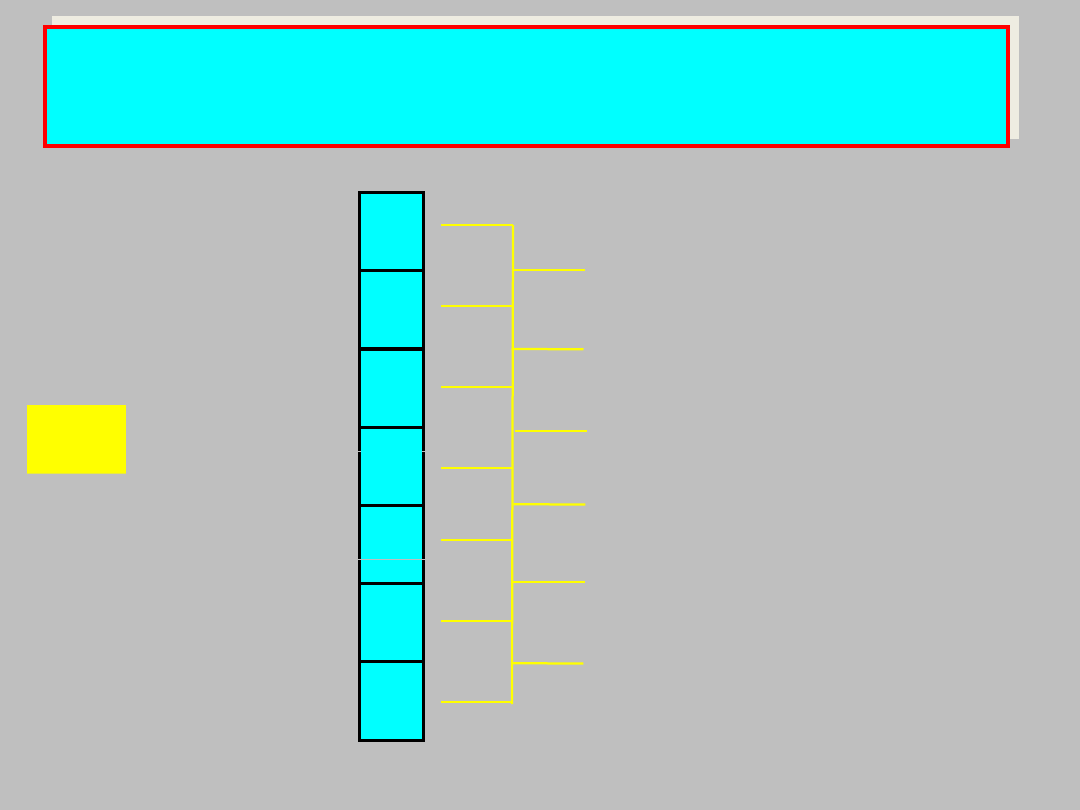
Analizując konfiguracje elektronowe POWŁOK WALENCYJNYCH
atomów, łatwo zauważyć, że konfiguracje te powtarzają się co
2, 8, 18 lub 32 pierwiastki

Analizując konfiguracje elektronowe POWŁOK WALENCYJNYCH
atomów, łatwo zauważyć, że konfiguracje te powtarzają się co
2, 8, 18 lub 32 pierwiastki

ns

1

1

H

3

Li

11

Na

19

K

37

Rb

55

Cs

87

Fr

1s

1

He2s

1

Ne3s

1

Ar4s

1

Kr5s

1

Xe6s

1

Rn7s

1

2

8

8

1
8

1
8

3
2

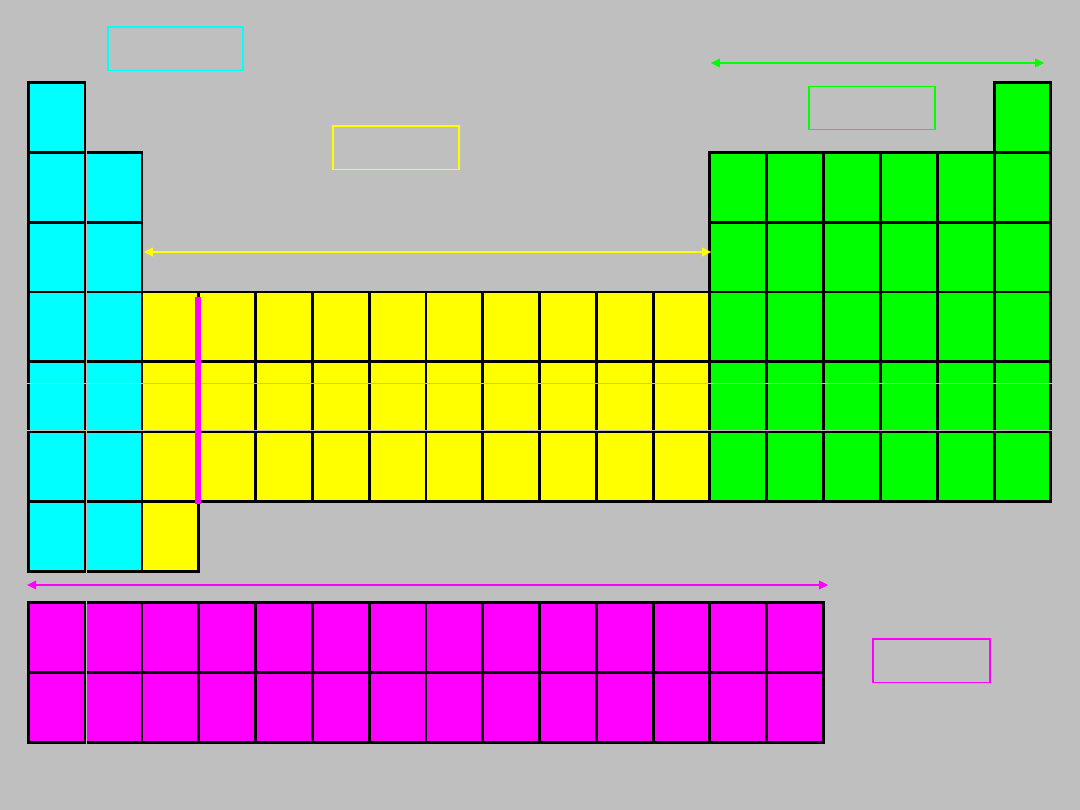
Możemy zatem ułożyć tablicę
pierwiastków, kierując się następującymi
zasadami:

Ustawiamy pierwiastki w ciąg

rosnących liczb atomowych

Ciąg ten „zawijamy” tak, aby pierwiastki o

podobnych konfiguracjach elektronowych

powłoki walencyjnej znalazły się w tych

samych kolumnach

...wynik jest następujący....

1

2

H

He

3

4

5

6

7

8

9

10

Li

Be

B

C

N

O

F

Ne

11

12

13

14

15

16

17

18

Na Mg

Al

Si

P

S

Cl Ar

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

K

Ca Sc

Ti

V

Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

Rb Sr

Y

Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te

I

Xe

55

56

57

72

73

74

75

76

77

78

79

80

81

82

83

84

85

86

Cs Ba La Hf Ta W Re Os Ir

Pt Au Hg Tl

Pb Bi

Po At Rn

87

88

89

Fr Ra Ac

58

59

60

61

62

63

64

65

66

67

68

69

70

71

Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm Yb Lu

90

91

92

93

94

95

96

97

98

99

100

101

102

103

Th Pa

U

Np Pu Am Cm Bk Cf

Es Fm Md No Lr

ns

1

ns

2

ns

2(1)

(n-1)d

x

ns

2

p

y

ns

2

(n-1)d

0(1)

(n-2)f

z

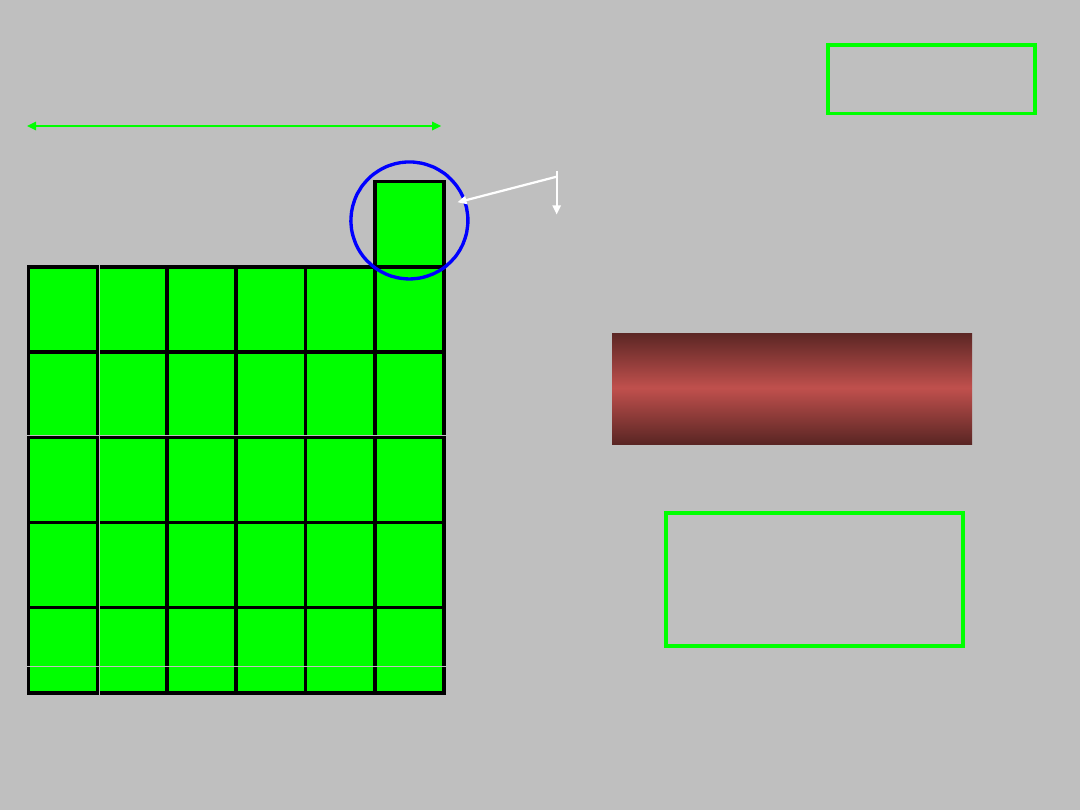
blok s

blok d

blok p

blok f

1

H

3

4

Li

Be

11

12

Na Mg

19

20

K

Ca

37

38

Rb Sr

55

56

Cs Ba

87

88

Fr Ra

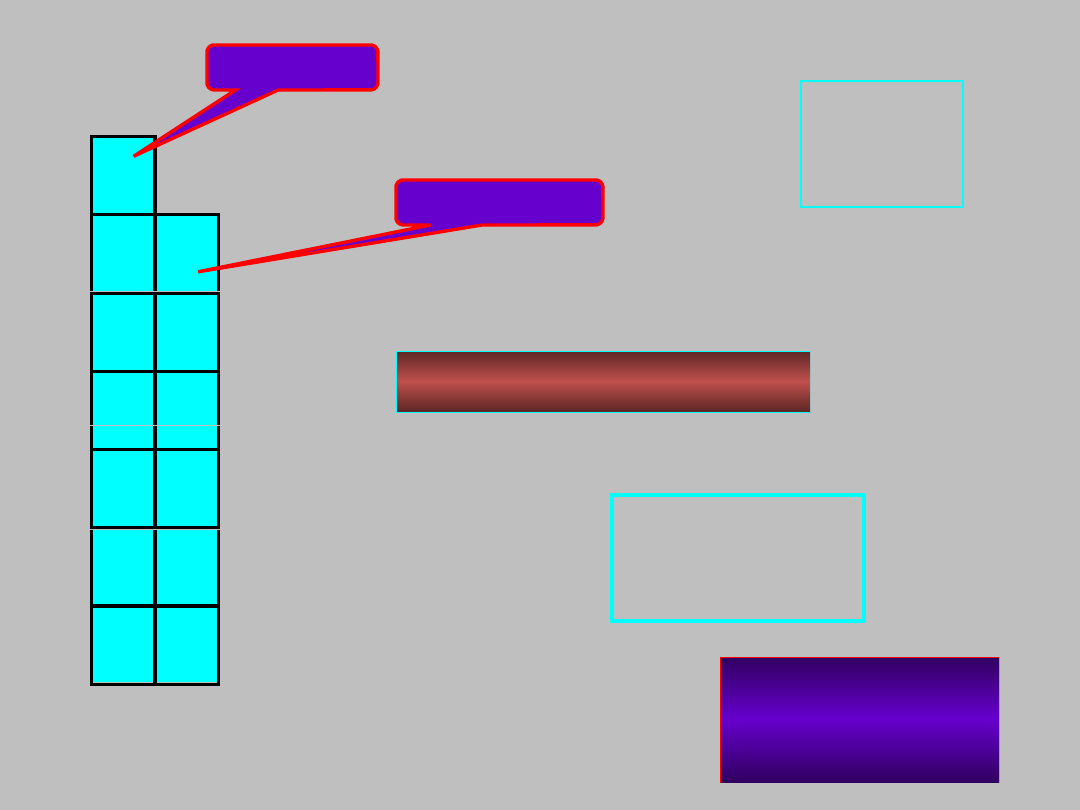
blok

s

ns

1

ns

2

n = 1 do

7

13 pierwiastków

1

2

3

4

5

6

7

litowce

berylowce

grupy 1 i

2

2

He

5

6

7

8

9

10

B

C

N

O

F

Ne

13

14

15

16

17

18

Al

Si

P

S

Cl Ar

31

32

33

34

35

36

Ga Ge As Se Br Kr

49

50

51

52

53

54

In Sn Sb Te

I

Xe

81

82

83

84

85

86

Tl

Pb Bi

Po At Rn

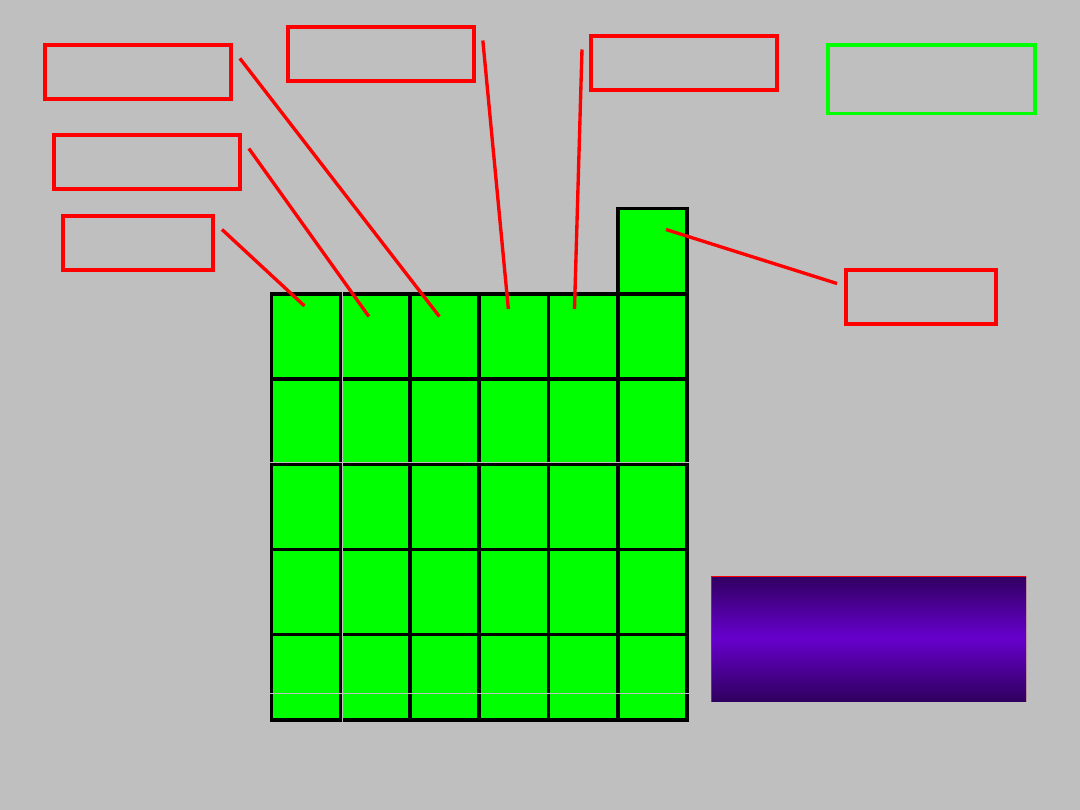
blok p

ns

2

p

y

30+1

pierwiastków

n = 2 do 6

y = 1 do 6

wyjątek 1s

2

2

3

4

5

6

2

He

5

6

7

8

9

10

B

C

N

O

F

Ne

13

14

15

16

17

18

Al

Si

P

S

Cl Ar

31

32

33

34

35

36

Ga Ge As Se Br Kr

49

50

51

52

53

54

In Sn Sb Te

I

Xe

81

82

83

84

85

86

Tl

Pb Bi

Po At Rn

blok p

borowce

węglowce

azotowce

tlenowce

fluorowce

helowce

grupy 13-

18

21

22

23

24

25

26

27

28

29

30

Sc

Ti

V

Cr Mn Fe Co Ni Cu Zn

39

40

41

42

43

44

45

46

47

48

Y

Zr Nb Mo Tc Ru Rh Pd Ag Cd

57

72

73

74

75

76

77

78

79

80

La Hf Ta W Re Os

Ir

Pt Au Hg

89

Ac

ns

2(1)

(n-

1)d

x

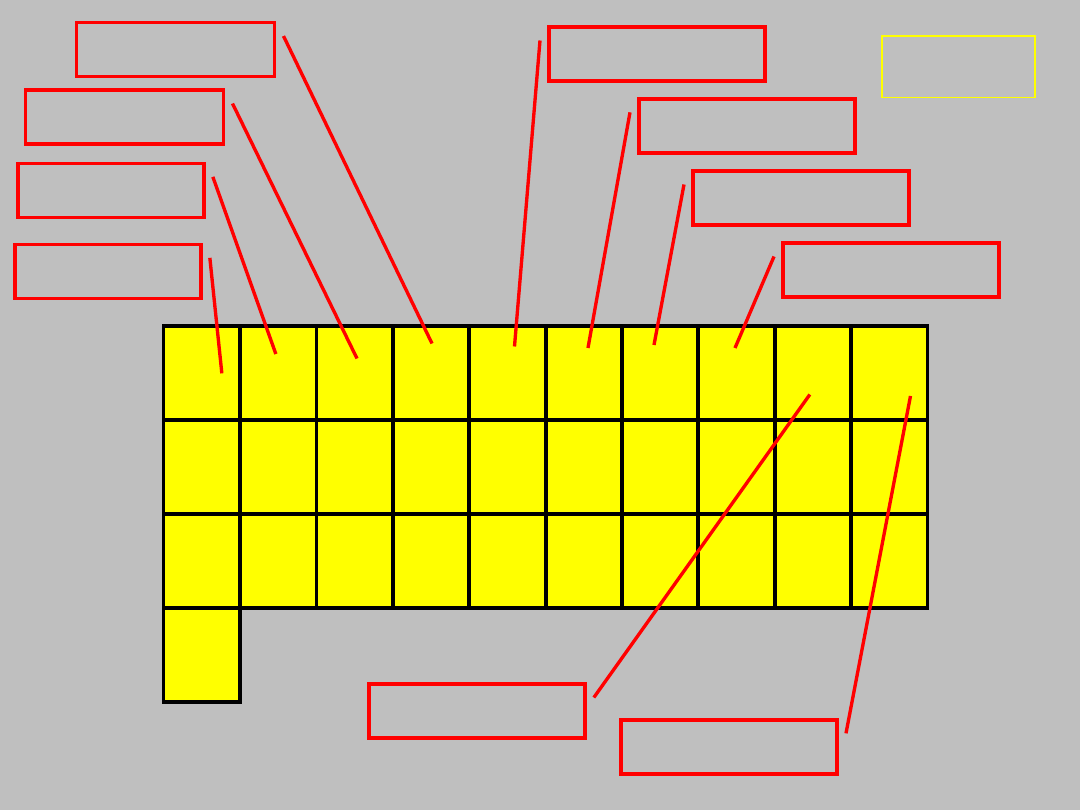
blok d

31+?

pierwiastków

n = 4 do 7

x = 1 do 10

....... są już dalsze...

grupy 3-

12

21

22

23

24

25

26

27

28

29

30

Sc

Ti

V

Cr Mn Fe Co Ni Cu Zn

39

40

41

42

43

44

45

46

47

48

Y

Zr Nb Mo Tc Ru Rh Pd Ag Cd

57

72

73

74

75

76

77

78

79

80

La Hf Ta W Re Os

Ir

Pt Au Hg

89

Ac

blok d

skandowce

tytanowce

wanadowce

chromowce

manganowce

żelazowce

kobaltowce

niklowce

miedziowce

cynkowce

58

59

60

61

62

63

64

65

66

67

68

69

70

71

Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm Yb Lu

90

91

92

93

94

95

96

97

98

99

100

101

102

103

Th Pa

U

Np Pu Am Cm Bk Cf

Es Fm Md No Lr

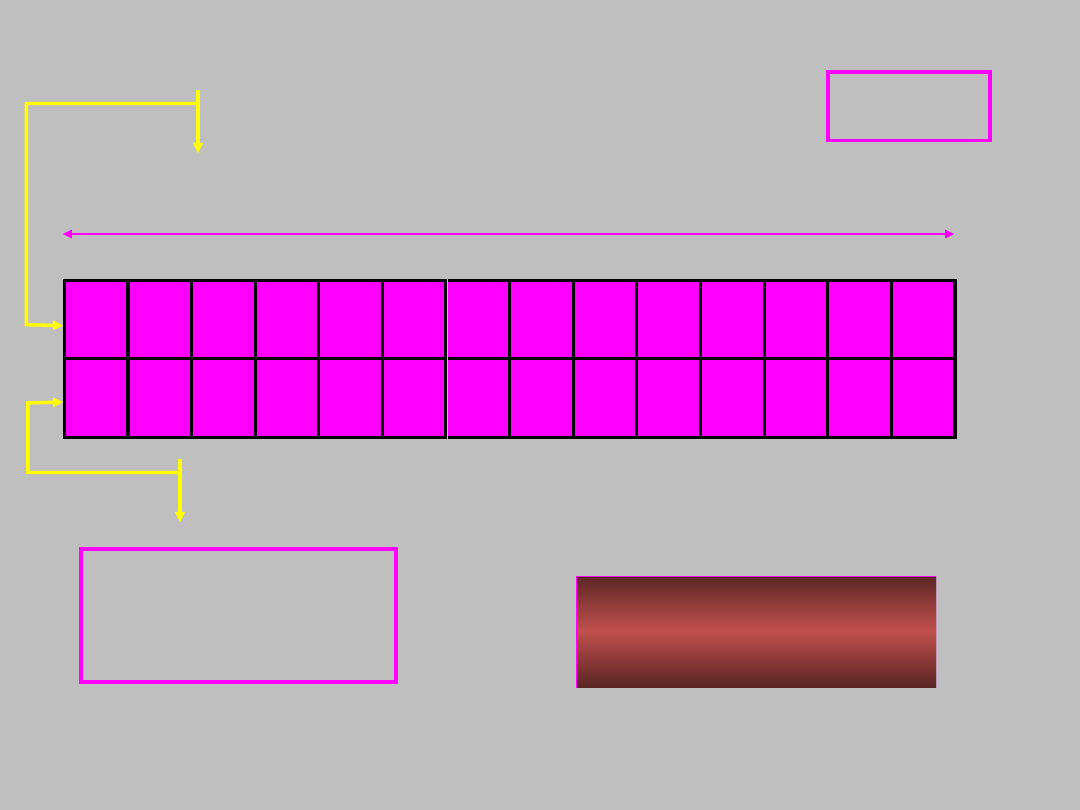
blok f

ns

2

(n-1)d

0(1)

(n-2)f

z

6
7

n = 6 lub 7

z = 1 do 14

28

pierwiastków

aktynowce

lantanowce

Podsumowanie:

Współczesna teoria budowy atomu

wyjaśniła PRAWO OKRESOWOŚCI

UKŁAD OKRESOWY PIERWIASTKÓW jest

pochodną konfiguracji elektronowej

atomów

Dzisiaj NIC JUŻ NIE WYNIKA z układu okresowego - to
układ okresowy WYNIKA ze współczesnej teorii budowy
atomu

•promienie atomowe
•gęstości pierwiastków
•potencjału jonizacyjne
pierwiastków

przykładowo
omówimy:

Popatrzmy jak kształtują się wybrane
wielkości fizyczne w zależności od
położenia pierwiastka w układzie
okresowym i od jego liczby atomowej
Z

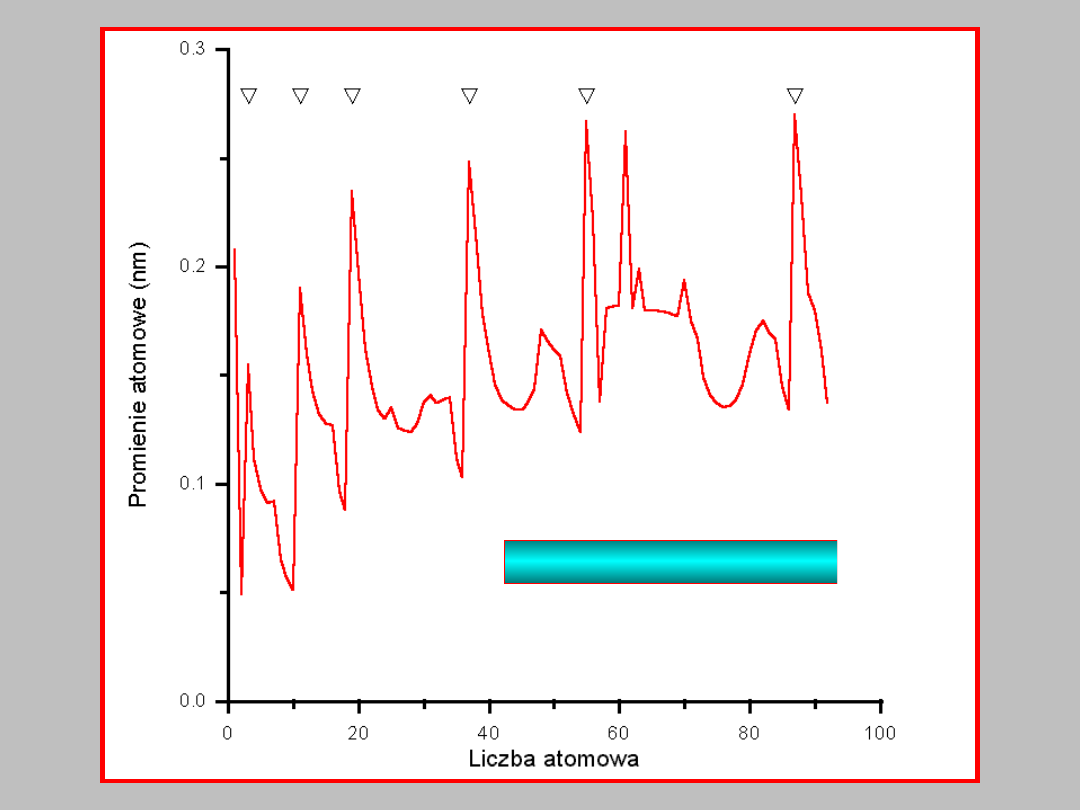
32

8

8

18

18

promienie atomowe

87

Fr

3

Li

11

N

a

19

K

37

Rb

55

Cs

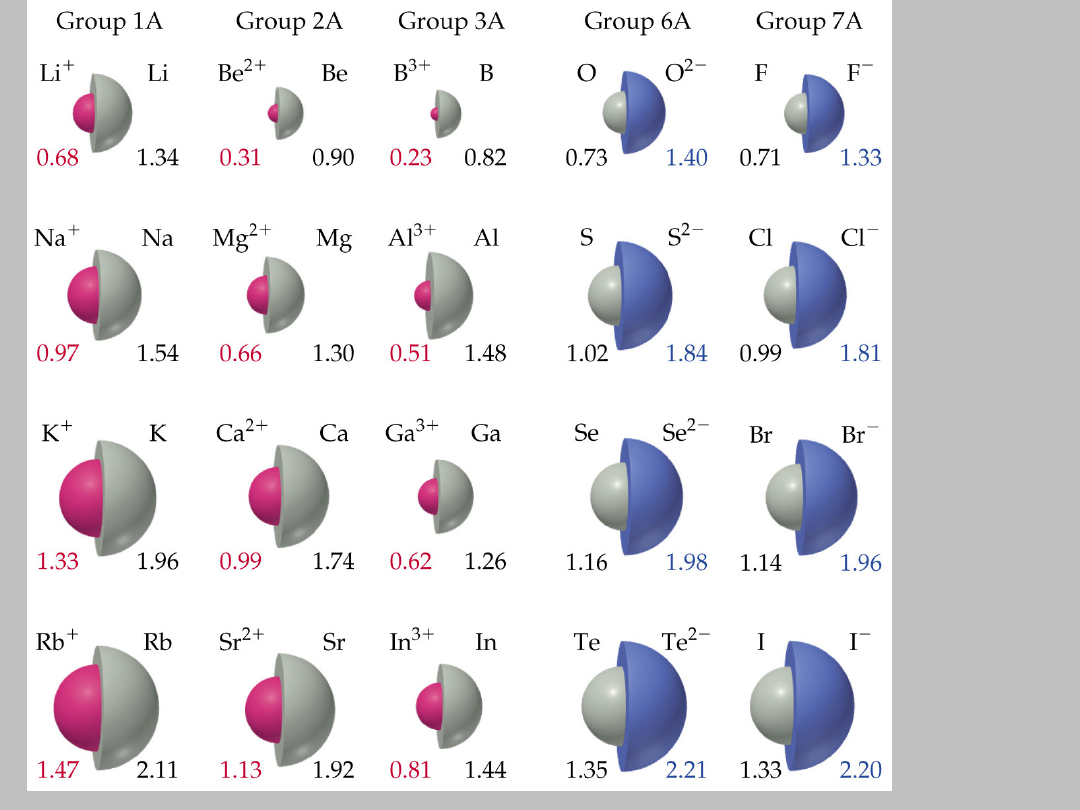
Figure
7.6

PROMIENIE ATOMOWE

PROMIENIE ATOMOWE

10

-10

m

32

8

8

18

18

87

Fr

55

Cs

37

Rb

19

K

11

N

a

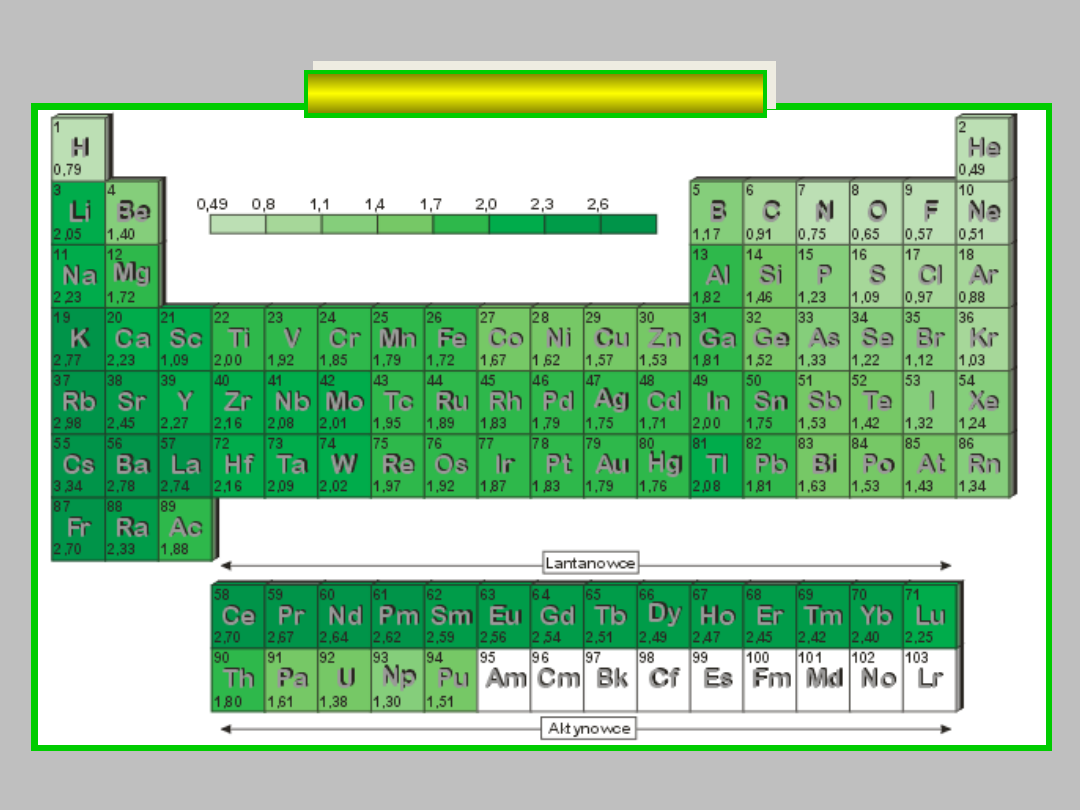
gęstość

g/cm

3

GĘSTOŚĆ PIERWIASTKÓW

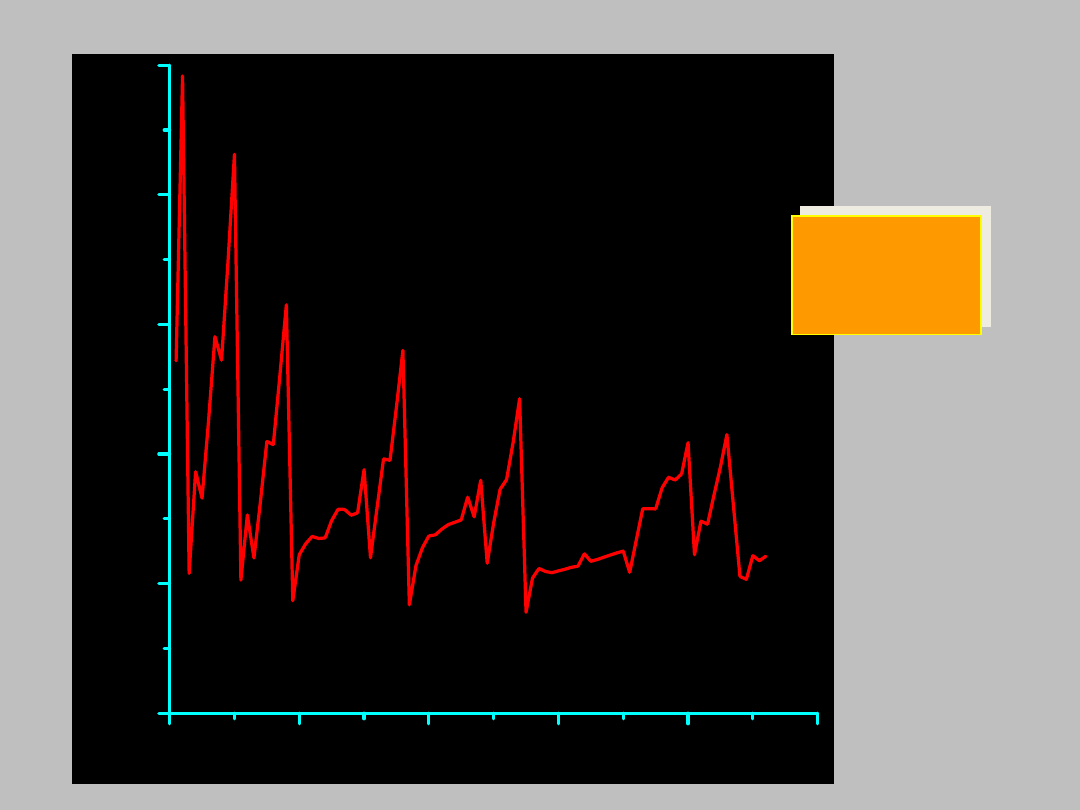
0

2 0

4 0

6 0

8 0

1 0 0

L ic z b a a to m o w a

0

5

1 0

1 5

2 0

2 5

P

ot

en

cj

ał

y

jo

ni

za

cj

i a

to

m

ów

(

V

)

N e

H e

A r

K r

X e

R n

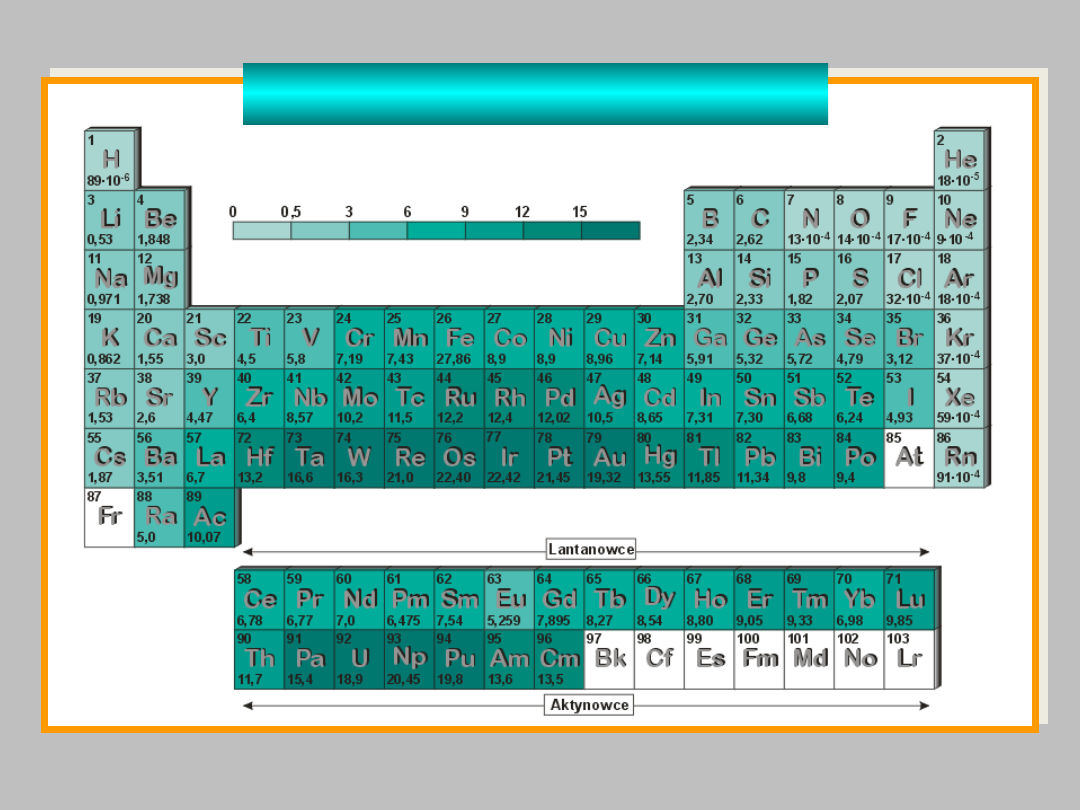
POTENCJAŁY JONIZACJI I

W =
q

e

·I

W =
q

e

·I

praca W potrzebna do usunięcia elektronu z atomu

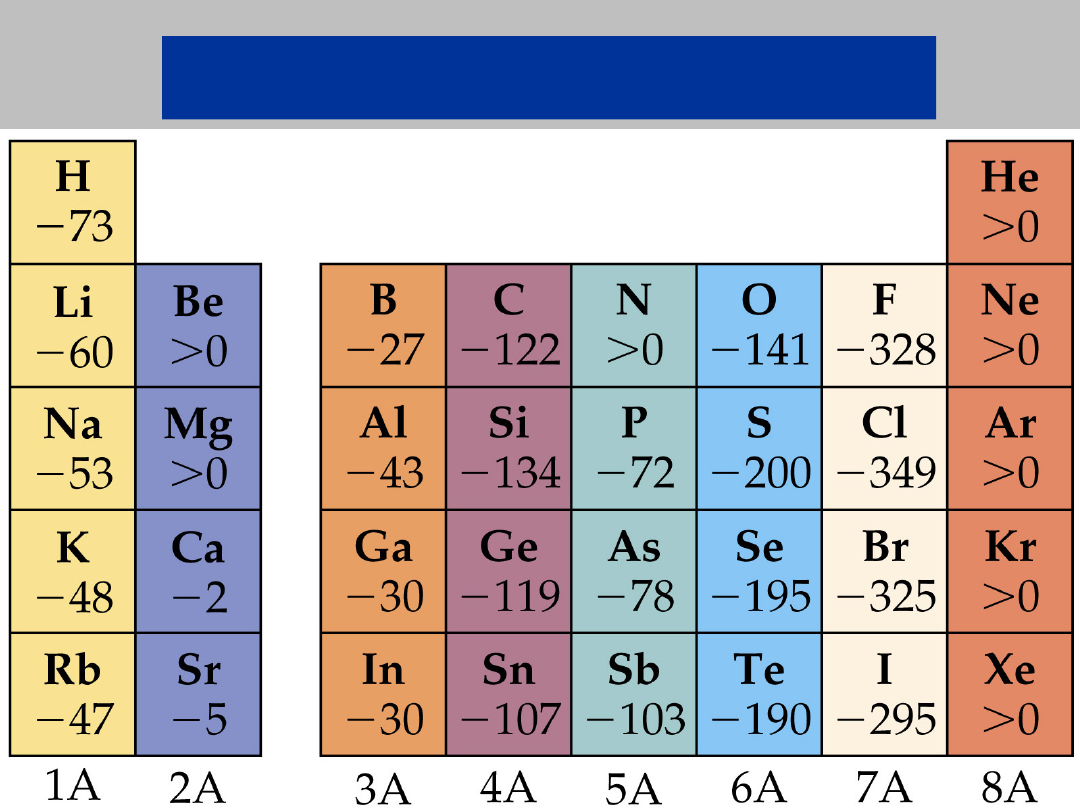
Elektroujemność

• Elektroujemność

jest przeciwna do energii

jonizacji

• Elektroujemność

: zmiana energii gdy atom

przyłącza elektron tworząc jon:

Cl(g) + e

-

 Cl

-

(g)

• Elektroujemność

może być egzo- lub

endoenergetyczna:

Ar(g) + e

-

 Ar

-

(g)

Elektroujemność

Właściwości metali

alkalicznych

Grupa 1: Metale alkaliczne

Group Trends for the Active

Metals

Grupa 2: Metale ziem alkalicznych

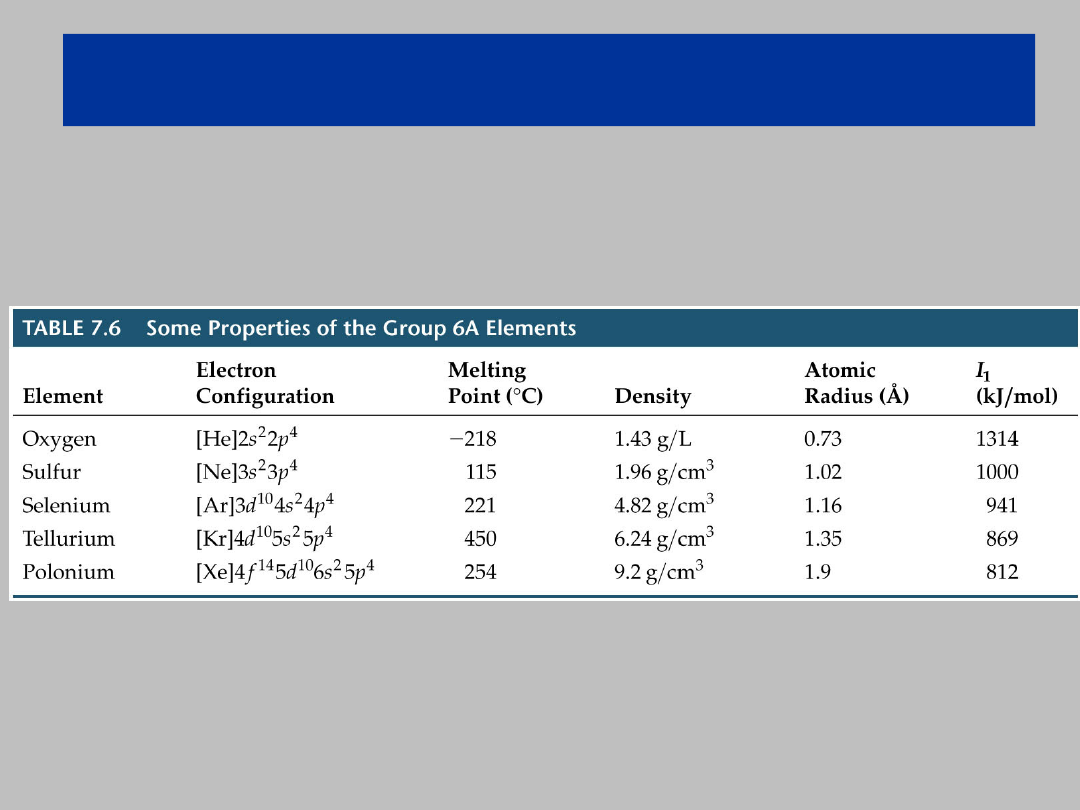
Właściwości wybranych

niemetali

Grupa 16: Tlenowce

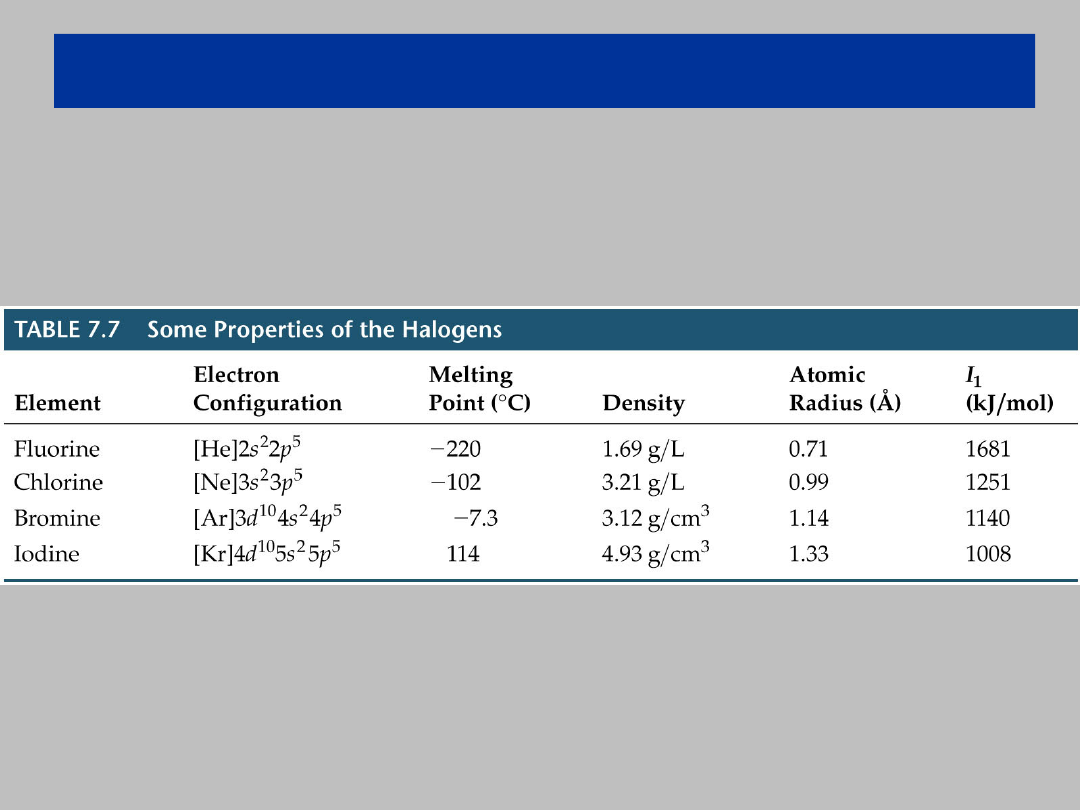
Właściwości niemetali

Grupa 17: Halogenki

Właściwości metali

alkalicznych

Grup 1A: Metale alkaliczne

• Wszystkie metale alkaliczne są miękkie.
• Chemia jest zdeterminowana przez utratę

elektronu s:

M  M

+

+ e

-

• Reaktywność wzrasta gdy przesuwamy się w

dół grupy.

• Metale alkaliczne reagują z wodą tworząc

wodorotlenek MOH i gazowy wodór:

2M(s) + 2H

2

O(l)  2MOH(aq) + H

2

(g)