Badanie dominacji sterowań 

okresowych nad optymalnym 

statycznym procesem 

sterowania

.

Henryk Zelek

2-MPS(s)

Prowadzący: prof. dr hab. inż. O. Petrov

Teoria sterowania

WPROWADZENIE TEORETYCZNE

Definicja stabilności asymptotycznej 

dyskretnego układu sterowania w 

obszarze: 

Punkt równowagi xr = 0 zredukowanego 

układu sterowania

z czasem dyskretnym nazywa sie 

punktem asymptotycznie stabilnym w 

obszarze

D obejmującym ten punkt

Definicja globalnej stabilności 

asymptotycznej dyskretnego 

układu

sterowania: 

Punkt równowagi xr = 0 zredukowanego 

układu sterowania z

czasem dyskretnym nazywa sie punktem 

globalnie asymptotycznie stabilnym,

jeżeli D = Rn

 Definicja lokalnej stabilności 

asymptotycznej dyskretnego układu

sterowania: 

Punkt równowagi xr = 0 zredukowanego 

układu sterowania

nazywa sie punktem lokalnie asymptotycznie 

stabilnym, jeżeli D jest zbiorem

ograniczonym (jeżeli D leży w kuli o 

promieniu ρ).

 

Przykład 1:chemiczny proces produkcyjny prowadzony 

jest w zbiornikowym reaktorze chemicznym w postaci 

reakcji A→B, A→C, gdzie A oznacza surowiec ,B - produkt 

użyteczny, C-produkt uboczny, x[1]-stężenie A w 

reaktorze, x[2]-stężenie B w reaktorze, u[1]-stężenie 

surowca A w strumieniu wejściowym , u[2]-natężenie 

dopływu katalizatora

(dane podstawowe statycznego procesu sterowania)

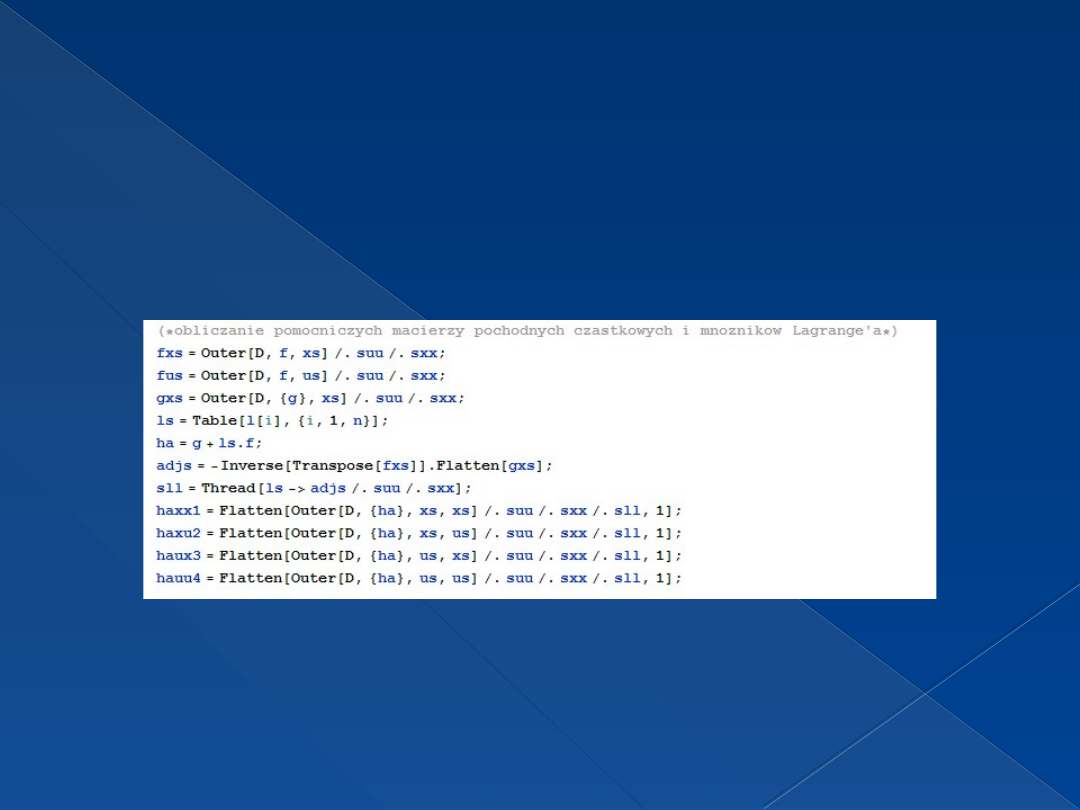
Obliczanie pomocniczych macierzy 

pochodnych cząstkowych i mnożników 

Lagrange’a

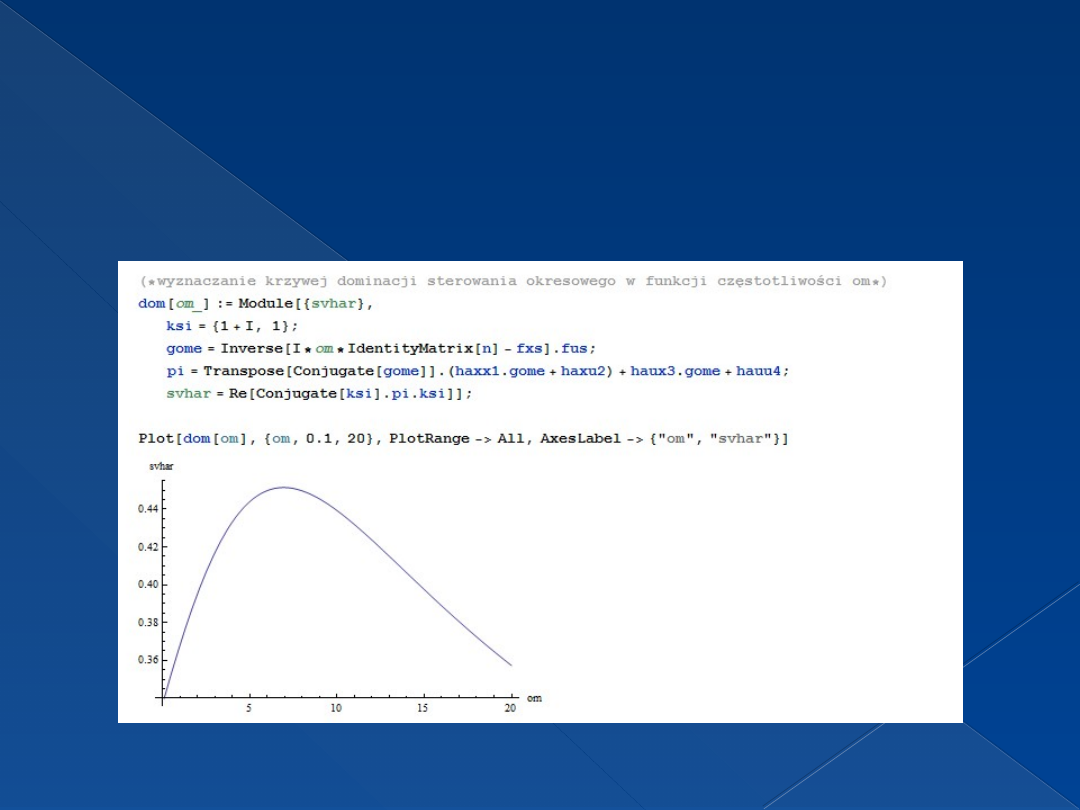
Wyznaczanie krzywej dominacji sterowania 

okresowego w funkcji częstotliwości om

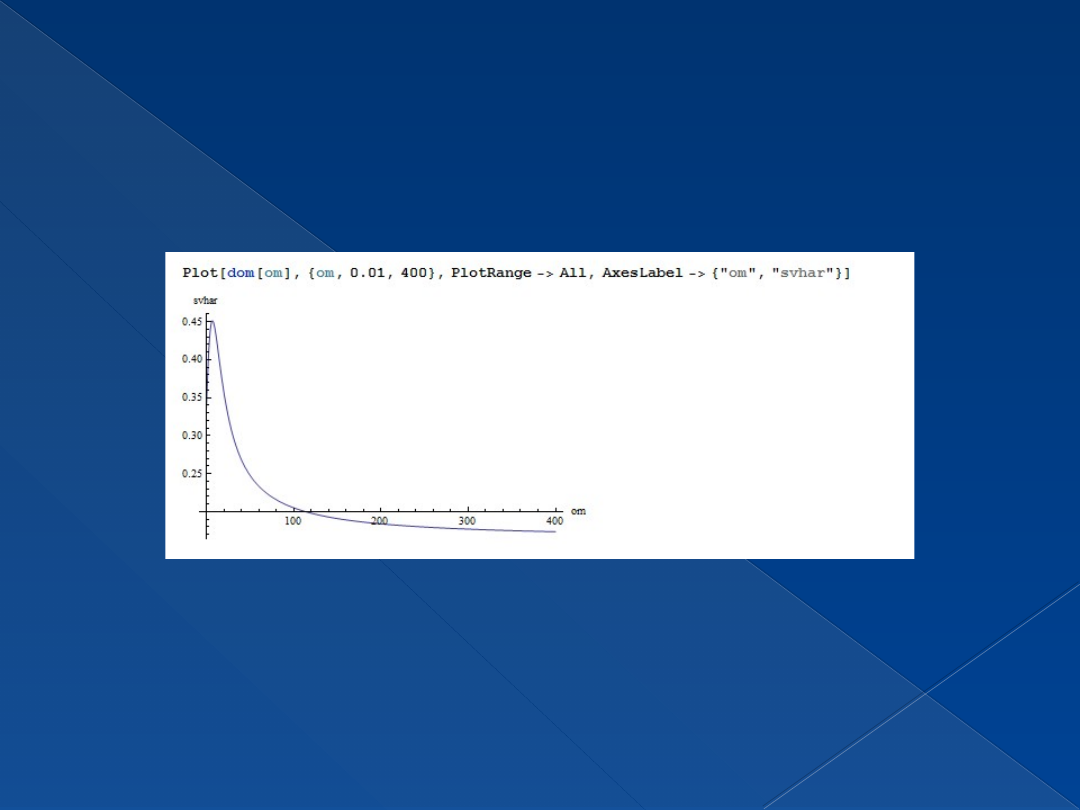
Wyznaczanie krzywej dominacji sterowania 

okresowego w funkcji częstotliwości om

 

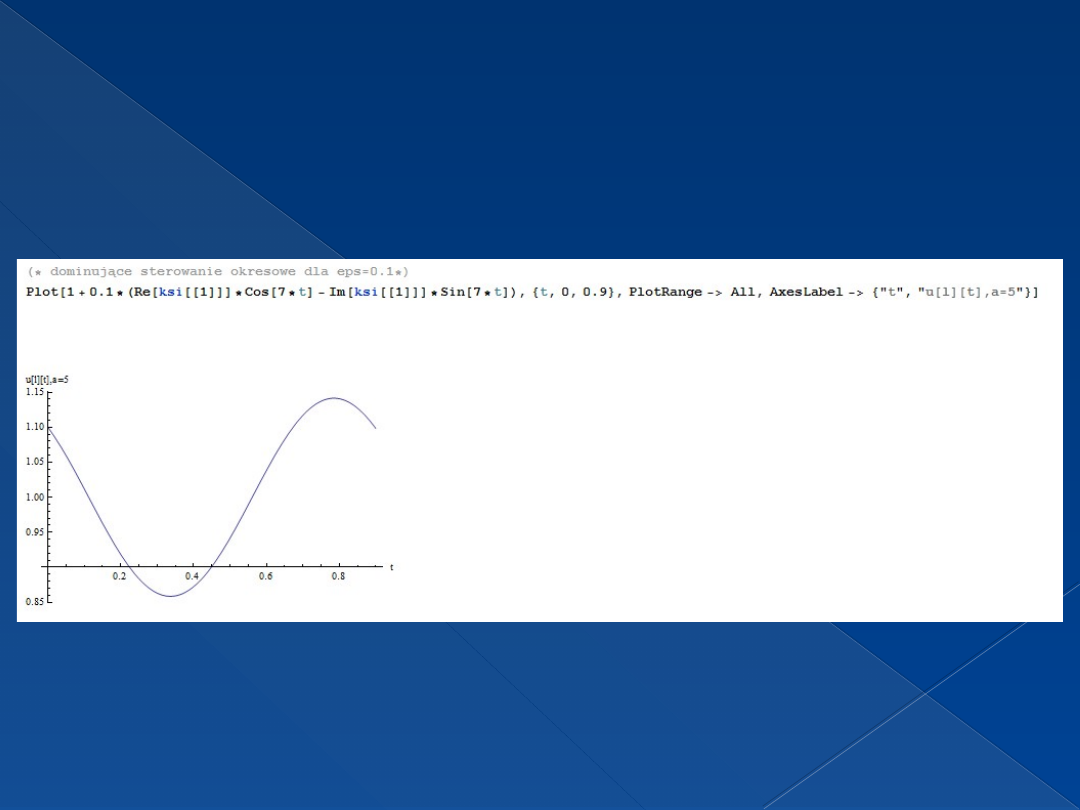
Dominujące sterowanie okresowe dla 

eps=0.1

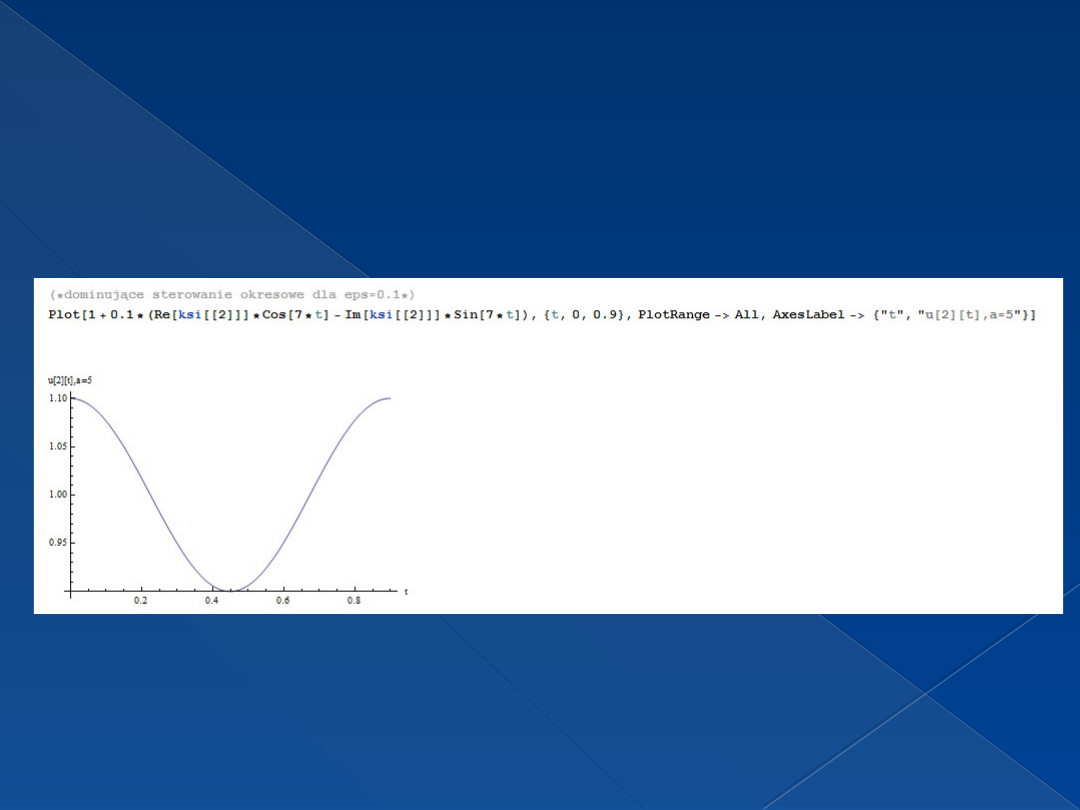
Dominujące sterowanie okresowe dla 

eps=0.1

 

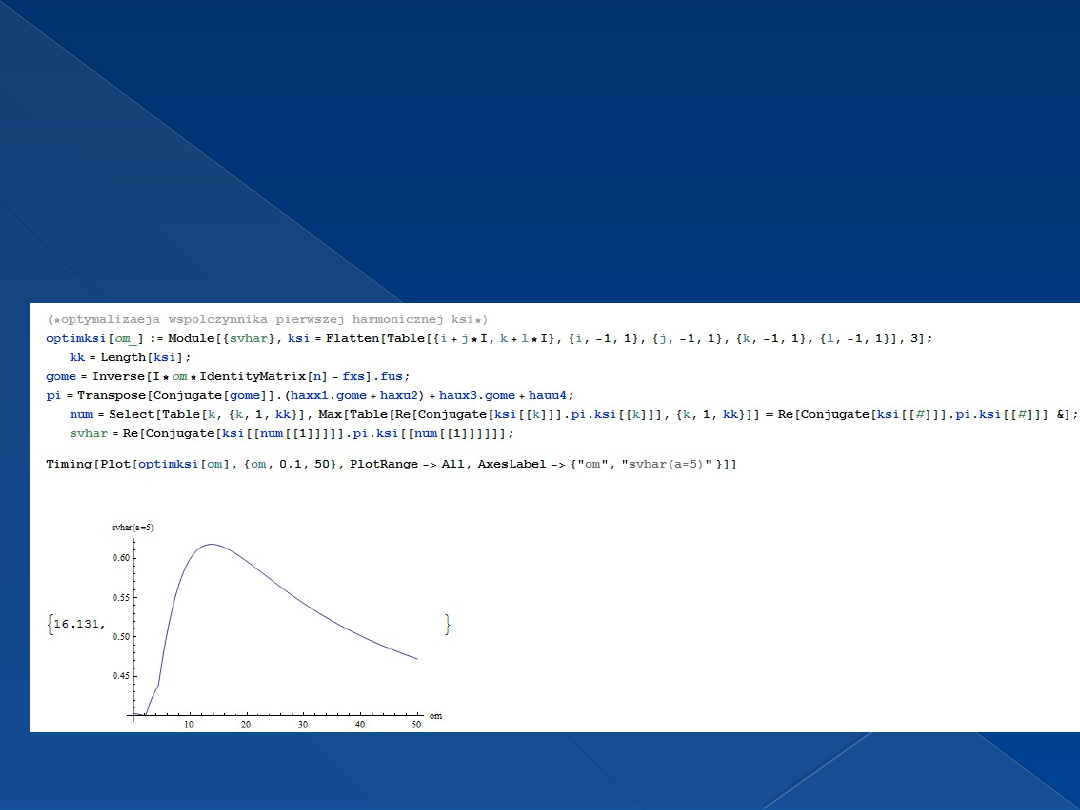
optymalizacja współczynnika 

pierwszej harmonicznej ksi

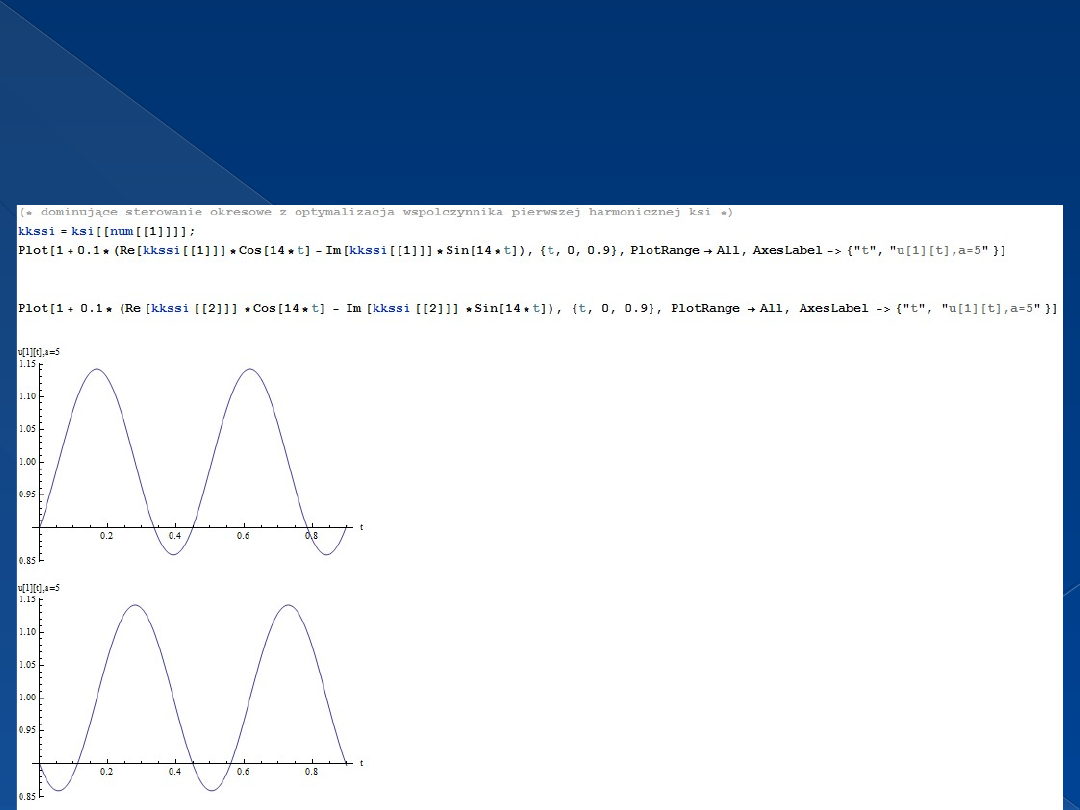
Dominujące sterowanie okresowe z 

optymalizacją współczynnika pierwszej 

harmonicznej ksi

 

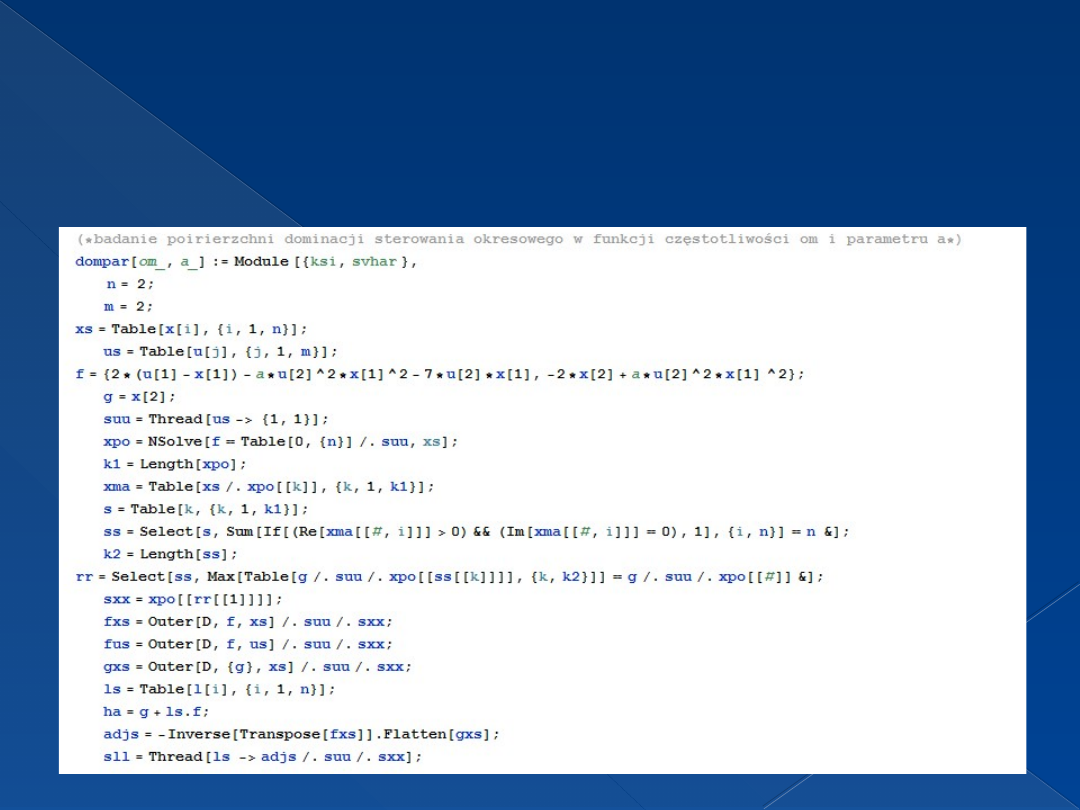
Badanie powierzchni dominacji sterowania 

okresowego w funkcji częstotliwości om i 

parametru a

Badanie powierzchni dominacji sterowania 

okresowego w funkcji częstotliwości om i 

parametru a

Wnioski:



Funkcja ta jest dodatnio określona w 
obszarze D



Różnica pierwszego rzędu tej funkcji 
względem czasu dyskretnego wzdłuż 
dyskretnej trajektorii stanu układu jest 
również dodatnio określona w tym obszarze



W przypadku nieograniczonego obszaru    
D = Rn funkcja ta spalenia warunek 
promieniowej nieograniczoności lim||x||
→+∞ V (x, k) = +∞.