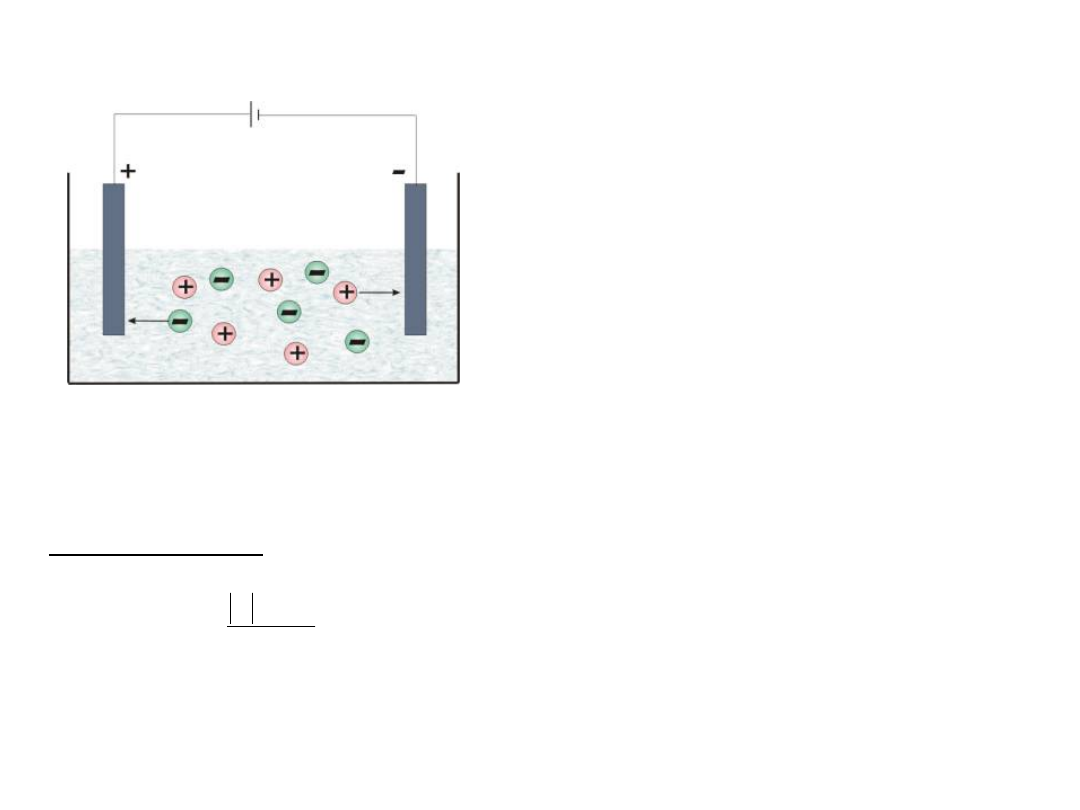
RUCH JONÓW W ROZTWORZE

W roztworze elektrolitu ładunek
elektryczny przenoszony jest
przez jony

Jony w roztworze poruszają się w polu elektrycznym ruchem
jednostajnym w wyniku równowagi między siłą tarcia wewnętrznego a
siłą z jaką działa pole elektryczne na ładunek jonu.

Prędkość jonu w roztworze jest określona przez
przyśpieszającą siłę pola elektrycznego i opóźniającą siłę tarcia
związaną z lepkością roztworu

z

i

e = q -

ładunek
r

i

-

hydrodynamiczny promień jonu
 - lepkość
roztworu

Prędkość wędrowania jonu jest wprost proporcjonalna do
natężenia pola elektrycznego

:

v

i

= u

i

 .

Ruch jonów w polu elektrycznym
zapewnia przewodnictwo
elektrolityczne roztworu.

Jony dodatnie (kationy)
przemieszczają się w kierunku
bieguna ujemnego, natomiast jony
ujemne (aniony) w kierunku bieguna
dodatniego (anody).

i

i

i

r

η

6π

Φ

e

z

v











Ruchliwość (u) jonu

w roztworze jest stałą
proporcjonalności między
prędkością wędrówki (v) tego
jonu i natężeniem pola
elektrycznego  : v

i

= u

i



Φ

v

u

i

i



z

i

e = q - ładunek

r

i

- hydrodynamiczny

promień jonu
 - lepkość roztworu

i

i

i

r

η

6π

e

z

u









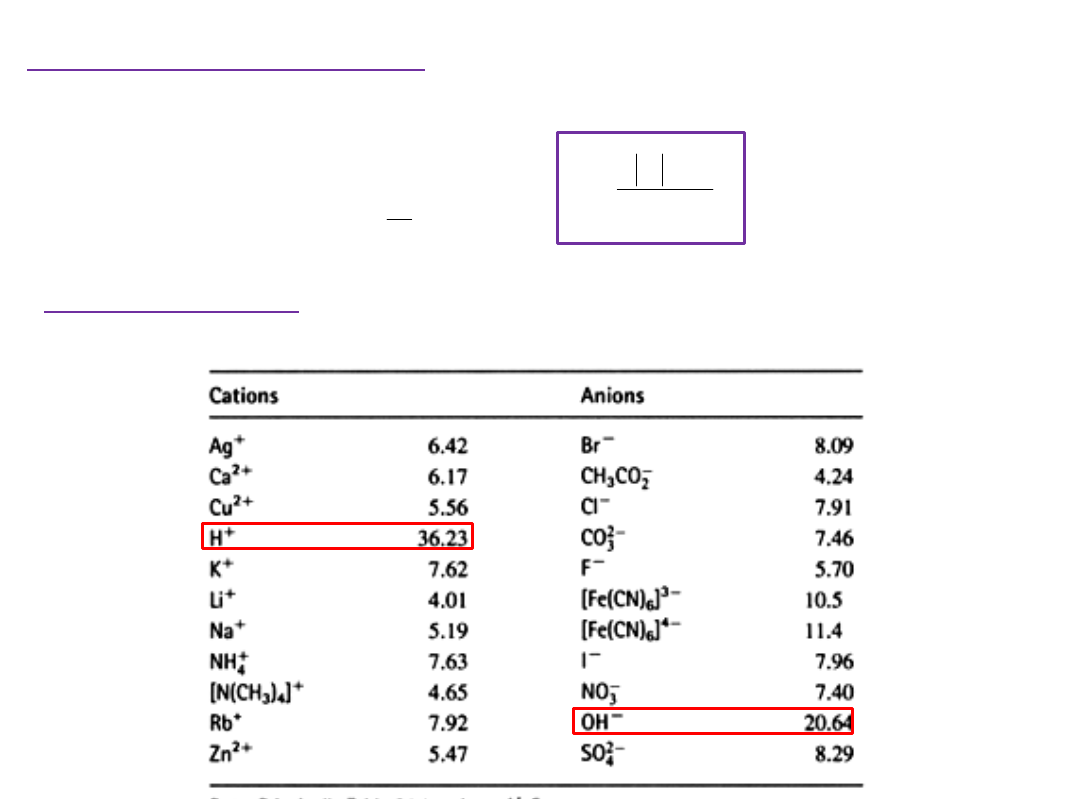
Ruchliwość jonu w roztworze zależy od jego ładunku,
rozmiaru i lepkości roztworu

Ruchliwości jonów u / 10

-8

[ m

2

s

-1

V

-1

] w wodzie w temp. 298 K

Przewodnictwo wody

Mechanizm przewodnictwa protonowego wody jest związany z
przeniesieniem protonu H

+

pomiędzy sąsiednimi cząsteczkami wody.

Liczba cząsteczek wody, z którymi jest związany proton H

+

jest sprawą

dyskusyjną.

Obecnie uwaga skupia się na strukturze
H

9

O

4

+

, w której prawie płaski

jon H

3

O

+

połączony jest z trzema

cząsteczkami H

2

O.

Cząsteczki wody połączone są
wiązaniami wodorowymi,
które ograniczają ich ruchy
rotacyjne.
Klaster H

9

O

4

+

jest również zhydratowany lecz wiązania wodorowe w

drugiej warstwie hydratacyjnej są słabsze .
Przeniesienie protonu zachodzi wówczas, gdy jedna z cząsteczek rotuje do
takiej pozycji, że wiązanie wodorowe może się przegrupować w wiązanie
kowalencyjne.
Czas charakterystyczny dla przeskoku protonu z jednej cząsteczki na
drugą wynosi ok. 1,5 ps. Jest on porównywalny z czasem potrzebnym na
reorientację cząsteczki wody o jeden radian.

Zgodnie z mechanizmem Grotthusa efektywny ruch protonu związany jest
z przegrupowaniem wiązań w szeregu cząsteczek H

2

O.

Przewodzenie w wodzie odbywa się poprzez bardzo szybkie przeskoki
protonu pomiędzy sąsiednimi klasterami.

Molowa przewodność protonów rośnie ze wzrostem ciśnienia, ponieważ
wzrost ciśnienia sprzyja rozrywaniu wiązań wodorowych.

Zdolność roztworu elektrolitu do przewodzenia prądu określa
PRZEWODNICTWO elektryczne roztworu .

Przewodność roztworu , jest odwrotnością jego oporu R

Jednostką przewodności jest 1 S (simens) = 1

-1

Przewodność próbki  maleje wraz z
jej długością l oraz rośnie ze
wzrostem przekroju poprzecznego S

l

S

κ

Γ





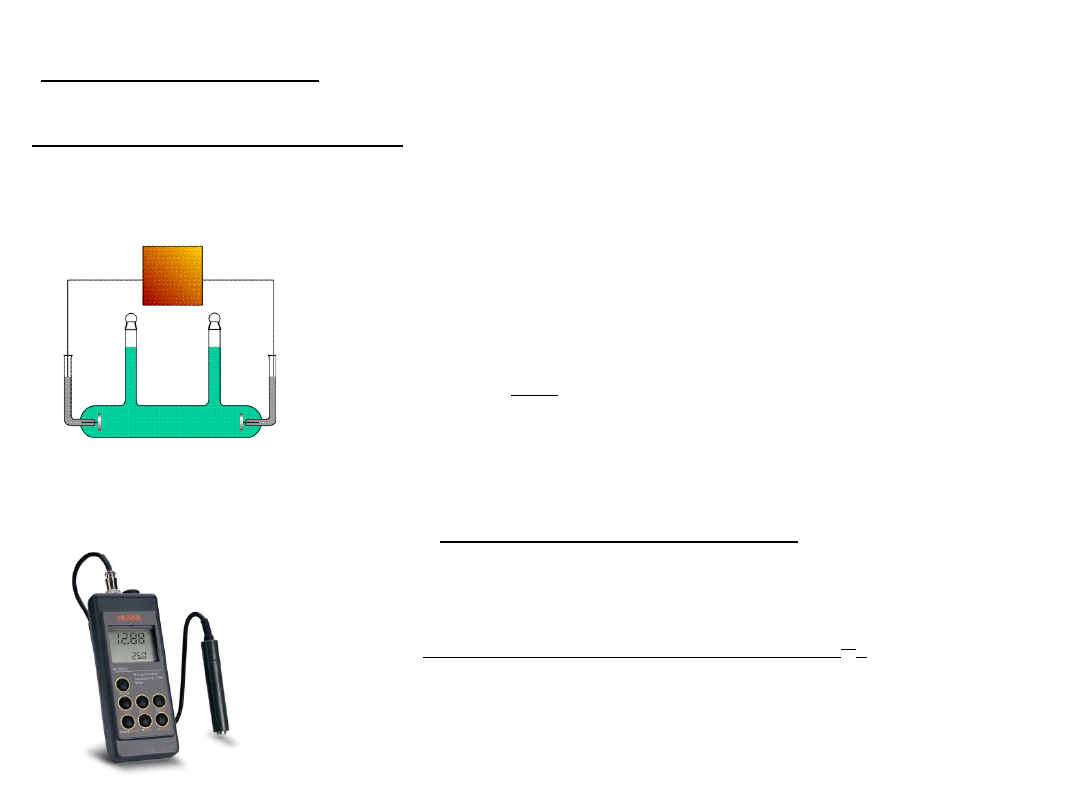
Do pomiaru przewodnictwa
elektrolitu wykorzystuje
się naczyńka
konduktometryczne.

l – odległość między elektrodami
S – powierzchnia efektywna
elektrod
l / S – stała naczyńka
konduktometrycznego

Miarą przewodnictwa elektrolitu jest
przewodnictwo właściwe , które
definiujemy jako zdolność przewodzenia
prądu przez jednostkową objętość
elektrolitu.

 - przewodność właściwa [S m

-1

] to

przewodność elektrolitu zawartego
pomiędzy elektrodami o powierzchni 1m

2

,

oddalonymi od siebie o 1m

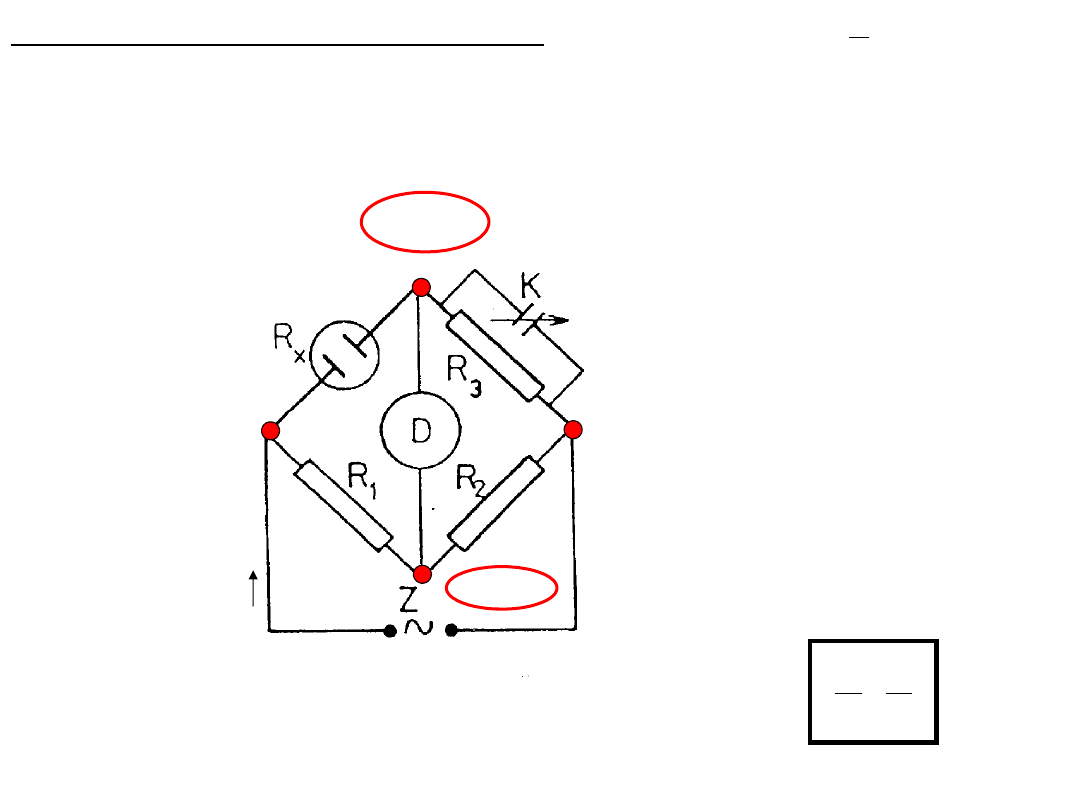
Pomiar przewodnictwa elektrolitu polega na
zmierzeniu jego oporu

Naczyńko konduktometryczne z badanym roztworem umieszcza się w
jednej z gałęzi mostka Wheatstone’a – R

x

.

Opory R

1

, R

2

i R

3

dobiera się tak, aby mostek był w równowadze tzn. aby

detektor D nie wykazywał przepływu prądu i

D

= 0.

2

1

3

x

R

R

R

R



gdy i

D

= 0

i

x

= i

3

oraz i

1

= i

2

U

1

= i

1

R

1

U

2

= i

2

R

2

U

x

= i

x

R

x

U

3

= i

3

R

3

U

D

= i

D

R

D

I

(a)

(b)

(c
)

(d)

I- natężenie prądu

I = i

1

+ i

x

i

x

= i

D

+ i

3

i

3

= i

2

+I

i

1

=i

2

+i

D

U

x

+U

D

+U

1

=0 ⇒ i

x

R

x

= - i

1

R

1

U

3

+U

D

+U

2

=0 ⇒ i

3

R

3

= - i

2

R

2

Kondensator o zmiennej
pojemności równoważący
pojemność naczyńka

Mostek jest zasilany prądem zmiennym o
częstotliwości ~ 1000 Hz Pozwala to uniknąć
zmian stężenia roztworu i polaryzacji elektrod.

R

1

Γ 

Przewodnictwo elektrolitu zależy
od:

 ruchliwości jonów



stężenia roztworu elektrolitu

 temperatury

 rodzaju rozpuszczalnika

i

i

i

r

η

6π

e

z

u









.

Kohlrausch - badał wpływ
stężenia elektrolitu na
przewodnictwo, sformułował
prawo niezależnego ruchu
jonów.

Historia badań ELEKTROLITÓW

Wilhelm Friedrich Ostwald

(1853-1932)

Ostwald - prawo rozcieńczeń:
wyznacza stałe równowagi dysocjacji
poprzez pomiar przewodnictwa

Friedrich Wilhelm Georg Kohlrausch

(1840 –1910)

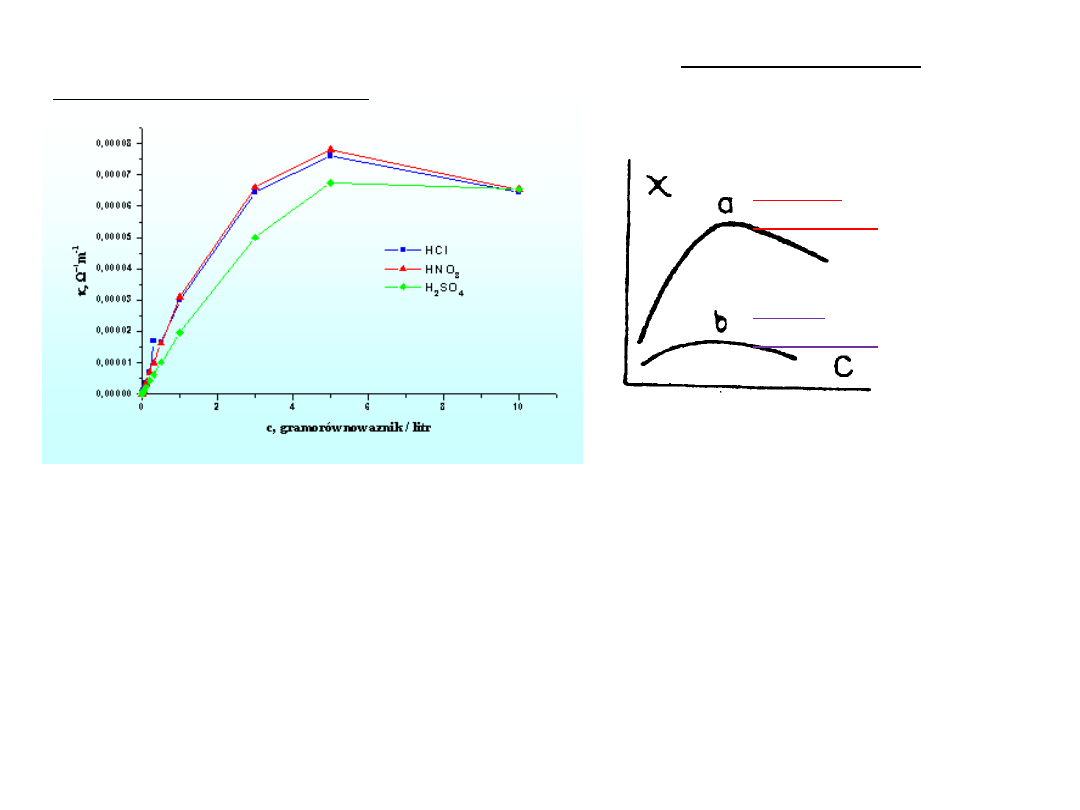
Wpływ stężenia roztworu elektrolitu na przewodnictwo
właściwe elektrolitu

Dla roztworów rozcieńczonych wzrost stężenia powoduje
wzrost przewodnictwa.

W przypadku roztworów stężonych wzajemne oddziaływanie
jonów ogranicza ich ruchliwość i może powodować
zmniejszenie przewodnictwa.

mocny
elektrolit

słaby
elektrolit

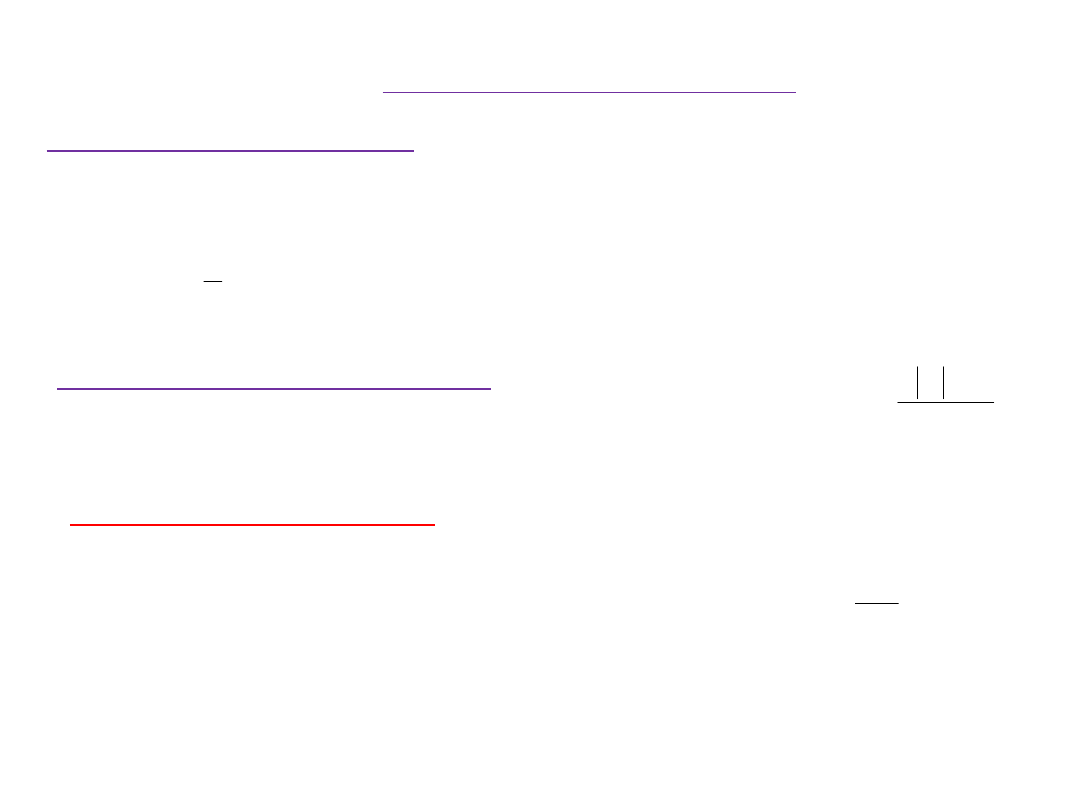
Przewodnictwo molowe zdolność przewodzenia prądu
przez warstwę elektrolitu o grubości jednostkowej zawierającej 1
mol elektrolitu.
(Atkins, Pigoń-Ruziewicz)

c

κ

10

λ

3





c – stężenie molowe [ mol
dm

-3

]

l - przewodność molowa [ S

m

2

mol

-1

]

l - przewodność molowa [ S m

2

mol

-1

] to przewodność 1 mola

ładunków (skrypt E.Hawlicka) zawartego pomiędzy elektrodami o
powierzchni 1 m

2

, oddalonymi od siebie o 1 m.

W celu porównywania przewodnictwa elektrolitów
wprowadzono pojęcie

przewodnictwa molowego

dawniej przewodnictwo równoważnikowe.

Wpływ stężenia elektrolitu na przewodnictwo
molowe badali
Kohlrausch, Debye, Hückle, i Onsager.



i

= F u

i

i

i

i

r

η

6π

e

z

u









Przewodnictwo molowe jonu
jest wprost proporcjonalne do
jego ruchliwości

i

i

i

z

Fu

λ 

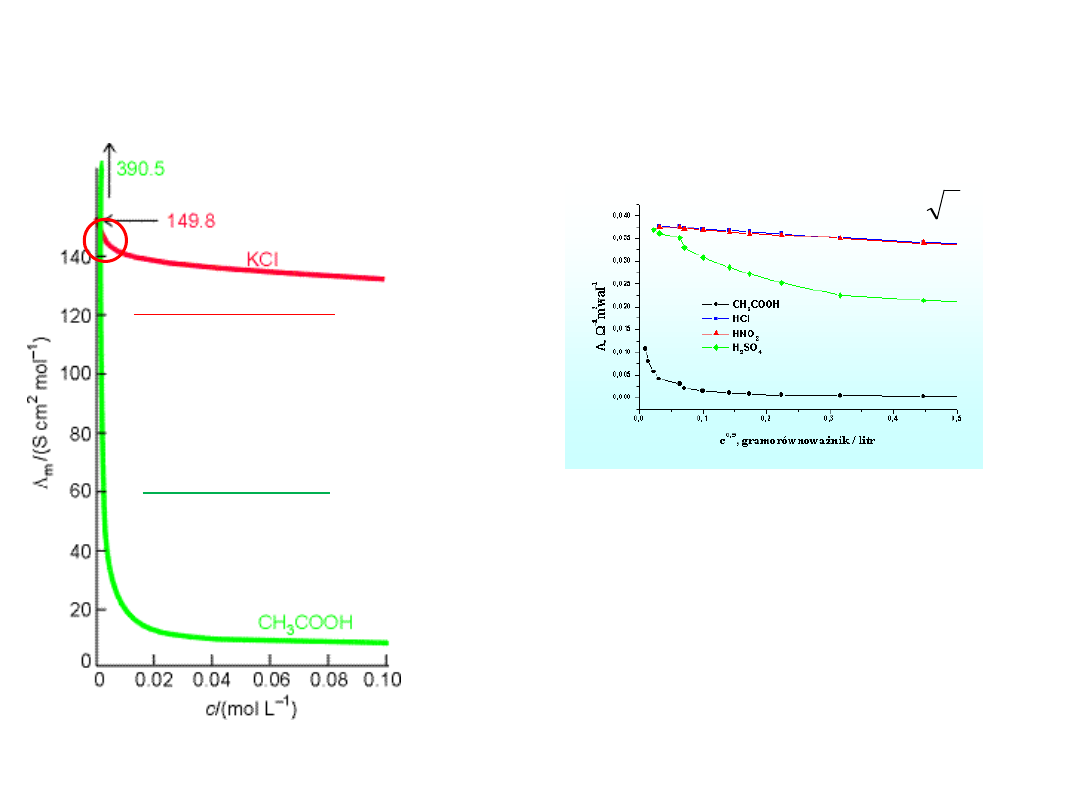
Zależność molowej
przewodności elektrolitu od
jego stężenia

mocny elektrolit

– przewodność molowa
nieznacznie maleje ze
wzrostem stężenia elektrolitu

słaby elektrolit

– wzrost stężenia
elektrolitu powoduje
gwałtowny spadek
przewodności
molowej

przewodnictwo molowe mocnych
elektrolitów (HCl, HNO

3

, H

2

SO

4

)

oraz elektrolitu słabego
(CH

3

COOH )

w funkcji c.

Wpływ stężenia elektrolitu na przewodnictwo molowe

c

a





0





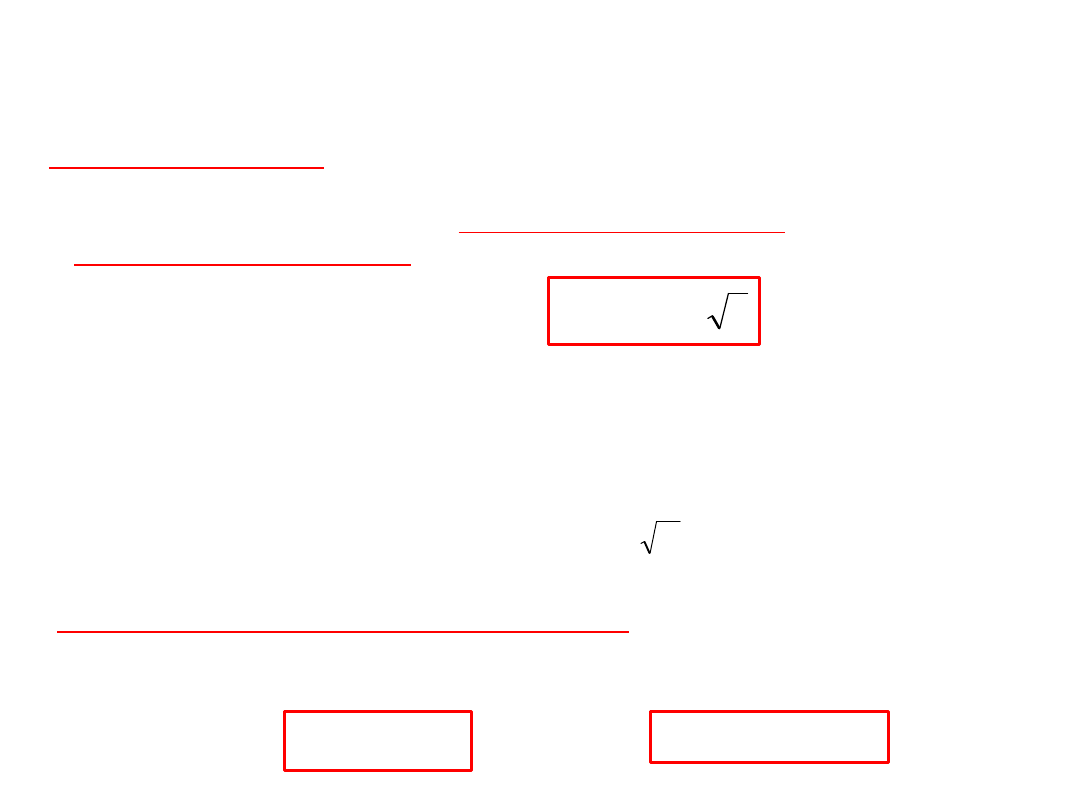
Prawa Kohlrausha

 Przy małych stężeniach przewodność molowa

mocnych elektrolitów zależy od pierwiastka
kwadratowego ze stężenia

c

a





0





Graniczną przewodność molową 

0

dla

elektrolitów mocnych wyznaczamy drogą
ekstrapolacji z wykresu

)

( c

f





Graniczna przewodność molowa
roztworu,
gdy stężenie elektrolitu dąży do
zera.





lim

0

0





c

 Prawo niezależnej wędrówki

jonów:

0

0

0















w roztworze nieskończenie rozcieńczonym jony poruszają się
niezależnie od siebie, a graniczna przewodność molowa jest
sumą granicznej przewodności molowej kationów i anionów.

F

)

u

u

(

o













0

0

Wpływ stężenia

mocnego elektrolitu

na przewodnictwo molowe

W

elektrolitach mocnych

wzrost stężenia elektrolitu powoduje

obniżenie przewodności molowej roztworu w wyniku wzrostu
oddziaływań między jonami .

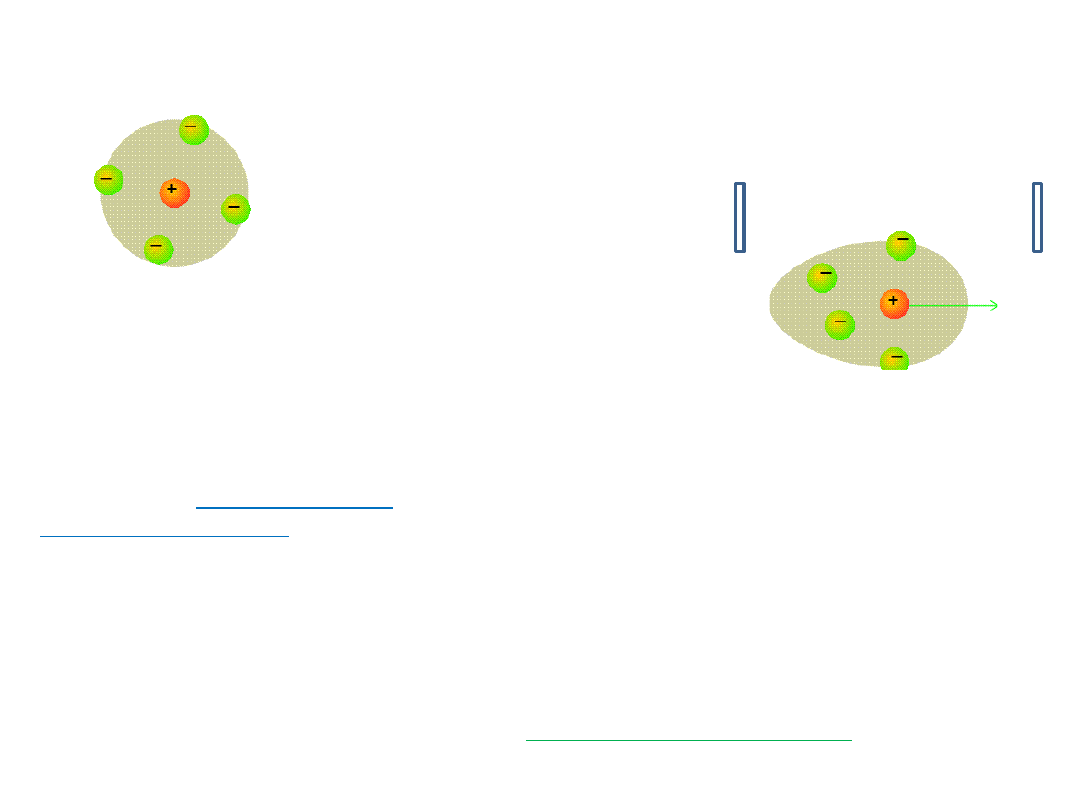
W nieobecności pola
elektrycznego chmura jonowa
ma symetrię kulistą.

Jeżeli jon ⊕ przesunie się z jednego położenia w drugie to musi upłynąć
jakiś czas -

czas relaksacji

- aby chmura jonowa mogła się odbudować.

Efekt relaksacyjny

zależy od grubości chmury jonowej i

ruchliwości jonów

tworzących

chmurę jonową.

Jon centralny i jego chmura jonowa poruszają się w przeciwnych
kierunkach, dlatego w roztworze pojawia się zjawisko „lepkiego oporu”,
co opóźnia ruch jonów- jest to tzw.

efekt elektroforetyczny

Efekt ten zależy od promienia poruszającej się „kuli” oraz od

lepkości

ośrodka

.

• EFEKT

relaksacyjny

Pole elektryczne deformuje chmurę jonową, bo
jon centralny i jego chmura jonowa maja
przeciwne ładunki.

• EFEKT

elektroforetyczny

+

-

Elektrolity mocne

teoria Debye’a – Hückle’a –
Onsagera

uwzględnia wpływ efektów elektroforetycznego i
relaksacyjnego na przewodnictwo elektrolitów i
podaje zależność przewodności molowej
elektrolitu od siły jonowej roztworu

.





I

B

A

0

0













Stałe A i B są zależne od
temperatury i właściwości
rozpuszczalnika takich jak
lepkość  i stała dielektryczna
.

dla I <
0,01

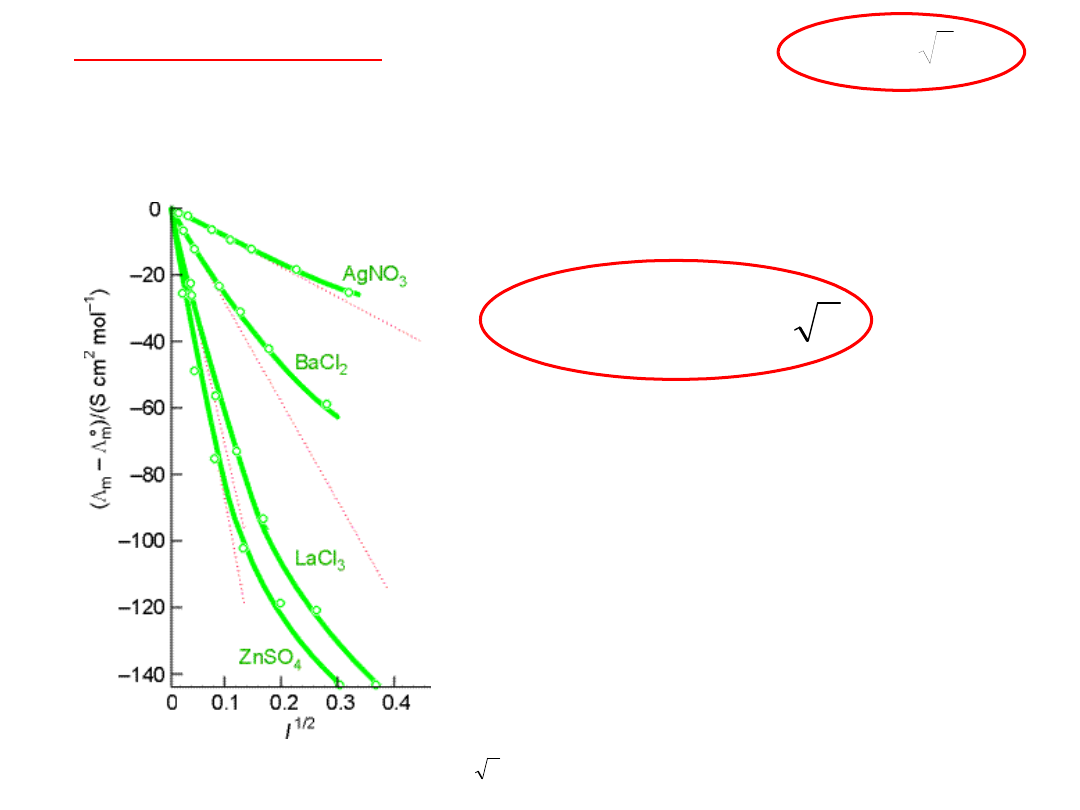
Zależność przewodności molowej  = f ( ) od pierwiastka z mocy
jonowej roztworu

I

c

a









0

Elektrolity słabe

Przewodność molową elektrolitów słabych można opisać
zależnością wyprowadzoną w oparciu o model D – H – O z
uwzględnieniem stopnia dysocjacji elektrolitu

0

λ

λ

α 

Przewodność elektrolitu zależy od liczby jonów
obecnych w roztworze, a więc od stopnia
dysocjacji elektrolitu 









c

α

Bλ

A

λ

α

λ

0

0









c – stężenie elektrolitu

Stałą równowagi dysocjacji kwasu HA o
stężeniu molowym c można wyrazić przez
przewodność molową kwasu





























0

0

2

2

1

c

c

K

a

 

2

0

0

1

1









a

K

c







Prawo rozcieńczeń Ostwalda

HA  H

+

+ A



c

c

c

c

]

HA

[

]

A

[

]

H

[

K























0

dla elektrolitów słabych

można obliczyć w oparciu o prawo niezależnej wędrówki jonów
z granicznych przewodności elektrolitów mocnych.

0

0

0

0

0

0

0

0

0

3

0

0

0

3

3

3

3

3

























































Cl

H

HCl

Cl

Na

NaCl

COO

CH

Na

COONa

CH

COO

CH

H

COOH

CH

HCl

NaCl

COONa

CH

COOH

CH

0

0

0

0

0

0

0

0

0

0

3

3

3



















































H

Cl

Cl

Na

Na

COO

CH

HCl

NaCl

COONa

CH

COOH

CH

0

0

0















LICZBA PRZENOSZENIA

JONU

Ładunek Q w roztworze elektrolitu jest przenoszony przez dwa rodzaje
jonów :
przez kationy ⊕ i aniony ⊖.
Wielkość ładunku przeniesionego przez każdy rodzaj jonów : kationy q

+

, i

aniony q

-

, zależy od właściwości jonów i od ich ruchliwości.

Liczbą przenoszenia jonu, t

jon

, nazywany jest stosunek ładunku

przeniesionego przez dany rodzaj jonów q

jon

do całkowitego ładunku Q =

q

jon

, który przepłynął przez roztwór podczas elektrolizy.

Dla roztworu zawierającego jeden elektrolit :

































q

q

q

Q

q

t

q

q

q

Q

q

t

i

Wielkość ładunku przeniesiona przez jeden rodzaj jonów q

jon

jest

proporcjonalna do ruchliwości tych jonów u

jon

, a liczbę przenoszenia t

jon

można zdefiniować jako:

























u

u

u

t

u

u

u

t

i

Wykorzystując zależność pomiędzy przewodnictwem molowym jonu 

jon

i ruchliwością jonu 

i

= F u

i

liczbę przenoszenia jonu można

przedstawić jako stosunek przewodności molowej jonu do przewodności
molowej elektrolitu :





































t

t

i

Transport ładunków w roztworze elektrolitu

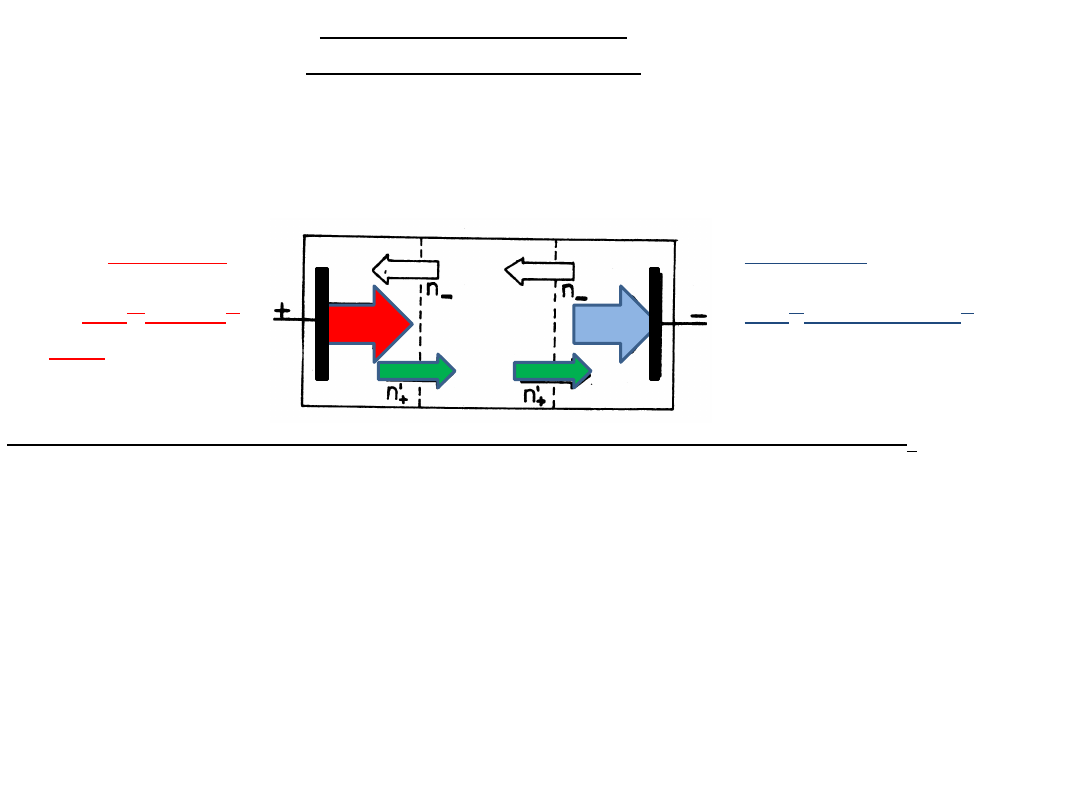
Wyznaczanie liczb

przenoszenia jonów

Podczas elektrolizy,

w wyniku wędrówki jonów

i

reakcji elektrodowych

, następuje zmiana

stężenia elektrolitu: początkowo w pobliżu elektrod, potem w całej
objętości roztworu.

Do wyznaczenia liczby przenoszenia wykorzystuje się

zmiany składu

roztworu

, które powstają

w przestrzeniach przy elektrodach

podczas

przepływu ładunku przez roztwór.

Liczba moli Ag

+

(n

+

) jest proporcjonalna do całkowitego ładunku Q, który

przepłynął przez roztwór.

n

+

= k· Q

(I prawo Faraday’a; k równoważnik elektrochemiczny

Ag)

W roztworze AgNO

3

ładunek jest przenoszony przez Ag

+

i NO

3

-

, które mają

różną ruchliwość.

Do przestrzeni przy kat.⊖ wpływa liczba moli Ag

+

(n

+

’

) proporcjonalna do

ładunku przenoszonego przez jony dodatnie q

+

:

n

+

’

=k· q

+

Stężenie jonów Ag

+

w przestrzeni przy katodzie zmienia się o wartość

 n = n

+

- n

+

’ =k Q – k q

+

= k (Q – q

+

) = k q

-

Zmiana stężenia Ag

+

przy katodzie jest proporcjonalna do ładunku

przeniesionego przez aniony

.

⊖ KATODA :

Ag

+

+ e → Ag

0

osadza się n

+

moli

Ag:

ANODA ⊕:

Ag

0

→ Ag

+

+ e

n

+

moli Ag

przechodzi do
roztworu

Elektrolizer zawierający elektrody Ag napełniony roztworem AgNO

3

.

n

+

n

+

+

-

+

+

-

C u S O

4

m A

3

2

-

+

1

k a to d a

a n o d a

A g N O

3

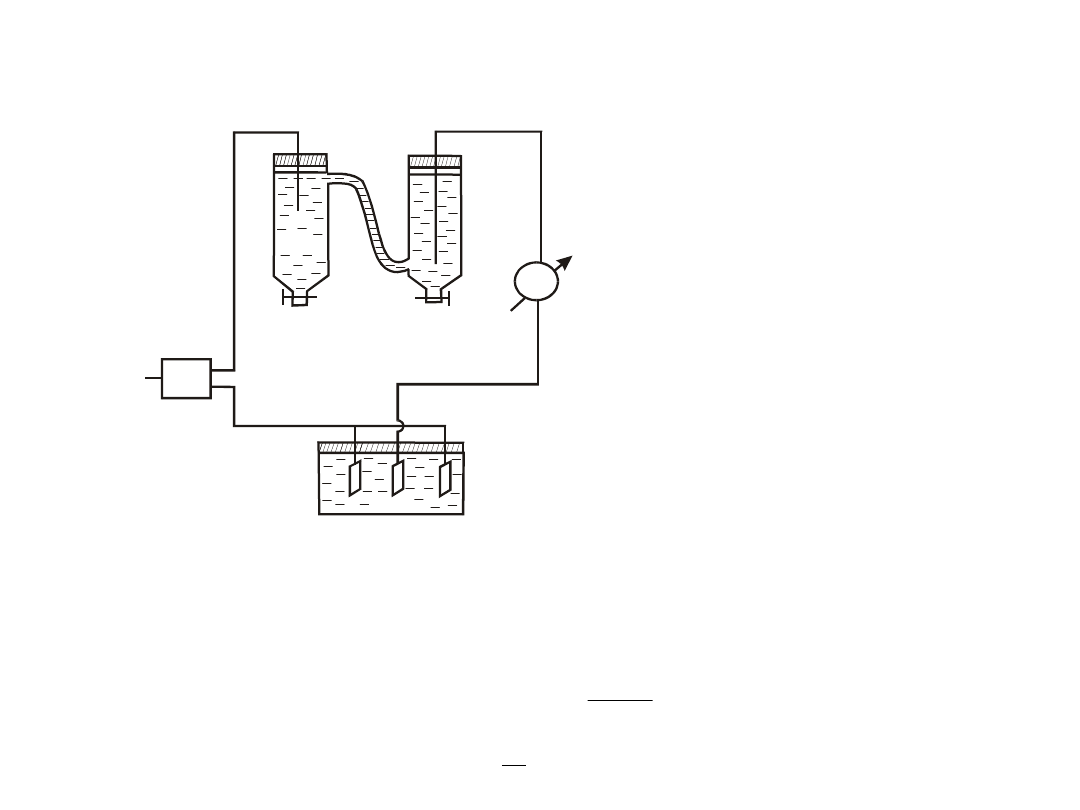
Do zmierzenia całkowitego
ładunku Q służy kulometr
miedziowy (2)

Budowa aparatu Hittorfa (1)
uniemożliwia wymieszanie się
roztworów z przestrzeni przy
elektrodach i pozwala na
swobodny przepływ jonów.

polega na elektrolizie badanego roztworu w aparacie Hittorfa

Wyznaczanie liczb przenoszenia metodą Hittorfa

układ
zasilany
jest
prądem
stałym ze
źródła (3).

Przez badany roztwór, o znanym stężeniu wyjściowym, podczas elektrolizy
przepływa ładunek Q, który mierzy się w połączonym szeregowo
kulometrze.
Po zakończeniu elektrolizy oznacza się ilościowo stężenie elektrolitu w
przestrzeni katodowej.
Z różnicy stężeń wyznacza się ubytek masy srebra w przestrzeni przy
katodzie  m

Ag

.

Ładunek przeniesiony przez aniony wynosi:

F

M

Δm

q

Ag

Ag







więc liczba przenoszenia anionu , a kationu t

+

= 1 – t

-

Q

q

t







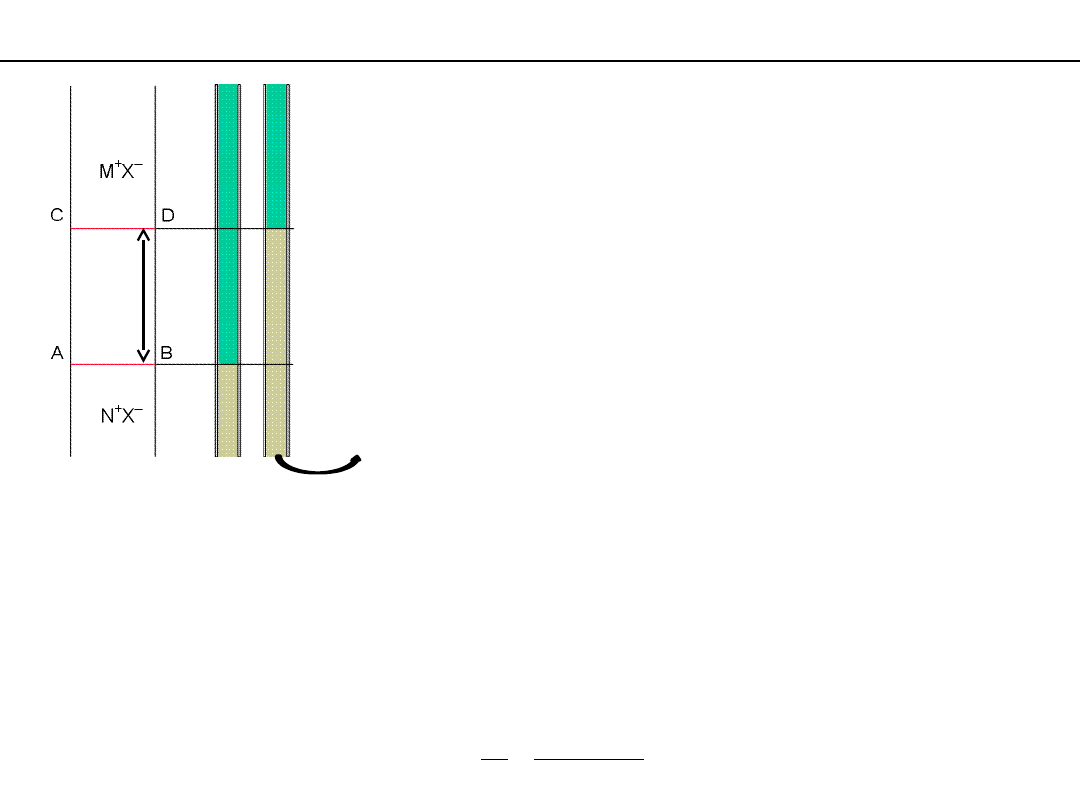
Wyznaczanie liczb przenoszenia jonów metodą ruchomej granicy

w czasie przepływu prądu obserwuje się ruch
granicy pomiędzy dwoma roztworami jonowymi
zawierającymi wspólny jon

Roztwór NX – roztwór wskaźnikowy –

o

gęstości większej

od

roztworu MX – roztworu

wznoszącego

-

znajduje się w dolnej części

pionowego elektrolizera

o polu przekroju S.

Oba roztwory tworzą wyraźną powierzchnię
graniczną.

Ruchliwość jonu M

+

musi być większa od

ruchliwości jonu N

+

.

Granica przesunęła się od AB do CD gdy prąd o natężeniu i przepłynął
przez roztwór w czasie t.
W tym czasie wszystkie jony

M

+

znajdujące się w objętości (S ‧ l)

musiały przejść przez przekrój CD.

Ich liczba wynosi c (stężenie) ‧ S ‧ l ‧ N

A

,

a przeniesiony przez nie ładunek to

q

+

= z

+

‧ e‧ c‧ S‧ l ‧N

A

= z

+

‧ c‧

S‧ l ‧F

Całkowity ładunek jaki przepłynął przez roztwór w tym czasie to

Q = i

t

Liczba przenoszenia jonu M

+

wynosi

Δt

i

F

l

S

c

z

Q

q

t



















S –

przekrój poprzeczny elektrolizera

l

czas

0

t

Zastosowanie pomiarów przewodnictwa

 Miareczkowanie konduktometryczne – oznaczenia

stężenia dowolnych jonów w roztworze, podstawę
stanowią różnice ruchliwości a tym samym
przewodnictwa jonów.

Miareczkowanie kwasów zasadami

Miareczkowanie strąceniowe

 wyznaczenia stałej dysocjacji słabego kwasu

 określania rozpuszczalności trudno rozpuszczalnych

elektrolitów

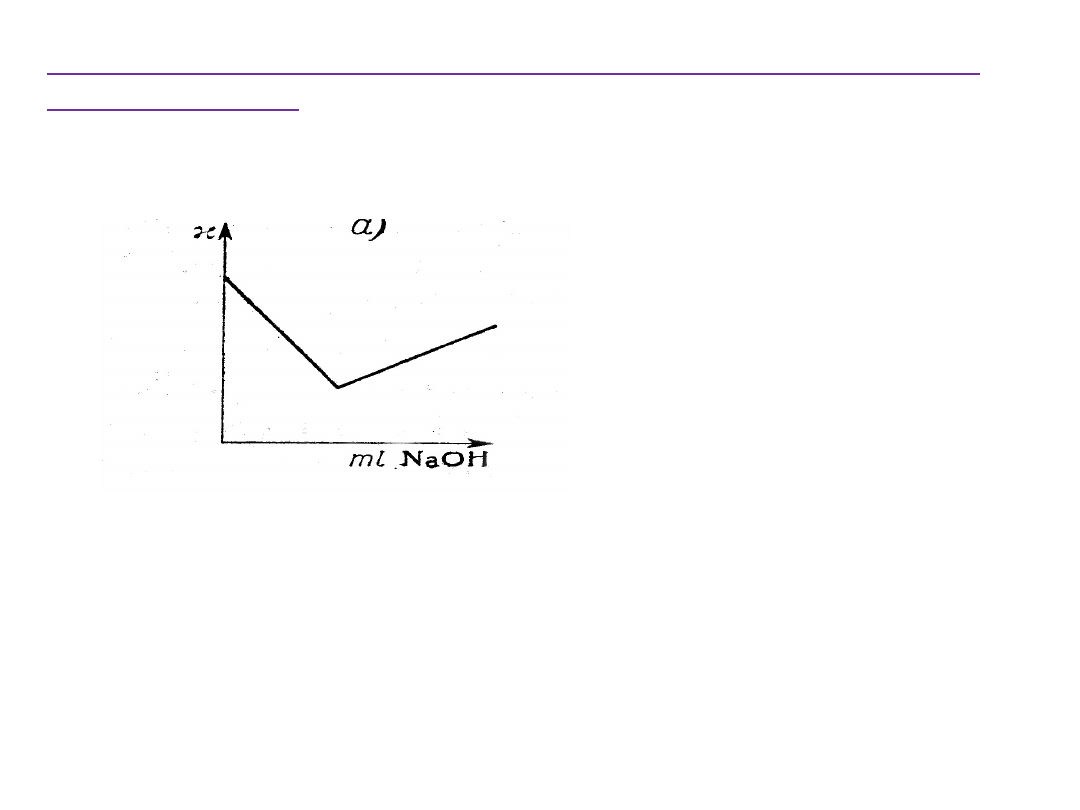
Miareczkowanie konduktometryczne mocnych kwasów
mocną zasadą:

Dodanie niewielkich porcji zasady powoduje znaczne zmiany przewodnictwa.

Przed osiągnięciem punktu równoważnikowego przewodnictwo roztworu
spada bo:
• bardzo ruchliwe jony H

+

,( 

298K

= 34,96 mS m

2

mol

-1

) są zastępowane przez

jony Na

+

, o znacznie mniejszym przewodnictwie molowym

• roztwór miareczkowany ulega rozcieńczeniu, gdyż zwiększa się jego

objętość.

Po przekroczeniu punktu równoważnikowego miareczkowania
przewodnictwo wzrasta, gdyż wzrasta całkowita liczba jonów w roztworze,
w tym jonów OH

-

( 

298K

= 19,91

mS m

2

mol

-1

.)



























































OH

O

H

Cl

2Na

O

H

Cl

Na

Cl

H

2

OH

Na

2

OH

Na

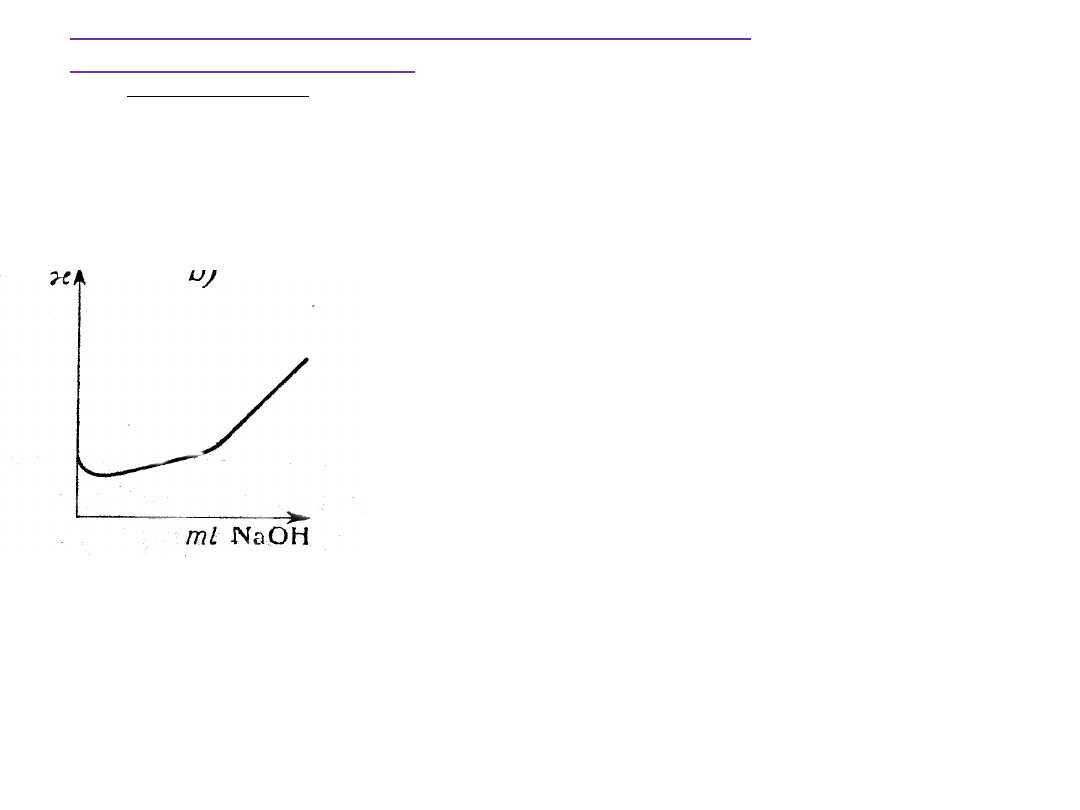
Miareczkowanie konduktometryczne słabych
kwasów mocną zasadą

























































OH

O

H

COO

CH

2Na

O

H

COO

CH

Na

H

COO

CH

2

3

OH

Na

2

3

OH

Na

-

3

Na początku miareczkowania nieznaczne obniżenie przewodnictwa
spowodowane jest zmniejszeniem stopnia dysocjacji kwasu octowego.
Przesunięcie stanu równowagi dysocjacji wynika z obecności wspólnego
jonu, CH

3

COO

-

, pochodzącego z tworzącego się w czasie miareczkowania

octanu sodu.

Po osiągnięciu punktu równoważnikowego () następuje silny wzrost
przewodnictwa wskutek wzrostu stężenia ruchliwych jonów OH

-

.

COOH]

[CH

]

COO

[CH

]

[H

K

3

3









Przewodnictwo roztworu słabego kwasu jest
małe, bo stężenie jonów, wynikające ze
stopnia dysocjacji kwasu jest małe.

Po niewielkim obniżeniu przewodnictwa
następuje wyraźny, stopniowy wzrost
spowodowany tym, że słabo zdysocjowany
CH

3

COOH jest zastępowany całkowicie

zdysocjowaną solą CH

3

COONa



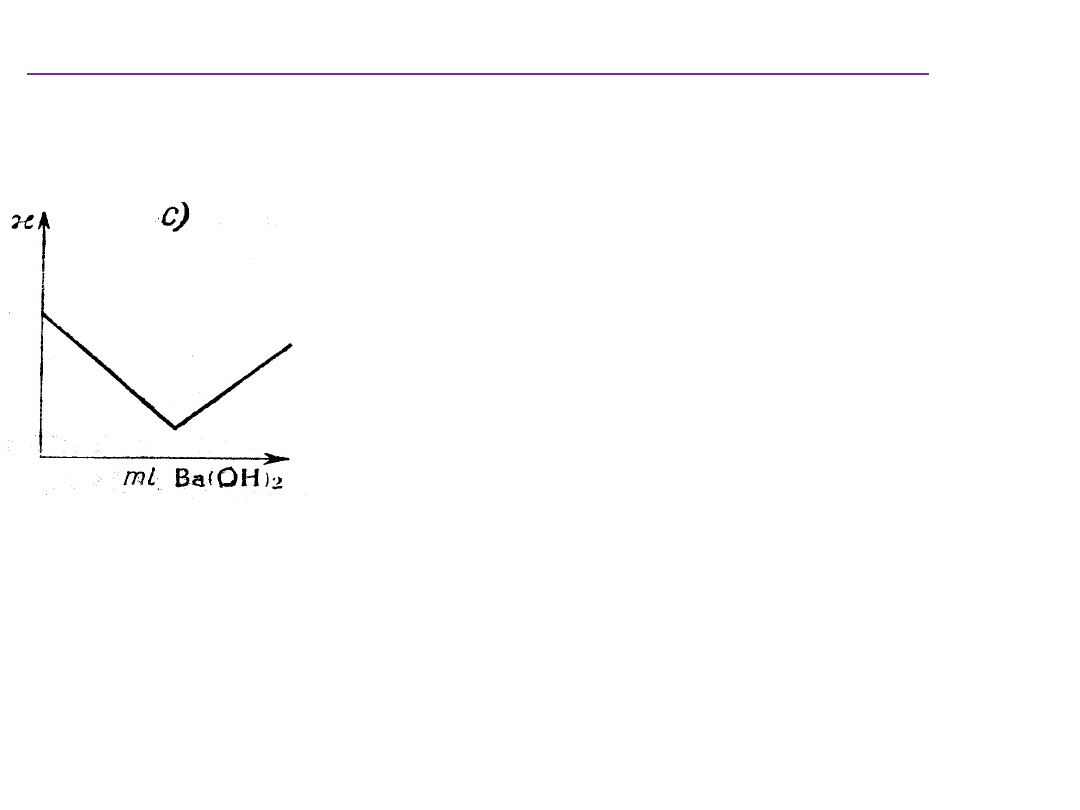
Miareczkowanie strąceniowe
oznaczenia stężenia dowolnych jonów w roztworze

.

Np.: miareczkowanie strąceniowe roztworu MgSO

4

roztworem Ba(OH)

2























































2OH

Ba

(s)

BaSO

2OH

Mg

(s)

BaSO

2OH

Mg

SO

Mg

2

4

2

Ba(OH)

4

2

Ba(OH)

2

4

2

2

2

Przewodnictwo roztworu maleje wskutek wytrącania się soli i ubywania z
roztworu jonu SO

4

2-

(

0

-

= 8,0 mS m

2

mol

-1

)

Ba

2+

( 

0

+

= 6,36 mS m

2

mol

-1

), Mg

2+

(

0

+

= 5,30 mS m

2

mol

-1

)

Jednocześnie roztwór zwiększa swoja objętość, co powoduje zmniejszenie
stężenia jonów.

Po przekroczeniu punktu równoważnikowego zwiększa się całkowita liczba
jonów w roztworze i przewodnictwo wzrasta.

W wyniku miareczkowania roztworu MgSO

4

wodorotlenkiem baru wytrąca się trudno
rozpuszczalna sól BaSO

4

.

 wyznaczanie stałej dysocjacji słabego kwasu

CH

3

COOH ⇆ H

+

+ CH

3

COO

-





























0

0

2

2

1

c

c

K

a

0

0

0

λ

λ

λ









]

mol

m

S

[

c

1

2

3

10













Mierzymy przewodność właściwą  roztworu słabego kwasu o
stężeniu c (mol dm

-3

).

Molową przewodność obliczamy ze wzoru

Graniczne przewodności molowe dla wybranych jonów
znajdujemy w tablicach

]

[

]

[

]

[

3

3

COOH

CH

COO

CH

H

K

a









W roztworze słabego kwasu stężenie jonów jest małe więc przyjmujemy,
że przewodność molowa słabego kwasu  jest równa granicznej
przewodności molowej 

0

Zadanie
Roztwór kwasu propionowego o stężeniu 0,015 mol dm

-3

ma

przewodnictwo właściwe równe 1,74 x 10

-2

S m

-1

, a jego

graniczne przewodnictwo molowe wynosi 385,6 x 10

-4

S m

2

mol

-1

.

Obliczyć stopień i stałą dysocjacji kwasu.

= 10

-3

/c = 1,160 x 10

-3

Sm

2

mol

-1

 = /

0

=0,03=3%





λ

λ

λ

c

λ

α

1

c

α

K

0

0

2

2

a













C

3

H

7

COOH ⇆ H

+

+ C

3

H

7

COO

-

 określenie rozpuszczalności trudno rozpuszczalnych elektrolitów

Roztwór trudno rozpuszczalnej soli można uważać za
nieskończenie rozcieńczony i przyjąć, że

c

κ

10

λ

3





0

0

0

λ

λ

λ

λ











rozpuszczalność [moldm

-3

]

trudno rozpuszczalnego
elektrolitu

0

0

3

λ

λ

κ

10

c













Mierzymy przewodność właściwą  nasyconego roztworu trudno
rozpuszczalnej soli

Graniczne przewodności molowe dla wybranych jonów znajdujemy w tablicach

Z wzoru obliczamy stężenie c elektrolitu w roztworze

λ

κ

10

c

3







Zadanie

W temperaturze 25

0

C przewodność właściwa nasyconego

roztworu Ag

2

CrO

4

wynosi

3,112 x 10

-3

Sm

-1

, a wody, z której sporządzono roztwór 1,2 x 10

-4

Sm

-1

.

Obliczyć iloczyn rozpuszczalności Ag

2

CrO

4

Graniczne przewodności molowe jonów wynoszą odpowiednio:


0

(Ag

+

)= 61,9 x 10

-4

Sm

2

mol

-1



0

( ½ CrO

4

2-

) = 83 x 10

-4

Sm

2

mol

-1

Przewodnictwo roztworu = przewodnictwo elektrolitu + przewodnictwo rozpuszczalnika



r-ru

= (Ag

2

CrO

4

) + (H

2

O)

(Ag

2

CrO

4

) = 

r-ru

- (H

2

O) = (3,112 x 10

-3

– 1,2 x 10

-4

)=2,992 x 10

-3

Sm

-1

dla r-ru soli trudno rozpuszczalnej przyjmujemy:   

0



0

+

 

0

-

 = 10

-3

 /

c(mol/dm

3

)

c(mol/dm

3

)=10

-3

 / (

0

+

 

0

-

) = 10

-3

x 2,992 x 10

-3

Sm

-1

/ 2 x (61,9+83) x 10

-4

S m

2

mol

-1

=

=1,03 x 10

-4

mol/dm

3

(stężenie elektrolitu)

IR

= c

Ag+

2

 c

CrO4

= (2c)

2

 c = 4c

3

= 4 x (1,03  10

-4

)

3

=

4,37  10

-12

Ag

2

CrO

4 (s)

⇋ 2 Ag

+

+ CrO

4

2-

IR = c

Ag+

2

 c

CrO4