www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
P
RÓBNY
E
GZAMIN
M
ATURALNY
Z
M
ATEMATYKI
Z
ESTAW PRZYGOTOWANY PRZEZ SERWIS
WWW
.
ZADANIA
.
INFO
POZIOM PODSTAWOWY
+
12
MARCA
2011
C
ZAS PRACY
: 170
MINUT
Zadania zamkni˛ete
Z
ADANIE
1
(1
PKT
.)
Liczba
|
√
5
−
2, 24
| − |
3, 14
−
π
|
jest równa
A)
−
0, 9
−
√
5
−
π
B) 5, 38
−
√
5
−
π
C) π
−
√
5
−
0, 9
D) 0, 9
+
√
5
−
π
R
OZWI ˛
AZANIE
Poniewa ˙z
√
5
≈
2, 236, oraz π
≈
3, 1415 mamy
|
√
5
−
2, 24
| − |
3, 14
−
π
| =
= (
2, 24
−
√
5
) − (
π
−
3, 14
) =
5, 38
−
√
5
−
π
.
Odpowied´z: B
Z
ADANIE
2
(1
PKT
.)
Iloczyn
1
9
5
·
√
27
·
81
3
·
√
3 jest równy
A) 3
3
2
B) 3
−
1
C) 3
1
D) 3
1
2
R
OZWI ˛
AZANIE
Liczymy
1
9
5
·
√
27
·
81
3
·
√
3
=
1
(
3
2
)
5
· (
3
3
)
1
2
· (
3
4
)
3
·
3
1
2
=
=
3
12
+
1
2
3
10
+
3
2
=
3
25
2
−
23
2
=
3.
Odpowied´z: C
Materiał pobrany z serwisu
1

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
3
(1
PKT
.)
Je ˙zeli liczba 3b jest o 50% wi˛eksza od połowy liczby 2a
+
b, to liczba a jest wi˛eksza od b o
A) 100%
B) 150%
C) 50%
D) 200%
R
OZWI ˛
AZANIE
Zapisujemy podany warunek
3b
=
1, 5
·
2a
+
b
2
=
3
4
(
2a
+
b
)
/
·
4
3
4b
=
2a
+
b
3b
=
2a
⇒
a
=
1, 5b.
Zatem a jest wi˛eksze od b o 50%.
Odpowied´z: C
Zadania
.info
Podobają Ci się nasze rozwiązania?
Pokaż je koleżankom i kolegom ze szkoły!
Z
ADANIE
4
(1
PKT
.)
Zbiór rozwi ˛
aza ´n nierówno´sci
|
x
−
2
| <
3 jest taki sam jak zbiór rozwi ˛
aza ´n nierówno´sci
A)
(
x
−
1
)(
x
+
5
) <
0
B)
(
x
−
2
)(
x
+
3
) <
0
C)
(
x
+
1
)(
5
−
x
) >
0
D)
(
x
−
1
)(
5
−
x
) >
0
R
OZWI ˛
AZANIE
Zbiorem rozwi ˛
aza ´n nierówno´sci
|
x
−
2
| <
3 jest zbiór liczb odległych od 2 o mniej ni ˙z 3,
czyli przedział
(
2
−
3, 2
+
3
) = (−
1, 5
)
.
Ten sam przedział jest zbiorem rozwi ˛
aza ´n nierówno´sci
(
x
+
1
)(
x
−
5
) <
0,
która jest równowa ˙zna nierówno´sci
(
x
+
1
)(
5
−
x
) >
0.
Odpowied´z: C
Materiał pobrany z serwisu
2
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
5
(1
PKT
.)
Prosta l ma równanie y
=
x log
3
3
√
3
+
3
√
3. Wska ˙z równanie prostej prostopadłej do prostej l.
A) y
= −
x log
3
1
3
√
3
+
3
B) y
=
x log
3
1
3
√
3
+
3
C) y
= −
3x
−
log
3
1
3
√
3
D) y
=
3x
−
log
3
1
3
√
3
R
OZWI ˛
AZANIE
Poniewa ˙z
log
3
3
√
3
=
log
3
3
1
3
=
1
3
,
prosta prostopadła do l musi mie´c współczynnik kierunkowy -3.
Odpowied´z: C
Z
ADANIE
6
(1
PKT
.)
Iloczyn wielomianów W
(
x
) = (
x
−
1
)
4
+
x
3
i P
(
x
) = (
2
−
x
+
3x
2
)
3
−
2x
4
jest wielomianem
stopnia
A) 24
B) 10
C) 12
D) 7
R
OZWI ˛
AZANIE
Zauwa ˙zmy, ˙ze wymna ˙zaj ˛
ac nawiasy
(
x
−
1
)(
x
−
1
)(
x
−
1
)(
x
−
1
)
otrzymamy wielomian stopnia 4, czyli W
(
x
)
jest wielomianem stopnia 4.
Podobnie, wyra ˙zenie
(
2
−
x
+
3x
2
)(
2
−
x
+
3x
2
)(
2
−
x
+
3x
2
)
jest wielomianem z najwy ˙zsz ˛
a pot˛eg ˛
a x postaci:
(
x
2
)
3
=
x
6
, czyli P
(
x
)
jest wielomianem
stopnia 6. Zatem iloczyn W
(
x
) ·
P
(
x
)
b˛edzie wielomianem stopnia 4
+
6
=
10 (bo x
4
·
x
6
=
x
10
).
Odpowied´z: B
Z
ADANIE
7
(1
PKT
.)
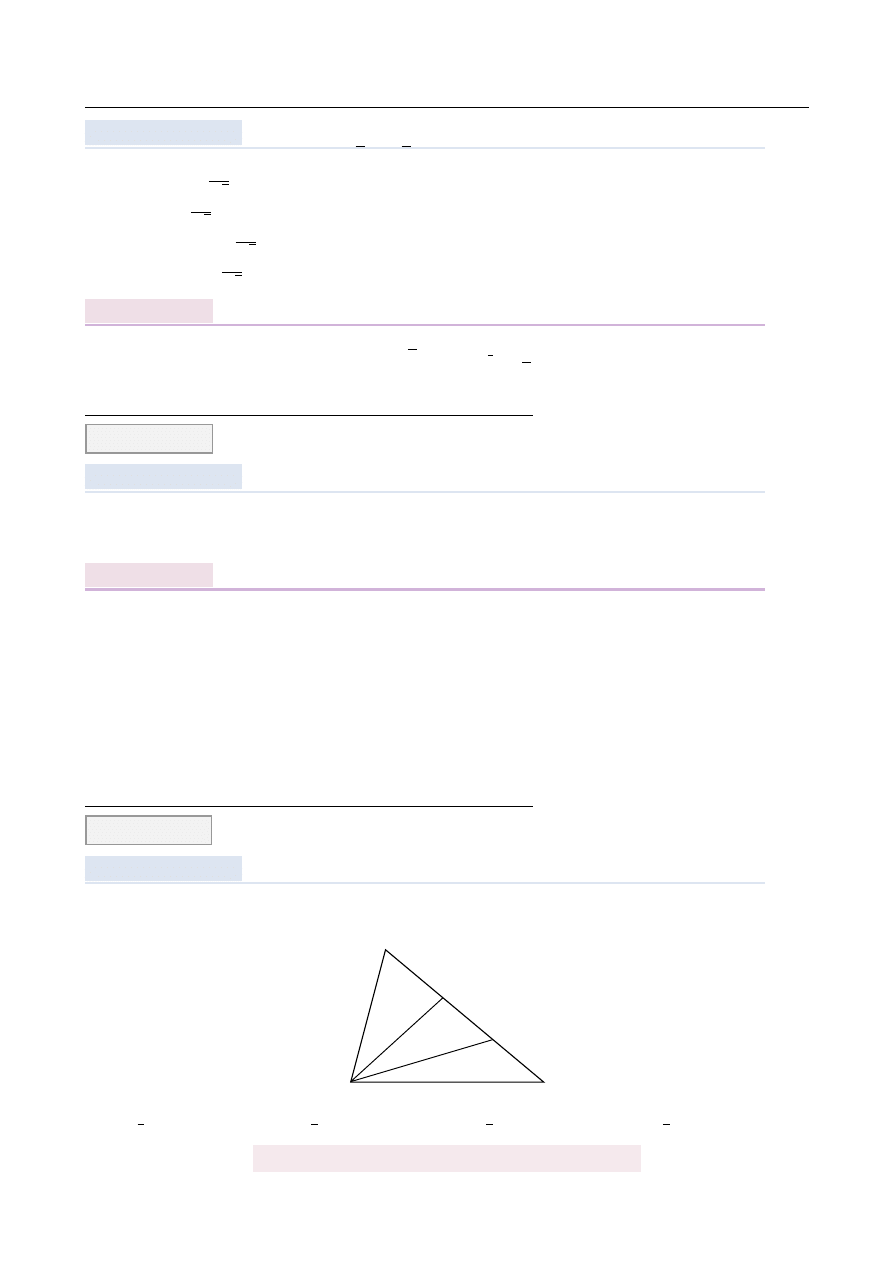
Punkty D i E dziel ˛
a bok BC trójk ˛
ata ABC na trzy równe cz˛e´sci (zobacz rysunek). Stosunek
pól trójk ˛
atów ABC i ABD jest równy
A
B
C
D
E
A)
3
2
B)
2
3
C)
9
4
D)
4
9
Materiał pobrany z serwisu
3
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
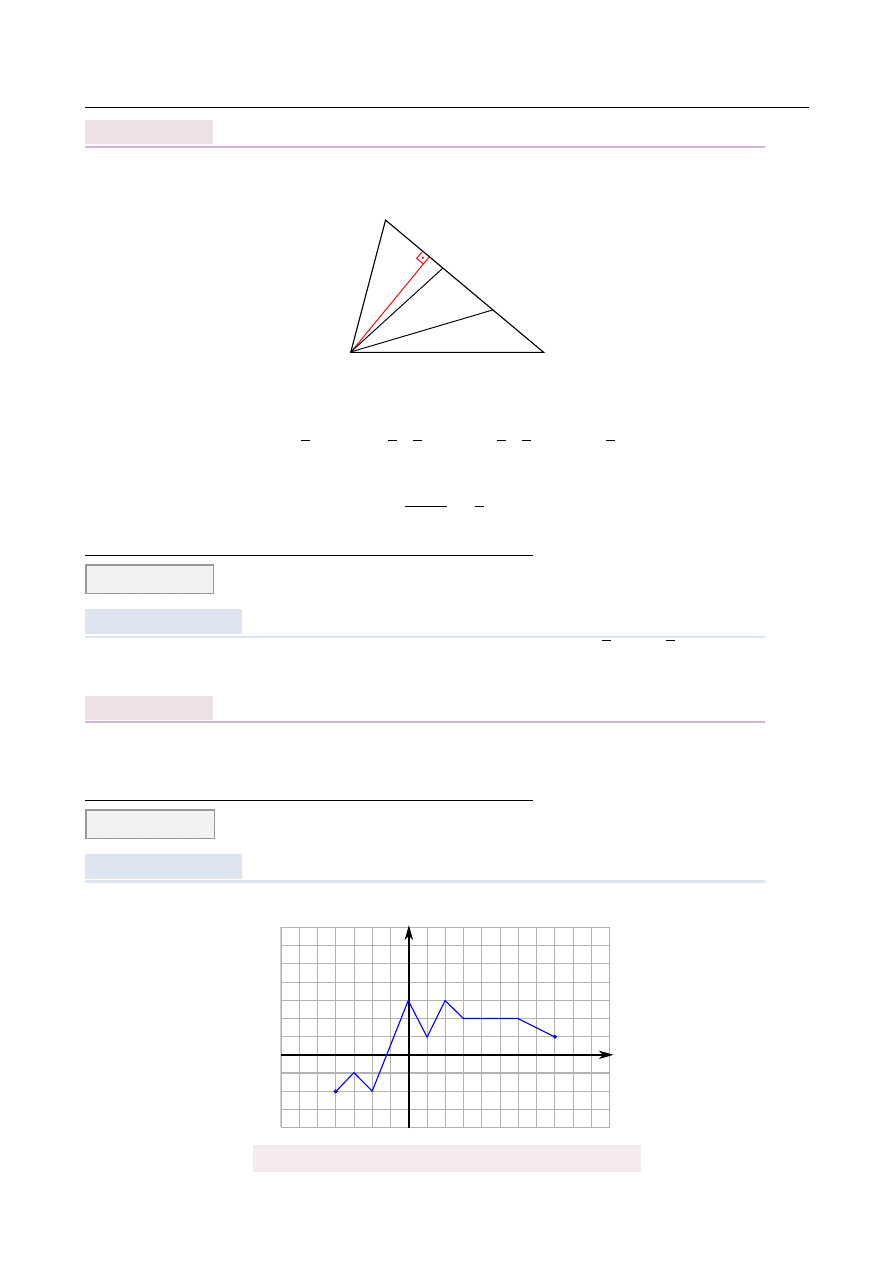
AZANIE
Wysoko´s´c opuszczona z wierzchołka A w trójk ˛
acie ABC jest jednocze´snie wysoko´sci ˛
a w
trójk ˛
acie ABD.
A
B
C
D
E
h
Je ˙zeli oznaczymy jej długo´s´c przez h to mamy
P
ABD
=
1
2
DB
·
h
=
1
2
·
2
3
BC
·
h
=
2
3
·
1
2
BC
·
h
=
2
3
P
ABC
.
Zatem
P
ABC
P
ABD
=
3
2
.
Odpowied´z: A
Z
ADANIE
8
(1
PKT
.)
Wykres funkcji y
=
mx
2
−
2mx
+
3 przechodzi przez punkty
(−
√
3, 3
)
,
(
√
3, 3
)
,
(
1, 3
)
. Wtedy
A) m
=
3
B) m
= −
3
C) m
=
2
D) m
=
0
R
OZWI ˛
AZANIE
Zauwa ˙zmy, ˙ze wszystkie trzy podane punkty le ˙z ˛
a na prostej y
=
3. Poniewa ˙z parabola nie
mo ˙ze mie´c trzech punktów wspólnych z poziom ˛
a prost ˛
a, wykresem danej funkcji musi by´c
prosta, czyli m
=
0.
Odpowied´z: D
Z
ADANIE
9
(1
PKT
.)
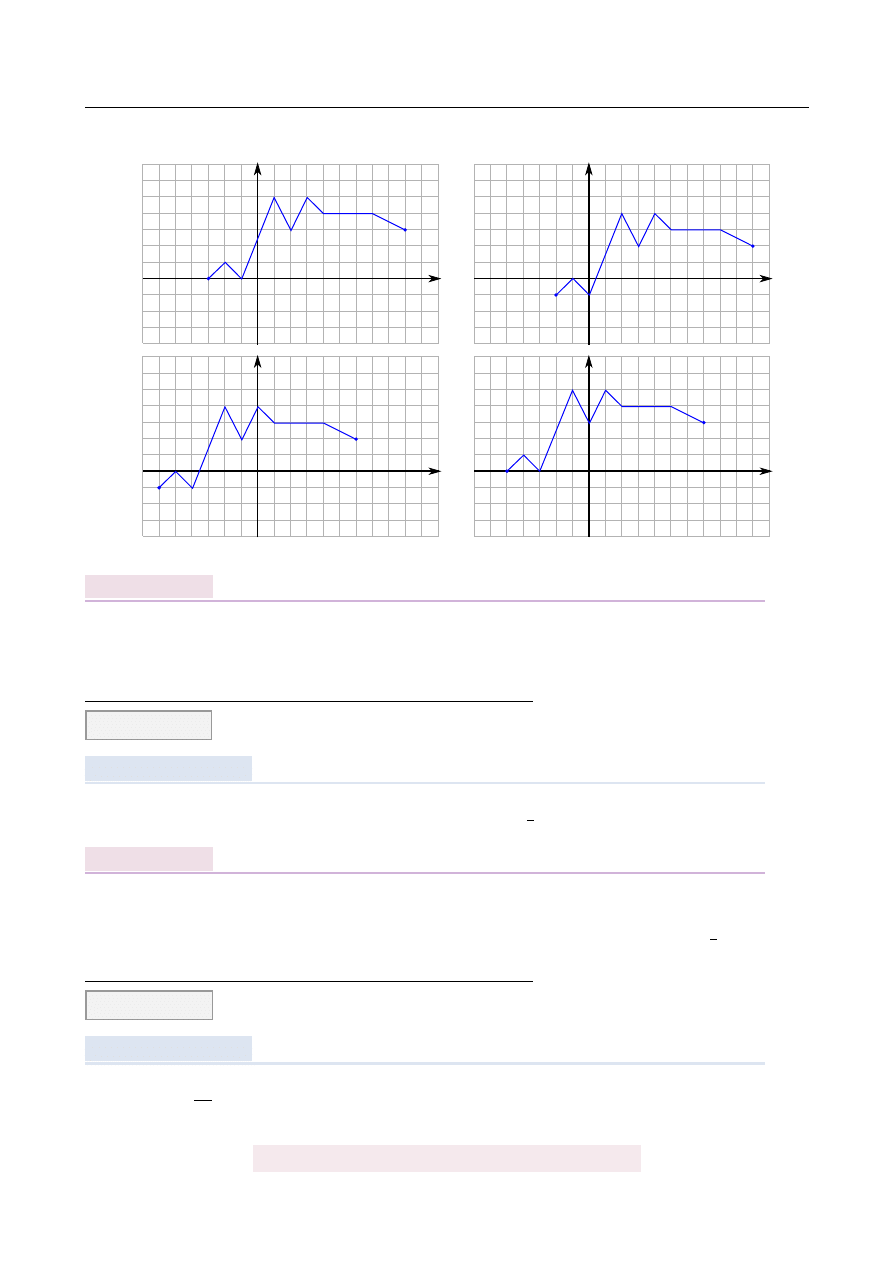
Rysunek przedstawia wykres funkcji y
=
f
(
x
)
.
x
y
1
2 3 4 5 6 7
8 9 10
1
2
3
4
5
6
-1
-1
-2
-2
-3
-4
-5
-6
-3
Materiał pobrany z serwisu
4
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Wska ˙z wykres funkcji g
(
x
) =
1
+
f
(
x
−
2
)
.
x
y
1
2 3 4 5 6 7
8 9 10
1
2
3
4
5
6
-1
-1
-2
-2
-3
-4
-5
-6
-3
x
y
1
2 3 4 5 6 7
8 9 10
1
2
3
4
5
6
-1
-1
-2
-2
-3
-4
-5
-6
-3
A)
B)
x
y
1
2 3 4 5 6 7
8 9 10
1
2
3
4
5
6
-1
-1
-2
-2
-3
-4
-5
-6
-3
x
y
1
2 3 4 5 6 7
8 9 10
1
2
3
4
5
6
-1
-1
-2
-2
-3
-4
-5
-6
-3
C)
D)
R
OZWI ˛
AZANIE
Wykres funkcji h
(
x
) =
f
(
x
−
2
)
powstaje z wykresu funkcji y
=
f
(
x
)
przez przesuni˛ecie o 2
jednostki w prawo, a wykres g
(
x
) =
1
+
h
(
x
) =
1
+
f
(
x
−
2
)
powstaje z wykresu y
=
h
(
x
)
przez przesuni˛ecie o 1 jednostk˛e do góry. Zatem wykres y
=
g
(
x
)
powstaje z wykresu y
=
f
(
x
)
przez przesuni˛ecie od 2 jednostki w prawo i jedn ˛
a do góry.
Odpowied´z: B
Z
ADANIE
10
(1
PKT
.)
Wska ˙z m, dla którego funkcja liniowa f
(
x
) = −
x
+
m
2
+
m
4
x
+
2 jest malej ˛
aca.
A) m
= −
2
B) m
= −
1
C) m
=
1
2
D) m
=
2
R
OZWI ˛
AZANIE
Poniewa ˙z
f
(
x
) = (
m
4
−
1
)
x
+ (
m
2
+
2
)
,
funkcja f jest malej ˛
aca je ˙zeli m
4
−
1
<
0. Wida´c, ˙ze z podanych liczb tylko m
=
1
2
spełnia ten
warunek.
Odpowied´z: C
Z
ADANIE
11
(1
PKT
.)
W ci ˛
agu arytmetycznym
(
a
n
)
wyraz a
29
jest dwa razy wi˛ekszy od wyrazu a
15
oraz a
11
6=
0.
Wtedy iloraz
a
31
a
11
jest równy
A) 1
B) 2
C) 3
D) 4
Materiał pobrany z serwisu
5

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Ze wzoru a
n
=
a
1
+ (
n
−
1
)
r na n-ty wyraz ci ˛
agu arytmetycznego mamy
a
29
=
2a
15
a
1
+
28r
=
2
(
a
1
+
14r
)
a
1
+
28r
=
2a
1
+
28r
0
=
a
1
.
Zatem
a
31
a
11
=
a
1
+
30r
a
1
+
10r
=
30r
10r
=
3.
Odpowied´z: C
Z
ADANIE
12
(1
PKT
.)
Liczby x
1
i x
2
s ˛
a pierwiastkami równania 2x
2
+
4x
+
1
=
0 i x
1
<
x
2
. Oblicz x
1
−
x
2
.
A)
√
2
B)
−
√
2
C) -2
D)
−
√
8
R
OZWI ˛
AZANIE
Rozwi ˛
azujemy dane równanie
2x
2
+
4x
+
1
=
0
∆
=
4
2
−
4
·
2
=
16
−
8
=
2
·
2
2
x
1
=
−
4
−
2
√
2
4
=
−
2
−
√
2
2
,
x
2
=
−
4
+
2
√
2
4
=
−
2
+
√
2
2
.
Zatem
x
1
−
x
2
=
−
2
−
√
2
2
−
−
2
+
√
2
2
=
−
2
√
2
2
= −
√
2.
Odpowied´z: B
Z
ADANIE
13
(1
PKT
.)
Warto´s´c wyra ˙zenia
tg 12,5
◦
·
tg 77,5
◦
sin 25
◦
cos 65
◦
+
cos 25
◦
sin 65
◦
jest równa
A) 1
B)
1
√
2
C)
√
2
D)
1
2
R
OZWI ˛
AZANIE
Materiał pobrany z serwisu
6
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Korzystamy ze wzorków
sin
(
90
◦
−
α
) =
cos α
cos
(
90
◦
−
α
) =
sin α
tg
(
90
◦
−
α
) =
ctg α
=
1
tg α
.
Liczymy
tg 12, 5
◦
·
tg 77, 5
◦
sin 25
◦
cos 65
◦
+
cos 25
◦
sin 65
◦
=
=
tg 12, 5
◦
·
tg
(
90
◦
−
12, 5
◦
)
sin 25
◦
cos
(
90
◦
−
25
◦
) +
cos 25
◦
sin
(
90
◦
−
25
◦
)
=
=
tg 12, 5
◦
·
1
tg 12,5
◦
sin 25
◦
sin 25
◦
+
cos 25
◦
cos 25
◦
=
=
1
sin
2
25
◦
+
cos
2
25
◦
=
1.
Mianownik mogli´smy te ˙z obliczy´c korzystaj ˛
ac ze wzoru
sin
(
α
+
β
) =
sin α cos β
+
sin β cos α.
Odpowied´z: A
Z
ADANIE
14
(1
PKT
.)
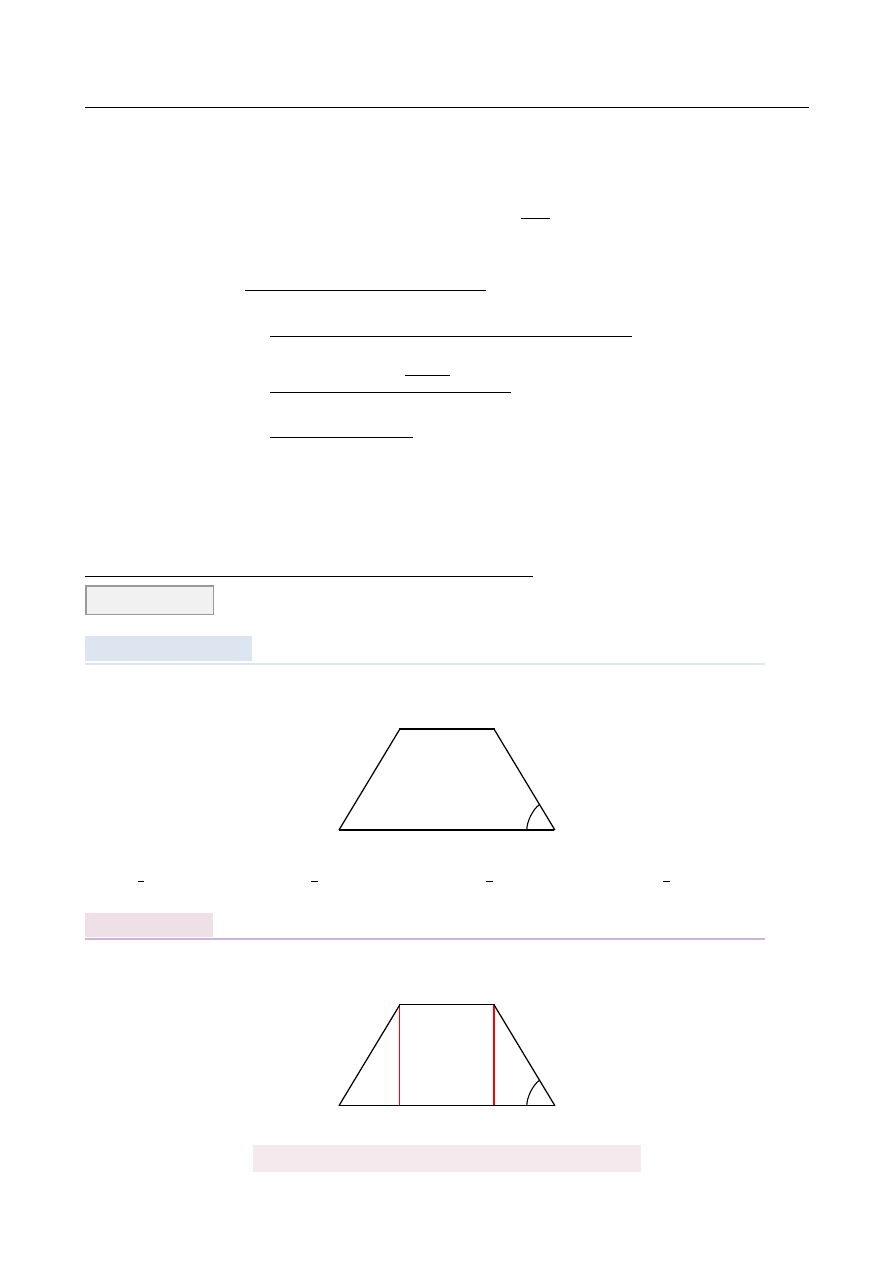
Dany jest trapez równoramienny (patrz rysunek). Wtedy tg α jest równy
α
10
10
7
19
A)
4
3
B)
3
4
C)
4
5
D)
3
5
R
OZWI ˛
AZANIE
Dorysujmy wysoko´sci trapezu.
α
10
10
7
7
6
6
8
8
Materiał pobrany z serwisu
7
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z twierdzenia Pitagorasa wyliczamy długo´s´c wysoko´sci.
h
=
p
10
2
−
6
2
=
√
64
=
8.
Zatem
tg α
=
8
6
=
4
3
.
Odpowied´z: A
Z
ADANIE
15
(1
PKT
.)
W malej ˛
acym ci ˛
agu geometrycznym
(
a
n
)
mamy a
1
= −
3
2
i a
2
a
3
a
4
= −
27
2
. Iloraz tego ci ˛
agu
równy
A)
−
√
2
B)
−
6
√
2
C)
−
3
√
2
D)
3
√
2
R
OZWI ˛
AZANIE
Poniewa ˙z a
2
=
a
1
q, a
3
=
a
1
q
2
, a
4
=
a
1
q
3
mamy równanie
a
2
a
3
a
4
=
a
1
q
·
a
1
q
2
·
a
1
q
3
=
a
3
1
q
6
−
27
2
=
−
3
2
3
·
q
6
= −
27
8
·
q
6
/
·
−
8
27
4
=
q
6
q
=
6
√
4
=
3
√
2
∨
q
= −
6
√
4
= −
3
√
2.
Poniewa ˙z ci ˛
ag ma by´c malej ˛
acy mamy q
=
3
√
2 (bo a
1
<
0).
Odpowied´z: D
Z
ADANIE
16
(1
PKT
.)
Ci ˛
ag
(
a
n
)
okre´slony jest wzorem a
n
=
n
2
−
11n
+
28, gdzie n
>
1. Liczba niedodatnich
wyrazów tego ci ˛
agu jest równa
A) 2
B) 3
C) 4
D) 7
R
OZWI ˛
AZANIE
Rozwi ˛
azujemy nierówno´s´c
n
2
−
11n
+
28
6
0
∆
=
121
−
4
·
28
=
9
n
=
11
−
3
2
=
4
∨
n
=
11
+
3
2
=
7
n
∈ h
4, 7
i
.
Zatem wyrazy niedodatnie to wyrazy o numerach 4,5,6,7.
Odpowied´z: C
Materiał pobrany z serwisu
8
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
17
(1
PKT
.)
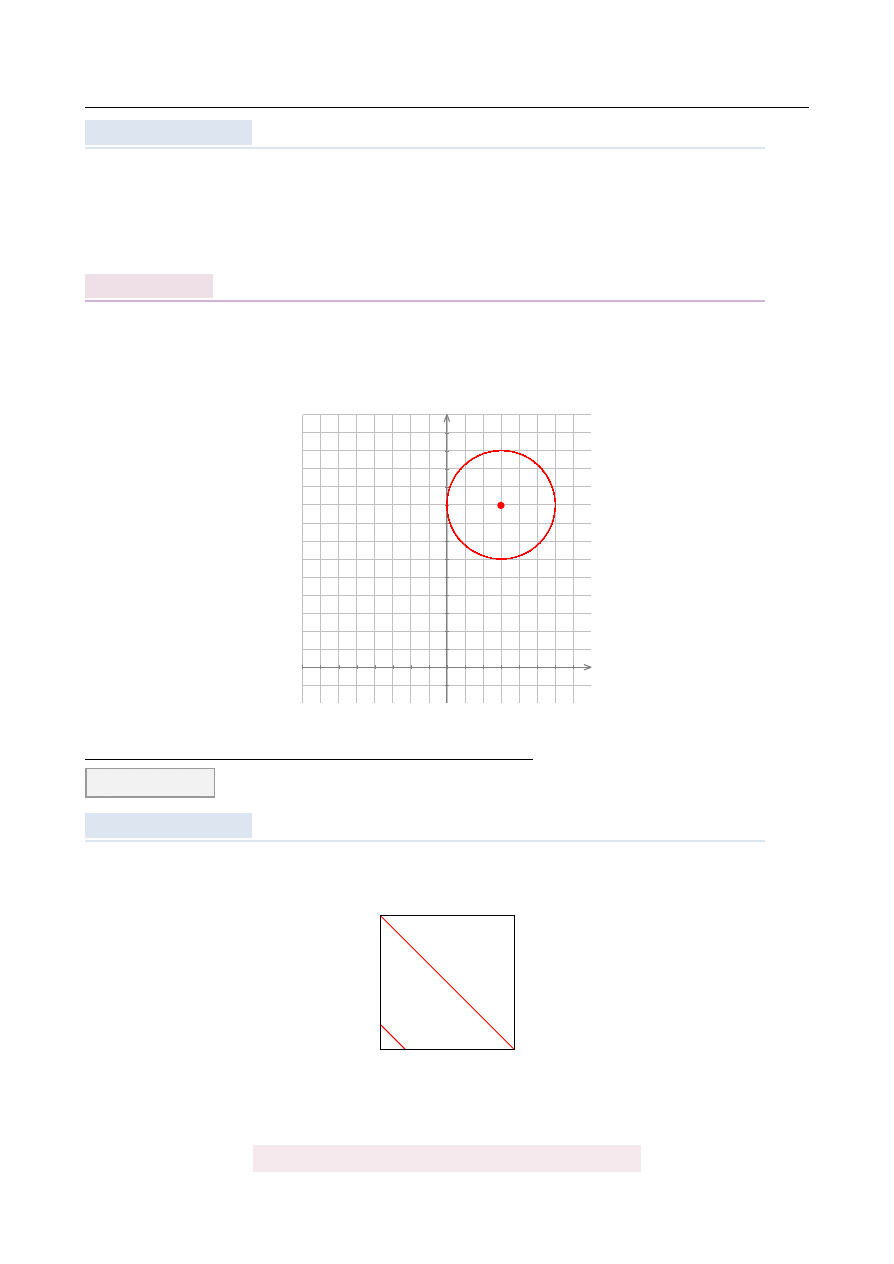
Wska ˙z równanie okr˛egu stycznego do osi Oy.
A)
(
x
−
3
)
2
+ (
y
−
3
)
2
=
3
B)
(
x
−
3
)
2
+ (
y
−
9
)
2
=
3
C)
(
x
−
9
)
2
+ (
y
−
3
)
2
=
9
D)
(
x
−
3
)
2
+ (
y
−
9
)
2
=
9
R
OZWI ˛
AZANIE
Szkicuj ˛
ac kolejne okr˛egi, łatwo zauwa ˙zy´c, ˙ze styczny do osi Oy jest tylko okr ˛
ag
(
x
−
3
)
2
+ (
y
−
9
)
2
=
3
2
,
który ma ´srodek
(
3, 9
)
i promie ´n 3.
-5
-1
+3
+5
x
-1
+1
+5
+10
y
Odpowied´z: D
Z
ADANIE
18
(1
PKT
.)
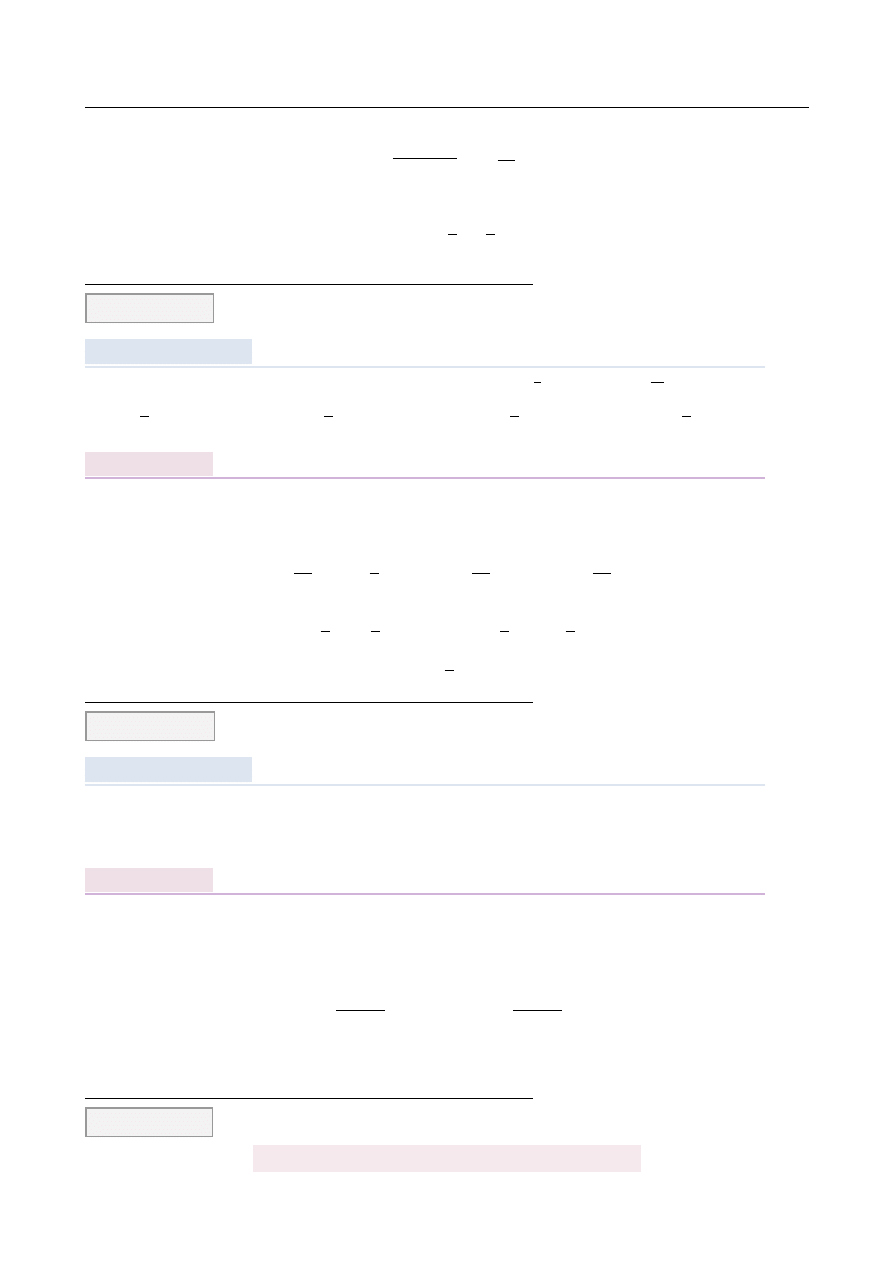
W kwadracie ABCD o boku długo´sci 20 poł ˛
aczono punkty E i F na bokach AB i AD w ten
sposób, ˙ze odcinek EF jest równoległy do przek ˛
atnej BD i jest od niej 5 razy krótszy.
A
B
C
D
E
F
Długo´s´c odcinka EB jest równa
A) 12
B) 15
C) 14
D) 16
Materiał pobrany z serwisu
9

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Poniewa ˙z odcinek EF stanowi
1
5
odcinka BD, wi˛ec trójk ˛
at AEF jest 5 razy mniejszy od trój-
k ˛
ata ABD. Zatem
AE
=
1
5
AB
=
4.
St ˛
ad EB
=
20
−
4
=
16.
Odpowied´z: D
Z
ADANIE
19
(1
PKT
.)
Punkty A, B, C, D, E, F, G s ˛
a wierzchołkami siedmiok ˛
ata foremnego.
B
C
D
E
F
G
A
Miara zaznaczonego na rysunku k ˛
ata AFC jest równa
A)
360
◦
14
B)
360
◦
7
C)
300
◦
14
D)
300
◦
7
R
OZWI ˛
AZANIE
Dorysujmy okr ˛
ag opisany na siedmiok ˛
acie i powiedzmy, ˙ze jego ´srodkiem jest punkt S.
B
C
D
E
F
G
A
S
Wida´c teraz, ˙ze na mocy zale ˙zno´sci mi˛edzy k ˛
atami: ´srodkowym i wpisanym opartymi
na tym samym łuku, mamy
]
AFC
=
1
2
]
ASC
= ]
ASB
=
1
7
·
360
◦
.
Odpowied´z: B
Materiał pobrany z serwisu
10

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
20
(1
PKT
.)
Pan Eugeniusz szykuj ˛
ac si˛e rano do pracy wybiera jeden spo´sród swoich 12 zegarków oraz
dwa spo´sród 22 wiecznych piór, przy czym jedno z nich traktuje jako pióro zapasowe. Na
ile sposobów mo ˙ze wybra´c zestaw składaj ˛
acy si˛e z zegarka i dwóch piór, głównego i zapa-
sowego?
A) 2777
B) 34
C) 5544
D) 5808
R
OZWI ˛
AZANIE
Zegarek wybiera na 12 sposobów, pierwsze pióro na 22 sposoby, a pióro zapasowe na 21
sposobów (bo jedno ju ˙z wybrał). Zatem w sumie mo ˙ze to zrobi´c na
12
·
22
·
21
=
5544
sposoby (zasada mno ˙zenia).
Odpowied´z: C
Z
ADANIE
21
(1
PKT
.)
Je ˙zeli dodamy do siebie liczby wierzchołków, kraw˛edzi i ´scian ostrosłupa otrzymamy 58. Ile
kraw˛edzi ma ten ostrosłup?
A) 29
B) 14
C) 28
D) 15
R
OZWI ˛
AZANIE
Je ˙zeli w podstawie ostrosłupa jest n–k ˛
at, to ma on n
+
1 ´scian, n
+
1 wierzchołków i 2n
kraw˛edzi. Mamy zatem równanie
n
+
1
+
n
+
1
+
2n
=
58
4n
=
56
⇒
n
=
14.
Zatem ostrosłup ten ma 2n
=
28 kraw˛edzi.
Odpowied´z: C
Z
ADANIE
22
(1
PKT
.)
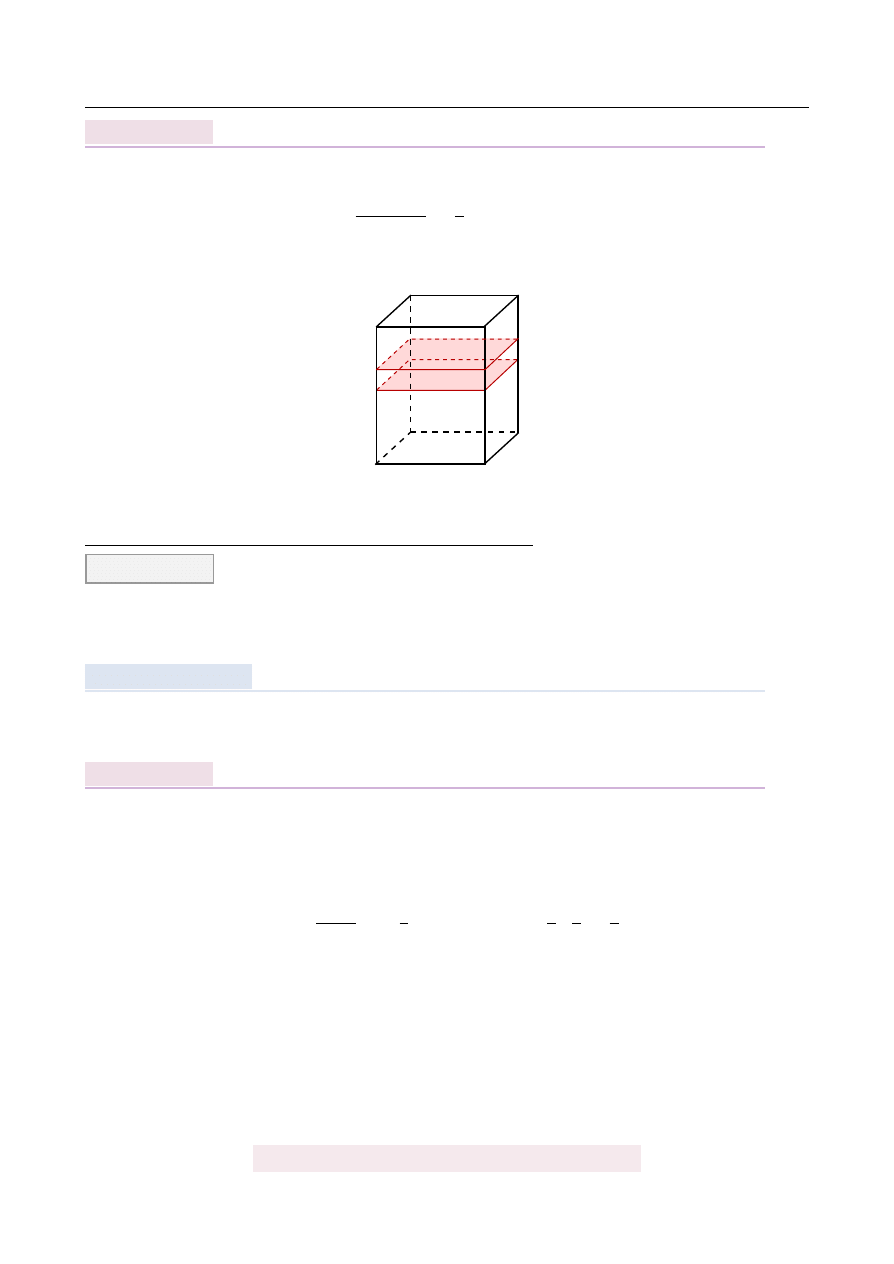
Prostopadło´scian dzielimy na cz˛e´sci prowadz ˛
ac dwie płaszczyzny równoległe do jego pod-
staw, które dziel ˛
a kraw˛ed´z boczn ˛
a w stosunku 5:1:2. Jaki procent obj˛eto´sci całego prostopa-
dło´scianu stanowi obj˛eto´s´c najwi˛ekszej z utworzonych cz˛e´sci?
A) 62,5%
B) 37,5%
C) 65%
D) 75%
Materiał pobrany z serwisu
11
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Wysoko´s´c najwi˛ekszej cz˛e´sci stanowi
5
5
+
1
+
2
=
5
8
=
62, 5%
wysoko´sci prostopadło´scianu.
Poniewa ˙z oba prostopadło´sciany maj ˛
a takie same pola podstaw, obj˛eto´s´c mniejszego z
nich stanowi 62,5% obj˛eto´sci wi˛ekszego.
Odpowied´z: A
Zadania otwarte
Z
ADANIE
23
(2
PKT
.)
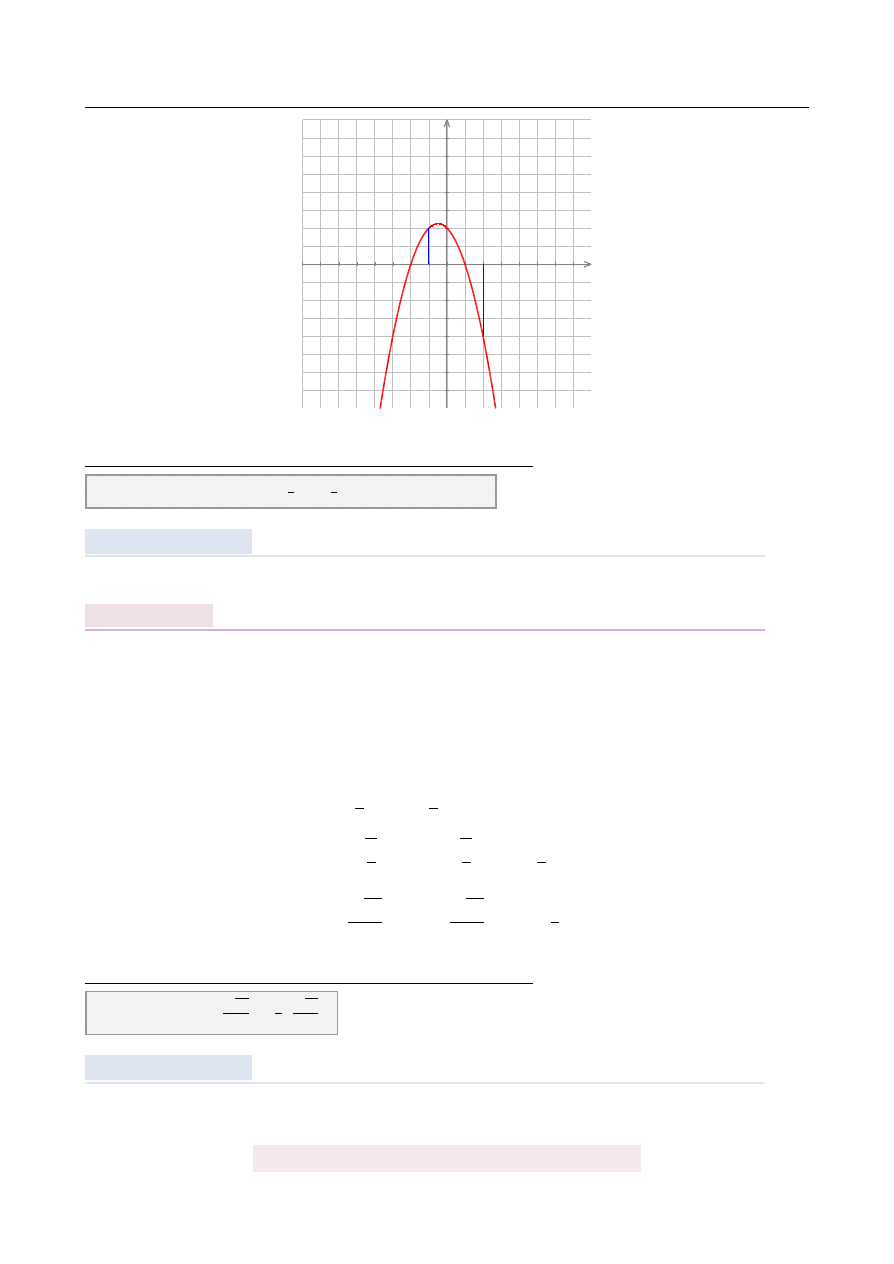
Wyznacz najmniejsz ˛
a i najwi˛eksz ˛
a warto´s´c funkcji f
(
x
) = −(
x
−
1
)(
x
+
2
)
w przedziale
h−
1; 2
i
.
R
OZWI ˛
AZANIE
Ramiona paraboli s ˛
a skierowane w dół, wi˛ec warto´s´c najwi˛eksza jest przyjmowana w jej
wierzchołku (je ˙zeli jest w podanym przedziale), a warto´s´c najmniejsza w jednym z ko ´nców
przedziału. W którym? – policzymy i sprawdzimy.
Wierzchołek paraboli znajduje si˛e dokładnie pomi˛edzy pierwiastkami, czyli w punkcie
x
w
=
1
−
2
2
= −
1
2
⇒
f
(
x
w
) =
3
2
·
3
2
=
9
4
.
Sprawd´zmy jeszcze ko ´nce przedziału.
f
(−
1
) = −(−
2
) ·
1
=
2
f
(
2
) = −
1
·
4
= −
4.
Na koniec obrazek.
Materiał pobrany z serwisu
12
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
-5
-1
+1
+5
x
-5
-1
+1
+5
y
Odpowied´z: f
max
=
f
(−
1
2
) =
9
4
, f
min
=
f
(
2
) = −
4
Z
ADANIE
24
(2
PKT
.)
Rozwi ˛
a ˙z równanie 4x
3
+
2x
2
−
10x
−
5
=
0.
R
OZWI ˛
AZANIE
Gdy si˛e przyjrzymy równaniu to mo ˙zna zauwa ˙zy´c, ˙ze z lewej strony mo ˙zemy wył ˛
aczy´c
(
2x
+
1
)
przed nawias.
4x
3
+
2x
2
−
10x
−
5
=
0
2x
2
(
2x
+
1
) −
5
(
2x
+
1
) =
0
(
2x
2
−
5
)(
2x
+
1
) =
0
4
x
2
−
5
2
x
+
1
2
=
0
4
x
−
r
5
2
!
x
+
r
5
2
!
x
+
1
2
=
0
4
x
−
√
10
2
!
x
+
√
10
2
!
x
+
1
2
=
0
Odpowied´z:
n
−
√
10
2
,
−
1
2
,
√
10
2
o
Z
ADANIE
25
(2
PKT
.)
Długo´s´c przeciwprostok ˛
atnej trójk ˛
ata prostok ˛
atnego o obwodzie 90 jest liczb ˛
a całkowit ˛
a i
jest o 1 wi˛eksza od długo´sci jednej z przyprostok ˛
atnych. Oblicz pole tego trójk ˛
ata.
Materiał pobrany z serwisu
13
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
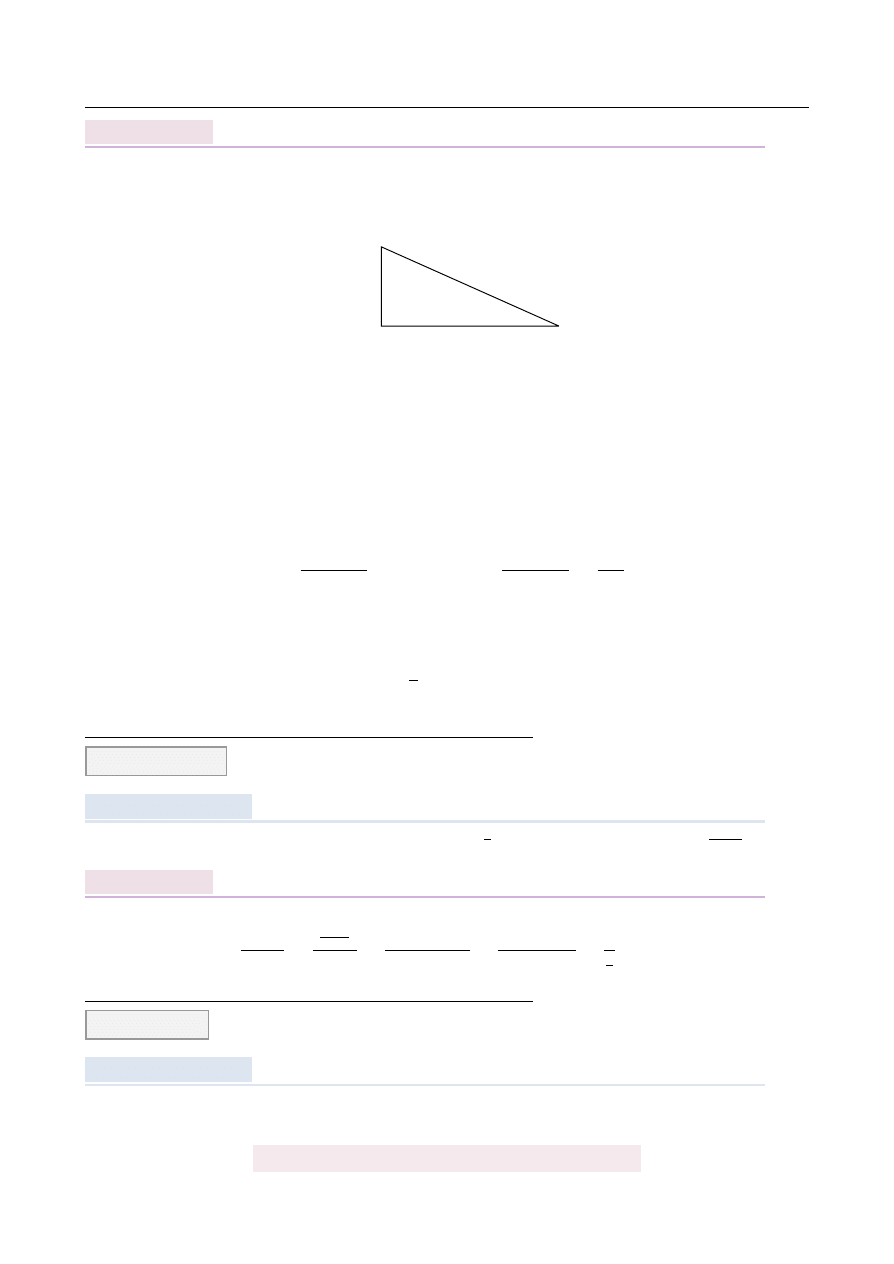
Je ˙zeli oznaczymy długo´s´c przeciwprostok ˛
atnej przez c to jedna z przyprostok ˛
atnych ma
długo´s´c c
−
1, a druga
90
−
c
− (
c
−
1
) =
91
−
2c.
c
c-1
91-2c
Zapisuj ˛
ac twierdzenie Pitagorasa otrzymujemy równanie
(
c
−
1
)
2
+ (
91
−
2c
)
2
=
c
2
c
2
−
2c
+
1
+
8281
−
364c
+
4c
2
=
c
2
4c
2
−
366c
+
8282
=
0
/ : 2
2c
2
−
183c
+
4141
=
0
∆
=
183
2
−
8
·
4141
=
361
=
19
2
c
=
183
−
19
4
=
41
∨
c
=
183
+
19
4
=
101
2
.
Poniewa ˙z przeciwprostok ˛
atna ma mie´c długo´s´c całkowit ˛
a, odrzucamy drugie rozwi ˛
azanie.
Zatem c
=
41 i przyprostok ˛
atne maj ˛
a długo´sci 9 i 40. Pole jest wi˛ec równe
P
=
1
2
·
9
·
40
=
180
Odpowied´z: 180
Z
ADANIE
26
(2
PKT
.)
K ˛
at α jest k ˛
atem ostrym. Wiedz ˛
ac, ˙ze sin α cos α
=
1
3
, oblicz warto´s´c wyra ˙zenia
tg α
sin
2
α
.
R
OZWI ˛
AZANIE
Liczymy
tg α
sin
2
α
=
sin α
cos α
sin
2
α
=
sin α
sin
2
α
cos α
=
1
sin α cos α
=
1
1
3
=
3.
Odpowied´z: 3
Z
ADANIE
27
(2
PKT
.)
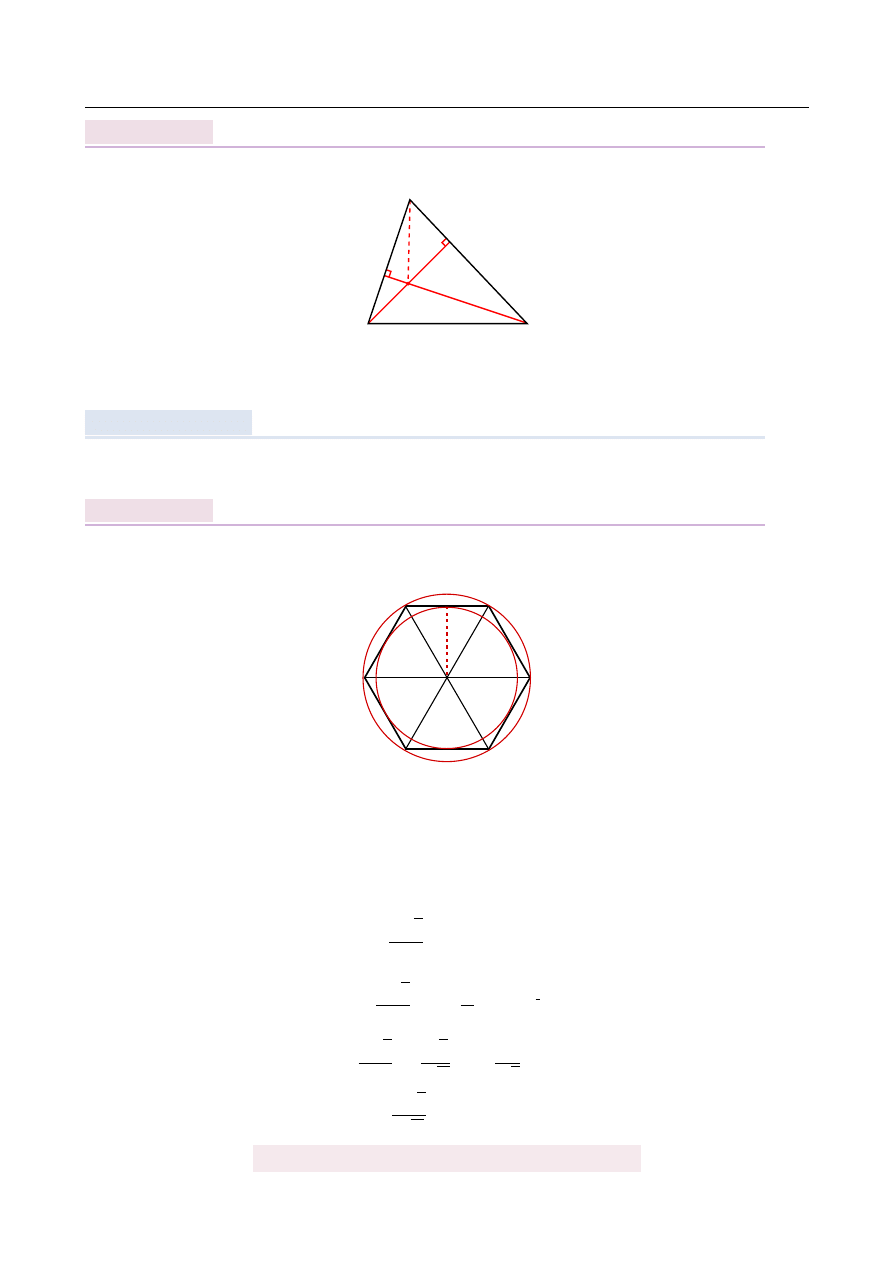
Odcinki AD i BE s ˛
a wysoko´sciami trójk ˛
ata ostrok ˛
atnego ABC, a punkt H jest punktem ich
przeci˛ecia. Uzasadnij, ˙ze punkty H, D, C i E le ˙z ˛
a na jednym okr˛egu.
Materiał pobrany z serwisu
14
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Rozpoczynamy oczywi´scie od rysunku.
A
B
C
D
E
H
Zauwa ˙zmy, ˙ze poniewa ˙z
]
CEH
= ]
CDH
=
90
◦
punkty E i D le ˙z ˛
a na okr˛egu o ´srednicy
CH. To oznacza, ˙ze okr ˛
ag ten przechodzi przez wszystkie cztery punkty H, D, C, E.
Z
ADANIE
28
(2
PKT
.)
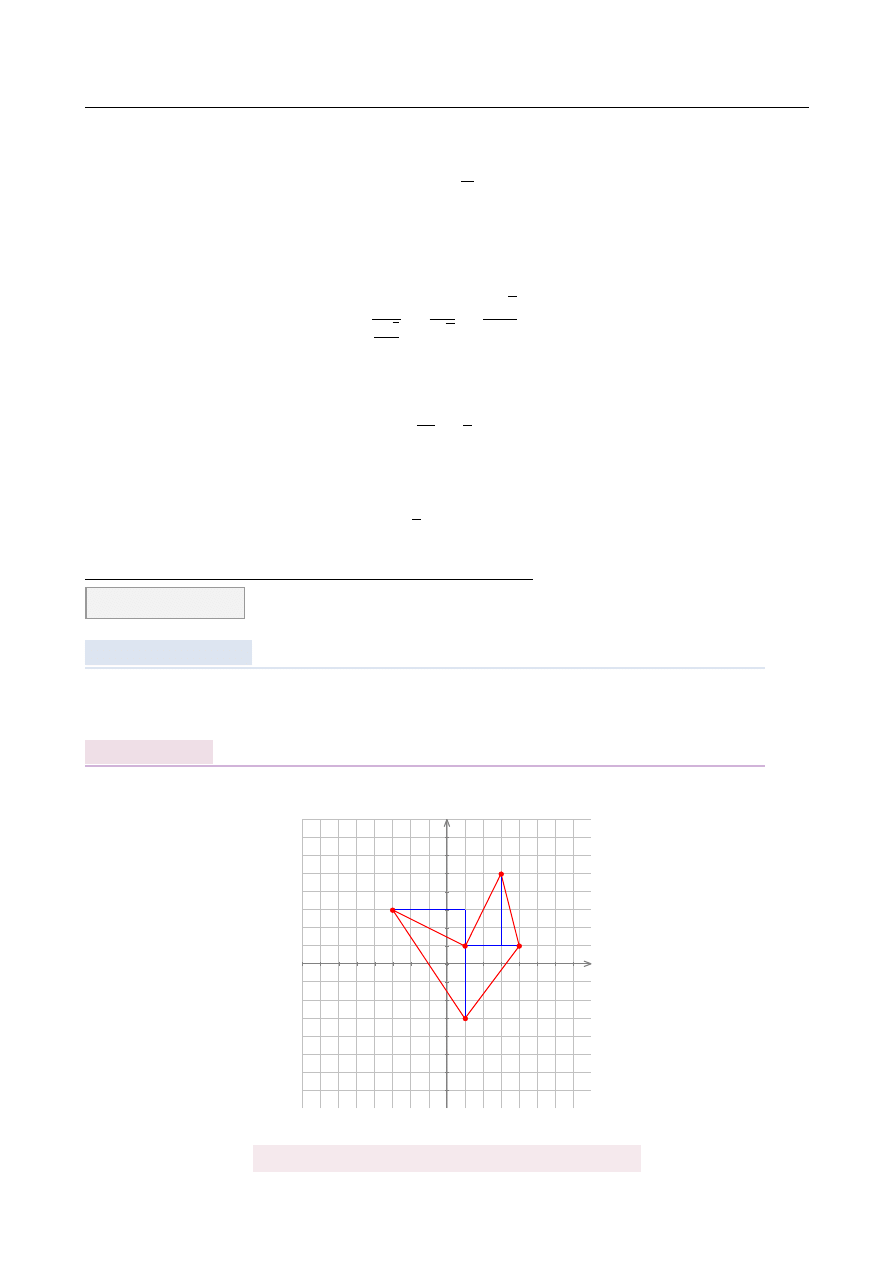
Pole koła wpisanego w sze´sciok ˛
at foremny wynosi 6 cm
2
. Oblicz pole koła opisanego na
tym sze´sciok ˛
acie.
R
OZWI ˛
AZANIE
Sze´sciok ˛
at składa si˛e z sze´sciu przystaj ˛
acych trójk ˛
atów równobocznych, oznaczmy ich bok
przez a.
A
B
C
S
D
E
F
a
a
a
Je ˙zeli narysujemy obrazek, to wida´c, ˙ze promie ´n okr˛egu opisanego na sze´sciok ˛
acie jest
równy a, a promie ´n okr˛egu wpisanego to wysoko´s´c trójk ˛
ata równobocznego.
Sposób I
Z powy ˙zszej uwagi mamy równanie.
π
a
√
3
2
!
2
=
6
/ : π
a
√
3
2
!
2
=
6
π
/ :
√
a
√
3
2
=
√
6
√
π
/
·
2
√
3
a
=
2
√
2
√
π
.
Materiał pobrany z serwisu
15
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Zatem pole koła opisanego wynosi
πa
2
=
π
·
8
π
=
8.
Sposób II
Jak ju ˙z zauwa ˙zyli´smy, stosunek promieni kół opisanego i wpisanego jest równy
a
a
√
3
2
=
2
√
3
=
2
√
3
3
.
Zatem stosunek pól tych kół jest kwadratem tej liczby
12
9
=
4
3
.
Tak wi˛ec pole koła opisanego jest równe
4
3
·
6
=
8.
Odpowied´z: 8 cm
2
Z
ADANIE
29
(4
PKT
.)
Oblicz pole pi˛eciok ˛
ata ABCDE, którego wierzchołki maj ˛
a współrz˛edne A
= (−
3, 3
)
, B
=
(
1,
−
3
)
, C
= (
4, 1
)
, D
= (
3, 5
)
, E
= (
1, 1
)
.
R
OZWI ˛
AZANIE
Rozpoczynamy od szkicowego rysunku.
-3
-1
+3 +4
x
-1
+1
+5
y
A
B
C
D
-3
E
Materiał pobrany z serwisu
16

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Zauwa ˙zmy, ˙ze interesuj ˛
acy nas pi˛eciok ˛
at składa si˛e z trzech trójk ˛
atów: ABE, BCE i ECD,
których pola jest do´s´c łatwo obliczy´c.
Trójk ˛
aty ABE i BCE maj ˛
a wspóln ˛
a podstaw˛e BE, która ma długo´s´c
BE
=
y
E
−
y
B
=
1
− (−
3
) =
4.
Wysoko´s´c trójk ˛
ata ABE jest równa
x
E
−
x
A
=
1
− (−
3
) =
4,
a wysoko´s´c trójk ˛
ata BCE jest równa
EC
=
x
C
−
x
E
=
4
−
1
=
3.
Zatem pola tych trójk ˛
atów s ˛
a równe
P
ABE
=
1
2
·
4
·
4
=
8
P
BCE
=
1
2
·
4
·
3
=
6.
Pozostało policzy´c pole trójk ˛
ata ECD. Wiemy ju ˙z, ˙ze EC
=
3, a wysoko´s´c opuszczona na t˛e
podstaw˛e jest równa
y
D
−
y
C
=
5
−
1
=
4.
Zatem
P
ECD
=
1
2
·
3
·
4
=
6.
St ˛
ad
P
ABCDE
=
P
ABE
+
P
BCE
+
P
ECD
=
8
+
6
+
6
=
20.
Odpowied´z: 20
Z
ADANIE
30
(6
PKT
.)
Linia kolejowa mi˛edzy miastami A i B ma długo´s´c 711 km. Poci ˛
ag jad ˛
acy z miasta A do
miasta B wyrusza 45 minut pó´zniej ni ˙z poci ˛
ag jad ˛
acy z miasta B do A. Poci ˛
agi te spotykaj ˛
a
si˛e w odległo´sci 450 km od miasta B. ´Srednia pr˛edko´s´c poci ˛
agu, który wyjechał z miasta A,
liczona od chwili wyjazdu z A do momentu spotkania, była o 34 km/h mniejsza od ´sred-
niej pr˛edko´sci drugiego poci ˛
agu liczonej od chwili wyjazdu z miasta B do chwili spotkania.
Oblicz ´sredni ˛
a pr˛edko´s´c ka ˙zdego z poci ˛
agów w chwili spotkania.
R
OZWI ˛
AZANIE
Oznaczmy szukane ´srednie pr˛edko´sci poci ˛
agów przez v
1
i v
2
odpowiednio. Do chwili spo-
tkania pierwszy poci ˛
ag przejechał 711
−
450
=
261 kilometrów, a drugi 450 kilometrów. To
Materiał pobrany z serwisu
17
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
oznacza, ˙ze pierwszy jechał przez
261
v
1
, a drugi przez
450
v
2
godzin. Wiemy, ˙ze pierwszy poci ˛
ag
wyruszył o
3
4
godziny pó´zniej ni ˙z drugi poci ˛
ag, co daje równanie
261
v
1
+
3
4
=
450
v
2
/
·
4
3
v
1
v
2
348v
2
+
v
1
v
2
=
600v
1
.
Wiemy ponadto, ˙ze v
1
=
v
2
−
34, co po podstawieniu do powy ˙zszego równania daje
348v
2
+ (
v
2
−
34
)
v
2
=
600
(
v
2
−
34
)
348v
2
+
v
2
2
−
34v
2
=
600v
2
−
20400
v
2
2
−
286v
2
+
20400
=
0
∆
=
286
2
−
4
·
20400
=
196
=
14
2
v
2
=
286
−
14
2
=
136
∨
v
2
=
286
+
14
2
=
150.
Daje to odpowiednio v
1
=
102 lub v
1
=
116.
Odpowied´z: 102 km/h i 136 km/h, lub 116 km/h i 150 km/h
Z
ADANIE
31
(6
PKT
.)
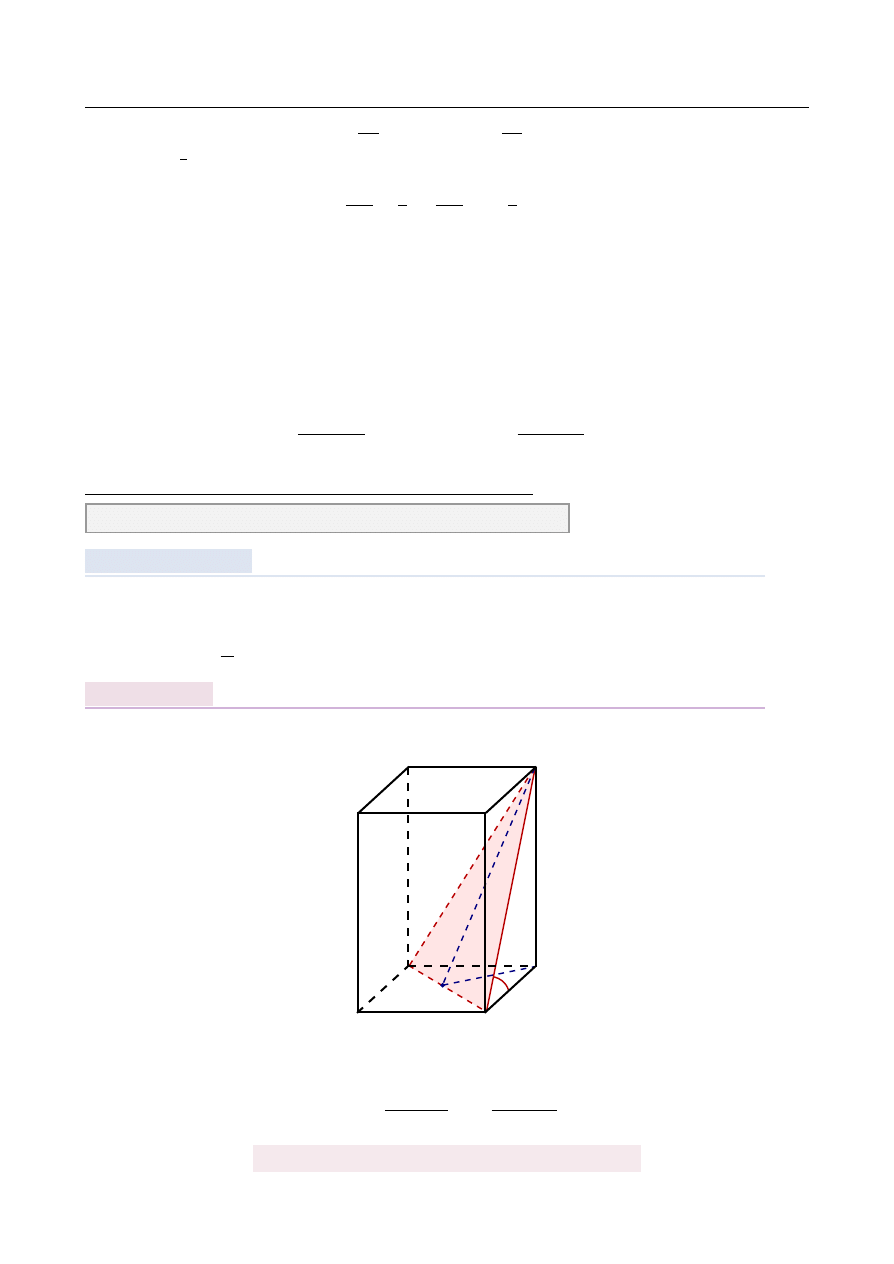
Dany jest graniastosłup prawidłowy czworok ˛
atny ABCDA
0
B
0
C
0
D
0
o podstawach ABCD i
A
0
B
0
C
0
D
0
, oraz kraw˛edziach bocznych AA
0
, BB
0
, CC
0
i DD
0
. Oblicz pole trójk ˛
ata BDC
0
wie-
dz ˛
ac, ˙ze przek ˛
atna ´sciany bocznej ma długo´s´c 13 i jest nachylona do podstawy pod α takim
k ˛
atem, ˙ze tg α
=
12
5
.
R
OZWI ˛
AZANIE
Rozpoczynamy od szkicowego rysunku.
D
A
B
C
A'
B'
C'
D'
a
a
b
α
b
E
13
Z podanego tangensa i długo´sci przek ˛
atnej ´sciany obliczymy długo´sci kraw˛edzi a i b
graniastosłupa. Na mocy twierdzenia Pitagorasa w trójk ˛
acie BCC
0
mamy
b
=
p
13
2
−
a
2
=
p
169
−
a
2
.
Materiał pobrany z serwisu
18
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Teraz korzystamy z podanego tangensa.
tg α
=
b
a
12
5
=
√
169
−
a
2
a
12a
=
5
p
169
−
a
2
/
()
2
144a
2
=
25
·
169
−
25a
2
169a
2
=
25
·
169
/ : 169
a
2
=
25
a
=
5.
Zatem b
=
√
169
−
a
2
=
12.
Znamy wi˛ec długo´s´c podstawy trójk ˛
ata równoramiennego BDC
0
:
BD
=
a
√
2
=
5
√
2.
Wysoko´s´c tego trójk ˛
ata obliczamy patrz ˛
ac na trójk ˛
at prostok ˛
atny ECC
0
.
EC
0
=
q
EC
2
+ (
CC
0
)
2
=
v
u
u
t
a
√
2
2
!
2
+
b
2
=
=
r
25
2
+
144
=
r
313
2
.
Zatem interesuj ˛
ace nas pole trójk ˛
ata BDC
0
jest równe
P
BDC
0
=
1
2
·
BD
·
EC
0
=
1
2
·
5
√
2
·
r
313
2
=
5
2
√
313.
Odpowied´z:
5
2
√
313
Materiał pobrany z serwisu
19
Wyszukiwarka
Podobne podstrony:
poziom podstawowy 24 marca 2012
REKOLEKCJE w Ziemi Świętej 5 12 marca 2011
Matura 12, matematyka, poziom podstawowy odpowiedzi
Egzamin maturalny z jęz włoskiego 2011 poziom podstawowy
Darmowa propozycja maturalna maj 2011 poziom podstawowy
Egzamin 2011 poziom podstawowy
Odpowiedzi do matury 2011 z WoS u Poziom podstawowy(1)
12.04.2011 Podstawy pedagogiki specjalnej wykład, podstawy pedagogiki specjalnej
Darmowa propozycja maturalna maj 2011 poziom podstawowy odpowiedzi
matematyka poziom podstawowy 2011 odpowiedzi pdf
Egzamin maturalny z jęz włoskiego 2011 poziom podstawowy
więcej podobnych podstron