
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
P
RÓBNY
E
GZAMIN
M
ATURALNY
Z
M
ATEMATYKI
Z
ESTAW PRZYGOTOWANY PRZEZ SERWIS
WWW
.
ZADANIA
.
INFO
POZIOM PODSTAWOWY
24
MARCA
2012
C
ZAS PRACY
: 170
MINUT
Zadania zamkni˛ete
Z
ADANIE
1
(1
PKT
.)
Liczba
3
√
3
·
√
3 jest równa
A)
4
√
3
B)
6
√
243
C)
3
√
81
D)
6
√
3
R
OZWI ˛
AZANIE
Liczymy
3
√
3
·
√
3
=
3
1
3
·
3
1
2
=
3
1
3
+
1
2
=
3
5
6
=
6
√
3
5
=
6
√
243.
Odpowied´z: B
Z
ADANIE
2
(1
PKT
.)
Rozwi ˛
azanie równania x
(
x
−
1
) +
36
=
x
(
x
+
3
)
nale ˙zy do przedziału
A)
(
3, 10
)
B)
(
11,
+
∞
)
C)
(−
5, 9
)
D)
(−
∞, 5
)
R
OZWI ˛
AZANIE
Przekształ´cmy dane równanie
x
(
x
−
1
) +
36
=
x
(
x
+
3
)
x
2
−
x
+
36
=
x
2
+
3x
36
=
4x
/ : 4
x
=
9.
Liczba ta nale ˙zy do przedziału
(
3, 10
)
.
Odpowied´z: A
Materiał pobrany z serwisu
1

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
3
(1
PKT
.)
Liczba b stanowi 40% liczby a. O ile procent liczba a jest wi˛eksza od liczby b?
A) 25%
B) 60%
C) 250%
D) 150%
R
OZWI ˛
AZANIE
Sposób I
Wiemy, ˙ze
b
=
0, 4a
Zatem
a
=
b
0, 4
=
2, 5b
=
b
+
1, 5b,
czyli liczba a jest wi˛eksza od b o 150%.
Sposób II
Aby ustali´c, która odpowied´z jest poprawna, posłu ˙zmy si˛e przykładem. Niech a
=
100,
wtedy b
=
40 i a jest wi˛eksze od b o 60, czyli o
60
40
=
1, 5
=
150%
liczby b.
Odpowied´z: D
Zadania
.info
Podobają Ci się nasze rozwiązania?
Pokaż je koleżankom i kolegom ze szkoły!
Z
ADANIE
4
(1
PKT
.)
Funkcja f
(
x
) = (
3
−
m
)
x
+
12 jest malej ˛
aca, gdy
A) m
> −
12
B) m
<
3
C) m
>
3
D) m
<
12
R
OZWI ˛
AZANIE
Funkcja liniowa jest malej ˛
aca je ˙zeli ma ujemny współczynnik kierunkowy (współczynnik
przy x), czyli
3
−
m
<
0
3
<
m.
Odpowied´z: C
Materiał pobrany z serwisu
2

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
5
(1
PKT
.)
Układ równa ´n
(
2x
−
4y
=
6
3x
+
ay
=
9
ma niesko ´nczenie wiele rozwi ˛
aza ´n, je´sli
A) a
= −
6
B) a
= −
2
C) a
=
6
D) a
=
3
R
OZWI ˛
AZANIE
Je ˙zeli układ ma mie´c niesko ´nczenie wiele rozwi ˛
aza ´n to drugie równanie musi by´c wielo-
krotno´sci ˛
a pierwszego. Poniewa ˙z 3x
=
3
2
·
2x tak b˛edzie, gdy
ay
=
3
2
· (−
4y
) = −
6y.
Zatem a
= −
6.
Odpowied´z: A
Z
ADANIE
6
(1
PKT
.)
Przez jakie wyra ˙zenie nale ˙zy przemno ˙zy´c sum˛e x
+
1, aby otrzyma´c sum˛e x
3
+
1?
A) x
2
+
1
B) x
2
−
1
C) x
2
−
x
+
1
D) x
2
+
x
+
1
R
OZWI ˛
AZANIE
Na mocy wzoru skróconego mno ˙zenia na sum˛e sze´scianów, mamy
x
3
+
1
= (
x
+
1
)(
x
2
−
x
+
1
)
.
Wyra ˙zenie x
+
1 musimy wi˛ec pomno ˙zy´c przez x
2
−
x
+
1.
Odpowied´z: C
Z
ADANIE
7
(1
PKT
.)
Je ˙zeli a
>
b
>
0 to wyra ˙zenie
|
2b
−
3a
| − |
2a
−
b
|
jest równe
A) a
−
3b
B) a
−
b
C) 3b
−
5a
D) 3b
−
2a
R
OZWI ˛
AZANIE
Je ˙zeli a
>
b
>
0 to
3a
>
3b
>
2b
oraz
2a
>
2b
>
b.
Zatem dane wyra ˙zenie jest równe
|
2b
−
3a
| − |
2a
−
b
| =
3a
−
2b
− (
2a
−
b
) =
3a
−
2b
−
2a
+
b
=
a
−
b.
Odpowied´z: B
Materiał pobrany z serwisu
3

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
8
(1
PKT
.)
Je ˙zeli log
x
1
9
= −
2 to liczba x jest równa
A) 3
B)
√
3
C)
1
81
D) 81
R
OZWI ˛
AZANIE
Z
mamy
log
x
1
9
= −
2
⇐⇒
x
−
2
=
1
9
,
czyli
1
x
2
=
1
9
x
2
=
9
=
3
2
x
=
3.
Odpowied´z: A
Z
ADANIE
9
(1
PKT
.)
Zbiorem rozwi ˛
aza ´n nierówno´sci
1
−
x
x
+
2
>
0 jest
A)
(
1,
+
∞
)
B)
(−
2, 1
)
C)
(−
∞, 1
)
D)
(−
∞,
−
2
) ∪ (
1,
+
∞
)
R
OZWI ˛
AZANIE
Nierówno´s´c b˛edzie spełniona je ˙zeli licznik i mianownik b˛ed ˛
a tego samego znaku, czyli do-
kładnie wtedy, gdy b˛edzie spełniona nierówno´s´c kwadratowa
(
1
−
x
)(
x
+
2
) >
0
/
· (−
1
)
(
x
−
1
)(
x
+
2
) <
0
x
∈ (−
2, 1
)
.
Odpowied´z: B
Z
ADANIE
10
(1
PKT
.)
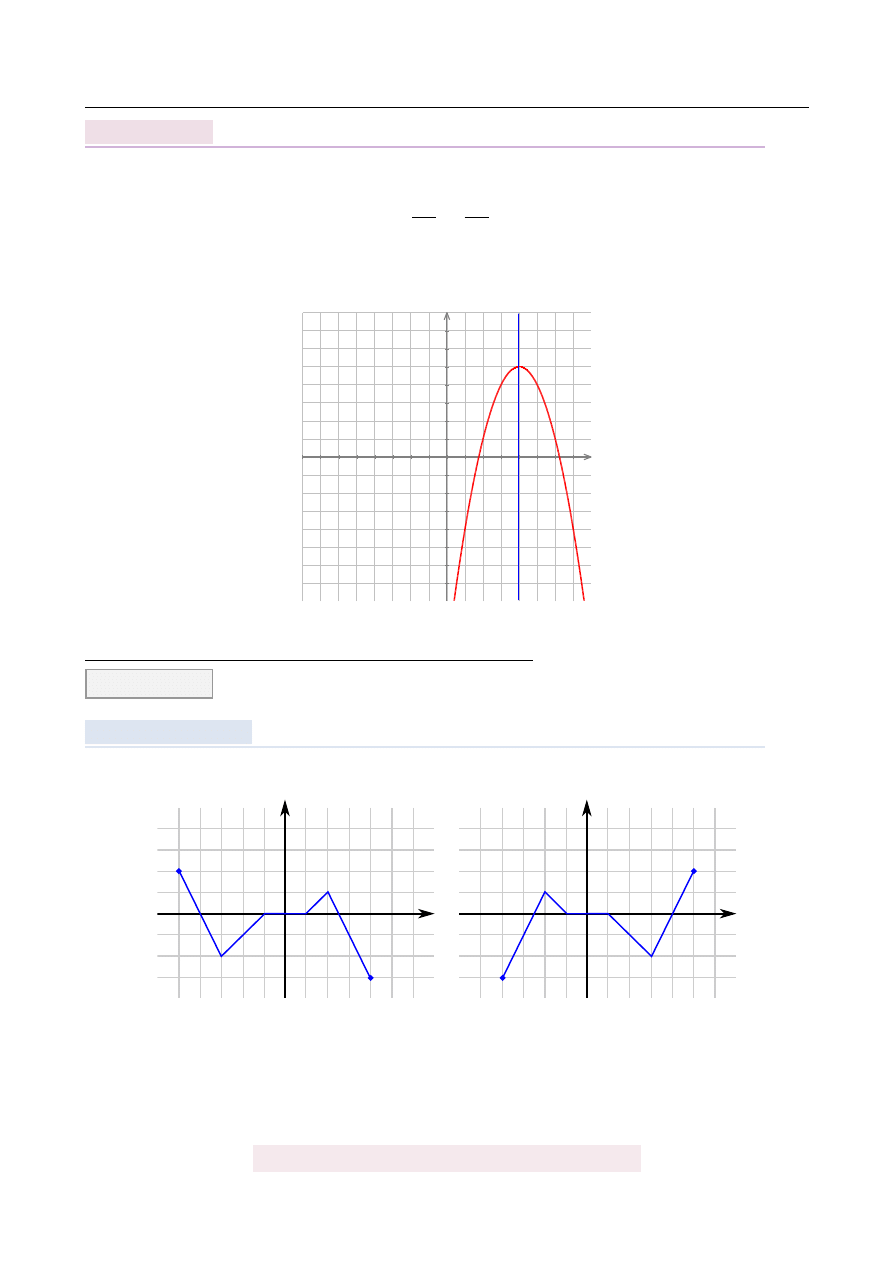
Wierzchołek paraboli y
= −
x
2
+
8x
−
11 le ˙zy na prostej o równaniu
A) x
= −
8
B) x
=
8
C) x
=
4
D) x
= −
4
Materiał pobrany z serwisu
4
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Liczymy pierwsz ˛
a współrz˛edn ˛
a wierzchołka
x
w
=
−
b
2a
=
−
8
−
2
=
4.
Zatem punkt ten le ˙zy na pionowej prostej x
=
4.
Na koniec obrazek.
-5
-1
+1
+5
x
-5
-1
+1
+5
y
x=4
Odpowied´z: C
Z
ADANIE
11
(1
PKT
.)
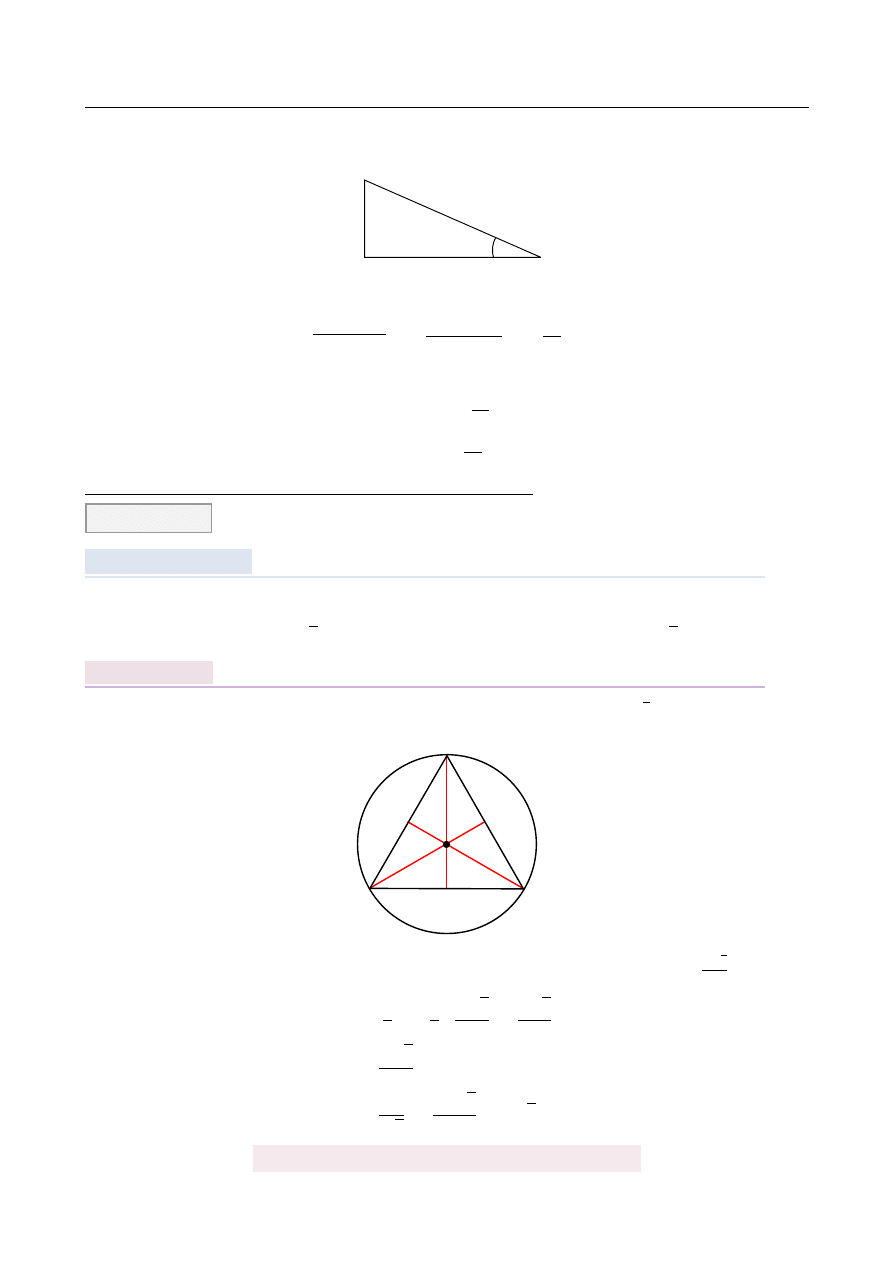
Na rysunku 1 jest przedstawiony wykres funkcji y
=
f
(
x
)
.
0
1
1
x
y
y=f(x)
0
1
1
x
y
Rys. 1
Rys. 2
Funkcja przedstawiona na rysunku 2 jest okre´slona wzorem
A) y
= −
f
(
x
)
B) y
=
f
(−
x
)
C) y
=
f
(
x
−
1
)
D) y
= −
1
+
f
(
x
)
Materiał pobrany z serwisu
5

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Wykres z rysunku 2 otrzymujemy odbijaj ˛
ac wykres y
=
f
(
x
)
wzgl˛edem osi Oy, czyli jest to
wykres g
(
x
) =
f
(−
x
)
.
Odpowied´z: B
Z
ADANIE
12
(1
PKT
.)
W ci ˛
agu geometrycznym
(
a
n
)
mamy a
4
=
54 i a
5
=
162. Wtedy wyraz a
3
jest równy
A) 6
B) 18
C) 2
D) 27
R
OZWI ˛
AZANIE
Skoro mamy podane dwa kolejne wyrazy ci ˛
agu geometrycznego, to wiemy, ˙ze jego iloraz
jest równy
q
=
a
5
a
4
=
162
54
=
3.
W takim razie
a
3
=
a
4
q
=
54
3
=
18.
Odpowied´z: B
Z
ADANIE
13
(1
PKT
.)
K ˛
at α jest ostry i cos α
=
12
13
. Wtedy
A) sin α
=
5
13
oraz tg α
=
12
5
B) sin α
=
5
13
oraz tg α
=
5
12
C) sin α
=
5
12
oraz tg α
=
5
13
D) sin α
=
5
13
oraz tg α
=
5
13
R
OZWI ˛
AZANIE
Sposób I
Na mocy jedynki trygonometrycznej
sin α
=
p
1
−
cos
2
α
=
r
1
−
144
169
=
r
25
169
=
5
13
.
Zatem
tg α
=
sin α
cos α
=
5
13
12
13
=
5
12
.
Sposób II
Materiał pobrany z serwisu
6
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Szkicujemy trójk ˛
at prostok ˛
atny o przyprostok ˛
atnej długo´sci 12 i przeciwprostok ˛
atnej długo-
´sci 13.
5
12
13
α
Ma mocy twierdzenia Pitagorasa druga przyprostok ˛
atna ma długo´s´c
p
13
2
−
12
2
=
√
169
−
144
=
√
25
=
5.
Zatem
sin α
=
5
13
tg α
=
5
12
.
Odpowied´z: B
Z
ADANIE
14
(1
PKT
.)
Promie ´n okr˛egu opisanego na trójk ˛
acie równobocznym ma długo´s´c 4. Zatem bok tego trój-
k ˛
ata ma długo´s´c
A) 12
B) 4
√
3
C) 4
D) 6
√
3
R
OZWI ˛
AZANIE
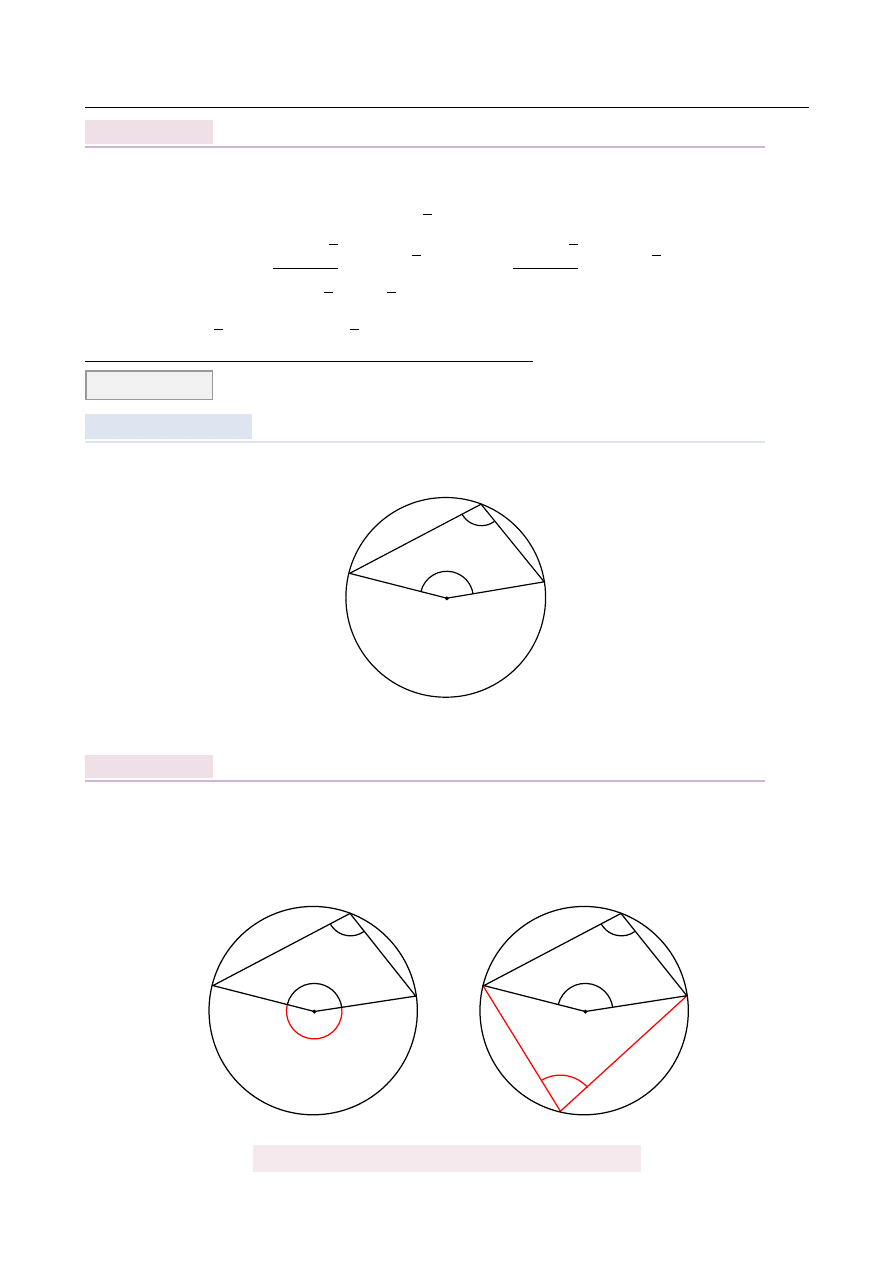
Promie ´n okr˛egu opisanego na trójk ˛
acie równobocznym to dokładnie
2
3
jego wysoko´sci (bo
dokładnie tak dziel ˛
a si˛e wysoko´sci w trójk ˛
acie równobocznym).
R
R
R
Zatem korzystaj ˛
ac ze wzoru na wysoko´s´c w trójk ˛
acie równobocznym h
=
a
√
3
2
mamy
R
=
2
3
h
=
2
3
·
a
√
3
2
=
a
√
3
3
4
=
a
√
3
3
a
=
12
√
3
=
12
√
3
3
=
4
√
3.
Materiał pobrany z serwisu
7

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Odpowied´z: B
Z
ADANIE
15
(1
PKT
.)
Suma wszystkich dwucyfrowych liczb parzystych jest równa
A) 2376
B) 2484
C) 2332
D) 2430
R
OZWI ˛
AZANIE
Sposób I
Dwucyfrowe liczby parzyste to
10, 12, . . . , 98.
Tworz ˛
a one ci ˛
ag arytmetyczny, w którym a
1
=
10 i r
=
2. Sprawd´zmy, którym wyrazem
tego ci ˛
agu jest liczba 98.
98
=
a
n
=
a
1
+ (
n
−
1
)
r
98
=
10
+
2
(
n
−
1
)
88
=
2
(
n
−
1
)
/ : 2
44
=
n
−
1
n
=
45.
Korzystaj ˛
ac ze wzoru na sum˛e pocz ˛
atkowych wyrazów ci ˛
agu arytmetycznego mamy
S
45
=
a
1
+
a
45
2
·
45
=
10
+
98
2
·
45
=
54
·
45
=
2430
Sposób II
Mamy obliczy´c sum˛e
S
=
10
+
12
+ · +
98
=
2
(
5
+
6
+ · · · +
49
)
.
W nawiasie mamy 49
−
4
=
45 kolejnych liczb naturalnych, wi˛ec ze wzoru na sum˛e kolej-
nych wyrazów ci ˛
agu arytmetycznego mamy
S
=
2
(
5
+
6
+ · · · +
49
) =
2
·
5
+
49
2
·
45
=
54
·
45
=
2430
Odpowied´z: D
Z
ADANIE
16
(1
PKT
.)
Ci ˛
ag
(
a
n
)
okre´slony jest wzorem a
n
=
n
2
−
4n
−
1, gdzie n
>
1. Liczba ujemnych wyrazów
tego ci ˛
agu jest równa
A) 2
B) 3
C) 4
D) 5
Materiał pobrany z serwisu
8
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Rozwi ˛
azujemy nierówno´s´c
n
2
−
4n
−
1
<
0
∆
=
16
+
4
=
20
= (
2
√
5
)
2
n
=
4
−
2
√
5
2
=
2
−
√
5
∨
n
=
4
+
2
√
5
2
=
2
+
√
5
n
∈ (
2
−
√
5, 2
+
√
5
)
.
Poniewa ˙z 2
−
√
5
≈ −
0, 2 i 2
+
√
5
≈
4, 2 wyrazami ujemnymi s ˛
a: a
1
, a
2
, a
3
i a
4
.
Odpowied´z: C
Z
ADANIE
17
(1
PKT
.)
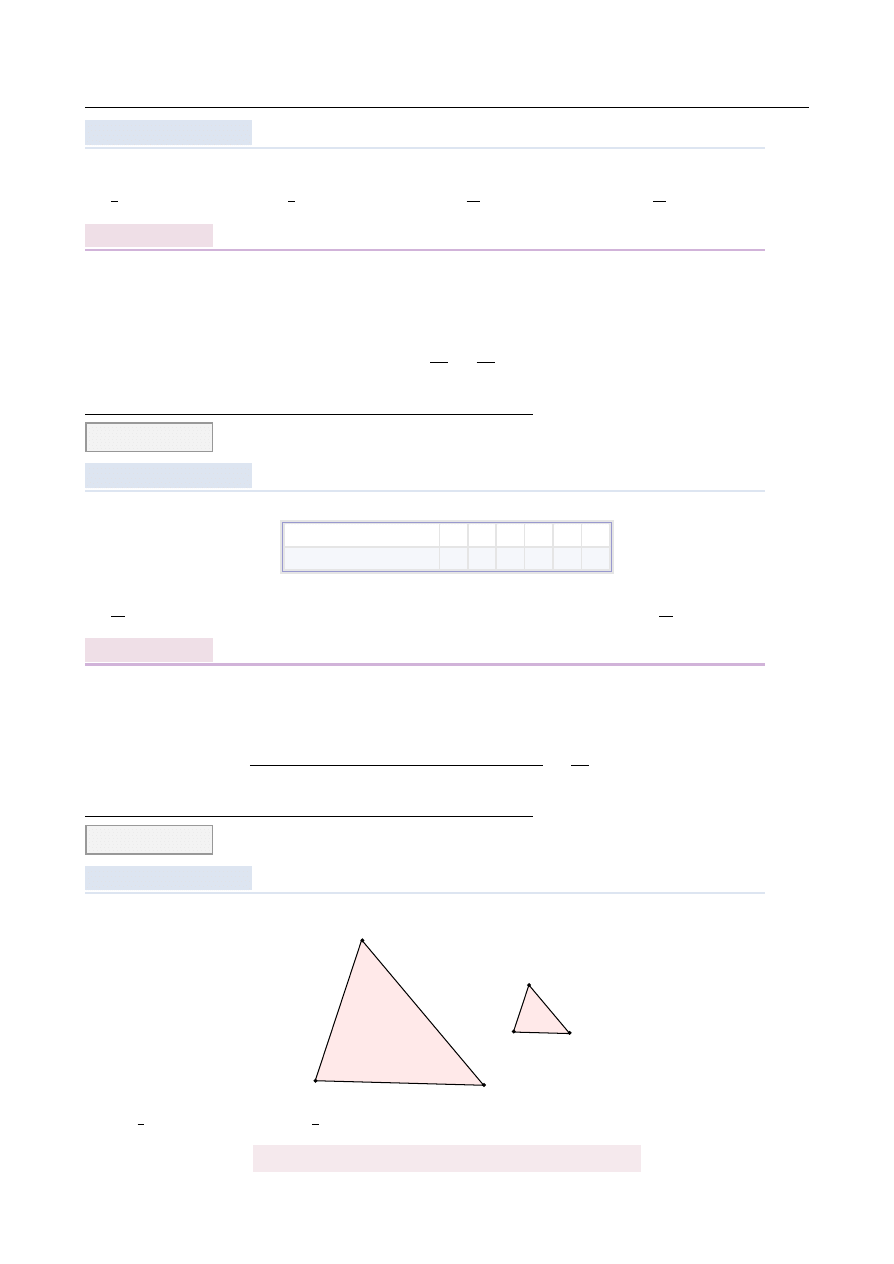
Punkt O jest ´srodkiem okr˛egu. K ˛
at wpisany α ma miar˛e
A
B
C
O
150
o
α
A) 75
◦
B) 95
◦
C) 105
◦
D) 110
◦
R
OZWI ˛
AZANIE
Sposób I
Na mocy twierdzenia o k ˛
atach wpisanym i ´srodkowym opartych na tym samym łuku, k ˛
at
wkl˛esły AOC ma miar˛e 2α.
A
B
C
O
150
o
α
2α
A
B
C
O
150
o
α
D
75
o
Materiał pobrany z serwisu
9

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Zatem
2α
+
150
◦
=
360
◦
2α
=
210
◦
α
=
105
◦
.
Sposób II
Wybierzmy punkt D na łuku AC tak jak na prawym obrazku. Wtedy
]
D
=
1
2
]
AOC
=
75
◦
.
Poniewa ˙z w czworok ˛
acie wpisanym w okr ˛
ag sumy przeciwległych k ˛
atów s ˛
a równe 180
◦
,
wi˛ec
α
= ]
B
=
180
◦
− ]
D
=
105
◦
.
Odpowied´z: C
Z
ADANIE
18
(1
PKT
.)
Przekrój osiowy walca jest kwadratem o polu 8. Pole powierzchni całkowitej tego walca jest
równe
A) 12π
B) 24π
C) 12
√
2π
D) 6π
R
OZWI ˛
AZANIE
Oznaczmy promie ´n podstawy walca przez r.
2r
r
r
Wtedy bok kwadratu w przekroju jest równy 2r, czyli
8
= (
2r
)
2
=
4r
2
2
=
r
2
r
=
√
2.
Liczymy pole powierzchni całkowitej.
P
c
=
2P
p
+
P
b
=
2
·
πr
2
+
2πr
· (
2r
) =
6πr
2
=
12π.
Odpowied´z: A
Materiał pobrany z serwisu
10
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
19
(1
PKT
.)
Rzucamy dwa razy symetryczn ˛
a sze´scienn ˛
a kostk ˛
a do gry. Prawdopodobie ´nstwo otrzyma-
nia sumy oczek równej cztery wynosi
A)
1
6
B)
1
9
C)
1
12
D)
1
18
R
OZWI ˛
AZANIE
Je ˙zeli za zdarzenia elementarne przyjmiemy pary otrzymanych liczb oczek to
|
Ω
| =
6
·
6
=
36.
Zdarzenia sprzyjaj ˛
ace s ˛
a trzy:
(
1, 3
)
,
(
2, 2
)
,
(
3, 1
)
. Zatem
p
=
3
36
=
1
12
.
Odpowied´z: C
Z
ADANIE
20
(1
PKT
.)
Rzucaj ˛
ac wielokrotnie symetryczn ˛
a kostk ˛
a do gry otrzymano nast˛epuj ˛
ace liczby oczek
Liczba oczek
1
2
3
4
5
6
Liczba wyników
5
3
4
1
5
2
´Srednia liczba oczek otrzymana w jednym rzucie jest równa.
A)
32
3
B) 3,5
C) 3,2
D)
10
3
R
OZWI ˛
AZANIE
Wszystkich danych jest
5
+
3
+
4
+
1
+
5
+
2
=
20,
wi˛ec ´srednia jest równa
1
·
5
+
2
·
3
+
3
·
4
+
4
·
1
+
5
·
5
+
6
·
2
20
=
64
20
=
3, 2.
Odpowied´z: C
Z
ADANIE
21
(1
PKT
.)
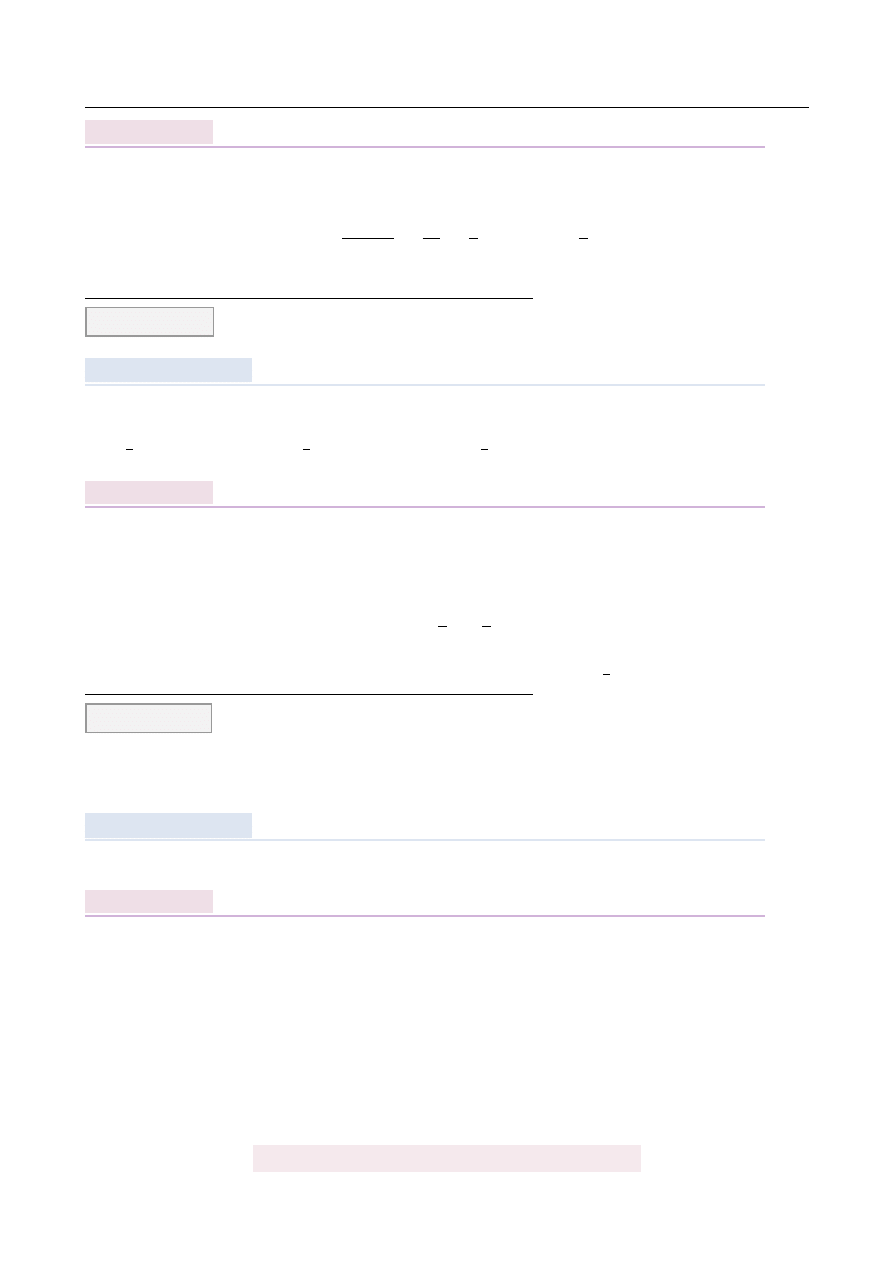
Znajd´z skal˛e podobie ´nstwa trójk ˛
ata A
0
B
0
C
0
do trójk ˛
ata ABC:
A
B
C
C'
B'
A'
Pole ABC=18
Pole A'B'C'=2
A)
1
3
B)
1
9
C) 3
D) 9
Materiał pobrany z serwisu
11
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Oznaczmy przez k szukan ˛
a skal˛e podobie ´nstwa trójk ˛
ata A
0
B
0
C
0
do trójk ˛
ata ABC. Poniewa ˙z
pole zmienia si˛e jak kwadrat skali podobie ´nstwa, mamy
k
2
=
P
A
0
B
0
C
0
P
ABC
=
2
18
=
1
9
⇒
k
=
1
3
.
Odpowied´z: A
Z
ADANIE
22
(1
PKT
.)
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 2x
−
3y
=
5 jest rów-
ny
A)
−
3
2
B)
2
3
C)
3
2
D) 2
R
OZWI ˛
AZANIE
Proste y
=
ax
+
b i y
=
cx
+
d s ˛
a równoległe je ˙zeli maj ˛
a takie same współczynniki kierun-
kowe, czyli gdy a
=
c. Równanie danej prostej mo ˙zna zapisa´c w postaci
3y
=
2x
−
5
y
=
2
3
x
−
5
3
Zatem współczynnik kierunkowy prostej równoległej jest równy
2
3
.
Odpowied´z: B
Zadania otwarte
Z
ADANIE
23
(2
PKT
.)
Rozwi ˛
a ˙z nierówno´s´c 9x
2
+
12x
+
4
6
0.
R
OZWI ˛
AZANIE
Liczymy
9x
2
+
12x
+
4
6
0
∆
=
12
2
−
4
·
9
·
4
=
144
−
144
=
0
Skoro
∆
=
0, parabola b˛ed ˛
aca wykresem lewej strony nierówno´sci jest styczna do osi Ox.
Materiał pobrany z serwisu
12

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
-5
-1
+1
+5
x
-5
-1
+1
+5
y
Rozwi ˛
azaniem nierówno´sci jest wi˛ec jedynie miejsce zerowe.
x
=
−
12
2
·
9
= −
2
3
.
Odpowied´z: x
= −
2
3
Z
ADANIE
24
(2
PKT
.)
Udowodnij, ˙ze iloczyn kolejnych liczb naturalnych od 1 do 21, czyli 1
·
2
·
3
·
. . .
·
21, jest
podzielny przez 3
9
.
R
OZWI ˛
AZANIE
Oczywi´scie iloczyn ten jest podzielny przez
3
·
6
·
9
·
12
·
15
·
18
·
21
=
=
3
· (
3
·
2
) ·
3
2
· (
3
·
4
) · (
3
·
5
) · (
3
2
·
2
) · (
3
·
7
) =
=
3
1
+
1
+
2
+
1
+
1
+
2
+
1
·
2
4
·
5
·
7
=
3
9
·
2
4
·
5
·
7.
W szczególno´sci, dany iloczyn dzieli si˛e przez 3
9
.
Z
ADANIE
25
(2
PKT
.)
Liczby
−
x
2
,
−
8, x w podanej kolejno´sci tworz ˛
a ci ˛
ag geometryczny. Oblicz x.
R
OZWI ˛
AZANIE
Je ˙zeli liczby a, b, c tworz ˛
a ci ˛
ag geometryczny to b
2
=
ac. Mamy zatem równanie
(−
8
)
2
= (−
x
2
) ·
x
64
= −
x
3
x
3
= −
64
x
= −
4.
Odpowied´z: x
= −
4
Materiał pobrany z serwisu
13
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
26
(2
PKT
.)
Rozwi ˛
a ˙z równanie x
4
+
2x
3
−
4x
2
−
8x
=
0.
R
OZWI ˛
AZANIE
Wida´c, ˙ze mo ˙zemy wył ˛
aczy´c x i
(
x
+
2
)
przed nawias.
x
4
+
2x
3
−
4x
2
−
8x
=
x
3
(
x
+
2
) −
4x
(
x
+
2
) = (
x
3
−
4x
)(
x
+
2
) =
= (
x
2
−
4
)
x
(
x
+
2
) = (
x
−
2
)(
x
+
2
)
x
(
x
+
2
)
.
Równanie ma wi˛ec 3 pierwiastki:
−
2, 0, 2.
Odpowied´z:
{−
2, 0, 2
}
Z
ADANIE
27
(2
PKT
.)
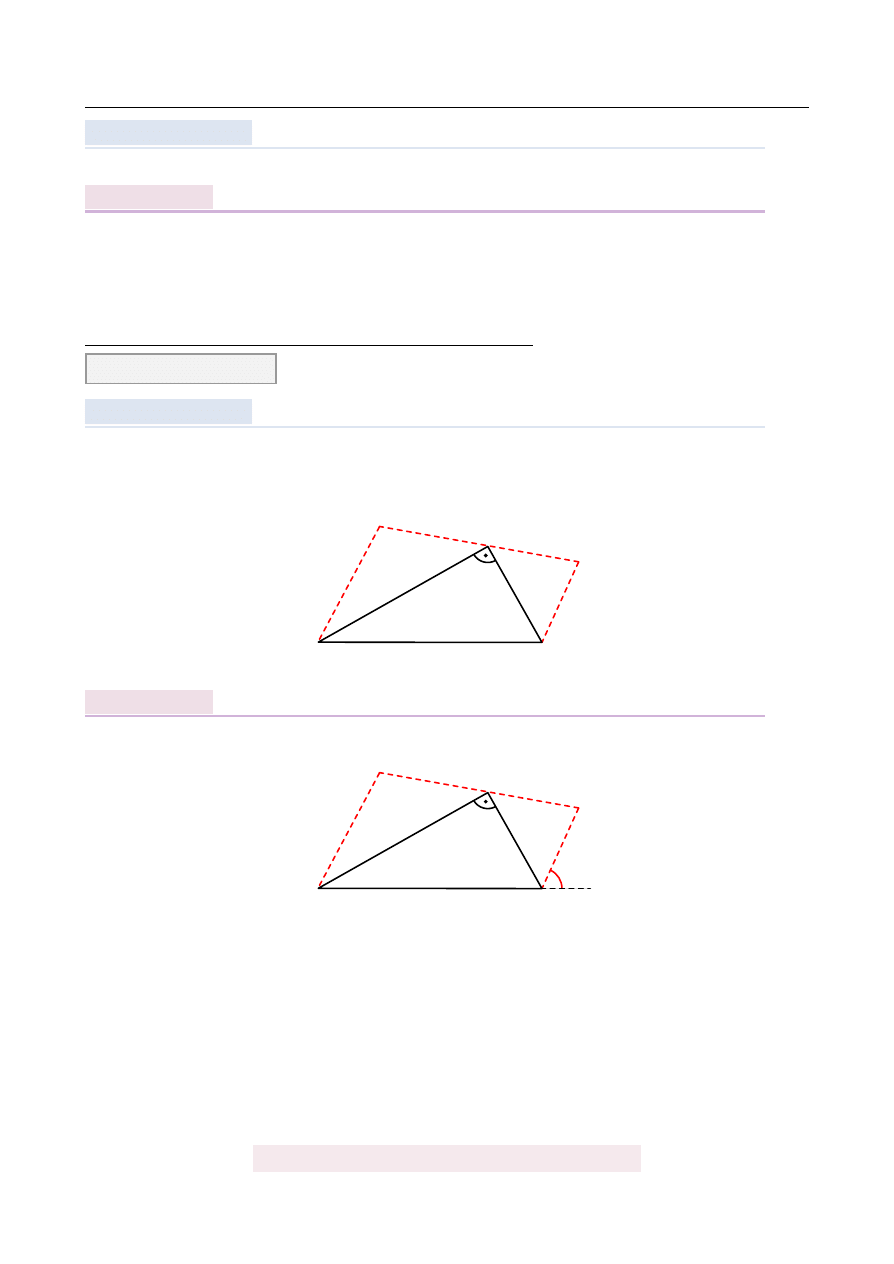
Na przyprostok ˛
atnych AC i BC trójk ˛
ata prostok ˛
atnego ABC zbudowano trójk ˛
aty równora-
mienne CDA i BEC w ten sposób, ˙ze
|
AD
| = |
CD
|
,
|
BE
| = |
CE
|
oraz punkty DCE le ˙z ˛
a na
jednej prostej. Wyka ˙z, ˙ze proste AD i BE s ˛
a równoległe.
A
B
C
E
D
R
OZWI ˛
AZANIE
Oznaczmy
]
CAD
= ]
ACD
=
α
oraz
]
BAC
=
β
.
A
B
C
E
D
α
α
β
α+β
Mamy wtedy
]
ABC
=
180
◦
− ]
BAC
−
90
◦
=
90
◦
−
β
]
CBE
= ]
BCE
=
180
◦
−
90
◦
− ]
ACD
=
90
◦
−
α
.
To oznacza, ˙ze
]
ABE
= ]
ABC
+ ]
CBE
=
90
◦
−
β
+
90
◦
−
α
=
180
◦
− (
α
+
β
)
.
To oznacza, ˙ze proste AD i BE przecinaj ˛
a prost ˛
a AB pod tym samym k ˛
atem, czyli s ˛
a równo-
ległe.
Materiał pobrany z serwisu
14
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
28
(2
PKT
.)
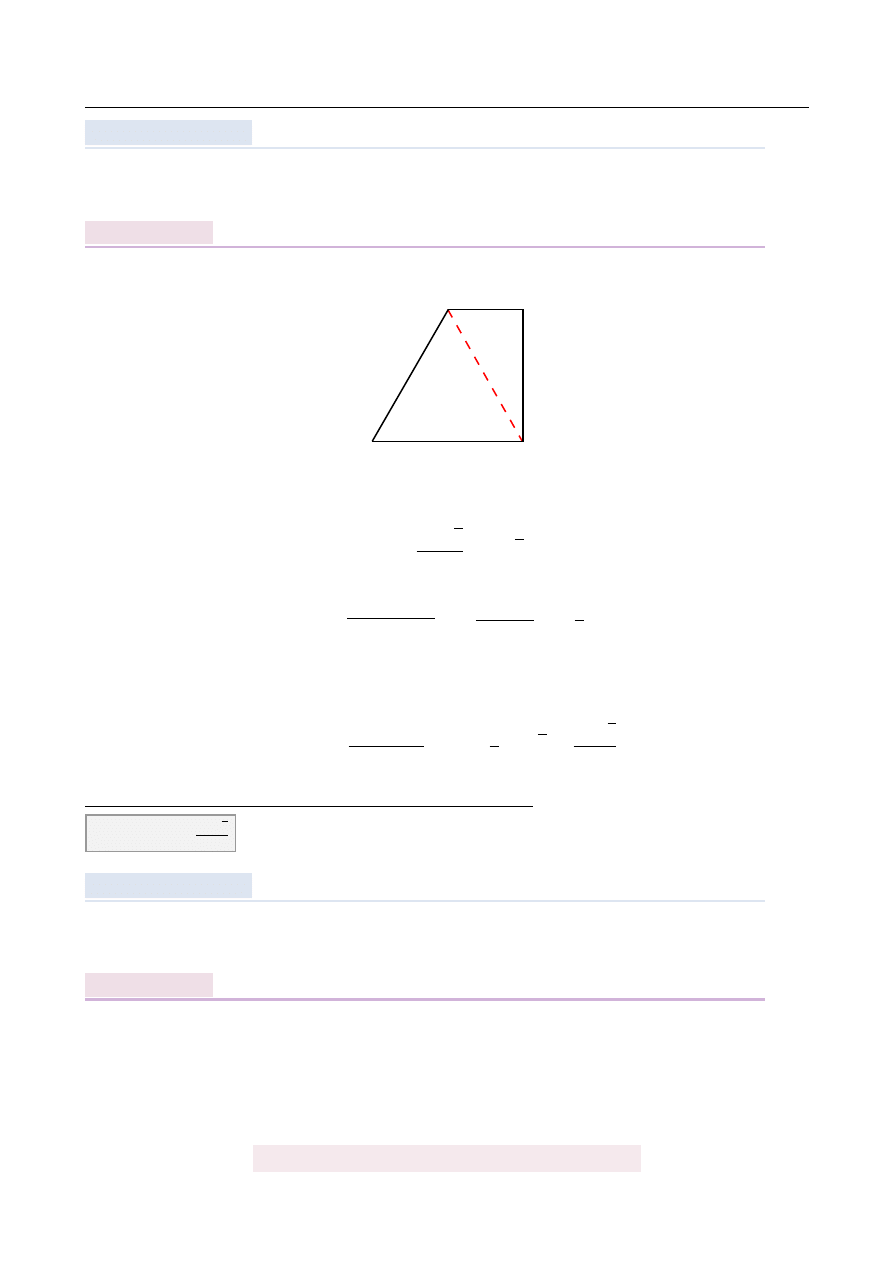
W trapezie prostok ˛
atnym krótsza przek ˛
atna dzieli go na trójk ˛
at prostok ˛
atny i trójk ˛
at rów-
noboczny. Dłu ˙zsza podstawa trapezu jest równa 6. Oblicz pole tego trapezu.
R
OZWI ˛
AZANIE
Rozpoczynamy od rysunku.
6
A
B
C
D
Zauwa ˙zmy, ˙ze wysoko´s´c BC trapezu ma długo´s´c równ ˛
a wysoko´sci trójk ˛
ata równobocz-
nego ABC, czyli
BC
=
6
·
√
3
2
=
3
√
3.
Długo´s´c podstawy CD wyliczamy z twierdzenia Pitagorasa w trójk ˛
acie BCD.
CD
=
p
BD
2
−
BC
2
=
√
36
−
27
=
√
9
=
3
(mogli´smy te ˙z zauwa ˙zy´c, ˙ze CD ma długo´s´c równ ˛
a połowie długo´sci podstawy AB).
Zatem pole trapezu jest równe
P
ABCD
=
AB
+
CD
2
·
BC
=
9
2
·
3
√
3
=
27
√
3
2
.
Odpowied´z:
27
√
3
2
Z
ADANIE
29
(2
PKT
.)
Napisz równanie symetralnej boku AB trójk ˛
ata ABC o wierzchołkach A
= (
3, 2
)
, B
= (
10, 2
)
i C
= (
5, 8
)
.
R
OZWI ˛
AZANIE
Zaczynamy od szkicowego rysunku.
Materiał pobrany z serwisu
15

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
-1
+5
+10
x
-1
+1
+5
+10
y
A
B
C
D
Z obrazka wida´c, ˙ze szukana prosta jest pionow ˛
a prost ˛
a przechodz ˛
ac ˛
a przez ´srodek D
odcinka AB. Punkt D ma współrz˛edne
D
=
3
+
10
2
,
2
+
2
2
=
13
2
, 2
.
Jest to wi˛ec prosta x
=
13
2
.
Odpowied´z: x
=
13
2
Z
ADANIE
30
(4
PKT
.)
Dane s ˛
a trzy sze´scienne kostki do gry: czerwona, niebieska i zielona. Oblicz prawdopodo-
bie ´nstwo zdarzenia polegaj ˛
acego na tym, ˙ze przy jednokrotnym rzucie trzema kostkami
liczba otrzymana na niebieskiej kostce jest wi˛eksza ni ˙z suma liczb otrzymanych na dwóch
pozostałych kostkach.
R
OZWI ˛
AZANIE
Za zdarzenia sprzyjaj ˛
ace przyjmijmy trójki wyrzuconych oczek, przy czym jako pierwszy
b˛edziemy zapisywa´c wynik otrzymany na niebieskiej kostce, jako drugi wynik otrzymany
na czerwonej kostce, i wreszcie na ko ´ncu wynik z zielonej kostki. Mamy zatem
|
Ω
| =
6
·
6
·
6
=
6
3
.
Policzmy ile jest zdarze ´n sprzyjaj ˛
acych.
Je ˙zeli na niebieskiej kostce wypadło 1 lub 2, to suma na pozostałych kostkach na pewno
nie jest mniejsza, wi˛ec nie ma zdarze ´n sprzyjaj ˛
acych tego typu.
Je ˙zeli na niebieskiej kostce wypadło 3, to na pozostałych kostkach musz ˛
a by´c dwie je-
dynki, wi˛ec mamy w tym przypadku jedno zdarzenie sprzyjaj ˛
ace:
(
3, 1, 1
)
.
Materiał pobrany z serwisu
16
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Wypisujemy zdarzenia sprzyjaj ˛
ace z 4 na pierwszym miejscu
(
4, 1, 1
)
,
(
4, 1, 2
)
,
(
4, 2, 1
)
.
Teraz zdarzenia z 5 na pierwszym miejscu
(
5, 1, 1
)
,
(
5, 1, 2
)
,
(
5, 1, 3
)
(
5, 2, 1
)
,
(
5, 2, 2
)
(
5, 3, 1
)
No i na koniec zdarzenia z 6 na pierwszym miejscu.
(
6, 1, 1
)
,
(
6, 1, 2
)
,
(
6, 1, 3
)
,
(
6, 1, 4
)
(
6, 2, 1
)
,
(
6, 2, 2
)
,
(
6, 2, 3
)
(
6, 3, 1
)
,
(
6, 3, 2
)
(
6, 4, 1
)
.
W sumie jest wi˛ec
1
+
3
+
6
+
10
=
20
zdarze ´n sprzyjaj ˛
acych i prawdopodobie ´nstwo wynosi
20
6
·
6
·
6
=
5
3
·
3
·
6
=
5
54
.
Odpowied´z:
5
54
Z
ADANIE
31
(4
PKT
.)
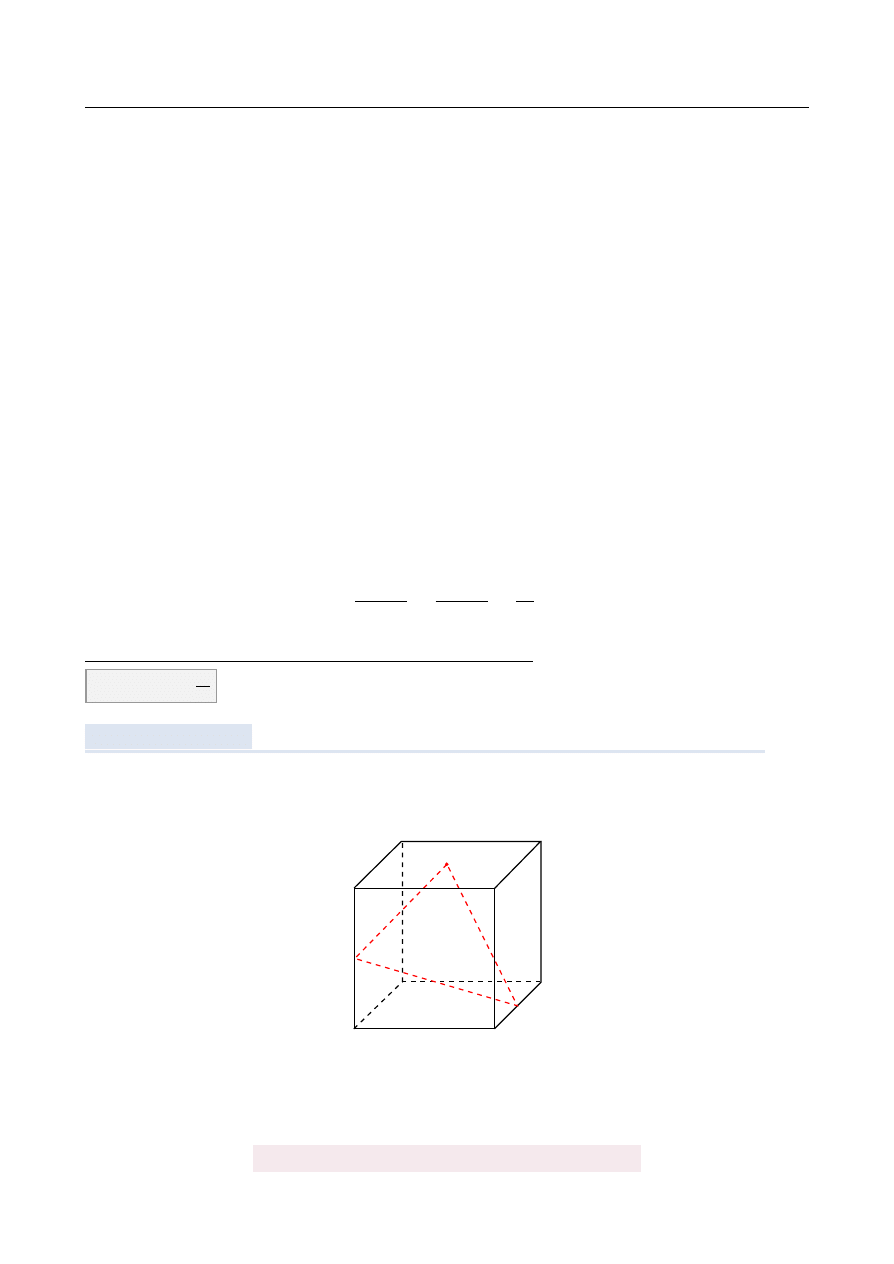
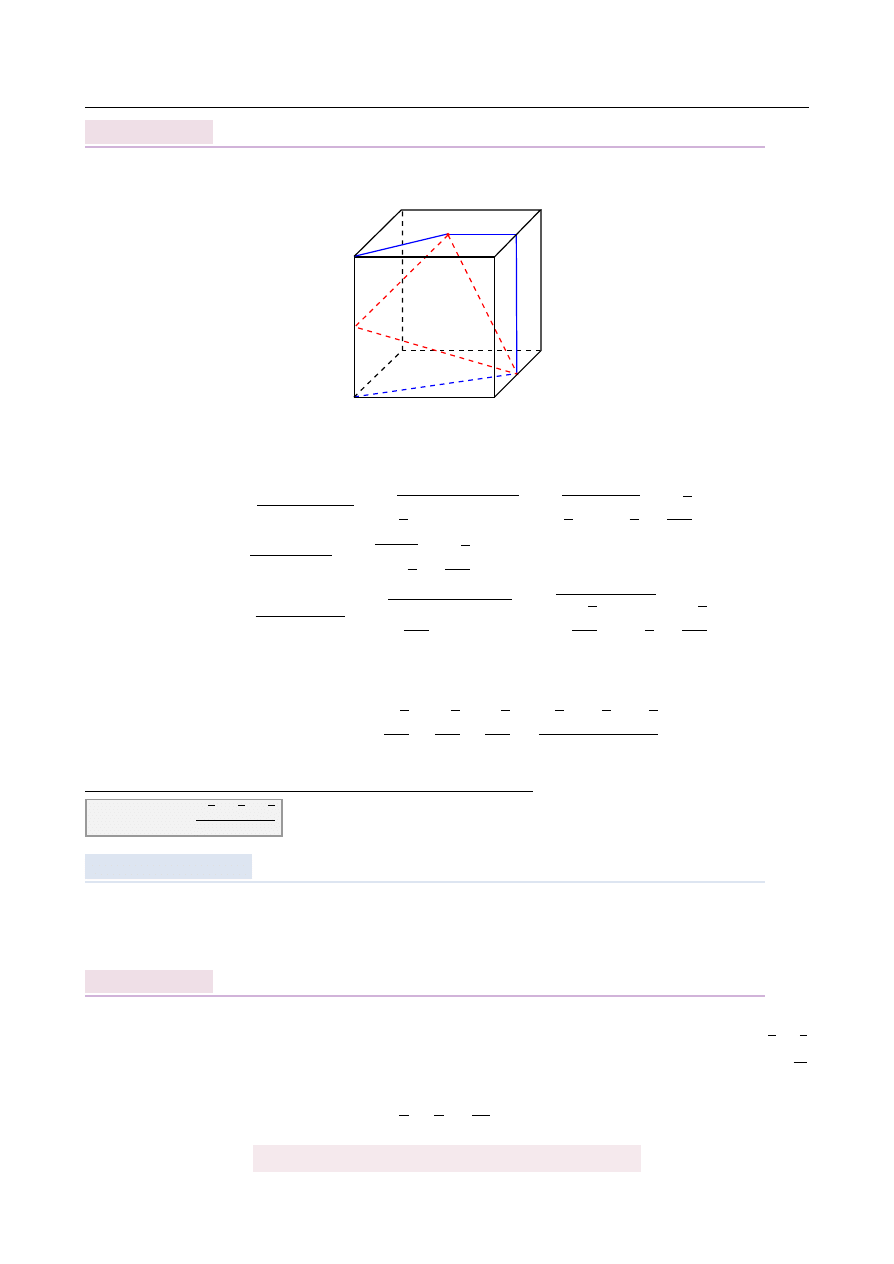
Punkty K i M s ˛
a ´srodkami kraw˛edzi BC i AE sze´scianu ABCDEFGH o kraw˛edzi długo´sci 1.
Punkt L jest ´srodkiem ´sciany EFGH (zobacz rysunek). Oblicz obwód trójk ˛
ata KLM.
A
B
C
D
E
F
G
H
M
K
L
Materiał pobrany z serwisu
17
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Niech S b˛edzie ´srodkiem kraw˛edzi FG i dorysujmy odcinki AK, KS, SL i LE.
A
B
C
D
E
F
G
H
M
K
L
S
Otrzymali´smy w ten sposób trzy trójk ˛
aty prostok ˛
atne AKM, KSL i LEM. W ka ˙zdym z
nich liczymy z twierdzenia Pitagorasa długo´s´c przeciwprostok ˛
atnej.
MK
=
p
AM
2
+
AK
2
=
r
1
4
+
AB
2
+
BK
2
=
r
1
4
+
1
+
1
4
=
√
6
2
KL
=
p
KS
2
+
SL
2
=
r
1
+
1
4
=
√
5
2
LM
=
p
LE
2
+
EM
2
=
s
EG
2
2
+
EM
2
=
v
u
u
t
√
2
2
!
2
+
1
4
=
√
3
2
.
Obwód trójk ˛
ata KLM jest wi˛ec równy
MK
+
KL
+
LM
=
√
6
2
+
√
5
2
+
√
3
2
=
√
3
+
√
5
+
√
6
2
.
Odpowied´z:
√
3
+
√
5
+
√
6
2
Z
ADANIE
32
(6
PKT
.)
Pierwsza pompa napełnia zbiornik w czasie o 15 godzin krótszym ni ˙z druga pompa. Je ˙zeli
obie pompy pracuj ˛
a jednocze´snie, to zbiornik zostaje napełniony w czasie 10 godzin. Ile
godzin potrzeba na napełnienie zbiornika przy pomocy ka ˙zdej z pomp?
R
OZWI ˛
AZANIE
Powiedzmy, ˙ze pierwsza pompa napełnia zbiornik w czasie x, a druga w czasie y godzin. W
takim razie x
=
y
−
15 oraz w ci ˛
agu jednej godziny pompy, pracuj ˛
ac razem, napełniaj ˛
a
1
x
+
1
y
cz˛e´s´c zbiornika. Z drugiej strony, z tre´sci zadania wiemy, ˙ze w ci ˛
agu godziny napełniaj ˛
a
1
10
zbiornika. Mamy st ˛
ad równanie
1
x
+
1
y
=
1
10
.
Materiał pobrany z serwisu
18

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Podstawiamy w tym równaniu x
=
y
−
15
1
y
−
15
+
1
y
=
1
10
/
·
10y
(
y
−
15
)
10y
+
10
(
y
−
15
) =
y
(
y
−
15
)
10y
+
10y
−
150
=
y
2
−
15y
y
2
−
35y
+
150
=
0
∆
=
35
2
−
4
·
150
=
625
=
25
2
y
=
35
−
25
2
=
5
lub
y
=
35
+
25
2
=
30.
Pierwsza odpowied´z daje x
=
y
−
15
= −
10, co nie jest mo ˙zliwe. Zatem y
=
30 i x
=
15.
Odpowied´z: 15 i 30 godzin.
Materiał pobrany z serwisu
19
Wyszukiwarka
Podobne podstrony:
poziom rozszerzony 24 marca 2012
psychologia wykład 24 marca 2012 roku, GWSH Żory Administracja, semestr II, Podstawy psychologii
Jezyk hiszpanski poziom podstawowy Egzamin maturalny 2012
Jezyk rosyjski poziom podstawowy Egzamin maturalny 2012
Jezyk francuski poziom podstawowy Egzamin maturalny 2012
Jezyk niemiecki poziom podstawowy Egzamin maturalny 2012
Jezyk rosyjski poziom podstawowy Egzamin maturalny 2012
Jezyk francuski poziom podstawowy Egzamin maturalny 2012
poziom podstawowy 12 marca 2011
Filozofia poziom podstawowy Egzamin maturalny 2012
Jezyk hiszpanski poziom podstawowy Egzamin maturalny 2012
Język Angielski i Niemiecki 2012 poziom podstawowy odpowiedzi
Egzamin 2012 poziom podstawowy
Egzamin 2012 poziom podstawowy
więcej podobnych podstron