www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
P
RÓBNY
E
GZAMIN
M
ATURALNY
Z
M
ATEMATYKI
Z
ESTAW PRZYGOTOWANY PRZEZ SERWIS
WWW
.
ZADANIA
.
INFO
POZIOM ROZSZERZONY
24
MARCA
2012
C
ZAS PRACY
: 180
MINUT
Z
ADANIE
1
(5
PKT
.)
Rozwi ˛
a ˙z nierówno´s´c
|
6
−
2x
| −
4
6 |
5
+
3x
|
.
R
OZWI ˛
AZANIE
Zapiszmy podan ˛
a nierówno´s´c w postaci
|
2x
−
6
| −
4
6 |
3x
+
5
|
.
Wyra ˙zenie pod pierwsz ˛
a warto´sci ˛
a bezwzgl˛edn ˛
a zeruje si˛e dla x
=
3, a wyra ˙zenie pod
drug ˛
a dla x
= −
5
3
, wi˛ec mamy do rozpatrzenia 3 przypadki.
Je ˙zeli x
< −
5
3
to wyra ˙zenia pod obydwiema warto´sciami bezwzgl˛ednymi s ˛
a ujemne i
mamy nierówno´s´c
− (
2x
−
6
) −
4
6 −(
3x
+
5
)
x
6 −
7.
Czyli w tym przypadku otrzymujemy przedział:
(−
∞,
−
7
i
.
Je ˙zeli
−
5
3
6
x
<
3 to mamy nierówno´s´c
− (
2x
−
6
) −
4
6
5
+
3x
−
3
6
5x
/ : 5
−
3
5
6
x.
W tym przypadku otrzymujemy wi˛ec przedział rozwi ˛
aza ´n:
−
3
5
, 3
.
Je ˙zeli wreszcie x
>
3 to wyra ˙zenia pod obydwiema warto´sciami bezwzgl˛ednymi s ˛
a do-
datnie i mamy nierówno´s´c
2x
−
6
−
4
6
3x
+
5
−
15
6
x.
W tym przypadku otrzymujemy wi˛ec zbiór rozwi ˛
aza ´n:
h
3,
+
∞
)
.
Rozwi ˛
azaniem nierówno´sci jest wi˛ec
(−
∞,
−
7
i ∪
−
3
5
,
+
∞
.
Odpowied´z:
(−
∞,
−
7
i ∪
−
3
5
,
+
∞
Materiał pobrany z serwisu
1

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
2
(4
PKT
.)
Uzasadnij, ˙ze 80
27
<
28
36
.
R
OZWI ˛
AZANIE
Sposób I
Poniewa ˙z oba wykładniki s ˛
a wielokrotno´sciami 9, zapiszmy obie liczby jako pot˛egi z wy-
kładnikiem 9.
80
27
=
80
3
9
=
512000
9
28
36
=
28
4
9
=
614656
9
.
Wida´c teraz, ˙ze 28
36
>
80
27
.
Sposób II
Tym razem spróbujemy obie liczby zapisa´c jako pot˛egi z wykładnikiem 36. W tym celu sza-
cujemy
80
27
<
81
27
= (
3
4
)
27
= (
3
3
)
36
=
27
36
.
Wida´c teraz, ˙ze ta liczba jest mniejsza od 28
36
.
Z
ADANIE
3
(4
PKT
.)
Wyka ˙z, ˙ze nie istnieje para liczb
(
a, b
)
spełniaj ˛
aca układ równa ´n
(
3b
+
2ab
=
1
a
2
+
b
2
+
3a
= −
4.
R
OZWI ˛
AZANIE
Sposób I
Dodajmy równania układu stronami.
a
2
+
b
2
+
3a
+
3b
+
2ab
= −
3
(
a
+
b
)
2
+
3
(
a
+
b
) = −
3
(
a
+
b
+
3
)(
a
+
b
) = −
3.
Podstawmy teraz x
=
a
+
b.
(
x
+
3
)
x
= −
3
x
2
+
3x
+
3
=
0
∆
=
9
−
12
<
0.
Otrzymane równanie kwadratowe jest sprzeczne, wi˛ec układ nie ma rozwi ˛
aza ´n.
Sposób II
Materiał pobrany z serwisu
2

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Przekształ´cmy drugie równanie – zwijamy do pełnego kwadratu.
a
2
+
3a
+
9
4
+
b
2
−
9
4
= −
4
a
+
3
2
2
+
b
2
= −
7
4
.
Oczywi´scie suma kwadratów nie mo ˙ze by´c liczb ˛
a ujemn ˛
a, wi˛ec drugie równanie układu jest
sprzeczne.
Sposób III
Podstawiamy b
=
1
3
+
2a
z pierwszego równania do drugiego.
a
2
+
1
(
3
+
2a
)
2
+
3a
= −
4
/
· (
3
+
2a
)
2
a
2
(
3
+
2a
)
2
+
1
+
3a
(
3
+
2a
)
2
= −
4
(
3
+
2a
)
2
(
3
+
2a
)
2
(
a
2
+
3a
+
4
) = −
1.
Teraz wystarczy zauwa ˙zy´c, ˙ze oba wyra ˙zenia z lewej strony s ˛
a nieujemne (
∆ trójmianu w
drugim nawiasie jest ujemna). Równanie to jest wi˛ec sprzeczne.
Zadania
.info
Podobają Ci się nasze rozwiązania?
Pokaż je koleżankom i kolegom ze szkoły!
Z
ADANIE
4
(4
PKT
.)
Wyznacz wszystkie rozwi ˛
azania równania 2 sin
2
x
+
sin x cos x
+
3 cos
2
x
=
3 nale ˙z ˛
ace do
przedziału
h
0, 2π
i
.
R
OZWI ˛
AZANIE
Przekształcamy (korzystaj ˛
ac z jedynki trygonometrycznej).
2 sin
2
x
+
sin x cos x
+
3 cos
2
x
=
3
2 sin
2
x
+
sin x cos x
+
3
(
1
−
sin
2
x
) =
3
−
sin
2
x
+
sin x cos x
=
0
sin x
(−
sin x
+
cos x
) =
0
sin x
=
0
∨
sin x
=
cos x.
Rozwi ˛
azaniem pierwszego równania (w danym przedziale) s ˛
a liczby
{
0, π, 2π
}
, a drugie
równanie mo ˙zemy przekształci´c nast˛epuj ˛
aco:
sin x
=
cos x
/ : cos x
tg x
=
1
(dzielili´smy przez cos x, bo wida´c, ˙ze je ˙zeli cos x
=
0 to równanie jest sprzeczne). Mamy
st ˛
ad dwa dodatkowe rozwi ˛
azania:
π
4
,
5π
4
.
Odpowied´z: x
∈
0,
π
4
, π,
5π
4
, 2π
Materiał pobrany z serwisu
3
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
5
(6
PKT
.)
Wyznacz wszystkie warto´sci parametru m, dla których suma odwrotno´sci pierwiastków
równania
3
x
+
3
=
1
m
−
8
−
2m
x
2
+
2x
−
3
jest równa
5
m
−
3
.
R
OZWI ˛
AZANIE
Oczywi´scie musi by´c x
6= −
3, m
6=
0 i m
6=
3. sprawd´zmy jeszcze kiedy zeruje si˛e trójmian
w mianowniku.
x
2
+
2x
−
3
=
0
∆
=
4
+
12
=
16
x
=
−
2
−
4
2
= −
3
∨
x
=
−
2
+
4
2
=
1.
Musimy wi˛ec dodatkowo zało ˙zy´c, ˙ze x
6=
1. Przy okazji okazało si˛e równie ˙z, ˙ze
x
2
+
2x
−
3
= (
x
−
1
)(
x
+
3
)
,
co pozwala do´s´c łatwo pozby´c si˛e ułamków w równaniu.
3
x
+
3
=
1
m
−
8
−
2m
(
x
−
1
)(
x
+
3
)
/
·
m
(
x
−
1
)(
x
+
3
)
3m
(
x
−
1
) =
x
2
+
2x
−
3
− (
8
−
2m
)
m
0
=
x
2
+
x
(
2
−
3m
) + (
2m
2
−
5m
−
3
)
.
Otrzymali´smy wi˛ec zwykłe równanie kwadratowe z parametrem. Sprawd´zmy, kiedy rów-
nanie to ma pierwiastki.
0
6
∆
= (
2
−
3m
)
2
−
4
(
2m
2
−
5m
−
3
) =
=
4
−
12m
+
9m
2
−
8m
2
+
20m
+
12
=
=
m
2
+
8m
+
16
= (
m
+
4
)
2
.
Równanie ma wi˛ec zawsze pierwiastki i mo ˙zemy skorzysta´c ze wzorów Viète’a.
5
m
−
3
=
1
x
1
+
1
x
2
=
x
1
+
x
2
x
1
x
2
=
−(
2
−
3m
)
2m
2
−
5m
−
3
5
m
−
3
=
3m
−
2
2m
2
−
5m
−
3
.
Zanim rozwi ˛
a ˙zemy to równanie, b ˛
ad´zmy ostro ˙zni i sprawd´zmy jakie s ˛
a miejsca zerowe
mianownika.
2m
2
−
5m
−
3
=
0
∆
=
25
+
24
=
49
m
=
5
−
7
4
= −
1
2
∨
m
=
5
+
7
4
=
3.
Materiał pobrany z serwisu
4
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Zakładamy wi˛ec dodatkowo, ˙ze m
6= −
1
2
. Przy okazji okazało si˛e, ˙ze
2m
2
−
5m
−
3
=
2
m
+
1
2
(
m
−
3
) = (
2m
+
1
)(
m
−
3
)
,
co pozwala łatwo upro´sci´c równanie
5
m
−
3
=
3m
−
2
(
2m
+
1
)(
m
−
3
)
/
· (
2m
+
1
)(
m
−
3
)
10m
+
5
=
3m
−
2
7m
= −
7
m
= −
1.
Na koniec sprawd´zmy, czy otrzymana warto´s´c m spełnia wszystkie poczynione wcze´sniej
zało ˙zenia. Wprawdzie nigdzie nie zało ˙zyli´smy, ˙ze m
6= −
1, ale zało ˙zyli´smy, ˙ze x
6= −
3 i
x
6=
1. Sprawd´zmy wi˛ec, czy rozwi ˛
azaniem równania dla m
= −
1 nie jest jedna z tych liczb.
Równanie kwadratowe dla m
= −
1 przyjmuje posta´c
0
=
x
2
+
5x
+
4
∆
=
25
−
16
=
9
x
1
=
−
5
−
3
2
= −
4,
x
2
=
−
5
+
3
2
= −
1.
Zatem wszystko jest w porz ˛
adku (wida´c te ˙z, ˙ze rzeczywi´scie
1
x
1
+
1
x
2
=
5
m
−
3
= −
5
4
).
Odpowied´z: m
= −
1
Z
ADANIE
6
(5
PKT
.)
Suma trzech liczb tworz ˛
acych ci ˛
ag geometryczny jest równa 63, a ich iloczyn jest równy
5832. Wyznacz ten ci ˛
ag.
R
OZWI ˛
AZANIE
Sposób I
Je ˙zeli trzy liczby tworz ˛
a ci ˛
ag geometryczny, to s ˛
a one postaci a, aq, aq
2
. Mamy zatem układ
równa ´n
(
a
+
aq
+
aq
2
=
63
a
(
aq
)(
aq
2
) =
5832
(
a
(
1
+
q
+
q
2
) =
63
a
3
q
3
=
5832.
Wida´c, ˙ze musimy wyci ˛
agn ˛
a´c pierwiastek 3 stopnia z liczby 5832. Mo ˙zna łatwo to zrobi´c
dziel ˛
ac j ˛
a przez sze´sciany, np. łatwo zauwa ˙zy´c, ˙ze dzieli si˛e ona przez 3, wi˛ec próbujemy
Materiał pobrany z serwisu
5

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
podzieli´c j ˛
a przez 27. Dzieli si˛e te ˙z przez 2, wi˛ec dzielimy j ˛
a przez 8. Otrzymamy w ten
sposób 5832
=
3
3
·
2
3
·
3
3
=
18
3
. Mamy zatem
(
a
(
1
+
q
+
q
2
) =
63
(
aq
)
3
=
18
3
(
a
(
1
+
q
+
q
2
) =
63
aq
=
18.
Prowadzi to do równania
18
q
(
1
+
q
+
q
2
) =
63
/
·
q
9
2
(
1
+
q
+
q
2
) =
7q
2q
2
−
5q
+
2
=
0
∆
=
25
−
16
=
9
q
=
5
−
3
4
=
1
2
∨
q
=
5
+
3
4
=
2.
Je ˙zeli q
=
1
2
to a
=
18
q
=
36 i otrzymujemy ci ˛
ag
(
36, 18, 9
)
. Je ˙zeli natomiast q
=
2 to a
=
18
q
=
9 i otrzymujemy ci ˛
ag
(
9, 18, 36
)
.
Sposób II
Szukamy trzech liczb a, b, c spełniaj ˛
acych warunki
a
+
b
+
c
=
63
abc
=
5832
b
2
=
ac.
Podstawiamy ac
=
b
2
z trzeciego równania do drugiego.
b
3
=
5832
⇒
b
=
18.
Mamy wi˛ec układ równa ´n
(
a
+
c
=
45
ac
=
324.
Podstawiamy a
=
45
−
c z pierwszego równania do drugiego.
(
45
−
c
)
c
=
324
0
=
c
2
−
45c
+
324
∆
=
45
2
−
324
·
4
=
729
=
27
2
c
=
45
−
27
2
=
9
∨
c
=
45
+
27
2
=
36.
Mamy wtedy a
=
45
−
c
=
36 i a
=
45
−
c
=
9 odpowiednio.
Odpowied´z:
(
36, 18, 9
)
oraz
(
9, 18, 36
)
Materiał pobrany z serwisu
6
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
7
(5
PKT
.)
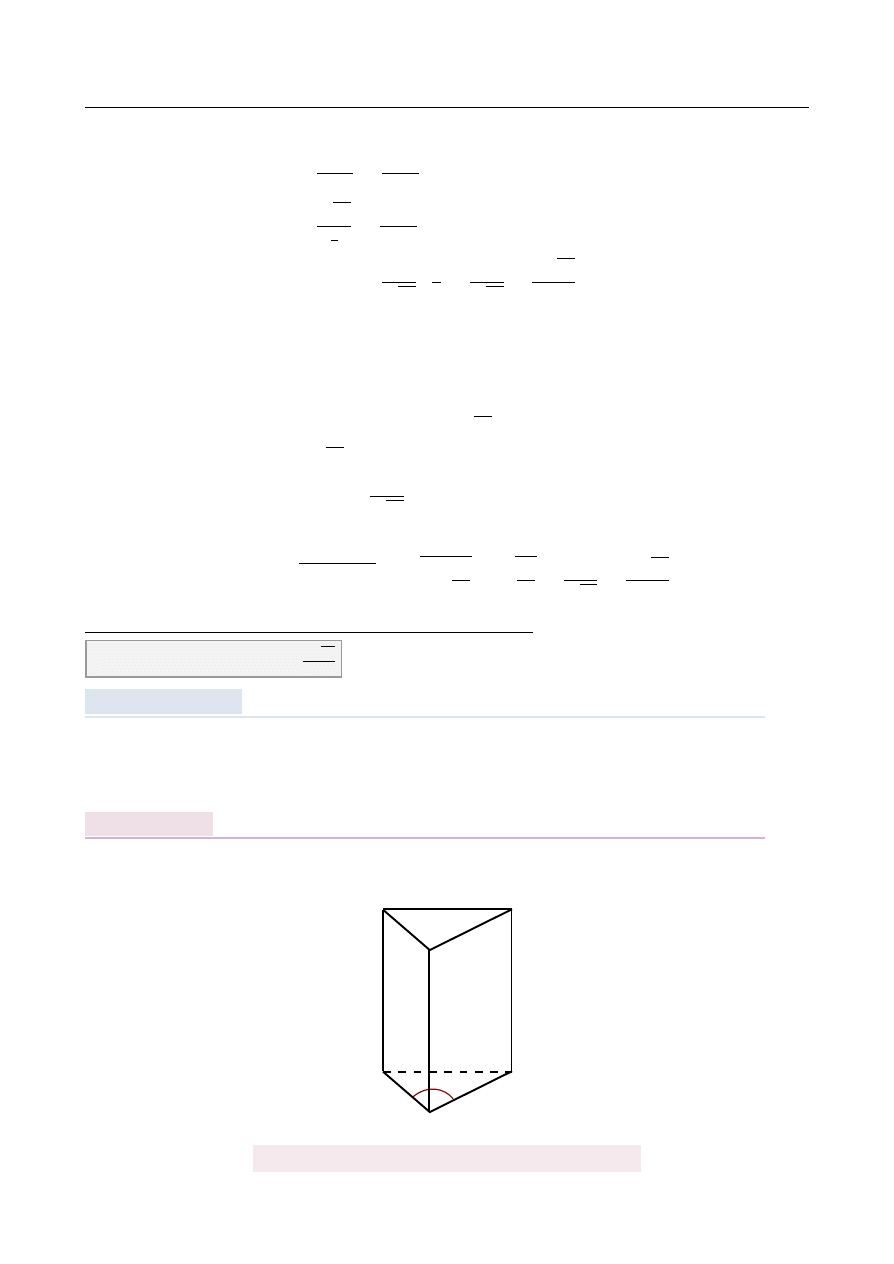
W trójk ˛
acie ABC, w którym
|
AC
| =
5,
|
BC
| =
4
√
2 i
|
AB
| =
7 na boku AB wybrano taki
punkt D, ˙ze
|
AD
| =
2. Oblicz sinus k ˛
ata ADC.
R
OZWI ˛
AZANIE
Rozpoczynamy od szkicowego rysunku.
A
B
C
D
α
β
5
5
2
4 2
Sinus k ˛
ata ADC mo ˙zemy wyliczy´c korzystaj ˛
ac z twierdzenia sinusów lub cosinusów
w trójk ˛
acie ADC, ale zanim to zrobimy musimy obliczy´c długo´s´c odcinka CD. Mo ˙zemy
obliczy´c t˛e długo´s´c pisz ˛
ac twierdzenie cosinusów w trójk ˛
acie ADC – do tego potrzebujemy
cos α
=
cos
]
CAD.
Liczymy. Piszemy twierdzenie cosinusów w trójk ˛
acie ABC.
BC
2
=
AB
2
+
AC
2
−
2AB
·
AC cos α
32
=
49
+
25
−
2
·
7
·
5 cos α
70 cos α
=
42
cos α
=
42
70
=
3
5
.
Teraz stosujemy twierdzenie cosinusów w trójk ˛
acie ADC.
CD
2
=
AD
2
+
AC
2
−
2AD
·
AC cos α
CD
2
=
4
+
25
−
2
·
2
·
5
·
3
5
CD
2
=
29
−
12
=
17
CD
=
√
17.
Interesuj ˛
acy nas sin β
=
sin
]
ADC obliczymy na dwa sposoby.
Sposób I
Chcemy skorzysta´c z twierdzenia sinusów w trójk ˛
acie ADC. Najpierw obliczmy jednak
sin α.
sin α
=
p
1
−
cos
2
α
=
r
1
−
9
25
=
4
5
.
Materiał pobrany z serwisu
7
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Teraz piszemy twierdzenie sinusów w trójk ˛
acie ADC.
CD
sin α
=
AC
sin β
√
17
4
5
=
5
sin β
sin β
=
5
√
17
·
4
5
=
4
√
17
=
4
√
17
17
.
Sposób II
Tym razem skorzystamy z twierdzenia cosinusów. Piszemy twierdzenie cosinusów w trój-
k ˛
acie ADC.
AC
2
=
AD
2
+
CD
2
−
2AD
·
CD cos β
25
=
4
+
17
−
2
·
2
·
√
17 cos β
4
√
17 cos β
= −
4
cos β
=
−
1
√
17
Pozostało skorzysta´c z jedynki trygonometrycznej.
sin β
=
q
1
−
cos
2
β
=
r
1
−
1
17
=
r
16
17
=
4
√
17
=
4
√
17
17
.
Odpowied´z: sin
]
ADC
=
4
√
17
17
Z
ADANIE
8
(4
PKT
.)
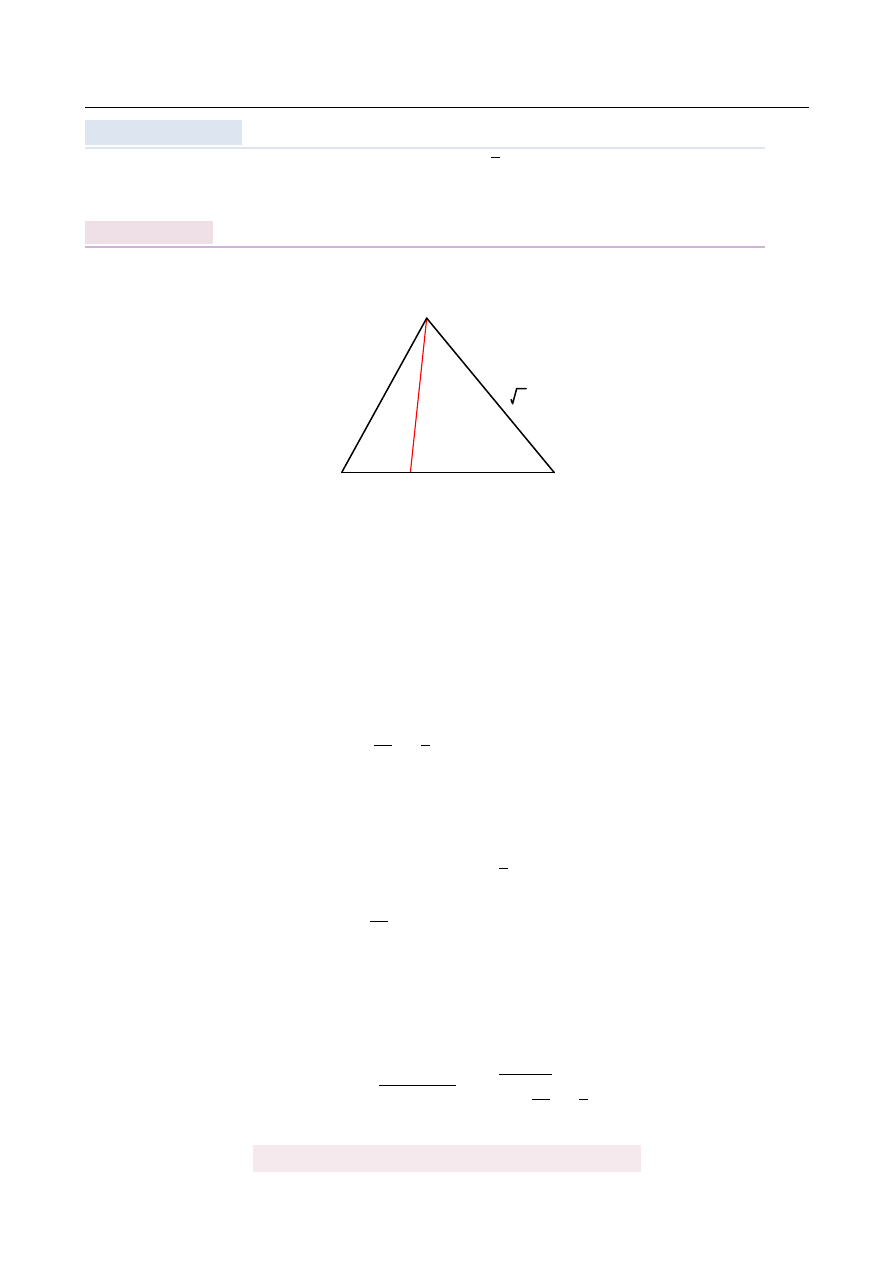
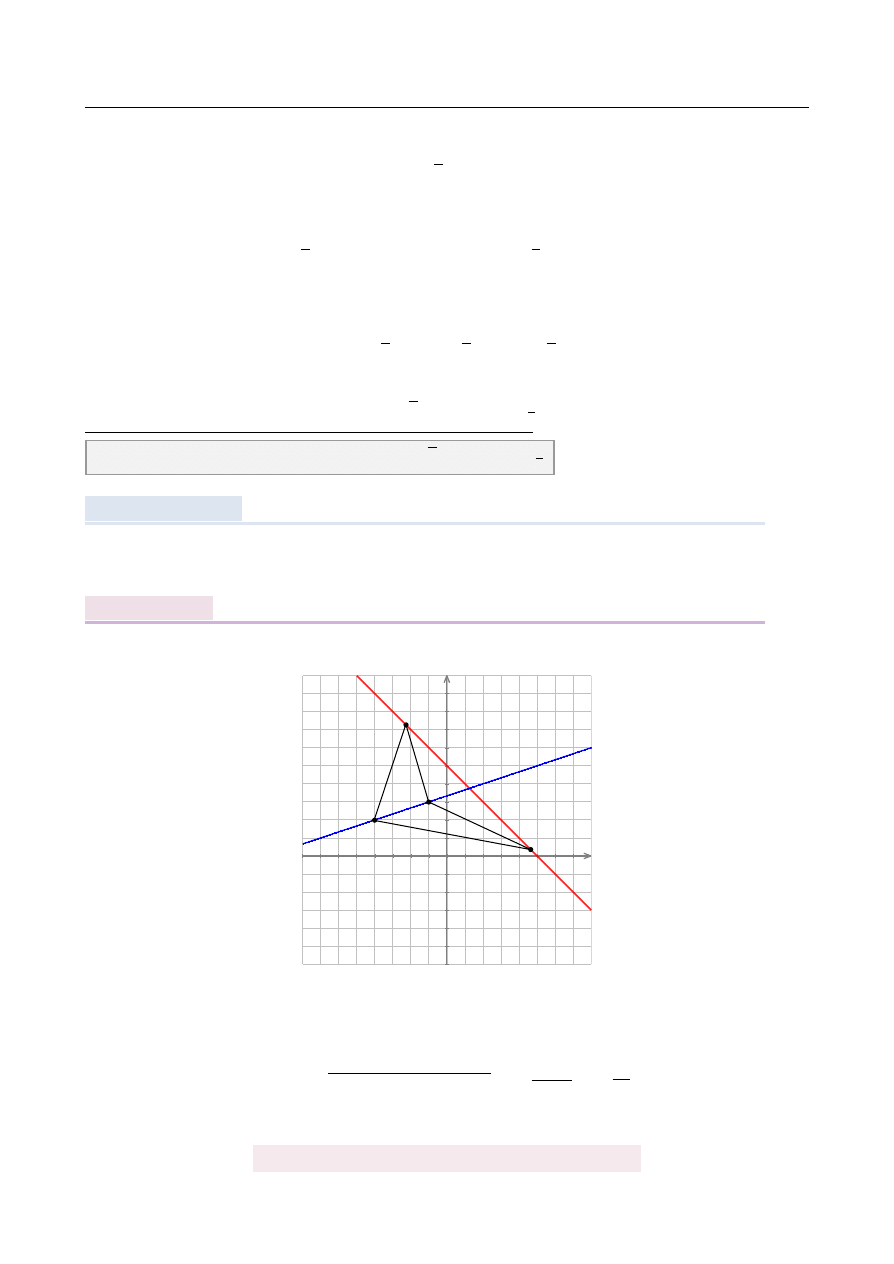
Podstaw ˛
a graniastosłupa prostego jest trójk ˛
at równoramienny o ramionach długo´sci a. Pole
podstawy jest równe sumie pól dwóch przystaj ˛
acych ´scian bocznych graniastosłupa. Jakie
powinny by´c długo´sci pozostałych kraw˛edzi graniastosłupa, aby jego obj˛eto´s´c była najwi˛ek-
sza?
R
OZWI ˛
AZANIE
Oznaczmy przez H długo´s´c wysoko´sci graniastosłupa, a przez α k ˛
at przy wierzchołku trój-
k ˛
ata równoramiennego w podstawie.
a
H
A
B
C
D
a
E
F
α
Materiał pobrany z serwisu
8
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Pole podstawy jest równe
P
p
=
1
2
a
2
sin α.
Z drugiej strony wiemy, ˙ze jest ono równe sumie pól dwóch ´scian bocznych, czyli
1
2
a
2
sin α
=
2aH
⇒
H
=
1
4
a sin α.
Zatem obj˛eto´s´c graniastosłupa jest równa
V
=
P
p
·
H
=
1
2
a
2
sin α
·
1
4
a sin α
=
1
8
a
3
sin
2
α
.
Obj˛eto´s´c b˛edzie najwi˛eksza, gdy sin α
=
1, czyli dla α
=
90
◦
. Wtedy podstawa trójk ˛
ata ABC
ma długo´s´c (twierdzenie Pitagorasa): a
√
2, a wysoko´s´c:
1
4
a.
Odpowied´z: Trójk ˛
at w podstawie: a
, a, a
√
2, wysoko´s´c:
a
4
.
Z
ADANIE
9
(4
PKT
.)
Dane s ˛
a punkty A
= (−
1, 3
)
i B
= (−
4, 2
)
. Wyznacz współrz˛edne punktu C na prostej
y
= −
x
+
5 tak, aby pole trójk ˛
ata ABC było równe 7.
R
OZWI ˛
AZANIE
Rozpoczynamy od szkicowego rysunku.
-5
-1
+1
+5
x
-5
-1
+1
+5
y
A
B
C
C
Sposób I
Obliczmy długo´s´c podstawy trójk ˛
ata ABC
AB
=
q
(−
4
+
1
)
2
+ (
2
−
3
)
2
=
√
9
+
1
=
√
10.
Materiał pobrany z serwisu
9

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z podanego pola obliczamy jaka jest długo´s´c wysoko´sci opuszczonej na bok AB.
7
=
1
2
AB
·
h
⇒
h
=
14
√
10
.
Co dalej? – szukamy punktu C na danej prostej, który jest w odległo´sci h od prostej AB.
Napiszmy najpierw równanie prostej AB. Mo ˙zna to zrobi´c korzystaj ˛
ac ze wzoru na rów-
nanie prostej przechodz ˛
acej przez dwa punkty, ale my zrobimy to wprost: szukamy prostej
w postaci y
=
ax
+
b. Podstawiamy współrz˛edne punktów A i B.
(
3
= −
a
+
b
2
= −
4a
+
b
Odejmujemy od pierwszego równania drugie ( ˙zeby skróci´c b) i mamy
1
= −
a
+
4a
⇒
a
=
1
3
.
Zatem b
=
3
+
a
=
10
3
i prosta AB ma równanie:
y
=
1
3
x
+
10
3
/
·
3
3y
−
x
−
10
=
0.
Sprawdzamy teraz, kiedy odległo´s´c punktu C
= (
x,
−
x
+
5
)
od prostej AB jest równa h.
|
3
(−
x
+
5
) −
x
−
10
|
√
9
+
1
=
14
√
10
/
·
√
10
| −
4x
+
5
| =
14
−
4x
+
5
= −
14
∨
−
4x
+
5
=
14
4x
=
19
∨
4x
= −
9
x
=
19
4
∨
x
= −
9
4
.
Wtedy y
= −
x
+
5
=
1
4
i y
= −
x
+
5
=
29
4
odpowiednio. Zatem C
=
19
4
,
1
4
lub C
=
−
9
4
,
29
4
.
Sposób II
Korzystamy ze wzoru na pole trójk ˛
ata o wierzchołkach A
= (
x
A
, y
A
)
, B
= (
x
B
, y
B
)
i C
=
(
x
C
, y
C
)
.
P
ABC
=
1
2
|(
x
B
−
x
A
)(
y
C
−
y
A
) − (
y
B
−
y
A
)(
x
C
−
x
A
)|
.
W naszej sytuacji C
= (
x,
−
x
+
5
)
, wi˛ec mamy równanie
7
=
1
2
|(−
4
+
1
)(−
x
+
5
−
3
) − (
2
−
3
)(
x
+
1
)|
14
= | −
3
(
2
−
x
) + (
x
+
1
)|
14
= |
4x
−
5
|
4x
−
5
= −
14
∨
4x
−
5
=
14
4x
= −
9
∨
4x
=
19
x
= −
9
4
∨
x
=
19
4
.
Materiał pobrany z serwisu
10

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Wtedy y
= −
x
+
5
=
1
4
i y
= −
x
+
5
=
29
4
odpowiednio. Zatem C
=
19
4
,
1
4
lub C
=
−
9
4
,
29
4
.
Odpowied´z: C
=
19
4
,
1
4
lub C
= −
9
4
,
29
4
Z
ADANIE
10
(5
PKT
.)
Ze zbioru liczb
{
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13
}
losujemy bez zwracania 4 liczby. Oblicz
jakie jest prawdopodobie ´nstwo, ˙ze w´sród 4 otrzymanych liczb jest dokładnie jedna para
liczb o sumie równej 14.
R
OZWI ˛
AZANIE
Wszystkich zdarze ´n elementarnych jest
13
4
=
13
·
12
·
11
·
10
4!
=
13
·
12
·
11
·
10
2
·
3
·
4
=
13
·
11
·
5.
Wypiszmy wszystkie pary liczb, które w sumie daj ˛
a 14.
(
1, 13
)
,
(
2, 12
)
,
(
3, 11
)
,
(
4, 10
)
,
(
5, 9
)
,
(
6, 8
)
.
Jest jeszcze liczba 7, która nie ma pary (bo losujemy bez zwracania).
Sposób I
O zdarzeniach sprzyjaj ˛
acych my´slimy nast˛epuj ˛
aco: musimy wybra´c jedn ˛
a z powy ˙zszych
par, a potem musimy dobra´c jeszcze dwie liczby tak, aby nie były z jednej pary.
Jedn ˛
a par˛e mo ˙zemy wybra´c na 6 sposobów. Po wybraniu tej pary pozostaje 13
−
2
=
11
liczb i z nich musimy wybra´c jeszcze dwie. Dwie pozostałe liczby mo ˙zemy wybra´c na
11
2
=
11
·
10
2
=
55
sposobów. Od tych 55 mo ˙zliwych par musimy jednak odj ˛
a´c 5 par, w których suma jest równa
14. W sumie 3 i 4 liczb˛e mo ˙zemy wi˛ec wybra´c na 55
−
5
=
50 sposobów. Jest wi˛ec
6
·
50
zdarze ´n sprzyjaj ˛
acych i prawdopodobie ´nstwo jest równe
6
·
50
13
·
11
·
5
=
6
·
10
13
·
11
=
60
143
.
Sposób II
Materiał pobrany z serwisu
11

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
O zdarzeniach sprzyjaj ˛
acych my´slimy nast˛epuj ˛
aco: musimy wybra´c jedn ˛
a z powy ˙zszych
par, a potem musimy dobra´c jeszcze dwie liczby tak, aby nie były z jednej pary.
Jedn ˛
a par˛e mo ˙zemy wybra´c na 6 sposobów. Gdy para ta jest ustalona to mo ˙zliwe s ˛
a dwie
sytuacje: albo jedn ˛
a z pozostałych liczb jest 7, albo nie. Je ˙zeli jest 7 w´sród wylosowanych
liczb to czwarta liczba mo ˙ze by´c któr ˛
akolwiek z pozostałych 13
−
2
−
1
=
10 liczb. Jest wi˛ec
6
·
10
=
60
zdarze ´n tego typu.
Je ˙zeli natomiast w´sród wylosowanych liczb nie ma 7, to pozostałe dwie liczby wybiera-
my spo´sród 5 par tak, aby dwie liczby nie były z jednej pary. W takim razie trzeci ˛
a liczb˛e
wybieramy dowolnie spo´sród 13
−
2
−
1
=
10 liczb (odejmujemy wybran ˛
a na pocz ˛
atku pa-
r˛e i 7), a czwart ˛
a liczb˛e wybieramy spo´sród 13
−
2
−
1
−
2
=
8 liczb (odejmujemy pierwsz ˛
a
par˛e, 7-k˛e, oraz par˛e trzeciej liczby). Teraz bardzo łatwo popełni´c bł ˛
ad – zauwa ˙zmy, ˙ze przy
takim sposobie liczenia, np. czwórk˛e
{
1, 13, 2, 3
}
policzyli´smy dwukrotnie: jako
(
1, 13, 2, 3
)
i
(
1, 13, 3, 2
)
! W takim razie zdarze ´n bez 7-ki jest
6
·
10
·
8
2
=
60
·
4.
Zdarzenia bez 7-ki mogli´smy te ˙z policzy´c inaczej: par˛e z sum ˛
a równ ˛
a 14 mo ˙zemy wybra´c na
6 sposobów, potem wybieramy dwie pary, z których b˛ed ˛
a pochodzi´c dwie pozostałe liczby
– mo ˙zemy to zrobi´c na
5
2
=
5
·
4
2
=
10
sposobów. Na koniec musimy jeszcze uwzgl˛edni´c, ˙ze w ka ˙zdej z tych dwóch ostatnich par
mamy mo ˙zliwo´s´c wyboru jednej z dwóch liczb. Daje to w sumie
6
·
10
·
2
·
2
=
60
·
40.
mo ˙zliwo´sci.
Prawdopodobie ´nstwo jest wi˛ec równe
p
=
60
+
60
·
4
13
·
11
·
5
=
60
·
5
13
·
11
·
5
=
60
13
·
11
=
60
143
.
Sposób III
Tym razem, zamiast oblicza´c prawdopodobie ´nstwo opisanego zdarzenia A, obliczymy praw-
dopodobie ´nstwo zdarzenia przeciwnego A
0
. S ˛
a dwa rodzaje zdarze ´n sprzyjaj ˛
acych zdarze-
niu A
0
: albo nie ma ˙zadnej pary z sum ˛
a równ ˛
a 14, albo takie pary s ˛
a dwie.
Łatwo obliczy´c liczb˛e zdarze ´n z dwoma parami z sum ˛
a równ ˛
a 14 – jest ich tyle, ile mo ˙z-
liwo´sci wybrania 2 par spo´sród 6 par wypisanych powy ˙zej. Jest wi˛ec
6
2
=
6
·
5
2
=
15
zdarze ´n tego typu.
Je ˙zeli natomiast nie ma ˙zadnej pary liczb z sum ˛
a równ ˛
a 14, to ka ˙zda z liczb musi pocho-
dzi´c z innej z wypisanych par, lub mo ˙ze by´c te ˙z 7-k ˛
a.
Materiał pobrany z serwisu
12

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Je ˙zeli w´sród wybranych liczb jest 7, to aby wybra´c pozostałe trzy liczby wybieramy 3
pary, z których b˛ed ˛
a pochodzi´c, mo ˙zemy to zrobi´c na
6
3
=
6
·
5
·
4
3!
=
20
sposobów. Ponadto w ka ˙zdej z 3 wybranych par mo ˙zemy wybra´c jedn ˛
a z dwóch liczb jest
wi˛ec
20
·
2
·
2
·
2
=
20
·
8
takich par.
Je ˙zeli wreszcie w´sród wybranych liczb nie ma 7-ki, to liczby pochodz ˛
a z 4 ró ˙znych par,
co mo ˙zemy wybra´c na
6
4
=
6
·
5
·
4
·
3
4!
=
15
sposobów. W ka ˙zdej parze mamy mo ˙zliwo´s´c wyboru jednej z 2 liczb. Jest wi˛ec
15
·
2
·
2
·
2
·
2
=
15
·
16
takich zdarze ´n.
Prawdopodobie ´nstwo jest wi˛ec równe.
P
(
A
) =
1
−
P
(
A
0
) =
1
−
15
+
20
·
8
+
15
·
16
13
·
11
·
5
=
=
1
−
3
+
4
·
8
+
3
·
16
13
·
11
=
1
−
83
143
=
60
143
.
Sposób IV
Tym razem b˛edziemy uwzgl˛ednia´c kolejno´s´c w jakiej losowane s ˛
a liczby, czyli za zdarzenia
elementarne przyjmiemy czwórki
(
a, b, c, d
)
wylosowanych liczb. Mamy zatem
|
Ω
| =
13
·
12
·
11
·
10.
Liczymy ile jest zdarze ´n sprzyjaj ˛
acych.
Najpierw zdarzenia w których jest 7. Do tej siódemki musimy dobra´c par˛e liczb z sum ˛
a
równ ˛
a 14 – mo ˙zemy to zrobi´c na 6 sposobów, a potem jeszcze jedn ˛
a dowoln ˛
a liczb˛e spo-
´sród pozostałych 10 liczb. Na koniec musimy ustali´c kolejno´s´c wybranych liczb, co mo ˙zemy
zrobi´c na 4! sposobów. W sumie jest wi˛ec
6
·
10
·
4!
=
60
·
24
takich zdarze ´n.
Teraz policzmy ile jest zdarze ´n bez 7-ki. Musimy wybra´c dwie liczby z sum ˛
a równ ˛
a 14 –
mo ˙zemy to zrobi´c na 6 sposobów, potem musimy jeszcze dobra´c dwie liczby, których suma
nie jest równa 14. Łatwo tu popełni´c bł ˛
ad, nie mo ˙zemy liczy´c tak: wybieramy liczb˛e spo-
´sród pozostałych 10, a potem ostatni ˛
a liczb˛e mo ˙zemy wybra´c na 8 sposobów – przy takim
sposobie liczenia ka ˙zd ˛
a par˛e liczymy podwójnie.
Materiał pobrany z serwisu
13

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
W takim razie liczmy ostro ˙zniej, aby wybra´c dwie liczby, których suma nie jest równa
14, wybieramy dwie pary, z których b˛ed ˛
a pochodzi´c te liczby – mo ˙zemy to zrobi´c na
5
2
=
5
·
4
2
=
10
sposobów, a potem z ka ˙zdej pary wybieramy jedn ˛
a z dwóch liczb w tej parze. W sumie jest
wi˛ec
10
·
2
·
2
=
40
mo ˙zliwo´sci wybrania dwóch liczb, których suma nie jest równa 14. Na koniec mo ˙zemy 4
wybrane liczby dowolnie permutowa´c, wi˛ec jest w sumie
6
·
40
·
4!
=
6
·
40
·
24
zdarze ´n bez 7-ki. Prawdopodobie ´nstwo jest wi˛ec równe
60
·
24
+
6
·
40
·
24
13
·
12
·
11
·
10
=
60
·
2
+
6
·
40
·
2
13
·
11
·
10
=
6
·
2
+
6
·
4
·
2
13
·
11
=
60
143
.
Odpowied´z:
60
143
Z
ADANIE
11
(4
PKT
.)
Stosunek pola powierzchni bocznej sto ˙zka do pola przekroju osiowego tego sto ˙zka jest rów-
ny
2π
√
3
. Oblicz k ˛
at rozwarcia sto ˙zka.
R
OZWI ˛
AZANIE
Rozpoczynamy od rysunku – oznaczmy k ˛
at rozwarcia k ˛
ata przez 2α.
r
r
A
B
C
D
α α
l
h
Sposób I
Materiał pobrany z serwisu
14
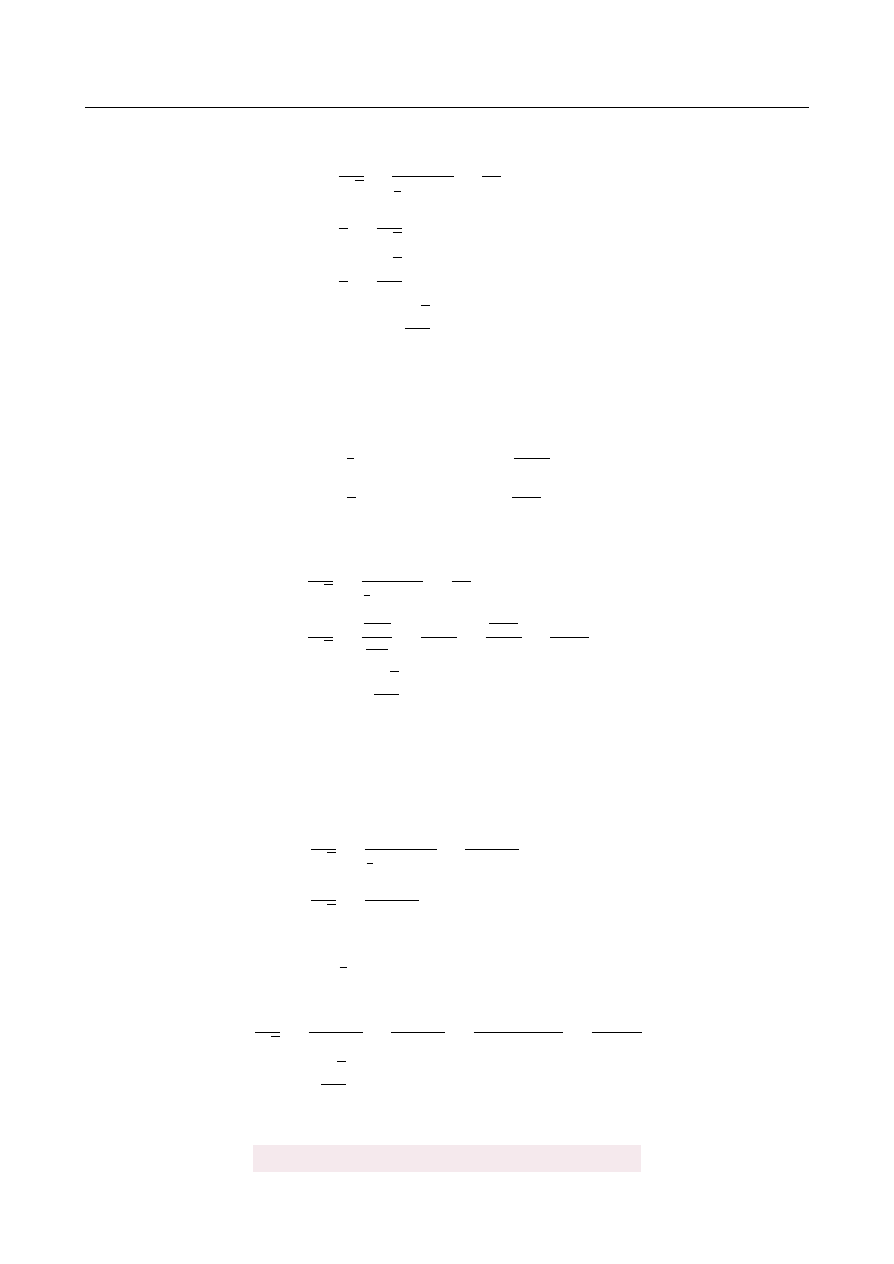
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Zapiszmy podan ˛
a informacj˛e o stosunku pól.
2π
√
3
=
πrl
1
2
·
2r
·
h
=
πl
h
/ : π
l
h
=
2
√
3
/
()
−
1
h
l
=
√
3
2
cos α
=
√
3
2
.
Zatem α
=
30
◦
i k ˛
at rozwarcia sto ˙zka jest równy 2α
=
60
◦
.
Sposób II
Zauwa ˙zmy, ˙ze
r
l
=
sin α
⇒
l
=
r
sin α
r
h
=
tg α
⇒
h
=
r
tg α
.
Zapiszmy podan ˛
a informacj˛e o stosunku pól.
2π
√
3
=
πrl
1
2
·
2r
·
h
=
πl
h
/ : π
2
√
3
=
r
sin α
r
tg α
=
tg α
sin α
=
sin α
cos α
sin α
=
1
cos α
cos α
=
√
3
2
.
Zatem α
=
30
◦
i k ˛
at rozwarcia sto ˙zka jest równy 2α
=
60
◦
.
Sposób III
Zapiszmy podan ˛
a informacj˛e o stosunku pól (korzystamy ze wzoru na pole trójk ˛
ata z sinu-
sem).
2π
√
3
=
πrl
1
2
l
2
sin 2α
=
2πr
l sin 2α
/ : 2π
1
√
3
=
r
l sin 2α
.
Zauwa ˙zmy, ˙ze ponadto
r
l
=
sin α
⇒
r
=
l sin α.
Mamy zatem
1
√
3
=
r
l sin 2α
=
l sin α
l sin 2α
=
sin α
2 sin α cos α
=
1
2 cos α
cos α
=
√
3
2
.
Zatem α
=
30
◦
i k ˛
at rozwarcia sto ˙zka jest równy 2α
=
60
◦
.
Materiał pobrany z serwisu
15
Wyszukiwarka
Podobne podstrony:
poziom podstawowy 24 marca 2012
Filozofia poziom rozszerzony Egzamin maturalny 2012
psychologia wykład 24 marca 2012 roku, GWSH Żory Administracja, semestr II, Podstawy psychologii
Filozofia poziom rozszerzony Egzamin maturalny 2012
Fizyka poziom rozszerzony Egzamin maturalny 2012
Egzamin 2012 poziom rozszerzony Nieznany (2)
Jezyk rosyjski, poziom rozszerzony transkrypcja Egzamin maturalny 2012
Jezyk francuski, poziom rozszerzony transkrypcja Egzamin maturalny 2012
Jezyk francuski poziom rozszerzony transkrypcja Egzamin maturalny 2012
Jezyk francuski poziom rozszerzony cz2 Egzamin maturalny 2012
PRZYGOTOWANIE DO SPRAWDZIANU - POLE TROJKATA KOLA - poziom rozszerzony 2012 2013, Sprawdziany,
Jezyk rosyjski poziom rozszerzony transkrypcja Egzamin maturalny 2012
matura chemia poziom rozszerzony czerwiec 2012
Jezyk francuski poziom rozszerzony cz1 Egzamin maturalny 2012
arkusz chemia probna cku umk luty 2012 poziom rozszerzony
Jezyk francuski poziom rozszerzony cz1 Egzamin maturalny 2012
więcej podobnych podstron