Biomaterials 22 (2001) 3085–3090

Mechanical properties of artificial tracheas composed

of a mesh cylinder and a spiral stent

Satoshi Kawaguchi

a

, Tatsuo Nakamura

b,

*, Yasuhiko Shimizu

b

, Toshiro Masuda

a

,

Toshikazu Takigawa

a

, Yu Liu

b

, Hiroki Ueda

b

, Takashi Sekine

b

, Kazuya Matsumoto

b

a

Department of Material Chemistry, Kyoto University, Yoshida, Sakyo-ku, Kyoto 606-8501, Japan

b

Institute for Frontier Medical Sciences, Kyoto University, Shogoin, Sakyo-ku, Kyoto 606-8507, Japan

Received 08 February 2000; accepted 20 January 2001

Abstract

Much work has been done on the materials used for mesh-type artificial tracheas, but a precise mechanical evaluation of these

structures has not yet been performed. In the present study, we determined the mechanical properties of typical mesh-type artificial
tracheas and compared them with those of native trachea. Four types of artificial trachea were made and used for the mechanical
tests. The basic frame of all the specimens was composed of a mesh cylinder and a spiral stent. The specimen whose mesh was sealed
with collagen sponge showed almost the same behavior in the force-strain curve under compression, suggesting that collagen sealing
has little effect on mechanical properties. Agreement between measured and estimated mechanical properties was good, especially in
the lowstrain region, suggesting that artificial tracheas can be designed in terms of mechanical properties by mainly considering the
basic frame structure. # 2001 Elsevier Science Ltd. All rights reserved.

Keywords:

Artificial trachea; Canine trachea; Compression test; Tensile test; Mechanical property; Young’s modulus

1. Introduction

Tracheal cartilage provides mechanical strength for

the trachea. Human tracheal cartilage is horseshoe
shaped; the dorsal portion of the trachea lacks cartilage
and is called the ‘‘membrane portion’’. Tracheal
cartilage prevents collapse of the air-way during
inspiration, and prevents over-expansion during expira-
tion.

Recently, the effectiveness and long-term safety of

mesh-type artificial tracheas have been demonstrated
in vivo [1,2], and a newtype of artificial trachea, with
collagen sponge layers added on both the inner and
outer surfaces of the prosthesis, has also been developed
[3]. With regard to the mechanical properties of native
tracheas, there have already been several studies on the
human trachea [4–10]. Although the mechanical proper-
ties of artificial tracheas play an important role in their
practical use, fewstudies have been done on artificial
tracheas [11,12] and a precise mechanical analysis has

not yet been performed for these structures. In the
design of currently used mesh-type artificial tracheas,
the main frame is composed of a mesh cylinder and a
polypropylene (PP) spiral [1–3]. The PP spiral gives the
mesh cylinder mechanical strength, acting like tracheal
cartilage. To make the mesh cylinder airtight and to
enhance the biocompatibility of the mesh, collagen or
collagen sponge may be coated on the mesh cylinder. In
this study, we studied the mechanical properties of
artificial tracheas and compared them with those of
native trachea. In addition, we analyzed the relationship
between structure and mechanical properties.

2. Materials and methods

2.1. Materials

Four typical types of artificial trachea were manu-

factured. They were composed of a fine Marlex

1

mesh

(C.R. Bard Inc., Billerica, MA) cylinder and an outer
spiral PP stent. The stent was attached to the outside of
the mesh cylinder by melting at several points and

*Corresponding author. Tel.: [phone]; fax:[phone]-

4844.

E-mail address:

[e-mail] (T. Nakamura).

0142-9612/01/$ - see front matter # 2001 Elsevier Science Ltd. All rights reserved.
PII: S 0 1 4 2 - 9 6 1 2 ( 0 1 ) 0 0 0 5 6 - 4

further fixed by 6-0 Prolene sutures (Ethicon Inc.,
Somerville, NJ). Table 1 summarizes the sample code,
cross-sectional shape of the stent, outer diameter of the
spiral and pitch of the spiral. The stent in Type-R is
rectangular in cross-section, and that in Type-C is
circular. Type-CC has the same main frame as Type-C,
but the surface of the specimen was coated with
collagen. Type-CS was made from Type-CC by laminat-
ing collagen sponge layers with a thickness of 0.5 mm on
both inner and outer surfaces. The lengths of the four
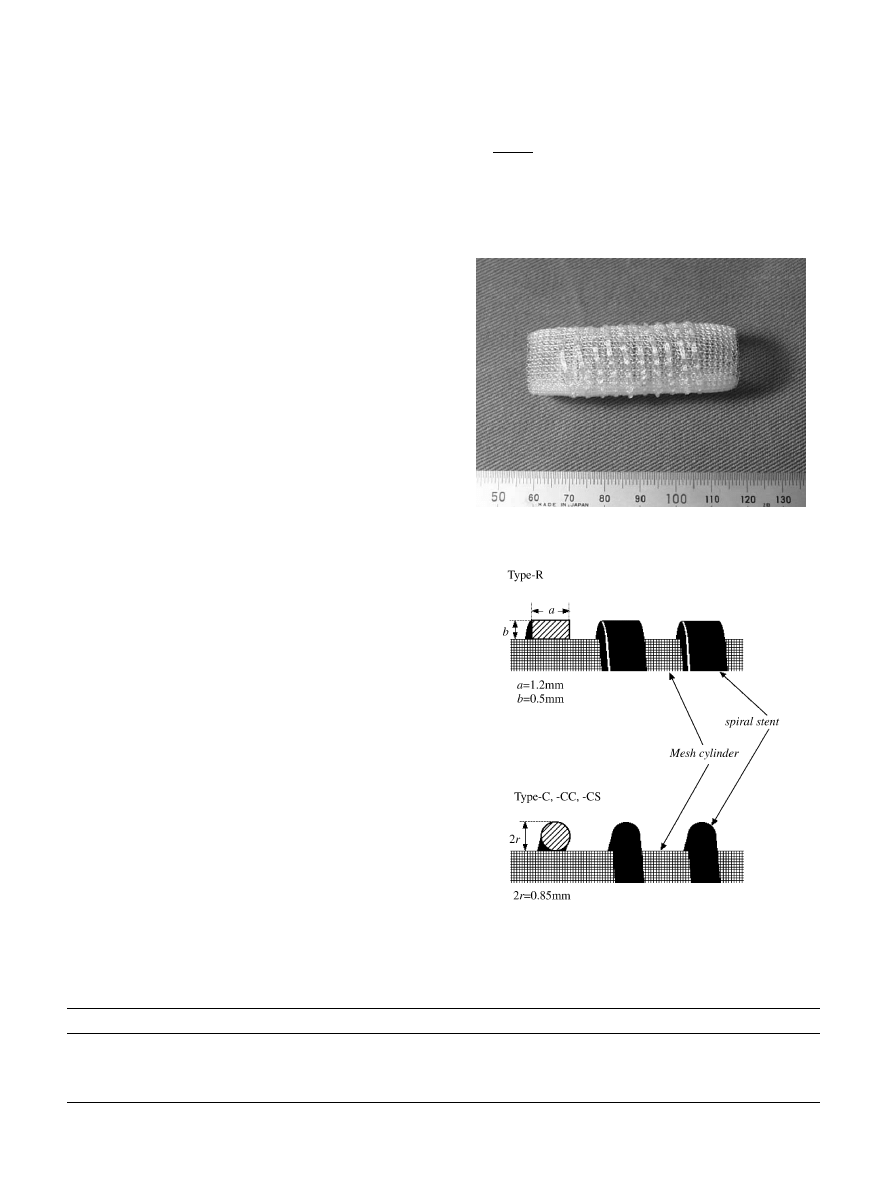
samples were 44–47 mm. Fig. 1 shows a macroscopic
viewof a Type-R specimen, and Fig. 2 show

s a

schematic representation of the specimens. For compar-
ison, we also examined the mechanical properties of
fresh canine trachea. Measurements on the canine
trachea were performed within four hours after removal.
The outer diameter of the canine trachea sample was
14 mm, and a length of 15 mm was used. Since the cross-
section was not exactly circular, the diameter given is the
shortest distance across. For tensile testing of the
cartilage, rectangular specimens (1.0 mm 0.7 mm) were
cut from the whole cartilage.

2.2. Mechanical testing

A tensile tester, RTM-500 (Orientec Co., Tokyo,

Japan), was used. Two parallel plates with diameters of
10 cm (upper plate) and 15 cm (bottom) were used for
the compression tests. The cross-head speed was set to
50 mm/min. Samples were compressed in the radial
direction (Fig. 3), and the force and displacement were
monitored. The same compression test was also done on
the canine trachea. Measurements were made in air for
Type-R and Type-C specimens, and in a saline solution
for Type-CC, Type-CS and canine trachea specimens.
The tensile properties of the tracheal cartilages in the
circumferential direction were examined using the same
apparatus as for the compression tests. In the tensile
test, the measurements were carried out in air and three
cross-head speeds (2, 10 and 100 mm/min) were em-
ployed to clarify the effect of tensile speed on the
mechanical properties of the tracheal cartilages.

2.3. Data analysis

The mechanical properties of the artificial tracheas

under compression were analyzed as force per pitch (f )

and strain (e

c

). e

c

was defined as

e

c

¼

d

0

d

d

0

ð1Þ

where d is the outer diameter of the specimen (stent) and
d

0

is the initial value of d. In data analysis of the

mechanical properties of the canine trachea, a combina-

Table 1
Sample codes and characteristic dimensions of artificial tracheas

Code

Cross-section of stent

Outer diameter of spiral stent (mm)

Pitch of spiral stent (mm)

Type-R

Rectangle

20.8

3.9

Type-C

Circle

20.5

3.9

Type-CC

Circle

18.5

2.7

Type-CS

Circle

18.3

3.2

Fig. 2. Schematic representation of the basic structure of the artificial
tracheas.

Fig. 1. Photograph of Type-R trachea.

S. Kawaguchi et al. / Biomaterials 22 (2001) 3085–3090

3086

tion of force per unit length (w) and e

c

was used. The

data for tensile testing were analyzed in terms of stress
(s) and tensile strain (e

t

). They are given by

s ¼

F

S

0

ð2Þ

e

t

¼

l l

0

l

0

ð3Þ

where F; S

0

and l are the force, the initial cross-sectional

area and the length, respectively, l

0

being the initial

value of l.

3. Results

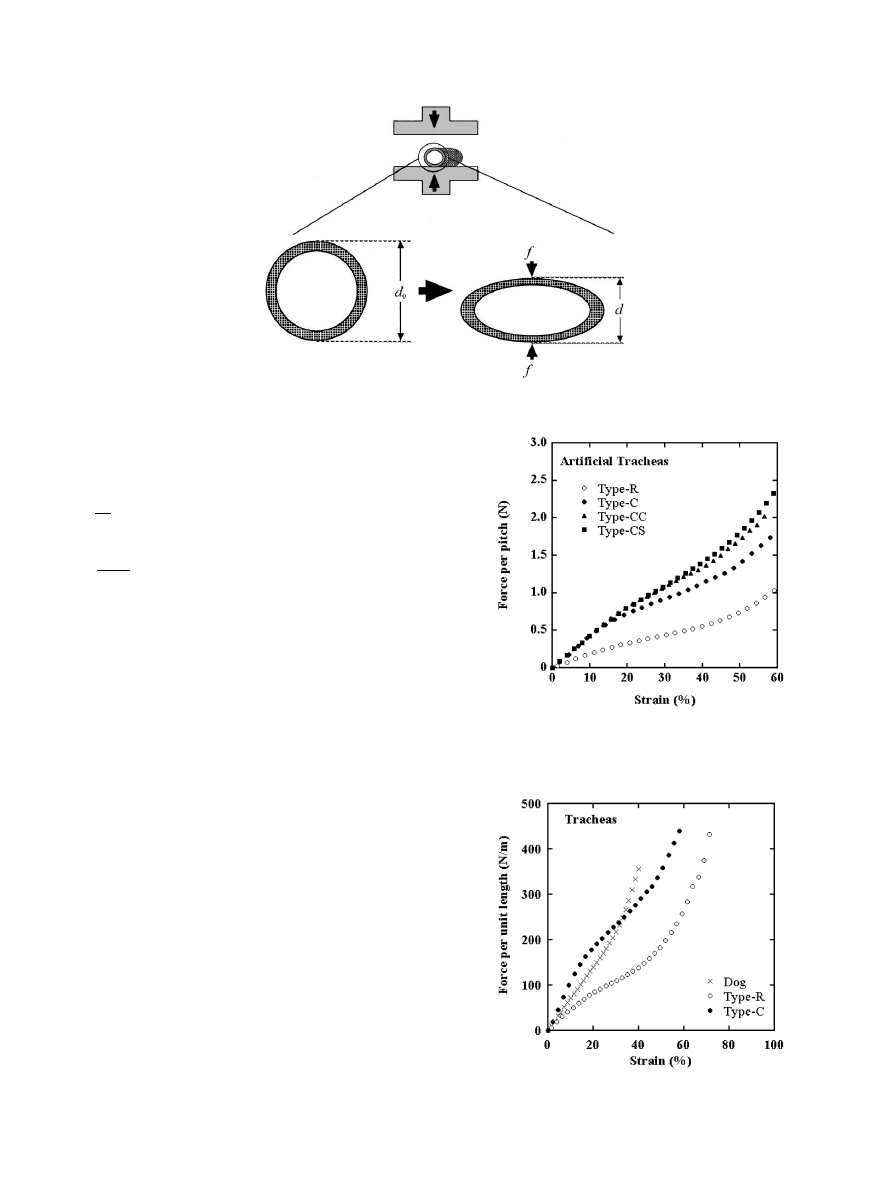
3.1. Force–strain curves of tracheal specimens

In Fig. 4, f is shown as a function of e

c

for all artificial

tracheas used. At lowstrains, f was proportional to e

c

for all the specimens. The values of f for the Type-C
group (namely, Type-C, Type-CC and Type-CS) were
almost the same in the lowstrain region of e

c

5 15

%.

The difference between the three curves was marked at
higher strains. The force level in this strain region
decreased in the order Type-CS, Type-CC and Type-C.
The values of f for the Type-C group were larger than
those for Type-R over the whole strain range.

In Fig. 5, the force per unit tube length (w) is shown as

a function of the strain (e

c

) for Type-R, Type-C and

canine tracheas. The w2e

c

curve of the canine trachea

lay between the curves of the artificial tracheas at low
strains, but was located above the curves of the artificial
tracheas at high strains. As far as the force level is
concerned, however, canine trachea resembled Type-C
rather than Type-R in its mechanical behavior under
compression.

Fig. 3. Schematic representation for the compression tests.

Fig. 4. Force per pitch vs. strain plots for Type-R, Type-C, Type-CC
and Type-CS artificial tracheas.

Fig. 5. Force per unit length vs. strain plots for Type-R and Type-C
artificial tracheas and canine trachea.

S. Kawaguchi et al. / Biomaterials 22 (2001) 3085–3090

3087

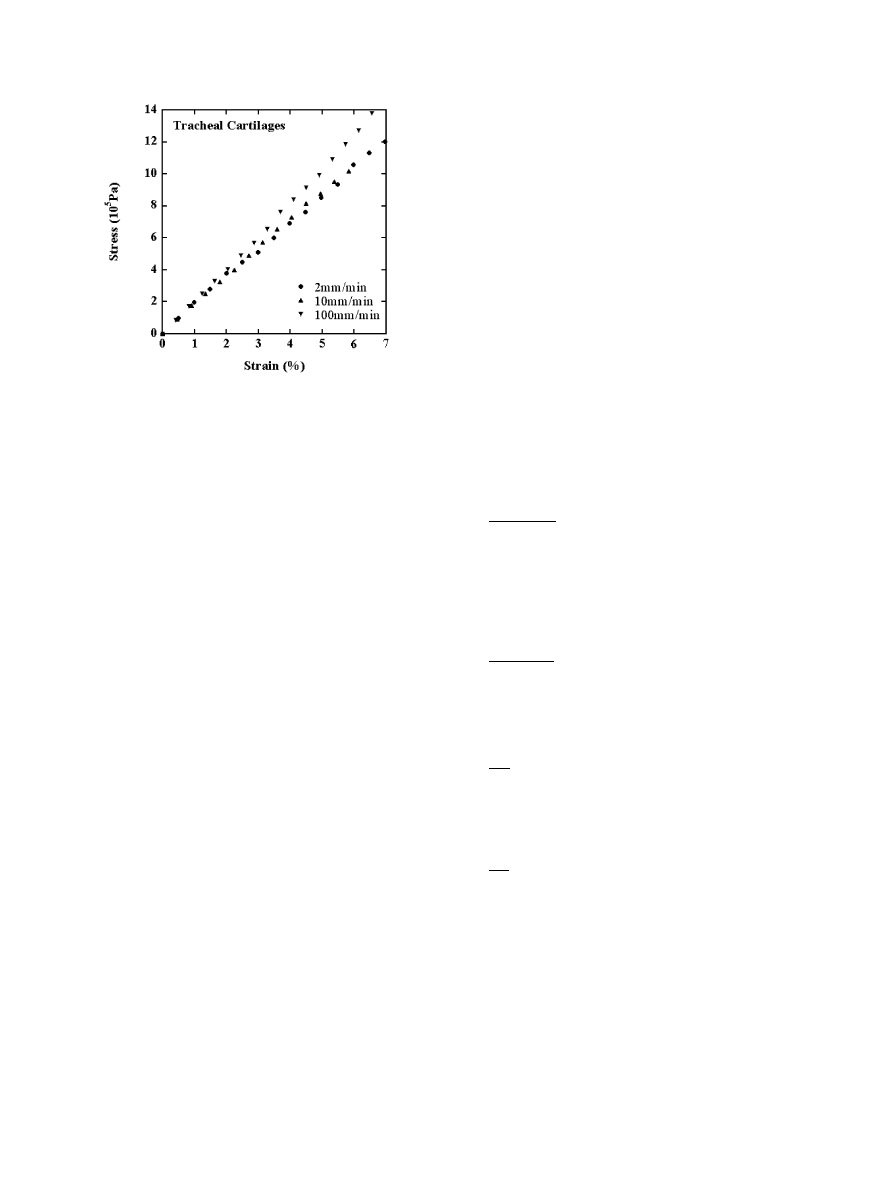
3.2. Stress–strain curves of tracheal cartilages

In Fig. 6, s is shown as a function of e

c

for tracheal

cartilages. The curve at 2 mm/min was almost identical
to that at 10 mm/min over the entire strain range
examined, whereas the curve at 100 mm/min was shifted
upwards compared with the others.

4. Discussion

Fine Marlex

1

mesh has a suitable pore size for

regeneration of tracheal tissue [13] and it has been used
clinically for reconstruction of the air-way. However, it
is necessary to support the mesh tube with a stent,
because a tube made from fine Marlex

1

mesh alone is

too soft (weak). However, there has never been any
systematic analysis of the relation between the mechan-
ical properties of stents and their material and shape.

An artificial trachea has to possess sufficient mechan-

ical strength to sustain the air-way, but a prosthesis that
is too stiff is also problematic. In this sense the initial
mechanical properties are of high importance for the
artificial trachea, since mismatch of these properties
often causes granulation at the anastomoses which
induces fatal obstruction or bleeding [14], or collapse of
the air-way.

4.1. Force–strain curves of trachea specimens

We calculated the ratio of f for Type-R to that for

Type-C over a wide range of e

c

. The ratio was almost

independent of e

c

, suggesting that the curves are similar

in shape, although the force level itself was different. As
mentioned previously, Type-C was composed of a mesh
cylinder and a spiral yarn with a circular cross-section.
Type-R had almost the same architecture as Type-C but

with a rectangular cross-section. The difference between
these two specimens was only the shape of the cross-
section of the stent, because the dimensions of both
specimens are almost the same, including the cross-
sectional area of the stents (see Fig. 2). The fact that the
shape of the two curves was almost the same suggests
that the shape of the f –e

c

curve is governed basically by

the architecture of the artificial trachea, whereas the
force level depends on the shape and dimensions of the
components.

As stated previously, the outer diameters of the

artificial tracheas were not the same (Fig. 4). Therefore,
direct comparison of the absolute values of the force is
not meaningful. The mechanical properties of the
artificial tracheas used here were chiefly provided by
the spiral stent around the mesh cylinder, as stated
previously. However, direct analysis of a spiral model is
complex, so for simplicity we here regard the spiral as a
series of hoops with the distance between the hoops set
equal to the pitch of the original spiral. When a
compression force (designated as f ) is imposed on a
hoop in the radial direction, f is given by

f ¼

8pEI DR

ðp

2

8ÞR

3
0

ð4Þ

where E is Young’s modulus, I is the second moment of
area, R

0

is the initial radius of curvature at the neutral

surface, and DR is the displacement of R

0

by loading

[15]. For the specimens used here, Eq. (4) can be
simplified to

f ¼

32pEI

ðp

2

8Þd

2

0

e

c

ð5Þ

because R

0

ffi d

0

=2 and DR

0

ffi ðd

0

dÞ=2. Here, e

c

is

the strain under compression as already defined by
Eq. (1). The quantity I is given by

I ¼

ab

3

12

ð6aÞ

for a Type-R specimen, where a and b are dimensions
characterizing the cross-section of the stent, as shown in
Fig. 2. Similarly, I is given by

I ¼

pr

4

4

ð6bÞ

for a Type-C specimen, where r is the radius of cross-
section (circle) of the stent (Fig. 2). In practice, the
validity of Eq. (4) (and also Eq. (5)) is limited to the low
strain region, because the equations are based on the
infinite deformation theory. At lowstrains, f was
proportional to e

c

for all specimens (Fig. 4), suggesting

that the experimental data for the artificial tracheas used
here can be analyzed by Eq. (5) as long as the applied
strain is low. The value of f depends on d

0

, and the

dependence of f on d

0

is clear from Eq. (5) at low

strains. Since the dependence of f on d

0

is not clear at

high strains, the corrected force per pitch (f

corr

) for the

Fig. 6. Stress vs. strain plots for canine tracheal cartilages under
extension. The cross-head speeds used are specified in the figure.

S. Kawaguchi et al. / Biomaterials 22 (2001) 3085–3090

3088

artificial tracheas was calculated based on Eq. (5) in the
whole strain range by

f

corr

¼ f

d

0

d

0;corr

2

ð7Þ

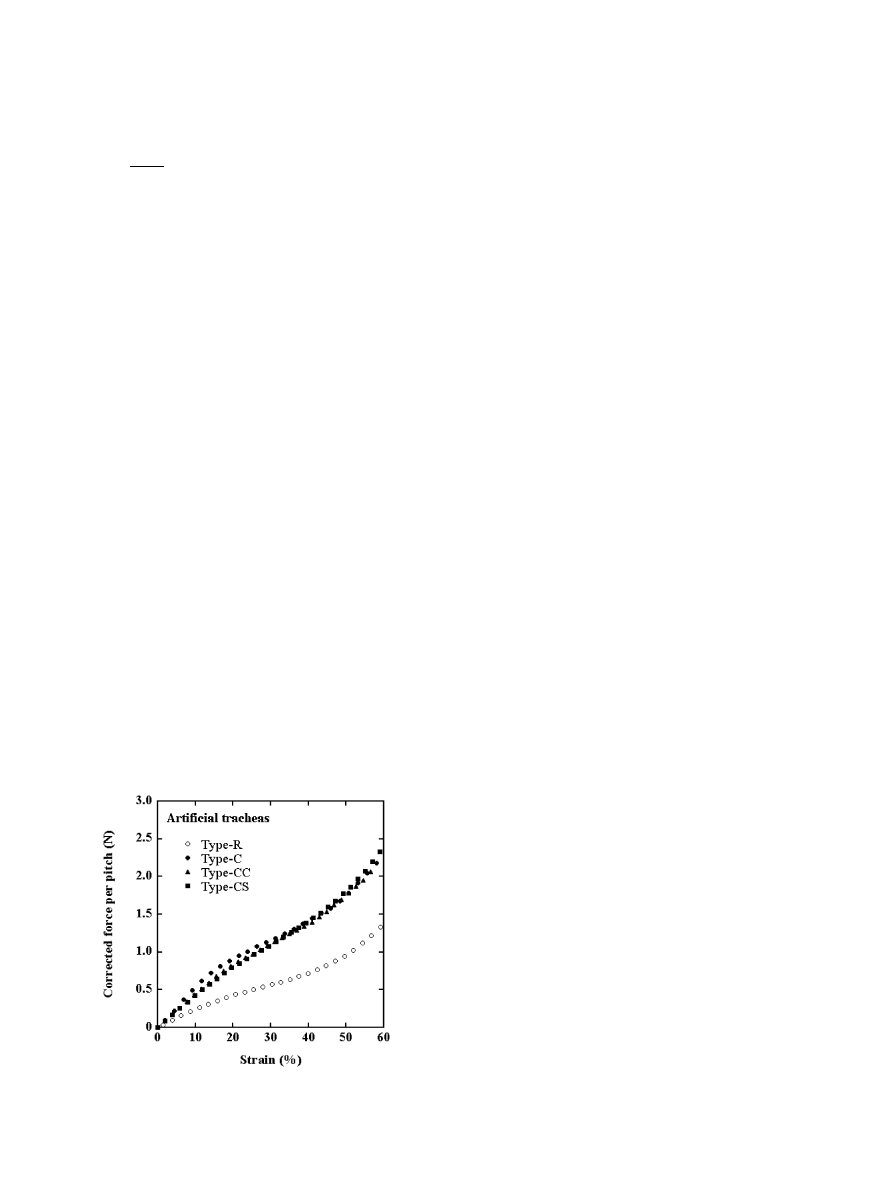
Fig. 7 shows force per pitch vs. strain plots for the
artificial tracheas similar to those in Fig. 4, but in these
plots the outer diameters of Type-C, Type-CC and
Type-R were reduced to that of Type-CS (18.3 mm),
which we designate hereafter d

0;corr

. The f

corr

2

e

c

curves

of the Type-C group (Type-C, Type-CC and Type-CS)
were located above the curve for Type-R. The curves for
the Type-C group almost overlapped over the whole
strain range examined, indicating that they have very
similar mechanical properties under compression. Spe-
cifically, coating with collagen as well as laminating with
collagen sponge did not affect the mechanical properties
of the tracheas.

By using Eq. (5), E of the stent is calculated from the

slope of the f –e

c

curve in the region of e

c

55%. The

values of E for the Type-R and Type-C stents were
evaluated from the curves shown in Fig. 4. In the
estimation of E; I was calculated by Eq. (6a) for Type-R
and by Eq. (6b) for Type-C, using the dimensions of the
stents shown in Fig. 2. The value of E was 1.2 10

9

Pa

for the Type-C stent and 1.1 10

9

Pa for the Type-R,

which agreed well with each other. The values of E for
the stents also agreed with the typical value for
polypropylene (1.17 10

9

Pa) reported in the literature

[16].

4.2. Stress–strain curves of tracheal cartilages

In Fig. 5, E for 100 mm/min was higher than those for

the others. Little difference was observed in E for 2 and
10 mm/min. The latter result may occur because the
difference in cross-head speed is small. In our experi-

ments, only one test was made for each cross-head
speed, so that we cannot say definitely that E of the
tracheal cartilages is cross-head speed dependent. We
are planning to make more repeats of the test to support
the above deduction. It is well known that articular
cartilages showthe viscoelasticity [17], and the visco-
elasticity originates from the collagen fibers in the
cartilages. This strongly suggests that the tracheal
cartilages behave viscoelastic bodies; namely, the
cross-head speed dependence appears in E in the
elongation tests.

E

for the tracheal cartilages could be obtained from

the slope of the s2e

t

curves. The values at 2, 10 and

100 mm/min were 1.9 10

7

, 1.9 10

7

and 2.1 10

7

Pa,

respectively. E can also be estimated independently from
the w2e

c

curve in Fig. 5. Assuming that the trachea is a

cylinder composed only of cartilage, with d

0

¼ 14 mm

and b ¼ 0:74 mm, E can be calculated to be 7.6 10

7

Pa.

E

estimated by both the deformation modes is of the

same order of magnitude, approximately 10

7

Pa.

5. Conclusions

Considering that the values of f correspond to

strength, the resistance of Type-C group tracheas to
collapse was greater than that of Type-R. The strength
of Type-C group tracheas was almost identical at all
values of strain when corrected for the outer diameter of
the stent. Therefore, neither collagen coating nor
laminating with collagen sponge appear to affect the
resistance of artificial tracheas to collapse. The resis-
tance of canine trachea to collapse was closer to that of
Type-C than to that of Type-R at high strains. The
shape of the w2e

c

curve of canine trachea was different

from that of artificial trachea. The shapes of the f 2e

c

curves of Type-R and Type-C artificial tracheas were
similar. The s2e

t

curves of tracheal cartilages were

suggested to be dependent on the tensile cross-head
speed. The Young’s modulus of tracheal cartilages was
estimated to be of the order of 10

7

Pa by both

compression and tensile tests.

As shown in this report, it is possible to estimate the

mechanical properties of a mesh-type artificial trachea
by using standard formulae. In other words, we can
design in advance artificial tracheas with adequate
mechanical properties. In this sense, these formulae will
contribute to the design of newprostheses for the
trachea.

Acknowledgements

This work was supported in part by Grant-in-Aid for

Scientific Research from the Ministry of Education,
Science, Sports and Culture of Japan (No. 10305069),

Fig. 7. Corrected force per pitch vs. strain plots for Type-R, Type-C,
Type-CC and Type-CS artificial tracheas.

S. Kawaguchi et al. / Biomaterials 22 (2001) 3085–3090

3089

and by JSPS Research for the Future Program,
Biological Tissue Engineering Project, No. JSPS-RFTF
98100201.

References

[1] Okumura N, Nakamura T, Natsume T, Tomihata K, Ikada Y,

Shimizu Y. Experimental study on a newtracheal prosthesis made
from collagen-conjugated mesh. J Thorac Cardiovasc Surg
1994;108:337–45.

[2] Teramachi M, Okumura N, Nakamura T, Kiyotani T, Takimoto

Y, Matsuda S, Ikada Y, Shimizu Y. Intrathoracic tracheal
reconstruction with a collagen-conjugated prosthesis: evaluation
of the efficacy of omental wrapping. J Thorac Cardiovasc Surg
1997;113:701–11.

[3] Teramachi M, Nakamura T, Yamamoto Y, Kiyotani T,

Takimoto Y, Shimizu Y. Porous-type tracheal prosthesis sealed
with collagen sponge. Ann Thorac Surg 1997;64:965–9.

[4] Rains JK, Bert JL, Roberts CR, Par

!ee PD. Mechanical properties

of human tracheal cartilage. J Appl Physiol 1992;72(1):219–25.

[5] Roberts CR, Rains JK, Par

!ee PD, Walker DC, Wiggs B, Bert JL.

Ultrastructure and tensile properties of human tracheal cartilage.
J Biomech 1998;31:81–6.

[6] Roberts CR, Par

!ee PD. Composition changes in human tracheal

cartilage in growth and aging, including changes in proteoglycan
structure. Am J Physiol 1991;261:L92–101.

[7] Lambert RK, Baile EM, Moreno R, Bert J, Par

!ee PD. A method

for estimating the Young’s modulus of complete tracheal cartilage
rings. J Appl Physiol 1991;70(3):1152–9.

[8] Ishida K, Par

!ee PD, Blogg T, Schellenberg RR. Effects of elastic

loading on porcine trachealis muscle mechanics. J Appl Physiol
1990;69(3):1033–9.

[9] Penn RB, Wolfson MR, Shaffer TH. Developmental differences in

tracheal cartilage mechanics. Pediatr Res 1989;26:429–33.

[10] Begis D, Delpuech C, Tallec PL, Loth L, Thiriet M, Vidrascu M.

A finite-element model of tracheal collapse. J Appl Physiol
1988;64(4):1359–68.

[11] Petrasch U, Hinrichsen G. On the further development of a

human alloplastic trachea prosthesis. Biomed Technik 1994;
39:244–50.

[12] Gustin B, G’Sell C, Cochelin B, Wourms P, Ferry MP. Finite

element determination of the forces exerted by endotracheal tubes
on the upper airways. Biomater 1996;17:1219–25.

[13] Shimizu Y, Tamura K, Tato H, Teramatsu T, Hino T. Study on

the artificial trachea using mesh. Jpn J Artif Org 1983;12:486–9.

[14] Deslauriens J, Ginsberg RJ, Nelems JM, Pearson FG. Innominate

artery rupture: a major complication of tracheal surgery. Ann
Thorac Surg 1975;20:671–7.

[15] Roark RJ, Young WC. Formulas for stress and strain. 5th ed.

Tokyo: McGraw-Hill Kogakusha, 1975.

[16] Brandrup J, Immergut EH, Grulke EA, editors. Polymer hand-

book. 4th ed. NewYork: Wiley, 1999.

[17] Fung YC. Biomechanics, mechanical properties of living tissues.

2nd ed. NewYork: Springer, 1993.

S. Kawaguchi et al. / Biomaterials 22 (2001) 3085–3090

3090