Fibrillar Structure and Mechanical Properties of Collagen

Peter Fratzl,

1

Klaus Misof, and Ivo Zizak

Materials Physics Institute and Ludwig-Boltzmann Institute of Osteology, University of Wien, Strudlhofgasse 4, A-1090 Wien, Austria

Gert Rapp

European Molecular Biology Laboratory Outstation, Notkestrasse 85, 22603 Hamburg, Germany

Heinz Amenitsch

Institute of Biophysics and X-Ray Structure Research, Austrian Academy of Sciences, Steyrerg. 17, A-8010 Graz, Austria

and

Sigrid Bernstorff

Sincrotrone Trieste, Strada Statale 14 - Km. 163.5, 34012, Basovizza, Trieste, Italy

Received November 13, 1997

Collagen type I is among the most important

stress-carrying protein structures in mammals. De-
spite their importance for the outstanding mechani-
cal properties of this tissue, there is still a lack of
understanding of the processes that lead to the
specific shape of the stress–strain curve of collagen.
Recent in situ synchrotron X-ray scattering experi-
ments suggest that several different processes could
dominate depending on the amount of strain. While
at small strains there is a straightening of kinks in
the collagen structure, first at the fibrillar then at
the molecular level, higher strains lead to molecular
gliding within the fibrils and ultimately to a disrup-
tion of the fibril structure. Moreover, it was ob-
served that the strain within collagen fibrils is
always considerably smaller than in the whole ten-
don. This phenomenon is still very poorly under-
stood but points toward the existence of additional
gliding processes occurring at the interfibrillar
level.

r

1997 Academic Press

INTRODUCTION

The outstanding mechanical properties of collagen-

rich tissues like, e.g., tendons, are largely deter-

mined by the collagen structure. Tendons are built of
parallel fibrils which are themselves assemblies of
parallel collagen molecules. There is still no com-
plete understanding of the relation between stress-
induced changes in the structure and the specific
shape of the stress/strain curve of collagen.

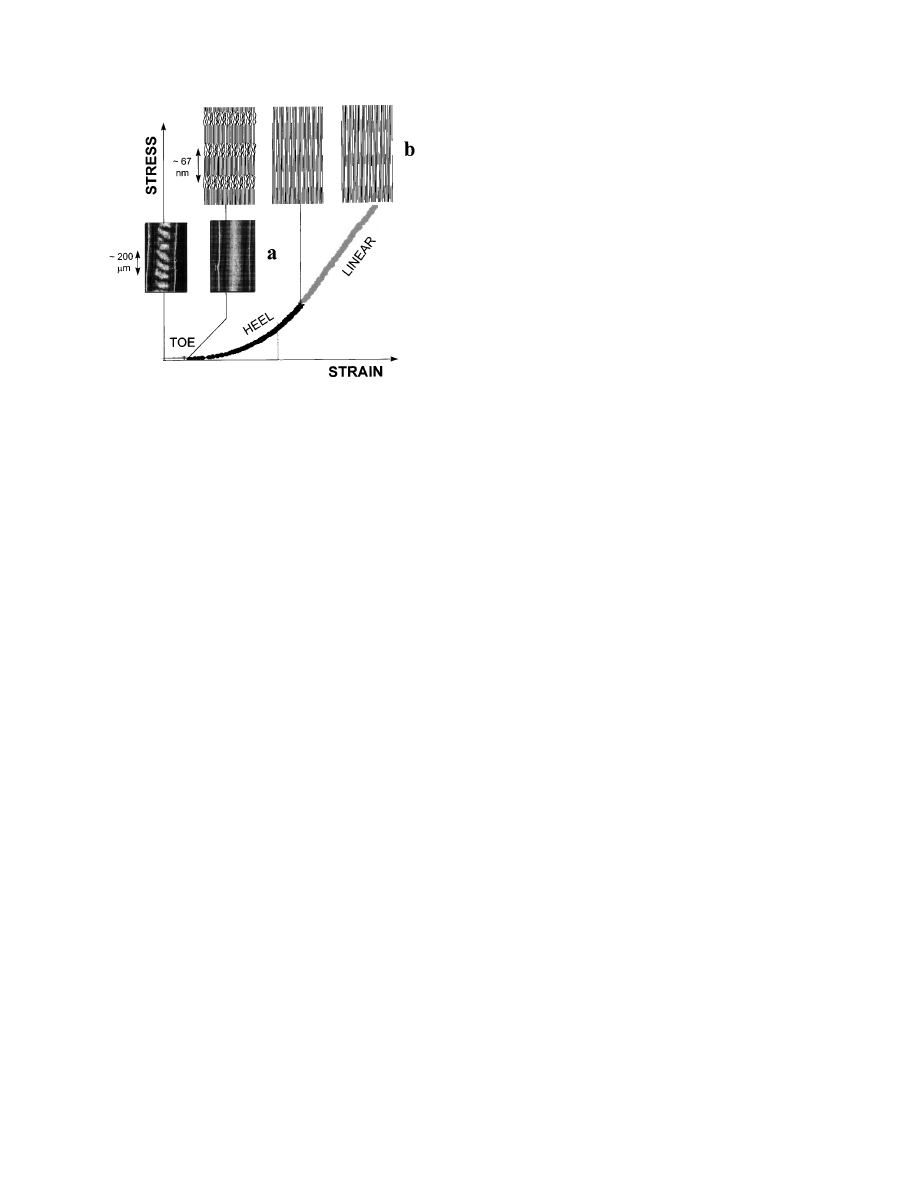
Typically, the stress/strain curve of collagen from

tendon can be subdivided into several regions (Vin-
cent, 1990), as outlined in Fig. 1. The region of small
strains (‘‘toe’’ region) corresponds to the removal of a
macroscopic crimp in the collagen fibrils, visible in
the light microscope (Diamant et al., 1972). At larger
strains (in the ‘‘heel’’ and the ‘‘linear’’ region of the
stress/strain curve, see Fig. 1), there is no further
structural change visible in the light microscope.
Hence, the processes affecting the collagen structure
occur in the submicrometer range and can be investi-
gated by (synchrotron) X-ray scattering.

HEEL REGION OF THE STRESS/STRAIN CURVE

At strains typically beyond 3%, the stiffness of rat

tail tendon increases considerably with the exten-
sion (heel region, Fig. 1). In a recent synchrotron
X-ray scattering experiment, Misof et al. (1997a)
have studied the structural changes occurring in this
part of the stress/strain curve. It was observed that
the intensity of the diffuse equatorial scattering,
which is due to the lateral arrangement of the
collagen molecules inside the fibrils (Fratzl et al.,

1

To whom correspondence and reprint requests should be

addressed at present address: Erich Schmid Institute of the
Austrian Academy of Sciences and University of Leoben, Jahnstr.12,
A-8700 Leoben, Austria. E-mail: [e-mail].

JOURNAL OF STRUCTURAL BIOLOGY

122, 119–122 (1997)

ARTICLE NO.

SB983966

119

1047-8477/97 $25.00

Copyright

r

1997 by Academic Press

All rights of reproduction in any form reserved.

1993; Hulmes et al., 1995), increased linearly with
the strain. This was interpreted as a reduction of the
disorder in the lateral molecular packing within
fibrils, resulting from the straightening of kinks in
the collagen molecules.

Indeed, kinks are thought to occur within the gap

region of the collagen fibril structure. In particular, a
recent refinement of the collagen fibril packing struc-
ture (Wess et al., 1998) points toward the existence of
kinks. They might occur in the gap region of the
collagen fibrils because of the greater flexibility of
collagen molecules due, first, to lower levels of
proline and hydroxyproline on the collagen chain
(Fraser and Trus, 1986) and, second, to the reduced
packing density as compared to the overlap region
(Fraser et al, 1983). Moreover, considerable azi-
muthal and lateral flexibility of collagen molecules
had been demonstrated in NMR measurements (Je-
linski et al., 1980).

The model outlined in Misof et al. (1997a) assumes

that spontaneously occurring molecular kinks (that
is, kinks appearing by thermal activation) lead to an
increased disorder and, hence, entropy of the gap
region. The straightening of the kinks would lead,
therefore, to an elongation of the fibril and to a
reduction in entropy which provides the force acting
against the elongation. This entropic force is increas-
ing when the number of kinks decreases leading to
the typical upwards curvature of stress/strain curve

(see Fig. 1). The model also implies a linear relation
between strain and degree of lateral order, which
was observed experimentally.

LINEAR REGION OF THE STRESS/STRAIN CURVE

When collagen is stretched beyond the heel region

of the stress/strain curve, most kinks are straight-
ened and no further extension is possible by the
entropic mechanism described above. Therefore, some
other process must prevail in the linear region of the
stress/strain curve. The most likely processes are a
stretching of the collagen triple-helices or of the
cross-links between the helices, implying a side by
side gliding of neighboring molecules. This process
has already been studied in the mid-eighties by use
of synchrotron radiation diffraction experiments
(Mosler et al., 1985; Folkhard et al., 1986). In these
experiments, a strain-induced change in the struc-
ture factor of the axial diffraction maximums was
observed. In particular, the second order maximum
increased with respect to the third order, when the
tendon was stretched. This was a clear indication
that stretching increased the length of the gap
region with respect to the length of the overlap
region, implying a considerable gliding of neighbor-
ing molecules (Folkhard et al., 1986).

In a very recent experiment, we have revisited this

problem by measuring the intensities of the meridi-
onal reflections of wet rat tail tendons and control-
ling the external stress and strain by means of the
apparatus described in Misof et al. (1997a). The
experiments were carried out at the SAXS beamline
of the synchrotron source ELETTRA in Trieste
(Amenitsch et al., 1995). The data were collected
using an X-ray CCD camera (AXS, Karlsruhe). This
two-dimensional data collection allowed an integra-
tion of the peak intensities accounting for the fact
that the unit cell of the collagen structure is tilted by
a few degrees with respect to the fibril axis (Wess,
1998), which leads to a splitting of higher order
meridional peaks. Both the applied stress and the
overall strain on the tendon were recorded during
the experiment.

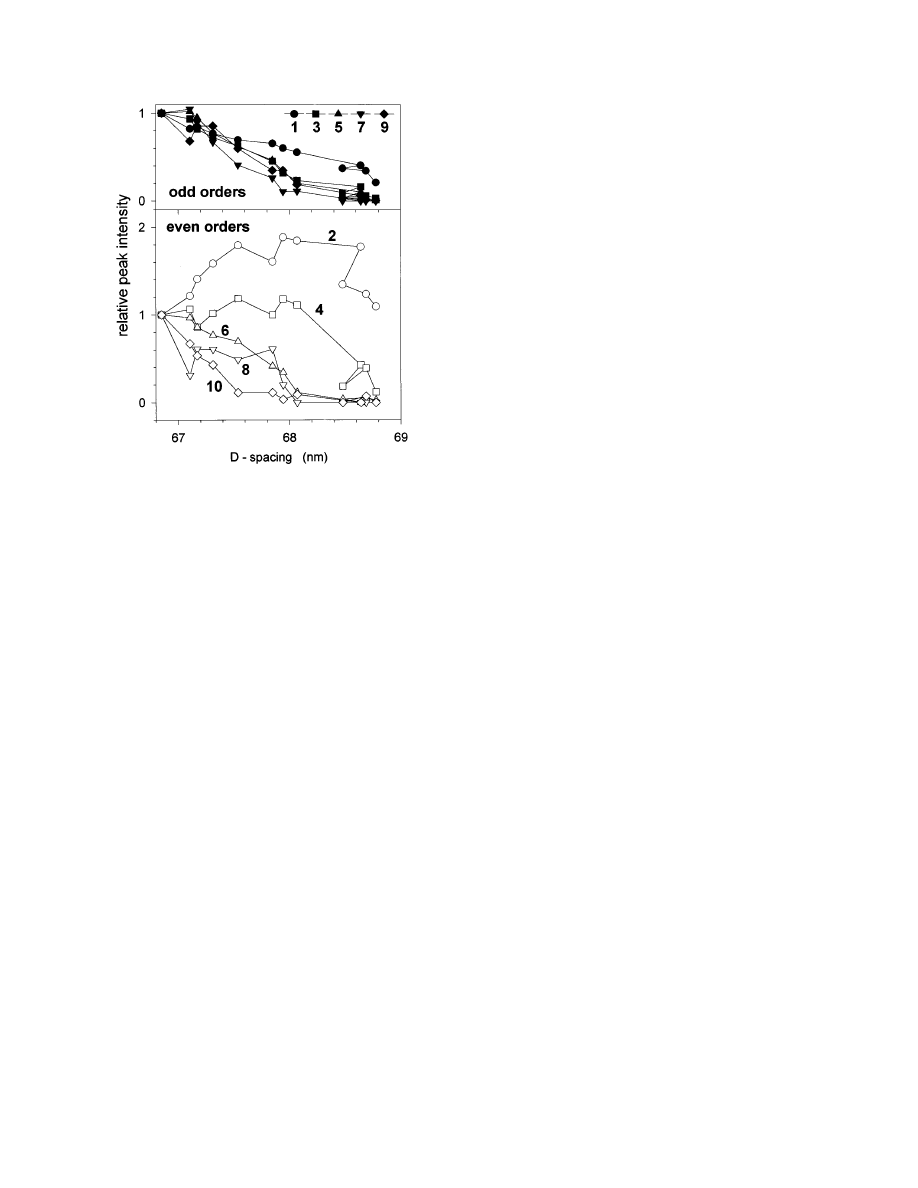
Figure 2 shows the evolution of peak intensities as

a function of the D-period during a typical stretching
experiment. There are two remarkable effects:

1. Odd and even orders behave in a qualitatively

different way. While odd orders always decrease with
strain, the lower even orders first increase and then
decrease (Fig. 2). This means that, in particular, the
ratio of second to third order increases drastically
during the stretching process, an effect that has been
observed before (Mosler et al., 1985). In normal
tendon this ratio is typically very small (Brodsky et
al., 1982) and its increase can be interpreted as the
growth of the gap in comparison to the overlap region

F

IG

. 1.

Typical stress–strain curve of a rat tail tendon. In the

toe region, where the tendon can be extended with very little force,
a macroscopic crimp of the fibrils with a typical period in the order
of 100 µm is removed (Diamant et al., 1972). This can be
visualized using polarized light (a). Further structural changes
occur at the fibrillar level (b). The heel region may correspond to a
straightening of molecular kinks in the gap (Misof et al., 1997a)
and the linear region to a gliding of molecules (Folkhart et al.,
1986). The most recent synchrotron diffraction data suggest that a
disruption of the fibrillar structure starts with an increased
fuzziness of the gap/overlap interface (see schematic picture, top
right).

120

FRATZL ET AL.

of the fibril, which indicates a gliding of neighboring
molecules with respect to each other.

The Hodge–Petruska staggering (1963) implies

that the gap length and the molecular length add up
to 5 D. Therefore, calling

e

D

and

e

M

the relative

increase of the D-period and of the length of the
triple-helical molecule,

g 2 g

0

5 5e

D

2 (5 2 g

0

)

e

M

,

where

g is the ratio of the gap length to the D-period,

with

g

0

being its value at the beginning of the

stretching process. Since the molecule is consider-
ably stiffer than the fibril (Sasaki and Odajima,
1996),

e

M

increases more slowly with the applied

stress than

e

D

, which means that

g, the fraction of

the D-period occupied by the gap, increases with
external stress. This may, in turn, explain qualita-
tively the experimentally observed increase of sec-
ond order peak in Fig. 2.

There is a systematic trend that higher reflections

decrease more rapidly than lower ones. This is
particularly visible for the even orders (Fig. 2) and it

means that the amount of disorder in the axial
staggering increases upon stretching. This was, how-
ever, not accompanied by a broadening of the axial
peaks during the stretching experiment.

A simple way to explain this observation is the

assumption that the interface between gap and
overlap region is getting increasingly fuzzy, as shown
schematically in the top right image of Fig. 1. This
may occur when the relative gliding of the molecules
is not exactly the same for each nearest neighbor
pair. Under this assumption, the axial projection of
the electron density would be smeared by a distribu-
tion function. Calling it P(r) and the electron density
without the smearing g

0

(r), the resulting electron

density along the fibril would be the convolution of P
and g

0

, P

3g

0

. Hence, the intensities of the axial

peaks would be determined by the Fourier-trans-
form squared of P

3g

0

, that is, the product of the

squared Fourier transforms of P and of g

0

. Conse-

quently, if P is, e.g., a Gaussian with width w, then
the axial peak intensities are multiplied by the
squared Fourier transform of P, which is a Gaussian
of a width proportional to 1/w. Hence, the stronger
the smearing, the larger the damping of higher order
peaks. As a result, the intensities of all axial reflec-
tions will eventually decrease with increasing strain,
higher orders faster than the lower ones. This may
explain, at least qualitatively, the effects observed in
Fig. 2.

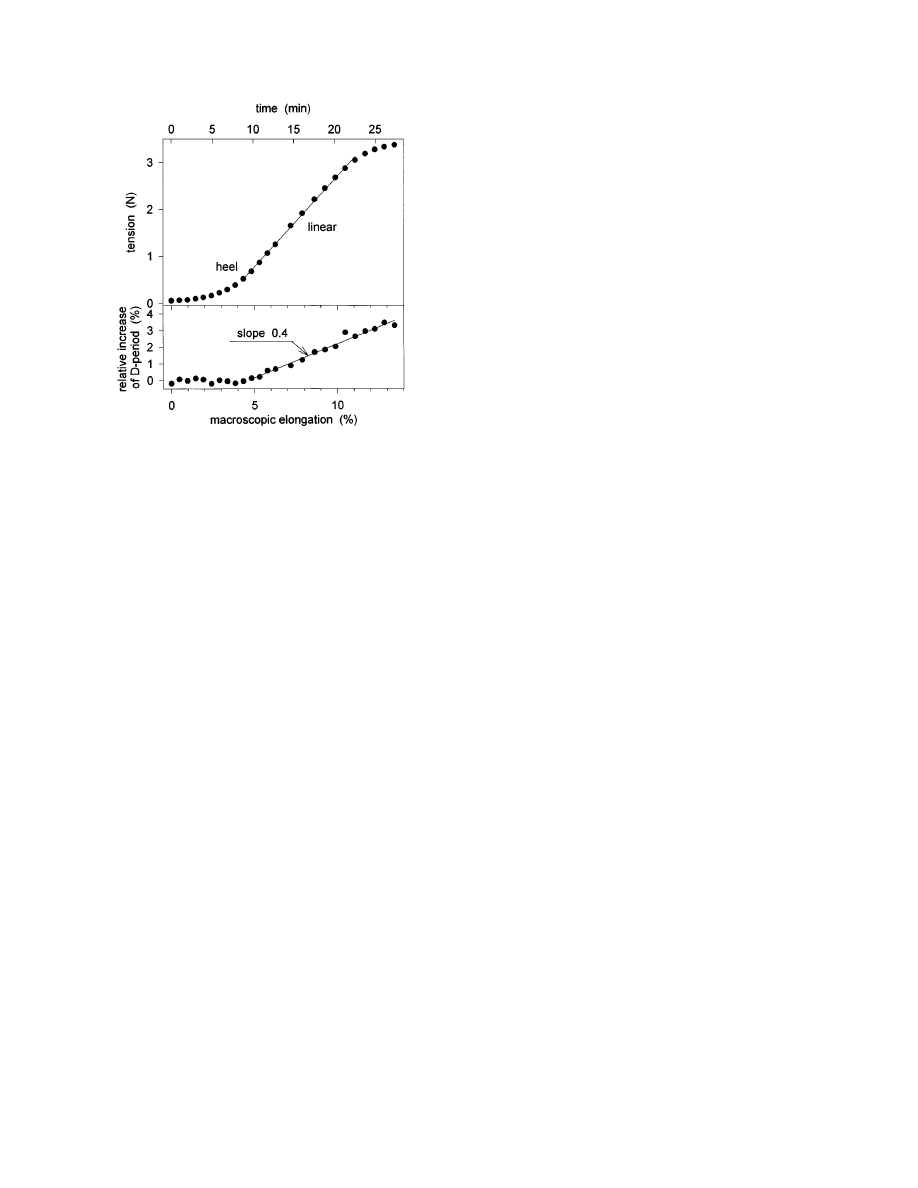
Finally, the relation between the increase of the

collagen D-period (that is, the strain at the fibrillar
level) and the macroscopic strain of the specimen is
shown in Fig. 3. In the linear region of the stress/
strain curve, the D-period increased by about 40% of
the macroscopic strain. This implies that not all the
elongation of the tendon is due to a stretching of the
fibrils (Sasaki and Odajima, 1996), and suggests
that some of the elongation of the tendon is due to a
relative movement of entire fibrils. At this point we
can only speculate about possible mechanisms, but it
is not unlikely that an interfibrillar gliding is medi-
ated by a highly viscous interfibrillar substance
containing water and proteoglycans.

OPEN QUESTIONS

Recent synchrotron X-ray scattering experiments

have revealed drastic changes in the molecular
packing of collagen fibrils under strain. While at low
strains a straightening of molecular kinks seems to
dominate, molecular gliding is observed at large
strains, leading to an increasingly irregular exten-
sion and ultimately to a disruption of the fibrillar
structure. The mechanisms are summarized in Fig.
1a, which shows the macroscopic effects occurring in
the toe-region of the stress/strain curve. Figure 1b
shows mechanisms at the fibrillar level. First, a
straightening of molecules and then an increase of

F

IG

. 2.

Evolution of the meridional peak intensities of rat tail

tendon under tensile stress, the length of the tendon being
increased at a constant rate. The intensities are shown as a
function of the D-period and were normalized to their value at D

5

66.85 nm, which was the D-period at the beginning of the
stretching process. The odd and even orders are shown separately
in the upper and lower panel, respectively. Some of the weak
orders (4 and, particularly, 8) are affected by large statistical
errors. Shortly before the tendons started to break, partial
relaxation of the D-period was occasionally observed (like between
the ninth and the tenth point in the graph, around D

5 68.6 nm).

This is most probably the result of a partial stress release due to
the failure of some of the collagen fibrils in the assembly.

121

FIBRILLAR STRUCTURE AND MECHANICAL PROPERTIES OF COLLAGEN

the gap region in the fibrils, accompanied by a
smearing of the gap/overlap interface. Nonetheless,
many important questions remain unsolved, among
which:

• A quantitative interpretation of the change in

axial scattering intensities (such as in Fig. 2) was
beyond the scope of this report, but work in this
direction is in progress. In particular, it seems
important to determine the strain-induced changes
in the electron density distribution along the fibril
axis to get a more detailed description of the gliding
process.

• The role of intermolecular cross-linking is still

unclear. Indeed, the molecular gliding described
above implies a considerable force on the cross-links.
Preliminary data on the stress/strain curves of cross-
link deficient rat tail tendons have shown that the
tendons break at very small forces and, in particular,
there is no linear region in the stress/strain curve.
Indeed, the tendons lacking cross-links were behav-
ing more like a viscous liquid than a solid fiber (Misof
et al., 1997c). Finally, collagen made of homotrimers
showed considerably reduced maximum strain, which
could also indicate an influence of cross-linking
(Misof et al., 1997b).

• Almost nothing is known about the role of the

interfibrillar substance for the mechanical proper-
ties and, in particular, on its role in mechanically
linking neighboring fibrils. The present data, how-

ever, suggest a considerable importance, since only
40% of the strain on the rat tail tendon is actually
transmitted to the fibrils.

This work has been supported by the Fonds zur Fo¨rderung der

Wissenschaftlichen Forschung (P11762-PHY).

REFERENCES

Amenitsch, H., Bernstorff, S., and Laggner, P. (1995) High flux

beamline for small-angle x-ray scattering at ELETTRA, Rev.
Sci. Instr. 66, 1624–1626.

Brodsky, B., Eikenberry, E. F., Belbruno, K. C., and Sterling, K.

(1982) Variations in collagen fibril structure in tendons, Biopoly-
mers 21, 935–951.

Diamant, J., Keller, A. , Baer, E., Litt, M., and Arridge, R. G. C.

(1972) Collagen: Ultrastructure and its relation to mechanical
properties as a function of aging, Proc. R. Soc. Lond. B. 180,
293–315.

Folkhard, W. E., Mosler, W., Geerken, E., Kno¨rzer, E., Nemetschek-

Gonsler, H., Nemetschck, Th., and Koch M. H. J. (1986)
Quantitative analysis of the molecular sliding mechanism in
native tendon collagen—Time-resolved dynamic studies using
synchrotron radiation, Int. J. Biol. Macromol. 9, 169–175.

Fraser, R. D. B., MacRae, T. P., Miller, A., and Suzuki, E. (1983).

Molecular conformation and packing in collagen fibrils, J. Mol.
Biol. 167, 497–521.

Fraser, R. D. B., and Trus B. L. (1986) Molecular mobility in the

gap regions of type I collagen fibrils, Bioscience Reports 6,
221–226.

Fratzl, P., Fratzl-Zelman, N., and Klaushofer, K. (1993) Collagen

packing and mineralization, Biophys. J. 64, 260–266.

Hodge, A. J., and Petruska, J. A. (1963) in Ramachandran, G. N.

(Ed.), Aspects of Protein Structure, pp. 289–300, Academic
Press, New York.

Hulmes, D. J. S, Wess, T. J., Prockop, D. J., and Fratzl, P. (1995)

Radial packing, order and disorder in collagen fibrils, Biophys.
J. 68, 1661–1670.

Jelinski, L. W., Sullivan, C. E., and Torchia, D. A. (1980) 2H NMR

study of molecular motion in collagen fibrils, Nature 284,
531–534.

Misof, K., Rapp, G., and Fratzl, P. (1997a) A new molecular model

for collagen based on synchrotron x-ray scattering evidence,
Biophys. J. 72, 1376–1381.

Misof, K., Landis, W. J., Klaushofer, K., and Fratzl, P. (1997b)

Collagen from the osteogenesis imperfecta mouse model (oim)
shows reduced resistence against tensile stress, J. Clin. Invest.
100, 40–45.

Misof, K. P., Rapp, G., Landis, W. J., Klaushofer, K., Hulmes,

D. J. S., and Fratzl, P. (1997c) Mechanical properties of normal
and defective collagen - implications for osteogenesis imper-
fecta, Bone 20 (Suppl. 4): 11S

Mosler, E., et al. 1985. Stress-induced molecular rearrangement

in tendon collagen, J. Mol. Biol. 182, 589–596.

Sasaki, N., and Odajima, S. (1996) Elongation mechanism of

collagen fibrils and force-strain relations of tendon at each level
of structural hierarchy, J. Biomech. 29, 1131–1136.

Vincent, J. 1990. Structural Biomaterials, Princeton Univ. Press,

New Jersey.

Wess, T. J, Hammersley, A. P., Wess, L., and Miller, A. (1998)

Molecular packing of type I collagen in tendon, J. Mol. Biol. 275,
255–267.

Wess, T. J. (1998) A consensus model for molecular packing of type

I collagen, J. Struct. Biol., this issue.

F

IG

. 3.

Tension required for the elongation of a typical rat tail

tendon (top) and corresponding relative change of the collagen
D-period (bottom). The (macroscopic) strain rate of the experi-
ment was constant at about 0.49% per minute. The time required
for the collection of an X-ray diffraction pattern was 50 s. The
onset of a change in the D-period occurred in the heel region. In
the linear region of the stress/strain curve, the relative change of
the D-period was 40% of the macroscopic elongation.

122

FRATZL ET AL.