c

c

Contents

J

!" # $%J%&

' () *

+%"' ,

) - ./,

0 )"' 1,

22.( 34"5672 /

) ' /

7"72 ,8/

! % 2 /9

7" :;4<; =:;2/,9

%2"9

46)2">9

:;4# 2&8

46 " ":4>8

46 " ":4>8

46 " " :4>8

7"2:;4%:;' 8

J"2:4J>-881

72 :;48111

72 6"1

0 ?

72 ":;41/*1&?

7 ":;4" %11?

5 :;4%46; ??

7"@ %(24*?

2 :;4*,?

J

eal Gas Non-Point Particles

J J

i„ u

i„ `

i„

!

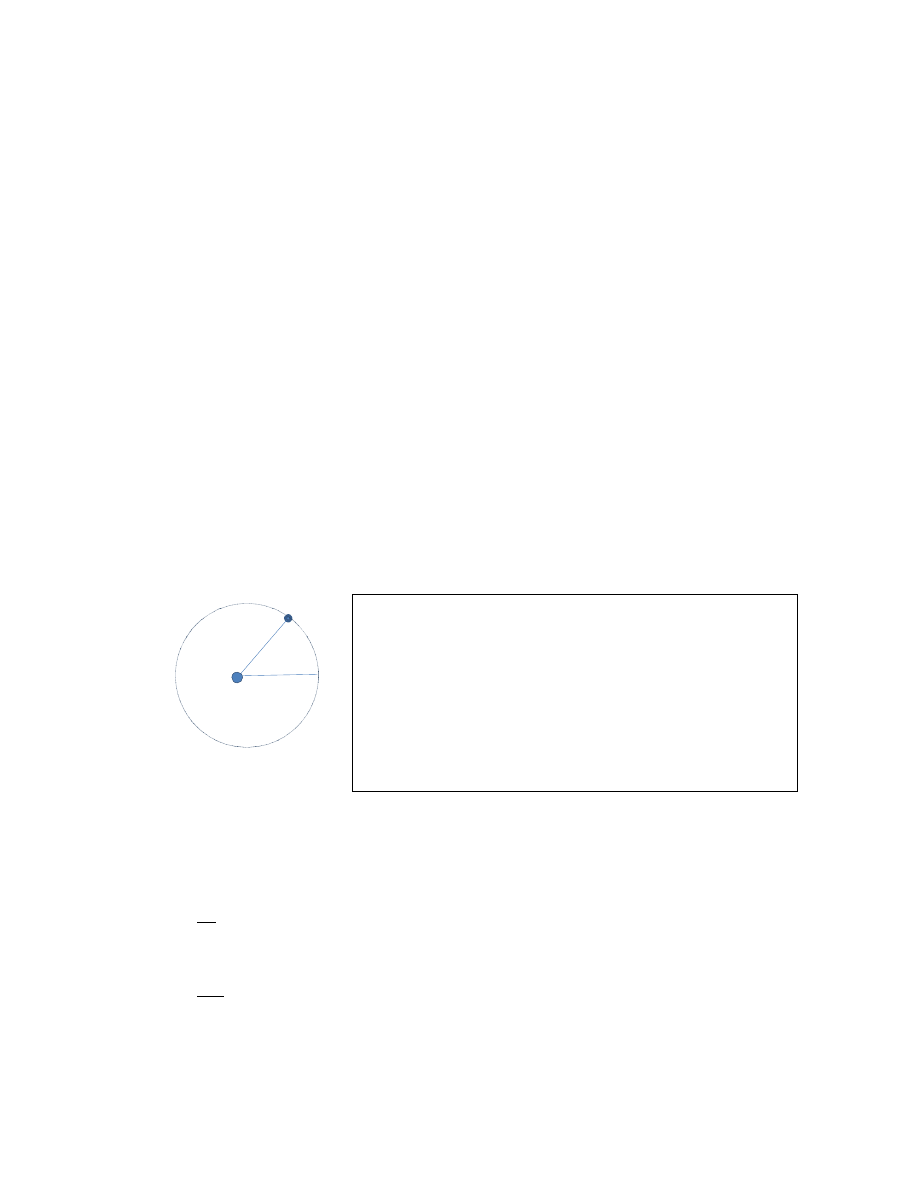
Problem in Rotating Atoms (02:30

Energy of a rotating system

`

m m " #

$%

†

"

&'

#

`

(

$

†

$

%

' *
&

**

A&3&26!3
&

)

*B

*

$

Convert rotational momentum to angular momentum

) $J

* +
$$ , $-
. "J#

w

/

ß

J" #". #

<= % 2 2<=. "

u

etermine the angular momentum (momenta conjugate to (Ʌ, J, r)

. /
"( 0

$

$

12 12

' 3 " #

Energy of a single molecule

$4

†

Partition Function for a Single Molecule (13:30

Ô

c " #$

532 "$$
# 6 )$

"$4# 6 3

$

!

"

`

%

7

`

$8

#$

!

%&$

!

9

"!

%

'(

%

'(

)

*

&

!

:

%(`

J

"

#

;<

$

+

,-

.

,

6$ $ '

log of Z , the Partition Function

$%

t

/ t - t # /

,

t

/

,

t

012345243

'"=>J#"J0

#

$

Energy of Molecular Gas Ȃ an a Para ox (23:25

$%%

†

67
6

689*

6

+

%

' &('`'` !
$
Ô

6!$

J ; < ?
) '`

"J0

#

`

! $-

" #$J &u
$ $

D

uantum Mechanical Formulation (28:00

`

! * $" #

Ô $

$4

†

"#

2:

*

$%

†

:

`

;< ">7

#$
5 6$ $ "$4# $%

$%&

;

:

6$ $

%(

$@ ! $

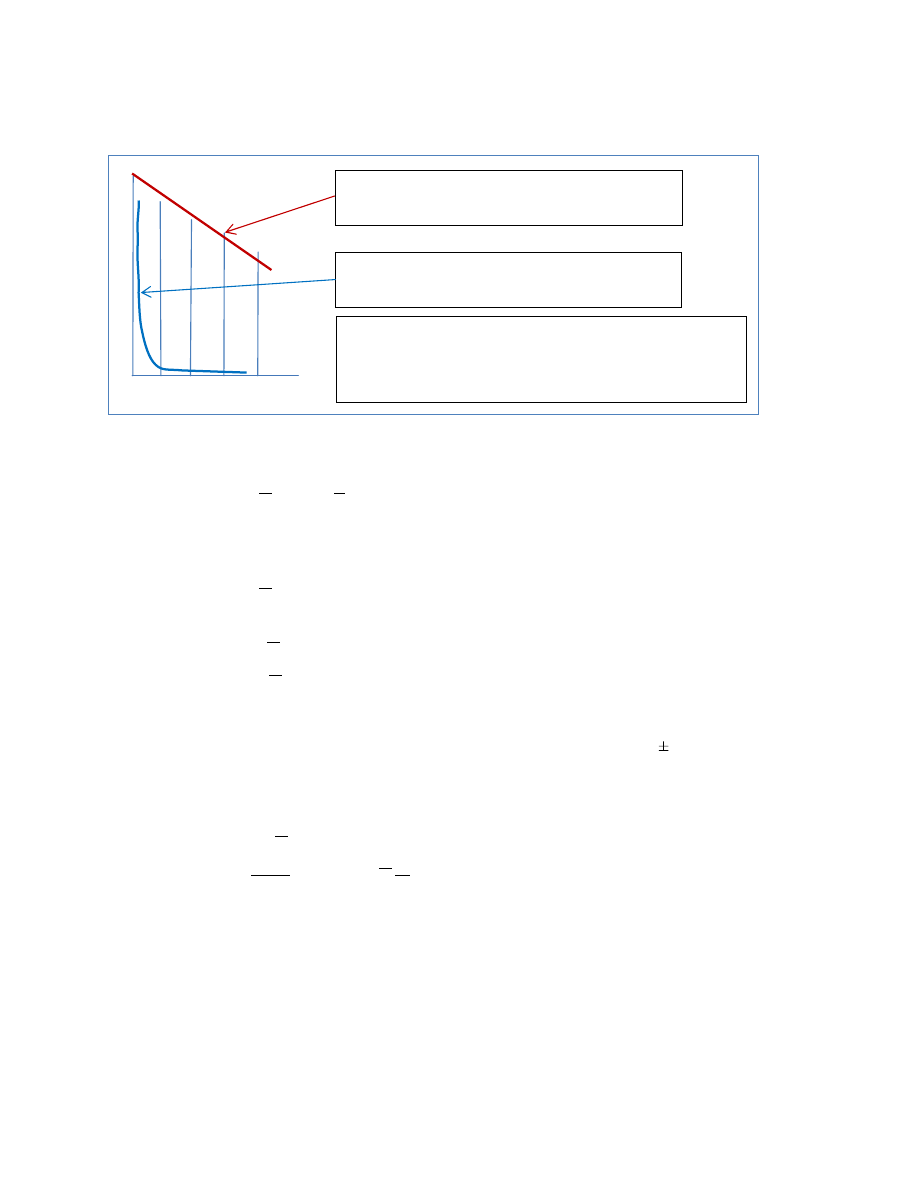
Approximate Solutions; High or Low Temperature

Ô: ! /
!

$%&

;

:

< ;

=

A 0`

Ô : !
!

$%&

;

:

"

>

0

+

%

'+

'??

:

0%A:

%

'

'??

:

0

70&

3

i„

;<

i„ J" 0

# :

i„ J ! !

Calculate Mo ifie Partition Function an Energy

$%

t

%

:

$%

†

@

6 ABC

6

/%

:

:

B :

3

i„

i„ '

i„

! %":

:

%

(J#

The Temperature Crossover Point (47:00

`

! /

C

*

‚

0%

"`0%(:#
;<

:

$%

=:

:"0%(` #

$%4

+

:

D`A

!

@ )E "F 0`#

+

+

D4

:

`G
! $H

!

u

iscussion on ifferent molecules, ifferent temperatures (50:00

" #

Thermo ynamics of a Black Hole Dzki s versionsdz (BekensteinEntropy
(54:20

1/ I ` @F,/
$

J + @F, 3

$%

Q

@EFG

Q

H

F

%$

„ 3+)

$

„ @F,

A

one bit of information, a photon.

`

F $

How Many bits of information in a photon?

,
@F,$` ") #*
*$

J *

) F * 3ummm m

`

)

/ $

Black Hole Premise (to just accept):

i„ Ô@F,

" @,#

i„ Ô c )5 @, 7

i„ @, $

- F

< )/

ummm m

ò Q

< c )5

How much energy oes the BH gain?

`

3 J

<5

c

$%8

†

I

J

:F

K

:F
L

M

J05

c

How much oes the mass of a BH increase?

“

:F

K

:F
L

M

@,

$

“

:F

K

:F
L

M

:

LF

" 20

#

How much oes the Ra ius of a BH increase?

"$%#Q

H

F

"$#“

:

LF

“Q

H

F

'

:

LF

$%

Q“Q

8N: 0

O * “Q

P “

@,

3

i„

i„ 5K5. K5

$ Ô

i„ ! / "=L#$ *

`

5,c

8N: 0

O *

)( @,

The Entropy of a Black Hole, Bekenstein Formula

' $ $M
3

8N: 0

O *Q

$

Q P 80

N:

O * '

@F

i„ @F,2 )

i„ M

: $

i„

:H

R

S

>T

UU

6FÔ

% "%3

J

s the Entropy of a B.H. Jnfinte? Ȃ No (77:00

`

2 @F,$J F

!2 N $` I

i„ I @, 7

i„ I @, $

Temperature of a Black Hole (78:28

J )"

83%8

#

@F,$

`

$` * 3" 7

7 7 #$

`

"‚20`‚c#

$J"$%8# ‚2 "‚c0%#
$%8

†

I

J

:F

K

:F
L

M

J05

c

V† J

:F

K

:F
L

M

W ??VQ >

"‚20`‚c#

$&

XY

X

:F
L

M

:F

H

`

/ $

" 8=#

Temperature ecreases with energy

$

P

+

Y

O

c ! $Ô
7 F $
P !

i„ P"

7

i„ Ô /

i„

i„ F

i„

`

@F,

P/ $@ @$,$

$

D

uestions

Temperature as seen by an observer far from the Black Hole (85:18)

Ô

$

' F " #/
$- $`

". )# $Ô

$`
$-
! $`!"

To an outsi e observer the Black Hole only has a surface, no interior (88:00

Ô

. )$`. " #

. )$M
@F, @F,$

u

`

2 @F,@F

Luminosity of a Black Hole, Hawking Ra iation (93:00

+

" 3

:000%#

.

D

c @ ) $
" F0%#

'Ô

P5

7`

P?>Z[\]^_`W? ?abc\P?>Zdcefcb\g_bc

%

\h]?\t` ?

dcefcb\g_bc?P?>Zi\``?

P

P

+

`

@F,/

F F $` ,F
$

Thermal Equilibrium, Specific Heat (100:00

`

F *$J /

" #$

/ $M.
/ *$

Entropy in universe is ominate by Black Holes (104:00

Ô

!$%

!$%

%

@F,F

#$`) A%

%

F F$