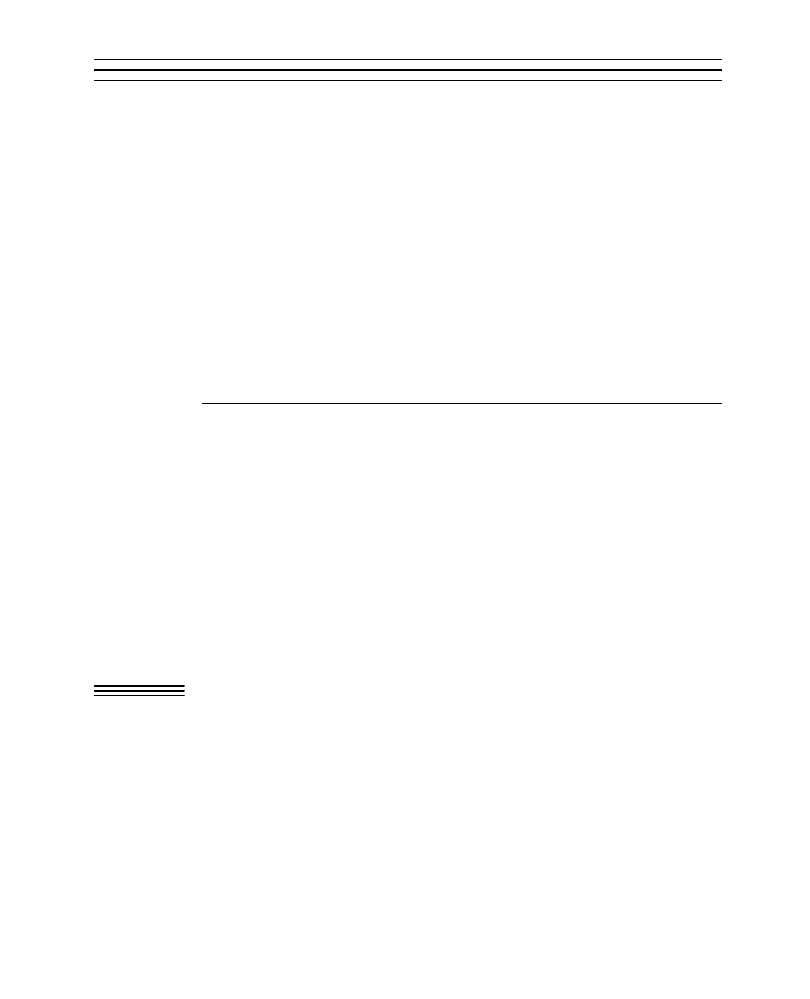
CHAPTER 22

Practical Aspects of Quantitative
Confocal Microscopy

John M. Murray

Department of Cell and Developmental Biology
School of Medicine, University of Pennsylvania
Philadelphia, Pennsylvania 19104

I. Introduction

II. Setting Up for Quantitative Imaging

A. Spot-Scanning Confocals
B. Disk-Scanning or Swept-Array Confocals

III. Correcting Nonuniformities (Flat-Fielding)

A. Additive Correction
B. Multiplicative Correction

IV. Limitations to Exact Quantitation

A. Limitations on Accuracy
B. Limitations on Precision

References

I. Introduction

In principle, confocal microscopes should be capable of generating excellent

quantitative data. The 3D fluorophore distribution in a specimen is transformed
by the microscope optics and detector into the 2D intensity distribution of a
digital image by a linear operation, a convolution. If multiple 2D images of the
specimen at di

Verent focal planes are obtained, then a low-pass spatially filtered

representation of the original 3D distribution in the specimen can be reconstructed
in a way that quantitatively preserves relative fluorophore concentrations, with of
course some limitations on accuracy and precision due to aberrations and noise.
Given appropriate calibration, absolute fluorophore concentrations are accessible.

METHODS IN CELL BIOLOGY, VOL. 81

0091-679X/07 $35.00

Copyright 2007, Elsevier Inc. All rights reserved.

467

DOI: 10.1016/S0091-679X(06)81022-8

To retain in the images all of the quantitative information passed by the micro-

scope, it is necessary to set up the system properly, but fortunately this is easy to do.

II. Setting Up for Quantitative Imaging

A. Spot-Scanning Confocals

Spot-scanning confocals typically utilize photomultiplier tube (PMT) detectors,

for which the gain is continuously adjustable over an enormous range by changing
the voltage applied to the dynode chain. The gain (PMT voltage) must be set carefully
on these instruments to avoid detector saturation. In addition, there is an ‘‘o

Vset’’

or ‘‘dark adjust’’ that needs to be set to avoid detector underflow. Finally, the laser
power must be set low enough to avoid depopulating the ground state of the
fluorophore. If significant ground state depletion occurs, then fluorescence emis-
sion does not increase linearly with illumination intensity (

Fig. 1

). In this situation,

fluorophores in the focal plane will give rise to less fluorescence than expected, and
will be underrepresented in the image relative to fluorophores out of the focal
plane. In that case, image intensities no longer truly reflect fluorophore distribution.

Here is a recipe for setting up the PMT detector and laser for quantitative

imaging, and for ensuring that the damage to the sample due to photobleaching or
phototoxicity is within acceptable limits.

For this preliminary setup, choose an area of the intended specimen that is

equivalent to the area to be imaged, but is not the best area. (It may be destroyed

Relative fluorescence

0

0.2

0.4

0.6

0.8

1.0

2

4

Laser power (% of maximum)

6

8

0

10

Ground state

depletion

Fig. 1

Nonlinear response of emitted fluorescence to illumination intensity. At low illumination intensity,

fluorescence emission increases in strict proportion to laser power. At higher intensity, emitted fluorescence
(solid line) is less than predicted (dashed line) because the population of molecules in the ground state has
been depleted.

468

John M. Murray

during this setup phase.) Steps 4–7 will probably have to be iterated several times
to optimize all the parameters.

1. Choose the appropriate filters/laser line combination.

2. Decide what pixel spacing is required to obtain the information needed

from this particular sample, and set the magnification/electronic zoom factor
accordingly. Do not oversample (i.e., pixel spacing should be close to the Nyquist
limit).

3. Get a ballpark estimate for the imaging parameters. Set the pinhole diameter

initially to be

1 Airy disk. Set the PMT voltage to maximum. Set the laser to the

minimum intensity that gives a decent signal at this PMT voltage.

4. Find the linear range of the detector. Use a look-up table (LUT) that high-

lights underflow and overflow in color, but is gray scale in between to display
the images.

a. Define the baseline. Scan with the laser o

V at the scan speed to be used for

data collection and set the o

Vset/dark adjust so that the screen intensity is

minimized, but there are no pixels at zero intensity.

b. Define the maximum intensity. Find a region of the specimen that is likely to
be the brightest, and with the laser on, decrease the PMT voltage until the
average intensity is

75% of the maximum, or lower if necessary to keep the

fraction of saturated pixels insignificant.

5. Find the linear range for the specimen. Check that the recorded fluorescence

emission increases linearly with increase in laser power up to at least twice the
intensity to be used for imaging. If the fluorescence does not increase exactly in
proportion to laser power (i.e., ground state depletion is occurring), one must
sacrifice temporal resolution (work with lower laser power and longer scan times)
or spatial resolution (decrease laser power and increase pinhole size, increase pixel
size) or both.

6. Determine the exposure required to achieve an acceptable image quality

[i.e., adjust the scan speed (pixel dwell time) and number of scans averaged per
frame to achieve a signal-to-noise ratio (SNR) that is adequate for the intended
observations or measurements].

7. Check that the level of illumination is below the ‘‘unacceptable damage’’

threshold. With the laser set to the intensity to be used for data collection, monitor
the intensity in a selected small area of the specimen over the course of numerous
repeated scans. One would like to be able to scan long enough to collect all
the needed information before the cumulative photobleaching reaches 50%
(probably

<20% for live cells). If the fluorescence is bleaching too much, you

will have to sacrifice spatial resolution (increase pixel size, decrease laser power) or
photometric resolution (decrease laser power, dwell time, or number of scans
averaged per frame) or both. For time-lapse imaging, one may also have to
sacrifice time resolution (work with lower laser power and longer intervals
between time points).

22. Quantitative Confocal Microscopy

469

B. Disk-Scanning or Swept-Array Confocals

Confocals in which multiple spots of illumination are used in parallel, such as

disk-scanning or ‘‘swept-field’’ instruments, typically use charge-coupled device
(CCD) cameras as detectors. The gain on these detectors is adjustable over a much
smaller range, and the number of photons needed to saturate the detector at
typical gain levels is much higher than for PMT detectors, making detector
saturation much less of a problem for most specimens. Additionally, because the
illumination is split among thousands of spots instead of being focused into a
single spot, it is di

Ycult to achieve laser powers suYcient to cause significant

ground state depletion. Setup of these instruments is thus much simpler than for
spot-scanning confocals. It is necessary merely to choose a combination of image
integration time and laser power that limits the intensities recorded from the
brightest regions of the specimen to something less than the detector full-well
value (i.e.,

<4095 for a 12-bit CCD camera).

III. Correcting Nonuniformities (Flat-Fielding)

Ideally, the proportionality factor relating fluorophore concentration in the

specimen to digital intensity in the image would be a constant, but in practice,
small variations in this factor over the field of view are common. Corrections for
these nonuniformities can and should be applied before the image data is used for
quantitative purposes. In general, two types of corrections need to be applied, one
additive, the other multiplicative.

A. Additive Correction

Additive corrections are applied to compensate for nonuniformities that are

independent of local image intensity.

Figure 2

shows examples for PMT and CCD

detectors. To measure this nonuniformity, an image is collected with the illumination
o

V (a ‘‘dark current’’ image). This image is first scaled to match the exposure time

used for collecting the real data, then subtracted from each image in the dataset. This
correction procedure is straightforward for CCD detectors, but often problematic for
PMT detectors because the nonuniformities arise from periodic noise in the detector
electronics and give rise to patterned fluctuations (

Fig. 2A

) that shift position with

every frame. Hence, the particular pattern of nonuniformities observed in the ‘‘dark
current’’ image is unlikely to match the pattern in the data images. Fortunately, with
proper adjustment of the o

Vset, the size of the nonuniformities in PMT dark current

is usually small compared to the noise in the data.

B. Multiplicative Correction

Multiplicative corrections are applied to compensate for nonuniformities that

are proportional to local image intensity. This type of nonuniformity is measured
by collecting an image of a thin (e.g.,

1-mm thick) sample known to have a spatially

470

John M. Murray

uniform distribution of fluorophore. It is important to maximize the SNR in the
image of this specimen, for example by using the longest possible exposure length
while avoiding detector saturation. It is also critical to use exactly the same magni-
fication, position within the field of view, and pinhole size as used for the real data.

Figure 3

shows examples for CCD- and PMT-based instruments. Nonuniformities

of this type are common due to defects in the optics of the system that lead to
nonuniform illumination intensity. Nonuniform transmittance of emitted fluores-
cence to the detector is also frequent, due to deviations from precise superposition of
the illuminated and detected focal spot. Nonuniformity arising from the latter
characteristically worsens with increasing lens numerical aperture (NA) and decreas-
ing pinhole diameter. Single-pixel defects in CCD chips are also common. The image
of the uniformly fluorescent specimen is adjusted by applying any necessary additive
corrections, and then normalized so that the local average in the brightest region of
the image has a value of 1.0. To avoid nonsensical values in the division to follow,
it is prudent to trim extremely low or extremely high pixels in the normalized result
(e.g., enforce a minimum value of 0.1 and a maximum of 10). Each image of the
specimen dataset is adjusted by the additive correction discussed above, and then
divided by this trimmed, normalized image of the uniform specimen.

IV. Limitations to Exact Quantitation

A. Limitations on Accuracy

If nonlinearities due to ground state depletion are avoided, then the remaining

significant photometric inaccuracy results from residual aberrations in the objec-
tive lens, particularly axial and lateral chromatic aberrations, and errors in the

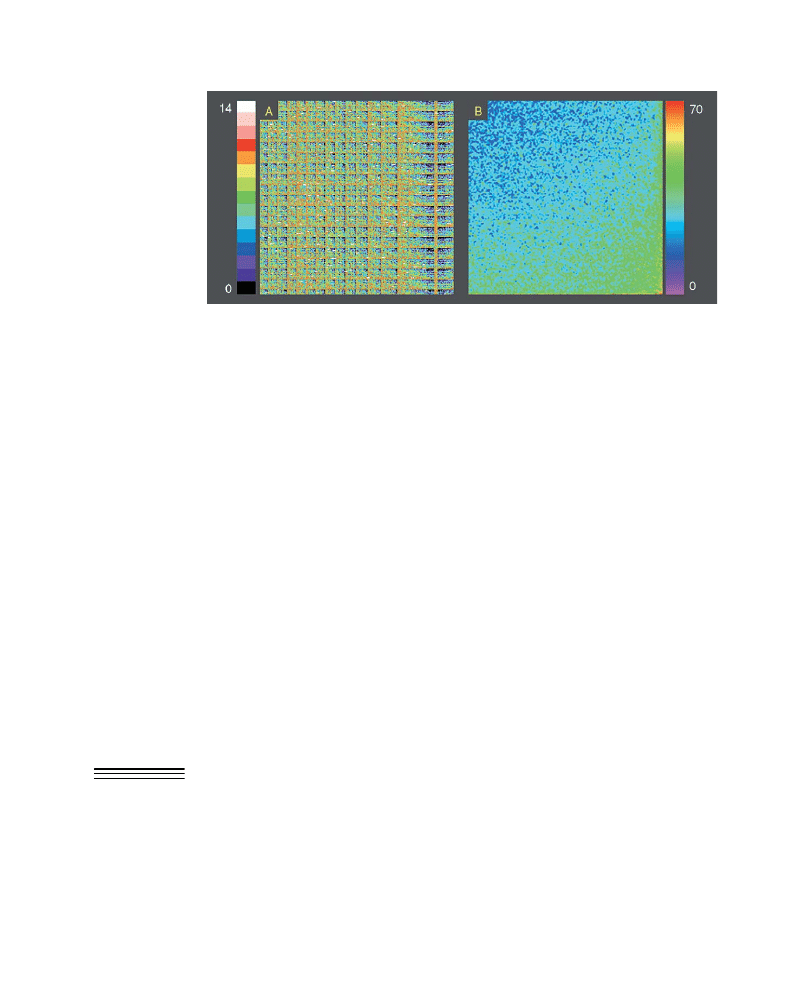
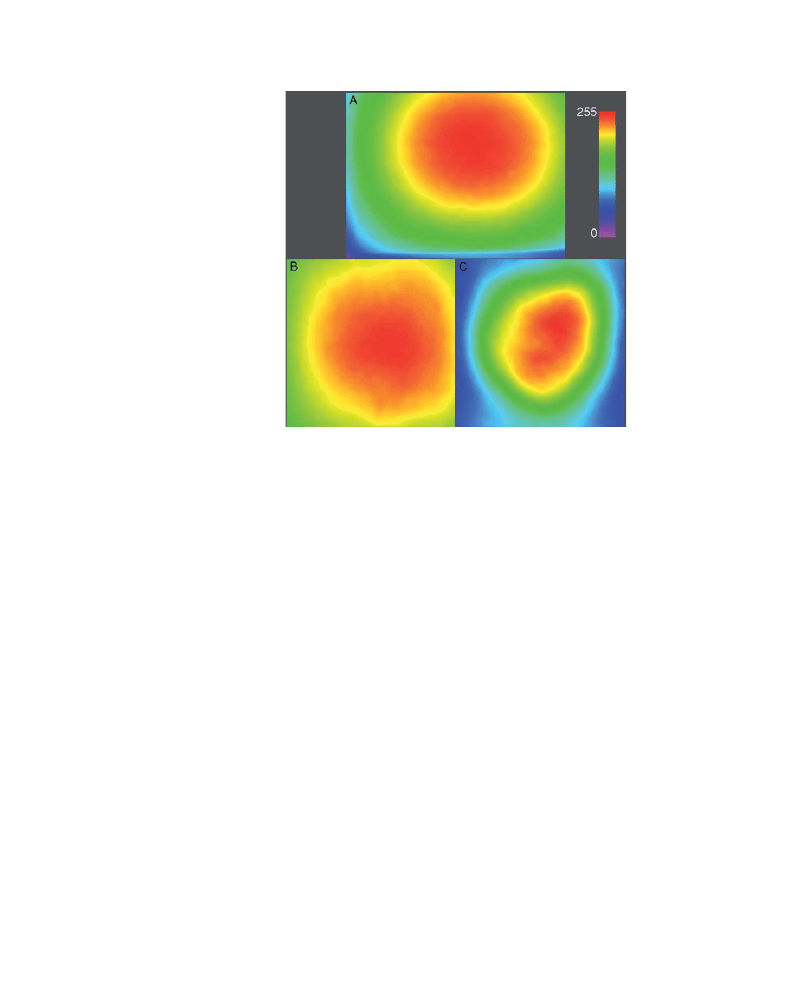
Fig. 2

Dark current images from spot-scanning and disk-scanning confocals. (A) 250

250 pixel region

from an image collected on the Zeiss LSM510 spot-scanning confocal, showing patterned noise artifacts
in the dark current. Displayed intensities range from 0 to 14 counts (255 maximum). (B) 512

512 pixel

image from a CCD detector showing a ‘‘hot spot’’ with higher dark current in the lower right corner.
Displayed intensities range from 0 to 70 counts (4095 maximum).

22. Quantitative Confocal Microscopy

471

scanning hardware that lead to variation in pixel dwell time across the field of
view. Confocal microscopes are particularly susceptible to chromatic aberrations
(

Keller, 1995; Sandison et al., 1995

). The e

Vect is to dramatically attenuate image

intensities in a nonuniform way across the field of view, generally worsening with
distance from the optical axis. The pattern of attenuation often di

Vers for diVerent

emission wavelengths.

Most errors due to the scanning hardware will be compensated by the flat-fielding

corrections described above. If the specimen is very thin (so thin that using a confocal
microscope would not be sensible), the multiplicative correction described above will
also su

Yce to compensate for the eVects of chromatic aberration. However, for a

specimen thicker than a micron or so, curvature of field interacts with axial and lateral
chromatic aberrations so as to make it impossible to compensate completely for their
e

Vects unless the precise 3D distribution of fluorophore in the specimen is already

known, a situation that would seem to render the entire e

Vort superfluous. A more

detailed description of this problem is given in Chapters 5 and 7 of

Pawley (1995)

.

B. Limitations on Precision

In considering the images obtained from a confocal microscope, the question

of whether their quality can be improved will always be faced if the goal is to
use the images for quantitative analysis. The defect that is most likely to interfere

Fig. 3

Images of a uniformly fluorescent thin specimen from a scanning disk (A) and spot-scanning

confocal with completely open pinhole (B) or pinhole set to 1 Airy disk radius (C).

472

John M. Murray

with quantitative applications is the limited SNR in confocal images, particu-
larly from spot-scanning confocals. In principle, the SNR achieved in an image
of a fluorescent specimen ought ultimately to be limited only by the inevitable
Poisson noise associated with stochastic absorption, excitation, and reemission
of a finite number of photons. The highest achievable SNR in a single image
will therefore never be greater than the square root of the number of photons
per pixel in the image. An upper limit to the achievable SNR is set by

ffiffiffiffiffiffi

W

p

,

where W is the ‘‘well capacity,’’ the number of photons per pixel at detector
saturation.

In practice, other sources of noise are usually present, degrading the SNR

to something less than

ffiffiffiffiffiffi

W

p

. The total noise in an image can be thought of as

the sum of a component that increases in proportion to the exposure time or signal
(e.g., Poisson or ‘‘shot’’ noise from signal, background, and dark current) plus an
exposure-independent component (e.g., camera read noise). These noise compo-
nents also can be characterized as ‘‘inescapable’’ (Poisson noise arising from the
signal itself ) and ‘‘possibly avoidable’’ (all other sources). Therefore, in order to
determine what the limits on precision in the data ought to be, that is, how much
of the noise in a dataset is ‘‘inescapable,’’ it is clearly necessary to know how many
photons went into making the image.

For a Poisson distribution, variance is numerically equal to mean. If the digital

intensity values were numerically equal to the number of photons detected for
each image pixel, then the image variances (‘‘noise’’ squared) would equal the
average intensity, and the expected SNR would be simply the square root of the
image intensities (SNR

¼ S=N ¼ S=

ffiffiffiffi

S

p

¼

ffiffiffiffi

S

p

). However, the digital intensity

values are related to the number of detected photons by an unknown proportion-
ality factor. One needs to know this proportionality factor in order to decide how
many photons contributed to the image, information that is necessary to decide
whether the observed noise in the image is the inescapable Poisson minimum, or
whether one could do better. The purpose of this section is to describe how that
proportionality factor can be measured.

Not every photon that arrives at the detector actually contributes to the

image. Some photons are simply not detected. The quantum e

Yciency (QE) relates

the number of photons arriving at the detector to the number of countable
events (defined below). The QE is always less than 1; some photons are simply
not detected at all and do not give rise to a countable event. A graph of QE
versus wavelength is usually on the specification sheet provided by the detector’s
manufacturer.

A countable event for a CCD detector is the generation of a photoelectron in the

CCD chip; for a PMT, a countable event is a pulse of electrons exiting at the end of
the dynode chain in response to a photon absorbed at the photocathode. For
either type of detector, the number of countable events in a given time interval is
simply a constant fraction (the QE) of the number of photons arriving in that
interval, and thus fluctuates with Poisson statistics just like the number of arriving
photons. In both the CCD- and PMT-based instruments, additional electronics

22. Quantitative Confocal Microscopy

473

downstream of the detector converts countable events to the digital number that is
output for each pixel. The proportionality factor relating number of countable
events to output digital value is the e

Vective quantization imposed by this addi-

tional electronics, that is, the number of countable events that corresponds to an
increment of 1 in the digital output value.

One can determine the quantization (call it q) by measuring the relationship

between the mean pixel intensity and the variance of pixel intensity. For a true
Poisson variate, the variance is equal to the mean. However, in the output digital
image, the number of countable events (which is a true Poisson variate) has been
multiplied by q, and thus the variance computed from image digital intensity
values is related to true variance by q

2

. The slope of a graph of variance versus

average digital intensity is q; the reciprocal of the slope is the number of countable
events needed for a digital intensity increment of 1. The intercept of the graph can
be used to find the sum of all noise components not correlated with the signal
(

Fig. 4

).

The protocol for collecting the needed data is described separately below for

CCD- and PMT-based confocals.

1. For a CCD detector:

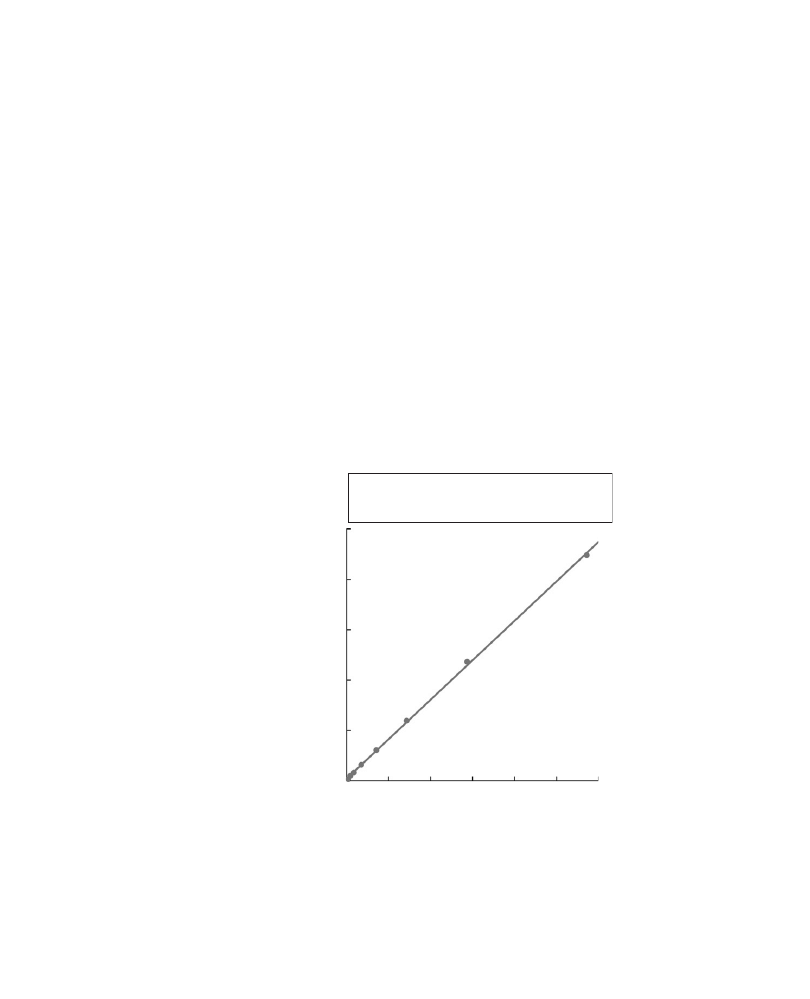
Variance = 0.313

⫻ Intensity + 8.72

Intensity increment of 1 = 1/0.313 = 3.2 photons
r = 9.9 photoelectrons

Variance

1000

800

600

400

200

0

Mean intensity

0

500

1000

1500

2000

2500

3000

Fig. 4

Calibration of a CCD detector by measuring variance as a function of intensity.

474

John M. Murray

a. With no light going to the camera (room lights and any nearby computer
monitors o

V, laser oV), but microscope otherwise configured as for image

collection, acquire an image with very short (e.g., 10 ms) exposure. Find
the mean intensity of this image. This is the ‘‘o

Vset,’’ a constant value

(i.e., variance

¼ 0), independent of exposure time and image intensity.

b. Turn the laser on. Adjust the laser power to give an image intensity just
above background noise with a 10-ms exposure.

c. Acquire two images in rapid succession with a 10-ms exposure, changing
nothing in between. These two images should be identical, so any di

Verence

between them can be attributed to noise. First, find the average pixel intensity
in the images (call it D). Then subtract one from the other. Add a constant to
avoid negative values (e.g., image1

image2 þ 1000). Find the standard

deviation of this di

Verence image, square it, and divide by 2. This number is

the variance of a single pixel in the image.

d. Repeat this acquisition and calculation for pairs of images taken at 20, 40,
80, 160,

. . . ms, up to 70% of detector saturation.

e. Plot variance versus (D

oVset) and from the least squares fit of a straight

line, obtain the slope (q) and intercept.

f. The arithmetic:

P

¼ average number of countable_events/pixel (variance ¼ P)

r

¼ exposure-independent noise (in countable_events/pixel, variance ¼ r

2

)

D

¼ pixel intensity, as a digital number (gray levels)

1/q

¼ number of countable_events needed to give an increment of 1 in the

digital intensity value

D

¼ qP þ qr þ offset

variance of D

¼ q

2

P

þ q

2

r

2

¼ qðD offsetÞ þ q

2

r

ðr 1Þ

To find the exposure-independent noise component, calculate:

r

¼

q

2

þ

ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi

q

4

þ 4 intercept q

2

p

2q

2

If this value is much larger than the camera read noise, then avoidable extra
noise is being added to the images, and some detective work is needed to find
the source.

2. For a PMT detector:

The protocol is messier than for the CCD detector. Due to the large fluctuations

in illumination intensity in most spot-scanning confocals (

Swedlow et al., 2002

),

22. Quantitative Confocal Microscopy

475

one cannot use the system lasers as illumination for this test (i.e., a significant
amount of the noise would be due to the laser fluctuations, not Poisson noise
correlated with the signal). The quartz-halogen lamp used for visual transmitted
light observation and the mercury arc lamp used for visual epifluorescence obser-
vation are also unsuitable due to residual line frequency (60 or 120 Hz) modula-
tion of their output. A stable illumination source can be obtained by simply
positioning a battery-powered light source (e.g., a flashlight) over the objective.
Unfortunately, the output of this type of light source is not easily controlled, so
the number of photons reaching the PMT must be varied by some other method.
With a little trial and error experimentation, the required wide range of signal
intensities can usually be achieved by combining di

Verent pinhole diameters with

di

Verent dichromatic mirrors and emission filters. The final complication is that

the measurement needs to be done for di

Verent PMT voltages spanning the range

normally used for real specimens.

Here is a recipe for collecting the needed data:

For display of the images, use a ‘‘pseudocolor’’ LUT that highlights underflow

and overflow in color, but is gray scale in between. It is also extremely useful to
display a continuously updated histogram of image pixel intensities.

a. With no light input, but microscope otherwise configured as for image
collection, acquire an image. Find the mean intensity of this image. This is
the ‘‘o

Vset,’’ a constant value (i.e., variance ¼ 0), independent of exposure

time and image intensity. Use the ‘‘o

Vset adjust’’ or ‘‘dark current’’ controls

to make this value small (

<10), but with no zero pixels. Repeat this mea-

surement for di

Verent PMT voltages over the range commonly used for data

collection with real specimens. The ‘‘o

Vset’’ will probably be nearly the same

over this range.

b. Turn the light source on. Set the PMT voltage to the lowest value used for
any specimen. Adjust the position of the flashlight, filters, pinhole diameter,
and other parameters to give an average intensity of

80% saturation.

c. Scan two images in rapid succession and store them. Adjust the filter, light
source, or pinhole to decrease the average intensity approximately twofold,
and collect another pair of images. Repeat with average intensities of

20%,

10%, and 5% of saturation.

d. These pairs of images should be identical, so any di

Verence between them

can be attributed to noise. First, find the average intensity in each pair (

¼D).

Subtract one member of each pair from the other, adding a constant to avoid
negative values (e.g., image1

image2 þ 128). Find the standard deviation

of this di

Verence image, square it, then divide by 2. This number is the

variance of D.

476

John M. Murray

e. Plot the variance versus (D

oVset), and obtain the slope (q) and intercept

of the best straight line through the data.

f. Repeat steps (b)–(e) for five or six PMT voltages spanning the range normal-
ly used for real specimens. As the PMT voltage is increased, the range of
intensities will need to be drastically reduced (e.g., average intensity restricted
to 5–20% of maximum) in order to avoid excessive detector saturation. The
proportion of saturated pixels (intensity

¼ 255 or 4095 for 8-bit or 12-bit

digitization) should be kept below 2% (

Fig. 5

).

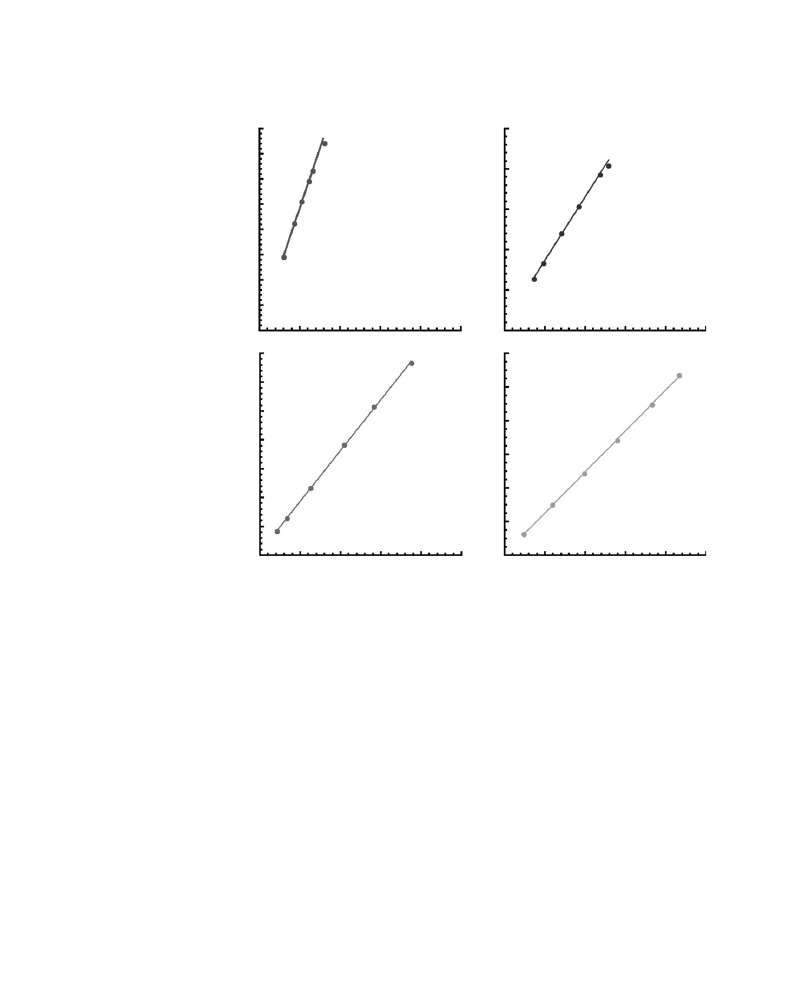
PMT gain calibration

1200 V

800 V

4000

3500

3000

2500

2000

1500

1000

500

0

Variance

Variance

700

600

500

400

300

200

100

0

0

50

100

150

200

250

Average intensity

0

0

500

1000

1500

2000

2500

20

40

60

80

100

120

0

50

100

150

200

250

Average intensity

1000 V

600 V

Fig. 5

Plots of data used to calibrate the gain of a PMT. Image variance was measured as a function

of image intensity for four di

Verent PMT voltage settings.

22. Quantitative Confocal Microscopy

477

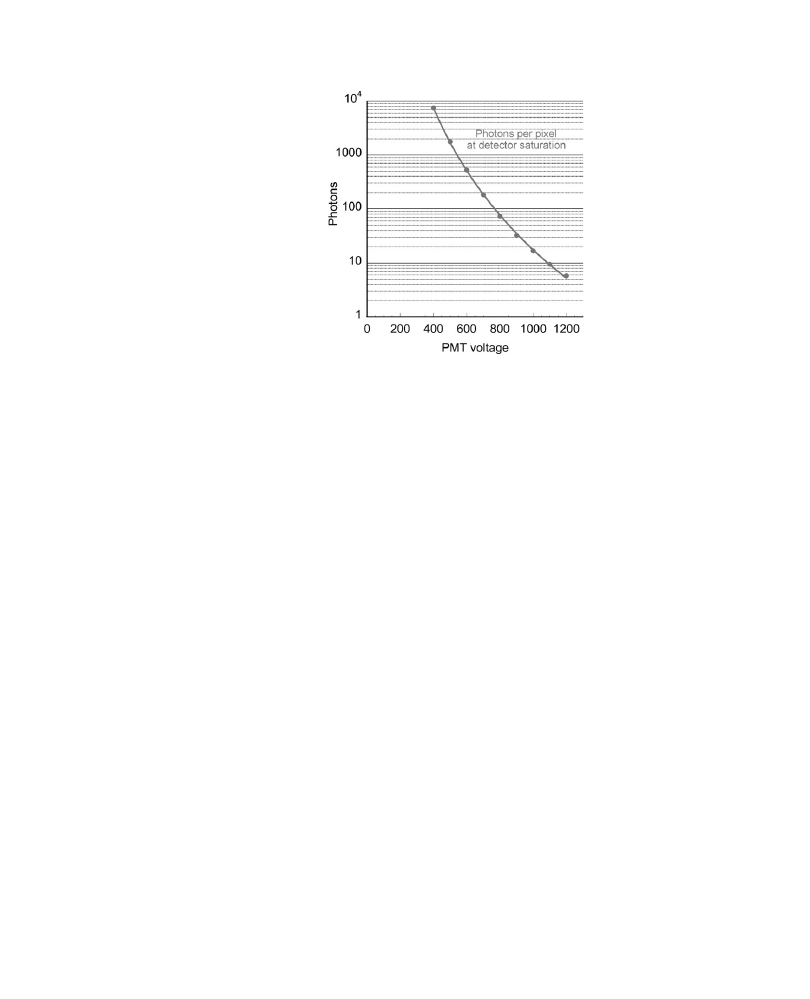
g. Plot log(1/q) versus PMT voltage. The data fall on a gently curved line,
with curvature low enough that linear interpolation is su

Ycient to generate

values for PMT voltages between the data points (

Fig. 6

).

References

Keller, H. E. (1995). Objective lenses for confocal microscopy. In ‘‘Handbook of Biological Confocal

Microscopy’’ (J. B. Pawley, ed.), pp. 111–126. Plenum Press, New York.

Pawley, J. B. (1995). ‘‘Handbook of Biological Confocal Microscopy.’’ Plenum Press, New York.
Sandison, D. R., Williams, R. M., Wells, K. S., Strickler, J., and Webb, W. W. (1995). Quantitative

fluorescence confocal laser scanning microscopy (CLSM). In ‘‘Handbook of Biological Confocal
Microscopy’’ (J. B. Pawley, ed.), pp. 39–53. Plenum Press, New York.

Swedlow, J. R., Hu, K., Andrews, P. D., Roos, D. S., and Murray, J. M. (2002). Measuring tubulin

content in Toxoplasma gondii: A comparison of laser-scanning confocal and wide-field fluorescence
microscopy. Proc. Natl. Acad. Sci. USA

99, 2014–2019.

Fig. 6

Calibration of a PMT detector. The number of detected photons required to give the maximum

pixel intensity value is plotted as a function of voltage applied to the PMT. Note that at the highest
voltage, only

6 photons are needed to saturate the detector.

478

John M. Murray