FIZYKA CZĄSTECZKOWA I TERMODYNAMIKA 

Fizyka 

 

 

   ‐ 

cząsteczkowa 

Dział fizyki badający budowę i własności materii przy założeniu, że 

każde ciało składa się z dużej liczby bardzo małych cząsteczek. Czą‐

steczki te znajdują się w ciągłym chaotycznym ruchu, którego inten‐

sywność zależy od temperatury. 

 

Termodynamika     

‐

  Bada jedynie makroskopowe własności ciał oraz makroskopowe zja‐

wiska, nie interesuje się ich obrazem mikroskopowym. Podstawą 

termodynamiki są zasady termodynamiki. 

 

Wielkości stosowane do opisu atomów i cząsteczek 

(Względna) Masa     ‐ 

atomowa, 

r

A  

 

Stosunek masy atomu danego pierwiastka do 1/12 masy atomu 

12

C.

(Względna) Masa     ‐ 

cząsteczkowa, 

r

M

 

Stosunek masy cząsteczki danej substancji do 1/12 masy atomu 

12

C.

 

Fizyka cząsteczkowa i termodynamika 1

 

Wielkości stosowane do opisu atomów i cząsteczek, cd. 

 

Atomowa 

 

   ‐ 

jednostka masy, 

j

m

 

Jednostka masy równa 1/12 masy atomu 

12

C.

27

1,66 10

kg 1D

j

m

−

=

⋅

=

  (dalton) 

1D

≈ masa atomu wodoru. 

 

Mol  

 

 

    ‐  Ilość substancji zawierająca taką samą liczbę cząstek co 0,012 kg izo‐

topu 

12

C. Wielokrotności i podwielokrotności: kilomol (kmol), mili‐

mol (mmol), mikromol (μmol). 

 

Liczba 

 

 

   ‐ 

Avogadra, 

A

N

    ‐ 

Liczba cząstek w molu substancji. 

23

1

6,022 10 mol

A

N

−

=

⋅

 

 

Masa molowa, 

μ

      ‐  Masa mola substancji.

A

r

j

N A m

μ

=

 

A

r

j

N M m

μ

=

 

Fizyka cząsteczkowa i termodynamika 2

 

Stan układu 

 

Układ 

 

 

 

‐  Zbiór rozważanych ciał.

 

Stan równowagi   

‐ 

Termodynamicznej 

(stan równowagowy) 

Stan, w którym układ może znajdować się dowolnie długo. W 

tym stanie wszystkie parametry stanu mają określone wartości 

i nie zmieniają się. 

 

Parametry stanu   

‐  Parametry fizyczne jednoznacznie określające stan równowagi 

termodynamicznej. 

 

Stan  

 

 

 

‐ 

nierównowagowy 

Stan, w którym niektóre parametry stanu nie mają określonej 

wartości. 

 

 

Jeżeli na osiach układu współrzędnych odkładamy wartości pewnych dwóch parametrów, to 

każdy stan równowagi układu jest reprezentowany na wykresie przez punkt. 

 

Fizyka cząsteczkowa i termodynamika 3

 

Przemiana 

 

Przemiana 

 

 

‐ 

(proces) 

Przejście układu z jednego stanu do drugiego (na ogół przez 

ciąg stanów nierównowagowych). 

 

Przemiana 

 

 

‐ 

równowagowa 

(kwazistatyczna, 

odwracalna)  

Przemiana składająca się z ciągłego zbioru kolejnych stanów 

równowagi. Rzeczywiste przemiany mogą być uważane za 

równowagowe, o ile zachodzą odpowiednio powoli. 

 

 

Wszystkie ilościowe rozważania termodynamiki dotyczą stanów równowagi i procesów od‐

wracalnych. 

 

 

Fizyka cząsteczkowa i termodynamika 4

 

Energia wewnętrzna układu 

 

Energia   

       ‐ 

wewnętrzna 

ciała 

Całkowita energia tego ciała z wyłączeniem jego energii kinetycznej 

jako całości oraz energii potencjalnej w zewnętrznych polach. 

Stanowi sumę energii oddziaływań międzycząsteczkowych i we‐

wnątrzcząsteczkowych układu oraz energii ruchu cieplnego cząste‐

czek. 

 

Energia wewnętrzna układu ciał jest równa sumie energii wewnętrznych każdego z tych ciał 

oraz energii oddziaływania między elementami układu. Energia wewnętrzna jest funkcją sta‐

nu układu. 

 

Funkcja stanu        ‐ 

układu 

Za każdym razem, gdy układ jest w danym stanie, funkcja stanu ma 

tę samą wartość, niezależnie od historii układu. 

 

Energię wewnętrzną oznaczamy literą  . 

 

U

Fizyka cząsteczkowa i termodynamika 5

 

Zmiany energii wewnętrznej 

 

Energia wewnętrzna może się zmieniać w wyniku dwóch procesów: 

‐ wykonywania pracy 

 przez układ nad ciałami zewnętrznymi, 

W

‐ dostarczania do układu ciepła  . 

Q

 

Wykonywanie pracy wiąże się z przemieszczaniem ciał zewnętrznych oddziaływujących na 

układ. 

 

Ciepło 

 

‐  Przepływ energii wywołany nieuporządkowanymi ruchami cząsteczek oto‐

czenia lub przyczyniający się do wzmożenia takich ruchów w otoczeniu. 

 

Ilość energii przekazywanej przez jedno ciało drugiemu określamy pracą 

 lub ilością ciepła 

, w zależności od rodzaju zjawisk odpowiedzialnych za transport energii. 

W

Q

 

 

Fizyka cząsteczkowa i termodynamika 6

 

Pierwsza zasada termodynamiki 

 

 

   

(zasada zachowania energii) 

2

1

U

U

Q W

−

= −

 

 

2

1

Q U

U

W

=

−

+

 

Pierwsza zasada termodynamiki

Ciepło dostarczone do układu jest zużywane na przyrost energii wewnętrznej tego 

układu i na wykonywanie przez układ pracy nad zewnętrznymi ciałami. 

 

Ilość ciepła   można wyrażać tymi samymi jednostkami, co pracę i energię. W układzie SI 

jednostką ciepła jest dżul (J). (1 J = 0,24 cal, 1 cal = 4,18 J). 

Q

 

W postaci różniczkowej pierwsza zasada termodynamiki zapisywana jest jako 

 

 

 

dQ

dU

dW

=

+

 

 

Fizyka cząsteczkowa i termodynamika 7

 

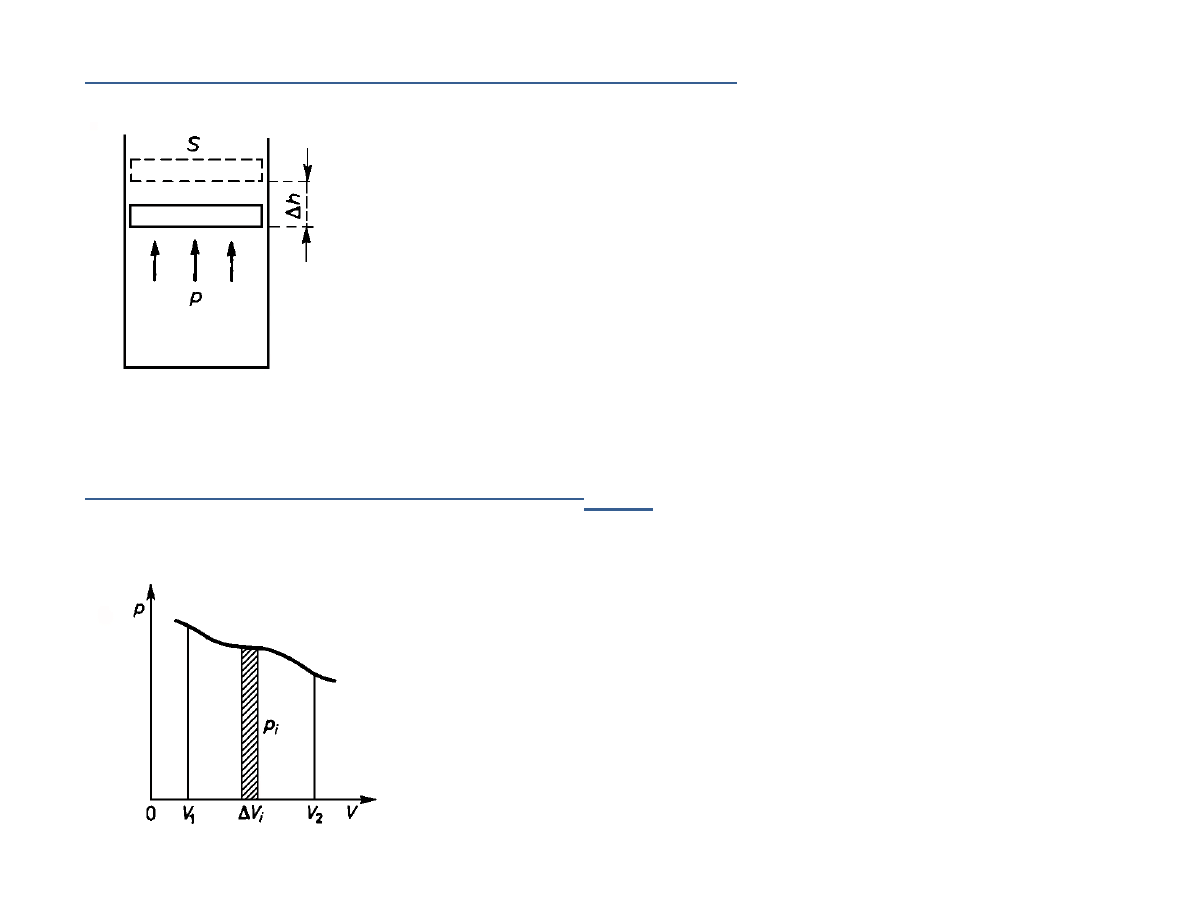
Praca wykonana przez ciało w przypadku zmiany objętości 

Infinitezymalne przesunięcie tłoka odpowiada pracy: 

 

W

F h

p S h

p V

Δ = Δ =

Δ = Δ  

W postaci różniczkowej:  

 

 

dW

p dV

=

 

Przy stałym ciśnieniu:   

 

 

12

2

1

(

)

W

p V

V

=

−

 

Ogólnie, dla dowolnych przemian: 

2

1

12

V

V

W

p dV

=

∫

 

 

Przedstawienie zmian objętości na wykresie 

( , )

p V

 

Praca przy zmianie objętości od   do 

jest liczbowo równa 

polu ograniczonemu osią  , krzywą 

)

1

V

2

V

 

V

(

p

f V

=

 oraz prostymi 

 i  . 

1

V

2

V

dQ

dU

p dV

 

Inna forma I zasady termodynamiki:  

 

 

=

+

 

Fizyka cząsteczkowa i termodynamika 8

 

Równanie stanu gazu doskonałego (równanie Clapeyrona) 

 

Równanie stanu  ‐  Równanie wiążące parametry stanu 

 

Gaz doskonały 

‐  Gaz, w którym oddziaływania międzycząsteczkowe są pomijalnie ma‐

łe. Każdy gaz rzeczywisty pod odpowiednio małym ciśnieniem ma 

własności zbliżone do gazu doskonałego. 

 

Stan gazu doskonałego jest określony przez trzy parametry: 

 

 

 

 

 

p

 ‐ ciśnienie, 

 ‐ objętość, 

 ‐ temperatura. 

V

T

 

Badania doświadczalne, a także rozważania teoretyczne pokazują, że w przypadku gazu do‐

skonałego parametry te łączy prosty związek. 

 

Równanie gazu doskonałego: 

const

pV

T

=

 

 

 

Fizyka cząsteczkowa i termodynamika 9

 

Równanie stanu gazu doskonałego, cd. 

 

const

pV

T

=

 

Prawo Avogadra  ‐  W warunkach, scharakteryzowanych przez te same parametry 

i  , 

p

T

mol każdego gazu zajmuje tę samą objętość. 

 

Np. w tzw. warunkach normalnych dla jednego mola gazu mamy: 

 

5

3

3

273,15 K (0 C)

J

1 atm 1, 013 10 Pa

8,31

mol K

22, 4 l

22, 4 10

m

m

m

T

pV

p

R

T

V

−

=

°

⎫

⎪

=

=

⋅

⇒

= =

⎬

⋅

⎪

=

=

⋅

⎭

 

 

 

 

 

 

 

 

 

 

 

 

 

 ‐ uniwersalna stała gazowa. 

R

Dla dowolnej masy m gazu:   

 

m

pV

RT

μ

=

 

Wprowadźmy stałą Boltzmanna:   

23

J

1,38 10

K

A

R

k

N

−

=

=

⋅

 

 

A

m

pV

N k T

N k T

,  

 

 ‐ liczba cząsteczek w masie  . 

 

μ

=

=

N

m

Fizyka cząsteczkowa i termodynamika 10

 

Równanie stanu gazu doskonałego, cd. 

 

 

pV

N k T

=

 

 

p

n k T

=

, 

 

N

n

V

=

 ‐ liczba cząsteczek w jednostce objętości. 

 

Przy ustalonej objętości ciśnienie gazu doskonałego jest wprost proporcjonalne do tempera‐

tury. Z tego względu gaz doskonały jest używany jako ciało termometryczne. Biorąc ciśnienie 

jako cechę termometryczną, otrzymuje się termometr o idealnie liniowej skali temperatur, 

tzw. doskonałej gazowej skali temperatur. 

 

Praktyczne znaczenie ma tzw. empiryczna skala temperatur, zbudowana w oparciu o zasto‐

sowanie równania  p

n k T

=

 dla wodoru. 

Fizyka cząsteczkowa i termodynamika 11

 

Pojemność cieplna 

 

Pojemność cieplna   ‐ 

ciała, 

 

c

C

Ilość ciepła potrzebna do tego, aby podwyższyć temperaturę ciała o 

jeden kelwin. 

 

c

dQ

C

dT

=

   

[ ]

J

K

c

C

=  

 

Ciepło właściwe,     ‐ 

c

Pojemność cieplna jednostki masy substancji

 

c

C

c

m

=

   

[ ]

J

kg K

c

=

⋅

 

 

Molowe ciepło          ‐ 

właściwe,   

C

Pojemność cieplna jednego mola substancji

 

C

c

μ

=

   

[ ]

J

mol K

C

=

⋅

 

 

 

Fizyka cząsteczkowa i termodynamika 12

 

Pojemność cieplna w stałej objętości 

Przy zmianach temperatury ciała w stałej objętości ciało nie wykonuje pracy nad otoczeniem 

0)

 i całe ciepło zamienia się na wzrost energii wewnętrznej 

(dW

=

(

)

V

dQ

dU

=

. 

 

V

cV

V

dQ

U

C

dT

T

∂

⎛

⎞

=

= ⎜

⎟

∂

⎝

⎠

 

 

Dla dowolnej masy gazu doskonałego zachodzi: 

V

m

U

C T

μ

=

 

 

Pojemność cieplna przy stałym ciśnieniu 

Przy zmianach temperatury ciała przy stałym ciśnieniu oprócz zmian energii wewnętrznej 

wykonywana jest praca 

(

)

p

dQ

dU

p dV

=

+

. 

 

Dla jednego mola gazu doskonałego mamy: 

 

 

p

V

C

C

R

=

+

 

 

Fizyka cząsteczkowa i termodynamika 13

 

Przemiany gazu doskonałego 

Spośród wielu możliwych przemian gazu doskonałego na wyróżnienie zasługują przemiany, 

w których ‐ oprócz równania stanu ‐ spełniony jest dodatkowy warunek określający rodzaj 

przemiany 

Rodzaj przemiany

Dodatkowy

warunek 

Równanie stanu

 

Izobaryczna 

const

p

=

/

con t

V T

=

s

 

 

Izochoryczna

const

V

=

 

p /

const

T

=

 

Izotermiczna

const

T

=

 

pV

= const

 

Adiabatyczna

0

dQ

=

const

pV

κ

=

/

p

V

C

C

,   

κ

≡

 

 

 

 

Fizyka cząsteczkowa i termodynamika 14

 

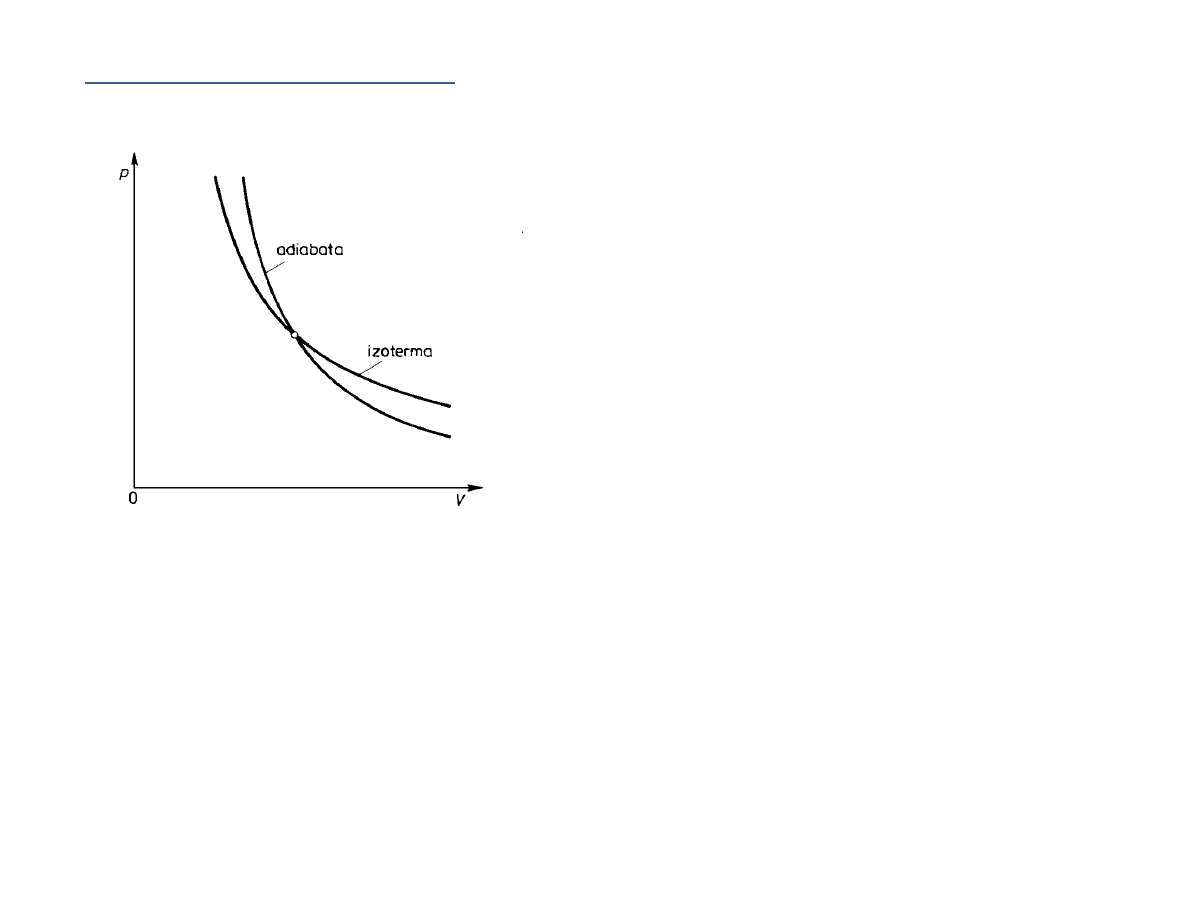
Fizyka cząsteczkowa i termodynamika 15

 

Przykładem przemiany adiabatycznej może być sprężanie i rozprężanie gazu przy rozchodze‐

niu się w gazie fali dźwiękowej, w odniesieniu do małych objętości. 

Adiabata:  

,  

)

const

pV

κ

=

(

1

κ

> . 

Izoterma:  

const

pV

=

 

 

 

 

 

 

 

 

 

Przemiany gazu doskonałego, cd.