Egzamin z Teorii Systemów luty 2004

Część teoretyczna

wersja A

1. Dla układu o transmitancji operatorowej
wyznaczyć wzór określający opóźnienie grupowe w funkcji pulsacji.

2. Dla filtru o transmitancji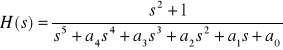
, dla dużych wartości częstotliwości należy wyznaczyć nachylenie wykresu tłumienia w funkcji pulsacji w skali logarytmicznej.

3. Napisać wzór określający transmitancję operatorową układu LTI w zależności od macierzy opisu w przestrzeni zmiennych stanu.

4. Starannie narysować wykres
w paśmie zaporowym dla filtru eliptycznego szóstego rzędu. Narysować odpowiednią linię łączącą ekstrema wykresu.

5. Dla pewnego filtru mającego wszystkie zera transmitancji w nieskończoności transmitancja spełnia zależność
, gdzie
jest wielomianem szóstego stopnia. Wyznaczyć bieguny transmitancji.

6. Podaj wzór określający wektor stanu
układu dyskretnego jako funkcję numeru próbki w czasie dla układu równań stanu
przy warunkach początkowych

7. Dla odpowiedzi skokowej
(odpowiedzi na skok jednostkowy) regulatora PI zachodzi
,
. Odpowiedź impulsowa tego regulatora

8. Źródło napięcia idealne o
obciążono odbiornikiem nieliniowym o charakterystyce
, gdzie natężenie prądu jest wyrażone w [mA], a napięcie w [V]. Do rozwiązania zastosowano metodę Newtona - Raphsona. Punkt startowy przyjęto
. Wyznaczyć kolejne przybliżenie

9. Dla stanu równowagi podać definicję stabilności w sensie Lapunowa.

10. Proszę napisać przykładowy wzór na transmitancję stabilnego (BIBO) układu wszechprzepustowego o trzech biegunach rzeczywistych.
(we wzorze mają występować współczynniki określone konkretnymi liczbami.