Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Modelowanie matematyczne jako podstawa obliczeń naukowo-
technicznych:

Wybór modelu opisowego, a w konsekwencji struktury
matematycznej modelu jest w znacznym stopniu arbitralny,

Struktura matematyczna użyta do modelowania powinna by
skończenie wymiarowa – tzn.: wyczerpująco opisana za pomocą
skończonej liczby parametrów,

Kryteria oceny modelu są ściśle związane z jego przeznaczeniem.

Wniosek:

Model uznany za adekwatny w jednym zastosowaniu może się

okazać nieadekwatny w innym.

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Zadanie programowania liniowego PL

przy ograniczeniach:

( )

x

c

x

T

f

=

max

0

2

2

1

1

≥

≥

≤

x

b

x

A

b

x

A

dim x=n, dim c=n

Macierze A

1

, A

2

odpowiadają za współczynniki w m

1

i m

2

ograniczeniach

dim A

1

=[m

1

x n], dim A

2

=[m

2

x n]

Wektory b

1

, b

2

odpowiadają za prawe strony ograniczeń

dim b

1

=m

1

, dim b

2

=m

2

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Zadanie programowania liniowego - przykłady

2

1

0

1

2

max

x

x

X

x

+

=

∈

x





















≥

≤

+

≤

+

−

≤

+

=

0

,

21

2

6

0

5

:

2

1

2

1

2

1

x

x

x

x

x

x

x

x

X

3

2

1

0

2

.

0

6

.

0

3

.

0

min

x

x

x

x

+

+

=

Przykład II System cięcia dłużyc

Przykład I System produkcji – maksymalizacja zysku

0

,

,

1200

2

1

0

2100

0

3

7

3

2

1

3

2

1

3

2

1

≥

≥

+

+

≥

+

+

x

x

x

x

x

x

x

x

x

przy ograniczeniach

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Przykład III
Maksymalizacja zysków w procesie produkcji w fabryce papieru.

Zakład przemysłowy produkuje papier niskiej i wysokiej jakości. Do produkcji
wykorzystywane są następujące składniki:

pulpa drzewna

chemikalia

szmaty lniane

woda

Cel: Optymalny poziom produkcji papieru niskiej i wysokiej jakości

przy uwzględnieniu ograniczeń.

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Ceny surowców kształtują się

następująco:

9

Szmaty lniane

4

Chemikalia

3

Pulpa

Cena jednost.

[zł/jedn.]

Surowiec

Woda jest wolna od opłat.

Jej zużycie jest nielimitowane.

W zależności od tego, czy

produkowany

jest papier niskiej, czy wysokiej

jakości zużywana jest różna

ilość surowców.

0,40

0,10

Szmaty

0,20

0,10

Chemikalia

1,50

1,10

Pulpa

Wysoka

Niska

Jakość papieru

Surowiec/jedn
ostkę

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Koszt wyprodukowania jednostki papieru:

niskiej jakości wynosi - 1,8 [zł], natomiast

wysokiej jakości - 1,5 [zł].

Cena sprzedaży jednostki produktu końcowego wynosi :

10 [zł] dla produktu niskiej jakości

16,5 [zł] dla produktu wysokiej jakości.

Efektem ubocznym przy produkcji papieru są ścieki. Podczas wytwarzania
jednostki papieru niskiej jakości powstają

3 jednostki ścieków

, zaś w przypadku

papieru o wysokiej jakości powstaje

6 jednostek ścieków.

Część ścieków poddawana jest procesowi oczyszczania w wyniku czego ilość
zanieczyszczenia jest redukowana o 50%. Pozostała część ścieków jest
odprowadzana do kanałów. Koszt tych operacji przedstawia się następująco:

Oczyszczanie ścieków powstałych przy produkcji papieru niskiej jakości = 0,11
[zł] na jednostkę produkcyjną,

oczyszczanie ścieków powstałych przy produkcji papieru wysokiej jakości =0,12

[zł] na jednostkę produkcyjną,

Koszt odprowadzenia jednostki ścieków do kanałów = 0,3 [zł].

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Proces produkcyjny obarczony jest z góry nałożonymi ograniczeniami:

Zakład może zakupić maksymalnie 50 jednostek pulpy drzewnej

Maksymalna przepustowość oczyszczalni ścieków wynosi 60 jednostek

Ze względu na kooperację zakład musi wytworzyć przynajmniej 12
jednostek papieru niskiej jakości

Cel: znalezienie optymalnego poziomu produkcji papieru niskiej i wysokiej

jakości, takiego aby zysk przedsiębiorstwa był maksymalny.

Uwzględnić należy wszystkie koszty generowane przez proces

produkcyjny oraz ograniczenia tegoż procesu.

W celu znalezienia maksymalnego dochodu , należy zmaksymalizować

funkcję celu przedstawiającą dochód zakładu produkcji papieru.

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Definicja problemu programowania liniowego PL

Wektor zmiennych decyzyjnych:

T

x

x

x

x

x

]

,

,

,

[

4

3

2

1

=

gdzie:

- wielkość produkcji papieru niskiej jakości

-wielkość produkcji papieru wysokiej jakości

-ilość oczyszczanych ścieków przy produkcji papieru niskiej jakości

- ilość oczyszczanych ścieków przy produkcji papieru wysokiej jakości.

4

3

2

1

x

x

x

x

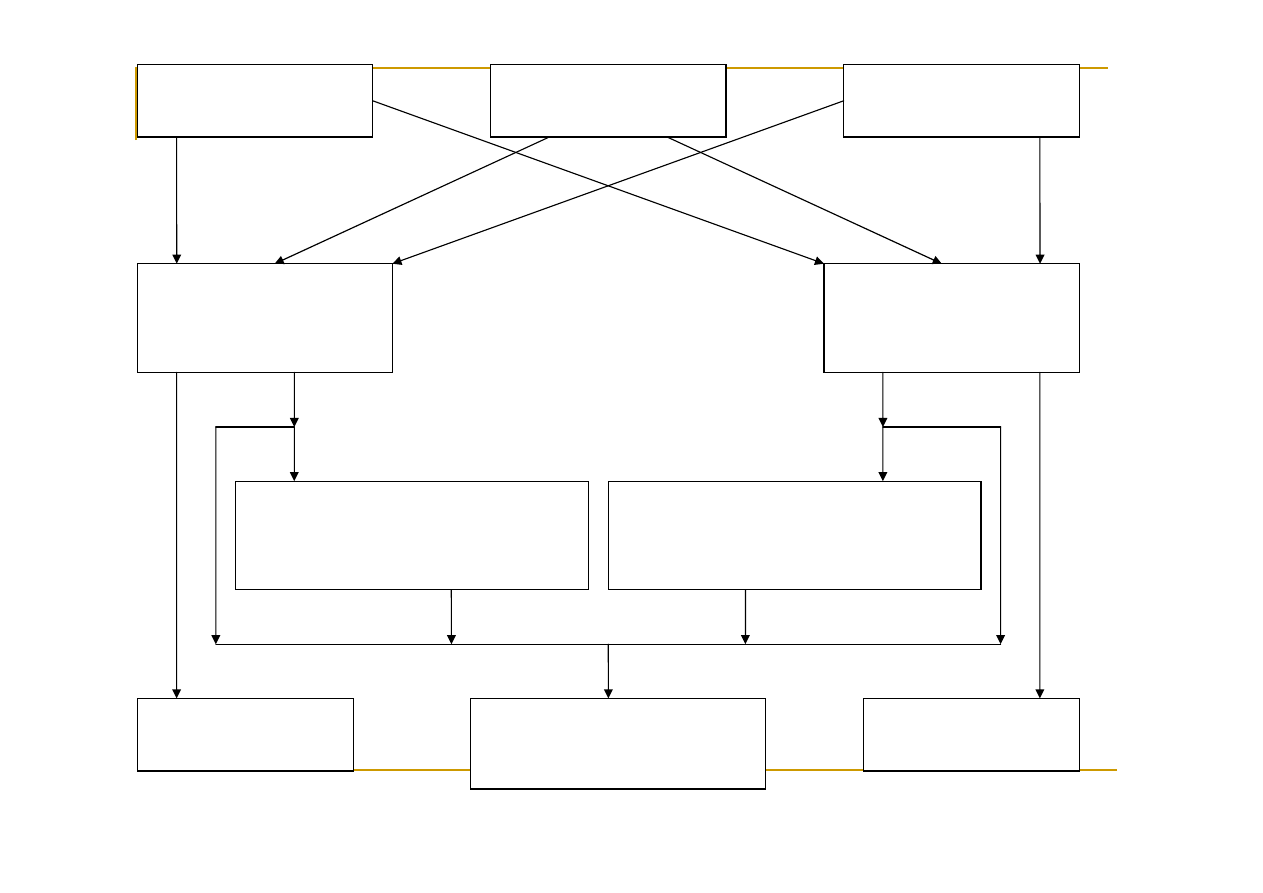
Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Pulpa drzewna
(koszt jednostki 3)

Chemikalia
(koszt jednostki 4)

Szmaty lniane
(koszt jednostki 9)

Koszt produkcji
jednostki papieru
niskiej jakości 1,8

Koszt produkcji
jednostki papieru
wysokiej jakości 1,5

Koszt oczyszczania jednostki
ścieków przy produkcji papieru
niskiej jakości 0,11

Koszt oczyszczania jednostki
ścieków przy produkcji papieru
wysokiej jakości 0,12

Cena sprzedaży
10

Cena sprzedaży
16,5

Koszt jednostki
usuwanych ścieków 0,3

1,1x

1

0,1x

1

0,1x

1

0,4x

2

0,2x

2

1,5x

2

x

1

x

2

3x

1

6x

2

x

3

x

4

3x

1-

x

3

6x

2-

x

4

0,5x

3

0,5x

4

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

dochód

koszty produkcji

koszty materiałów do produkcji papieru niskiej jakości

koszty materiałów do produkcji papieru wysokiej jakości

koszty oczyszczania ścieków

koszt odprowadzenia ścieków

W celu znalezienia maksymalnego zysku, należy maksymalizować funkcję celu w
postaci: dochód – koszty.

Wyznaczenie funkcji celu i ograniczeń zadania produkcji papieru

2

1

5

,

16

10

x

x +

2

1

5

,

1

8

,

1

x

x +

1

1

1

1

,

0

9

1

,

0

4

1

,

1

3

x

x

x

⋅

+

⋅

+

⋅

2

2

2

4

,

0

9

2

,

0

4

5

,

1

3

x

x

x

⋅

+

⋅

+

⋅

4

3

12

,

0

11

,

0

x

x +

(

)

(

)

[

]

4

4

2

3

3

1

5

,

0

6

5

,

0

3

3

,

0

x

x

x

x

x

x

+

−

+

+

−

(

) (

)

(

) (

)

(

)

(

)

[

]

(

)

4

3

2

1

4

4

2

3

3

1

4

3

2

2

1

1

2

1

2

1

03

,

0

04

,

0

4

,

4

7

,

2

5

,

0

6

5

,

0

3

3

,

0

12

,

0

11

,

0

4

,

0

9

2

,

0

4

5

,

1

3

1

,

0

9

1

,

0

4

1

,

1

3

5

,

1

8

,

1

5

,

16

10

)

(

max

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

X

F

X

+

+

+

=

=

+

−

+

+

−

−

+

+

−

⋅

+

⋅

+

⋅

−

+

⋅

+

⋅

+

⋅

−

+

−

+

=

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Zatem funkcja celu jest postaci:

Uwzględniając następujące ograniczenia :

maksymalna ilość pulpy

maksymalna przepustowość oczyszczalni
ścieków

wymaganie nieujemnego przepływu

wymaganie nieujemnego przepływu

wymaganie wyprodukowania określonej
liczby papieru niskiej jakości

Wymaganie produkowania określonej liczby
papieru wysokiej jakości:

4

3

2

1

03

,

0

04

,

0

4

,

4

7

,

2

)

(

max

x

x

x

x

X

F

X

+

+

+

=

50

5

,

1

1

,

1

2

1

≤

+

x

x

60

4

3

≤

+ x

x

0

3

3

1

≤

− x

x

0

6

4

2

≤

− x

x

12

1

≥

x

0

2

≥

x

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Zadanie maksymalizacji zysku produkcji papieru

4

3

2

1

0

03

.

0

04

.

0

5

.

1

7

.

2

max

x

x

x

X

x

+

+

+

=

∈

x

x

































≥

≥

−

≥

≥

−

≤

+

≤

+

12

0

6

0

,

0

3

60

50

5

.

1

1

.

1

1

4

2

3

1

2

1

2

1

x

x

x

x

x

x

x

x

x

x

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Zadanie programowania nieliniowego PN

przy ograniczeniach:

( )













=

∧

∈

x

x

x

f

f

X

min

{

}

m

i

g

x

X

i

,...,

1

,

0

)

(

=

≤

=

x

Zadanie programowania nieliniowego polega na znalezieniu wektora zmiennych
decyzyjnych

, należącego do zbioru rozwiązań dopuszczalnych X w postaci:

takiego, że dla

X

∈

∀x

( )

x

x

f

f

≤













∧

∧

x

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Przykład zadania programowania nieliniowego

Przykład IV. Zadania sterowania siecią dystrybucji wody minimalizujące

zużycie energii elektrycznej

Dana jest sieć dystrybucji wody w postaci:

m- węzłów,

s - odbiorców z odpowiednimi potrzebami, w których utrzymywane jest

odpowiednie ciśnienie oraz n łuków,

każdy łuk „i” charakteryzuje się przepływem y

i

:

Opis sieci:

spadek ciśnienia x

i

na łuku „i”:

gdzie: r

i

- opór hydrauliczny łuku „i”

d

i

- różnica wysokości geodezyjnych łuku „i”

Ograniczenia wynikające ze struktury sieci:

I prawo Kirchhoff’a:

A – macierz incydencji dla węzłów sieci wodociągowej,

II prawo Kirchhoff’a:

B – macierz oczkowa dla węzłów sieci wodociągowej.

i

i

i

i

i

d

y

y

r

x

+

=

sgn

2

n

R

y∈

n

R

x∈

s

R

∈

σ

σ

=

y

A

0

=

x

B

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Sterowanie siecią dystrybucji wody minimalizujące zużycie energii
elektrycznej

( )

i

n

i

i

y

f

y

f

∑

=

=

1

)

(

min

gdzie:

( )

i

i

i

i

i

i

i

i

i

y

d

y

y

r

y

x

y

f

+

=

=

sgn

3

przy ograniczeniach

:

σ

=

y

A

0

=

x

B

i

i

i

i

i

d

y

y

r

x

+

=

sgn

2

n

R

y∈

n

R

x∈

s

R

∈

σ

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Przykład V: Znaleźć najlepszą liniową aproksymację nieznanej funkcji
określonej poprzez tabelę 20 pomiarów.

Wyznaczyć optymalne wartości wektora współczynników b=[b

1

, b

2

, b

3

, b

4

] formy liniowej :

gdzie: u - wektor wielkości sterujących, y - wektor wielkości wyjściowych

Dane: tabela z 20 pomiarami wektora u wielkości sterujących oraz wektora wielkości

wyjściowych

dla następujących kryteriów jakości:

1.

minimum sumy wartości bezwzględnych różnic między wartościami wektora wyjść a
wartościami otrzymanymi z modelu liniowego:

gdzie:

- wartości zmierzone wielkości wyjściowych

i=1,...,20 - wielkości wyjściowe obliczone na podstawie

modelu

Zadanie trudne do rozwiązania, ponieważ funkcja celu jest nie-różniczkowalna.

u

b

y

T

=

( )

∑

=

−

=

20

1

~

)

(

[

min

i

i

i

b

y

y

b

f

20

,...,

1

~

=

i

y

i

)

(b

y

i

( )

i

i

i

i

i

u

b

u

b

u

b

u

b

b

y

4

4

3

3

2

2

1

1

+

+

+

=

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Równoważne zadanie programowania liniowego

Wprowadzono nową zmienną:

-

Zwiększenie wymiaru zadania: 24 zmienne niezależne

przy ograniczeniach:

dla i=1,...,20

Zadanie programowania liniowego:

-

funkcja celu jest wypukła

-

rozwiązano metodą dwufazową simpleks

.

.

Wektor b optymalnych wsp

Wektor b optymalnych wsp

ó

ó

ł

ł

czynnik

czynnik

ó

ó

w :

w :

( )

b

y

y

z

i

i

i

−

= ~

∑

=

=

20

1

)

(

min

i

i

z

b

f

i

i

i

i

i

i

i

z

u

b

u

b

u

b

u

b

y

z

≤

−

−

−

−

≤

−

4

4

3

3

2

2

1

1

~

87

,

51

1

=

b

232

,

1

2

=

b

122

,

0

3

−

=

b

08

,

1

4

−

=

b

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Drugie kryterium jakości

2. minimum sumy kwadratów różnic między wartościami wektora wyjść a

wartościami otrzymanymi z modelu liniowego:

gdzie:

- wartości zmierzone wielkości wyjściowych

- i=1,...,20 - wielkości wyjściowe obliczone na podstawie

modelu

Zadanie programowania nieliniowego:

funkcja celu jest wypukła

rozwiązano metodą gradientów sprzężonych w wersji Polak’a-Ribiere’y.

( )

(

)

2

20

1

~

)

(

[

min

∑

=

−

=

i

i

i

b

y

y

b

f

20

,...,

1

~

=

i

y

i

)

(b

y

i

( )

i

i

i

i

i

u

b

u

b

u

b

u

b

b

y

4

4

3

3

2

2

1

1

+

+

+

=

Wyniki identyfikacji zależą od wyboru kryterium optymalizacji i przyjętej

dokładności obliczeń.

28

,

39

1

=

b

07

,

1

2

=

b

16

,

0

3

=

b

94

,

0

4

−

=

b

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Przykład VI- Symulacja ruchu ramienia robota przemysłowego

Adekwatny model matematyczny dla szerokiej klasy obiektów sterowania- to układ równań
różniczkowych zwyczajnych pierwszego rzędu.

W tym celu:

1.

Konkretne ustalenie liczby równań

2.

Oznaczenie wartości parametrów tych równań

3.

Ustalenie warunków początkowych

4.

Jeżeli to możliwe - uproszczenie modelu do postaci równań liniowych

5.

Poszukiwanie rozwiązania, minimalizującego błędy, wynikające z opisu w postaci modelu
matematycznego – układu równań różniczkowych .

Proces symulacji:

Numeryczne rozwiązanie równań różniczkowych poprzez:

•

Zastąpienie pochodnych – ilorazami różnicowymi

•

Rozwiązanie wynikającego z tego faktu układu równań liniowych.

•

Minimalizacja błędu dla układu równań różniczkowych.

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Przykład VII- Zadanie lokalizacji magazynu i ustalania tras dostaw
optymalizacji sieci tras dostaw z wyborem najlepszego położenia dla
magazynu

Przykład VIII –
Zadania klasy VRP
np..: Firma CorbitConnect - obsługa rynku dostaw
np.: - procedury logistyczne:

-

Route scheduling, optimisation and disposition

-

Fleet management and controlling

-

Fleet controlling

-

Mobile navigation with tour management

-

Mobile tour management

np.: Program PLANTOUR - Firma CorbitConnect

Wydział Elektroniki studia II st.

kier. Automatyka i Robotyka

Teoria i metody optymalizacji
Dr inż. Ewa Szlachcic

Rozwiązywanie zadań inżynierskich – to umiejętność sprowadzania tych

zadań do standardowych problemów numerycznych, takich jak:

Rozwiązywanie układu liniowych równań algebraicznych,

Rozwiązywanie układu nieliniowych równań algebraicznych,

Aproksymacja i interpolacja funkcji jednej i wielu zmiennych,

Różniczkowanie funkcji jednej i wielu zmiennych,

Całkowanie układów równań różniczkowych zwyczajnych,

Rozwiązywanie zadań optymalizacji liniowej,

Rozwiązywanie zadań optymalizacji nieliniowej.

Zadanie numeryczne – to proces przetwarzania pewnego elementu zbioru
danych

D

D

w taki element zbioru wyników

W,

W,

który spełnia zadane wymagania

R

1

, R

2

,….

Układ

{

}

,...

,

,

,

2

1

R

R

W

D

To klasa zadań numerycznych.