Spis rzeczy

1 Pierwszy rzut oka na kryptogra

,

e

4

1.0.1 Szyfrowanie danych

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

4

1.0.2 Podstawowe zastosowania technik szyfrowania

:

:

:

:

:

:

:

:

:

5

1.0.3 Historia kryptograi

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

8

1.0.4 Kontrowersje zwi

,

azane ze stosowaniem kryptograi

:

:

:

:

:

:

9

1.0.5 Korzystanie z produktow kryptogracznych

:

:

:

:

:

:

:

:

:

:

10

2 Podstawowe techniki szyfrowania

12

2.0.6 Podstawienie

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

12

2.0.7 XOR i one-time pad

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

13

2.0.8 S-boksy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

15

3 Algorytmy symetryczne

18

3.1 DES { Data Encryption Standard

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

18

3.1.1 Szyfrowanie DES-em

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

19

3.1.2 Deszyfrowanie DES-em

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

21

3.2 Trzykrotny DES

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

21

3.3 Szyfrowanie tekstow dowolnej dlugosci

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

21

3.3.1 Elektroniczna ksi

,

a_zka kodowa

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

22

3.3.2 Cipher Block Chaining

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

23

3.3.3 Cypher Feedback

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

23

3.4 IDEA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

24

3.4.1 Szyfrowanie poprzez algorytm IDEA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

25

3.4.2 Generowanie podkluczy dla algorytmu IDEA

:

:

:

:

:

:

:

:

:

25

3.4.3 Deszyfrowanie przez IDEA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

25

4 Algorytmy niesymetryczne

29

4.0.4 Teoria zlo_zonosci obliczeniowej a kryptograa

:

:

:

:

:

:

:

:

:

29

4.0.5 Szyfry plecakowe

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

30

4.1 RSA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

32

4.1.1 Opis algorytmu RSA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

33

4.1.2 Testy pierwszosci

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

35

4.1.3 Aspekty bezpieczenstwa RSA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

37

4.1.4 Trudne bity kryptogramow RSA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

39

4.2 Algorytm ElGamala

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

41

5 Funkcje jednokierunkowe

43

5.0.1 Kandydaci na funkcje jednokierunkowe

:

:

:

:

:

:

:

:

:

:

:

:

:

44

5.0.2 Hard-core bit

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

45

i

SPIS

RZECZY

ii

6 Jednokierunkowe funkcje hashuj

,

ace

46

6.0.3 Wlasnosci i zastosowania funkcji hashuj

,

acych

:

:

:

:

:

:

:

:

:

46

6.0.4 Ataki przeciw funkcjom hashuj

,

acym

:

:

:

:

:

:

:

:

:

:

:

:

:

:

47

6.1 Techniki o dowodliwych wlasnosciach

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

49

6.1.1 Hashowanie przy pomocy dyskretnego logarytmu

:

:

:

:

:

:

:

49

6.1.2 Rozszerzenie na teksty dowolnej dlugosci

:

:

:

:

:

:

:

:

:

:

:

:

50

6.2 Praktyczne algorytmy hashuj

,

ace

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

51

6.2.1 MD5

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

51

6.2.2 Hashowanie dowolnie dlugich tekstow

:

:

:

:

:

:

:

:

:

:

:

:

:

52

7 Ci

,

agi pseudolosowe

55

7.0.3 Wlasnosci ci

,

agow pseudolosowych

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

55

7.0.4 Generatory ci

,

agow pseudolosowych

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

57

7.0.5 Pseudolosowosc generatora BBS

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

59

7.1 Zastosowania ci

,

agow pseudolosowych

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

59

7.1.1 Szyfrowanie strumieniowe

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

59

7.1.2 Szyfrowanie probabilistyczne

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

60

8 Podpisy cyfrowe

61

8.0.3 Podpisy cyfrowe ElGamala

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

62

8.0.4 DSA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

63

8.0.5 Slepe podpisy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

64

8.0.6 Kanal podprogowy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

65

8.0.7 Podpisy niezaprzeczalne

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

66

9 Uwierzytelnianie

69

9.0.8 Protokol challenge and response

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

69

9.0.9 Dowody interakcyjne

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

70

9.0.10 Dowody z wiedz

,

a zerow

,

a

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

71

9.0.11 Protokol Fiege-Fiata-Shamira

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

73

9.0.12 Protokol Schnorra

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

74

9.0.13 Protokol Guillou-Quisquartera

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

75

9.0.14 Podpisy cyfrowe poprzez uwierzytelnianie

:

:

:

:

:

:

:

:

:

:

:

76

10 Administracja kluczami

77

10.1 Praktyka gospodarki kluczami

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

77

10.1.1 Urz

,

adzenie kryptograczne

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

77

10.1.2 Generowanie kluczy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

78

10.1.3 Hierarchia kluczy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

79

10.1.4 Przechowywanie kluczy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

79

10.2 Protokoly uzgadniania kluczy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

80

10.2.1 Uzgadnianie kluczy poprzez szyfrowanie symetryczne

:

:

:

:

:

81

10.2.2 Uzgadnianie klucza przez szyfrowanie asymetryczne

:

:

:

:

:

82

10.2.3 Protokol Die-Hellmana i jego pochodne

:

:

:

:

:

:

:

:

:

:

:

82

11 Protokoly kryptograczne

85

11.0.4 Atak man in the middle

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

85

11.0.5 Dzielenie tajemnic

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

87

11.0.6 Zobowi

,

azanie bitowe

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

88

11.0.7 Pieni

,

adze cyfrowe

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

90

11.0.8 Elektroniczne wybory

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

93

SPIS

RZECZY

iii

12 Kryptoanaliza

95

12.0.9 Kryptoanaliza ro_znicowa

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

96

12.0.10Kryptoanaliza liniowa

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

99

12.0.11Ro_znicowa kryptoanaliza bl

,

edow

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

100

13 Wybrane implementacje

102

13.0.12Smart cards

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

102

13.0.13Krzywe eliptyczne

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

103

13.0.14Kerberos

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

103

13.0.15Zabezpieczanie komunikacji telefonicznej

:

:

:

:

:

:

:

:

:

:

:

:

106

13.0.16PGP { Pretty Good Privacy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

107

13.0.17Zabezpieczanie poczty elektronicznej { PEM

:

:

:

:

:

:

:

:

:

108

13.0.18Bezpieczenstwo w WWW

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

109

13.0.19Protokoly obrotu nansowego

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

109

A Wybrane aspekty teorii liczb

112

B Teoria algorytmow

116

Przedmowa

Do niedawna kryptograa byla obiektem zainteresowania w wi

,

ekszym stopniu slu_zb

wywiadowczych i wojska ni_z przedmiotow gospodarczych i prywatnych osob. Post

,

ep

w dziedzinie elektroniki a zwlaszcza gwaltowny rozwoj sieci komputerowych sytuacj

,

e

t

,

e zmienily w radykalny sposob.

Dawniej, gdy prywatny u_zytkownik dysponowal jedynie komputerem PC nie

wl

,

aczonym do sieci, ochrona danych byla stosunkowo prosta i zapewniona przez

zyczny dost

,

ep do komputera. Na tej samej zasadzie chronione byly dane przecho-

wywane w postaci elektronicznej przez male rmy, dzialy rm, organizacje politycz-

ne. Nie skomplikowaneprotokoly kryptograczne, ale klucz do pomieszczenia z kom-

puterem, czy koperta, w ktorej przesylana byla dyskietka, stanowily ochron

,

e przed

niepowolanym dost

,

epem. Oczywiscie zdarzaly si

,

e kradzie_ze dyskietek, komputerow,

wlamania do siedzib partii politycznych

:

:

:

. Wi

,

ekszosc u_zytkownikow nie czulo

jednak potrzeby skuteczniejszej ochrony swych danych.

Sytuacja zacz

,

ela si

,

e radykalnie zmieniac z chwil

,

a gwaltownego wzrostu sieci

komputerowych. Dotyczylo to nie tylko sieci obejmuj

,

acych szereg dzialow pojedyn-

czych rm, ale i sieci globalne, takie jak Internet (w tym zwlaszcza World Wide

Web). Zapewnienie bezpieczenstwa w tych sieciach stalo si

,

e jednym z pierwszo-

planowych zadan decyduj

,

acych o ich dalszym rozwoju. Nowe techniki telekomu-

nikacyjne, takie jak telefonia komorkowa, telewizja cyfrowa, telebanking, itp., nie

moglyby znalezc swego miejsca w codziennej praktyce, gdyby nie stosowanie technik

kryptogracznych dla ochrony dost

,

epu.

Najpierw rewolucja obj

,

ela komunikacj

,

e w srodowisku naukowym. Pojawienie

si

,

e poczty elektronicznej umo_zliwilo blyskawiczne kontaktowanie sie naukowcow z

najdalszych krajow. Pozwolilo to na olbrzymi wzrost wydajnosci w wielu dziedzi-

nach badan. Mo_znaby si

,

e spodziewac, _ze konkurencja i ostra walka o przodownictwo

doprowadzi w srodowisku naukowym do wielu nadu_zyc poczty elektronicznej. Tym

bardziej, _ze nie jest trudne na przyklad przeslac list w ten sposob, by nadawca po

naglowku mogl byc przekonany, _ze pochodzi on od innej osoby. Mo_zliwe jest rownie_z

przechwytywanie korespondencji przeznaczonej do innych adresatow. Zjawiska te

jednak stanowily dotychczas w calymsrodowisku naukowymbardzo w

,

aski margines.

Powodem zapewne bylo to, i_z komunikowaly si

,

e osoby, ktore i tak obdarzaly si

,

e

pelnym zaufaniem. Tak wi

,

ec metody, ktore pozwalalyby na zabezpieczenie przed

odczytem, modykacj

,

a czy te_z preparowaniem listow elektronicznych przez osoby

trzecie nie byly stosowane.

Te czasy min

,

ely. Wraz z pojawieniem si

,

e World Wide Web Internet stal si

,

e

atrakcyjny dla "szaregou_zytkownika\. WInternecie pojawilysi

,

e interesuj

,

ace zasoby

informacyjne, dzi

,

eki czemu ilosc u_zytkownikow zacz

,

ela rosn

,

ac gwaltownie. Co

wi

,

ecej, Internet coraz cz

,

esciej jest u_zywany nie jako narz

,

edzie zabawy czy rozwijania

zainteresowan, ale do celow komercyjnych. Ju_z dzis bilety lotnicze kupuj

,

e przez

Internet, literatur

,

e naukow

,

a wybieram przez World Wide Web, a zamiast kupowac

gazet

,

e z lokalnymi ogloszeniami si

,

egam do jej elektronicznego odpowiednika. W

takiej sytuacji b

,

edzie coraz wi

,

ecej osob: hardware tanieje, software staje si

,

e coraz

latwiejszy do obslugi przez laika, w wielu krajach pol

,

aczenia telefoniczne wskutek

1

SPIS

RZECZY

2

konkurencji na rynku telekomunikacyjnym staj

,

a si

,

e tansze i wy_zszej jakosci. Coraz

latwiejsze b

,

edzie zatem stanie si

,

e kolejnym u_zytkownikiem Internetu. Za par

,

e lat

b

,

edziemy miec zapewne do czynienia z sytuacj

,

a, gdy Internet b

,

edzie najwi

,

ekszym

supermarketem, najobszerniejsz

,

a gazet

,

a, najwi

,

ekszym Hyde Parkiem,

:

:

:

{przynaj-

mniej w krajach, gdzie uslugi telekomunikacyjne b

,

ed

,

a wystarczaj

,

aco tanie.

Jak ka_zdy wynalazek, rozwoj globalnych sieci komputerowych przynosi korzysci,

ale i niebezpieczenstwa. Wiele dyskutuje si

,

e na przyklad na temat mo_zliwosci

wykorzystywania Internetu przez organizacje przest

,

epcze. Sytuacja przypomina

nieco spory po wynalezieniu samochodu. Nie sposob cz

,

esciowo nie przyznac racji

przeciwnikom automobili maj

,

ac przed oczyma tragiczne statystki o tysi

,

acach ludzi

zabitych na drogach. Nie cofn

,

elo to jednak motoryzacji, tak jak nie do odwrocenia

jest ju_z rozwoj globalnej sieci komputerowej na swiecie.

Poniewa_z poprzez Internet komunikowac si

,

e b

,

ed

,

a nie dobrzy i ufaj

,

acy sobie

znajomi, lecz cz

,

esto anonimowi czy wrodzy sobie u_zytkownicy, mijaj

,

a czasy, gdy

niezbyt wiele myslano o bezpieczenstwie danych i komunikacji. Z jednej strony

podl

,

aczenie do sieci komputerowych stanowic b

,

edzie warunek wst

,

epny istnienia

rm (tak jak posiadanie telefonu, faxu, czy skrzynki pocztowej), z drugiej strony

podl

,

aczenie to stanowi o mo_zliwosci wlaman, dewastacji danych i innych dzialan o

charakterze przest

,

epczym.

Oczywiscie u_zytkownicy sieci komputerowych b

,

ed

,

a sie bronic przed niepowo-

lanym dost

,

epem do danych czy manipulacjami dokonywanymi na nich. Pierwsz

,

a

lini

,

a obrony b

,

ed

,

a oczywiscie systemy operacyjne zarz

,

adzaj

,

ace prac

,

a komputerow i

wykonywaniem zlecen na rzecz u_zytkownikow. W wielu miejscach ruchu w sieciach

komputerowych (ktore uzyskaly ju_z modn

,

a nazw

,

e

infostr

ad

) "sprawdzane b

,

ed

,

a

bilety\, a "pasa_zerowie na gap

,

e\ b

,

ed

,

a usuwani z ruchu. Rownoczesnie zadaniem

systemu operacyjnego b

,

edzie przestrzeganie, czy u_zytkownicy dokonuj

,

a jedynie do-

zwolonych operacji.

Wskutek zlo_zonosci stawianych zadan systemy operacyjne b

,

ed

,

a stawac si

,

e coraz

bardziej skomplikowane. Tym samymcoraz trudniej b

,

edzie ich tworcom przewidziec

wszystkie mo_zliwosci, tak aby uniemo_zliwicomini

,

ecie zabezpieczen zainstalowanych

poprzez system operacyjny. Dotychczasowe doniesienia z tego pola walki s

,

a raczej

pesymistyczne dla systemow operacyjnych. Stoj

,

a one w obliczu mia_zd_z

,

acej przewagi

wlamywaczy zwanych hackerami. Hackerzy nie s

,

a, jakby si

,

e chcialo wierzyc, jedynie

grup

,

a nastoletnich maniakow komputerowych (czy lagodniej mowi

,

ac, milosnikow

technik komputerowych). Jest to grupa o olbrzymim potencjale intelektualnym,

nierzadko doskonalym zapleczu sprz

,

etowym i nansowym.

Ostatni

,

a szans

,

a na zagwarantowanie bezpieczenstwa danych jest kryptograa.

Nie mo_ze ona usun

,

ac wszelkich niebezpieczenstw (jak na przyklad zniszczenie da-

nych przez wlamywacza komputerowego), ale w wielu sytuacjach skutecznie pomaga

(na przyklad uniemo_zliwia odczyt danych przez niepowolan

,

a osob

,

e). W odro_znieniu

do innych metod kryptograa dostarcza metod wzgl

,

ednie bezpiecznych. Tak bez-

piecznych, _ze liniami telekomunikacyjnymi dokonuje si

,

e co chwila przelewow nie-

wyobra_zalnych dla szarego czlowieka sum. I nikt si

,

e nie martwi, _ze ktos wl

,

aczy si

,

e

na lini

,

e i t

,

a drog

,

a powi

,

ekszy stan swego konta o iles milionow dolarow (z ktorymi

odleci natychmiast na wyspy poludniowego Pacyku do kraju, z ktorym zapomniano

zawrzec umow

,

e o ekstardycji przest

,

epcow).

Miroslaw Kutylowski

Wst

,

ep

Niniejsza ksi

,

a_zka ma za zadanie w bardzo zwi

,

ezly sposob przedstawic podstawowe

metody kryptograczne. Wiele interesuj

,

acych technik kryptogracznych zostalo w

niej pomini

,

etych. Nacisk polo_zony zostal na te aspekty, ktore maj

,

a b

,

adz miec mog

,

a

praktyczne zastosowanie. Wskutek tego wiele teoretycznie ciekawych zagadnien

swiadomie nie poruszamy w tej ksi

,

a_zce. Z drugiej strony, naszym zamyslem bylo, na

tyle na ile to jest mo_zliwe w tak krotkiej pozycji, umo_zliwicczytelnikowi zrozumienie

matematycznych mechanizmow tkwi

,

acych w kryptograi. Tym ksi

,

a_zka ta ro_zni si

,

e

na przyklad od dost

,

epnej na polskim rynku pozycji Bruce'a Schneiera 6], maj

,

acej

bardziej charakter encyklopedii ni_z podr

,

ecznika.

Niniejsza ksi

,

a_zka przeznaczona jest dla studentow informatyki i pokrewnych

dziedzin. Mo_ze byc wykorzystana jako podr

,

ecznik do semestralnego wykladu z kry-

ptograi, jak rownie_z jako material do samodzielnego studiowania. Do zrozumie-

nia niektorych cz

,

esci ksi

,

a_zki niezb

,

edna jest znajomosc pewnych faktow z algebry.

Czytelnik nieobeznany z tymi zagadnieniami mo_ze znalezc brakuj

,

ace informacje w

Dodatku A. Niekiedy konieczna jest znajomosc standardowych faktow z podstaw

informatyki wykladanych na pierwszych latach studiow informatycznych. Cz

,

esc

tych poj

,

ec skrotowo przedstawiamy w Dodatku B.

Niniejsza ksi

,

a_zka oparta jest na cz

,

esci skryptu do wykladu Miroslawa Kutylow-

skiego. Wyklad ten odbyl si

,

e na Wydziale Matematyki i Informatyki Uniwersytetu

Paderborn w semestrze zimowym 1995 roku. Wspomniany skrypt obejmuje procz

kryptograi zagadnienia kodow samokoryguj

,

acych bl

,

edy i kompresji danych. Jest

on dost

,

epny poprzez World Wide Web pod adresem

http://www.uni-paderborn.de/fachbereich/AG/agmadh/WWW/german/LehreKuty/ikk95/skript.ps.gz

Lista zauwa_zonych bl

,

edow, uzupelnienia, itp. znajduj

,

a si

,

e w World Wide Web

pod adresem

http://www.uni-paderborn.de/fachbereich/AG/agmadh/WWW/german/LehreKuty/kryptograa/

Pragniemy podzi

,

ekowac licznym studentom za udzielon

,

a pomoc. W szczegolno-

sci wymienic chcielibysmy Guido Haeselera, ktorego notatki do wykladu w Latex-u

byly podstaw

,

a pierwszej wersji skryptu (i szeregu rysunkow zawartych w ksi

,

a_zce).

Cz

,

esc rysunkow zostala wykonana przez Franka Beste i Ew

,

e Kutylowsk

,

a.

3

Rozdzia

l

1

Pierwszy

rzut

ok

a

na

kryptogra

,

e

1.0.1 Szyfrowanie danych

Najwa_zniejsze pole zainteresowan kryptograi (ale obecnie ju_z nie jedyne) to szyf-

rowanie dokumentow. Z orginalnego dokumentu (mo_ze to byc tekst, zakodowany

cyfrowo obraz, zakodowany cyfrowo dzwi

,

ek,

:

:

:

) zwanego

tekstem jawnym

mo_zna

stworzyc jego zaszyfrowan

,

a wersj

,

e zwan

,

a

kryptogramem

. Do zaszyfrowania i de-

szyfrowania niezb

,

edny jest dodatkowo

klucz

lub klucze. Ze wzgl

,

edu na wlasnosci

kluczy rozro_zniamy nast

,

epuj

,

ace metody szyfrowania:

Algorytmy symetryczne:

klucz do szyfrowania i deszyfrowania s

,

a identyczne

(lub latwo wyprowadzalne jeden z drugiego).

tekst jawny

zaszyfrowany tekst (kryptogram)

6

6

?

?

-

szyfrowanie kluczem

K

deszyfrowanie kluczem

K

Rysunek 1.1: Symetryczna metoda szyfrowania

Algorytmy asymetryczne:

(zwane tak_ze algorytmami z

kluczem jawnym

lub

kluczem publicznym

) klucze do szyfrowania i deszyfrowania s

,

a ro_zne prak-

tycznie nie powinno byc mo_zliwe wyprowadzenie z jednego z nich pasuj

,

acego

drugiego klucza umo_zliwiaj

,

acego operacj

,

e odwrotn

,

a.

Jako podstawow

,

a zasad

,

e nale_zy przyj

,

ac, _ze deszyfrowanie przy pomocy niewlas-

ciwego klucza nie powinno praktycznie dostarczac

_zadnych

informacji o tekscie

jawnym.

W ramach kryptograi rozwa_zamy rownie_z metody

lamania szyfrow

, lub ina-

czej

kryptoanalizy

. Chodzi o to by, na przyklad, na podstawie kryptogramu

znalezc odpowiadaj

,

acy mu tekst jawny lub zastosowany do szyfrowania klucz.

4

R

OZDZIA

L

1.

PIER

WSZY

RZUT

OKA

NA

KR

YPTOGRAFI

,

E

5

1.0.2 Podstawowe zastosowania technik szyfrowania

Ochrona danych przed niepowolanym odczytem

Realizacja tego celu nast

,

epuje poprzez szyfrowanie danych przy pomocy algorytmow

symetrycznych.

Pola zastosowan:

Zapis danych na nosnikach (dyski itp.) nie gwarantuj

,

acych ochrony przed odczy-

tem przez niepowolane osoby

: Dane te s

,

a zapisywane jedynie w postaci krypto-

gramu tylko posiadacz odpowiedniego klucza mo_ze z kryptogramu odtworzyc

orginalny tekst.

Zabezpieczenie komunikacji przeprowadzanej liniami nara_zonami na podsluch

: na

przyklad tego rodzaju zabezpieczenie niezb

,

edne jest w przypadku elektro-

nicznego dokonywania operacji gieldowych { podsluch dokonywanych zamo-

wien dostarczalby informacji pozwalaj

,

acy na efektywn

,

a spekulacj

,

e gieldow

,

a.

Jeszcze wi

,

eksze niebezpieczenstwa wi

,

azac si

,

e mog

,

a z mo_zliwosciami zmian w

przesylanych informacjach, na przyklad w wypadku elektronicznego obrotu

pieni

,

edzy pomi

,

edzy bankami. Szyfrowanie nie eliminuje zycznej mo_zliwosci

zaklocenia komunikacji b

,

adz dokonywania w niej zmian. Jednak zmiany do-

konywane bez znajomosci odpowiedniego klucza powoduj

,

a powstawanie chao-

tycznych tekstow po odszyfrowaniu przez prawowitego odbiorc

,

e u_zywaj

,

acego

prawidlowego klucza. W ten sposob proba oszustwa zostaje wykryta.

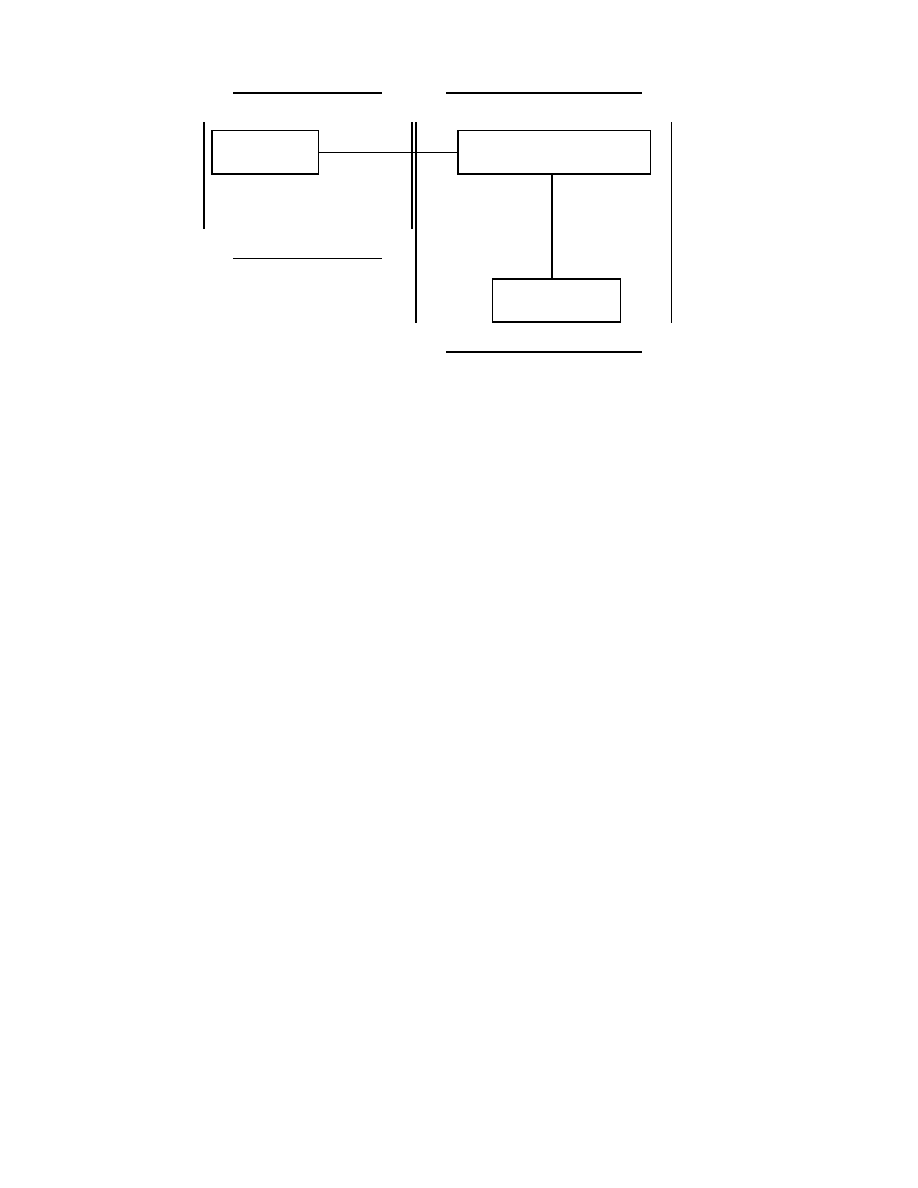
Uwierzytelnianie dokumentow

Uwierzytelnianie dokumentow mo_ze nast

,

apic przy pomocy algorytmow asymetry-

cznych. Alice publikuje (na przyklad na swej stronie w World Wide Web) jeden z

dwu pasuj

,

acych do siebie kluczy, mianowicie ten slu_z

,

acy do deszyfrowania (dlatego

klucz ten nazywamy

kluczem jawnym

lub

kluczem publicznym

). Drugi z pary

kluczy jest przez Alice pilnie strze_zony i nie jest podawany do niczyjej wiadomosci.

Klucz ten nazywamy

kluczem prywatnym

. Uwierzytelnianie dokumentow przez

Alice odbywa si

,

e poprzez szyfrowanie ich przy pomocy jej prywatnego klucza (patrz

rys. 1.2). Jest to mo_zliwe poniewa_z:

Ka_zdy mo_ze przy pomocy publicznego klucza Alice odzyskac orginalny tekst.
Jesli kryptogram nie byl wygenerowany przy pomocy prywatnego klucza Alice,

to deszyfrowanie przy pomocy klucza Alice daje w wyniku tekst b

,

ed

,

acy chao-

tycznym ci

,

agiem znakow bez _zadnego sladu sensu. Gwarantuje to, _ze jedynie

posiadacz prywatnego klucza Alice mo_ze t

,

a drog

,

a uwierzytelniac dokumenty

w imieniu Alice.
Na tej samej zasadzie pomylenie klucza publicznego w trakcie deszyfrowania

rownie_z daje w wyniku tekst b

,

ed

,

acy chaotycznym ci

,

agiem znakow. Dzi

,

eki

temu nie jest mo_zliwe przypisanie tekstu niewlasciwemu autorowi.

Ochrona prywatnosci elektronicznej korespondencji

Asymetryczne algorytmy szyfrowania mo_zna u_zyc rownie_z dla ochrony elektronicz-

nej korespondencji. Przesylanie korespondencji elektronicznej l

,

aczy si

,

e bowiem z

wieloma niebezpieczenstwami. Ktos maj

,

acy kontrol

,

e nad w

,

ezlem Internetu, przez

ktory przesylany jest list, mo_ze list ten zniszczyc, zmodykowac, albo wreszcie

przekazac go komus innemu. Aby zapobiec przynajmniej dwom ostatnim mo_z-

liwosciom mo_zna u_zyc scenariusza opisanego poni_zej. Przed niszczeniem listow

kryptograa nie jest nas w stanie uchronic.

R

OZDZIA

L

1.

PIER

WSZY

RZUT

OKA

NA

KR

YPTOGRAFI

,

E

6

'

&

$

%

'

&

$

%

Alice

Bob

tekst orginalny

kryptogram

tekst orginalny

?

deszyfrowanie

kluczem

publicznym

K

0

szyfrowanie

kluczem

prywatnym

K

-

Rysunek 1.2: Uwierzytelnianie przez szyfrowanie

Zalo_zmy, i_z Alice chce bezpiecznie otrzymywac korespondencj

,

e. W tym celu

Alice musi dysponowac par

,

a pasuj

,

acych kluczy dla asymetrycznego algorytmu szy-

fruj

,

acego. Klucz do

szyfr

owania

zostaje przez Alice opublikowany, na przyklad po-

przez World Wide Web. Gdy Bob pragnie wyslac list do Alice, wtedy wykonywane

s

,

a nast

,

epuj

,

ace kroki (patrz rys. 1.3):

Bob zaopatruje si

,

e w klucz

K

, publiczny klucz Alice.

Bob szyfruje tekst swego listu do Alice przy pomocy klucza

K

.

Bob wysyla zaszyfrowany list poczt

,

a elektroniczn

,

a do Alice (w zale_znosci od

stosowanego systemu, konieczna mo_ze byc konwersja z pliku zawieraj

,

acego

kryptogram z postaci binarnej na tekstow

,

a, by unikn

,

ac zmian wprowadzanych

przez program pocztowy).
Alice deszyfruje otrzymany list przy pomocy swego prywatnego klucza i otrzy-

muje w ten sposob orginalny list.

Powy_zszy protokol gwarantuje, _ze tylko Alice jest w stanie odkodowac prze-

znaczone do niej listy. Tak wi

,

ec przechwycenie korespondencji przez osoby trzecie

przestaje byc niebezpieczne. Rownie_z proby wprowadzania zmian w zaszyfrowanym

liscie (nawet na slepo) jest skazana na niepowodzenie { wszystkie rozs

,

adne algo-

rytmy szyfruj

,

ace maj

,

a wlasnosc, _ze zmiana chocby jednego bitu w kryptogramie

powoduje olbrzymie zmiany w tekscie po deszyfrowaniu, wskutek czego tekst ten

ma postac przypadkowego ci

,

agu znakow.

Oczywiscie bezpieczenstwo korespondencji mi

,

edzy Alice i Bobem mo_zna zagwa-

rantowac poprzez stosowanie szyfrowania algorytmem symetrycznym z kluczem

znanym jedynie Alice i Bobowi. Zalet

,

a protokolu z u_zyciem asymetrycznego al-

gorytmu jest to, _ze Alice i Bob nie musz

,

a uzgadniac stosowanych kluczy, oraz

_ze Alice mo_ze ograniczyc si

,

e do posiadania jednej pary kluczy dla korespondencji

prowadzonej z du_z

,

a ilosci

,

a osob. Protokol nadaje si

,

e wi

,

ec dobrze dla korespondencji

pomi

,

edzy osobami sporadycznie kontaktuj

,

acymi si

,

e oraz gdy Alice otrzymuje listy

od du_zej ilosci osob.

Elektroniczny notariusz

Do notariusza zglaszamy si

,

e w dwoch wa_znych sytuacjach:

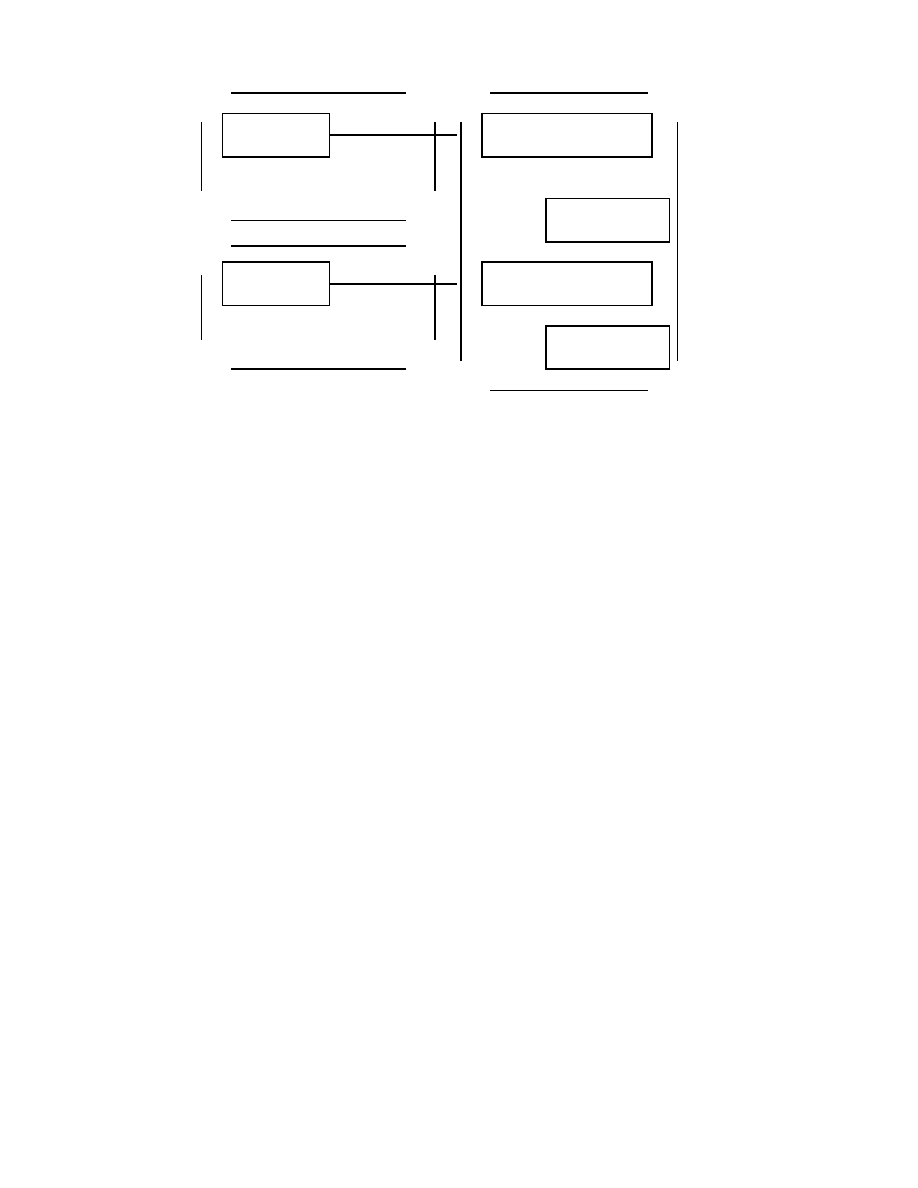
R

OZDZIA

L

1.

PIER

WSZY

RZUT

OKA

NA

KR

YPTOGRAFI

,

E

7

'

&

$

%

'

&

$

%

List 1

List 2

-

-

szyfrowanie

szyfrowanie
kluczem

publicznym

K

kluczem

publicznym

K

Bob

Mike

Kryptogram 1

Kryptogram 2

List 1

List 2

'

&

$

%

J

J

J

^

deszyfrowanie
kluczem

K

0

S

S

w

prywatnym

K

0

Alice, posiadaczka

K

0

Rysunek 1.3: Ochrona korespondencji przy u_zyciu asymetrycznych algorytmow

szyfruj

,

acych

1. Jesli chcemy urz

,

edowo potwierdzic istnienie jakiegos dokumentu. W tym

wypadku mo_zemy dodatkowo pragn

,

ac by proces potwierdzania nie ujawnial

tresci dokumentu (bo mo_ze byc to na przyklad opis nowej, wartosciowej tech-

nologii).

2. Jesli chcemy zagwarantowac by w dokumencie (na przyklad umowie handlo-

wej) nie byly dokonywane pozniej jakiekolwiek zmiany przez nieuczciwego

partnera.

W obu przypadkach wystarcza sporz

,

adzenie dla wspomnianego dokumentu czegos

w rodzaju odciskow palcow { krotkiego ci

,

agu symboli, ktory

pr

aktycznie

jest dla

ka_zdego tekstu inny. Takie "odciski palcow\ mo_zna na przyklad opublikowac jako

ogloszenie w codziennej prasie. Zdobywamy w ten sposob dowod istnienia doku-

mentu. Aby dowod ten byl niezaprzeczalny musimy zagwarantowac kilka wlasnosci.

Do sporz

,

adzania "odciskow palcow\ u_zywamy tak zwanych

jednokierunkowych

funkcji hashuj

,

acych

. Mowimy, _ze

H

jest jednokierunkow

,

a funkcj

,

a hashuj

,

ac

,

a o

ile spelnione s

,

a nast

,

epuj

,

ace warunki:

Dla ka_zdego

X

latwo jest obliczyc

H

(

X

).

H

(

X

) ma ustalon

,

a dlugosc dla wszystkich tekstow

X

(w ten sposob dlugosc

H

(

X

) nie zdradza _zadnych informacji o tekscie

X

).

Dla zadanego

Y

znalezienie

X

takiego, _ze

H

(

X

) =

Y

, jest praktycznie niemo-

_zliwe. Dotyczy to w szczegolnosci systematycznego przeszukiwania wszystkich

mo_zliwych tekstow. Tak wi

,

ec ci

,

agi

H

(

X

) musz

,

a byc wystarczaj

,

aco dlugie,

by takie systematyczne przeszukiwanie bylo praktycznie beznadziejne. Jesli

wartosci funkcji hashuj

,

acej skladaj

,

a si

,

e z 128 bitow to mamy do dyspozycji

2

128

mo_zliwych wartosci. Jest to praktycznie nieskonczona ilosc (dla porow-

nania calkowity okres od pocz

,

atku do konca Wszechswiata bywa szacowany

wedlug niektorych teorii na 2

61

sekund!).

W rzeczywistosci nakladane s

,

a jeszcze bardziej rygorystyczne warunki na wlasnosci

jednokierunkowych funkcji hashuj

,

acych (patrz Rozdzial 6).

R

OZDZIA

L

1.

PIER

WSZY

RZUT

OKA

NA

KR

YPTOGRAFI

,

E

8

W celu "notarialnego\ potwierdzenia posiadania dokumentu

X

nale_zy obliczyc

wartosc

H

(

X

) i opublikowac j

,

a lub umiescic u notariusza (rol

,

e notariusza mo_ze

przej

,

ac odpowiedni specjalnie zabezpieczony program sieciowy). Pozniej, gdy pra-

gniemy udowodnic posiadanie dokumentu

X

, przedstawiamy

X

i wskazujemy na

miejsce, gdzie podalismywczesniej wartosc

H

(

X

). Sprawdzenie polega na obliczeniu

wartosci

H

(

X

) dla podanego tekstu

X

i porownaniu jej z wartosci

,

a opublikowan

,

a

wczesniej lub zlo_zon

,

a u notariusza.

W celu zagwarantowania, i_z tekst

X

(na przyklad umowa) nie ulegnie mody-

kacjom, rownie_z obliczamy wartosc

H

(

X

). Wartosc t

,

e mo_zemy nast

,

epnie dol

,

aczyc

do dokumentu (na przyklad dla wykrycia przypadkowych bl

,

edow powstalych w

trakcie transmisji danych) lub opublikowac, czy zlo_zyc u notariusza (dla ochrony

przed post

,

epowaniem nieuczciwego partnera umowy).

Zauwa_zmy, _ze opisana metoda moglaby na przyklad pozwalac na proste spraw-

dzanie autentycznosci programow komputerowych. Jeden z trudniejszych do wy-

krycia atakow na system komputerowy jest wprowadzanie tzw. koni trojanskich {

programow zachowuj

,

acych si

,

e z punktu widzenia u_zytkownika w sposob dokladnie

taki sam jak programy orginalne, jednak wykonuj

,

ace pewne dodatkowe funkcje (na

przyklad samopowielanie w przypadku wirusow, czy przekazywanie informacji na

zewn

,

atrz w wypadku szpiegostwa gospodarczego). O ile jednak producent programu

X

zamiesci wartosc

H

(

X

) na przyklad w World Wide Web, wtedy osoba posiadaj

,

aca

program

X

mo_ze w ka_zdym momencie obliczyc wartosc funkcji

H

dla posiadanego

programu i porownac j

,

a z wartosci

,

a

H

(

X

) dost

,

epn

,

a publicznie. Zauwa_zmy, _ze

metoda ta pozwala na wykrycie zmian dokonywanych w programie przez

jakie-

kolwiek

wirusy, te znane jak i nieznane lub nienapisane jeszcze. Istotn

,

a cech

,

a tej

metody jest to, _ze producent nie musi upubliczniac programu

X

, a mimo wszystko

pelna werykacja orginalnosci jest mo_zliwa. Tym samym producent ma szanse

sprzeda_zy dalszych kopii programu

X

.

O ile wybierzemy funkcj

,

e hashuj

,

ac

,

a generuj

,

ac

,

a krotkie ci

,

agi liter, wtedy telefo-

nicznie mo_zna sprawdzic orginalnoscdokumentow przeslanych elektronicznie (osoby

znaj

,

ace si

,

e po glosie mog

,

a sprawdzic czy wartosci funkcji hashuj

,

acej dla wyslanego

i otrzymanego dokumentu s

,

a takie same). T

,

a drog

,

a mo_zna na przyklad drog

,

a

telefoniczn

,

a sprawdzic orginalnosc kluczy publicznych generowanych przez system

PGP.

|||||||||||||||||||||||||||||||||||

Przyklady, jakie przedstawilismy powy_zej to tylko niektore z dzisiejszych per-

spektyw zastosowania kryptograi. Ju_z po tych przykladach widac jednak, _ze pole

zastosowan kryptograi wykracza daleko poza klasyczne szyfrowanie danych (na

przyklad do celow militarnych). Niektore inne zastosowania b

,

ed

,

a przedstawione w

dalszej cz

,

esci tej ksi

,

a_zki. Poza tym Czytelnik mo_ze odwolac si

,

e do bogatej literatury

fachowej dotycz

,

acej kryptograi.

1.0.3 Historia kryptograi

Ju_z w staro_zytnosci stosowane byly pewne metody szyfrowania wiadomosci o cha-

rakterze strategicznym. Ciekawe jest, _ze stopien wyranowania tych metod byl

znacz

,

aco ni_zszy od stanu wiedzy matematycznej w ka_zdej wlasciwie epoce. Sto-

sowane metody byly dawniej zazwyczaj dosc prymitywne i pozwalaly na zlamanie

szyfrow dostatecznie zdeterminowanemu przeciwnikowi. Sytuacja ulegla zmianie

ju_z w pierwszej polowie dwudziestego wieku. Zbudowano wtedy szereg systemow

szyfrowania przy pomocy urz

,

adzen mechanicznych wykorzystywanych powszechnie

podczas II Wojny Swiatowej. Cz

,

esc z tych systemow zostala skutecznie zlamana

(na przyklad niemiecki system Enigma). Prawdziw

,

a rewolucj

,

e pod wzgl

,

edem pro-

jektowania systemow szyfruj

,

acych przyniosl rozwoj elektroniki daj

,

acy olbrzymie

mo_zliwosci operacji obliczeniowych niskim kosztem.

R

OZDZIA

L

1.

PIER

WSZY

RZUT

OKA

NA

KR

YPTOGRAFI

,

E

9

Rozwoj kryptograi od swych pocz

,

atkow byl bardzo silnie zwi

,

azany z celami

wojskowymi. W zwi

,

azku z tym wszelkie prace z dziedziny kryptograi mialy cha-

rakter tajny i ich rezultaty nie byly publikowane lub wykorzystywane w sektorze

cywilnym do lat siedemdziesi

,

atych. Naukowcy prowadz

,

acy badania w kryptogra-

i znajdowali si

,

e pod scisl

,

a kontrol

,

a organow bezpieczenstwa. Publikowanie prac

nast

,

epowalo sporadycznie i niekiedy jedynie poprzez niedopatrzenie organow kon-

trolnych.

Prawdziwy przelom pod wzgl

,

edem rozwoju kryptograi nast

,

apil w latach sie-

demdziesi

,

atych wraz z odkryciem asymetrycznych algorytmow szyfruj

,

acych. Ol-

brzymie zainteresowanie w srodowiskach naukowych spowodowalo lawinowy wzrost

ilosci prowadzonych badan, ju_z poza kontrol

,

a aparatow bezpieczenstwa poszcze-

golnych panstw. Wymiana informacji jaka ma miejsce od tego czasu pozwolila na

ogromny rozwoj wiedzy w tej dziedzinie.

W wielu krajach stosowanie metod kryptogracznych jest nadal zabronione lub

ograniczone. W wielu krajach, sk

,

adinn

,

ad demokratycznych, gdzie obywatele ciesz

,

a

si

,

e du_zym zakresem wolnosci, podejmowane s

,

a proby ustanowienia kontroli panstwa

nad stosowaniem metod kryptogracznych. W szczegolnosci dotyczy to przyklad

Wspolnoty Europejskiej i USA (forsowanie u_zywania Clippera, tj. ukladu elektro-

nicznego slu_z

,

acego do szyfrowania, jednak pozwalaj

,

acego na lamanie kryptogramow

przez slu_zby bezpieczenstwa). Doprowadzilo to te_z do tak spektakularnych krokow

jak zakaz u_zywania technik kryptogracznych do celow prywatnych w Rosji.

Ograniczaniu mo_zliwosci stosowania metod kryptogracznych sprzeciwiaj

,

a si

,

e

bardzo gwaltownie srodowiska buzinessu. Wskazuj

,

a na niezb

,

ednosc jej stosowania

w gospodarce w niereglamentowany sposob. W obecnej chwili wydaje si

,

e, _ze jednym

z niezb

,

ednych warunkow rozwoju gospodarczego panstwa jest rozbudowa globalnej

sieci komputerowej pelni

,

acej funkcj

,

e infrastruktury informacyjnej gospodarki. Po-

niewa_z w sieciach tego typu nie da si

,

e raczej zagwarantowac bezpieczenstwa przed

wlamaniamikomputerowymi,dane musz

,

a byc zabezpieczane w inny sposob. Jedyna

droga do realizacji tego celu wiedzie poprzez wykorzystanie technik kryptogra-

cznych. Podnoszone s

,

a argumenty, i_z wprowadzenie ograniczen stosowania kry-

ptograi nieuchronie powoduje spadek atrakcyjnosci danego kraju dla inwestycji

gospodarczych.

1.0.4 Kontrowersje zwi

,

azane ze stosowaniem kryptograi

Kryptograa w obecnym stadium rozwoju potra zagwarantowac ochron

,

e danych

przed dost

,

epem niepowolanych osob. Jest to mo_zliwe nawet wtedy, gdy wlasciciel

danych za takowe uwa_za organy scigania. Dopuszczenie stosowania tych metod

uniemo_zliwiazatem skutecznie dokonywanie "rewizji\ policyjnychwsystemachkom-

puterowych. Umo_zliwia to dokonywanie elektronicznego przetwarzania danych w

ramach dzialalnosci przest

,

epczej bez niebezpieczenstwa dostarczenia organom sci-

gania materialu dowodowego w wypadku ich przechwycenia. Pozwala to rownie_z

na korzystanie z powszechnie dost

,

epnych sieci takich jak Internet do dzialalnosci

przest

,

epczej. Z mo_zliwosci tych korzystaj

,

a zapewne ju_z teraz organizacje dzialaj

,

ace

na kraw

,

edzi prawa, lub te_z wbrew prawu.

W obliczu powy_zszych zagro_zen w wielu panstwach organy bezpieczenstwa (cza-

sami demokratycznie wybrane, czasami b

,

ed

,

ace aparatem politycznej represji) stara-

j

,

a si

,

e zabronic b

,

adz ograniczyc stosowanie metod kryptogracznych. Druga z tych

opcji polega na dopuszczeniu jedynie takich metod, ktore mog

,

a zostac zlamane

przez organy bezpieczenstwa (wskutek slabosci tych metod, koniecznosci przekazy-

wania u_zywanych kluczy organom bezpieczenstwa, b

,

adz dzi

,

eki wbudowanym do

algorytmow "tylnym drzwiom\ pozwalaj

,

acym na deszyfrowanie bez znajomosci

kluczy).

R

OZDZIA

L

1.

PIER

WSZY

RZUT

OKA

NA

KR

YPTOGRAFI

,

E

10

Przeciwnicy stosowania ograniczen w stosowaniu kryptograi wskazuj

,

a, i_z sro-

dowiska przest

,

epcze bylyby i tak w stanie korzystac z technik kryptogracznych

bez mo_zliwosci udowodnienia im tego poprzez organy scigania. Problem polega

na tym, i_z kryptogramy maj

,

a charakter losowych ci

,

agow znakow i s

,

a od nich

nieodro_znialne. Z drugiej strony losowy charakter maj

,

a szumy zawarte w ka_zdym

kodowanym cyfrowo obrazie czy dzwi

,

eku. Tym samym przest

,

epca dzialaj

,

acy w

ramach zorganizowanych grup mo_ze ukryc przekazywan

,

a wiadomosc na przyklad w

zdj

,

eciu Tatr umieszczonym na swej stronie WWW, czy te_z na dysku CD specjalnie w

tym celu spreparowanym. Co wi

,

ecej, z niektorych form kryptograi nie jestesmy w

stanie ju_z zrezygnowac, chocby w obrocie bankowym. Poniewa_z wiele metod u_zywa

jako niezb

,

ednych parametrow losowych ci

,

agow znakow, przest

,

epca mo_ze zamiast

nich u_zywac kryptogramow z przest

,

epczymi informacjami. Znow, nie wzbudzi to

_zadnych podejrzen, a wiadomosci tak przekazywane b

,

ed

,

a odro_znialne od naprawd

,

e

losowych ci

,

agow jedynie dla posiadaczy tajnego klucza (przyklad takiej sytuacji

opisujemy dokladniej w Rozdziale 8.0.6).

Reasumuj

,

ac, wydaje si

,

e i_z postulowane ograniczenia s

,

a w stanie byc skuteczne

jedynie w odniesieniu do osob czy organizacji nie paraj

,

acych si

,

e dzialalnosci

,

a prze-

st

,

epcz

,

a. Spowodowaloby to zatem skutek odwrotny do zamierzonego { stawialoby

organizacje przest

,

epcze w uprzywilejowanej pozycji wobec reszty spoleczenstwa,

ktora nie bylaby w stanie bronic swych danych wobec dzialan kryminalnych.

1.0.5 Korzystanie z produktow kryptogracznych

Upublicznienie kryptograi pozwala na bardziej wiarygodn

,

a werykacj

,

e oferowa-

nych programow i sprz

,

etu kryptogracznego. Nie mo_zna bowiem w tym wzgl

,

edzie

polegac na reklamie samych rm. Wadliwoscoferowanego produktu nie jest widocz-

na bowiem golym okiem, a cz

,

esto bez nieslychanie kosztownego badania produktu

nie jest si

,

e rownie_z w stanie o tym przekonac.

Sformulowacmo_zna nast

,

epuj

,

ace zasady dotycz

,

ace praktycznego stosowania pro-

duktow kryptogracznych w sytuacjach, gdy rzeczywiscie bezpieczenstwo ma klu-

czowe znaczenie:

Jako wzgl

,

ednie bezpieczne mog

,

a byc uznane jedynie programy czy te_z spe-

cjalny hardware oferowany poprzez znane rmy o niezaprzeczalnej reputacji.

Najlepiej, gdy produkty te posiadaj

,

a certykaty odpowiednich panstwowych

urz

,

edow kontrolnych (jak na przyklad NIST w USA).

Programy i urz

,

adzenia kryptograczne powinny realizowac powszechnie zna-

ne, popularne i przetestowane rozwi

,

azania. Proces testowania powinien miec

nast

,

epuj

,

acy przebieg:

1.

Propozycja metody, wraz z jej szczegolowym opisem musi byc podana do

wiadomosci publicznej.

Bezpieczenstwo metody nie mo_ze opierac si

,

e na

utajnieniu jej sposobu dzialania. Wiadomo, _ze i tak pewna grupa osob

uzyska do takich informacji dost

,

ep (chocby pracownicy rmy oferuj

,

acej

produkt). Grupa ta mo_ze nast

,

epnie wykorzystywac je na szkod

,

e u_zyt-

kownika produktu.

2.

Propozycja musi wzbudzic powszechne zainteresowanie srodowiska nauko-

wego i businessu i musz

,

a byc prowadzone nad ni

,

a intensywne badania.

3.

Jesli po dlu_zszym czasie nie ma znacz

,

acych post

,

epow prowadz

,

acych do

zlamania metody

a teoretyczne badania zdaj

,

a si

,

e potwierdzac jej bez-

pieczenstwo (na przyklad poprzez redukcj

,

e znanych trudnych zagadnien

obliczeniowych do zagadnienia zlamania proponowanego szyfru),

wtedy

metod

,

e t

,

e mo_zna uznac za wzgl

,

ednie bezpieczn

,

a i dopuscic do u_zytku

.

R

OZDZIA

L

1.

PIER

WSZY

RZUT

OKA

NA

KR

YPTOGRAFI

,

E

11

Jesli jakikolwiek z powy_zszych warunkow nie jest spelniony, algorytm nie

mo_zna uznac za bezpieczny.
Niezb

,

edne jest ci

,

agle sledzenie rozwoju stanu wiedzy kryptogracznej. Post

,

e-

py w tej dziedzinie mog

,

a spowodowac mo_zliwosclamania algorytmow dawniej

uznawanych za bezpieczne. (Tego typu sytuacja nast

,

apila na przyklad w

odniesieniu do dlugosci kluczy dla systemu RSA wskutek post

,

epow w zakresie

algorytmow rozkladaj

,

acych liczby na czynniki pierwsze.)

Czasami jakosc oferty software'u i hardware'u kryptogracznego jest powi

,

azana

z czynnikami politycznymi, takimi jak ograniczenia eksportowe. Na przyklad tak

zwane "wersje mi

,

edzynarodowe\ programow rm amerykanskich maj

,

ace dostarczyc

prywatnemu u_zytkownikowi narz

,

edzia kryptograczne gwarantuj

,

a jedynie bardzo

niski poziom bezpieczenstwa. Poziom ten jest tak niski, _ze programy te nie wyma-

gaj

,

a zezwolen eksportowych w bardzo restrykcyjnym ustawodawstwie USA.

Rozdzia

l

2

P

o

dsta

w

o

w

e

tec

hniki

szyfro

w

ania

W niniejszym rozdziale przedstawiamy kilka klasycznych technik szyfrowania. Tech-

niki te bywaj

,

a skladnikami wielu bardziej zaawansowanych algorytmow, dlatego

poswi

,

ecimy im chwil

,

e uwagi.

2.0.6 Podstawienie

Niech :

!

b

,

edzie permutacj

,

a, zas zbiorem u_zywanych liter. Tekst jawny

a

1

a

2

:

:

:

a

n

(gdzie

a

i

2

) jest szyfrowany jako (

a

1

) (

a

2

)

:

:

:

(

a

n

). Kryptogram

b

1

:

:

:

b

n

odszyfrowywany jest jako

;

1

(

b

1

)

:

:

:

;

1

(

b

n

).

Przyklad: szyfry Cesara

Litery alfabetu mo_zna uto_zsamiac z liczbami. W

systemie Cesara u_zywanych jest 26 liter odpowiadaj

,

acych liczbom od 0 do 25.

(

i

) :=

i

+ 3 mod 26 dla

i

2

f

0

:

:

:

25

g

.

Analiza cz

,

estotliwosci

Slabosci

,

a szyfrow opartych na podstawieniach jest to, _ze mog

,

a one byc zlamane

poprzez analiz

,

e cz

,

estotliwosci wyst

,

epowania poszczegolnych liter alfabetu. Litery

alfabetu nie wyst

,

epuj

,

a bowiem z jednakow

,

a cz

,

estotliwosci

,

a { analiza tych cz

,

e-

stotliwosci w zaszyfrowanych tekstach pozwala na zgadni

,

ecie niektorych wartosci

permutacji . Dla przykladu przyjrzyjmy si

,

e przeci

,

etnej cz

,

estotliwosci wyst

,

epo-

wania liter w tekstach w j

,

ezyku angielskim (wedlug 1]):

E - 12.31 % L - 4.03 % B - 1.62 %

T - 9.59 % D - 3.65 % G - 1.61 %

A - 8.05 % C - 3.20 % V - 0.93 %

O - 7.94 % U - 3.10 % K - 0.52 %

N - 7.19 % P - 2.29 % Q - 0.20 %

I - 7.18 % F - 2.28 % X - 0.20 %

S - 6.59 % M - 2.25 % J - 0.10 %

R - 6.03 % W - 2.03 % Z - 0.09 %

H - 5.14 % Y - 1.88 %

Kryptoanaliza polega na sporz

,

adzeniu tabeli cz

,

estotliwosci wyst

,

epowania liter

w zaszyfrowanym tekscie i porownania go z powy_zsz

,

a tabel

,

a. Na tej podstawie

mo_zna na przyklad zlokalizowac prawdopodobne wartosci dla (

E

), (

T

), (

A

). Po

przyj

,

eciu hipotetycznych wartosci dla tych liter szukamy w kryptogramie sekwencji

12

R

OZDZIA

L

2.

PODST

A

W

O

WE

TECHNIKI

SZYFR

O

W

ANIA

13

liter odpowiadaj

,

acych typowym slowom takim jak na przyklad "the\. Pozwala

to na zwerykowanie hipotezy i przyj

,

ecie prawidlowych wartosci dla E, T, A. Po

ustaleniu tych wartosci mo_zemy pokusic si

,

e o odgadni

,

ecie (

H

) - tak by utworzyc

odpowiednio du_zo kryptogramow dla "the\. Post

,

epowanie to kontynuujemy dyspo-

nuj

,

ac coraz to wi

,

ekszymi porcjami tekstu jawnego.

Sposobem na utrudnienie analizy cz

,

estotliwosci jest szyfrowanie poprzez podsta-

wienie nie pojedynczych liter, ale blokow liter okreslonej dlugosci (tj. :

k

!

k

).

Mamy wtedy bowiem do czynienia z mniejszymi dysproporcjami w zakresie sredniej

cz

,

estotliwosci wyst

,

epowania poszczegolnych konguracji liter w bloku w szczegol-

nosci poszczegolne prawdopodobienstwa s

,

a stosunkowo malymi liczbami. Utrudnia

to odgadni

,

ecie wartosci podstawienia . W szczegolnosci kryptoanaliza wymaga

du_zo dlu_zszych kryptogramow, aby moc skorzystac z jakichkolwiek statystycznych

prawidlowosci.

Przykladem systemu, w ktorym koduje si

,

e bloki dlugosci 2 jest system Fairplay'a

przedstawiony na rys. 2.1. Jest to prosty system, w ktorym wszelkie operacje szy-

frowania i deszyfrowania mog

,

a byc z latwosci

,

a dokonane r

,

ecznie. System oczywiscie

gwarantuje tylko bardzo niewielki zakres bezpieczenstwa i mo_ze byc traktowany jako

dygresja w stron

,

e metod historycznych (stosowanych w trakcie I Wojny Swiatowej).

Szyfrowaniu podlegaj

,

a pary liter, przy czym u_zywamy 25 liter (25 du_zych liter

alfabetu angielskiego, jedna z liter, mianowicie J, jest w tekstach zast

,

apiona przez

I). Do szyfrowania i deszyfrowania u_zywamy jest kwadrat 5

5, w ktory wpisujemy

kolejne litery wyst

,

epuj

,

ace w hasle (na rys. 2.1 haslem jest "POSZLA MALPA

DO PIWNICY\), przy czym pomijamy powtarzaj

,

ace si

,

e litery. Gdy po wpisaniu

tych liter zostaly jeszcze wolne miejsca w kwadracie, to umieszczamy tam jeszcze

niewpisane litery w kolejnosci alfabetycznej. W ten sposob wypelniamy kwadrat

25 literami. Szyfrowanie przebiega nast

,

epuj

,

aco. Zalo_zmy dla przykladu, _ze chcemy

zaszyfrowac par

,

e OH wedlug klucza z rys. 2.1. Litery O oraz H wyznaczaj

,

a pro-

stok

,

at

w kwadracie do szyfrowania, w ktorego pozostalych rogach znajduj

,

a si

,

e S

i G. Regula szyfrowania mowi, _ze OH zast

,

epujemy wlasnie tymi literami, tj. SG.

Gdy para liter jak

,

a zamierzamy zaszyfrowac le_zy w jednej kolumnie lub jednym

wierszu (i wobec tego nie deniuje prostok

,

ata), to litery te zast

,

epujemy par

,

a liter

le_z

,

ac

,

a na prawo od nich, na przyklad SY zast

,

epujemy przez ZB, zas WE przez AN

(litery le_z

,

ace w pierwszej kolumnie z prawej strony zast

,

epujemy literami z ostatniej

kolumny).

Ogolnie rzecz bior

,

ac podstawienie nie oparte o dlugie bloki lub o prostych

zasadach generowania permutacji z klucza mo_ze byc podatne na analiz

,

e cz

,

estotliwo-

sci. Z tego wzgl

,

edu podstawienie nale_zy traktowac raczej jako technik

,

e pomocnicz

,

a

do wykorzystania jako element pomocniczy bardziej zlo_zonych metod.

2.0.7 XOR i one-time pad

Operacja

X

OR

(

eXclusive OR

) jest zdeniowana jak nast

,

epuje:

0

X

OR

0 = 1

X

OR

1 = 0

1

X

OR

0 = 0

X

OR

1 = 1.

Szyfrowanie przy pomocy XOR:

zalo_zmy, _ze tekst jawny jest ci

,

agiem bit-

ow

a

1

:

:

:

a

n

, zas klucz ci

,

agiem bitow

k

1

:

:

:

k

n

. Wtedy kryptogramem jest ci

,

ag

c

1

:

:

:

c

n

, gdzie

c

i

:=

a

i

X

OR

k

i

dla

i

= 1

:

:

:

n

. Deszyfrowanie oparte jest na

trzech latwych do sprawdzenia rownosciach:

x

X

OR

x

= 0

x

X

OR

0 =

x

x

X

OR

(

y

X

OR

z

) = (

x

X

OR

y

)

X

OR

z

)

:

St

,

ad

c

i

X

OR

k

i

= (

a

i

X

OR

k

i

)

X

OR

k

i

=

a

i

X

OR

(

k

i

X

OR

k

i

) =

a

i

X

OR

0 =

a

i

:

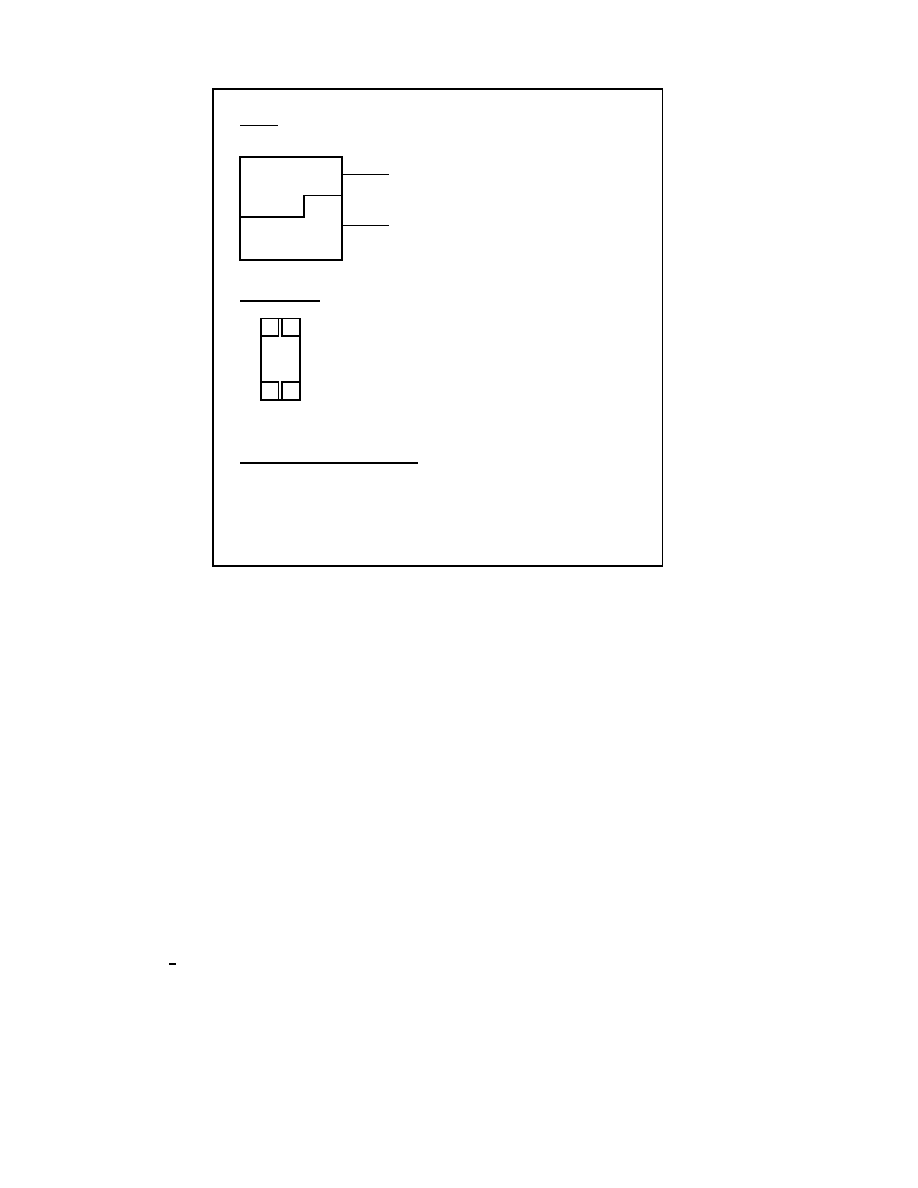
R

OZDZIA

L

2.

PODST

A

W

O

WE

TECHNIKI

SZYFR

O

W

ANIA

14

R T U V X

F G H K Q

N C Y B E

A M D I W

P O S Z L

(KR) = FV, (OW) = LM,

(AI) = MW, (WE) = AN

(SZ) = ZL

OH - rogi prostok

,

ata

OH

zast

,

epowany jest poprzez litery

znajduj

,

ace si

,

e w pozostalych rogach

prostok

,

ata

tj. przez SG

szyfrowanie:

szyfrowanie tekstu jawnego KR

j

OW

j

A I

j

WE

j

SZ

R T U V X

F G H K Q

N C Y B E

A M D I W

P O S Z L

pozostale litery

w kolejnosci alfabetycznej

haslo:

"POSZLA MALPA DO PIWNICY\

klucz: kwadrat 5

5 zawiera wszystkie litery z waj

,

atkiem J,

ktore w tekscie jawnym zast

,

epujemy poprzez I

Rysunek 2.1: System Playfair'a

Szyfrowanie przy pomocy

X

OR

ma wielorakie zastosowania. Jednym z nich jest

one-time pad

.

One-time pad

Jest to metoda szyfrowania, w ktorej u_zywany jest losowo wy-

brany klucz

k

1

:

:

:

k

n

. Samo szyfrowanie odbywa si

,

e przy pomocy

X

OR

. Istotne

jest, by do ka_zdego szyfrowania u_zywac

innego, wygenerowanego niezale_znie

klucza

. Zasadzie tej metoda zawdzi

,

ecza sw

,

a nazw

,

e.

Nast

,

epuj

,

ace wlasnosci s

,

a kluczowe dla metody one-time pad:

Kryptogram jest tak_ze ci

,

agiem losowym

n

bitow, tzn. ma ten sam rozklad

prawdopodobienstwa co ci

,

agi bitow wygenerowane przez rzucanie monet

,

a

(wyrzucenie reszki powoduje dopisanie 1, wyrzucenie orla { dopisanie 0).

Bez znajomosci klucza

_zadna

informacja dotycz

,

aca tekstu jawnego nie mo_ze

byc wydedukowana z kryptogramu (bez wzgl

,

edu na zastosowane moce obli-

czeniowe itp.). Wlasnosc ta bywa nazywana bezpieczenstwem doskonalym.

Dla udowodnienia pierwszej wlasnosci zauwa_zmy, _ze jesli

k

i

=

a

i

, to

c

i

= 0, oraz

_ze

c

i

= 1 w przeciwnym wypadku. Zatem prawdopodobienstwo, _ze

c

i

= 0 jest rowne

1

2

niezale_znie od wartosci

a

i

. Zatem

i

-ty bit kryptogramu jest losowy. Poniewa_z

bity

k

i

s

,

a losowane niezale_znie od siebie, wi

,

ec i bity kryptogramu s

,

a niezale_zne, tak

jak w przypadku ci

,

agow jakie otrzymujemy rzucaj

,

ac monet

,

a.

Niech

c

1

:

:

:

c

n

b

,

edzie dowolnym ci

,

agiem bitow. Dla udowodnienia drugiej wlas-

nosci zauwa_zmy, _ze dla ka_zdego tekstu jawnego

d

1

:

:

:

d

n

istnieje dokladnie jeden

R

OZDZIA

L

2.

PODST

A

W

O

WE

TECHNIKI

SZYFR

O

W

ANIA

15

klucz

k

1

:

:

:

k

n

taki, _ze poprzez szyfrowanie otrzymujemy kryptogram

c

1

:

:

:

c

n

. Istot-

nie, dla

i

= 1

:

:

:

n

spelniona musi byc rownosc

c

i

=

d

i

X

OR

k

i

, sk

,

ad

k

i

=

d

i

X

OR

c

i

.

Poniewa_z kryptogram

c

1

:

:

:

c

n

odpowiada ka_zdemu mo_zliwemu tekstowi jawnemu

z takim samym prawdopodobienstwem, nic nie mo_zna wywnioskowac o ksztalcie

tekstu jawnego bez znajomosci klucza.

Zastosowania one-time pad:

jedn

,

a dziedzin

,

a zastosowan jest szyfrowanie sto-

sunkowo krotkich, ale bardzo wa_znych informacji, jak rozkazy wojskowe o strate-

gicznym znaczeniu (na przyklad o wystrzeleniu rakiet j

,

adrowych). U_zywanie w

tej sytuacji szyfrow mo_zliwych do zlamania (chocby olbrzymim nakladem obliczen)

niesie niebezpieczenstwo, _ze faktycznie szyfry zostan

,

a zlamane.

Problemy ze stosowaniem one-time pad:

zasady u_zywania one-time pad

mowi

,

a, _ze klucz

musi byc zawczasu uzgodniony przez osoby komunikuj

,

ace si

,

e

musi byc wybrany naprawd

,

e losowo (co technicznie nie jest latwe,

patrz rozdzial 7)

musi byc przechowywany w bezpieczny sposob

musi byc co najmniej tak dlugi jak szyfrowany tekst.

Ka_zdy z powy_zszych warunkow stwarza niedogodnosci dla u_zytkownikow i zaw

,

e_za

pole praktycznych zastosowan one-time pad.

Niebezpieczenstwo u_zycia wielokrotnie tego samego klucza:

Zalo_zmy, _ze

szyfrujemy dlugi tekst

a

0

a

1

:

:

:

przy pomocy klucza dlugosci

n

. Poniewa_z brakuje

nam bitow klucza, u_zywamy nast

,

epuj

,

acej formuly:

c

i

=

a

i

X

OR

k

i

mod

n

:

Inaczej mowi

,

ac, bloki dlugosci

n

szyfrujemy ka_zdorazowo przy pomocy tego samego

klucza

k

0

:

:

:

k

n;

1

. Zauwa_zmy, _ze wtedy

c

j

X

OR

c

n

+

j

= (

a

j

X

OR

k

j

)

X

OR

(

a

n

+

j

X

OR

k

j

) =

a

j

X

OR

a

n

+

j

:

Zatem z latwosci

,

a mo_zna bez znajomosci klucza na podstawie samego kryptogramu

obliczyc

a

j

X

OR

a

n

+

j

!

Zlamanie tak skonstruowanego kryptogramu mo_ze si

,

e odbywac wedlug nast

,

e-

puj

,

acego scenariusza. Z du_zym prawdopodobienstwem ka_zdy tekst zawiera dlugie

ci

,

agi spacji. Zakladaj

,

ac, _ze

a

j

jest spacj

,

a mo_zna obliczyc

a

j

+

n

. Czyni

,

ac tak dla

ka_zdego

j

otrzymujemy pewien tekst. Szukamy w nim zrozumialych fragmentow.

W miejscach, gdzie

n

pozycji do tylu w tekscie jawnym wyst

,

epuje blok spacji

otrzymamy w ten sposob fragmenty tekstu jawnego. Jesli potramy je rozpoznac,

to dysponujemy bitami

a

i

,

c

i

dla odpowiednich

i

. St

,

ad wyliczamy

k

i

mod

n

=

a

i

X

OR

c

i

. Znalezione wartosci klucza u_zywamy nast

,

epnie dla calego kryptogramu w

celu odszyfrowania innych fragmentow tekstu jawnego. Prac

,

e mo_zna kontynuowac

probuj

,

ac zgadn

,

ac kolejne wartosci

k

i

na granicy odszyfrowanych regionow spraw-

dzaj

,

ac czy prowadzi to do sensownego uzupelnienia odgadni

,

etych fragmentow tekstu

jawnego.

2.0.8 S-boksy

S-boksy s

,

a nadzwyczaj istotnymi skladnikami algorytmu DES (

D

ata

E

ncryption

S

tandard) najwa_zniejszego w praktyce algorytmu szyfruj

,

acego w momencie powsta-

wania tej ksi

,

a_zki. Ka_zdy S-boks jest zdeniowany poprzez macierz rozmiaru 4

16

zawieraj

,

ac

,

a liczby z przedzialu od 0 do 15 (patrz rys. 2.2).

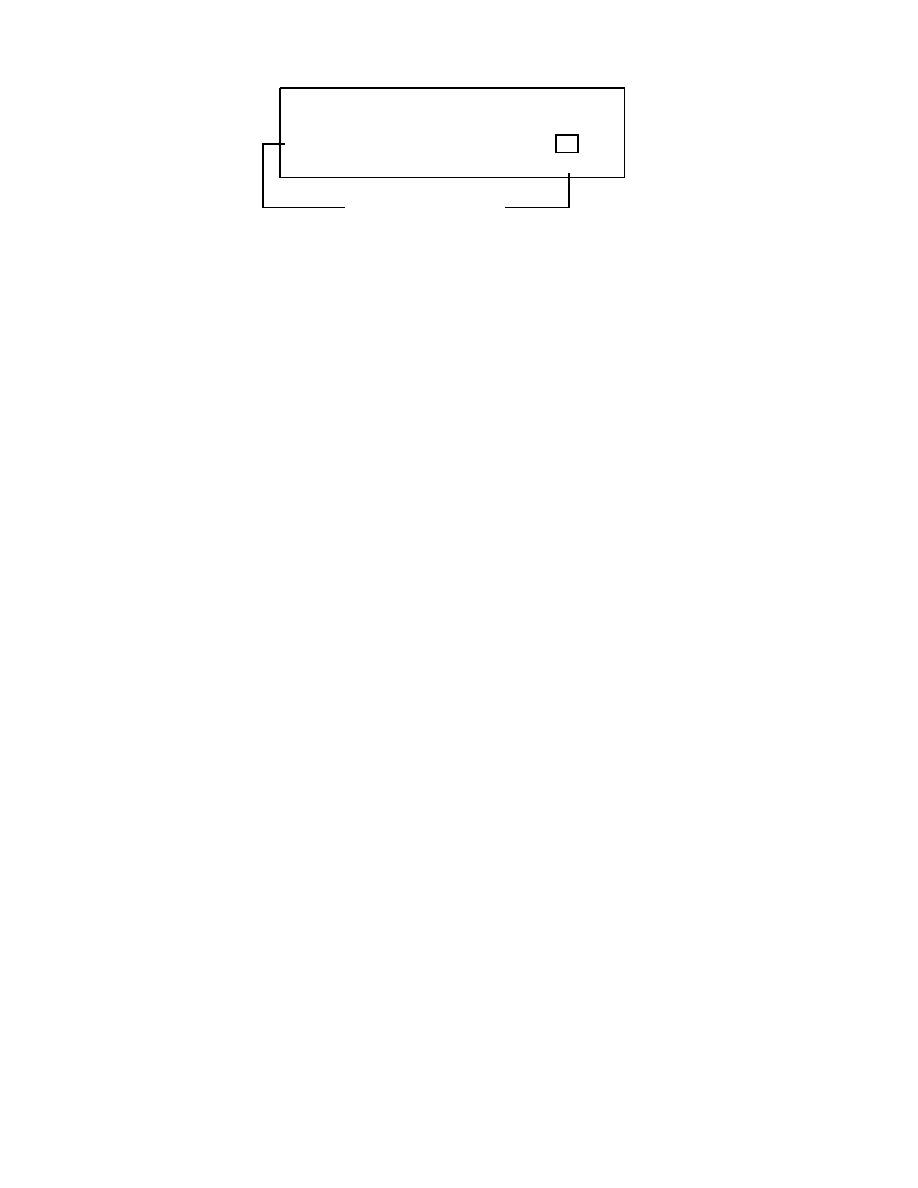
R

OZDZIA

L

2.

PODST

A

W

O

WE

TECHNIKI

SZYFR

O

W

ANIA

16

15 12 8 2 4 9 1 7 5 11 3 14 10 0 6 13

4 1 14 8 13 6 2 11 15 12 9 7 9 10 5 0

0 15 7 4 14 2 13 1 10 6 12 11 9 5 3 8

14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7

argument= 111010, wynik= 10

10

= 1010

2

wiersz 2, kolumna 13

-

6

Rysunek 2.2: Szyfrowanie przy pomocy S-boksow (rysunek przedstawia S-boks o

nazwie S1)

Sposob dzialania S-boksow.

S-boks deniuje funkcj

,

e, ktorej argumentami s

,

a

ci

,

agi zlo_zone z 6 bitow, a wartosciami ci

,

agi zlo_zone z 4 bitow. Obliczenie wartosci

dla argumentu

x

ma nast

,

epuj

,

acy przebieg:

pierwszy i ostatni bit argumentu

x

tworz

,

a liczb

,

e w systemie dwojkowym wy-

znaczaj

,

ac

,

a numer wiersza (wiersze numerujemy od 0 do 3),

pozostale 4 bity

x

wyznaczaj

,

a numer kolumny (kolumny numerujemy od 0 do

15),

na przeci

,

eciu wyznaczonych kolumny i wiersza znajduje si

,

e pojedynczy ele-

ment, liczba ta jest szukan

,

a wartosci

,

a funkcji.

Wybor liczb znajduj

,

acych si

,

e w S-boksie ma fundamentalne znaczenie dla jakosci

szyfrowania. Wybor S-boksow stosowanych w praktyce nie byl do konca procesem

jawnym, znanych jest jednak kilka regul, ktore wzi

,

eto pod uwag

,

e. Nie jest znana

_zadna prosta i elegancka analiza matematyczna, ktora prowadzilaby do wyboru

takich a nie innych S-boksow. W praktyce stosowane s

,

a S-boksy o nazwach S1, S2,

:

:

:

, S8.

Efekt lawinowy:

Jedn

,

a z podstawowych zasad szyfrowania jest to, by zmiana

pojedynczego bitu w tekscie jawnym powodowala zmian

,

e wielu bitow w kryptogra-

mie. W idealnej sytuacji powinno to powodowac zmian

,

e mniej wi

,

ecej tylu bitow,

ile bysmy zmienili w wypadku ich ustawienia wedlug rzutow monet

,

a. Tym samym

podobne teksty jawne nie maj

,

a podobnych kryptogramow! Wlasnosc ta utrudnia

w znacz

,

acy sposob kryptoanaliz

,

e. W tej sytuacji mowimy o

efekcie lawinowym

,

dla podkreslenia, _ze zmiana pojedynczego bitu w tekscie jawnym powoduje lawin

,

e

zmian w kryptogramie.

Przy pomocy S-boksow mo_za zrealizowac efekt lawinowy. O ile S-boks stosujemy

do bitow (

x

y

z

u

v

w

) to zmiana

x

lub

w

powoduje zmian

,

e numeru wiersza. Rzut

oka na S-boks z rys. 2.2 pozwala stwierdzic, _ze wiersze nie s

,

a do siebie podobne.

Dlatego nie ma _zadnego powodu, by po zmianie

x

lub

w

wynik przypominal w

jakikolwiek sposob stary wynik. Podobne zjawisko odnosi si

,

e do kolumn, gdy_z

kolumny S-boksu rownie_z nie s

,

a podobne.

Gdy S-boksy s

,

a u_zywane wielokrotnie, wtedy efekt lawinowy ulega spot

,

egowaniu

i sposob w jaki zmiana pojedynczego bitu wplywa na zmian

,

e koncowego wyniku jest

coraz bardziej skomplikowany.

Kryteria wyboru S-boksow:

Poni_zej omawiamy niektore wa_zne wlasnosci, ja-

kie powinny byc spelnione przez dobre S-boksy. Ka_zda z nich zostala sformulowana

na zasadzie

\jesli wlasnosc nie jest spelniona, to kryptoanaliza mo_ze byc ulatwiona\

.

R

OZDZIA

L

2.

PODST

A

W

O

WE

TECHNIKI

SZYFR

O

W

ANIA

17

Ka_zdy wiersz S-boksu zawiera wszystkie liczby calkowite od

0

do

15

.

Wlasnosc ta zapewnia, _ze sama znajomosc wiersza nie daje _zadnej informacji

o wartosci koncowej.

Funkcja obliczana przez S-boks nie jest funkcj

,

a aniczn

,

a,

tzn. _zaden bit wyniku nie da si

,

e przedstawic jako

c

0

+

P

6

i

=1

c

i

x

i

, gdzie

x

i

oznacza

i

-ty bit argumentu, zas operacje arytmetyczne wykonywane s

,

a

modulo 2. Gdyby bity wyniku byly wyra_zalne za pomoc

,

a funkcji anicznych,

to kryptoanaliza bylaby powa_znie ulatwiona. Istotnie, po pierwsze skladanie

S-boksow nie mialoby sensu { dalej poruszalibysmy si

,

e w obr

,

ebie funkcji

anicznych, bo zlo_zenie funkcji anicznych jest funkcj

,

a aniczn

,

a. Po drugie,

kryptoanaliza ograniczalaby si

,

e do rozwi

,

azywania ukladow rownan liniowych,

co nie jest trudnym zadaniem.

Zmiana jednego bitu argumentu zmienia co najmniej dwa bity wyniku.

Wlasnosc ta ma zapewnic efekt lawinowy w przypadku wielokrotnego zasto-

sowania S-boksow.

Dla ka_zdego argumentu

x

wartosci obliczane przez S-boks dla argumentow

x

oraz

x

X

OR

001100

ro_zni

,

a si

,

e co najmniej na dwoch pozycjach.

Dla ka_zdego argumentu

x

oraz

e

f

2

f

0

1

g

wartosci obliczane przez S-boks dla

x

oraz

x

X

OR

11

ef

00

ro_zni

,

a si

,

e co najmniej na dwoch pozycjach.

Jesli ustalimy wartosc jednego bitu argumentu oraz jedn

,

a pozycj

,

e wyniku, to dla

okolo polowy ustawien pozostalych bitow argumentu na wybranej pozycji wyniku

otrzymamy

0

.

Wlasnoscta gwarantuje, _ze nawet gdy znamy wartosc jednego bitu argumentu,

to na dowolnej pozycji wyniku otrzymujemy 1 w przybli_zeniu z takimi cz

,

esto-

sciami jak w wypadku losowania bitow przy pomocy rzutow monet

,

a.

Bardzo wskazany jest rownie_z taki wybor wartosci w tablicy S-boksu, by jak najbar-

dziej utrudnione byly znane techniki kryptoanalizy, takie jak kryptoanaliza ro_zni-

cowa i liniowa (patrz rozdz. 12).

Rozdzia

l

3

Algorytmy symetryczne

3.1

DES

{

Data

Encryption

Standard

Zanim przejdziemy do technicznego opisu algorytmu DES, sformulujmy kilka ogol-

nych uwag na jego temat:

DES jest symetrycznym algorytmem szyfruj

,

acym, ten sam klucz jest u_zywany

do szyfrowania i deszyfrowania.
Szczegolowy opis algorytmu DES zostal celowo opublikowany. Chodzilo o

przekonanie potencjalnych u_zytkownikow, _ze bezpieczenstwo metody nie tkwi

w tajnosci jej budowy, ale w konstrukcji odpornej na kryptoanaliz

,

e. Bowiem

ka_zda metoda, ktorej szczegoly nie zostaly ujawnione, mo_ze zawierac w sobie

tzw.

tylne drzwi

, czyli miejsce w algorytmie, ktore mo_ze byc wykorzystane

przez przeciwnika znaj

,

acego szczegoly algorytmu na zdobycie informacji nie-

dost

,

epnych w zwyklym trybie (na przyklad dotycz

,

ace u_zywanych kluczy).

DES jest znacz

,

aco szybszy, gdy jest zaimplementowany jako hardware a nie

jako software. Algorytm zostal celowo tak zaprojektowany, aby zniecz

,

ecic do

u_zywania implementacji software'owych uwa_zanych za bardziej podatne na

atak (latwiej jest si

,

e wlamac do systemu i niepostrze_zenie wymienic software,

ni_z dokonac zycznego wlamania by wymienic hardware). Uklady realizuj

,

ace

DES s

,

a bardzo szybkie (na przyklad 1 GB/sek.) dla porownania dobry soft-

ware na PC mo_ze miec pr

,

edkosc tysi

,

ace razy ni_zsz

,

a.

DES szyfruje bloki zlo_zone z 64 bitow, co daje 8 liter ASCII, ka_zda zao-

patrzona w bit parzystosci. Klucze skladaj

,

a si

,

e rownie_z z 64 bitow, przy

czym 8 bitow jest bitami parzystosci. Tak wi

,

ec w istocie w trakcie wyboru

klucza mo_zna okreslic jedynie 56 bitow, reszta jest generowana automatycznie.

Post

,

ep w dziedzinie technologii i zwi

,

azane z tym obni_zenie kosztow kry-

ptoanalizy wyzwolily dyskusje, czy dlugosc kluczy DES-a nie jest za mala.

Koszty znalezienia klucza na podstawie dostatecznej ilosci par tekst jawny{

kryptogram zaszyfrowany tym kluczem bywaj

,

a szacowane jedynie na miliony

dolarow USA.
DES zostal w USA uznany za standard dla celow niemilitarnych. Zostal

wst

,

epnie zaprojektowany w osrodku badawczym IBM w Yorktown Heights,

a nast

,

epnie zmodykowany przez NSA (National Security Agency), rz

,

adowy

organ w USA zajmuj

,

acy si

,

e problemami bezpieczenstwa narodowego. Wywo-

lalo to wiele podejrzen, _ze NSA zna

tylne drzwi

umo_zliwiaj

,

acejlamanieszyfrow

generowanych przy pomocy DES-a. Poniewa_z DES stal si

,

e w mi

,

edzyczasie

18

R

OZDZIA

L

3.

ALGOR

YTMY

SYMETR

YCZNE

19

standardem w zastosowaniach komercyjnych na calym swiecie, dawaloby to

USA olbrzymie korzyscie w zakresie militarnym i gospodarczym.
W odniesieniu do DES-a nie zostaly opublikowane _zadne prace daj

,

ace tej

metodzie solidne podstawy matematyczne. Jednak_ze ponad 20 lat badan

akademickich potwierdzaj

,

a, _ze konstrukcja DES-a jest bardzo wyranowana.

Jakkolwiek w zakresie kryptoanalizy DES-a osi

,

agni

,

eto du_ze post

,

epy, nie za-

grozily one znacz

,

aco stosowaniu tej metody w praktyce. Z drugiej strony

uproszczone wersje DES-a mog

,

a byc zlamane znacz

,

aco mniejszym kosztem.

Interesuj

,

ace jest, _ze proby ulepszen DES-a dotychczas nie doprowadzily do

znacz

,

acych post

,

epow i DES nie doczekal si

,

e nowej, lepszej wersji.

3.1.1 Szyfrowanie DES-em

Szyfrowanie i deszyfrowanie przy pomocy DES-a sklada si

,

e z 16

rund

. W trakcie

ka_zdej rundy dokonywane s

,

a te same obliczenia, ale na wynikach obliczen z poprzed-

niej rundy i specjalnym podkluczu generowanym z 64-bitowego klucza. Dodatkowo,

przed pierwsz

,

a rund

,

a i po ostatniej rundzie bity s

,

a permutowane w ustalony sposob.

Generowanie podkluczy

W celu uzyskania podkluczy u_zywanych podczas poszczegolnych rund usuwamy

najpierw 8 bitow parzystosci zawartych w kluczu. Nast

,

epnie z pozostalych 56 bitow

tworzonych jest 16 podkluczy, ka_zdy skladaj

,

acy si

,

e z 48 bitow. Tak utworzony

i

-

ty klucz oznaczac b

,

edziemy przez

K

i

b

,

edzie on u_zywany w trakcie

i

-tej rundy.

Ka_zdy podklucz sklada si

,

e ze z gory okreslonych bitow orginalnego klucza { dla

ka_zdego podklucza s

,

a to inne bity i ustawione w innej kolejnosci. Sposob tworzenia

podkluczy jest jawny i zostal opublikowany wraz z opisem DES-a. Maj

,

ac na uwadze

koszty hardware'u wybrano taki sposob wybierania bitow podkluczy, jaki latwo

daj

,

e si

,

e zrealizowac hardware'owo. Interesuj

,

ace jest, i_z znane metody kryptoana-

lizy DES-a w najbardziej istotnym momencie nie wykorzystuj

,

a zale_znosci mi

,

edzy

wartosciami bitow podkluczy.

Permutacja pocz

,

atkowa i koncowa

Na pocz

,

atku bity tekstu jawnego s

,

a permutowane. Nie ma to _zadnego celu kry-

ptogracznego. Zauwa_zmy jednak, _ze permutacja ta mo_ze byc z latwosci

,

a zaim-

plementowana hardware'owo. Po prostu poszczegolne bity doprowadzone s

,

a za

pomoc

,

a drutow (dokladniej pol

,

aczen w ukladzie VLSI) na odpowiednie miejsca.

Czas obliczen permutacji odpowiada tu jedynie czasowi w jakim informacje dotr

,

a

po drutach na miejsca przeznaczenia. W przeciwienstwie do tego implementacja

software'owa wymaga dlugich obliczen: ka_zdy bit oddzielnie musi byc przekopio-

wany na miejsce przeznaczenia.

Pod koniec szyfrowania uzyskane bity s

,

a permutowane permutacj

,

a odwrotn

,

a do

pocz

,

atkowej. Permutacja ta jest nazywana

permutacj

,

a koncow

,

a

.

Runda DES-a

Dane wejsciowe rundy

i

+1 skladaj

,

a si

,

e z dwu ci

,

agow 32-bitowych:

L

i

(pierwszych

32 bitow b

,

ed

,

acych wynikiem rundy

i

) oraz

R

i

(pozostale 32 bity uzyskane w rundzie

i

). Zachodz

,

a nast

,

epuj

,

ace zwi

,

azki:

L

i+1

=

R

i

R

i+1

=

L

i

X

OR

f

(

R

i

K

i+1

)

(3.1)

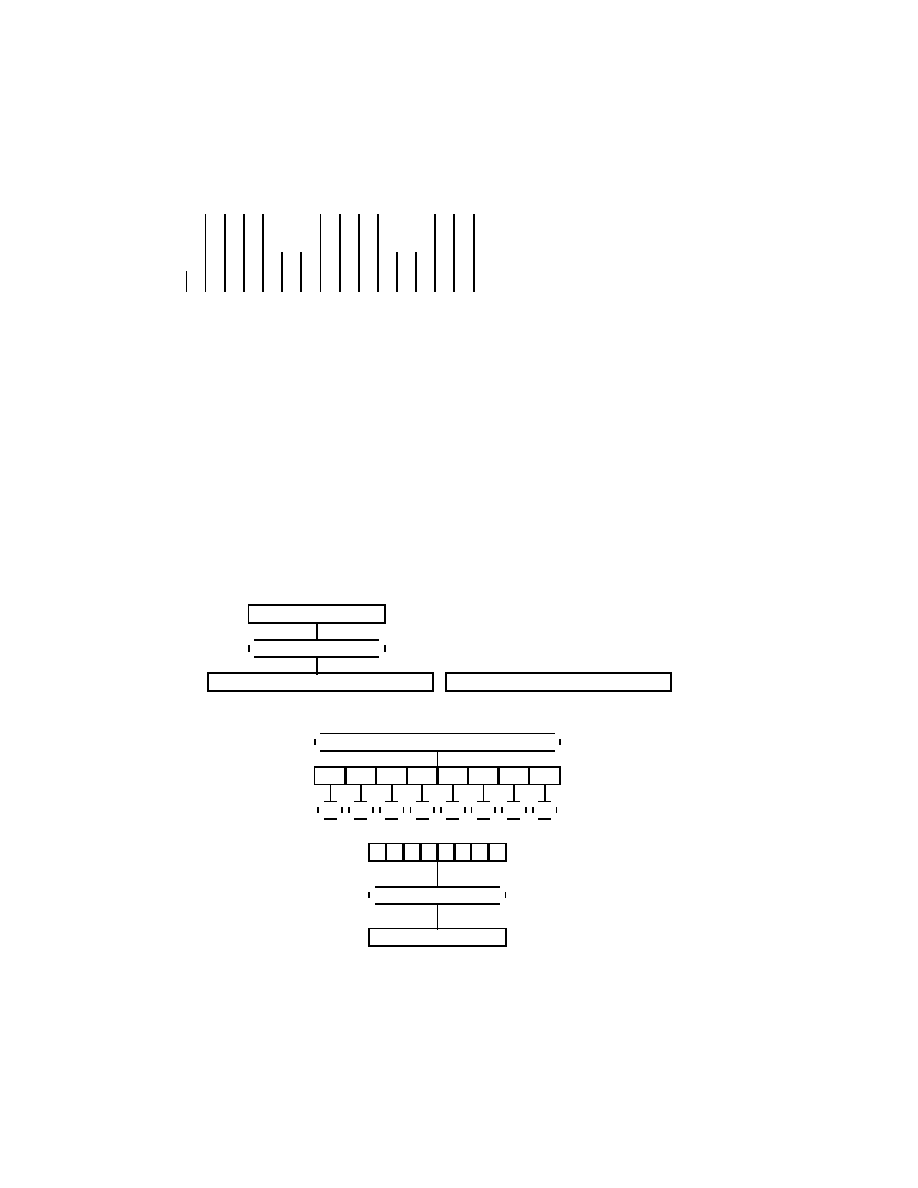
R

OZDZIA

L

3.

ALGOR

YTMY

SYMETR

YCZNE

20

gdzie

f

jest funkcj

,

a, ktora posiada zasadnicze znaczenie dla szyfrowania. Obliczenie

wartosci funkcji

f

jest przedstawione na rys. 3.2 i dokonuje si

,

e w nast

,

epuj

,

acy sposob:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

numery bitow na wejsciu

numery bitow na wyjsciu

...

pol

,

aczenia realizuj

,

ace

permutacj

,

e z

rozszerzeniem

@

@

@

@

@

@

;

;

;

;

;

;

(

(

(

(

(

(

(

(

(

(

(

(

(

(

(

(

(

(

(

(

(

(

(

(

32

1 2 3 4

5 6 7 8

9 10 11

Rysunek 3.1: Permutacja z rozszerzeniem

1. Poprzez tzw.

permutacj

,

e z rozszerzeniem

otrzymuje si

,

e ci

,

ag zlo_zony z 48

bitow z 32 bitow

R

i

(32 bity

R

i

s

,

a kopiowane na 48 pozycji, niektore z nich

dwukrotnie, patrz rys. 3.1).

2. Na otrzymanych 48 bitach jest dokonywana operacja XOR z odpowiadaj

,

acymi

im bitami podklucza

K

i+1

.

3. Otrzymane 48 bitow dzielone jest na 8 grup po 6 bitow. Ka_zda grupa pod-

dawana jest dzialaniu S-boksu. (S-Boks u_zywany przez

i

-t

,

a grup

,

e nazywany

jest Si.)

4. Otrzymane 32 bity s

,

a na koniec permutowane.

f

(

R

i

K

i+1

)

?

permutacja

?

S

1

S

2

S

3

S

4

S

5

S

6

S

7

S

8

H

H

H

H

j

Q

Q

Q

s

S

S

w

B

B

N

+

/

?

?

?

?

?

?

?

?

XOR

?

K

i+1

H

H

H

H

H

H

j

permut. z rozszerz.

?

R

i

?

Rysunek 3.2: Funkcja

f

DES-a

R

OZDZIA

L

3.

ALGOR

YTMY

SYMETR

YCZNE

21

3.1.2 Deszyfrowanie DES-em

Nale_zaloby oczekiwac, _ze aby deszyfrowac kryptogram nale_zy cale obliczenie skla-

daj

,

ace si

,

e na szyfrowanie odtworzyc od konca do pocz

,

atku. Ale dla S-boksow nie

jest to mo_zliwe! Jednemu wynikowi otrzymanemu przez S-boks odpowiada wiele

mo_zliwych argumentow. Pomaga tu jednak nast

,

epuj

,

acy wybieg: z rownosci (3.1)

wynika, i_z:

R

i;1

=

L

i

L

i;1

=

R

i

X

OR

f

(

R

i;1

K

i

) =

R

i

X

OR

f

(

L

i

K

i

)

Jesli wi

,

ec znamy

L

i

,

R

i

oraz podklucz

K

i

, to na podstawie powy_zszych rownosci

mo_zemy obliczyc

L

i;1

i

R

i;1

. Tak wi

,

ec nie musimywcale obliczacfunkcji odwrotnej

do funkcji obliczanych przez S-boksy.

Latwo widac, _ze podczas deszyfrowania dokonywane s

,

a te same operacje co

podczas szyfrowania (tylko podklucze wyst

,

epuj

,

a w odwrotnej kolejnosci). Z tego

wzgl

,

edu ten sam hardware mo_ze byc u_zyty do szyfrowania i deszyfrowania.

Zauwa_zylismy, _ze wzory (3.1) stwarzaj

,

a dogodne mo_zliwoscideszyfrowania. Inte-

resuj

,

ace jest, _ze szyfrowanie wedlug schematu danego tymi wzorami zdaje si

,

e miec

solidne podstawy teoretyczne (por. 4]). Jest to jeden z argumentow przemawiaj

,

a-

cych na korzysc DES-a.

3.2

T

rzykrotn

y

DES

Wielkosc klucza u_zywanego przez algorytm DES wydaje si

,

e byc niewystarczaj

,

aca.

Z tego wzgl

,

edu podj

,

eto szereg prob modykacji DES-a, tak aby w istotny sposob

wykorzystywac dlu_zsze klucze. Wiele tych prob skonczylo si

,

e niepowodzeniem.

Okazywalo si

,

e bowiem, i_z koszty zwi

,

azane ze zlamaniem kryptogramow utworzo-

nych przy pomocy tych metod s

,

a porownywalne z kosztami zlamania kryptogramow

utworzonych przy pomocy DES-a (przynajmniej przy u_zyciu znanych metod la-

mania szyfrow). Bardziej skomplikowana budowa algorytmu i dlu_zsze klucze nie

oferowaly wi

,

ec wi

,

ekszego bezpieczenstwa.

Metod

,

a niekiedy stosowan

,

a w praktyce jest

trzykrotny DES

. U_zywamy w nim

dwoch kluczy

S

1

,

S

2

, ka_zdy b

,

ed

,

acy zwyklym kluczem DES-a. Szyfrowanie tekstu

jawnego ma nast

,

epuj

,

acy przebieg:

1. tekst jawny szyfrowany jest kluczem

S

1

,

2. wynik kroku 1 jest deszyfrowany kluczem

S

2

,

3. wynik kroku 2 jest powtornie szyfrowany kluczem

S

1

.

Aby z kryptogramu otrzymac z powrotem tekst jawny wystarczy oczywiscie wyko-

nac nast

,

epuj

,

ace kroki:

1. kryptogram deszyfrowany jest kluczem

S

1

,

2. wynik kroku 1 jest szyfrowany kluczem

S

2

,

3. wynik kroku 2 jest powtornie deszyfrowany kluczem

S

1

.

3.3

Szyfro

w

anie

tekst

ow

do

w

olnej

d

lugo

sci

DES szyfruje tylko bardzo krotkie teksty (8 liter ASCII!). Aby DES uczynic

u_zytecznym trzeba znalezc sposob na szyfrowanie tekstow dowolnej dlugosci. Po-

ni_zej przedstawiamy trzy takie ogolne metody rozszerzaj

,

ace szyfrowanie tekstow

ustalonej dlugosci, powiedzmy

k

, na teksty dowolnej dlugosci.

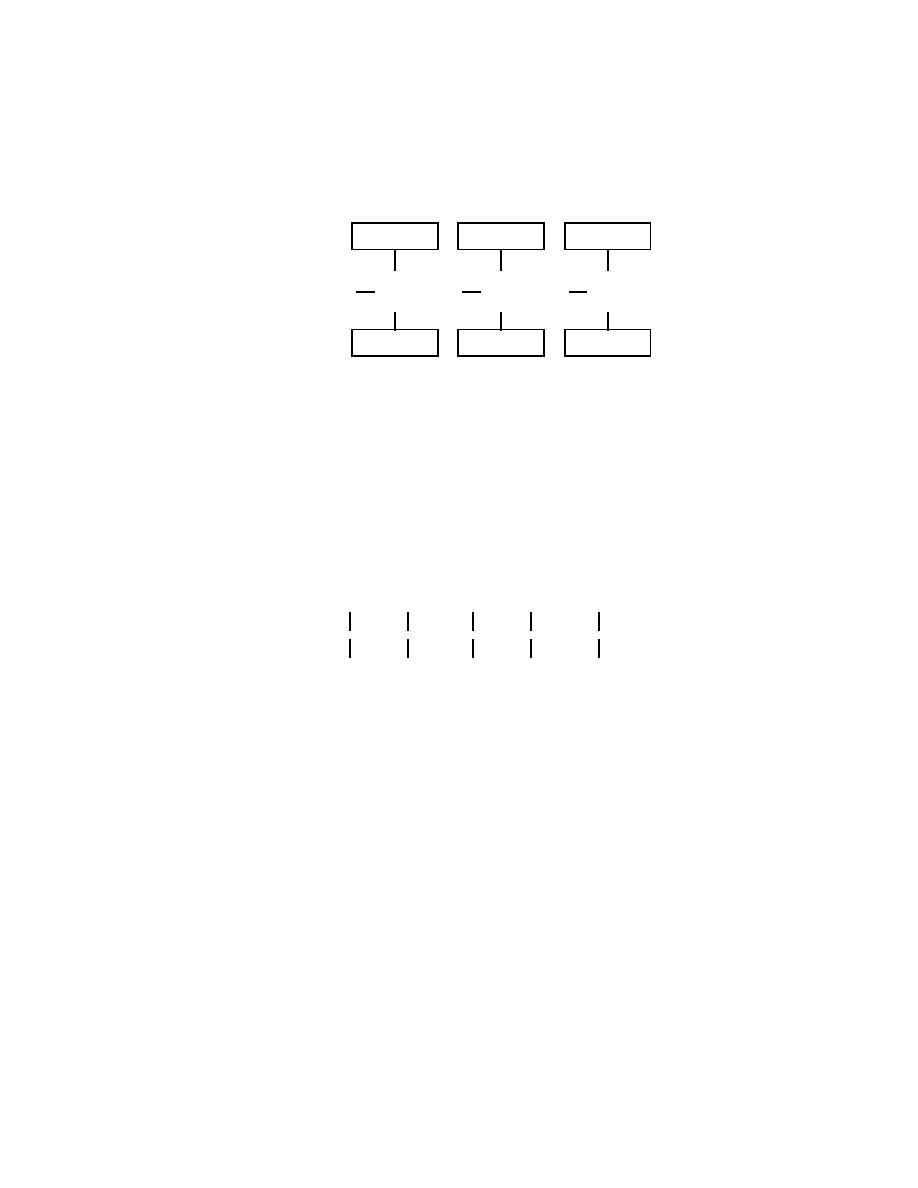
R

OZDZIA

L

3.

ALGOR

YTMY

SYMETR

YCZNE

22

3.3.1 Elektroniczna ksi

,

a_zka kodowa

Elektroniczna ksi

,

a_zka kodowa

(inaczej

ECB

, czyli

Electronic Codebook

) funkcjo-

nuje jak nast

,

epuje (patrz rys. 3.3): tekst jawny dzielony jest na bloki dlugosci

k

.

Ka_zdy z tych blokow jest oddzielnie szyfrowany przy pomocy tego samego klucza.

kryptogram

tekst jawny

blok 1

blok 2

blok 3

DES

DES

DES

-

-

-

K

K

K

?

?

?

?

?

?

Rysunek 3.3: Schemat trybu ECB

Tryb ECB ma t

,

a zalet

,

e, _ze uszkodzenie lub utrata pojedynczych blokow nie

ma wplywu na mo_zliwosc deszyfrowania pozostalych cz

,

esci kryptogramu. Z drugiej

strony mo_zliwy jest atak nie wymagaj

,

acy zlamania szyfru. Przesledzimy to na

nast

,

epuj

,

acym przykladzie:

Przyklad ataku na ECB:

Zalo_zmy, _ze komunikacja pomi

,

edzy dwoma bankami

odbywa si

,

e w trybie ECB. W ten sposob szyfrowane s

,

a przelewy mi

,

edzy kontami

obu bankow. Zalo_zmy, _ze specykacja kont, na jakie nale_zy dokonac przelewow ma

nast

,

epuj

,

ac

,

a postac:

przelew =

kon-

to

odbior- ca

wartosc przelewu

kryptogram = blok 1 blok 2 blok 3 blok 4 blok 5 blok 6

Przest

,

epca Mallet, ktory jest w stanie modykowac tresc kryptogramow naply-

waj

,

acych do banku, mo_ze przeprowadzic nast

,

epuj

,

acy atak:

1. Mallet dokonuje 17 przelewow na swe konto, zawsze t

,

e sam

,

a kwot

,

e pieni

,

edzy.

Nast

,

epnie identykuje w przesylanych kryptogramach taki kryptogram konta,

na ktory dokonano dokladnie 17 przelewow i w dodatku na t

,

e sam

,

a kwot

,

e.

Mallet mo_ze w tym momencie zalo_zyc, _ze chodzi tu o jego konto. W ten sposob

poznaje kryptogram numeru swego konta mimo, i_z nie zna klucza u_zytego do

szyfrowania.

2. Mallet zamienia w pewnej ilosci przeplywaj

,

acych kryptogramow kod numeru

konta, wstawiaj

,

ac na to miejsce kryptogram numeru swego konta. Dzi

,

eki temu

bank dopisuje do konta Malleta kwoty przeznaczone pierwotnie dla innych

osob.

3. Mallet sprawdza stan swego konta i dokonuje przelewu na swe konto w kraju,

z ktorym nie podpisano umowy o ekstradycji. Nast

,

epnie udaje si

,

e sladem

pieni

,

edzy zanim ktos si

,

e zorientuje.

Aby unikn

,

ac sytuacji opisanej powy_zej trzeba u_zyc bezpieczniejszego trybu szy-

frowania. Dwa takie tryby opisujemy poni_zej.

Jako ciekawostk

,

e dodajmy, _ze mimo wskazanych powy_zej zagro_zen instytucje

nansowe cz

,

esto lekkomyslnie u_zywaj

,

a trybu ECB do transmisji wa_znych danych.

R

OZDZIA

L

3.

ALGOR

YTMY

SYMETR

YCZNE

23

3.3.2 Cipher Block Chaining

Cipher Block Chaining

(CBC) jest metod

,

a, dzi

,

eki ktorej ten sam blok tekstu

jawnego jest szyfrowany w ro_znych miejscach w ro_zny sposob. Osi

,

agane jest to

w nast

,

epuj

,

acy sposob. Rozwa_zmy algorytm szyfruj

,

acy bloki dlugosci

k

. Niech

E

K

(

X

) oznacza kryptogram uzyskany z tekstu jawnego

X

przy pomocy klucza

K

. Jesli tekst jawny sklada si

,

e z blokow

P

1

P

2

P

3

:

:

:

dlugosci

k

, to kryptogram

uzyskany przy pomocy klucza

K

sklada si

,

e blokow

C

1

C

2

C

3

:

:

:

(rownie_z dlugosci

k

) zdeniowanych nast

,

epuj

,

aco:

C

1

=

E

K

(

P

1

X

OR

I

)

C

i

=

E

K

(

P

i

X

OR

C

i;1

)

:

Ci

,

ag

I

wyst

,

epuj

,

acy w powy_zszym wzorze jest generowany losowo i przesylany w

sposob niezaszyfrowany. Zauwa_zmy, _ze kryptogramy poszczegolnych blokow s

,

a ze

sob

,

a powi

,

azane: dla otrzymania

C

i

wykorzystujemy

C

i;1

, a nie tylko

P

i

. Poniewa_z

C

i

zale_zy od

C

i;1

, a

C

i+1

od

C

i

, wi

,

ec posrednio

C

i+1

zale_zy od

C

i;1

. Zale_znosci

tego typu przenosz

,

a si

,

e dalej i ostatecznie ka_zdy blok

C

j

jest zale_zny od wszystkich

blokow

C

1

:

:

:

C

j

;1

, a co za tym idzie rownie_z od

I

P

1

P

2

:

:

:

P

j

;1

.

Deszyfrowywanie tak uzyskanych kryptogramow jest stosunkowo proste (poni_zej

D

oznacza funkcj

,

e deszyfruj

,

ac

,

a dla blokow dlugosci

k

):

P

1

=

D

K

(

C

1

)

X

OR

I

P

i

=

D

K

(

C

i

)

X

OR

C

i;1

:

(3.2)

Odnotujmy kilka wlasnosci szyfrowania w trybie CBC:

Zaleta: takie same bloki z reguly s

,

a reprezentowane z reguly poprzez bloki

ro_znej postaci w kryptogramie. Co wi

,

ecej, ten sam tekst jawny jest szyfrowany

w inny sposob, o ile wybierzemy inny ci

,

ag pocz

,

atkowy

I

.

Wada: nie mo_zna _zadnego bloku

C

i

usun

,

ac z kryptogramu. Stwarza to

klopoty, o ile pragn

,

elibysmy przy pomocy CBC szyfrowac zawartosc baz da-

nych. Podobne problemy napotykamyprzy probie wprowadzenia dodatkowego

bloku w srodku tekstu jawnego: od tego miejsca caly kryptogram musi byc

utworzony na nowo.
Wada: podzial na bloki musi byc odporny na zaklocenia (dodatkowy bit lub

utrata pojedynczego bitu prowadz

,

a do desynchronizacji szyfrowania i deszy-

frowania).
Zaleta: przeklamania wewn

,

atrz jednego bloku (bez zmiany ilosci bitow) pro-

wadz

,

a do przeklaman po deszyfrowaniu, ale jedynie w bloku, w ktorym na-

st

,

apilo przeklamanie i bloku nast

,

epuj

,

acym po nim. Wlasnosc ta wynika

bezposrednio z wzoru (3.2).

3.3.3 Cypher Feedback

CFB

, czyli

cypher feedback

, jest drugim bezpiecznym trybem szyfrowania dlugich

tekstow. W odro_znieniu do CBC szyfrowane s

,

a nie cale bloki, ale fragmenty zlo_zone

z 8 bitow, czyli w praktyce 1 litera. Tryb ten mo_ze byc u_zyty na przyklad dla

zabezpieczenia komunikacji pomi

,

edzy klawiatur

,

a i serwerem. Oczywiste jest, _ze

w tej sytuacji niezb

,

edne jest natychmiastowe przesylanie pojedynczych znakow

bez czekania na zgromadzenie bloku 8 znakow, jak to mialo miejsce w przypadku

korzystania z trybu CBC. Mo_zliwe jest rownie_z przesylanie t

,

a metod

,

a na przyklad

pojedynczych bitow.

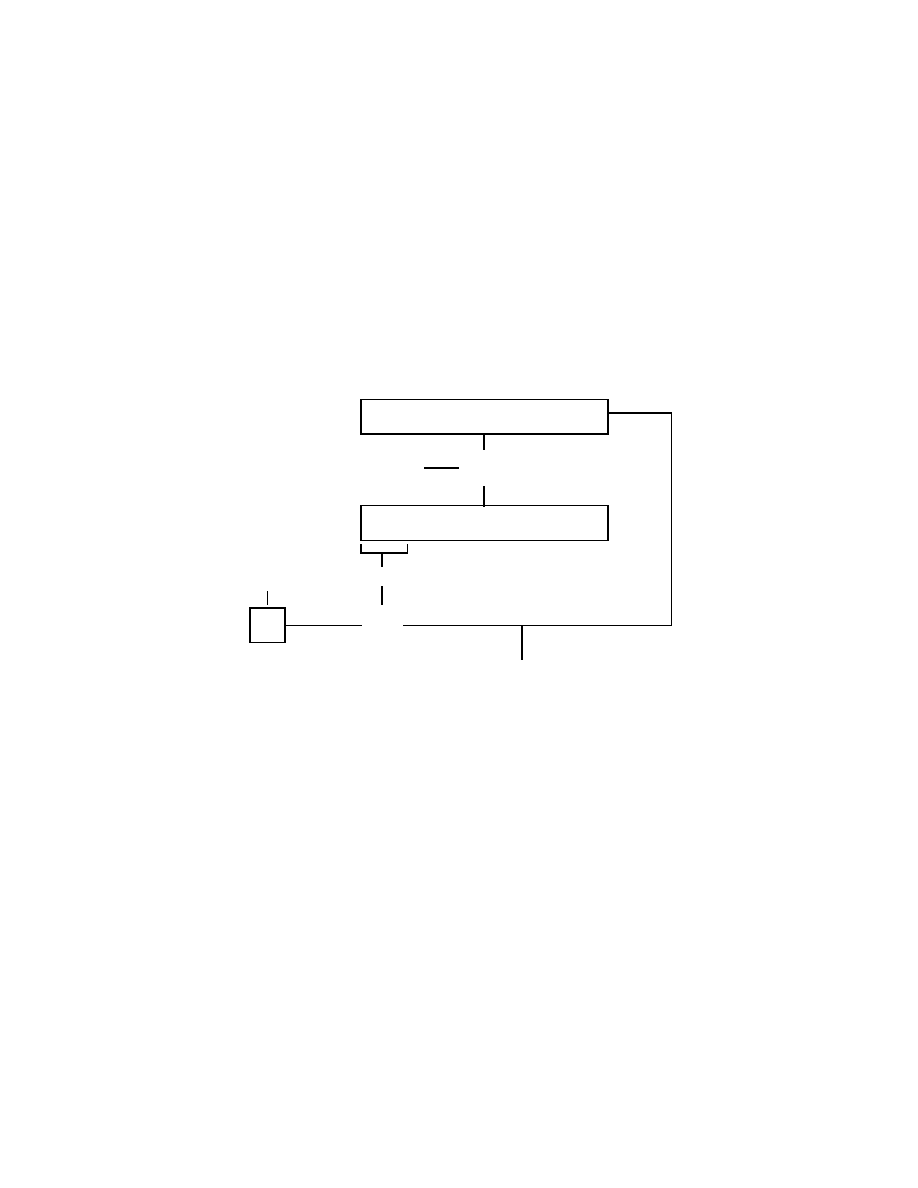
R

OZDZIA

L

3.

ALGOR

YTMY

SYMETR

YCZNE

24

Schemat dzialania CFB przedstawiony jest na rys. 3.4, przy czym wykorzystano

DES jako metod

,

e szyfrowania pojedynczych blokow. Jednym z zasadniczych sklad-

nikow CFB jest rejestr przesuwaj

,

acy. Na pocz

,

atku zawiera on losowo wygenerowany

ci

,

ag, ktory jest przesylany w niezaszyfrowanej postaci. W trakcie ka_zdego taktu

pracy CFB przy u_zyciu klucza

K

wykonywane s

,

a nast

,

epuj

,

ace operacje:

1. Zawartosc rejestru przesuwaj

,

acego jest szyfrowana przy pomocy klucza

K

.

2. Z wytworzonego kryptogramu pobieranych jest pierwszych 8 bitow, bity te

slu_z

,

a do operacji

X

OR

z 8 bitami koduj

,

acymi nast

,

epn

,

a liter

,

e

P

podawan

,

a

na wejsciu. W wyniku otrzymujemy ci

,

ag osmiu bitow

Z

.

3. Ci

,

ag

Z

tworzy kolejnych 8 bitow wyniku. Ponadto w rejestrze przesuwaj

,

acym

wykonujemy przesuni

,

ecie o 8 pozycji. Jest to przesuni

,

ecie niecykliczne { 8

bitow z lewej strony ulega usuni

,

eciu. Z kolei na osmiu zwolnionych pozycjach

zapisywany jest ci

,

ag

Z

.

P

?

nast

,

epna litera

-

X

OR

-

?

wyjscie

?

8 bitow

Z

?

kryptogram

rejestr przesuwaj

,

acy

?

?

-

DES

klucz

K

Rysunek 3.4: Schemat trybu CFB

3.4

IDEA

Wiele prob podejmowanych bylo nad zaprojektowaniem algorytmu, ktory zast

,

apilby

DES. Jedn

,

a z przyczyn bylo przekonanie, _ze wielkosc kluczy DES-a jest za mala.

Inn

,

a wa_zn

,

a przyczyn

,

a byly regulacje prawne w USA uznaj

,

ace DES za produkt o

znaczeniu militarnym i u_zywanie go poza granicami USA bez stosownych licencji

za czyn przest

,

epczy. Poniewa_z utrudnia to stosowanie kryptograi w kontaktach z

partnerami z USA i spoza USA, istnieje potrzeba znalezienia algorytmu, ktorego

stosowanie nie prowadziloby do koniktow z amerykanskimi organami bezpieczen-

stwa. Cele te przyswiecaly powstaniu algorytmu (

I

nternational

D

ata

E

ncryption

S

tandard), wskrocie

IDEA

.

Wlasnosci IDEA:

IDEA jest algorytmem, z ktorego mo_zna korzystac bezplatnie do celow nie-

komercyjnych. Algorytm jest opatentowany w Europie.

R

OZDZIA

L

3.

ALGOR

YTMY

SYMETR

YCZNE

25

IDEA jest algorytmem nowym, wprowadzonym w latach dziewi

,

ecdziesi

,

atych.

Algorytm spotkal si

,

e z du_zym zainteresowaniem, w tym rownie_z jesli chodzi

o proby jego kryptoanalizy. Wobec stosunkowo krotkiego okresu od momentu

jego opublikowania nale_zy z ostro_znosci

,

a podchodzic do jego bezpieczenstwa.

IDEA wchodzi jako jeden z komponentow w sklad PGP, popularnego pakietu

kryptogracznego (patrz rozdz. 13.0.16).
Klucze u_zywane przez IDEA s

,

a zlo_zone z 128 bitow. W praktyce oznacza

to, _ze poszukiwanie pasuj

,

acego klucza do pary kryptogram{tekst jawny po-

przez wyprobowywanie wszystkich kluczy po kolei jest niewykonalne. Mimo

wielkosci kluczy programy szyfruj

,

ace i deszyfruj

,

ace wedlug algorytmu IDEA

nie s

,

a wolniejsze ni_z programy realizuj

,

ace DES.

3.4.1 Szyfrowanie poprzez algorytm IDEA

Szyfrowanie sklada si

,

e z 8 rund. Pojedyncz

,

a rund

,

e schematycznie przedstawia

rys. 3.5. Oprocz tego po ostatniej rundzie dokonywane jest przeksztalcenie

koncowe (patrz rys. 3.8). Jego znaczenie stanie si

,

e jasne, gdy omawiacb

,

edzie-

my deszyfrowanie.
Ka_zda runda przeprowadza rozmaite operacje na 16-bitowych blokach. Trzy

operacje s

,

a u_zywane:

{

X

OR

dokonywany na poszczegolnych bitach,

{

dodawanie modulo 2

16

(oznaczane dalej symbolem +),

{

mno_zenie modulo (2

16

+ 1) (oznaczane dalej symbolem

).

Klucz zawiera 128 bitow. Z niego generowanych jest szereg podkluczy. W

trakcie rundy

i

u_zywanych jest szesc podkluczy

Z

(i)

1

:

:

:

Z

(i)

6

.

W odro_znieniu do kluczy, tekst jawny zawiera 64 bitow.

Przebieg rundy algorytmu IDEA zostal przedstawiony na rys. 3.5. Dane wejsciowe

dla rundy

i

skladaj

,

a si

,

e z 4 blokow po 16 bitow oznaczonych

X

1

:

:

:

X

4

. Rezultat

sklada si

,

e z blokow 16-bitowych oznaczonych

Y

1

:

:

:

Y

4

.

3.4.2 Generowanie podkluczy dla algorytmu IDEA

Szyfrowanie przy pomocy algorytmu IDEA wymaga 6

8+4 podkluczy (8 jest ilosci

,

a

rund, ka_zda z rund wykorzystuje 6 podkluczy, dodatkowo przeksztalcenie koncowe

u_zywa 4 kluczy). Podklucze s

,

a generowane w nast

,

epuj

,

acy sposob:

1. Klucz jest dzielony na bloki 16-bitowe. Daje to pierwszych 8 podkluczy (6

podkluczy dla pierwszej rundy, 2 dla drugiej rundy).

2. Na kluczu wykonuje si

,

e przesuni

,

ecie cykliczne o 25 pozycji. Wynik jest na

nowo dzielony na bloki dlugosci 16. Daje to nast

,

epnych 8 podkluczy (4

brakuj

,

ace podklucze dla drugiej rundy, 4 dla trzeciej rundy).

3. Operacje z punktu 2 powtarzamy a_z wygenerujemy wszystkie potrzebne pod-

klucze.

3.4.3 Deszyfrowanie przez IDEA

Tak jak w przypadku DES-a potrzebna jest jakas sprytna metoda, albowiem bez-

posrednio wyliczyc dane wejsciowe dla rundy na podstawie danych wyjsciowych dla

rundy byloby trudno (porownaj rys. 3.5).

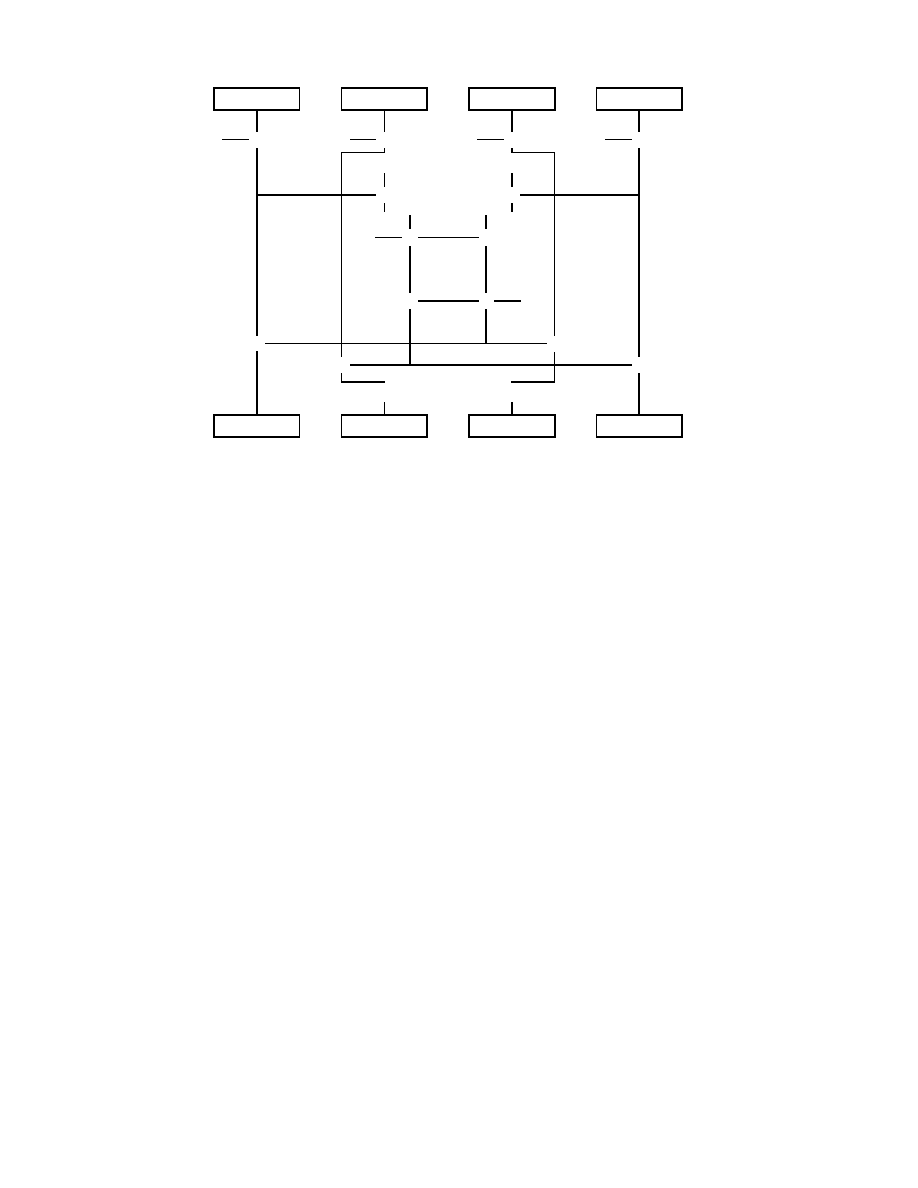
R

OZDZIA

L

3.

ALGOR

YTMY

SYMETR

YCZNE

26

X

1

: 16 bitow

X

2

: 16 bitow

X

3

: 16 bitow

X

4

: 16 bitow

?

?

?

?

j

j

+

j

+

j

Z

(i)

4

-

Z

(i)

3

-

Z

(i)

2

-

Z

(i)

1

-

?

?

j

X

j

X

?

?

-

(

(

(

(

(

(

(

(

(

h

h

h

h

h

h

h

h

h

r

r

r

r

h

h

?

(

(

?

j

-

j

+

Z

(i)

5

-

j

+

j

Z

(i)

6

?

?

j

X

?

-

r

j

X

j

X

?

-

r

j

X

?

h

h

h

h

h

h

h

h

h

?

(

(

(

(

(

(

(

(

(

?

?

Y

1

: 16 bitow

Y

2

: 16 bitow

Y

3

: 16 bitow

Y

4

: 16 bitow

...

...

...

...

j

mno_zenie

j

+ dodawanie

j

X

X

OR

Z

1

(

i

)

Z

2

(

i

)

:::

- podklucze rundy

i

Rysunek 3.5: Runda

i

algorytmu IDEA

Idea deszyfrowania dla jednej rundy:

Wprowadzmy nast

,

epuj

,

ace oznaczenia

(patrz rys. 3.6):

A

=

X

1

Z

(i)

1

B

=

X

2

+

Z

(i)

2

C

=

X

3

+

Z

(i)

3

D

=

X

4

Z

(i)

4

:

Niech

E

=

B

X

OR

Y

3

F

=

C

X

OR

Y

2

(porownaj rys. 3.6). Latwo zauwa_zyc korzystaj

,

ac z rys. 3.6, _ze

Y

3

X

OR

Y

4

= (

B

X

OR

E

)

X

OR

(

E

X

OR

D

) =

B

X

OR

D :

Zatem mo_zemy obliczyc wartosc

B

X

OR

D

. Podobnie mo_zna obliczyc

A

X

OR

C

.

Zauwa_zmy, _ze

B

X

OR

D

i

A

X

OR

C

s

,

a wynikami otrzymywanymi przez dwa w

,

ezly

obliczaj

,

ace

X

OR

w srodkowej cz

,

esci ukladu przedstawionego na rys. 3.6. Tak wi

,

ec

znaj

,

ac klucze

Z

(i)

5

i

Z

(i)

6

mo_zna obliczyc

E

i

F

. Przy ich pomocy otrzymujemy:

A

=

Y

1

X

OR

F

B

=

Y

3

X

OR

E

C

=

Y

2

X

OR

F

D

=

Y

4

X

OR

E

:

Znaj

,

ac

A

B

C

D

i podklucze

Z

(i)

1

:

:

:

Z

(i)

4

mo_zna na koniec wyliczyc

X

1

:

:

:

X

4

.

W opisany powy_zej sposob znaj

,

ac podklucze wyprowadzilismy dane wejsciowe

rundy z jej wyniku. W celu przeprowadzenia deszyfrowania czynimy to dla wszyst-

kich rund, poczynaj

,

ac od ostatniej.

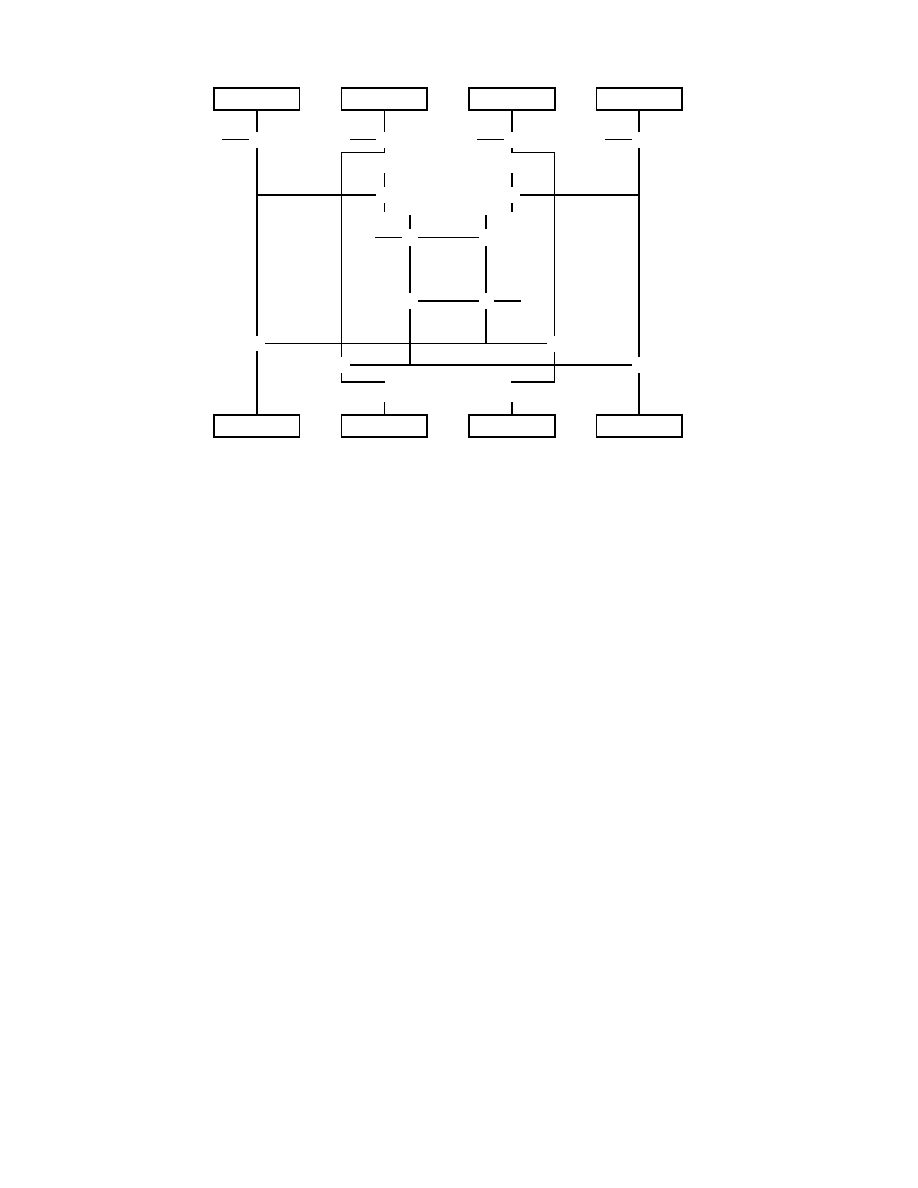
R

OZDZIA

L

3.

ALGOR

YTMY

SYMETR

YCZNE

27

X

1

X

2

X

3

X

4

?

?

?

?

j

j

+

j

+

j

Z

(i)

4

-

Z

(i)

3

-

Z

(i)

2

-

Z

(i)

1

-

?

?

j

X

j

X

?

?

-

(

(

(

(

(

(

(

(

(

h

h

h

h

h

h

h

h

h

r

r

r

r

h

h

?

(

(

?

j

l

k

-

j

+

l

k

Z

(i)

5

-

j

+

j

Z

(i)

6

?

?

j

X

?

-

r

j

X

j

X

?

-

r

j

X

?

h

h

h

h

h

h

h

h

h

?

(

(

(

(

(

(

(

(

(

?

?

Y

1

Y

2

Y

3

Y

4

...

...

...

...

B

E

F

C

D

A

A

X

OR

C

B

X

OR

D

Rysunek 3.6: Metoda deszyfrowania dla algorytmu IDEA

Realizacja deszyfrowania:

Powy_zej zauwa_zylismy jak deszyfrowac w przypadku

algorytmu IDEA. Jesli wykonywane operacje przedstawimy schematycznie (patrz

rys. 3.7), to zauwa_zamy uderzaj

,

ace podobienstwo do operacji wykonywanych pod-

czas rundy szyfrowania. Jedyna ro_znica polega na tym, _ze arytmetyczne operacje

wykonywane przy u_zyciu 4 podkluczy s

,

a wykonywane nie na pocz

,

atku, ale na koncu

rundy deszyfrowania. Dzi

,

eki temu ten sam uklad elektroniczny mo_ze byc u_zyty w

celu szyfrowania i deszyfrowania. Jedynie logiczny podzial na rundy jest nieco inny:

najpierw przeprowadzamy operacj

,

e pocz

,

atkow

,

a, odpowiadaj

,

ac

,

a operacji koncowej

szyfrowania, a nast

,

epnie wykonujemy 8 rund, ka_zda z nich zaczynaj

,

aca si

,

e od

operacji

X

OR

.

Podklucze u_zywane podczas deszyfrowania odpowiadaj

,

a podkluczom szyfrowa-

nia wylistowanym w innej kolejnosci. Ponadto by otrzymac podklucze deszyfrowa-

nia musimy cz

,

esc podkluczy odwrocic (te u_zywane do mno_zenia) lub zanegowac (te

u_zywane do dodawania).

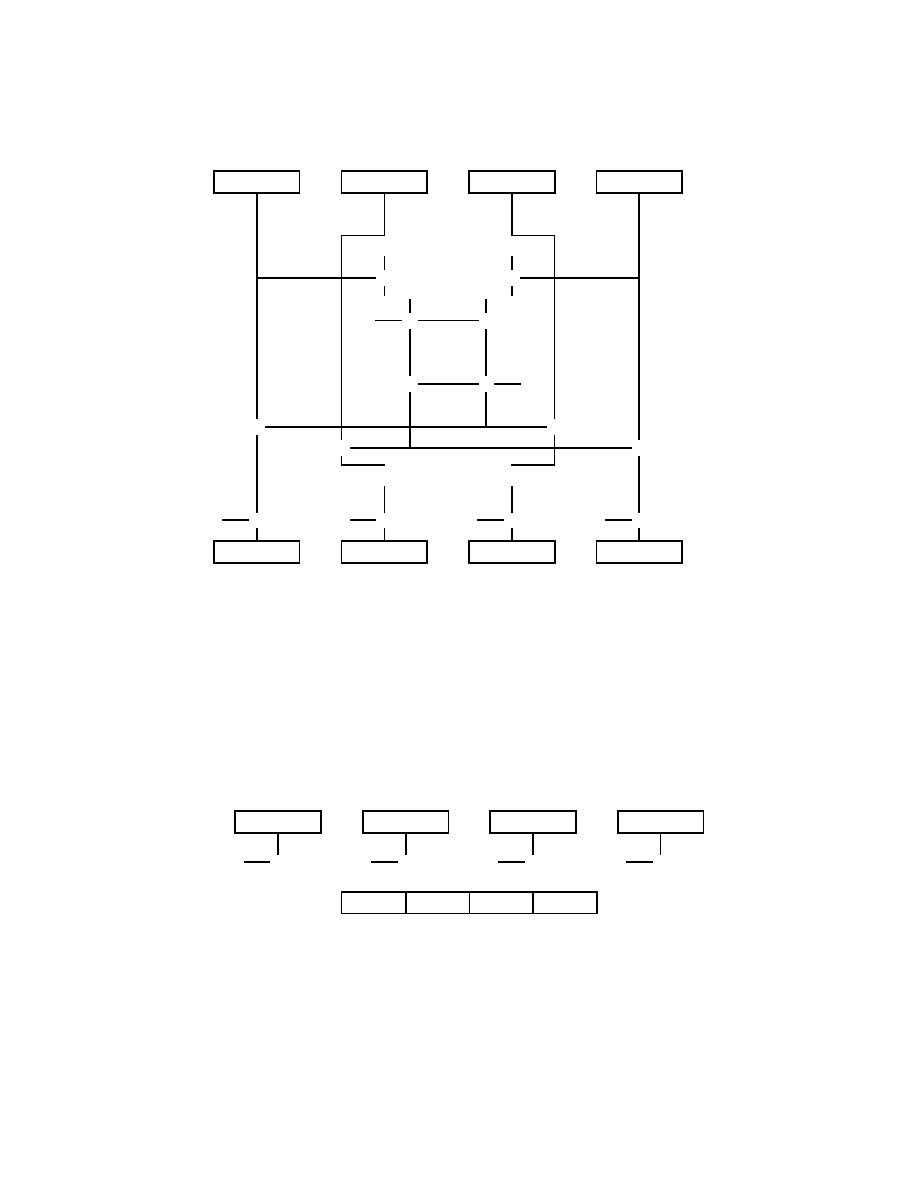
R

OZDZIA

L

3.

ALGOR

YTMY

SYMETR

YCZNE

28

Y

1

Y

3

Y

2

Y

4

?

?

?

?

?

?

?

?

j

j

+

j

+

j

Z

(i)

4

;1

-

;Z

(i)

3

-

;Z

(i)

2

-

Z

(i)

1

;1

-

?

?

j

X

j

X

?

?

-

(

(

(

(

(

(

(

(

(

h

h

h

h

h

h

h

h

h

r

r

r

r

h

h

?

(

(

?

j

-

j

+

Z

(i)

5

;1

-

j

+

j

;Z

(i)

6

?

?

j

X

?

-

r

j

X

j

X

?

-

r

j

X

?

h

h

h

h

h

h

h

h

h

?

(

(

(

(

(

(

(

(

(

?

?

X

1

X

3

X

2

X

4

Rysunek 3.7: Schemat deszyfrowania w algorytmie IDEA

16 bitow

16 bitow

16 bitow

16 bitow

16 bitow

16 bitow

?

?

?

?

j

.

j

+

j

j

+

.

Z

(9)

4

-

Z

(9)

3

-

Z

(9)

2

-

Z

(9)

1

-

Z

Z

~

=

9

X

X

X

X

X

X

z

kryptogram

Rysunek 3.8: Przeksztalcenie koncowe w algorytmie IDEA

Spis rzeczy

1 Pierwszy rzut oka na kryptogra

,

e

4

1.0.1 Szyfrowanie danych

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

4

1.0.2 Podstawowe zastosowania technik szyfrowania

:

:

:

:

:

:

:

:

:

5

1.0.3 Historia kryptograi

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

8

1.0.4 Kontrowersje zwi

,

azane ze stosowaniem kryptograi

:

:

:

:

:

:

9

1.0.5 Korzystanie z produktow kryptogracznych

:

:

:

:

:

:

:

:

:

:

10

2 Podstawowe techniki szyfrowania

12

2.0.6 Podstawienie

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

12

2.0.7 XOR i one-time pad

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

13

2.0.8 S-boksy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

15

3 Algorytmy symetryczne

18

3.1 DES { Data Encryption Standard

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

18

3.1.1 Szyfrowanie DES-em

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

19

3.1.2 Deszyfrowanie DES-em

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

21

3.2 Trzykrotny DES

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

21

3.3 Szyfrowanie tekstow dowolnej dlugosci

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

21

3.3.1 Elektroniczna ksi

,

a_zka kodowa

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

22

3.3.2 Cipher Block Chaining

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

23

3.3.3 Cypher Feedback

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

23

3.4 IDEA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

24

3.4.1 Szyfrowanie poprzez algorytm IDEA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

25

3.4.2 Generowanie podkluczy dla algorytmu IDEA

:

:

:

:

:

:

:

:

:

25

3.4.3 Deszyfrowanie przez IDEA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

25

4 Algorytmy niesymetryczne

29

4.0.4 Teoria zlo_zonosci obliczeniowej a kryptograa

:

:

:

:

:

:

:

:

:

29

4.0.5 Szyfry plecakowe

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

30

4.1 RSA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

32

4.1.1 Opis algorytmu RSA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

33

4.1.2 Testy pierwszosci

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

35

4.1.3 Aspekty bezpieczenstwa RSA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

37

4.1.4 Trudne bity kryptogramow RSA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

39

4.2 Algorytm ElGamala

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

41

5 Funkcje jednokierunkowe

43

5.0.1 Kandydaci na funkcje jednokierunkowe

:

:

:

:

:

:

:

:

:

:

:

:

:

44

5.0.2 Hard-core bit

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

45

i

SPIS

RZECZY

ii

6 Jednokierunkowe funkcje hashuj

,

ace

46

6.0.3 Wlasnosci i zastosowania funkcji hashuj

,

acych

:

:

:

:

:

:

:

:

:

46

6.0.4 Ataki przeciw funkcjom hashuj

,

acym

:

:

:

:

:

:

:

:

:

:

:

:

:

:

47

6.1 Techniki o dowodliwych wlasnosciach

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

49

6.1.1 Hashowanie przy pomocy dyskretnego logarytmu

:

:

:

:

:

:

:

49

6.1.2 Rozszerzenie na teksty dowolnej dlugosci

:

:

:

:

:

:

:

:

:

:

:

:

50

6.2 Praktyczne algorytmy hashuj

,

ace

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

51

6.2.1 MD5

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

51

6.2.2 Hashowanie dowolnie dlugich tekstow

:

:

:

:

:

:

:

:

:

:

:

:

:

52

7 Ci

,

agi pseudolosowe

55

7.0.3 Wlasnosci ci

,

agow pseudolosowych

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

55

7.0.4 Generatory ci

,

agow pseudolosowych

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

57

7.0.5 Pseudolosowosc generatora BBS

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

59

7.1 Zastosowania ci

,

agow pseudolosowych

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

59

7.1.1 Szyfrowanie strumieniowe

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

59

7.1.2 Szyfrowanie probabilistyczne

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

60

8 Podpisy cyfrowe

61

8.0.3 Podpisy cyfrowe ElGamala

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

62

8.0.4 DSA

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

63

8.0.5 Slepe podpisy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

64

8.0.6 Kanal podprogowy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

65

8.0.7 Podpisy niezaprzeczalne

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

66

9 Uwierzytelnianie

69

9.0.8 Protokol challenge and response

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

69

9.0.9 Dowody interakcyjne

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

70

9.0.10 Dowody z wiedz

,

a zerow

,

a

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

71

9.0.11 Protokol Fiege-Fiata-Shamira

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

73

9.0.12 Protokol Schnorra

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

74

9.0.13 Protokol Guillou-Quisquartera

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

75

9.0.14 Podpisy cyfrowe poprzez uwierzytelnianie

:

:

:

:

:

:

:

:

:

:

:

76

10 Administracja kluczami

77

10.1 Praktyka gospodarki kluczami

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

77

10.1.1 Urz

,

adzenie kryptograczne

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

77

10.1.2 Generowanie kluczy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

78

10.1.3 Hierarchia kluczy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

79

10.1.4 Przechowywanie kluczy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

79

10.2 Protokoly uzgadniania kluczy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

80

10.2.1 Uzgadnianie kluczy poprzez szyfrowanie symetryczne

:

:

:

:

:

81

10.2.2 Uzgadnianie klucza przez szyfrowanie asymetryczne

:

:

:

:

:

82

10.2.3 Protokol Die-Hellmana i jego pochodne

:

:

:

:

:

:

:

:

:

:

:

82

11 Protokoly kryptograczne

85

11.0.4 Atak man in the middle

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

85

11.0.5 Dzielenie tajemnic

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

87

11.0.6 Zobowi

,

azanie bitowe

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

88

11.0.7 Pieni

,

adze cyfrowe

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

90

11.0.8 Elektroniczne wybory

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

93

SPIS

RZECZY

iii

12 Kryptoanaliza

95

12.0.9 Kryptoanaliza ro_znicowa

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

96

12.0.10Kryptoanaliza liniowa

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

99

12.0.11Ro_znicowa kryptoanaliza bl

,

edow

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

100

13 Wybrane implementacje

102

13.0.12Smart cards

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

102

13.0.13Krzywe eliptyczne

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

103

13.0.14Kerberos

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

103

13.0.15Zabezpieczanie komunikacji telefonicznej

:

:

:

:

:

:

:

:

:

:

:

:

106

13.0.16PGP { Pretty Good Privacy

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

107

13.0.17Zabezpieczanie poczty elektronicznej { PEM

:

:

:

:

:

:

:

:

:

108

13.0.18Bezpieczenstwo w WWW

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

109

13.0.19Protokoly obrotu nansowego

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

:

109

A Wybrane aspekty teorii liczb

112

B Teoria algorytmow

116

Przedmowa

Do niedawna kryptograa byla obiektem zainteresowania w wi

,

ekszym stopniu slu_zb

wywiadowczych i wojska ni_z przedmiotow gospodarczych i prywatnych osob. Post

,

ep

w dziedzinie elektroniki a zwlaszcza gwaltowny rozwoj sieci komputerowych sytuacj

,

e

t

,

e zmienily w radykalny sposob.

Dawniej, gdy prywatny u_zytkownik dysponowal jedynie komputerem PC nie

wl

,

aczonym do sieci, ochrona danych byla stosunkowo prosta i zapewniona przez

zyczny dost

,

ep do komputera. Na tej samej zasadzie chronione byly dane przecho-

wywane w postaci elektronicznej przez male rmy, dzialy rm, organizacje politycz-

ne. Nie skomplikowaneprotokoly kryptograczne, ale klucz do pomieszczenia z kom-

puterem, czy koperta, w ktorej przesylana byla dyskietka, stanowily ochron

,

e przed

niepowolanym dost

,

epem. Oczywiscie zdarzaly si

,

e kradzie_ze dyskietek, komputerow,

wlamania do siedzib partii politycznych

:

:

:

. Wi

,

ekszosc u_zytkownikow nie czulo

jednak potrzeby skuteczniejszej ochrony swych danych.

Sytuacja zacz

,

ela si

,

e radykalnie zmieniac z chwil

,

a gwaltownego wzrostu sieci

komputerowych. Dotyczylo to nie tylko sieci obejmuj

,

acych szereg dzialow pojedyn-

czych rm, ale i sieci globalne, takie jak Internet (w tym zwlaszcza World Wide

Web). Zapewnienie bezpieczenstwa w tych sieciach stalo si

,

e jednym z pierwszo-

planowych zadan decyduj

,

acych o ich dalszym rozwoju. Nowe techniki telekomu-

nikacyjne, takie jak telefonia komorkowa, telewizja cyfrowa, telebanking, itp., nie

moglyby znalezc swego miejsca w codziennej praktyce, gdyby nie stosowanie technik

kryptogracznych dla ochrony dost

,

epu.

Najpierw rewolucja obj

,

ela komunikacj

,

e w srodowisku naukowym. Pojawienie

si

,

e poczty elektronicznej umo_zliwilo blyskawiczne kontaktowanie sie naukowcow z

najdalszych krajow. Pozwolilo to na olbrzymi wzrost wydajnosci w wielu dziedzi-

nach badan. Mo_znaby si

,

e spodziewac, _ze konkurencja i ostra walka o przodownictwo

doprowadzi w srodowisku naukowym do wielu nadu_zyc poczty elektronicznej. Tym

bardziej, _ze nie jest trudne na przyklad przeslac list w ten sposob, by nadawca po

naglowku mogl byc przekonany, _ze pochodzi on od innej osoby. Mo_zliwe jest rownie_z

przechwytywanie korespondencji przeznaczonej do innych adresatow. Zjawiska te

jednak stanowily dotychczas w calymsrodowisku naukowymbardzo w

,

aski margines.

Powodem zapewne bylo to, i_z komunikowaly si

,

e osoby, ktore i tak obdarzaly si

,

e

pelnym zaufaniem. Tak wi

,

ec metody, ktore pozwalalyby na zabezpieczenie przed

odczytem, modykacj

,

a czy te_z preparowaniem listow elektronicznych przez osoby

trzecie nie byly stosowane.

Te czasy min

,

ely. Wraz z pojawieniem si

,

e World Wide Web Internet stal si

,

e

atrakcyjny dla "szaregou_zytkownika\. WInternecie pojawilysi

,

e interesuj

,

ace zasoby

informacyjne, dzi

,

eki czemu ilosc u_zytkownikow zacz

,

ela rosn

,

ac gwaltownie. Co

wi

,

ecej, Internet coraz cz

,

esciej jest u_zywany nie jako narz

,

edzie zabawy czy rozwijania

zainteresowan, ale do celow komercyjnych. Ju_z dzis bilety lotnicze kupuj

,

e przez

Internet, literatur

,

e naukow

,

a wybieram przez World Wide Web, a zamiast kupowac

gazet

,

e z lokalnymi ogloszeniami si

,

egam do jej elektronicznego odpowiednika. W

takiej sytuacji b

,

edzie coraz wi

,

ecej osob: hardware tanieje, software staje si

,

e coraz

latwiejszy do obslugi przez laika, w wielu krajach pol

,

aczenia telefoniczne wskutek

1

SPIS

RZECZY

2

konkurencji na rynku telekomunikacyjnym staj

,

a si

,

e tansze i wy_zszej jakosci. Coraz

latwiejsze b

,

edzie zatem stanie si

,

e kolejnym u_zytkownikiem Internetu. Za par

,

e lat

b

,

edziemy miec zapewne do czynienia z sytuacj

,

a, gdy Internet b

,

edzie najwi

,

ekszym

supermarketem, najobszerniejsz

,

a gazet

,

a, najwi

,

ekszym Hyde Parkiem,

:

:

:

{przynaj-

mniej w krajach, gdzie uslugi telekomunikacyjne b

,

ed

,

a wystarczaj

,

aco tanie.

Jak ka_zdy wynalazek, rozwoj globalnych sieci komputerowych przynosi korzysci,

ale i niebezpieczenstwa. Wiele dyskutuje si

,

e na przyklad na temat mo_zliwosci

wykorzystywania Internetu przez organizacje przest

,

epcze. Sytuacja przypomina

nieco spory po wynalezieniu samochodu. Nie sposob cz

,

esciowo nie przyznac racji

przeciwnikom automobili maj

,

ac przed oczyma tragiczne statystki o tysi

,

acach ludzi

zabitych na drogach. Nie cofn

,

elo to jednak motoryzacji, tak jak nie do odwrocenia

jest ju_z rozwoj globalnej sieci komputerowej na swiecie.

Poniewa_z poprzez Internet komunikowac si

,

e b

,

ed

,

a nie dobrzy i ufaj

,

acy sobie

znajomi, lecz cz

,

esto anonimowi czy wrodzy sobie u_zytkownicy, mijaj

,

a czasy, gdy

niezbyt wiele myslano o bezpieczenstwie danych i komunikacji. Z jednej strony

podl

,

aczenie do sieci komputerowych stanowic b

,

edzie warunek wst

,

epny istnienia

rm (tak jak posiadanie telefonu, faxu, czy skrzynki pocztowej), z drugiej strony

podl

,

aczenie to stanowi o mo_zliwosci wlaman, dewastacji danych i innych dzialan o

charakterze przest

,

epczym.

Oczywiscie u_zytkownicy sieci komputerowych b

,

ed

,

a sie bronic przed niepowo-

lanym dost

,

epem do danych czy manipulacjami dokonywanymi na nich. Pierwsz

,

a

lini

,

a obrony b

,

ed

,

a oczywiscie systemy operacyjne zarz

,

adzaj

,

ace prac

,

a komputerow i

wykonywaniem zlecen na rzecz u_zytkownikow. W wielu miejscach ruchu w sieciach

komputerowych (ktore uzyskaly ju_z modn

,

a nazw

,

e

infostr

ad

) "sprawdzane b

,

ed

,

a

bilety\, a "pasa_zerowie na gap

,

e\ b

,

ed

,

a usuwani z ruchu. Rownoczesnie zadaniem

systemu operacyjnego b

,

edzie przestrzeganie, czy u_zytkownicy dokonuj

,

a jedynie do-

zwolonych operacji.

Wskutek zlo_zonosci stawianych zadan systemy operacyjne b

,

ed

,

a stawac si

,

e coraz

bardziej skomplikowane. Tym samymcoraz trudniej b

,

edzie ich tworcom przewidziec

wszystkie mo_zliwosci, tak aby uniemo_zliwicomini

,

ecie zabezpieczen zainstalowanych

poprzez system operacyjny. Dotychczasowe doniesienia z tego pola walki s

,

a raczej

pesymistyczne dla systemow operacyjnych. Stoj

,

a one w obliczu mia_zd_z

,

acej przewagi

wlamywaczy zwanych hackerami. Hackerzy nie s

,

a, jakby si

,

e chcialo wierzyc, jedynie

grup

,

a nastoletnich maniakow komputerowych (czy lagodniej mowi

,

ac, milosnikow

technik komputerowych). Jest to grupa o olbrzymim potencjale intelektualnym,

nierzadko doskonalym zapleczu sprz

,

etowym i nansowym.

Ostatni

,

a szans

,

a na zagwarantowanie bezpieczenstwa danych jest kryptograa.

Nie mo_ze ona usun

,

ac wszelkich niebezpieczenstw (jak na przyklad zniszczenie da-

nych przez wlamywacza komputerowego), ale w wielu sytuacjach skutecznie pomaga

(na przyklad uniemo_zliwia odczyt danych przez niepowolan

,

a osob

,

e). W odro_znieniu

do innych metod kryptograa dostarcza metod wzgl

,

ednie bezpiecznych. Tak bez-

piecznych, _ze liniami telekomunikacyjnymi dokonuje si

,

e co chwila przelewow nie-

wyobra_zalnych dla szarego czlowieka sum. I nikt si

,

e nie martwi, _ze ktos wl

,

aczy si

,

e

na lini

,

e i t

,

a drog

,

a powi

,

ekszy stan swego konta o iles milionow dolarow (z ktorymi

odleci natychmiast na wyspy poludniowego Pacyku do kraju, z ktorym zapomniano

zawrzec umow

,

e o ekstardycji przest

,

epcow).

Miroslaw Kutylowski

Wst

,

ep

Niniejsza ksi

,

a_zka ma za zadanie w bardzo zwi

,

ezly sposob przedstawic podstawowe

metody kryptograczne. Wiele interesuj

,

acych technik kryptogracznych zostalo w

niej pomini

,

etych. Nacisk polo_zony zostal na te aspekty, ktore maj

,

a b

,

adz miec mog

,

a

praktyczne zastosowanie. Wskutek tego wiele teoretycznie ciekawych zagadnien

swiadomie nie poruszamy w tej ksi

,

a_zce. Z drugiej strony, naszym zamyslem bylo, na

tyle na ile to jest mo_zliwe w tak krotkiej pozycji, umo_zliwicczytelnikowi zrozumienie

matematycznych mechanizmow tkwi

,

acych w kryptograi. Tym ksi

,

a_zka ta ro_zni si

,

e

na przyklad od dost

,

epnej na polskim rynku pozycji Bruce'a Schneiera 6], maj

,

acej

bardziej charakter encyklopedii ni_z podr

,

ecznika.

Niniejsza ksi

,

a_zka przeznaczona jest dla studentow informatyki i pokrewnych

dziedzin. Mo_ze byc wykorzystana jako podr

,

ecznik do semestralnego wykladu z kry-

ptograi, jak rownie_z jako material do samodzielnego studiowania. Do zrozumie-

nia niektorych cz

,

esci ksi

,

a_zki niezb

,

edna jest znajomosc pewnych faktow z algebry.

Czytelnik nieobeznany z tymi zagadnieniami mo_ze znalezc brakuj

,

ace informacje w

Dodatku A. Niekiedy konieczna jest znajomosc standardowych faktow z podstaw

informatyki wykladanych na pierwszych latach studiow informatycznych. Cz

,

esc

tych poj

,

ec skrotowo przedstawiamy w Dodatku B.

Niniejsza ksi

,

a_zka oparta jest na cz

,

esci skryptu do wykladu Miroslawa Kutylow-

skiego. Wyklad ten odbyl si

,

e na Wydziale Matematyki i Informatyki Uniwersytetu

Paderborn w semestrze zimowym 1995 roku. Wspomniany skrypt obejmuje procz

kryptograi zagadnienia kodow samokoryguj

,

acych bl

,

edy i kompresji danych. Jest

on dost

,

epny poprzez World Wide Web pod adresem

http://www.uni-paderborn.de/fachbereich/AG/agmadh/WWW/german/LehreKuty/ikk95/skript.ps.gz

Lista zauwa_zonych bl

,

edow, uzupelnienia, itp. znajduj

,

a si

,

e w World Wide Web

pod adresem

http://www.uni-paderborn.de/fachbereich/AG/agmadh/WWW/german/LehreKuty/kryptograa/

Pragniemy podzi

,

ekowac licznym studentom za udzielon

,

a pomoc. W szczegolno-

sci wymienic chcielibysmy Guido Haeselera, ktorego notatki do wykladu w Latex-u

byly podstaw

,

a pierwszej wersji skryptu (i szeregu rysunkow zawartych w ksi

,

a_zce).

Cz

,

esc rysunkow zostala wykonana przez Franka Beste i Ew

,

e Kutylowsk

,

a.

3