UZUPE£NIA ZESPÓ£
NADZORUJ¥CY
miejsce
na naklejkê
z kodem
WPISUJE UCZEÑ
dysleksja
MAJ 2002
EGZAMIN
W TRZECIEJ KLASIE GIMNAZJUM
Z ZAKRESU PRZEDMIOTÓW
MATEMATYCZNO-PRZYRODNICZYCH
Poznaj zainteresowania rówieników
Instrukcja dla ucznia
1.
Sprawd, czy zestaw egzaminacyjny zawiera 14 stron.
Ewentualny brak stron lub inne usterki zg³o nauczycielowi.
2. Na tej stronie i na karcie odpowiedzi wpisz swój kod
i datê urodzenia.
3.
Czytaj uwa¿nie wszystkie teksty i zadania.
4.
Rozwi¹zania zapisuj d³ugopisem lub piórem z czarnym lub granatowym
tuszem/atramentem. Nie u¿ywaj korektora.
5.
W zadaniach od 1. do 25. s¹ podane cztery odpowiedzi: A, B, C, D.
Odpowiada im nast
êpuj¹cy uk³ad na karcie odpowiedzi:
A
B
C
D
Wybierz tylko
jedn¹ odpowied i zamaluj kratkê z odpowiadaj¹c¹ jej
liter¹ - np. gdy wybra³e odpowied "A":
6.
Staraj siê nie pope³niæ b³êdów przy zaznaczaniu odpowiedzi, ale jeli siê
pomylisz,
b³êdne zaznaczenie otocz kó³kiem i zamaluj inn¹ odpowied.
7.
Rozwi¹zania zadañ od 26. do 36. zapisz czytelnie i starannie
w
wyznaczonych miejscach. Pomy³ki przekrelaj.
8.
Redaguj¹c odpowiedzi do zadañ, mo¿esz wykorzystaæ miejsca opatrzone
napisem Brudnopis
. Zapisy w brudnopisie nie bêd¹ sprawdzane
i oceniane.
Powodzenia!
Czas pracy:
120 minut
Liczba punktów
do uzyskania: 50
GM-A1-021
KOD UCZNIA
DATA URODZENIA UCZNIA
dzieñ miesi¹c
rok
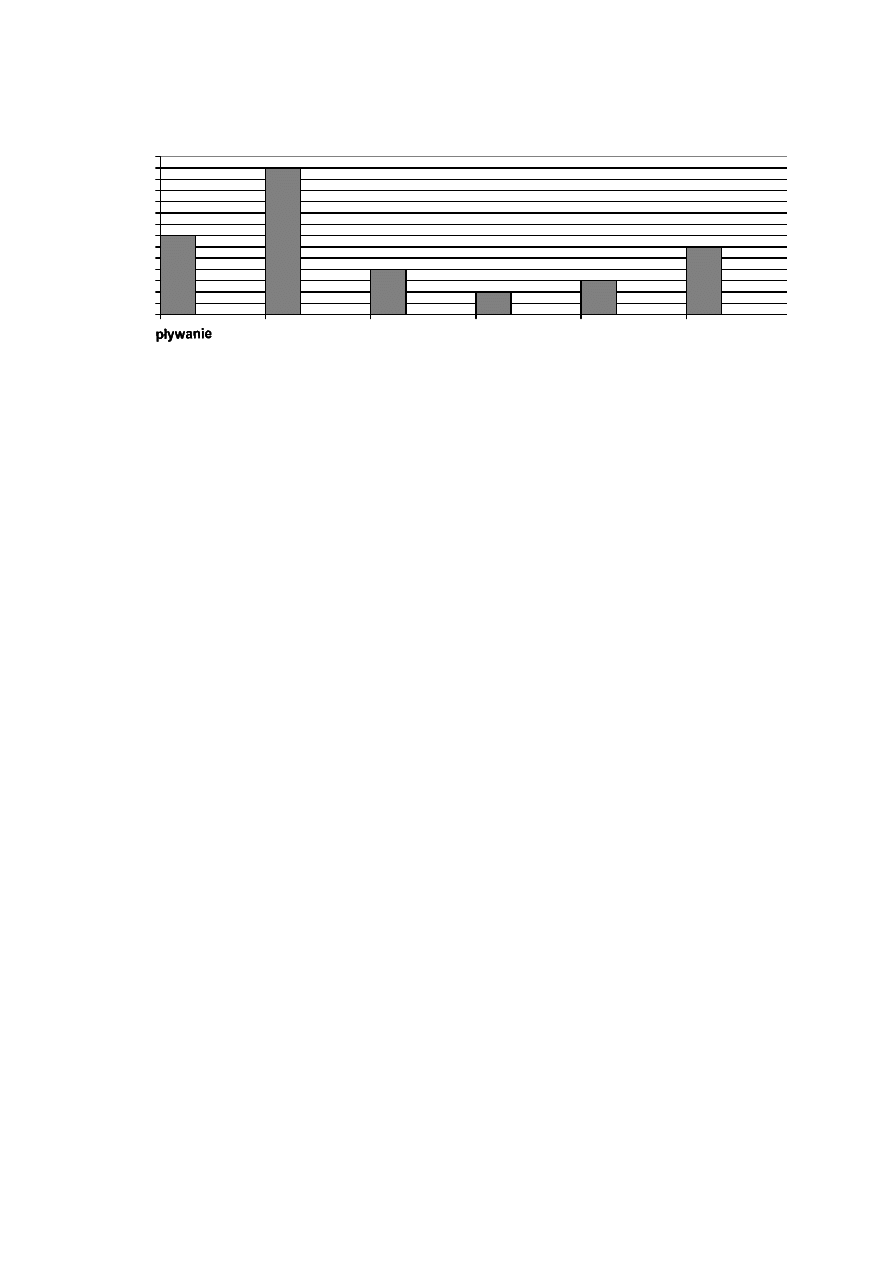
Wród gimnazjalistów przeprowadzono ankietê na temat ich zainteresowañ.
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
informatyka
narciarstwo
filatelistyka
modelarstwo
kolarstwo
rodzaje zainteresowañ
Wiedz¹c, ¿e ka¿dy uczeñ poda³ tylko jeden rodzaj zainteresowañ, rozwi¹¿ zadania 1 – 3.
Zadanie 1. (0–1)
Ilu uczniów bra³o udzia³ w ankiecie?
A.
250
B.
320
C.
350
D.
370
Zadanie 2. (0–1)
O ilu mniej uczniów interesuje siê kolarstwem ni¿ informatyk¹?
A.
70
B.
110
C.
120
D.
130
Zadanie 3. (0–1)
Ile procent wszystkich uczniów interesuje siê p³ywaniem?
A. 5%
B. 20%
C. 50%
D. 70%
Kolekcjonerzy znaczków
Zadanie 4. (0–1)
Jacek i Pawe³ zbieraj¹ znaczki. Jacek ma o 30 znaczków wiêcej ni¿ Pawe³. Razem maj¹
350 znaczków. Ile znaczków ma Pawe³?
A.
145
B.
160
C.
190
D.
205
Zadanie 5. (0–1)
Pawe³ kupi³ australijski znaczek i 3 znaczki krajowe. Ka¿dy znaczek krajowy
kosztowa³
tyle samo. Za wszystkie znaczki zap³aci³ 16 z³. Ile kosztowa³ znaczek australijski, jeli by³
piêciokrotnie dro¿szy ni¿ znaczek krajowy?
A. 4 z³
B. 10 z³
C. 12 z³
D. 13 z³
li
czba u
czni
ó
w
Strona 2 z 14
Zadanie 6. (0–1)
Krokodyla przedstawionego na australijskim znaczku Paw³a mo¿na opisaæ nastêpuj¹co:
A. w¹¿, zmiennocieplny, drapie¿ca, jajorodny
B. gad, sta³ocieplny, wody ciep³e
C. drapie¿ca, gad, zmiennocieplny, jajorodny
D. sta³ocieplny, p³az, jajorodny, zêby jadowe
Zadanie 7. (0–1)
Znaczek z kolekcji Jacka upamiêtnia wydarzenie, które mia³o miejsce 8 czerwca 2000 roku.
Wówczas z miejscowoci Yulara w rodkowej Australii wyruszy³a sztafeta nios¹ca znicz
olimpijski przed olimpiad¹ w Sydney. W Australii by³o to:
A. pod koniec kalendarzowej wiosny
B. na pocz¹tku kalendarzowego lata
C. pod koniec kalendarzowej jesieni
D. na pocz¹tku kalendarzowej zimy
Zadanie 8. (0–1)
Entuzjaci kolarstwa
Zadanie 9. (0–1)
Marta i Jacek, wyje¿d¿aj¹c na wycieczkê rowerow¹, spotkali siê w po³owie drogi od
swoich miejsc zamieszkania oddalonych o 8 km. Marta jecha³a ze redni¹ szybkoci¹
16
km/h, a Jacek 20 km/h. Marta wyjecha³a z domu o godzinie 14
00
. O której godzinie
wyjecha³ Jacek, jeli na miejsce spotkania dotar³ o tej samej godzinie co Marta?
A. 13
53
B. 13
57
C. 14
03
D. 14
12
Brudnopis
Zadanie 10. (0–1)
Marta przygotowa³a prowiant na wycieczkê rowerow¹. Pakowane przez ni¹ produkty
¿ywnociowe zawieraj¹ wa¿ne dla organizmu zwi¹zki chemiczne. Które z nich s¹ dla
organizmu g³ównie ród³em energii?
A. bia³ka
B. cukry
C. sole mineralne
D. witaminy
Zamieszczona obok figura ma:
A.
dok³adnie 4 osie symetrii i ma rodek symetrii
B.
co najmniej 4 osie symetrii i nie ma rodka symetrii
C.
dok³adnie 2 osie symetrii i nie ma rodka symetrii
D.
dok³adnie 2 osie symetrii i ma rodek symetrii
Strona 3 z 14
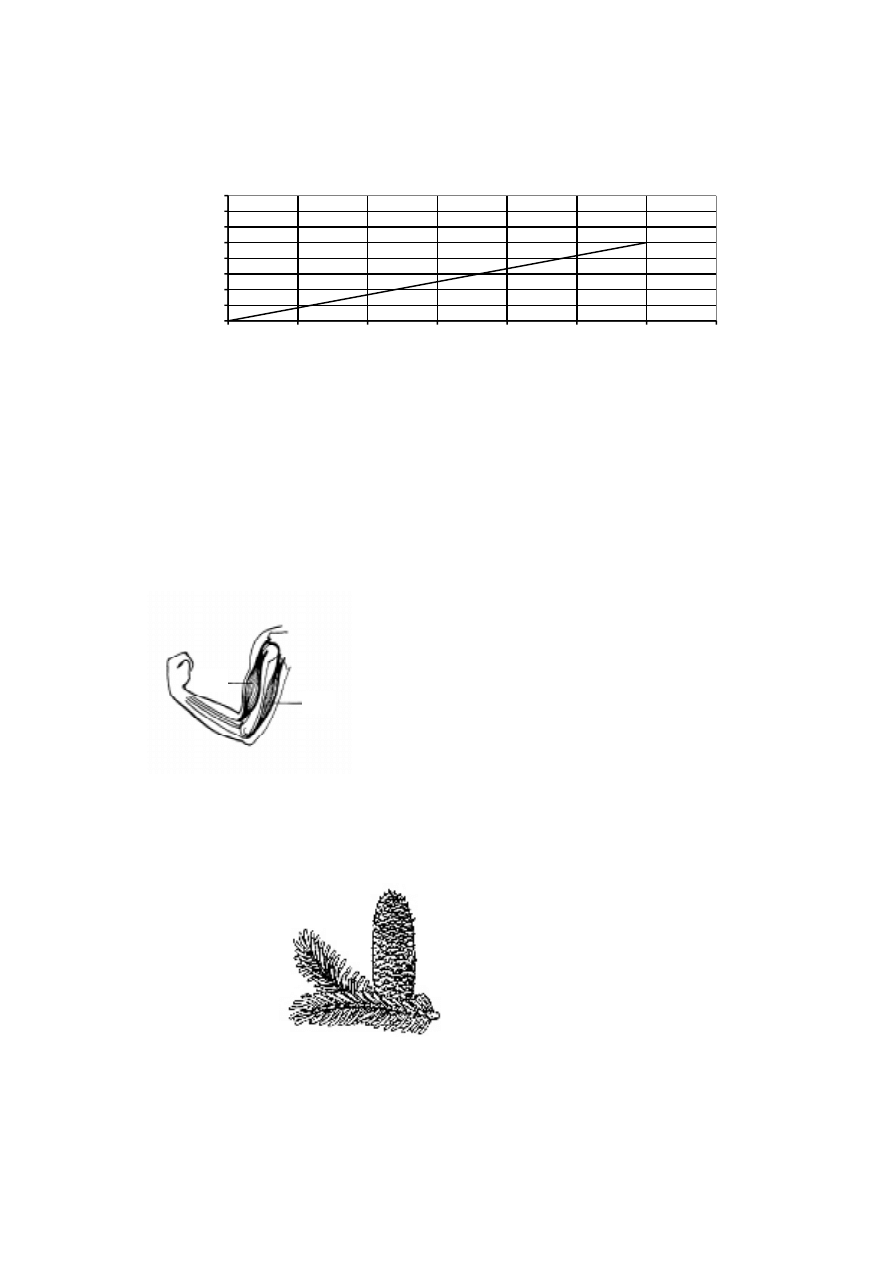
A. miêsieñ I
B. miêsieñ II
C. miêsieñ I i II
D. ¿aden z nich
II
I
Zadanie 11. (0–1)
Na wykresie poni¿ej przedstawiono zale¿noæ drogi – przebytej przez turystê
poruszaj¹cego siê na rowerze – od czasu.
Turysta ten porusza³ siê ruchem:
A. jednostajnym
B. przyspieszonym
C.
opónionym
D. zmiennym
Zadanie 12. (0–1)
Podczas jazdy na
rowerze pracuj¹ miênie stanowi¹ce czêæ uk³adu ruchu cz³owieka.
Który z miêni przedstawionych na poni¿szym rysunku jest zginaczem?
Zadanie 13. (0–1)
Na podstawie rysunku rozpoznaj drzewo obserwowane przez Jacka w trakcie
przeja¿d¿ki rowerowej.
A. wierk
B. sosna
C. modrzew
D. jod³a
0
2
4
6
8
10
12
14
16
0
5
10
15
20
25
30
35
czas [min]
droga [km]
Strona 4 z 14
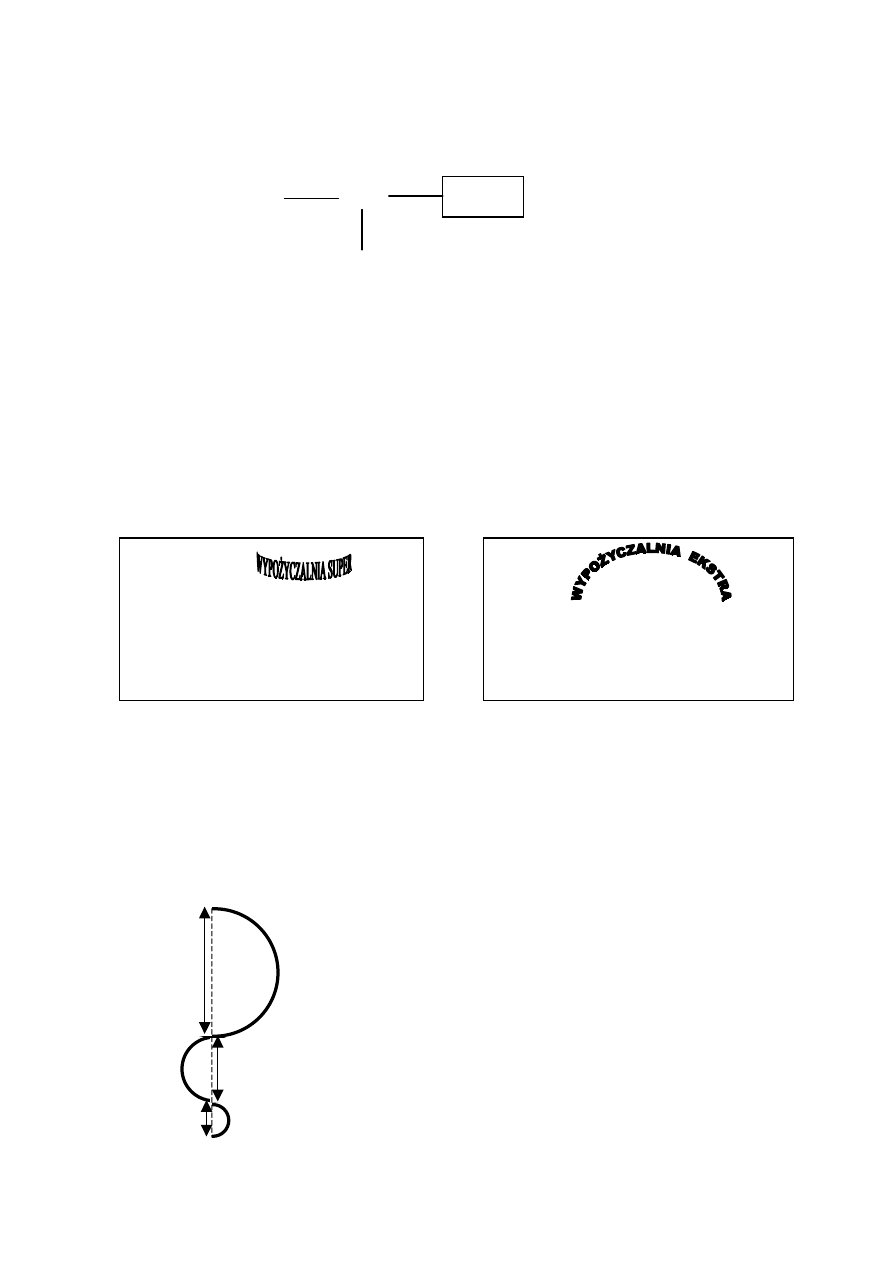
Zadanie 14. (0–1)
Po ca³odniowej wycieczce rowerowej Marta odczu³a ból w miêniach spowodowany
miêdzy innymi wytworzeniem siê kwasu mlekowego. Zwi¹zek ten mo¿na opisaæ
wzorem:
Zamieszczona w ramce grupa funkcyjna, charakterystyczna dla kwasów organicznych,
nazywa siê:
A. wêglowodorow¹
B. wodorotlenow¹
C. karboksylow¹
D. estrow¹
Narciarze
Zadanie 15. (0–1)
Podczas pobytu w miejscowoci górskiej Adam wypo¿yczy³ narty w wypo¿yczalni
SUPER, a Bartek w wypo¿yczalni EKSTRA.
Koszt wypo¿yczenia nart w obu firmach bêdzie taki sam, je¿eli ch³opcy bêd¹ u¿ywaæ
nart przez:
A. 4 godziny
B. 6 godzin
C. 8 godzin
D. 10 godzin
Zadanie 16. (0–1)
Rysunek przedstawia lad na niegu, który pozostawi³ jad¹cy na nartach Adam.
Cena za wypo¿yczenie nart: 10 z³
i dodatkowo
5 z³ za ka¿d¹ godzinê u¿ywania
Cena za wypo¿yczenie nart: 18 z³
i dodatkowo
3 z³ za ka¿d¹ godzinê u¿ywania
D³ugoæ trasy przebytej przez Adama równa jest:
A. 350
π
m
B. 700
π
m
C. 1400
π
m
D. 2100
π
m
COOH
CH
CH
3
OH
400 m
200 m
800 m
Strona 5 z 14
Wykorzystuj¹c zamieszczony poni¿ej fragment mapy poziomicowej, rozwi¹¿ zadania
17 i 18.
skala:
1:75000
Zadanie 17. (0–1)
Bartek korzysta z wyci¹gu narciarskiego. Ile wynosi ró¿nica wysokoci pomiêdzy doln¹
a górn¹ stacj¹ tego wyci¹gu?
A. 1200 m
B. 1800 m
C. 2800 m
D. 3200 m
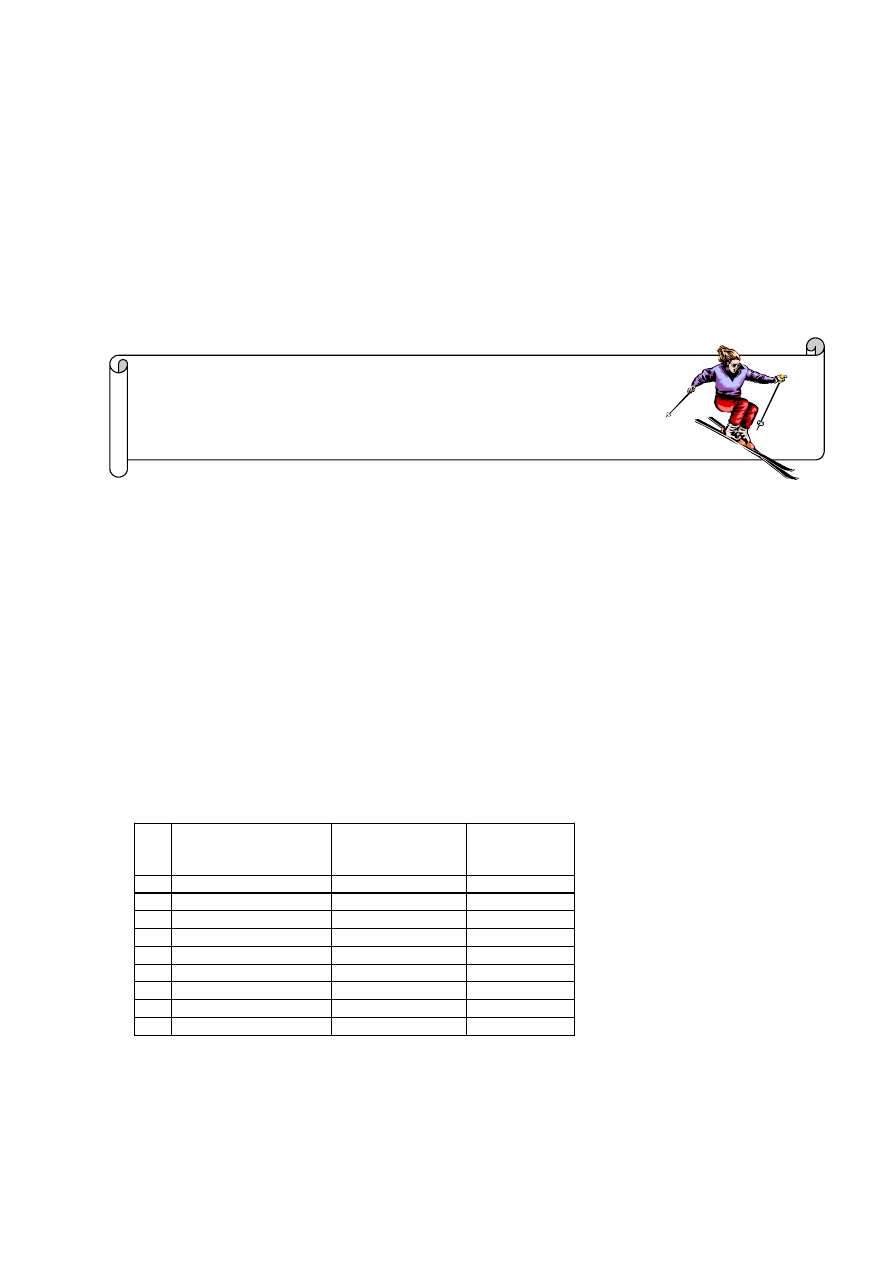
Zadanie 18. (0–1)
Przekrój góry (patrz mapa poziomicowa), w której wydr¹¿ono tunel, ilustruje:
A. rysunek I
B. rysunek II
C. rysunek III
D. rysunek IV
I II
III IV
= = =
tunel
wyci¹g
14
0
0
1200
1400
1600
1800
2000
2200
2400
2600
2800
3000
3200
3400
wysokoæ w m n.p.m
.
s kala 1:75 000
1600
1800
2000
2200
2400
2600
2800
3000
3200
3400
wysokoæ w m n.p.m
.
skala 1:75 000
1200
1400
1600
1800
2000
2200
2400
2600
2800
3000
3200
3400
wysokoæ w m n.p.m.
skala 1:75 000
1200
1400
1600
1800
2000
2200
2400
2600
2800
3000
3200
3400
wysokoæ w m n.p.m.
skala 1:75 000
Strona 6 z 14
= = =
tunel
wyci¹g
Zadanie 19. (0–1)
Ró¿nica wysokoci pomiêdzy wjazdem do tunelu a najwy¿szym wzniesieniem wynosi
1800 m. Ró¿nica temperatur wynosi rednio 0,6
°
C na ka¿de 100 metrów ró¿nicy
wysokoci. Ile wynosi temperatura powietrza przy wjedzie do tunelu, je¿eli na szczycie
jest -10
°
C?
A. oko³o – 21
°
C
B. oko³o – 6
°
C
C. oko³o 1
°
C
D. oko³o 6
°
C
Zadanie 20. (0–1)
Maciek wjecha³ na szczyt góry kolejk¹ linow¹ w czasie 10 minut.
Z jak¹ redni¹ szybkoci¹ porusza³a siê ta kolejka? Wykorzystaj informacje
zamieszczone na tablicy
zawieszonej przed wejciem do kas.
Tablica informacyjna
D³ugoæ trasy kolejki
1200
metrów
Cena biletu w górê
10 z³
A. 2 m/s
B. 4 m/s
C. 15 m/s
D. 150 m/s
Mi³onicy komputerów
Zadanie 21. (0–1)
Pasj¹ Filipa s¹ komputery. Filip wie, ¿e elementarn¹ jednostk¹ informacji jest bit. Jeden bit
informacji jest kodowany jedn¹ z dwóch wartoci 0 lub 1. Dwóm bitom odpowiadaj¹ cztery
mo¿liwoci: 00, 01, 10, 11. Ile mo¿liwoci odpowiada trzem bitom?
A. 2
B. 4
C. 6
D. 8
Zadanie 22. (0–1)
Fili
p zamieci³ na swojej stronie internetowej nastêpuj¹ce informacje dotycz¹ce planet
Uk³adu S³onecznego.
Lp.
Nazwa planety
Masa planety w
stosunku do masy
Ziemi
Liczba
ksiê¿yców
1. Merkury
0,06
0
2. Wenus
0,82
0
3. Ziemia
1
1
4. Mars
0,11
2
5. Jowisz
317,9
16
6. Saturn
95,18
20
7. Uran
14,5
17
8. Neptun
17,24
8
9. Pluton
0,002
1
Tablice geograficzne, Wyd. Adamantan, Warszawa 1998
Która z planet o masie mniejszej ni¿ masa Ziemi ma najwiêcej ksiê¿yców?
A. Mars
B. Saturn
C. Neptun
D. Pluton
Strona 7 z 14
Tablica informacyjna
D³ugoæ trasy kolejki
1200
metrów
Cena biletu w górê
10 z³
Zadanie 23. (0–1)
Dorota stworzy³a bazê danych o krajach azjatyckich. Zamieci³a w niej nastêpuj¹ce
informacje na temat Mongolii:
Mongolia
ludnoæ stolica
w tysi¹cach
nazwa
ludnoæ w tys.
2538
U³an Bator 627
Tablice geograficzne, Wyd. Adamantan, Warszawa 1998
W stolicy Mongolii mieszka:
A. prawie co drugi mieszkaniec Mongolii
B. prawie co czwarty mieszkaniec Mongolii
C. prawie co dziesi¹ty mieszkaniec Mongolii
D. prawie co trzysta czterdziesty mieszkaniec Mongolii
Zadanie 24. (0–1)
Do pracowni
komputerowej zakupiono 8 nowych monitorów i 6 drukarek za ³¹czn¹
kwotê 9400 z³. Drukarka by³a o 300 z³ tañsza ni¿ monitor. Cenê monitora mo¿na
obliczyæ, rozwi¹zuj¹c równanie:
A. 8x + 6(x + 300) = 9400
B. 8x + 6(x – 300) = 9400
C. 8(x-300) + 6x = 9400
D. 8(x + 300) + 6(x-300) = 9400
Zadanie 25. (0–1)
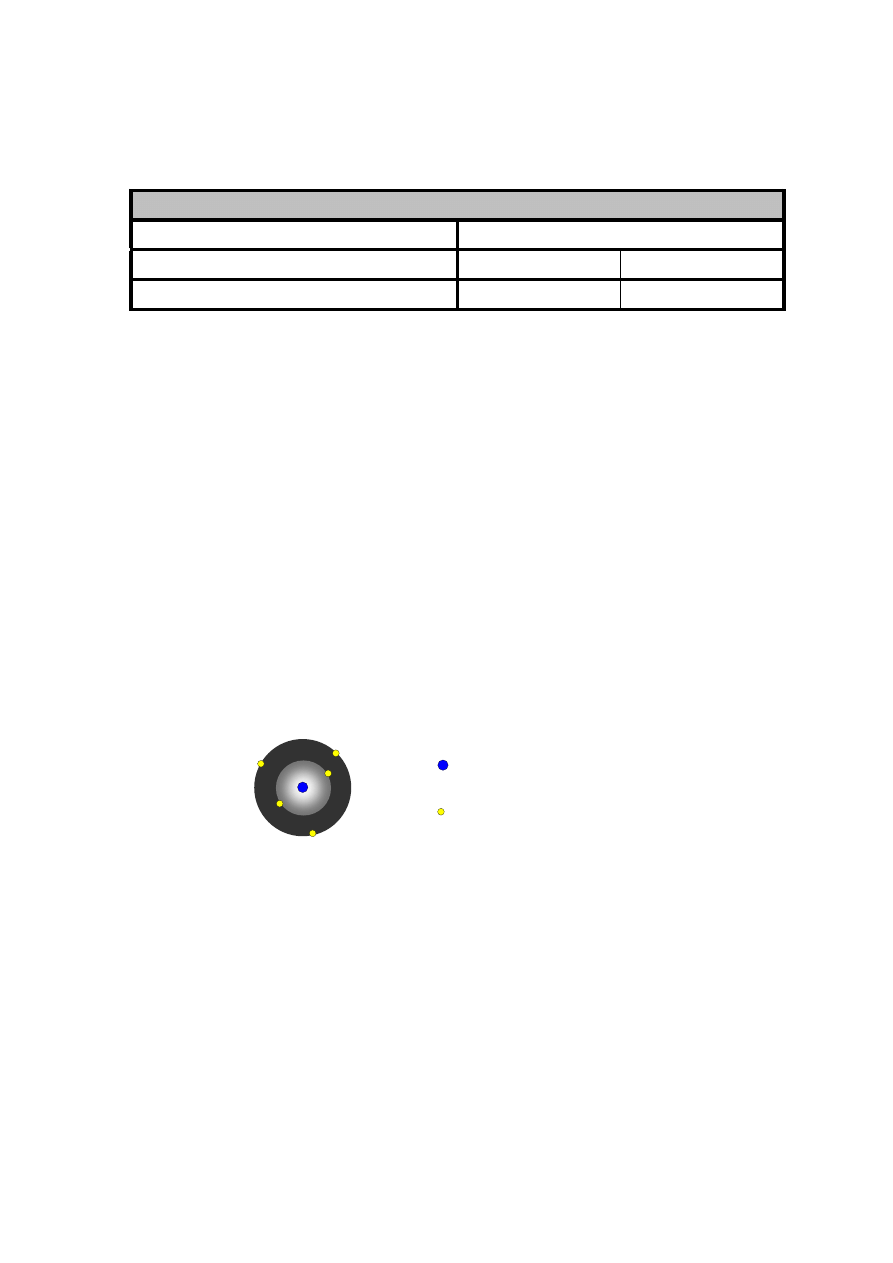
W programie komputerowym do nauki chemii Marta znalaz³a nastêpuj¹cy rysunek:
uproszczony model atomu
Na podstawie rysunku mo¿na stwierdziæ, ¿e atom tego pierwiastka:
A. nie zawiera protonów
B. zawiera jeden neutron
C. zawiera szeæ cz¹stek elementarnych
D. posiada trzy elektrony walencyjne
j¹dro atomowe
elektron
Strona 8 z 14
Zadanie 26. (0–3)
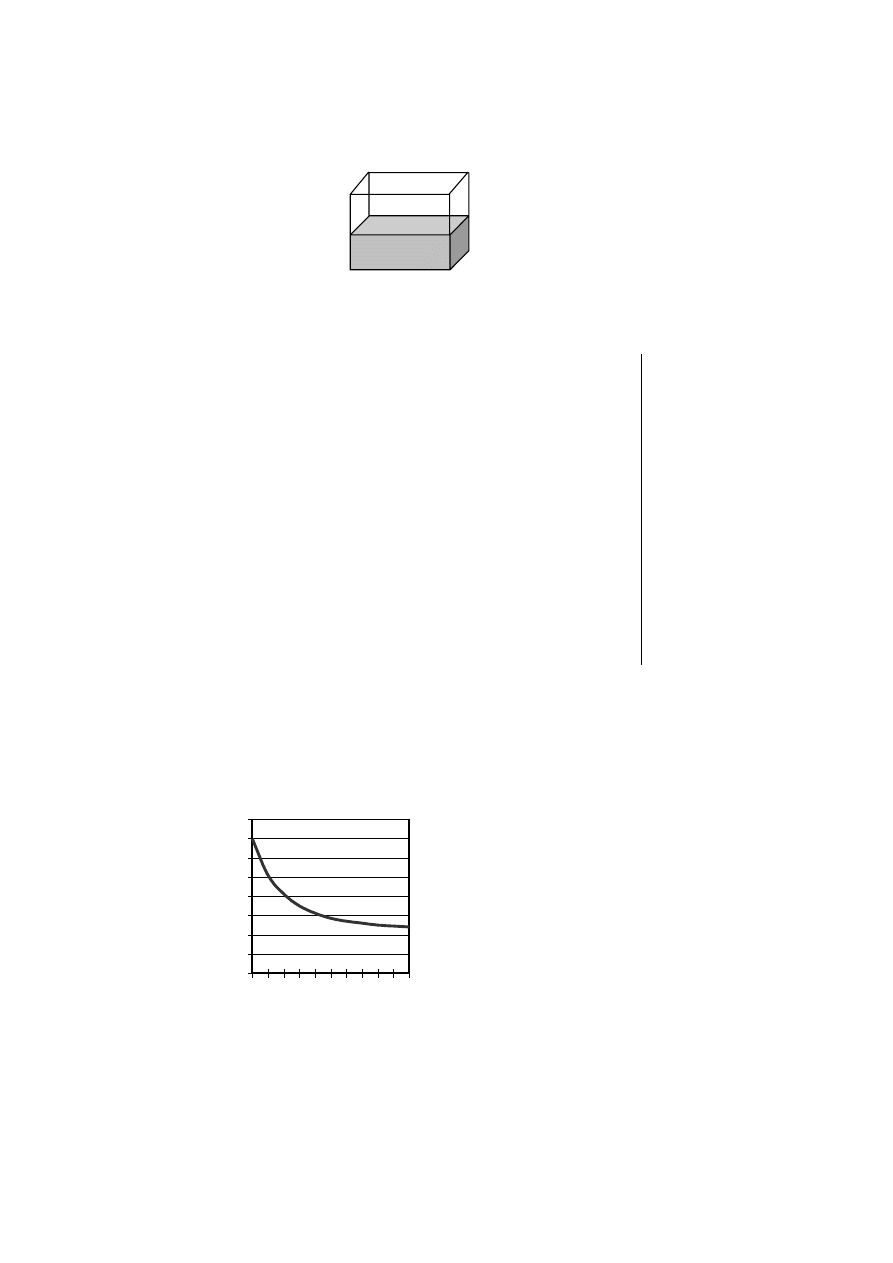
Akwarium, w którym Marek hoduje rybki, ma wymiary 5 dm, 8 dm, 6 dm. Marek
wlewa do niego wodê przep³ywaj¹c¹ przez kran z szybkoci¹ 8 dm
3
na minutê.
Do jakiej wysokoci woda w akwarium bêdzie siêgaæ po 10 minutach. Zapisz obliczenia.
Brudnopis
Zadanie 27. (0–1)
Jednym z warunków istnienia ¿ycia w rodowisku wodnym jest obecnoæ
rozpuszczonego w wodzie tlenu. Przeanalizuj poni¿szy wykres i wyjanij jednym
zdaniem, dlaczego wzrost temperatury wody w akwarium mo¿e przyczyniæ siê do niêcia
ryb.
.....................................................................................................................................................
.....................................................................................................................................................
6 dm
5 dm
8 dm
0
0,001
0,002
0,003
0,004
0,005
0,006
0,007
0,008
0
20
40
60
80
100
temperatura [
0
C]
rozpu
szczal
noæ tl
enu
[w gramach na 100 gramów
wody]
Strona 9 z 14
Zadanie 28. (0–2)
Rysunek przedstawia g³owê ryby. Wskazany strza³k¹ narz¹d to..........................................
Narz¹d ten odpowiada za proces ............................................... .
Mi³onicy p³ywania
Zadanie 29. (0–3)
Marcin przebywa autobusem
4
3 drogi do jeziora, a pozosta³¹ czêæ piechot¹. Oblicz
odleg³oæ miêdzy domem Marcina a jeziorem, je¿eli trasa, któr¹ przebywa pieszo, jest
o 8 km krótsza ni¿ trasa, któr¹ przebywa autobusem. Zapisz obliczenia.
Brudnopis
Strona 10 z 14
kie
runek ruchu ³ódki
jezioro
³ódka
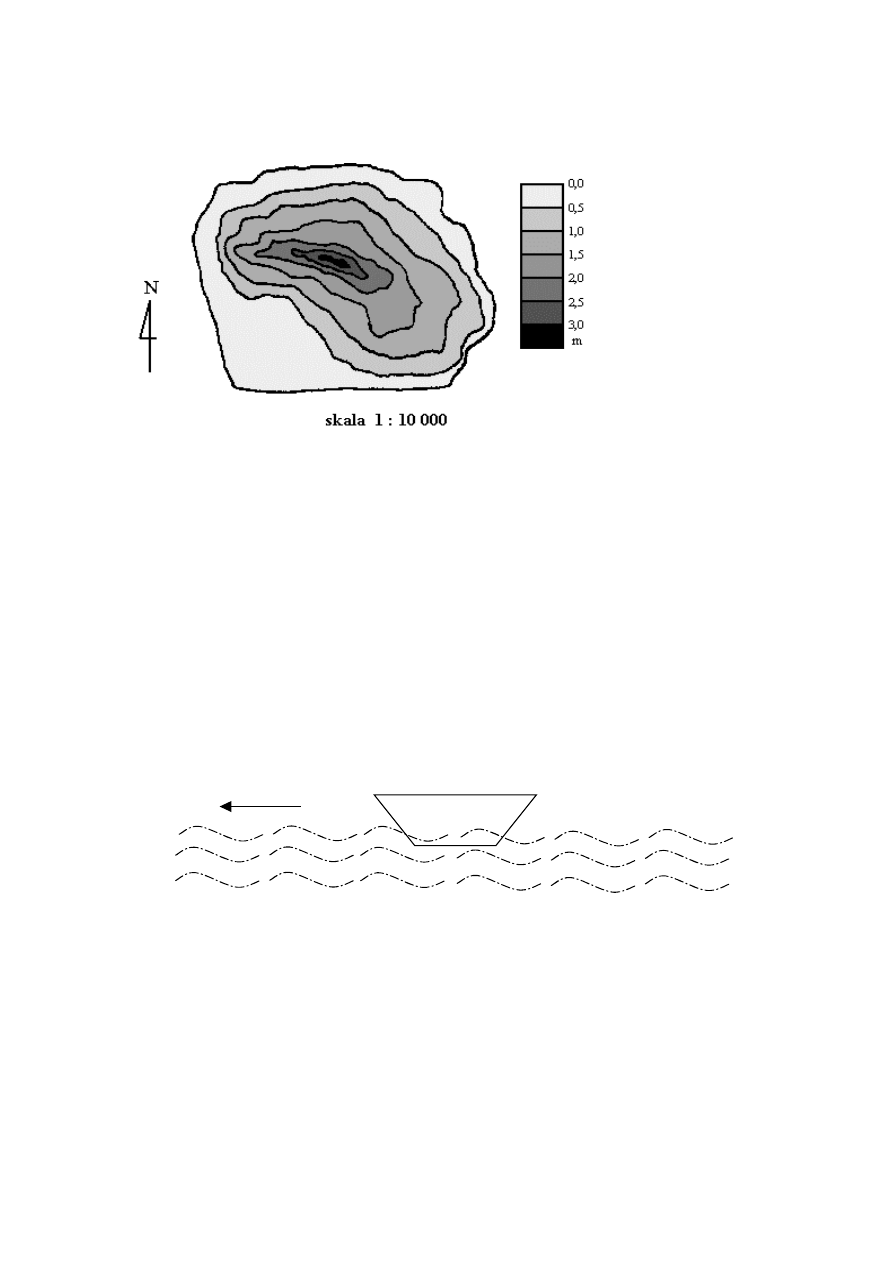
Zadanie 30. (0–3)
Przerywan¹ lini¹ zaznacz na mapie w po³udniowo-zachodniej czêci jeziora bezpieczne
k¹pielisko dla doros³ych – o g³êbokoci do 1,5 m.
Jaka jest najwiêksza g³êbokoæ tego jeziora?
Zadanie 31. (0–2)
Na ³ódkê poruszaj¹c¹ siê ruchem jednostajnym po jeziorze dzia³aj¹ cztery si³y:
si³a ciê¿aru ³ódki
)
(Q
r
, si³a wyporu
)
(
w
F
r
,
si³a ci¹gu silnika
)
( F
r
, si³a oporu ruchu
)
(
op
F
r
Na powy¿szym schemacie narysuj wektory wymienionych si³ i podpisz je zgodnie
z oznaczeniami podanymi w nawiasach.
Odpowied: ..............................................................................
Strona 11 z 14
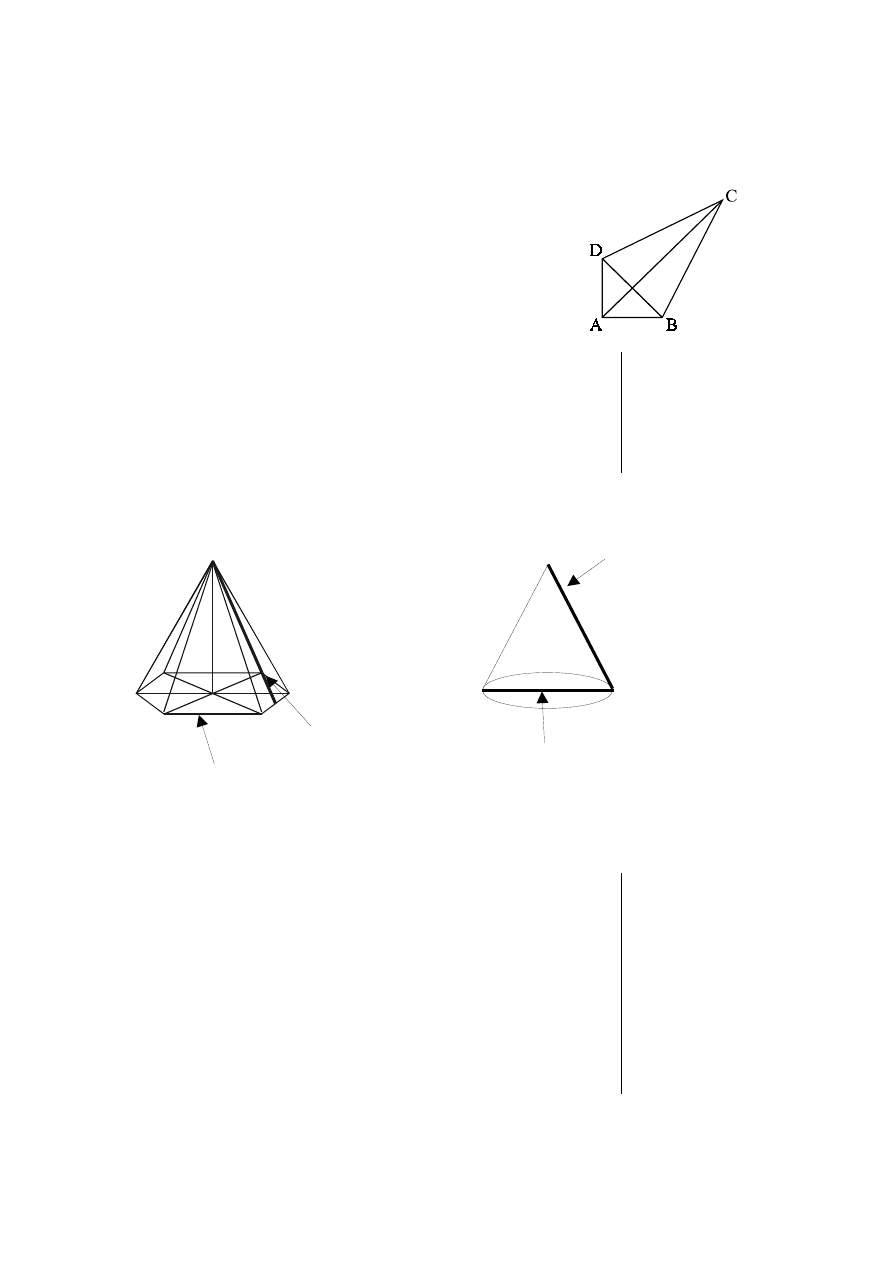
Majsterkowicze
Zadanie 32. (0–2)
Przed przyst¹pieniem do budowy latawca Janek rysuje jego model. Model ten
przedstawiono na rysunku w skali 1:10. Oblicz pole powierzchni latawca zbudowanego
przez Janka, wiedz¹c, ¿e d³ugoci odcinków AC i BD równe s¹ odpowiednio 4 cm i 2 cm,
oraz AC
⊥
BD i S –
rodek BD. Zapisz obliczenia.
Brudnopis
Zadanie 33. (0–3)
Na zabawê karnawa³ow¹ Beata wykona³a kartonowe czapeczki w kszta³cie bry³
narysowanych poni¿ej:
Ile papieru zu¿y³a na ka¿d¹ z czapeczek? Na któr¹ czapeczkê zu¿y³a wiêcej papieru?
Zapisz obliczenia.
Brudnopis
30 cm
d³ugoæ tworz¹cej
d³ugoæ rednicy 20 cm
S
30 cm
wysokoæ ciany
bocznej
10 cm
d³ugoæ krawêdzi podstawy
w kszta³cie szeciok¹ta foremnego
Strona 12 z 14
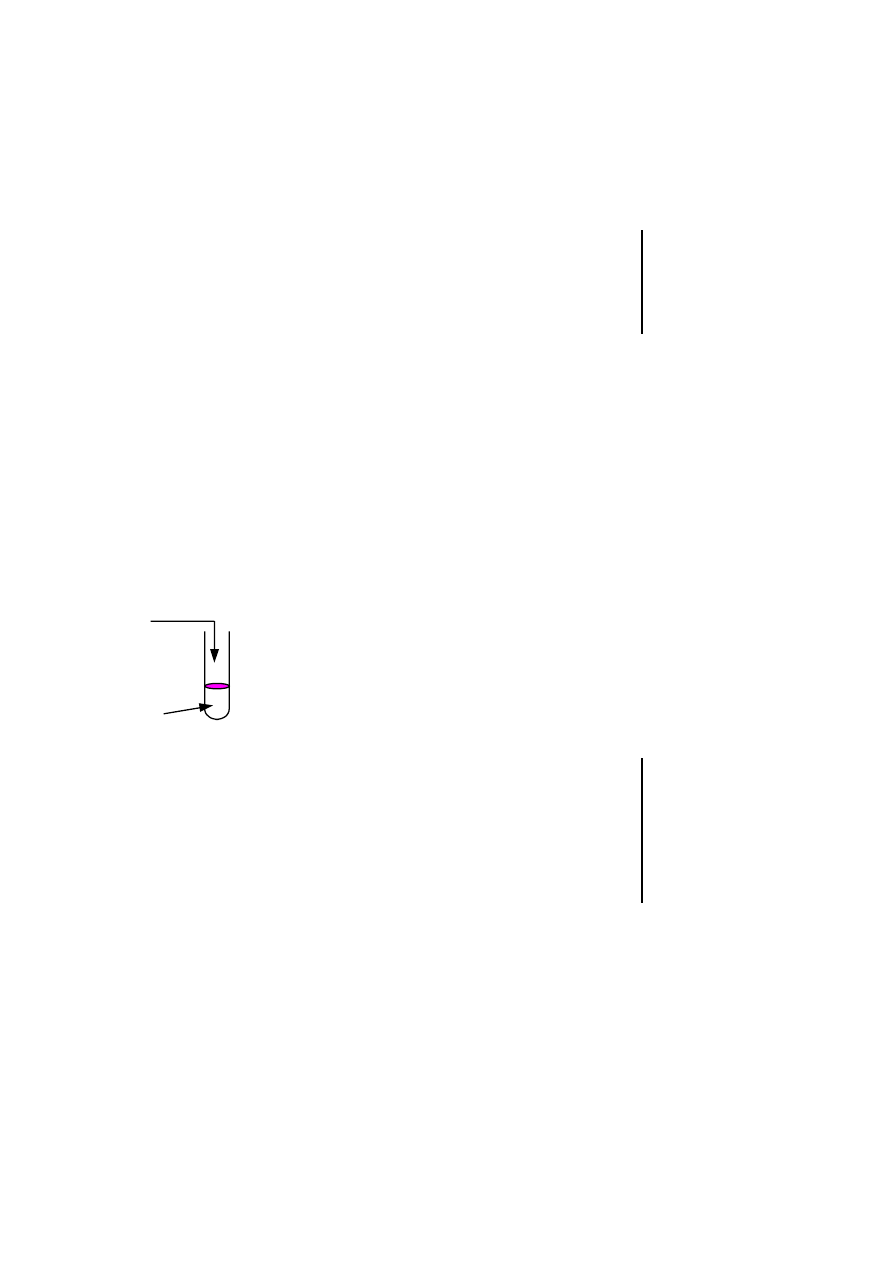
Zadanie 34. (0–1)
Zbyszek postanowi³ zbudowaæ samodzielnie owietlenie choinkowe zasilane napiêciem
220 woltów. W tym celu kupi³ w sklepie elektrycznym ¿aróweczki dostosowane do
napiêcia 11 woltów ka¿da.
Oblicz, ile ¿aróweczek Zbyszek powinien po³¹czyæ szeregowo, aby ¿aróweczki dzia³a³y
w takich warunkach, do jakich s¹ dostosowane.
Brudnopis
Uczestnicy kó³ zainteresowañ
Zadanie 35. (0–3)
Na zajêciach kó³ka chemicznego uczniowie przeprowadzali reakcjê zobojêtniania. Do
roztworu wodorotlenku sodu (M
NaOH
= 40u) dodali fenoloftaleinê, a nastêpnie wkraplali
rozcieñczony roztwór kwasu mrówkowego (M
HCOOH
= 46u). Punkt zobojêtnienia
uzyskali w momencie odbarwienia wskanika. Zapisz równanie przeprowadzonej
reakcji i oblicz, ile gramów kwasu potrzeba do z
obojêtnienia roztworu zawieraj¹cego
10 gramów NaOH.
Brudnopis
Zadanie 36. (0–2)
Na zajêciach ko³a biologicznego uczniowie prowadzili obserwacje mikroskopowe tkanek
zwierzêcych. Robert nastêpuj¹co opisa³ obserwowan¹ tkankê:
„Komórki tej
tkanki cile przylegaj¹ do siebie, ³¹czy je niewielka iloæ substancji
miêdzykomórkowej. Mog¹ tworzyæ jedn¹ lub kilka warstw.
Opis Roberta dotyczy tkanki ..............................................
G³ówn¹ funkcj¹ tej tkanki jest ...........................................
+ fenoloftaleina
HCOOH
NaOH
Strona 13 z 14
Brudnopis
Strona 14 z 14
SCHEMAT PUNKTOWANIA ARKUSZA EGZAMINACYJNEGO DLA GIMNAZJUM Z ZAKRESU
PRZEDMIOTÓW MATEMATYCZNO – PRZYRODNICZYCH (A1)
Poznaj zainteresowania rówieśników
Z a d a n i a z a m k n i ę t e
N r
z a d a n i a
P o p r a w n e
o d p o w i e d z i
L i c z b a
p u n k t ó w
N r
z a d a n i a
P o p r a w n e
o d p o w i e d z i
L i c z b a
p u n k t ó w
1 C 0 - 1
1 4 C 0 - 1
2 A 0 - 1
1 5 A 0 - 1
3 B 0 - 1
1 6 B 0 - 1
4 B 0 - 1
1 7 B 0 - 1
5 B 0 - 1
1 8 C 0 - 1
6 C 0 - 1
1 9 C 0 - 1
7 C 0 - 1
2 0 A 0 - 1
8 D 0 - 1
2 1 D 0 - 1
9 C 0 - 1
2 2 A 0 - 1
1 0 B 0 - 1
2 3 B 0 - 1
1 1 A 0 - 1
2 4 B 0 - 1
1 2 B 0 - 1
2 5 D 0 - 1
1 3 D 0 - 1
- 1 -
Z a d a n i a o t w a r t e ( A 1 )
Nr
zad
Liczba
pkt
Poprawna odpowiedź
Punktacja
26
0-3
Pole podstawy prostopadłościanu
2
40
5
8
dm
dm
dm
=
⋅
Objętość wody przepływającej przez kran
w ciągu 10 min
3
3
80
min
8
min
10
dm
dm
=
⋅
h – wysokość do jakiej woda w akwarium
będzie sięgać po 10 min
dm
h
dm
h
dm
2
80
40
3
2
=
=
⋅
Po 10 min woda w akwarium sięgać będzie
na wysokość 2 dm.
obliczenie pola podstawy
akwarium –1pkt
obliczenie objętości wody
wpływającej przez kran w ciągu
10 min –1 pkt
obliczenie wysokości, do jakiej
woda sięgać będzie po 10 min
–1
pkt
27
0-1
Wraz ze wzrostem temperatury
rozpuszczalność tlenu w wodzie maleje
Ilość tlenu w wodzie maleje, ryby duszą
się.
poprawne uzasadnienie –1 pkt.
28
0-2
skrzela , wymiana gazowa
skrzela –1pkt
wymiany gazowej –1pkt
29 0-3
x-szukana
odległość
4
1
x –odległość pokonana pieszo
-ustalenie zależności między
poszczególnymi odcinkami
szukanej drogi
–1pkt
- 2 -
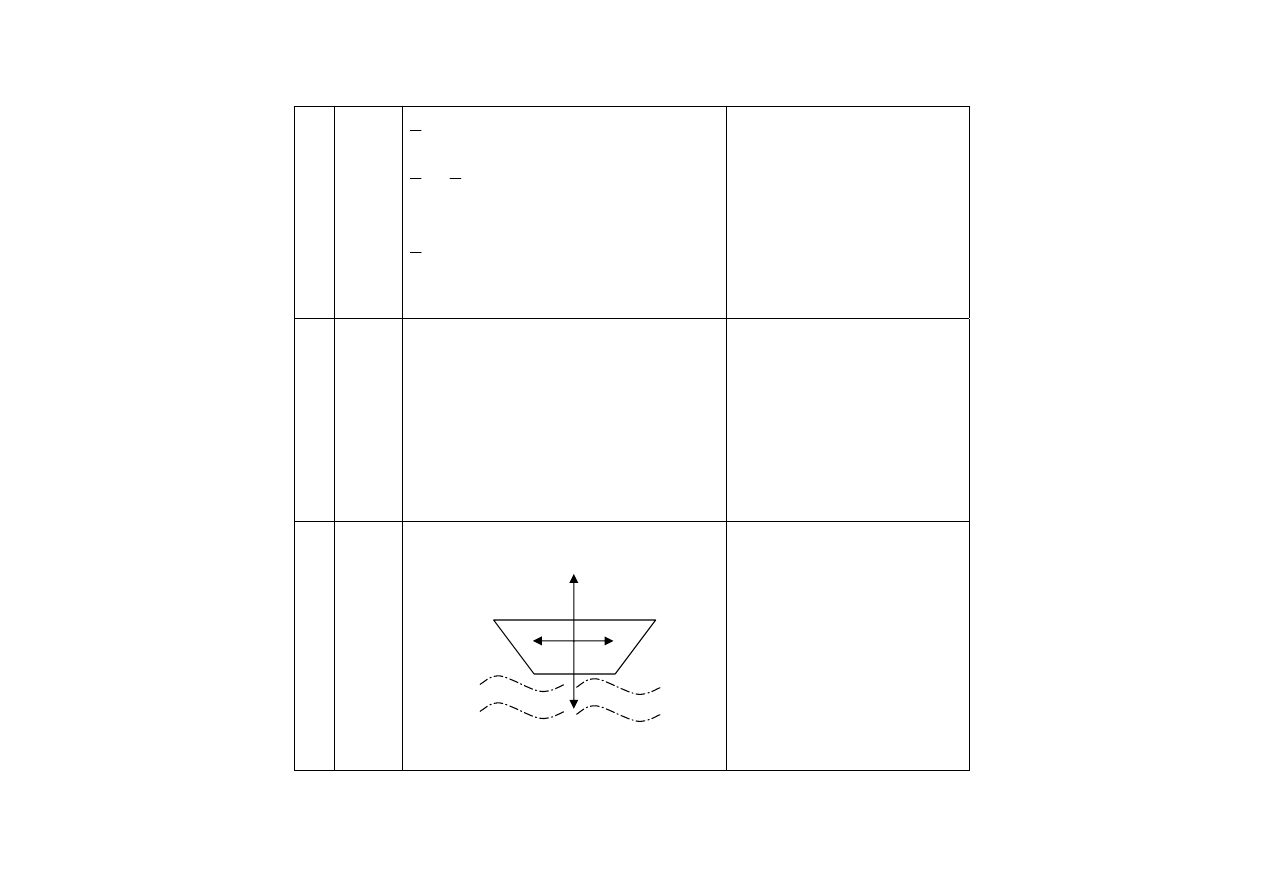
4
3
x- odległość pokonana autobusem
8
4
1
4
3
=
− x
x
16
8
2
1
=
=
x
x
-ułożenie równania –1pkt
-rozwiązanie równania
( zapisanie poprawnego
wyniku) –1pkt
30 0-3
Głębokość jeziora nie mniejsza niż 3 m.
-zaznaczenie obszaru nie
przekraczającego głębokości
1,5
m. –1
pkt
-zaznaczenie dowolnego
obszaru w południowo-
zachodniej części jeziora–1 pkt
-poprawne odczytanie
głębokości
–1pkt
31
0 - 2
w
F
r
F
r
op
F
r
Q
r
-narysowanie i oznaczenie
wektorów sił (F
w
, Q) o
kierunku pionowym, tych
samych wartościach i
przeciwnych zwrotach –1pkt
-narysowanie i oznaczenie
wektorów sił (F, F
op
) o
kierunku poziomym, tych
samych wartościach i
przeciwnych zwrotach –1pkt
- 3 -
32
0-2
Pole deltoidu ABCD:
2
4
2
4
2
1
2
1
cm
P
cm
cm
P
BD
AC
P
=
⋅
⋅
=
⋅
⋅
=
Pole latawca w skali 1 :1
2
2
2
2
400
4
100
4
10
cm
cm
cm
=
⋅
=
⋅
Pole powierzchni latawca
jest równe 400 cm
2
.
obliczenie pola deltoidu ABCD
–1pkt
obliczenie pola latawca w skali
1:1 –1
pkt
33 0-3
2
1
1
900
30
10
2
1
6
cm
P
cm
cm
P
=
⋅
⋅
⋅
=
2
2
2
2
2
942
300
30
10
cm
P
cm
P
cm
cm
P
≈
=
⋅
⋅
=
π
π
P
2
> P
1
Na wykonanie czapeczki w
kształcie stożka Beata zużyła więcej
papieru.
obliczenie P
1
-pow. bocznej
ostrosłupa
–1 pkt
obliczenie P
2
-pow. bocznej
stożka –1
pkt
porównanie
–1
pkt
34 0-1
220V:11V=20
odp. 20 żaróweczek
podanie liczby żarówek–1pkt
35
0-3
równanie reakcji:
NaOH + HCOOH → HCOONa + H
2
O
obliczenie ilości kwasu:
40 u NaOH --- 46 u HCOOH
10 g NaOH --- x g HCOOH
x = 11,5 gramów
poprawne zapisanie równania
reakcji –1
pkt
ułożenie proporcji –1 pkt
podanie wyniku –1 pkt
36 0-2
nabłonkowa,
np. ochronna
poprawna nazwa tkanki–1 pkt
nazwa
funkcji
–1
pkt
- 4 -
- 5 -
-
1 -
Kartoteka gimnazjalnego arkusza egzaminacyjnego
z zakresu przedmiotów matematyczno – przyrodniczych (A1)
Poznaj zainteresowania rówieśników
Sprawdzana umiejętność
Nr
zadania
Standard
Uczeń:
Punktacja
1 II/1d
odczytuje
wskazaną wielkość z diagramu
0 – 1
2 II/2b
porównuje
wielkości odczytane z diagramu
0 – 1
3
I/2b
oblicza jakim procentem jednej liczby jest druga liczba,
wykorzystując wielkości odczytane z diagramu
0 – 1
4 I/2a
rozwiązuje zadanie tekstowe stosując w praktyce
różnicowe porównywanie dwóch wielkości
0 – 1
5 I/2a
rozwiązuje zadanie tekstowe stosując w praktyce
ilorazowe porównywanie dwóch wielkości
0 – 1
6
I/1b
wskazuje cechy gadów
0 – 1
7 III/1d
określa porę roku na półkuli południowej
0 – 1
8 I/3a
ustala
liczbę osi symetrii oraz istnienie środka symetrii
przedstawionej na rysunku figury
0 – 1
9
IV/ 1a
na podstawie szybkości średniej oblicza czas trwania
ruchu i na podstawie warunków zadania ustala godzinę
rozpoczęcia ruchu
0 – 1
10 I/1b
wskazuje
związki organiczne pełniące w organizmie
funkcję energetyczną
0 – 1
11
III/3c
rozpoznaje ruch jednostajny na podstawie wykresu
0 – 1
12
II/1f
rozpoznaje na rysunku mięsień zginacz
0 – 1
13
II/1e
na podstawie rysunku rozpoznaje jodłę
0 – 1
14 I/1b
nazywa
grupę charakterystyczną dla kwasów
organicznych
0 – 1
15
III/3c
wskazuje argument, dla którego dwie funkcje opisane
słownie w tabelach przyjmują tą samą wartość
0 – 1
16 I/3b
oblicza
sumę długości trzech półokręgów o podanych
średnicach
0 – 1
17 II/1b
określa różnicę wysokości na podstawie mapy
poziomicowej
0 – 1
18
II/2c
dokonuje porównania przekroju góry z mapą poziomicową
0 – 1
19 III/4a
oblicza
temperaturę u podnóża góry na podstawie
informacji
0 – 1
20 I/2d
uczeń oblicza szybkość średnią na podstawie danych
zamieszczonych w tabeli
0 – 1
21 IV/1b
wskazuje
liczbę wszystkich ustawień zero-jedynkowych
w ciągu 3 elementowym
0 – 1
22
II/1c
analizuje dane dotyczące planet Układu Słonecznego
0 – 1
23
I/2c
oblicza stosunek wielkości odczytanych z tabeli
0 – 1
24
III/2d
wskazuje równanie opisujące zależności podane w treści
zadania
0 – 1
25
II/1e
wnioskuje o budowie atomu na podstawie jego modelu
0 – 1
26 I/3b,
I/3b,
I/3b
oblicza objętość wody wlewanej do naczynia o podanych
wymiarach oraz wysokość do jakiej będzie ona sięgać w
0 – 3
-
2 -
tym naczyniu
27
II/1d
analizuje wykres rozpuszczalności tlenu w wodzie
0 – 1
28
II/2d, III/1a rozpoznaje skrzela i określa ich funkcję
0 - 2
29 IV/2a,
IV/3b,
IV4a
układa i rozwiązuje równanie odpowiadające warunkom
zadania
0 - 3
30 II/2f,
II/2f,
II/2f
zaznacza na rysunku obszar uwzględniając odpowiedni
kierunek i głębokość, odczytuje głębokość jeziora
0 – 3
31
III/2a, III/1d nanosi na rysunku wektory sił
0 – 2
32
I/3b, I/3c
oblicza pole deltoidu oraz deltoidu podobnego w skali
10:1
0 – 2
33 IV/2a,
IV/3b,
IV/5b
oblicza i porównuje pole powierzchni bocznej
graniastosłupa prawidłowego sześciokątnego oraz pole
powierzchni bocznej stożka
0 – 3
34 III/1a
oblicza
liczbę żarówek w szeregowym obwodzie
elektrycznym
0 – 1
35 III/2d
IV/4b, IV/4a
pisze równanie reakcji zobojętniania
oblicza liczbę gramów kwasu potrzebną do zobojętnienia
danej ilości zasady
0 – 1
0 – 2
36
II/1a, II/2e
na podstawie opisu rozpoznaje tkankę nabłonkową i
określa jej główną funkcję
0 – 2
Document Outline