wspólny cel...

© Copyright by ZamKor

P. Sagnowski i Wspólnicy sp. j.

ul. Tetmajera 19, 31-352 Kraków

tel. [phone]

faks [phone]

e-mail: [e-mail]

adres ser wisu: www.zamkor.pl

ZamKor

Zadania z fizyki z czêœci matematyczno-przyrodniczej

egzaminu gimnazjalnego 2010

Zadan ie 21. (0-1)

Na ¿arówkach do latarek znajduj¹ siê informacje o warunkach ich pracy.

Je¿eli w tym samym czasie ka¿da z ¿arówek pracuje w warunkach zgodnych z umieszczon¹ na niej
informacj¹, to
A. pierwsza ¿arówka pobiera pr¹d o wiêkszej mocy.
B. do pierwszej ¿arówki przy³o¿one jest mniejsze napiêcie.
C. przez drug¹ ¿arówkê p³ynie pr¹d o wiêkszym natê¿eniu.
D. opór pierwszej ¿arówki jest wiêkszy ni¿ drugiej.

Zadanie 22. (0-1)

Pawe³ uchyli³ drzwi z ciep³ego pokoju do zimnego korytarza. Wzd³u¿ pionowej szczeliny
powsta³ej miêdzy drzwiami i framug¹ przesuwa³ zapalon¹ œwieczkê. W którym
fragmencie szczeliny p³omieñ œwieczki powinien odchyliæ siê od pionu najmniej?
A. W œrodkowym.
B. W dolnym.
C. W górnym.
D. Wszêdzie jednakowo.

Zadanie 27. (0-3)

Oblicz, jak¹ objêtoœæ mia³ Cullinan (najwiêkszy znaleziony diament). Przyjmij, ¿e gêstoœæ diamentu wynosi
3 2

3

, g cm . Zapisz obliczenia. Wynik zaokr¹glij do ca³oœci.

Zadanie 28. (0-3)

Ola wla³a æwieræ litra wody o temperaturze 20

o

C do czajnika o mocy 1000 W. Do ogrzania 1 kg wody o 1

o

C

potrzeba 4200 J energii. Oblicz, po jakim czasie woda w czajniku osi¹gnie temperaturê wrzenia 100

o

C.

Przyjmij, ¿e 1 litr wody ma masê 1 kg, a ca³e ciep³o wydzielane w grza³ce jest pobierane przez wodê. Zapisz
obliczenia.

Do kum ent zosta³ po brany z ser wisu Zam Kor.

Wszel kie prawa zastr ze¿one.

Data utwor zenia:

2010-05-26

Stro na 1

2,4 V 0,75 A

pierwsza ¿arówka

2,4 V 0,5 A

druga ¿arówka

wspólny cel...

© Copyright by ZamKor

P. Sagnowski i Wspólnicy sp. j.

ul. Tetmajera 19, 31-352 Kraków

tel. [phone]

faks [phone]

e-mail: [e-mail]

adres ser wisu: www.zamkor.pl

ZamKor

Informacje do zadañ 29. i 30.
Pracownik ochrony chodzi wzd³u¿ ogrodzenia parkingu (w kszta³cie trapezu prostok¹tnego) ze sta³¹ prêd -
koœci¹ 1 m/s. Obchód zaczyna od wartowni A. Na rysunku przedstawiono plan jego trasy, a obok podano
wymiary parkingu.

AB = 125 m
BC = 65 m
CD = 100 m
AD = 60 m

Zadanie 29. (0-2)

Minê³o 10 minut od chwili rozpoczêcia obchodu. Na którym odcinku znajduje siê pracownik ochrony? Zapisz
obliczenia.

Informacje do zadañ 33. i 34.
Roœliny wbudowuj¹ w swoje tkanki zarówno wêgiel

12

C, jak i promieniotwórczy wêgi

14

C. Na skutek

samoistnego rozpadu

14

C jeden gram wêgla w ¿ywym drzewie emituje oko³o 16 cz¹stek beta na minutê.

Kiedy roœlina obumiera, proces przyswajania wêgla ustaje i zawartoœæ izotopu

14

C w jej tkankach zaczyna

maleæ. Czas po³owicznego rozpadu wêgla

14

C wynosi 5700 lat.

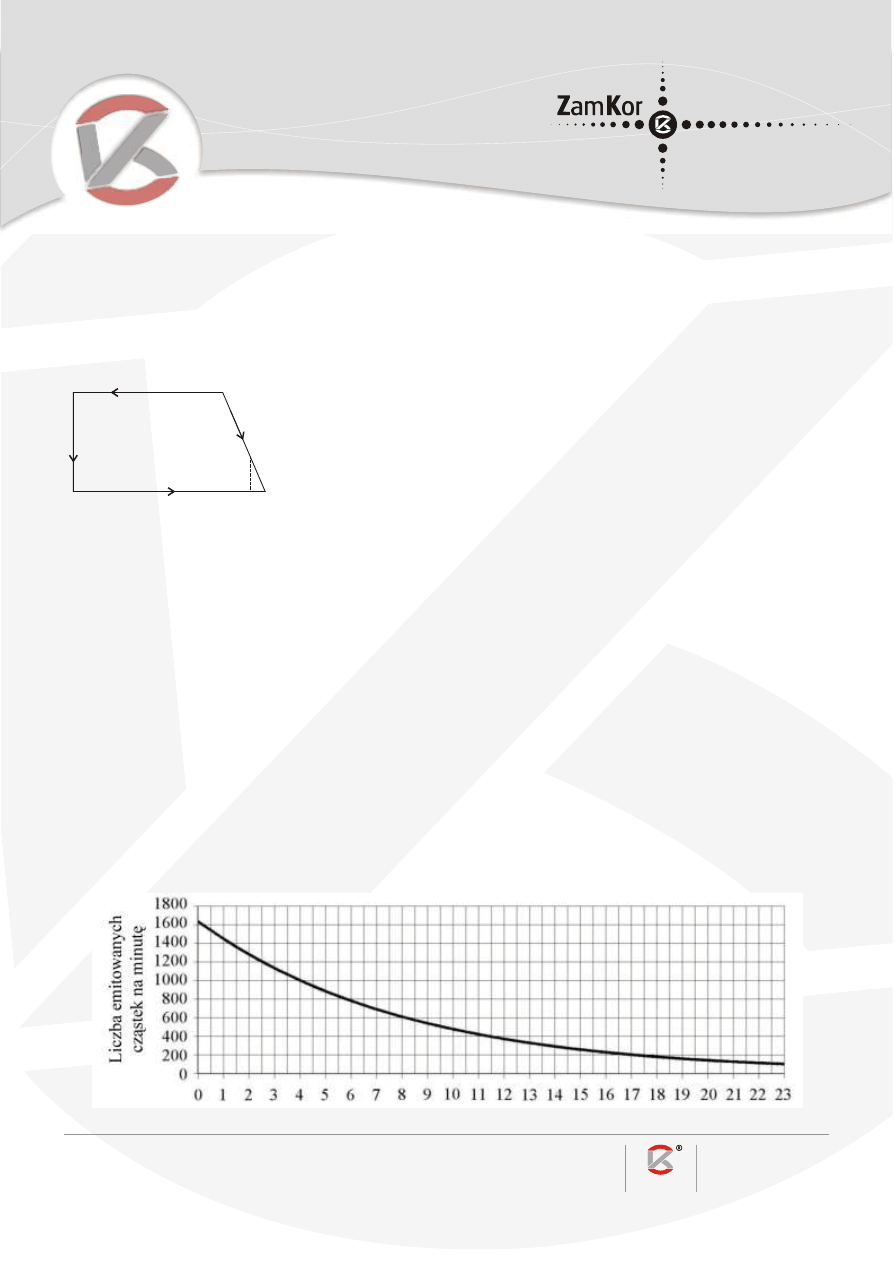
Na wykresie przedstawiono, jak zmienia³a siê emisja cz¹stek beta ze 100 g wêgla w ci¹gu 23 000 lat po
obumarciu drzewa.

Liczba cz¹stek beta emitowanych przez 100 g wêgla na minutê w zale¿noœci od czasu, jaki up³yn¹³ od

chwili obumarcia drzewa

Do kum ent zosta³ po brany z ser wisu Zam Kor.

Wszel kie prawa zastr ze¿one.

Data utwor zenia:

2010-05-26

Stro na 2

A

F B

C

D

F

Zadanie 33. (0-1)

Sto gramów wêgla zawartego w drewnie ze szcz¹tków prehistorycznych narzêdzi emituje 500 cz¹stek beta na
minutê. Ile tysiêcy lat temu obumar³o drzewo, z którego wykonano te narzêdzia?

Zadanie 34. (0-1)

Przedstaw, uzupe³niaj¹c tabelê, jak zmienia³a siê emisja cz¹stek beta z 50 g wêgla w ci¹gu 17 100 lat od
chwili obumarcia drzewa.

Czas od chwi li obumarc ia drze wa w latach

0

5 700

11 400

17 100

Licz

ba cz¹stek beta wyemit

owa

nych przez 50 g

wêgla w ci¹gu minuty

100

Do kum ent zosta³ po brany z ser wisu Zam Kor.

Wszel kie prawa zastr ze¿one.

Data utwor zenia:

2010-05-26

Stro na 3

Rozwi¹zania zadañ z fizyki z czêœci matematyczno-przyrodniczej

egzaminu gimnazjalnego 2010

Zadan ie 21. (0-1)

Moc urz¹dzenia wyra¿a siê wzorem

P

UI

=

Na tej podstawie wnioskujemy, ¿e pierwsza ¿arówka pracuje z wieksz¹ moc¹.
OdpowiedŸ poprawna A.

Zadanie 22. (0-1)

Zadanie dotyczy zjawiska konwekcji. Jest to sposób transportu energii, któremu towarzyszy trans port masy
gazu lub cieczy.
Gêstoœæ zimnego powietrza w korytarzu jest wiêksza od gêstoœci ciep³ego powietrza w pokoju. Przy pod³odze
powietrze z korytarza przemieszcza siê do pokoju (tak, jak w zimie powietrze przez uchylone okno wp³ywa do
pokoju i ch³odzi nasze stopy). P³omieñ umieszczonej tam œwieczki jest odchylony w stronê pokoju. Powietrze,
wp³ywaj¹ce z korytarza jest ogrzewane, rozszerza siê, jego gêstoœæ maleje i zgodnie z prawem Archimedesa
unosi siê w górê. Pod sufitem ciep³e powietrze przemieszcza siê do korytarza. P³omieñ umieszczonej pod
sufitem œwieczki odchyla siê w stronê korytarza. Najwiêksza szansa na to, ¿e p³omieñ ustawi siê pionowo
jest w œrodkowej czêœci szczeliny.
OdpowiedŸ poprawna A.

Zadanie 27. (0-3)

Do rozwi¹zania tego zadania nale¿y skorzystaæ z „Informacji do zadañ 25–27”.

Dane: m =

×

=

3106 0 2

621 2

,

,

g

g, r = 3 2

3

,

g

cm

Szukane: V
Rozwi¹zanie:

r =

m

V

sk¹d V

m

=

r

V =

»

621 2

3 2

194

3

3

,

,

g

g

cm

cm

OdpowiedŸ: Cullinan mia³ objêtoœæ oko³o 194

3

cm .

Do kum ent zosta³ po brany z ser wisu Zam Kor.

Wszel kie prawa zastr ze¿one.

Data utwor zenia:

2010-05-26

Stro na 4

Zadanie 28. (0-3)

Sposób rozwi¹zania zadania zale¿y od tego, czy uczeñ pozna³ w gimnazjum i rozumie pojêcie ciep³a
w³aœciwego.
Jeœli tak, to potrafi³ na podstawie tematu zadania wywnioskowaæ, ¿e ciep³o w³aœciwe wody wynosi

c

w

=

×°

4200

J

kg C

. Pozosta³e dane to:

m =

1

4

kg, Dt =

° -

° =

°

100

20

80

C

C

C, P = 1000 W

Szukane: czas ogrzewania t
Rozwi¹zanie:
Praca W

P

= t wykonana przez pr¹d elektryczny p³yn¹cy w grza³ce czajnika powoduje wzrost energii

wewnêtrznej DE

w

grza³ki. Na skutek ró¿nicy temperatur pomiêdzy grza³k¹ i wod¹, zostaje wodzie przekazane

ciep³o:

Q

E

W

P

w

=

=

=

D

t

Przekazane wodzie ciep³o mo¿na wyraziæ tak¿e wzorem

Q

mc

t

w

=

D

Porównuj¹c oba wyra¿enia, otrzymujemy:

P

mc

t

w

t =

D sk¹d t =

mc

t

P

w

D

t =

×

×°

×

°

=

×

=

1

4

4200

80

1000

4200 20

1000

84

kg

J

kg C

C

W

J

J

s

s

OdpowiedŸ: Woda osi¹gnê³a temperaturê wrzenia po 84 s.

Jeœli z informacji, ¿e „do ogrzania 1 kg wody o 1° C potrzeba 4200 J” uczeñ nie potrafi wywnioskowaæ, ¿e

ciep³o w³aœciwe wody wynosi c

w

=

×°

4200

J

kg C

, mo¿e skorzystaæ z proporcji.

Jeœli do ogrzania 1 kg wody o 1° C potrzeba 4200 J,

to do ogrzania

1

4

kg wody o 1° C potrzeba

1

4

4200

1050

×

=

J

J.

Jeœli do ogrzania

1

4

kg wody o 1° C potrzeba 1050 J,

to do ogrzania

1

4

kg wody o 80° C potrzeba 80 1050

84 000

×

=

J

J.

Taka energia (ciep³o) zostaje przekazana wodzie przez grza³kê czajnika o mocy 1000 W w pewnym czasie t.

Do kum ent zosta³ po brany z ser wisu Zam Kor.

Wszel kie prawa zastr ze¿one.

Data utwor zenia:

2010-05-26

Stro na 5

P t = 84 000 J t =

=

84 000

1000

84

J

J

s

s

Zadanie 29. (0-2)

W celu obliczenia czasu potrzebnego na przejœcie ka¿dego z prostoliniowych odcinków korzystamy ze wzoru:

u =

s

t

sk¹d t

s

=

u

t

AB

=

=

125

1

125

m

m

s

s, t

BC

=

=

65

1

65

m

m

s

s, t

CD

= 100 s, t

DA

= 60 s

Sumujemy kolejne czasy dopóty, dopóki ca³kowity czas nie przekroczy 10 min, tj. 600 s.

t

t

t

t

t

AB

BC

CD

DA

1

350

=

+

+

+

=

s

t

t

t

t

AB

BC

CD

2

290

=

+

+

=

s

t

c

=

+

=

350

290

640

s

s

s

OdpowiedŸ: Pracownik ochrony jest na odcinku CD.

Zadanie 33. (0-1)

Z wykresu odczytujemy, ¿e skoro obecnie 100 g wêgla emituje 500 cz¹stek b na minutê, to drzewo obumar³o
9500 lat temu.

Zadanie 34. (0-1)

Z wykresu odczytujemy, ¿e w chwili obumarcia drzewa 100 g wêgla emitowa³o 1600 cz¹stek b na minutê,

wiêc 50 g wêgla emitowa³o w jednej minucie

1
2

1600

800

×

=

cz¹stek b. Po czasie równym okresowi

po³owicznego rozpadu (5700 lat) 50 g wêgla emitowa³o po³owê, czyli 400 cz¹stek b. Po up³ywie czasu
równego dwóm okresom po³owicznego rozpadu (11400 lat) liczba emitowanych cz¹stek zmala³a do 200
cz¹stek b, a po czasie 3 5700

17100

×

=

lat

lat zmala³a do 100 cz¹stek na minutê.

Do kum ent zosta³ po brany z ser wisu Zam Kor.

Wszel kie prawa zastr ze¿one.

Data utwor zenia:

2010-05-26

Stro na 6