D. McRuer “Man-Machine Systems”
The Electrical Engineering Handbook
Ed. Richard C. Dorf
Boca Raton: CRC Press LLC, 2000

© 2000 by CRC Press LLC

105

Man-Machine Systems

105.1 Introduction
105.2 Several Natures of Man-Machine Control—A Catalog

of Behavioral Complexities

105.3 Full-Attention Compensatory Operations—The

Crossover Model

Crossover Frequency for Full-Attention Operations • Remnant •
Effects of Changes in the Task Variables • Effects of Divided
Attention

105.1 Introduction

In principle the dynamic behavior of the human element in man-machine systems can be described in terms
similar to those used to describe other system elements. There are, however, major complications in quantifi-
cation because of the enormous versatility of the human engaged, simultaneously, as the on-going

architect

and

modifier of the man-machine system itself and as an operating entity within that system. In other words, the
adaptive and learning capabilities of the human permit both set-up and modification of the effective system
structure and the subsequent self-improvement and tuning of the human dynamic characteristics within that
structure.

The situations which are simplest to quantify are those in which the

machine

has time-stationary dynamic

properties and the human has, after architectural, learning, and adaptation phases, achieved a similar state.
Under these circumstances human dynamic operations can be characterized by quasi-linear describing functions
and a remnant [Graham and McRuer, 1961] or operator-induced noise. This is the context here.

105.2 Several Natures of Man-Machine Control—A Catalog

of Behavioral Complexities

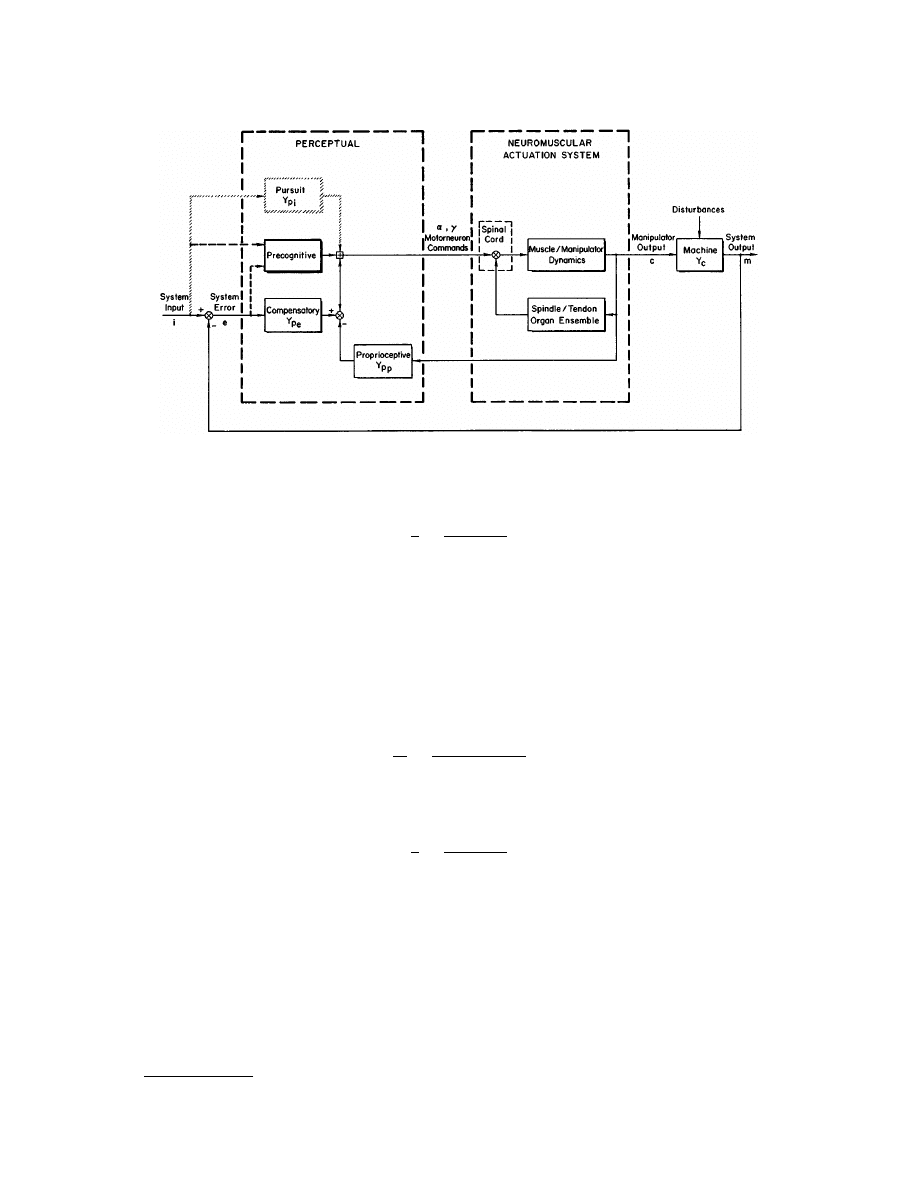
Figure 105.1 [McRuer and Krendel, 1974] shows a general quasi-linear man-machine system with time-
stationary properties. This diagram is suitable for the description of human behavior in an interactive man-
machine system wherein the human responds to visually sensed inputs and communicates with the machine
via a manipulator of some sort (e.g., control stick, wheel, pedal, etc.). This block diagram indicates the minimum
needed number of major functional signal pathways internal to the human operator to characterize different
behavioral features. The constituent human sensing, data processing, computing, and actuating elements are
connected as internal signal processing pathways which can be “reconfigured” as the situation changes. Such
reconfiguration is an aspect of human behavior as a system architect. Functional operations on internal signals
within a given pathway may also be modified.

The specific internal signal organizational possibilities depicted in

Fig. 105.1

have been discovered by manip-

ulating experimental situations (e.g., by changing system inputs and machine dynamics) to isolate different
combinations of the specific blocks shown [McRuer and Jex, 1967; McRuer and Krendel 1974; McRuer 1980].

To describe the parts of the figure start at the far right with the

controlled element

. This is the machine being

controlled by the human. To its left is the actual interface between the human and the machine—the neuromuscular

Duane McRuer

Systems Technology, Inc.

© 2000 by CRC Press LLC

actuation system, which is the human’s output mechanism. This in itself is a complicated feedback control
system capable of operating as an open-loop or combined open-loop/closed-loop system, although that level
of complication is not explicit in the simple feedback control system shown here. In the diagram the neuro-
muscular system comprises limb, muscle, and manipulator dynamics in the forward loop and muscle spindle
and tendon organ ensembles as feedback elements. Again, many more biological sensors and other elements
are actually involved; this description is intended only to be generally indicative of the minimum level of
complexity associated with the

human actuation elements.

All of these elements operate within the human at

the level from the spinal cord to the periphery.

There are other sensor systems, such as joint receptors and peripheral vision, which indicate limb output

position. These operate through higher centers and are subsumed in the

proprioceptive

feedback loop incorpo-

rating a block at the perceptual level further to the left in the diagram. If motion cues are present, these too
can be associated in similar proprioceptive blocks with feedbacks from the controlled element output.

The other three pathways shown at the perceptual level correspond to three different types of control

operations on the visually presented system inputs. Depending on which pathway is effectively present, the

H

AZARDOUS

E

NVIRONMENT

R

OBOTICS

eneb Robotics, Inc. is an internationally known leader in 3D graphics-based factory simulation,
telerobotics, and virtual reality software used widely in the aerospace, automotive, defense, envi-
ronmental, medical, nuclear, and research communities.

Among the company’s broad software product line is TELEGRIP™, which provides 3D graphical interface

for previewing, interactive programming, and real-time bilateral control of remote robotic devices. It
provides operators a system for safe, quick, and efficient remediation of hazardous environments from a
single point of control and input that is isolated from virtually all operator hazards.

Accurate 3D kinematic models of the robot and work space components allow the operator to preplan

and optimize robot trajectories before the program is automatically generated. Control commands are
monitored when running in autonomous, teleoperational, or shared control modes to assure procedural safety.

A video camera provides a Deneb Robotics engineer with a view of the robot. (Photo courtesy of National Aeronautics
and Space Administration.)

D

© 2000 by CRC Press LLC

control structure of the man-machine system can appear to be

open-loop

, or

combination open-loop/closed-loop

,

or totally

closed-loop

with respect to visual stimuli.

When the

compensatory

block is appropriate at the perceptual level, the human controller acts in response

to errors or controlled-element output quantities only. Only the

Y

pe

block “exists”, with

Y

pi

and the precognitive

block both equal to zero. With the compensatory pathway operational, continuous closed-loop control is exerted
on the machine so as to minimize system errors in the presence of commands and disturbances.

Compensatory

behavior

will characteristically be present when the commands and disturbances are random-appearing and

when the only information displayed to the human controller consists of system errors or machine outputs. In
the simple case where the describing function

Y

pe

is defined so as to account for the perceptual and neuromus-

cular components, the system is single-input/single-output, and the operator-induced noise is neglected, the
closed-loop system output/input dynamics will be

(105.1)

m

i

Y Y

Y Y

pe c

pe c

=

+

1

A key feature of TELEGRIP is a video overlay option that utilizes video to calibrate 3D computer models

with the actual environment. The video overlay technique is especially useful for on-line planning applica-
tions or teleoperations in remote, hazardous, or complex environments such as space, undersea, or nuclear
sites.

A virtual reality calibration technique was developed for reliable and accurate matching of a graphically

simulated environment in 3D geometry with actual video camera views. The system was designed for
predictive displays with calibrated graphics that overlay in live video for telerobotics applications. For
example, the system allows an operator to designate precise movements of a robot arm before sending the
command to execute.

Following successful test of the video overlay techniques, an agreement was concluded with Deneb

Robotics that allows the company to integrate video overlay into the commercially available TELEGRIP to
expand its use in hazardous environment robotics. (Courtesy of National Aeronautics and Space Adminis-
tration.)

The operator can view the video image of the real world environment (upper right) and the computer’s interpretation
of the same scene using TELEGRIP. (Photo courtesy of National Aeronautics and Space Administration.)

© 2000 by CRC Press LLC

and the error/input

(105.2)

Thus, for compensatory situations, the man-machine system emulates the classic single-input/single-output

feedback system. The output can be made to follow the input and the error can be reduced only by making
the open-loop describing function large compared to 1 over the operating bandwidth of the system.

When the command inputs can be distinguished from the system outputs by virtue of the display (e.g.,

i

and

m

are shown or detectable as separate entities relative to a reference) or preview (e.g., as in following a

curved course) the

pursuit

block in Fig. 105.1 comes into play and joins the compensatory. The introduction

of this new signal pathway provides an open-loop control in conjunction with the compensatory closed-loop
error correcting action. The output/input dynamics of the man-machine system will then become

(105.3)

and the error/input describing function is

(105.4)

With the pursuit system organization the error can be reduced by the human’s operations in two ways: by
making the open-loop describing function large compared with 1 and by generating a pursuit path describing
function which tends to be the inverse of the controlled element. This can, of course, only be done over a
limited range of frequencies. The quality of the overall control in the pursuit case can, in principle, be much
superior to that where only compensatory operations are possible.

An even higher level of control is possible. When complete familiarity with the controlled element dynamics

and the entire perceptual field is achieved, the highly skilled human operator can, under certain conditions,
generate neuromuscular commands which are deft, discrete, properly timed, scaled, and sequenced so as to
result in machine outputs which are almost exactly as desired. These neuromuscular commands are selected

FIGURE 105.1

Major human operator pathways in a man-machine system.

e

i

Y Y

pe c

=

+

1

1

m

i

Y

Y

Y

Y Y

pi

pe

c

pe

c

=

+

+

(

)

1

e

i

Y Y

Y Y

pi c

pe c

=

-

+

1

1

© 2000 by CRC Press LLC

from a repertoire of previously learned control movements. They are conditioned responses which may be
triggered by the situation and the command and control quantities, but they are not continuously dependent
on these quantities. This pure open-loop programmed-control-like behavior is called

precognitive

. Like the

pursuit pathway, it often appears in company with compensatory follow-up or simultaneous operations. This
forms a dual-mode form of control in which the human’s manual output is initially dominated by the precognitive
action, which does most of the job, and is then completed when needed by compensatory error-reduction actions.

The above description of human action pathways available in man-machine systems has emphasized the

visual modality. Similar behavior patterns can be exhibited to some extent in other modalities as well. Thus
the human’s interactions with machines can be even more extraordinarily varied than described here and can
range completely over the spectrum from open-loop to closed-loop in character in one or more modalities.

105.3 Full-Attention Compensatory Operations—

The Crossover Model

The compensatory pathways with manual control operations using the visual modality have been extensively
studied. Thousands of experiments have been performed, and most of the adaptive features of human behavior
associated with these kinds of operations are well understood. There are both classical control [e.g., McRuer
and Krendel, 1974; and McRuer et al., 1990] and optimal control [e.g., Baron and Kleinman, 1969; Kleinman
et al., 1970; Curry et al., 1976; and Thompson, 1990] theoretical formulations available to predict steady-state
and dynamic performance.

By far the simplest human behavioral “law” for compensatory systems is the

crossover model.

This states that,

for a particular controlled element transfer function,

Y

c

,

the human operator adopts a describing function,

Y

pe

,

such that the open-loop man-machine transfer characteristics appear as

(105.5)

The two parameters in the crossover model are the crossover
frequency,

w

c

, and an effective pure time delay,

t

. The model

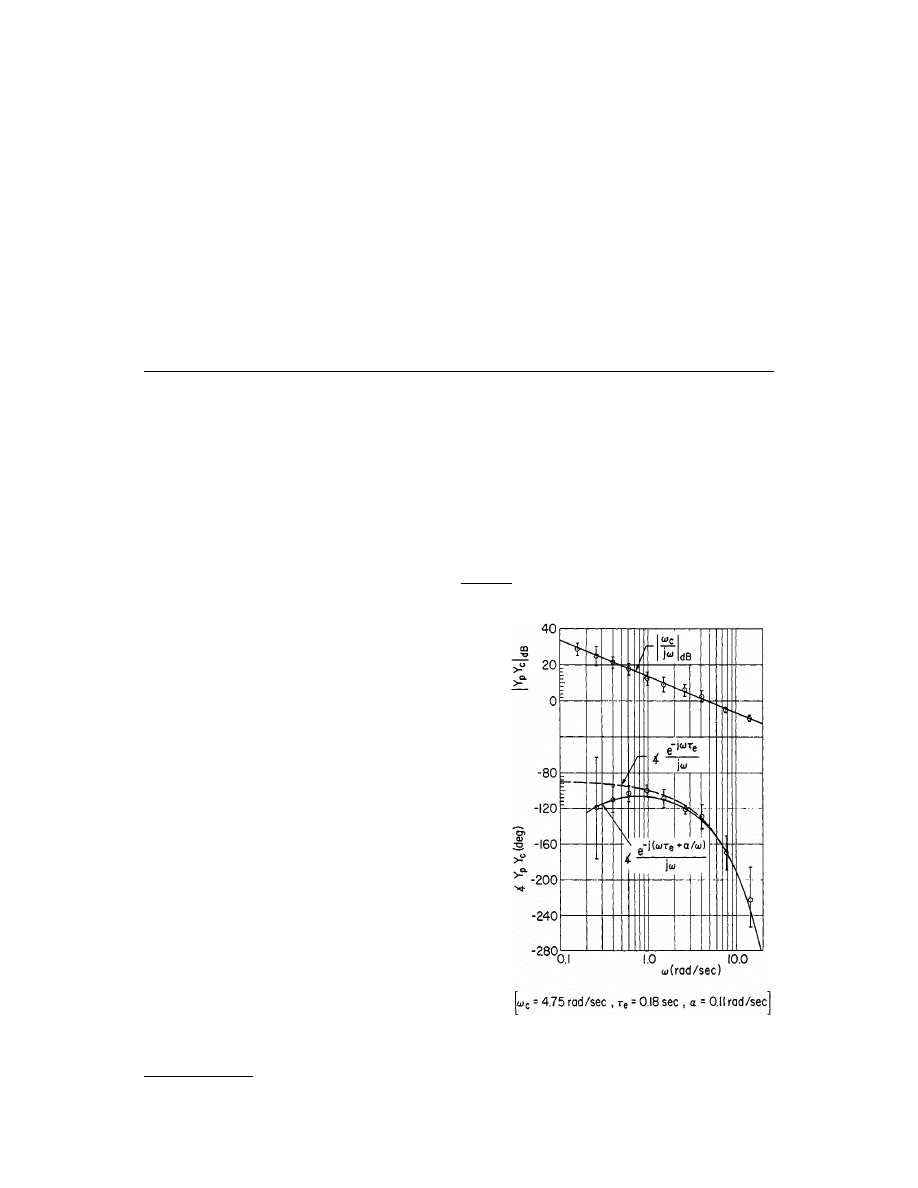
applies only in the immediate region of the crossover fre-
quency. The typical data shown in

Fig. 105.2

illustrate how

well this relationship is obeyed for a variety of subjects and
a particular controlled element. The agreement with the
amplitude ratio is excellent over a broad range of frequencies.
The phase agreement is good in the region of the crossover
frequency,

w

c

, but departs somewhat at lower frequencies.

Figure 105.2 also shows the

extended crossover model

. Here

the effects in the crossover region of a potentially large num-
ber of low-frequency lags and leads (in the machine and/or
the operator) are represented by a phase contribution given
by exp(–

j

a

/

w

). Here the time constant 1/

a

is a lumped-

constant representation of myriad low-frequency phase char-
acteristics. It is an appropriate approximation

only

in the

general region of crossover and is not intended to extend to
extremely low frequencies.

Fundamentally, the crossover model states that the human’s

transfer characteristics will be different for each set of machine
dynamics, but that the form of the composite total open-loop
dynamics will be substantially invariant. The effective time
delay in Eq. (105.5) is a low-frequency approximation to the
combination of all manner of high-frequency pure delays, lags,
and leads, including a component representing the effects of

Y Y

e

j

p c

c

j

=

-

w

w

t w

FIGURE 105.2

Data and crossover models for a

simple rate-control-like controlled element.

© 2000 by CRC Press LLC

the neuromuscular actuation system reflected to the crossover region. It follows that the effective time delay,

t

, is not a constant. Its two major components are (1) the effective composite time delay of the controlled

element (including manipulator effects)—the sum of the machine’s lags minus leads at frequencies well above
crossover and (2) the high-frequency dynamics of the human operator approximated by a pure delay which
has an equivalent phase shift at frequencies within the crossover region. The latter includes a minimum of 0.1
second for the neuromuscular system and an additional increment which depends on the amount of lead
generation required of the human to offset the controlled element deficiencies in order to make good the
crossover model form.

Figure 105.3

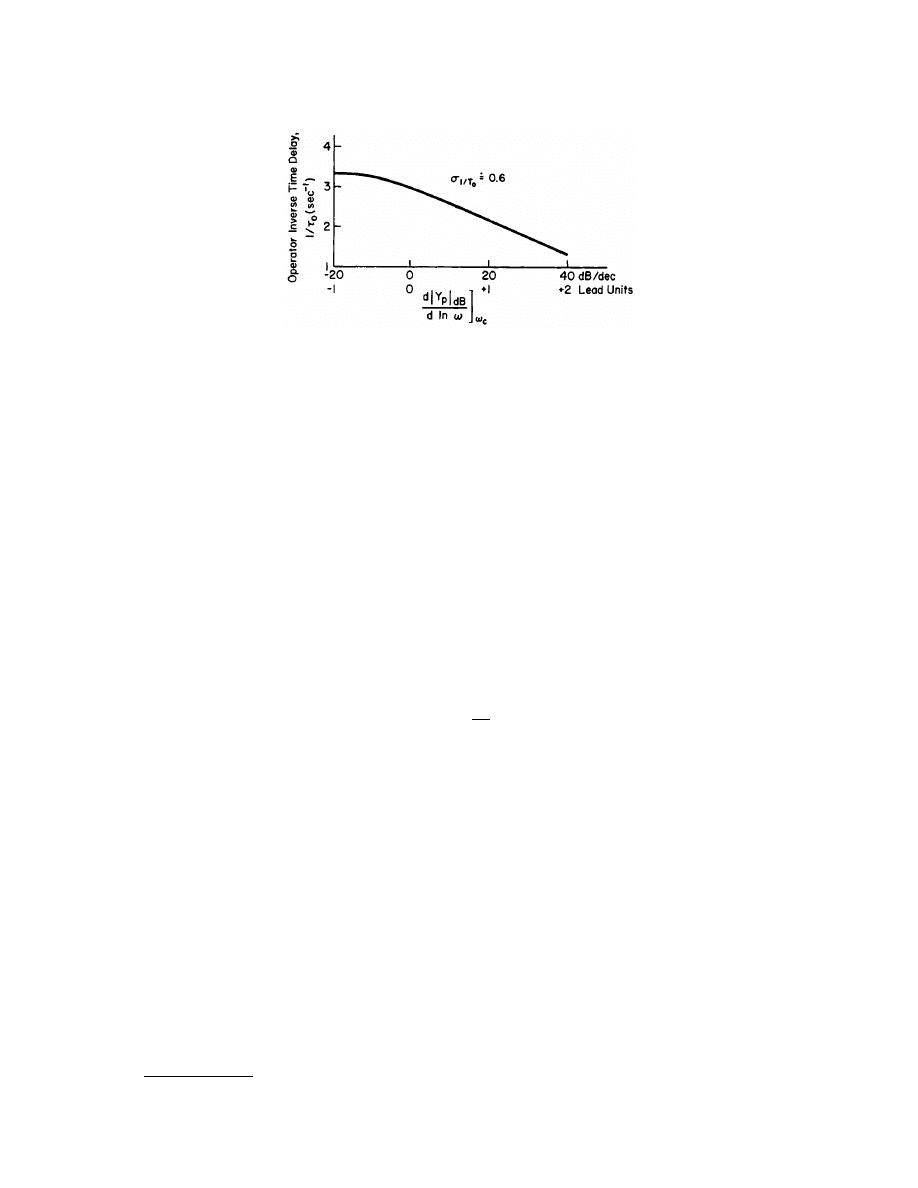
[McRuer and Krendel, 1974] shows this variation for a wide range of

controlled elements (the neuromuscular delay component is included). More refined estimates are available
[e.g., McRuer et al., 1990], but the above description is suitable for first-order estimates of behavior and dynamic
performance.

Crossover Frequency for Full-Attention Operations

The crossover frequency tends to be constant for a given set of task variables (controlled-element form, inputs,
disturbances, etc.). For example, as a controlled-element gain is changed, the human will change gain to
compensate, resulting in the same crossover frequency. The maximum attainable crossover frequency,

w

u

, will be

(105.6)

This corresponds to zero phase margin. The nominal crossover frequency and associated pilot gain can be
estimated from the condition to provide minimum mean-squared error in the presence of the appropriate form
of continuous attention remnant. “Remnant” is operator-induced noise; as described below it depends on the
nature of the operator’s equalization and is larger when low-frequency lead is required to make good the
crossover model. Thus, the need to generate lead impacts both the effective time delay and the remnant and,
accordingly, the crossover frequency for which the minimum mean-squared error is obtained. The nominal
crossover frequency for full-attention operations can be estimated [McRuer et al., 1990] using

w

c

/

w

u

No Operator Lead 0.78
Low-Frequency Operator Lead 0.66

Remnant

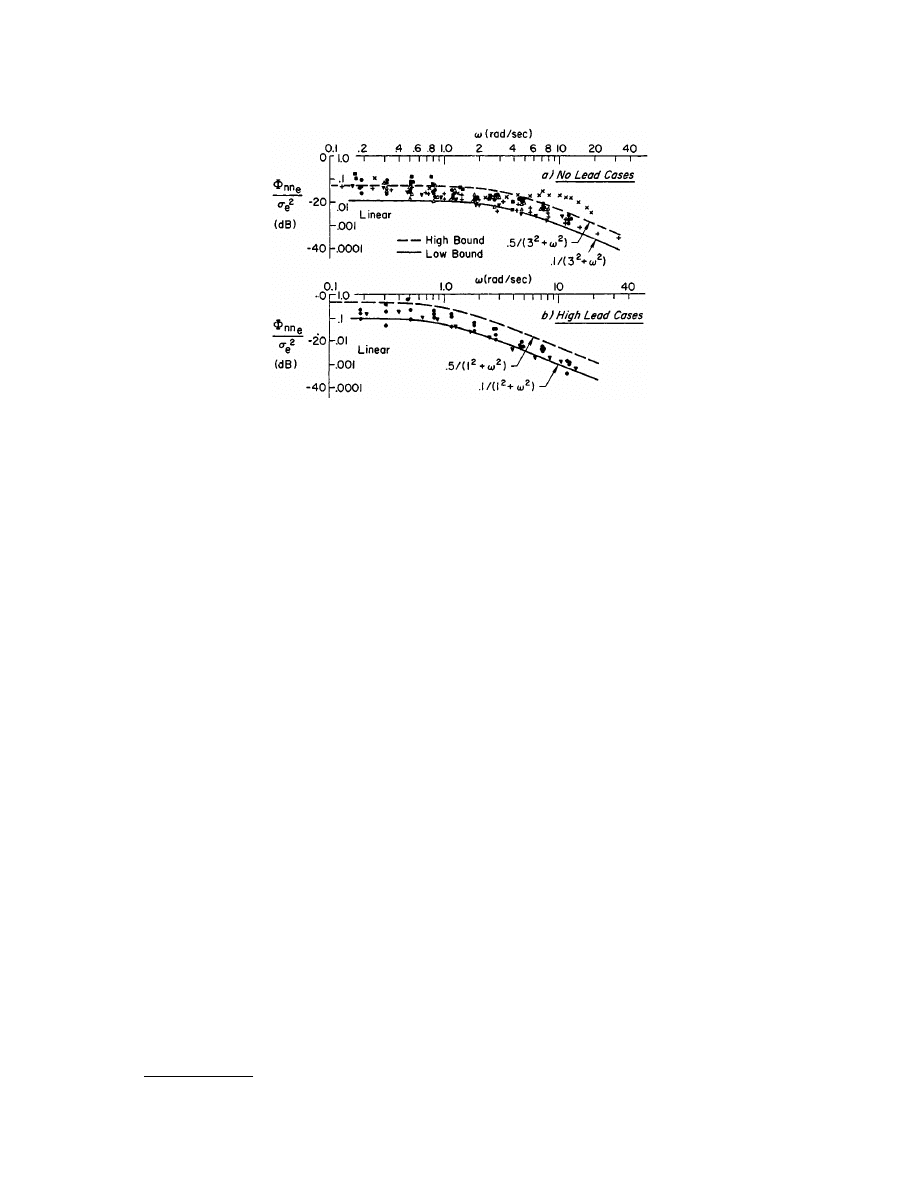
The second component of the operator’s response is operator-induced noise or remnant. Remnant can, in
principle, result from several sources, but in single-loop systems with ideal linear manipulator characteristics

FIGURE 105.3

Variation of crossover model dynamic stimulus-response latency with degree of operator lead equalization.

w

p

t

u

=

2

© 2000 by CRC Press LLC

and no significant nonlinearities in the controlled element, the basic cause appears to be random time-varying
behavior within the operator, which can be thought of as continuous random fluctuations in the effective time
delay. The remnant can be described as a continuous, relatively broadband, power spectral density.

Fig. 105.4

provides a cross-section of remnant data from several sources. It is very important to note that the magnitude
of the power spectral density scales approximately with the mean-squared error.

Effects of Changes in the Task Variables

The task variable which has the most important effect on the trained operator’s behavior is the controlled
element dynamics. Indeed, the natures of human adaptive changes in adjusting to the controlled element is the
main thrust of the crossover model and remnant discussion above. More generally, task variables other than
the machine dynamics, as well as environmental and operator-centered variables, can change operator gain,
and hence crossover frequency, effective time delay, and remnant. Accordingly,

w

c

and

t

variations become

quantification measures of changes or differences in the task, environmental, and operator-centered variables
expressed directly in terms of the operator’s control actions.

A common example is the reduction of crossover frequency when the amplitude of the command or

disturbance signals are very small. This reflects the human’s indifference to small errors and constitutes the
principal human behavioral nonlinearity in the crossover model context. Another example occurs in measuring
the effects of training, where

w

c

increases with trials until stable conditions are obtained for that particular

subject and set of constant task and environmental conditions. Similarly, operator gain and remnant can be
modified as a consequence of changes in operator-centered variables. A notable example is the decrease in gain
and increase in remnant which accompanies alcohol ingestion.

Effects of Divided Attention

Human operators in man-machine systems are, in general, involved in two types of operations—control tasks
and a diverse combination of monitoring/supervising/communicating/data-gathering/decision making activi-
ties referred to as “managerial tasks.” While the operator’s attention is “divided” between the control and
managerial tasks, these are often performed nearly simultaneously as parallel processing operations.

By definition, control workload is highest when the operator’s full attention is required for control purposes

and when this attention is focused on only the most critical input information needed for closed-loop control.
For this reason the full-attention crossover model and remnant for compensatory behavior treated above has
received the major attention here. Estimates and considerations based on full-attention compensatory assumptions
will generally be conservative. For instance, the dynamic performance of the overall man-machine system will
typically be improved when additional cues and information provide the basis for the generation of pursuit behavior.

Figure 105.4

Normalized remnant spectra.

© 2000 by CRC Press LLC

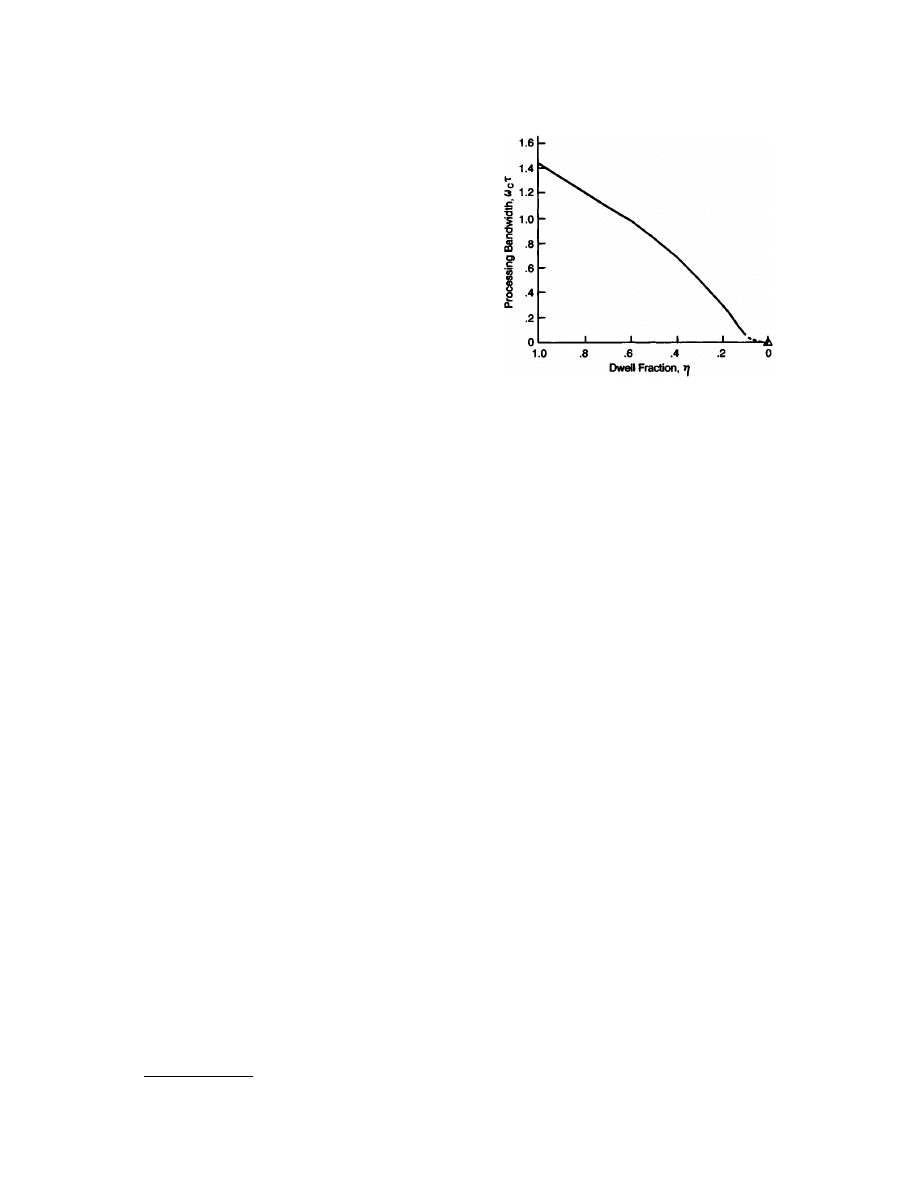
For a given situation the minimum divided attention

level should be established by the demands of the control
task. When divided attention conditions are present in com-
pensatory situations the major effects on the control per-
formance are reduced crossover frequency and increased
system error. To a first order the divided attention effects
on average crossover frequency are given in

Fig. 105.5

. Here

the “control dwell fraction,” is

h

, the proportion of the total

time spent on the control task. There are many other com-
plications and considerations [McRuer et al., 1990], but
these require more than handbook treatment.

Defining Terms

Compensatory behavior:

Human dynamic behavior in

which the operator’s actions are conditioned prima-
rily by the closed-loop man-machine system errors.

Compensatory display:

For the simplest case, a display

which shows only the difference between the desired
input command and the system output.

Precognitive behavior:

Conditioned responses triggered by the total situation; essentially pure open-loop

control.

Pursuit behavior:

The human operator’s outputs depend on system errors, as in compensatory behavior, but

may also be direct functions of system inputs and outputs. The human response pathways make the
man-machine system a combined open-loop, closed-loop system.

Pursuit display:

In the simplest case, a display which shows input command, system output, and the system

error as separable entities.

Related Topics

100.3 Frequency Response Methods: Bode Diagram Approach • 100.7 Nonlinear Control Systems

References

S. Baron, and D.L. Kleinman, “The Human As An Optimal Controller and Information Processor,” NASA CR-

1151, 1969.

R.E. Curry, W.C. Hoffman, and L.R. Young, “Pilot Modeling for Manned Simulation,” AFFDL-TR-76-124, 1976.
D.Graham and D. McRuer,

Analysis of Nonlinear Control Systems,

New York: John Wiley & Sons, 1961 (also

Dover, 1971).

D.L. Kleinman, S. Baron, and W.H. Levison, “An optimal control model of human response,”

Automatica,

vol.

9, no. 3, 1970.

D.T. McRuer, “Human dynamics in man-machine systems,”

Automatica,

vol. 16, no. 3, 1980.

D.T. McRuer, W.E. Clement, P.M. Thompson, and R.E. Magdaleno, “Pilot Modeling for Flying Qualities

Applications,” WRDC-TR-89-3125, vol. II, 1990.

D.T. McRuer, and H.R. Jex, “A review of quasi-linear pilot models,”

IEEE Trans. Human Factors in Electronics,

vol. HFE-8, no. 3, 1967.

D.T. McRuer, and E.S. Krendel, “Mathematical Models of Human Pilot Behavior,” AGARD-AG-188, 1974.
P.M. Thompson, “Program CC’s Implementation of the Human Optimal Control Model,” WRDC-TR-89-3125,

vol. III, 1990.

Figure 105.5

Effect of divided attention on process-

ing bandwidth.

© 2000 by CRC Press LLC

Further Information

The references of the chapter, especially Kleinman et al. [1970], McRuer and Krendel [1974], and McRuer et al.
[1990], comprise a good cross section of detailed information on modeling aspects of man-machine systems.
An excellect general text is T.B. Sheridan and W.R. Farrell,

Man-Machine Systems: Information, Control, and

Decision Models of Human Performance

, Cambridge: MIT Press, 1974.

Encyclopedic coverage appears in K.R. Boff, L. Kaufman, and J.P. Thomas,

Handbook of Perception and

Human Performance

, New York: Wiley, 1986, and K.R. Boff and J.E. Lincoln, “Engineering Data Compendium:

Human Perception and Performance,” Harry G. Armstrong Aerospace Medical Research Laboratory, Wright-
Patterson Air Force Base, Ohio, 1988.

The aperiodic proceedings of the so-called “Annual Manual” contain a great deal of information about man-

machine system developments. Since 1965 these have been published by NASA as SP’s (NASA Special Publi-
cations) under the general heading of

NASA—University Conference on Manual Control

.

The text article emphasizes the dynamic behavior of the human, not the design of machine dynamics to

achieve optimum characteristics in terms of man-machine system dynamic performance and human subjective
approval. For these aspects of design, a comprehensive summary of models, references, and applications appears
in “Advances in Flying Qualities,”

AGARD Lecture Series LS-157,

1988. Although the applications there are

specifically for aerospace vehicle control, the principles illustrated apply to vehicles in general and to other
machines subject to continuous control by a human operator.

As with other feedback control systems, system stability is a major consideration. In spite of the extraordinary

adaptive properties intrinsic to human controllers, system instability is a rare but often unfavorable event. The
nature of such man-machine oscillations and the design steps required to avoid them is treated extensively in
Duane McRuer,

Pilot-Induced Oscillations and Human Dynamic Behavior,

NASA Contractor Report 4683, July 1995.