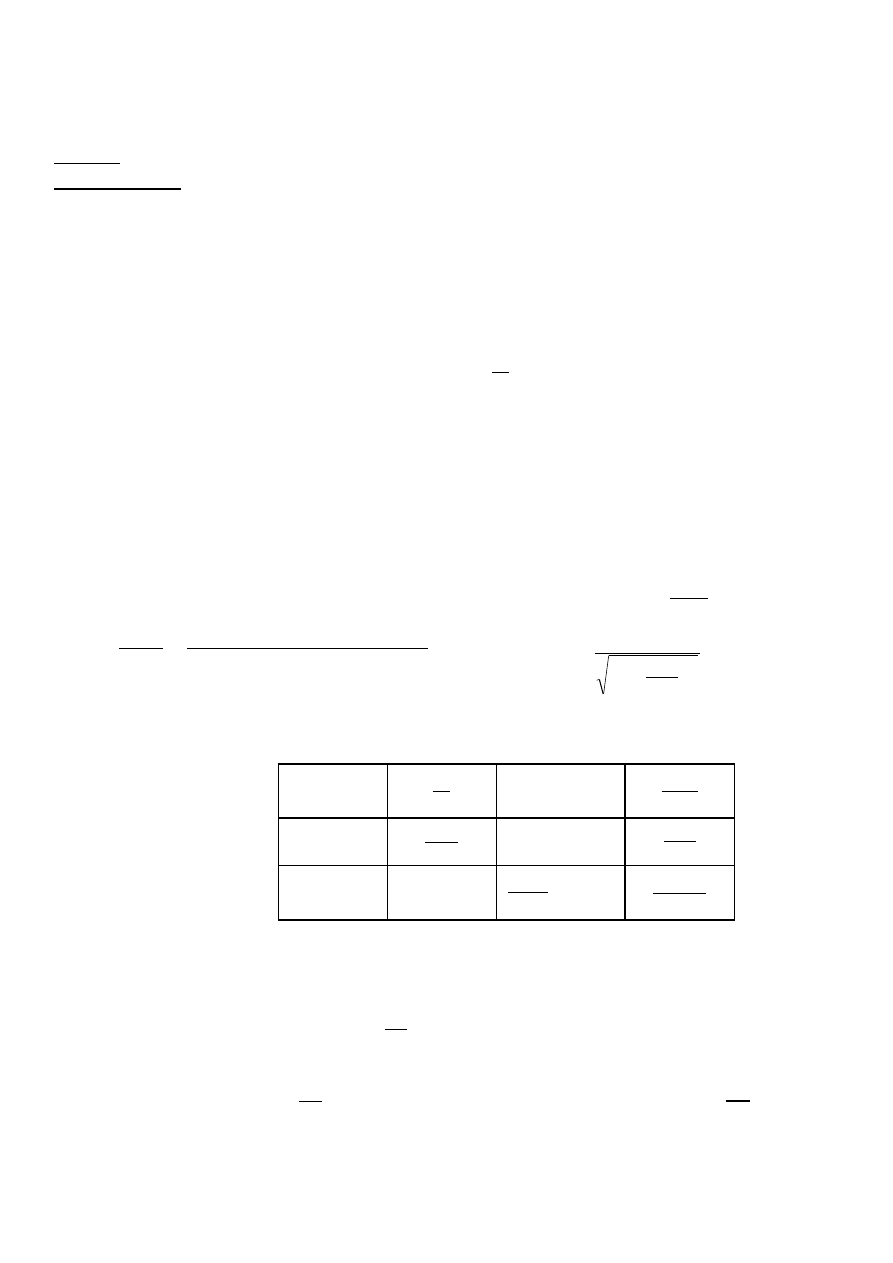
Rozwiązaniem równania różniczkowego jest (znalezienie funkcji mając jej pochodną)
równanie które wyznacza zależność pomiędzy nieznaną funkcją a jej pochodnymi. Polega na
znalezieniu funkcji której pochodne spełniają to równanie: (rr zwyczajne, rr cząstkowe) aby
je powiązać należy sprowadzić je do jednej ze standardowych form a nastepnie użyc
odpowiadającego tej formie przekształcenia.
Metody: całkowanie obu stron równania, liniowe równania różniczk. Jednorodne
Równania różn.: transmitancja, równanie różniczk.
Rozkład masy radioaktywnej:
drgająca masa na sprężynie:
)
(
.
)
(
1
0
),
(
),
(
),...
(
),
(
:
ln
.
.
.
.
.
)
(
)
(
'
.]
[
:
/
)
(
)
(
)
(
1
,
0
1
1
nor
rozwik
p
itd
y
t
y
rz
poch
zatkowydla
warunekpoc
t
t
y
t
y
t
y
t
y
F
ntegorzęte
apostać
ogó
r
m
r
r
r
t
km
t
m
itd
h
h
t
km
h
t
m
t
m
n
n
n
n
>
−
=
<
=
−
>
−
−
−
=
⋅
=
+
−
−
−
•
−
)
(
)
(
...
)
(
)
(
)
(
)
(
)
(
...
)
(
)
(
.
.
/
.
.
)
(
)
(
(
1
)
(
)
(
)
(
);
(
)
(
)
(
)
(
)
(
0
1
1
1
0
1
2
1
1
2
2
1
t
u
b
t
u
b
t
u
b
t
u
b
t
g
t
y
a
t
y
a
a
t
y
a
t
y
pocz
zerowewar
e
stacjonarn
lin
dyn
sys
t
px
t
x
k
F
m
t
x
t
x
t
x
t
x
t
x
t
px
t
x
k
F
t
x
m
n
n
n
n
n
n
n
n
+
+
+
+
=
+
+
+
+
=
−
−
−
=
>
−
=
=
−
−
=
•
−
−
•
−
−
−
•
•
•
•
•
•
•
Transmitancja G(s)-iloraz transformaty laplace’a wyjścia do wejścia:
0
1
1
1
0
1
1
1
...
...
)
(
)
(
)
(
a
s
a
s
a
s
a
b
s
b
s
b
s
b
s
U
s
Y
t
G
n
n
n
n
n
n
n
n
+
+
+
+
+
+
+
+
=
=
−
−
−
−
)
(
'
'
)
(
1
)
(
)
(
'
'
)
(
)
(
,
|
2
2
t
s
s
t
v
m
t
F
t
ms
t
ma
t
F
r
mM
G
F
ma
F
⋅
−
=
=
=
=
=
Przekształcenie laplacea (warunki początkowe musza być zerowe) f(t)F(s)
CI
s
R
t
dt
e
t
f
s
F
st
def
∈
∈
=
∫
∞
∞
−
−
,
)
(
)
(
Podstawowe wymuszenia:
∫
=
∂
1
)
( dt
t
-Skok jednost.:
s
u
s
U
t
u
t
U
0
0
)
(
);
(
1
)
(
=
=
-impulsowe:
1
)
(
:
0
:
0
:
0
)
(
=
=
∞
≠
=
s
U
t
t
t
u
-liniowe:
2
)
(
;
)
(
s
a
s
u
at
t
u
=
=
-paraboliczne:
2
2
2
)
(
;
)
(
s
a
s
u
at
t
u
=
=
t
2
1
s
∫
dt
t
f )
(
s
s
F )
(
R
a
e
at
∈
;
a
s
−
1
∫∫
dt
t
f )
(
2
)
(
s
s
F
)
(
0
t
f
sF(s)-f(0)
)
(cos
2
sin
at
v
at
2
2
)
(
1
a
s
s
v
+

Rozwiązanie-to jakas funkcja dziedziny czasu a wartosciami przedzial. y:T->R [t0,tn]; [t0,&]
CO-rodzina funkcji zależnych od n-parametrów tak dobranych aby spełniały dowolne
warunki początkowe i otrzymywały dla nich rozwiązanie
CS-zbiór funkcji spełniających równanie różniczk (bez warunków początkowych)
•
CORJ-(sztucznie wyznaczona prawa str)-spelnia każdy warunek początkowy dla
wyzerowanych
CORN-(prawa strona narzucona)-spelnia war. pocz. Dla narzuconej prawej str
CSRJ
•
CSRN (w liczeniu będziemy jakos łączyć z CORJ)
METODA UZMIENNIANIA STAŁEJ:
a(t)-cg
; g(t)-cg
1krok: równanie I stopnia /rzędu:
warunek początkowy: y(t0)=y0
)
(
)
(
)
(
)
(
t
g
t
y
t
a
t
y
=
+
•
(gdyby równanie było stacjonarne to wynik=0)
RJ:
)
(
)
(
)
(
)
(
t
g
t
y
t
a
t
y
=
+
•
||
∫
=
−
dt
t
a
Ce
t
y
)
(
)
(
jest rozwiąż RJ bo:
))
(
(
)
(
)
(
t
a
Ce
t
y
dt
t
a
−
∫
=
−
•
∫
=
dt
t
a
t
oznA
)
(
)
(
)
(
)
(
0
0
0
/
)
(
|
t
A
t
A
e
Ce
t
y
y
t
t
−
=
=
=
C
e
y
x
A
=
)
(
0
---->-
CORJ
Ce
t
y
dt
t
a
>
−
∫
=
−
)
(
)
(
//
/ szukamy roz postaci:
)
(
)
(
)
(
)
(
t
g
t
y
t
a
t
y
=
+
•
(niejednorodne)
))
(
(
)
(
)
(
)
(
)
(
)
(
t
a
e
t
C
e
t
C
t
y
dt
t
a
dt
t
a
−
∫
+
∫
=
−
−
•
•
∫
⋅
=
∫
−
•
dt
t
a
dt
t
a
e
t
g
e
t
C
)
(
)
(
/
)
(
)
(
∫
⋅
=
•
dt
t
a
e
t
g
t
C
)
(
)
(
)
(
1
)
(
)
(
)
(
C
e
t
g
t
C
dt
t
a
+
∫
⋅
=
∫
(
)
1
)
(
)
(
)
(
)
(
C
dt
e
t
g
e
t
y
t
a
dt
t
a
+
⋅
⋅
∫
=
∫
−
∫
∫
−
>
−
−
=
∫
⋅
⋅
∫
=
−
−
CORN
po
dt
e
t
g
e
dt
e
t
g
e
t
y
ozn
t
A
t
A
t
a
dt
t
a
)
(
)
(
)
(
)
(
1
)
(
)
(
)
(
:
)
(
)
(
1
1
/
)
(
)
(
t
A
t
A
e
e
C
t
y
t
y
−
+
=
(
)
)
(
1
1
)
(
)
(
t
A
e
t
y
t
y
C
⋅
−
=
dla t=t0 mamy w szczególności:
(
)
)
(
0
1
0
1
0
)
(
t
A
e
t
y
y
C
⋅
−
=
C1 dla każdego w.p możemy wyliczyc i będzie spełniony czyli było corn
∫
∫
∫
+
∫
=
−
−
dt
e
t
g
e
e
C
t
y
t
a
dt
t
a
dt
t
a
)
(
)
(
)
(
1
)
(
)
(
CORN= CORJ
+ CSRN
CORJ-mowi jak zachowuje się układ sam w sobie na w.p bez ingerencji sterowania
CSRN-nic nie mowi o w.p ,tym co w srodku, ale mowi jak odpowiada na nasze wymuszenie
Wyszukiwarka
Podobne podstrony:
03 ScilabControl, 2 ROK, 3ci SEMESTR, Modele ukladow dynamicznych, materialy na lab i cw
Modelowanie układów dynamicznych na elektronicznej maszynie analogowej, STUDIA - Kierunek Transport,
LTS 2 Modelowanie ukladow dynamicznyc
PAcw2 Modelowanie ukladów dynamicznych
więcej podobnych podstron