Laboratorium z Teorii Sterowania

Sprawozdanie z ćwiczenia nr 2

Temat: Modelowanie układów dynamicznych w języku symulacyjnym SIMULINK.

Skład grupy:

Sebastian Kowalewicz

Paweł Wyszyński

Arkadiusz Żanowski

Zadanie 1.

Dla transmitancji:

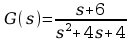
należało sformułować równania stanu i zaproponować model blokowy: Macierz opisująca w przestrzeni stanu układ dynamiczny drugiego rzędu: A=[0 1 ;-4 -4]

A =

0 1

-4 -4

B=[0;1]

B =

0

1

C=[6 1]

C =

6 1

D=[0]

D =0

Proponowany model blokowy (rys. 1)

Zadanie 2.

Portret fazowy układu.

Wyznaczenie zmiennych stanu

yout =

5.0000 5.0000

5.0005 4.9960

5.3420 1.2579

5.3085 -1.5033

4.9673 -3.0872

4.4364 -3.8118

3.8140 -3.9446

3.1740 -3.7069

2.5550 -3.2573

1.9916 -2.7129

1.5056 -2.1595

1.1045 -1.6509

0.7858 -1.2148

0.5411 -0.8606

0.3593 -0.5852

0.2207 -0.3677

0.1207 -0.2054

0.0545 -0.0947

0.0241 -0.0426

0.0100 -0.0180

0.0038 -0.0070

0.0013 -0.0023

0.0003 -0.0006

0.0001 -0.0001

0.0000 0.0000

0.0000 0.0000

0.0000 0.0000

0.0000 0.0000

0.0000 0.0000

0.0001 -0.0003

Tworzenie portretu fazowego, dla różnych warunków początkowych.

» plot(yout(:,1),yout(:,2))

» hold on

» who

yout

» plot(yout(:,1),yout(:,2))

» hold on

» who

yout

» plot(yout(:,1),yout(:,2))

» hold on

» plot(yout-(:,1),yout-(:,2))

|

» axis ([-10 10 -10 10])

» who

yout

» plot(yout(:,1),yout(:,2))

» hold on

» who

yout

» plot(yout(:,1),yout(:,2))

» hold on

» who

» plot(yout(:,1),yout(:,2))

» hold on

» who

yout

» plot(yout(:,1),yout(:,2))

» hold on

» who

yout

» plot(yout(:,1),yout(:,2))

» hold on

» who

yout

» plot(yout(:,1),yout(:,2))

» hold on

» who

yout

» plot(yout(:,1),yout(:,2))

» hold on

» who

yout

» plot(yout(:,1),yout(:,2))

» hold on

» gtext('Portret fazowy')

» gtext('x0=-1')

» gtext('x0=-5')

» gtext('x0=-9')

» gtext('x0=9')

» gtext('x0=5')

Zadanie 3

Wyznaczenie charakterystyki skokowej i impulsowej oraz na wymuszenie sinusoidalne układu za pomocą bloku GRAPH.

Schemat układu do wyznaczenia tych odpowiedzi znajduje się na rys nr2.

Odpowiedzi:

• skokowa rys.3;

• impulsowa rys 4;

• sinusoidalne rys 5;

Zadanie 4

Badanie stabilności układu.

a=[0,1;-4,-4]

a =

0 1

-4 -4

» b=[0;1]

b =

0

1

» c=[6,1]

c =

6 1

» d=[0]

d =

0

nyquist(a,b,c,d,1)

Wyznaczanie granicy stabilności k_kr

m=[conv([1 0],conv([3 1],[5 1]))]

m =

15 8 1 0

l=1

l =

1

margin(l,m)

» z=5.46/20

z =

0.2730

» 10^.2730

ans =

1.8750

» k=1/1.8750

k_kr= k =

0.5333

Następnym podpunktem zadania było sprawdzenie odpowiedzi dla różnych stałych czasowych przy k_kr= k = 0.5333, rys 6. Wszystkie stałe czasowe zostały zmienione o +-25%. Jak widać na wykresie odpowiedzi zostały przesunięte w czasie i nie nastąpiło przesunięcie k_kr.

Dla zmiany k przy tych samych stałych czasowych wykresy pokazane są na rys 7.

Laboratorium

z

Teorii Sterowania

Sprawozdanie z ćwiczenia nr 2

Temat: Modelowanie układów dynamicznych w języku symulacyjnym SIMULINK.

Skład grupy:

Sebastian Kowalewicz

Paweł Wyszyński

Arkadiusz Żanowski