E. Michlowicz.: IMW – Modelowanie układów dynamicznych
1
WYKŁAD 3
MODELOWANIE UKŁADÓW DYNAMICZNYCH
MODEL WCIĄGARKI PRZEJEZDNEJ
1. Ogólne zasady modelowania układów dynamicznych
Układ rzeczywisty to obiekt techniczny istniejący w rzeczywistości lub w
postaci projektu technicznego. Badanie własności dynamicznych układu
rzeczywistego realizujemy w sposób doświadczalny lub teoretyczny.
Pierwszy z tych sposobów można zastosować jedynie do obiektu
istniejącego w rzeczywistości, np. w postaci prototypu. Sposób teoretyczny
jest bardziej uniwersalny. Umożliwia on określenie i optymalizację własności
dynamicznych obiektu już na etapie jego konstruowania. Badania
doświadczalne
przeprowadza
się
w
warunkach
rzeczywistych
lub
laboratoryjnych,
tzn.
w
warunkach
stworzonych
sztucznie
przez
eksperymentatora. Badania teoretyczne natomiast wymagają stworzenia
pewnego modelu myślowego, nazywanego modelem obliczeniowym, a
następnie opisu jego własności równaniami ruchu.
Opis matematyczny obiektu jako zbiór formuł opisujących
zachodzące w nim procesy dynamiczne nazywamy modelem matematycznym
obiektu.
Układ rzeczywisty można analizować według różnych kryteriów i
zjawisk. Dla każdego obiektu można również opracować nowe modele
matematyczne, zależnie od przyjętego sposobu opisu ruchu, pewnych założeń
i uproszczeń natury matematycznej itp. Najistotniejszymi kryteriami przy
doborze modelu jest uwzględnienie tych właściwości układu rzeczywistego,
które w rozważanym przypadku mają decydujący wpływ na analizowane
zjawisko.
Opracowanie
modelu
polega
na
przyjęciu
szeregu
założeń
upraszczających, które ułatwiają opis matematyczny i analizę procesów
dynamicznych zachodzących w danym obiekcie. Wnikliwość, z jaką
wprowadzone są te uproszczenia, ma zasadniczy wpływ na uzyskane wyniki
analizy. Przyjęcie zbyt dużych uproszczeń może spowodować pominięcie
istotnych cech układu rzeczywistego, natomiast nadmierna złożoność modelu
prowadzi zazwyczaj do skomplikowanego opisu matematycznego. Na obecnym
etapie rozwoju wiedzy nie ma ścisłych i jednoznacznych metod tworzenia
modeli obliczeniowych. Proces ten opiera się w dużej mierze na intuicji i
doświadczeniu inżynierskim.
Najczęściej stosowane przybliżenia, które są przydatne w modelowaniu
obiektów:
a) zastępowanie parametrów rozłożonych parametrami skupionymi,
b) uproszczenie kształtu geometrycznego obiektu,
c) pomijanie mało istotnych oddziaływań zewnętrznych,
d) założenie
jednorodności
materiału
poszczególnych
elementów
rozpatrywanego układu,
E. Michlowicz.: IMW – Modelowanie układów dynamicznych
2
e) pomijanie odkształcalności lub masy niektórych wielkości fizycznych
badanego obiektu,
f) przyjęcie liniowych charakterystyk niektórych wielkości fizycznych
badanego obiektu,
g) założenie, że własności fizyczne układu są niezmienne w czasie,
h) zastępowanie procesów stochastycznych w układzie rzeczywistym
procesami deterministycznymi w jego modelu.
2. Modelowanie wg zasady d’Alamberta:
Układ znajduje się w stanie równowagi dynamicznej, jeśli dla
dowolnego elementu bezwładnego – związanego z sąsiednimi
elementami układu poprzez więzy (sprężyste, z tłumieniem) – suma
wszystkich
sił
uogólnionych:
zewnętrznych,
masowych
i
przenoszonych przez więzy wynosi zero.
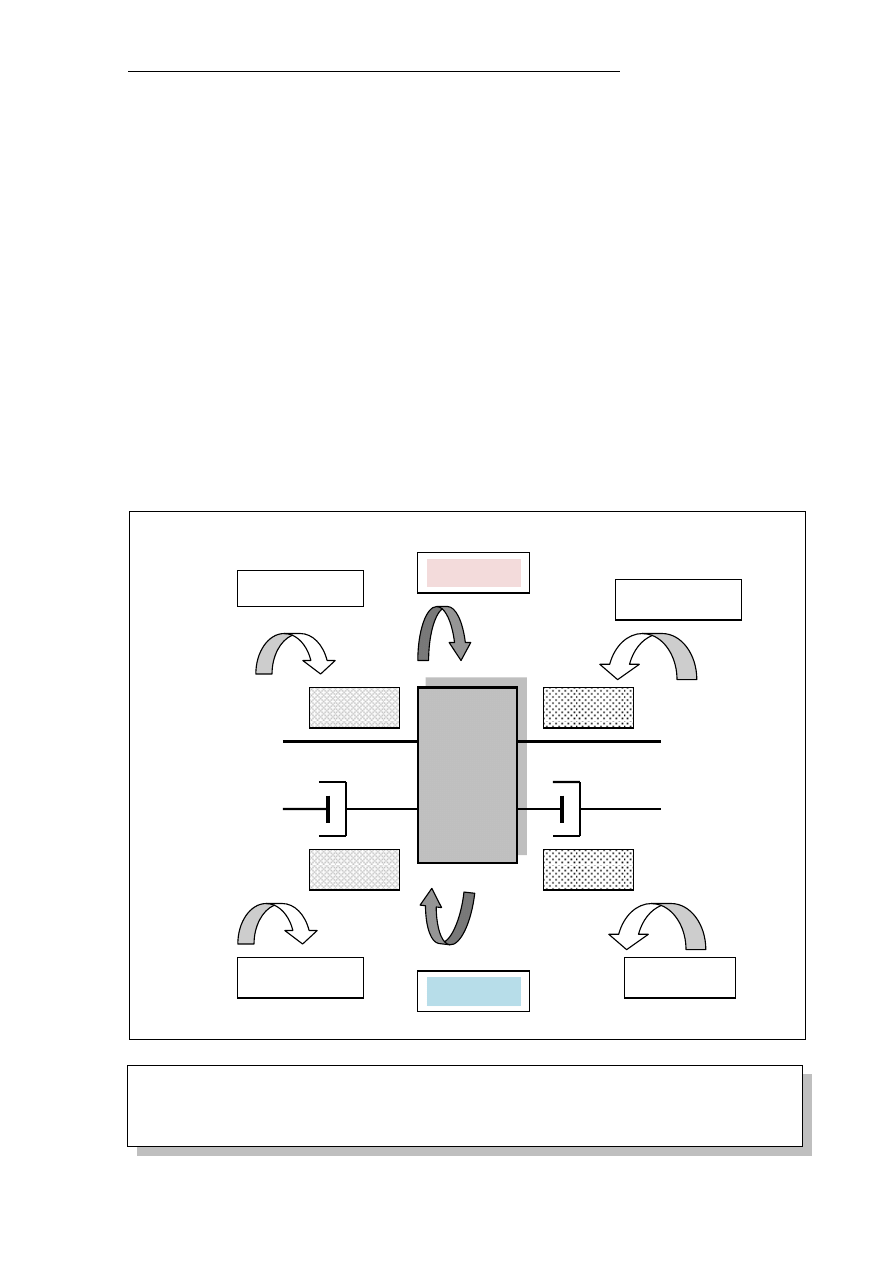
Model d’Alamberta
Rys. 1. Schemat obciążenia elementu z więzami
Element
„n”
I
n
(m
n
)
k
n-1
k
n
h
n-1
h
n
M
sn-1
(S
sn-1
)
M
n
(S
n
)
M
tn-1
(S
n-1
)
M
s
(S
sn
)
M
tn
(S
tn
)
M
bn
(S
bn
)
M
bn
+ M
sn
+ M
tn
- M
sn-1
- M
tn-1
– M
n
= 0
E. Michlowicz.: IMW – Modelowanie układów dynamicznych
3
gdzie:
M
sn
lub S
sn
– moment lub siła sprężystości w więzi n,
M
tn
lub S
tn
– moment lub siła tłumienia w więzi n,
M
n
lub S
n
– moment lub siła wymuszająca ruch (zewnętrzna) elementu n,
M
bn
lub S
bn
– moment lub siła bierna (oporu) elementu n,
k
n
– współczynnik sprężystości (sztywności) więzi n,
h
n
– współczynnik tłumienia (wiskotycznego) więzi n.
3. Równania ruchu
Układanie równań ruchu w przypadku układów mechanicznych najlepiej
rozpocząć od zasady Hamiltona.
Zasada Hamiltona dla układu zachowawczego:
całka
2
1
t
t
Ldt
przyjmuje wartość ekstremalną
Funkcja L jest nazwana funkcją Lagrange’a i reprezentuje nadwyżkę
energii kinetycznej nad potencjalną.
p
k
E
E
L
Przykładowo:
Masa skupiona o stałym momencie bezwładności I porusza się
ruchem obrotowym:
E
k
= I q
2
/ 2 = I ω
2
/ 2
Energia potencjalna jest całką momentu czynnego M
c
na
elementarnym przesunięciu obrotowym dα :
E
p
=
∫
M
c
dα
Po obliczeniu wariacji całki względem kolejnych zmiennych (współrzędnych
uogólnionych) otrzymuje się równania Lagrange’a drugiego rodzaju:
dla układu zachowawczego –
tj. układu bez strat i bez wymuszenia zewnętrznego:
0
)
(
j
j
q
L
q
L
dt
d
dla układu niezachowawczego –
tj. układu ze stratami i z wymuszeniem:
j
j
j
j
Q
q
R
q
L
q
L
dt
d
)
(
gdzie:
j = 1…k; przy czym k jest liczbą stopni swobody;
q
j
– współrzędna uogólniona;
funkcja strat
)
(
j
q
f
R
funkcja wymuszeń
)
,
,
(
t
q
q
f
Q
j
E. Michlowicz.: IMW – Modelowanie układów dynamicznych
4
Układy rzeczywiste są układami niezachowawczymi.
Po odpowiednich podstawieniach (do równania Lagrange’a) i zróżniczkowaniu
otrzymujemy równanie ruchu:
2
2
d
dI
dt
d
I
M
M
M
o b c
s
d
4. Moment dynamiczny i stany nieustalone
Moment dynamiczny jest różnicą pomiędzy momentem silnika
(wymuszeniem zewnętrznym) a momentem oporu (obciążeniem); I = const.
dt
ω
d
I
M
M
M
obc
s
d
Układ znajduje się w stanie równowagi,
Gdy: M
d
= 0, tj. dla M
s
= M
obc
.
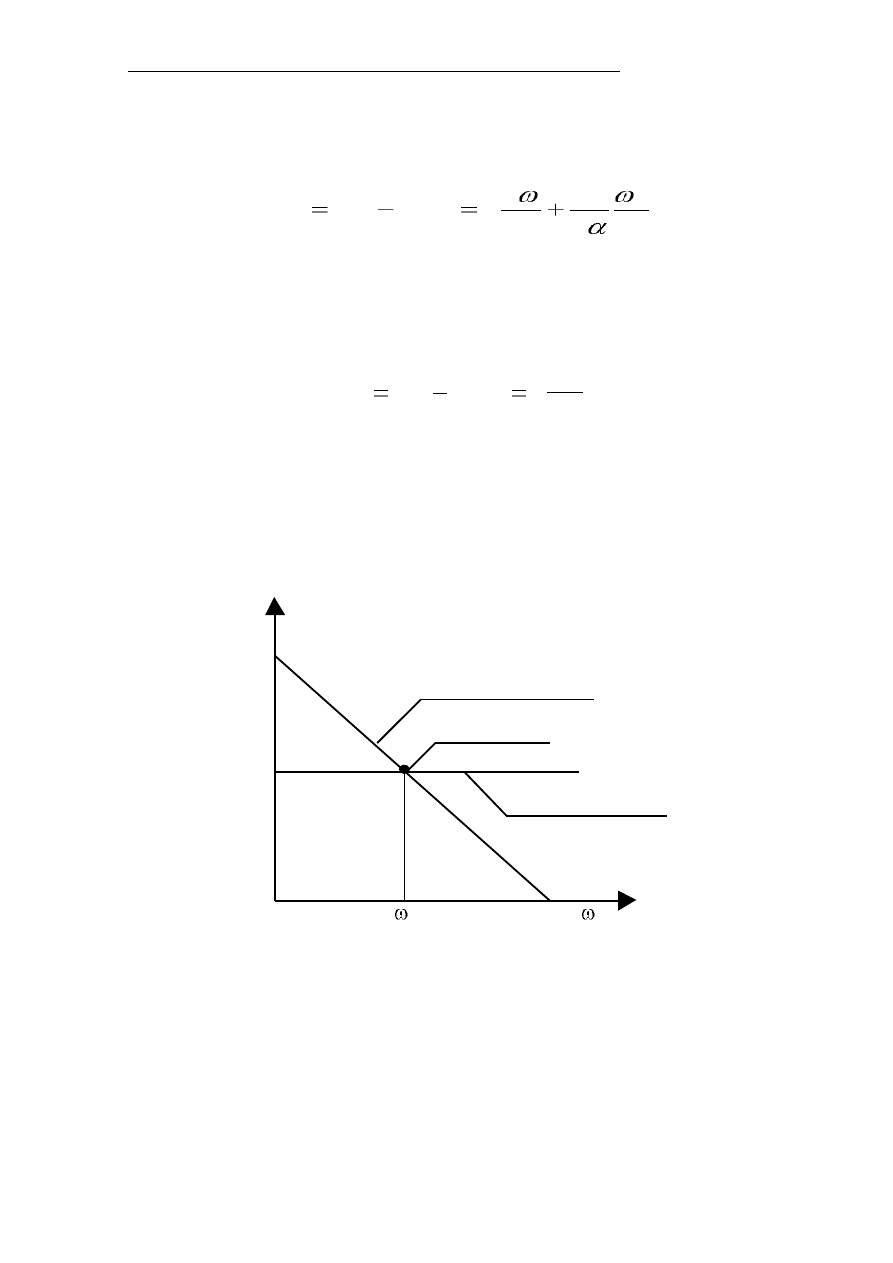
Stan równowagi dynamicznej jest punktem pracy układu napędowego. Na
wykresie statycznej charakterystyki mechanicznej silnika jest to punkt
przecięcia się charakterystyki silnika z charakterystyką obciążenia
(rys.2.).
Rys.2. Punkt pracy układu napędowego
Zmiana wartości obciążenia lub siły elektromotorycznej silnika powoduje
zmianę momentu dynamicznego oraz prędkości ruchu.
Zakłócenie równowagi ruchu napędu nazywamy stanem nieustalonym,
który trwa aż do osiągnięcia nowej stałej prędkości ruchu układu napędowego.
Stabilność układu to skłonność powracania do warunków równowagi
statycznej gdy zostanie z nich wytrącony.
M
M
obc
p
Charakterystyka
momentu silnika Ms
P unkt pracy
Charakterystyka
momentu obciążenia
E. Michlowicz.: IMW – Modelowanie układów dynamicznych
5
5. Więzy sprężyste
Więzy sprężyste charakteryzuje współczynnik sztywności k określony jako
wartość siły potrzebnej dla jednostkowego przesunięcia jednego końca więzów
względem drugiego.
Dla przesunięcia prostoliniowego wartość tego współczynnika można
wyznaczyć ze wzoru:
l
EQ
l
F
k
r
gdzie:
F - siła rozciągająca więzy [N],
Δl - wydłużenie liniowe [m],
E - moduł sprężystości Younga [N/m
2
],
Q - przekrój poprzeczny [m
2
],
l - długość więzi [m].
Dla przesunięcia obrotowego współczynnik sztywności jest równy:
l
d
G
M
k
s
32
4
gdzie:
M - moment skracający więzy [Nm],
Δα - skręcenie więzi [rad],
G - moduł sprężystości poprzecznej [N/m
2
],
d - średnica więzi [m].
cz. 2. MODEL FIZYCZNY WCIĄGARKI PRZEJEZDNEJ
Przy badaniu dynamiki wciągarki przejezdnej przyjęto następujące
uproszczenia:
a) dyskretyzacja układu, tzn. masy układu są skupione w punktach
materialnych,
b) więzy odkształcają się w granicach sprężystości i nie posiadają
bezwładności,
c) siły i momenty sił działających w układzie przyłożone są do mas
skupionych,
d) straty energii towarzyszące odkształceniom są skutkiem tłumienia
wiskotycznego.
Redukcja sił, momentów sił, mas i momentów bezwładności jest konieczna i
polega
na
zastąpieniu
modelu
rzeczywistego
wciągarki
modelem
uproszczonym, który znacznie ułatwia obliczenia.
Poszczególne elementy modelu charakteryzują:
- prędkość ruchu,
- bezwładność (zastępcza masa lub moment bezwładności),
- zredukowana siła lub moment siły przyłożony do elementu.
E. Michlowicz.: IMW – Modelowanie układów dynamicznych
6
1.Redukcja więzów sprężystych (rys. 1.)
W przypadku gdy więzy składają się z szeregowo połączonych części o
różnych współczynnikach sztywności k
1
i k
2
, w obliczeniach można je zastąpić
więzami zastępczymi, których całkowite odkształcenie jest równe sumie
odkształceń więzów składowych.
Dla więzów skręcanych będzie to:
=
1
+
2
=
2
1
2
1
1
1
k
k
M
k
M
k
M
skręcanie więzów zastępczych charakteryzuje
=
z
k
M
,
stąd ich współczynnik sztywności jest następujący:
......
1
1
1
2
1
k
k
k
z
Gdy elementy układu połączone są dwoma równoległymi więzami
odkształcenia obu więzów są jednakowe:
=
1
=
2
.
Jednak moment przenoszony przez więzy rozkłada się na obie więzi, to:
M = M
1
= M
2
zależnie od sztywności każdej z nich M
i
= k
i
,
zatem:
k
z
= k
1
+ k
2
a stąd otrzymujemy:
k
z
= k
1
+ k
2
Układ szeregowo połączonych więzów poruszających się z różnymi
prędkościami (np. poprzez przekładnie zębatą), może być zastąpiony poprzez
więzy zastępcze mające współczynnik sztywności k
z
-
gdy więzy poruszają się z prędkością kątową silnika:
2
2
1
1
1
k
i
k
k
z
,
-
gdy więzy poruszają się z prędkością kątową elementu roboczego:
2
1
2
1
1
1
k
k
i
k
z
,
gdzie: i - jest przełożeniem między elementami napędu.
E. Michlowicz.: IMW – Modelowanie układów dynamicznych
7
2. Model 2-masowy (wciągarki przejezdnej)
Podczas rozpatrywania skutków oddziaływania podnoszonego ciężaru na
ustrój nośny wciągarki, wielomasowy układ podtrzymujący może być
zastąpiony odpowiednio dobranym modelem masowym o zmniejszonej liczbie
elementów składowych. Układ dwumasowy służy do opisu dynamicznego
oddziaływania podnoszonego ładunku na ustrój podtrzymujący.
Poniższy rysunek 3 przedstawia model fizyczny mechanizmu podnoszenia
sprowadzony do układu dwóch mas zredukowanych połączonych ze sobą
elementem sprężysto – tłumiącym. Masa m
1
jest to masa zredukowana na wał
wolnoobrotowy reduktora, która zastępuje momenty bezwładności elementów
obrotowych: wirnika silnika, sprzęgieł, bębna hamulcowego, kół zębatych i
bębna z nawiniętą liną. Masa m
2
jest to masa zredukowana zastępująca masę
ładunku zawieszonego na linie oraz masę zblocza.
W mechanizmie jazdy elementy wykonują ruch obrotowy zarówno od strony
napędowej (wał silnika, sprzęgło hamulcowe, koła zębate) jak i od strony
napędzanej (sprzęgła zębate koła jezdne). Dlatego model fizyczny
mechanizmu (rys. 4.) sprowadzono do modelu dwóch mas poruszających się
względem siebie ruchem obrotowym.
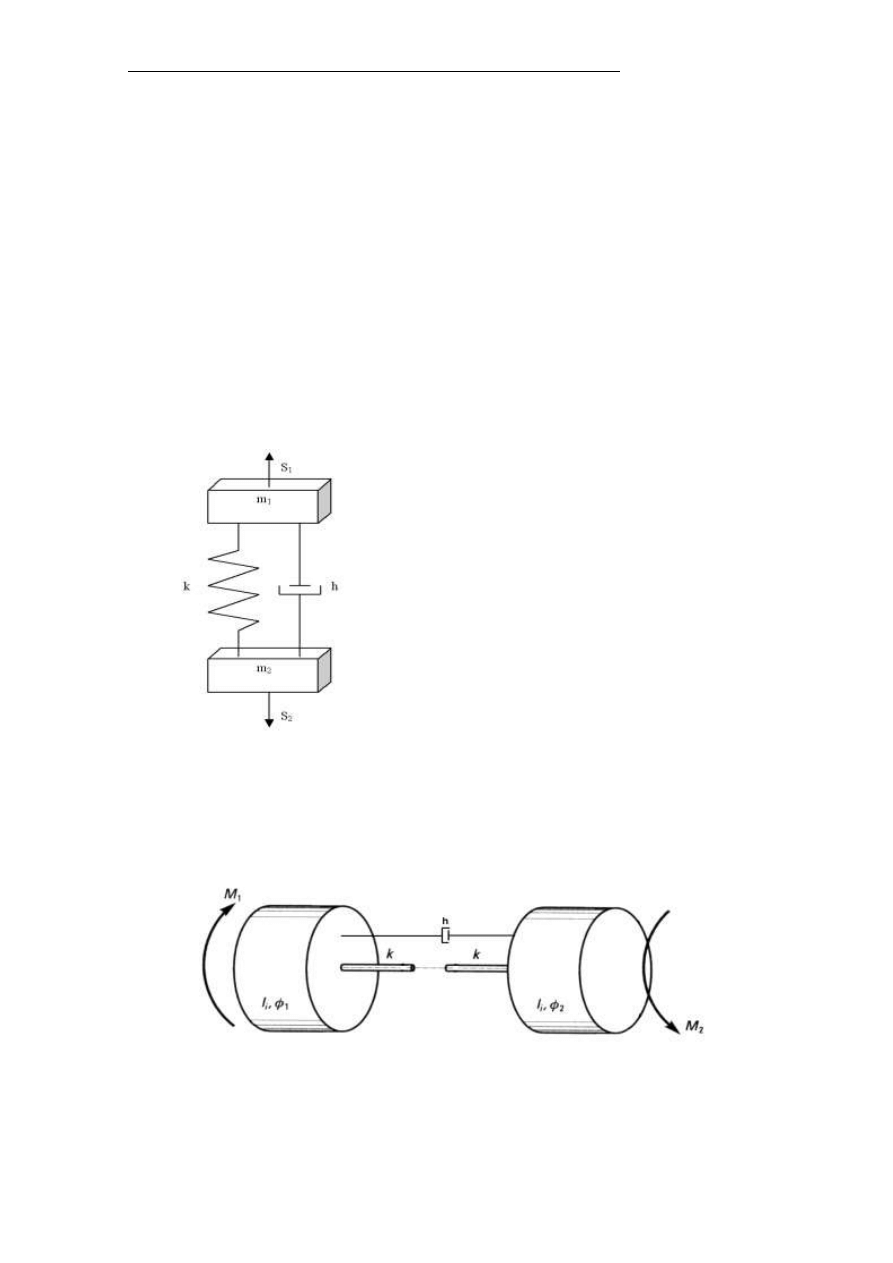
Rys. 4. Mechanizm jazdy sprowadzony do modelu obrotowego
M
1
,M
2
- momenty czynne i bierne, I
1
,I
2
– momenty bezwładności, k – zastępczy
współczynnik sztywności wałów napędzających koła jezdne h – zastępczy
współczynnik tłumienia w wałach napędzających koła jezdne.
Rys.3. Model obliczeniowy
mechanizmu podnoszenia
sprowadzony do układu dwóch mas
zredukowanych,
k – zredukowana sztywność liny
zastępczej,
h – zredukowany współczynnik
tłumienia liny,
S
1
, S
2
– siły zastępcze.
E. Michlowicz.: IMW – Modelowanie układów dynamicznych
8
Równania ruchu mas w modelach dwumasowych wyprowadzono posługując się
równaniami Lagrange’a II rodzaju dla układu niezachowawczego tj. układu ze
stratami i wymuszeniami.
j
j
j
j
Q
q
R
q
L
q
L
dt
d
gdzie:
L = E
k
- E
p
=f (
t
q
q
j
j
,
,
) jest funkcją Lagrange’a,
E
k
– jest energią kinetyczną,
E
p
- jest energią potencjalną,
R = f (
j
q
) – jest funkcją strat,
t
q
q
f
Q
j
j
j
,
,
- jest funkcją wymuszenia,
q
i
– jest współrzędną uogólnioną, a wskaźnik j = 1,...,k
przy czym k jest liczbą stopni swobody układu.
3. Równania ruchu dla mechanizmów wciągarki
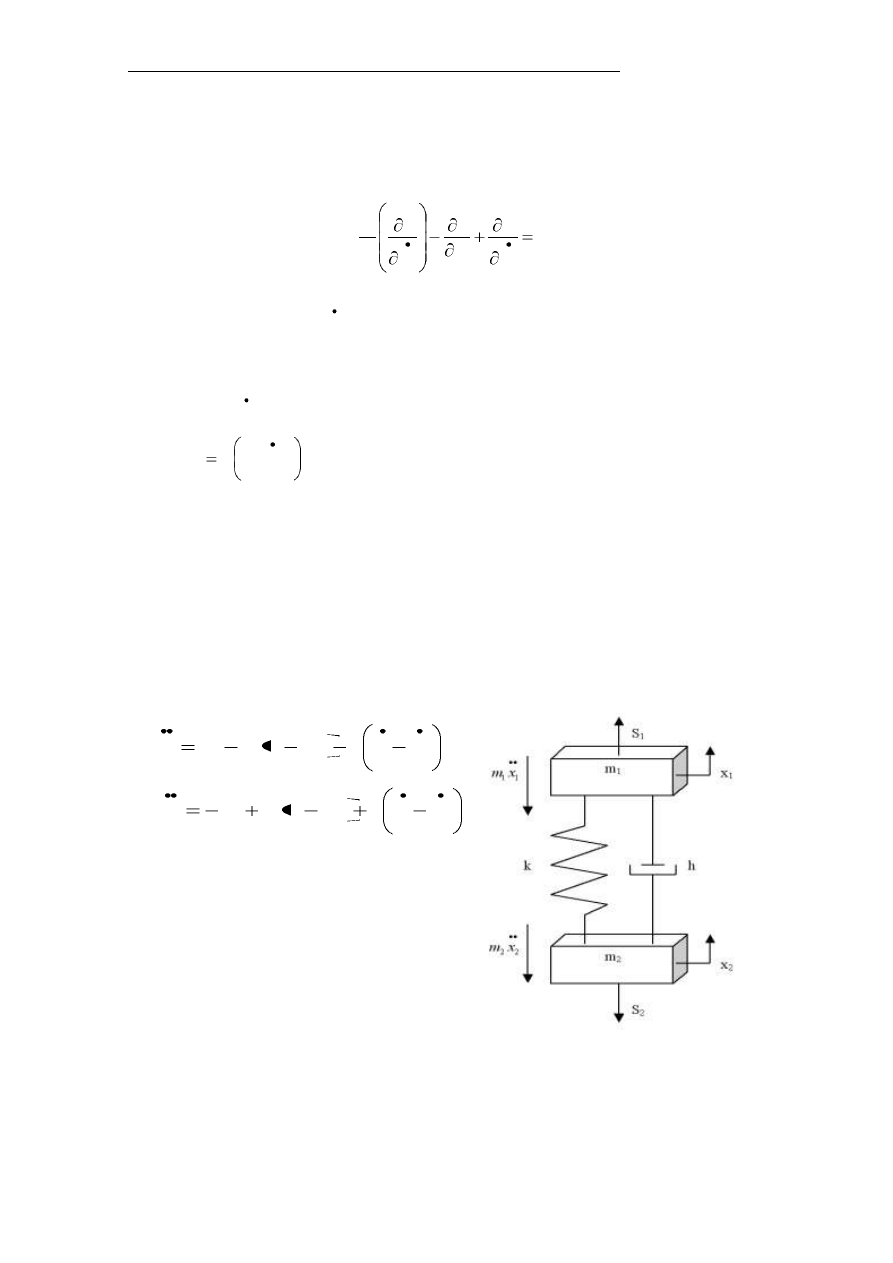
Równania ruchu dla mechanizmu podnoszenia
Układ mechanizmu podnoszenia (rys.5.) ma dwa stopnie swobody i opisany
jest dwoma równaniami:
2
1
2
1
1
1
1
x
x
h
x
x
k
S
x
m
2
1
2
1
2
2
2
x
x
h
x
x
k
S
x
m
Rys. 5. Model obliczeniowy mechanizmu podnoszenia sprowadzony do układu
dwóch mas zredukowanych, k – zredukowana sztywność liny zastępczej, h –
zredukowany współczynnik tłumienia, S
1
,S
2
– siły zastępcze.
E. Michlowicz.: IMW – Modelowanie układów dynamicznych
9
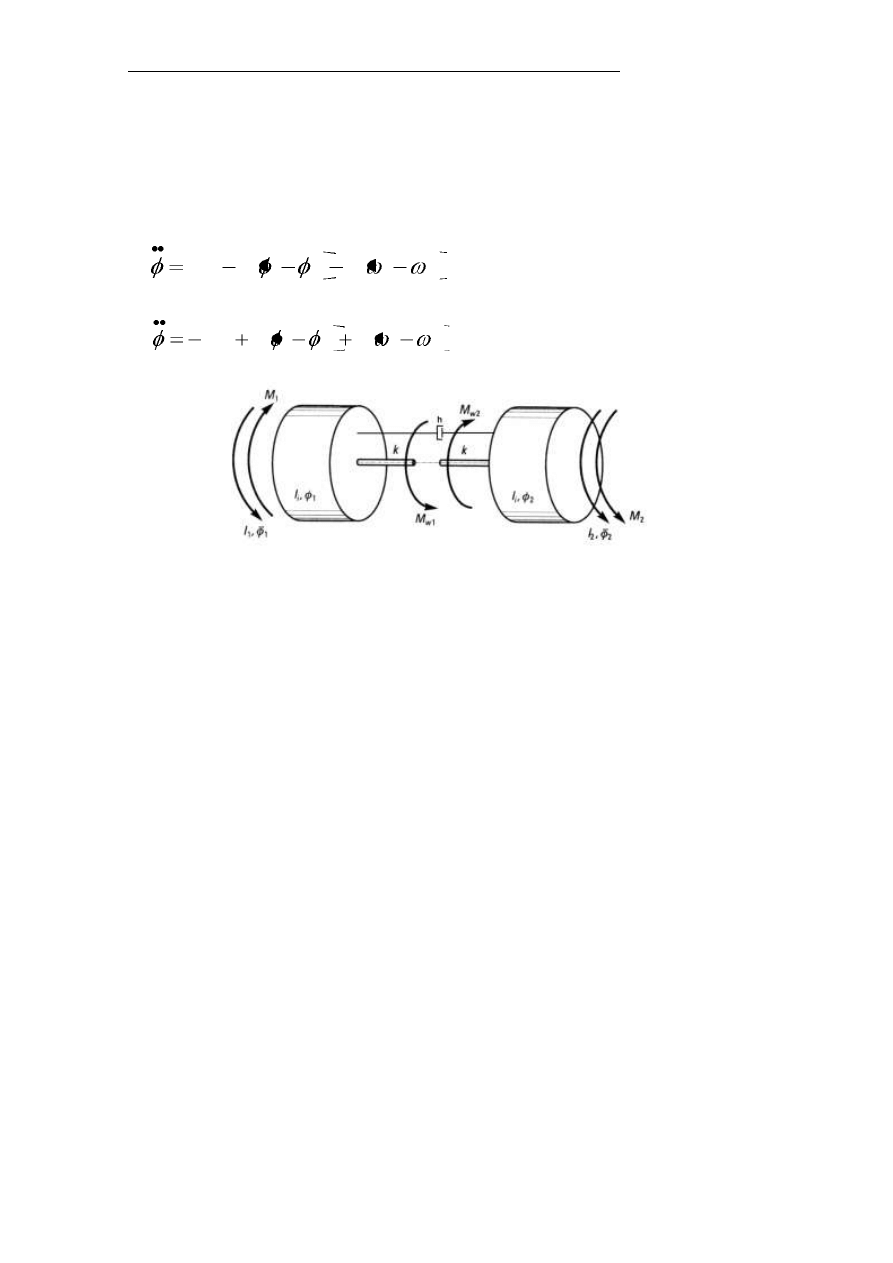
Równania ruchu dla mechanizmu jazdy
Układ mechanizmu jazdy, układ dwumasowy (rys.6.) z więzami sprężystymi
ma dwa stopnie swobody i opisany jest dwoma równaniami:
2
1
2
1
2
2
h
k
M
I
Rys. 6. Model dwumasowy mechanizmu jazdy wciągarki sprowadzony do
modelu obrotowego, k –zastępczy współczynnik sztywności wałów
napędzających koła jezdne, M
1
,M
2
– momenty czynne i bierne, I
1
,I
2
–
momenty bezwładności, h –zastępczy współczynnik tłumienia w wałach
napędzających koła jezdne.
2
1
2
1
1
1
h
k
M
I