2. Dynamika układów liniowych

Str.

16

2

DYNAMIKA UKŁADÓW LINIOWYCH

Podstawową formą opisu dynamiki elementów automatyki są równania różniczkowe. Inną

formą opisu dynamiki układów liniowych jest transmitancja operatorowa wynikająca z zastoso-
wania transformacji Laplace’a do równań różniczkowych liniowych. Również charakterystyka
czasowa będąca rozwiązaniem równania różniczkowego dla określonego sygnału wymuszającego
reprezentuje właściwości dynamiczne. Specjalną formą wyrażania dynamiki są charakterystyki
częstotliwościowe. Opisują one parametry sygnału sinusoidalnego przechodzącego przez badany
element (amplitudę i przesunięcie fazowe).

2.1

Zwyczajne równania różniczkowe

Szczególne znaczenie w automatyce mają zwyczajne równania różniczkowe liniowe o stałych

współczynnikach, które mają rozwiązania analityczne (znane są metody rozwiązywania tych rów-
nań). Chociaż rzeczywiste obiekty regulacji są w różnym stopniu nieliniowe, jednak w wielu
przypadkach zupełnie wystarcza opis przybliżony oparty na przyjęciu przybliżonych równaniach
różniczkowych (zastosowanie linearyzacji).

W teorii regulacji wyjątkowe miejsce zajmują równania różniczkowe liniowe o stałych

współczynnikach. W ogólnym przypadku równanie różniczkowe liniowe ma postać:

)

t

(

x

b

dt

)

t

(

x

d

b

)

t

(

y

dt

)

t

(

dy

a

dt

)

t

(

y

d

a

o

m

m

m

1

n

n

n

+

+

=

+

+

+

L

L

(2.1)

Współczynniki:

o

1

1

m

m

o

1

1

n

n

b

,

b

,

b

,

b

,

1

a

,

a

,

a

,

a

L

L

−

−

=

+

są stałe, a rząd (m) najwyższej

pochodnej sygnału wejściowego x(t) nie jest większy od rzędu (n) najwyższej pochodnej sygnału
wyjściowego y(t), m

≤

n.

2.2

Transmitancja operatorowa

Transmitancję operatorową G(s) otrzymuje się przez zastosowanie przekształcenia Laplace’a

do równania różniczkowego liniowego o stałych współczynnikach. W celu wykonanie transfor-

maty Laplace’a mnożymy równanie (2.1) przez funkcję wykładniczą (

st

e

−

), następnie wykonu-

jemy całkowanie po czasie w granicach od t = 0 do t = ∞. Otrzymamy:

=

+

+

+

∫

∫

∫

∞

−

∞

−

∞

−

0

st

0

st

1

0

st

n

n

n

dt

e

)

t

(

y

dt

e

dt

)

t

(

dy

a

dt

e

dt

)

t

(

y

d

a

L

∫

∫

∞

−

∞

−

+

+

=

0

st

o

0

st

m

m

m

dt

e

)

t

(

x

b

dt

e

dt

)

t

(

x

d

b

L

(2.2)

2. Dynamika układów liniowych

Str.

17

Zakłada się, że wartości początkowe sygnałów oraz ich pochodnych są równe zero.

0

)

0

(

x

,

0

t

d

)

t

(

x

d

,

,

0

t

d

)

t

(

x

d

0

t

0

t

1

m

1

m

=

=

=

=

=

−

−

L

(2.3)

0

)

0

(

y

,

0

t

d

)

t

(

y

d

,

,

0

t

d

)

t

(

y

d

0

t

0

t

1

n

1

n

=

=

=

=

=

−

−

L

(2.4)

Po zastosowania przekształcenia Laplace’a występujące w równaniu (2.2) funkcje czasowe

x(t), y(t) przechodzą w funkcje operatorowe x(s), y(s). Zamiast symbolu pochodnej (d/dt) pojawi
się operator Laplace’a (s). Pierwszej pochodnej czasowej odpowiada mnożenie funkcji operato-
rowej przez „s”, drugiej pochodnej odpowiada mnożenie przez

2

s , pochodnej rzędu n - odpowia-

da mnożenie przez

n

s , i.t.d.. Wyrażenia odpowiadające warunkom początkowym są równe zero

na mocy przyjętych założeń (2.3), (2.4) o ich zerowych wartościach.

)

s

(

x

b

)

s

(

x

s

b

)

s

(

y

)

s

(

y

s

a

)

s

(

y

s

a

o

m

m

1

n

n

+

+

=

+

+

+

L

L

Po uporządkowaniu otrzymamy równanie operatorowe (2.5)

)

s

(

x

)

b

s

b

s

b

(

)

s

(

y

)

1

s

a

s

a

(

o

1

m

m

1

n

n

+

+

+

=

+

+

+

L

L

(2.5)

Z równania (2.5) obliczamy operatorowy sygnał wyjściowy y(s), - równanie (2.6) oraz trans-

mitancję operatorową G(s), - równanie (2.7).

)

s

(

x

)

s

(

G

)

s

(

x

1

s

a

s

a

b

s

b

s

b

)

s

(

y

1

n

n

o

1

m

m

⋅

=

+

+

+

+

+

+

=

L

L

(2.6)

1

s

a

s

a

b

s

b

s

b

)

s

(

x

)

s

(

y

)

s

(

G

1

n

n

o

1

m

m

+

+

+

+

+

+

=

=

L

L

(2.7)

Równanie (2.7) przyjmujemy jako definicję transmitancji operatorowej.

Transmitancja operatorowa G(s) jest to iloraz operatorowego sygnału wyjściowego y(s) do opera-
torowego sygnału wejściowego x(s) i jest równa ilorazowi wielomianów operatorowych utworzo-
nych z prawej i lewej strony równania różniczkowego po wstawieniu operatora Lapace’a „s” w
miejsce pochodnych czasowych. Transmitancja operatorowa stanowi operatorową formę zapisu
równania różniczkowego; występują w niej współczynniki równania oraz operator Laplace’a w
potędze wskazującej na rząd pochodnej czasowej sygnału. Dzięki wprowadzeniu pojęcia transmi-
tancji można nadać matematyczne znaczenie schematom blokowym układów regulacji. Wewnątrz
bloku wpisuje się transmitancję przyporządkowaną temu blokowi.

)

s

(

x

)

s

(

G

)

s

(

y

⋅

=

(2.8)

Sygnał wyjściowy y(s) w postaci operatorowej jest równy iloczynowi transmitancji

operatorowej G(s) i operatorowego sygnału wejściowego x(s). Przykłady obliczania
transmitancji podano w rozdziale 3 przy omawianiu elementów automatyki.

2. Dynamika układów liniowych

Str.

18

2.3

Łączenie elementów automatyki - transmitancja wypadkowa

Z pośród różnych połączeń elementów automatyki można wyróżnić trzy podstawowe: połą-

czenie szeregowe, połączenie równoległe i połączenie tworzące układ ze sprzężeniem zwrotnym.
Dla tych połączeń obliczamy transmitancję zastępczą (wypadkową).

2.3.1

Połączenie szeregowe elementów

Połączenie szeregowe dwóch elementów o transmitancjach:

)

s

(

G

i

)

s

(

G

2

1

polega na tym, że

sygnał wyjściowy z pierwszego elementu jest podawany na wejście drugiego elementu, (rys. 2.1).

Z równań:

)

s

(

x

)

s

(

G

)

s

(

x

1

1

⋅

=

)

s

(

x

)

s

(

G

)

s

(

y

1

2

⋅

=

otrzymamy

)

s

(

x

)

s

(

G

)

s

(

G

)

s

(

y

1

2

⋅

⋅

=

)

s

(

G

)

s

(

G

)

s

(

x

)

s

(

y

)

s

(

G

2

1

⋅

=

=

(2.9)

Transmitancja zastępcza połączenia szeregowego jest równa iloczynowi transmitancji połą-

czonych elementów.

2.3.2

Połączenie równoległe elementów

Połączenie równoległe

dwóch elementów (rys. 2.2) realizowane jest w ten sposób, że ten sam

sygnał wejściowy x jest podawany na wejścia dwóch elementów o transmitancjach

,

)

s

(

G

i

)

s

(

G

2

1

a ich sygnały wyjściowe są algebraicznie dodawane (ze znakiem + lub - ) w su-

matorze. Dla dodawania sygnałów

)

s

(

y

,

)

s

(

y

2

1

w sumatorze otrzymujemy układ równań:

)

s

(

x

)

s

(

G

)

s

(

y

1

1

⋅

=

)

s

(

x

)

s

(

G

)

s

(

y

2

2

⋅

=

)

s

(

y

)

s

(

y

)

s

(

y

2

1

+

=

z którego obliczamy transmitancję zastępczą G(s) połączenia równoległego:

[

]

)

s

(

x

)

s

(

G

)

s

(

G

)

s

(

y

2

1

⋅

+

=

)

s

(

G

)

s

(

G

)

s

(

x

)

s

(

y

)

s

(

G

2

1

+

=

=

(2.10)

x(s)

x

1

(s)

y(s)

G

1

(s)

G

2

(s)

.

G

1

(s) G

2

(s)

x(s)

y(s)

Rys. 2.1. Połączenie szeregowe elementów automatyki

2. Dynamika układów liniowych

Str.

19

Transmitancja zastępcza połączenia równoległego jest równa sumie transmitancji połączonych
elementów.

2.3.3

Układ z ujemnym sprzężeniem zwrotnym

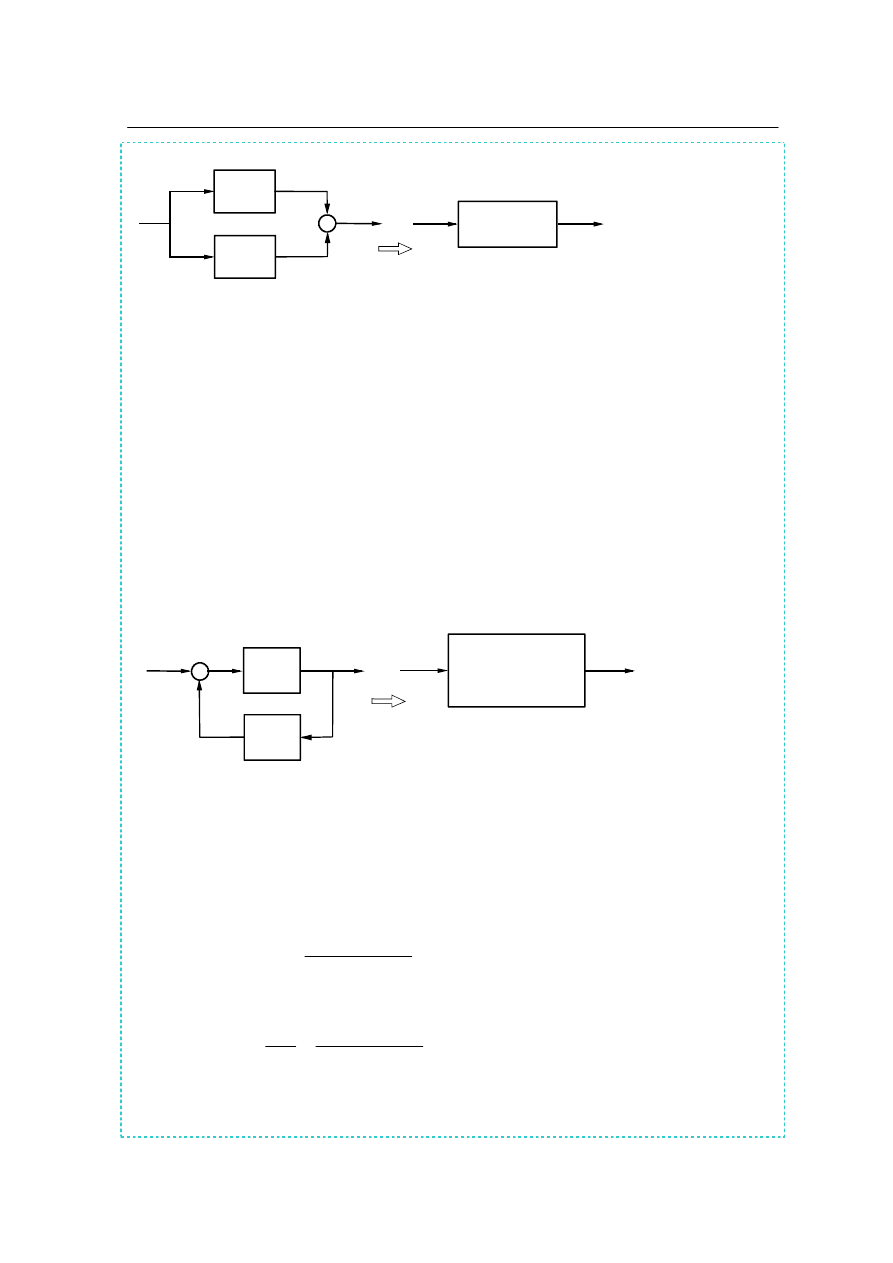
Połączenie elementów tworzące układ z ujemnym sprzężeniem zwrotnym (rys. 2.3) opisują

następujące równania:

)

s

(

y

)

s

(

x

)

s

(

y

1

e

−

=

)

s

(

y

)

s

(

G

)

s

(

y

e

1

⋅

=

)

s

(

y

)

s

(

G

)

s

(

y

2

1

⋅

=

Obliczamy sygnał y(s).

[

]

)

s

(

y

)

s

(

G

)

s

(

x

)

s

(

G

)

s

(

y

2

1

−

⋅

=

[

]

)

s

(

x

)

s

(

G

)

s

(

y

)

s

(

G

)

s

(

G

1

1

2

1

⋅

=

+

)

s

(

x

)

s

(

G

)

s

(

G

1

)

s

(

G

)

s

(

y

2

1

1

⋅

+

=

Transmitancja zastępcza układu z ujemnym sprzężeniem zwrotnym jest równa:

)

s

(

G

)

s

(

G

1

)

s

(

G

)

s

(

x

)

s

(

y

)

s

(

G

2

1

1

+

=

=

(2.11)

Rys. 2.2. Połączenie równoległe elementów automatyki

+

+

y

1

(s)

y(s)

G

1

(s)

G

2

(s)

+

G

1

(s)

G

2

(s)

x(s)

y(s)

x(s)

x(s)

y

2

(s)

x(s)

Rys.2.3. Układ z ujemnym sprzężeniem zwrotnym

_

x(s)

y(s)

G

1

(s)

1 +

_____________

G

2

(s)

G

1

(s)

.

x(s)

y

1

(s)

y(s)

G

1

(s)

G

2

(s)

y

e

(s)

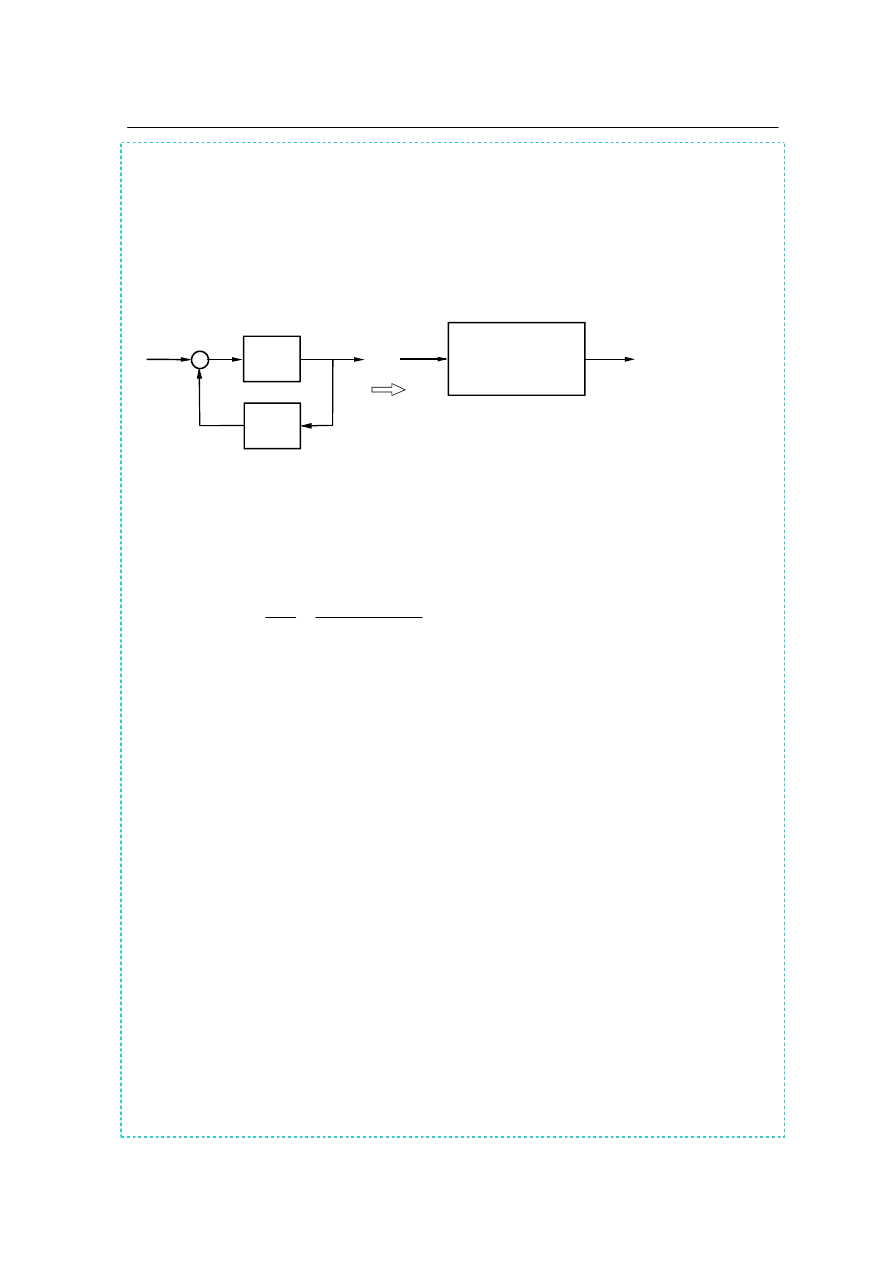
2. Dynamika układów liniowych

Str.

20

2.3.4

Układ z dodatnim sprzężeniem zwrotnym

Układ z dodatnim sprzężeniem zwrotnym

(rys. 2.4) opisują następujące równania:

)

s

(

y

)

s

(

x

)

s

(

y

1

e

+

=

)

s

(

y

)

s

(

G

)

s

(

y

e

1

⋅

=

)

s

(

y

)

s

(

G

)

s

(

y

2

1

⋅

=

Transmitancja zastępcza układu z dodatnim sprzężeniem zwrotnym jest równa.

)

s

(

G

)

s

(

G

1

)

s

(

G

)

s

(

x

)

s

(

y

)

s

(

G

2

1

1

−

=

=

(2.12)

2.3.5

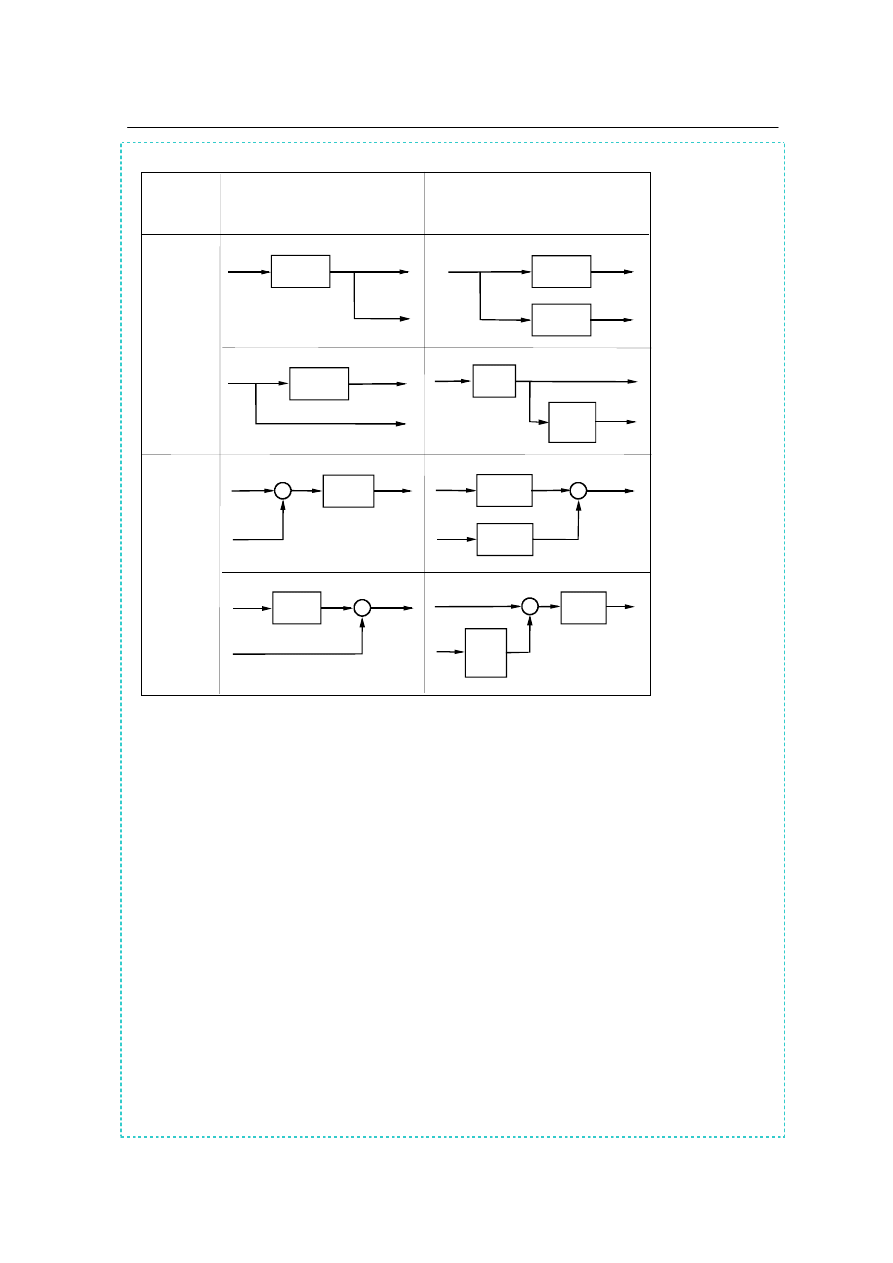
Przestawienie węzłów zaczepowych i sumacyjnych względem bloku

Złożone schematy blokowe można przekształcać i upraszczać. Do podstawowych przekształ-

ceń należy zaliczyć:

przestawienie węzła zaczepowego względem bloku i przestawienie sumatora

względem bloku. Obowiązujące zasady tych przekształceń przedstawiono w tabeli 2.1.

+

x(s)

y(s)

G

1

(s)

1

-

_____________

G

2

(s)

G

1

(s)

.

x(s)

y

1

(s)

y(s)

G

1

(s)

G

2

(s)

y

e

(s)

Rys.2.4. Układ z dodatnim sprzężeniem zwrotnym

2. Dynamika układów liniowych

Str.

21

Układ wyj

ś

ciowy

Układ równowa

ż

ny

Rodzaj
operacji

P

rz

e

s

ta

w

ie

n

ie

w

ę

z

ła

z

a

c

z

e

p

o

w

e

g

o

P

rz

e

s

ta

w

ie

n

ie

w

ę

z

ła

s

u

m

a

c

y

jn

e

g

o

x

x

x

x

1

x

x

1

x

1

x

1

x

2

x

2

x

2

x

2

x

x

y

y

y

y

y

y

y

y

y

y

G

G

G

G

G

G

G

G

G

G

1

G

__

1

G

__

Tabela 2.1 Przestawienie w

ę

zła zaczepowego i sumacyjnego wzgl

ę

dem bloku

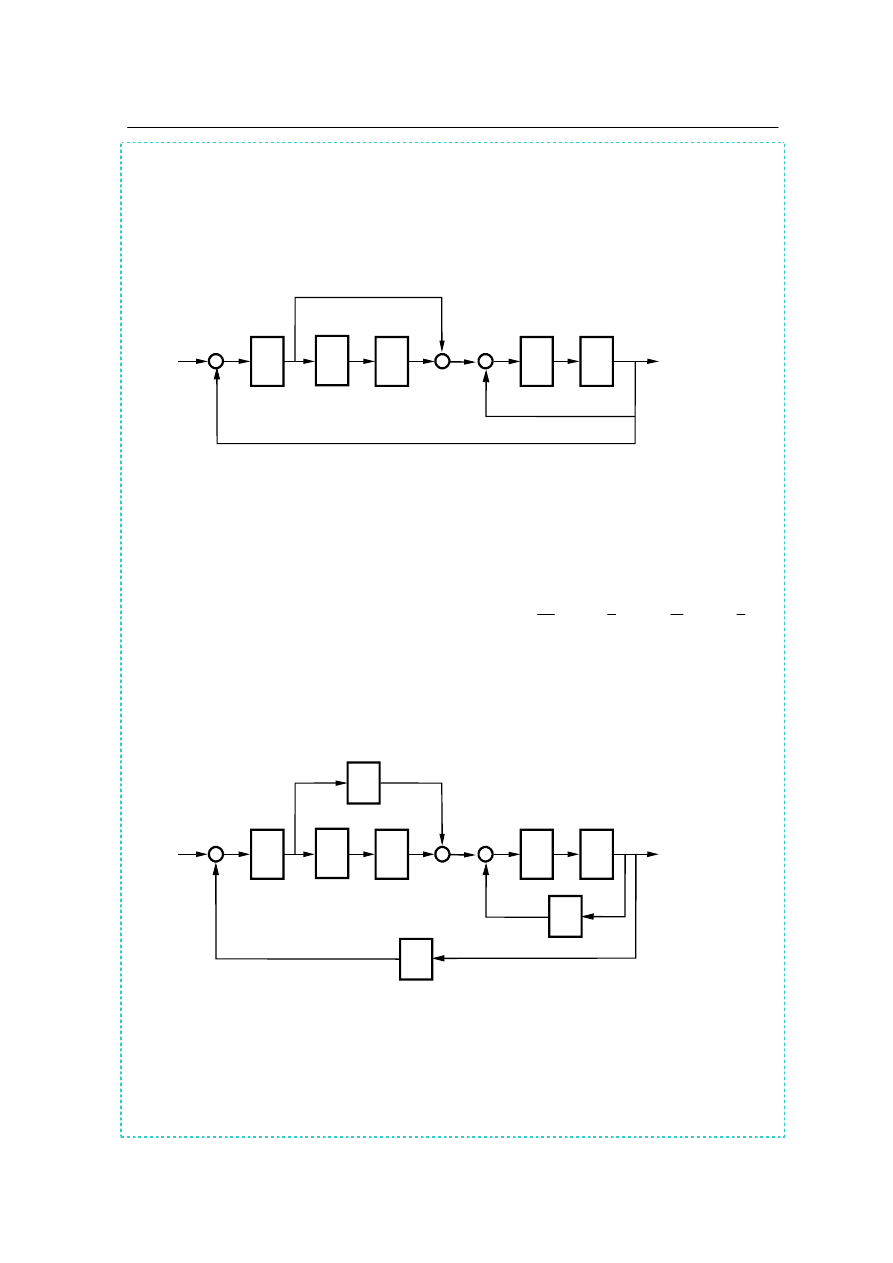
2. Dynamika układów liniowych

Str.

22

2.3.6

Zadania – schematy blokowe

Zadanie 2.1

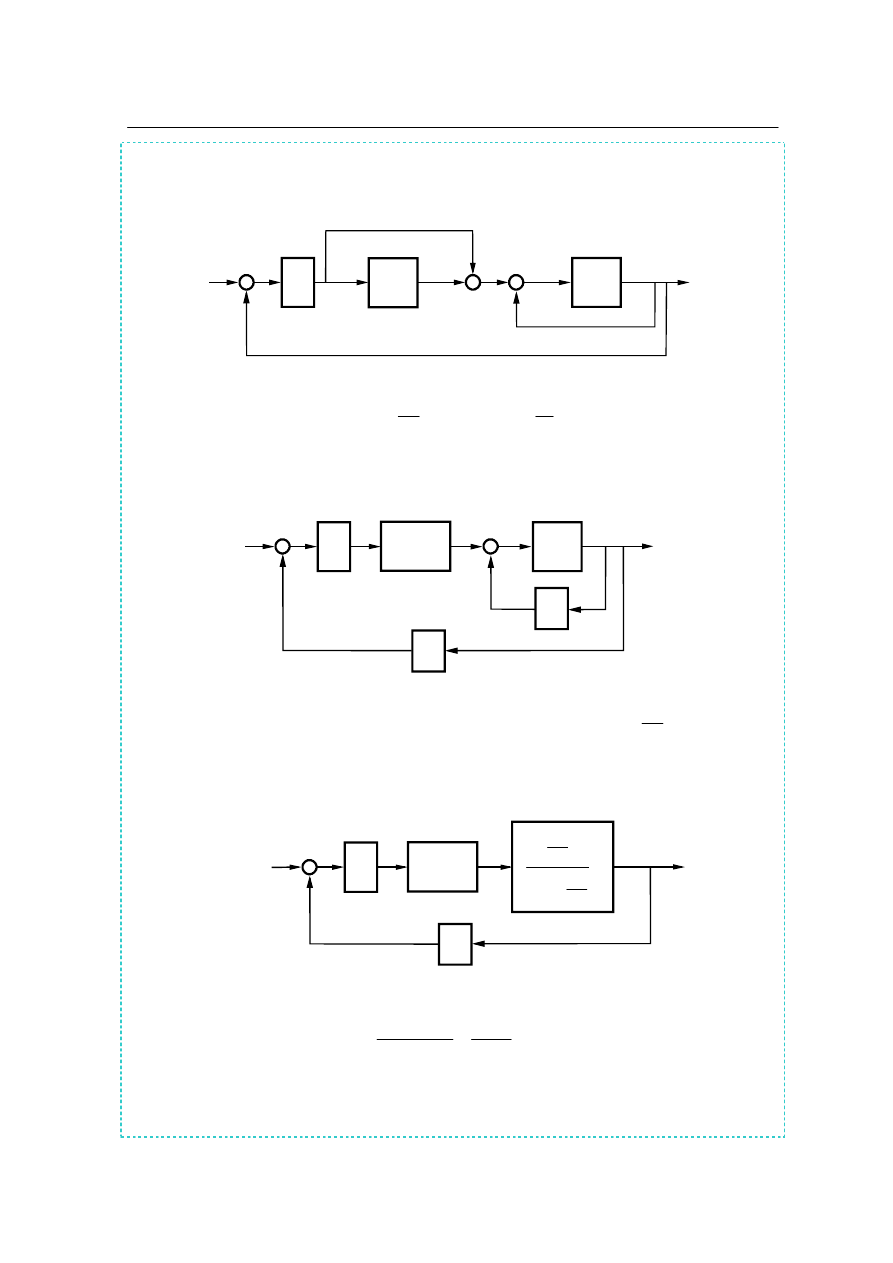
Przekształcić schemat blokowy przedstawiony na rys. 2.5 do prostszej postaci.

R o z w i ą z a n i e i a n a l i z a z a d a n i a 2 . 1 .

Układ zawiera: 5 bloków o transmitancjach:

p

1

K

G

=

,

i

2

T

1

G

=

,

s

1

G

3

=

,

T

1

G

4

=

,

s

1

G

5

=

;

połączenia szeregowe, jedno połączenie równoległe, dwa połączenia ze sprzężeniem zwrotnym
ujemnym. Linia sygnałowa od punktu zaczepowego do sumatora nie zawierająca bloku ma do-
myślną transmitancję

1

G

6

=

. Kolejne etapy przekształcania schematu blokowego przedstawiono

na poniższych rysunkach.

y

w

y

e

K

p

x

r

_

_

y

_

1

s

_

1

s

T

i

__

1

1

T

__

1

1

1

G

1

G

2

G

3

G

4

G

5

G

6

G

6

G

6

Rys. 2.5a. Wstawienie domyślnych bloków o transmitancji

1

G

6

=

i rozdzielenie

dwóch obwodów sprzężeń zwrotnych przez przesunięcie węzła
zaczepowego na linii sygnału „y”.

Rys. 2.5. Rozwinięty schemat blokowy układu regulacji

y

w

y

e

K

p

x

r

_

_

y

_

1

s

_

1

s

T

i

__

1

1

T

__

G

1

G

2

G

3

G

4

G

5

2. Dynamika układów liniowych

Str.

23

y

w

y

e

K

p

x

r

_

_

y

1

Ts

__

1

1

T

i

s

__

1

1 +

G

9

G

8

Rys. 2.5c. Redukcja połączenia równoległego:

s

T

1

1

G

G

G

i

7

6

9

+

=

+

=

.

y

w

y

e

K

p

x

r

_

y

1

T

i

s

__

1

1 +

Ts

Ts

1

1

1

1

⋅

+

G

1

G

9

G

10

Rys. 2.5d. Redukcja wewnętrznego obwodu sprzężenia zwrotnego:

Ts

1

1

G

G

1

G

G

8

6

8

10

+

=

⋅

+

=

Rys. 2.5b. Redukcja dwóch połączeń szeregowych:

s

T

1

G

G

G

i

3

2

7

=

⋅

=

,

Ts

1

G

G

G

5

4

8

=

⋅

=

.

y

w

y

e

K

p

x

r

_

_

y

1

Ts

__

T

i

s

__

1

G

7

G

8

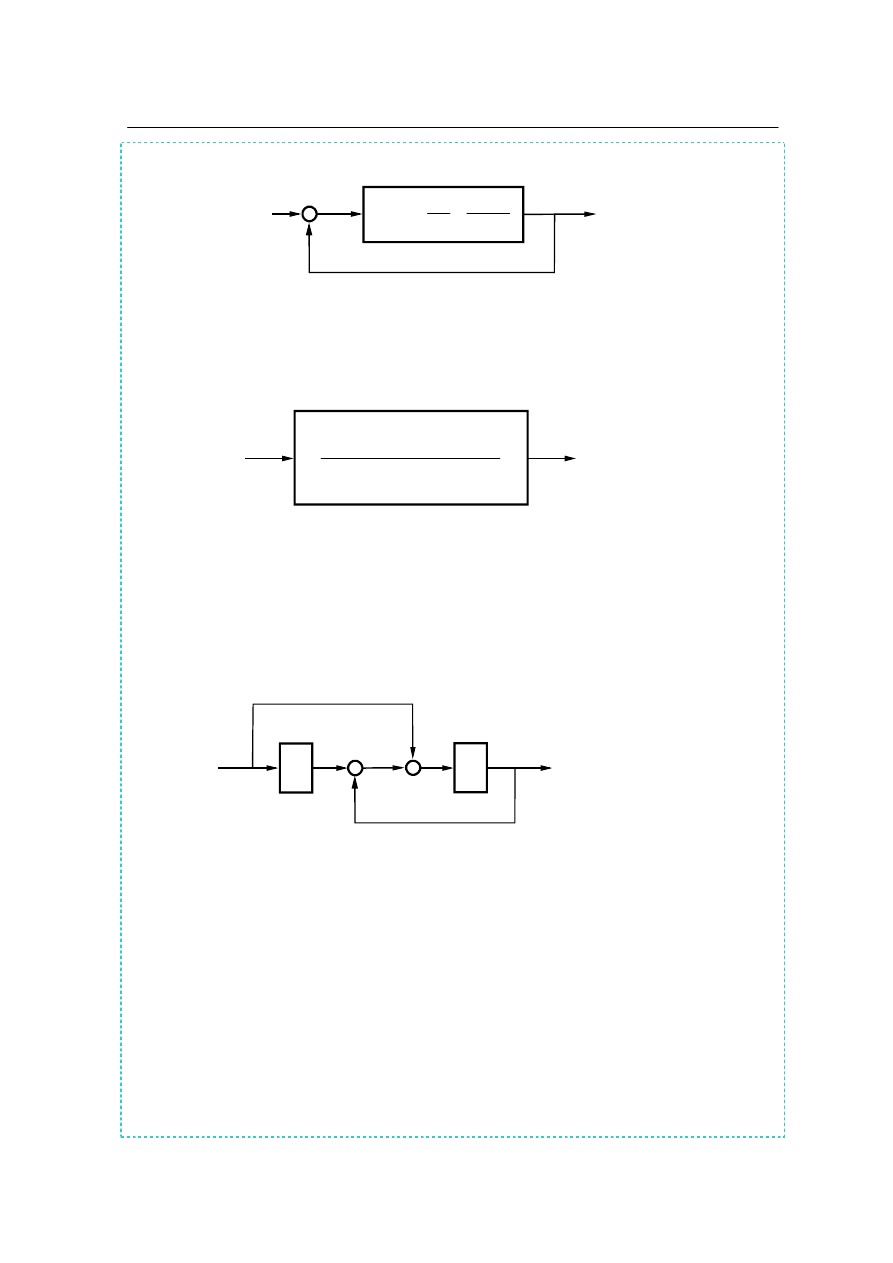
2. Dynamika układów liniowych

Str.

24

Wynik końcowy:











Zadanie 2.2

Obliczyć transmitancję wypadkową układu przedstawionego na rys. 2.6.

R o z w i ą z a n i e i a n a l i z a z a d a n i a 2 . 2 .

Splecione układy można rozdzielić przez przestawienie węzłów sumacyjnych, lub przez uło-

ż

enie układu równań opisujących wszystkie elementy i węzły sumacyjne i rozwiązać te równania

tak, aby obliczyć sygnał wyjściowy jako funkcję sygnału wejściowego. Zostaną przedstawione
obie metody. Przestawienie węzłów sumacyjnych pokazano na rys.2.6a.

Rys. 2.5e. Redukcja połączenia szeregowego.

y

w

y

e

_

y

1

1

1

1

+

⋅

+

Ts

)

s

T

(

K

i

p

Rys. 2.6. Schemat blokowy zawierający połączenie równoległe splecio-

ne obwodem sprzężenia zwrotnego

_

y

Ts

__

1

1

Ts

__

x

x

1

x

2

x

3

x

3

= x + x

1

- y

x

2

= x

1

- y

y

w

y

)

s

T

(

K

)

Ts

(

s

T

)

s

T

(

K

i

p

i

i

p

1

1

1

+

+

+

⋅

+

Rys. 2.5f. Redukcja sprzężenia zwrotnego:

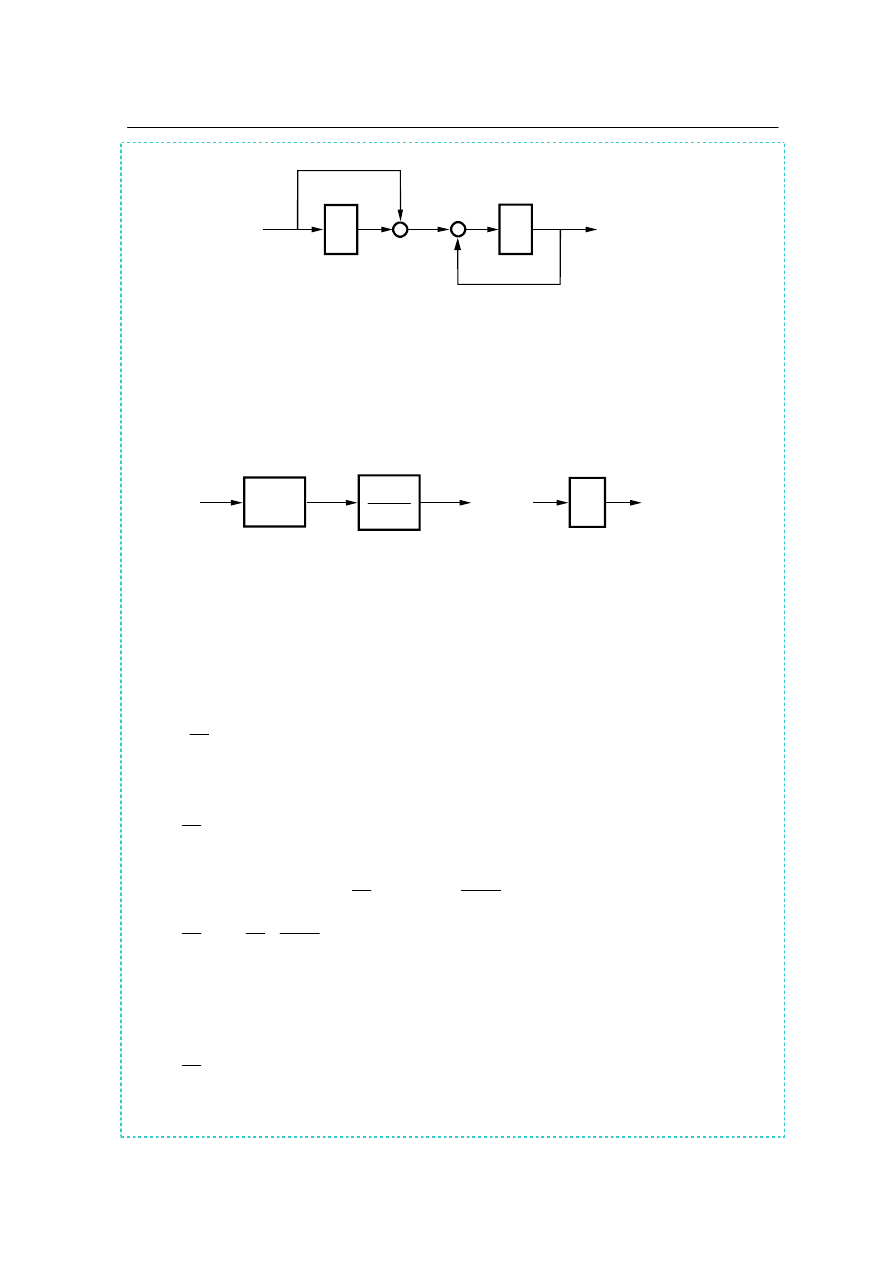
2. Dynamika układów liniowych

Str.

25

Układ na rys.2.6a jest równoważny układowi z ras. 2.6, ponieważ sygnał

3

x w obu układach

jest taki sam.

Metoda upraszczania schematu blokowego przez rozwiązywania równań.

Piszemy równania elementów dla schematu z rys. 2.6:

x

Ts

1

x

1

⋅

=

y

x

x

1

2

−

=

x

x

x

2

3

+

=

3

x

Ts

1

y

⋅

=

Obliczamy:

y

x

Ts

Ts

1

x

)

y

x

Ts

1

(

x

)

y

x

(

x

x

x

1

2

3

−

⋅

+

=

+

−

⋅

=

+

−

=

+

=

)

y

x

Ts

Ts

1

(

Ts

1

x

Ts

1

y

3

−

⋅

+

⋅

=

⋅

=

y

)

Ts

(

x

)

Ts

1

(

y

)

Ts

(

)

Ts

(

⋅

−

⋅

+

=

⋅

⋅

x

)

1

Ts

(

y

)

1

Ts

(

)

Ts

(

⋅

+

=

⋅

+

⋅

x

y

)

Ts

(

=

⋅

Wynik końcowy:

x

Ts

1

y

⋅

=

_

y

Ts

__

1

1

Ts

__

x

1

x

4

x

3

x

3

= x

1

+ x - y

x

4

= x

1

+ x

x

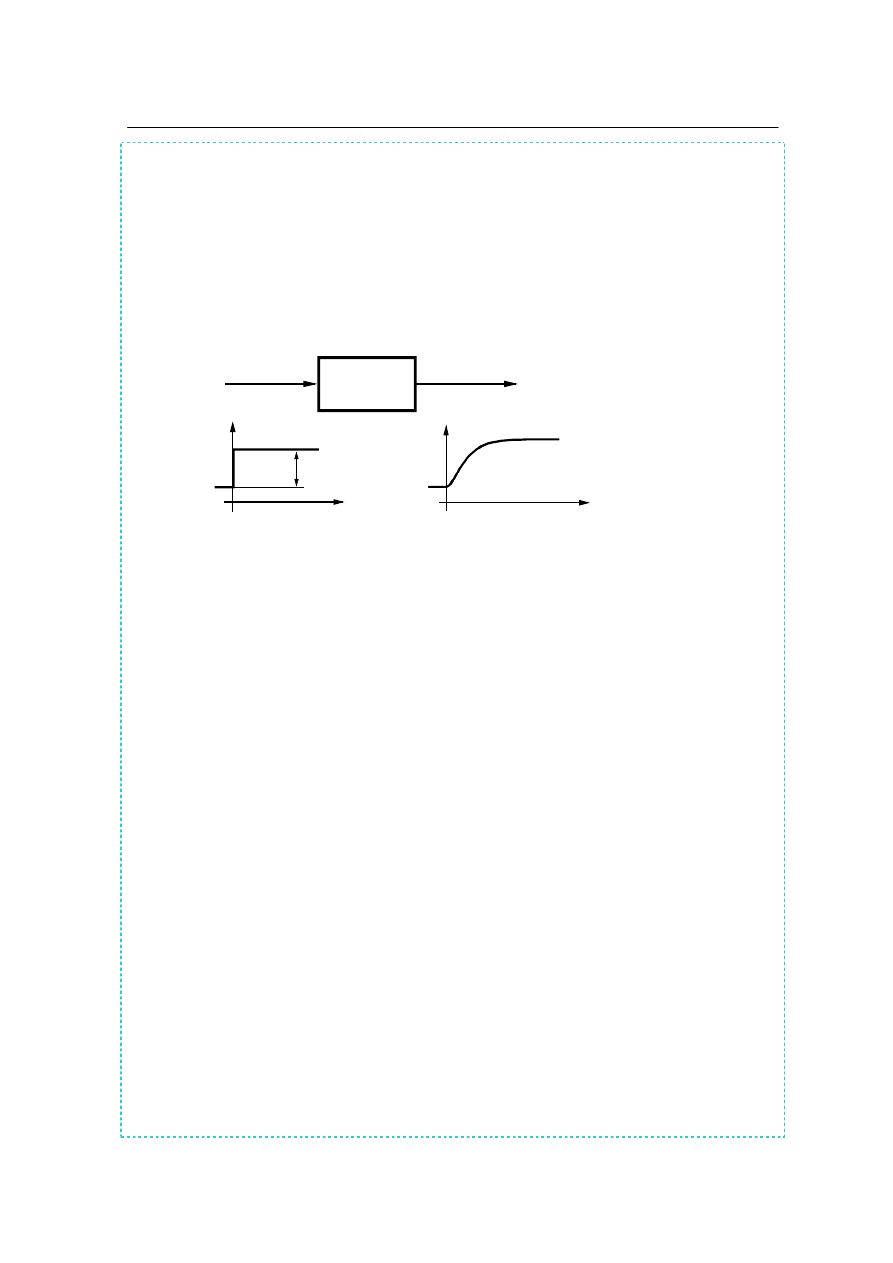
Rys.2.6a. Rozdzielenie połączenia równoległego od układu

ze sprzężeniem zwrotnym.

Ts

__

1

1 +

1

1

+

Ts

x

x

4

y

x

y

Ts

__

1

Rys. 2.6b. Końcowe etapy przekształceń: redukcja połączenia równoległe-

go i układu ze sprzężeniem zwrotnym, redukcja połączenia sze-
regowego i końcowy wynik.

2. Dynamika układów liniowych

Str.

26

2.4 Charakterystyki czasowe

Charakterystyka czasowa wyraża nazywana dynamiczne właściwości elementu automatyki.

Definicja charakterystyki czasowej została wstępnie podana w rozdziale 1.3, (rys. 1.8). Charakte-
rystykę czasową można zmierzyć lub obliczyć.

2.4.1

zależności między charakterystykami czasowymi

Jeżeli znana jest transmitancja G(s) elementu automatyki oraz sygnał wymuszający, wówczas

z równania

)

s

(

x

)

s

(

G

)

s

(

y

⋅

=

obliczamy operatorowy sygnał wyjściowy y(s), następnie przy po-

mocy tablic funkcji operatorowych znajdujemy równanie charakterystyki czasowej y(t).

Jako sygnały wymuszające najczęściej stosuje się: skok jednostkowy

x(t) =

1(t), sygnał liniowo narastający

)

t

(

t

)

t

(

x

1

⋅

=

, lub sygnał impulsowy opisany impulsową

funkcją delta Diraca x(t) =

δ

(t), a odpowiadające im charakterystyki oznaczamy przez: h(t) – cha-

rakterystyka dla wymuszenia skokowego , f(t) – dla wymuszenia liniowego, g(t) – dla wymusze-
nia impulsowego. Pomiędzy charakterystykami h(t), f(t), g(t) zachodzą poniżej przedstawione za-
leżności:

Równanie charakterystyki impulsowej g(t)

obliczamy dla sygnału wymuszającego x(t) =

δ

(t), x(s) = 1, otrzymamy:

)

s

(

G

)

s

(

g

=

(2.13)

[

]

)

s

(

G

1

L

)

t

(

g

−

=

(2.14)

Charakterystyka czasowa impulsowa g(t) jest równa odwrotnej transformacji Laplace’a

transmitancji operatorowej G(s).

Rys. 2.7. Charakterystyka czasowa

x(s)

y(s)

x(t)

y(t)

t

t

G(s)

∆

x

2. Dynamika układów liniowych

Str.

27

Równanie charakterystyki skokowej h(t)

obliczamy dla sygnału wymuszającego x(t) =

1

(t), czyli x(s) = 1/s, otrzymamy:

)

s

(

g

s

1

)

s

(

G

s

1

)

s

(

h

⋅

=

⋅

=

.

(2.15)

Dzieleniu funkcji operatorowej g(s) przez „s” odpowiada całkowanie funkcji czasowej g(t),

wobec tego:

∫

=

t

0

dt

)

t

(

g

)

t

(

h

(2.16)

Charakterystyka czasowa skokowa h(t) jest równa całce charakterystyki impulsowej g(t).

Równanie charakterystyki f(t) dla wymuszenia liniowego obliczamy dla sygnału wymusza-

jącego x(t) = t

1(t), x(s) = 1/s

2

. Wstawiając tę funkcję do równania (2.8) i uwzględniając równanie

(2.15) otrzymamy:

)

s

(

h

s

1

2

s

1

)

s

(

G

)

s

(

f

⋅

=

⋅

=

(2.17)

Charakterystyka czasowa f(t) dla wymuszenia liniowego jest równa całce charakterystyki

skokowej h(t).

∫

=

t

0

dt

)

t

(

h

)

t

(

f

(2.18)

Zależności pomiędzy charakterystykami można również wyrazić przy pomocy pochodnych

)

t

(

f

t

d

d

)

t

(

h

=

(2.19)

)

t

(

h

t

d

d

)

t

(

g

=

(2.20)

Jeżeli znana jest charakterystyka impulsowa g(t), wówczas odpowiedź elementu na dowolne wy-
muszenie x(t) możemy obliczyć z twierdzenia o splocie.

∫

τ

τ

−

τ

=

t

0

d

)

t

(

x

)

(

g

)

t

(

y

(2.21)

Przykłady obliczania charakterystyk czasowych z transmitancji podano w rozdziale 3 przy

omawianiu elementów automatyki.

2. Dynamika układów liniowych

Str.

28

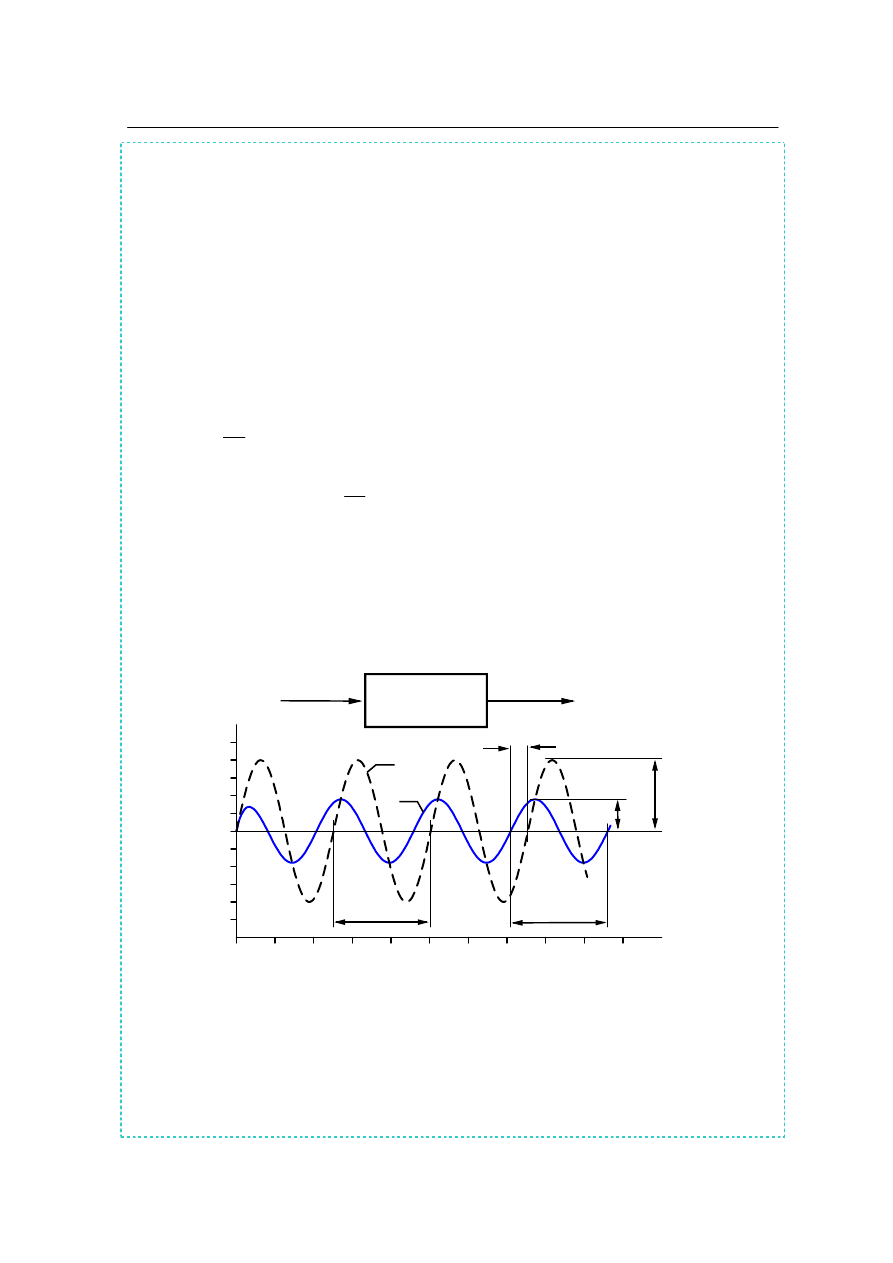
2.5 Charakterystyki częstotliwościowe

2.5.1

Definicja charakterystyki częstotliwościowej

Jeżeli na wejście elementu liniowego zostanie wprowadzony sygnał sinusoidalny

)

t

sin(

x

)

t

(

x

o

ω

=

o pulsacji

ω

i amplitudzie

o

x wówczas sygnał wyjściowy będzie sumą dwóch

sygnałów: składowej przejściowej

p

y i składowej okresowej sinusoidalnej (harmonicznej)

h

y .

Po zaniku składowej przejściowej pozostanie tylko składowa sinusoidalna

)

t

sin(

y

)

t

(

y

y(t)

o

h

ϕ

+

ω

=

=

o tej samej pulsacji

ω

; jaką ma sygnał wymuszający; o amplitu-

dzie

o

y , przesunięta o kąt

ϕ

względem sygnału wymuszającego. Pulsacja

ω

jest równa

f

2

T

2

o

π

=

π

=

ω

(2.22)

gdzie:

o

T jest okresem,

o

T

1

f

=

częstotliwością drgań.

Przesunięcie fazowe jest równe

ϕ

=

∆

t

⋅ω

(2.23)

gdzie

∆

t jest przesunięciem czasowym sygnału wyjściowego względem sygnału wejściowego

(rys. 2.8).

Aby badany obiekt pozostawał w strefie liniowości amplituda sygnału wymuszającego nie

powinna przekraczać 5% znamionowej wartości sygnału wejściowego (

zn

o

x

05

,

0

x

≤

).

Rys.2.8. Odpowiedź elementu liniowego na wymuszenie sinusoidalne

x(s)

y(s)

G(s) =

Ts

Ts + 1

______

0

10

20

30

40

50

-1.0

-0.5

0.0

0.5

1.0

T

o

∆

t

x

o

y

o

[s]

czas t

y

x

T

o

y

x

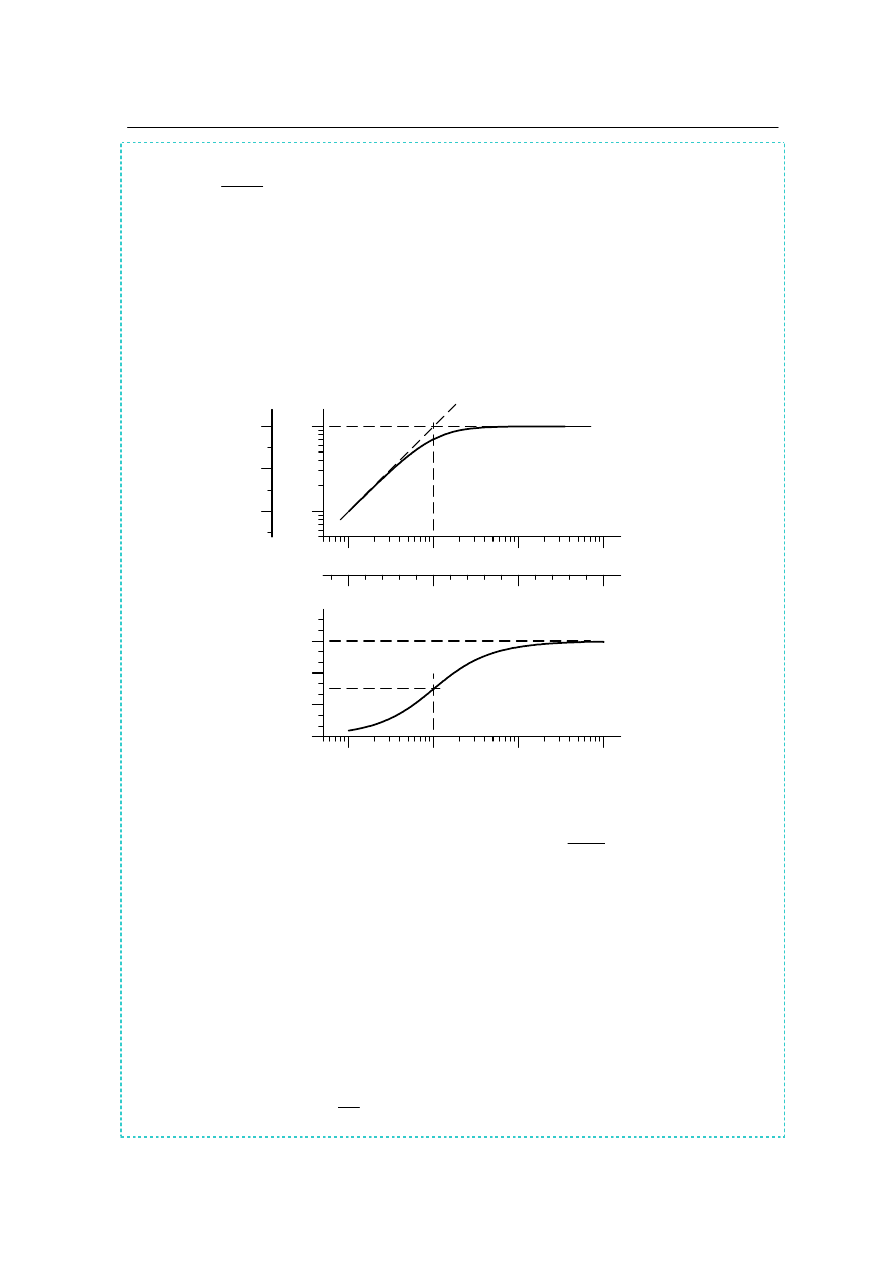
2. Dynamika układów liniowych

Str.

29

Na rys. 2.9 przedstawiono pełną odpowiedź elementu różniczkującego rzeczywistego o transmi-

tancji

1

Ts

Ts

)

s

(

G

+

=

, (T = 1 [s]) na wymuszenie sinusoidalne

)

t

sin(

x

)

t

(

x

o

ω

=

,

(

1

x

o

=

,

ω

= 0,5 [rad/s], okres sinusoidy

566

,

12

T

o

≅

[s]).

Sygnał wyjściowy

)

t

(

y

)

t

(

y

)

t

(

y

n

h

+

=

zawiera składową harmoniczną (sinusoidalną):

)

10715

,

1

t

5

,

0

sin(

4472

,

0

)

t

5

,

0

cos(

4

,

0

)

t

5

,

0

sin(

2

,

0

y

h

+

⋅

⋅

≅

⋅

⋅

−

⋅

⋅

=

oraz składową nieharmoniczną (przejściową):

t

n

e

4

,

0

y

−

⋅

=

.

Składowa przejściowa po czasie t > 5T = 5 [s] (czyli po czasie krótszym od jednego okresu)

praktycznie zanika i pozostaje składowa harmoniczna o amplitudzie

4472

,

0

y

o

≅

przesunięta

względem sygnału wymuszającego o kąt

ϕ

= +1,10715 [rad] = 63,4 stopnia. Przesunięcie fazowe

ϕ

składowej harmonicznej jest dodatnie, ponieważ wszystkie okresy sygnału wyjściowego y(t)

począwszy od okresu drugiego wyprzedzają okresy sygnału wymuszającego o kąt

ϕ

= 63,4 stop-

nia. Tylko nieliczne elementy wprowadzają dodatnie przesunięcie fazowe. Większość elementów
wprowadza ujemne przesunięcie fazowe.

Stosunek amplitud

o

o

x

y

)

(

A

=

ω

oraz przesunięcie fazowe

ϕ

(

ω

) zależą od pulsacji

ω

(często-

0.1

1.0

10.0

100.0

ω

0.1

1.0

-20

-10

0

0.1

1.0

10.0

100.0

ω

0

30

60

90

ϕ

-1

0

1

2

rad/s

rad/s

stopnie

Rys. 2.9. Charakterystyki częstotliwościowe: amplitudowa A(

ω

) oraz fazowa

ϕ(ω)

elementu różniczkującego rzeczywistego,

1

Ts

Ts

)

s

(

G

+

=

, T = 1 [s].

20 lg A(

ω

)

dB

A(

ω

)

lg

ω

T

ω

T = 1

A(

ω

)

ϕ

(

ω

)

2. Dynamika układów liniowych

Str.

30

tliwości) sygnału wymuszającego. Wykres stosunku amplitud A(

ω

) od częstotliwości

ω

jest na-

zwana

charakterystyką częstotliwościową amplitudową, a wykres przesunięcia fazowego

ϕ

(

ω

) od

częstotliwości –

charakterystyką częstotliwościową fazową, (rys.2.9).

Charakterystykę amplitudową sporządza się we współrzędnych logarytmicznych. Na osi po-

ziomej podawane są wartości funkcji log(

ω

) lub log(f), a na osi pionowej wartości funkcji

log[A(

ω

)] lub funkcji L(

ω

) = 20 log[A(

ω

)] określającej moc sygnału wyjściowego w dB (decybe-

lach).

Charakterystykę fazową sporządza się we współrzędnych półlogarytmicznych. Częstotliwość

jest podawana w skali logarytmicznej, a faza w skali liniowej. Obie te charakterystyki są rysowa-
ne, razem charakterystyka fazowa pod charakterystyką amplitudową, a podziałki częstotliwości są
jednakowe dla charakterystyki amplitudowej i fazowej.

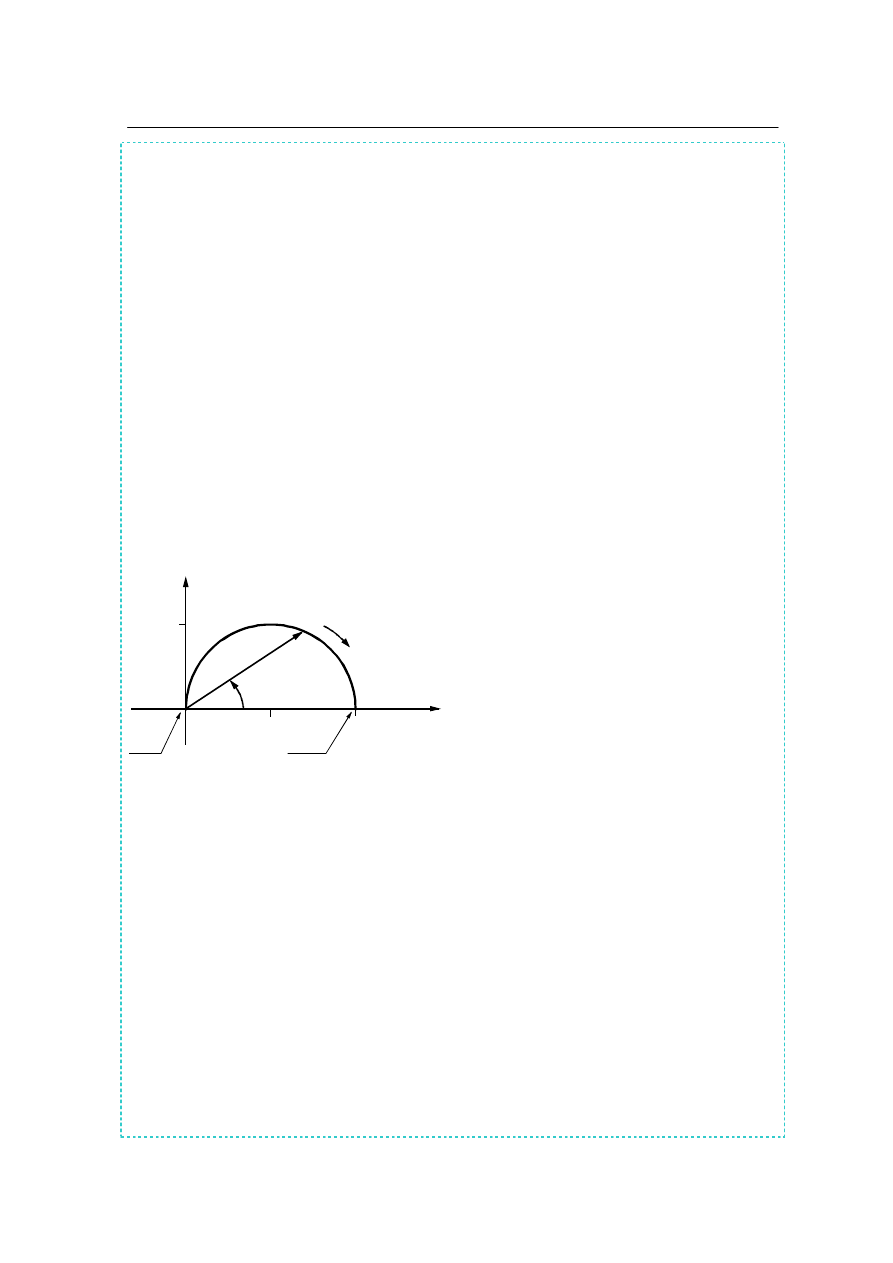
Używana jest również

charakterystyka amplitudowo – fazowa przedstawiona w postaci parame-

trycznej na płaszczyźnie liczb zespolonych (w układzie współrzędnych biegunowych; rys.2. 10).

Długość wektora poprowadzonego z początku układu współrzędnych do punktu na charakte-

rystyce przedstawia stosunek amplitud A(

ω

), a kąt między osią poziomą (osią liczb rzeczywi-

stych) i wektorem – przedstawia kąt przesu-
nięcia fazowego

ϕ

(

ω

). Pulsacja (

ω

) jest para-

metrem zmieniającym się wzdłuż charaktery-
styki od (

ω

= 0) do (

ω

= ∞). Charakterystyka

amplitudowo – fazowa nazwana jest

charakte-

rystyką Nyquista.

Charakterystyka amplitudowo fazowa jest

równocześnie wykresem sporządzonym na
płaszczyźnie liczb zespolonych. Wynika to ze
związku między transmitancją operatorową i
odpowiedzią elementu na wymuszenie sinuso-
idalne (następny punkt 2.6.2).

Re[G(i

ω

)]

Im[G(i

ω

)]

ϕ

A

ω = 0

ω

P(

ω

)

1

0.5

0

0

0.5

Q(

ω

)

∞

=

ω

Rys. 2.10. Charakterystyka częstotliwościowa

amplitudowo - fazowa (charaktery-
styka Nyqwista) elementu różniczku-
jącego rzeczywistego

2. Dynamika układów liniowych

Str.

31

2.5.2.

Wyprowadzenie równań wiążących transmitancję operatorową

z charakterystyką częstotliwościową

Jeżeli na wejście elementu o transmitancji G(s) zostanie wyprowadzony sygnał sinusoidalny

)

t

sin(

x

)

t

(

x

o

ω

=

, wówczas sygnał wyjściowy y(t) może być obliczony w następujący sposób:

Sygnałowi czasowemu

)

t

sin(

x

)

t

(

x

o

ω

=

odpowiada funkcja operatorowa

2

2

o

s

x

)

s

(

x

ω

+

ω

⋅

=

(2.24)

Obliczamy sygnał wyjściowy w postaci operatorowej

)

i

s

)(

i

s

(

x

)

s

(

G

s

x

)

s

(

G

)

s

(

x

)

s

(

G

)

s

(

y

o

2

2

o

ω

+

ω

−

ω

⋅

⋅

=

ω

+

ω

⋅

⋅

=

=

(2.25)

Rozkładając funkcję y(s) na ułamki proste otrzymamy:

)

s

(

y

i

s

1

C

i

s

1

B

)

i

s

)(

i

s

(

x

)

s

(

G

)

s

(

y

)

s

(

y

)

s

(

y

n

o

n

h

+

ω

+

+

ω

−

=

ω

+

ω

−

ω

⋅

=

+

=

(2.26)

Sygnał wyjściowy zawiera składowe harmoniczne reprezentowane przez funkcję operatorową:

ω

+

+

ω

−

=

i

s

1

C

i

s

1

B

)

s

(

y

h

(2.27)

i składowe nieharmoniczne reprezentowane przez funkcję

)

s

(

y

n

.

Składowa nieharmoniczna

)

s

(

y

n

w mianowniku nie zawiera pierwiastków urojonych

ω

±

=

i

s

, ani dodatnich, wobec tego odpowiadająca jej funkcja czasowa

)

t

(

y

n

po pewnym cza-

sie zanika, w rezultacie pozostaje tylko składowa harmoniczna

)

t

(

y

h

. W celu obliczenia współ-

czynników: B oraz C przy składowej harmonicznej wykonujemy następujące działania:

W celu obliczenia współczynnika B mnożymy równanie (2.27) przez

)

i

-

(s

ω

, następnie pod-

stawiamy

ω

=

i

s

, w wyniku otrzymamy

)

i

(

G

2

x

i

B

o

ω

−

=

(2.28)

W podobny sposób obliczamy współczynnik C.

)

i

(

G

2

x

i

C

o

ω

−

=

(2.29)

2. Dynamika układów liniowych

Str.

32

Funkcja G(i

ω

) otrzymana z transmitancji operatorowej G(s) w wyniku podstawienia

ω

=

i

s

jest nazywana

transmitancją widmową. Transmitancja widmowa jak każda funkcja zespolona ma

składową rzeczywistą P(

ω

) i składową urojoną Q(

ω

).

)

(

Q

i

)

(

P

)]

i

(

G

Im[

i

)]

i

(

G

Re[

)

G(i

ω

+

ω

=

ω

+

ω

=

ω

(2.30)

Transmitancja widmowa sprzężona G(-i

ω

) ze względu na symetrię liczb zespolonych sprzę-

ż

onych ma tę samą składową rzeczywistą co transmitancja G(i

ω

),

)

(

P

)]

i

(

G

Re[

ω

=

ω

−

i składową

urojoną ze znakiem przeciwnym

)

(

Q

)

i

(

G

Im[

ω

−

=

ω

−

)

(

Q

i

)

(

P

)]

i

(

G

Im[

i

)]

i

(

G

Re[

)

i

G(-

ω

−

ω

=

ω

−

+

ω

−

=

ω

(2.31)

Po wstawieniu (2.28), (2.29) do (2.27) otrzymujemy sygnał wyjściowy składowej okresowej

w postaci operatorowej:













ω

+

ω

−

+

ω

−

ω

−

=

i

s

)

i

(

G

i

i

s

)

i

(

G

i

2

x

)

s

(

y

o

h

(2.32)

W celu wyeliminowania liczb urojonych wykonujemy przekształcenia:

[

] [

]













ω

+

ω

−

ω

+

ω

−

ω

+

ω

−

=

i

s

)

(

Q

i

)

(

P

i

i

s

)

(

Q

i

)

(

P

i

2

x

)

s

(

y

o

h

(2.33)

[

]

[

]













ω

−

ω

−

ω

+

ω

−

ω

+

ω

+

ω

+

ω

−

ω

+

ω

−

=

i

s

i

s

i

s

)

(

Q

i

)

(

P

i

i

s

i

s

i

s

)

(

Q

i

)

(

P

i

2

x

)

s

(

y

o

h

[

] [

]













ω

+

ω

−

ω

−

−

+

ω

+

ω

−

ω

+

+

−

=

2

2

2

2

o

h

s

Q

P

i

Q

s

i

P

s

i

s

Q

P

i

Q

s

i

P

s

i

2

x

)

s

(

y

Ostatecznie otrzymujemy













ω

+

ω

ω

+

ω

=

2

2

o

h

s

)

(

P

)

(

Q

s

x

)

s

(

y

(2.34)

W tablicy funkcji operatorowych znajdziemy funkcję czasową

)

t

(

y

h

odpowiadającą funkcji

operatorowej

)

s

(

y

h

, (2.34).

[

]

)

t

cos(

)

(

Q

)

t

sin(

)

(

P

x

)

t

(

y

o

h

ω

ω

+

ω

ω

=

(2.35)

Składową harmoniczną (2.35) możemy przedstawić w postaci:

)

t

sin(

y

)

t

(

y

o

h

ϕ

+

ω

=

(2.36)

2. Dynamika układów liniowych

Str.

33

W tym celu korzystamy z tożsamości trygonometrycznej.

)

t

cos(

)

sin(

)

t

sin(

)

cos(

)

t

sin(

ω

⋅

ϕ

+

ω

⋅

ϕ

=

ϕ

+

ω

(2.37)

Łącząc równania: (2.35), (2.36) oraz (2.37) otrzymamy:

[

]

[

]

)

t

cos(

)

(

Q

)

t

sin(

)

(

P

x

)

t

cos(

)

sin(

)

t

sin(

)

cos(

y

o

o

ω

ω

+

ω

ω

=

ω

⋅

ϕ

+

ω

⋅

ϕ

(2.38)

Tożsamości (2.38) jest spełniona w każdej chwili t wówczas, gdy zachodzą związki:

[

]

[

]

)

t

cos(

)

(

Q

)

t

sin(

)

(

P

x

)

t

cos(

)

sin(

)

t

sin(

)

cos(

y

o

o

ω

ω

+

ω

ω

=

ω

⋅

ϕ

+

ω

⋅

ϕ

)

(

P

x

)

cos(

y

o

o

ω

=

ϕ

(2.39)

)

(

Q

x

)

sin(

y

o

o

ω

=

ϕ

(2.40)

Z tych dwóch równań możemy obliczać stosunek amplitud oraz przesunięcie fazowe składo-

wej harmonicznej sygnału wyjściowego.

)

(

Q

)

(

P

)

i

(

G

)

(

A

x

y

2

2

o

o

ω

+

ω

=

ω

=

ω

=

(2.41)

[

]

ϕ

ω

=

ω

=

ω

cos

)

(

A

)

i

(

G

Re

)

(

P

(2.42)

[

]

ϕ

ω

=

ω

=

ω

sin

)

(

A

)

i

(

G

Im

)

(

Q

(2.43)

)

(

P

)

(

Q

)]

(

[

tg

ω

ω

=

ω

ϕ

(2.44)

[

]













ω

ω

=

ω

=

ω

ϕ

)

(

P

)

(

Q

arct

)

i

(

G

arg

)

(

(2.45)

Wzory: (2.41), ..., (2.45), wyrażają związki pomiędzy składowymi charakterystyki częstotli-

wościowej i transmitancji widmowej. Stosunek amplitud jest równy wartości bezwzględnej
transmitancji widmowej, a przesunięcie fazowe argumentowi transmitancji widmowej.

Jeżeli wykorzystamy wzór (2.46)

)

(

i

e

)]

(

sin[

i

)]

(

cos[

ω

ϕ

=

ω

ϕ

+

ω

ϕ

(2.46)

to transmitancję widmową G(i

ω

) możemy przedstawić w postaci wykładniczej, wzór (2.47).

)

(

i

e

)

(

A

)

(

Q

i

)

(

P

)

G(i

ω

ϕ

ω

=

ω

+

ω

=

ω

(2.47)